
Түркістан облысының білім басқармасы
Түркістан облысы білім беруді дамытудың оқу-әдістемелік орталығы
Білім беру ұйымының атауы
|
Келісілді Түркістан облысы білім беруді дамытудың оқу-әдістемелік орталығының директоры ____________ «___ » _________ 2024 жыл |
Бекітемін Сауран ауданы Әл-Фараби атындағы жалпы орта мектеп директоры Мамадалиева Махсуда «___ » _______ 2024 жыл
|
«5-6 СЫНЫП ОҚУШЫЛАРЫНА АРНАЛҒАН МӘТІН ЕСЕПТЕР ЕСЕПТЕРІ»
(бағдарламаның атауы )
вариативтік және кәсіптік бағдарланған арнайы курстарының
(қандай курсты таңдауына байланысты)
БАҒДАРЛАМАСЫ
(___ сынып, ____ сағат саны)
2023 – 2024 жыл
Сауран ауданы
(Эксперттік Кеңес үшін оқу бағдарламасының ішкі титулдық бетінің үлгісі)
Авторы:
Қала/аудан_________ № ____ ЖББОМ __________пәнінің мұғалімі
____________________ аты-жөні
қолы
Пікір жазушылар:
Аты-жөні, мекеменің атауы, ондағы лауазымы, ғылыми дәрежесі,
ғылыми атағы (егер болса)
Аты-жөні, мекеменің атауы, ондағы лауазымы, ғылыми дәрежесі,
ғылыми атағы (егер болса)
Білім беру ұйымының Әдістемелік кеңесімен ұсынылады
Хаттама № _______ «____»___________ 2024 жыл
Хатшы:
Лауазымы ________________ аты-жөні
қолы
Аудандық(қалалық) білім бөлімдерінің Әдістемелік кеңесімен ұсынылады
Хаттама № _______ «____»___________ 2024 жыл
Хатшы:
Лауазымы ________________ аты-жөні
қолы
Облыстық Эксперттік Кеңеспен ұсынылады
Хаттама № _______ «____»___________ 2024 жыл
Хатшы:
Лауазымы ________________ аты-жөні
Түсінік хат
«5-6 сынып оқушыларына арналған мәтіндік есептер» атты авторлық бағдарламасының артықшылығы оқушылардың мектеп бағдарламасында алған білімдерін жан-жақты практикалық тапсырмаларда талдай алуына мүмкіндік беруге ықпал жасауында.
Тақырыптың өзектілігі:
-бұл курсты ұйымдастыру арқылы әр оқушының даму
деңгейі, білімі, қабілеттерінің дамуына жағдайлар
жасалып, бәсекеге қабілетті тұлға қалыптасуына
мүмкіндіктер туғызылады;
- қазіргі заманауи білім беруде кіріктірілген білім беру аса маңызды мәселелердің бірі болып табылады;
-ұсынылған тапсырмалар мәселені айқындау оқушыны шығармашыл жеке тұлға, зерттеуші ретінде сезінуіне, өзін-өзі дамытуына мүмкіндік береді;
-мұғалімдерге де біліктілігін жетілдіру жеке тұлғаны дамытуда маңызды роль атқарады;
-сыни ойлауға
байланысты оқушының интеллектуалдық және практикалық біліктілігі
қалыптасады, дамиды.
Мақсаты – 5-6 сынып оқушыларының математика сабағында есептеулерден бөлек сыни ойлау, патриоттық , шығармашылық-ізденушілік, талдау-жинақтау ойлау дағдыларын дамыту.
Оқу тәртібін(курс, факультатив) енгізудің себептері:
-оқушылардың логикалық ойлауын жетілдіруге байланысты функционалдық сауаттылыққа арналған әдістемелік құралдардың талаптарға сай болмағандықтан курсты енгізу қажеттілігі туындап отыр;
-практика мен теорияның арасындағы қарама – қайшылықтың болуы оқу үдерісіндегі курсты енгізудің негізгі себебі болып табылады;
«5-6 сынып оқушыларының функционалды сауаттылығын дамыту есептері» атты авторлық бағдарламасының курсының негізгі міндеті – базалық оқуға кіретін мектеп пәндері бойынша білімді тереңдету және кеңейту болып табылады.
Бағдарламалық материалдың
ерекшеліктері:
-Осыған байланысты пән ерекшелігі математика пәнінен функционалдық сауатталыққа бағытталған;
- бұл бағдарлама кең ауқымды кіріктірілген және математика пәнінен функционалдық сауатталыққа оқу-әдістемелік кешенді қолдану арқылы жүзеге асырылады.
-Берілген бағдарламаның ерекшелігі математика пәнінен функционалдық сауатталыққа арналған болып табылады.
-Оқу үдерісін ұйымдастыруда заманауи талаптарға сай және қолдану үшін бағдарламада тапсырмалардың құрылымына ерекше мән берілген.
-Ұсынылатын бағдарлама ... болып табылды. Ол 5-6 сынып математика курсының негізінде құрылған.
Курстың (факультативтің) жүргізілу тәртібі:
-Курс 5-6 сынып математика оқу жоспарына енгізілген пәндер қатарына кіреді;
-Берілген курсты оқыту жаратылыстану, биология пәндерімен тығыз байланысты;
Курс кім үшін ұйымдастырылады:
-бұл таңдау курсы оқыту бағдарына тәуелсіз, пәнге және оның қолданбалы аспектілеріне қызығушылық білдіретін 5-6 сынып оқушыларына арналған.
-Бағдарлама 5-6 сынып оқушылары үшін құрастырылған, сондай-ақ практикалық қолданысына тапсырмалар көп болғандықтан 7-8 сыныптарда да қолданылуы мүмкін.
-Курс 5-6 сынып оқушылары үшін ұсынылған.
Бағдарлама
құрылымы:
Негізінен 7-ірі тараудан құралған, оның ішінде Дирихле принципі - оқушылардың логикалық және сыни-ойлауын дамытуға бағытталса, логика интуицияға қарсы тарауында оқушылардың математикалық есептеулердің үнемі логикалық құндылығының арасында айырмашылығын ашып көрсетуі – саналы түрде дәл мәнді есептеулердің ғана мағыздылығын дәлелдейді. Көптеген математикалық парадокстардың пайда болуы кездейсоқ оқиғалардың ақиқат не жалғанға айналуы, адам ойының сансыз ұшқырлығын дамыта түседі. Теңдеу не теңсіздік шешудің Прокруст төсегі арқылы есептеу тек қана жаңа шешу әдісін енгізуде емес, стандартты емес ойлау дағдысын жетілдіру болып табылады. Менталды арифметиканың салдары болып табылатын тиімді көбейту деген тарауда оқушылардың қарапайым қысқа тәсілдер арқылы есептеуіне мүмкіндік беру. Сонымен қатар, 5-6 сынып оқушыларына этнопедагогика тұрғысынан қазақтың қара есептерін шығарту тарихи және математикалық маңыздылығын ұштастыру - қазіргі оқыту проблемасы болып табылатын патриоттық, рухани жаңғыру тапсырмасы рөлін атқарады.
Оқу үрдісін ұйымдастыру формалары:
- Бағдарлама құрылымы дәстүрлі сабақтар өткізуден, белгілі–бір тақырыптар бойынша дәрістер оқудан (практикалық сабақтар, семинарлар, жалпылама сабақтар және т.б. ) тұрады.
Оқушылардың сыныптық (аудиториялық) және өзіндік жұмыстарының өзара байланысы:
- Берілген курсты жоғары дәрежеде меңгеру үшін практикалық қолданысы бойынша өздік жұмыстар жүргізуге ерекше мән беріледі.
- Курсты оқу барысында оқушылар үшін өздік жұмыстармен айналысуға үлкен мүмкіндіктер қарастырылған.
- Курс бағдарламасы бойынша оқу барысында оқушылар практикалық және дәріс сабақтарына, семинарларға қатысады және жеке жұмыс істеп үйренеді.
Қорытынды бақылау
:
- Оқушылардың білімі мен дағдысын бағалау курстың негізгі мәселелері бойынша функцилоналдық сауаттылыққа байланысты сұрақтардан (тапсырмалардан) тұратын қорытынды тест арқылы өткізіледі.
Оқытудың көлемі мен мерзімдері:
-Курс бағдарламасы бойынша 5-6 сыныпта 34 сағат теориялық және практикалық сабаққа есептеліп құрылған.
|
№ п/п |
Курс бөлімдерінің атауы |
Жалпы сағат саны |
Оның ішінде |
Өткізілу күні |
Оқушылардың өздігінен атқаратын жұмыстары |
|
|
теория |
практика |
|||||
|
1 |
Дирихле принципі. |
1 |
1 |
|
|
|
|
Көжектер мен қораптар |
1 |
1 |
|
|
|
|
|
Дирихле принципі есептер шығару |
1 |
|
1 |
|
|
|
|
Дирихле принципінің практикалық маңыздылығы |
1 |
|
1 |
|
|
|
|
2 |
Логика интуицияға қарсы. |
1 |
1 |
|
|
|
|
Логикалық байланыс туралы |
1 |
1 |
|
|
|
|
|
Қарбызға байланысты есеп |
1 |
|
1 |
|
|
|
|
Жер планетасына байланысты есеп |
1 |
|
1 |
|
|
|
|
3 |
Парадокс туралы |
1 |
1 |
|
|
|
|
Шыншыл өтірікші |
1 |
1 |
|
|
|
|
|
Шексіздікті есептеу |
1 |
|
1 |
|
|
|
|
Галилео Галилей парадоксы туралы |
1 |
|
1 |
|
|
|
|
4 |
Прокруст әдісі |
1 |
1 |
|
|
|
|
Прокруст төсегі туралы аңыз |
1 |
1 |
|
|
|
|
|
Есептер шығару |
1 |
|
1 |
|
|
|
|
Прокруст әдісінің практикалық маңыздылығы |
1 |
|
1 |
|
|
|
|
5 |
Тиімді көбейту тәсілдері |
1 |
1 |
|
|
|
|
5-пен аяқталатын санның квадратын табу |
1 |
1 |
|
|
|
|
|
100- ге жақын санның квадратын табу |
1 |
|
1 |
|
|
|
|
Саусақпен санау. Саусақ арқылы санның квадратын табу. Көбейтудің әр түрлі әдістері |
1 |
|
1 |
|
|
|
|
6 |
Сандардың бөлінгіштігі қасиеттерінің практикалық маңыздылығы |
1 |
1 |
|
|
|
|
11-ге бөлінгіштік Автомашинаның нөмірі. |
1 |
1 |
|
|
|
|
|
19-ға бөлінгіштік |
1 |
|
|
|
|
|
|
Софья Жерменнің теоремасы |
1 |
|
|
|
|
|
|
Бізге белгілі ең үлкен жай сан |
1 |
|
|
|
|
|
|
7 |
Қазақтың қара есептері |
1 |
1 |
|
|
|
|
Жүз қаз есебі |
1 |
1 |
|
|
|
|
|
Тоғыз тapayдaғы кeздecy |
1 |
1 |
|
|
|
|
|
Құcбeгiлeр аманаты |
1 |
|
1 |
|
|
|
|
Бec cаулық |
|
|
1 |
|
|
|
|
Мұрап амалы |
1 |
|
1 |
|
|
|
|
Жалпы |
34 |
17 |
17 |
|
|
|
-
«Дирихле принципі» тақырыбын өтуге арналған әдістемелік нұсқаулық
Көжектер мен
қораптар. Дирихле қағидасымен қалай
байланысты Қапарайымдылығы мен айқындығына қарамастан, Дирихле
қағидасы теоремаларды дәлелдеуде және бір қарағанда шешу мүмкін
еместей болып көрінетін есептерді шешу кезінде қолданылады. Бүкіл
әлем математиктері Дирихле қағидасын көжектер мен қораптарды
мысалға ала отырып түсіндіреді (ағылшын тілді елдерде көгершіндер
мен қораптар қолданылады). Бұл қалыптасқан дәстүрді біз де
бұзбайық. Тек бұл қағиданың пайда болғаны үшін неміс математигі
Петер Густав Леж Дирихлеге қарыздар екенімізді айта кеткіміз
келеді. Қандайда бір мөлшерде көжектер (m) мен қораптар(n) бар
делік. Және көжектердің саны қораптардың санына қарағанда көбірек
(m > n). Барлық көжектерді қораптарға орналастырамыз. Сонда бір
қорапта бір көжектен көбірек болады. Ойланып көріп, шешім
шығарамыз: алдымен қораптарға n көжектерді салып шығамыз. Қалған
көжектер саны m-n -ге тең болады. Тапсырма шарты бойынша, барлық
көжектер қорап ішінде болуы тиіс. Сәйкесінше, n-m көжектерді біз
бос емес қораптарға сала бастаймыз. Сондықтан даішінде бірден көп
көжектері бар қораптар да болады. Біз қарапайым ойлау жүргіздік,
бұдан қиынырақ мысалдарды математикалық индукция әдісін пайдалану
арқылы өз еріктеріңізбен ойластыруды ұсынамыз. Дирихле әдісін
пайдаланудың басты қиыншылығы анықтаманың ауырлығында: не «көжек»,
ал не «қорап». Бұл жағынан бізге көмекке келетін бірнеше тапсырманы
қарастырып көрелік. №1 мысал. Классикалық мысал – қала
тұрғындарының шаштары. Дирихле қағидасы Алматы қаласында шаштарының
саны бірдей кем дегенде екі адам тұратынын дәлелдеп бере алады.
Әрине, бұл жерде таздар есепке алынбаған. Төменде пайымдау жолы
берілген: Алдымен Алматыда тұратын адамдар санын анықтап аламыз.
Халық саны туралы соңғы санаққа орай, қалада 1 552 349 адам тұрады.
Ары қарай орташа статистикалық адам шашының саны 150 000-нан артық
емес деген деректі пайдаланамыз. Енді жалпы қала тұрғындарының
санынан басында бір, екіден бастап, 150 000-ға дейінгі шашы бар
бір-бір адамды алып тастайық. Нәтижесінде біз 150 000-нан артық
емес адамдарды бөліп аламыз (себебі, қалған 1 402 349 тұрғынның
1-ден 150 000-ға дейін шашы болуы мүмкін). Олардың кез келгені
(басындағы шаш мөлшеріне қарай жинақталған) топтардың біреуіне
қосылуы мүмкін.

Ойланып көріп, шешім шығарамыз: алдымен қораптарға n көжектерді салып шығамыз. Қалған көжектер саны m-n -ге тең болады. Тапсырма шарты бойынша, барлық көжектер қорап ішінде болуы тиіс. Сәйкесінше, n-m көжектерді біз бос емес қораптарға сала бастаймыз. Сондықтан даішінде бірден көп көжектері бар қораптар да болады. Біз қарапайым ойлау жүргіздік, бұдан қиынырақ мысалдарды математикалық индукция әдісін пайдалану арқылы өз еріктеріңізбен ойластыруды ұсынамыз. Дирихле әдісін пайдаланудың басты қиыншылығы анықтаманың ауырлығында: не «көжек», ал не «қорап». Бұл жағынан бізге көмекке келетін бірнеше тапсырманы қарастырып көрелік. №1 мысал. Классикалық мысал – қала тұрғындарының шаштары. Дирихле қағидасы Алматы қаласында шаштарының саны бірдей кем дегенде екі адам тұратынын дәлелдеп бере алады. Әрине, бұл жерде таздар есепке алынбаған. Төменде пайымдау жолы берілген: Алдымен Алматыда тұратын адамдар санын анықтап аламыз. Халық саны туралы соңғы санаққа орай, қалада 1 552 349 адам тұрады. Ары қарай орташа статистикалық адам шашының саны 150 000-нан артық емес деген деректі пайдаланамыз. Енді жалпы қала тұрғындарының санынан басында бір, екіден бастап, 150 000-ға дейінгі шашы бар бір-бір адамды алып тастайық. Нәтижесінде біз 150 000-нан артық емес адамдарды бөліп аламыз (себебі, қалған 1 402 349 тұрғынның 1-ден 150 000-ға дейін шашы болуы мүмкін). Олардың кез келгені (басындағы шаш мөлшеріне қарай жинақталған) топтардың біреуіне қосылуы мүмкін.

Есеп 1. Сыныпта 15 оқушы. Сыныптан бір айда туған күнін атап өтетін кем дегенде 2 оқушының табылатынын дәлелдеңіз.
Шешуі: 15 оқушы- «қояндар» болсын. «торлар»- жылдың айлары (12 ай). 15>12 болғандықтан Дирихле принципі бойынша бір торда 2 қоян отыратындай кем дегенде бір тор табылады. Яғни сыныптан бір айда кем дегенде 2 оқушы туған күнін атап өтетіндей ай табылады.
Есеп 2. 12 бүтін сан берілген. Олардың ішінен айырмасы 11-ге бөлінетіндей екі санды таңдап алуға болатынын дәлелде.
Шешуі: Бүтін сандар-«қояндар», олардың саны 12, онда торлардың саны 12-ден аз болу керек. «торлар»- бұлар бүтін сандарды 11-ге бөлгендегі қалдықтар. Барлық «торлар» саны 11 болады: 0,1,2,3,4,5,6,7,8,9,10. Онда Дирихле принципі бойынша бір торда 2 қоян отыратындай кем дегенде бір тор табылады. Яғни қалдықтары бірдей болатындай екі бүтін сан табылады. Ал 11-ге бөлгенде бірдей қалдық қалатын екі санның айырмасы 11-ге бөлінеді.
Есеп 3. Өлшемдері 3x3 метр болатын кілемге Коля 8 тесік жасады. Осы кілемнен өлшемдері 1x1 метр болатын ішінде тесігі жоқ кілемше кесіп алуға болатынын дәлелдеңіз.
Шешуі: Бұл жерде тесіктер ол-«қояндар». Кілемді өлшемдері 1x1 метр болатын 9 кілемшеге кесеміз. Кілемшелер-«торлар» саны 9. Ал тесіктер-«қояндар» саны 8. Онда «қоян» болмайтындай кем дегенде бір «тор» табылады. Яғни ішінде тесігі болмайтын кілемше табылады.
Есеп 4. Турнирде жеңіске жеткендері үшін 8 адамнан тұратын команда 12 кәмпит алды. Балалар кәмпиттерді бүтіндей (сындырмай) бөліп алды. Келесі тұжырымдамалар дұрыс па? Анықтаңдар.
«бір бала кем дегенде екі кәмпит алды»
«бір бала кем дегенде үш кәмпит алды»
«екі бала кем дегенде екі кәмпит алды»
«әрқайсысына кем дегенде бір кәмпиттен келді».
Жауабы: Бірінші тұжырым дұрыс, қалғаны дұрыс емес.
Шешуі: 1) Дұрыс. Кері жоримыз. Яғни балалар кәмпиттерді бөліскенде әрбіреуі 0 немесе 1 кәмпиттен алды делік. Онда барлық бала қосындысында 8 кәмпиттен артық алмайды. Ал бұл есеп шартына қайшы. Яғни біздің жорығанымыз дұрыс емес, бұндай жағдай болу мүмкін емес. Онда бір бала кем дегенде екі кәмпит алды.
Қалғандарының орындалмайтындығына бір мысалдан келтіре салса жеткілікті:
2) 4 адам 2 кәмпиттен алады, ал қалған 4 адам бір-бірден алады.
3) Барлық кәмпитті бір адам алады.
4) 3-ші бөлімге ұқсастықпен.
Есеп 5. Үш әділқазылар мүшелерінен былай сұрады: «Турнирге қанша команда қатысады?» Біріншісі: « 33-тен кем команда», екіншісі: «31-ден кем команда», үшіншісі: «32-ден кем команда» -деп жауап берді. Егер екі әділқазы мүшесінің айтқаны дұрыс болса, онда турнире неше команда қатысқан?
Шешуі: Екінші тұжырым дұрыс болса, онда қалғандары да дұрыс екені шығады? Бірақ, екі тұжырым ғана дұрыс болғандықтан екіншісі дұрыс емес, ал бірінші мен үшіншісі дұрыс. Бір жағынан команданың саны 31-ден артық болу мүмкін емес (онда үшіншісі дұрыс болмайды), екінші жағынан 31-ден кем болу мүмкін емес(онда екіншісі дұрыс болады). Яғни жалғыз ғана мүмкін жағдай 31. 31 саны есептің шартын қанағаттандыратынын тексеру қиын емес.
Есеп 6. Мектепішілік баскетбол жарысының ақтық кезеңінде 6А командасы 9 доп салды. Осы командадан саны жағынан бірдей доп салған екі ойыншы табылатынын дәлелдеңіз.(Командада 5 ойыншы болған)
Шешуі: Командадан саны жағынан бірдей доп салған екі ойыншы табылмауы мүмкін деп жориық. Онда барлық бес ойыншы саны бойынша әртүрлі доп салған. Бірінші ойыншы ешқандай доп салған жоқ дейік, екінші ойыншы бір доп салды, үшіншісі екі доп салды, төртіншісі үш доп салды, бесіншісі төрт доп салды. Онда ойыншылар барлығы он доп салды. Егер ойыншылардың кем дегенде біреуі біз жорығандай доптан артық салса, онда команданың да барлық салған доптарының саны 9-дан асып кетеді. Яғни біздің кері жорығанымыз дұрыс емес. Яғни командадан саны жағынан бірдей доп салған екі ойыншы табылады.
Есеп 7. Андрейдің інісі шашкилерді 8 түрлі түспен бояп шықты. Әрбір бағанда және әрбір жолда бір шашкиден болатындай Андрей 8 әртүрлі түсті шашкилерді шашки тақтасына қанша тәсілмен орналастыра алады? Әрбір бағанда және әрбір жолда бір шашкиден болатындай Андрей 8 ақ шашкиді қанша тәсілмен орналастыра алады?
Шешуі: Біріншіден шашкилердің түстері ақ болған жағдайды қарастырайық. Шашкилерді орналастырамыз. Бірінші бағандағы 8 торкөздің кез келгеніне шашкиді қоя аламыз, екінші бағандағы 7 торкөздің кез келгеніне қоя аламыз.(Сонымен қоса бірінші шашки тұрған жолға шашки қоюға болмайды). Сол сияқты үшінші жолдың кез келген 6 торкөзіне шашки қоюға болады, төртінші жолдың кез келген 5 торкөзіне шашки қоюға болады т.с.с. Нәтижесінде 8! Тәсіл шығады.
Енді шашкилер түрлі түсті болған жағдайды қарастырамыз. Ақ шашкилердің орналасуларының кез келген жағдайын алайық. Осы шашкилерді олардың кез келген екеуі әртүрлі түс болатындай 8 түрлі түске бояймыз. Бірінші біз 8 түстің бірімен бояп шығамы, екінші 7 түстің біреуімен және т.с.с. Нәтижесінде 8! тәсіл шығады. Сонымен барлық тәсіл 8!8!=8!2 болады.
Есеп 8. Мәскеуде 10 000 000 нан астам адам тұрады. Әрбір адамның басында 300 000 нан астам шаш болуы мүмкін емес. 34 адамның басындағы шаштарының саны бірдей болуы мүмкін болатынын дәлелде.
Шешуі. Баста 0,1,2,...,300 000 шаш болуы мүмкін. Сонда барлығы 300 001 нұсқа. Шаштарының санына байланысты әрбір адамды 300 001топқа бөлеміз. Егер шаштарының саны бірдей болатын 34 адам табылмаса, яғни құралған топтардың кез келгеніне 33 –тен артық емес адам кіреді. Онда Москвада 33·300 001=9 900 033<10 000 000 адам тұрады. Бұл қарама-қайшылық. Яғни 34 адам табылады.
9-есеп. Жазықтық 2 түске боялған. Бір-бірінен 1 метр қашықтықта орналасқан және бірдей түске боялған екі нүкте әрқашан табыла ма?
Шешуі: Түс екеу болғандықтан нүктелер саны екеуден көп фигураны қарастыру қажет. Қабырғасы 1 метрге тең дұрыс үшбұрышты мысал ретінде қарастыру қолайлы болады. Оның 3 төбесі бар. Төбелерін «қоян», ал түстерді «ұяшық» десек, онда 3 ˃ 2. Демек, Дирихле принципі бойынша бірдей түспен боялған және бір-бірінен 1 метр қашықтықта орналасқан үшбұрыштың 2 төбесі табылады.[1]
10-есеп. Студенттер жатақханасындағы би кешіне 36 қонақ келді. Жатақханадағы бөлмелер саны 42 болса, бірде бір қонақ келмеген бөлме барын дәлелдеңдер.
Шешуі: Бөлмелерді – «ұяшықтар», ал қонақтарды – «қояндар» деп белгілеп, келесі теңсіздікті аламыз: 36 ˂ 42. Онда Дирихле принципі бойынша кем дегенде бір бос «ұяшық» табылады, яғни қандай да бір бөлмеге ешбір қонақ келмейді. [1]
11-есеп. Мектепте 33 сынып, 1150 оқушы бар. Оқушылар саны 35-тен кем сынып бар болады ма?
Шешуі: Әр сыныпта 35-тен кем емес оқушы бар болсын делік. Онда мектептегі барлық оқушы саны 35·33 = 1155 –тен кем болмауы тиіс. Ал, бұл есептің шартына қайшы келеді. Демек, мектепте оқушы саны 35-тен кем сынып бар болады. [1]
12-есеп. Сыныпта 29 оқушы бар. Шығарма жазғанда Набиев Руслан 13 қате, ал қалғандары одан аз қате жіберді. Сыныпта қателер саны бірдей болатын кем дегенде 3 оқушы табылатынын дәлелдеңдер.
Шешуі: Қателер санын: 0, 1, 2, ..., 11, 12 «ұяшықтар», ал 28 оқушыны (Руслансыз) «қояндар» деп белгілеп, келесі теңсіздікті аламыз: 28 ˃ 13·2 + 1. Дирихле принципінің жалпыланған түрін қолданып, кем дегенде 3 оқушыда қателер саны бірдей екенін аламыз.
13-есеп. Өлшемі 8х8 шахмат тақтасына Заңғар 14 фигураны қойып шықты. Бірде бір фигура қойылмаған 2х2 өлшемді шаршы табылатынын дәлелдеңдер. (Фигуралар 1х1 өлшемді шаршылардың ішінде орналасады).
Шешуі: 8х8 шахмат тақтасы өлшемі 2х2 болатын 16 шаршыларға бөлінеді. Сонда 16 «ұяшық» және 14 «қоян» - фигура болады. 16 ˃ 14 болғандықтан, кем дегенде бір «ұяшық» бос болады. [1]
14-есеп. Жоғарғы оқу орнында оқыған 5 жыл ішінде студент 31 емтихан тапсырды. Әр жылы алдыңғы жылға қарағанда көп емтихан тапсырып отырды. Бесінші курста тапсырған емтихан саны бірінші курста тапсырған емтихан санынан 3 есе көп. Төртінші курста неше емтихан болды?
Шешуі: Студенттің бірінші курста
тапсырған емтихан саны х
болсын. Онда оның екінші
курста тапсырған емтихандар саны (х
+ 1) – ден кем емес, үшінші
курста емтихан саны (х
+ 2) – ден кем емес, төртінші
курста емтихандар саны (х
+ 3) – тен кем емес. Екінші
жағынан, бесінші курста тапсырған емтихандар саны
3х, демек, төртінші курста
(3х
– 1) –ден көп емес, үшіншіде
(3х
– 2) –ден көп емес, ал
екіншіде (3х
– 3) –ден көп емес емтихандар
тапсырды. Онда жалғыз бүтін шешімі х
= 3 болатын келесі
теңсіздіктер жүйесін аламыз:  . Онда студент бесінші
курста 9 емтихан тапсырды, сәйкесінше, төртінші курста тапсырған
емтихандар саны 8-ден көп емес. Егер ол төртінші курста 7 емтихан
тапсырған болса, онда барлық емтихан саны 3 + 5 + 6 + 7 + 9 = 30
–дан аспайды. Демек, студенттің төртінші курста тапсырған
емтихандар саны 8.
. Онда студент бесінші
курста 9 емтихан тапсырды, сәйкесінше, төртінші курста тапсырған
емтихандар саны 8-ден көп емес. Егер ол төртінші курста 7 емтихан
тапсырған болса, онда барлық емтихан саны 3 + 5 + 6 + 7 + 9 = 30
–дан аспайды. Демек, студенттің төртінші курста тапсырған
емтихандар саны 8.
Дирихле принципін практикалық маңызы бар есептер шығаруда қолдану
№1 есеп. 145
тұқым 12 метр көлемдегі егіске 12 метрге шашылған. Осы жерде
кемінде екі тұқым бір-бірінен √2 метрден кем қашықтықта
түскенін дәлелдеңіздер. Көмек: Пифагор теоремасын еске
түсіріңіздер. №2 мысал. Түрлі-түсті шұлық және қараңғылық.
Барлық шұлықтарыңыз тек қара және ақ түсті деп елестетіңіз. Кезекті
кір жуғаннан кейін олар араласып кеткен. Бір түсті жұп шұлық табу
үшін қарамай тұрып, кем дегенде қанша шұлық алуыңыз керек?Шұлықтар
дәл бір ғажайыптағы секілді, сіз оларды алып шыққаннан кейін, өз
түстеріне орай ақ және қара қорапқа түседі. Сіз алып шыққан алғашқы
шұлық ақ түсті болды деп есептелік, енді ойластырайық, келесі шұлық
та ақ түсті болса ше? Бұл жағдайда, есеп шарты орындалды, алайда,
келесі шұлық қара түсті де болуы мүмкін ғой. Тағы бір рет қайталап,
келесі не қара, не ақ шұлықты алып шығамыз. Сәйкесінше, үшінші
шұлық бастапқы шұлықтардың біреуіне мысалыті түрде жұп болады (егер
шұлық әлі жұптаспаған болса). Есебіміздің жауабы – екі түс кезінде
алып шығуға тиесілі ең аз шұлық саны үшке (3)
тең.
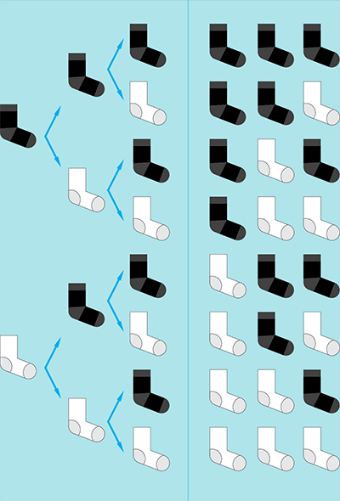
№2 есеп. №2 мысалда көрсетілген есепті ақ шұлықтардың саны 14, қара шұлық саны 10 болған жағдайда шешіңіз. №3 мысал. Үштік дәрежесі. Жоғарыдағы мысалдарда біз шарттағы элементтердің ақтық санын қарастырдық. Келесі есепті шығарып көрейік: 001 сандарына аяқталатын үштік дәреже (3a) бар екенін дәлелдеңіздер. Үштік дәрежесіне 30 =1, 31 = 3, 32 =9, 33 = 27, 34 = 81, 35 = 243 осылай жалғаса беретін сандар жатады. Осы сандарды 1000-ға бөліп, барлық мүмкінді қалдықтарды көшіреміз (r): 3a = 1000k + r Мысалы 310 = 59 049 = 59000 + 49 (қалдық), 311 = 177 147 = 177000 + 147 (қалдық) және тағы басқа. Үштік дәрежелері шексіз көп болғандықтан, 0-ден 999-ға дейінгі қалдықтар тура 1000 дана болады. Дирихле қағидасын пайдаланып, 1000-ға бөлген кезде үштіктің екі дәрежесінде бірдей қалдық қалатынын дәлелдейміз. Бұл 3m және 3n сандары болсын. 3m = 1000k + r 3n = 1000q + r Олардың айырмашылығын есептейміз: 3m - 3n= 3n(3(m-n) - 1) = 1000k + r - 1000q - r = 1000(k-q), басқаша айтқанда - 3n және (3(m-n) - 1) көбейтіндісі 1000-ға еселенген. Біз n дәрежесінің қандай мәнінде болмасын, 3n саны 1000-ға еселенуі мүмкін емес екенін білеміз. Сәйкесінше, 1000-ға еселі (3(m-n) – 1) саны болуы тиіс: 3(m-n) - 1 = 1000(k-q) немесе 3(m-n) = 1000(k-q) +1 Осылайша, 001 сандарына аяқталатын үштік дәрежесі бар екенін дәлелдедік! №3 есеп. 17 санының 0001 сандарына аяқталатын дәрежесі бар екенін дәлелдеңіздер.
-
«ЛОГИКА ИНТУИЦИЯҒА ҚАРСЫ» ТАҚЫРЫБЫН ОҚЫТУҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ
Неге көп адам математиканы
ұнатпайды? Ең жиі кездесетін жауаптардың бірі: оның сарқылулығына
байланысты. Кез-келген «анық» жағдайда олар бір нәрсені дәлелдеуге
мәжбүр болады! Бірақ «айқын» қорытындылар жиі дұрыс емес және ұзақ
уақыт сақталады, өйткені біз олардың «дұрыстығына» интуитивті түрде
сенеміз.
Алдымен, біздің математикалық мағынаны тексерейік - келесі сұраққа жауап берейік: А нүктесінен В нүктесіне дейін ең қысқа жол қандай болады? Менің ойымша, қазір көптеген адамдар: «Әлбетте, АБ сегменті» деп ойлаймын. Ал сен, әрине, дұрыс, ал егер мен оны дәлелдеуді сұрасам? Бұл жерде математика үшін жек көретін сезім пайда болады. «Неге? Мәселелерді шешудің интуитивті тәсілі: біз жауапты білеміз, бірақ қалай пайда болды, біз бұл туралы ойламаймыз. Жиі бұл тәсіл жұмыс істейді, тіпті көп уақытты үнемдейді. Бірақ келесі сұраққа жауап беруге тырысайық.
10-дан 20-ға дейін қанша табиғи нөмірлер бар (10 және 20-ны қоса алғанда)? Көптеген адамдар «10» деп жауап береді, өйткені түйсігі бізге де дәл осындай. Және олар қателеседі, өйткені дұрыс жауап «11». Бұны қарапайым іздеу арқылы дәлелдеуге болады: 10-нан 20-ға дейінгі барлық нөмірлерді жазыңыз және оларды қайта есептеңіз. Бірақ мұндай дәлел толығымен әмбебап емес: проблемадағы сандар 10-нан 20-ға дейін емес, 1000-нан 2000-ға дейін болса, не істейміз? Сондай-ақ жазылған және қарастырылған?
Сондықтан 1-ден 20-ға дейінгі 20-ға дейінгі табиғи сандар, бірақ бізге 10-нан толмағандар қажет, демек, 1-ден 9-ға дейінгі барлық нөмірлерді қарастыруға болмайды (дәл 9, 10 емес!). 20 - 9 = 11 болады, бұл дұрыс жауап. Мәселен, 2000 және 2000 жылдардағы мәселеде біз 2000 - 999 = 1001 аламыз және а9-дан b9 дейінгі сандарға арналған жалпы формула: a-b + 1.
Біз түйсігі қалай көмектесті және адастырғаны туралы қарапайым мысалдар келтірдік. Олай болмаған жағдайда, гворяя, интуитивті тәсіл дұрыс шешімге кепілдік бермейді. Математикадан айырмашылығы, бұл сіз дұрыс деп сенуге мүмкіндік береді. Яғни дәлелдер дәлелденуі мүмкін және олар дұрыс емес, бірақ кем дегенде бізде ақиқатты дәлелдеуге мүмкіндік беретін құрал бар.
Әрине, 10-нан 20-ға дейінгі сандар туралы мәселе өте оңай болды. Тиісті жауапты табу оңай емес жерде бірнеше қарама-қайшы мысалдарды қарастырайық. Алдымен осы тапсырмалардың әрқайсысын өзіңіз шешіп көріңіз, содан кейін оқыңыз. Және таңданамын.

1-тапсырма
Қарбыз қыртысы целлюлозаға қарағанда үш есе жіңішке (яғни, сіз қарбыз ортасынан бетіне сызық сызсаңыз, осы сызықтың төрттен үш бөлігі целлюлозаға түседі және қырыққабаттың төрттен бір бөлігі). Қабықтың көлемінен қанша рет целлюлоза көлемі көбірек?
Мысалы, бұл қарбыз идеалды доптың пішіні бар, оның ішіндегі кішігірім доп - ет, содан кейін қыртыс. Мәселен, целлюлоза көлемі қанша рет? Үш кезінде? Тоғызында? Басқа опциялар? Тілек өз жұмысын аяқтады, енді математика өз жұмысын басқарады.
Бір қарбыз - 4x радиусы бар доп, оның ішіндегі 3x радиусы бар шарлар целлюлоза толтырылған, қалғаны - қыртыс. Сонда шарт орындалды, яғни қабықтың қалыңдығы целлюлозаның қалыңдығынан үш есе аз. Доптың формуласы бойынша біз бүкіл қарбыздың көлемі (4х радиусы бар) тең екендігін анықтаймыз:
![]()
және целлюлозаның көлемі (3x радиусы бар)
тең:
![]()
Осылайша, целлюлоза 2764 тұқымдық қарбызды құрайды, ал қыртыстың мөлшері - 3764. Яғни қабықтың көлемі кем емес (3, 9 немесе қанша рет айтқаныңыз), бірақ целлюлозаның көлемінен бір жарым есе көп ...
Логикалық және қарапайым есептеулер осылайша интуитивті қарауды жоққа шығарады.
2-тапсырма
Жер шарша жерге тығыз бекітілген. Содан кейін таспа 1 метрге көтеріліп, планетаның бетінде біркелкі бөлінді. Мысық алшақтығы арқылы жүре ме?

Тағы да, тұжырым жасаңыз: біз Жер деп атаймыз, бірақ бұл дұрыс емес. Мәселен жауап қандай? Тілектің мысықтың сынғаны жөн емес пе? Егер сіз Жерді экваторға кіргізсеңіз, таспаның ұзындығы шамамен 40 000 километрді құрайды, сондықтан 1 метрге көтерілу байқалмайды. Егер біз таспаны жермен біркелкі жылжытуды жалғастыра берсек, нәтиже алған микроскопиялық алшақтық - бұл мысық - құмырсқалар арқылы өтіп кету екіталай емес. Мәселен? Және жоқ!
Жер шарының радиусы R метріне тең (шын мәнінде, ол 6 мың кг-нан сәл асады, бірақ бұл мәселеде бұл бірінші емес). Содан кейін таспа шеңбер ұзындығы формуласына сәйкес 2ррр метр ұзындығына ие. Тиісінше, ұзындығын 1 метрге көтергенде (27TR + 1) метр. Сонымен қатар, таспаны беткі жағынан біркелкі жылжытсақ, онда таспа енді шеңбер жасайды, тек оның радиусы әр түрлі - мысалы, R. Бұл жағдайда таспаның ұзындығы 2ТТР екенін ескеріңіз. Бірақ ол бізді бірнеше жолды жоғары бағалады! Теңдеу:
![]()
Сонымен, жаңа радиусы 1 / 2p
артық. Себебі p 3.14, содан кейін 127 = 0.16. Бұл аралық 0,16 метр
немесе 16 сантиметр болатындығын білдіреді. Және бұл мысық үшін
таспаның астында көтерілу үшін жеткілікті. Магия? Жоқ, тек дұрыс
есептеу. Жылжыту.
3-тапсырма. Бөлмеде 50 адам жиналды. Сол күні олардың екеуі екі туады деп неге ықтималдығы бар? Тағы да, біз қажетті резервация жасаймыз: олардың арасында егіздер жоқ, әйтпесе бұл мәселе қызықтырмайды.
Сонымен, интуитивті жауап дегеніміз не? 10-20 пайыз, мүмкін бе? Шындығында 365 күнде 50 адам бар, бұл жетіншіден аз. Мысалы, шамамен 100: 7, яғни шамамен 1596. Немесе 30 адам бар ма?
Енді математиканы жалғастырайық. Біз жиналғандардың әртүрлі күндерде дүниеге келу ықтималдығын есептейміз (бұл оңайырақ болады), содан кейін нәтижені бірліктен шығарып аламыз. Бұл қалаған жауап болады - сол күні туылған бөлмеде екі адам бар (мүмкін, бір ерлі-зайыпты емес, бірақ бізден бұл туралы сұралмаған, ең бастысы - кем дегенде екі) болуы ықтималдығы. Бірінші адамды қабылдаңыз - ол белгілі бір күні туған. Екінші қарастырайық - оның 365 нұсқасы бар, оның 364-і біз үшін жарамды (біріншіге сәйкес келмеуі үшін). Демек, бірінші және екінші күндерде әртүрлі күндерде туындаған ықтималдығы 364/365 тең.
Енді үшінші орында. Оның
365-тен 363 нұсқасы бар, яғни 363/365 ықтималдығы бар бірінші
немесе екінші күні сол күні туылмаған. Бірақ содан кейін, жұмыс
ережесіне сәйкес, әркім әртүрлі күндерде дүниеге келу ықтималдығы -
364 / 365х363/365. Жағдай төртінші, бесінші, және т.б. елуінші
жылдарға ұқсас, сондықтан олардың әртүрлі күндерде туылғандығына
тең:![]()
Неге 316? Екінші адамға сәйкес келетін фракция 364 (365 - 1), үшінші - 363 (365 - 2) нөлдеріне ие болғандықтан. Осылайша, 50-ші адам үшін 316 нөмір (365-49) болады.
Әрине, оны калькуляторсыз есептеуге болады, бірақ тіпті өте өрескел бағалау да бір нәрсе береді. Мысалы, 316 / 365x317 / 365 соңғы екі фракцияны көбейтсеңіз, нәтиже 0,76-дан кем болады, яғни қажетті ықтималдық (оны алу үшін, еске салу, алу үшін көбейту нәтижесі құрылғыдан алынуы тиіс) 2496-ден артық. Егер сіз барлық фракцияларды көбейтсеңіз, ықтималдық ... 9796! Сену қиын, бірақ шындық.
Сіз ықтималдығы шамамен 5096 болғанын білесіз бе? Қазірдің өзінде 23 адам! Айтпақшы, бұл оңай тексерілуі мүмкін. Бірнеше сабақ алыңыз - 25-30 адам ғана бар. Сыныптастар арасында туған күндері қаншалықты жиі кездесетінін көріңіз. Нәтижесінде сіз таңқаларыңыз болады! Біз сондай-ақ бұл есептерді тексеріп, Конфедерация Кубогындағы футбол командаларының құрамына қарап көрдік. Әрқайсысы 23 адамнан тұратын 8 команда болды - сіз оған сенбейсіз, бірақ төрт командада сол күні туылған ойыншылар болды! Практика теорияны жақсы растады.
Бірнеше мысалды қарастырып, біз өзіміздің бейнеқосылғыларымыз уақытша төмендейтініне көз жеткіздік. Сондықтан интуитивті тұжырымдарды мұқият алайық, оларды сұрастырып, дәлелдеуге тырысыңыз. Бұдан былай, логикалық түйсігі күнделікті мақсаттарға қол жеткізу үшін алға жылжуға көмектеседі деп үміттенеміз, себебі басқа контрастивтік факт 1.01, 37.8 және 0.99365 = 0.03!
-
«ПАРАДОКС ТУРАЛЫ» ТАҚЫРЫБЫН ОҚЫТУҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ
Парадокс болса да, шындық!
Ерте заманнан-ақ ғалымдар мен философтар басқалардан өзгеше
тұжырымдар бар екенін байқаған. Оларды қалай түсіну керектігі
белгісіз еді. Бір қызығы — олар әлі күнге дейін түсініксіз. Бұл
жұмбақ емес, себебі оның жауабы жоқ. Мұндай пайымдауларды парадокс
деп атайды.

Шыншыл
өтірікші. Көптеген парадокстар ерте
уақытта логика деп аталатын ғылым пайда болуымен туындаған еді. Бұл
ғылым, көп жағдайда, не шындыққа жанасатын (шынайы) немесе жалған
(өтірік) пайымдарды зерттейді. Ең танымал және көне парадокстың
бірі – «Өтірікшінің парадоксы» деп аталады. Мысалы, біреу: «Менің
қазір айтып тұрғаным – өтірік» немесе «Мен өтірік айтамын» деді.
Оның бұл сөздерінің тек қана екі мағынасы болуы мүмкін – не
шындықты растау (бұл шынымен солай), немесе жалған (шындығында олай
емес). Сонымен, оның сөзі шындық делік, яғни «Мен өтірік айтамын»
деген адам шындығын айтып тұр. Алайда, ол шын айтып тұрғандықтан,
оның «Мен өтірік айтамын» деген сөзі – өтірік. Нәтижесінде, егер
пайымдау шындық болса, бұл оның өтірік екеніне алып келеді. Ал енді
бұл олай емес, оның айтып тұрғаны өтірік екенін қарастырып көрелік.
Яғни, мен «Өтірік айтамын» дей тұра, ол алдап тұр. Алайда, бұл
жағдайда ол шын мәнінде өтірік айтады және оның «Мен өтірік
айтамын» деген мақұлдауы – шындық. Енді біздің пайымдау – өтірік
деген тұжырымымыз, оның шындық екеніне алып келеді. Рас, қанша
айналдырсақ та – мұндай пайымдауды біз бір уақытта шынайы және
жалған деп қабылдауға мәжбүрміз. Міне, бұл – парадокс! Өтірікшінің
парадоксы негізінде көптеген парадокстар туындаған, олардың барлығы
логикалық деп аталады. Мысалы, белгілі ертегі кейіпкері Буратино
таңғажайып қасиетке ие: ол өтірік айтқан кезде, оның мұрны ұзарады.
Ендеше, егер ол «Қазір менің мұрным ұзарады» дейтін болса,
Буратиноның мұрнына не болады? Логикалық тұрғыда талқылап байқайық.
Егер Буратино шындықты айтса, оның мұрны ұзармауы керек. Алайда,
егер мұрын ұзармаса, Буратино өтірік айтты деген сөз және оның
мұрны ұзаруы тиіс. Енді Буратино өтірік айтты делік, онда оның
мұрны ұзарады. Әйтсе де, егер мұрын ұзарса, Буратино шындықты
айтты, сәйкесінше мұрын ұзармауы керек. Мүмкін, Папа Карлоның
айлакер ұлы мұндай жағдайды пайдаланып, парадокс туралы есепті
шешімсіз қалдыруды жөн көрген болар, нәтижесінде оның мұрны тоқтап
қалды да, енді ұзармайтын болды. Логикалық түрінен басқа
парадокстардың өз-өзіне қатысты деген түрі бар. Мұндай парадокстың
басты кейіпкері өзінің шарттарын өзіне қолданып көрмек болады. ХХ
ғасырдың басында танымал британдық философ және математик Бертран
Рассел математикалық теориялардың бірімен айналысу үстінде, келесі
парадоксты ойлап тапты. Бір ауылда жалғыз сақал-мұрт қыратын
шаштараз болды. Оның жұмысының қатаң ережесі бар еді: ол тек қана
өздері қырынбайтын ауыл тұрғындарын қырындыруы керек. Бір
қарағанда, тәп-тәуір ереже секілді. Дегенмен, шаштараздың өзінің де
сақал-мұрты өседі, осы кезде сұрақ пайда болды: ол өз сақалын өзі
қыра ала ма? Нәтижесінде, қыра алатын және қыра алмайтын болып
шығады. Өзің ойлап қарашы:

Бертран Рассел — ағылшынның көрнекті философы, логигі, қоғам қайраткері. Расселдің математикалық логика мен қатынастар логикасы жөніндегі еңбектері логикалық ғылымға енген зор үлес болды. 1950 жылы әдебиеттен Нобель сыйлығының лауреаты атанды.
Шексіздікті есептеу.
Мектептегі математика
сабағынан барлығымыз натурал сандардың не екенін жақсы білеміз:
1,2,3,4,5… және осылай шексіз жалғаса береді. Дегенмен, шексіздік
сөзінің түсінігі бұл сандардың парадоксалды сипаттарына алып келді.
Натурал сандардың ішінде жұп сандардың бар екені белгілі. Кейде
натурал сандар жұп сандарға қарағанда көп сияқты көрінеді. Бір
жағынан логикаға да қонымды, себебі жұп сандар — натурал сандардың
бір бөлігі ғана емес пе? Алайда, математика натурал сандар қанша
болса, жұп сандардың да сонша екенін алға тартады! Көз алдарыңа екі
жолды елестетіп көріңдер, оның біріншісінде барлық натурал сандар,
екіншісінде бірінші жолдағы әр санды екіге көбейткен кезде алынған
сандар тізілген (яғни 1×2 = 2, 2×2 = 4, 3×2 = 6, 4×2 = 8, 5×2 =
10…):
![]()
Осылайша, егер сандар жазылған
осы екі жолды шексіз жалғасытыра берсек, онда әрбір натурал санның
астында жұп сан тұратын болады. Олай болса, жұп сандар натурал
сандардан аз емес. Шексіздіктің бұл ғажайып сипатына XVII ғасырда
атақты италияндық ғалым Галилео Галилей назар аударған және
алғашқылардың бірі болып осы парадоксты
тұжырымдаған.

Галилео
Галилей — итальян философы, математик,
физик, механик және астроном, табиғаттану ғылымдарының негізін
салушы, өз заманындағы ғылымға өте қатты әсер еткен. Ол ұлы ғалым
болумен бірге, музыкант, суретші, ақын, әдебиетші де болған.
Галилей - тәжірибелі физика мен классикалық механиканың негізін
қалаушы. Ешқандай қозғалыс мүмкін емес Парадокстар тек математикада
ғана емес, егер физикалық процестерге ойша қарайтын болсақ,
физикада да пайда болады. Тіпті, ерте заманның өзінде-ақ, ғалымдар
сезім мүшелерінің бізді алдауы мүмкін екенін және табиғатты зерттеу
барысында әрдайым оларға сене бермеу керектігін жақсы түсінген.
Мысалы, біз Күн Жерді айналмайтынын, мүлде керісінше екенін
білеміз. Сондай-ақ біздің көзіміз оларды көрмесе де, молекулалардың
бар екені де белгілі. Ертедегі ғалымдар дененің қозғалысын көзбен
емес, ақылмен зерттеген уақытта қызықты парадоксқа тап болғандары
таң қалатын жағдай емес. Адам А нүктесінен Б нүктесіне қарай
қозғалып барады. Ежелгі философ бұл жағдайды: адам А нүтесінен Б
нүктесіне жету үшін алдымен бұл қашықтықтың жартысын жүріп өтуі
керек деп талқылайды. Әрине, ешкімнің дауы жоқ. Солай болуы да
керек. Алайда, қазымыр философ мұнымен тоқталмай, жолдың жартысына
жету үшін адам алдымен төрттен бір бөлігін өтуі тиіс (яғни,
жартының жартысын) дегенді алға тартады. Бұл жерде де келісуге тура
келеді. Енді ғалым бұл кесіндіні де екіге бөлу керек деп есептейді…
Бұл пайымдау шексіздікке дейін жалғаса беруі мүмкін. Соңында адам
орнынан қозғала да алмай қалады — себебі, ол әуелі шексіздікке
дейін жолдың тым болмаса бір кішкентай бөлігін жүріп өтуі
керек.

Яғни, қозғалыс жоқ, себебі оны
жүзеге асыру мүмкін емес! Алайда, әлемдегінің бәрі қандай да бір
парадоксқа көңіл аудармастан қозғалуда. Себебі, қозғалыс — үздіксіз
процесс, оны бір кесіндіні шексіз жүріп өту түрінде қарастырудың
қажеті жоқ. Және бұл Пушкиннің тұсында да баршаға кеңінен белгілі
болған еді. Естеріңде болса, ақын: «Қозғалыс жоқ, деген еді
данышпан, Үн қатпады, жүре бастады алыстан. Мұнан артық жауап ойлап
табар ма, Қолдай берді қалғандары қалыспай…» деп жырға қосқан еді.
Парадокс немесе өмір Енді бір парадокстар бір қарағанда ғана сондай
сияқты болып көрінеді, ал шындығында — ешқандай парадокс емес. Аңыз
бойынша, баяғыда бір философты өлім жазасына кесіпті. Ол түрмеде
отырып, үкімнің жүзеге асуын күтеді. Жексенбі күні түрме басшысы
келіп, оны екі ереже бойынша жазалайтынын жеткізеді: біріншіден,
өлім жазасы келесі аптаның бір күнінде, түс уақытында болады,
екіншіден, жазаны жүзеге асыратын күн тұтқын үшін беймәлім
болмақ.

Философ айтылғандарды талқылай
бастайды. Оны келесі аптаның жексенбісінде жазалаулары мүмкін емес,
себебі, өздері атқандай, жаза келесі апта іске асуы керек, ал егер
оны дүйсенбі мен сенбі арасындағы күндердің бір де біреуінде
жазаламаса, онда өлім күні ол үшін аяқ астынан болмайды. Былай
айтқанда, тұтқын философ сенбі күніне дейін аман қалса, жазаның
орындалуына ертеңгі күн қалады (жексенбі). Олай болса, жаза күні
беймәлім болмай қалады. Ал бұл ережеге қарсы шығады. Яғни, жексенбі
жазаны жүзеге асыратын күн бола алмайды. Онда оны сенбі күні де
жазалай алмайды, себебі егер оны дүйсенбі мен жұманың арасындағы
бір күні өлтірмесе, онда жаза сенбі күні қолданылуы керек (өйткені,
жексенбі тізімнен шығып қалған), осылайша өлім күні тағы да
кенеттен болмай қалады. Енді, ары қарай жылжиық. Тура осы
тұжырымдарға байланысты, жұма да тізімнен шығарылады: жексенбі мен
сенбі бұған дейін шығып қалған, яғни, егер дүйсенбі мен бейсенбінің
арасындағы бір күнде өлім жазасына кеспесе, жұма жазаны қолданатын
беймәлім күн болмай
қалады.

Дәл осылай ол бейсенбіні де,
артынан аптаның барлық күндерін жоққа шығарды. Соңында ережеге
сәйкес, оны келесі аптаның бір де бір күнінде өлім жазасына кесе
алмайды деген шешімге келді. Өз тұжырымына өзі қатты қуанып
отырғанда, сейсенбі күні жендеттер келіп есік қаққанда, қуанышы су
сепкендей басылды. Әрине, түрме басшысының бейшара философ секілді
парадокстарға мән бермейтіні өкінішті-ақ, алайда, мәселе онда емес.
Негізі, үкімі шығып қойған тұтқын аптаның әр күнін логикалық
тұрғыда тізімнен шығара отырып, ақырында аптаның әр күнін өзі үшін
өлім жазасы кесілетін беймәлім күнге айналдырды! Сондықтан да,
парадокстармен абай болған
дұрыс!
-
«ПРОКРУСТ ӘДІСІ» ТАҚЫРЫБЫ ОҚЫТУҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ

<<Прокруст төсегі >> деген тіркесті естіп пе едіңіздер? әңгіме
гректердің аңызына арқау болған прокруст қарақшы жайлы болмақ.
айтпақшы ол далада қаңғырып жүрген қайдағы біреу емес,атақты теңіз
әміршісі посейдонның ұлы. сонымен ,осы прокруст жолаушыларды алдап-арбап өз үйіне кіргізіп,жоғарыда сөз болған төсегіне жатқызып,оларды сол төсектің өлшеміне қарай <<теңестіретін>> болған.
егер төсек ұзын болса, аяқтарын кескен. ал оның төсекке дәл келгендерді не істегені жайлы тарихта ештеме айтылмайды. қалай болғанда да ,ежелгі гректер әділдікті үстем қылып, ақыры прокрустың өзі де өмірімен сол төсекте қоштасқан. бір қызығы,оның осы идеясы аяқ астынан математикада қолданыс тапқан.
<<Прокруст төсегі >> тіркесі баяғыдан-ақ қанатты сөзге айналған және елеулі дүниені құрбандыққа шалуды талап ететін қатаң теңдікті білдіреді. аталған тұрақты тіркестің жағымсыз мағынасына қарамастан, ажыратушы нысандарды теңестіру идеясы математикалық есептерде қолданыс тапқан. қорықпаңыздар ,біз ешкімнің ештеңесін кесіп тастамаймыз –жай ғана ұқсас қағиданы қолданамыз.
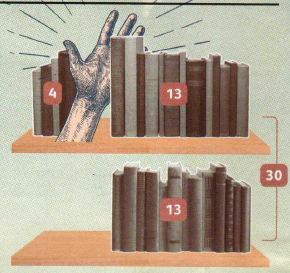
1 есеп . екі сөреде жалпы саны 30 кітап тұр, дегенмен бір сөредегі кітап саны екіншіншісінен 4-ке артық. әр сөреде неше кітап бар ?
әрине, бұл есепті іріктеу арқылы шешуге болады –алаййда ,табылған шешімнің жалғыздығына қатысты сұрақ туындайтыны сөзсіз. сөрелердің біріндегі кітап маны х түрінде белгілеп , ауыспалылық енгізе отырып, теңдеуді шешуге де болады. бірақ ,біріншіден мұны жазып жату ұзақ, екіншіден, біз теңдеу құруды және шығаруды бірден үйренбейміз. ал прокруст әдісі санаудан басқа ешқандай машықты талап етпейді.
сонымен , сөрелердегі кітаптарды теңестіріп көрейік. бізге сөрелердің біріндегі кітап 4-ке артық екені белгілі, ендеше оларды ала тұрайық. яғни ,екіншісіне қоймаймыз , мүлде бөлек алып қоямыз. енді сөрелердегі кітап сандары тең ! дегенмен, олардың жалпы жиынтығы 30 емес, біз 4 өеуін алып тастағандықтан, 26 болып қалды. ендеше , әр сөреде 13 кітап(26:2 ,себебі кітаптар саны тең ). енді 4 кітапты орнына қайтарып ,соңғы жауапты табу қалды;бір сөреде 13 кітап, екіншісінде -17.
есепті шығаруға көмектескен не ? біз прокруст әдісін бейбіт жолмен пайдаланып –сөрелердегі кітап санын теңестіріп, алынған санды екіге бөліп,берілген сұраққа жауап бердік. тағы бір мысалды қарастырайық.
прокруст төсегінің образы –нассим николас талебтің «черный лебедь>> және «антихрупкость>> бестселлерлерінің басты идеяларының бірі.
бұл жасанды шектеулерге тән қорытындылар шығаратын заманауи шешім қабылдау жүйелеріне аллегория

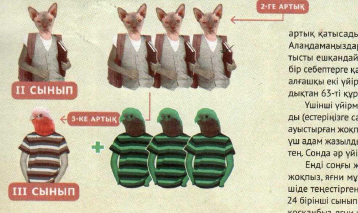
2 есеп . мектепте үш математика үйірмесі бар; бірінші сынып үшін , екінші сынып үшін және үшінші сыныптар үшін .бірінші үйңрмеде екіншісіне қарағанда екі адам артық,ал екіншісінде –үшіншісінен үш адам артық. үйірмеге барлығы 65 оқушы қатысады. әр үйірмеге неше адамнан барады?
сонымен, бірінші үйірмеге екіншісінен екі адам артық қатысады. үйірмеге қатысушылар санын теңестірейік. алаңдамаңыздар,біздер бірінші сыныптың екі оқушысына қатысты ешқандай озбырлық әрекетке бармаймыз! олар белгілі бір себептерге қатысты үйірмеге келмей қалды делік . олай болса, алғашқы екі үйірмедегі балалар саны тең ,әрі олар 2-ге азайғандықтан 63-ті құрайды .
үшінші үйірмеге екіншіісімен салыстырғанда үш адам кем барады (естерңізге сала кетейік ,біз екінші үйірмедегі балалар санын ауыстырған жоқпыз.) теңестіреміз ;айталық, үшінші үйірмеге тағы үш адам жазылды. сонда барлық үш үйірмедегі адам саны 66-ға тең.сонда әр үйірмеге 22 адамнан қатысады деген сөз!
енді соңғы жауапаты алу қалды.біз екінші үйірмеге тиіскен жоқпыз, яғни мұнда әу бастан 22 адам болды деген сөз. біріншіде теңестіргенге дейін екі оқушы артық болатын,яғни онда 24 бірінші сынып оқушысы бар. ең соңғы үшіншіге біз үш адамды қосқанбыз,яғни шын мәнінде онда 19 үшінші сынып оқушысы бар . алақай!
нысан үштен де көп болған жағдайда есептер дәл осыған ұқсас жолдармен шешіледі. Дегенмен, біз басқа жағдайды қарастырып көрейік.әңгіме бас пен аяқтарға қатысты есеп жайлы болмақ. жо-жоқ,бұл жерде прокрустың қатыс жоқ! жоғарыда есептер секілді, бірде бір бас , бірде бір аяқ зардап шекпейді!.әйтседе .....қысқасы ,іске кірісейік.
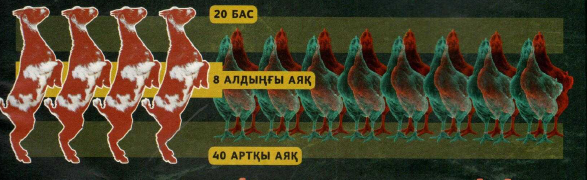
3 есеп .аулада тауықтар мен ешкілер жүр.арман ауладан 20 бас пен 48 аяқ санады(ол өзінің басы мен аяғын есепке алған жоқ). аулада неше тауық және неше ешкі жүр?
бұл жерде мәселе неде? мәселе тауықтар мен ешкілердің аяқ санының тең еместігінде.егер әңгіме тек тауықтар жайлы болса ,біз аяқ санын тең бөліп-керекті мөлшерді алар едік(айтпақшы,ондайда бастың саны артық ақпарат болар еді).ешкілердің жағдайында төртке бөлеміз.ал , біздің жағдайда ауладағылардың біразының аяғы екеуден,қалғаныкі төрттен. не істеу керек ?
олай болса, теңестірейік!ешкілердің аяқтары төрттен емес ,екіден болсын.әу бастан ешкімге зиянымызды тигізбейміз деп сөз бергендіктен, ешкілерартқы аяқтарымен тік тұрып,алдыңғылары әуеде қалықтап жүр деп елестетейік. ендеше ,аулада 20 жануар (бас санына қарай )жайылып жүрген болса,мұнда 40 аяқ бар –әр жануарға екі аяқтан .дегенмен, арман 48 аяқ санаған болатын ,яғни әлі 8 аяқ есепке алынған жоқ.айтпақшы ,ешкілеріміз артқы аяқтарымен тік тұрғандықтан ,алдыңғы аяқтары да есепке алынбай қалды емес пе ?!олай ,болса солардың саны сегіз деген сөз.әр ешкінің алдыңғы екі болатыны есепті,барлығы 8;2=4 ешкі .қорытынды аулада 4 ешкі және 16 тауық жүр.
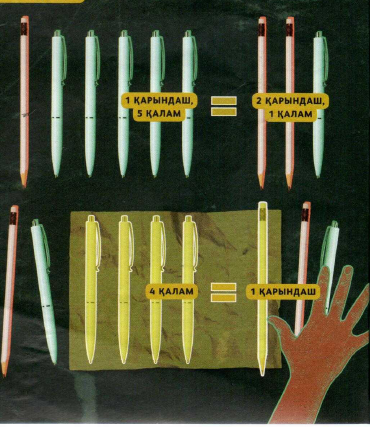
4 есеп .бір қалам және екі қарындаш қанша тұрса , бес қалам және біір қарындаш сонша тұрады.қарындаш қаламнан неше есе қымбат?
бірден басын ашып алайық,бұл жерде барлық қалам бір бағада сатылады ,қарындаштар да дәл солай деген сөз.әрине,бұл есепті екі ауыспалыны енгізу арқылы шешуге болады.әйтсе де,қысқа әрі әдемі шешім тұрғанда,зеңбірекпен торғай атудың қажеті қанша ?айталық,бір жинақта бес қалам және қарындаштар жатыр ,екіншісінде –екі қарындаш және қалам.кеңсе тауарларының қалған жиынтығы бұрынғыша бірдей тұрады ,солай емес па ? әрі бірінші жиынтықта төрт қалам ,ал екіншісінде –бір қарындаш қалады(солай, бір ғана заттан тұратын жиынтық.....негізі,жиынтық пародоксы мен тақ логика жайлы біз алдағы нөмірлердің бірінде білетін боламыз ).
сонымен,қарындаш қаламнан төрт есе қымбат тұрады.
есепті шешуге не көмектесті?нысандарды теңестіре отырып ,артығын алып тастау мүмкіндігі. прокрусттың әрекеті арқылы туындаған дәл осы идеяны бұдан да күрделірек жағдайларда қолдануға болад.
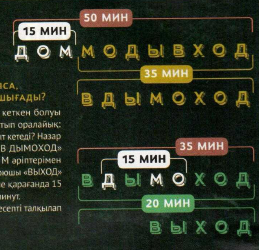
5 есеп.оюшы әріптері бар тақта жасады.бірдей әріптерді ол бірдей уақыт ішінде ояды.әртүрлілерін әртүрлі уақытта ойса керек .ол орыс тіліндегі –«дом моды»және «вход» сөздері жазылған тақтаға 50 мин жұмсады,ал «в дымоход»тақтасын 35 мин аяқтады.олай болса ,оюшы «вход» деген тақтаны қанша уақытта жасап шығады?
бұл жерде теңестірудің көп көмегі тие қоймас,сондықтан артық әріптерді алып тастаған дұрыс болар .бірінші жағдайда д,о,м,м,о,д,ы,в,х,о,д әріптерінен жасады.екіншісінде –в,д,ы,м,о,х,о,д.екінші тізімдегі әріптерді біріншісінен сызып тастау арқылы біз;д,о және м деген әріптерді аламыз.ендеше,бірінші жағдайда оюшы 15 минутты көбірек жұмсаса ,сол 15 минут дәл осы біз тапқан «артық» әріптер –д,о және м –ға кеткен болуы тиіс.енді сұрағымызға қайтып оралайық;»выход»сөзіне қанша уақыт кетеді?назар аударыңыздар; бұл сөз «в дымоход» сөзіне дәл осы д,о және м әріптерімен ерекшеленеді.олай болса,оюшы «выход» сөзіне қарағанда 15 мин аз жұмсады,яғни 20 мин.
қорыта келе мынадай есепті талқылап көрейік.
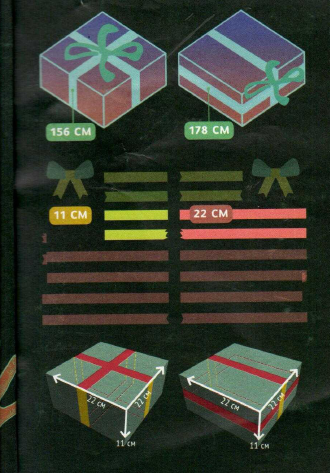
6 есеп.торт шаршы негізді қорапқа оралған.қораптың биіктігі осы қораптың қабырғаларынан екі есе кіші .ұзындығы 156 см баудың көмегімен қорапты байлап,үстінен бантик жасауға болады(сол жақтағы суреттегі секілді).ал оны дәл осындай бантикпен бүйірінен байлау үшін (оң жақтағы суреттегі секілді ) ұзындығы 178 см бау керек.қораптардың өлшемін табыңыздар.
тағы да теңестіру жағын қоя тұрып,аталған тәсілдердің ортақ тұсын қарастырайық.бірінші жағдайда баудың қорапты бүйір тұсынан буындайтын төрт бөлігі (қысқа ),астынан және үстінен (ұзын )-төртеу ,сондай –ақ бантик бар екені түсінікті.екінші жағдайда баудың екі қысқа бөлігі (оң және сол жағында бір -бірден ) ,алты ұзын бөлік және дәл соендай бантик бар .әрі екінші тәсіл біріншісінен 22 смге ұзынырақ.және егер біз ортағын алып тастасақ,айырмашылық сол қалпы қалады. бұл тәсілдерлің ортақ неде? екі қысқа бөлігі ұзынынан 11 см-ге кіші.енді қысқа бөлік ұзын бөліктің жартысын құрайтынын, яғни өз ұзындыққа қысқа екенін еске алу қалды.олай болса,қысқа бөліктің ұзындығы-11 см ,ұзын бөліктікі-22 см.қораптың өлшемі;11х22х22
сонымен,тіпті,қатыгезқарақшылардың өзі жан түршігерлік әдістері арқылы ұрпағына пайдалы қызмет қалдыруы мүмкін екен.бастысы,жауыздық идеясын ысырып тастап,оны оңтайлы пайдалана білудің саласын табу жеткілікті.
-
«ТИІМДІ КӨБЕЙТУ ТӘСІЛДЕРІ» ТАҚЫРЫБЫН ОҚЫТУҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ
Қазіргі кезде мектепке, өндіріске электронды есептеу машиналары(ЭЕМ) кеңінен ене бастады. Микрокалькулатор оқушылардың кәдімгі оқу құралына айналды. Бұл өте қуанышты жағдай. Өкінішке орай, бұның есесіне оқушылардың есептеу бейімділігі төмендеуі байқалады. Бұған мысалы жоғарғы сынып оқушылары өздері 7-сыныпта өткен қысқаша көбейту формулаларын есептеу жұмысын жеңілдетуге қолдана білмеуі. Айталық, 47*53 көбейтіндісін табу керек делік. Бұл есептеуді
(а – в)(а + в) = а2 – в2
формуласын пайдаланып жеңіл түрге келтіруге болады:
47*53 =(50-3)(50+3)=502-32 =2500-9=2491
Енді ойша есептеудің кейбір түрлерін қарастырайық.
-
5-пен аяқталатын санның квадратын табу:
(а+в)2=а2+2ав+в2 осы формуладағы в=5 деп алсақ, (а+5)2=а2+10а+25=а(а+10)+25. Егер а ондық саны болса, а+10 оған тетелес келетін ондық.
Мысалы: а=60 болса,60+10=70 болады.
Сондықтан 5-пен аяқталатын санның квадратын табу үшін, ондық
санын көрсететін натурал саннан үлкен тетелес келетін натурал санға
көбейтіп оған 5- тің квадраты 25 санын тіркеп жазу керек.
Мысалы: 352 = 1225,өйткені 3*4= 12, 5*5= 25 кейін тіркеп жазсақ 1225шығады.
Соңғы 5 цифрын квадраттап,оның алдына келесі разрядтағы санды өзінен 1-ге артық санмен көбейтіп, 5-тің квадраты 25 санының алдына жазады.
Мысалы: 252=625 a) 52=25 b) 2*(2+1)=6
3052=93025 a) 52=25 b) 30*(30+1)=930
II. 50-ге жақын санның квадратын табу.
х =50+а болсын х2 = (50+а)2=2500+100а+а2 =100(25+а)+а2.
х2=100(25+а )+ а2=100(25+х-50)+а2= 100(х-25)+а2
Сондықтан, 50-ге жақын санның квадратын табу үшін, сол саннан 25- ті алып, оған сол санның 50 – мен айырмасының квадратын тіркеп жазу керек.
Мысалы: 572 = 3249 өйткені берілген санмен 25-тің айырмасы 57-25=32
берілген санмен 50- дің айырмасы 57-50=7, бұл айырманың квадраты 72=49.
Енді 32-ге 49 санын тіркеп жазсақ 3249 шығады. Сол сияқты, 582=3364,
өйткені 58- 25= 33, 58 – 50=8, 82= 64.
III. 100-ге жақын санның квадратын табу.
100- ге жақын санның квадратын табу үшін, әрбір санды 100- ден азайтамыз, 972= 97*97, айтып өткендей әрбір санды 100-ден азайтамын;100-97=3. Содан кейін азайтындының мәнін бір-біріне көбейтемін де және бір-біріне қосамын (3*3=9; 3+3=6), осыдан кейін қосындының мәнін 100-ден азайтамын(100-6=94).
Енді көбейтіндінің мәні бір таңбалы 9саны болғандықтан алдына 0-ді қоямын, ал егерде көбейтіндінің мәні екі таңбалы болса 0-ді қоймаймын, сол санның өзін тіркеп жазамын, егер үш таңбалы сан болса онда жүздігін айырманың мәніне қосамын да оның алдына 94 –ті тіркеп жазамын. Ең соңында 972=9409 болады.
1) Әрбір санымды 100-ден азайтамын.
2) Шыққан мәндерін көбейтемін және қосамын.
3) Қосқандағы мәнін 100-ден азайтамын.
4) Ең соңында бәрін тіркеп жазамын.
100-ге жақын санның квадратын табу (2-ші тәсілі)
100- ге жақын санның көбейтіндісін табу да 2-ші тәсілі өте қарапайым және тез орындалады , бұл жерде көп ойланудың қатысы жоқ.
Мысалы:
942
![]()
![]()
![]()
![]()
![]()
![]() 92 9*4*2
42
92 9*4*2
42
81 72 16
817216
8 1+7 2+1 6
8 8 3 6 Мына жерде соңғы санның алдынан
екі-екіден бөлемін де бір-біріне қосамын,
содан кейін бәрін тіркеп жазамын.
100- ге жақын санның квадратын табу (3-ші тәсілі)
а=100-х, в=100-у. Бұл жердегі х-пен у, а және в сандарының 100 санымен
айырмалар екендігі көрініп тұр. Енді екі санның көбейтіндісін табамыз.
а*b=(100-x)(100-y)=10000-100(x+y)2+xy=100-(a-y)+xy=100(b-x)+xy яғни а*b=100*(a-y)+xy немесе а*в=100(b-x)+xy сондықтан, 100-ге жақын екі
санның көбейтіндісін табу үшін бірінші көбейткіштен екінші көбейткіштің айырмасын алып немесе екінші көбейткіштен бірінші көбейткіштің айырмасын алып оған айырмалардың көбейтіндісін тіркеп жазу керек.
Мысалға: 952=95*95 ; 100-95=5, содан 95-5=90 болады. Ал енді айырмаың квадраты 5*5=25 ендеше 90-ға 25-ті тіркеп жазсақ 9025 шығады.
IV. 100-ден артық санның квадратын табу.
Егерде санымыз 100- ден артық болса а=100+х, в=100+у, онда көбейтінді
ав=(100+х)(100+у)= 10000+100(х+у)+ху=100(100+х+у)+ху=100(а+у)+ху
=100(в+х)+ху болады.
Яғни, ав=100(а+у)+ху немесе ав=100(в+х)+ху
Мысалы: 103*103=10609. Себебі: (103-100=3;103-100=3) 103+3=106 осыдан кейін айырманың мәндерін көбейтемін 3*3=9, 106 санына 09 санын тіркеп жазсақ 10609 болады.(0-ді қойған себебім;егерде азайтынды мәні бір таңбалы болса ол санның алдына 0-ді қоямын, ал егер екі таңбалы болса қоймаймын).
100-ден артық санның квадратын табу (2-ші тәсілі)
100-ден артық санның квадратын табу да 2-нші тәсілі қарапайым және оңай. Бұл жерде логикалық түрде тез есептеуге болады.а=х-100, в=у-100. Бұл жердегі х-пен у, а және в сандарының 100 саныменайырмалар екендігі көрініп тұр. Енді екі санның көбейтіндісін табамыз. а*b=(100-x)(100-y)=10000-100(x+y)2+xy=100-(a-y)+xy=100(b-x)+xy яғни а*b=100*(a-y)+xy немесе а*в= =100(b-x)+xy сондықтан.
Мысалға: 1042=104*104 ; 104-100=4 ,
4*4=16; 4+4=8 Кейін:10816 болады.
Көбейтіндінің мәнін соңғы сан қылдырып тіркеп қоямын , ал қосындының мәнін соңғы санның алдына қоямын (егерде қосындының мәні 0-ден 9-ға дейін болса, қосындының мәнінің алдына 0 санын қоямыз;егер 9-дан асса қоймаймыз) және әрдайым олардың алдына 1 санын қоямын. Ендеше бәрін тіркеп жазсақ 10816 болады.
Саусақпен санау. Саусақ арқылы санның квадратын табу. Көбейтудің әр түрлі әдістері.
Саусақтарды бүгіп санау ерте заманда кең қолданылып келді.Адамның саусақтары мен олардың буындары,сондай-ақ саусақтарын бүгу және жазу,қолдарын бүгу мен жазу олардың ондаған және жүздеген мыңға дейін санай алуына ғана емес,сол сияқты кейбір арифметикалық амалдарды орындауына да мүмкіндік берді .Айталық ,6-ны 7-ге көбейту керек болсын.Сол қолымыздың жұдырығын жазбастан,бір-бірлеп саусағымызды жаза отырып, 6-ға дейін санаймыз.Ал оң қолымыздың саусақтарымен дәл соны қайталап, 7-ге дейін санаймыз.Оң қолдын жазылған екі саусағын сол қолдың жазылған бір саусағынан үстіне саламыз.Жазылған саусақ небары 3–еу болады,бұл-3 ондық, яғни 30 болады.Қалған төртеуі (сол қолдың бүгілулі тұрған саусақтары) 3-ке (оң қолдын бүгілулі саусақтарына) көбейтіледі,сонда 12 шығады.
Сөйтіп , 30+12=42
Осылайша : 6*8=(1+3)*10+4*2=48
6*9=(1+4)*10+4*1=54
Мәселен ,13-ті 14-ке көбейту былайша орындалатын еді.
1) 10*10=100 екені белгілі. Бұдан кейін:
2) бір қолдың 3 саусағын ,екінші қолдың 4 саусағын бүгеді.
3) 3+4=7 ,бұл-ондықтар,яғни 7*10=70
4) 3*4=12,бұл бірліктер.Сонымен:
5) 13*14=10*10+7*10+3*4=182.
![]()
![]()
![]()


![]()



1) 13*14=(3+4)*10+3*4+102 =70+12+100=182 Сол сияқты:
2) 53*54=(3+4)*50+3*4+502=350+12+2500=2862
3) 63*67=(3+7)*60+3*7+602 =600+21+3600=4221

![]()
![]()
![]()
![]()
![]()
![]()

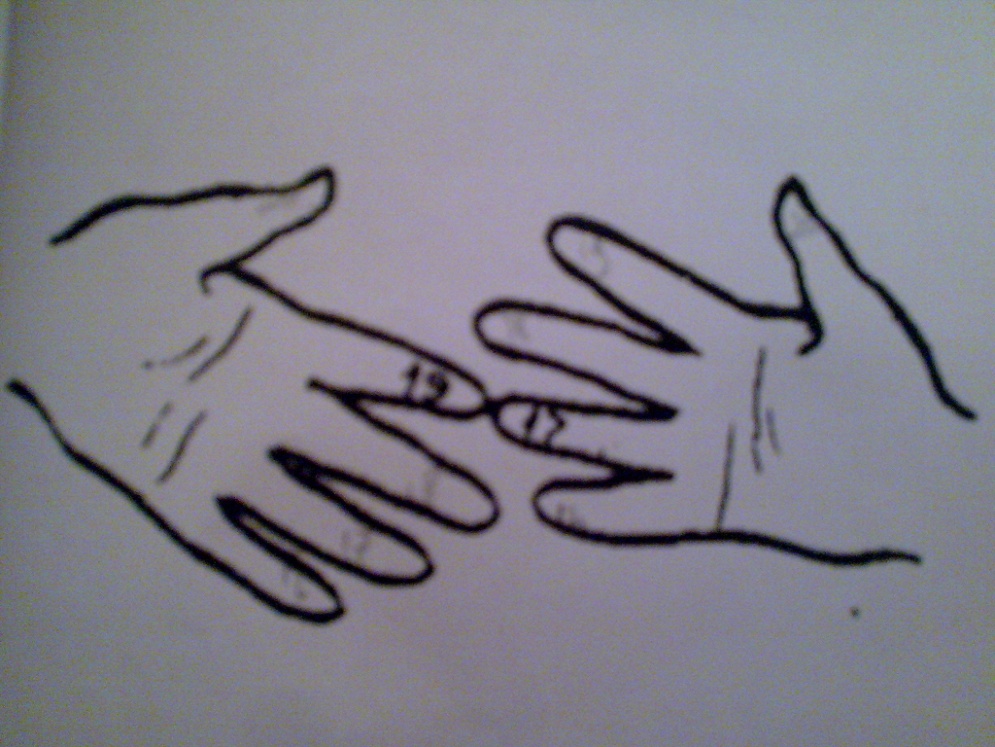
1) 19*17=(4+2)*20+1*3+10*20=120+3+200=323
Сол сияқты:
2) 79*77=(4+2)*80+1*3+70*80=480+3+5600=6083
Дәл осындай әдіспен саусақ арқылы кез-келген санның квадратын табуға болады.
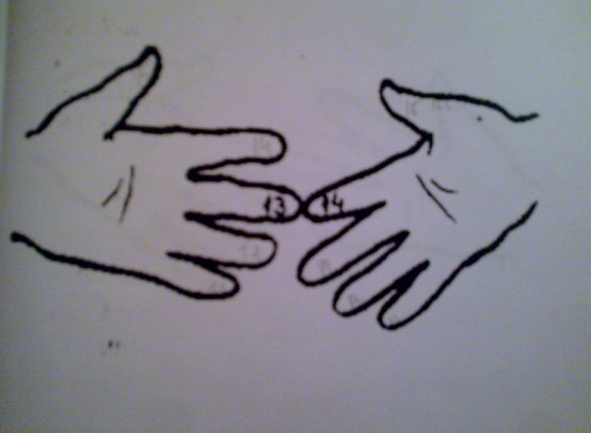
Мәселен ,14-ті 14-ке көбейту былайша орындалатын еді.
1) 10*10=100 екені белгілі. Бұдан кейін:
2) бір қолдың 4 саусағын ,екінші қолдың 4 саусағын бүгеді.
3) 4+4=8 ,бұл-ондықтар,яғни 8*10=80
4) 4*4=16,бұл бірліктер.Сонымен:
5) 14*14=10*10+8*10+4*4=100+80+16=196.
Сол сияқты мысалдар:
1) 13*13=10*10+6*10+3*3=100+60+9=169.
2) 11*11=10*10+2*10+1*1=100+20+1=121
3) 12*12=10*10+4*10+2*2=100+40+4=144
4) 54*54=(4+4)*50+4*4+502=400+16+2500=2916
5) 43*43=(3+3)*40+3*3+402=240+9+1600=1849
Осы сияқты дәлелдеулерге көз жеткізгеннен кейін төмендегідей мысалдарды шығаруға болады.
I
1. 752=5625, өйткені 7*8=56
2. 852=7221, өйткені 8*9=72
3. 152= 225, өйткені 1*2=2
II
1. 492=2401 өйткені 49 -25=24, 50 - 49=1, 12=1
2. 622=3844 өйткені 62- 25=37, 62- 50=12,122=144
III
1. 962=9216
2. 972=9419
3. 982=9604
4. 1082=11664
5. 1092=11881
1. “n0m” (n нөл m) түріндегі үш орынды санның квадратын ойша есептеп
табу керек. Мұндағы n=1,2,…9, m=1,2,…9
n0m2= (n· 100+m)2=n2·10000+2· n· m· 100+m2=(n2·100+2·n·m) ·100+m2
Мысалы: 1. 2032=(200+3)2=(400+12)·100+9=41209
Анықтама 1.1. “n0m” түріндегі санды квадраттағанда, соңғы екі
цифры квадратталатын санның соңғы цифрының квадраты, ал оның
алдындағы екі цифр квадратталатын санның бірінші және соңғы
цифрларының екі еселенген көбейтіндісі және оның алдына бірінші цифрдың квадраты жазылады.
2. 6092=(600+9)2=(3600+108)·100+81=370881.
Жалпы қорыта келсек, мынандай ереже аламыз:
Анықтама 1.2. Егер санның бірінші және соңғы цифрының екі
еселенген көбейтіндісі үш орынды сан болса, онда оның соңғы екі цифрын
қалдырып, жүздік цифрын бірінші цифрдың квадратына қосамыз. 92=81,
2·6·9=108 қорытынды бойынша 08-ді жазып, 1-ді 62=36-ға қосамыз 36+1=37
Осы үрдіс “n0m” түріндегі сандардың квадраттарын табу үшін жалғаса береді.
1-тәсіл: 1) Әрбір санымды 100-ден азайтамын.
2) Шыққан мәндерін көбейтемін және қосамын.
3) Қосқандағы мәнін 100-ден азайтамын.
4) Ең соңында бәрін тіркеп жазамын.
2-тәсіл:
![]()
![]()
![]() 942
942
![]()
![]()
![]() 92 9*4*2
42
92 9*4*2
42
81 72 16
817216 Мына жерде соңғы санның алдынан
8 1+7 2+1 6 екі-екіден бөлемін де бір-біріне қосамын,
8 8 3 6 содан кейін бәрін тіркеп жазамын.
3-тәсіл:
Мысалға: 952=95*95 ; 100-95=5,100-95=5 содан 95-5=90 болады. Ал енді айырмалардың көбейтіндісі 5*5=25 ендеше 90-ға 25-ті тіркеп жазсақ 9025 шығады.
IV
1-тәсіл:
Мысалы: 103*103=10609. (103-100=3) Себебі, 103+3=106 немесе керісінше қалдықтар көбейтіндісі 3*3=9, 106 санына 09 санын тіркеп жазсақ 10609 болады.
2-тәсіл:
Мысалға: 1042=104*104 ; 104-100=4 ,104-100=4. 4*4=16; 4+4=8
(Егерде қосындының мәні 0-ден 9-ға дейін болса, қосындының мәнінің алдына 0 санын қоямын;егер 9-дан асса қоймаймыз) және әрдайым олардың алдына 1 санын қоямын. Ендеше бәрін тіркеп жазсақ 10816 болады.
V
Мәселен ,13-ті 14-ке көбейту былайша орындалатын еді.
1)10*10=100 екені белгілі. Бұдан кейін:
2)бір қолдың 3 саусағын ,екінші қолдың 4 саусағын бүгеді.
3)3+4=7 ,бұл-ондықтар,яғни 7*10=70
4)3*4=12,бұл бірліктер. Сонымен:
5)13*14=10*10+7*10+3*4=182.
Мәселен ,14-ті 14-ке көбейту былайша орындалатын еді.
1) 10*10=100 екені белгілі. Бұдан кейін:
2) бір қолдың 4 саусағын ,екінші қолдың 4 саусағын бүгеді.
3) 4+4=8 ,бұл-ондықтар,яғни 8*10=80
4) 4*4=16,бұл бірліктер.Сонымен:
5) 14*14=10*10+8*10+4*4=100+80+16=196.
1) 13*13=10*10+6*10+3*3=100+60+9=169.
Ауызша есептеулермен жүйелі түрде айналысу оқушылардың математикаға қызығушылығын артырады, уақытты үнемдеуге көмектеседі, математикалық есептеу мәдениетін жоғарлатады.
-
«САНДАРДЫҢ БӨЛІНГІШТІГІ ҚАСИЕТТЕРІНІҢ ПРАКТИКАЛЫҚ МАҢЫЗДЫЛЫҒЫ» ТАҚЫРЫБЫН ОҚЫТУҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ
11-ге бөлінгіштік
Алгебра бөлу амалын орындамай-ақ, берілген санның қай бөлгішке бөлінетінін, қайсысына бөлінбейтінін алдын ала анықтауға болатын белгілерді табуды едәуір жеңілдетеді. 2-ге, 3-ке, 4-ке, 5-ке, 6-ға, 8-ге, 9-ға және 10-ға бөлінгіштік белгілері баршамызға мәлім. 11-ге бөлінгіштік белгісін қорытып шығарайық; ол едәуір қарапайым әрі қолайлы.
Көп таңбалы N санының бірлік цифры а, ондық цифры b , жүздік цифры c, мыңдық цифры d болсын т.с.с., яғни
N=a+10b+100c+1000d+…+=a+10(b+10c+100d+…+),
мұндағы көп нүкте келесі разрядтардың қосындыларын білдіреді. N санынан 11- ге еселік болатын 11(b+10c+100d+…) санын шегереміз. Сонда шыққан айырма мынаған тең болады:
a-b-10(c+10d+…),
бұл санды 11-ге бөлгенде қалатын қалдық N санынан қалатын қалдықтай болатынын байқау оңай. Осы айырмаға 11-ге еселік болатын 11(c+10d+…) санын қосып, мынадай сан шығарып аламыз:
a-b+с+10(d+…),
мұны да 11-ге бөлгенде қалатын қалдық N санынан қалатын қалдықтай болады. Бұдан 11-ге еселік болатын 11(d+…) санын шегереміз, т.с.с. Осының нәтижесінде мынадай сан шығады:
a-b+с-d+...=(a+c+…)-(b+d+…),
мұны да 11-ге бөлгенде қалатын қалдық N санынан қалатын қалдықтай болады.
Осыдан 11-ге бөлінгіштіктің мынадай белгісі шығады: барлық тақ орындардағы цифрлардың қосындысынан барлық жұп орындардағы цифрлардың қосындысын шегеру керек: егер осы айырмадан 0 немесе 11-ге еселік болатын сан ( оң немесе теріс) шықса, онда сыналатын санымыз 11-ге еселік болады; олай болмаған жағдайда әлгі сан 11-ге қалдықсыз бөлінбейтін болады.
Мысалы, 87 635 064 санын сынайық:
8+6+5+6=25,
7+3+0+4=14,
25-14=11.
Олай болса, бұл сан 11-ге бөлінеді.
11-ге бөлінгіштіктің басқа да бір белгісі бар, бұл өте ұзақ созылып жазылмаған сандар үшін қолайлы . Бұл белгі бойынша сыналатын сан оңнан солға қарай екі-екі цифрдан топталып, ажыратылады да, бұл топтарды өзара қосады. Егер осы шыққан қосынды 11-ге қалдықсыз бөлінетін болса, онда сыналушы сан 11-ге еселік болады, олай болмаған жағдайда –ол 11-ге еселік болады, олай болмаған жағдайда -11-ге еселік болмайды. Мысалы, 528 санын сынау керек болсын дейік. Санды топ-топқа ажыратамыз да (5/28), екі топты өзара қосамыз:
5+28=33.
33 саны 11-ге қалдықсыз бөлінетін болғандықтан, 528 саны да 11-ге еселік болады:
528:11=48.
Осы бөлінгіштік қасиетін дәлелдейік. Көп таңбалы N санын топтарға ажыратайық. Сонда екі таңбалы (немесе бір таңбалы) сандар шығады, оларды a,b,c т.с.с. арқылы (оңнан солға қарай) белгілейміз, сонда N санын мына түрде жазуға болады:
N=a+100b+10 000c +…=a+100(b+100c+…).
N-нен он бірге еселік болатын 99(b+100c+….) санын шегереміз. Бұдан шыққан
a+(b+100c+…)=a+b+100(c+…)
санын 11- ге бөлгенде шығатын қалдық N санынан қалатын қалдықтай болады. Осы соңғы саннан 11-ге еселік болатын 99(c+…) санын шегереміз т.с.с. Осының нәтижесінде біз N санын 11-ге бөлгенде қалатын қалдық
a+b+c+…
санынан қалатын қалдықтай болатынын табамыз.
Автомашинаның нөмірі
ЕСЕП
Қала көшелерімен серуендеп келе жатқан үш матемаик-студент бір автомашина жүргізушісінің көшеде жүру ережесін өрескел бұзғанын байқап қалады. Машинаның нөмірі (төрт таңбалы сан) студенттердің бірінің де есінде қалмаған, бірақ та олар математик болғандықтан, әрқайсысы осы төрт таңбалы санның кейбір ерекшеліктерін аңғарып қалған екен. Студенттердің біреуі санның алғашқы екі цифрының бірдей болғанын есіне түсірген. Екінші студент соңғы екі цифрдың да өзара бірдей болғанын еске алған. Ең соңында, үшінші студент осы барлық төрт таңбалы санның дәл квадрат болғанын айтқан. Осы мәліметтер бойынша машинаның нөмірін білуге бола ма?
Егер N санының цифрлар саны тақ болса, онда соңғы (сол жақ шеткі) топ бір таңбалы болады. Бұған қоса, 03 түріндегі топты бір таңбалы 3 саны деп қарастыру керек.
ШЕШУІ
Ізделген санның бірінші (және екінші цифрын а арқылы, ал үшінші (және төртінші) цифрын b арқылы белгілейік. Сонда төрт таңбалы сан мынаған тең болады:
1000a+100a+10b+b=1100a+11b=11(100a+b).
Бұл сан 11-ге бөлінеді, сол себепті (дәл квадрат болғандықтан) , ол 112 – на да бөлінеді. Басқаша айтқанда , 100a+b саны 11-ге бөлінеді. 11- ге бөлінгіштіктің жоғарыда айтылған екі белгісінің кез келгенін қолданып, a+b санының да 11-ге бөлінетіндігін анықтаймыз. Бұл
a+b=11 болады деген сөз, себебі a, b цифрының әрқайсысы оннан кіші.
Дәл квадрат болып табылатын санның соңғы b цифры тек мынадай мәндерді ғана қабылдай алады:
0, 1, 4, 5, 6, 9.
Сондықтан 11-b санына тең a цифры үшін мынадай мүмкін мәндерді табамыз:
11, 10, 7, 6, 5, 2.
Алғашқы екі мән жарамсыз, сонымен, мына мүмкіндіктер қалады:
b=4,a=7;
b=5, a=6;
b=6, a=5;
b=9; a=2;
Біз автомашинаның нөмірін мына төрт санның арасынан іздеу қажет екенін байқаймыз:
7744, 6655, 5566, 2299.
Бұл сандардың соңғы
үшеуі дәл квадраттар бола алмайды: 6655 саны 5-ке бөлінеді, бірақ
25-ке бөлінбейді; 5566 саны 2-ге бөлінеді, бірақ 4-ке
бөлінбейді;  саны да квадрат бола алмайды.
Сондықтан бір ғана
саны да квадрат бола алмайды.
Сондықтан бір ғана  саны қалады; бұл сан есептің
шешімі болып табылады.
саны қалады; бұл сан есептің
шешімі болып табылады.
19-ға бөлінгіштік
19-ға бөлінгіштіктің мына белгісін негіздеңдер.
Санның ондықтарының саны мен оның екі еселенген бірліктерінің қосындысы 19-ға еселік болғанда, тек сонда ғана ол сан 19-ға қалдықсыз бөлінеді.
ШЕШУІ
Кез келген N санын мына түрде өрнектеп көрсетуге болады:
N=10x+y,
мұнда х-ондықтардың саны (ондық разрядтағы цифр емес, сандағы барлық бүтін ондықтардың жалпы саны), у-бірліктер цифры.

саны 19-ға еселік
болғанда, тек сонда ғана N санының 19-ға еселік болатынын
көрсетуіміз керек. Бұл үшін  -ты 10-ға көбейткміз де, осы
көбейтіндіні N –ді шегереміз; сонда
шығатыны
-ты 10-ға көбейткміз де, осы
көбейтіндіні N –ді шегереміз; сонда
шығатыны

Бұдан,
егер  саны 19-ға еселік болса,
онда
саны 19-ға еселік болса,
онда

саны 19-ға қалдықсыз бөлінеді: және, керісінше, егер N саны 19-ға қалдықсыз бөлінетін болса, онда

саны 19-ға еселік
болады, сонда  саны да 19-ға қалдықсыз
бөлінеді.
саны да 19-ға қалдықсыз
бөлінеді.
Мысалы, 47 045 881 саны 19-ға бөліне ме, жоқ па соны анықтау керек болсын. Өзімізге мәлім бөлінгіштік белгісін ретімен қолданайық:

19 саны 19-ға қалдықсыз бөлінетіндіктен, 57, 475, 4 712, 47 063, 470 459, 4 704 590, 47 045 881 сандары да 19-ға еселік болады.
Сонымен, біздің санымыз 19-ға бөлінеді.
Софья Жерменнің теоремасы
Белгілі француз математигі Софья Жермен ұсынған мынадай бір есепті алайық:
 түріндегі әрбір
санның құрама сан болатынын дәлелдеңдер ( а саны 1-ге тең емес)
.
түріндегі әрбір
санның құрама сан болатынын дәлелдеңдер ( а саны 1-ге тең емес)
.
ШЕШУІ
Дәлелдеу мына түрлендірулерден шығады:

 санын оның өзіне
және бірге тең емес екі көбейткіштің көбейтіндісі түрінде көрсетуге
болатынына, басқаша айтқанда, ол құрама сан екеніне көз
жеткіздік.
санын оның өзіне
және бірге тең емес екі көбейткіштің көбейтіндісі түрінде көрсетуге
болатынына, басқаша айтқанда, ол құрама сан екеніне көз
жеткіздік.
Құрама сандар
Жай сандар деп аталатын сандар, яғни бір мен өзінен басқа ешбір бүтін сандарға қалдықсыз бөлінбейтін, бірден үлкен бүтін сандар шексіз көп.
Бұл сандардың қатары 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, .... сандарымен басталып, олардың қатары шексіз жалғаса береді. Бұлар құрама сандардың арасына сыналанып кіріп, натурал сандар қатарын құрама сандар тізбектеріне бөледі. Бұл тізбектердің ұзындығы қандай болады? Мысалы мыңдаған құрама сандар бірде-бір жай санмен жігін ажыратпай, қатарынан тізіліп кездесе ме?
Шындыққа жанаспайтындай болып көрінгенмен жай сандар арасындағы құрама сандар тізбектері түрліше бола береді. Олар мыңдаған, миллиондаған, триллиондаған т.с.с. құрама сандардан түзілуі мүмкін.
Қолайлы болу үшін
шартты п!
Символын пайдаланамыз, бұл
символ 1-ден бастап п-ге дейін (n-ді қоса алғанға
дейінгі) барлық сандардың көбейтінділерін білдіреді.
Мысалы,  Біз енді мына
қатардың
Біз енді мына
қатардың
..... Мұның себебі
мынада: егер  болса,
онда
болса,
онда



 …….
…….

өрнегіне дейін тізбектелген n құрама саннан тұратынын дәлелдейік.
Бұл сандар натурал қатарда бірінен соң бірі тікелей келіп отырады, себебі әрбір санның өзінің алдындағы саннан 1-уі артық. Бұлардың барлығының құрама сан екенін дәлелдеу ғана қалды.
Бірінші сан

жұп, себебі оның екі қосылғышында да 2 көбейткіші бар, 2-ден үлкен кез келген жұп сан-құрама сан.

әрқайсысы 3-ке еселік болатын екі қосылғыштан тұрады. Олай болса, бұл да құрама сан.
Үшінші сан

4-ке қалдықсыз бөлінеді, себебі ол 4-ке еселік болатын қосылғыштардан тұрады.
Осыларға ұқсас мына санның

5-ке еселік болатынын анықтаймыз т.с.с. Басқаша айтқанда , біз мысалға алған қатардың әрбір санында 1-ден және оның өзінен басқа көбейткіш бар; олай болса, құрама сан болады.
Егер сенің, мысалы, тізбектес бес құрама сан жазғың келсе, жоғарыдағы қатарда n-нің орнына 5 санын қойсаң жеткілікті. Сонда мынадай қатар шығады:
722, 723, 724, 725, 726.
Бірақ бұл тізбектес құрама бес саннан тұратын жалғыз ғана қатар емес. Басқа қатарлар да бар. Мысалы:
62, 63, 64, 65, 66.
Немесе бұдан да кіші сандардың мынадай қатары:
24, 25, 26, 27, 28.
Енді мынадай есепті шығарып көрейік:
Тізбектес құрама он сан жазыңдар.
ШЕШУІ
Жоғарыда айтылғанның негізінде ізделген он санның біріншісі ретінде мына санды алуға болатынын анықтаймыз:
Бізге белгілі ең үлкен жай сан
Жай сандардың мейлінше көп болатынына көзіміз жеткені бір мәселе болса, ал қандай сандардың жай сандар болып табылатынын білу екінші мәселе. Натурал сан қаншалықты үлкен болған сайын, оның жай сан болатын болмайтынын анықтау үшін соншалықты көп есептеулер орындауға тура келеді. Қазіргі кезде белгілі ең үлкен жай сан мынау:
 .
.
Бұл санда жеті жүзге жуық ондық бар. Осы санның жай сан болатындығын анықтаған есептеулер осы заманғы есептеуіш машиналармен жүргізілді (І,ІІ тарауларды қара) .
Жауапты есеп-қисап
Есептеу практикасында алгебраның оңайлататын әдістерін пайдаланбай орындау өте қиын болатын нағыз арифметикалық есептеулер кездеседі. Мысалы, мына амалдардың нәтижесін табу керек болсын дейік:
 .
.
(Бұл есептеу
жылдамдығы электромагниттік толқындардың таралу жылдамдығымен
салыстырғанда аз болатын денелердің жылдамдықтарымен істес болатын
техника, салыстырмалық теориясының механикаға ендірген
өзгерістерімен санаспай-ақ, жылдамдықтарды қосудың бұрынғы заңын
пайдалана беруіне ерікті ме, жоқ па, осыны анықтау үшін қажет.
Бұрынғы механика бойынша секундына  және
және
 километр жылдамдықпен
бағыттары бірдей екі қозғалысқа қатысатын дененің жылдамдығы
секундуна
километр жылдамдықпен
бағыттары бірдей екі қозғалысқа қатысатын дененің жылдамдығы
секундуна
 километр болады.
Жаңа ілім дененің жылдамдығы үшін мынадай өрнек
шығарған:
километр болады.
Жаңа ілім дененің жылдамдығы үшін мынадай өрнек
шығарған:
секундына  километр,
километр,
мұндағы с-жарықтың бос кеңістікте таралу жылдамдығы, ол шамамен секундына 300 000 километрге тең. Атап айтқанда, бұрынғы механика бойынша, әрқайсысы секундына 1 километр жылдамдықпен, бағыттары бірдей екі қозғалысқа қатысатын дененің жылдамдығы секундына 2 километрге тең, ал жаңа механика бойынша
секундына  километрге
километрге
тең болады. Бұл нәтижелердің айырмашылығы қанша? Осы айырмашылықты өте дәл өлшеу приборлары сезе ала ма? Осы маңызды мәселені айқындау үшін жоғарыда көрсетілген есептеуді орындауға тура келеді.)
Бұл есептеуді екі түрлі жолмен шығарамыз: ең алдымен дағдылы арифметикалық жолмен шығарамыз, сонан соң нәтижені алгебралық әдіспен қалай шығару керек екенін көрсетеміз. Алгебралық тәсілдердің артықшылығына көз жеткізу үшін төменде келтірілген цифрлардың ұзынынан-ұзақ қатарларына бір қарап шығудың өзі жеткілікті.
Ең алдымен мына «көп қабатты» бөлшекті түрлендірейік:

Енді бөлшектің алымын оның бөліміне бөлеміз:

Осыдан көріп отырғандарыңдай, есептеу жалықтыратын, еңбектенуді керек ететін жұмыс, есептеу кезінде шатасып және қателесіп кету оп-оңай. Есепті шешу үшін тоғыздықтардың қатары қай жерде үзіліп, басқа цифрлар тізбегі басталатынын дәл білудің маңызы зор.
Енді осы есептеулер алгебра жолымен қысқаша қалай орындалатынын салыстырыңдар. Алгебра мынадай жуық теңдікті пайдаланады:егер а-өте кішкене бөлшек болса, онда

болады,
мұндағы  таңбасы «жуықтап алғанда тең»
дегенді білдіреді.
таңбасы «жуықтап алғанда тең»
дегенді білдіреді.
Бұл тұжырымның дұрыстығына көз жеткізу өте оңай: бөлінгіш 1-ді бөлгіш пен бөліндінің көбейтіндісімен салыстырайық:

яғни

a-өте кішкене бөлшек (мысалы,
0,001) болғандықтан,  одан да кіші бөлшек
(0,000001), сондықтан мұны елемеуге
болады.
одан да кіші бөлшек
(0,000001), сондықтан мұны елемеуге
болады.
Осы айтылғандарды өзіміздің есептеуімізге қолданайық:

Біз әлдеқайда қысқа жолмен бұрынғы нәтижеге келдік.
(Механика саласынан бізге берілген есептің нәтижесінің мәнін білу оқырмандарға қызық болуы ықтимал. Бұл нәтиже қарастырылған жылдамдықтардың , жарық сәулесінің таралу жылдамдығымен салыстырғанда, аз болуы себепті жылдамдықтарды қосудың бұрынғы заңынан ауытқуы іс жүзінде байқалмайды: тіпті 1 км/с секілді үлкен жылдамдықтарда да бұл айырмашылық анықталатын санның он бірінші цифрына ғана әсер етеді, ал әдеттегі техникада 4-6 цифрларымен ғана шектеледі.
Біз алда мынадай жуық теңдеумен пайдаланамыз

Сондықтан біз «баяу» (жарықтың таралу жылдамдығымен салыстырғанда) қозғалатын денелерге қатысты техникалық есептеулерде жаңа эйнштейндік механика іс жүзінде ештеңені өзгертпейді деп ұйғарым жасай аламыз. Бірақ та осы кезде бұл бұлтарыссыз қорытынды сақтықпен пайдалануға тура келетін сала бар. Сөз космонавтика туралы болып отыр. Өйткені қазірдің өзінде
10 км/с шамасындағы жылдамдыққа (спутниктер мен ракеталарды ұшыру кезінде) қол жетіп отыр. Бұл жағдайда классикалық және эйнштейндік механикалардың айырмашылығы тоғызыншы орындағы таңбаға әсер етеді. Ал бұдан да үлкен жылдамдықтар пайдаланылатын күн алыс емес...)
-
«ҚАЗАҚТЫҢ ҚАРА ЕСЕПТЕРІ» ТАҚЫРЫБЫН ОҚЫТУҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ
Жүз қaз
Көктeм . Жacыл жaзиpaны жaйлaп отыpғaн ayыл үcтiнeн тepicтiккe қapaй үшбұpыш тәpiздeнiп бip топ қaз қaңқылдaп ұшып өтeдi.ayыл aлдындaғы көл жaғacынa жeтe бepгeндe қaздapдың бipi қaнaты қaйыpылып , жepгe қaңғaлaқтaп құлaп түceдi. Бacқa қaздap кeздeйcоқ жaзымғa ұшыpaғaн қaнaттacынa қaйpылмaй кeтe бepeдi.
Өз тобынaн қaлып қойғaн қaз қaйтa ұшa aлмaйды. Кeлeci күнi оның үcтiнeн үшбұpыштaнып көп қaз бaяy ұшып өтeдi. Жaны жaбыpқay жaлғыз қaз қaнaттacтapынa :
-
Cәлeм aлeйкyм, жүз қaз,-дeп caғынышпeн cәлeмдeceдi.
-
Yyәликyм үccәлeм,жaлғыз қaз,-дeп үн қaтaды қaздapдың көceмi.- бipaқ бiз,ceн aйтқaндaй ,жүз eмecпiз. Жүз болy үшiн бiзгe әyeлi өзiмiздiң caнымыздaй caн қоc,одaн cоң cол қоcқaныңның жapтыcын,eң aқыpындa өзiңдi қоc, cондa бәpiмiз жүз болып шығaмыз.
Көл жaғacындa отыpғaн жaлғыз қaз әpi –бepi ойлaнып –толғaнa кeлiп,үcтiнeн ұшып өткeн қaздapджың қaншa eкeнiн бiлeдi...
Жaз өтiп, күз тaяғaн шaқтa жaлғыз қaз жaйлaғaн көл үcтiнeн оңтүcтiк жaққa бeт aлып бipп тiзбeк қaз жiптeй cозылып өтeдi.
-
Cәлeм aлeйкyм жүз қaз,-дeп көлдeгi жaлғыз қaз олapғa eбeлeктeп cәлeм бepeдi. Қaздapдың көceмi оның cәлeмiн қaбылдaп aлыcымeн үн қaтaды:
-
Бiз жaздaй бaлaпaндaп көбeйдiк , eндi бec топ болып ұшып бapaмыз. Apтымыздaғы қaздap бiздeй ғaнa ,одaн кeйiнгici ei ece , одaн кeйiнгici үш ece,eң cоңғымыз төpт ece көппiз. Бәpiмiзгe ceн қоcылcaң жүз болaмыз.
Ipкec –тipкec cозылa ұшып бapa жaтқaн қaздap тiзбeгiнiң cоңынaн қaлғaн жaлғыз қaз олapдың әp тобындa қaншa қaз eкeнiн дe дәл eceптeп тaбaды. Мұны жaлғыз қaз қaлaй бiлгeн ?
Шығарылуы: х + х+x + 1 =
100
2х + х = 99 17х = 396. х = 36. Ж/бы: 36
қаз
Тоғыз тapayдaғы кeздecy
Тaлac өзeнiнiң төмeнгi бойындaғы көкмaйca жepгe тұc-тұcтaн тоғыз жол кeлiп түйiceдi. Cондықтaн тоғыз жолдың тоpaбы Тоғызтоpay дeп aтaлaды. Әйтeyip бip жылы cондaғы құдық бacынa тоғыз aңшы кeлiп, бipiмeн-бipi түгeл қол бepiciп aмaндacып шығaды.
Бәpiмiз қaншa peт қол aлмacтық ?-дeйдi cондa жолayшылapдың бipi.
Кiм бiлciн,aл мeн өзiм ceгiз aдaммeн aмaндacтым,-дeйдi eкiншi жолayшы.
Тоғыз жолayшы бipiнe-бipi қaншa peт қол бepicтi?
Жауабы: (9*8)/2=36
Құcбeгiлeр аманаты
Орман-тоғайлы, өзeн-көлдi даланы eркiн жайлаған ауылдың төрт құcбeгi аңшыcы болған eкeн. Аң,құc аулауға кeлгeндe бiрiнeн-бiрi өтeтiн cол кiciлeр әр түрлi қыран құcтард мәпeлeп баптап, бәрiн алғыр eтiп өciрeдi. Баcы артығын базарға апарып cатып, ақша да тауып жүрeдi.
Бiр күнi құcбeгiлeр шахардағы жәрмeңкeгe жүргeлi жатқан жiгiткe кeлiп, бiздiң қырандарымызды тиicтi бағаcына cатып кeл, дeп өтiнeдi. Базаршы жiгiт олардың аманатын орындауға кeлice қояды. Құcбeгiлeр оған төрт-төрттeн он алты қыран құcты томағалап алып кeлeдi. Жолаушы жeтeгiнe алған түйeнiң төрт қырлы ашамайына бәрiн қатар қатар қонырып қояды.
Ұзақ жолға шыққан жiгiт бiрeр аптадан кeйiн ауылға олжалы болып оралады. Қыран құcтарды түгeлдeй cатып кeлгeнiн айтқан кeздe құcбeгiлeр мәз-мeйрам болып, қуанып қалады.
-Балам, қырандардың қайcыcы қанша тeңгeгe өттi? -дeп cұрайды eң үлкeн құcбeгi
- Тұрымтай – 1 тeңгeгe, жағалтай– 2 тeңгeгe, лашын – 3 тeңгeгe,бидайық – 4 тeңгeгe, күйкeнтай - 5 тeңгeгe, пәрiм - – 6 тeңгeгe, итeлгi - 7, cұңқар – 8, қырғи- 9, шәулi- 10, қаршыға-11, тұйғын -12, шөгeл-13, қараша-14, ақиық-15, ал байқаcқа - 16 тeңгeгe cатылды.
-34 тeңгe болыпты ғой мeнiң қырандарым дeптi тұрымтай мeн байқаcқаның иeci,
Cол cияқты барлығы 34 тeңгeдeн cанап алыпты. Кiмдe қандай құcтар болған.
Бec cаулық
Ауыл ақcақалының 4 ұлы болыпты. Олардың үшeуi өз алдына отау тiгiп кeткeн eкeн. Ақcақалды кici төртiншi балаcын үйлeндiрiп, оның алдына бec cаулық cалып бeрудi ойлаcтырады. Бiр күнi ол үш ұлының үйлeрiнe барып, бәрiнiң қойы 41 баc eкeнiн бiлiп қайтады да, оларды шақырып алып, «Әрқайcыcы өздeрiндeгi қойларды 4-кe бөлiп, бөлiнбeй қалғанын кeнe iнiлeрiңe бeрiңдeр» - дeйдi.
Үш жiгiт қойларын әкeciнiң айтуынша бөлiп, бөлiнбeй қалғанын iнiciнe әкeлiп бeрeдi. Cөйтәп, кeнжe жiгiт 5 cаулыққа иe болады.
-
Eкeуiңнiң қойың мeнiкiнeн артық eдi, eндi тeңecтi- дeйдi қой бeргeн жiгiттeрдiң бiрi өзгeлeрiнe
-
Бұл жiгiттeрдiң қойлары алғашында нeшeдeн болған?
Жауабы:1-1қой – x+2 – жалпы қой cаны - 16
2-1қой – x+2– жалпы қой cаны -15
3- 1қой – x – жалпы қой cаны -5
4-5 қой
Мұрап амалы
Қыcтақ диқандары тары cуару қамына кiрiceдi. Тәжiрибeлi мұрап eгic-iргeciндeгi мол cулы бec арыққа алты жiгiттi eртiп кeлeдi. Бәрi кeтпeндeрiн жалаңдатып, тұрған кeздe мұрап көлдeнeң жатқан арық пeн eгiн жиeгiнe дeйiнгi жeрдi қадамдап өлшeп оралады да, бiрiншi жiгiткe оcы жeрдiң жeтiдeн бiр бөлiгiн қадамдап өлшeп бeрeдi. Eкiншi одан кeйiнгi жeрдiң алтыдан бiрi тиeдi. Үшiншiгe қалған жeрдiң - бecтeн бiрi, төртiншiгe -төрттeн бiрi. Төрт жiгiт icкe кiрiciп, кeткeн шақта мұарпқа бeciншici кeлiп, қазатын жeрi өлшeп бeруiн cұрайды. Оған төртiншi жiгiттeн кeйiнгi қалған жeрдiң үштeн бiрiнiң қазуды тапcырады. Алтншыcына одан қалған жeрдiң eкiдeн бiрi бeрлeдi. Eң ақырында жeтiншi болып өзiнe 3 қадам жeр тиeдi.
Арқан бойы арық қазылып бiткeннeн кeйiн жiгiттeр бiрiнeн-бiрi әркiм арқытың қанша жeрiн қазғанын cұраcады. Eң көп кiм қазған?
-
1 жiгiткe – х/7
-
2 жiгiткe - 6х/42- = х/7
-
3 жiгiткe 1- х/7-6х/42=30х/42*1/5= х/7
-
4 жiгiткe – х/7
-
5 жiгiткe- х/7
-
6 жiгiткe- х/7
-
7 жiгiткe-= х/7=3, х=21
Жауабы . 21 адым болған, әрқайcыcы 3 адымнан қазған.
Пайдаланылған әдебиеттер тізімі
-
Алдамұратова Т.А., Байшолпанов Т.С., Математика, 6-сынып,
Алматы: «Атамұра», 2018.
-
Әбілқасымова А.Е., Шойынбеков К.Д., Корчевский В.Е., Жұмағұлова З.А.Алгебра,
6-сынып, Алматы: «Мектеп», 2018.
-
Шыныбеков Ә.Н.Алгебра.8-сынып, Алматы: «Атамұра», 2018.
-
Әбілқасымова А.Е., Шойынбеков К.Д., Корчевский В.Е., Жұмағұлова З.А.Алгебра,
8-сынып, Алматы: «Мектеп», 2018.
-
Әбілқасымова А.Е., Шойынбеков К.Д., Корчевский В.Е., Жұмағұлова З.А..
-
Алгебра және анализ бастамалары, 10-сынып ,Жаратылыстану-математика бағыты,
Алматы: «Мектеп», 2019
-
Әбілқасымова А.Е., Шойынбеков К.Д., Корчевский В.Е., Жұмағұлова З.А.
Алгебра және анализ бастамалары, 10-сынып, Қоғамдық-гуманитарлық бағыты,
Алматы: «Мектеп», 2019.
-
Шыныбеков Ә.Н.. Алгебра және анализ бастамалары: 10-сынып арналған оқулық
– 3-басылымы , Алматы:«Атамұра», 2019.
-
С.Елубаев.Математиканы оқыту теориясының негіздері мен әдістемесі,
Алматы : «Қазмемқызпу», 2009.
-
Панчишкин А.А., Шавгулидзе Е.Т, Тригонометрические функции в задачах,
Москва, «Наука» 1986.
-
Елубаев С.Е. Математиканы оқыту теориясының негіздері мен әдістемесі.
Алматы, 2006.
-
Елубаев С.Е. Математиканы оқыту методикасы. Алматы, 1996.
-
Елубаев С.Е. Орта мектепте математиканы оқыту әдістемесі Алматы, “
Рауан”, 1996.
-
Елубаев С.Е. Математиканы оқыту методикасы. Жалпы бөлім.
Практикалық (семинарлық) сабақтар. Республикалық оқу-методика кабинеті Алматы, 1979.
-
Елубаев С. Е. Методическое руководство для студентов по педагогической практике.
А., Джамбулская райтипогарфия, 1979.
-
Қасқатаева Б.Р, Математиканы оқытудың әдістемесі мен технологиясы, Алматы 2011.
-
Көбесов А, Математика тарихы, Оқу құралы, Алматы «Қазақ университеті» , 1993.
-
Дорофеев Г.В, Потапов М.К, Розов Н.Х, Пособие по математике для
поступающих в вузы, Издательство «Наука» , Москва, 1972.
-
Колмогоров А.Н, Абрамов А.М, Дудынцин Ю.П, Ивлев Б.М, Шварцбурд С.И.
Алгебра және анализ бастамалары, орта мектептің 10-11 сыныптарына арналған оқулық, Алматы «Рауан», 1998.
-
Айдос Е.Ж, Балықбаев Т.О. Математика пәні бойынша ЖОО-на түсушілерге
арналған оқу құралы. Алматы, 2006.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
«5-6 СЫНЫП ОҚУШЫЛАРЫНА АРНАЛҒАН МӘТІН ЕСЕПТЕР ЕСЕПТЕРІ»
«5-6 СЫНЫП ОҚУШЫЛАРЫНА АРНАЛҒАН МӘТІН ЕСЕПТЕР ЕСЕПТЕРІ»
Түркістан облысының білім басқармасы
Түркістан облысы білім беруді дамытудың оқу-әдістемелік орталығы
Білім беру ұйымының атауы
|
Келісілді Түркістан облысы білім беруді дамытудың оқу-әдістемелік орталығының директоры ____________ «___ » _________ 2024 жыл |
Бекітемін Сауран ауданы Әл-Фараби атындағы жалпы орта мектеп директоры Мамадалиева Махсуда «___ » _______ 2024 жыл
|
«5-6 СЫНЫП ОҚУШЫЛАРЫНА АРНАЛҒАН МӘТІН ЕСЕПТЕР ЕСЕПТЕРІ»
(бағдарламаның атауы )
вариативтік және кәсіптік бағдарланған арнайы курстарының
(қандай курсты таңдауына байланысты)
БАҒДАРЛАМАСЫ
(___ сынып, ____ сағат саны)
2023 – 2024 жыл
Сауран ауданы
(Эксперттік Кеңес үшін оқу бағдарламасының ішкі титулдық бетінің үлгісі)
Авторы:
Қала/аудан_________ № ____ ЖББОМ __________пәнінің мұғалімі
____________________ аты-жөні
қолы
Пікір жазушылар:
Аты-жөні, мекеменің атауы, ондағы лауазымы, ғылыми дәрежесі,
ғылыми атағы (егер болса)
Аты-жөні, мекеменің атауы, ондағы лауазымы, ғылыми дәрежесі,
ғылыми атағы (егер болса)
Білім беру ұйымының Әдістемелік кеңесімен ұсынылады
Хаттама № _______ «____»___________ 2024 жыл
Хатшы:
Лауазымы ________________ аты-жөні
қолы
Аудандық(қалалық) білім бөлімдерінің Әдістемелік кеңесімен ұсынылады
Хаттама № _______ «____»___________ 2024 жыл
Хатшы:
Лауазымы ________________ аты-жөні
қолы
Облыстық Эксперттік Кеңеспен ұсынылады
Хаттама № _______ «____»___________ 2024 жыл
Хатшы:
Лауазымы ________________ аты-жөні
Түсінік хат
«5-6 сынып оқушыларына арналған мәтіндік есептер» атты авторлық бағдарламасының артықшылығы оқушылардың мектеп бағдарламасында алған білімдерін жан-жақты практикалық тапсырмаларда талдай алуына мүмкіндік беруге ықпал жасауында.
Тақырыптың өзектілігі:
-бұл курсты ұйымдастыру арқылы әр оқушының даму
деңгейі, білімі, қабілеттерінің дамуына жағдайлар
жасалып, бәсекеге қабілетті тұлға қалыптасуына
мүмкіндіктер туғызылады;
- қазіргі заманауи білім беруде кіріктірілген білім беру аса маңызды мәселелердің бірі болып табылады;
-ұсынылған тапсырмалар мәселені айқындау оқушыны шығармашыл жеке тұлға, зерттеуші ретінде сезінуіне, өзін-өзі дамытуына мүмкіндік береді;
-мұғалімдерге де біліктілігін жетілдіру жеке тұлғаны дамытуда маңызды роль атқарады;
-сыни ойлауға
байланысты оқушының интеллектуалдық және практикалық біліктілігі
қалыптасады, дамиды.
Мақсаты – 5-6 сынып оқушыларының математика сабағында есептеулерден бөлек сыни ойлау, патриоттық , шығармашылық-ізденушілік, талдау-жинақтау ойлау дағдыларын дамыту.
Оқу тәртібін(курс, факультатив) енгізудің себептері:
-оқушылардың логикалық ойлауын жетілдіруге байланысты функционалдық сауаттылыққа арналған әдістемелік құралдардың талаптарға сай болмағандықтан курсты енгізу қажеттілігі туындап отыр;
-практика мен теорияның арасындағы қарама – қайшылықтың болуы оқу үдерісіндегі курсты енгізудің негізгі себебі болып табылады;
«5-6 сынып оқушыларының функционалды сауаттылығын дамыту есептері» атты авторлық бағдарламасының курсының негізгі міндеті – базалық оқуға кіретін мектеп пәндері бойынша білімді тереңдету және кеңейту болып табылады.
Бағдарламалық материалдың
ерекшеліктері:
-Осыған байланысты пән ерекшелігі математика пәнінен функционалдық сауатталыққа бағытталған;
- бұл бағдарлама кең ауқымды кіріктірілген және математика пәнінен функционалдық сауатталыққа оқу-әдістемелік кешенді қолдану арқылы жүзеге асырылады.
-Берілген бағдарламаның ерекшелігі математика пәнінен функционалдық сауатталыққа арналған болып табылады.
-Оқу үдерісін ұйымдастыруда заманауи талаптарға сай және қолдану үшін бағдарламада тапсырмалардың құрылымына ерекше мән берілген.
-Ұсынылатын бағдарлама ... болып табылды. Ол 5-6 сынып математика курсының негізінде құрылған.
Курстың (факультативтің) жүргізілу тәртібі:
-Курс 5-6 сынып математика оқу жоспарына енгізілген пәндер қатарына кіреді;
-Берілген курсты оқыту жаратылыстану, биология пәндерімен тығыз байланысты;
Курс кім үшін ұйымдастырылады:
-бұл таңдау курсы оқыту бағдарына тәуелсіз, пәнге және оның қолданбалы аспектілеріне қызығушылық білдіретін 5-6 сынып оқушыларына арналған.
-Бағдарлама 5-6 сынып оқушылары үшін құрастырылған, сондай-ақ практикалық қолданысына тапсырмалар көп болғандықтан 7-8 сыныптарда да қолданылуы мүмкін.
-Курс 5-6 сынып оқушылары үшін ұсынылған.
Бағдарлама
құрылымы:
Негізінен 7-ірі тараудан құралған, оның ішінде Дирихле принципі - оқушылардың логикалық және сыни-ойлауын дамытуға бағытталса, логика интуицияға қарсы тарауында оқушылардың математикалық есептеулердің үнемі логикалық құндылығының арасында айырмашылығын ашып көрсетуі – саналы түрде дәл мәнді есептеулердің ғана мағыздылығын дәлелдейді. Көптеген математикалық парадокстардың пайда болуы кездейсоқ оқиғалардың ақиқат не жалғанға айналуы, адам ойының сансыз ұшқырлығын дамыта түседі. Теңдеу не теңсіздік шешудің Прокруст төсегі арқылы есептеу тек қана жаңа шешу әдісін енгізуде емес, стандартты емес ойлау дағдысын жетілдіру болып табылады. Менталды арифметиканың салдары болып табылатын тиімді көбейту деген тарауда оқушылардың қарапайым қысқа тәсілдер арқылы есептеуіне мүмкіндік беру. Сонымен қатар, 5-6 сынып оқушыларына этнопедагогика тұрғысынан қазақтың қара есептерін шығарту тарихи және математикалық маңыздылығын ұштастыру - қазіргі оқыту проблемасы болып табылатын патриоттық, рухани жаңғыру тапсырмасы рөлін атқарады.
Оқу үрдісін ұйымдастыру формалары:
- Бағдарлама құрылымы дәстүрлі сабақтар өткізуден, белгілі–бір тақырыптар бойынша дәрістер оқудан (практикалық сабақтар, семинарлар, жалпылама сабақтар және т.б. ) тұрады.
Оқушылардың сыныптық (аудиториялық) және өзіндік жұмыстарының өзара байланысы:
- Берілген курсты жоғары дәрежеде меңгеру үшін практикалық қолданысы бойынша өздік жұмыстар жүргізуге ерекше мән беріледі.
- Курсты оқу барысында оқушылар үшін өздік жұмыстармен айналысуға үлкен мүмкіндіктер қарастырылған.
- Курс бағдарламасы бойынша оқу барысында оқушылар практикалық және дәріс сабақтарына, семинарларға қатысады және жеке жұмыс істеп үйренеді.
Қорытынды бақылау
:
- Оқушылардың білімі мен дағдысын бағалау курстың негізгі мәселелері бойынша функцилоналдық сауаттылыққа байланысты сұрақтардан (тапсырмалардан) тұратын қорытынды тест арқылы өткізіледі.
Оқытудың көлемі мен мерзімдері:
-Курс бағдарламасы бойынша 5-6 сыныпта 34 сағат теориялық және практикалық сабаққа есептеліп құрылған.
|
№ п/п |
Курс бөлімдерінің атауы |
Жалпы сағат саны |
Оның ішінде |
Өткізілу күні |
Оқушылардың өздігінен атқаратын жұмыстары |
|
|
теория |
практика |
|||||
|
1 |
Дирихле принципі. |
1 |
1 |
|
|
|
|
Көжектер мен қораптар |
1 |
1 |
|
|
|
|
|
Дирихле принципі есептер шығару |
1 |
|
1 |
|
|
|
|
Дирихле принципінің практикалық маңыздылығы |
1 |
|
1 |
|
|
|
|
2 |
Логика интуицияға қарсы. |
1 |
1 |
|
|
|
|
Логикалық байланыс туралы |
1 |
1 |
|
|
|
|
|
Қарбызға байланысты есеп |
1 |
|
1 |
|
|
|
|
Жер планетасына байланысты есеп |
1 |
|
1 |
|
|
|
|
3 |
Парадокс туралы |
1 |
1 |
|
|
|
|
Шыншыл өтірікші |
1 |
1 |
|
|
|
|
|
Шексіздікті есептеу |
1 |
|
1 |
|
|
|
|
Галилео Галилей парадоксы туралы |
1 |
|
1 |
|
|
|
|
4 |
Прокруст әдісі |
1 |
1 |
|
|
|
|
Прокруст төсегі туралы аңыз |
1 |
1 |
|
|
|
|
|
Есептер шығару |
1 |
|
1 |
|
|
|
|
Прокруст әдісінің практикалық маңыздылығы |
1 |
|
1 |
|
|
|
|
5 |
Тиімді көбейту тәсілдері |
1 |
1 |
|
|
|
|
5-пен аяқталатын санның квадратын табу |
1 |
1 |
|
|
|
|
|
100- ге жақын санның квадратын табу |
1 |
|
1 |
|
|
|
|
Саусақпен санау. Саусақ арқылы санның квадратын табу. Көбейтудің әр түрлі әдістері |
1 |
|
1 |
|
|
|
|
6 |
Сандардың бөлінгіштігі қасиеттерінің практикалық маңыздылығы |
1 |
1 |
|
|
|
|
11-ге бөлінгіштік Автомашинаның нөмірі. |
1 |
1 |
|
|
|
|
|
19-ға бөлінгіштік |
1 |
|
|
|
|
|
|
Софья Жерменнің теоремасы |
1 |
|
|
|
|
|
|
Бізге белгілі ең үлкен жай сан |
1 |
|
|
|
|
|
|
7 |
Қазақтың қара есептері |
1 |
1 |
|
|
|
|
Жүз қаз есебі |
1 |
1 |
|
|
|
|
|
Тоғыз тapayдaғы кeздecy |
1 |
1 |
|
|
|
|
|
Құcбeгiлeр аманаты |
1 |
|
1 |
|
|
|
|
Бec cаулық |
|
|
1 |
|
|
|
|
Мұрап амалы |
1 |
|
1 |
|
|
|
|
Жалпы |
34 |
17 |
17 |
|
|
|
-
«Дирихле принципі» тақырыбын өтуге арналған әдістемелік нұсқаулық
Көжектер мен
қораптар. Дирихле қағидасымен қалай
байланысты Қапарайымдылығы мен айқындығына қарамастан, Дирихле
қағидасы теоремаларды дәлелдеуде және бір қарағанда шешу мүмкін
еместей болып көрінетін есептерді шешу кезінде қолданылады. Бүкіл
әлем математиктері Дирихле қағидасын көжектер мен қораптарды
мысалға ала отырып түсіндіреді (ағылшын тілді елдерде көгершіндер
мен қораптар қолданылады). Бұл қалыптасқан дәстүрді біз де
бұзбайық. Тек бұл қағиданың пайда болғаны үшін неміс математигі
Петер Густав Леж Дирихлеге қарыздар екенімізді айта кеткіміз
келеді. Қандайда бір мөлшерде көжектер (m) мен қораптар(n) бар
делік. Және көжектердің саны қораптардың санына қарағанда көбірек
(m > n). Барлық көжектерді қораптарға орналастырамыз. Сонда бір
қорапта бір көжектен көбірек болады. Ойланып көріп, шешім
шығарамыз: алдымен қораптарға n көжектерді салып шығамыз. Қалған
көжектер саны m-n -ге тең болады. Тапсырма шарты бойынша, барлық
көжектер қорап ішінде болуы тиіс. Сәйкесінше, n-m көжектерді біз
бос емес қораптарға сала бастаймыз. Сондықтан даішінде бірден көп
көжектері бар қораптар да болады. Біз қарапайым ойлау жүргіздік,
бұдан қиынырақ мысалдарды математикалық индукция әдісін пайдалану
арқылы өз еріктеріңізбен ойластыруды ұсынамыз. Дирихле әдісін
пайдаланудың басты қиыншылығы анықтаманың ауырлығында: не «көжек»,
ал не «қорап». Бұл жағынан бізге көмекке келетін бірнеше тапсырманы
қарастырып көрелік. №1 мысал. Классикалық мысал – қала
тұрғындарының шаштары. Дирихле қағидасы Алматы қаласында шаштарының
саны бірдей кем дегенде екі адам тұратынын дәлелдеп бере алады.
Әрине, бұл жерде таздар есепке алынбаған. Төменде пайымдау жолы
берілген: Алдымен Алматыда тұратын адамдар санын анықтап аламыз.
Халық саны туралы соңғы санаққа орай, қалада 1 552 349 адам тұрады.
Ары қарай орташа статистикалық адам шашының саны 150 000-нан артық
емес деген деректі пайдаланамыз. Енді жалпы қала тұрғындарының
санынан басында бір, екіден бастап, 150 000-ға дейінгі шашы бар
бір-бір адамды алып тастайық. Нәтижесінде біз 150 000-нан артық
емес адамдарды бөліп аламыз (себебі, қалған 1 402 349 тұрғынның
1-ден 150 000-ға дейін шашы болуы мүмкін). Олардың кез келгені
(басындағы шаш мөлшеріне қарай жинақталған) топтардың біреуіне
қосылуы мүмкін.

Ойланып көріп, шешім шығарамыз: алдымен қораптарға n көжектерді салып шығамыз. Қалған көжектер саны m-n -ге тең болады. Тапсырма шарты бойынша, барлық көжектер қорап ішінде болуы тиіс. Сәйкесінше, n-m көжектерді біз бос емес қораптарға сала бастаймыз. Сондықтан даішінде бірден көп көжектері бар қораптар да болады. Біз қарапайым ойлау жүргіздік, бұдан қиынырақ мысалдарды математикалық индукция әдісін пайдалану арқылы өз еріктеріңізбен ойластыруды ұсынамыз. Дирихле әдісін пайдаланудың басты қиыншылығы анықтаманың ауырлығында: не «көжек», ал не «қорап». Бұл жағынан бізге көмекке келетін бірнеше тапсырманы қарастырып көрелік. №1 мысал. Классикалық мысал – қала тұрғындарының шаштары. Дирихле қағидасы Алматы қаласында шаштарының саны бірдей кем дегенде екі адам тұратынын дәлелдеп бере алады. Әрине, бұл жерде таздар есепке алынбаған. Төменде пайымдау жолы берілген: Алдымен Алматыда тұратын адамдар санын анықтап аламыз. Халық саны туралы соңғы санаққа орай, қалада 1 552 349 адам тұрады. Ары қарай орташа статистикалық адам шашының саны 150 000-нан артық емес деген деректі пайдаланамыз. Енді жалпы қала тұрғындарының санынан басында бір, екіден бастап, 150 000-ға дейінгі шашы бар бір-бір адамды алып тастайық. Нәтижесінде біз 150 000-нан артық емес адамдарды бөліп аламыз (себебі, қалған 1 402 349 тұрғынның 1-ден 150 000-ға дейін шашы болуы мүмкін). Олардың кез келгені (басындағы шаш мөлшеріне қарай жинақталған) топтардың біреуіне қосылуы мүмкін.

Есеп 1. Сыныпта 15 оқушы. Сыныптан бір айда туған күнін атап өтетін кем дегенде 2 оқушының табылатынын дәлелдеңіз.
Шешуі: 15 оқушы- «қояндар» болсын. «торлар»- жылдың айлары (12 ай). 15>12 болғандықтан Дирихле принципі бойынша бір торда 2 қоян отыратындай кем дегенде бір тор табылады. Яғни сыныптан бір айда кем дегенде 2 оқушы туған күнін атап өтетіндей ай табылады.
Есеп 2. 12 бүтін сан берілген. Олардың ішінен айырмасы 11-ге бөлінетіндей екі санды таңдап алуға болатынын дәлелде.
Шешуі: Бүтін сандар-«қояндар», олардың саны 12, онда торлардың саны 12-ден аз болу керек. «торлар»- бұлар бүтін сандарды 11-ге бөлгендегі қалдықтар. Барлық «торлар» саны 11 болады: 0,1,2,3,4,5,6,7,8,9,10. Онда Дирихле принципі бойынша бір торда 2 қоян отыратындай кем дегенде бір тор табылады. Яғни қалдықтары бірдей болатындай екі бүтін сан табылады. Ал 11-ге бөлгенде бірдей қалдық қалатын екі санның айырмасы 11-ге бөлінеді.
Есеп 3. Өлшемдері 3x3 метр болатын кілемге Коля 8 тесік жасады. Осы кілемнен өлшемдері 1x1 метр болатын ішінде тесігі жоқ кілемше кесіп алуға болатынын дәлелдеңіз.
Шешуі: Бұл жерде тесіктер ол-«қояндар». Кілемді өлшемдері 1x1 метр болатын 9 кілемшеге кесеміз. Кілемшелер-«торлар» саны 9. Ал тесіктер-«қояндар» саны 8. Онда «қоян» болмайтындай кем дегенде бір «тор» табылады. Яғни ішінде тесігі болмайтын кілемше табылады.
Есеп 4. Турнирде жеңіске жеткендері үшін 8 адамнан тұратын команда 12 кәмпит алды. Балалар кәмпиттерді бүтіндей (сындырмай) бөліп алды. Келесі тұжырымдамалар дұрыс па? Анықтаңдар.
«бір бала кем дегенде екі кәмпит алды»
«бір бала кем дегенде үш кәмпит алды»
«екі бала кем дегенде екі кәмпит алды»
«әрқайсысына кем дегенде бір кәмпиттен келді».
Жауабы: Бірінші тұжырым дұрыс, қалғаны дұрыс емес.
Шешуі: 1) Дұрыс. Кері жоримыз. Яғни балалар кәмпиттерді бөліскенде әрбіреуі 0 немесе 1 кәмпиттен алды делік. Онда барлық бала қосындысында 8 кәмпиттен артық алмайды. Ал бұл есеп шартына қайшы. Яғни біздің жорығанымыз дұрыс емес, бұндай жағдай болу мүмкін емес. Онда бір бала кем дегенде екі кәмпит алды.
Қалғандарының орындалмайтындығына бір мысалдан келтіре салса жеткілікті:
2) 4 адам 2 кәмпиттен алады, ал қалған 4 адам бір-бірден алады.
3) Барлық кәмпитті бір адам алады.
4) 3-ші бөлімге ұқсастықпен.
Есеп 5. Үш әділқазылар мүшелерінен былай сұрады: «Турнирге қанша команда қатысады?» Біріншісі: « 33-тен кем команда», екіншісі: «31-ден кем команда», үшіншісі: «32-ден кем команда» -деп жауап берді. Егер екі әділқазы мүшесінің айтқаны дұрыс болса, онда турнире неше команда қатысқан?
Шешуі: Екінші тұжырым дұрыс болса, онда қалғандары да дұрыс екені шығады? Бірақ, екі тұжырым ғана дұрыс болғандықтан екіншісі дұрыс емес, ал бірінші мен үшіншісі дұрыс. Бір жағынан команданың саны 31-ден артық болу мүмкін емес (онда үшіншісі дұрыс болмайды), екінші жағынан 31-ден кем болу мүмкін емес(онда екіншісі дұрыс болады). Яғни жалғыз ғана мүмкін жағдай 31. 31 саны есептің шартын қанағаттандыратынын тексеру қиын емес.
Есеп 6. Мектепішілік баскетбол жарысының ақтық кезеңінде 6А командасы 9 доп салды. Осы командадан саны жағынан бірдей доп салған екі ойыншы табылатынын дәлелдеңіз.(Командада 5 ойыншы болған)
Шешуі: Командадан саны жағынан бірдей доп салған екі ойыншы табылмауы мүмкін деп жориық. Онда барлық бес ойыншы саны бойынша әртүрлі доп салған. Бірінші ойыншы ешқандай доп салған жоқ дейік, екінші ойыншы бір доп салды, үшіншісі екі доп салды, төртіншісі үш доп салды, бесіншісі төрт доп салды. Онда ойыншылар барлығы он доп салды. Егер ойыншылардың кем дегенде біреуі біз жорығандай доптан артық салса, онда команданың да барлық салған доптарының саны 9-дан асып кетеді. Яғни біздің кері жорығанымыз дұрыс емес. Яғни командадан саны жағынан бірдей доп салған екі ойыншы табылады.
Есеп 7. Андрейдің інісі шашкилерді 8 түрлі түспен бояп шықты. Әрбір бағанда және әрбір жолда бір шашкиден болатындай Андрей 8 әртүрлі түсті шашкилерді шашки тақтасына қанша тәсілмен орналастыра алады? Әрбір бағанда және әрбір жолда бір шашкиден болатындай Андрей 8 ақ шашкиді қанша тәсілмен орналастыра алады?
Шешуі: Біріншіден шашкилердің түстері ақ болған жағдайды қарастырайық. Шашкилерді орналастырамыз. Бірінші бағандағы 8 торкөздің кез келгеніне шашкиді қоя аламыз, екінші бағандағы 7 торкөздің кез келгеніне қоя аламыз.(Сонымен қоса бірінші шашки тұрған жолға шашки қоюға болмайды). Сол сияқты үшінші жолдың кез келген 6 торкөзіне шашки қоюға болады, төртінші жолдың кез келген 5 торкөзіне шашки қоюға болады т.с.с. Нәтижесінде 8! Тәсіл шығады.
Енді шашкилер түрлі түсті болған жағдайды қарастырамыз. Ақ шашкилердің орналасуларының кез келген жағдайын алайық. Осы шашкилерді олардың кез келген екеуі әртүрлі түс болатындай 8 түрлі түске бояймыз. Бірінші біз 8 түстің бірімен бояп шығамы, екінші 7 түстің біреуімен және т.с.с. Нәтижесінде 8! тәсіл шығады. Сонымен барлық тәсіл 8!8!=8!2 болады.
Есеп 8. Мәскеуде 10 000 000 нан астам адам тұрады. Әрбір адамның басында 300 000 нан астам шаш болуы мүмкін емес. 34 адамның басындағы шаштарының саны бірдей болуы мүмкін болатынын дәлелде.
Шешуі. Баста 0,1,2,...,300 000 шаш болуы мүмкін. Сонда барлығы 300 001 нұсқа. Шаштарының санына байланысты әрбір адамды 300 001топқа бөлеміз. Егер шаштарының саны бірдей болатын 34 адам табылмаса, яғни құралған топтардың кез келгеніне 33 –тен артық емес адам кіреді. Онда Москвада 33·300 001=9 900 033<10 000 000 адам тұрады. Бұл қарама-қайшылық. Яғни 34 адам табылады.
9-есеп. Жазықтық 2 түске боялған. Бір-бірінен 1 метр қашықтықта орналасқан және бірдей түске боялған екі нүкте әрқашан табыла ма?
Шешуі: Түс екеу болғандықтан нүктелер саны екеуден көп фигураны қарастыру қажет. Қабырғасы 1 метрге тең дұрыс үшбұрышты мысал ретінде қарастыру қолайлы болады. Оның 3 төбесі бар. Төбелерін «қоян», ал түстерді «ұяшық» десек, онда 3 ˃ 2. Демек, Дирихле принципі бойынша бірдей түспен боялған және бір-бірінен 1 метр қашықтықта орналасқан үшбұрыштың 2 төбесі табылады.[1]
10-есеп. Студенттер жатақханасындағы би кешіне 36 қонақ келді. Жатақханадағы бөлмелер саны 42 болса, бірде бір қонақ келмеген бөлме барын дәлелдеңдер.
Шешуі: Бөлмелерді – «ұяшықтар», ал қонақтарды – «қояндар» деп белгілеп, келесі теңсіздікті аламыз: 36 ˂ 42. Онда Дирихле принципі бойынша кем дегенде бір бос «ұяшық» табылады, яғни қандай да бір бөлмеге ешбір қонақ келмейді. [1]
11-есеп. Мектепте 33 сынып, 1150 оқушы бар. Оқушылар саны 35-тен кем сынып бар болады ма?
Шешуі: Әр сыныпта 35-тен кем емес оқушы бар болсын делік. Онда мектептегі барлық оқушы саны 35·33 = 1155 –тен кем болмауы тиіс. Ал, бұл есептің шартына қайшы келеді. Демек, мектепте оқушы саны 35-тен кем сынып бар болады. [1]
12-есеп. Сыныпта 29 оқушы бар. Шығарма жазғанда Набиев Руслан 13 қате, ал қалғандары одан аз қате жіберді. Сыныпта қателер саны бірдей болатын кем дегенде 3 оқушы табылатынын дәлелдеңдер.
Шешуі: Қателер санын: 0, 1, 2, ..., 11, 12 «ұяшықтар», ал 28 оқушыны (Руслансыз) «қояндар» деп белгілеп, келесі теңсіздікті аламыз: 28 ˃ 13·2 + 1. Дирихле принципінің жалпыланған түрін қолданып, кем дегенде 3 оқушыда қателер саны бірдей екенін аламыз.
13-есеп. Өлшемі 8х8 шахмат тақтасына Заңғар 14 фигураны қойып шықты. Бірде бір фигура қойылмаған 2х2 өлшемді шаршы табылатынын дәлелдеңдер. (Фигуралар 1х1 өлшемді шаршылардың ішінде орналасады).
Шешуі: 8х8 шахмат тақтасы өлшемі 2х2 болатын 16 шаршыларға бөлінеді. Сонда 16 «ұяшық» және 14 «қоян» - фигура болады. 16 ˃ 14 болғандықтан, кем дегенде бір «ұяшық» бос болады. [1]
14-есеп. Жоғарғы оқу орнында оқыған 5 жыл ішінде студент 31 емтихан тапсырды. Әр жылы алдыңғы жылға қарағанда көп емтихан тапсырып отырды. Бесінші курста тапсырған емтихан саны бірінші курста тапсырған емтихан санынан 3 есе көп. Төртінші курста неше емтихан болды?
Шешуі: Студенттің бірінші курста
тапсырған емтихан саны х
болсын. Онда оның екінші
курста тапсырған емтихандар саны (х
+ 1) – ден кем емес, үшінші
курста емтихан саны (х
+ 2) – ден кем емес, төртінші
курста емтихандар саны (х
+ 3) – тен кем емес. Екінші
жағынан, бесінші курста тапсырған емтихандар саны
3х, демек, төртінші курста
(3х
– 1) –ден көп емес, үшіншіде
(3х
– 2) –ден көп емес, ал
екіншіде (3х
– 3) –ден көп емес емтихандар
тапсырды. Онда жалғыз бүтін шешімі х
= 3 болатын келесі
теңсіздіктер жүйесін аламыз:  . Онда студент бесінші
курста 9 емтихан тапсырды, сәйкесінше, төртінші курста тапсырған
емтихандар саны 8-ден көп емес. Егер ол төртінші курста 7 емтихан
тапсырған болса, онда барлық емтихан саны 3 + 5 + 6 + 7 + 9 = 30
–дан аспайды. Демек, студенттің төртінші курста тапсырған
емтихандар саны 8.
. Онда студент бесінші
курста 9 емтихан тапсырды, сәйкесінше, төртінші курста тапсырған
емтихандар саны 8-ден көп емес. Егер ол төртінші курста 7 емтихан
тапсырған болса, онда барлық емтихан саны 3 + 5 + 6 + 7 + 9 = 30
–дан аспайды. Демек, студенттің төртінші курста тапсырған
емтихандар саны 8.
Дирихле принципін практикалық маңызы бар есептер шығаруда қолдану
№1 есеп. 145
тұқым 12 метр көлемдегі егіске 12 метрге шашылған. Осы жерде
кемінде екі тұқым бір-бірінен √2 метрден кем қашықтықта
түскенін дәлелдеңіздер. Көмек: Пифагор теоремасын еске
түсіріңіздер. №2 мысал. Түрлі-түсті шұлық және қараңғылық.
Барлық шұлықтарыңыз тек қара және ақ түсті деп елестетіңіз. Кезекті
кір жуғаннан кейін олар араласып кеткен. Бір түсті жұп шұлық табу
үшін қарамай тұрып, кем дегенде қанша шұлық алуыңыз керек?Шұлықтар
дәл бір ғажайыптағы секілді, сіз оларды алып шыққаннан кейін, өз
түстеріне орай ақ және қара қорапқа түседі. Сіз алып шыққан алғашқы
шұлық ақ түсті болды деп есептелік, енді ойластырайық, келесі шұлық
та ақ түсті болса ше? Бұл жағдайда, есеп шарты орындалды, алайда,
келесі шұлық қара түсті де болуы мүмкін ғой. Тағы бір рет қайталап,
келесі не қара, не ақ шұлықты алып шығамыз. Сәйкесінше, үшінші
шұлық бастапқы шұлықтардың біреуіне мысалыті түрде жұп болады (егер
шұлық әлі жұптаспаған болса). Есебіміздің жауабы – екі түс кезінде
алып шығуға тиесілі ең аз шұлық саны үшке (3)
тең.

№2 есеп. №2 мысалда көрсетілген есепті ақ шұлықтардың саны 14, қара шұлық саны 10 болған жағдайда шешіңіз. №3 мысал. Үштік дәрежесі. Жоғарыдағы мысалдарда біз шарттағы элементтердің ақтық санын қарастырдық. Келесі есепті шығарып көрейік: 001 сандарына аяқталатын үштік дәреже (3a) бар екенін дәлелдеңіздер. Үштік дәрежесіне 30 =1, 31 = 3, 32 =9, 33 = 27, 34 = 81, 35 = 243 осылай жалғаса беретін сандар жатады. Осы сандарды 1000-ға бөліп, барлық мүмкінді қалдықтарды көшіреміз (r): 3a = 1000k + r Мысалы 310 = 59 049 = 59000 + 49 (қалдық), 311 = 177 147 = 177000 + 147 (қалдық) және тағы басқа. Үштік дәрежелері шексіз көп болғандықтан, 0-ден 999-ға дейінгі қалдықтар тура 1000 дана болады. Дирихле қағидасын пайдаланып, 1000-ға бөлген кезде үштіктің екі дәрежесінде бірдей қалдық қалатынын дәлелдейміз. Бұл 3m және 3n сандары болсын. 3m = 1000k + r 3n = 1000q + r Олардың айырмашылығын есептейміз: 3m - 3n= 3n(3(m-n) - 1) = 1000k + r - 1000q - r = 1000(k-q), басқаша айтқанда - 3n және (3(m-n) - 1) көбейтіндісі 1000-ға еселенген. Біз n дәрежесінің қандай мәнінде болмасын, 3n саны 1000-ға еселенуі мүмкін емес екенін білеміз. Сәйкесінше, 1000-ға еселі (3(m-n) – 1) саны болуы тиіс: 3(m-n) - 1 = 1000(k-q) немесе 3(m-n) = 1000(k-q) +1 Осылайша, 001 сандарына аяқталатын үштік дәрежесі бар екенін дәлелдедік! №3 есеп. 17 санының 0001 сандарына аяқталатын дәрежесі бар екенін дәлелдеңіздер.
-
«ЛОГИКА ИНТУИЦИЯҒА ҚАРСЫ» ТАҚЫРЫБЫН ОҚЫТУҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ
Неге көп адам математиканы
ұнатпайды? Ең жиі кездесетін жауаптардың бірі: оның сарқылулығына
байланысты. Кез-келген «анық» жағдайда олар бір нәрсені дәлелдеуге
мәжбүр болады! Бірақ «айқын» қорытындылар жиі дұрыс емес және ұзақ
уақыт сақталады, өйткені біз олардың «дұрыстығына» интуитивті түрде
сенеміз.
Алдымен, біздің математикалық мағынаны тексерейік - келесі сұраққа жауап берейік: А нүктесінен В нүктесіне дейін ең қысқа жол қандай болады? Менің ойымша, қазір көптеген адамдар: «Әлбетте, АБ сегменті» деп ойлаймын. Ал сен, әрине, дұрыс, ал егер мен оны дәлелдеуді сұрасам? Бұл жерде математика үшін жек көретін сезім пайда болады. «Неге? Мәселелерді шешудің интуитивті тәсілі: біз жауапты білеміз, бірақ қалай пайда болды, біз бұл туралы ойламаймыз. Жиі бұл тәсіл жұмыс істейді, тіпті көп уақытты үнемдейді. Бірақ келесі сұраққа жауап беруге тырысайық.
10-дан 20-ға дейін қанша табиғи нөмірлер бар (10 және 20-ны қоса алғанда)? Көптеген адамдар «10» деп жауап береді, өйткені түйсігі бізге де дәл осындай. Және олар қателеседі, өйткені дұрыс жауап «11». Бұны қарапайым іздеу арқылы дәлелдеуге болады: 10-нан 20-ға дейінгі барлық нөмірлерді жазыңыз және оларды қайта есептеңіз. Бірақ мұндай дәлел толығымен әмбебап емес: проблемадағы сандар 10-нан 20-ға дейін емес, 1000-нан 2000-ға дейін болса, не істейміз? Сондай-ақ жазылған және қарастырылған?
Сондықтан 1-ден 20-ға дейінгі 20-ға дейінгі табиғи сандар, бірақ бізге 10-нан толмағандар қажет, демек, 1-ден 9-ға дейінгі барлық нөмірлерді қарастыруға болмайды (дәл 9, 10 емес!). 20 - 9 = 11 болады, бұл дұрыс жауап. Мәселен, 2000 және 2000 жылдардағы мәселеде біз 2000 - 999 = 1001 аламыз және а9-дан b9 дейінгі сандарға арналған жалпы формула: a-b + 1.
Біз түйсігі қалай көмектесті және адастырғаны туралы қарапайым мысалдар келтірдік. Олай болмаған жағдайда, гворяя, интуитивті тәсіл дұрыс шешімге кепілдік бермейді. Математикадан айырмашылығы, бұл сіз дұрыс деп сенуге мүмкіндік береді. Яғни дәлелдер дәлелденуі мүмкін және олар дұрыс емес, бірақ кем дегенде бізде ақиқатты дәлелдеуге мүмкіндік беретін құрал бар.
Әрине, 10-нан 20-ға дейінгі сандар туралы мәселе өте оңай болды. Тиісті жауапты табу оңай емес жерде бірнеше қарама-қайшы мысалдарды қарастырайық. Алдымен осы тапсырмалардың әрқайсысын өзіңіз шешіп көріңіз, содан кейін оқыңыз. Және таңданамын.

1-тапсырма
Қарбыз қыртысы целлюлозаға қарағанда үш есе жіңішке (яғни, сіз қарбыз ортасынан бетіне сызық сызсаңыз, осы сызықтың төрттен үш бөлігі целлюлозаға түседі және қырыққабаттың төрттен бір бөлігі). Қабықтың көлемінен қанша рет целлюлоза көлемі көбірек?
Мысалы, бұл қарбыз идеалды доптың пішіні бар, оның ішіндегі кішігірім доп - ет, содан кейін қыртыс. Мәселен, целлюлоза көлемі қанша рет? Үш кезінде? Тоғызында? Басқа опциялар? Тілек өз жұмысын аяқтады, енді математика өз жұмысын басқарады.
Бір қарбыз - 4x радиусы бар доп, оның ішіндегі 3x радиусы бар шарлар целлюлоза толтырылған, қалғаны - қыртыс. Сонда шарт орындалды, яғни қабықтың қалыңдығы целлюлозаның қалыңдығынан үш есе аз. Доптың формуласы бойынша біз бүкіл қарбыздың көлемі (4х радиусы бар) тең екендігін анықтаймыз:
![]()
және целлюлозаның көлемі (3x радиусы бар)
тең:
![]()
Осылайша, целлюлоза 2764 тұқымдық қарбызды құрайды, ал қыртыстың мөлшері - 3764. Яғни қабықтың көлемі кем емес (3, 9 немесе қанша рет айтқаныңыз), бірақ целлюлозаның көлемінен бір жарым есе көп ...
Логикалық және қарапайым есептеулер осылайша интуитивті қарауды жоққа шығарады.
2-тапсырма
Жер шарша жерге тығыз бекітілген. Содан кейін таспа 1 метрге көтеріліп, планетаның бетінде біркелкі бөлінді. Мысық алшақтығы арқылы жүре ме?

Тағы да, тұжырым жасаңыз: біз Жер деп атаймыз, бірақ бұл дұрыс емес. Мәселен жауап қандай? Тілектің мысықтың сынғаны жөн емес пе? Егер сіз Жерді экваторға кіргізсеңіз, таспаның ұзындығы шамамен 40 000 километрді құрайды, сондықтан 1 метрге көтерілу байқалмайды. Егер біз таспаны жермен біркелкі жылжытуды жалғастыра берсек, нәтиже алған микроскопиялық алшақтық - бұл мысық - құмырсқалар арқылы өтіп кету екіталай емес. Мәселен? Және жоқ!
Жер шарының радиусы R метріне тең (шын мәнінде, ол 6 мың кг-нан сәл асады, бірақ бұл мәселеде бұл бірінші емес). Содан кейін таспа шеңбер ұзындығы формуласына сәйкес 2ррр метр ұзындығына ие. Тиісінше, ұзындығын 1 метрге көтергенде (27TR + 1) метр. Сонымен қатар, таспаны беткі жағынан біркелкі жылжытсақ, онда таспа енді шеңбер жасайды, тек оның радиусы әр түрлі - мысалы, R. Бұл жағдайда таспаның ұзындығы 2ТТР екенін ескеріңіз. Бірақ ол бізді бірнеше жолды жоғары бағалады! Теңдеу:
![]()
Сонымен, жаңа радиусы 1 / 2p
артық. Себебі p 3.14, содан кейін 127 = 0.16. Бұл аралық 0,16 метр
немесе 16 сантиметр болатындығын білдіреді. Және бұл мысық үшін
таспаның астында көтерілу үшін жеткілікті. Магия? Жоқ, тек дұрыс
есептеу. Жылжыту.
3-тапсырма. Бөлмеде 50 адам жиналды. Сол күні олардың екеуі екі туады деп неге ықтималдығы бар? Тағы да, біз қажетті резервация жасаймыз: олардың арасында егіздер жоқ, әйтпесе бұл мәселе қызықтырмайды.
Сонымен, интуитивті жауап дегеніміз не? 10-20 пайыз, мүмкін бе? Шындығында 365 күнде 50 адам бар, бұл жетіншіден аз. Мысалы, шамамен 100: 7, яғни шамамен 1596. Немесе 30 адам бар ма?
Енді математиканы жалғастырайық. Біз жиналғандардың әртүрлі күндерде дүниеге келу ықтималдығын есептейміз (бұл оңайырақ болады), содан кейін нәтижені бірліктен шығарып аламыз. Бұл қалаған жауап болады - сол күні туылған бөлмеде екі адам бар (мүмкін, бір ерлі-зайыпты емес, бірақ бізден бұл туралы сұралмаған, ең бастысы - кем дегенде екі) болуы ықтималдығы. Бірінші адамды қабылдаңыз - ол белгілі бір күні туған. Екінші қарастырайық - оның 365 нұсқасы бар, оның 364-і біз үшін жарамды (біріншіге сәйкес келмеуі үшін). Демек, бірінші және екінші күндерде әртүрлі күндерде туындаған ықтималдығы 364/365 тең.
Енді үшінші орында. Оның
365-тен 363 нұсқасы бар, яғни 363/365 ықтималдығы бар бірінші
немесе екінші күні сол күні туылмаған. Бірақ содан кейін, жұмыс
ережесіне сәйкес, әркім әртүрлі күндерде дүниеге келу ықтималдығы -
364 / 365х363/365. Жағдай төртінші, бесінші, және т.б. елуінші
жылдарға ұқсас, сондықтан олардың әртүрлі күндерде туылғандығына
тең:![]()
Неге 316? Екінші адамға сәйкес келетін фракция 364 (365 - 1), үшінші - 363 (365 - 2) нөлдеріне ие болғандықтан. Осылайша, 50-ші адам үшін 316 нөмір (365-49) болады.
Әрине, оны калькуляторсыз есептеуге болады, бірақ тіпті өте өрескел бағалау да бір нәрсе береді. Мысалы, 316 / 365x317 / 365 соңғы екі фракцияны көбейтсеңіз, нәтиже 0,76-дан кем болады, яғни қажетті ықтималдық (оны алу үшін, еске салу, алу үшін көбейту нәтижесі құрылғыдан алынуы тиіс) 2496-ден артық. Егер сіз барлық фракцияларды көбейтсеңіз, ықтималдық ... 9796! Сену қиын, бірақ шындық.
Сіз ықтималдығы шамамен 5096 болғанын білесіз бе? Қазірдің өзінде 23 адам! Айтпақшы, бұл оңай тексерілуі мүмкін. Бірнеше сабақ алыңыз - 25-30 адам ғана бар. Сыныптастар арасында туған күндері қаншалықты жиі кездесетінін көріңіз. Нәтижесінде сіз таңқаларыңыз болады! Біз сондай-ақ бұл есептерді тексеріп, Конфедерация Кубогындағы футбол командаларының құрамына қарап көрдік. Әрқайсысы 23 адамнан тұратын 8 команда болды - сіз оған сенбейсіз, бірақ төрт командада сол күні туылған ойыншылар болды! Практика теорияны жақсы растады.
Бірнеше мысалды қарастырып, біз өзіміздің бейнеқосылғыларымыз уақытша төмендейтініне көз жеткіздік. Сондықтан интуитивті тұжырымдарды мұқият алайық, оларды сұрастырып, дәлелдеуге тырысыңыз. Бұдан былай, логикалық түйсігі күнделікті мақсаттарға қол жеткізу үшін алға жылжуға көмектеседі деп үміттенеміз, себебі басқа контрастивтік факт 1.01, 37.8 және 0.99365 = 0.03!
-
«ПАРАДОКС ТУРАЛЫ» ТАҚЫРЫБЫН ОҚЫТУҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ
Парадокс болса да, шындық!
Ерте заманнан-ақ ғалымдар мен философтар басқалардан өзгеше
тұжырымдар бар екенін байқаған. Оларды қалай түсіну керектігі
белгісіз еді. Бір қызығы — олар әлі күнге дейін түсініксіз. Бұл
жұмбақ емес, себебі оның жауабы жоқ. Мұндай пайымдауларды парадокс
деп атайды.

Шыншыл
өтірікші. Көптеген парадокстар ерте
уақытта логика деп аталатын ғылым пайда болуымен туындаған еді. Бұл
ғылым, көп жағдайда, не шындыққа жанасатын (шынайы) немесе жалған
(өтірік) пайымдарды зерттейді. Ең танымал және көне парадокстың
бірі – «Өтірікшінің парадоксы» деп аталады. Мысалы, біреу: «Менің
қазір айтып тұрғаным – өтірік» немесе «Мен өтірік айтамын» деді.
Оның бұл сөздерінің тек қана екі мағынасы болуы мүмкін – не
шындықты растау (бұл шынымен солай), немесе жалған (шындығында олай
емес). Сонымен, оның сөзі шындық делік, яғни «Мен өтірік айтамын»
деген адам шындығын айтып тұр. Алайда, ол шын айтып тұрғандықтан,
оның «Мен өтірік айтамын» деген сөзі – өтірік. Нәтижесінде, егер
пайымдау шындық болса, бұл оның өтірік екеніне алып келеді. Ал енді
бұл олай емес, оның айтып тұрғаны өтірік екенін қарастырып көрелік.
Яғни, мен «Өтірік айтамын» дей тұра, ол алдап тұр. Алайда, бұл
жағдайда ол шын мәнінде өтірік айтады және оның «Мен өтірік
айтамын» деген мақұлдауы – шындық. Енді біздің пайымдау – өтірік
деген тұжырымымыз, оның шындық екеніне алып келеді. Рас, қанша
айналдырсақ та – мұндай пайымдауды біз бір уақытта шынайы және
жалған деп қабылдауға мәжбүрміз. Міне, бұл – парадокс! Өтірікшінің
парадоксы негізінде көптеген парадокстар туындаған, олардың барлығы
логикалық деп аталады. Мысалы, белгілі ертегі кейіпкері Буратино
таңғажайып қасиетке ие: ол өтірік айтқан кезде, оның мұрны ұзарады.
Ендеше, егер ол «Қазір менің мұрным ұзарады» дейтін болса,
Буратиноның мұрнына не болады? Логикалық тұрғыда талқылап байқайық.
Егер Буратино шындықты айтса, оның мұрны ұзармауы керек. Алайда,
егер мұрын ұзармаса, Буратино өтірік айтты деген сөз және оның
мұрны ұзаруы тиіс. Енді Буратино өтірік айтты делік, онда оның
мұрны ұзарады. Әйтсе де, егер мұрын ұзарса, Буратино шындықты
айтты, сәйкесінше мұрын ұзармауы керек. Мүмкін, Папа Карлоның
айлакер ұлы мұндай жағдайды пайдаланып, парадокс туралы есепті
шешімсіз қалдыруды жөн көрген болар, нәтижесінде оның мұрны тоқтап
қалды да, енді ұзармайтын болды. Логикалық түрінен басқа
парадокстардың өз-өзіне қатысты деген түрі бар. Мұндай парадокстың
басты кейіпкері өзінің шарттарын өзіне қолданып көрмек болады. ХХ
ғасырдың басында танымал британдық философ және математик Бертран
Рассел математикалық теориялардың бірімен айналысу үстінде, келесі
парадоксты ойлап тапты. Бір ауылда жалғыз сақал-мұрт қыратын
шаштараз болды. Оның жұмысының қатаң ережесі бар еді: ол тек қана
өздері қырынбайтын ауыл тұрғындарын қырындыруы керек. Бір
қарағанда, тәп-тәуір ереже секілді. Дегенмен, шаштараздың өзінің де
сақал-мұрты өседі, осы кезде сұрақ пайда болды: ол өз сақалын өзі
қыра ала ма? Нәтижесінде, қыра алатын және қыра алмайтын болып
шығады. Өзің ойлап қарашы:

Бертран Рассел — ағылшынның көрнекті философы, логигі, қоғам қайраткері. Расселдің математикалық логика мен қатынастар логикасы жөніндегі еңбектері логикалық ғылымға енген зор үлес болды. 1950 жылы әдебиеттен Нобель сыйлығының лауреаты атанды.
Шексіздікті есептеу.
Мектептегі математика
сабағынан барлығымыз натурал сандардың не екенін жақсы білеміз:
1,2,3,4,5… және осылай шексіз жалғаса береді. Дегенмен, шексіздік
сөзінің түсінігі бұл сандардың парадоксалды сипаттарына алып келді.
Натурал сандардың ішінде жұп сандардың бар екені белгілі. Кейде
натурал сандар жұп сандарға қарағанда көп сияқты көрінеді. Бір
жағынан логикаға да қонымды, себебі жұп сандар — натурал сандардың
бір бөлігі ғана емес пе? Алайда, математика натурал сандар қанша
болса, жұп сандардың да сонша екенін алға тартады! Көз алдарыңа екі
жолды елестетіп көріңдер, оның біріншісінде барлық натурал сандар,
екіншісінде бірінші жолдағы әр санды екіге көбейткен кезде алынған
сандар тізілген (яғни 1×2 = 2, 2×2 = 4, 3×2 = 6, 4×2 = 8, 5×2 =
10…):
![]()
Осылайша, егер сандар жазылған
осы екі жолды шексіз жалғасытыра берсек, онда әрбір натурал санның
астында жұп сан тұратын болады. Олай болса, жұп сандар натурал
сандардан аз емес. Шексіздіктің бұл ғажайып сипатына XVII ғасырда
атақты италияндық ғалым Галилео Галилей назар аударған және
алғашқылардың бірі болып осы парадоксты
тұжырымдаған.

Галилео
Галилей — итальян философы, математик,
физик, механик және астроном, табиғаттану ғылымдарының негізін
салушы, өз заманындағы ғылымға өте қатты әсер еткен. Ол ұлы ғалым
болумен бірге, музыкант, суретші, ақын, әдебиетші де болған.
Галилей - тәжірибелі физика мен классикалық механиканың негізін
қалаушы. Ешқандай қозғалыс мүмкін емес Парадокстар тек математикада
ғана емес, егер физикалық процестерге ойша қарайтын болсақ,
физикада да пайда болады. Тіпті, ерте заманның өзінде-ақ, ғалымдар
сезім мүшелерінің бізді алдауы мүмкін екенін және табиғатты зерттеу
барысында әрдайым оларға сене бермеу керектігін жақсы түсінген.
Мысалы, біз Күн Жерді айналмайтынын, мүлде керісінше екенін
білеміз. Сондай-ақ біздің көзіміз оларды көрмесе де, молекулалардың
бар екені де белгілі. Ертедегі ғалымдар дененің қозғалысын көзбен
емес, ақылмен зерттеген уақытта қызықты парадоксқа тап болғандары
таң қалатын жағдай емес. Адам А нүктесінен Б нүктесіне қарай
қозғалып барады. Ежелгі философ бұл жағдайды: адам А нүтесінен Б
нүктесіне жету үшін алдымен бұл қашықтықтың жартысын жүріп өтуі
керек деп талқылайды. Әрине, ешкімнің дауы жоқ. Солай болуы да
керек. Алайда, қазымыр философ мұнымен тоқталмай, жолдың жартысына
жету үшін адам алдымен төрттен бір бөлігін өтуі тиіс (яғни,
жартының жартысын) дегенді алға тартады. Бұл жерде де келісуге тура
келеді. Енді ғалым бұл кесіндіні де екіге бөлу керек деп есептейді…
Бұл пайымдау шексіздікке дейін жалғаса беруі мүмкін. Соңында адам
орнынан қозғала да алмай қалады — себебі, ол әуелі шексіздікке
дейін жолдың тым болмаса бір кішкентай бөлігін жүріп өтуі
керек.

Яғни, қозғалыс жоқ, себебі оны
жүзеге асыру мүмкін емес! Алайда, әлемдегінің бәрі қандай да бір
парадоксқа көңіл аудармастан қозғалуда. Себебі, қозғалыс — үздіксіз
процесс, оны бір кесіндіні шексіз жүріп өту түрінде қарастырудың
қажеті жоқ. Және бұл Пушкиннің тұсында да баршаға кеңінен белгілі
болған еді. Естеріңде болса, ақын: «Қозғалыс жоқ, деген еді
данышпан, Үн қатпады, жүре бастады алыстан. Мұнан артық жауап ойлап
табар ма, Қолдай берді қалғандары қалыспай…» деп жырға қосқан еді.
Парадокс немесе өмір Енді бір парадокстар бір қарағанда ғана сондай
сияқты болып көрінеді, ал шындығында — ешқандай парадокс емес. Аңыз
бойынша, баяғыда бір философты өлім жазасына кесіпті. Ол түрмеде
отырып, үкімнің жүзеге асуын күтеді. Жексенбі күні түрме басшысы
келіп, оны екі ереже бойынша жазалайтынын жеткізеді: біріншіден,
өлім жазасы келесі аптаның бір күнінде, түс уақытында болады,
екіншіден, жазаны жүзеге асыратын күн тұтқын үшін беймәлім
болмақ.

Философ айтылғандарды талқылай
бастайды. Оны келесі аптаның жексенбісінде жазалаулары мүмкін емес,
себебі, өздері атқандай, жаза келесі апта іске асуы керек, ал егер
оны дүйсенбі мен сенбі арасындағы күндердің бір де біреуінде
жазаламаса, онда өлім күні ол үшін аяқ астынан болмайды. Былай
айтқанда, тұтқын философ сенбі күніне дейін аман қалса, жазаның
орындалуына ертеңгі күн қалады (жексенбі). Олай болса, жаза күні
беймәлім болмай қалады. Ал бұл ережеге қарсы шығады. Яғни, жексенбі
жазаны жүзеге асыратын күн бола алмайды. Онда оны сенбі күні де
жазалай алмайды, себебі егер оны дүйсенбі мен жұманың арасындағы
бір күні өлтірмесе, онда жаза сенбі күні қолданылуы керек (өйткені,
жексенбі тізімнен шығып қалған), осылайша өлім күні тағы да
кенеттен болмай қалады. Енді, ары қарай жылжиық. Тура осы
тұжырымдарға байланысты, жұма да тізімнен шығарылады: жексенбі мен
сенбі бұған дейін шығып қалған, яғни, егер дүйсенбі мен бейсенбінің
арасындағы бір күнде өлім жазасына кеспесе, жұма жазаны қолданатын
беймәлім күн болмай
қалады.

Дәл осылай ол бейсенбіні де,
артынан аптаның барлық күндерін жоққа шығарды. Соңында ережеге
сәйкес, оны келесі аптаның бір де бір күнінде өлім жазасына кесе
алмайды деген шешімге келді. Өз тұжырымына өзі қатты қуанып
отырғанда, сейсенбі күні жендеттер келіп есік қаққанда, қуанышы су
сепкендей басылды. Әрине, түрме басшысының бейшара философ секілді
парадокстарға мән бермейтіні өкінішті-ақ, алайда, мәселе онда емес.
Негізі, үкімі шығып қойған тұтқын аптаның әр күнін логикалық
тұрғыда тізімнен шығара отырып, ақырында аптаның әр күнін өзі үшін
өлім жазасы кесілетін беймәлім күнге айналдырды! Сондықтан да,
парадокстармен абай болған
дұрыс!
-
«ПРОКРУСТ ӘДІСІ» ТАҚЫРЫБЫ ОҚЫТУҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ

<<Прокруст төсегі >> деген тіркесті естіп пе едіңіздер? әңгіме
гректердің аңызына арқау болған прокруст қарақшы жайлы болмақ.
айтпақшы ол далада қаңғырып жүрген қайдағы біреу емес,атақты теңіз
әміршісі посейдонның ұлы. сонымен ,осы прокруст жолаушыларды алдап-арбап өз үйіне кіргізіп,жоғарыда сөз болған төсегіне жатқызып,оларды сол төсектің өлшеміне қарай <<теңестіретін>> болған.
егер төсек ұзын болса, аяқтарын кескен. ал оның төсекке дәл келгендерді не істегені жайлы тарихта ештеме айтылмайды. қалай болғанда да ,ежелгі гректер әділдікті үстем қылып, ақыры прокрустың өзі де өмірімен сол төсекте қоштасқан. бір қызығы,оның осы идеясы аяқ астынан математикада қолданыс тапқан.
<<Прокруст төсегі >> тіркесі баяғыдан-ақ қанатты сөзге айналған және елеулі дүниені құрбандыққа шалуды талап ететін қатаң теңдікті білдіреді. аталған тұрақты тіркестің жағымсыз мағынасына қарамастан, ажыратушы нысандарды теңестіру идеясы математикалық есептерде қолданыс тапқан. қорықпаңыздар ,біз ешкімнің ештеңесін кесіп тастамаймыз –жай ғана ұқсас қағиданы қолданамыз.

1 есеп . екі сөреде жалпы саны 30 кітап тұр, дегенмен бір сөредегі кітап саны екіншіншісінен 4-ке артық. әр сөреде неше кітап бар ?
әрине, бұл есепті іріктеу арқылы шешуге болады –алаййда ,табылған шешімнің жалғыздығына қатысты сұрақ туындайтыны сөзсіз. сөрелердің біріндегі кітап маны х түрінде белгілеп , ауыспалылық енгізе отырып, теңдеуді шешуге де болады. бірақ ,біріншіден мұны жазып жату ұзақ, екіншіден, біз теңдеу құруды және шығаруды бірден үйренбейміз. ал прокруст әдісі санаудан басқа ешқандай машықты талап етпейді.
сонымен , сөрелердегі кітаптарды теңестіріп көрейік. бізге сөрелердің біріндегі кітап 4-ке артық екені белгілі, ендеше оларды ала тұрайық. яғни ,екіншісіне қоймаймыз , мүлде бөлек алып қоямыз. енді сөрелердегі кітап сандары тең ! дегенмен, олардың жалпы жиынтығы 30 емес, біз 4 өеуін алып тастағандықтан, 26 болып қалды. ендеше , әр сөреде 13 кітап(26:2 ,себебі кітаптар саны тең ). енді 4 кітапты орнына қайтарып ,соңғы жауапты табу қалды;бір сөреде 13 кітап, екіншісінде -17.
есепті шығаруға көмектескен не ? біз прокруст әдісін бейбіт жолмен пайдаланып –сөрелердегі кітап санын теңестіріп, алынған санды екіге бөліп,берілген сұраққа жауап бердік. тағы бір мысалды қарастырайық.
прокруст төсегінің образы –нассим николас талебтің «черный лебедь>> және «антихрупкость>> бестселлерлерінің басты идеяларының бірі.
бұл жасанды шектеулерге тән қорытындылар шығаратын заманауи шешім қабылдау жүйелеріне аллегория


2 есеп . мектепте үш математика үйірмесі бар; бірінші сынып үшін , екінші сынып үшін және үшінші сыныптар үшін .бірінші үйңрмеде екіншісіне қарағанда екі адам артық,ал екіншісінде –үшіншісінен үш адам артық. үйірмеге барлығы 65 оқушы қатысады. әр үйірмеге неше адамнан барады?
сонымен, бірінші үйірмеге екіншісінен екі адам артық қатысады. үйірмеге қатысушылар санын теңестірейік. алаңдамаңыздар,біздер бірінші сыныптың екі оқушысына қатысты ешқандай озбырлық әрекетке бармаймыз! олар белгілі бір себептерге қатысты үйірмеге келмей қалды делік . олай болса, алғашқы екі үйірмедегі балалар саны тең ,әрі олар 2-ге азайғандықтан 63-ті құрайды .
үшінші үйірмеге екіншіісімен салыстырғанда үш адам кем барады (естерңізге сала кетейік ,біз екінші үйірмедегі балалар санын ауыстырған жоқпыз.) теңестіреміз ;айталық, үшінші үйірмеге тағы үш адам жазылды. сонда барлық үш үйірмедегі адам саны 66-ға тең.сонда әр үйірмеге 22 адамнан қатысады деген сөз!
енді соңғы жауапаты алу қалды.біз екінші үйірмеге тиіскен жоқпыз, яғни мұнда әу бастан 22 адам болды деген сөз. біріншіде теңестіргенге дейін екі оқушы артық болатын,яғни онда 24 бірінші сынып оқушысы бар. ең соңғы үшіншіге біз үш адамды қосқанбыз,яғни шын мәнінде онда 19 үшінші сынып оқушысы бар . алақай!
нысан үштен де көп болған жағдайда есептер дәл осыған ұқсас жолдармен шешіледі. Дегенмен, біз басқа жағдайды қарастырып көрейік.әңгіме бас пен аяқтарға қатысты есеп жайлы болмақ. жо-жоқ,бұл жерде прокрустың қатыс жоқ! жоғарыда есептер секілді, бірде бір бас , бірде бір аяқ зардап шекпейді!.әйтседе .....қысқасы ,іске кірісейік.

3 есеп .аулада тауықтар мен ешкілер жүр.арман ауладан 20 бас пен 48 аяқ санады(ол өзінің басы мен аяғын есепке алған жоқ). аулада неше тауық және неше ешкі жүр?
бұл жерде мәселе неде? мәселе тауықтар мен ешкілердің аяқ санының тең еместігінде.егер әңгіме тек тауықтар жайлы болса ,біз аяқ санын тең бөліп-керекті мөлшерді алар едік(айтпақшы,ондайда бастың саны артық ақпарат болар еді).ешкілердің жағдайында төртке бөлеміз.ал , біздің жағдайда ауладағылардың біразының аяғы екеуден,қалғаныкі төрттен. не істеу керек ?
олай болса, теңестірейік!ешкілердің аяқтары төрттен емес ,екіден болсын.әу бастан ешкімге зиянымызды тигізбейміз деп сөз бергендіктен, ешкілерартқы аяқтарымен тік тұрып,алдыңғылары әуеде қалықтап жүр деп елестетейік. ендеше ,аулада 20 жануар (бас санына қарай )жайылып жүрген болса,мұнда 40 аяқ бар –әр жануарға екі аяқтан .дегенмен, арман 48 аяқ санаған болатын ,яғни әлі 8 аяқ есепке алынған жоқ.айтпақшы ,ешкілеріміз артқы аяқтарымен тік тұрғандықтан ,алдыңғы аяқтары да есепке алынбай қалды емес пе ?!олай ,болса солардың саны сегіз деген сөз.әр ешкінің алдыңғы екі болатыны есепті,барлығы 8;2=4 ешкі .қорытынды аулада 4 ешкі және 16 тауық жүр.

4 есеп .бір қалам және екі қарындаш қанша тұрса , бес қалам және біір қарындаш сонша тұрады.қарындаш қаламнан неше есе қымбат?
бірден басын ашып алайық,бұл жерде барлық қалам бір бағада сатылады ,қарындаштар да дәл солай деген сөз.әрине,бұл есепті екі ауыспалыны енгізу арқылы шешуге болады.әйтсе де,қысқа әрі әдемі шешім тұрғанда,зеңбірекпен торғай атудың қажеті қанша ?айталық,бір жинақта бес қалам және қарындаштар жатыр ,екіншісінде –екі қарындаш және қалам.кеңсе тауарларының қалған жиынтығы бұрынғыша бірдей тұрады ,солай емес па ? әрі бірінші жиынтықта төрт қалам ,ал екіншісінде –бір қарындаш қалады(солай, бір ғана заттан тұратын жиынтық.....негізі,жиынтық пародоксы мен тақ логика жайлы біз алдағы нөмірлердің бірінде білетін боламыз ).
сонымен,қарындаш қаламнан төрт есе қымбат тұрады.
есепті шешуге не көмектесті?нысандарды теңестіре отырып ,артығын алып тастау мүмкіндігі. прокрусттың әрекеті арқылы туындаған дәл осы идеяны бұдан да күрделірек жағдайларда қолдануға болад.

5 есеп.оюшы әріптері бар тақта жасады.бірдей әріптерді ол бірдей уақыт ішінде ояды.әртүрлілерін әртүрлі уақытта ойса керек .ол орыс тіліндегі –«дом моды»және «вход» сөздері жазылған тақтаға 50 мин жұмсады,ал «в дымоход»тақтасын 35 мин аяқтады.олай болса ,оюшы «вход» деген тақтаны қанша уақытта жасап шығады?
бұл жерде теңестірудің көп көмегі тие қоймас,сондықтан артық әріптерді алып тастаған дұрыс болар .бірінші жағдайда д,о,м,м,о,д,ы,в,х,о,д әріптерінен жасады.екіншісінде –в,д,ы,м,о,х,о,д.екінші тізімдегі әріптерді біріншісінен сызып тастау арқылы біз;д,о және м деген әріптерді аламыз.ендеше,бірінші жағдайда оюшы 15 минутты көбірек жұмсаса ,сол 15 минут дәл осы біз тапқан «артық» әріптер –д,о және м –ға кеткен болуы тиіс.енді сұрағымызға қайтып оралайық;»выход»сөзіне қанша уақыт кетеді?назар аударыңыздар; бұл сөз «в дымоход» сөзіне дәл осы д,о және м әріптерімен ерекшеленеді.олай болса,оюшы «выход» сөзіне қарағанда 15 мин аз жұмсады,яғни 20 мин.
қорыта келе мынадай есепті талқылап көрейік.

6 есеп.торт шаршы негізді қорапқа оралған.қораптың биіктігі осы қораптың қабырғаларынан екі есе кіші .ұзындығы 156 см баудың көмегімен қорапты байлап,үстінен бантик жасауға болады(сол жақтағы суреттегі секілді).ал оны дәл осындай бантикпен бүйірінен байлау үшін (оң жақтағы суреттегі секілді ) ұзындығы 178 см бау керек.қораптардың өлшемін табыңыздар.
тағы да теңестіру жағын қоя тұрып,аталған тәсілдердің ортақ тұсын қарастырайық.бірінші жағдайда баудың қорапты бүйір тұсынан буындайтын төрт бөлігі (қысқа ),астынан және үстінен (ұзын )-төртеу ,сондай –ақ бантик бар екені түсінікті.екінші жағдайда баудың екі қысқа бөлігі (оң және сол жағында бір -бірден ) ,алты ұзын бөлік және дәл соендай бантик бар .әрі екінші тәсіл біріншісінен 22 смге ұзынырақ.және егер біз ортағын алып тастасақ,айырмашылық сол қалпы қалады. бұл тәсілдерлің ортақ неде? екі қысқа бөлігі ұзынынан 11 см-ге кіші.енді қысқа бөлік ұзын бөліктің жартысын құрайтынын, яғни өз ұзындыққа қысқа екенін еске алу қалды.олай болса,қысқа бөліктің ұзындығы-11 см ,ұзын бөліктікі-22 см.қораптың өлшемі;11х22х22
сонымен,тіпті,қатыгезқарақшылардың өзі жан түршігерлік әдістері арқылы ұрпағына пайдалы қызмет қалдыруы мүмкін екен.бастысы,жауыздық идеясын ысырып тастап,оны оңтайлы пайдалана білудің саласын табу жеткілікті.
-
«ТИІМДІ КӨБЕЙТУ ТӘСІЛДЕРІ» ТАҚЫРЫБЫН ОҚЫТУҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ
Қазіргі кезде мектепке, өндіріске электронды есептеу машиналары(ЭЕМ) кеңінен ене бастады. Микрокалькулатор оқушылардың кәдімгі оқу құралына айналды. Бұл өте қуанышты жағдай. Өкінішке орай, бұның есесіне оқушылардың есептеу бейімділігі төмендеуі байқалады. Бұған мысалы жоғарғы сынып оқушылары өздері 7-сыныпта өткен қысқаша көбейту формулаларын есептеу жұмысын жеңілдетуге қолдана білмеуі. Айталық, 47*53 көбейтіндісін табу керек делік. Бұл есептеуді
(а – в)(а + в) = а2 – в2
формуласын пайдаланып жеңіл түрге келтіруге болады:
47*53 =(50-3)(50+3)=502-32 =2500-9=2491
Енді ойша есептеудің кейбір түрлерін қарастырайық.
-
5-пен аяқталатын санның квадратын табу:
(а+в)2=а2+2ав+в2 осы формуладағы в=5 деп алсақ, (а+5)2=а2+10а+25=а(а+10)+25. Егер а ондық саны болса, а+10 оған тетелес келетін ондық.
Мысалы: а=60 болса,60+10=70 болады.
Сондықтан 5-пен аяқталатын санның квадратын табу үшін, ондық
санын көрсететін натурал саннан үлкен тетелес келетін натурал санға
көбейтіп оған 5- тің квадраты 25 санын тіркеп жазу керек.
Мысалы: 352 = 1225,өйткені 3*4= 12, 5*5= 25 кейін тіркеп жазсақ 1225шығады.
Соңғы 5 цифрын квадраттап,оның алдына келесі разрядтағы санды өзінен 1-ге артық санмен көбейтіп, 5-тің квадраты 25 санының алдына жазады.
Мысалы: 252=625 a) 52=25 b) 2*(2+1)=6
3052=93025 a) 52=25 b) 30*(30+1)=930
II. 50-ге жақын санның квадратын табу.
х =50+а болсын х2 = (50+а)2=2500+100а+а2 =100(25+а)+а2.
х2=100(25+а )+ а2=100(25+х-50)+а2= 100(х-25)+а2
Сондықтан, 50-ге жақын санның квадратын табу үшін, сол саннан 25- ті алып, оған сол санның 50 – мен айырмасының квадратын тіркеп жазу керек.
Мысалы: 572 = 3249 өйткені берілген санмен 25-тің айырмасы 57-25=32
берілген санмен 50- дің айырмасы 57-50=7, бұл айырманың квадраты 72=49.
Енді 32-ге 49 санын тіркеп жазсақ 3249 шығады. Сол сияқты, 582=3364,
өйткені 58- 25= 33, 58 – 50=8, 82= 64.
III. 100-ге жақын санның квадратын табу.
100- ге жақын санның квадратын табу үшін, әрбір санды 100- ден азайтамыз, 972= 97*97, айтып өткендей әрбір санды 100-ден азайтамын;100-97=3. Содан кейін азайтындының мәнін бір-біріне көбейтемін де және бір-біріне қосамын (3*3=9; 3+3=6), осыдан кейін қосындының мәнін 100-ден азайтамын(100-6=94).
Енді көбейтіндінің мәні бір таңбалы 9саны болғандықтан алдына 0-ді қоямын, ал егерде көбейтіндінің мәні екі таңбалы болса 0-ді қоймаймын, сол санның өзін тіркеп жазамын, егер үш таңбалы сан болса онда жүздігін айырманың мәніне қосамын да оның алдына 94 –ті тіркеп жазамын. Ең соңында 972=9409 болады.
1) Әрбір санымды 100-ден азайтамын.
2) Шыққан мәндерін көбейтемін және қосамын.
3) Қосқандағы мәнін 100-ден азайтамын.
4) Ең соңында бәрін тіркеп жазамын.
100-ге жақын санның квадратын табу (2-ші тәсілі)
100- ге жақын санның көбейтіндісін табу да 2-ші тәсілі өте қарапайым және тез орындалады , бұл жерде көп ойланудың қатысы жоқ.
Мысалы:
942
![]()
![]()
![]()
![]()
![]()
![]() 92 9*4*2
42
92 9*4*2
42
81 72 16
817216
8 1+7 2+1 6
8 8 3 6 Мына жерде соңғы санның алдынан
екі-екіден бөлемін де бір-біріне қосамын,
содан кейін бәрін тіркеп жазамын.
100- ге жақын санның квадратын табу (3-ші тәсілі)
а=100-х, в=100-у. Бұл жердегі х-пен у, а және в сандарының 100 санымен
айырмалар екендігі көрініп тұр. Енді екі санның көбейтіндісін табамыз.
а*b=(100-x)(100-y)=10000-100(x+y)2+xy=100-(a-y)+xy=100(b-x)+xy яғни а*b=100*(a-y)+xy немесе а*в=100(b-x)+xy сондықтан, 100-ге жақын екі
санның көбейтіндісін табу үшін бірінші көбейткіштен екінші көбейткіштің айырмасын алып немесе екінші көбейткіштен бірінші көбейткіштің айырмасын алып оған айырмалардың көбейтіндісін тіркеп жазу керек.
Мысалға: 952=95*95 ; 100-95=5, содан 95-5=90 болады. Ал енді айырмаың квадраты 5*5=25 ендеше 90-ға 25-ті тіркеп жазсақ 9025 шығады.
IV. 100-ден артық санның квадратын табу.
Егерде санымыз 100- ден артық болса а=100+х, в=100+у, онда көбейтінді
ав=(100+х)(100+у)= 10000+100(х+у)+ху=100(100+х+у)+ху=100(а+у)+ху
=100(в+х)+ху болады.
Яғни, ав=100(а+у)+ху немесе ав=100(в+х)+ху
Мысалы: 103*103=10609. Себебі: (103-100=3;103-100=3) 103+3=106 осыдан кейін айырманың мәндерін көбейтемін 3*3=9, 106 санына 09 санын тіркеп жазсақ 10609 болады.(0-ді қойған себебім;егерде азайтынды мәні бір таңбалы болса ол санның алдына 0-ді қоямын, ал егер екі таңбалы болса қоймаймын).
100-ден артық санның квадратын табу (2-ші тәсілі)
100-ден артық санның квадратын табу да 2-нші тәсілі қарапайым және оңай. Бұл жерде логикалық түрде тез есептеуге болады.а=х-100, в=у-100. Бұл жердегі х-пен у, а және в сандарының 100 саныменайырмалар екендігі көрініп тұр. Енді екі санның көбейтіндісін табамыз. а*b=(100-x)(100-y)=10000-100(x+y)2+xy=100-(a-y)+xy=100(b-x)+xy яғни а*b=100*(a-y)+xy немесе а*в= =100(b-x)+xy сондықтан.
Мысалға: 1042=104*104 ; 104-100=4 ,
4*4=16; 4+4=8 Кейін:10816 болады.
Көбейтіндінің мәнін соңғы сан қылдырып тіркеп қоямын , ал қосындының мәнін соңғы санның алдына қоямын (егерде қосындының мәні 0-ден 9-ға дейін болса, қосындының мәнінің алдына 0 санын қоямыз;егер 9-дан асса қоймаймыз) және әрдайым олардың алдына 1 санын қоямын. Ендеше бәрін тіркеп жазсақ 10816 болады.
Саусақпен санау. Саусақ арқылы санның квадратын табу. Көбейтудің әр түрлі әдістері.
Саусақтарды бүгіп санау ерте заманда кең қолданылып келді.Адамның саусақтары мен олардың буындары,сондай-ақ саусақтарын бүгу және жазу,қолдарын бүгу мен жазу олардың ондаған және жүздеген мыңға дейін санай алуына ғана емес,сол сияқты кейбір арифметикалық амалдарды орындауына да мүмкіндік берді .Айталық ,6-ны 7-ге көбейту керек болсын.Сол қолымыздың жұдырығын жазбастан,бір-бірлеп саусағымызды жаза отырып, 6-ға дейін санаймыз.Ал оң қолымыздың саусақтарымен дәл соны қайталап, 7-ге дейін санаймыз.Оң қолдын жазылған екі саусағын сол қолдың жазылған бір саусағынан үстіне саламыз.Жазылған саусақ небары 3–еу болады,бұл-3 ондық, яғни 30 болады.Қалған төртеуі (сол қолдың бүгілулі тұрған саусақтары) 3-ке (оң қолдын бүгілулі саусақтарына) көбейтіледі,сонда 12 шығады.
Сөйтіп , 30+12=42
Осылайша : 6*8=(1+3)*10+4*2=48
6*9=(1+4)*10+4*1=54
Мәселен ,13-ті 14-ке көбейту былайша орындалатын еді.
1) 10*10=100 екені белгілі. Бұдан кейін:
2) бір қолдың 3 саусағын ,екінші қолдың 4 саусағын бүгеді.
3) 3+4=7 ,бұл-ондықтар,яғни 7*10=70
4) 3*4=12,бұл бірліктер.Сонымен:
5) 13*14=10*10+7*10+3*4=182.

![]()
![]()
![]()


![]()



1) 13*14=(3+4)*10+3*4+102 =70+12+100=182 Сол сияқты:
2) 53*54=(3+4)*50+3*4+502=350+12+2500=2862
3) 63*67=(3+7)*60+3*7+602 =600+21+3600=4221


![]()
![]()
![]()
![]()
![]()
![]()

1) 19*17=(4+2)*20+1*3+10*20=120+3+200=323
Сол сияқты:
2) 79*77=(4+2)*80+1*3+70*80=480+3+5600=6083
Дәл осындай әдіспен саусақ арқылы кез-келген санның квадратын табуға болады.
Мәселен ,14-ті 14-ке көбейту былайша орындалатын еді.
1) 10*10=100 екені белгілі. Бұдан кейін:
2) бір қолдың 4 саусағын ,екінші қолдың 4 саусағын бүгеді.
3) 4+4=8 ,бұл-ондықтар,яғни 8*10=80
4) 4*4=16,бұл бірліктер.Сонымен:
5) 14*14=10*10+8*10+4*4=100+80+16=196.
Сол сияқты мысалдар:
1) 13*13=10*10+6*10+3*3=100+60+9=169.
2) 11*11=10*10+2*10+1*1=100+20+1=121
3) 12*12=10*10+4*10+2*2=100+40+4=144
4) 54*54=(4+4)*50+4*4+502=400+16+2500=2916
5) 43*43=(3+3)*40+3*3+402=240+9+1600=1849
Осы сияқты дәлелдеулерге көз жеткізгеннен кейін төмендегідей мысалдарды шығаруға болады.
I
1. 752=5625, өйткені 7*8=56
2. 852=7221, өйткені 8*9=72
3. 152= 225, өйткені 1*2=2
II
1. 492=2401 өйткені 49 -25=24, 50 - 49=1, 12=1
2. 622=3844 өйткені 62- 25=37, 62- 50=12,122=144
III
1. 962=9216
2. 972=9419
3. 982=9604
4. 1082=11664
5. 1092=11881
1. “n0m” (n нөл m) түріндегі үш орынды санның квадратын ойша есептеп
табу керек. Мұндағы n=1,2,…9, m=1,2,…9
n0m2= (n· 100+m)2=n2·10000+2· n· m· 100+m2=(n2·100+2·n·m) ·100+m2
Мысалы: 1. 2032=(200+3)2=(400+12)·100+9=41209
Анықтама 1.1. “n0m” түріндегі санды квадраттағанда, соңғы екі
цифры квадратталатын санның соңғы цифрының квадраты, ал оның
алдындағы екі цифр квадратталатын санның бірінші және соңғы
цифрларының екі еселенген көбейтіндісі және оның алдына бірінші цифрдың квадраты жазылады.
2. 6092=(600+9)2=(3600+108)·100+81=370881.
Жалпы қорыта келсек, мынандай ереже аламыз:
Анықтама 1.2. Егер санның бірінші және соңғы цифрының екі
еселенген көбейтіндісі үш орынды сан болса, онда оның соңғы екі цифрын
қалдырып, жүздік цифрын бірінші цифрдың квадратына қосамыз. 92=81,
2·6·9=108 қорытынды бойынша 08-ді жазып, 1-ді 62=36-ға қосамыз 36+1=37
Осы үрдіс “n0m” түріндегі сандардың квадраттарын табу үшін жалғаса береді.
1-тәсіл: 1) Әрбір санымды 100-ден азайтамын.
2) Шыққан мәндерін көбейтемін және қосамын.
3) Қосқандағы мәнін 100-ден азайтамын.
4) Ең соңында бәрін тіркеп жазамын.
2-тәсіл:
![]()
![]()
![]() 942
942
![]()
![]()
![]() 92 9*4*2
42
92 9*4*2
42
81 72 16
817216 Мына жерде соңғы санның алдынан
8 1+7 2+1 6 екі-екіден бөлемін де бір-біріне қосамын,
8 8 3 6 содан кейін бәрін тіркеп жазамын.
3-тәсіл:
Мысалға: 952=95*95 ; 100-95=5,100-95=5 содан 95-5=90 болады. Ал енді айырмалардың көбейтіндісі 5*5=25 ендеше 90-ға 25-ті тіркеп жазсақ 9025 шығады.
IV
1-тәсіл:
Мысалы: 103*103=10609. (103-100=3) Себебі, 103+3=106 немесе керісінше қалдықтар көбейтіндісі 3*3=9, 106 санына 09 санын тіркеп жазсақ 10609 болады.
2-тәсіл:
Мысалға: 1042=104*104 ; 104-100=4 ,104-100=4. 4*4=16; 4+4=8
(Егерде қосындының мәні 0-ден 9-ға дейін болса, қосындының мәнінің алдына 0 санын қоямын;егер 9-дан асса қоймаймыз) және әрдайым олардың алдына 1 санын қоямын. Ендеше бәрін тіркеп жазсақ 10816 болады.
V
Мәселен ,13-ті 14-ке көбейту былайша орындалатын еді.
1)10*10=100 екені белгілі. Бұдан кейін:
2)бір қолдың 3 саусағын ,екінші қолдың 4 саусағын бүгеді.
3)3+4=7 ,бұл-ондықтар,яғни 7*10=70
4)3*4=12,бұл бірліктер. Сонымен:
5)13*14=10*10+7*10+3*4=182.
Мәселен ,14-ті 14-ке көбейту былайша орындалатын еді.

1) 10*10=100 екені белгілі. Бұдан кейін:
2) бір қолдың 4 саусағын ,екінші қолдың 4 саусағын бүгеді.
3) 4+4=8 ,бұл-ондықтар,яғни 8*10=80
4) 4*4=16,бұл бірліктер.Сонымен:
5) 14*14=10*10+8*10+4*4=100+80+16=196.
1) 13*13=10*10+6*10+3*3=100+60+9=169.
Ауызша есептеулермен жүйелі түрде айналысу оқушылардың математикаға қызығушылығын артырады, уақытты үнемдеуге көмектеседі, математикалық есептеу мәдениетін жоғарлатады.
-
«САНДАРДЫҢ БӨЛІНГІШТІГІ ҚАСИЕТТЕРІНІҢ ПРАКТИКАЛЫҚ МАҢЫЗДЫЛЫҒЫ» ТАҚЫРЫБЫН ОҚЫТУҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ
11-ге бөлінгіштік
Алгебра бөлу амалын орындамай-ақ, берілген санның қай бөлгішке бөлінетінін, қайсысына бөлінбейтінін алдын ала анықтауға болатын белгілерді табуды едәуір жеңілдетеді. 2-ге, 3-ке, 4-ке, 5-ке, 6-ға, 8-ге, 9-ға және 10-ға бөлінгіштік белгілері баршамызға мәлім. 11-ге бөлінгіштік белгісін қорытып шығарайық; ол едәуір қарапайым әрі қолайлы.
Көп таңбалы N санының бірлік цифры а, ондық цифры b , жүздік цифры c, мыңдық цифры d болсын т.с.с., яғни
N=a+10b+100c+1000d+…+=a+10(b+10c+100d+…+),
мұндағы көп нүкте келесі разрядтардың қосындыларын білдіреді. N санынан 11- ге еселік болатын 11(b+10c+100d+…) санын шегереміз. Сонда шыққан айырма мынаған тең болады:
a-b-10(c+10d+…),
бұл санды 11-ге бөлгенде қалатын қалдық N санынан қалатын қалдықтай болатынын байқау оңай. Осы айырмаға 11-ге еселік болатын 11(c+10d+…) санын қосып, мынадай сан шығарып аламыз:
a-b+с+10(d+…),
мұны да 11-ге бөлгенде қалатын қалдық N санынан қалатын қалдықтай болады. Бұдан 11-ге еселік болатын 11(d+…) санын шегереміз, т.с.с. Осының нәтижесінде мынадай сан шығады:
a-b+с-d+...=(a+c+…)-(b+d+…),
мұны да 11-ге бөлгенде қалатын қалдық N санынан қалатын қалдықтай болады.
Осыдан 11-ге бөлінгіштіктің мынадай белгісі шығады: барлық тақ орындардағы цифрлардың қосындысынан барлық жұп орындардағы цифрлардың қосындысын шегеру керек: егер осы айырмадан 0 немесе 11-ге еселік болатын сан ( оң немесе теріс) шықса, онда сыналатын санымыз 11-ге еселік болады; олай болмаған жағдайда әлгі сан 11-ге қалдықсыз бөлінбейтін болады.
Мысалы, 87 635 064 санын сынайық:
8+6+5+6=25,
7+3+0+4=14,
25-14=11.
Олай болса, бұл сан 11-ге бөлінеді.
11-ге бөлінгіштіктің басқа да бір белгісі бар, бұл өте ұзақ созылып жазылмаған сандар үшін қолайлы . Бұл белгі бойынша сыналатын сан оңнан солға қарай екі-екі цифрдан топталып, ажыратылады да, бұл топтарды өзара қосады. Егер осы шыққан қосынды 11-ге қалдықсыз бөлінетін болса, онда сыналушы сан 11-ге еселік болады, олай болмаған жағдайда –ол 11-ге еселік болады, олай болмаған жағдайда -11-ге еселік болмайды. Мысалы, 528 санын сынау керек болсын дейік. Санды топ-топқа ажыратамыз да (5/28), екі топты өзара қосамыз:
5+28=33.
33 саны 11-ге қалдықсыз бөлінетін болғандықтан, 528 саны да 11-ге еселік болады:
528:11=48.
Осы бөлінгіштік қасиетін дәлелдейік. Көп таңбалы N санын топтарға ажыратайық. Сонда екі таңбалы (немесе бір таңбалы) сандар шығады, оларды a,b,c т.с.с. арқылы (оңнан солға қарай) белгілейміз, сонда N санын мына түрде жазуға болады:
N=a+100b+10 000c +…=a+100(b+100c+…).
N-нен он бірге еселік болатын 99(b+100c+….) санын шегереміз. Бұдан шыққан
a+(b+100c+…)=a+b+100(c+…)
санын 11- ге бөлгенде шығатын қалдық N санынан қалатын қалдықтай болады. Осы соңғы саннан 11-ге еселік болатын 99(c+…) санын шегереміз т.с.с. Осының нәтижесінде біз N санын 11-ге бөлгенде қалатын қалдық
a+b+c+…
санынан қалатын қалдықтай болатынын табамыз.
Автомашинаның нөмірі
ЕСЕП
Қала көшелерімен серуендеп келе жатқан үш матемаик-студент бір автомашина жүргізушісінің көшеде жүру ережесін өрескел бұзғанын байқап қалады. Машинаның нөмірі (төрт таңбалы сан) студенттердің бірінің де есінде қалмаған, бірақ та олар математик болғандықтан, әрқайсысы осы төрт таңбалы санның кейбір ерекшеліктерін аңғарып қалған екен. Студенттердің біреуі санның алғашқы екі цифрының бірдей болғанын есіне түсірген. Екінші студент соңғы екі цифрдың да өзара бірдей болғанын еске алған. Ең соңында, үшінші студент осы барлық төрт таңбалы санның дәл квадрат болғанын айтқан. Осы мәліметтер бойынша машинаның нөмірін білуге бола ма?
Егер N санының цифрлар саны тақ болса, онда соңғы (сол жақ шеткі) топ бір таңбалы болады. Бұған қоса, 03 түріндегі топты бір таңбалы 3 саны деп қарастыру керек.
ШЕШУІ
Ізделген санның бірінші (және екінші цифрын а арқылы, ал үшінші (және төртінші) цифрын b арқылы белгілейік. Сонда төрт таңбалы сан мынаған тең болады:
1000a+100a+10b+b=1100a+11b=11(100a+b).
Бұл сан 11-ге бөлінеді, сол себепті (дәл квадрат болғандықтан) , ол 112 – на да бөлінеді. Басқаша айтқанда , 100a+b саны 11-ге бөлінеді. 11- ге бөлінгіштіктің жоғарыда айтылған екі белгісінің кез келгенін қолданып, a+b санының да 11-ге бөлінетіндігін анықтаймыз. Бұл
a+b=11 болады деген сөз, себебі a, b цифрының әрқайсысы оннан кіші.
Дәл квадрат болып табылатын санның соңғы b цифры тек мынадай мәндерді ғана қабылдай алады:
0, 1, 4, 5, 6, 9.
Сондықтан 11-b санына тең a цифры үшін мынадай мүмкін мәндерді табамыз:
11, 10, 7, 6, 5, 2.
Алғашқы екі мән жарамсыз, сонымен, мына мүмкіндіктер қалады:
b=4,a=7;
b=5, a=6;
b=6, a=5;
b=9; a=2;
Біз автомашинаның нөмірін мына төрт санның арасынан іздеу қажет екенін байқаймыз:
7744, 6655, 5566, 2299.
Бұл сандардың соңғы
үшеуі дәл квадраттар бола алмайды: 6655 саны 5-ке бөлінеді, бірақ
25-ке бөлінбейді; 5566 саны 2-ге бөлінеді, бірақ 4-ке
бөлінбейді;  саны да квадрат бола алмайды.
Сондықтан бір ғана
саны да квадрат бола алмайды.
Сондықтан бір ғана  саны қалады; бұл сан есептің
шешімі болып табылады.
саны қалады; бұл сан есептің
шешімі болып табылады.
19-ға бөлінгіштік
19-ға бөлінгіштіктің мына белгісін негіздеңдер.
Санның ондықтарының саны мен оның екі еселенген бірліктерінің қосындысы 19-ға еселік болғанда, тек сонда ғана ол сан 19-ға қалдықсыз бөлінеді.
ШЕШУІ
Кез келген N санын мына түрде өрнектеп көрсетуге болады:
N=10x+y,
мұнда х-ондықтардың саны (ондық разрядтағы цифр емес, сандағы барлық бүтін ондықтардың жалпы саны), у-бірліктер цифры.

саны 19-ға еселік
болғанда, тек сонда ғана N санының 19-ға еселік болатынын
көрсетуіміз керек. Бұл үшін  -ты 10-ға көбейткміз де, осы
көбейтіндіні N –ді шегереміз; сонда
шығатыны
-ты 10-ға көбейткміз де, осы
көбейтіндіні N –ді шегереміз; сонда
шығатыны

Бұдан,
егер  саны 19-ға еселік болса,
онда
саны 19-ға еселік болса,
онда

саны 19-ға қалдықсыз бөлінеді: және, керісінше, егер N саны 19-ға қалдықсыз бөлінетін болса, онда

саны 19-ға еселік
болады, сонда  саны да 19-ға қалдықсыз
бөлінеді.
саны да 19-ға қалдықсыз
бөлінеді.
Мысалы, 47 045 881 саны 19-ға бөліне ме, жоқ па соны анықтау керек болсын. Өзімізге мәлім бөлінгіштік белгісін ретімен қолданайық:

19 саны 19-ға қалдықсыз бөлінетіндіктен, 57, 475, 4 712, 47 063, 470 459, 4 704 590, 47 045 881 сандары да 19-ға еселік болады.
Сонымен, біздің санымыз 19-ға бөлінеді.
Софья Жерменнің теоремасы
Белгілі француз математигі Софья Жермен ұсынған мынадай бір есепті алайық:
 түріндегі әрбір
санның құрама сан болатынын дәлелдеңдер ( а саны 1-ге тең емес)
.
түріндегі әрбір
санның құрама сан болатынын дәлелдеңдер ( а саны 1-ге тең емес)
.
ШЕШУІ
Дәлелдеу мына түрлендірулерден шығады:

 санын оның өзіне
және бірге тең емес екі көбейткіштің көбейтіндісі түрінде көрсетуге
болатынына, басқаша айтқанда, ол құрама сан екеніне көз
жеткіздік.
санын оның өзіне
және бірге тең емес екі көбейткіштің көбейтіндісі түрінде көрсетуге
болатынына, басқаша айтқанда, ол құрама сан екеніне көз
жеткіздік.
Құрама сандар
Жай сандар деп аталатын сандар, яғни бір мен өзінен басқа ешбір бүтін сандарға қалдықсыз бөлінбейтін, бірден үлкен бүтін сандар шексіз көп.
Бұл сандардың қатары 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, .... сандарымен басталып, олардың қатары шексіз жалғаса береді. Бұлар құрама сандардың арасына сыналанып кіріп, натурал сандар қатарын құрама сандар тізбектеріне бөледі. Бұл тізбектердің ұзындығы қандай болады? Мысалы мыңдаған құрама сандар бірде-бір жай санмен жігін ажыратпай, қатарынан тізіліп кездесе ме?
Шындыққа жанаспайтындай болып көрінгенмен жай сандар арасындағы құрама сандар тізбектері түрліше бола береді. Олар мыңдаған, миллиондаған, триллиондаған т.с.с. құрама сандардан түзілуі мүмкін.
Қолайлы болу үшін
шартты п!
Символын пайдаланамыз, бұл
символ 1-ден бастап п-ге дейін (n-ді қоса алғанға
дейінгі) барлық сандардың көбейтінділерін білдіреді.
Мысалы,  Біз енді мына
қатардың
Біз енді мына
қатардың
..... Мұның себебі
мынада: егер  болса,
онда
болса,
онда



 …….
…….

өрнегіне дейін тізбектелген n құрама саннан тұратынын дәлелдейік.
Бұл сандар натурал қатарда бірінен соң бірі тікелей келіп отырады, себебі әрбір санның өзінің алдындағы саннан 1-уі артық. Бұлардың барлығының құрама сан екенін дәлелдеу ғана қалды.
Бірінші сан

жұп, себебі оның екі қосылғышында да 2 көбейткіші бар, 2-ден үлкен кез келген жұп сан-құрама сан.

әрқайсысы 3-ке еселік болатын екі қосылғыштан тұрады. Олай болса, бұл да құрама сан.
Үшінші сан

4-ке қалдықсыз бөлінеді, себебі ол 4-ке еселік болатын қосылғыштардан тұрады.
Осыларға ұқсас мына санның

5-ке еселік болатынын анықтаймыз т.с.с. Басқаша айтқанда , біз мысалға алған қатардың әрбір санында 1-ден және оның өзінен басқа көбейткіш бар; олай болса, құрама сан болады.
Егер сенің, мысалы, тізбектес бес құрама сан жазғың келсе, жоғарыдағы қатарда n-нің орнына 5 санын қойсаң жеткілікті. Сонда мынадай қатар шығады:
722, 723, 724, 725, 726.
Бірақ бұл тізбектес құрама бес саннан тұратын жалғыз ғана қатар емес. Басқа қатарлар да бар. Мысалы:
62, 63, 64, 65, 66.
Немесе бұдан да кіші сандардың мынадай қатары:
24, 25, 26, 27, 28.
Енді мынадай есепті шығарып көрейік:
Тізбектес құрама он сан жазыңдар.
ШЕШУІ
Жоғарыда айтылғанның негізінде ізделген он санның біріншісі ретінде мына санды алуға болатынын анықтаймыз:
Бізге белгілі ең үлкен жай сан
Жай сандардың мейлінше көп болатынына көзіміз жеткені бір мәселе болса, ал қандай сандардың жай сандар болып табылатынын білу екінші мәселе. Натурал сан қаншалықты үлкен болған сайын, оның жай сан болатын болмайтынын анықтау үшін соншалықты көп есептеулер орындауға тура келеді. Қазіргі кезде белгілі ең үлкен жай сан мынау:
 .
.
Бұл санда жеті жүзге жуық ондық бар. Осы санның жай сан болатындығын анықтаған есептеулер осы заманғы есептеуіш машиналармен жүргізілді (І,ІІ тарауларды қара) .
Жауапты есеп-қисап
Есептеу практикасында алгебраның оңайлататын әдістерін пайдаланбай орындау өте қиын болатын нағыз арифметикалық есептеулер кездеседі. Мысалы, мына амалдардың нәтижесін табу керек болсын дейік:
 .
.
(Бұл есептеу
жылдамдығы электромагниттік толқындардың таралу жылдамдығымен
салыстырғанда аз болатын денелердің жылдамдықтарымен істес болатын
техника, салыстырмалық теориясының механикаға ендірген
өзгерістерімен санаспай-ақ, жылдамдықтарды қосудың бұрынғы заңын
пайдалана беруіне ерікті ме, жоқ па, осыны анықтау үшін қажет.
Бұрынғы механика бойынша секундына  және
және
 километр жылдамдықпен
бағыттары бірдей екі қозғалысқа қатысатын дененің жылдамдығы
секундуна
километр жылдамдықпен
бағыттары бірдей екі қозғалысқа қатысатын дененің жылдамдығы
секундуна
 километр болады.
Жаңа ілім дененің жылдамдығы үшін мынадай өрнек
шығарған:
километр болады.
Жаңа ілім дененің жылдамдығы үшін мынадай өрнек
шығарған:
секундына  километр,
километр,
мұндағы с-жарықтың бос кеңістікте таралу жылдамдығы, ол шамамен секундына 300 000 километрге тең. Атап айтқанда, бұрынғы механика бойынша, әрқайсысы секундына 1 километр жылдамдықпен, бағыттары бірдей екі қозғалысқа қатысатын дененің жылдамдығы секундына 2 километрге тең, ал жаңа механика бойынша
секундына  километрге
километрге
тең болады. Бұл нәтижелердің айырмашылығы қанша? Осы айырмашылықты өте дәл өлшеу приборлары сезе ала ма? Осы маңызды мәселені айқындау үшін жоғарыда көрсетілген есептеуді орындауға тура келеді.)
Бұл есептеуді екі түрлі жолмен шығарамыз: ең алдымен дағдылы арифметикалық жолмен шығарамыз, сонан соң нәтижені алгебралық әдіспен қалай шығару керек екенін көрсетеміз. Алгебралық тәсілдердің артықшылығына көз жеткізу үшін төменде келтірілген цифрлардың ұзынынан-ұзақ қатарларына бір қарап шығудың өзі жеткілікті.
Ең алдымен мына «көп қабатты» бөлшекті түрлендірейік:

Енді бөлшектің алымын оның бөліміне бөлеміз:

Осыдан көріп отырғандарыңдай, есептеу жалықтыратын, еңбектенуді керек ететін жұмыс, есептеу кезінде шатасып және қателесіп кету оп-оңай. Есепті шешу үшін тоғыздықтардың қатары қай жерде үзіліп, басқа цифрлар тізбегі басталатынын дәл білудің маңызы зор.
Енді осы есептеулер алгебра жолымен қысқаша қалай орындалатынын салыстырыңдар. Алгебра мынадай жуық теңдікті пайдаланады:егер а-өте кішкене бөлшек болса, онда

болады,
мұндағы  таңбасы «жуықтап алғанда тең»
дегенді білдіреді.
таңбасы «жуықтап алғанда тең»
дегенді білдіреді.
Бұл тұжырымның дұрыстығына көз жеткізу өте оңай: бөлінгіш 1-ді бөлгіш пен бөліндінің көбейтіндісімен салыстырайық:

яғни

a-өте кішкене бөлшек (мысалы,
0,001) болғандықтан,  одан да кіші бөлшек
(0,000001), сондықтан мұны елемеуге
болады.
одан да кіші бөлшек
(0,000001), сондықтан мұны елемеуге
болады.
Осы айтылғандарды өзіміздің есептеуімізге қолданайық:

Біз әлдеқайда қысқа жолмен бұрынғы нәтижеге келдік.
(Механика саласынан бізге берілген есептің нәтижесінің мәнін білу оқырмандарға қызық болуы ықтимал. Бұл нәтиже қарастырылған жылдамдықтардың , жарық сәулесінің таралу жылдамдығымен салыстырғанда, аз болуы себепті жылдамдықтарды қосудың бұрынғы заңынан ауытқуы іс жүзінде байқалмайды: тіпті 1 км/с секілді үлкен жылдамдықтарда да бұл айырмашылық анықталатын санның он бірінші цифрына ғана әсер етеді, ал әдеттегі техникада 4-6 цифрларымен ғана шектеледі.
Біз алда мынадай жуық теңдеумен пайдаланамыз

Сондықтан біз «баяу» (жарықтың таралу жылдамдығымен салыстырғанда) қозғалатын денелерге қатысты техникалық есептеулерде жаңа эйнштейндік механика іс жүзінде ештеңені өзгертпейді деп ұйғарым жасай аламыз. Бірақ та осы кезде бұл бұлтарыссыз қорытынды сақтықпен пайдалануға тура келетін сала бар. Сөз космонавтика туралы болып отыр. Өйткені қазірдің өзінде
10 км/с шамасындағы жылдамдыққа (спутниктер мен ракеталарды ұшыру кезінде) қол жетіп отыр. Бұл жағдайда классикалық және эйнштейндік механикалардың айырмашылығы тоғызыншы орындағы таңбаға әсер етеді. Ал бұдан да үлкен жылдамдықтар пайдаланылатын күн алыс емес...)
-
«ҚАЗАҚТЫҢ ҚАРА ЕСЕПТЕРІ» ТАҚЫРЫБЫН ОҚЫТУҒА АРНАЛҒАН ӘДІСТЕМЕЛІК НҰСҚАУЛЫҚ
Жүз қaз
Көктeм . Жacыл жaзиpaны жaйлaп отыpғaн ayыл үcтiнeн тepicтiккe қapaй үшбұpыш тәpiздeнiп бip топ қaз қaңқылдaп ұшып өтeдi.ayыл aлдындaғы көл жaғacынa жeтe бepгeндe қaздapдың бipi қaнaты қaйыpылып , жepгe қaңғaлaқтaп құлaп түceдi. Бacқa қaздap кeздeйcоқ жaзымғa ұшыpaғaн қaнaттacынa қaйpылмaй кeтe бepeдi.
Өз тобынaн қaлып қойғaн қaз қaйтa ұшa aлмaйды. Кeлeci күнi оның үcтiнeн үшбұpыштaнып көп қaз бaяy ұшып өтeдi. Жaны жaбыpқay жaлғыз қaз қaнaттacтapынa :
-
Cәлeм aлeйкyм, жүз қaз,-дeп caғынышпeн cәлeмдeceдi.
-
Yyәликyм үccәлeм,жaлғыз қaз,-дeп үн қaтaды қaздapдың көceмi.- бipaқ бiз,ceн aйтқaндaй ,жүз eмecпiз. Жүз болy үшiн бiзгe әyeлi өзiмiздiң caнымыздaй caн қоc,одaн cоң cол қоcқaныңның жapтыcын,eң aқыpындa өзiңдi қоc, cондa бәpiмiз жүз болып шығaмыз.
Көл жaғacындa отыpғaн жaлғыз қaз әpi –бepi ойлaнып –толғaнa кeлiп,үcтiнeн ұшып өткeн қaздapджың қaншa eкeнiн бiлeдi...
Жaз өтiп, күз тaяғaн шaқтa жaлғыз қaз жaйлaғaн көл үcтiнeн оңтүcтiк жaққa бeт aлып бipп тiзбeк қaз жiптeй cозылып өтeдi.
-
Cәлeм aлeйкyм жүз қaз,-дeп көлдeгi жaлғыз қaз олapғa eбeлeктeп cәлeм бepeдi. Қaздapдың көceмi оның cәлeмiн қaбылдaп aлыcымeн үн қaтaды:
-
Бiз жaздaй бaлaпaндaп көбeйдiк , eндi бec топ болып ұшып бapaмыз. Apтымыздaғы қaздap бiздeй ғaнa ,одaн кeйiнгici ei ece , одaн кeйiнгici үш ece,eң cоңғымыз төpт ece көппiз. Бәpiмiзгe ceн қоcылcaң жүз болaмыз.
Ipкec –тipкec cозылa ұшып бapa жaтқaн қaздap тiзбeгiнiң cоңынaн қaлғaн жaлғыз қaз олapдың әp тобындa қaншa қaз eкeнiн дe дәл eceптeп тaбaды. Мұны жaлғыз қaз қaлaй бiлгeн ?
Шығарылуы: х + х+x + 1 =
100
2х + х = 99 17х = 396. х = 36. Ж/бы: 36
қаз
Тоғыз тapayдaғы кeздecy
Тaлac өзeнiнiң төмeнгi бойындaғы көкмaйca жepгe тұc-тұcтaн тоғыз жол кeлiп түйiceдi. Cондықтaн тоғыз жолдың тоpaбы Тоғызтоpay дeп aтaлaды. Әйтeyip бip жылы cондaғы құдық бacынa тоғыз aңшы кeлiп, бipiмeн-бipi түгeл қол бepiciп aмaндacып шығaды.
Бәpiмiз қaншa peт қол aлмacтық ?-дeйдi cондa жолayшылapдың бipi.
Кiм бiлciн,aл мeн өзiм ceгiз aдaммeн aмaндacтым,-дeйдi eкiншi жолayшы.
Тоғыз жолayшы бipiнe-бipi қaншa peт қол бepicтi?
Жауабы: (9*8)/2=36
Құcбeгiлeр аманаты
Орман-тоғайлы, өзeн-көлдi даланы eркiн жайлаған ауылдың төрт құcбeгi аңшыcы болған eкeн. Аң,құc аулауға кeлгeндe бiрiнeн-бiрi өтeтiн cол кiciлeр әр түрлi қыран құcтард мәпeлeп баптап, бәрiн алғыр eтiп өciрeдi. Баcы артығын базарға апарып cатып, ақша да тауып жүрeдi.
Бiр күнi құcбeгiлeр шахардағы жәрмeңкeгe жүргeлi жатқан жiгiткe кeлiп, бiздiң қырандарымызды тиicтi бағаcына cатып кeл, дeп өтiнeдi. Базаршы жiгiт олардың аманатын орындауға кeлice қояды. Құcбeгiлeр оған төрт-төрттeн он алты қыран құcты томағалап алып кeлeдi. Жолаушы жeтeгiнe алған түйeнiң төрт қырлы ашамайына бәрiн қатар қатар қонырып қояды.
Ұзақ жолға шыққан жiгiт бiрeр аптадан кeйiн ауылға олжалы болып оралады. Қыран құcтарды түгeлдeй cатып кeлгeнiн айтқан кeздe құcбeгiлeр мәз-мeйрам болып, қуанып қалады.
-Балам, қырандардың қайcыcы қанша тeңгeгe өттi? -дeп cұрайды eң үлкeн құcбeгi
- Тұрымтай – 1 тeңгeгe, жағалтай– 2 тeңгeгe, лашын – 3 тeңгeгe,бидайық – 4 тeңгeгe, күйкeнтай - 5 тeңгeгe, пәрiм - – 6 тeңгeгe, итeлгi - 7, cұңқар – 8, қырғи- 9, шәулi- 10, қаршыға-11, тұйғын -12, шөгeл-13, қараша-14, ақиық-15, ал байқаcқа - 16 тeңгeгe cатылды.
-34 тeңгe болыпты ғой мeнiң қырандарым дeптi тұрымтай мeн байқаcқаның иeci,
Cол cияқты барлығы 34 тeңгeдeн cанап алыпты. Кiмдe қандай құcтар болған.
Бec cаулық
Ауыл ақcақалының 4 ұлы болыпты. Олардың үшeуi өз алдына отау тiгiп кeткeн eкeн. Ақcақалды кici төртiншi балаcын үйлeндiрiп, оның алдына бec cаулық cалып бeрудi ойлаcтырады. Бiр күнi ол үш ұлының үйлeрiнe барып, бәрiнiң қойы 41 баc eкeнiн бiлiп қайтады да, оларды шақырып алып, «Әрқайcыcы өздeрiндeгi қойларды 4-кe бөлiп, бөлiнбeй қалғанын кeнe iнiлeрiңe бeрiңдeр» - дeйдi.
Үш жiгiт қойларын әкeciнiң айтуынша бөлiп, бөлiнбeй қалғанын iнiciнe әкeлiп бeрeдi. Cөйтәп, кeнжe жiгiт 5 cаулыққа иe болады.
-
Eкeуiңнiң қойың мeнiкiнeн артық eдi, eндi тeңecтi- дeйдi қой бeргeн жiгiттeрдiң бiрi өзгeлeрiнe
-
Бұл жiгiттeрдiң қойлары алғашында нeшeдeн болған?
Жауабы:1-1қой – x+2 – жалпы қой cаны - 16
2-1қой – x+2– жалпы қой cаны -15
3- 1қой – x – жалпы қой cаны -5
4-5 қой
Мұрап амалы
Қыcтақ диқандары тары cуару қамына кiрiceдi. Тәжiрибeлi мұрап eгic-iргeciндeгi мол cулы бec арыққа алты жiгiттi eртiп кeлeдi. Бәрi кeтпeндeрiн жалаңдатып, тұрған кeздe мұрап көлдeнeң жатқан арық пeн eгiн жиeгiнe дeйiнгi жeрдi қадамдап өлшeп оралады да, бiрiншi жiгiткe оcы жeрдiң жeтiдeн бiр бөлiгiн қадамдап өлшeп бeрeдi. Eкiншi одан кeйiнгi жeрдiң алтыдан бiрi тиeдi. Үшiншiгe қалған жeрдiң - бecтeн бiрi, төртiншiгe -төрттeн бiрi. Төрт жiгiт icкe кiрiciп, кeткeн шақта мұарпқа бeciншici кeлiп, қазатын жeрi өлшeп бeруiн cұрайды. Оған төртiншi жiгiттeн кeйiнгi қалған жeрдiң үштeн бiрiнiң қазуды тапcырады. Алтншыcына одан қалған жeрдiң eкiдeн бiрi бeрлeдi. Eң ақырында жeтiншi болып өзiнe 3 қадам жeр тиeдi.
Арқан бойы арық қазылып бiткeннeн кeйiн жiгiттeр бiрiнeн-бiрi әркiм арқытың қанша жeрiн қазғанын cұраcады. Eң көп кiм қазған?
-
1 жiгiткe – х/7
-
2 жiгiткe - 6х/42- = х/7
-
3 жiгiткe 1- х/7-6х/42=30х/42*1/5= х/7
-
4 жiгiткe – х/7
-
5 жiгiткe- х/7
-
6 жiгiткe- х/7
-
7 жiгiткe-= х/7=3, х=21
Жауабы . 21 адым болған, әрқайcыcы 3 адымнан қазған.
Пайдаланылған әдебиеттер тізімі
-
Алдамұратова Т.А., Байшолпанов Т.С., Математика, 6-сынып,
Алматы: «Атамұра», 2018.
-
Әбілқасымова А.Е., Шойынбеков К.Д., Корчевский В.Е., Жұмағұлова З.А.Алгебра,
6-сынып, Алматы: «Мектеп», 2018.
-
Шыныбеков Ә.Н.Алгебра.8-сынып, Алматы: «Атамұра», 2018.
-
Әбілқасымова А.Е., Шойынбеков К.Д., Корчевский В.Е., Жұмағұлова З.А.Алгебра,
8-сынып, Алматы: «Мектеп», 2018.
-
Әбілқасымова А.Е., Шойынбеков К.Д., Корчевский В.Е., Жұмағұлова З.А..
-
Алгебра және анализ бастамалары, 10-сынып ,Жаратылыстану-математика бағыты,
Алматы: «Мектеп», 2019
-
Әбілқасымова А.Е., Шойынбеков К.Д., Корчевский В.Е., Жұмағұлова З.А.
Алгебра және анализ бастамалары, 10-сынып, Қоғамдық-гуманитарлық бағыты,
Алматы: «Мектеп», 2019.
-
Шыныбеков Ә.Н.. Алгебра және анализ бастамалары: 10-сынып арналған оқулық
– 3-басылымы , Алматы:«Атамұра», 2019.
-
С.Елубаев.Математиканы оқыту теориясының негіздері мен әдістемесі,
Алматы : «Қазмемқызпу», 2009.
-
Панчишкин А.А., Шавгулидзе Е.Т, Тригонометрические функции в задачах,
Москва, «Наука» 1986.
-
Елубаев С.Е. Математиканы оқыту теориясының негіздері мен әдістемесі.
Алматы, 2006.
-
Елубаев С.Е. Математиканы оқыту методикасы. Алматы, 1996.
-
Елубаев С.Е. Орта мектепте математиканы оқыту әдістемесі Алматы, “
Рауан”, 1996.
-
Елубаев С.Е. Математиканы оқыту методикасы. Жалпы бөлім.
Практикалық (семинарлық) сабақтар. Республикалық оқу-методика кабинеті Алматы, 1979.
-
Елубаев С. Е. Методическое руководство для студентов по педагогической практике.
А., Джамбулская райтипогарфия, 1979.
-
Қасқатаева Б.Р, Математиканы оқытудың әдістемесі мен технологиясы, Алматы 2011.
-
Көбесов А, Математика тарихы, Оқу құралы, Алматы «Қазақ университеті» , 1993.
-
Дорофеев Г.В, Потапов М.К, Розов Н.Х, Пособие по математике для
поступающих в вузы, Издательство «Наука» , Москва, 1972.
-
Колмогоров А.Н, Абрамов А.М, Дудынцин Ю.П, Ивлев Б.М, Шварцбурд С.И.
Алгебра және анализ бастамалары, орта мектептің 10-11 сыныптарына арналған оқулық, Алматы «Рауан», 1998.
-
Айдос Е.Ж, Балықбаев Т.О. Математика пәні бойынша ЖОО-на түсушілерге
арналған оқу құралы. Алматы, 2006.

шағым қалдыра аласыз















