
-
Көпбұрыш. Дөңес көпбұрыш
А деңгей:
-
Көпбұрыш дегеніміз не? Мысал келтіріңіз.
-
Үшбұрыш қандай көпбұрыш? Оның элементтерін атаңыз.
-
Төртбұрыштың неше қабырғасы бар?
-
Дөңес көпбұрыш дегеніміз не? Дөңес емес көпбұрыштың мысалын келтіріңіз.
-
Бесбұрыштың неше бұрышы бар?
-
Көпбұрыштың диагоналі дегеніміз не? Төртбұрыштың неше диагоналі бар?
-
Алтыбұрыштың неше қабырғасы және неше бұрышы бар?
-
Көпбұрыштың периметрі дегеніміз не? Қабырғалары 5 см, 7 см және 8 см болатын үшбұрыштың периметрін табыңыз.
-
Квадрат дөңес көпбұрыш па? Неге?
-
Тіктөртбұрыш қандай көпбұрыш? Оның элементтерін атаңыз.
В деңгей:
-
Қабырғаларының ұзындықтары 4 см, 6 см, 8 см, 10 см және 12 см болатын бестікбұрыштың периметрін табыңыз.
-
Дөңес бесбұрыштың диагональдарының санын анықтаңыз.
-
Дөңес көпбұрыштың барлық бұрыштарының қосындысын табу формуласын жазыңыз. Сегізбұрыштың барлық бұрыштарының қосындысын табыңыз.
-
Қабырғалары тең ұзындықтағы дөңес көпбұрыштың атауын атаңыз.
-
Егер дөңес көпбұрыштың бұрыштарының қосындысы 1080° болса, онда оның неше қабырғасы бар?
С деңгей:
-
Дөңес жетібұрыштың диагональдарының санын табыңыз.
-
Дөңес көпбұрыштың барлық бұрыштарының қосындысы 1800° болса, оның неше қабырғасы бар?
-
Сыртқы бұрыштарының қосындысы 360° болатын кез келген дөңес көпбұрыштың қасиетін атаңыз.
-
Егер дөңес көпбұрыштың бір бұрышы 150° болса, ал қалған бұрыштары тең болса және олардың саны 5 болса, онда қалған бұрыштардың әрқайсысының шамасын табыңыз.
-
Тұрақты сегізбұрыштың бір бұрышының шамасын табыңыз.
-
Сегізбұрыштың ішкі бұрыштарының қосындысын табыңыз. Формуланы қолданыңыз.
-
Онбұрыштың ішкі бұрыштарының қосындысын табыңыз. Формуланы қолданыңыз.
-
Егер дөңес көпбұрыштың ішкі бұрыштарының қосындысы 1260° болса, оның неше қабырғасы бар?
-
Дөңес көпбұрыштың ішкі бұрыштарының қосындысы 180(n-2) формуласын қорытып шығарыңыз (n - қабырғалар саны).
-
Дөңес көпбұрыштың сыртқы бұрыштарының қосындысы 360° екенін геометриялық тұрғыдан дәлелдеңіз.
-
Дөңес көпбұрыштың ішкі бұрыштарының орташа шамасы 140° болса, оның неше қабырғасы бар?
-
Тұрақты он бесбұрыштың бір ішкі бұрышының шамасын табыңыз. Формуланы қолданыңыз.
-
Тұрақты он бесбұрыштың бір сыртқы бұрышының шамасын табыңыз.
-
Дөңес көпбұрыштың ішкі және сыртқы бұрыштарының қосындыларын пайдаланып, көпбұрыштың қабырғалар санын табудың формуласын жазыңыз.
-
Егер дөңес көпбұрыштың ішкі бұрыштарының қосындысы оның сыртқы бұрыштарының қосындысынан 1440°-қа артық болса, онда оның неше қабырғасы бар?
2. Параллелограмм, ромб, тіктөртбұрыш, шаршы және олардың қасиеттері мен белгілері
А деңгей (қасиеттерді қолдану):
-
Параллелограммның қарама-қарсы жақтары тең екенін біле отырып, егер параллелограммның бір жағы 8 см, ал екіншісі 5 см болса, қалған жақтарының ұзындықтарын табыңыз.
-
Параллелограммның қарама-қарсы бұрыштары тең екенін біле отырып, егер параллелограммның бір бұрышы 70° болса, қарама-қарсы бұрышының шамасын табыңыз.
-
Параллелограммның көрші бұрыштарының қосындысы 180° екенін біле отырып, егер параллелограммның бір бұрышы 110° болса, оның көрші бұрышының шамасын табыңыз.
-
Параллелограммның диагональдары қиылысқан нүктеде жартылай бөлінетінін біле отырып, егер параллелограммның бір диагоналының ұзындығы 12 см болса, оның жартысының ұзындығын табыңыз.
-
Параллелограммның қарама-қарсы жақтары параллель екенін біле отырып, егер параллелограммның бір жағына перпендикуляр сызық жүргізілсе, онда ол екінші жағына да перпендикуляр болатынын түсіндіріңіз.
-
Параллелограммның ауданын табу формуласын жазыңыз (табан және биіктік арқылы). Егер табаны 10 см, биіктігі 6 см болса, ауданын табыңыз.
-
Ромбының қабырғалары тең екенін біле отырып, егер ромбының бір қабырғасы 7 см болса, қалған қабырғаларының ұзындықтарын табыңыз.
-
Квадраттың барлық қабырғалары тең және барлық бұрыштары 90° екенін біле отырып, квадрат параллелограмм болып табыла ма? Түсіндіріңіз.
-
Тіктөртбұрыштың қарама-қарсы жақтары тең және параллель, ал барлық бұрыштары 90° екенін біле отырып, тіктөртбұрыш параллелограмм болып табыла ма? Түсіндіріңіз.
-
Параллелограммның диагональдары қиылысқан нүктеде жартылай бөлінетінін пайдаланып, есепті шешіңіз: Диагональдарының ұзындықтары 10 см және 14 см болатын параллелограмм берілген. Диагональдарының жартысының ұзындықтарын табыңыз.
В деңгей (қасиеттерді қолдану және есептеу):
-
Параллелограммның екі көрші бұрышының шамасының қатынасы 2:3. Бұрыштардың шамасын табыңыз.
-
Параллелограммның периметрі 36 см, ал бір жағы 8 см. Қалған жақтарының ұзындықтарын табыңыз.
-
Параллелограммның ауданы 48 см², ал биіктігі 6 см. Табанының ұзындығын табыңыз.
-
Ромбының диагональдарының ұзындықтары 6 см және 8 см. Ромбының ауданын табыңыз.
-
Тіктөртбұрыштың диагоналы 13 см, ал бір жағы 5 см. Екінші жағының ұзындығын табыңыз.
Сдеңгей (қасиеттерді қорытып шығару):
-
Параллелограммның қарама-қарсы жақтарының тең екенін дәлелдеңіз.
-
Параллелограммның қарама-қарсы бұрыштарының тең екенін дәлелдеңіз.
-
Параллелограммның көрші бұрыштарының қосындысы 180° екенін дәлелдеңіз.
-
Параллелограммның диагональдары қиылысқан нүктеде жартылай бөлінетінін дәлелдеңіз.
-
Ромбының диагональдары перпендикуляр және жартылай бөлінетінін дәлелдеңіз (бұл дәлелдеу үшін қосымша конструкциялар жасау қажет болуы мүмкін).
Тіктөртбұрыш, ромб және шаршы геометриялық фигураларын анықтау, қасиеттерін және белгілерін қолдану
А (анықтамаларды және негізгі қасиеттерді қолдану):
-
Тіктөртбұрыштың анықтамасын беріңіз. Оның кем дегенде үш қасиетін атаңыз.
-
Ромбтың анықтамасын беріңіз. Оның кем дегенде үш қасиетін атаңыз.
-
Шаршының анықтамасын беріңіз. Оның кем дегенде төрт қасиетін атаңыз.
-
Тіктөртбұрыштың қарама-қарсы жақтары қалай орналасқан?
-
Ромбтың барлық жақтарының ұзындығы қалай?
-
Шаршының барлық бұрыштарының шамасы қандай?
-
Тіктөртбұрыштың диагональдарының қасиетін атаңыз.
-
Ромбтың диагональдарының екі қасиетін атаңыз.
-
Шаршының диагональдарының үш қасиетін атаңыз.
-
Тіктөртбұрыштың ауданын табу формуласын жазыңыз.
-
Ромбтың ауданын табу формуласын жазыңыз (диагональдары арқылы).
-
Шаршының ауданын табу формуласын жазыңыз.
-
Егер тіктөртбұрыштың бір жағы 5 см, ал екіншісі 12 см болса, оның диагоналының ұзындығын табыңыз.
-
Егер ромбтың диагональдары 6 см және 8 см болса, оның ауданын табыңыз.
-
Егер шаршының қабырғасы 10 см болса, оның ауданын және диагоналының ұзындығын табыңыз.
В деңгей (қасиеттерді қолдану және есептеулер):
-
Тіктөртбұрыштың периметрі 28 см, ал бір жағы 5 см. Екінші жағының ұзындығын табыңыз.
-
Ромбтың периметрі 40 см. Оның бір жағының ұзындығын табыңыз.
-
Шаршының ауданы 64 см². Оның қабырғасының ұзындығын табыңыз.
-
Тіктөртбұрыштың ауданы 60 см², ал бір жағы 10 см. Екінші жағының ұзындығын табыңыз.
-
Ромбтың ауданы 24 см², ал бір диагоналы 6 см. Екінші диагоналының ұзындығын табыңыз.
С деңгей (қасиеттерді қорытып шығару және қолдану):
-
Тіктөртбұрыштың диагональдары тең екенін дәлелдеңіз. (Пифагор теоремасын қолдану арқылы)
-
Ромбтың диагональдары бір-біріне перпендикуляр екенін дәлелдеңіз. (үшбұрыштардың теңдігін қолдану арқылы)
-
Шаршының диагональдары тең және перпендикуляр екенін дәлелдеңіз.
-
Егер параллелограммның диагональдары тең болса және бір-біріне перпендикуляр болса, онда ол шаршы екенін дәлелдеңіз.
-
Егер тіктөртбұрыштың диагональдары бір-біріне перпендикуляр болса, онда ол шаршы екенін дәлелдеңіз.
Бұл есептердегі сандарды және шарттарды өзгертуге болады. Кейбір есептерді шешу үшін геометриялық теоремалар мен аксиомаларды қолдану қажет болуы мүмкін. Қиын деңгейдегі есептер геометриялық дәлелдеуді талап етеді. Есептер оқушылардың геометриялық ойлау қабілетін дамытуға бағытталған.
-
Фалес теоремасы. Пропорционал кесінділер
1-5 есептер (А деңгей):
-
Екі параллель түзуді қиып өтетін екі қиюшы түзу берілген. Бірінші қиюшы түзудің кесінділері 4 см және 6 см. Екінші қиюшы түзудің сәйкес кесіндісі 8 см. Екінші кесіндіні табыңыз.
-
Параллель түзулерді қиып өтетін екі қиюшы түзудің бірінші қиюшы түзудегі кесінділері 5 және 10. Екінші қиюшы түзудегі бірінші кесінді 6. Екінші кесіндіні табыңыз.
-
Үшбұрыштың екі қабырғасына параллель түзу жүргізілген. Параллель түзу үшбұрыштың қабырғаларын 3 және 6 болатын екі кесіндіге бөледі. Үшбұрыштың сәйкес келетін қабырғасы 9 болса, параллель түзудің кесіндісін табыңыз.
-
Суретте екі параллель түзу берілген. Оларды қиып өтетін қиюшы түзулердің біреуіндегі кесінділер 2 және 3. Екінші қиюшы түзудегі бірінші кесінді 4. Екінші кесіндіні табыңыз.
-
Фалес теоремасы бойынша екі параллель түзуді қиып өтетін қиюшы түзудің кесінділерінің қатынасын табыңыз, егер бір қиюшы түзудегі кесінділер 8 және 12, ал екінші қиюшы түзудегі сәйкес кесінділер 6 және х болса.
6-15 есептер (В деңгей:
-
Үшбұрыштың қабырғаларына параллель түзу жүргізілген. Бұл түзу үшбұрыштың қабырғаларын 4:6 қатынасында бөледі. Үлкен үшбұрыштың периметрі 30 см. Кіші үшбұрыштың периметрін табыңыз.
-
Екі параллель түзуді үш қиюшы түзу қиып өтеді. Бірінші қиюшы түзудегі кесінділер 2, 3 және 4. Екінші қиюшы түзудегі сәйкес кесінділер 4, 6 және х. х-ті табыңыз.
-
Үшбұрыштың екі қабырғасына параллель түзу жүргізілген. Бұл түзу үшбұрыштың қабырғаларын 5 және 10 кесінділерге бөледі. Параллель түзудің ұзындығы 12 см болса, үшбұрыштың сәйкес қабырғасының ұзындығын табыңыз.
-
Тіктөртбұрыштың қабырғаларына параллель екі түзу жүргізілген. Бұл түзулер тіктөртбұрыштың қабырғаларын 3:2 қатынасында бөледі. Тіктөртбұрыштың ауданы 60 см² болса, кіші тіктөртбұрыштың ауданын табыңыз.
-
Екі параллель түзуді қиып өтетін екі қиюшы түзу берілген. Бірінші қиюшы түзудің кесінділері 7 және 14. Екінші қиюшы түзудегі сәйкес кесінділердің қосындысы 27. Екінші қиюшы түзудің кесінділерін табыңыз.
11-15. (Осы есептер үшін суреттер беру қажет. Суреттерде параллель түзулер мен қиюшы түзулер арқылы құрылған кесінділер берілген. Кесінділердің ұзындықтары беріліп, белгісіз кесінділерді табу тапсырылады.)
16-20 есептер (С деңгей):
-
Екі параллель түзуді үш қиюшы түзу қиып өтеді. Бірінші қиюшы түзудегі кесінділер 3, x және 5. Екінші қиюшы түзудегі сәйкес кесінділер 6, 10 және 12. x-ті табыңыз.
-
Үшбұрыштың медианасы оны екі тең үшбұрышқа бөледі. Бұл үшбұрыштардың аудандарының қатынасын Фалес теоремасы арқылы дәлелдеңіз.
-
Екі параллель түзудің арақашықтығы 10 см. Оларды қиып өтетін қиюшы түзулердің біріндегі кесінділер 4 және 6 см. Екінші қиюшы түзудің сәйкес кесінділерінің арақашықтығын табыңыз.
-
Екі параллель түзудің арақашықтығы 8 см. Оларды қиып өтетін қиюшы түзулердің біреуіндегі кесінділер 3 және 5 см. Екінші қиюшы түзудің сәйкес кесінділердің қосындысы 16 см. Екінші кесінділерді табыңыз.
-
Үшбұрыштың екі қабырғасына параллель түзу жүргізілген. Бұл түзу үшбұрыштың қабырғаларын 2:3 қатынасында бөледі. Параллель түзу үшбұрыштың периметрін 25 см-ге тең екі үшбұрышқа бөледі. Үлкен және кіші үшбұрыштардың периметрлерін табыңыз.
1. Екі параллель түзуді қиып өтетін екі қиюшы түзу берілген. Бірінші қиюшы түзудің кесінділері 6 см және 9 см. Екінші қиюшы түзудің сәйкес кесіндісі 12 см. Екінші кесіндіні табыңыз.
a) 18 см b) 9 см c) 15 см d) 6 см
2. Параллель түзулерді қиып өтетін екі қиюшы түзудің бірінші қиюшы түзудегі кесінділері 4 және 8. Екінші қиюшы түзудегі бірінші кесінді 3. Екінші кесіндіні табыңыз.
a) 12 b) 6 c) 9 d) 3
3. Үшбұрыштың екі қабырғасына параллель түзу жүргізілген. Параллель түзу үшбұрыштың қабырғаларын 2 және 4 болатын екі кесіндіге бөледі. Үшбұрыштың сәйкес келетін қабырғасы 9 болса, параллель түзудің кесіндісін табыңуз.
a) 6 b) 3 c) 4.5 d) 18
4. Суретте екі параллель түзу берілген (суретті қосу керек). Оларды қиып өтетін қиюшы түзулердің біреуіндегі кесінділер 5 және 10. Екінші қиюшы түзудегі бірінші кесінді 6. Екінші кесіндіні табыңыз.
a) 12 b) 3 c) 18 d) 24
Бір немесе бірнеше дұрыс жауабы бар тест тапсырмасы
1. Екі параллель түзуді қиып өтетін екі қиюшы түзудің кесінділерінің қатынасы туралы қандай тұжырымдар дұрыс?
a) Кесінділердің қатынасы әрқашан тең.
b) Кесінділердің қатынасы бір-біріне тәуелді емес.
c) Кесінділердің қатынасы қиюшы түзудің орнына тәуелді.
d) Кесінділердің қатынасы параллель түзулердің арақашықтығына тәуелді емес.
e) Фалес теоремасы осы қатынасты анықтайды.
f) Кесінділердің қатынасы әрқашан 1-ге тең.
2. Фалес теоремасын қолдана отырып, қандай шамаларды есептеуге болады?
a) Үшбұрыштың ауданын.
b) Үшбұрыштың периметрін.
c) Параллель түзулер арасындағы қашықтықты.
d) Пропорционал кесінділердің ұзындықтарын.
e) Бұрыштардың шамаларын.
f) Үшбұрыштың биіктігін.
1-тапсырма: 1-a, 2-b, 3-b, 4-a
2-тапсырма: 1-a, e, 2-d, f,
4.Трапеция, оның түрлері мен қасиеттері. Трапеция мен үшбұрыштың орта сызықтары
А деңгей
1. Үшбұрыштың орта сызығын табу формуласы.
2. Трапецияның орта сызығын табу формуласы.
3. Үшбұрыштың орта сызығы 8 см-ге тең. Осы орта сызығына параллель қабырғасын табыңыз.
4. Үшбұрыштың орта сызығы 5 см-ге тең. Осы орта сызығына параллель қабырғасын табыңыз.
5. Үшбұрыштың орта сызығы 7 см-ге тең. Осы орта сызығына параллель қабырғасын табыңыз.
6. Үшбұрыштың бір қабырғасы 12 см – ге тең. Осы қабырғасына параллель орта сызығын табыңыз.
7. Үшбұрыштың бір қабырғасы 20 см – ге тең. Осы қабырғасына параллель орта сызығын табыңыз.
8. Трапецияның табандары 6 см және 8 см. Оның орта сызығын табыңыз.
9. Трапецияның табандары 3 см және 9 см. Оның орта сызығын табыңыз.
10. Трапецияның табандары 4 см және 12 см. Оның орта сызығын табыңыз.
11. Трапецияның табандары 6 см және 8 см. Оның орта сызығын табыңыз.
В деңгей
12. Тең қабырғалы үшбұрыштың орта сызығы 3 см. Оның периметрін табыңдар.
13. Тең қабырғалы АВС үшбұрышының орта сызығы - ДЕ. Егер АВС үшбұрышының қабырғасы 14 см болса, онда ЕВД үшбұрышының периметрін табыңдар.
14. Тең қабырғалы үшбұрыштың орта сызығы 4 см. Оның периметрін табыңдар.
15. Тең қабырғалы үшбұрыштың орта сызығы 5 см. Оның периметрін табыңдар.
16. Тең қабырғалы үшбұрыштың орта сызығы 2 см. Оның периметрін табыңдар.
17. Тең қабырғалы үшбұрыштың орта сызығы 4,5 см. Оның периметрін табыңдар.
18. Тең бүйірлі үшбұрыштың табанына параллель орта сызығы 3 см. Үшбұрыштың периметрі 16 см болса, онда оның қабырғаларын табыңыз.
19. Тең бүйірлі үшбұрыштың табанына параллель орта сызығы 4 см. Үшбұрыштың периметрі 18 см болса, онда оның қабырғаларын табыңыз.
20. Тең бүйірлі үшбұрыштың табанына параллель орта сызығы 5 см. Үшбұрыштың периметрі 26 см болса, онда оның қабырғаларын табыңыз.
С деңгей
21. Табандары АД=12 см және
ВС=4 см болатын АВСД трапециясының ЕF орта сызығы, ВД диагоналын К
нүктесінде қияды. F , онда FК және КЕ
кесінділердің ұзындықтарын табыңдар.
, онда FК және КЕ
кесінділердің ұзындықтарын табыңдар.
22.Табандары АД=10 см және
ВС=2 см болатын АВСД трапециясының ЕF орта сызығы, ВД диагоналын К
нүктесінде қияды. F , онда FК және КЕ
кесінділердің ұзындықтарын табыңдар.
, онда FК және КЕ
кесінділердің ұзындықтарын табыңдар.
23. АВСД тең бүйірлі трапецияның ЕF орта сызығы жүргізілген. Егер табандары АД=14 см, ВС=10 см, ал бүйір қабырғасы АВ=6 см болса, онда ЕВСF трапецияның периметрін табыңдар.
24. АВСД тең бүйірлі трапецияның ЕF орта сызығы жүргізілген. Егер табандары АД=12 см, ВС=8 см, ал бүйір қабырғасы АВ=4 см болса, онда ЕВСF трапецияның периметрін табыңдар.
25. Табандары ВС=5 см және АД=19 см, бүйір қабырғасы 12 см болатын тең бүйірлі АВСД трапециясының ВF биіктігі жүргізілген, онда АВF үшбұрышының периметрін табыңдар.
26.Төмендегі суретте, А, В, С
үш үй бір түзудің бойында түзу сызықты жолдан әртүрлі қашықтықта
орналасқан және  . Шеткі екі үй жолдан
сәйкесінше 72 м және 54 м қашықтықта болса, ортадағы үй жолдан
қандай қашықтықта орналасқан?
. Шеткі екі үй жолдан
сәйкесінше 72 м және 54 м қашықтықта болса, ортадағы үй жолдан
қандай қашықтықта орналасқан?
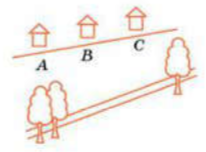
27.Төмендегі суретте, А, В, С
үш үй бір түзудің бойында түзу сызықты жолдан әртүрлі қашықтықта
орналасқан және  . Шеткі екі үй жолдан
сәйкесінше 52 м және 26 м қашықтықта болса, ортадағы үй жолдан
қандай қашықтықта орналасқан?
. Шеткі екі үй жолдан
сәйкесінше 52 м және 26 м қашықтықта болса, ортадағы үй жолдан
қандай қашықтықта орналасқан?

28.Төмендегі суретте, А, В, С
үш үй бір түзудің бойында түзу сызықты жолдан әртүрлі қашықтықта
орналасқан және  . Шеткі екі үй жолдан
сәйкесінше 100 м және 90 м қашықтықта болса, ортадағы үй жолдан
қандай қашықтықта орналасқан?
. Шеткі екі үй жолдан
сәйкесінше 100 м және 90 м қашықтықта болса, ортадағы үй жолдан
қандай қашықтықта орналасқан?

1-тапсырма (4 жауапты):
1. Трапеция дегеніміз не?
a) Төртбұрыштың екі қабырғасы параллель.
b) Төртбұрыштың барлық қабырғалары тең.
c) Төртбұрыштың барлық бұрыштары тең.
d) Төртбұрыштың екі қабырғасы перпендикуляр.
2. Тік трапеция дегеніміз не?
a) Екі қабырғасы параллель, ал екі қабырғасы перпендикуляр
. b) Екі қабырғасы параллель, ал бүйір қабырғалары биіктіктер.
c) Екі қабырғасы параллель, ал барлық бұрыштары тең.
d) Екі қабырғасы параллель, ал негіздері тең.
3. Тең бүйірлі трапеция дегеніміз не?
a) Екі қабырғасы параллель, ал бүйір қабырғалары тең
b) Екі қабырғасы параллель, ал барлық қабырғалары тең.
c) Екі қабырғасы параллель, ал бұрыштары тең.
d) Екі қабырғасы параллель, ал негіздері тең.
.
2-тапсырма (6 жауапты):
1. Тең бүйірлі трапецияның қандай қасиеттері бар?
a) Бүйір қабырғалары тең.
b) Негіздері тең.
c) Диагональдары тең.
d) Бұрыштары тең.
e) Бүйір бұрыштары тең.
f) Ауданды есептеу формуласы тіктөртбұрыштың ауданына тең.
2. Тік трапецияның қандай қасиеттері бар?
a) Бүйір қабырғалары биіктіктер.
b) Бүйір бұрыштары тік бұрыштар.
c) Диагональдары тең.
d) Негіздері тең.
e) Ауданды есептеу формуласы тіктөртбұрыштың ауданына тең.
f) Бүйір қабырғалары тең.
3. Трапецияның медианасы дегеніміз не?
a) Трапецияның екі негізін жалғайтын кесінді.
b) Трапецияның ең ұзын диагоналы.
c) Трапецияның негіздерінің ортаңғы нүктелерін жалғайтын кесінді.
d) Трапецияның биіктігі.
e) Трапецияның ауданы.
f) Трапецияның периметрі.
Жауаптар:
1-тапсырма: 1-a, 2-b, 3-a,
2-тапсырма: 1-a, c, e, 2-a, b, 3-c
5.Үшбұрыштың тамаша нүктелері
1-5. А деңгей:
-
Тең бүйірлі үшбұрышта биіктік, медиана және биссектриса бірдей бола ма? Егер иә болса, неге?
-
Тікбұрышты үшбұрышта медиана гипотенузаның жартысына тең бола ма? Дәлелдеңіз.
-
Тең қабырғалы үшбұрышта биіктіктер, медианалар және биссектрисалар қалай орналасады?
-
Үшбұрыштың ауырлық центрі дегеніміз не және ол қалай табылады?
-
Биіктіктердің қиылысу нүктесін атаңыз.
6-10. В деңгей:
-
Үшбұрыштың екі медианасының ұзындығы 6 см және 8 см. Үшінші медиананың ұзындығы қандай болуы мүмкін? (шешімде үшбұрыш теңсіздігін қолдану қажет)
-
Үшбұрыштың биіктігінің ұзындығы 5 см, негізі 10 см. Үшбұрыштың ауданын табыңыз.
-
Үшбұрыштың ауырлық центрі медианаларды қандай қатынаста бөледі?
-
Тең бүйірлі үшбұрышта биіктік негізді екі тең бөлікке бөле ме? Неге?
-
Тікбұрышты үшбұрышта ортоцентр қайда орналасады?
11-15. С деңгей:
-
Үшбұрыштың ауырлық центрі, ортоцентрі және айналдыру центрі бір нүктеде қиылысатын үшбұрышты атаңыз.
-
Егер үшбұрыштың екі медианасы перпендикуляр болса, онда бұл үшбұрыш қандай болуы мүмкін?
-
Үшбұрыштың ауданы 24 см², биіктігі 6 см болса, негізінің ұзындығын табыңыз.
-
Тең бүйірлі үшбұрышта биіктіктің ұзындығы 8 см, ал негізінің ұзындығы 12 см болса, үшбұрыштың ауданын табыңыз.
-
Үшбұрыштың бір медианасы 10 см, ал ауырлық центрінен осы медиананың ұшына дейінгі қашықтық 6 см болса, ауырлық центрінен медиананың басқа ұшына дейінгі қашықтықты табыңыз.
(графикалық шешімді қажет етеді):
-
Берілген үшбұрыш үшін ауырлық центрін, ортоцентрін және инцентрін салыңыз. (Сурет берілуі керек)
-
Берілген үшбұрыш үшін биіктіктерді салыңыз және ортоцентрін табыңыз. (Сурет берілуі керек)
-
Берілген үшбұрыш үшін медианаларды салыңыз және ауырлық центрін табыңыз. (Сурет берілуі керек)
-
Берілген үшбұрыш үшін биссектрисаларды салыңыз және инцентрін табыңыз. (Сурет берілуі керек)
-
Екі медианасы 6 см және 8 см болатын үшбұрыш салыңыз. Үшінші медиананың ұзындығын өлшеңіз.
1. Үшбұрыштың медианасы дегеніміз не?
a) Үшбұрыштың төбесінен қарсы жатқан қабырғаға түсірілген перпендикуляр.
b) Үшбұрыштың төбесінен қарсы жатқан қабырғаның ортасына жүргізілген кесінді. c) Үшбұрыштың бұрышын екіге бөлетін сәуле.
d) Үшбұрыштың екі қабырғасын қосатын кесінді.
2. Үшбұрыштың биіктігі дегеніміз не?
a) Үшбұрыштың төбесінен қарсы жатқан қабырғаға түсірілген перпендикуляр.
b) Үшбұрыштың төбесінен қарсы жатқан қабырғаның ортасына жүргізілген кесінді. c) Үшбұрыштың бұрышын екіге бөлетін сәуле.
d) Үшбұрыштың екі қабырғасын қосатын кесінді.
3. Үшбұрыштың биссектрисасы дегеніміз не?
a) Үшбұрыштың төбесінен қарсы жатқан қабырғаға түсірілген перпендикуляр.
b) Үшбұрыштың төбесінен қарсы жатқан қабырғаның ортасына жүргізілген кесінді. c) Үшбұрыштың бұрышын екіге бөлетін сәуле.
d) Үшбұрыштың екі қабырғасын қосатын кесінді.
2-тапсырма (6 жауапты):
1. Тең бүйірлі үшбұрышта қандай тамаша нүктелер бірдей нүктеде орналасады?
a) Ауырлық центрі
b) Ортоцентр
c) Инцентр
d) Айналдыру центрі
e) Медиана
f) Биіктік
2. Үшбұрыштың ауырлық центрі медианаларды қандай қатынаста бөледі?
a) 1:1 b) 1:2 c) 2:1 d) 2:3 e) 3:1 f) 3:2
Жауаптар:
1-тапсырма: 1-b, 2-a, 3-c,
2-тапсырма: 1-a, b, c, f, 3-c
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
8-сынып 1- тоқсан бойынша Геометриядан тақырыптық тапсырмалар жинағы
8-сынып 1- тоқсан бойынша Геометриядан тақырыптық тапсырмалар жинағы
-
Көпбұрыш. Дөңес көпбұрыш
А деңгей:
-
Көпбұрыш дегеніміз не? Мысал келтіріңіз.
-
Үшбұрыш қандай көпбұрыш? Оның элементтерін атаңыз.
-
Төртбұрыштың неше қабырғасы бар?
-
Дөңес көпбұрыш дегеніміз не? Дөңес емес көпбұрыштың мысалын келтіріңіз.
-
Бесбұрыштың неше бұрышы бар?
-
Көпбұрыштың диагоналі дегеніміз не? Төртбұрыштың неше диагоналі бар?
-
Алтыбұрыштың неше қабырғасы және неше бұрышы бар?
-
Көпбұрыштың периметрі дегеніміз не? Қабырғалары 5 см, 7 см және 8 см болатын үшбұрыштың периметрін табыңыз.
-
Квадрат дөңес көпбұрыш па? Неге?
-
Тіктөртбұрыш қандай көпбұрыш? Оның элементтерін атаңыз.
В деңгей:
-
Қабырғаларының ұзындықтары 4 см, 6 см, 8 см, 10 см және 12 см болатын бестікбұрыштың периметрін табыңыз.
-
Дөңес бесбұрыштың диагональдарының санын анықтаңыз.
-
Дөңес көпбұрыштың барлық бұрыштарының қосындысын табу формуласын жазыңыз. Сегізбұрыштың барлық бұрыштарының қосындысын табыңыз.
-
Қабырғалары тең ұзындықтағы дөңес көпбұрыштың атауын атаңыз.
-
Егер дөңес көпбұрыштың бұрыштарының қосындысы 1080° болса, онда оның неше қабырғасы бар?
С деңгей:
-
Дөңес жетібұрыштың диагональдарының санын табыңыз.
-
Дөңес көпбұрыштың барлық бұрыштарының қосындысы 1800° болса, оның неше қабырғасы бар?
-
Сыртқы бұрыштарының қосындысы 360° болатын кез келген дөңес көпбұрыштың қасиетін атаңыз.
-
Егер дөңес көпбұрыштың бір бұрышы 150° болса, ал қалған бұрыштары тең болса және олардың саны 5 болса, онда қалған бұрыштардың әрқайсысының шамасын табыңыз.
-
Тұрақты сегізбұрыштың бір бұрышының шамасын табыңыз.
-
Сегізбұрыштың ішкі бұрыштарының қосындысын табыңыз. Формуланы қолданыңыз.
-
Онбұрыштың ішкі бұрыштарының қосындысын табыңыз. Формуланы қолданыңыз.
-
Егер дөңес көпбұрыштың ішкі бұрыштарының қосындысы 1260° болса, оның неше қабырғасы бар?
-
Дөңес көпбұрыштың ішкі бұрыштарының қосындысы 180(n-2) формуласын қорытып шығарыңыз (n - қабырғалар саны).
-
Дөңес көпбұрыштың сыртқы бұрыштарының қосындысы 360° екенін геометриялық тұрғыдан дәлелдеңіз.
-
Дөңес көпбұрыштың ішкі бұрыштарының орташа шамасы 140° болса, оның неше қабырғасы бар?
-
Тұрақты он бесбұрыштың бір ішкі бұрышының шамасын табыңыз. Формуланы қолданыңыз.
-
Тұрақты он бесбұрыштың бір сыртқы бұрышының шамасын табыңыз.
-
Дөңес көпбұрыштың ішкі және сыртқы бұрыштарының қосындыларын пайдаланып, көпбұрыштың қабырғалар санын табудың формуласын жазыңыз.
-
Егер дөңес көпбұрыштың ішкі бұрыштарының қосындысы оның сыртқы бұрыштарының қосындысынан 1440°-қа артық болса, онда оның неше қабырғасы бар?
2. Параллелограмм, ромб, тіктөртбұрыш, шаршы және олардың қасиеттері мен белгілері
А деңгей (қасиеттерді қолдану):
-
Параллелограммның қарама-қарсы жақтары тең екенін біле отырып, егер параллелограммның бір жағы 8 см, ал екіншісі 5 см болса, қалған жақтарының ұзындықтарын табыңыз.
-
Параллелограммның қарама-қарсы бұрыштары тең екенін біле отырып, егер параллелограммның бір бұрышы 70° болса, қарама-қарсы бұрышының шамасын табыңыз.
-
Параллелограммның көрші бұрыштарының қосындысы 180° екенін біле отырып, егер параллелограммның бір бұрышы 110° болса, оның көрші бұрышының шамасын табыңыз.
-
Параллелограммның диагональдары қиылысқан нүктеде жартылай бөлінетінін біле отырып, егер параллелограммның бір диагоналының ұзындығы 12 см болса, оның жартысының ұзындығын табыңыз.
-
Параллелограммның қарама-қарсы жақтары параллель екенін біле отырып, егер параллелограммның бір жағына перпендикуляр сызық жүргізілсе, онда ол екінші жағына да перпендикуляр болатынын түсіндіріңіз.
-
Параллелограммның ауданын табу формуласын жазыңыз (табан және биіктік арқылы). Егер табаны 10 см, биіктігі 6 см болса, ауданын табыңыз.
-
Ромбының қабырғалары тең екенін біле отырып, егер ромбының бір қабырғасы 7 см болса, қалған қабырғаларының ұзындықтарын табыңыз.
-
Квадраттың барлық қабырғалары тең және барлық бұрыштары 90° екенін біле отырып, квадрат параллелограмм болып табыла ма? Түсіндіріңіз.
-
Тіктөртбұрыштың қарама-қарсы жақтары тең және параллель, ал барлық бұрыштары 90° екенін біле отырып, тіктөртбұрыш параллелограмм болып табыла ма? Түсіндіріңіз.
-
Параллелограммның диагональдары қиылысқан нүктеде жартылай бөлінетінін пайдаланып, есепті шешіңіз: Диагональдарының ұзындықтары 10 см және 14 см болатын параллелограмм берілген. Диагональдарының жартысының ұзындықтарын табыңыз.
В деңгей (қасиеттерді қолдану және есептеу):
-
Параллелограммның екі көрші бұрышының шамасының қатынасы 2:3. Бұрыштардың шамасын табыңыз.
-
Параллелограммның периметрі 36 см, ал бір жағы 8 см. Қалған жақтарының ұзындықтарын табыңыз.
-
Параллелограммның ауданы 48 см², ал биіктігі 6 см. Табанының ұзындығын табыңыз.
-
Ромбының диагональдарының ұзындықтары 6 см және 8 см. Ромбының ауданын табыңыз.
-
Тіктөртбұрыштың диагоналы 13 см, ал бір жағы 5 см. Екінші жағының ұзындығын табыңыз.
Сдеңгей (қасиеттерді қорытып шығару):
-
Параллелограммның қарама-қарсы жақтарының тең екенін дәлелдеңіз.
-
Параллелограммның қарама-қарсы бұрыштарының тең екенін дәлелдеңіз.
-
Параллелограммның көрші бұрыштарының қосындысы 180° екенін дәлелдеңіз.
-
Параллелограммның диагональдары қиылысқан нүктеде жартылай бөлінетінін дәлелдеңіз.
-
Ромбының диагональдары перпендикуляр және жартылай бөлінетінін дәлелдеңіз (бұл дәлелдеу үшін қосымша конструкциялар жасау қажет болуы мүмкін).
Тіктөртбұрыш, ромб және шаршы геометриялық фигураларын анықтау, қасиеттерін және белгілерін қолдану
А (анықтамаларды және негізгі қасиеттерді қолдану):
-
Тіктөртбұрыштың анықтамасын беріңіз. Оның кем дегенде үш қасиетін атаңыз.
-
Ромбтың анықтамасын беріңіз. Оның кем дегенде үш қасиетін атаңыз.
-
Шаршының анықтамасын беріңіз. Оның кем дегенде төрт қасиетін атаңыз.
-
Тіктөртбұрыштың қарама-қарсы жақтары қалай орналасқан?
-
Ромбтың барлық жақтарының ұзындығы қалай?
-
Шаршының барлық бұрыштарының шамасы қандай?
-
Тіктөртбұрыштың диагональдарының қасиетін атаңыз.
-
Ромбтың диагональдарының екі қасиетін атаңыз.
-
Шаршының диагональдарының үш қасиетін атаңыз.
-
Тіктөртбұрыштың ауданын табу формуласын жазыңыз.
-
Ромбтың ауданын табу формуласын жазыңыз (диагональдары арқылы).
-
Шаршының ауданын табу формуласын жазыңыз.
-
Егер тіктөртбұрыштың бір жағы 5 см, ал екіншісі 12 см болса, оның диагоналының ұзындығын табыңыз.
-
Егер ромбтың диагональдары 6 см және 8 см болса, оның ауданын табыңыз.
-
Егер шаршының қабырғасы 10 см болса, оның ауданын және диагоналының ұзындығын табыңыз.
В деңгей (қасиеттерді қолдану және есептеулер):
-
Тіктөртбұрыштың периметрі 28 см, ал бір жағы 5 см. Екінші жағының ұзындығын табыңыз.
-
Ромбтың периметрі 40 см. Оның бір жағының ұзындығын табыңыз.
-
Шаршының ауданы 64 см². Оның қабырғасының ұзындығын табыңыз.
-
Тіктөртбұрыштың ауданы 60 см², ал бір жағы 10 см. Екінші жағының ұзындығын табыңыз.
-
Ромбтың ауданы 24 см², ал бір диагоналы 6 см. Екінші диагоналының ұзындығын табыңыз.
С деңгей (қасиеттерді қорытып шығару және қолдану):
-
Тіктөртбұрыштың диагональдары тең екенін дәлелдеңіз. (Пифагор теоремасын қолдану арқылы)
-
Ромбтың диагональдары бір-біріне перпендикуляр екенін дәлелдеңіз. (үшбұрыштардың теңдігін қолдану арқылы)
-
Шаршының диагональдары тең және перпендикуляр екенін дәлелдеңіз.
-
Егер параллелограммның диагональдары тең болса және бір-біріне перпендикуляр болса, онда ол шаршы екенін дәлелдеңіз.
-
Егер тіктөртбұрыштың диагональдары бір-біріне перпендикуляр болса, онда ол шаршы екенін дәлелдеңіз.
Бұл есептердегі сандарды және шарттарды өзгертуге болады. Кейбір есептерді шешу үшін геометриялық теоремалар мен аксиомаларды қолдану қажет болуы мүмкін. Қиын деңгейдегі есептер геометриялық дәлелдеуді талап етеді. Есептер оқушылардың геометриялық ойлау қабілетін дамытуға бағытталған.
-
Фалес теоремасы. Пропорционал кесінділер
1-5 есептер (А деңгей):
-
Екі параллель түзуді қиып өтетін екі қиюшы түзу берілген. Бірінші қиюшы түзудің кесінділері 4 см және 6 см. Екінші қиюшы түзудің сәйкес кесіндісі 8 см. Екінші кесіндіні табыңыз.
-
Параллель түзулерді қиып өтетін екі қиюшы түзудің бірінші қиюшы түзудегі кесінділері 5 және 10. Екінші қиюшы түзудегі бірінші кесінді 6. Екінші кесіндіні табыңыз.
-
Үшбұрыштың екі қабырғасына параллель түзу жүргізілген. Параллель түзу үшбұрыштың қабырғаларын 3 және 6 болатын екі кесіндіге бөледі. Үшбұрыштың сәйкес келетін қабырғасы 9 болса, параллель түзудің кесіндісін табыңыз.
-
Суретте екі параллель түзу берілген. Оларды қиып өтетін қиюшы түзулердің біреуіндегі кесінділер 2 және 3. Екінші қиюшы түзудегі бірінші кесінді 4. Екінші кесіндіні табыңыз.
-
Фалес теоремасы бойынша екі параллель түзуді қиып өтетін қиюшы түзудің кесінділерінің қатынасын табыңыз, егер бір қиюшы түзудегі кесінділер 8 және 12, ал екінші қиюшы түзудегі сәйкес кесінділер 6 және х болса.
6-15 есептер (В деңгей:
-
Үшбұрыштың қабырғаларына параллель түзу жүргізілген. Бұл түзу үшбұрыштың қабырғаларын 4:6 қатынасында бөледі. Үлкен үшбұрыштың периметрі 30 см. Кіші үшбұрыштың периметрін табыңыз.
-
Екі параллель түзуді үш қиюшы түзу қиып өтеді. Бірінші қиюшы түзудегі кесінділер 2, 3 және 4. Екінші қиюшы түзудегі сәйкес кесінділер 4, 6 және х. х-ті табыңыз.
-
Үшбұрыштың екі қабырғасына параллель түзу жүргізілген. Бұл түзу үшбұрыштың қабырғаларын 5 және 10 кесінділерге бөледі. Параллель түзудің ұзындығы 12 см болса, үшбұрыштың сәйкес қабырғасының ұзындығын табыңыз.
-
Тіктөртбұрыштың қабырғаларына параллель екі түзу жүргізілген. Бұл түзулер тіктөртбұрыштың қабырғаларын 3:2 қатынасында бөледі. Тіктөртбұрыштың ауданы 60 см² болса, кіші тіктөртбұрыштың ауданын табыңыз.
-
Екі параллель түзуді қиып өтетін екі қиюшы түзу берілген. Бірінші қиюшы түзудің кесінділері 7 және 14. Екінші қиюшы түзудегі сәйкес кесінділердің қосындысы 27. Екінші қиюшы түзудің кесінділерін табыңыз.
11-15. (Осы есептер үшін суреттер беру қажет. Суреттерде параллель түзулер мен қиюшы түзулер арқылы құрылған кесінділер берілген. Кесінділердің ұзындықтары беріліп, белгісіз кесінділерді табу тапсырылады.)
16-20 есептер (С деңгей):
-
Екі параллель түзуді үш қиюшы түзу қиып өтеді. Бірінші қиюшы түзудегі кесінділер 3, x және 5. Екінші қиюшы түзудегі сәйкес кесінділер 6, 10 және 12. x-ті табыңыз.
-
Үшбұрыштың медианасы оны екі тең үшбұрышқа бөледі. Бұл үшбұрыштардың аудандарының қатынасын Фалес теоремасы арқылы дәлелдеңіз.
-
Екі параллель түзудің арақашықтығы 10 см. Оларды қиып өтетін қиюшы түзулердің біріндегі кесінділер 4 және 6 см. Екінші қиюшы түзудің сәйкес кесінділерінің арақашықтығын табыңыз.
-
Екі параллель түзудің арақашықтығы 8 см. Оларды қиып өтетін қиюшы түзулердің біреуіндегі кесінділер 3 және 5 см. Екінші қиюшы түзудің сәйкес кесінділердің қосындысы 16 см. Екінші кесінділерді табыңыз.
-
Үшбұрыштың екі қабырғасына параллель түзу жүргізілген. Бұл түзу үшбұрыштың қабырғаларын 2:3 қатынасында бөледі. Параллель түзу үшбұрыштың периметрін 25 см-ге тең екі үшбұрышқа бөледі. Үлкен және кіші үшбұрыштардың периметрлерін табыңыз.
1. Екі параллель түзуді қиып өтетін екі қиюшы түзу берілген. Бірінші қиюшы түзудің кесінділері 6 см және 9 см. Екінші қиюшы түзудің сәйкес кесіндісі 12 см. Екінші кесіндіні табыңыз.
a) 18 см b) 9 см c) 15 см d) 6 см
2. Параллель түзулерді қиып өтетін екі қиюшы түзудің бірінші қиюшы түзудегі кесінділері 4 және 8. Екінші қиюшы түзудегі бірінші кесінді 3. Екінші кесіндіні табыңыз.
a) 12 b) 6 c) 9 d) 3
3. Үшбұрыштың екі қабырғасына параллель түзу жүргізілген. Параллель түзу үшбұрыштың қабырғаларын 2 және 4 болатын екі кесіндіге бөледі. Үшбұрыштың сәйкес келетін қабырғасы 9 болса, параллель түзудің кесіндісін табыңуз.
a) 6 b) 3 c) 4.5 d) 18
4. Суретте екі параллель түзу берілген (суретті қосу керек). Оларды қиып өтетін қиюшы түзулердің біреуіндегі кесінділер 5 және 10. Екінші қиюшы түзудегі бірінші кесінді 6. Екінші кесіндіні табыңыз.
a) 12 b) 3 c) 18 d) 24
Бір немесе бірнеше дұрыс жауабы бар тест тапсырмасы
1. Екі параллель түзуді қиып өтетін екі қиюшы түзудің кесінділерінің қатынасы туралы қандай тұжырымдар дұрыс?
a) Кесінділердің қатынасы әрқашан тең.
b) Кесінділердің қатынасы бір-біріне тәуелді емес.
c) Кесінділердің қатынасы қиюшы түзудің орнына тәуелді.
d) Кесінділердің қатынасы параллель түзулердің арақашықтығына тәуелді емес.
e) Фалес теоремасы осы қатынасты анықтайды.
f) Кесінділердің қатынасы әрқашан 1-ге тең.
2. Фалес теоремасын қолдана отырып, қандай шамаларды есептеуге болады?
a) Үшбұрыштың ауданын.
b) Үшбұрыштың периметрін.
c) Параллель түзулер арасындағы қашықтықты.
d) Пропорционал кесінділердің ұзындықтарын.
e) Бұрыштардың шамаларын.
f) Үшбұрыштың биіктігін.
1-тапсырма: 1-a, 2-b, 3-b, 4-a
2-тапсырма: 1-a, e, 2-d, f,
4.Трапеция, оның түрлері мен қасиеттері. Трапеция мен үшбұрыштың орта сызықтары
А деңгей
1. Үшбұрыштың орта сызығын табу формуласы.
2. Трапецияның орта сызығын табу формуласы.
3. Үшбұрыштың орта сызығы 8 см-ге тең. Осы орта сызығына параллель қабырғасын табыңыз.
4. Үшбұрыштың орта сызығы 5 см-ге тең. Осы орта сызығына параллель қабырғасын табыңыз.
5. Үшбұрыштың орта сызығы 7 см-ге тең. Осы орта сызығына параллель қабырғасын табыңыз.
6. Үшбұрыштың бір қабырғасы 12 см – ге тең. Осы қабырғасына параллель орта сызығын табыңыз.
7. Үшбұрыштың бір қабырғасы 20 см – ге тең. Осы қабырғасына параллель орта сызығын табыңыз.
8. Трапецияның табандары 6 см және 8 см. Оның орта сызығын табыңыз.
9. Трапецияның табандары 3 см және 9 см. Оның орта сызығын табыңыз.
10. Трапецияның табандары 4 см және 12 см. Оның орта сызығын табыңыз.
11. Трапецияның табандары 6 см және 8 см. Оның орта сызығын табыңыз.
В деңгей
12. Тең қабырғалы үшбұрыштың орта сызығы 3 см. Оның периметрін табыңдар.
13. Тең қабырғалы АВС үшбұрышының орта сызығы - ДЕ. Егер АВС үшбұрышының қабырғасы 14 см болса, онда ЕВД үшбұрышының периметрін табыңдар.
14. Тең қабырғалы үшбұрыштың орта сызығы 4 см. Оның периметрін табыңдар.
15. Тең қабырғалы үшбұрыштың орта сызығы 5 см. Оның периметрін табыңдар.
16. Тең қабырғалы үшбұрыштың орта сызығы 2 см. Оның периметрін табыңдар.
17. Тең қабырғалы үшбұрыштың орта сызығы 4,5 см. Оның периметрін табыңдар.
18. Тең бүйірлі үшбұрыштың табанына параллель орта сызығы 3 см. Үшбұрыштың периметрі 16 см болса, онда оның қабырғаларын табыңыз.
19. Тең бүйірлі үшбұрыштың табанына параллель орта сызығы 4 см. Үшбұрыштың периметрі 18 см болса, онда оның қабырғаларын табыңыз.
20. Тең бүйірлі үшбұрыштың табанына параллель орта сызығы 5 см. Үшбұрыштың периметрі 26 см болса, онда оның қабырғаларын табыңыз.
С деңгей
21. Табандары АД=12 см және
ВС=4 см болатын АВСД трапециясының ЕF орта сызығы, ВД диагоналын К
нүктесінде қияды. F , онда FК және КЕ
кесінділердің ұзындықтарын табыңдар.
, онда FК және КЕ
кесінділердің ұзындықтарын табыңдар.
22.Табандары АД=10 см және
ВС=2 см болатын АВСД трапециясының ЕF орта сызығы, ВД диагоналын К
нүктесінде қияды. F , онда FК және КЕ
кесінділердің ұзындықтарын табыңдар.
, онда FК және КЕ
кесінділердің ұзындықтарын табыңдар.
23. АВСД тең бүйірлі трапецияның ЕF орта сызығы жүргізілген. Егер табандары АД=14 см, ВС=10 см, ал бүйір қабырғасы АВ=6 см болса, онда ЕВСF трапецияның периметрін табыңдар.
24. АВСД тең бүйірлі трапецияның ЕF орта сызығы жүргізілген. Егер табандары АД=12 см, ВС=8 см, ал бүйір қабырғасы АВ=4 см болса, онда ЕВСF трапецияның периметрін табыңдар.
25. Табандары ВС=5 см және АД=19 см, бүйір қабырғасы 12 см болатын тең бүйірлі АВСД трапециясының ВF биіктігі жүргізілген, онда АВF үшбұрышының периметрін табыңдар.
26.Төмендегі суретте, А, В, С
үш үй бір түзудің бойында түзу сызықты жолдан әртүрлі қашықтықта
орналасқан және  . Шеткі екі үй жолдан
сәйкесінше 72 м және 54 м қашықтықта болса, ортадағы үй жолдан
қандай қашықтықта орналасқан?
. Шеткі екі үй жолдан
сәйкесінше 72 м және 54 м қашықтықта болса, ортадағы үй жолдан
қандай қашықтықта орналасқан?

27.Төмендегі суретте, А, В, С
үш үй бір түзудің бойында түзу сызықты жолдан әртүрлі қашықтықта
орналасқан және  . Шеткі екі үй жолдан
сәйкесінше 52 м және 26 м қашықтықта болса, ортадағы үй жолдан
қандай қашықтықта орналасқан?
. Шеткі екі үй жолдан
сәйкесінше 52 м және 26 м қашықтықта болса, ортадағы үй жолдан
қандай қашықтықта орналасқан?

28.Төмендегі суретте, А, В, С
үш үй бір түзудің бойында түзу сызықты жолдан әртүрлі қашықтықта
орналасқан және  . Шеткі екі үй жолдан
сәйкесінше 100 м және 90 м қашықтықта болса, ортадағы үй жолдан
қандай қашықтықта орналасқан?
. Шеткі екі үй жолдан
сәйкесінше 100 м және 90 м қашықтықта болса, ортадағы үй жолдан
қандай қашықтықта орналасқан?

1-тапсырма (4 жауапты):
1. Трапеция дегеніміз не?
a) Төртбұрыштың екі қабырғасы параллель.
b) Төртбұрыштың барлық қабырғалары тең.
c) Төртбұрыштың барлық бұрыштары тең.
d) Төртбұрыштың екі қабырғасы перпендикуляр.
2. Тік трапеция дегеніміз не?
a) Екі қабырғасы параллель, ал екі қабырғасы перпендикуляр
. b) Екі қабырғасы параллель, ал бүйір қабырғалары биіктіктер.
c) Екі қабырғасы параллель, ал барлық бұрыштары тең.
d) Екі қабырғасы параллель, ал негіздері тең.
3. Тең бүйірлі трапеция дегеніміз не?
a) Екі қабырғасы параллель, ал бүйір қабырғалары тең
b) Екі қабырғасы параллель, ал барлық қабырғалары тең.
c) Екі қабырғасы параллель, ал бұрыштары тең.
d) Екі қабырғасы параллель, ал негіздері тең.
.
2-тапсырма (6 жауапты):
1. Тең бүйірлі трапецияның қандай қасиеттері бар?
a) Бүйір қабырғалары тең.
b) Негіздері тең.
c) Диагональдары тең.
d) Бұрыштары тең.
e) Бүйір бұрыштары тең.
f) Ауданды есептеу формуласы тіктөртбұрыштың ауданына тең.
2. Тік трапецияның қандай қасиеттері бар?
a) Бүйір қабырғалары биіктіктер.
b) Бүйір бұрыштары тік бұрыштар.
c) Диагональдары тең.
d) Негіздері тең.
e) Ауданды есептеу формуласы тіктөртбұрыштың ауданына тең.
f) Бүйір қабырғалары тең.
3. Трапецияның медианасы дегеніміз не?
a) Трапецияның екі негізін жалғайтын кесінді.
b) Трапецияның ең ұзын диагоналы.
c) Трапецияның негіздерінің ортаңғы нүктелерін жалғайтын кесінді.
d) Трапецияның биіктігі.
e) Трапецияның ауданы.
f) Трапецияның периметрі.
Жауаптар:
1-тапсырма: 1-a, 2-b, 3-a,
2-тапсырма: 1-a, c, e, 2-a, b, 3-c
5.Үшбұрыштың тамаша нүктелері
1-5. А деңгей:
-
Тең бүйірлі үшбұрышта биіктік, медиана және биссектриса бірдей бола ма? Егер иә болса, неге?
-
Тікбұрышты үшбұрышта медиана гипотенузаның жартысына тең бола ма? Дәлелдеңіз.
-
Тең қабырғалы үшбұрышта биіктіктер, медианалар және биссектрисалар қалай орналасады?
-
Үшбұрыштың ауырлық центрі дегеніміз не және ол қалай табылады?
-
Биіктіктердің қиылысу нүктесін атаңыз.
6-10. В деңгей:
-
Үшбұрыштың екі медианасының ұзындығы 6 см және 8 см. Үшінші медиананың ұзындығы қандай болуы мүмкін? (шешімде үшбұрыш теңсіздігін қолдану қажет)
-
Үшбұрыштың биіктігінің ұзындығы 5 см, негізі 10 см. Үшбұрыштың ауданын табыңыз.
-
Үшбұрыштың ауырлық центрі медианаларды қандай қатынаста бөледі?
-
Тең бүйірлі үшбұрышта биіктік негізді екі тең бөлікке бөле ме? Неге?
-
Тікбұрышты үшбұрышта ортоцентр қайда орналасады?
11-15. С деңгей:
-
Үшбұрыштың ауырлық центрі, ортоцентрі және айналдыру центрі бір нүктеде қиылысатын үшбұрышты атаңыз.
-
Егер үшбұрыштың екі медианасы перпендикуляр болса, онда бұл үшбұрыш қандай болуы мүмкін?
-
Үшбұрыштың ауданы 24 см², биіктігі 6 см болса, негізінің ұзындығын табыңыз.
-
Тең бүйірлі үшбұрышта биіктіктің ұзындығы 8 см, ал негізінің ұзындығы 12 см болса, үшбұрыштың ауданын табыңыз.
-
Үшбұрыштың бір медианасы 10 см, ал ауырлық центрінен осы медиананың ұшына дейінгі қашықтық 6 см болса, ауырлық центрінен медиананың басқа ұшына дейінгі қашықтықты табыңыз.
(графикалық шешімді қажет етеді):
-
Берілген үшбұрыш үшін ауырлық центрін, ортоцентрін және инцентрін салыңыз. (Сурет берілуі керек)
-
Берілген үшбұрыш үшін биіктіктерді салыңыз және ортоцентрін табыңыз. (Сурет берілуі керек)
-
Берілген үшбұрыш үшін медианаларды салыңыз және ауырлық центрін табыңыз. (Сурет берілуі керек)
-
Берілген үшбұрыш үшін биссектрисаларды салыңыз және инцентрін табыңыз. (Сурет берілуі керек)
-
Екі медианасы 6 см және 8 см болатын үшбұрыш салыңыз. Үшінші медиананың ұзындығын өлшеңіз.
1. Үшбұрыштың медианасы дегеніміз не?
a) Үшбұрыштың төбесінен қарсы жатқан қабырғаға түсірілген перпендикуляр.
b) Үшбұрыштың төбесінен қарсы жатқан қабырғаның ортасына жүргізілген кесінді. c) Үшбұрыштың бұрышын екіге бөлетін сәуле.
d) Үшбұрыштың екі қабырғасын қосатын кесінді.
2. Үшбұрыштың биіктігі дегеніміз не?
a) Үшбұрыштың төбесінен қарсы жатқан қабырғаға түсірілген перпендикуляр.
b) Үшбұрыштың төбесінен қарсы жатқан қабырғаның ортасына жүргізілген кесінді. c) Үшбұрыштың бұрышын екіге бөлетін сәуле.
d) Үшбұрыштың екі қабырғасын қосатын кесінді.
3. Үшбұрыштың биссектрисасы дегеніміз не?
a) Үшбұрыштың төбесінен қарсы жатқан қабырғаға түсірілген перпендикуляр.
b) Үшбұрыштың төбесінен қарсы жатқан қабырғаның ортасына жүргізілген кесінді. c) Үшбұрыштың бұрышын екіге бөлетін сәуле.
d) Үшбұрыштың екі қабырғасын қосатын кесінді.
2-тапсырма (6 жауапты):
1. Тең бүйірлі үшбұрышта қандай тамаша нүктелер бірдей нүктеде орналасады?
a) Ауырлық центрі
b) Ортоцентр
c) Инцентр
d) Айналдыру центрі
e) Медиана
f) Биіктік
2. Үшбұрыштың ауырлық центрі медианаларды қандай қатынаста бөледі?
a) 1:1 b) 1:2 c) 2:1 d) 2:3 e) 3:1 f) 3:2
Жауаптар:
1-тапсырма: 1-b, 2-a, 3-c,
2-тапсырма: 1-a, b, c, f, 3-c

шағым қалдыра аласыз















