
Геометрия 9 сынып
Тапсырмалардың сипаттамасы
Ұзақтығы – 45 минут
Балл саны – 20
Тапсырмалар түрлері
КТБ – көп таңдауы бар тапсырмалар
ҚЖ – қысқа жауапты қажет ететін тапсырмалар
ТЖ – толық жауапты қажет ететін тапсырмалар
|
№ |
Тақырып |
№ |
Тапсырма түрі |
Тексерілетін мақсаты |
|
1 |
Көпбұрыштың ішкі бұрыштарының қосындысы. Көпбұрыштың сыртқы бұрыштарының қосындысы. |
1 |
КТБ |
8.1.1.2 Көпбұрыштың ішкі бұрыштарының қосындысы мен сыртқы бұрыштарының қосындысы формуласын щығару |
|
2 |
Параллелограмм, тіктөртбұрыш, ромб, шаршы, олардың қасиеттері мен белгілері. |
2 |
КТБ |
8.1.1.6, тіктөртбұрыш, ромб, шаршының анықтамасын білу, қасиеттері мен белгілерін шығарып көрсету 8.1.1.4 Параллелограммның қасиеттері мен белгілерін шығарып көрсету |
|
3 |
Үшбұрыштың орта сызығы. |
3 a) |
КТБ |
8.1.1.12 Үшбұрыштың орта сызығының қасиетін дәлелдеу және есеп шығаруда қолдану |
|
4 |
Трапецияның орта сызығы.. |
3 b) |
КТБ |
8.1.1.13 Трапецияның орта сызығының қасиетін дәлелдеу және есеп шығаруда қолдану |
|
5 |
Үшбұрыштың медианасының қаситтері. Пифагор теоремасы |
4 |
ТЖ |
8.1.3.1 Үшбұрыштың медианасы, биссектрисасы, биіктігі және орта перпендикулярларының қаситтерін білу және есеп шығаруда қолдану. 8.1.3.3 Пифагор теоремасын дәлелдеу және есеп шығаруда қолдану |
|
6 |
Шаршы, тіктөртбұрыш және ромбтың аудандары |
5 |
КТБ |
8.1.3.11 Шаршы, параллелограм және ромбтың аудандарының формуласын шығару және есеп шығаруда қолдану |
|
7 |
Жазықтықтағы тікбұрышты координаталар жүйесі
|
6 |
КТБ |
8.1.3.17 центрі (a,b) нүктесінде және радиуысы r болатын шеңбердің теңдеуін жаза білу:
|
|
8 |
Пифагор теормеасы. Тікбұрышты үшбұрыштың сүйір бұрышының тригонометриялық функциясы. Тікбұрышты үшбұрыштарды шешу |
7 |
ТЖ |
8.1.3.2 қабырғалардың қатынасымен берілген синус, косинус, тангенс және котангенстың анықтамаларын біледі; 8.1.3.3 Пифагор теоремасын дәлелдеу; 8.1.3.8 тікбұрышты үшбұрыштың екі элементы бойынша белгісіз бұрыштары мен қабырғаларын табу |
I нұсқа
1. Жеті бұрыштың ішкі бұрыштарның қосындысын тап. [1 б]
2. Ақиқатты / жалғанды орнатыңыз:
|
Мәлімдемелер |
Ақиқат/жалған |
|
1. параллелограммның диагональдары перпендикуляр және қиылысу нүктесінде тең бөлінеді |
|
|
2. Шаршы дегеніміз ол барлық қабырғлары және бұрыштары тең параллелограмм |
|
|
4. Егер ромбтың көршілес жатқан қабырғаларының орталарын қосса, онда тіктөртбұрыш шығады |
|
[3 б]
3. а) АC табаны 12-ге тең болатын АВС теңбүйірлі үшбұрышы берілген. КF орта сызығының ұзындығын тап. [1 б]
b) Трапецияның орта сызығының ұзындығы 8,5 см, ал бір табанының ұзындығы 5 см. Екінші табанының ұзындығын тап.
[1 б]
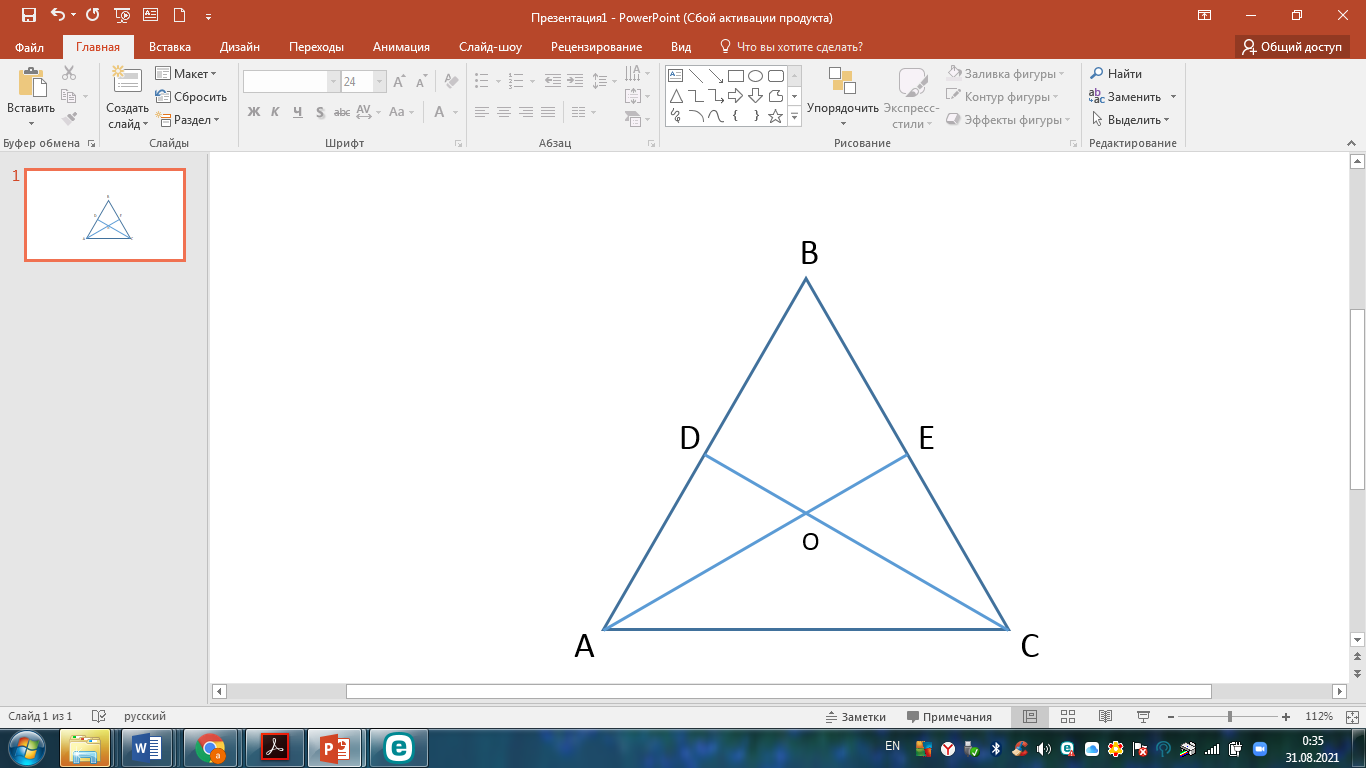
4. АС=ВС
болатын АВС теңбүйірлі
үшбұрышы берілген. АВ=
 см, АЕ= 21 см. Егер О нүктесі
AE и CD медианаларының қиылысу нүктесі болса, ОD-ны
тап.
см, АЕ= 21 см. Егер О нүктесі
AE и CD медианаларының қиылысу нүктесі болса, ОD-ны
тап.
[5 б]
5. Фигураларды олардың ауданымен сәйкестендір:
|
I.
|
|
a) 16 см2 |
|
II.
|
|
b) 32 см2 |
|
III.
|
|
c) 20 см2 d) 36 см2 |
[4 б]
6. Центрі О нүктесінде және
радиусы R
болатын шеңбердің теңдеуі
берілген ( )+(
)+( ) = 27. О нүктесінің координатасы
мен радиустың ұзындығын тап.
) = 27. О нүктесінің координатасы
мен радиустың ұзындығын тап.
а) О (-9; 4), R=27. b) O
(-3;2), R=3 с) О (-9; 4), R=3
с) О (-9; 4), R=3
d) О (9;- 4), R=3 e) О (3; -2), R=27
e) О (3; -2), R=27
[1 б]
7. Тікбұрышты үшбұрыштың
гипотенузасының ұзындығы 5 , ал бір катеті 5 см.
Осы үшбұрыштың сүйір бүрыщтарын тап.
[4 б]
, ал бір катеті 5 см.
Осы үшбұрыштың сүйір бүрыщтарын тап.
[4 б]
IІ нұсқа
1. Бес бұрыштың ішкі бұрыштарның қосындысын тап. [1 б]
2. Ақиқатты / жалғанды орнатыңыз:
|
Мәлімдемелер |
Ақиқат/жалған |
|
1. Трапецияның диагональдары перпендикуляр және қиылысу нүктесінде тең бөлінеді |
|
|
2. Егер ромбтың көршілес жатқан қабырғаларының орталарын қосса, онда тіктөртбұрыш шығады |
|
|
3. Шаршы дегеніміз ол барлық қабырғлары және бұрыштары тең параллелограмм |
|
[3 б]
3. а) АC табаны 16-ге тең болатын АВС теңбүйірлі үшбұрышы берілген. КF орта сызығының ұзындығын тап. [1 б]
b) Трапецияның орта сызығының ұзындығы 6,5 см, ал бір табанының ұзындығы 6 см. Екінші табанының ұзындығын тап.
[1 б]
4. АВ=ВС
болатын АВС теңбүйірлі
үшбұрышы берілген. ВС=
 см, СД= 21 см. Егер О нүктесі
AE и CD медианаларының қиылысу нүктесі болса, ОЕ-ны
тап.
см, СД= 21 см. Егер О нүктесі
AE и CD медианаларының қиылысу нүктесі болса, ОЕ-ны
тап.

[5 б]
5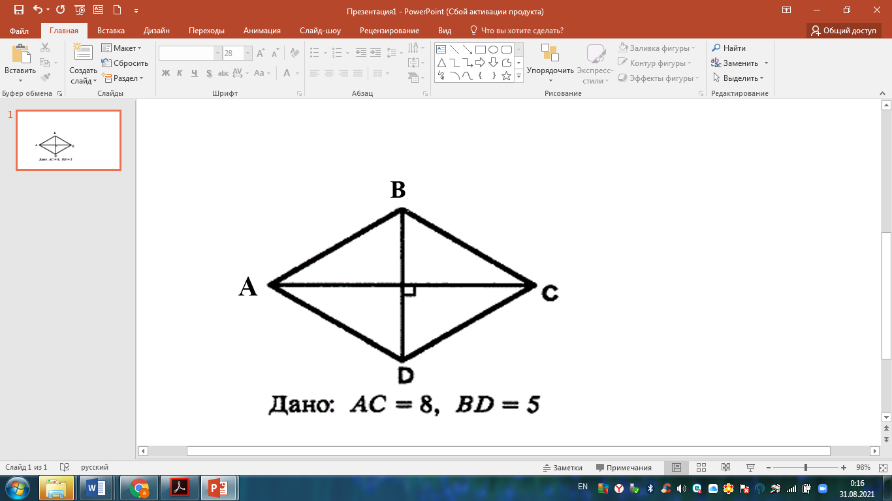 .
Фигураларды олардың ауданымен
сәйкестендір:
.
Фигураларды олардың ауданымен
сәйкестендір:
|
I. |
|
a) 32 см2 |
|
II.
|
|
b) 16 см2 |
|
III.
|
|
c) 36 см2 d) 20 см2 |
[4 б]
6. Центрі О нүктесінде және
радиусы R
болатын шеңбердің теңдеуі
берілген ( )+(
)+( ) = 12. О нүктесінің координатасы
мен радиустың ұзындығын тап.
) = 12. О нүктесінің координатасы
мен радиустың ұзындығын тап.
а) О (-7; 5), R=12. b) O
(-3;2), R=2 с) О (-7; 5), R=2
с) О (-7; 5), R=2
d) О (7;- 5), R=2 e) О (3; -2), R=27
e) О (3; -2), R=27
[1 б]
7. Тікбұрышты үшбұрыштың
гипотенузасының ұзындығы 7 , ал бір катеті 7 см.
Осы үшбұрыштың сүйір бүрыщтарын тап. [4
б]
, ал бір катеті 7 см.
Осы үшбұрыштың сүйір бүрыщтарын тап. [4
б]
|
№ |
Дескриптор |
Балл |
|
1 |
Көпбұрыштың ішкі бұрыштарының қосындысы уралы формуланы қолданады. Сыртқы бұрыштарының қосындысын табу үшін осы теореманың салдарын қолданады |
1 |
|
2 |
Жалғандығын анықтайды Жалғандығын анықтайды Ақиқаттығын анықтайды |
1 1 1 |
|
3 b) |
Үшбұрыштың орта сызығының қасиетін дәлелдейді және есеп шығаруда қолданады |
1 |
|
|
Трапецияның орта сызығының қасиетін дәлелдейді және есеп шығаруда қолданады |
|
|
3 а) |
Применяет теорему о средней линии треугольника и находит среднюю линию треугольника |
1 |
|
4 |
Медиананың қасиетін қолданып АD-ны табады . Медиананың қасиетін
қолданып AO= AD-ны табады Медиананың қасиетін қолданып AOD- тікбұрышты екенін дәлелдейді. Пифагор теоремасы бойынша ОD-ны табады |
1 1 1 1 1 |
|
5 |
параллелограммның биіктігін табады параллелограммның ауданын табады Тіктөртбұрыштың ауданын табады ромбтың ауданын табады |
1 1 1 1 |
|
6 |
центрі (a,b) нүктесінде және радиуысы R болатын шеңбердің теңдеуін қолданады |
1 |
|
|
Сызбасын жасап берілгенін жазады |
1 |
|
Пифагор теоремасын қолданып екінші катеттің ұзындығын табады. |
1 |
|
|
синус, косинус, тангенстың анықтамаларын қолданып үшбұрыштың бұрыштарын табады |
1 1 |
|
|
|
|
20 |
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
9 геометрия 0-дік бақылау срез
9 геометрия 0-дік бақылау срез
Геометрия 9 сынып
Тапсырмалардың сипаттамасы
Ұзақтығы – 45 минут
Балл саны – 20
Тапсырмалар түрлері
КТБ – көп таңдауы бар тапсырмалар
ҚЖ – қысқа жауапты қажет ететін тапсырмалар
ТЖ – толық жауапты қажет ететін тапсырмалар
|
№ |
Тақырып |
№ |
Тапсырма түрі |
Тексерілетін мақсаты |
|
1 |
Көпбұрыштың ішкі бұрыштарының қосындысы. Көпбұрыштың сыртқы бұрыштарының қосындысы. |
1 |
КТБ |
8.1.1.2 Көпбұрыштың ішкі бұрыштарының қосындысы мен сыртқы бұрыштарының қосындысы формуласын щығару |
|
2 |
Параллелограмм, тіктөртбұрыш, ромб, шаршы, олардың қасиеттері мен белгілері. |
2 |
КТБ |
8.1.1.6, тіктөртбұрыш, ромб, шаршының анықтамасын білу, қасиеттері мен белгілерін шығарып көрсету 8.1.1.4 Параллелограммның қасиеттері мен белгілерін шығарып көрсету |
|
3 |
Үшбұрыштың орта сызығы. |
3 a) |
КТБ |
8.1.1.12 Үшбұрыштың орта сызығының қасиетін дәлелдеу және есеп шығаруда қолдану |
|
4 |
Трапецияның орта сызығы.. |
3 b) |
КТБ |
8.1.1.13 Трапецияның орта сызығының қасиетін дәлелдеу және есеп шығаруда қолдану |
|
5 |
Үшбұрыштың медианасының қаситтері. Пифагор теоремасы |
4 |
ТЖ |
8.1.3.1 Үшбұрыштың медианасы, биссектрисасы, биіктігі және орта перпендикулярларының қаситтерін білу және есеп шығаруда қолдану. 8.1.3.3 Пифагор теоремасын дәлелдеу және есеп шығаруда қолдану |
|
6 |
Шаршы, тіктөртбұрыш және ромбтың аудандары |
5 |
КТБ |
8.1.3.11 Шаршы, параллелограм және ромбтың аудандарының формуласын шығару және есеп шығаруда қолдану |
|
7 |
Жазықтықтағы тікбұрышты координаталар жүйесі
|
6 |
КТБ |
8.1.3.17 центрі (a,b) нүктесінде және радиуысы r болатын шеңбердің теңдеуін жаза білу:
|
|
8 |
Пифагор теормеасы. Тікбұрышты үшбұрыштың сүйір бұрышының тригонометриялық функциясы. Тікбұрышты үшбұрыштарды шешу |
7 |
ТЖ |
8.1.3.2 қабырғалардың қатынасымен берілген синус, косинус, тангенс және котангенстың анықтамаларын біледі; 8.1.3.3 Пифагор теоремасын дәлелдеу; 8.1.3.8 тікбұрышты үшбұрыштың екі элементы бойынша белгісіз бұрыштары мен қабырғаларын табу |
I нұсқа
1. Жеті бұрыштың ішкі бұрыштарның қосындысын тап. [1 б]
2. Ақиқатты / жалғанды орнатыңыз:
|
Мәлімдемелер |
Ақиқат/жалған |
|
1. параллелограммның диагональдары перпендикуляр және қиылысу нүктесінде тең бөлінеді |
|
|
2. Шаршы дегеніміз ол барлық қабырғлары және бұрыштары тең параллелограмм |
|
|
4. Егер ромбтың көршілес жатқан қабырғаларының орталарын қосса, онда тіктөртбұрыш шығады |
|
[3 б]
3. а) АC табаны 12-ге тең болатын АВС теңбүйірлі үшбұрышы берілген. КF орта сызығының ұзындығын тап. [1 б]
b) Трапецияның орта сызығының ұзындығы 8,5 см, ал бір табанының ұзындығы 5 см. Екінші табанының ұзындығын тап.
[1 б]
4. АС=ВС
болатын АВС теңбүйірлі
үшбұрышы берілген. АВ=
 см, АЕ= 21 см. Егер О нүктесі
AE и CD медианаларының қиылысу нүктесі болса, ОD-ны
тап.
см, АЕ= 21 см. Егер О нүктесі
AE и CD медианаларының қиылысу нүктесі болса, ОD-ны
тап.

[5 б]
5. Фигураларды олардың ауданымен сәйкестендір:
|
I.
|
|
a) 16 см2 |
|
II.
|
|
b) 32 см2 |
|
III.
|
|
c) 20 см2 d) 36 см2 |
[4 б]
6. Центрі О нүктесінде және
радиусы R
болатын шеңбердің теңдеуі
берілген ( )+(
)+( ) = 27. О нүктесінің координатасы
мен радиустың ұзындығын тап.
) = 27. О нүктесінің координатасы
мен радиустың ұзындығын тап.
а) О (-9; 4), R=27. b) O
(-3;2), R=3 с) О (-9; 4), R=3
с) О (-9; 4), R=3
d) О (9;- 4), R=3 e) О (3; -2), R=27
e) О (3; -2), R=27
[1 б]
7. Тікбұрышты үшбұрыштың
гипотенузасының ұзындығы 5 , ал бір катеті 5 см.
Осы үшбұрыштың сүйір бүрыщтарын тап.
[4 б]
, ал бір катеті 5 см.
Осы үшбұрыштың сүйір бүрыщтарын тап.
[4 б]
IІ нұсқа
1. Бес бұрыштың ішкі бұрыштарның қосындысын тап. [1 б]
2. Ақиқатты / жалғанды орнатыңыз:
|
Мәлімдемелер |
Ақиқат/жалған |
|
1. Трапецияның диагональдары перпендикуляр және қиылысу нүктесінде тең бөлінеді |
|
|
2. Егер ромбтың көршілес жатқан қабырғаларының орталарын қосса, онда тіктөртбұрыш шығады |
|
|
3. Шаршы дегеніміз ол барлық қабырғлары және бұрыштары тең параллелограмм |
|
[3 б]
3. а) АC табаны 16-ге тең болатын АВС теңбүйірлі үшбұрышы берілген. КF орта сызығының ұзындығын тап. [1 б]
b) Трапецияның орта сызығының ұзындығы 6,5 см, ал бір табанының ұзындығы 6 см. Екінші табанының ұзындығын тап.
[1 б]
4. АВ=ВС
болатын АВС теңбүйірлі
үшбұрышы берілген. ВС=
 см, СД= 21 см. Егер О нүктесі
AE и CD медианаларының қиылысу нүктесі болса, ОЕ-ны
тап.
см, СД= 21 см. Егер О нүктесі
AE и CD медианаларының қиылысу нүктесі болса, ОЕ-ны
тап.

[5 б]
5 .
Фигураларды олардың ауданымен
сәйкестендір:
.
Фигураларды олардың ауданымен
сәйкестендір:
|
I. |
|
a) 32 см2 |
|
II.
|
|
b) 16 см2 |
|
III.
|
|
c) 36 см2 d) 20 см2 |
[4 б]
6. Центрі О нүктесінде және
радиусы R
болатын шеңбердің теңдеуі
берілген ( )+(
)+( ) = 12. О нүктесінің координатасы
мен радиустың ұзындығын тап.
) = 12. О нүктесінің координатасы
мен радиустың ұзындығын тап.
а) О (-7; 5), R=12. b) O
(-3;2), R=2 с) О (-7; 5), R=2
с) О (-7; 5), R=2
d) О (7;- 5), R=2 e) О (3; -2), R=27
e) О (3; -2), R=27
[1 б]
7. Тікбұрышты үшбұрыштың
гипотенузасының ұзындығы 7 , ал бір катеті 7 см.
Осы үшбұрыштың сүйір бүрыщтарын тап. [4
б]
, ал бір катеті 7 см.
Осы үшбұрыштың сүйір бүрыщтарын тап. [4
б]
|
№ |
Дескриптор |
Балл |
|
1 |
Көпбұрыштың ішкі бұрыштарының қосындысы уралы формуланы қолданады. Сыртқы бұрыштарының қосындысын табу үшін осы теореманың салдарын қолданады |
1 |
|
2 |
Жалғандығын анықтайды Жалғандығын анықтайды Ақиқаттығын анықтайды |
1 1 1 |
|
3 b) |
Үшбұрыштың орта сызығының қасиетін дәлелдейді және есеп шығаруда қолданады |
1 |
|
|
Трапецияның орта сызығының қасиетін дәлелдейді және есеп шығаруда қолданады |
|
|
3 а) |
Применяет теорему о средней линии треугольника и находит среднюю линию треугольника |
1 |
|
4 |
Медиананың қасиетін қолданып АD-ны табады . Медиананың қасиетін
қолданып AO= AD-ны табады Медиананың қасиетін қолданып AOD- тікбұрышты екенін дәлелдейді. Пифагор теоремасы бойынша ОD-ны табады |
1 1 1 1 1 |
|
5 |
параллелограммның биіктігін табады параллелограммның ауданын табады Тіктөртбұрыштың ауданын табады ромбтың ауданын табады |
1 1 1 1 |
|
6 |
центрі (a,b) нүктесінде және радиуысы R болатын шеңбердің теңдеуін қолданады |
1 |
|
|
Сызбасын жасап берілгенін жазады |
1 |
|
Пифагор теоремасын қолданып екінші катеттің ұзындығын табады. |
1 |
|
|
синус, косинус, тангенстың анықтамаларын қолданып үшбұрыштың бұрыштарын табады |
1 1 |
|
|
|
|
20 |

шағым қалдыра аласыз


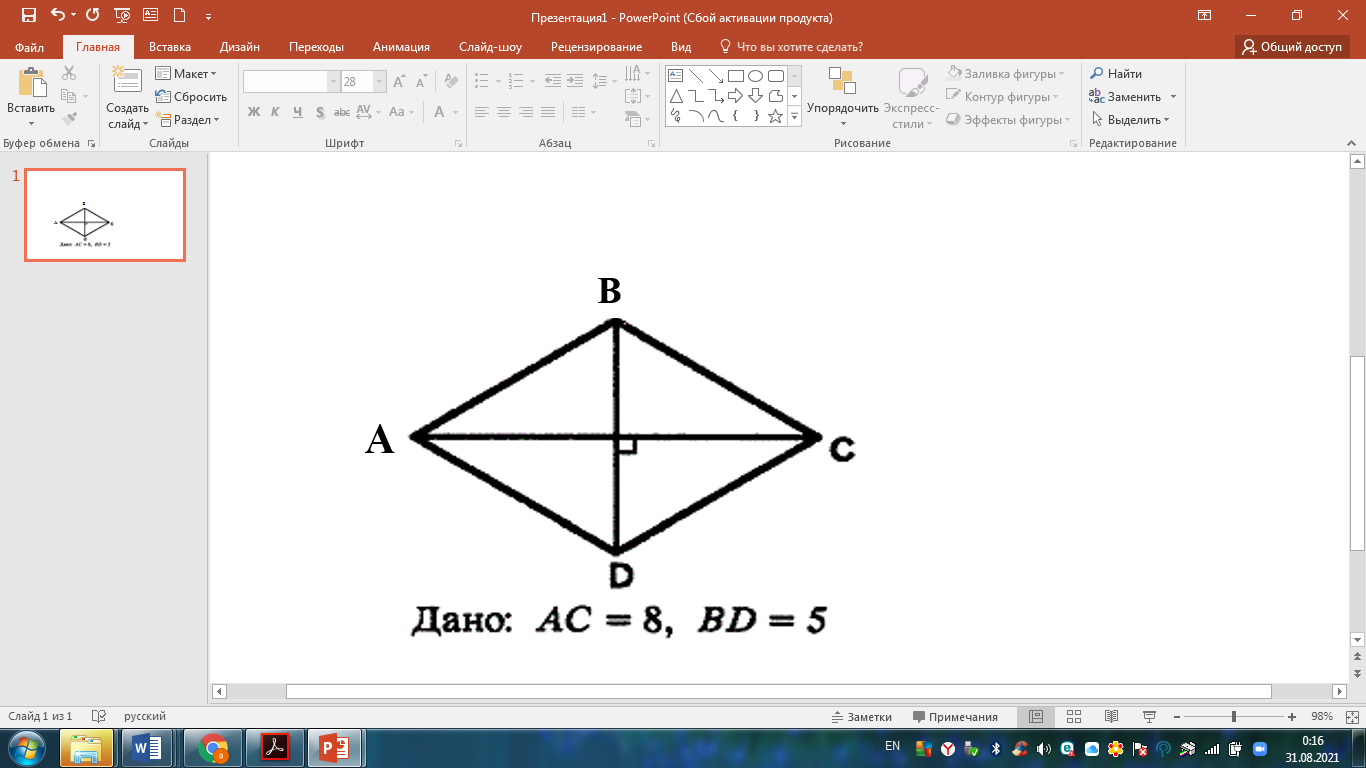
 AD
AD













