
«Екі айнымалысы бар теңдеулер,теңсіздіктер және олардың жүйелері»
-
нұсқа
-
Екі айнымалысы бар теңдеулер жүйесін шешіңіздер:
 [4 балл ]
[4 балл ]
-
Тіктөртбұрыштың периметрі 26см, ал ауданы 42см2. Тіктөртбұрыштың қабырғаларын теңдеулер жүйесін құрып табыңыз. [4 балл ]
-
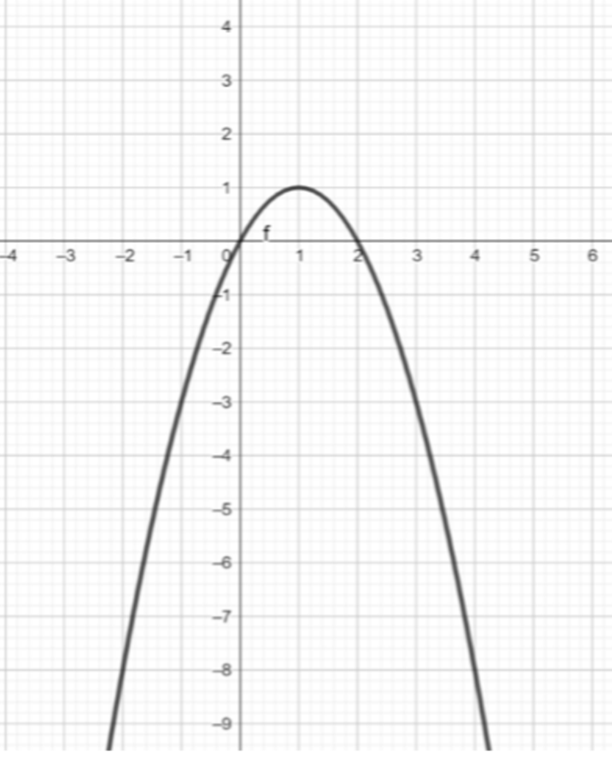
 Функцияның графигі суретте көрсетілген. [2 балл
]
Функцияның графигі суретте көрсетілген. [2 балл
]
а)
 ; координаталық жазықтықта теңсіздігінің шешімі болатын
қандай да бір сандар жұбын көрсетіңдер.
; координаталық жазықтықта теңсіздігінің шешімі болатын
қандай да бір сандар жұбын көрсетіңдер.
б) А(3;4), В( -1;-5) нүктелерінің қайсысы, а пунктының шешімі болады?
-
Екі айнымалысы бар теңсіздіктер жүйесін шешіңіздер:
 [5 балл ]
[5 балл ]
«Екі айнымалысы бар теңдеулер,теңсіздіктер және олардың жүйелері»
-
нұсқа
-
Екі айнымалысы бар теңдеулер жүйесін шешіңіздер:
 [4 балл ]
[4 балл ]
-
Тіктөртбұрыштың периметрі 26см, ал ауданы 42см2. Тіктөртбұрыштың қабырғаларын теңдеулер жүйесін құрып табыңыз. [4 балл ]
-
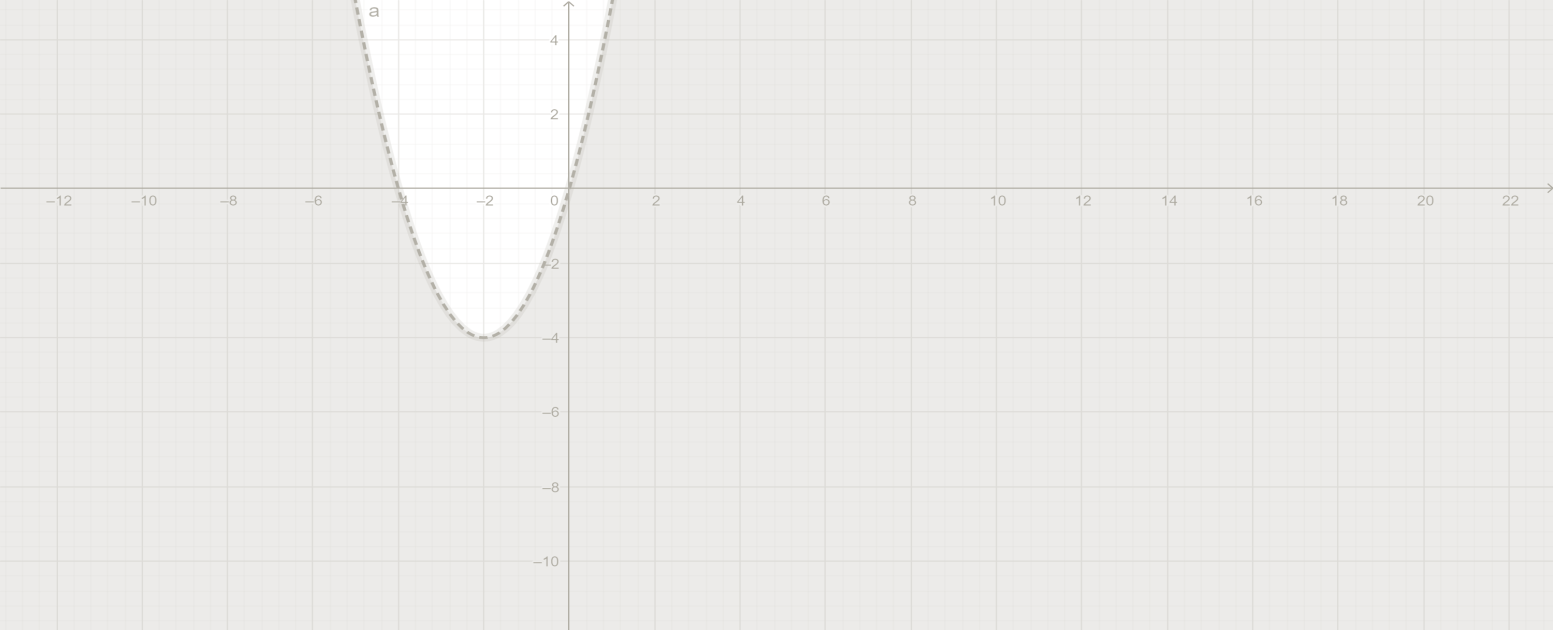
 Функцияның графигі суретте көрсетілген. [2 балл
]
Функцияның графигі суретте көрсетілген. [2 балл
]
а)
 ; координаталық жазықтықта теңсіздігінің шешімі болатын
қандай да бір сандар жұбын көрсетіңдер.
; координаталық жазықтықта теңсіздігінің шешімі болатын
қандай да бір сандар жұбын көрсетіңдер.
б) А(-1;4), В( -2;-5) нүктелерінің қайсысы, а пунктының шешімі болады?
-
Екі айнымалысы бар теңсіздіктер жүйесін шешіңіздер:
 [5 балл ]
[5 балл ]
|
Бағалау критерийлері |
№ |
Дескриптор |
Балл |
|
Білім алушы |
|||
|
Екі айнымалысы бар сызықтық емес теңдеулер жүйесін шешу әдістерін қолданады |
1 |
бір айнымалыны екінші айнымалы арқылы өрнектейді |
1 |
|
екінші теңдеудегі айнымалыны ауыстырады |
1 |
||
|
бір айнымалыдан тәуелді теңдеуді шешеді |
1 |
||
|
теңдеулер жүйесінің шешімін табады және жауабын жазады |
1 |
||
|
Мәтінді есептерді теңдеулер жүйесін құру арқылы шешеді |
2 |
шарты бойынша бірінші теңдеуді құрады |
1 |
|
шарты бойынша екінші теңдеуді құрады |
1 |
||
|
теңдеулер жүйесінің шешімін табады |
1 |
||
|
есеп шартына сәйкес жауабын жазады |
1 |
||
|
Екі айнымалысы бар теңсіздікті шешеді |
3 |
тікбұрышты координаттар жүйесінде теңсіздіктің өптеген шешімдерін көрсетеді |
1 |
|
берілген координаттары бар нүктелер осы теңсіздіктің шешімі болып табылатындығын тексереді |
1 |
||
|
Екі айнымалысы бар сызықты емес теңсіздіктер жүйесін шешеді |
4 |
координаталардың тікбұрышты жүйесінде жүйенің бірінші теңдеуімен берілген қисық графигін құрастырады |
1 |
|
теңсіздіктің біріншісін кӛптеген шешімдерді бейнелейді; |
1 |
||
|
жүйенің екінші теңдеуімен берілген қисық графигін дәл сол тікбұрышты координаттар жүйесінде салады; |
1 |
||
|
теңсіздіктің екіншісінің көптеген шешімдерін бейнелейді; |
1 |
||
|
көптеген шешімдердің қиылысуын көрсетеді |
1 |
||
|
Барлығы |
15 |
||

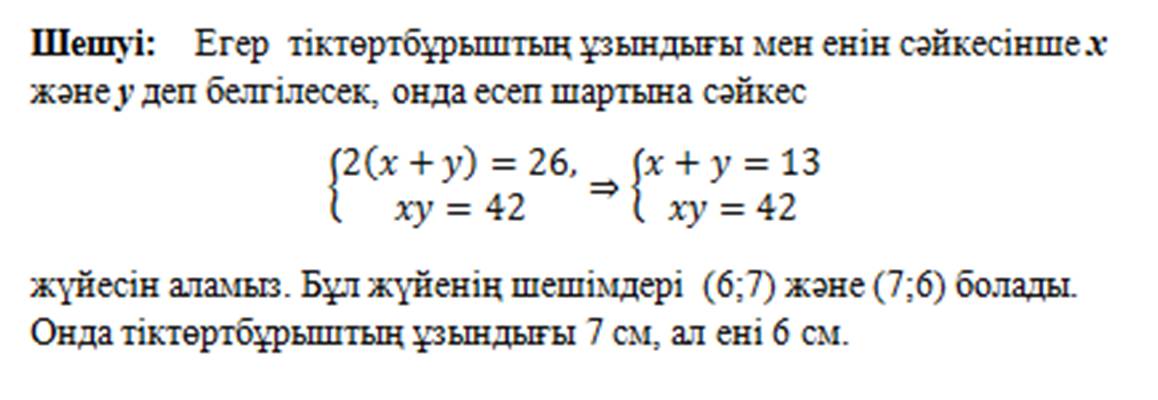
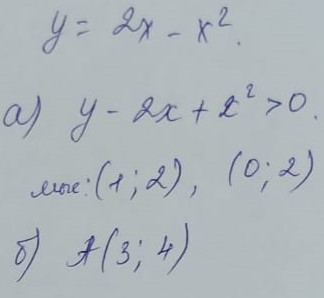
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
9 сынып алгебра бжб№1
9 сынып алгебра бжб№1
«Екі айнымалысы бар теңдеулер,теңсіздіктер және олардың жүйелері»
-
нұсқа
-
Екі айнымалысы бар теңдеулер жүйесін шешіңіздер:
 [4 балл ]
[4 балл ]
-
Тіктөртбұрыштың периметрі 26см, ал ауданы 42см2. Тіктөртбұрыштың қабырғаларын теңдеулер жүйесін құрып табыңыз. [4 балл ]
-
 Функцияның графигі суретте көрсетілген. [2 балл
]
Функцияның графигі суретте көрсетілген. [2 балл
]
а)
 ; координаталық жазықтықта теңсіздігінің шешімі болатын
қандай да бір сандар жұбын көрсетіңдер.
; координаталық жазықтықта теңсіздігінің шешімі болатын
қандай да бір сандар жұбын көрсетіңдер.
б) А(3;4), В( -1;-5) нүктелерінің қайсысы, а пунктының шешімі болады?

-
Екі айнымалысы бар теңсіздіктер жүйесін шешіңіздер:
 [5 балл ]
[5 балл ]
«Екі айнымалысы бар теңдеулер,теңсіздіктер және олардың жүйелері»
-
нұсқа
-
Екі айнымалысы бар теңдеулер жүйесін шешіңіздер:
 [4 балл ]
[4 балл ]
-
Тіктөртбұрыштың периметрі 26см, ал ауданы 42см2. Тіктөртбұрыштың қабырғаларын теңдеулер жүйесін құрып табыңыз. [4 балл ]
-
 Функцияның графигі суретте көрсетілген. [2 балл
]
Функцияның графигі суретте көрсетілген. [2 балл
]
а)
 ; координаталық жазықтықта теңсіздігінің шешімі болатын
қандай да бір сандар жұбын көрсетіңдер.
; координаталық жазықтықта теңсіздігінің шешімі болатын
қандай да бір сандар жұбын көрсетіңдер.
б) А(-1;4), В( -2;-5) нүктелерінің қайсысы, а пунктының шешімі болады?

-
Екі айнымалысы бар теңсіздіктер жүйесін шешіңіздер:
 [5 балл ]
[5 балл ]
|
Бағалау критерийлері |
№ |
Дескриптор |
Балл |
|
Білім алушы |
|||
|
Екі айнымалысы бар сызықтық емес теңдеулер жүйесін шешу әдістерін қолданады |
1 |
бір айнымалыны екінші айнымалы арқылы өрнектейді |
1 |
|
екінші теңдеудегі айнымалыны ауыстырады |
1 |
||
|
бір айнымалыдан тәуелді теңдеуді шешеді |
1 |
||
|
теңдеулер жүйесінің шешімін табады және жауабын жазады |
1 |
||
|
Мәтінді есептерді теңдеулер жүйесін құру арқылы шешеді |
2 |
шарты бойынша бірінші теңдеуді құрады |
1 |
|
шарты бойынша екінші теңдеуді құрады |
1 |
||
|
теңдеулер жүйесінің шешімін табады |
1 |
||
|
есеп шартына сәйкес жауабын жазады |
1 |
||
|
Екі айнымалысы бар теңсіздікті шешеді |
3 |
тікбұрышты координаттар жүйесінде теңсіздіктің өптеген шешімдерін көрсетеді |
1 |
|
берілген координаттары бар нүктелер осы теңсіздіктің шешімі болып табылатындығын тексереді |
1 |
||
|
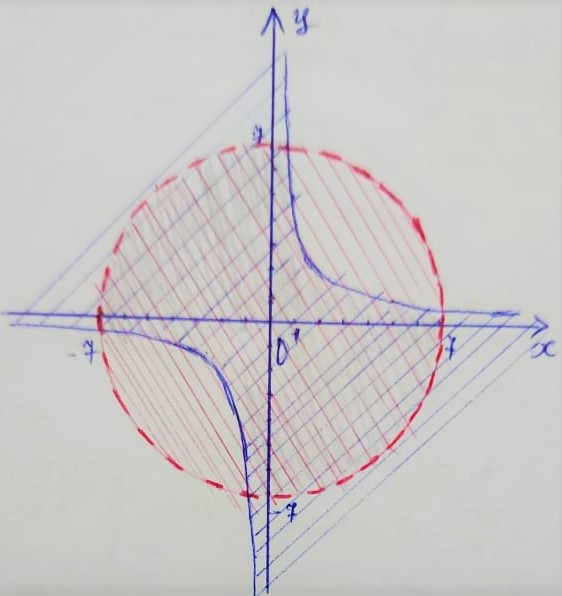
Екі айнымалысы бар сызықты емес теңсіздіктер жүйесін шешеді |
4 |
координаталардың тікбұрышты жүйесінде жүйенің бірінші теңдеуімен берілген қисық графигін құрастырады |
1 |
|
теңсіздіктің біріншісін кӛптеген шешімдерді бейнелейді; |
1 |
||
|
жүйенің екінші теңдеуімен берілген қисық графигін дәл сол тікбұрышты координаттар жүйесінде салады; |
1 |
||
|
теңсіздіктің екіншісінің көптеген шешімдерін бейнелейді; |
1 |
||
|
көптеген шешімдердің қиылысуын көрсетеді |
1 |
||
|
Барлығы |
15 |
||

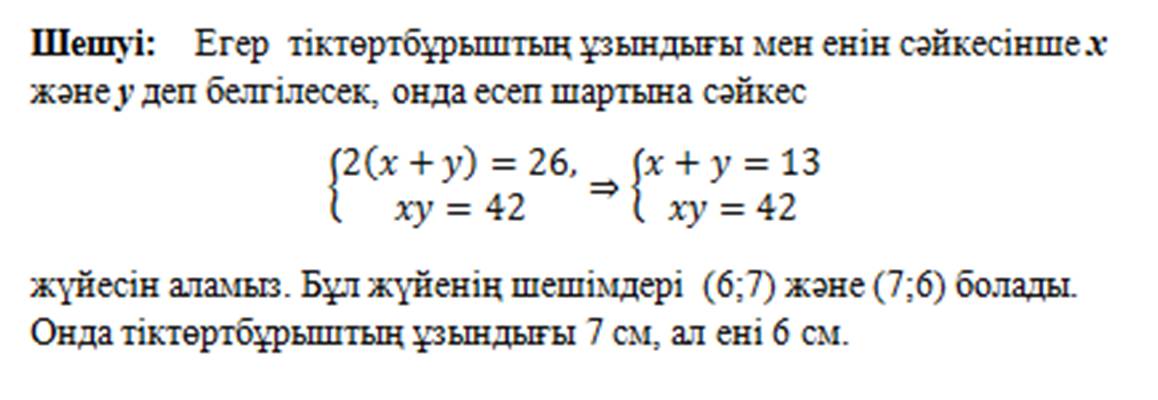

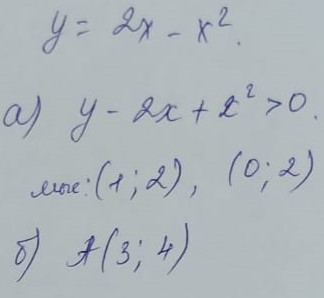

шағым қалдыра аласыз















