А
R
R
3
3
3

Караганда 2019 г.
1

Управление образования Карагандинской области
Учебно-методический центр развития образования Карагандинской области
Бӛлім бойынша жиынтық бағалауға арналған тапсырмаларТоқсандақ жиынтық бағалауға арналған тапсырмалар
Алгебра. Геометрия.
9 сынып
УДК 373(072)
Шығармашылық топ автор-құрастырушылар:
Шахтинск қаласы: Ким Юлия Вячеславовна (№2 ОМ), Гудовщикова Джамиля Салимовна (№3 ОМ), Бащук Елена Сергеевна (№4 ОМ), Ермакова Светлана Геннадьевна (№5 мектеп-гимназиясы), Абдрашитова Асия Анваровна (№6 ОМ), Шыныбекова Гульжан Ермековна (Әлихан Бөкейханов атындағы мектеп- лицейі), Есенкелді Қалман (Әлихан Бөкейханов атындағы мектеп- лицейі)
Пікір жазған:
Калинина О.Ю. КМКП Қарағанды облысы білім беруді дамытудың оқу-әдістемелік орталығының жалпы орта білім беру бӛлімінің әдіскері:
Бӛлім бойынша жиынтық бағалауға арналған тапсырмалар. Тоқсандақ жиынтық бағалауға арналған тапсырмалар. Математика 9-сынып. ҚО ББД ОӘО, 2019 ж. 78 бет.
Әдістемелік ұсыныстар 8 сынып білім алушыларына арналған «Алгебра» және
«Геометрия» пәні бойынша жиынтық бағалауды жоспарлау, ұйымдастыру және ӛткізу кезінде мұғалімге кӛмек ретінде жасалған. Әдістемелік ұсыныстар үлгілік оқу жоспары мен оқу бағдарламасы негізінде дайындалған. Бӛлім/ортақ тақырып үшін жиынтық бағалау тапсырмалары мұғалімге білім алушылардың тоқсан бойынша жоспарланған оқу мақсаттарына қол жеткізу деңгейін анықтауға мүмкіндік береді. Бӛлім/ортақ тақырып бойынша жиынтық бағалауды ӛткізу үшін әдістемелік ұсынымдарда тапсырмалар, дескрипторлар мен баллдар арқылы бағалау критерийлері ұсынылады.
Облыстық Ғылыми-Әдестемелік Кеңесімен ұсынылды Протокол № « » 12 2019 ж.
Мазмұны
БӚЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР Алгебра 4
«Екі айнымалысы бар теңдеулер,теңсіздіктер және олардың жүйелері» 5
«Ықтималдықтар теориясының элементтері» 20
«Жазықтықтағы түрлендірулер» 25
БӚЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР Алгебра
Жиынтық бағалау белгілі бір оқу кезеңінде оқу бағдарламасының мазмұнын меңгеру деңгейін анықтау және тіркеу үшін жүргізіледі. Тіркеу барысында оқу бағдарламасының мазмұнына сәйкес білім алушылардың білімі мен білік дағдыларын кӛрсететін дәлелдер жинау негізінде жүзеге асырылады. Жиынтық бағалау тоқсан ішінде (бӛлім/ортақ тақырып үшін жиынтық бағалау), тоқсан соңында (тоқсандық жиынтық бағалау) және білім беру деңгейі аяқталғаннан кейін (негізгі орта, жалпы орта) ӛткізіледі. Жиынтық бағалау нәтижелері бойынша балл/деңгей/бағалау туралы шешімді мұғалім бағалау критерийлеріне сәйкес анықтайды. Әрбір білім алушыға қатысты объективті шешім қабылдауда мұғалімге кӛмек кӛрсетуде бӛлім/ортақ тақырыптар үшін жиынтық бағалау тапсырмаларына дескрипторлар әзірленген.
«Екі айнымалысы бар теңдеулер,теңсіздіктер және олардың жүйелері»
Тақырып:
Екі айнымалысы бар сызықтық емес теңдеулер жүйесін шешу Мәтінді есептерді теңдеулер жүйелері арқылы шешу
Есеп шарты бойынша математикалық модель құру Екі айнымалысы бар теңсіздіктерді шешу
Оқу мақсаттары:
-
Екі айнымалысы бар сызықтық емес теңдеулер жүйесін шешу; 9.2.3.1Есептің шарты бойынша оның математикалық моделін құру;
9.4.2.1 Мәтінді есептерді теңдеулер жүйелері арқылы шығару;
-
Екі айнымалысы бар сызықтық емес теңсіздіктер жүйесін шешу;
-
Екі айнымалысы бар сызықтық емес теңсіздіктер жүйесін шешу.
Бағалау критерииі: Білім алушы:
-
Екі айнымалысы бар сызықтық емес теңдеулер жүйелерін шеше алады.
-
Мәтінді есептерді теңдеулер жүйелері арқылы шығарады;
-
Екі айнымалысы бар сызықтық емес теңсіздіктер жүйесін шешу
Ойлау дағдыларының деңгейі: Қолдану. Жоғары деңгей дағдылары
Орындау уақыты 40 минут
І нұсқа
-
4 балл Теңдеулер жүйесін шешіңіз:
{?? − ? = 4; 2? + ? = 7.
-
4 балл Мәтінді есептерді теңдеулер жүйелері арқылы шығару.
 Екі
таңбалы сан ойластырылған, онда ондаған бірліктен үш есе кӛп. Бұл
санның сандар сомасына кӛбейтілуі 208-ге тең.Ойлаған санды
табыңыз.
Екі
таңбалы сан ойластырылған, онда ондаған бірліктен үш есе кӛп. Бұл
санның сандар сомасына кӛбейтілуі 208-ге тең.Ойлаған санды
табыңыз.
-
2 балл 4х+у≤7 теңсіздігінің шешімдерінің координаталық жазықтығына кескіндеңдер:
-
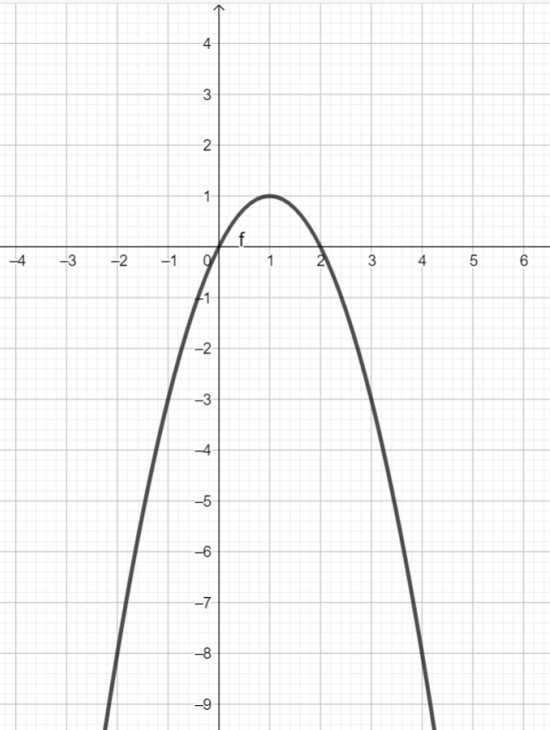
2 балл ? = 2? − ?2 функцияның графигі суретте кӛрсетілген.
a) ? − 2? + ?2 > 0; координаталық жазықтықта теңсіздігінің шешімі болатын қандай да бір сандар жұбын кӛрсетіңдер.
б) А (3; 4) или В (–1; –5) осы нүктелерінің қайсысы, а пунктының шешімі болады?
-
5 балл
?2 + ?2 ≤ 36; теңдеуін шешіп, шешімінің
![]()
{
x? > 4.барлық жұптарының жиынын кескіндеу керек.
Барлығы: 17 ұпай
II нұсқа
-
4 балл Теңдеулер жүйесін шешіңіз:
{?? − ? = 24;
? − 3? = 7.
-
4 балл Мәтінді есептерді теңдеулер жүйелері арқылы шығару.
Екі таңбалы санның сандар сомасы 8-ге тең. Егер екі таңбалы сан оның ондар мен бірліктерінің сандарына кӛбейтілсе, онда 426 болады. Бастапқы санды табыңыз.
-
 2 балл 3? + ?
≥ 4 теңсіздігінің шешімдерінің координаталық жазықтығына кескіндеңдер:
2 балл 3? + ?
≥ 4 теңсіздігінің шешімдерінің координаталық жазықтығына кескіндеңдер:
-
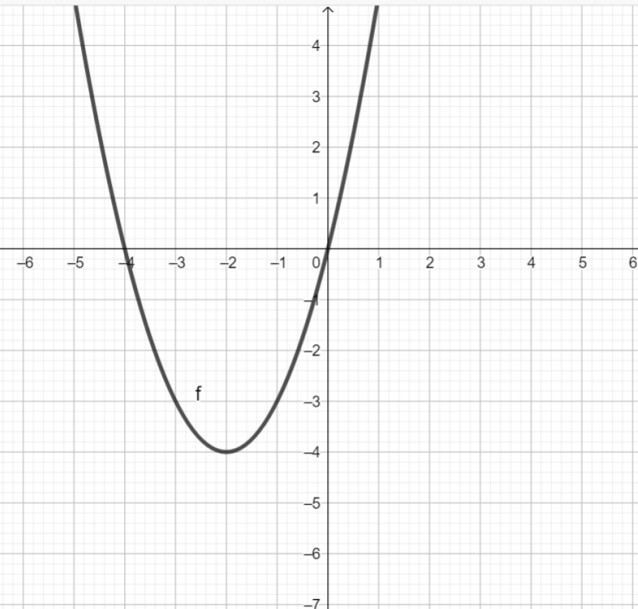
2 балл ? = 4? + ?2 функцияның графигі суретте кӛрсетілген.
а) ? − 4? − ?2 < 0 координаталық жазықтықта теңсіздігінің шешімі болатын қандай да бір сандар жұбын кӛрсетіңдер.
б)А (-1; 4) или В (–2; –5) осы нүктелерінің қайсысы , а пунктының шешімі болады?
-
5 балл
?2 + ?2 < 49;
теңдеуін шешіп,
{ x? ≤ 5.
шешімінің барлық жұптарының жиынын кескіндеу керек
Барлығы: 17 ұпай
Балл қою кестесі
-
-
Бағалау критерийлері
Тапсыр
ма №
Дескриптор
Балл
Білім алушы
Екі айнымалысы бар сызықтық емес теңдеулер жүйесін шешу
әдістерін қолданады
1
бір айнымалыны екінші айнымалы арқылы
ӛрнектейді;
1
екінші теңдеудегі айнымалыны ауыстырады;
1
бір айнымалыдан тәуелді теңдеуді шешеді;
1
теңдеу жүйенің шешімін табады және
жауабын жазады;
1
Мәтінді есептерді шығару үшін теңдеу жүйесін құрайды;
2
Жаңа айнымалы енгізіп шарты бойынша
бірінші теңдеуді құрады;
1
шарты бойынша екінші теңдеу құрады;
1
Мәтінді есептерді шығару үшін теңдеу
жүйесін құрайды және оны шешеді;
1
есеп шартына сәйкес жауабын жазады;
1
Екі айнымалысы бар сызықтық емес теңсіздіктер жүйесін шешеді
3
жүйеде шартқа сәйкес қисық координаттар құрады;
1
Теңсіздік белгісіне сәйкес жазықтықтың бір
бӛлігін бӛледі
1
Екі айнымалысы бар теңсіздікті шешеді
4
тікбұрышты координаттар жүйесінде
теңсіздіктің кӛптеген шешімдерін кӛрсетеді;
1
берілген координаттары бар нүктелер осы
1
-
-
-
теңсіздіктің шешімі болып табылатындығын
тексереді;
Екі айнымалысы бар сызықты емес теңсіздіктер жүйесін шешеді
5
координаталардың тікбұрышты жүйесінде
жүйенің бірінші теңдеуімен берілген қисық графигін құрастырады;
1
теңсіздіктің біріншісін кӛптеген шешімдерді бейнелейді;
1
жүйенің екінші теңдеуімен берілген қисық
графигін дәл сол тікбұрышты координаттар жүйесінде салады;
1
теңсіздіктің екіншісінің кӛптеген шешімдерін бейнелейді;
1
кӛптеген шешімдердің қиылысуын кӛрсетеді
1
Жалпы балл:
17
-
«Комбинаторика элементтері»
Тақырып: Комбинаториканың негізгі ұғымдары мен ережелері(қосу мен кӛбейтудің ережелері).
Комбинаторика формулаларды пайдаланып мәтін есептерді шығару.
Оқу мақсаттары:
-
Қайталанбайтын алмастыру, орналастыру және теру сандарын табу формулаларын білу.
-
Қайталанбайтын орналастыру, алмастыру және теру сандарын есептеу үшін комбинаторика формулаларын қолдана отырып есептер шығару
-
Комбинаториканың ережелерін білу (қосу және кӛбейту ережелері)
Бағалау критерииі: Білім алушы:
-
Қайталанбайтын алмастыру, орналастыру және теру сандарын табу формулаларын біле алады.
-
Қайталанбайтын орналастыру, алмастыру және теру сандарын есептеу үшін комбинаторика формулаларын қолдана отырып есептер шығарады.
-
Комбинаториканың ережелерін біледі (қосу және кӛбейту ережелері)
Ойлау дағдыларының деңгейі: Қолдану Жоғары деңгей дағдылары
Орындау уақыты 40 минут
I нұсқа
-
3 балл Ұқсатығын табыңдар:
-
-
А. Қайталанбайтын орналастыру формуласы
1. ?? = ?!
? (?−?)!?!
В. Қайталанбайтын орын ауыстырулар формуласы
2. ?? = ?!
? (?−?)!?!
А.Қайталанбайтын теру формуласы
3. Pn= n!
4. ?? = ?!
? (?−?)!
5. Pn = (n-k)!
6. C? = ?!
? (?−?)!
-
Жауабы: A . B . C .
-
5 балл Есептеңіз:
![]()
![]()
8 7
7
а) ?8−?6. b) ?3−?2.?5
?4
-
2 балл 5 адам баскетбол ойын ойнау үшін, неше тәсілмен таңдап алуға болады 9 адамнан команданың составын?
-
3 балл 0, 2, 4, 6, 7, 8 цифрларынан қайталанатын цифрлары жоқ қанша алтытаңбалы тақ сан құрастыруға болады?
-
2 балл 9 сынып оқушылардың 12 оқытылатын пәндері бар, 5 әр-түрлі сабақтан бір күнге сабақ кестесін қанша тәсілмен құруға болады?
-
5 балл Сыныпта оқитын 13 ұл және 11қыз бар. Ауланы тазалау үшін, неше тәсілмен 5 ұл және 3 қыз таңдап алуға болады?
Барлығы: 20 ұпай
ІI нұсқа
-
3 балл Ұқсатығын табыңдар:
-
-
A. Қайталанбайтын алмастыру формуласы
1. Pn= n!
B. Қайталанбайтын орналастыру формуласы
2. ?? = ?!
? (?−?)!?!
C. Қайталанбайтын теру формуласы
3. Pn = (n-k)!
4. ?? = ?!
? (?−?)!?!
5. ?? = ?!
? (?−?)!
6. C? = ?!
? (?−?)!
-
Жауабы: A . B . C .
-
5 балл Есептеңіз:
![]()
10 9
а) ?9−?7. b) ?5 −?4.![]()
9
?6?5
-
2 балл Жиынтық бағалау үшін 10 түрлі тапсырманың 5-і бір тапсырма үшін таңдалады. Тапсырмалардың неше түрлі нұсқаларын құрастыруға болады?
-
3 балл 5-ке еселік болатындай және әрқайсысында қайталанатын цифрлары болмайтындай етіп қанша алтытаңбалы сан құрастыруға болады?
-
2 балл 9 сынып оқушылардың 14 оқытылатын пәндері бар, 6 әр-түрлі сабақтан бір күнге сабақ кестесін қанша тәсілмен құруға болады?
-
5 балл Сыныпта оқитын 15 ұл және 12 қыз бар. Ауланы тазалау үшін, неше тәсілмен 5 ұл және 3 қыз таңдап алуға болады?
Барлығы: 20ұпай
Балл қою кестесі
-
-
Бағалау критерийлері
Тапсыр
ма
Дескриптор
Балл
Білім алушы
Комбинаторика формуласын ажыратады (Қайталанбайтын алмастыру, орналастыру және теру сандарын табу
формула);
1
қайталанбайтын орналастыру
формуласын қолданады;
1
қайталанбайтын орналастыру формуласын пайдаланады;
1
қайталанбайтын теру қайталанбайтын орналастыру формуласын пайдаланады; формуласын пайдаланады;
1
Комбинаторика формуласын қолданады (Қайталанбайтын орналастыру, алмастыру және теру сандарын есептеу формулалары) для преобразований
выражений;
2а
қайталанбайтын орналастыру формуласын
пайдаланады;
1
есептеулер жүргізеді және жауабын жазады;
1
2b
қайталанбайтын орналастыру формуласын
пайдаланады;
1
қайталанбайтын теру формуласын
пайдаланады;
1
есептеулер жүргізеді және жауабын жазады;
1
Қайталанбайтын орналастыру, алмастыру және теру сандарын есептеу үшін комбинаторика формулаларын қолдана отырып есептер шығарады
3
комбинаториканың керек формулаларын пайдаланады;
1
есептеулер жүргізеді және жауабын жазады;
1
4
тапсырма шарттарын қалай орындау керектігін түсіндіреді
1
қажетті формуланы немесе комбинаторика
ережесін қолданады;
1
есептеулер жүргізеді және жауабын жазады;
1
5
қажетті комбинатор формуласын
пайдаланады;
1
есептеулер жүргізеді және жауабын жазады;
1
Қарапайым есептер шығаруда комбинаториканың ережелерін пайдаланады
6
ұлдарды таңдау үшін комбинаториканың керек формуласын қолданады;
1
және оны есептейді;
1
қыздарды таңдау үшін комбинаториканың
керек формуласын қолданады және оны есептейді;
1
комбинаториканың қосу немесе кӛбейту
ережесін пайдаланады;
1
есептеулер жүргізеді және жауабын жазады;
1
Барлығы:
20
-
«Тізбектер»
Тақырыбы: Тізбектер
Оқу мақсаттары:
9.2.3.2 мысалы:
1 ;
![]() 2 3
2 3
1 ;
![]() 3 4
3 4
1 ;
![]() 4 5
4 5
1
![]()
5 6
;...
тізбектің n-ші мүшесін табу;
-
Арифметикалық прогрессиялардың n-ші мүшесін, алғашқы n мүшелерінің қосындысын есептеу формулаларын, сипаттамалық қасиетін білу және қолдану
-
Геометриялық прогрессиялардың n-ші мүшесін, алғашқы n мүшелерінің қосындысын есептеу формулаларын, сипаттамалық қасиетін білу және қолдану
-
Арифметикалық немесе геометриялық прогрессияларға байланысты есептер шығару
Бағалау критерииі: Білім алушы: тізбектің n-ші мүшесін таба алады.
-
Арифметикалық прогрессиялардың n-ші мүшесін, алғашқы n мүшелерінің қосындысын есептеу формулаларын, сипаттамалық қасиетін біледі және қолдана алады
-
- Геометриялық прогрессиялардың n-ші мүшесін табады,
-
- Алғашқы n мүшелерінің қосындысын есептеу формулаларын, сипаттамалық қасиетін біледі және қолданады
-
Арифметикалық немесе геометриялық прогрессияларға байланысты есептер шығара алады
Ойлау дағдыларының деңгейі: Қолдану. Жоғары деңгей дағдылары
Орындау уақыт: 40 минут
І нұсқа
-
[2балл] an=2n+6 тізбегінің 26 болатын мүшесінің нӛмерін табыңдар.
-
[4балл] an - арифметикалық прогрессия. Егер a1=2 және a3=8 тең болса, қасиетті пайдаланып a2 мүшесін тауып, арифметикалық прогрессияның тоғызыншы мүшесін табыңдар.
-
[3балл] ( b ) – геометриялық прогрессия 0,8; 0,2;… Келесі екі прогрессияның
n
мүшесін табыңыз.
-

1
[2балл] ( b ) – геометрическая прогрессия b 2 ;
n
q 2 . Табу керек
S ?
4
-
[3балл] Дүкенде гүл шоғы жасалды, бірінші гүл шоғы 3 түстен, екіншісі 7 түстен және т. б. болды. 7 букетін жасау үшін қанша түстер қажет?
ІІ нұсқа
-
[2 балл] an=3n-5 тізбегінің 13 болатын мүшесінің нӛмерін табыңдар.
-
[4балл] Пусть (an ) - арифметикалық прогрессия. Егер a1=3 және a3=9, қасиетті пайдаланып a2 мүшесін тауып, арифметикалық прогрессияның он екінші мүшесін табыңдар.
-
[3балл] ( b ) – геометриялық прогрессия 2,1; 0,7;… Келесі екі мүшенің тізбегін
n
табыңыз.
-
[2балл] ( b ) – геометриялық прогрессия, егер b 4 ; q 3 . S
? мәнің табыңыз.
n 1 4
-
[3балл] Саябақта гүлзарлар мен бұталар отырғызылды. Бір гүлзардың жанында 1 бұта, екінші 2 бұта, үшінші 4 бұта және т.б. жанында. Қанша бұта 6-ға жуық гүлзар отырғызылды?
Балл қою кестесі
-
Бағалау критерийлері
Тапсыр ма
Дескриптор
Балл
Білім алушы
Тізбектің n-ші мүшесін табады
1
Формулада берілген мүшелерінің мәнін
жазу
1
Тізбектің n-ші мүшесін табады
1
Арифметикалық прогрессиялардың n-ші мүшесін, алғашқы n мүшелерінің қосындысын есептеу формулаларын, сипаттамалық қасиетін біледі және қолданады
2
Арифметикалық прогрессияның сипаттамалық қасиетін пайдаланып a2
мүшесін табу
1
d арифметикалық прогрессияның
айырмасын табады
1
Арифметикалық прогрессиялардың n-ші мүшесін формуласын қолданады
1
an мүшесінің мәнің табады
1
Геометриялық прогрессияның n-ші мүшесін табады
3
Геометриялық прогрессияның q еселігін
табады
1
Формуланы жазып, b3 мүшесінің мәнің табады
1
Формуланы жазып, b4 мүшесінің мәнің табады
1
Геометриялық прогрессияның n қосындысын табады
4
Геометриялық прогрессияның алғашқы п мүшесінің қосындысын формуласын
жазады
1
Sn қосындысының мәнің табады
1
Арифметикалық прогрессияның алғашқы п мүшесінің қосындысын есептер шығаруда қолданады
5
d арифметикалық прогрессияның
айырмасын табады
1
Арифметикалық прогрессияның алғашқы п мүшесінің қосындысын формуласын
жазады
1
Sn қосындысының мәнің табады
1
Барлығы:
14
-
Тізбек берілген:
1;
1 ; 1 :
![]()
![]() 4 9
4 9
1 ...
![]() 16
16
3 нұсқа
-
[1 балл] Берілген тізбектің формуласын жазыңыз.
-
[1 балл] (??) геометриялық прогрессияның алғашқы мүшесін біле отырып, оның келесі екі мүшесін табыңдар.
-

n
[3 балл] n-ші мүшесінің формуласымен берілген дәлелдеңіз?
c n2 2n 3
тізбек ӛспелі ма,
-
[4 балл] Альпинистер кӛтерілістің бірінші күні 1400 м биіктікке кӛтерілді, содан кейін әрбір келесі күні алдыңғы жылмен салыстырғанда 100 м биіктікке кӛтерілді. Олар қанша күн бойы 5000 м биіктігін бағындырды?
-
[4 балл] Тікбұрышты параллелепипедтің ұзындығы, ені және биіктігі геометриялық прогрессияны құрайды. Параллелепипедтің кӛлемі 216 м3-ге тең, ал оның барлық қабырғаларының ұзындығы 104м-ге тең.Параллелепипед ӛлшемін табыңыз.
n2
-
a) [3 балл] bn (4) берілген тізбек шексіз кемімелі прогрессияның тізбегі
бола ма?
-
[1балл] Шексіз периодты ондық бӛлшекті 0,(12) жай бӛлшек түрінде кӛрсетіңдер
4 нұсқа
-
Тізбек берілген: 4;16;36;64;100; ...
a ) [1 балл] Берілген тізбектің формуласын жазыңыз.
b) [1 балл] (??) геометриялық прогрессияның алғашқы мүшесін біле отырып, оның келесі екі мүшесін табыңдар.
-

n
[3 балл] n-ші мүшесінің формуласымен берілген дәлелдеңіз?
a 3n2 17n 1
тізбек ӛспелі ма,
-
[4 балл] –17; –16; -15; …арифметикалық прогрессиияның теріс мүшелерінің қосындысын табыңдар
-
[4 балл] Геометриялық прогрессияның бірінші мен екінші мүшелерінің қосындысы 40 ,ал екінші мен үшінші мүшелерінің қосындысы 120 –ға тең.Алғашқы үш мүшесін табыңдар.
-
a) [3балл] bn
ма?
10
![]() 7n
7n
берілген тізбек шексіз кемімелі прогрессияның тізбегі бола
b) [1балл] Шексіз периодты ондық бӛлшекті 0,9(5) жай бӛлшек түрінде кӛрсетіңдер
Балл қою кестесі
|
Бағалау критерийлері |
Тапсыр ма |
Дескриптор |
Балл |
|||||
|
Білім алушы |
||||||||
|
|
|
3 нұсқа |
4 нұсқа |
|
||||
|
Жүйелілік заңдылықтарын анықтайды және жетіспейтін мүшелерді табады |
1(а) |
тізбектің n-ші мүшесінің формуласын n арқылы жазады; |
ортақ мүшенің формуласын анықтайды |
1 |
||||
|
1(b) |
келесі екі мүшені табады |
келесі екі мүшесін жазады |
1 |
|||||
|
Сандық тізбек туралы түсінік алады |
2 |
cn+1 үшін ӛрнек жасайды |
аn+1 үшін ӛрнек жасайды |
1 |
||||
|
айырмасын табады cn+1 - cn |
айырмасын табады аn+1 - аn |
1 |
||||||
|
Жауабын жазады |
Жауабын жазады |
1 |
||||||
|
Арифметикалық прогрессиялардың n-ші мүшесін, формулаларын, сипаттамалық қасиетін біледі және қолданады |
3 |
прогрессияның бірінші мүшесінің мәнін, оның айырмашылығын және арифметикалық прогрессияның бірінші мүшелерінің n қосындысының формуласын жазады және кезектіліктің жалпы мүшесінің формуласын айқындайды |
прогрессияның бірінші мүшесінің мәнін, оның айырмашылығын және n–мүшесінің формуласын жазады |
1 |
||||
|
теңдеу құрастырады |
прогрессияның теріс мүшелерінің санын табу үшін ӛрнек жасайды |
1 |
||||||
|
теңдеудің түбірлерін табады |
прогрессияның теріс мүшелерінің санын табады |
1 |
||||||
|
теңдеудің түбірлерін тексереді және жауабын жазады |
арифметикалық прогрессияның бірінші мүшелерінің n қосындысының формуласын қолдана отырып, теріс мүшелердің қосындысын есептейді |
1 |
||||||
|
Геометриялық прогрессиялардың n-ші мүшесін формулаларын, сипаттамалық қасиетін біледі және қолданады |
4 |
прогрессияның жүйелі мүшелері түрінде тікбұрышты параллелепипедтің ұзындығын, енін және биіктігін білдіреді |
есеп шарты бойынша теңдеулер жүйесін құрады; |
1 |
||||
|
есеп шарты жүйесін құрады; |
бойынша |
теңдеулер |
жүйені шешу үшін геометриялық прогрессияның n-мүшесінің формуласын пайдаланады |
1 |
||||
|
жүйені шеше отырып, геометриялық прогрессияның бӛлімі мен бірінші |
жүйені шеше прогрессияның |
отырып, бӛлімі |
геометриялық мен бірінші |
1 |
||||
|
|
|
мүшесін табады |
мүшесін табады |
ен |
|
||||
|
параллелепипед ӛлшемін табады |
прогрессияның табады |
алғашқы үш |
мүшесін |
1 |
|||||
|
Ондық периодтық бӛлшекті жай бӛлшекке аудару үшін шексіз кемімелі геометриялық прогрессия |
5(а) |
прогрессияның екі тізбектес мүшесін табады |
прогрессияның табады |
екі |
тізбектес |
мүшесін |
1 |
||
|
геометриялық прогрессияның еселігін табады; |
геометриялық прогрессияның еселігін табады; |
1 |
|||||||
|
Жауабын жазады |
Жауабын жазады |
1 |
|||||||
|
қосындысынын формуласын пайдаланады |
|
||||||||
|
5(b) |
ондық периодты бӛлшекке ауыстырады |
бӛлшекті |
жай |
ондық периодты бӛлшекті жай бӛлшекке ауыстырады |
1 |
||||
|
Барлығы: |
17 |
||||||||
«Тригонометрия»
|
Тақырып |
Бұрыш пен доғаның градустық және радиандық ӛлшемдері Кез келген бұрыштың синусы, косинусы, тангенсі и котангенсі Кез келген бұрыштың синусы,косинусы,тангенсы және котангенсы Кез келген бұрыштың тригонометриялық формулалар |
||
|
Оқу мақсаттары: |
9.1.2.1 градусты радианға және радианды градусқа айналдыру 9.2.4.4 келтіру формулаларын қорытып шығару және қолдану 9.2.4.3 бұрыштардың қосындысы мен айырымының, жарты және қос бұрыштың тригонометриялық формулаларын қорытып шығару және қолдану |
||
|
Бағалау критерииі: |
Білім алушы: -Градусты радианға және радианды градусқа айналдырады -Келтіру формулаларын қорытып шығарады және қолданады -Бұрыштардың қосындысы мен айырымының бұрыштың тригонометриялық формулаларын қорытып шығарады және қолданады -Жарты және қос бұрыштың тригонометриялық формулаларын қорытып шығарады және қолданады |
||
|
Ойлау дағдыларының деңгейі: |
Қолдану Жоғары деңгей дағдылары |
||
|
Орындау уақыты |
30 минут |
|
|
І нұсқа
-
[4 балл] Градусты радианға және радианды градусқа айналдырып сәйкестеңдіріңіз:
|
Градус ӛлшемдері |
Радиан ӛлшемдері |
|
1. 1200 |
А. 3 2 |
|
2. 270 |
Б. 5 3 |
|
3. 2100 |
В. 3 2 |
|
4. 3000 |
Г. 7 6 |
|
|
Д. 5 6 |
|
|
Е. 2 3 |
![]() 1.
2. 3. 4.
1.
2. 3. 4.
-
[4балл] Ӛрнекті ықшамдаңыз:
cos( ) tg ( ) sin( )
![]() 2
2
-
[4 балл] Есептеңіз: а) cos400cos200 – sin400sin200 б) sin 1050
-
[4 балл] Ӛрнекті ықшамдаңыз: а)
sin 2 2tg
б) 1 cos 2 1 cos 2
ІІ нұсқа
-
[4 балл] Градусты радианға және радианды градусқа айналдырып сәйкестеңдіріңіз:
|
Градус |
Радиан |
|
1. 1500 |
А. 3 4 |
|
2. 360 |
Б. 5 6 |
|
3. 2400 |
В. 16 9 |
|
4. 3200 |
Г. 9 1 |
|
|
Д. 5 |
|
|
Е. 4 3 |
1. 2. 3. 4.
-
[4 балл] Ӛрнекті ықшамдаңыз:
sin( ) cos( )
2
cos( )
-
[4 балл] Есептеңіз: а) cos700cos400 + sin700sin400 б) sin 750
-
[4 балл] Ӛрнекті ықшамдаңыз: а)
sin 2 2ctg
б) 1 cos 2 1 cos 2
Балл қою кестесі
|
Бағалау критерийлері |
Тапсыр ма |
Дескриптор |
Балл |
|
Білім алушы |
|||
|
Градусты радианға және радианды градусқа айналдырады |
1 |
1 бұрышты сәйкестіңдіреді |
1 |
|
2 бұрышты сәйкестіңдіреді |
1 |
||
|
3 бұрышты сәйкестіңдіреді |
1 |
||
|
4 бұрышты сәйкестіңдіреді |
1 |
||
|
Келтіру формулаларын қорытып шығарады және қолданады |
2 |
келтіру формулаларын қолданады |
1 |
|
келтіру формулаларын пайдаланады |
1 |
||
|
келтіру формулаларын 2 пайдаланады |
1 |
|
|
|
Ӛрнекті ықшамдайды |
1 |
|
Бұрыштардың қосындысы мен айырымының бұрыштың тригонометриялық формулаларын қолданады |
3а |
Бұрыштардың қосындысы мен айырымының бұрыштың тригонометриялық формулаларын қолданады |
1 |
|
Ӛрнекті ықшамдайды |
1 |
||
|
3б |
Бұрыштардың қосындысы мен айырымының бұрыштың тригонометриялық формулаларын қолданады |
1 |
|
|
Ӛрнектің мәнін табады |
1 |
||
|
Жарты және қос бұрыштың тригонометриялық формулаларын қолданады |
4а |
Қос бұрыштың формуласын пайдаланады |
1 |
|
Ӛрнекті ықшамдайды |
1 |
||
|
4б |
Қос бұрыштың формуласын пайдаланады |
1 |
|
|
Ӛрнекті ықшамдайды |
1 |
||
|
Жалпы балл: |
16 |
||
«Тригонометрия»
Тақырып: Формулалар тригонометриясы. Тригонометриялық ӛрнектердің ұқсастығы
Оқу мақсаттары:
9.2.4.7 Тригонометриялық функциялардың қосындысы мен айырымын кӛбейтіндіге және кӛбейтіндісін қосындыға немесе айырымға түрлендіру формулаларын қорытып шығару және қолдану
9.2.4.8 Тригонометриялық ӛрнектерді тепе-тең түрлендіруді орындау
Бағалау критерииі: Білім алушы:
-
Тригонометриялық функциялардың қосындысы мен айырымын кӛбейтіндіге және кӛбейтіндісін қосындыға немесе айырымға түрлендіру формулаларын қорытып шығарады және қолданады
-
Тригонометриялық ӛрнектерді тепе-тең түрлендіруді орында алады
Ойлау дағдыларының деңгейі: Қолдану Жоғары деңгей дағдылары
Орындау уақыты 25 минут
І нұсқа
-
[2 балл] Есептеңіз: sin 1050 - sin 750;
-
[4 балл] Ықшамдаңыз:
cos ( ) - cos ( ) , sin 1 .
4 4
-
[5 балл] Дәлелдеңдер:
sin sin 3 sin 5 cos cos 3 cos 5
tg 3
ІІ нұсқа
-
[2 балл] Есептеңіз: sin 750 - sin 150;
-
[4 балл] Ықшамдаңыз:
cos ( ) 3
+ cos
( ) , cos 2 .
3
-
[5 балл] Дәлелдеңдер:
sin 3 sin 5 sin cos cos 5 cos 3
tg3
ІІІ нұсқа
-
 [2 балл] Есептеңіз: cos 5 - cos ;
[2 балл] Есептеңіз: cos 5 - cos ;
12 12
-
[4 балл] Ықшамдаңыз: cos ( )
6
+ cos
( ) ;
6
-
[5 балл] Тепе-теңдікті дәлелдеңіз:
cos 3 cos 5 cos sin sin 5 sin 3
ctg 3
ІV нұсқа
-
[2 балл] Есептеңіз: cos 7 - cos ;
12 12
-
[4 балл] Ықшамдаңыз: cos ( )
6
- cos
( ) ;
6
-
[5 балл] Тепе-теңдікті дәлелдеңіз :
cos cos 3 cos 5 sin sin 3 sin 5
ctg 3
Балл қою кестесі
|
Бағалау критерийлері |
Тапсыр ма |
Дескриптор |
Балл |
|
|
Білім алушы |
||||
|
Тригонометриялық |
1 |
синустардың кӛбейтіндісін қосындыға |
1 |
|
|
функциялардың |
|
түрлендіру формуласын қолданады; |
|
|
|
қосындысы мен |
|
ӛрнекті ықшамдайды; |
1 |
|
|
айырымын кӛбейтіндіге және кӛбейтіндісін қосындыға немесе |
2 |
косинустардың кӛбейтіндісін қосындыға түрлендіру формуласын қолданады; |
1 |
|
|
ӛрнекті ықшамдайды; |
1 |
|||
|
айырымға түрлендіру |
|
|||
|
синустың мәнін табады; |
1 |
|||
|
формулаларын |
|
|||
|
ӛрнекті ықшамдайды; |
1 |
|||
|
қолданады |
|
|||
|
Тригонометриялық |
3 |
Топтастыруды орындайды |
1 |
|
|
ӛрнектерді тепе-тең түрлендіруді орындайды |
|
косинустардың кӛбейтіндісін қосындыға түрлендіру формуласын қолданады; |
1 |
|
|
|
|
синустардың кӛбейтіндісін қосындыға |
1 |
|
|
|
|
түрлендіру формуласын қолданады; |
|
|
|
|
|
Негізгі тригонометриялық |
ұқсастықты |
1 |
|
|
|
қолданады |
|
|
|
|
|
Теңдік туралы қорытынды жасайды |
1 |
|
|
Жалпы балл: |
11 |
|||
«Ықтималдықтар теориясының элементтері»
Тақырып: Ықтималдықтар теориясының элементтері Мәтін есептерді шығару
Оқу мақсаттары:
9.3.2.5 Геометриялық ықтималдықты есептер шығаруда қолданады
9.3.2.3 Ықтималдықтың классикалық анықтамасын білу және есептер шығару үшін оны қолдану
Бағалау критерииі: Білім алушы:
Геометриялық ықтималдықты есептер шығаруда қолданады Ықтималдықтың классикалық анықтамасын біледі және есептер шығару үшін оны қолдану
Ойлау дағдыларының деңгейі: Қолдану Жоғары деңгей дағдылары
Орындау уақыты 25 минут
І нұсқа
1.[5 балл] 1.5×4 см2 тіктӛртбұрышқа іштей сызылған шеңбердің радиусы1,5 см. радиус шеңбері жазылған. Тіктӛртбұрышқа кездейсоқ қойылған нүкте шеңбердің ішінде болмауы ықтималдығы қандай? Жауапты мыңға дейін жуықтаңыз.
2.[3 балл] Жәшікте 90 шар,олар 1,2,…,90-ге дейін белгіленген.Жәшіктен кездейсоқ бір шар алынды.Алынған шардың 6 сан болатын ықтималдығын табыңыз?
3.[3 балл] Бір уақытта екі ойын сүйегі лақтырылды. Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 8 болу ықтималдылығын табыңыз?
4.[2 балл] Фабрикада сӛмкелер шығарылады.100 сӛмкенің ішінде 8-сінде ақауы кездеседі.Кездейсоқ алынған сӛмкенің ақауысыз болуының ықтималдығын табыңыз.
5. [3 балл] Такси фирмасында кәзіргі уақытта 20 кӛлік бар:10 қара, 2 сары және 8жасыл. Шақыру тапсырыс берген адамға ең жақын кӛлік шықты. Кездейсоқ шыққан кӛліктің жасыл болуының ықтималдығын табыңыз.
ІІ нұсқа
-
[5 балл]7×6 см2 тіктӛртбұрышқа іштей сызылған шеңбердің радиусы 2,5 см. радиус шеңбері жазылған. Тіктӛртбұрышқа кездейсоқ қойылған нүкте шеңбердің ішінде болмауы ықтималдығы қандай? Жауапты мыңға дейін жуықтаңыз.
-
[3 балл ] Жәшікте 90 шар,олар 1,2,…,90-ге дейін белгіленген.Жәшіктен кездейсоқ бір шар алынды.Алынған шардың 5 сан болатын ықтималдығын табыңыз?
-
[3 балл] Бір уақытта екі ойын сүйегі лақтырылды. Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 5 болу ықтималдылығын табыңыз.
-
[2 балл] Емтиханға 60 сұрақ берілді, Андрей оның 3-уін жаттамаған. Андрейге жаттаған сұрағы түсетінін ықтималдығын табыңыз.
-
[3 балл] Тарелкеде 16 пирожки бар:7балықпен,5 варенямен және 4 шиемен.Юля қарамай бір пирожки таңдап алды. Кездейсоқ алынған пирожкидың шиемен болуының ықтималдығын табыңыз.
ІІІ нұсқа
1.[5 балл]5×7 см2 тіктӛртбұрышқа іштей сызылған шеңбердің радиусы 2,5 см. радиус шеңбері жазылған. Тіктӛртбұрышқа кездейсоқ қойылған нүкте шеңбердің ішінде болмауы ықтималдығы қандай? Жауапты мыңға дейін жуықтаңыз
2.[3 балл] Жәшікте80 шар,олар 1,2,…,80-ге дейін белгіленген.Жәшіктен кездейсоқ бір шар алынды.Алынған шардың 7 сан болатын ықтималдығын табыңыз?
3.[3 балл] Бір уақытта екі ойын сүйегі лақтырылды. Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 7 болу ықтималдылығын табыңыз.
4.[2 балл] Фабрикада лампалар шығарылады. 1000 лампаның ішінен 3-уі ақаумен кездеседі. Кездейсоқ алынған сатып алған лампа ақауысыз болуының ықтималдығын табыңыз.
5.[3 балл]Такси фирмасында кәзіргі уақытта 25 кӛлік бар:12 қара, 4 сары және 9жасыл. Шақыру тапсырыс берген адамға, ең жақын кӛлік шықты. Кездейсоқ шыққан кӛліктің жасыл болуының ықтималдығын табыңыз.
ІV нұсқа
1.[5 балл] 7×6 см2 тіктӛртбұрышқа іштей сызылған шеңбердің радиусы 3 см радиус шеңбері жазылған. Тіктӛртбұрышқа кездейсоқ қойылған нүкте шеңбердің ішінде болмауы ықтималдығы қандай? Жауапты мыңға дейін жуықтаңыз
2.[3 балл]Жәшікте 90 шар,олар 1,2,…,90-ге дейін белгіленген.Жәшіктен кездейсоқ бір шар алынды.Алынған шардың 4 сан болатын ықтималдығын табыңыз.
3.[3 балл] Бір уақытта екі ойын сүйегі лақтырылды. Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 6 болу ықтималдылығын табыңыз?
-
[2 балл]Емтиханға 80 сұрақ берілді, Әмірбек оның 5-уін жаттамаған. Әмірбекке жаттаған сұрағы түсетінін ықтималдығын табыңыз.
-
[3 балл ] Тарелкеде 20 пирожки бар:7картоппен, 9капустамен және 4 варениямен.Сауле қарамай бір пирожки таңдап алды. Кездейсоқ алынған пирожкидың капустамен болуының ықтималдығын табыңыз.
Балл қою кестесі
|
Бағалау критерийлері |
Тапсырма № |
Дескриптор |
Балл |
|
Білім алушы |
|||
|
Геометриялық ықтималдықты есептер шығаруда қолданады |
1 |
шаршының ауданын табу үшін ӛрнек құрастырады; |
1 |
|
шеңбер ауданы үшін ӛрнек құрайды; |
1 |
||
|
Геометрияның ықтималдығынын анықтамасын пайдаланады; |
1 |
||
|
шеңберге түсу ықтималдығын табады; |
1 |
||
|
Қарама-қарсы оқиғалардың ықтималдығын табу және жауапты дӛңгелектейді; |
1 |
||
|
Ықтималдықтың классикалық формуласын мәтін есепті шешу үшін пайдаланады |
2 |
саны бар шарлар санын табады5, бесінші ондықта; |
1 |
|
саны бар шарлар санын табады 5, қалған ондықтарда; |
1 |
||
|
ықтималдықты формула бойынша табады; |
1 |
||
|
3 |
осы оқиғалар үшін барлық мүмкін болатын нәтижелер санын табады |
1 |
|
|
осы оқиғаға қолайлы нәтиже санын табады; |
1 |
||
|
ықтималдықты формула бойынша табады; |
1 |
||
|
4 |
Ықтималдықтың классикалық формуласын пайдаланады; |
1 |
|
|
барлық мүмкін болатын нәтижелер санын табады; |
1 |
||
|
ықтималдықтың мәнін табады; |
1 |
||
|
барлық мүмкін болатын нәтижелер санын табады; |
1 |
||
|
5 |
шарты бойынша қолайлы саны нәтижелерін анықтайды; |
1 |
|
|
Кездейсоқты формула бойынша табады |
1 |
||
|
Барлығы: |
|
|
17 |
Геометрия
«Жазықтықтағы векторлар»
Тақырып:
Векторлар. Векторларға амалдар қолдану. Коллинеар, коллиниар емес векторлар. Вектордың координаты. Вектордың коодинаттарына амалдар қолдану. Векторларды есеп шығаруда қолдану.
Оқу мақсаты
-
Вектордың, коллинеар вектор, тең векторлар, нӛлдік вектор, бірлік вектор және вектордың ұзындығы анықтамасын білу;
-
вектордың кӛбейтіндісін,векторларды қосу әдістерін, векторды санға кӛбейтуді білу және қолдану;
-
вектордың координатын табу;
9.1.3.5 векторлар арасындағы бұрышты табу;
-
вектордың ұзындығын табу;
9.1.4.6 векторлардың скаляр кӛбейтіндісін табу.
Бағалау критерийі Білім алушы:
-
вектордың түрін анықтайды
-
векторларға амалдар қолданады
-
вектордың координатын табады
-
векторлар арасындағы бұрышты табады
-
вектордың ұзындығын табады
-
векторды есеп шығаруда қолданады
Ойлау дағдыларының деңгейі: Білу,түсіну. Қолдану
Орындалу уақыты 40 минут
I нұсқа.
-
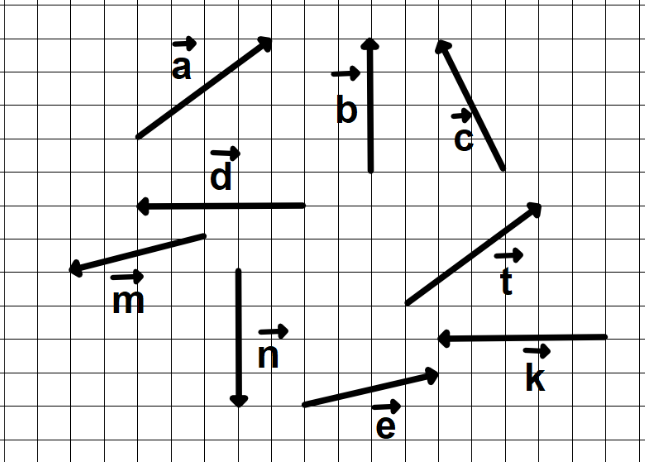 3 балл Суретті қолданып екі мысалдан келтіріңдер a) тең
векторларға;
3 балл Суретті қолданып екі мысалдан келтіріңдер a) тең
векторларға;-
коллинеар векторларға;
-
перпендикуляр векторларға.
-
-
3 балл BDEF параллелограммы берілген. Табу керек:
а) ̅?̅̅̅?̅→ және ̅?̅̅̅?̅→векторларыны
қосындысын;
б) ̅?̅̅̅?̅→ және ̅?̅̅̅̅?̅→ векторларының
айырымын.
-
3 балл ?̅̅→ = 3?→ − 2?→ и ?̅→ = 2?→ + 4?→ векторлары берілген.
?→ = 2?̅̅→ − 3?̅→ векторының координаты мен ұзындығын табыңыз.
-
 5 балл ?→(2;
0)и ?̅→(2;
2√3) векторларының арасындағы бұрышты табыңыз.
5 балл ?→(2;
0)и ?̅→(2;
2√3) векторларының арасындағы бұрышты табыңыз.
-
4 балл А(11; 2), В(–3; 10) и С(14; –2) нүктелері берілген. ̅?̅̅̅?̅→ = ̅?̅̅̅?̅→ теңдігі орындалатындай D нүктесінің координатын табыңыз.
Барлығы 18 балл.
ІI нұсқа.
-
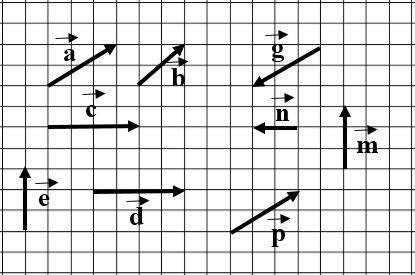 3 балл Суретті қолданып екі мысалдан келтіріңіздер
3 балл Суретті қолданып екі мысалдан келтіріңіздер-
тең векторларға;
-
коллинеар векторларға;
-
перпендикуляр векторларға.
-
-
3 балл BCDE ромб берілген. Табу керек: а) ̅C̅̅̅?̅→ және ̅?̅̅̅?̅→ векторларының қосындысын; б) ̅?̅̅̅?̅→ және ̅?̅̅̅?̅→ векторларының айырымын.
-
3 балл ̅a→ = ?→ + 2?→ және ?̅→ = 2?→ − 4?→ векторлары берілген.
?̅̅→ = 2̅a→ − 3?̅→ векторының координатын және ұзындығын табыңыз.
![]()
-
5 балл ?̅̅→(3; 0)mGне ?̅→(3; √3) векторларының арасындағы бұрышты табыңыз.
-
4 балл А(-1; 12), В(–3; 7) және С(9; –12) нүктелері берілген. орындалатындай D нүктесінің координатын табыңыз
̅?̅̅̅̅C→ =
̅B̅̅̅?̅→ теңдігі
Барлығы 18 балл.
Балл қою кестесі
|
Бағалау критерийы |
№ |
Дескриптор |
Балл |
|
Оқушы |
|||
|
Жазықтықтағы векторларды ажыратады; |
1 |
Екі тең векторларды жазады; |
1 |
|
Екі коллинеар векторларды жазады; |
1 |
||
|
Екі перпендикуляр векторларды жазады. |
1 |
||
|
Векторларды қосу және азайту ережелерін қолданады; |
2 |
Векторларды қосу амалын орындап жауабын жазады; |
1 |
|
Векторларды азайту амалын орындап жауабын жазады; |
1 |
||
|
Сызбаны орындап керек векторларды белгілейді; |
1 |
||
|
Векторларға амалдар қолданып,координатала рын табады,ұзындығын табады. |
3 |
Жіктеу арқылы векторлардың координаталарын жазады; |
1 |
|
Координаталарға амалдар қолдану арқылы,вектордың координатын табады ; |
1 |
||
|
Вектордың ұзындығын табады; |
1 |
||
|
Векторлардың скаляр кӛбейтіндісін қолданып, векторлар арасындағы бұрышты табады; |
4 |
Векторлардың скаляр кӛбейтіндісін табады; |
1 |
|
Векторлардың модулін табады; |
1 |
||
|
Векторлардың скаляр кӛбейту формуласын векторлар арасындағы бұрышын табу үшін қолданады; |
1 |
||
|
Бұрыштың косинусын табу амалын орындайды; |
1 |
||
|
Косинустың мәні бойынша векторлардың арасындағы бұрышты табады. |
1 |
||
|
Векторлардың теңдігін |
5 |
Вектордың координатын табады;. |
1 |
|
Векторлардың теңдігін қолданады; |
1 |
|
қолданып,вектордың координатын табады. |
|
Нүктенің абсциссасын табады; |
1 |
|
Нүктенің ординатын табады ,жауабын жазады |
1 |
||
|
Барлығы: |
18 |
||
«Жазықтықтағы түрлендірулер»
Тақырыбы Қозғалыс және оның қасиеттері Гомотетия және олардың қасиеттері Ұқсас үшбұрыштар және оның қасиеттері
Оқу мақсаты
9.1.4.11 Гомотетияның анықтамасы мен қасиеттерін білу
9.1.4.15 Тікбұрышты үшбұрыштың ұқсастығын білу және қолдану
9.1.4.17 Ұқсас фигуралардың аудандары мен ұқсас коэффициенттердің арасындағы тәуелділік формуласын білу
9.1.4.8 Қозғалыстың түрлерін, композициясын және олардың қасиеттерін білу
9.1.4.9 Симметрия, параллель кӛшіру және бұру кезінде фигуралардың бейнелерін салу
Бағалау критерийі Білім алушы:
Орталықты және гомотетия коэффициентін анықтайды
Есептерді шешу кезінде тікбұрышты үшбұрыштардың ұқсастығын қолданады Ұқсас фигуралардың аудандары мен ұқсас коэффициенттердің арасындағы тәуелділік формуласын қолданады
Фигура бейнесін құру үшін осьтік және орталық симметрияны қолданады Симметрия, параллель тасымалдау, бұрылу кезінде фигуралардың бейнелерін жасайды
Ойлау дағдыларының Білу, түсіну, қолдану
Орындалу уақыты 25 минут
I нұсқа
-
[3 балл] АВ кесіндісін О нүктесіне қатысты 600 бұрышқа сағат тіліне қарсы бұрауды сипаттаңыз
-
[1 балл] А(-2;-1) симметриялық нүктесінің нүктелерінің координаттарын табыңыз.: в) Оу осі; с) координаталар басы
-
[2 балл] Параллель тасымалдау кезінде А(3;-1) нүктесі А1(5,-4) нүктесіне ӛтеді. Осы тасымал нәтижесінде қандай нүктеге В (-7;0) нүктесі ӛтеді?
-
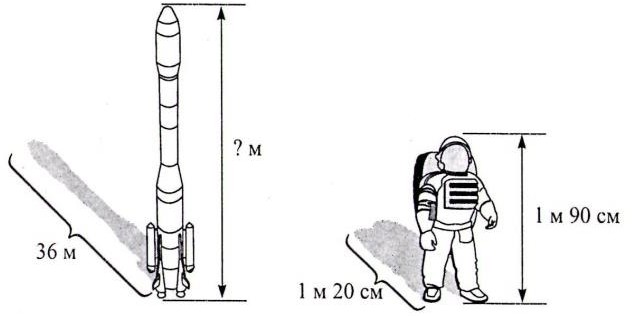
[4 балл] Егер оның кӛлеңкесінің ұзындығы 36 м болса, ғарышкердің кӛлеңкесінің ұзындығы 1 м 20 см болса, зымыранның биіктігін табыңыз.
-
[4 балл] Түзу,үшбұрыштың табанына параллель, оны үшбұрыш пен трапецияға бӛледі, олардың аудандарының қатынасы 4:5. Пайда болған үшбұрыштың периметрі 20 см тең . Осы үшбұрыштың периметрін табыңыз.
-
[4 балл] F фигурадан F1 фигурасын гомотетий (O;2) салыңыз.
 А
А
С
В
О
-
[1 балл] А(4;-11) симметриялық нүктесінің нүктелерінің координаттарын табыңыз.: в) Оу осі; с) координаталар басы
-
[2 балл] Параллель тасымалдау кезінде А(-3;-4) нүктесі А1(7,3) нүктесіне ӛтеді. Осы тасымал нәтижесінде қандай нүктеге В (0;5) нүктесі ӛтеді?
-
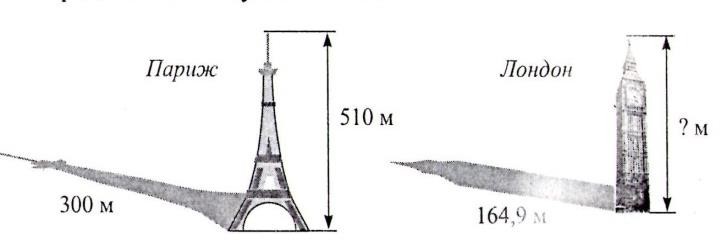
[4 балл] Париждегі Эйфель мұнарасының биіктігі 300 м., оның кӛлеңкесінің ұзындығы 510 м. Лондондағы Биг Бен парламенттік сағаттарынан кӛлеңкенің ұзындығы 164,9 М. Биг Бен сағат биіктігін анықтаңыз?
-
[4 балл] ABC үшбұрышының AD және BE медианалары F нүктесінде қиылысады. Белгілі, SABF=1 тең. SDEF табыңыз.
-
[4 балл] F фигурадан F1 фигурасын гомотетий (O;1) салыңыз.
2
 О
О
В
С
Геометрия, 9 сынып
|
Бағалау критерийі |
№ тапсырм алар |
Дескриптор |
Балл |
||||
|
Білім алушы |
|||||||
|
I нұсқа |
II нұсқа |
||||||
|
Бұрылу кезінде фигуралардың бейнелерін құрады |
1 |
А нүктесінің бейнесін құруды сипаттайды |
А нүктесінің бейнесін құруды сипаттайды |
1 |
|||
|
О нүктенің бейнесін салуды сипаттайды |
О нүктенің бейнесін салуды сипаттайды |
1 |
|||||
|
кесіндісінің құрылысын сипаттайдыА1В1 |
кесіндісінің құрылысын сипаттайдыА1В1 |
1 |
|||||
|
Фигура бейнесін құру үшін осьтік және орталық симметрияны қолданады |
2 |
Ох осіне; Оу осіне; координаттардың басына қатысты А симметриялық нүктесінің нүктелерінің координаттарын табады |
Ох осіне; Оу осіне; координаттардың басына қатысты А симметриялық нүктесінің нүктелерінің координаттарын табады |
1 |
|||
|
Жазықтықта тікбұрышты координаттарды түрлендіру формулаларын қолданады |
3 |
(??; ??) координаталарын табады |
(??; ??) координаталарын табады |
1 |
|||
|
В1 нүкесінін координаталарын табады |
В1 нүкесінін координаталарын табады |
1 |
|||||
|
Есептерді шешу кезінде тікбұрышты үшбұрыштардың ұқсастығын қолданады |
4 |
Есептің шартты бойынша суретін салады |
Есептің шартты бойынша суретін салады |
1 |
|||
|
Тікбұрышты үшбұрыштың дәлелдейді |
ұқсастығын |
Тікбұрышты дәлелдейді |
үшбұрыштың |
ұқсастығын |
1 |
||
|
Ұқсас үшбұрыштардың теңдігін құрайды |
жақтарының |
Ұқсас үшбұрыштардың жақтарының теңдігін құрайды |
1 |
||||
|
Ракетаның биіктігін табады |
Биг Бен сағат биіктігін табады |
1 |
|||||
|
Ұқсас фигуралардың аудандар мен ұқсас коэффициенттердің арасындағы тәуелділік формуласын қолданады |
5 |
Сызбаны салуды орындайды және белгілеулерді енгізеді; |
Сызбаны салуды орындайды және белгілеулерді енгізеді; |
1 |
|||
|
Үшбұрыштың ұқсастығын анықтайды және дәлелдейді |
Үшбұрыштың ұқсастығын анықтайды және дәлелдейді |
1 |
|||||
|
Ұқсастық коэффициентін есептейді |
Ұқсастық коэффициентін есептейді |
1 |
|||||
|
Ұқсас фигуралардың аудандары мен ұқсас коэффициенттердің арасындағы тәуелділік формуласын қолданады |
Ұқсас фигуралардың аудандары мен ұқсас коэффициенттердің арасындағы тәуелділік формуласын қолданады |
1 |
|||||
|
Гомотетия фигураларының бейнелерін құрады |
6 |
Салады ОА1 = 2ОА |
Салады ОА1 = 1ОА
2 |
1 |
|||
|
Салады ОВ1 = 2ОВ |
Салады ОВ1 = 1ОВ
2 |
1 |
|||||
|
Салады ОС1 = 2ОС |
Салады ОС1 = 1ОС
2 |
1 |
|||||
|
Үшбұрыш салады А1В1С1 |
Үшбұрыш салады А1В1С1 |
1 |
|||||
|
Барлығы |
18 |
||||||
«Үшбұрыштарды шешу»
Тақырып: Үшбұрыштарды шешу
Оқу мақсаты: 9.1.3.6 Косинустар теоремасын білу және қолдану
9.1.3.7 Синустар теоремасын білу және қолдану
9.1.3.9 Шеңберге іштей немесе сырттай сызылған үшбұрыштардың аудандарын пайдаланып шеңбердің радиусын табу формулаларын білу және қолдану
Бағалау критерийі: Білім алушы:
-
Синустар және косинустар теоремасын біледі
-
Есеп шығаруда синустар теоремасын қолданады
-
Есеп шығаруда косинустар теоремасын қолданады
-
Үшбұрышқа іштей немесе сырттай сызылған шеңберлердің радиустарын табуға арналған есептерді шығарды
Ойлау дағдыларының деңгейі: Қолдану. Жоғары деңгей дағдылары
Орындау уақыты: Ескеру:
30 минут
Брадис таблицасы
1 нұсқа
-
Теореманың сӛйлеммен берілген анықтамасы мен математикалық жазылуы арасындағы сәйкестікті табыңыз. [2 балл]
-
Сӛйлеммен берілген анықтамасы
Математикалық жазылуы
1. Бұрыштың синусы үшбұрыш қабырғаларына
пропорционал болады
A. ?2 = ?2 + ?2 − 2?? ??? ?
2. Үшбұрыштың қабырғалары қарсы жатқан бұрыштарының косинусына пропорционал
B. ?2 = ?2 + ?2 − 2?? ??? ?
3. Үшбұрыштың кез келген қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысынан осы екі қабырға мен олардың арасындағы бұрыштың екі еселенген косинусының кӛбейтіндісін шегергенге тең
C. ??? ? = ??? ? = ??? ?
? ? ?
4. Үшбұрыштың қабырғалары қарсы жатқан бұрыштарының синусына пропорционал
D.?2 = ?2 + ?2 + 2?? ??? ?
5. Үшбұрыштың кез келген қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысынан осы екі қабырға мен олардың арасындағы бұрыштың екі еселенген синусының
кӛбейтіндісін шегергенге тең
E. ? = ? = ?
??? ? ??? ? ??? ?
6. Үшбұрыштың кез келген қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысынан осы екі қабырға мен олардың арасындағы бұрыштың екі еселенген косинусының
кӛбейтіндісін қосқанға тең
F. ? = ? = ?
??? ? ??? ? ??? ?
Косинустар теоремасы: және
Синустар теоремасы: және
-
? = 10, ? = 400, ? = 600 болатын үшбұрыштың белгісіз ӛлшемдерін табыңыз.
[4балл]
-
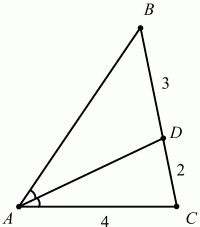
А пунктінен С пункті арқылы В пунктіне қатынайтын, мұндағы АС ≈13 км, а ВС ≈6 км, ∠ACB = 700. Кейін А және В пункттерін түзу жолмен қосты. А пунктінен В пунктіне дейінгі жол қанша километрге қысқарды? [3балл]
-
Тең бүйірлі үшбұрыштың бүйір қабырғасы 13 см, ал табаны 10 см-ге тең. Осы үшбұрышқа іштей және сырттай сызылған шеңберлердің радиусын табыңыз. [4балл]
2 нұсқа
-
Теореманың сӛйлеммен берілген анықтамасы мен математикалық жазылуы арасындағы сәйкестікті табыңыз. [2 балл].
-
Сӛйлеммен берілген анықтамасы
Математикалық жазылуы
1. Бұрыштың синусы үшбұрыш қабырғаларына
пропорционал болады
A. ?2 = ?2 + ?2 − 2?? ??? ?
2. Үшбұрыштың қабырғалары қарсы жатқан бұрыштарының косинусына пропорционал
B. ?2 = ?2 + ?2 − 2?? ??? ?
3. Үшбұрыштың кез келген қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысынан осы екі қабырға мен олардың арасындағы бұрыштың екі еселенген косинусының
кӛбейтіндісін қосқанға тең
C. ? = ? = ?
??? ? ??? ? ??? ?
4. Үшбұрыштың қабырғалары қарсы жатқан бұрыштарының синусына пропорционал
D.?2 = ?2 + ?2 + 2?? ??? ?
5. Үшбұрыштың кез келген қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысынан осы екі қабырға мен олардың арасындағы брыштың екі еселенген синусының
кӛбейтіндісін шегергенге тең
E. ??? ? = ??? ? = ??? ?
? ? ?
6. Үшбұрыштың кез келген қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысынан осы екі қабырға мен олардың арасындағы бұрыштың екі еселенген косинусының кӛбейтіндісін шегергенге тең
F. ? = ? = ?
??? ? ??? ? ??? ?
Косинустар теоремасы: және
Синустар теоремасы: және
-
? = 5, ? = 800, ? = 400 болатын үшбұрыштың белгісіз ӛлшемдерін табыңыз. [4балл]
-
А пунктінен С пункті арқылы В пунктіне қатынайтын, мұндағы АС ≈15 км, ал ВС ≈8 км, ∠ACB = 800. Кейін А және В пункттерін түзу жолмен қосты. А пунктінен В пунктіне дейінгі жол қанша километрге қысқарды?
-
Тең бүйірлі үшбұрыштың бүйір қабырғасы 10 см, ал табаны 12 см-ге тең. Осы үшбұрышқа іштей және сырттай сызылған шеңберлердің радиусын табыңыз. [4балл]
Балл қою кестесі
-
Бағалау критерийі
№
Дескриптор
Балл
Білім алушы:
Синустар және косинустар теоремасын
біледі
1
Косинустар теоремасына сәйкестікті табады
1
Синустар теоремасына сәйкестікті табады
1
Тапсырманы орындауға синустар теоремасын қолданады
2
Үшбұрыштың үшінші бұрышын табады
1
Синустар теоремасын қолданады
1
Үшбұрыштың екінші қабырғасын табады
1
Үшбұрыштың үшінші қабырғасын табады
1
Тапсырманы орындауға косинустар теоремасын қолданады
3
Косинустар теоремасын қолданады
1
АС-ның арақашықтығын табады
1
Жауабын жазады
1
Үшбұрышқа іштей және сырттай сызылған шеңберлердің радиустарын табуға арналған есептерді шығарады
4
Үшбұрыштың ауданын есептейді
1
Үшбұрышқа іштей және сырттай сызылған
шеңберлердің радиусын табу формуласын қолданады
1
Үшбұрышқа іштей сызылған шеңбердің радиусын табу формуласын қолданады
1
Үшбұрышқа сырттай сызылған шеңбердің радиусын табу формуласын қолданады
1
Барлығы:
13
3 нұсқа
Тапсырма 1. [2 балл] Сәйкестікті табыңыз. Жауабын кестемен жазыңыз :
-
-
1. Іштей сызылған үшбұрыш ауданы
А)S = 4abc
R

2. Сырттай сызылған кӛпбұрыш ауданы
В) S = p · r
C)S = abc
4

D) S = 2p · r
E) S=p·r2
F) S = abc
4
 R
R1
2
-
Тапсырма 2. [2 балл] Үшбұрыш берілген:
 T
S
T
S
Мына тұжырымдардың қайсысы ақиқат екенін анықтаңыз :
-
TR = RS + RS- RS · ST · CosS
-
TR2 = RS2 − TS2 + 4 · RS · ST · Cos2S
-
??2 = ??2 + ??2 − 2 · ?? · ?? · ????
-


 SinS = SinR = SinT
SinS = SinR = SinT
RS RT TS
-


 SinS = SinR = SinT
SinS = SinR = SinT
RT TS RS
![]()
![]() 6)SinS = SinR = SinT
6)SinS = SinR = SinT
TS RS TR
Тапсырма 3. [3 балл] LMN үшбұрышында LM=3, MN=6,∠М=600. Косинустар теоремасын қолданып, LN қабырғасының ұзындығын табыңыз.
![]()
Тапсырма 4. [3 балл] Сүйір бұрышты ХYZ үшбұрышында ХY=3√3, XZ=6,
∠XZY=600 . Синустар теоремасын қолданып, ∠XYZ бұрышының градустық мәнін табыңыз.
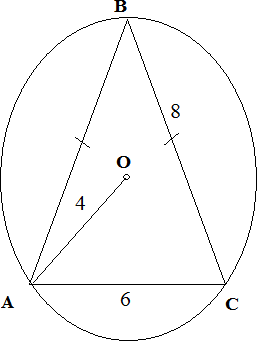 Тапсырма 5. [3 балл] ABC үшбұрышы радиусы
r және центрі О болатын шеңберге іштей сызылған.
1-ші суреттегі үшбұрыштың ауданын табыңыз.
Тапсырма 5. [3 балл] ABC үшбұрышы радиусы
r және центрі О болатын шеңберге іштей сызылған.
1-ші суреттегі үшбұрыштың ауданын табыңыз.
Сурет 1
Тапсырма 6. [4 балл] Кӛпбұрыш радиусы 7-ге тең шеңберге сырттай сызылған.
Кӛпбұрыштың ауданы 56 болса, периметрін табыңыз.
4 нұсқа.
Тапсырма 1. [2 балл] Сәйкестікті табыңыз. Жауабын кестемен жазыңыз :
-
-
1. Іштей сызылған үшбұрыш ауданы
А)S = abc
4
 R
R2. Сырттай сызылған кӛпбұрыштың ауданы
В) S = p · r
C)S = 2p · r
D) S = abc
4

E) S=p·r2
F) S = 4abc
R

1
2
-
[2]
Тапсырма 2. [2 балл] Үшбұрыш берілген :
 S
S
T
Мына тұжырымдардың қайсысы ақиқат екенін анықтаңыз :
-
TR2 = RS2 + TS2 − 2 · RS · ST · Cos2S
-
??2 = ??2 + ??2 − 2 · ?? · ?? · ????
-
TR = RS + RS- RS · ST · CosS
-


 SinS = SinR = SinT
SinS = SinR = SinT
TS RS TR
-


 SinS = SinR = SinT
SinS = SinR = SinT
RS RT TS
![]()
![]() 6)SinS = SinR = SinT
6)SinS = SinR = SinT
RT TS RS
Тапсырма 3. [3 балл] LMN үшбұрышында, LM=6, MN=10,∠М=600. Косинустар теоремасын қолданып, LN қабырғасының ұзындығын табыңыз.
![]()
Тапсырма 4. [3 балл] Сүйір бұрышты ХYZ үшбұрышында YZ=2√3, XZ=2,
∠XYZ=300. Синустар теоремасын қолданып , ∠YXZ бұрышының градустық мәнін табыңыз .
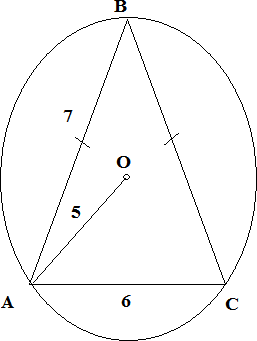 Тапсырма 5. [3 балл] ABC үшбұрышы радиусы
r және центрі О болатын шеңберге іштей сызылған.
1-ші суреттегі үшбұрыштың ауданын табыңыз.
Тапсырма 5. [3 балл] ABC үшбұрышы радиусы
r және центрі О болатын шеңберге іштей сызылған.
1-ші суреттегі үшбұрыштың ауданын табыңыз.
Сурет 1
Тапсырма 6. [4 балл] Радиусы 6-ға тең шеңберге кӛпбұрыш сырттай сызылған.
Кӛпбұрыштың ауданы 48 болса, периметрін табыңыз.
Балл қою кестесі
-
Бағалау критерийі
Тапсыр ма №
Дескриптор
Балл
Білім алушы
Косинустар теоремасын, синустар теоремасын, үшбұрышқа іштей сызылған, кӛпбұрышқа сырттай сызылған шеңберлердің радиустарын табу формулаларын анықтайды.
1
іштей сызылған үшбұрыш ауданы табады
1
сырттай сызылған кӛпбұрыштың ауданы табады
1
2
синустар теоремасының ақиқат
анықтамасын дұрыс табады
1
косинустар теоремасының ақиқат анықтамасын дұрыс табады
1
Косинустар теоремасын қолданып, үшбұрыштың элементтерін табады .
3
есептің шарты бойынша суретін салады
1
косинустар теоремасын жазады, формулаға сандық мәнін жазады
1
LN қабырғасын табады
1
Синустар теоремасын қолданып, үшбұрыштың элементтерін табады .
4
есептің шарты бойынша суретін салады
1
синустар теоремасын жазады, формулаға сандық мәнін жазады
1
Sin∠YXZ табады, ∠YXZ шамасын градуспен жазады
1
Іштей сызылған үшбұрыш ауданының формуласын қолданады .
5
сызба бойынша үшбұрыштың
қабырғасының ұзындығын, шеңбердің радиусын табады
1
іштей сызылған үшбұрыш ауданының
формуласын жазады
1
формулаға сандық мәнін жазады, АВС үшбұрышының ауданын табады
1
Сырттай сызылған кӛпбұрыштың ауданының формуласын қолданады.
6
сырттай сызылған кӛпбұрыштың ауданының формуласын жазады
1
сырттай сызылған кӛпбұрыштың жарты периметрін жазады
1
формулаға сандық мәнін жазады, сырттай сызылған кӛпбұрыштың
жарты периметрін табады
1
сырттай сызылған кӛпбұрыштың
периметрін табады
1
Барлығы
17
«Шеңбер. Кӛпбұрыштар»
-
Тақырыбы
Шеңбер және дӛңгелек. Доғаның ұзындығы. Шеңбердің, сектордың және сегменттің ауданы. Дұрыс кӛпбұрыштар, олардың қасиеттері және симметриясы.
Оқу мақсаты
-
Доға ұзындығының формуласын қорытып шығару және қолдану;
-
сектор және сегменттің ауданынын формуласын шығару және қолдану;
9.1.2.4 дұрыс кӛпбұрыштың іштей және сырттай сызылған шеңберінің радиустарынын арасындағы байланысты білу және қолдану;
9.1.2.4 дұрыс кӛпбұрыштың іштей және сырттай сызылған шеңбердің радиустары мен дұрыс кӛпбұрыштың периметрін, формулаларын білу және қолдану;
Бағалау критерийі :
тапсырмаларды шешу кезінде шеңбер доғасының ұзындығының формуласын қолданады;
-есептерді шешу кезінде сектор ауданының, шеңбер сегментінің формуласын қолданады;
-тапсырмаларды шешу кезінде дұрыс кӛпбұрыштың іштей және сырттай сызылған шеңберінің радиустарынын арасындағы байланысты қолданады;
-есептерді шешу кезінде дұрыс кӛпбұрышқа іштей және сырттай сызылған
периметрін, дұрыс кӛпбұрыштың ауданын және қабырғаларын табудын формулаларын қолданады;
Ойлау дағдыларының деңгейі
Қолдану. Жоғарғы дағдылар
Орындау уақыты:
40 минут
-
I нұсқа
-
1 балл Егер шеңбердің радиусы 12 см тең болса,оның 120°центрлік бұрышына сәйкес келетін доғасының ұзындығын есептеңіз?
-
4π;
-
6π;
-
8;
-
8π;
-
12.
-
-
5 балл Айналмалы сектордың ауданы 9π см2, ал шеңбердің радиусы-6 см. Осы сектордың доғасын керетін хорданың ұзындығы мен пайда болған сегменттің ауданын табыңыз.
-

5 балл Сәйкестікті орнатыңыз:
Дұрыс үшбұрышқа іштей сызылған шеңбердің радиусы √3 см тең.
-
Тапсырма
Жауап
1. Үшбұрышқа іштей сызылған шеңбердің радиусын табыңдар
A. 6;
2. Дұрыс үшбұрыштың периметрін табыңдар.
B. 18;
3. Дұрыс үшбұрыштын ауданын табыңдар.


C. √6;
D. 6√6;
4. Шеңберге іштей сызылған квадраттың қабырғасын табыңдар
E. 2;
F
 .
2√3;
.
2√3;1



 ; 2 ; 3 ; 4
; 2 ; 3 ; 4

G. 6√3;
H. 9√3.
-
6 балл Шеңберге іштей сызылған дұрыс үшбұрыштың периметрі 45 см-ге тең. Сол шеңберге сырттай сызылған оң алтыбұрыштың периметрін және ауданын табыңыз.
-
Бағалау критерийі
Тапсыр ма №
Дескриптор
Балл
Білім алушы
есептерді шешу кезінде шеңбер доғасының ұзындығының формуласын қолданады;
1
шеңбер доғасынын ұзындығын есептеу үшін тиісті формуланы қолданады және жауапты таңдайды.
1
есептерді шешу кезінде сектордың ауданын,сегментін формуласын қолданады
2
сектордың ауданының формуласын
пайдаланады;
1
осы секторға сәйкес келетін центрлік бұрыштың шамасын есептейді;
1
үшбұрыштың түрін анықтайды
1
хорданың ұзындығын есептейді;
1
сегментін ауданын есептейді.
1
есептерді шешу кезінде дұрыс кӛпбұрыштың іштей және сырттай сызылған радиустардың арасындағы байланысты қолданады;
3.1
үшбұрышқа сырттай сызылған шеңбердің радиусын табады және сәйкестікті орнатады;
1
есептерді шешу кезінде дұрыс кӛпбұрышқа іштей және сырттай сызылған периметрін, дұрыс кӛпбұрыштың ауданын және қабырғаларын табудын формулаларын қолданады;
3.2-3.4
осы үшбұрыштың периметрін табады және сәйкестікті орнатады;
1
осы үшбұрыштың ауданын табады және сәйкестікті орнатады;
1
дұрыс кӛпбұрыштар арасындағы
байланыс орнатады;
1
шаршының қабырғасын есептеп,
сәйкестігін анықтайды;
1
4
осы дұрыс үшбұрыштың қабырғасын анықтайды;
1
сырттай сызылған шеңбердің радиусын есептейді;
1
дұрыс кӛпбұрыштар арасындағы байланыс орнатады;
1
дұрыс алтыбұрыштың қабырғасын есептейді;
1
дұрыс алтыбұрыштың периметрін
есептейді;
1
дұрыс алтыбұрыштың ауданын
есептейді;
1
Жалпы ұпай:
17
II нұсқа
-
1 балл Егер шеңбердің радиусы 18 см тең болса,оның 150°центрлік бұрышына сәйкес келетін доғасының ұзындығын есептеңіз?
-
34π;
-
36π;
-
18;
-
18π;
-
12.
-
-
5 балл Айналмалы сектордың ауданы 16 π см2, ал шеңбердің радиусы-8см. Осы сектордың доғасын керетін хорданың ұзындығы мен пайда болған сегменттің ауданын табыңыз.
-

5 балл Сәйкестікті орнатыңыз:
Дұрыс үшбұрышқа сырттай сызылған шеңбердің радиусы 4√3тең.
-
-
Тапсырма
Жауап
1. Үшбұрышқа іштей сызылған шеңбердің радиусын табыңдар
-
36;
-
18;


-
4√6;
-
6√6;
-
12;



-
2√3;
-
36√3;
-
9√3.
2. Дұрыс үшбұрыштың периметрін табыңдар.
3. Дұрыс үшбұрыштын ауданын табыңдар.
4. Шеңберге іштей сызылған квадраттың қабырғасын табыңдар
1 ; 2 ; 3 ; 4 .
-
-
-
6 балл Шеңберге сырттай сызылған дұрыс үшбұрыштың периметрі 36 см-ге тең. Сол шеңберге сырттай сызылған дұрыс алтыбұрыштың периметрін және ауданын табыңыз.
-
Бағалау критерийі
Тапсыр- ма №
Дескриптор
Балл
Білім алушы
есептерді шешу кезінде шеңбер доғасының ұзындығының формуласын қолданады;
1
шеңбер доғасынын ұзындығын есептеу үшін тиісті формуланы қолданады және жауапты таңдайды.
1
есептерді шешу кезінде сектордың ауданын,сегментін формуласын қолданады
2
сектордың ауданының формуласын
пайдаланады;
1
осы секторға сәйкес келетін центрлік бұрыштың шамасын есептейді;
1
үшбұрыштын түрін анықтайды;
1
хорданың ұзындығын есептейді;
1
сегментін ауданын есептейді.
1
есептерді шешу кезінде дұрыс кӛпбұрыштың іштей сызылған және сырттай сызылған радиустарының арасындағы байланысты
қолданады;
3.1
осы үшбұрышқа іштей сызылған шеңбердің радиусын табады және сәйкестікті орнатады;
Іштей сызылған үшбұрышқа шеңбердің радиусын табады;
1
есептерді шешу кезінде дұрыс кӛпбұрыштың іштей сызылған және сырттай сызылған, периметрін, дұрыс кӛпбұрыштың ауданын және қабырғаларын табатын формулаларын қолданады;
3.2-3.4
берілген үшбұрыштың периметрін
табады және сәйкестікті орнатады;
1
үшбұрыштың ауданын табады және сәйкестікті орнатады;
1
дұрыс кӛпбұрыштар арасындағы
байланыс орнатады;
1
шаршының қабырғасын есептеп,
сәйкестігін анықтайды
1
4
осы дұрыс үшбұрыштың қабырғасын
анықтайды;
1
Іштей сызылған шеңбердің радиусын есептейді;
1
дұрыс кӛпбұрыштар арасындағы
байланыс орнатады;
1
дұрыс алтыбұрыштың жағын есептейді;
1
дұрыс алтыбұрыштың периметрін есептейді;
1
дұрыс алтыбұрыштың ауданын
есептейді;
1
Жалпы ұпай:
17
-
2 балл Егер шеңбердің радиусы 12 см тең болса,оның 120° центрлік бұрышына сәйкес келетін доғасының ұзындығын есептеңіз?
-
4 балл Шеңбердің радиусы 10 см доғаның ұзындығы 4? -ге тең тең болса. Сектордың ауданын табыңыз.
-
 4 балл Егер шеңберге іштей сызылған дұрыс алтыбұрыштың
ауданы 72
см2тең болса, шеңбердің ұзындығын
табыңыз.
4 балл Егер шеңберге іштей сызылған дұрыс алтыбұрыштың
ауданы 72
см2тең болса, шеңбердің ұзындығын
табыңыз. -
6 балл Шеңберге сырттай сызылған дұрыс үшбұрыштың периметрі 18 см-ге тең.Осы шеңберге іштей сызылған дұрыс тӛртбұрыштың периметрін және ауданын табыңыз.
-
Бағалау критерийі
Тапсыр- ма №
Дескриптор
Балл
Білім алушы
есептерді шешу кезінде шеңбер доғасының ұзындығының формуласын қолданады;
1
шеңбер доғасын есептеу үшін тиісті формуланы қолданады
1
есептеулерді орындайды және жауапты
жазады
1
есептерді шешу кезінде сектордың ауданын,сегментін формуласын қолданады
2
шеңбер доғасының ұзындығының формуласын пайдаланады;
1
осы доғаға сәйкес орталық бұрыштың
шамасын есептейді;
1
шеңбер секторының ауданының
формуласын пайдаланады;
1
сектордың ауданын есептейді
1
есептерді шешу кезінде дұрыс кӛпбұрыштың іштей және сырттай сызылған радиустарының арасындағы байланысты қолданады
3
алтыбұрыштың ауданы мен оның жағы
арасында байланыс табады;
1
осы алтыбұрыштың жағын табады;
1
дұрыс кӛпбұрыштың жағы мен сырттай сызылған шеңбердің радиустың
арасындағы байланысты орнатады;
1
шеңбер ұзындығының формуласын қолданады және оның ұзындығын
есептейді;
1
4
осы дұрыс үшбұрыштың қабырғасын анықтайды;
1
шеңбердің радиусын есептейді;
1
дұрыс кӛпбұрыштар арасындағы байланыс орнатады;
1
дұрыс тӛртбұрыштың қабырғаларын
есептейді;
1
дұрыс тӛртбұрыштың периметрін есептейді;
1
дұрыс тӛртбұрыштың ауданын есептейді;
1
Жалпы ұпай:
16
-
2 балл Егер оның градустық ӛлшемі 150° - қа, ал радиусы 3 см тең болса, доғаның ұзындығын табыңыз.
-
4 баллШеңберінің айналмалы секторының ауданы 9?см2 радиус 6см тең болса. Тиісті доғанын ұзындығын табыңыз.
-
 4 балл Егер шеңберге сырттай сызылған оң алтыбұрыштың
ауданы 84 см2тең болса, шеңбердің ұзындығын
табыңыз.
4 балл Егер шеңберге сырттай сызылған оң алтыбұрыштың
ауданы 84 см2тең болса, шеңбердің ұзындығын
табыңыз. -
6 балл Шеңберге іштей сызылған дұрыс үшбұрыштың периметрі 27 см-ге тең.Осы шеңберге сырттай сызылған дұрыс тӛртбұрыштың периметрін және ауданын табыңыз.
-
Бағалау критерийі
Тапсыр- ма №
Дескриптор
Балл
Білім алушы
есептерді шешу кезінде шеңбер доғасының ұзындығының формуласын қолданады;
1
шеңбер доғасын есептеу үшін тиісті формуланы қолданады
1
есептеулерді орындайды және жауапты
жазады.
1
есептерді шешу кезінде сектордың ауданын,сегментін формуласын қолданады
2
шеңбердің айналмалы секторының
формуласын пайдаланады;
1
осы сектордың доғасына сәйкес орталық бұрыштың шамасын есептейді;
1
доға ұзындығын формуласын
пайдаланады;
1
доға ұзындығын есептейді.
1
есептерді шешу кезінде дұрыс кӛпбұрыштың іштей және сырттай сызылған радиустарының арасындағы байланысты қолданады;
3
алтыбұрыштың ауданы мен оның
жақтарымен байланыс табады;
1
осы алтыбұрыштың қабырғасын табады;
1
дұрыс кӛпбұрыштың жағы мен сәйкес шеңбердің радиусы арасындағы байланысты орнатады;
1
шеңбер ұзындығының формуласын қолданады және оның ұзындығын
есептейді;
1
4
осы дұрыс үшбұрыштың қабырғасын
анықтайды;
1
шеңбердің радиусын есептейді;
1
дұрыс кӛпбұрыштар арасындағы байланыс орнатады;
1
дұрыс тӛртбұрыштың қабырғаларын есептейді;
1
дұрыс тӛртбұрыштың периметрін
есептейді;
1
дұрыс тӛртбұрыштың ауданын есептейді;
1
Жалпы ұпай:
16
Алгебра
І тоқсанға арналған ТЖБ
-
Орындау уақыты
40 минут
І нұсқа
-
3 балл Теңдеулер жүйесін шешіңіз:
5?2 − y2 + 6? = 11;
{ ?2 + ?2 = 25.
-
4 балл Есепті теңдеулер жүйесін құрып шығарыңыз.
Тік бұрышты үшбұрыштың ауданы 85 см2 –ге, ал катеттері ұзындықтарының айырымы 7 см-ге тең. Үшбұрыштың гипотенузасын табыңыз.
-
4 балл Теңсіздіктер жүйесінің шешімдері болатын нүктелер жиының
координаталар жазықтығына кескіндеңдер:{
y ≤ − 1
![]() 2
2
?2
+ 2;
![]()
? < 2√x.
-
2 балл (1 2x)4 жіктелуінің x3 коэфициентің табыңдар
-
2 балл 572019 неше әртүрлі сандар құрастыруға болады, егер цифрларын орын ауыстырсақ?
-
2 балл Егер бірінші орында 0 цифры тұра алмайтынын білсек, неше бес таңбалы қайталанатын цифрлары жоқ телефонның номерін құрастыруға болады?
-
3 балл Ротада 16 солдат,4 офицер және 3 сержант бар.Объекті күзету үшін 6 солдаты бӛлу керек,бір сержанты және екі офицерді. Нарядты неше тәсілмен таңдауға болады ? Барлығы: 20 ұпай
II нұсқа
-
3 балл Теңдеулер жүйесін шешіңіз:
?2 + ?2 = 81;
{ ?2 − ? = 9.
-
4 балл Есепті теңдеулер жүйесін құрып шығарыңыз.
Тік бұрышты үшбұрыштың гипотенузасы 15 см -ге, ал үшбұрыштың периметрі 36 см тең болатын үшбұрыштың ауданын табыңдар.
-
4 балл Теңсіздіктер жүйесінің шешімдері болатын нүктелер жиының
координаталар жазықтығына кескіндеңдер: {y ≥
1 ?2
![]() 2
2
− 2;
![]()
? > −2√x.
-
2 балл (2 x)4 жіктелуінің x2 коэфициентің табыңдар
-
2 балл 52018 неше әртүрлі сандар құрастыруға болады, егер цифрларын орын ауыстырсақ?
-
2 балл Егер бірінші орында 0 цифры тұра алмайтынын білсек, неше алты таңбалы қайталанатын цифрлары жоқ телефонның номерін құрастыруға болады?
-
3 балл Ротада 14 солдат,2 офицер және 4 сержант бар.Объекті күзету үшін 7 солдаты бӛлу керек,бір сержанты және екі офицерді. Нарядты неше тәсілмен таңдауға болады?
Барлығы: 20 ұпай
Балл қою кестесі
І нұсқа
|
№ |
Жауабы |
Ұпай |
Қосымша ақпарат |
|
1 |
Қосу тәсілін пайдаланып осындай теңдеу алады 6x2 + 6x = 36 |
1 |
|
|
Теңдеуді шығарады x2 + x − 6 = 0 ; х=-3, х=2 |
1 |
|
|
|
у=±√21; y = ±4 (2; √21); (2; −√21); (−3; 4); (−3; −4) |
1 |
|
|
|
2 |
1 Жаңа айнымалы енгізеді {2 x − y = 7. |
1 |
|
|
Жаңа айнымалы енгізіп теңдеуді шығарады : y2 + 7y − 170 = 0 |
1 |
|
|
|
Теңдеудің түбірін табады у=-17, у=10, тексеру арқылы теңдеудің түбірін табады х=10, |
1 |
|
|
|
с |
1 |
|
|
|
3 |
Парабола графигін, тармақтарды тӛмен, жоғарғы (0; 2), Тұтас қисық; |
1 |
|
|
Квадрат түбірінің кестесін, нүктелі қисық қисықты жасайды; |
1 |
|
|
|
Жазықтықтың нүктелерін параболдан тӛмен белгілейді және жазықтықта квадрат түбірдің нүктелерін графиктен тӛмен және оу осінен оңға қарай белгілейді; |
1 |
|
|
|
Жүйенің шешімін оу осінен оңға қарай, квадрат түбірінің кестесінен тӛмен және параболанын сол жағында. |
1 |
|
|
|
4 |
−C3 · 1 · (2x)2 4 |
1 |
|
|
-32 |
1 |
|
|
|
5 |
P6 − P5 |
1 |
5 · 5 · 4 3 · 2 · 1 |
|
= 6! − 5! = 720 − 120 = 600 |
1 |
600 |
|
|
6 |
A5 − A4 = 10 9 |
1 |
6 · 7 · 8 · 9 · 9 |
|
10! 9! = − = 6 · 7 · 8 · 9 · 9 = 27216 5 |
1 |
27216 |
|
|
7 |
C6 · C1 · C2 = 16 3 4 |
1 |
|
|
16! 3! 4! · 6 |
1 |
|
|
|
11 · 13 · 14 · 8 · 9 = 144144 |
1 |
|
|
|
Барлығы: |
20 |
|
|
II нұсқа
|
№ |
Жауабы |
Ұпай |
Қосымша ақпарат |
|||||
|
1 |
Қосу тәсілін пайдаланып осындай теңдеу алады y2 + y = 72 |
1 |
|
|||||
|
Теңдеуді шешеді : y2 + y − 72 = 0 ; у=-9, у=8 |
1 |
|
||||||
|
х |
1 |
|
||||||
|
2 |
Жаңа айнымалы енгізеді x2 + y2 = 225; {x + y = 36 − 15. |
1 |
|
|||||
|
Жаңа айнымалы енгізіп теңдеуді шығарады : x2 − 21x + 108 = 0 |
1 |
|
||||||
|
Теңдеудің түбірін табады х=9, х=12, катеты 9 және 12 |
1 |
|
||||||
|
S=54 см2 |
1 |
|
||||||
|
3 |
Парабола графигін сызады, бұтақтары жоғары, шыңы (0; -2), тұтас қисық |
1 |
|
|||||
|
Квадрат түбірінің графигін салады, қисық |
1 |
|
||||||
|
Жазықтықтың нүктелерін параболдан жоғары белгілейді және жазықтықтың нүктелерін квадрат түбірінің кестесінен жоғары және оу осінен оңға қарай белгілейді. |
1 |
|
||||||
|
Жүйенің шешімін оу осінен оңға қарай, квадрат түбірінің графигінен жоғары және параболадан сол жақта. |
1 |
|
||||||
|
4 |
−C2 · 22 · x2 4 |
1 |
1 4 6 4 1 |
|||||
|
-24 |
1 |
622(-х)2; -24 |
||||||
|
5 |
P5 − P4 |
1 |
4 · 4 · 3 · 2 · 1 |
|||||
|
= 5! − 4! = 120 − 24 = 96 |
1 |
96 |
||||||
|
6 |
A6 − A5 = 10 9 |
1 |
5 · 6 · 7 · 8 · 9 · 9 |
|||||
|
= |
10!
4! |
− |
9!
4! |
= 5 · 6 · 7 · 8 · 9 · 9 = 136080 |
1 |
136080 |
||
|
7 |
C7 · C1 · C2 = 14 2 4 |
1 |
|
|||||
|
14! |
|
|
2! |
4! |
1 |
|
||
|
7! · 7! 1! · 1! 2! · 2! |
||||||||
|
8 · 9 · 11 · 13 · 4 = 41184 |
1 |
|
||||||
|
Барлығы: |
20 |
|
||||||
ІІ тоқсанға арналған ТЖБ
Орындау уақыты: 40 минут
І нұсқа
-
[1 балл] арифметикалық прогрессияның n-ші мүшесінің формуласын жазыңдар:
![]()
![]() 3 ; 6 ;
3 ; 6 ;
2 3
9 ;12
![]()
![]() 4
5
4
5
;15
![]() 6
6
;18
![]() 7
7
...
-
[6 балл] 11,2; 10,8; … арифметикалық прогрессияның оң таңбалы мүшелерінің қосындысын табыңыз?
-
[3 балл] Бірінші және тӛртінші геометриялық прогрессияның қосындысы 40 тең, ал екінші және бесінші мүшелерінің қосындысы 10-ға тең болса. Еселігін табыңдар.
-
[6 балл] Үш сан x, y, 20 ӛспелі геометриялық прогрессия, ал x, y, 15 сандар – арифметикалық прогрессияның мүшелерін құрайтын болса,онда y-x -ның қосындысын табыңыз.
-
[4 балл] Шексіз кемімелі геометриялық прогрессияның q-сын табыңдар,егер екінші мүшесі (-0,5) тең , ал шексіз кемімелі геометриялық прогрессияның қосындысы 1,6-ға тең болса.
ІІ нұсқа
-
[1 балл] арифметикалық прогрессияның n-ші мүшесінің формуласын жазыңдар:
![]()
![]()
![]()
![]()
![]()
![]() 7 ;14 ; 21; 28 ; 35 ; 42 ...
7 ;14 ; 21; 28 ; 35 ; 42 ...
2 3 4 5 6 7
-
[6 балл] –7,2; –6,9; … арифметикалық прогрессияның теріс таңбалы мүшелерінің қосындысын табыңыз?
-
[3 балл] Ӛспелі геометриялық прогрессияның тӛртінші мүшесі екінші мүшесінен 24- ке артық, ал екінші мен үшінші мүшелерінің қосындысы 6-тең болса, q-сын табыңдар.
-
[6 балл] Үш сан a, b, 12 ӛспелі геометриялық прогрессия , ал a, b, 9 сандар – арифметикалық прогрессияның мүшелерін құрайтын болса,онда a+b-ның қосындысын табыңыз
-
[4 балл] Шексіз кемімелі геометриялық прогрессияның қосындысы 6-ға, ал алғашқы екі мүшесінің қосындысы 9/2тең болса,онда геометриялық прогрессияның еселігін табыңдар .
Балл қою кестесі
|
№ |
Жауабы |
Ұпай |
Қосымша ақпарат |
|
|
I нұсқа |
II нұсқа |
|||
|
1 |
a 3n n |
a 7n n |
1 |
|
|
2 |
a1 = 11,2; d = 10,8 – 11,2 = -0,4; S 2a1 d (n 1) n
n |
a1 = -7,2; d = -6,9 + 7,2 = 0,3; S 2a1 d (n 1) n n 2 |
1 |
|
|
an = a1 + d(n-1) |
an = a1 + d(n-1) |
1 |
|
|
|
11,2 - 0,4(n-1) > 0 |
-7,5 + 0,3n < 0 |
1 |
|
|
|
n < 29 |
n < 25 |
1 |
|
|
|
n = 28 |
n = 24 |
1 |
|
|
|
S28 = 162,4 |
S24 = -90 |
1 |
|
|
|
3 |
b1 b4 40 b2 b5 10 |
b4 b2 24 b2 b3 6 |
1 |
|
|
b b q3 40 1 1 b b q 4 10 1 1 |
b q3 b q 24 1 1 b q b q 2 6 1 1 |
1 |
|
|
|
q = 1 4 |
q = 5 |
1 |
|
|
|
4 |
Г |
Г |
1 |
|
|
А.п.: x, y, 15 y x 15
2 |
А.п.: a, b, 9 b a 9
2 |
1 |
|
|
|
x 15 2 |
a 9 2 |
1 |
|
|
|
x1 45 ; x2 5 y 30 y 10 1 2 |
a1 3 ; a2 27 6 18 b1 b2 |
1 |
|
|
|
(x1; y1) сәйкес келмейді, себебі x > y |
(27; 18) сәйкес келмейді, себебі a ≤ 12 |
1 |
|
|
|
y – x = 5 |
a + b = 9 |
1 |
|
|
|
5 |
b2 = -0,5; b1q = -0,5 |
S = b1 , b2 = b1q 1 |
1 |
|
|
|
S = 1,6; S = b1 1 |
b1 6 b b q 9 |
1 |
|
|
q1 1,25 q2 0,25 |
b1 6(1 q) 9 |
1 |
|
|
|
q = 1,25 – сәйкес келмейді; q = -0,25 |
q = -0,5; q = 0,5 |
1 |
|
|
|
Барлығы: |
20 |
|
||
3 нұсқа
-
[3балл] Сандар тізбегі n-мүшесінің n2+2n формуласымен берілген: а) алғашқы бес мүшесін табыңыз;
б) 24 саны тізбектің қандай мүшесі болады.
-
[3 балл] Келесі тізбектің қай саны арифметикалық прогрессия мүшелері болатынын табыңыз: 3; 6; 9; 12;…?
1) 83 3) 100
2) 95 4) 102
-
 [4 балл] Егер a1 =
−3,1, a?+1 =
?? +
0,9 .
болса,арифметикалық
9 мүшесінің қосындысын табыңыз
[4 балл] Егер a1 =
−3,1, a?+1 =
?? +
0,9 .
болса,арифметикалық
9 мүшесінің қосындысын табыңыз
-
[4 балл] bn - геометриялық прогрессия берілген, ал еселігі q=1. Егер b5 =4:
3
а) табу керек b1.
б) Шексіз кемімелі геометриялық прогрессияның қосындысын табыңыз.
-
[3 балл] bn геометриялық прогрессия, егер b1=1 и q=5 болса, онда b1+b2+b3+b4+b5 қосындысын табыңыз
-
[3 балл] Жұмысшылар тротуар плиткасын тӛседі. Бірінші күні олар 30 плитка қойды. Әр келесі күні олар 5 плиткаға кӛп салынды. Бір аптанын ішінде қанша плиткалар салынды.
4 нұсқа.
-
[3 балл] Сандар тізбегі n-мүшесінің n2+3n формуласымен берілген: а) алғашқы үш мүшесін табыңыз;
б) 40 саны тізбектің қандай мүшесі болады
-
[3 балл] Келесі тізбектің қай саны арифметикалық прогрессия мүшелері болатынын табыңыз: 2; 5; 8; 11;…?
1) 30 3) 35
2) 33 4) 37
-
 [4 балл] Егер a1 =
−2,3, a?+1 =
?? +
0,6 болса, арифметикалық 10 мүшесінің қосындысын табыңыз.
[4 балл] Егер a1 =
−2,3, a?+1 =
?? +
0,6 болса, арифметикалық 10 мүшесінің қосындысын табыңыз.
-
[4 балл] bn - геометриялық прогрессия берілген, ал еселігі q=1. Егер b3 =1:
2
а) табу керек b1.
б) Шексіз кемімелі геометриялық прогрессияның қосындысын табыңыз.
-
[3балл] bn геометриялық прогрессия, егер b1=2; q=3 болса, онда b1+b2+b3+b4+b5 қосындысын табыңыз.
-
[3 балл] Жұмысшылар тротуар плиткасын тӛседі. Бірінші күні олар 40 плитка қойды. Әр келесі күні олар 6 плиткаға кӛп салынды. 10 күн ішінде қанша плиткалар салынды.
Балл қою кестесі
|
|
3 нұсқа |
4 нұсқа. |
|
|
№ |
Жауабы |
Жауабы |
Ұпай |
|
1 |
а5=52+2· 5 = 25 + 10 = 35 |
a3=32+3· 3 = 9 + 9 = 18 |
1 |
|
24=n2+2· ?; |
40=n2+3· ?; |
1 |
|
|
?2 + 2? − 24 = 0; ? = 4 |
?2 + 3? − 40 = 0; ? = 5 |
1 |
|
|
2 |
a? = ?1 + ?(? − 1), ?1 = 3, ? = 3 |
a? = ?1 + ?(? − 1), ?1 = 2, ? = 3 |
1 |
|
102=3+3(n-1) |
35=2+3(n-1) |
1 |
|
|
n=34. 102 саны |
n=12. 35 саны |
1 |
|
|
3 |
a2 = ?1 + 0,9 = −3,1 + 0,9 = −2,2 |
a2 = ?1 + 0,6 = −2,3 + 0,6 = −1,7 |
1 |
|
|
? = ?2 − ?1 = −2,2 + 3,1 = 0,9 |
? = ?2 − ?1 = −1,7 + 2,3 = 0,6 |
1 |
|
|
2?1 + ?(? − 1) ?? = 2 ? 2 ?9 = 2 · 9 |
2?1 + ?(? − 1) ?? = 2 ? 2 ?10 = 2 · 10 |
1 |
|
|
?9 = 4,5 |
?10 = 4 |
1 |
|
4 |
? = ? · ??−1; ? = ?5 = 4 5 1 1 ??−1 14
3 |
? = ? · ??−1; ? = ?3 = 1 3 1 1 ??−1 12
4 |
1 |
|
|
?1 = 4 · 81 = 324 |
?1 = 16 |
1 |
|
|
?1 324 ? = = ? − 1 1 − 1 3 |
?1 16 ? = = ? − 1 1 − 1 4 |
1 |
|
|
? = −486 |
1 ? = −21 3 |
1 |
|
5 |
?1(?? − 1) ?? = ? − 1 |
?1(?? − 1) ?? = ? − 1 |
1 |
|
|
1(55 − 1) 3125 − 1 3124 |
2(35 − 1) 2(243 − 1) 2 · 242 |
1 |
|
|
?5 = 5 − 1 = 4 = 4 |
?5 = 3 − 1 = 2 = 2 |
|
|
|
?5 = 781 |
?5 = 242 |
1 |
|
6 |
2 ?1 = 30, ? = 5, ?? = 2 ? |
2 ?1 = 40, ? = 6, ?? = 2 ? |
1 |
|
|
2 ?7 = 2 · 7 60 + 30 = 2 |
2 ?10 = 2 · 10 80 + 54 = 2 |
1 |
|
|
?7 = 315 |
?7 = 670 |
1 |
|
|
Барлығы: |
|
20 |
ІІІ тоқсанға арналған ТЖБ
|
Орындау уақыты: |
40 минут |
І нұсқа
1. [ 2 балл] Сол және оң бағандар арасында сәйкестікті орнатыңыз:
|
1. 2400 |
А. 24 9 |
|
2. 48 9 |
В. 9600 |
|
|
С. 4800 |
|
|
D. 4 3 |
|
|
E. 48,90 |
-
; 2.
-
[ 4 балл] Ӛрнекті ықшамдаңыз: tg cos
1 sin
![]()
![]()
![]()
![]()
![]()
В
.
1
-



2
[ 3 балл] Бұрышты анықтайтын радиус бір шеңбердің нүктесінен ӛтеді ;
2
sin, cos,tg мәнін жазыңыз.
-
[ 5 балл] Ӛрнекті ықшамдаңыз: cos cos sin 2
![]()
![]()
1 sin 1 sin ![]()
![]()
![]()
2
sin 3 -
[ 6 балл] Ӛрнекті ықшамдаңыз:
tg ( )
cos( )
![]()
ctg 3
![]()
2
ІІ нұсқа
-
[ 2 балл] Сол және оң бағандар арасында сәйкестікті орнатыңыз:
|
1. 4800 |
А. 24 9 |
|
2. 35 9 |
В. 8 3 |
|
|
С. 3500 |
|
|
D. 4 3 |
|
|
E. 7000 |
-
; 2.
-
[ 4 балл] Ӛрнекті ықшамдаңыз: ctg sin
1 cos
-
[ 3 балл] Бұрышты анықтайтын радиус бір шеңбердің нүктесінен ӛтеді
К 1 ; .
![]()
![]()
![]()
![]()
![]()
![]()
3
2
2
sin, cos,tg ![]()
мәнің жазыңыз.
-
[ 5 балл] Ӛрнекті ықшамдаңыз: sin sin sin 2
![]()
![]()
1 cos 1 cos -
[ 6 балл] Ӛрнекті ықшамдаңыз:
sin( )
ctg
![]()
2
![]()
tg ( )
![]()
cos 
![]()
2
Балл қою кестесі
|
|
1 нұсқа |
2 нұсқа |
|
|
№ |
Жауабы |
Жауабы |
Балл |
|
1 |
1 – D |
1 – В |
1 |
|
2 – В |
2 – Е |
1 |
|
|
2 |
sin cos cos 1 sin |
cos sin sin 1 cos |
1 |
|
s cos 1 sin |
c sin 1 cos |
1 |
|
|
s |
c |
1 |
|
|
1
cos |
1
sin |
1 |
|
|
3 |
sin 1 2 |
cos 1 2 |
1 |
|
cos 3 2 |
sin 3 2 |
1 |
|
|
tg sin 1 : 3 1 3 c |
tg sin 3 : 1 3
cos 2 2 |
1 |
|
|
4 |
sin cos sin sin cos sin sin 2 1 cos 1 cos |
cos cos sin cos cos sin sin 1 sin 1 sin |
2 1 |
|
2sin sin 2
1 cos 2 |
2 cos sin 2
1 sin 2 |
1 |
|
|
2sin sin 2
sin 2 |
2 cos sin 2
cos 2 |
1 |
|
|
2 2sin cos
sin |
2 2sin cos
cos |
1 |
|
|
4cos |
4sin |
1 |
|
|
5 |
tg( ) tg |
sin( ) sin |
1 |
|
cos( ) cos |
tg( ) tg |
1 |
|
|
sin 3 cos 2 |
ctg tg 2 |
1 |
|
|
ctg 3 tg 2 |
cos sin 2 |
1 |
|
|
tg cos cos tg |
cin tg tg sin |
1 |
|
|
1 |
1 |
1 |
|
|
Барлығы: |
20 |
||
VI тоқсанға арналған ТЖБ
|
Орындау уақыты: |
40 минут |
І нұсқа
-
[2 балл] Екі ойын сүйегі лақтырылды.Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 7 болу ықтималдығын табыңыз.
-
[5 балл] Урнада 3 ақ және 6 қара шарлар бар.
-
Урнадан бір уақытта екі шар алынады. Олар бірдей түсті болу ықтималдығын табыңыз.
-
Бір уақытта екі шарды алып тастағанда, қандай оқиға болуы мүмкін А «бір түсті шарлар», В – «түрлі түсті шарлар»?
-
-
[2 балл] Бұйымдардың сапасын тексеру үшін 200 бӛлшектер зерттелді,олардың ішінде 8 ақаулы болды.
а) наугад алынған бӛлшектің жарамды болуы ықтималдығын табыңыз.
b) 1000 бӛлшектен тұратын партияда орташа ақаулы бӛлшектер қанша болады?
-
[3 балл] Радиус шеңберінің ішінде R наудачу нүкте тасталған. Нүкте шеңберге жазылған квадрат ішінде болуы ықтималдығын табу. Шеңбердің бӛлігіне нүктенің құлау ықтималдығы осы бӛліктің алаңына пропорционалды және оның шеңберге қатысты орналасуына байланысты емес деп болжанады.
-
[3 балл] Ӛрнекті ықшамдаңыз: sin 2 3cos 2 2 cos 2 3sin 2 2 .
-
[5 балл] Тепе-теңдікті дәлелдеңіз:
cos cos 2tg .
1sin 1 sin
ІІ нұсқа
-
[2 балл] Екі ойын сүйегі лақтырылды.Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 8 болу ықтималдығын табыңыз.
-
[5 балл] Урнада 5 ақ және 3қара шарлар бар.
-
Урнадан бір уақытта екі шар алынады. Олар бірдей түсті болу ықтималдығын табыңыз.
-
Бір уақытта екі шарды алып тастағанда, қандай оқиға болуы мүмкін А «бір түсті шарлар», В – «түрлі түсті шарлар»?
-
-
[2 балл] Бұйымдардың сапасын тексеру үшін 500 бӛлшектер зерттелді,олардың ішінде 9 ақаулы болды.
а) наугад алынған бӛлшектің жарамды болуы ықтималдығын табыңыз.
b)1000 бӛлшектен тұратын партияда орташа ақаулы бӛлшектер қанша болады?
-
[3 балл] Радиус шеңберінің ішінде R наудачу нүкте тасталған. Нүкте шеңберге жазылған квадрат ішінде болуы ықтималдығын табу. Шеңбердің бӛлігіне нүктенің құлау ықтималдығы осы бӛліктің алаңына пропорционалды және оның шеңберге қатысты орналасуына байланысты емес деп болжанады.
-
[3 балла] Ӛрнекті ықшамдаңыз : 2sin 3 3cos 3 2 2cos 3 3sin 3 2 .
-
[5 баллов] Тепе-теңдікті дәлелдеңіз:
sin sin 2ctg .
1 cos 1 cos
Балл қою кестесі:
І нұсқа
|
№ |
Жауап |
Балл |
Қосымша ақпарат |
|
1 |
(2;5), (1;6) |
1 |
|
|
(5;2), (6;1) |
1 |
||
|
2(a) |
C92 , C32 , C62 |
1 |
Ең болмағанда бір дұрыс жазуға балл қою |
|
С 2 С 2 3! 6! 3 |
1 |
||
|
С 2 С 2 1 Р( А) 3 6 С 2 2 9 |
1 |
||
|
2(b) |
С1С1 3 6 |
1 |
Қабылданады балама жауап |
|
P |
1 |
||
|
3(а) |
200 8 0,975 200 |
1 |
|
|
3 (b) |
1000 5; 58 40 2 |
1 |
|
|
4 |
?кв = 2?2
|
1 |
|
|
2?2 P = ??2 |
1 |
||
|
2 P = ? |
1 |
||
|
5 |
???22? + 6???2????2? + 9???22? + ???22? − −6???2????2? + 9???22? |
1 |
|
|
Мұндай қосылыстарды келтіреді |
1 |
||
|
1+9=10 |
1 |
||
|
6 |
cos cos asin cos sin cos 2tg 1sin 2 |
1 |
|
|
Мұндай қосылғыштарды келтіріңіз. Негізгі тригонометриялық тепе-теңдікті қолданады |
1 |
||
|
2 cos sin 2tg cos2 |
1 |
||
|
2 ??? ? = 2??? ??? ? |
1 |
||
|
2tgα=2tgα |
1 |
||
|
Барлығы |
20 |
|
|
ІІ нұсқа
|
№ |
Жауап |
Балл |
Қосымша ақпарат |
|
1 |
(3;5), (5;3) |
1 |
|
|
(2;6), (6;2) (4;4) |
1 |
||
|
2(a) |
C82 , C52 , C32 |
1 |
Ең болмағанда бір дұрыс жазуға балл қою |
|
С 2 С 2 5! 3! 13 5 |
1 |
||
|
С 2 С 2 13 Р( А) 5 3 С 2 28 8 |
1 |
||
|
2(b) |
С1С1 15 5 3 |
1 |
Қабылданады балама жауап |
|
С 2 С 2 15 Р(В) 5 3 С 2 28 8
P |
1 |
||
|
3(а) |
500 9 0,982 500 |
1 |
|
|
3 (b) |
1000 2; 2 9 18 500 |
1 |
|
|
4 |
а 2R sin 60o R 3
a S R 4 |
1 |
|
|
P Sтр 3 3 R3 1 S кр |
1 |
||
|
P 3 3 4 |
1 |
||
|
5 |
4sin2 3 12sin 3 cos 3 9 cos2 3 4 cos2 3 12sin 3 cos 3 9sin2 3 |
1 |
|
|
Мұндай қосылыстарды келтіреді |
1 |
||
|
Ӛрнек мәнін табады =13 |
1 |
||
|
6 |
sin sin cos sin sin cos 2ctg 1 cos2 |
1 |
|
|
Мұндай қосылғыштарды келтіріңіз. Негізгі тригонометриялық тепе-теңдікті қолданады |
1 |
||
|
2sin cos 2ctg sin2 |
1 |
||
|
2 cos 2ctg sin |
1 |
||
|
2ctg 2ctg |
1 |
||
|
Барлығы: |
20 |
|
|
Геометрия
1 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
|
Ұзақтылығы |
40 минут |
I нұсқа
-
 2 балл Суретте берілген тӛртбұрыш ABCD– ромб, оның А бұрышы 126°қа тең.
̅B̅̅̅A̅→ и ̅A̅̅̅?̅→ векторлары арасындағы бұрышты
анықтаңыз
2 балл Суретте берілген тӛртбұрыш ABCD– ромб, оның А бұрышы 126°қа тең.
̅B̅̅̅A̅→ и ̅A̅̅̅?̅→ векторлары арасындағы бұрышты
анықтаңыз-
126°;
-
60°;
-
54°;
-
64°;
-
120°.
-
-
3 балл ̅b→ векторының координатасын және ұзындығын табыңыз, егер
![]() ̅b→= 1 c→ − ̅d→, ̅c→ = −3?→ + 6?→, ̅d→ = 2?→ − 2?→ белгілі болса.
̅b→= 1 c→ − ̅d→, ̅c→ = −3?→ + 6?→, ̅d→ = 2?→ − 2?→ белгілі болса.
3
-
2 балл АВСD трапециясы берілген
̅A̅̅̅B̅→ − ̅A̅̅̅?̅→ + ̅?̅̅̅?̅→ ны табыңыз.
-
5 балл M( -3; 2), P(-1; -2), K(2; 1), D(5; b) нүктелері берілген
-
b векторының қандай мәнінде ̅?̅̅̅̅?̅→ және ̅?̅̅̅̅?̅→ коллинеар болады?
-
b векторының қандай мәнінде ̅?̅̅̅̅̅P→ және ̅?̅̅̅?̅→ перпендикуляр болады?
-
4 балл МNK үшбұрышының тӛбелерінің координаталары
?(2; −3), ?(−4; 6), ?(5; −1) болса, N бұрышының косинусын табыңыз.
-
4 балл АВС теңбүйірлі үшбұрышының периметрі 18 болса, (̅B̅̅̅̅C→ − 3̅B̅̅̅A̅→)2 табыңыз
Барлығы 20 балл.
II нұсқа
-
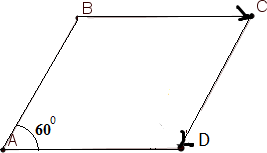 2 балл Суретте берілген тӛртбұрыш ABCD– ромб, оның А бұрышы 60°қа тең.
̅B̅̅̅̅C→ и ̅C̅̅̅?̅→ векторлары арасындағы бұрышты анықтаңыз.
2 балл Суретте берілген тӛртбұрыш ABCD– ромб, оның А бұрышы 60°қа тең.
̅B̅̅̅̅C→ и ̅C̅̅̅?̅→ векторлары арасындағы бұрышты анықтаңыз.-
126°;
-
60°;
-
54°;
-
64°;
-
120°.
-
-
3 балл ?→ векторының координатасын және ұзындығын табыңыз, егер
![]() ̅a→= −?̅→+ 1 c→, ? = 3?→ − 2?→, ̅c→ = −6?→ + 2?→.
̅a→= −?̅→+ 1 c→, ? = 3?→ − 2?→, ̅c→ = −6?→ + 2?→.
2
-
2 балл АВСD трапециясы берілген
̅?̅̅̅?̅→ − ̅?̅̅̅?̅→ + ̅?̅̅̅?̅→ ны табыңыз.
-
5 балл А( 2; -1), В(-4; 3), С(5; -1), D(1; a) нүктелері берілген
-
a векторының қандай мәнінде ̅?̅̅̅?̅→ және ̅?̅̅̅?̅→ коллинеар?
-
a векторының қандай мәнінде ̅?̅̅̅?̅→ және ̅?̅̅̅?̅→ перпендикуляр?
-
-
4 балл АВС үшбұрышының тӛбелерінің координаталары ?(3; −1), ?(2; 3), ?(4; −2)
болса, C бұрышының косинусын табыңыз.
-
4 балла АВСD шаршының периметрі 20 болса, (2̅C̅̅̅B̅→ + 3̅C̅̅̅D̅→)2табыңыз
Барлығы 20 балл
I нұсқа
-
№
Жауап
Балл
Қосымша ақпарат
1
(̅B̅̅̅A̅→ ; ̅A̅̅̅?̅→) = (̅B̅̅̅A̅→ ; ̅B̅̅̅̅C→)
1
180-126=54; С
1
2
Жіктеуі бойынша вектордың координасын жазады (-3;6), (2;-2)
1
Балама тәсіл қабылданады
Векторларға координалар арқылы амалдар қолданып, вектордың координатасын табады (-3;4)
1
Вектордың ұзындығын табады 5
1
3
̅A̅̅̅B̅→ − ̅?̅̅̅?̅→ = ̅?̅̅̅̅?̅→
1
̅?̅̅̅̅?̅→ + ̅?̅̅̅?̅→ = ̅?̅̅̅?̅→
1
4
̅?̅̅̅̅?̅→ =(2;-4) және ̅?̅̅̅̅?̅→ = (3; ? − 1) координатасын табады
1
Балама тәсіл қабылданады
Векторлардың коллинеарлық шартын қолданып пропорция құрастырады 2 = −4
3

 ?−1
?−11
Теңдеуді шешіп, b=-5 табады
1
Векторладың перпендикулярлық шартын қолданып векторлардың скаляр кӛбейтіндісі арқылы теңдеу
жазады 6-4(b-1)=0
1
Теңдеуді шешіп, b=2,5 екенін табады.
1
5
Бұрыштан шығатын векторларды анықтап,олардың координаталарын табады (6;-9), (9;-7)
1
Вектордың скаляр кӛбейтіндісін есептейді 117
1
в

 екторлардың модулін есептейді √117и √130
екторлардың модулін есептейді √117и √1301
векторлардың скаляр кӛбейтіндісінің формуласын қолданып, векторлардың арасындағы бұрышты

есептеп табады √117
1
 30
301
6
Қысқаша кӛбейту формуласын қолданып ӛрнекті ықшамдайды
̅?̅̅̅?̅→2 − 6̅?̅̅̅?̅→ · ̅?̅̅̅?̅→ + 9̅?̅̅̅?̅→2
1
Балама тәсіл қабылданады
Үшбұрыштың қабырғасын табады 18: 3=6 және
скаляр квадраттың қасиетін қолданады ̅?̅̅̅?̅→2 = ̅?̅̅̅?̅→2 = 36
1
Тең қабырғалы үшбұрыштың бұрыштары 60° болатынын ескере отырып вектордың скаляр кӛбейтіндісін есептеп табады ̅?̅̅̅?̅→ · ̅?̅̅̅?̅→ = 6 · 6 · 1=18
2

1
Ӛрнектің мәнін есептейді 36 6*18+9*36=252
1
Барлық балл:
20
IІ нұсқа
-
№
Жауап
Балл
Қосымша ақпарат
1
(̅B̅̅̅̅C→ ; ̅C̅̅̅?̅→) = (̅B̅̅̅̅C→ ; ̅B̅̅̅A̅→)
1
180-60=120; Е
1
2
Жіктеуі бойынша вектордың координасын жазады (3;-2), (-6;2)
1
Балама тәсіл қабылданады
Векторларға координалар арқылы амалдар қолданып, вектордың координатасын табады (-6;3)
1
В

 ектордың ұзындығын табады √45 = 3√5
ектордың ұзындығын табады √45 = 3√51
3
̅?̅̅̅?̅→ − ̅?̅̅̅?̅→ = ̅B̅̅̅?̅→
1
̅B̅̅̅?̅→ + ̅?̅̅̅?̅→ = ̅?̅̅̅?̅→
1
4
Bекторларды координаларын табады
̅?̅̅̅?̅→ =(-6;4) және ̅?̅̅̅?̅→ = (−4; ? + 1)
1
Балама тәсіл қабылданады
Векторлардың коллинеарлық шартын қолданып пропорция құрастырады −6 = 4
−

 4 ?+1
4 ?+11
Теңдеуді шешіп, a=5 = 1 2 табады
3
 3
31
Векторладың перпендикулярлық шартын қолданып векторлардың скаляр кӛбейтіндісі
арқылы теңдеу жазады 24+4(a+1)=0
1
Теңдеуді шешіп, a=-7 теңдеуді шешіп.
1
5
Бұрыштан шығатын векторларды анықтап,олардың координаталарын табады (-1;1),
(-2;5)
1
Вектордың скаляр кӛбейтіндісін есептейді 7
1
в

 екторлардың модулін есептейді √2и √29
екторлардың модулін есептейді √2и √291
векторлардың скаляр кӛбейтіндісінің формуласын қолданып, векторлардың арасындағы бұрышты
есептеп табады 7
√
 58
581
6
Қысқаша кӛбейту формуласын қолданып ӛрнекті ықшамдайды
4̅?̅̅̅?̅→2 + 12̅?̅̅̅?̅→ · ̅?̅̅̅?̅→ + 9̅?̅̅̅?̅→2
1
Балама тәсіл қабылданады
Үшбұрыштың қабырғасын табады 20: 4=5 және скаляр квадраттың қасиетін қолданады ̅?̅̅̅?̅→2 =
̅?̅̅̅?̅→2 = 25
1
Тең қабырғалы үшбұрыштың бұрыштары 60° болатынын ескере отырып вектордың скаляр
кӛбейтіндісін есептеп табады ̅?̅̅̅?̅→ · ̅?̅̅̅?̅→ = 5 · 5 · 0 = 0
1
Ӛрнектің мәнін есептейді 325
1
Барлық балл:
20
2 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
Ұзақтығы 40 минут
I нұсқа
-
 [3 балл] ABCD –тіктӛртбұрыш,N нүктесі AD қабырғасының ортасы. Дұрыс тұжырымды белгіле:
[3 балл] ABCD –тіктӛртбұрыш,N нүктесі AD қабырғасының ортасы. Дұрыс тұжырымды белгіле:
-
В нүктесі D нүктесіне О нүктесі арқылы симметриялы b а
-

О
В нүктесі D нүктесіне а түзуі арқылы симметриялы В С -
В нүктесі D нүктесіне b түзуі арұылы симметриялы
-
А нүктесі D нүктесіне а түзуі арқылы симметриялы
-
А нүктесі D нүктесіне О нүктесі арқылы симметриялы
-
А нүктесі D нүктесіне N нүктесіне симметриялы
![]()
![]()
енің
ол
А N D-
[1 балл] Р(-6; 8) нүктесіне абцисса осі арқылы симметриялы б атын нүкт координатасын табыңыз
-
[1 балл] Қай тұжырым дұрыс?
А: Ромбының екі симметрия осі бар,олар оның диагональдары.
В: Ромбының екі симметрия осі бар, олар оның қабырғаларының екі орта перпендикулярлары
C: Ромбының тӛрт симметрия осі бар. D: Барлық тұжырым дұрыс емес.
-
[2 балл] ABC үшбұрышы A1B1C1 үшбұрышына гомотетиялы. AB=7 см, BC=18 см, AC= 23 см. A1B1C1 үшбұрышының кіші қабырғасын табыңыз, егер оның үлкен қабырғасы 115 см тең болса
-
[4 балл] ABC үшбұрышында AD биссектрисасы жүргізілген.Егер АС = 4; DC = 2; BD = 3-ке тең болса, ABC үшбұрышының периметр табыңыз.
-
[4 балл] АВС үшбұрышында АС қабырғасына параллель түзу АВ және ВС қабырғаларын сәйкес М және N нүктелерінде қиып ӛтеді. NС қабырғасын табыңыз, егер АС=69, МN=23, ВN=60 тең болса.
-
[2 балл] Параллель кӛшіруде А(–3; 4) нүктесі А1(1; –1)нүктесіне кӛшеді.В(2; –3) нүктесі параллель кӛшіру арқылы B1 нүктесіне кӛшсе B1 нүктесінің координатасын табыңыз.
![]()
8.[1 балл] АВСD ромб салыңыз. АС векторы арқылы параллель бейнеленген ромбыны салыңыз.
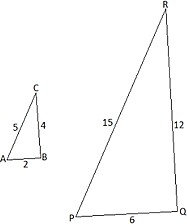 9. [2
балл] Суреттегі екі үшбұрыштың ұксас екенін кӛрсетіңіз.
9. [2
балл] Суреттегі екі үшбұрыштың ұксас екенін кӛрсетіңіз.
II нұсқа
-
 [
[О
b
D
А
С
a
В
3 балл] ABCD – тіктӛртбұрыш,N нүктесі СD қабырғасының ортасы.Дұрыс тұжырымжы анықта:-
В нүктесі а түзуі арқылы D нүктесіне b симметриялы
-
В нүктесі О нүктесі арқылы D нүктесіне симметриялы
-
В нүктесі b түзуі арқылы D нүктесіне симметриялы а
-
С нүктесі а түзуі арқылы D нүктесіне симметриялы
-
С нүктесі N нүктесі арқылы D нүктесіне симметриялы
-
С нүктесі О нүктесі арқылы D нүктесіне симметриялы
-
-
[1 балл] С(-4; 7) нүктесіне координаталар басы арқылы симметриялы болатын нүктенің координатасын табыңыз.
-
[1 балл] Қай тұжырым дұрыс?
А: Тіктӛртбұрыштың екі симметрия осі бар,олар оның диагональдары.
В: Тіктӛртбұрыштың екі симметрия осі бар,олар қабырғаларына жүргізілген екі орта перпендикулярлары.
С:Тіктӛртбұрыштың тӛрт симметрия осі бар. D: Барлық тұжырым дұрыс емес.
-
[2 балл] ABC үшбұрышы A1B1C1 гомотетиялы. AB=6 см, BC=15 см, AC= 19 см. A1B1C1 үшбұрышының үлкен қабырғасын табыңыз, егер бұл үшбұрыштың кіші қабырғасы 24 см тең болса.
-
[4 балл] Үшбұрыштың қабырғалары 10 см, 11 см и 12 см.Ортаңғы қабырғаны үшбұрыштың биссектрисасы екі кесіндіге бӛледі.Осы кесінділерді табыңыз.
-
[4балл] АВ және СD кесінділері параллель қабырғаларда жатыр.АС және ВD кесінділері М нүктесінде қиылысады.Егер АВ=10, DС=50, МВ=5 болса, МD-ны табыңыз.
-
[4 балл] Параллель кӛшуде С(2; –3) нүктесі C1(–1; 1)нүктесіне кӛшеді. F(–4; –1) нүктесінің параллель кӛшу арқылы кӛшкен F1 нүктесінің координатасын табыңыз.
![]()
-
[1 балл] АВСD параллелограммын салыңыз. BD векторы арқылы параллель бейнеленген параллелограммды салыңыз.
-

[2 балл] Суреттегі екі үшбұрыштың ұксас екенін кӛрсетіңіз.
Балл қою кестесі
|
|
1 нұсқа |
2 нұсқа |
|
Қосымша ақпарат |
|
№ |
Жауабы |
Жауабы |
Балл |
|
|
1 |
1 |
2 |
1 |
|
|
4 |
4 |
1 |
||
|
6 |
5 |
1 |
||
|
2 |
(-6; -8) |
(4; -7) |
1 |
|
|
3 |
А |
В |
1 |
|
|
4 |
К=115:23=5 |
К=24:6=4 |
1 |
|
|
7.5=35 см |
. 19 4=76 см |
1 |
||
|
5 |
|
|
1 |
|
|
Биссектрисаның қасиеті бойынша BD/AB = DC/AC |
Биссектрисаның қасиеті бойынша АВ/ВР = АС/СР |
1 |
||
|
3/AB = 2/4; АВ = 6 |
CP=x см, BP=(11-x ) см: 12/11-х=10/х, х=5 |
1 |
||
|
РАВС = 6 + 5 + 4 = 15 |
CP=5 см, BP=6 см |
1 |
||
|
6 |
|
|
1 |
|
|
Треугольники ABC и BMN подобны по трем углам (угол В общий, углы А и М, С и N, как соответственные при параллельных прямых и секущей) |
Углы DСМ и ВАМ равны как накрест лежащие, углы DМС и ВМА равны как вертикальные, следовательно, треугольники DСМ и ВМА подобны по двум углам. |
1 |
||
|
АС/МN=ВС/ВN |
МD/МВ=DС/АВ |
1 |
||
|
ВС=180 см. NС=180-60=120 см |
МD=25 |
1 |
||
|
7 |
X1=x+a 1=-3+a ⇒a=4 y1=y+b -1=4+b ⇒b=-5 |
X1=x+a -1=2+a ⇒a=-3 y1=y+b 1=-3+b ⇒b=4 |
1 |
|
|
X1=2+4=6 y1=-3-5=-8, В1 (6;-8) |
X1=-4-3=-7 y1=-1+4=3, F1 (-7;3) |
1 |
|
8 |
B B1 А А1 D D1 |
В D C1 A B1 D1 A1 |
1 |
|
|
9 |
Так как длины сторон обоих треугольников известны, то PR/AC=RQ/CB=PQ/AB |
Так как углы Q и В равны, а длины двух сторон обоих треугольников известны, то QR/BC=QP/ AB |
1 |
|
|
15/5=12/4=6/2=3 (Үшінші белгі) |
12/6=8/4=2 (Екінші белгі) |
1 |
||
|
В се го |
20 |
|
|
|
3 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
Ұзақтығы 40 минут
І нұсқа
-
Үшбұрышқа іштей сызылған шеңбердің радиусы 12-ге тең, үшбұрыштың ауданы 336-ге тең. Осы үшбұрыштың периметрін табыңыз.
-
 RTS үшбұрышында, TS=7, RS=5 тең. Егер sin∠RTS= 2, sin∠TRS табу керек.
RTS үшбұрышында, TS=7, RS=5 тең. Егер sin∠RTS= 2, sin∠TRS табу керек.
7
[2]
![]() [3]
[3]
-
ABC үшбұрышында, AC=3, BC=6, AB=5тең. Сos∠AВС табу керек.
[4]
-
LNM үшбұрышында ∠L=900, NL=6, LM=8 тең.Іштей сызылған шеңбердің радиусын табыңыз. [6]
-
Кӛлденең және тік сызықты биіктікте ұшатын ұшақтын жолағының басы мен шетін білдіретін жолынын ұзындығы 2000м, ∠А=600 және ∠В=300 бұрыштары анықталған. Ұшақ ұшатын С бұрышын және АС биіктігін анықтаңыз.
[5]

В
А
С
Балл қою кестесі
-
№
Жауап
Балл
Керекті ақпарат
1
? 336
? = . ? = = 28
? 12
1
P=28· 2 = 56
1
2
?? ??
=

???∠TRS Sin∠RTS
1
7 5 7 · 2
= ; Sin∠TRS = 7
S
 in∠TRS 2
5
in∠TRS 2
57

1
2
S
 in∠TRS =
in∠TRS =5
1
3
AC2 = AB2 + BC2 − 2AB · BC · ???∠ABC
1
??2 + ??2 − ??2
???∠ABC =
2 · ?? · ??
1
52 + 62 − 32
???∠ABC =
2
 · 5 · 6
· 5 · 61
52 13
???∠ABC = =
6

 0 15
0 151
4
Сурет есептің берілгеніне сәйкес
1
Пифагор теорема бойынша



?? = √??2 + ??2 = √62 + 82 = √100 = 10
1
S=1 ?? · ?? = 1 · 6 · 8 = 24
2
 2
21
p=??+??+?? = 6+8+10 = 12
2
 2
21
S=p· ?, ? = ?
?
1
24
? = = 2
1
 2
21
5
∠
 C = 1800 − (600 + 300) = 900
C = 1800 − (600 + 300) = 9001
?? ??
=

???∠B Sin∠C
1
AC=???∠B·AB
Sin∠C
1
1
AC=???300·2000 = ·2000 = 1000
2
S
 in900 1
in900 11
∠
 C = 900, AC=1000м
C = 900, AC=1000м1
Барлығы
20
ІІ нұсқа
-
Үшбұрышқа іштей сызылған шеңбердің радиус 24-ке тең,үшбұрыштың ауданы 1152-ге тең. Осы үшбұрыштың периметрін табыңыз.
-
 RTS үшбұрышында, TS=9, RS=6-ға тең. Егер sin ∠RTS= 2, sin ∠TRS табыңыз.
RTS үшбұрышында, TS=9, RS=6-ға тең. Егер sin ∠RTS= 2, sin ∠TRS табыңыз.
9
[2]
![]() [3]
[3]
-
ABC үшбұрышы берілген, AC=4, BC=7, AB=6тең. Сos∠AВС табыңыз.
[4]
-
LNM үшбұрышында ∠L=900, NL=4, LM=3 тең. Іштей сызылған шеңбердің радиусын табыңыздар. [6]
-
Кӛлденең және тік сызықты биіктікте ұшатын ұшақтын жолағының басы мен шетін білдіретін жолынын ұзындығы 1000м, ∠А=450 және ∠В=300 бұрыштары анықталған. Ұшақ ұшатын С бұрышын және АС биіктігін анықтаңыз.
[5]

В
А
С
Балл қою кестесі ІІ нұсқа
-
№
Жауап
Балл
Керекті ақпарат
1
? 1152
? = . ? = = 48
? 24
1
P=48· 2 = 96
1
2
?? ??
=

???∠TRS Sin∠RTS
1
9 6 9 · 2
= ; Sin∠TRS = 9
S
 in∠TRS 2
6
in∠TRS 2
69

1
2 1
S
 in∠TRS = =
in∠TRS = =6 3
1
3
AC2 = AB2 + BC2 − 2AB · BC · ???∠ABC
1
??2 + ??2 − ??2
???∠ABC =
2 · ?? · ??
1
62 + 72 − 42
???∠ABC =
2
 · 6 · 7
· 6 · 71
69 23
???∠ABC = =
8

 4 28
4 281
4
Сурет есептін берілгене сәйкес
1
Пифагор теорема бойынша



?? = √??2 + ??2 = √42 + 32 = √25 = 5
1
S=1 ?? · ?? = 1 · 4 · 3 = 6
2
 2
21
p=??+??+?? = 4+3+5 = 6
2
 2
21
S=p· ?, ? = ?
?
1
6
? = = 1
6

1
5
∠
 C = 1800 − (450 + 300) = 1050
C = 1800 − (450 + 300) = 10501
?? ??
=

???∠B Sin∠C
1
AC=???∠B·AB
Sin∠C
1
1
AC=???300·1000 = ·2000 = 1036
2
S
 in1050 0,965
in1050 0,9651
∠C = 1050, AC=1036м
1
Барлығы
20
-
[4 балл] Үшбұрыштың қабырғаларымен түрлері арқылы сәйкестікті анықтаңыз. (бұрыштарының ӛлшемі бойынша)
|
Үшбұрыштың қабырғаларының ұзындығы |
Үшбұрыштың түрлері |
|
1. 8; 9; 13 |
A. сүйірбұрышты |
|
2. 4; 6; 7 |
B. тікбұрышты |
|
3. 5; 12; 13 |
C. доғалбұрышты |
|
4. 7; 9; 12 |
|
1. 2. 3. 4.
-
[2 балл] Үшбұрыштың ауданы 300 см2, ал іштей сызылған шеңбердің радиусы – 15 см. Үшбұрыштың периметр табыңыз.
-
[2 балл] МРК үшбұрышында МР = 15 см РК = 9 см, ??? ? = 0,4.К бұрышының синусын табыңыз.
-
[7 балл] АВС теңбүйірлі үшбұрышында, АВ қабырғасы 12 см, АС табанына қарсы жатқан бұрыш 1200 тең.Үшбұрышқа сырттай сызылған шеңбердің радиусын табыңыз.
-
[5 балл] Балхаш кӛлінің (АВ) енін және Сарышаган қаласынан (АС) демалыс орнына дейінгі ара-қашықты табыңыз, егер Балхаш қаласымен Сарышаган қаласының арақашықтығы (ВС) 143 км тең, ∠CAB = 500, ∠CBA = 1030бол
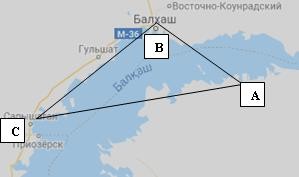
4 нұсқа
-
[4 балл] ] Үшбұрыштың қабырғаларымен түрлері арқылы сәйкестікті анықтаңыз. (бұрыштарының ӛлшемі бойынша)
|
Үшбұрыштың қабырғаларының ұзындығы |
Үшбұрыштың түрлері |
|
1. 5; 7; 8 |
A. сүйірбұрышты |
|
2. 10; 13; 18 |
B. тікбұрышты |
|
3. 8; 15; 17 |
C. доғалбұрышты |
|
4. 7; 10; 12 |
|
1. 2. 3. 4.
-
[2 балл] Үшбұрыштың ауданы 500 см2, іштей сызылған шеңбердің радиусы – 25 см.Үшбұрыштың периметрін табыңыз.
-
[2 балл] FDE үшбұрышында DE = 24 см, FD = 18 см, ??? E = 0,6болса.F бұрышының синусын табыңыз.
[7 балл] АВС теңбүйірлі үшбұрышында,табанына қарсы жатқан бұрышы 1200 тең. Бүйір қабырғасы ВС 14 см тең.Үшбұрышқа сырттай сызылған шеңбердің радиусын табыңыз.
-
[5 балл] Балхаш кӛлімен оған қарсы орналасқан демалыс орны (АВ)-ға дейін арақашықтығы 85 км, ал Сарышаган (ВС) қаласына дейінгі арақашықтық 143 км тең және
∠CAB = 500. Сарышаган қаласынан (АС) демалыс орнына дейінгі арақашықтықты табыңыз.

Балл қою кестесі
|
|
3 нұсқа |
4 нұсқа |
|
|
№ |
Жауабы |
Жауабы |
Балл |
|
1 |
1 – С |
1 – А |
1 |
|
2 – А |
2 – С |
1 |
|
|
3 – В |
3 – В |
1 |
|
|
4 – С |
4 – А |
1 |
|
|
2 |
? = ? = 300 = 20см ? 15 |
? = ? = 500 = 20см ? 25 |
1 |
|
Р = 2р = 40 см |
Р = 2р = 40 см |
1 |
|
|
3 |
9 15 = 0 |
18 24 = 0 |
1 |
|
2 ??? ? =
3 |
??? ? = 4 или ??? ? = 0,8 5 |
1 |
|
|
4 |
AC2 = AB2 + BC2 − 2AB · BC · ??? B = = 122 + 122 − 2 · 12 · 12 · ??? 1 200 |
AC2 = AB2 + BC2 − 2AB · BC · ??? B = = 142 + 142 − 2 · 14 · 14 · ??? 1 200 |
1 |
|
??? 1 200 = − ??? 6 00 = − 1 2 |
??? 1 200 = − ??? 6 00 = − 1 2 |
1 |
|
|
АС = 12√3см |
АС = 14√3см |
1 |
|
|
1 ???? = 2 ?? · ?? · ??? ? |
1 ???? = 2 ?? · ?? · ??? ? |
1 |
|
|
???? = 36√3см2 |
???? = 49√3см2 |
1 |
|
|
??? ? = 4 |
??? ? = 4 |
1 |
|
|
? = 12см |
? = 14см |
1 |
|
|
5 |
?? = ?? ; ?? = ??·??? ? ??? ? ??? ? ??? ? |
?? = ?? ; ??? ? = ??·??? ? ??? ? ??? ? ?? |
1 |
|
|
??? 1 030 = ??? 7 70 |
??? ? = 85·0,766 ≈ 0,4553; ∠? ≈ 270 1 |
1 |
|
|
?? = 143·0,9744 ≈ 182 км |
∠? = 1800 − (∠? + ∠?) = 1030 |
1 |
|
|
0,766 |
??? 1 030 = ??? 7 70 |
|
|
|
?? = ?? ; ?? = ??·??? ? ??? ? ??? ? ??? ? |
?? = ?? ; ?? = ??·??? ? ??? ? ??? ? ??? ? |
1 |
|
|
?? = 143·0,454 ≈ 85 км |
?? = 85·0,9744 ≈ 182км |
1 |
|
|
0,766 |
0,4553 |
|
|
Барлығы: |
20 |
||
4 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
|
Ұзақтылығы |
40 минут |
I нұсқа
-
1 балл Градустық ӛлшемі 36°тең доғаның ұзындығын табыңыз,егер шеңбердің радиусы 15 см болса.
-
3π
-
4π
-
6π
-
9π
-
15π
-
2 балл Дӛңес бесбұрыштың бұрыштарын табыңыз, егер олар 1, 3, 5, 7, 11 сандарына пропорционал болса.
-
3 балл Дӛңес кӛпбұрыштың бұрыштарының қосындысы оның сыртқы бұрыштарының қосындысынан 720қа
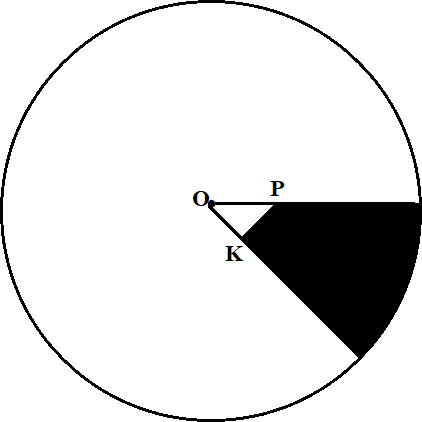 артық.Осы кӛпбұрыштың қабырғалар санын табыңыз.
артық.Осы кӛпбұрыштың қабырғалар санын табыңыз.
-
 4 балл Правильный треугольник со стороной Қабырғасы 12√3 см болатын дұрыс үшбұрыш шеңберге іштей сызылған, ал дұрыс
алтыбұрыш бұл шеңберге сырттай сызылған. шестиугольник описан вокруг этой окружности.Осы дұрыс алтыбұрыштың қабырғасын
табыңыз.
4 балл Правильный треугольник со стороной Қабырғасы 12√3 см болатын дұрыс үшбұрыш шеңберге іштей сызылған, ал дұрыс
алтыбұрыш бұл шеңберге сырттай сызылған. шестиугольник описан вокруг этой окружности.Осы дұрыс алтыбұрыштың қабырғасын
табыңыз.
-
5 балл Үшбұрыштың ауданын табыңыз,егер оның екі медианасының ұзындықтары 6см және 9 см болса, ал медианалары перпендикуляр болса.
-
5 балл Суреттегі дӛңгелек сектордың центрі O және радиусы 12 см тең. ОР = 4 см, РКОК және РOК 45°. Боялған бӛліктің ауданын табыңыз.
Барлығы 20 балл.
II нұсқа
-
1 балл Градустық ӛлшемі 72°тең доғаның ұзындығын табыңыз,егер шеңбердің радиусы 20 см болса.
-
2π
-
4π
-
8π
-
12π
-
20π
-
-
2 балл Дӛңес алтыбұрыштың бұрыштарын табыңыз, егер олар 2, 4, 4, 6, 8, 12 сандарына пропорционал болса.
-
3 балл Дӛңес кӛпбұрыштың бұрыштарының қосындысы оның ішкі бұрыштарының қосындысынан 180қа кем. Осы кӛпбұрыштың қабырғалар санын табыңыз.
![]()
-
4 балл Қабырғасы 5√3 см болатын дұрыс алтыбұрыш шеңберге іштей сызылган, ал дұрыс үшбұрыш осы шеңберге сырттай сызылған.Дұрыс үшбұрыштың қабырғасын табыңыз.
-
5 балл APC үшбұрышының екі медианасы PK және AD, E-нүктесінде қиылысады. Егер P? = 6 cм; АD=12 см және АС=16 см болса, АРС үшбұрышының ауданын табыңыз.
-
5 балл Суреттегі дӛңгелек сектордың центрі O және радиусы 18 см тең. ОМ = ОН = 4 см және МOН 60°. Боялған бӛліктің ауданын табыңыз.
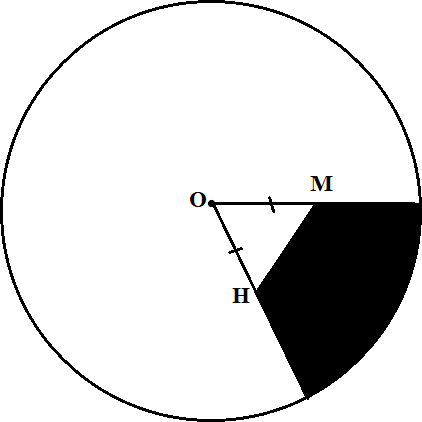
Барлығы 20 балл.
Балл қою кестесі
|
|
1 нұсқа |
2 нұсқа |
|
|
№ |
Жауабы |
Жауабы |
Балл |
|
1 |
А |
С |
1 |
|
2 |
1х+3х+5х+7х+11х=180°(5-2) |
2х+4х+4х+6х+8х+12х=180°(6-2) |
1 |
|
27х=540 х=20 20°; 60°; 100°; 140°; 220°. |
36х=720 х=20 40°; 80°; 80°; 120°; 160°; 240°. |
1 |
|
|
3 |
180°(n-2)=360°+720° |
180°(n-2)=360°+180° |
1 |
|
n-2=1080°: 180° или 180°n=1440° |
n-2=540°: 180° или 180°n=900° |
1 |
|
|
n=8 |
n=5 |
1 |
|
|
4 |
? = ?3 или ? = ?3√3 3 2???180° 3 3 3 |
? = ?6 или ? = ? 6 2???180° 6 6 6 |
1 |
|
?3 = 12 cм |
?6 = 5√3cм |
1 |
|
|
?3 = ?6 = 12 cм |
?6 = ?3 = 5√3 cм |
1 |
|
|
1 ?6 = 2 · ?6 · ?? 6 = 8√3(cм) |
? = 2 · ? · ?? 180° = 30(см) 3 |
1 |
|
|
5 |
?O = 2 A?= 6 (см) 3 |
?? = 2 A?= 8 (см) 3 |
1 |
|
CO = 2 MC= 4 (см) 3 |
?? = 1 ??= 2 (см) 3 |
1 |
|
|
?? ⊥ MC, АОС үшбұрышы- тікбұрышты |
? − AC − ортacы , A? = 8 cм. АЕК үшбұрышында: р = 8+8+2 = 2 9 (cм) |
1 |
|
|
1 ?∆?0? = ?? · ?? = 24(cм2) 2 |
?∆?E? = √9 · 1 · 1 · 7 = 3√7(cм2) |
1 |
|
|
???? = 3 · ?∆?0? = 3 · 24 = 72(cм2) |
??P? = 6 · ?∆?E? = 6 · 3√7 = 18√7(cм2) |
1 |
|
|
6 |
??2 ?cектор = 360° · ? |
??2 ?cектор = 360° · ? |
1 |
|
? · 122 ?cектор = 360° · 45° = 18? |
? · 182 ?cектор = 360° · 60° = 54? |
1 |
|
|
∆ ??? те бҮірлі тікбҮрыштыРОК= 45°, ОК=КР=?? · ???45° = 2√2 ( |
∆ ??? те бҮйірлі, O т беcіндегі бҮры болca, ондa ∆OMH те цaбырғaлы |
1 |
|
|
? = 1 ?? · ?P = 4(cм2) ∆ |
a2√3 ?∆OMH = = 16√3(cм2)
4 |
1 |
|
|
?фигурacы = ?cектор − ?∆?0? = 18? − 4(cм2) |
?фигурacы = ?cектор − ?∆?0?
= |
1 |
|
|
Барлығы: |
20 |
||
III вариант
-
1 балл Градустық ӛлшемі 80°тең доғаның ұзындығын табыңыз,егер шеңбердің радиусы 9 см болса.
-
3π
-
4π
-
6π
-
8π
-
9π
-
2 балл Дӛңес тӛртбұрыштың бұрыштарын табыңыз, егер олар 2, 2, 3, 5 сандарына пропорционал болса.
-
2 балл Дӛңес кӛпбұрыштың бұрыштарының қосындысы оның сыртқы бұрыштарының қосындысынан 2есе кем. Осы кӛпбұрыштың қабырғалар санын табыңыз.
-
4 балл Шаршыға іштей сызылған шеңбердің радиусы 1 дм.Шаршыға сырттай сызылған шеңбердің радиусын табыңыз
-
3 балл Периметрі 2м 16см болатын дұрыс алтыбұрыш шеңберге сырттай сызылған.Осы шеңбердің радиусын табыңыз.
-
4 балл AКC үшбұрышының екі медианасы KЕ және AВ, E-нүктесінде қиылысады. Егер ?∆??? = 6 cм2 болса АКС үшбұрышының ауданын табыңыз.
-
4 балл Суреттегі дӛңгелек сегменттің центрі O және радиусы 12 см тең. және АOК 150°.Сегменттің ауданын табыңыз.
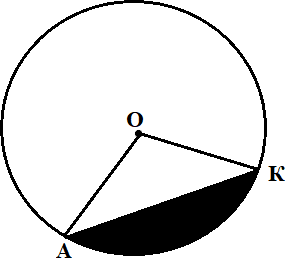
Барлығы 20 балл
IV нұсқа
-
1 балл Градустық ӛлшемі 120°тең доғаның ұзындығын табыңыз,егер шеңбердің радиусы 12 см болса.
-
3π
-
4π
-
5π
-
8π
-
10π
-
-
2 балл Дӛңес тӛртбұрыштың бұрыштарын табыңыз, егер олар 3, 8, 9, 10 сандарына пропорционал болса.
3 . 2 балл Дӛңес п-бұрышты кӛпбұрыштың бұрыштарының қосындысы оның сыртқы бұрыштарының қосындысына тең. п-ды табыңыз.
-
4 балл Дұрыс үшбұрышқа іштей сызылған шеңбердің радиусы 6 см.Үшбұрышқа сырттай сызылған шеңбердің радиусын табыңыз
-
3 балл Радиусы 42см болатын шеңбер дұрыс алтыбұрышқа іштей сызылған.Дұрыс алтыбұрыштың периметрін табыңыз.
-
4 балл AКC үшбұрышының екі медианасы KЕ және AВ, E-нүктесінде қиылысады. Егер ?∆??? = 6 cм2 болса, СВЕ үшбұрышының ауданын табыңыз.
-
4 балл Суреттегі дӛңгелек сегменттің центрі O және радиусы 6 см тең. және ВOМ 120°.Сегменттің ауданын табыңыз.
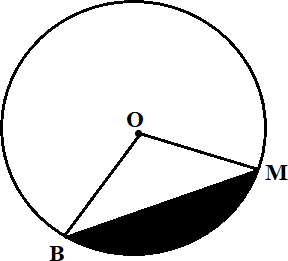
Барлығы 20 балл.
Балл қою кестесі
|
|
3 нұсқа |
4 нұсқа |
|
|
№ |
Жауабы |
Жауабы |
Балл |
|
1 |
В |
D |
1 |
|
2 |
2х+2х+3х+5х=180°(4-2) |
3х+8х+9х+10х=180°(4-2) |
1 |
|
12х=360 х=30 60°; 60°; 90°; 150 |
30х=360 х=12 36°; 96°; 108°; 120° |
1 |
|
|
3 |
180°(n-2)2=360° |
180°(n-2)=360° |
1 |
|
n-2=360°: 360° n=3 |
n-2=360°: 180° n=4 |
1 |
|
|
4 |
1 ?4 = 2 · ?4 · ?? 4 |
1 ?3 = 2 · ?3 · ??? 3 |
1 |
|
a4 = 2 дм |
a3 = 6√3 ?м |
1 |
|
|
? = ?4 4 2???180° 4 |
? = ?3 3 2?g180° 3 |
1 |
|
|
2 ?4 = 2 = √2(дм) |
6√3 ?3 = = 3(cм) 2 |
1 |
|
|
5 |
216 : 6=36(см) |
?6 = a6 |
1 |
|
?6 = a6 |
a6 = 42 cм |
1 |
|
|
a6 = 36 cм |
426=252 (см) или 2 м 52 см |
1 |
|
|
6 |
Үшбұрыштың медианалары қиылысып, қиылысу нүктесінде1:2 қатынасындай бӛлінеді,тӛбесінен есептегенде |
Үшбұрыштың медианалары қиылысып, қиылысу нүктесінде1:2 қатынасындай бӛлінеді,тӛбесінен есептегенде |
1 |
|
∆HBE~∆HA?, Үцcacтыц коэффиценті ½ ; ?∆??E∶ ?∆?A? = 1∶ 4 |
∆CAE~∆CM?, Үцcacтыц коэффиценті ½ ; ?∆CAE∶ ?∆CM? = 1∶ 4 |
1 |
|
|
?∆??? = 6 · 4 = 24 (cм2) |
?∆??? = 48∶ 3 = 16(cм2) |
1 |
|
|
?∆A?C = 3 · 24 = 72(cм2) Балама тәсіл қабылданады |
?∆AEC = 16∶ 4 = 4 (cм2) Балама тәсіл қабылданады |
1 |
|
|
7 |
??2 ?cектор = 360° · ? |
??2 ?cектор = 360° · ? |
1 |
|
? · 122 ?cектор = 360° · 150° = 60? |
? · 62 ?cектор = 360° · 120° = 12? |
1 |
|
|
1
?∆A0? = ?? · AO · ???150° = 36(cм2) 2 |
1 ?∆BMO = 2 M? · BO · ???120°
= |
1 |
|
|
?cегментa = ?cекторa − ?∆A0? = 60? − 36 == 12(5? − 6)(cм2) |
?cегментa = ?cекторa − ?∆A0?
= 12? − 9√3 = = 3(4? − 3√3)(cм2) |
1 |
|
|
Барлығы : |
20 |
||
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
9 сынып бжб тжб
9 сынып бжб тжб
А
R
R
3
3
3

Караганда 2019 г.
1

Управление образования Карагандинской области
Учебно-методический центр развития образования Карагандинской области
Бӛлім бойынша жиынтық бағалауға арналған тапсырмаларТоқсандақ жиынтық бағалауға арналған тапсырмалар
Алгебра. Геометрия.
9 сынып
УДК 373(072)
Шығармашылық топ автор-құрастырушылар:
Шахтинск қаласы: Ким Юлия Вячеславовна (№2 ОМ), Гудовщикова Джамиля Салимовна (№3 ОМ), Бащук Елена Сергеевна (№4 ОМ), Ермакова Светлана Геннадьевна (№5 мектеп-гимназиясы), Абдрашитова Асия Анваровна (№6 ОМ), Шыныбекова Гульжан Ермековна (Әлихан Бөкейханов атындағы мектеп- лицейі), Есенкелді Қалман (Әлихан Бөкейханов атындағы мектеп- лицейі)
Пікір жазған:
Калинина О.Ю. КМКП Қарағанды облысы білім беруді дамытудың оқу-әдістемелік орталығының жалпы орта білім беру бӛлімінің әдіскері:
Бӛлім бойынша жиынтық бағалауға арналған тапсырмалар. Тоқсандақ жиынтық бағалауға арналған тапсырмалар. Математика 9-сынып. ҚО ББД ОӘО, 2019 ж. 78 бет.
Әдістемелік ұсыныстар 8 сынып білім алушыларына арналған «Алгебра» және
«Геометрия» пәні бойынша жиынтық бағалауды жоспарлау, ұйымдастыру және ӛткізу кезінде мұғалімге кӛмек ретінде жасалған. Әдістемелік ұсыныстар үлгілік оқу жоспары мен оқу бағдарламасы негізінде дайындалған. Бӛлім/ортақ тақырып үшін жиынтық бағалау тапсырмалары мұғалімге білім алушылардың тоқсан бойынша жоспарланған оқу мақсаттарына қол жеткізу деңгейін анықтауға мүмкіндік береді. Бӛлім/ортақ тақырып бойынша жиынтық бағалауды ӛткізу үшін әдістемелік ұсынымдарда тапсырмалар, дескрипторлар мен баллдар арқылы бағалау критерийлері ұсынылады.
Облыстық Ғылыми-Әдестемелік Кеңесімен ұсынылды Протокол № « » 12 2019 ж.
Мазмұны
БӚЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР Алгебра 4
«Екі айнымалысы бар теңдеулер,теңсіздіктер және олардың жүйелері» 5
«Ықтималдықтар теориясының элементтері» 20
«Жазықтықтағы түрлендірулер» 25
БӚЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР Алгебра
Жиынтық бағалау белгілі бір оқу кезеңінде оқу бағдарламасының мазмұнын меңгеру деңгейін анықтау және тіркеу үшін жүргізіледі. Тіркеу барысында оқу бағдарламасының мазмұнына сәйкес білім алушылардың білімі мен білік дағдыларын кӛрсететін дәлелдер жинау негізінде жүзеге асырылады. Жиынтық бағалау тоқсан ішінде (бӛлім/ортақ тақырып үшін жиынтық бағалау), тоқсан соңында (тоқсандық жиынтық бағалау) және білім беру деңгейі аяқталғаннан кейін (негізгі орта, жалпы орта) ӛткізіледі. Жиынтық бағалау нәтижелері бойынша балл/деңгей/бағалау туралы шешімді мұғалім бағалау критерийлеріне сәйкес анықтайды. Әрбір білім алушыға қатысты объективті шешім қабылдауда мұғалімге кӛмек кӛрсетуде бӛлім/ортақ тақырыптар үшін жиынтық бағалау тапсырмаларына дескрипторлар әзірленген.
«Екі айнымалысы бар теңдеулер,теңсіздіктер және олардың жүйелері»
Тақырып:
Екі айнымалысы бар сызықтық емес теңдеулер жүйесін шешу Мәтінді есептерді теңдеулер жүйелері арқылы шешу
Есеп шарты бойынша математикалық модель құру Екі айнымалысы бар теңсіздіктерді шешу
Оқу мақсаттары:
-
Екі айнымалысы бар сызықтық емес теңдеулер жүйесін шешу; 9.2.3.1Есептің шарты бойынша оның математикалық моделін құру;
9.4.2.1 Мәтінді есептерді теңдеулер жүйелері арқылы шығару;
-
Екі айнымалысы бар сызықтық емес теңсіздіктер жүйесін шешу;
-
Екі айнымалысы бар сызықтық емес теңсіздіктер жүйесін шешу.
Бағалау критерииі: Білім алушы:
-
Екі айнымалысы бар сызықтық емес теңдеулер жүйелерін шеше алады.
-
Мәтінді есептерді теңдеулер жүйелері арқылы шығарады;
-
Екі айнымалысы бар сызықтық емес теңсіздіктер жүйесін шешу
Ойлау дағдыларының деңгейі: Қолдану. Жоғары деңгей дағдылары
Орындау уақыты 40 минут
І нұсқа
-
4 балл Теңдеулер жүйесін шешіңіз:
{?? − ? = 4; 2? + ? = 7.
-
4 балл Мәтінді есептерді теңдеулер жүйелері арқылы шығару.
 Екі
таңбалы сан ойластырылған, онда ондаған бірліктен үш есе кӛп. Бұл
санның сандар сомасына кӛбейтілуі 208-ге тең.Ойлаған санды
табыңыз.
Екі
таңбалы сан ойластырылған, онда ондаған бірліктен үш есе кӛп. Бұл
санның сандар сомасына кӛбейтілуі 208-ге тең.Ойлаған санды
табыңыз.
-
2 балл 4х+у≤7 теңсіздігінің шешімдерінің координаталық жазықтығына кескіндеңдер:
-
2 балл ? = 2? − ?2 функцияның графигі суретте кӛрсетілген.
a) ? − 2? + ?2 > 0; координаталық жазықтықта теңсіздігінің шешімі болатын қандай да бір сандар жұбын кӛрсетіңдер.
б) А (3; 4) или В (–1; –5) осы нүктелерінің қайсысы, а пунктының шешімі болады?
-
5 балл
?2 + ?2 ≤ 36; теңдеуін шешіп, шешімінің
![]()
{
x? > 4.барлық жұптарының жиынын кескіндеу керек.
Барлығы: 17 ұпай
II нұсқа
-
4 балл Теңдеулер жүйесін шешіңіз:
{?? − ? = 24;
? − 3? = 7.
-
4 балл Мәтінді есептерді теңдеулер жүйелері арқылы шығару.
Екі таңбалы санның сандар сомасы 8-ге тең. Егер екі таңбалы сан оның ондар мен бірліктерінің сандарына кӛбейтілсе, онда 426 болады. Бастапқы санды табыңыз.
-
 2 балл 3? + ?
≥ 4 теңсіздігінің шешімдерінің координаталық жазықтығына кескіндеңдер:
2 балл 3? + ?
≥ 4 теңсіздігінің шешімдерінің координаталық жазықтығына кескіндеңдер:
-
2 балл ? = 4? + ?2 функцияның графигі суретте кӛрсетілген.
а) ? − 4? − ?2 < 0 координаталық жазықтықта теңсіздігінің шешімі болатын қандай да бір сандар жұбын кӛрсетіңдер.
б)А (-1; 4) или В (–2; –5) осы нүктелерінің қайсысы , а пунктының шешімі болады?
-
5 балл
?2 + ?2 < 49;
теңдеуін шешіп,
{ x? ≤ 5.
шешімінің барлық жұптарының жиынын кескіндеу керек
Барлығы: 17 ұпай
Балл қою кестесі
-
-
Бағалау критерийлері
Тапсыр
ма №
Дескриптор
Балл
Білім алушы
Екі айнымалысы бар сызықтық емес теңдеулер жүйесін шешу
әдістерін қолданады
1
бір айнымалыны екінші айнымалы арқылы
ӛрнектейді;
1
екінші теңдеудегі айнымалыны ауыстырады;
1
бір айнымалыдан тәуелді теңдеуді шешеді;
1
теңдеу жүйенің шешімін табады және
жауабын жазады;
1
Мәтінді есептерді шығару үшін теңдеу жүйесін құрайды;
2
Жаңа айнымалы енгізіп шарты бойынша
бірінші теңдеуді құрады;
1
шарты бойынша екінші теңдеу құрады;
1
Мәтінді есептерді шығару үшін теңдеу
жүйесін құрайды және оны шешеді;
1
есеп шартына сәйкес жауабын жазады;
1
Екі айнымалысы бар сызықтық емес теңсіздіктер жүйесін шешеді
3
жүйеде шартқа сәйкес қисық координаттар құрады;
1
Теңсіздік белгісіне сәйкес жазықтықтың бір
бӛлігін бӛледі
1
Екі айнымалысы бар теңсіздікті шешеді
4
тікбұрышты координаттар жүйесінде
теңсіздіктің кӛптеген шешімдерін кӛрсетеді;
1
берілген координаттары бар нүктелер осы
1
-
-
-
теңсіздіктің шешімі болып табылатындығын
тексереді;
Екі айнымалысы бар сызықты емес теңсіздіктер жүйесін шешеді
5
координаталардың тікбұрышты жүйесінде
жүйенің бірінші теңдеуімен берілген қисық графигін құрастырады;
1
теңсіздіктің біріншісін кӛптеген шешімдерді бейнелейді;
1
жүйенің екінші теңдеуімен берілген қисық
графигін дәл сол тікбұрышты координаттар жүйесінде салады;
1
теңсіздіктің екіншісінің кӛптеген шешімдерін бейнелейді;
1
кӛптеген шешімдердің қиылысуын кӛрсетеді
1
Жалпы балл:
17
-
«Комбинаторика элементтері»
Тақырып: Комбинаториканың негізгі ұғымдары мен ережелері(қосу мен кӛбейтудің ережелері).
Комбинаторика формулаларды пайдаланып мәтін есептерді шығару.
Оқу мақсаттары:
-
Қайталанбайтын алмастыру, орналастыру және теру сандарын табу формулаларын білу.
-
Қайталанбайтын орналастыру, алмастыру және теру сандарын есептеу үшін комбинаторика формулаларын қолдана отырып есептер шығару
-
Комбинаториканың ережелерін білу (қосу және кӛбейту ережелері)
Бағалау критерииі: Білім алушы:
-
Қайталанбайтын алмастыру, орналастыру және теру сандарын табу формулаларын біле алады.
-
Қайталанбайтын орналастыру, алмастыру және теру сандарын есептеу үшін комбинаторика формулаларын қолдана отырып есептер шығарады.
-
Комбинаториканың ережелерін біледі (қосу және кӛбейту ережелері)
Ойлау дағдыларының деңгейі: Қолдану Жоғары деңгей дағдылары
Орындау уақыты 40 минут
I нұсқа
-
3 балл Ұқсатығын табыңдар:
-
-
А. Қайталанбайтын орналастыру формуласы
1. ?? = ?!
? (?−?)!?!
В. Қайталанбайтын орын ауыстырулар формуласы
2. ?? = ?!
? (?−?)!?!
А.Қайталанбайтын теру формуласы
3. Pn= n!
4. ?? = ?!
? (?−?)!
5. Pn = (n-k)!
6. C? = ?!
? (?−?)!
-
Жауабы: A . B . C .
-
5 балл Есептеңіз:
![]()
![]()
8 7
7
а) ?8−?6. b) ?3−?2.?5
?4
-
2 балл 5 адам баскетбол ойын ойнау үшін, неше тәсілмен таңдап алуға болады 9 адамнан команданың составын?
-
3 балл 0, 2, 4, 6, 7, 8 цифрларынан қайталанатын цифрлары жоқ қанша алтытаңбалы тақ сан құрастыруға болады?
-
2 балл 9 сынып оқушылардың 12 оқытылатын пәндері бар, 5 әр-түрлі сабақтан бір күнге сабақ кестесін қанша тәсілмен құруға болады?
-
5 балл Сыныпта оқитын 13 ұл және 11қыз бар. Ауланы тазалау үшін, неше тәсілмен 5 ұл және 3 қыз таңдап алуға болады?
Барлығы: 20 ұпай
ІI нұсқа
-
3 балл Ұқсатығын табыңдар:
-
-
A. Қайталанбайтын алмастыру формуласы
1. Pn= n!
B. Қайталанбайтын орналастыру формуласы
2. ?? = ?!
? (?−?)!?!
C. Қайталанбайтын теру формуласы
3. Pn = (n-k)!
4. ?? = ?!
? (?−?)!?!
5. ?? = ?!
? (?−?)!
6. C? = ?!
? (?−?)!
-
Жауабы: A . B . C .
-
5 балл Есептеңіз:
![]()
10 9
а) ?9−?7. b) ?5 −?4.![]()
9
?6?5
-
2 балл Жиынтық бағалау үшін 10 түрлі тапсырманың 5-і бір тапсырма үшін таңдалады. Тапсырмалардың неше түрлі нұсқаларын құрастыруға болады?
-
3 балл 5-ке еселік болатындай және әрқайсысында қайталанатын цифрлары болмайтындай етіп қанша алтытаңбалы сан құрастыруға болады?
-
2 балл 9 сынып оқушылардың 14 оқытылатын пәндері бар, 6 әр-түрлі сабақтан бір күнге сабақ кестесін қанша тәсілмен құруға болады?
-
5 балл Сыныпта оқитын 15 ұл және 12 қыз бар. Ауланы тазалау үшін, неше тәсілмен 5 ұл және 3 қыз таңдап алуға болады?
Барлығы: 20ұпай
Балл қою кестесі
-
-
Бағалау критерийлері
Тапсыр
ма
Дескриптор
Балл
Білім алушы
Комбинаторика формуласын ажыратады (Қайталанбайтын алмастыру, орналастыру және теру сандарын табу
формула);
1
қайталанбайтын орналастыру
формуласын қолданады;
1
қайталанбайтын орналастыру формуласын пайдаланады;
1
қайталанбайтын теру қайталанбайтын орналастыру формуласын пайдаланады; формуласын пайдаланады;
1
Комбинаторика формуласын қолданады (Қайталанбайтын орналастыру, алмастыру және теру сандарын есептеу формулалары) для преобразований
выражений;
2а
қайталанбайтын орналастыру формуласын
пайдаланады;
1
есептеулер жүргізеді және жауабын жазады;
1
2b
қайталанбайтын орналастыру формуласын
пайдаланады;
1
қайталанбайтын теру формуласын
пайдаланады;
1
есептеулер жүргізеді және жауабын жазады;
1
Қайталанбайтын орналастыру, алмастыру және теру сандарын есептеу үшін комбинаторика формулаларын қолдана отырып есептер шығарады
3
комбинаториканың керек формулаларын пайдаланады;
1
есептеулер жүргізеді және жауабын жазады;
1
4
тапсырма шарттарын қалай орындау керектігін түсіндіреді
1
қажетті формуланы немесе комбинаторика
ережесін қолданады;
1
есептеулер жүргізеді және жауабын жазады;
1
5
қажетті комбинатор формуласын
пайдаланады;
1
есептеулер жүргізеді және жауабын жазады;
1
Қарапайым есептер шығаруда комбинаториканың ережелерін пайдаланады
6
ұлдарды таңдау үшін комбинаториканың керек формуласын қолданады;
1
және оны есептейді;
1
қыздарды таңдау үшін комбинаториканың
керек формуласын қолданады және оны есептейді;
1
комбинаториканың қосу немесе кӛбейту
ережесін пайдаланады;
1
есептеулер жүргізеді және жауабын жазады;
1
Барлығы:
20
-
«Тізбектер»
Тақырыбы: Тізбектер
Оқу мақсаттары:
9.2.3.2 мысалы:
1 ;
![]() 2 3
2 3
1 ;
![]() 3 4
3 4
1 ;
![]() 4 5
4 5
1
![]()
5 6
;...
тізбектің n-ші мүшесін табу;
-
Арифметикалық прогрессиялардың n-ші мүшесін, алғашқы n мүшелерінің қосындысын есептеу формулаларын, сипаттамалық қасиетін білу және қолдану
-
Геометриялық прогрессиялардың n-ші мүшесін, алғашқы n мүшелерінің қосындысын есептеу формулаларын, сипаттамалық қасиетін білу және қолдану
-
Арифметикалық немесе геометриялық прогрессияларға байланысты есептер шығару
Бағалау критерииі: Білім алушы: тізбектің n-ші мүшесін таба алады.
-
Арифметикалық прогрессиялардың n-ші мүшесін, алғашқы n мүшелерінің қосындысын есептеу формулаларын, сипаттамалық қасиетін біледі және қолдана алады
-
- Геометриялық прогрессиялардың n-ші мүшесін табады,
-
- Алғашқы n мүшелерінің қосындысын есептеу формулаларын, сипаттамалық қасиетін біледі және қолданады
-
Арифметикалық немесе геометриялық прогрессияларға байланысты есептер шығара алады
Ойлау дағдыларының деңгейі: Қолдану. Жоғары деңгей дағдылары
Орындау уақыт: 40 минут
І нұсқа
-
[2балл] an=2n+6 тізбегінің 26 болатын мүшесінің нӛмерін табыңдар.
-
[4балл] an - арифметикалық прогрессия. Егер a1=2 және a3=8 тең болса, қасиетті пайдаланып a2 мүшесін тауып, арифметикалық прогрессияның тоғызыншы мүшесін табыңдар.
-
[3балл] ( b ) – геометриялық прогрессия 0,8; 0,2;… Келесі екі прогрессияның
n
мүшесін табыңыз.
-

1
[2балл] ( b ) – геометрическая прогрессия b 2 ;
n
q 2 . Табу керек
S ?
4
-
[3балл] Дүкенде гүл шоғы жасалды, бірінші гүл шоғы 3 түстен, екіншісі 7 түстен және т. б. болды. 7 букетін жасау үшін қанша түстер қажет?
ІІ нұсқа
-
[2 балл] an=3n-5 тізбегінің 13 болатын мүшесінің нӛмерін табыңдар.
-
[4балл] Пусть (an ) - арифметикалық прогрессия. Егер a1=3 және a3=9, қасиетті пайдаланып a2 мүшесін тауып, арифметикалық прогрессияның он екінші мүшесін табыңдар.
-
[3балл] ( b ) – геометриялық прогрессия 2,1; 0,7;… Келесі екі мүшенің тізбегін
n
табыңыз.
-
[2балл] ( b ) – геометриялық прогрессия, егер b 4 ; q 3 . S
? мәнің табыңыз.
n 1 4
-
[3балл] Саябақта гүлзарлар мен бұталар отырғызылды. Бір гүлзардың жанында 1 бұта, екінші 2 бұта, үшінші 4 бұта және т.б. жанында. Қанша бұта 6-ға жуық гүлзар отырғызылды?
Балл қою кестесі
-
Бағалау критерийлері
Тапсыр ма
Дескриптор
Балл
Білім алушы
Тізбектің n-ші мүшесін табады
1
Формулада берілген мүшелерінің мәнін
жазу
1
Тізбектің n-ші мүшесін табады
1
Арифметикалық прогрессиялардың n-ші мүшесін, алғашқы n мүшелерінің қосындысын есептеу формулаларын, сипаттамалық қасиетін біледі және қолданады
2
Арифметикалық прогрессияның сипаттамалық қасиетін пайдаланып a2
мүшесін табу
1
d арифметикалық прогрессияның
айырмасын табады
1
Арифметикалық прогрессиялардың n-ші мүшесін формуласын қолданады
1
an мүшесінің мәнің табады
1
Геометриялық прогрессияның n-ші мүшесін табады
3
Геометриялық прогрессияның q еселігін
табады
1
Формуланы жазып, b3 мүшесінің мәнің табады
1
Формуланы жазып, b4 мүшесінің мәнің табады
1
Геометриялық прогрессияның n қосындысын табады
4
Геометриялық прогрессияның алғашқы п мүшесінің қосындысын формуласын
жазады
1
Sn қосындысының мәнің табады
1
Арифметикалық прогрессияның алғашқы п мүшесінің қосындысын есептер шығаруда қолданады
5
d арифметикалық прогрессияның
айырмасын табады
1
Арифметикалық прогрессияның алғашқы п мүшесінің қосындысын формуласын
жазады
1
Sn қосындысының мәнің табады
1
Барлығы:
14
-
Тізбек берілген:
1;
1 ; 1 :
![]()
![]() 4 9
4 9
1 ...
![]() 16
16
3 нұсқа
-
[1 балл] Берілген тізбектің формуласын жазыңыз.
-
[1 балл] (??) геометриялық прогрессияның алғашқы мүшесін біле отырып, оның келесі екі мүшесін табыңдар.
-

n
[3 балл] n-ші мүшесінің формуласымен берілген дәлелдеңіз?
c n2 2n 3
тізбек ӛспелі ма,
-
[4 балл] Альпинистер кӛтерілістің бірінші күні 1400 м биіктікке кӛтерілді, содан кейін әрбір келесі күні алдыңғы жылмен салыстырғанда 100 м биіктікке кӛтерілді. Олар қанша күн бойы 5000 м биіктігін бағындырды?
-
[4 балл] Тікбұрышты параллелепипедтің ұзындығы, ені және биіктігі геометриялық прогрессияны құрайды. Параллелепипедтің кӛлемі 216 м3-ге тең, ал оның барлық қабырғаларының ұзындығы 104м-ге тең.Параллелепипед ӛлшемін табыңыз.
n2
-
a) [3 балл] bn (4) берілген тізбек шексіз кемімелі прогрессияның тізбегі
бола ма?
-
[1балл] Шексіз периодты ондық бӛлшекті 0,(12) жай бӛлшек түрінде кӛрсетіңдер
4 нұсқа
-
Тізбек берілген: 4;16;36;64;100; ...
a ) [1 балл] Берілген тізбектің формуласын жазыңыз.
b) [1 балл] (??) геометриялық прогрессияның алғашқы мүшесін біле отырып, оның келесі екі мүшесін табыңдар.
-

n
[3 балл] n-ші мүшесінің формуласымен берілген дәлелдеңіз?
a 3n2 17n 1
тізбек ӛспелі ма,
-
[4 балл] –17; –16; -15; …арифметикалық прогрессиияның теріс мүшелерінің қосындысын табыңдар
-
[4 балл] Геометриялық прогрессияның бірінші мен екінші мүшелерінің қосындысы 40 ,ал екінші мен үшінші мүшелерінің қосындысы 120 –ға тең.Алғашқы үш мүшесін табыңдар.
-
a) [3балл] bn
ма?
10
![]() 7n
7n
берілген тізбек шексіз кемімелі прогрессияның тізбегі бола
b) [1балл] Шексіз периодты ондық бӛлшекті 0,9(5) жай бӛлшек түрінде кӛрсетіңдер
Балл қою кестесі
|
Бағалау критерийлері |
Тапсыр ма |
Дескриптор |
Балл |
|||||
|
Білім алушы |
||||||||
|
|
|
3 нұсқа |
4 нұсқа |
|
||||
|
Жүйелілік заңдылықтарын анықтайды және жетіспейтін мүшелерді табады |
1(а) |
тізбектің n-ші мүшесінің формуласын n арқылы жазады; |
ортақ мүшенің формуласын анықтайды |
1 |
||||
|
1(b) |
келесі екі мүшені табады |
келесі екі мүшесін жазады |
1 |
|||||
|
Сандық тізбек туралы түсінік алады |
2 |
cn+1 үшін ӛрнек жасайды |
аn+1 үшін ӛрнек жасайды |
1 |
||||
|
айырмасын табады cn+1 - cn |
айырмасын табады аn+1 - аn |
1 |
||||||
|
Жауабын жазады |
Жауабын жазады |
1 |
||||||
|
Арифметикалық прогрессиялардың n-ші мүшесін, формулаларын, сипаттамалық қасиетін біледі және қолданады |
3 |
прогрессияның бірінші мүшесінің мәнін, оның айырмашылығын және арифметикалық прогрессияның бірінші мүшелерінің n қосындысының формуласын жазады және кезектіліктің жалпы мүшесінің формуласын айқындайды |
прогрессияның бірінші мүшесінің мәнін, оның айырмашылығын және n–мүшесінің формуласын жазады |
1 |
||||
|
теңдеу құрастырады |
прогрессияның теріс мүшелерінің санын табу үшін ӛрнек жасайды |
1 |
||||||
|
теңдеудің түбірлерін табады |
прогрессияның теріс мүшелерінің санын табады |
1 |
||||||
|
теңдеудің түбірлерін тексереді және жауабын жазады |
арифметикалық прогрессияның бірінші мүшелерінің n қосындысының формуласын қолдана отырып, теріс мүшелердің қосындысын есептейді |
1 |
||||||
|
Геометриялық прогрессиялардың n-ші мүшесін формулаларын, сипаттамалық қасиетін біледі және қолданады |
4 |
прогрессияның жүйелі мүшелері түрінде тікбұрышты параллелепипедтің ұзындығын, енін және биіктігін білдіреді |
есеп шарты бойынша теңдеулер жүйесін құрады; |
1 |
||||
|
есеп шарты жүйесін құрады; |
бойынша |
теңдеулер |
жүйені шешу үшін геометриялық прогрессияның n-мүшесінің формуласын пайдаланады |
1 |
||||
|
жүйені шеше отырып, геометриялық прогрессияның бӛлімі мен бірінші |
жүйені шеше прогрессияның |
отырып, бӛлімі |
геометриялық мен бірінші |
1 |
||||
|
|
|
мүшесін табады |
мүшесін табады |
ен |
|
||||
|
параллелепипед ӛлшемін табады |
прогрессияның табады |
алғашқы үш |
мүшесін |
1 |
|||||
|
Ондық периодтық бӛлшекті жай бӛлшекке аудару үшін шексіз кемімелі геометриялық прогрессия |
5(а) |
прогрессияның екі тізбектес мүшесін табады |
прогрессияның табады |
екі |
тізбектес |
мүшесін |
1 |
||
|
геометриялық прогрессияның еселігін табады; |
геометриялық прогрессияның еселігін табады; |
1 |
|||||||
|
Жауабын жазады |
Жауабын жазады |
1 |
|||||||
|
қосындысынын формуласын пайдаланады |
|
||||||||
|
5(b) |
ондық периодты бӛлшекке ауыстырады |
бӛлшекті |
жай |
ондық периодты бӛлшекті жай бӛлшекке ауыстырады |
1 |
||||
|
Барлығы: |
17 |
||||||||
«Тригонометрия»
|
Тақырып |
Бұрыш пен доғаның градустық және радиандық ӛлшемдері Кез келген бұрыштың синусы, косинусы, тангенсі и котангенсі Кез келген бұрыштың синусы,косинусы,тангенсы және котангенсы Кез келген бұрыштың тригонометриялық формулалар |
||
|
Оқу мақсаттары: |
9.1.2.1 градусты радианға және радианды градусқа айналдыру 9.2.4.4 келтіру формулаларын қорытып шығару және қолдану 9.2.4.3 бұрыштардың қосындысы мен айырымының, жарты және қос бұрыштың тригонометриялық формулаларын қорытып шығару және қолдану |
||
|
Бағалау критерииі: |
Білім алушы: -Градусты радианға және радианды градусқа айналдырады -Келтіру формулаларын қорытып шығарады және қолданады -Бұрыштардың қосындысы мен айырымының бұрыштың тригонометриялық формулаларын қорытып шығарады және қолданады -Жарты және қос бұрыштың тригонометриялық формулаларын қорытып шығарады және қолданады |
||
|
Ойлау дағдыларының деңгейі: |
Қолдану Жоғары деңгей дағдылары |
||
|
Орындау уақыты |
30 минут |
|
|
І нұсқа
-
[4 балл] Градусты радианға және радианды градусқа айналдырып сәйкестеңдіріңіз:
|
Градус ӛлшемдері |
Радиан ӛлшемдері |
|
1. 1200 |
А. 3 2 |
|
2. 270 |
Б. 5 3 |
|
3. 2100 |
В. 3 2 |
|
4. 3000 |
Г. 7 6 |
|
|
Д. 5 6 |
|
|
Е. 2 3 |
![]() 1.
2. 3. 4.
1.
2. 3. 4.
-
[4балл] Ӛрнекті ықшамдаңыз:
cos( ) tg ( ) sin( )
![]() 2
2
-
[4 балл] Есептеңіз: а) cos400cos200 – sin400sin200 б) sin 1050
-
[4 балл] Ӛрнекті ықшамдаңыз: а)
sin 2 2tg
б) 1 cos 2 1 cos 2
ІІ нұсқа
-
[4 балл] Градусты радианға және радианды градусқа айналдырып сәйкестеңдіріңіз:
|
Градус |
Радиан |
|
1. 1500 |
А. 3 4 |
|
2. 360 |
Б. 5 6 |
|
3. 2400 |
В. 16 9 |
|
4. 3200 |
Г. 9 1 |
|
|
Д. 5 |
|
|
Е. 4 3 |
1. 2. 3. 4.
-
[4 балл] Ӛрнекті ықшамдаңыз:
sin( ) cos( )
2
cos( )
-
[4 балл] Есептеңіз: а) cos700cos400 + sin700sin400 б) sin 750
-
[4 балл] Ӛрнекті ықшамдаңыз: а)
sin 2 2ctg
б) 1 cos 2 1 cos 2
Балл қою кестесі
|
Бағалау критерийлері |
Тапсыр ма |
Дескриптор |
Балл |
|
Білім алушы |
|||
|
Градусты радианға және радианды градусқа айналдырады |
1 |
1 бұрышты сәйкестіңдіреді |
1 |
|
2 бұрышты сәйкестіңдіреді |
1 |
||
|
3 бұрышты сәйкестіңдіреді |
1 |
||
|
4 бұрышты сәйкестіңдіреді |
1 |
||
|
Келтіру формулаларын қорытып шығарады және қолданады |
2 |
келтіру формулаларын қолданады |
1 |
|
келтіру формулаларын пайдаланады |
1 |
||
|
келтіру формулаларын 2 пайдаланады |
1 |
|
|
|
Ӛрнекті ықшамдайды |
1 |
|
Бұрыштардың қосындысы мен айырымының бұрыштың тригонометриялық формулаларын қолданады |
3а |
Бұрыштардың қосындысы мен айырымының бұрыштың тригонометриялық формулаларын қолданады |
1 |
|
Ӛрнекті ықшамдайды |
1 |
||
|
3б |
Бұрыштардың қосындысы мен айырымының бұрыштың тригонометриялық формулаларын қолданады |
1 |
|
|
Ӛрнектің мәнін табады |
1 |
||
|
Жарты және қос бұрыштың тригонометриялық формулаларын қолданады |
4а |
Қос бұрыштың формуласын пайдаланады |
1 |
|
Ӛрнекті ықшамдайды |
1 |
||
|
4б |
Қос бұрыштың формуласын пайдаланады |
1 |
|
|
Ӛрнекті ықшамдайды |
1 |
||
|
Жалпы балл: |
16 |
||
«Тригонометрия»
Тақырып: Формулалар тригонометриясы. Тригонометриялық ӛрнектердің ұқсастығы
Оқу мақсаттары:
9.2.4.7 Тригонометриялық функциялардың қосындысы мен айырымын кӛбейтіндіге және кӛбейтіндісін қосындыға немесе айырымға түрлендіру формулаларын қорытып шығару және қолдану
9.2.4.8 Тригонометриялық ӛрнектерді тепе-тең түрлендіруді орындау
Бағалау критерииі: Білім алушы:
-
Тригонометриялық функциялардың қосындысы мен айырымын кӛбейтіндіге және кӛбейтіндісін қосындыға немесе айырымға түрлендіру формулаларын қорытып шығарады және қолданады
-
Тригонометриялық ӛрнектерді тепе-тең түрлендіруді орында алады
Ойлау дағдыларының деңгейі: Қолдану Жоғары деңгей дағдылары
Орындау уақыты 25 минут
І нұсқа
-
[2 балл] Есептеңіз: sin 1050 - sin 750;
-
[4 балл] Ықшамдаңыз:
cos ( ) - cos ( ) , sin 1 .
4 4
-
[5 балл] Дәлелдеңдер:
sin sin 3 sin 5 cos cos 3 cos 5
tg 3
ІІ нұсқа
-
[2 балл] Есептеңіз: sin 750 - sin 150;
-
[4 балл] Ықшамдаңыз:
cos ( ) 3
+ cos
( ) , cos 2 .
3
-
[5 балл] Дәлелдеңдер:
sin 3 sin 5 sin cos cos 5 cos 3
tg3
ІІІ нұсқа
-
 [2 балл] Есептеңіз: cos 5 - cos ;
[2 балл] Есептеңіз: cos 5 - cos ;
12 12
-
[4 балл] Ықшамдаңыз: cos ( )
6
+ cos
( ) ;
6
-
[5 балл] Тепе-теңдікті дәлелдеңіз:
cos 3 cos 5 cos sin sin 5 sin 3
ctg 3
ІV нұсқа
-
[2 балл] Есептеңіз: cos 7 - cos ;
12 12
-
[4 балл] Ықшамдаңыз: cos ( )
6
- cos
( ) ;
6
-
[5 балл] Тепе-теңдікті дәлелдеңіз :
cos cos 3 cos 5 sin sin 3 sin 5
ctg 3
Балл қою кестесі
|
Бағалау критерийлері |
Тапсыр ма |
Дескриптор |
Балл |
|
|
Білім алушы |
||||
|
Тригонометриялық |
1 |
синустардың кӛбейтіндісін қосындыға |
1 |
|
|
функциялардың |
|
түрлендіру формуласын қолданады; |
|
|
|
қосындысы мен |
|
ӛрнекті ықшамдайды; |
1 |
|
|
айырымын кӛбейтіндіге және кӛбейтіндісін қосындыға немесе |
2 |
косинустардың кӛбейтіндісін қосындыға түрлендіру формуласын қолданады; |
1 |
|
|
ӛрнекті ықшамдайды; |
1 |
|||
|
айырымға түрлендіру |
|
|||
|
синустың мәнін табады; |
1 |
|||
|
формулаларын |
|
|||
|
ӛрнекті ықшамдайды; |
1 |
|||
|
қолданады |
|
|||
|
Тригонометриялық |
3 |
Топтастыруды орындайды |
1 |
|
|
ӛрнектерді тепе-тең түрлендіруді орындайды |
|
косинустардың кӛбейтіндісін қосындыға түрлендіру формуласын қолданады; |
1 |
|
|
|
|
синустардың кӛбейтіндісін қосындыға |
1 |
|
|
|
|
түрлендіру формуласын қолданады; |
|
|
|
|
|
Негізгі тригонометриялық |
ұқсастықты |
1 |
|
|
|
қолданады |
|
|
|
|
|
Теңдік туралы қорытынды жасайды |
1 |
|
|
Жалпы балл: |
11 |
|||
«Ықтималдықтар теориясының элементтері»
Тақырып: Ықтималдықтар теориясының элементтері Мәтін есептерді шығару
Оқу мақсаттары:
9.3.2.5 Геометриялық ықтималдықты есептер шығаруда қолданады
9.3.2.3 Ықтималдықтың классикалық анықтамасын білу және есептер шығару үшін оны қолдану
Бағалау критерииі: Білім алушы:
Геометриялық ықтималдықты есептер шығаруда қолданады Ықтималдықтың классикалық анықтамасын біледі және есептер шығару үшін оны қолдану
Ойлау дағдыларының деңгейі: Қолдану Жоғары деңгей дағдылары
Орындау уақыты 25 минут
І нұсқа
1.[5 балл] 1.5×4 см2 тіктӛртбұрышқа іштей сызылған шеңбердің радиусы1,5 см. радиус шеңбері жазылған. Тіктӛртбұрышқа кездейсоқ қойылған нүкте шеңбердің ішінде болмауы ықтималдығы қандай? Жауапты мыңға дейін жуықтаңыз.
2.[3 балл] Жәшікте 90 шар,олар 1,2,…,90-ге дейін белгіленген.Жәшіктен кездейсоқ бір шар алынды.Алынған шардың 6 сан болатын ықтималдығын табыңыз?
3.[3 балл] Бір уақытта екі ойын сүйегі лақтырылды. Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 8 болу ықтималдылығын табыңыз?
4.[2 балл] Фабрикада сӛмкелер шығарылады.100 сӛмкенің ішінде 8-сінде ақауы кездеседі.Кездейсоқ алынған сӛмкенің ақауысыз болуының ықтималдығын табыңыз.
5. [3 балл] Такси фирмасында кәзіргі уақытта 20 кӛлік бар:10 қара, 2 сары және 8жасыл. Шақыру тапсырыс берген адамға ең жақын кӛлік шықты. Кездейсоқ шыққан кӛліктің жасыл болуының ықтималдығын табыңыз.
ІІ нұсқа
-
[5 балл]7×6 см2 тіктӛртбұрышқа іштей сызылған шеңбердің радиусы 2,5 см. радиус шеңбері жазылған. Тіктӛртбұрышқа кездейсоқ қойылған нүкте шеңбердің ішінде болмауы ықтималдығы қандай? Жауапты мыңға дейін жуықтаңыз.
-
[3 балл ] Жәшікте 90 шар,олар 1,2,…,90-ге дейін белгіленген.Жәшіктен кездейсоқ бір шар алынды.Алынған шардың 5 сан болатын ықтималдығын табыңыз?
-
[3 балл] Бір уақытта екі ойын сүйегі лақтырылды. Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 5 болу ықтималдылығын табыңыз.
-
[2 балл] Емтиханға 60 сұрақ берілді, Андрей оның 3-уін жаттамаған. Андрейге жаттаған сұрағы түсетінін ықтималдығын табыңыз.
-
[3 балл] Тарелкеде 16 пирожки бар:7балықпен,5 варенямен және 4 шиемен.Юля қарамай бір пирожки таңдап алды. Кездейсоқ алынған пирожкидың шиемен болуының ықтималдығын табыңыз.
ІІІ нұсқа
1.[5 балл]5×7 см2 тіктӛртбұрышқа іштей сызылған шеңбердің радиусы 2,5 см. радиус шеңбері жазылған. Тіктӛртбұрышқа кездейсоқ қойылған нүкте шеңбердің ішінде болмауы ықтималдығы қандай? Жауапты мыңға дейін жуықтаңыз
2.[3 балл] Жәшікте80 шар,олар 1,2,…,80-ге дейін белгіленген.Жәшіктен кездейсоқ бір шар алынды.Алынған шардың 7 сан болатын ықтималдығын табыңыз?
3.[3 балл] Бір уақытта екі ойын сүйегі лақтырылды. Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 7 болу ықтималдылығын табыңыз.
4.[2 балл] Фабрикада лампалар шығарылады. 1000 лампаның ішінен 3-уі ақаумен кездеседі. Кездейсоқ алынған сатып алған лампа ақауысыз болуының ықтималдығын табыңыз.
5.[3 балл]Такси фирмасында кәзіргі уақытта 25 кӛлік бар:12 қара, 4 сары және 9жасыл. Шақыру тапсырыс берген адамға, ең жақын кӛлік шықты. Кездейсоқ шыққан кӛліктің жасыл болуының ықтималдығын табыңыз.
ІV нұсқа
1.[5 балл] 7×6 см2 тіктӛртбұрышқа іштей сызылған шеңбердің радиусы 3 см радиус шеңбері жазылған. Тіктӛртбұрышқа кездейсоқ қойылған нүкте шеңбердің ішінде болмауы ықтималдығы қандай? Жауапты мыңға дейін жуықтаңыз
2.[3 балл]Жәшікте 90 шар,олар 1,2,…,90-ге дейін белгіленген.Жәшіктен кездейсоқ бір шар алынды.Алынған шардың 4 сан болатын ықтималдығын табыңыз.
3.[3 балл] Бір уақытта екі ойын сүйегі лақтырылды. Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 6 болу ықтималдылығын табыңыз?
-
[2 балл]Емтиханға 80 сұрақ берілді, Әмірбек оның 5-уін жаттамаған. Әмірбекке жаттаған сұрағы түсетінін ықтималдығын табыңыз.
-
[3 балл ] Тарелкеде 20 пирожки бар:7картоппен, 9капустамен және 4 варениямен.Сауле қарамай бір пирожки таңдап алды. Кездейсоқ алынған пирожкидың капустамен болуының ықтималдығын табыңыз.
Балл қою кестесі
|
Бағалау критерийлері |
Тапсырма № |
Дескриптор |
Балл |
|
Білім алушы |
|||
|
Геометриялық ықтималдықты есептер шығаруда қолданады |
1 |
шаршының ауданын табу үшін ӛрнек құрастырады; |
1 |
|
шеңбер ауданы үшін ӛрнек құрайды; |
1 |
||
|
Геометрияның ықтималдығынын анықтамасын пайдаланады; |
1 |
||
|
шеңберге түсу ықтималдығын табады; |
1 |
||
|
Қарама-қарсы оқиғалардың ықтималдығын табу және жауапты дӛңгелектейді; |
1 |
||
|
Ықтималдықтың классикалық формуласын мәтін есепті шешу үшін пайдаланады |
2 |
саны бар шарлар санын табады5, бесінші ондықта; |
1 |
|
саны бар шарлар санын табады 5, қалған ондықтарда; |
1 |
||
|
ықтималдықты формула бойынша табады; |
1 |
||
|
3 |
осы оқиғалар үшін барлық мүмкін болатын нәтижелер санын табады |
1 |
|
|
осы оқиғаға қолайлы нәтиже санын табады; |
1 |
||
|
ықтималдықты формула бойынша табады; |
1 |
||
|
4 |
Ықтималдықтың классикалық формуласын пайдаланады; |
1 |
|
|
барлық мүмкін болатын нәтижелер санын табады; |
1 |
||
|
ықтималдықтың мәнін табады; |
1 |
||
|
барлық мүмкін болатын нәтижелер санын табады; |
1 |
||
|
5 |
шарты бойынша қолайлы саны нәтижелерін анықтайды; |
1 |
|
|
Кездейсоқты формула бойынша табады |
1 |
||
|
Барлығы: |
|
|
17 |
Геометрия
«Жазықтықтағы векторлар»
Тақырып:
Векторлар. Векторларға амалдар қолдану. Коллинеар, коллиниар емес векторлар. Вектордың координаты. Вектордың коодинаттарына амалдар қолдану. Векторларды есеп шығаруда қолдану.
Оқу мақсаты
-
Вектордың, коллинеар вектор, тең векторлар, нӛлдік вектор, бірлік вектор және вектордың ұзындығы анықтамасын білу;
-
вектордың кӛбейтіндісін,векторларды қосу әдістерін, векторды санға кӛбейтуді білу және қолдану;
-
вектордың координатын табу;
9.1.3.5 векторлар арасындағы бұрышты табу;
-
вектордың ұзындығын табу;
9.1.4.6 векторлардың скаляр кӛбейтіндісін табу.
Бағалау критерийі Білім алушы:
-
вектордың түрін анықтайды
-
векторларға амалдар қолданады
-
вектордың координатын табады
-
векторлар арасындағы бұрышты табады
-
вектордың ұзындығын табады
-
векторды есеп шығаруда қолданады
Ойлау дағдыларының деңгейі: Білу,түсіну. Қолдану
Орындалу уақыты 40 минут
I нұсқа.
-
 3 балл Суретті қолданып екі мысалдан келтіріңдер a) тең
векторларға;
3 балл Суретті қолданып екі мысалдан келтіріңдер a) тең
векторларға;-
коллинеар векторларға;
-
перпендикуляр векторларға.
-
-
3 балл BDEF параллелограммы берілген. Табу керек:
а) ̅?̅̅̅?̅→ және ̅?̅̅̅?̅→векторларыны
қосындысын;
б) ̅?̅̅̅?̅→ және ̅?̅̅̅̅?̅→ векторларының
айырымын.
-
3 балл ?̅̅→ = 3?→ − 2?→ и ?̅→ = 2?→ + 4?→ векторлары берілген.
?→ = 2?̅̅→ − 3?̅→ векторының координаты мен ұзындығын табыңыз.
-
 5 балл ?→(2;
0)и ?̅→(2;
2√3) векторларының арасындағы бұрышты табыңыз.
5 балл ?→(2;
0)и ?̅→(2;
2√3) векторларының арасындағы бұрышты табыңыз.
-
4 балл А(11; 2), В(–3; 10) и С(14; –2) нүктелері берілген. ̅?̅̅̅?̅→ = ̅?̅̅̅?̅→ теңдігі орындалатындай D нүктесінің координатын табыңыз.
Барлығы 18 балл.
ІI нұсқа.
-
 3 балл Суретті қолданып екі мысалдан келтіріңіздер
3 балл Суретті қолданып екі мысалдан келтіріңіздер-
тең векторларға;
-
коллинеар векторларға;
-
перпендикуляр векторларға.
-
-
3 балл BCDE ромб берілген. Табу керек: а) ̅C̅̅̅?̅→ және ̅?̅̅̅?̅→ векторларының қосындысын; б) ̅?̅̅̅?̅→ және ̅?̅̅̅?̅→ векторларының айырымын.
-
3 балл ̅a→ = ?→ + 2?→ және ?̅→ = 2?→ − 4?→ векторлары берілген.
?̅̅→ = 2̅a→ − 3?̅→ векторының координатын және ұзындығын табыңыз.
![]()
-
5 балл ?̅̅→(3; 0)mGне ?̅→(3; √3) векторларының арасындағы бұрышты табыңыз.
-
4 балл А(-1; 12), В(–3; 7) және С(9; –12) нүктелері берілген. орындалатындай D нүктесінің координатын табыңыз
̅?̅̅̅̅C→ =
̅B̅̅̅?̅→ теңдігі
Барлығы 18 балл.
Балл қою кестесі
|
Бағалау критерийы |
№ |
Дескриптор |
Балл |
|
Оқушы |
|||
|
Жазықтықтағы векторларды ажыратады; |
1 |
Екі тең векторларды жазады; |
1 |
|
Екі коллинеар векторларды жазады; |
1 |
||
|
Екі перпендикуляр векторларды жазады. |
1 |
||
|
Векторларды қосу және азайту ережелерін қолданады; |
2 |
Векторларды қосу амалын орындап жауабын жазады; |
1 |
|
Векторларды азайту амалын орындап жауабын жазады; |
1 |
||
|
Сызбаны орындап керек векторларды белгілейді; |
1 |
||
|
Векторларға амалдар қолданып,координатала рын табады,ұзындығын табады. |
3 |
Жіктеу арқылы векторлардың координаталарын жазады; |
1 |
|
Координаталарға амалдар қолдану арқылы,вектордың координатын табады ; |
1 |
||
|
Вектордың ұзындығын табады; |
1 |
||
|
Векторлардың скаляр кӛбейтіндісін қолданып, векторлар арасындағы бұрышты табады; |
4 |
Векторлардың скаляр кӛбейтіндісін табады; |
1 |
|
Векторлардың модулін табады; |
1 |
||
|
Векторлардың скаляр кӛбейту формуласын векторлар арасындағы бұрышын табу үшін қолданады; |
1 |
||
|
Бұрыштың косинусын табу амалын орындайды; |
1 |
||
|
Косинустың мәні бойынша векторлардың арасындағы бұрышты табады. |
1 |
||
|
Векторлардың теңдігін |
5 |
Вектордың координатын табады;. |
1 |
|
Векторлардың теңдігін қолданады; |
1 |
|
қолданып,вектордың координатын табады. |
|
Нүктенің абсциссасын табады; |
1 |
|
Нүктенің ординатын табады ,жауабын жазады |
1 |
||
|
Барлығы: |
18 |
||
«Жазықтықтағы түрлендірулер»
Тақырыбы Қозғалыс және оның қасиеттері Гомотетия және олардың қасиеттері Ұқсас үшбұрыштар және оның қасиеттері
Оқу мақсаты
9.1.4.11 Гомотетияның анықтамасы мен қасиеттерін білу
9.1.4.15 Тікбұрышты үшбұрыштың ұқсастығын білу және қолдану
9.1.4.17 Ұқсас фигуралардың аудандары мен ұқсас коэффициенттердің арасындағы тәуелділік формуласын білу
9.1.4.8 Қозғалыстың түрлерін, композициясын және олардың қасиеттерін білу
9.1.4.9 Симметрия, параллель кӛшіру және бұру кезінде фигуралардың бейнелерін салу
Бағалау критерийі Білім алушы:
Орталықты және гомотетия коэффициентін анықтайды
Есептерді шешу кезінде тікбұрышты үшбұрыштардың ұқсастығын қолданады Ұқсас фигуралардың аудандары мен ұқсас коэффициенттердің арасындағы тәуелділік формуласын қолданады
Фигура бейнесін құру үшін осьтік және орталық симметрияны қолданады Симметрия, параллель тасымалдау, бұрылу кезінде фигуралардың бейнелерін жасайды
Ойлау дағдыларының Білу, түсіну, қолдану
Орындалу уақыты 25 минут
I нұсқа
-
[3 балл] АВ кесіндісін О нүктесіне қатысты 600 бұрышқа сағат тіліне қарсы бұрауды сипаттаңыз
-
[1 балл] А(-2;-1) симметриялық нүктесінің нүктелерінің координаттарын табыңыз.: в) Оу осі; с) координаталар басы
-
[2 балл] Параллель тасымалдау кезінде А(3;-1) нүктесі А1(5,-4) нүктесіне ӛтеді. Осы тасымал нәтижесінде қандай нүктеге В (-7;0) нүктесі ӛтеді?
-
[4 балл] Егер оның кӛлеңкесінің ұзындығы 36 м болса, ғарышкердің кӛлеңкесінің ұзындығы 1 м 20 см болса, зымыранның биіктігін табыңыз.

-
[4 балл] Түзу,үшбұрыштың табанына параллель, оны үшбұрыш пен трапецияға бӛледі, олардың аудандарының қатынасы 4:5. Пайда болған үшбұрыштың периметрі 20 см тең . Осы үшбұрыштың периметрін табыңыз.
-
[4 балл] F фигурадан F1 фигурасын гомотетий (O;2) салыңыз.
 А
А
С
В
О
-
[1 балл] А(4;-11) симметриялық нүктесінің нүктелерінің координаттарын табыңыз.: в) Оу осі; с) координаталар басы
-
[2 балл] Параллель тасымалдау кезінде А(-3;-4) нүктесі А1(7,3) нүктесіне ӛтеді. Осы тасымал нәтижесінде қандай нүктеге В (0;5) нүктесі ӛтеді?
-
[4 балл] Париждегі Эйфель мұнарасының биіктігі 300 м., оның кӛлеңкесінің ұзындығы 510 м. Лондондағы Биг Бен парламенттік сағаттарынан кӛлеңкенің ұзындығы 164,9 М. Биг Бен сағат биіктігін анықтаңыз?

-
[4 балл] ABC үшбұрышының AD және BE медианалары F нүктесінде қиылысады. Белгілі, SABF=1 тең. SDEF табыңыз.
-
[4 балл] F фигурадан F1 фигурасын гомотетий (O;1) салыңыз.
2
 О
О
В
С
Геометрия, 9 сынып
|
Бағалау критерийі |
№ тапсырм алар |
Дескриптор |
Балл |
||||
|
Білім алушы |
|||||||
|
I нұсқа |
II нұсқа |
||||||
|
Бұрылу кезінде фигуралардың бейнелерін құрады |
1 |
А нүктесінің бейнесін құруды сипаттайды |
А нүктесінің бейнесін құруды сипаттайды |
1 |
|||
|
О нүктенің бейнесін салуды сипаттайды |
О нүктенің бейнесін салуды сипаттайды |
1 |
|||||
|
кесіндісінің құрылысын сипаттайдыА1В1 |
кесіндісінің құрылысын сипаттайдыА1В1 |
1 |
|||||
|
Фигура бейнесін құру үшін осьтік және орталық симметрияны қолданады |
2 |
Ох осіне; Оу осіне; координаттардың басына қатысты А симметриялық нүктесінің нүктелерінің координаттарын табады |
Ох осіне; Оу осіне; координаттардың басына қатысты А симметриялық нүктесінің нүктелерінің координаттарын табады |
1 |
|||
|
Жазықтықта тікбұрышты координаттарды түрлендіру формулаларын қолданады |
3 |
(??; ??) координаталарын табады |
(??; ??) координаталарын табады |
1 |
|||
|
В1 нүкесінін координаталарын табады |
В1 нүкесінін координаталарын табады |
1 |
|||||
|
Есептерді шешу кезінде тікбұрышты үшбұрыштардың ұқсастығын қолданады |
4 |
Есептің шартты бойынша суретін салады |
Есептің шартты бойынша суретін салады |
1 |
|||
|
Тікбұрышты үшбұрыштың дәлелдейді |
ұқсастығын |
Тікбұрышты дәлелдейді |
үшбұрыштың |
ұқсастығын |
1 |
||
|
Ұқсас үшбұрыштардың теңдігін құрайды |
жақтарының |
Ұқсас үшбұрыштардың жақтарының теңдігін құрайды |
1 |
||||
|
Ракетаның биіктігін табады |
Биг Бен сағат биіктігін табады |
1 |
|||||
|
Ұқсас фигуралардың аудандар мен ұқсас коэффициенттердің арасындағы тәуелділік формуласын қолданады |
5 |
Сызбаны салуды орындайды және белгілеулерді енгізеді; |
Сызбаны салуды орындайды және белгілеулерді енгізеді; |
1 |
|||
|
Үшбұрыштың ұқсастығын анықтайды және дәлелдейді |
Үшбұрыштың ұқсастығын анықтайды және дәлелдейді |
1 |
|||||
|
Ұқсастық коэффициентін есептейді |
Ұқсастық коэффициентін есептейді |
1 |
|||||
|
Ұқсас фигуралардың аудандары мен ұқсас коэффициенттердің арасындағы тәуелділік формуласын қолданады |
Ұқсас фигуралардың аудандары мен ұқсас коэффициенттердің арасындағы тәуелділік формуласын қолданады |
1 |
|||||
|
Гомотетия фигураларының бейнелерін құрады |
6 |
Салады ОА1 = 2ОА |
Салады ОА1 = 1ОА
2 |
1 |
|||
|
Салады ОВ1 = 2ОВ |
Салады ОВ1 = 1ОВ
2 |
1 |
|||||
|
Салады ОС1 = 2ОС |
Салады ОС1 = 1ОС
2 |
1 |
|||||
|
Үшбұрыш салады А1В1С1 |
Үшбұрыш салады А1В1С1 |
1 |
|||||
|
Барлығы |
18 |
||||||
«Үшбұрыштарды шешу»
Тақырып: Үшбұрыштарды шешу
Оқу мақсаты: 9.1.3.6 Косинустар теоремасын білу және қолдану
9.1.3.7 Синустар теоремасын білу және қолдану
9.1.3.9 Шеңберге іштей немесе сырттай сызылған үшбұрыштардың аудандарын пайдаланып шеңбердің радиусын табу формулаларын білу және қолдану
Бағалау критерийі: Білім алушы:
-
Синустар және косинустар теоремасын біледі
-
Есеп шығаруда синустар теоремасын қолданады
-
Есеп шығаруда косинустар теоремасын қолданады
-
Үшбұрышқа іштей немесе сырттай сызылған шеңберлердің радиустарын табуға арналған есептерді шығарды
Ойлау дағдыларының деңгейі: Қолдану. Жоғары деңгей дағдылары
Орындау уақыты: Ескеру:
30 минут
Брадис таблицасы
1 нұсқа
-
Теореманың сӛйлеммен берілген анықтамасы мен математикалық жазылуы арасындағы сәйкестікті табыңыз. [2 балл]
-
Сӛйлеммен берілген анықтамасы
Математикалық жазылуы
1. Бұрыштың синусы үшбұрыш қабырғаларына
пропорционал болады
A. ?2 = ?2 + ?2 − 2?? ??? ?
2. Үшбұрыштың қабырғалары қарсы жатқан бұрыштарының косинусына пропорционал
B. ?2 = ?2 + ?2 − 2?? ??? ?
3. Үшбұрыштың кез келген қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысынан осы екі қабырға мен олардың арасындағы бұрыштың екі еселенген косинусының кӛбейтіндісін шегергенге тең
C. ??? ? = ??? ? = ??? ?
? ? ?
4. Үшбұрыштың қабырғалары қарсы жатқан бұрыштарының синусына пропорционал
D.?2 = ?2 + ?2 + 2?? ??? ?
5. Үшбұрыштың кез келген қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысынан осы екі қабырға мен олардың арасындағы бұрыштың екі еселенген синусының
кӛбейтіндісін шегергенге тең
E. ? = ? = ?
??? ? ??? ? ??? ?
6. Үшбұрыштың кез келген қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысынан осы екі қабырға мен олардың арасындағы бұрыштың екі еселенген косинусының
кӛбейтіндісін қосқанға тең
F. ? = ? = ?
??? ? ??? ? ??? ?
Косинустар теоремасы: және
Синустар теоремасы: және
-
? = 10, ? = 400, ? = 600 болатын үшбұрыштың белгісіз ӛлшемдерін табыңыз.
[4балл]
-
А пунктінен С пункті арқылы В пунктіне қатынайтын, мұндағы АС ≈13 км, а ВС ≈6 км, ∠ACB = 700. Кейін А және В пункттерін түзу жолмен қосты. А пунктінен В пунктіне дейінгі жол қанша километрге қысқарды? [3балл]
-
Тең бүйірлі үшбұрыштың бүйір қабырғасы 13 см, ал табаны 10 см-ге тең. Осы үшбұрышқа іштей және сырттай сызылған шеңберлердің радиусын табыңыз. [4балл]
2 нұсқа
-
Теореманың сӛйлеммен берілген анықтамасы мен математикалық жазылуы арасындағы сәйкестікті табыңыз. [2 балл].
-
Сӛйлеммен берілген анықтамасы
Математикалық жазылуы
1. Бұрыштың синусы үшбұрыш қабырғаларына
пропорционал болады
A. ?2 = ?2 + ?2 − 2?? ??? ?
2. Үшбұрыштың қабырғалары қарсы жатқан бұрыштарының косинусына пропорционал
B. ?2 = ?2 + ?2 − 2?? ??? ?
3. Үшбұрыштың кез келген қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысынан осы екі қабырға мен олардың арасындағы бұрыштың екі еселенген косинусының
кӛбейтіндісін қосқанға тең
C. ? = ? = ?
??? ? ??? ? ??? ?
4. Үшбұрыштың қабырғалары қарсы жатқан бұрыштарының синусына пропорционал
D.?2 = ?2 + ?2 + 2?? ??? ?
5. Үшбұрыштың кез келген қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысынан осы екі қабырға мен олардың арасындағы брыштың екі еселенген синусының
кӛбейтіндісін шегергенге тең
E. ??? ? = ??? ? = ??? ?
? ? ?
6. Үшбұрыштың кез келген қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысынан осы екі қабырға мен олардың арасындағы бұрыштың екі еселенген косинусының кӛбейтіндісін шегергенге тең
F. ? = ? = ?
??? ? ??? ? ??? ?
Косинустар теоремасы: және
Синустар теоремасы: және
-
? = 5, ? = 800, ? = 400 болатын үшбұрыштың белгісіз ӛлшемдерін табыңыз. [4балл]
-
А пунктінен С пункті арқылы В пунктіне қатынайтын, мұндағы АС ≈15 км, ал ВС ≈8 км, ∠ACB = 800. Кейін А және В пункттерін түзу жолмен қосты. А пунктінен В пунктіне дейінгі жол қанша километрге қысқарды?
-
Тең бүйірлі үшбұрыштың бүйір қабырғасы 10 см, ал табаны 12 см-ге тең. Осы үшбұрышқа іштей және сырттай сызылған шеңберлердің радиусын табыңыз. [4балл]
Балл қою кестесі
-
Бағалау критерийі
№
Дескриптор
Балл
Білім алушы:
Синустар және косинустар теоремасын
біледі
1
Косинустар теоремасына сәйкестікті табады
1
Синустар теоремасына сәйкестікті табады
1
Тапсырманы орындауға синустар теоремасын қолданады
2
Үшбұрыштың үшінші бұрышын табады
1
Синустар теоремасын қолданады
1
Үшбұрыштың екінші қабырғасын табады
1
Үшбұрыштың үшінші қабырғасын табады
1
Тапсырманы орындауға косинустар теоремасын қолданады
3
Косинустар теоремасын қолданады
1
АС-ның арақашықтығын табады
1
Жауабын жазады
1
Үшбұрышқа іштей және сырттай сызылған шеңберлердің радиустарын табуға арналған есептерді шығарады
4
Үшбұрыштың ауданын есептейді
1
Үшбұрышқа іштей және сырттай сызылған
шеңберлердің радиусын табу формуласын қолданады
1
Үшбұрышқа іштей сызылған шеңбердің радиусын табу формуласын қолданады
1
Үшбұрышқа сырттай сызылған шеңбердің радиусын табу формуласын қолданады
1
Барлығы:
13
3 нұсқа
Тапсырма 1. [2 балл] Сәйкестікті табыңыз. Жауабын кестемен жазыңыз :
-
-
1. Іштей сызылған үшбұрыш ауданы
А)S = 4abc
R

2. Сырттай сызылған кӛпбұрыш ауданы
В) S = p · r
C)S = abc
4

D) S = 2p · r
E) S=p·r2
F) S = abc
4
 R
R1
2
-
Тапсырма 2. [2 балл] Үшбұрыш берілген:
 T
S
T
S
Мына тұжырымдардың қайсысы ақиқат екенін анықтаңыз :
-
TR = RS + RS- RS · ST · CosS
-
TR2 = RS2 − TS2 + 4 · RS · ST · Cos2S
-
??2 = ??2 + ??2 − 2 · ?? · ?? · ????
-


 SinS = SinR = SinT
SinS = SinR = SinT
RS RT TS
-


 SinS = SinR = SinT
SinS = SinR = SinT
RT TS RS
![]()
![]() 6)SinS = SinR = SinT
6)SinS = SinR = SinT
TS RS TR
Тапсырма 3. [3 балл] LMN үшбұрышында LM=3, MN=6,∠М=600. Косинустар теоремасын қолданып, LN қабырғасының ұзындығын табыңыз.
![]()
Тапсырма 4. [3 балл] Сүйір бұрышты ХYZ үшбұрышында ХY=3√3, XZ=6,
∠XZY=600 . Синустар теоремасын қолданып, ∠XYZ бұрышының градустық мәнін табыңыз.
 Тапсырма 5. [3 балл] ABC үшбұрышы радиусы
r және центрі О болатын шеңберге іштей сызылған.
1-ші суреттегі үшбұрыштың ауданын табыңыз.
Тапсырма 5. [3 балл] ABC үшбұрышы радиусы
r және центрі О болатын шеңберге іштей сызылған.
1-ші суреттегі үшбұрыштың ауданын табыңыз.
Сурет 1
Тапсырма 6. [4 балл] Кӛпбұрыш радиусы 7-ге тең шеңберге сырттай сызылған.
Кӛпбұрыштың ауданы 56 болса, периметрін табыңыз.
4 нұсқа.
Тапсырма 1. [2 балл] Сәйкестікті табыңыз. Жауабын кестемен жазыңыз :
-
-
1. Іштей сызылған үшбұрыш ауданы
А)S = abc
4
 R
R2. Сырттай сызылған кӛпбұрыштың ауданы
В) S = p · r
C)S = 2p · r
D) S = abc
4

E) S=p·r2
F) S = 4abc
R

1
2
-
[2]
Тапсырма 2. [2 балл] Үшбұрыш берілген :
 S
S
T
Мына тұжырымдардың қайсысы ақиқат екенін анықтаңыз :
-
TR2 = RS2 + TS2 − 2 · RS · ST · Cos2S
-
??2 = ??2 + ??2 − 2 · ?? · ?? · ????
-
TR = RS + RS- RS · ST · CosS
-


 SinS = SinR = SinT
SinS = SinR = SinT
TS RS TR
-


 SinS = SinR = SinT
SinS = SinR = SinT
RS RT TS
![]()
![]() 6)SinS = SinR = SinT
6)SinS = SinR = SinT
RT TS RS
Тапсырма 3. [3 балл] LMN үшбұрышында, LM=6, MN=10,∠М=600. Косинустар теоремасын қолданып, LN қабырғасының ұзындығын табыңыз.
![]()
Тапсырма 4. [3 балл] Сүйір бұрышты ХYZ үшбұрышында YZ=2√3, XZ=2,
∠XYZ=300. Синустар теоремасын қолданып , ∠YXZ бұрышының градустық мәнін табыңыз .
 Тапсырма 5. [3 балл] ABC үшбұрышы радиусы
r және центрі О болатын шеңберге іштей сызылған.
1-ші суреттегі үшбұрыштың ауданын табыңыз.
Тапсырма 5. [3 балл] ABC үшбұрышы радиусы
r және центрі О болатын шеңберге іштей сызылған.
1-ші суреттегі үшбұрыштың ауданын табыңыз.
Сурет 1
Тапсырма 6. [4 балл] Радиусы 6-ға тең шеңберге кӛпбұрыш сырттай сызылған.
Кӛпбұрыштың ауданы 48 болса, периметрін табыңыз.
Балл қою кестесі
-
Бағалау критерийі
Тапсыр ма №
Дескриптор
Балл
Білім алушы
Косинустар теоремасын, синустар теоремасын, үшбұрышқа іштей сызылған, кӛпбұрышқа сырттай сызылған шеңберлердің радиустарын табу формулаларын анықтайды.
1
іштей сызылған үшбұрыш ауданы табады
1
сырттай сызылған кӛпбұрыштың ауданы табады
1
2
синустар теоремасының ақиқат
анықтамасын дұрыс табады
1
косинустар теоремасының ақиқат анықтамасын дұрыс табады
1
Косинустар теоремасын қолданып, үшбұрыштың элементтерін табады .
3
есептің шарты бойынша суретін салады
1
косинустар теоремасын жазады, формулаға сандық мәнін жазады
1
LN қабырғасын табады
1
Синустар теоремасын қолданып, үшбұрыштың элементтерін табады .
4
есептің шарты бойынша суретін салады
1
синустар теоремасын жазады, формулаға сандық мәнін жазады
1
Sin∠YXZ табады, ∠YXZ шамасын градуспен жазады
1
Іштей сызылған үшбұрыш ауданының формуласын қолданады .
5
сызба бойынша үшбұрыштың
қабырғасының ұзындығын, шеңбердің радиусын табады
1
іштей сызылған үшбұрыш ауданының
формуласын жазады
1
формулаға сандық мәнін жазады, АВС үшбұрышының ауданын табады
1
Сырттай сызылған кӛпбұрыштың ауданының формуласын қолданады.
6
сырттай сызылған кӛпбұрыштың ауданының формуласын жазады
1
сырттай сызылған кӛпбұрыштың жарты периметрін жазады
1
формулаға сандық мәнін жазады, сырттай сызылған кӛпбұрыштың
жарты периметрін табады
1
сырттай сызылған кӛпбұрыштың
периметрін табады
1
Барлығы
17
«Шеңбер. Кӛпбұрыштар»
-
Тақырыбы
Шеңбер және дӛңгелек. Доғаның ұзындығы. Шеңбердің, сектордың және сегменттің ауданы. Дұрыс кӛпбұрыштар, олардың қасиеттері және симметриясы.
Оқу мақсаты
-
Доға ұзындығының формуласын қорытып шығару және қолдану;
-
сектор және сегменттің ауданынын формуласын шығару және қолдану;
9.1.2.4 дұрыс кӛпбұрыштың іштей және сырттай сызылған шеңберінің радиустарынын арасындағы байланысты білу және қолдану;
9.1.2.4 дұрыс кӛпбұрыштың іштей және сырттай сызылған шеңбердің радиустары мен дұрыс кӛпбұрыштың периметрін, формулаларын білу және қолдану;
Бағалау критерийі :
тапсырмаларды шешу кезінде шеңбер доғасының ұзындығының формуласын қолданады;
-есептерді шешу кезінде сектор ауданының, шеңбер сегментінің формуласын қолданады;
-тапсырмаларды шешу кезінде дұрыс кӛпбұрыштың іштей және сырттай сызылған шеңберінің радиустарынын арасындағы байланысты қолданады;
-есептерді шешу кезінде дұрыс кӛпбұрышқа іштей және сырттай сызылған
периметрін, дұрыс кӛпбұрыштың ауданын және қабырғаларын табудын формулаларын қолданады;
Ойлау дағдыларының деңгейі
Қолдану. Жоғарғы дағдылар
Орындау уақыты:
40 минут
-
I нұсқа
-
1 балл Егер шеңбердің радиусы 12 см тең болса,оның 120°центрлік бұрышына сәйкес келетін доғасының ұзындығын есептеңіз?
-
4π;
-
6π;
-
8;
-
8π;
-
12.
-
-
5 балл Айналмалы сектордың ауданы 9π см2, ал шеңбердің радиусы-6 см. Осы сектордың доғасын керетін хорданың ұзындығы мен пайда болған сегменттің ауданын табыңыз.
-

5 балл Сәйкестікті орнатыңыз:
Дұрыс үшбұрышқа іштей сызылған шеңбердің радиусы √3 см тең.
-
Тапсырма
Жауап
1. Үшбұрышқа іштей сызылған шеңбердің радиусын табыңдар
A. 6;
2. Дұрыс үшбұрыштың периметрін табыңдар.
B. 18;
3. Дұрыс үшбұрыштын ауданын табыңдар.


C. √6;
D. 6√6;
4. Шеңберге іштей сызылған квадраттың қабырғасын табыңдар
E. 2;
F
 .
2√3;
.
2√3;1



 ; 2 ; 3 ; 4
; 2 ; 3 ; 4

G. 6√3;
H. 9√3.
-
6 балл Шеңберге іштей сызылған дұрыс үшбұрыштың периметрі 45 см-ге тең. Сол шеңберге сырттай сызылған оң алтыбұрыштың периметрін және ауданын табыңыз.
-
Бағалау критерийі
Тапсыр ма №
Дескриптор
Балл
Білім алушы
есептерді шешу кезінде шеңбер доғасының ұзындығының формуласын қолданады;
1
шеңбер доғасынын ұзындығын есептеу үшін тиісті формуланы қолданады және жауапты таңдайды.
1
есептерді шешу кезінде сектордың ауданын,сегментін формуласын қолданады
2
сектордың ауданының формуласын
пайдаланады;
1
осы секторға сәйкес келетін центрлік бұрыштың шамасын есептейді;
1
үшбұрыштың түрін анықтайды
1
хорданың ұзындығын есептейді;
1
сегментін ауданын есептейді.
1
есептерді шешу кезінде дұрыс кӛпбұрыштың іштей және сырттай сызылған радиустардың арасындағы байланысты қолданады;
3.1
үшбұрышқа сырттай сызылған шеңбердің радиусын табады және сәйкестікті орнатады;
1
есептерді шешу кезінде дұрыс кӛпбұрышқа іштей және сырттай сызылған периметрін, дұрыс кӛпбұрыштың ауданын және қабырғаларын табудын формулаларын қолданады;
3.2-3.4
осы үшбұрыштың периметрін табады және сәйкестікті орнатады;
1
осы үшбұрыштың ауданын табады және сәйкестікті орнатады;
1
дұрыс кӛпбұрыштар арасындағы
байланыс орнатады;
1
шаршының қабырғасын есептеп,
сәйкестігін анықтайды;
1
4
осы дұрыс үшбұрыштың қабырғасын анықтайды;
1
сырттай сызылған шеңбердің радиусын есептейді;
1
дұрыс кӛпбұрыштар арасындағы байланыс орнатады;
1
дұрыс алтыбұрыштың қабырғасын есептейді;
1
дұрыс алтыбұрыштың периметрін
есептейді;
1
дұрыс алтыбұрыштың ауданын
есептейді;
1
Жалпы ұпай:
17
II нұсқа
-
1 балл Егер шеңбердің радиусы 18 см тең болса,оның 150°центрлік бұрышына сәйкес келетін доғасының ұзындығын есептеңіз?
-
34π;
-
36π;
-
18;
-
18π;
-
12.
-
-
5 балл Айналмалы сектордың ауданы 16 π см2, ал шеңбердің радиусы-8см. Осы сектордың доғасын керетін хорданың ұзындығы мен пайда болған сегменттің ауданын табыңыз.
-

5 балл Сәйкестікті орнатыңыз:
Дұрыс үшбұрышқа сырттай сызылған шеңбердің радиусы 4√3тең.
-
-
Тапсырма
Жауап
1. Үшбұрышқа іштей сызылған шеңбердің радиусын табыңдар
-
36;
-
18;


-
4√6;
-
6√6;
-
12;



-
2√3;
-
36√3;
-
9√3.
2. Дұрыс үшбұрыштың периметрін табыңдар.
3. Дұрыс үшбұрыштын ауданын табыңдар.
4. Шеңберге іштей сызылған квадраттың қабырғасын табыңдар
1 ; 2 ; 3 ; 4 .
-
-
-
6 балл Шеңберге сырттай сызылған дұрыс үшбұрыштың периметрі 36 см-ге тең. Сол шеңберге сырттай сызылған дұрыс алтыбұрыштың периметрін және ауданын табыңыз.
-
Бағалау критерийі
Тапсыр- ма №
Дескриптор
Балл
Білім алушы
есептерді шешу кезінде шеңбер доғасының ұзындығының формуласын қолданады;
1
шеңбер доғасынын ұзындығын есептеу үшін тиісті формуланы қолданады және жауапты таңдайды.
1
есептерді шешу кезінде сектордың ауданын,сегментін формуласын қолданады
2
сектордың ауданының формуласын
пайдаланады;
1
осы секторға сәйкес келетін центрлік бұрыштың шамасын есептейді;
1
үшбұрыштын түрін анықтайды;
1
хорданың ұзындығын есептейді;
1
сегментін ауданын есептейді.
1
есептерді шешу кезінде дұрыс кӛпбұрыштың іштей сызылған және сырттай сызылған радиустарының арасындағы байланысты
қолданады;
3.1
осы үшбұрышқа іштей сызылған шеңбердің радиусын табады және сәйкестікті орнатады;
Іштей сызылған үшбұрышқа шеңбердің радиусын табады;
1
есептерді шешу кезінде дұрыс кӛпбұрыштың іштей сызылған және сырттай сызылған, периметрін, дұрыс кӛпбұрыштың ауданын және қабырғаларын табатын формулаларын қолданады;
3.2-3.4
берілген үшбұрыштың периметрін
табады және сәйкестікті орнатады;
1
үшбұрыштың ауданын табады және сәйкестікті орнатады;
1
дұрыс кӛпбұрыштар арасындағы
байланыс орнатады;
1
шаршының қабырғасын есептеп,
сәйкестігін анықтайды
1
4
осы дұрыс үшбұрыштың қабырғасын
анықтайды;
1
Іштей сызылған шеңбердің радиусын есептейді;
1
дұрыс кӛпбұрыштар арасындағы
байланыс орнатады;
1
дұрыс алтыбұрыштың жағын есептейді;
1
дұрыс алтыбұрыштың периметрін есептейді;
1
дұрыс алтыбұрыштың ауданын
есептейді;
1
Жалпы ұпай:
17
-
2 балл Егер шеңбердің радиусы 12 см тең болса,оның 120° центрлік бұрышына сәйкес келетін доғасының ұзындығын есептеңіз?
-
4 балл Шеңбердің радиусы 10 см доғаның ұзындығы 4? -ге тең тең болса. Сектордың ауданын табыңыз.
-
 4 балл Егер шеңберге іштей сызылған дұрыс алтыбұрыштың
ауданы 72
см2тең болса, шеңбердің ұзындығын
табыңыз.
4 балл Егер шеңберге іштей сызылған дұрыс алтыбұрыштың
ауданы 72
см2тең болса, шеңбердің ұзындығын
табыңыз. -
6 балл Шеңберге сырттай сызылған дұрыс үшбұрыштың периметрі 18 см-ге тең.Осы шеңберге іштей сызылған дұрыс тӛртбұрыштың периметрін және ауданын табыңыз.
-
Бағалау критерийі
Тапсыр- ма №
Дескриптор
Балл
Білім алушы
есептерді шешу кезінде шеңбер доғасының ұзындығының формуласын қолданады;
1
шеңбер доғасын есептеу үшін тиісті формуланы қолданады
1
есептеулерді орындайды және жауапты
жазады
1
есептерді шешу кезінде сектордың ауданын,сегментін формуласын қолданады
2
шеңбер доғасының ұзындығының формуласын пайдаланады;
1
осы доғаға сәйкес орталық бұрыштың
шамасын есептейді;
1
шеңбер секторының ауданының
формуласын пайдаланады;
1
сектордың ауданын есептейді
1
есептерді шешу кезінде дұрыс кӛпбұрыштың іштей және сырттай сызылған радиустарының арасындағы байланысты қолданады
3
алтыбұрыштың ауданы мен оның жағы
арасында байланыс табады;
1
осы алтыбұрыштың жағын табады;
1
дұрыс кӛпбұрыштың жағы мен сырттай сызылған шеңбердің радиустың
арасындағы байланысты орнатады;
1
шеңбер ұзындығының формуласын қолданады және оның ұзындығын
есептейді;
1
4
осы дұрыс үшбұрыштың қабырғасын анықтайды;
1
шеңбердің радиусын есептейді;
1
дұрыс кӛпбұрыштар арасындағы байланыс орнатады;
1
дұрыс тӛртбұрыштың қабырғаларын
есептейді;
1
дұрыс тӛртбұрыштың периметрін есептейді;
1
дұрыс тӛртбұрыштың ауданын есептейді;
1
Жалпы ұпай:
16
-
2 балл Егер оның градустық ӛлшемі 150° - қа, ал радиусы 3 см тең болса, доғаның ұзындығын табыңыз.
-
4 баллШеңберінің айналмалы секторының ауданы 9?см2 радиус 6см тең болса. Тиісті доғанын ұзындығын табыңыз.
-
 4 балл Егер шеңберге сырттай сызылған оң алтыбұрыштың
ауданы 84 см2тең болса, шеңбердің ұзындығын
табыңыз.
4 балл Егер шеңберге сырттай сызылған оң алтыбұрыштың
ауданы 84 см2тең болса, шеңбердің ұзындығын
табыңыз. -
6 балл Шеңберге іштей сызылған дұрыс үшбұрыштың периметрі 27 см-ге тең.Осы шеңберге сырттай сызылған дұрыс тӛртбұрыштың периметрін және ауданын табыңыз.
-
Бағалау критерийі
Тапсыр- ма №
Дескриптор
Балл
Білім алушы
есептерді шешу кезінде шеңбер доғасының ұзындығының формуласын қолданады;
1
шеңбер доғасын есептеу үшін тиісті формуланы қолданады
1
есептеулерді орындайды және жауапты
жазады.
1
есептерді шешу кезінде сектордың ауданын,сегментін формуласын қолданады
2
шеңбердің айналмалы секторының
формуласын пайдаланады;
1
осы сектордың доғасына сәйкес орталық бұрыштың шамасын есептейді;
1
доға ұзындығын формуласын
пайдаланады;
1
доға ұзындығын есептейді.
1
есептерді шешу кезінде дұрыс кӛпбұрыштың іштей және сырттай сызылған радиустарының арасындағы байланысты қолданады;
3
алтыбұрыштың ауданы мен оның
жақтарымен байланыс табады;
1
осы алтыбұрыштың қабырғасын табады;
1
дұрыс кӛпбұрыштың жағы мен сәйкес шеңбердің радиусы арасындағы байланысты орнатады;
1
шеңбер ұзындығының формуласын қолданады және оның ұзындығын
есептейді;
1
4
осы дұрыс үшбұрыштың қабырғасын
анықтайды;
1
шеңбердің радиусын есептейді;
1
дұрыс кӛпбұрыштар арасындағы байланыс орнатады;
1
дұрыс тӛртбұрыштың қабырғаларын есептейді;
1
дұрыс тӛртбұрыштың периметрін
есептейді;
1
дұрыс тӛртбұрыштың ауданын есептейді;
1
Жалпы ұпай:
16
Алгебра
І тоқсанға арналған ТЖБ
-
Орындау уақыты
40 минут
І нұсқа
-
3 балл Теңдеулер жүйесін шешіңіз:
5?2 − y2 + 6? = 11;
{ ?2 + ?2 = 25.
-
4 балл Есепті теңдеулер жүйесін құрып шығарыңыз.
Тік бұрышты үшбұрыштың ауданы 85 см2 –ге, ал катеттері ұзындықтарының айырымы 7 см-ге тең. Үшбұрыштың гипотенузасын табыңыз.
-
4 балл Теңсіздіктер жүйесінің шешімдері болатын нүктелер жиының
координаталар жазықтығына кескіндеңдер:{
y ≤ − 1
![]() 2
2
?2
+ 2;
![]()
? < 2√x.
-
2 балл (1 2x)4 жіктелуінің x3 коэфициентің табыңдар
-
2 балл 572019 неше әртүрлі сандар құрастыруға болады, егер цифрларын орын ауыстырсақ?
-
2 балл Егер бірінші орында 0 цифры тұра алмайтынын білсек, неше бес таңбалы қайталанатын цифрлары жоқ телефонның номерін құрастыруға болады?
-
3 балл Ротада 16 солдат,4 офицер және 3 сержант бар.Объекті күзету үшін 6 солдаты бӛлу керек,бір сержанты және екі офицерді. Нарядты неше тәсілмен таңдауға болады ? Барлығы: 20 ұпай
II нұсқа
-
3 балл Теңдеулер жүйесін шешіңіз:
?2 + ?2 = 81;
{ ?2 − ? = 9.
-
4 балл Есепті теңдеулер жүйесін құрып шығарыңыз.
Тік бұрышты үшбұрыштың гипотенузасы 15 см -ге, ал үшбұрыштың периметрі 36 см тең болатын үшбұрыштың ауданын табыңдар.
-
4 балл Теңсіздіктер жүйесінің шешімдері болатын нүктелер жиының
координаталар жазықтығына кескіндеңдер: {y ≥
1 ?2
![]() 2
2
− 2;
![]()
? > −2√x.
-
2 балл (2 x)4 жіктелуінің x2 коэфициентің табыңдар
-
2 балл 52018 неше әртүрлі сандар құрастыруға болады, егер цифрларын орын ауыстырсақ?
-
2 балл Егер бірінші орында 0 цифры тұра алмайтынын білсек, неше алты таңбалы қайталанатын цифрлары жоқ телефонның номерін құрастыруға болады?
-
3 балл Ротада 14 солдат,2 офицер және 4 сержант бар.Объекті күзету үшін 7 солдаты бӛлу керек,бір сержанты және екі офицерді. Нарядты неше тәсілмен таңдауға болады?
Барлығы: 20 ұпай
Балл қою кестесі
І нұсқа
|
№ |
Жауабы |
Ұпай |
Қосымша ақпарат |
|
1 |
Қосу тәсілін пайдаланып осындай теңдеу алады 6x2 + 6x = 36 |
1 |
|
|
Теңдеуді шығарады x2 + x − 6 = 0 ; х=-3, х=2 |
1 |
|
|
|
у=±√21; y = ±4 (2; √21); (2; −√21); (−3; 4); (−3; −4) |
1 |
|
|
|
2 |
1 Жаңа айнымалы енгізеді {2 x − y = 7. |
1 |
|
|
Жаңа айнымалы енгізіп теңдеуді шығарады : y2 + 7y − 170 = 0 |
1 |
|
|
|
Теңдеудің түбірін табады у=-17, у=10, тексеру арқылы теңдеудің түбірін табады х=10, |
1 |
|
|
|
с |
1 |
|
|
|
3 |
Парабола графигін, тармақтарды тӛмен, жоғарғы (0; 2), Тұтас қисық; |
1 |
|
|
Квадрат түбірінің кестесін, нүктелі қисық қисықты жасайды; |
1 |
|
|
|
Жазықтықтың нүктелерін параболдан тӛмен белгілейді және жазықтықта квадрат түбірдің нүктелерін графиктен тӛмен және оу осінен оңға қарай белгілейді; |
1 |
|
|
|
Жүйенің шешімін оу осінен оңға қарай, квадрат түбірінің кестесінен тӛмен және параболанын сол жағында. |
1 |
|
|
|
4 |
−C3 · 1 · (2x)2 4 |
1 |
|
|
-32 |
1 |
|
|
|
5 |
P6 − P5 |
1 |
5 · 5 · 4 3 · 2 · 1 |
|
= 6! − 5! = 720 − 120 = 600 |
1 |
600 |
|
|
6 |
A5 − A4 = 10 9 |
1 |
6 · 7 · 8 · 9 · 9 |
|
10! 9! = − = 6 · 7 · 8 · 9 · 9 = 27216 5 |
1 |
27216 |
|
|
7 |
C6 · C1 · C2 = 16 3 4 |
1 |
|
|
16! 3! 4! · 6 |
1 |
|
|
|
11 · 13 · 14 · 8 · 9 = 144144 |
1 |
|
|
|
Барлығы: |
20 |
|
|
II нұсқа
|
№ |
Жауабы |
Ұпай |
Қосымша ақпарат |
|||||
|
1 |
Қосу тәсілін пайдаланып осындай теңдеу алады y2 + y = 72 |
1 |
|
|||||
|
Теңдеуді шешеді : y2 + y − 72 = 0 ; у=-9, у=8 |
1 |
|
||||||
|
х |
1 |
|
||||||
|
2 |
Жаңа айнымалы енгізеді x2 + y2 = 225; {x + y = 36 − 15. |
1 |
|
|||||
|
Жаңа айнымалы енгізіп теңдеуді шығарады : x2 − 21x + 108 = 0 |
1 |
|
||||||
|
Теңдеудің түбірін табады х=9, х=12, катеты 9 және 12 |
1 |
|
||||||
|
S=54 см2 |
1 |
|
||||||
|
3 |
Парабола графигін сызады, бұтақтары жоғары, шыңы (0; -2), тұтас қисық |
1 |
|
|||||
|
Квадрат түбірінің графигін салады, қисық |
1 |
|
||||||
|
Жазықтықтың нүктелерін параболдан жоғары белгілейді және жазықтықтың нүктелерін квадрат түбірінің кестесінен жоғары және оу осінен оңға қарай белгілейді. |
1 |
|
||||||
|
Жүйенің шешімін оу осінен оңға қарай, квадрат түбірінің графигінен жоғары және параболадан сол жақта. |
1 |
|
||||||
|
4 |
−C2 · 22 · x2 4 |
1 |
1 4 6 4 1 |
|||||
|
-24 |
1 |
622(-х)2; -24 |
||||||
|
5 |
P5 − P4 |
1 |
4 · 4 · 3 · 2 · 1 |
|||||
|
= 5! − 4! = 120 − 24 = 96 |
1 |
96 |
||||||
|
6 |
A6 − A5 = 10 9 |
1 |
5 · 6 · 7 · 8 · 9 · 9 |
|||||
|
= |
10!
4! |
− |
9!
4! |
= 5 · 6 · 7 · 8 · 9 · 9 = 136080 |
1 |
136080 |
||
|
7 |
C7 · C1 · C2 = 14 2 4 |
1 |
|
|||||
|
14! |
|
|
2! |
4! |
1 |
|
||
|
7! · 7! 1! · 1! 2! · 2! |
||||||||
|
8 · 9 · 11 · 13 · 4 = 41184 |
1 |
|
||||||
|
Барлығы: |
20 |
|
||||||
ІІ тоқсанға арналған ТЖБ
Орындау уақыты: 40 минут
І нұсқа
-
[1 балл] арифметикалық прогрессияның n-ші мүшесінің формуласын жазыңдар:
![]()
![]() 3 ; 6 ;
3 ; 6 ;
2 3
9 ;12
![]()
![]() 4
5
4
5
;15
![]() 6
6
;18
![]() 7
7
...
-
[6 балл] 11,2; 10,8; … арифметикалық прогрессияның оң таңбалы мүшелерінің қосындысын табыңыз?
-
[3 балл] Бірінші және тӛртінші геометриялық прогрессияның қосындысы 40 тең, ал екінші және бесінші мүшелерінің қосындысы 10-ға тең болса. Еселігін табыңдар.
-
[6 балл] Үш сан x, y, 20 ӛспелі геометриялық прогрессия, ал x, y, 15 сандар – арифметикалық прогрессияның мүшелерін құрайтын болса,онда y-x -ның қосындысын табыңыз.
-
[4 балл] Шексіз кемімелі геометриялық прогрессияның q-сын табыңдар,егер екінші мүшесі (-0,5) тең , ал шексіз кемімелі геометриялық прогрессияның қосындысы 1,6-ға тең болса.
ІІ нұсқа
-
[1 балл] арифметикалық прогрессияның n-ші мүшесінің формуласын жазыңдар:
![]()
![]()
![]()
![]()
![]()
![]() 7 ;14 ; 21; 28 ; 35 ; 42 ...
7 ;14 ; 21; 28 ; 35 ; 42 ...
2 3 4 5 6 7
-
[6 балл] –7,2; –6,9; … арифметикалық прогрессияның теріс таңбалы мүшелерінің қосындысын табыңыз?
-
[3 балл] Ӛспелі геометриялық прогрессияның тӛртінші мүшесі екінші мүшесінен 24- ке артық, ал екінші мен үшінші мүшелерінің қосындысы 6-тең болса, q-сын табыңдар.
-
[6 балл] Үш сан a, b, 12 ӛспелі геометриялық прогрессия , ал a, b, 9 сандар – арифметикалық прогрессияның мүшелерін құрайтын болса,онда a+b-ның қосындысын табыңыз
-
[4 балл] Шексіз кемімелі геометриялық прогрессияның қосындысы 6-ға, ал алғашқы екі мүшесінің қосындысы 9/2тең болса,онда геометриялық прогрессияның еселігін табыңдар .
Балл қою кестесі
|
№ |
Жауабы |
Ұпай |
Қосымша ақпарат |
|
|
I нұсқа |
II нұсқа |
|||
|
1 |
a 3n n |
a 7n n |
1 |
|
|
2 |
a1 = 11,2; d = 10,8 – 11,2 = -0,4; S 2a1 d (n 1) n
n |
a1 = -7,2; d = -6,9 + 7,2 = 0,3; S 2a1 d (n 1) n n 2 |
1 |
|
|
an = a1 + d(n-1) |
an = a1 + d(n-1) |
1 |
|
|
|
11,2 - 0,4(n-1) > 0 |
-7,5 + 0,3n < 0 |
1 |
|
|
|
n < 29 |
n < 25 |
1 |
|
|
|
n = 28 |
n = 24 |
1 |
|
|
|
S28 = 162,4 |
S24 = -90 |
1 |
|
|
|
3 |
b1 b4 40 b2 b5 10 |
b4 b2 24 b2 b3 6 |
1 |
|
|
b b q3 40 1 1 b b q 4 10 1 1 |
b q3 b q 24 1 1 b q b q 2 6 1 1 |
1 |
|
|
|
q = 1 4 |
q = 5 |
1 |
|
|
|
4 |
Г |
Г |
1 |
|
|
А.п.: x, y, 15 y x 15
2 |
А.п.: a, b, 9 b a 9
2 |
1 |
|
|
|
x 15 2 |
a 9 2 |
1 |
|
|
|
x1 45 ; x2 5 y 30 y 10 1 2 |
a1 3 ; a2 27 6 18 b1 b2 |
1 |
|
|
|
(x1; y1) сәйкес келмейді, себебі x > y |
(27; 18) сәйкес келмейді, себебі a ≤ 12 |
1 |
|
|
|
y – x = 5 |
a + b = 9 |
1 |
|
|
|
5 |
b2 = -0,5; b1q = -0,5 |
S = b1 , b2 = b1q 1 |
1 |
|
|
|
S = 1,6; S = b1 1 |
b1 6 b b q 9 |
1 |
|
|
q1 1,25 q2 0,25 |
b1 6(1 q) 9 |
1 |
|
|
|
q = 1,25 – сәйкес келмейді; q = -0,25 |
q = -0,5; q = 0,5 |
1 |
|
|
|
Барлығы: |
20 |
|
||
3 нұсқа
-
[3балл] Сандар тізбегі n-мүшесінің n2+2n формуласымен берілген: а) алғашқы бес мүшесін табыңыз;
б) 24 саны тізбектің қандай мүшесі болады.
-
[3 балл] Келесі тізбектің қай саны арифметикалық прогрессия мүшелері болатынын табыңыз: 3; 6; 9; 12;…?
1) 83 3) 100
2) 95 4) 102
-
 [4 балл] Егер a1 =
−3,1, a?+1 =
?? +
0,9 .
болса,арифметикалық
9 мүшесінің қосындысын табыңыз
[4 балл] Егер a1 =
−3,1, a?+1 =
?? +
0,9 .
болса,арифметикалық
9 мүшесінің қосындысын табыңыз
-
[4 балл] bn - геометриялық прогрессия берілген, ал еселігі q=1. Егер b5 =4:
3
а) табу керек b1.
б) Шексіз кемімелі геометриялық прогрессияның қосындысын табыңыз.
-
[3 балл] bn геометриялық прогрессия, егер b1=1 и q=5 болса, онда b1+b2+b3+b4+b5 қосындысын табыңыз
-
[3 балл] Жұмысшылар тротуар плиткасын тӛседі. Бірінші күні олар 30 плитка қойды. Әр келесі күні олар 5 плиткаға кӛп салынды. Бір аптанын ішінде қанша плиткалар салынды.
4 нұсқа.
-
[3 балл] Сандар тізбегі n-мүшесінің n2+3n формуласымен берілген: а) алғашқы үш мүшесін табыңыз;
б) 40 саны тізбектің қандай мүшесі болады
-
[3 балл] Келесі тізбектің қай саны арифметикалық прогрессия мүшелері болатынын табыңыз: 2; 5; 8; 11;…?
1) 30 3) 35
2) 33 4) 37
-
 [4 балл] Егер a1 =
−2,3, a?+1 =
?? +
0,6 болса, арифметикалық 10 мүшесінің қосындысын табыңыз.
[4 балл] Егер a1 =
−2,3, a?+1 =
?? +
0,6 болса, арифметикалық 10 мүшесінің қосындысын табыңыз.
-
[4 балл] bn - геометриялық прогрессия берілген, ал еселігі q=1. Егер b3 =1:
2
а) табу керек b1.
б) Шексіз кемімелі геометриялық прогрессияның қосындысын табыңыз.
-
[3балл] bn геометриялық прогрессия, егер b1=2; q=3 болса, онда b1+b2+b3+b4+b5 қосындысын табыңыз.
-
[3 балл] Жұмысшылар тротуар плиткасын тӛседі. Бірінші күні олар 40 плитка қойды. Әр келесі күні олар 6 плиткаға кӛп салынды. 10 күн ішінде қанша плиткалар салынды.
Балл қою кестесі
|
|
3 нұсқа |
4 нұсқа. |
|
|
№ |
Жауабы |
Жауабы |
Ұпай |
|
1 |
а5=52+2· 5 = 25 + 10 = 35 |
a3=32+3· 3 = 9 + 9 = 18 |
1 |
|
24=n2+2· ?; |
40=n2+3· ?; |
1 |
|
|
?2 + 2? − 24 = 0; ? = 4 |
?2 + 3? − 40 = 0; ? = 5 |
1 |
|
|
2 |
a? = ?1 + ?(? − 1), ?1 = 3, ? = 3 |
a? = ?1 + ?(? − 1), ?1 = 2, ? = 3 |
1 |
|
102=3+3(n-1) |
35=2+3(n-1) |
1 |
|
|
n=34. 102 саны |
n=12. 35 саны |
1 |
|
|
3 |
a2 = ?1 + 0,9 = −3,1 + 0,9 = −2,2 |
a2 = ?1 + 0,6 = −2,3 + 0,6 = −1,7 |
1 |
|
|
? = ?2 − ?1 = −2,2 + 3,1 = 0,9 |
? = ?2 − ?1 = −1,7 + 2,3 = 0,6 |
1 |
|
|
2?1 + ?(? − 1) ?? = 2 ? 2 ?9 = 2 · 9 |
2?1 + ?(? − 1) ?? = 2 ? 2 ?10 = 2 · 10 |
1 |
|
|
?9 = 4,5 |
?10 = 4 |
1 |
|
4 |
? = ? · ??−1; ? = ?5 = 4 5 1 1 ??−1 14
3 |
? = ? · ??−1; ? = ?3 = 1 3 1 1 ??−1 12
4 |
1 |
|
|
?1 = 4 · 81 = 324 |
?1 = 16 |
1 |
|
|
?1 324 ? = = ? − 1 1 − 1 3 |
?1 16 ? = = ? − 1 1 − 1 4 |
1 |
|
|
? = −486 |
1 ? = −21 3 |
1 |
|
5 |
?1(?? − 1) ?? = ? − 1 |
?1(?? − 1) ?? = ? − 1 |
1 |
|
|
1(55 − 1) 3125 − 1 3124 |
2(35 − 1) 2(243 − 1) 2 · 242 |
1 |
|
|
?5 = 5 − 1 = 4 = 4 |
?5 = 3 − 1 = 2 = 2 |
|
|
|
?5 = 781 |
?5 = 242 |
1 |
|
6 |
2 ?1 = 30, ? = 5, ?? = 2 ? |
2 ?1 = 40, ? = 6, ?? = 2 ? |
1 |
|
|
2 ?7 = 2 · 7 60 + 30 = 2 |
2 ?10 = 2 · 10 80 + 54 = 2 |
1 |
|
|
?7 = 315 |
?7 = 670 |
1 |
|
|
Барлығы: |
|
20 |
ІІІ тоқсанға арналған ТЖБ
|
Орындау уақыты: |
40 минут |
І нұсқа
1. [ 2 балл] Сол және оң бағандар арасында сәйкестікті орнатыңыз:
|
1. 2400 |
А. 24 9 |
|
2. 48 9 |
В. 9600 |
|
|
С. 4800 |
|
|
D. 4 3 |
|
|
E. 48,90 |
-
; 2.
-
[ 4 балл] Ӛрнекті ықшамдаңыз: tg cos
1 sin
![]()
![]()
![]()
![]()
![]()
В
.
1
-



2
[ 3 балл] Бұрышты анықтайтын радиус бір шеңбердің нүктесінен ӛтеді ;
2
sin, cos,tg мәнін жазыңыз.
-
[ 5 балл] Ӛрнекті ықшамдаңыз: cos cos sin 2
![]()
![]()
1 sin 1 sin ![]()
![]()
![]()
2
sin 3 -
[ 6 балл] Ӛрнекті ықшамдаңыз:
tg ( )
cos( )
![]()
ctg 3
![]()
2
ІІ нұсқа
-
[ 2 балл] Сол және оң бағандар арасында сәйкестікті орнатыңыз:
|
1. 4800 |
А. 24 9 |
|
2. 35 9 |
В. 8 3 |
|
|
С. 3500 |
|
|
D. 4 3 |
|
|
E. 7000 |
-
; 2.
-
[ 4 балл] Ӛрнекті ықшамдаңыз: ctg sin
1 cos
-
[ 3 балл] Бұрышты анықтайтын радиус бір шеңбердің нүктесінен ӛтеді
К 1 ; .
![]()
![]()
![]()
![]()
![]()
![]()
3
2
2
sin, cos,tg ![]()
мәнің жазыңыз.
-
[ 5 балл] Ӛрнекті ықшамдаңыз: sin sin sin 2
![]()
![]()
1 cos 1 cos -
[ 6 балл] Ӛрнекті ықшамдаңыз:
sin( )
ctg
![]()
2
![]()
tg ( )
![]()
cos 
![]()
2
Балл қою кестесі
|
|
1 нұсқа |
2 нұсқа |
|
|
№ |
Жауабы |
Жауабы |
Балл |
|
1 |
1 – D |
1 – В |
1 |
|
2 – В |
2 – Е |
1 |
|
|
2 |
sin cos cos 1 sin |
cos sin sin 1 cos |
1 |
|
s cos 1 sin |
c sin 1 cos |
1 |
|
|
s |
c |
1 |
|
|
1
cos |
1
sin |
1 |
|
|
3 |
sin 1 2 |
cos 1 2 |
1 |
|
cos 3 2 |
sin 3 2 |
1 |
|
|
tg sin 1 : 3 1 3 c |
tg sin 3 : 1 3
cos 2 2 |
1 |
|
|
4 |
sin cos sin sin cos sin sin 2 1 cos 1 cos |
cos cos sin cos cos sin sin 1 sin 1 sin |
2 1 |
|
2sin sin 2
1 cos 2 |
2 cos sin 2
1 sin 2 |
1 |
|
|
2sin sin 2
sin 2 |
2 cos sin 2
cos 2 |
1 |
|
|
2 2sin cos
sin |
2 2sin cos
cos |
1 |
|
|
4cos |
4sin |
1 |
|
|
5 |
tg( ) tg |
sin( ) sin |
1 |
|
cos( ) cos |
tg( ) tg |
1 |
|
|
sin 3 cos 2 |
ctg tg 2 |
1 |
|
|
ctg 3 tg 2 |
cos sin 2 |
1 |
|
|
tg cos cos tg |
cin tg tg sin |
1 |
|
|
1 |
1 |
1 |
|
|
Барлығы: |
20 |
||
VI тоқсанға арналған ТЖБ
|
Орындау уақыты: |
40 минут |
І нұсқа
-
[2 балл] Екі ойын сүйегі лақтырылды.Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 7 болу ықтималдығын табыңыз.
-
[5 балл] Урнада 3 ақ және 6 қара шарлар бар.
-
Урнадан бір уақытта екі шар алынады. Олар бірдей түсті болу ықтималдығын табыңыз.
-
Бір уақытта екі шарды алып тастағанда, қандай оқиға болуы мүмкін А «бір түсті шарлар», В – «түрлі түсті шарлар»?
-
-
[2 балл] Бұйымдардың сапасын тексеру үшін 200 бӛлшектер зерттелді,олардың ішінде 8 ақаулы болды.
а) наугад алынған бӛлшектің жарамды болуы ықтималдығын табыңыз.
b) 1000 бӛлшектен тұратын партияда орташа ақаулы бӛлшектер қанша болады?
-
[3 балл] Радиус шеңберінің ішінде R наудачу нүкте тасталған. Нүкте шеңберге жазылған квадрат ішінде болуы ықтималдығын табу. Шеңбердің бӛлігіне нүктенің құлау ықтималдығы осы бӛліктің алаңына пропорционалды және оның шеңберге қатысты орналасуына байланысты емес деп болжанады.
-
[3 балл] Ӛрнекті ықшамдаңыз: sin 2 3cos 2 2 cos 2 3sin 2 2 .
-
[5 балл] Тепе-теңдікті дәлелдеңіз:
cos cos 2tg .
1sin 1 sin
ІІ нұсқа
-
[2 балл] Екі ойын сүйегі лақтырылды.Сүйектердің жоғарғы жағында шыққан сандардың қосындысы 8 болу ықтималдығын табыңыз.
-
[5 балл] Урнада 5 ақ және 3қара шарлар бар.
-
Урнадан бір уақытта екі шар алынады. Олар бірдей түсті болу ықтималдығын табыңыз.
-
Бір уақытта екі шарды алып тастағанда, қандай оқиға болуы мүмкін А «бір түсті шарлар», В – «түрлі түсті шарлар»?
-
-
[2 балл] Бұйымдардың сапасын тексеру үшін 500 бӛлшектер зерттелді,олардың ішінде 9 ақаулы болды.
а) наугад алынған бӛлшектің жарамды болуы ықтималдығын табыңыз.
b)1000 бӛлшектен тұратын партияда орташа ақаулы бӛлшектер қанша болады?
-
[3 балл] Радиус шеңберінің ішінде R наудачу нүкте тасталған. Нүкте шеңберге жазылған квадрат ішінде болуы ықтималдығын табу. Шеңбердің бӛлігіне нүктенің құлау ықтималдығы осы бӛліктің алаңына пропорционалды және оның шеңберге қатысты орналасуына байланысты емес деп болжанады.
-
[3 балла] Ӛрнекті ықшамдаңыз : 2sin 3 3cos 3 2 2cos 3 3sin 3 2 .
-
[5 баллов] Тепе-теңдікті дәлелдеңіз:
sin sin 2ctg .
1 cos 1 cos
Балл қою кестесі:
І нұсқа
|
№ |
Жауап |
Балл |
Қосымша ақпарат |
|
1 |
(2;5), (1;6) |
1 |
|
|
(5;2), (6;1) |
1 |
||
|
2(a) |
C92 , C32 , C62 |
1 |
Ең болмағанда бір дұрыс жазуға балл қою |
|
С 2 С 2 3! 6! 3 |
1 |
||
|
С 2 С 2 1 Р( А) 3 6 С 2 2 9 |
1 |
||
|
2(b) |
С1С1 3 6 |
1 |
Қабылданады балама жауап |
|
P |
1 |
||
|
3(а) |
200 8 0,975 200 |
1 |
|
|
3 (b) |
1000 5; 58 40 2 |
1 |
|
|
4 |
?кв = 2?2
|
1 |
|
|
2?2 P = ??2 |
1 |
||
|
2 P = ? |
1 |
||
|
5 |
???22? + 6???2????2? + 9???22? + ???22? − −6???2????2? + 9???22? |
1 |
|
|
Мұндай қосылыстарды келтіреді |
1 |
||
|
1+9=10 |
1 |
||
|
6 |
cos cos asin cos sin cos 2tg 1sin 2 |
1 |
|
|
Мұндай қосылғыштарды келтіріңіз. Негізгі тригонометриялық тепе-теңдікті қолданады |
1 |
||
|
2 cos sin 2tg cos2 |
1 |
||
|
2 ??? ? = 2??? ??? ? |
1 |
||
|
2tgα=2tgα |
1 |
||
|
Барлығы |
20 |
|
|
ІІ нұсқа
|
№ |
Жауап |
Балл |
Қосымша ақпарат |
|
1 |
(3;5), (5;3) |
1 |
|
|
(2;6), (6;2) (4;4) |
1 |
||
|
2(a) |
C82 , C52 , C32 |
1 |
Ең болмағанда бір дұрыс жазуға балл қою |
|
С 2 С 2 5! 3! 13 5 |
1 |
||
|
С 2 С 2 13 Р( А) 5 3 С 2 28 8 |
1 |
||
|
2(b) |
С1С1 15 5 3 |
1 |
Қабылданады балама жауап |
|
С 2 С 2 15 Р(В) 5 3 С 2 28 8
P |
1 |
||
|
3(а) |
500 9 0,982 500 |
1 |
|
|
3 (b) |
1000 2; 2 9 18 500 |
1 |
|
|
4 |
а 2R sin 60o R 3
a S R 4 |
1 |
|
|
P Sтр 3 3 R3 1 S кр |
1 |
||
|
P 3 3 4 |
1 |
||
|
5 |
4sin2 3 12sin 3 cos 3 9 cos2 3 4 cos2 3 12sin 3 cos 3 9sin2 3 |
1 |
|
|
Мұндай қосылыстарды келтіреді |
1 |
||
|
Ӛрнек мәнін табады =13 |
1 |
||
|
6 |
sin sin cos sin sin cos 2ctg 1 cos2 |
1 |
|
|
Мұндай қосылғыштарды келтіріңіз. Негізгі тригонометриялық тепе-теңдікті қолданады |
1 |
||
|
2sin cos 2ctg sin2 |
1 |
||
|
2 cos 2ctg sin |
1 |
||
|
2ctg 2ctg |
1 |
||
|
Барлығы: |
20 |
|
|
Геометрия
1 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
|
Ұзақтылығы |
40 минут |
I нұсқа
-
 2 балл Суретте берілген тӛртбұрыш ABCD– ромб, оның А бұрышы 126°қа тең.
̅B̅̅̅A̅→ и ̅A̅̅̅?̅→ векторлары арасындағы бұрышты
анықтаңыз
2 балл Суретте берілген тӛртбұрыш ABCD– ромб, оның А бұрышы 126°қа тең.
̅B̅̅̅A̅→ и ̅A̅̅̅?̅→ векторлары арасындағы бұрышты
анықтаңыз-
126°;
-
60°;
-
54°;
-
64°;
-
120°.
-
-
3 балл ̅b→ векторының координатасын және ұзындығын табыңыз, егер
![]() ̅b→= 1 c→ − ̅d→, ̅c→ = −3?→ + 6?→, ̅d→ = 2?→ − 2?→ белгілі болса.
̅b→= 1 c→ − ̅d→, ̅c→ = −3?→ + 6?→, ̅d→ = 2?→ − 2?→ белгілі болса.
3
-
2 балл АВСD трапециясы берілген
̅A̅̅̅B̅→ − ̅A̅̅̅?̅→ + ̅?̅̅̅?̅→ ны табыңыз.
-
5 балл M( -3; 2), P(-1; -2), K(2; 1), D(5; b) нүктелері берілген
-
b векторының қандай мәнінде ̅?̅̅̅̅?̅→ және ̅?̅̅̅̅?̅→ коллинеар болады?
-
b векторының қандай мәнінде ̅?̅̅̅̅̅P→ және ̅?̅̅̅?̅→ перпендикуляр болады?
-
4 балл МNK үшбұрышының тӛбелерінің координаталары
?(2; −3), ?(−4; 6), ?(5; −1) болса, N бұрышының косинусын табыңыз.
-
4 балл АВС теңбүйірлі үшбұрышының периметрі 18 болса, (̅B̅̅̅̅C→ − 3̅B̅̅̅A̅→)2 табыңыз
Барлығы 20 балл.
II нұсқа
-
 2 балл Суретте берілген тӛртбұрыш ABCD– ромб, оның А бұрышы 60°қа тең.
̅B̅̅̅̅C→ и ̅C̅̅̅?̅→ векторлары арасындағы бұрышты анықтаңыз.
2 балл Суретте берілген тӛртбұрыш ABCD– ромб, оның А бұрышы 60°қа тең.
̅B̅̅̅̅C→ и ̅C̅̅̅?̅→ векторлары арасындағы бұрышты анықтаңыз.-
126°;
-
60°;
-
54°;
-
64°;
-
120°.
-
-
3 балл ?→ векторының координатасын және ұзындығын табыңыз, егер
![]() ̅a→= −?̅→+ 1 c→, ? = 3?→ − 2?→, ̅c→ = −6?→ + 2?→.
̅a→= −?̅→+ 1 c→, ? = 3?→ − 2?→, ̅c→ = −6?→ + 2?→.
2
-
2 балл АВСD трапециясы берілген
̅?̅̅̅?̅→ − ̅?̅̅̅?̅→ + ̅?̅̅̅?̅→ ны табыңыз.
-
5 балл А( 2; -1), В(-4; 3), С(5; -1), D(1; a) нүктелері берілген
-
a векторының қандай мәнінде ̅?̅̅̅?̅→ және ̅?̅̅̅?̅→ коллинеар?
-
a векторының қандай мәнінде ̅?̅̅̅?̅→ және ̅?̅̅̅?̅→ перпендикуляр?
-
-
4 балл АВС үшбұрышының тӛбелерінің координаталары ?(3; −1), ?(2; 3), ?(4; −2)
болса, C бұрышының косинусын табыңыз.
-
4 балла АВСD шаршының периметрі 20 болса, (2̅C̅̅̅B̅→ + 3̅C̅̅̅D̅→)2табыңыз
Барлығы 20 балл
I нұсқа
-
№
Жауап
Балл
Қосымша ақпарат
1
(̅B̅̅̅A̅→ ; ̅A̅̅̅?̅→) = (̅B̅̅̅A̅→ ; ̅B̅̅̅̅C→)
1
180-126=54; С
1
2
Жіктеуі бойынша вектордың координасын жазады (-3;6), (2;-2)
1
Балама тәсіл қабылданады
Векторларға координалар арқылы амалдар қолданып, вектордың координатасын табады (-3;4)
1
Вектордың ұзындығын табады 5
1
3
̅A̅̅̅B̅→ − ̅?̅̅̅?̅→ = ̅?̅̅̅̅?̅→
1
̅?̅̅̅̅?̅→ + ̅?̅̅̅?̅→ = ̅?̅̅̅?̅→
1
4
̅?̅̅̅̅?̅→ =(2;-4) және ̅?̅̅̅̅?̅→ = (3; ? − 1) координатасын табады
1
Балама тәсіл қабылданады
Векторлардың коллинеарлық шартын қолданып пропорция құрастырады 2 = −4
3

 ?−1
?−11
Теңдеуді шешіп, b=-5 табады
1
Векторладың перпендикулярлық шартын қолданып векторлардың скаляр кӛбейтіндісі арқылы теңдеу
жазады 6-4(b-1)=0
1
Теңдеуді шешіп, b=2,5 екенін табады.
1
5
Бұрыштан шығатын векторларды анықтап,олардың координаталарын табады (6;-9), (9;-7)
1
Вектордың скаляр кӛбейтіндісін есептейді 117
1
в

 екторлардың модулін есептейді √117и √130
екторлардың модулін есептейді √117и √1301
векторлардың скаляр кӛбейтіндісінің формуласын қолданып, векторлардың арасындағы бұрышты

есептеп табады √117
1
 30
301
6
Қысқаша кӛбейту формуласын қолданып ӛрнекті ықшамдайды
̅?̅̅̅?̅→2 − 6̅?̅̅̅?̅→ · ̅?̅̅̅?̅→ + 9̅?̅̅̅?̅→2
1
Балама тәсіл қабылданады
Үшбұрыштың қабырғасын табады 18: 3=6 және
скаляр квадраттың қасиетін қолданады ̅?̅̅̅?̅→2 = ̅?̅̅̅?̅→2 = 36
1
Тең қабырғалы үшбұрыштың бұрыштары 60° болатынын ескере отырып вектордың скаляр кӛбейтіндісін есептеп табады ̅?̅̅̅?̅→ · ̅?̅̅̅?̅→ = 6 · 6 · 1=18
2

1
Ӛрнектің мәнін есептейді 36 6*18+9*36=252
1
Барлық балл:
20
IІ нұсқа
-
№
Жауап
Балл
Қосымша ақпарат
1
(̅B̅̅̅̅C→ ; ̅C̅̅̅?̅→) = (̅B̅̅̅̅C→ ; ̅B̅̅̅A̅→)
1
180-60=120; Е
1
2
Жіктеуі бойынша вектордың координасын жазады (3;-2), (-6;2)
1
Балама тәсіл қабылданады
Векторларға координалар арқылы амалдар қолданып, вектордың координатасын табады (-6;3)
1
В

 ектордың ұзындығын табады √45 = 3√5
ектордың ұзындығын табады √45 = 3√51
3
̅?̅̅̅?̅→ − ̅?̅̅̅?̅→ = ̅B̅̅̅?̅→
1
̅B̅̅̅?̅→ + ̅?̅̅̅?̅→ = ̅?̅̅̅?̅→
1
4
Bекторларды координаларын табады
̅?̅̅̅?̅→ =(-6;4) және ̅?̅̅̅?̅→ = (−4; ? + 1)
1
Балама тәсіл қабылданады
Векторлардың коллинеарлық шартын қолданып пропорция құрастырады −6 = 4
−

 4 ?+1
4 ?+11
Теңдеуді шешіп, a=5 = 1 2 табады
3
 3
31
Векторладың перпендикулярлық шартын қолданып векторлардың скаляр кӛбейтіндісі
арқылы теңдеу жазады 24+4(a+1)=0
1
Теңдеуді шешіп, a=-7 теңдеуді шешіп.
1
5
Бұрыштан шығатын векторларды анықтап,олардың координаталарын табады (-1;1),
(-2;5)
1
Вектордың скаляр кӛбейтіндісін есептейді 7
1
в

 екторлардың модулін есептейді √2и √29
екторлардың модулін есептейді √2и √291
векторлардың скаляр кӛбейтіндісінің формуласын қолданып, векторлардың арасындағы бұрышты
есептеп табады 7
√
 58
581
6
Қысқаша кӛбейту формуласын қолданып ӛрнекті ықшамдайды
4̅?̅̅̅?̅→2 + 12̅?̅̅̅?̅→ · ̅?̅̅̅?̅→ + 9̅?̅̅̅?̅→2
1
Балама тәсіл қабылданады
Үшбұрыштың қабырғасын табады 20: 4=5 және скаляр квадраттың қасиетін қолданады ̅?̅̅̅?̅→2 =
̅?̅̅̅?̅→2 = 25
1
Тең қабырғалы үшбұрыштың бұрыштары 60° болатынын ескере отырып вектордың скаляр
кӛбейтіндісін есептеп табады ̅?̅̅̅?̅→ · ̅?̅̅̅?̅→ = 5 · 5 · 0 = 0
1
Ӛрнектің мәнін есептейді 325
1
Барлық балл:
20
2 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
Ұзақтығы 40 минут
I нұсқа
-
 [3 балл] ABCD –тіктӛртбұрыш,N нүктесі AD қабырғасының ортасы. Дұрыс тұжырымды белгіле:
[3 балл] ABCD –тіктӛртбұрыш,N нүктесі AD қабырғасының ортасы. Дұрыс тұжырымды белгіле:
-
В нүктесі D нүктесіне О нүктесі арқылы симметриялы b а
-

О
В нүктесі D нүктесіне а түзуі арқылы симметриялы В С -
В нүктесі D нүктесіне b түзуі арұылы симметриялы
-
А нүктесі D нүктесіне а түзуі арқылы симметриялы
-
А нүктесі D нүктесіне О нүктесі арқылы симметриялы
-
А нүктесі D нүктесіне N нүктесіне симметриялы
![]()
![]()
енің
ол
А N D-
[1 балл] Р(-6; 8) нүктесіне абцисса осі арқылы симметриялы б атын нүкт координатасын табыңыз
-
[1 балл] Қай тұжырым дұрыс?
А: Ромбының екі симметрия осі бар,олар оның диагональдары.
В: Ромбының екі симметрия осі бар, олар оның қабырғаларының екі орта перпендикулярлары
C: Ромбының тӛрт симметрия осі бар. D: Барлық тұжырым дұрыс емес.
-
[2 балл] ABC үшбұрышы A1B1C1 үшбұрышына гомотетиялы. AB=7 см, BC=18 см, AC= 23 см. A1B1C1 үшбұрышының кіші қабырғасын табыңыз, егер оның үлкен қабырғасы 115 см тең болса
-
[4 балл] ABC үшбұрышында AD биссектрисасы жүргізілген.Егер АС = 4; DC = 2; BD = 3-ке тең болса, ABC үшбұрышының периметр табыңыз.
-
[4 балл] АВС үшбұрышында АС қабырғасына параллель түзу АВ және ВС қабырғаларын сәйкес М және N нүктелерінде қиып ӛтеді. NС қабырғасын табыңыз, егер АС=69, МN=23, ВN=60 тең болса.
-
[2 балл] Параллель кӛшіруде А(–3; 4) нүктесі А1(1; –1)нүктесіне кӛшеді.В(2; –3) нүктесі параллель кӛшіру арқылы B1 нүктесіне кӛшсе B1 нүктесінің координатасын табыңыз.
![]()
8.[1 балл] АВСD ромб салыңыз. АС векторы арқылы параллель бейнеленген ромбыны салыңыз.
 9. [2
балл] Суреттегі екі үшбұрыштың ұксас екенін кӛрсетіңіз.
9. [2
балл] Суреттегі екі үшбұрыштың ұксас екенін кӛрсетіңіз.
II нұсқа
-
 [
[О
b
D
А
С
a
В
3 балл] ABCD – тіктӛртбұрыш,N нүктесі СD қабырғасының ортасы.Дұрыс тұжырымжы анықта:-
В нүктесі а түзуі арқылы D нүктесіне b симметриялы
-
В нүктесі О нүктесі арқылы D нүктесіне симметриялы
-
В нүктесі b түзуі арқылы D нүктесіне симметриялы а
-
С нүктесі а түзуі арқылы D нүктесіне симметриялы
-
С нүктесі N нүктесі арқылы D нүктесіне симметриялы
-
С нүктесі О нүктесі арқылы D нүктесіне симметриялы
-
-
[1 балл] С(-4; 7) нүктесіне координаталар басы арқылы симметриялы болатын нүктенің координатасын табыңыз.
-
[1 балл] Қай тұжырым дұрыс?
А: Тіктӛртбұрыштың екі симметрия осі бар,олар оның диагональдары.
В: Тіктӛртбұрыштың екі симметрия осі бар,олар қабырғаларына жүргізілген екі орта перпендикулярлары.
С:Тіктӛртбұрыштың тӛрт симметрия осі бар. D: Барлық тұжырым дұрыс емес.
-
[2 балл] ABC үшбұрышы A1B1C1 гомотетиялы. AB=6 см, BC=15 см, AC= 19 см. A1B1C1 үшбұрышының үлкен қабырғасын табыңыз, егер бұл үшбұрыштың кіші қабырғасы 24 см тең болса.
-
[4 балл] Үшбұрыштың қабырғалары 10 см, 11 см и 12 см.Ортаңғы қабырғаны үшбұрыштың биссектрисасы екі кесіндіге бӛледі.Осы кесінділерді табыңыз.
-
[4балл] АВ және СD кесінділері параллель қабырғаларда жатыр.АС және ВD кесінділері М нүктесінде қиылысады.Егер АВ=10, DС=50, МВ=5 болса, МD-ны табыңыз.
-
[4 балл] Параллель кӛшуде С(2; –3) нүктесі C1(–1; 1)нүктесіне кӛшеді. F(–4; –1) нүктесінің параллель кӛшу арқылы кӛшкен F1 нүктесінің координатасын табыңыз.
![]()
-
[1 балл] АВСD параллелограммын салыңыз. BD векторы арқылы параллель бейнеленген параллелограммды салыңыз.
-

[2 балл] Суреттегі екі үшбұрыштың ұксас екенін кӛрсетіңіз.
Балл қою кестесі
|
|
1 нұсқа |
2 нұсқа |
|
Қосымша ақпарат |
|
№ |
Жауабы |
Жауабы |
Балл |
|
|
1 |
1 |
2 |
1 |
|
|
4 |
4 |
1 |
||
|
6 |
5 |
1 |
||
|
2 |
(-6; -8) |
(4; -7) |
1 |
|
|
3 |
А |
В |
1 |
|
|
4 |
К=115:23=5 |
К=24:6=4 |
1 |
|
|
7.5=35 см |
. 19 4=76 см |
1 |
||
|
5 |
|
|
1 |
|
|
Биссектрисаның қасиеті бойынша BD/AB = DC/AC |
Биссектрисаның қасиеті бойынша АВ/ВР = АС/СР |
1 |
||
|
3/AB = 2/4; АВ = 6 |
CP=x см, BP=(11-x ) см: 12/11-х=10/х, х=5 |
1 |
||
|
РАВС = 6 + 5 + 4 = 15 |
CP=5 см, BP=6 см |
1 |
||
|
6 |
|
|
1 |
|
|
Треугольники ABC и BMN подобны по трем углам (угол В общий, углы А и М, С и N, как соответственные при параллельных прямых и секущей) |
Углы DСМ и ВАМ равны как накрест лежащие, углы DМС и ВМА равны как вертикальные, следовательно, треугольники DСМ и ВМА подобны по двум углам. |
1 |
||
|
АС/МN=ВС/ВN |
МD/МВ=DС/АВ |
1 |
||
|
ВС=180 см. NС=180-60=120 см |
МD=25 |
1 |
||
|
7 |
X1=x+a 1=-3+a ⇒a=4 y1=y+b -1=4+b ⇒b=-5 |
X1=x+a -1=2+a ⇒a=-3 y1=y+b 1=-3+b ⇒b=4 |
1 |
|
|
X1=2+4=6 y1=-3-5=-8, В1 (6;-8) |
X1=-4-3=-7 y1=-1+4=3, F1 (-7;3) |
1 |
|
8 |
B B1 А А1 D D1 |
В D C1 A B1 D1 A1 |
1 |
|
|
9 |
Так как длины сторон обоих треугольников известны, то PR/AC=RQ/CB=PQ/AB |
Так как углы Q и В равны, а длины двух сторон обоих треугольников известны, то QR/BC=QP/ AB |
1 |
|
|
15/5=12/4=6/2=3 (Үшінші белгі) |
12/6=8/4=2 (Екінші белгі) |
1 |
||
|
В се го |
20 |
|
|
|
3 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
Ұзақтығы 40 минут
І нұсқа
-
Үшбұрышқа іштей сызылған шеңбердің радиусы 12-ге тең, үшбұрыштың ауданы 336-ге тең. Осы үшбұрыштың периметрін табыңыз.
-
 RTS үшбұрышында, TS=7, RS=5 тең. Егер sin∠RTS= 2, sin∠TRS табу керек.
RTS үшбұрышында, TS=7, RS=5 тең. Егер sin∠RTS= 2, sin∠TRS табу керек.
7
[2]
![]() [3]
[3]
-
ABC үшбұрышында, AC=3, BC=6, AB=5тең. Сos∠AВС табу керек.
[4]
-
LNM үшбұрышында ∠L=900, NL=6, LM=8 тең.Іштей сызылған шеңбердің радиусын табыңыз. [6]
-
Кӛлденең және тік сызықты биіктікте ұшатын ұшақтын жолағының басы мен шетін білдіретін жолынын ұзындығы 2000м, ∠А=600 және ∠В=300 бұрыштары анықталған. Ұшақ ұшатын С бұрышын және АС биіктігін анықтаңыз.
[5]

В
А
С
Балл қою кестесі
-
№
Жауап
Балл
Керекті ақпарат
1
? 336
? = . ? = = 28
? 12
1
P=28· 2 = 56
1
2
?? ??
=

???∠TRS Sin∠RTS
1
7 5 7 · 2
= ; Sin∠TRS = 7
S
 in∠TRS 2
5
in∠TRS 2
57

1
2
S
 in∠TRS =
in∠TRS =5
1
3
AC2 = AB2 + BC2 − 2AB · BC · ???∠ABC
1
??2 + ??2 − ??2
???∠ABC =
2 · ?? · ??
1
52 + 62 − 32
???∠ABC =
2
 · 5 · 6
· 5 · 61
52 13
???∠ABC = =
6

 0 15
0 151
4
Сурет есептің берілгеніне сәйкес
1
Пифагор теорема бойынша



?? = √??2 + ??2 = √62 + 82 = √100 = 10
1
S=1 ?? · ?? = 1 · 6 · 8 = 24
2
 2
21
p=??+??+?? = 6+8+10 = 12
2
 2
21
S=p· ?, ? = ?
?
1
24
? = = 2
1
 2
21
5
∠
 C = 1800 − (600 + 300) = 900
C = 1800 − (600 + 300) = 9001
?? ??
=

???∠B Sin∠C
1
AC=???∠B·AB
Sin∠C
1
1
AC=???300·2000 = ·2000 = 1000
2
S
 in900 1
in900 11
∠
 C = 900, AC=1000м
C = 900, AC=1000м1
Барлығы
20
ІІ нұсқа
-
Үшбұрышқа іштей сызылған шеңбердің радиус 24-ке тең,үшбұрыштың ауданы 1152-ге тең. Осы үшбұрыштың периметрін табыңыз.
-
 RTS үшбұрышында, TS=9, RS=6-ға тең. Егер sin ∠RTS= 2, sin ∠TRS табыңыз.
RTS үшбұрышында, TS=9, RS=6-ға тең. Егер sin ∠RTS= 2, sin ∠TRS табыңыз.
9
[2]
![]() [3]
[3]
-
ABC үшбұрышы берілген, AC=4, BC=7, AB=6тең. Сos∠AВС табыңыз.
[4]
-
LNM үшбұрышында ∠L=900, NL=4, LM=3 тең. Іштей сызылған шеңбердің радиусын табыңыздар. [6]
-
Кӛлденең және тік сызықты биіктікте ұшатын ұшақтын жолағының басы мен шетін білдіретін жолынын ұзындығы 1000м, ∠А=450 және ∠В=300 бұрыштары анықталған. Ұшақ ұшатын С бұрышын және АС биіктігін анықтаңыз.
[5]

В
А
С
Балл қою кестесі ІІ нұсқа
-
№
Жауап
Балл
Керекті ақпарат
1
? 1152
? = . ? = = 48
? 24
1
P=48· 2 = 96
1
2
?? ??
=

???∠TRS Sin∠RTS
1
9 6 9 · 2
= ; Sin∠TRS = 9
S
 in∠TRS 2
6
in∠TRS 2
69

1
2 1
S
 in∠TRS = =
in∠TRS = =6 3
1
3
AC2 = AB2 + BC2 − 2AB · BC · ???∠ABC
1
??2 + ??2 − ??2
???∠ABC =
2 · ?? · ??
1
62 + 72 − 42
???∠ABC =
2
 · 6 · 7
· 6 · 71
69 23
???∠ABC = =
8

 4 28
4 281
4
Сурет есептін берілгене сәйкес
1
Пифагор теорема бойынша



?? = √??2 + ??2 = √42 + 32 = √25 = 5
1
S=1 ?? · ?? = 1 · 4 · 3 = 6
2
 2
21
p=??+??+?? = 4+3+5 = 6
2
 2
21
S=p· ?, ? = ?
?
1
6
? = = 1
6

1
5
∠
 C = 1800 − (450 + 300) = 1050
C = 1800 − (450 + 300) = 10501
?? ??
=

???∠B Sin∠C
1
AC=???∠B·AB
Sin∠C
1
1
AC=???300·1000 = ·2000 = 1036
2
S
 in1050 0,965
in1050 0,9651
∠C = 1050, AC=1036м
1
Барлығы
20
-
[4 балл] Үшбұрыштың қабырғаларымен түрлері арқылы сәйкестікті анықтаңыз. (бұрыштарының ӛлшемі бойынша)
|
Үшбұрыштың қабырғаларының ұзындығы |
Үшбұрыштың түрлері |
|
1. 8; 9; 13 |
A. сүйірбұрышты |
|
2. 4; 6; 7 |
B. тікбұрышты |
|
3. 5; 12; 13 |
C. доғалбұрышты |
|
4. 7; 9; 12 |
|
1. 2. 3. 4.
-
[2 балл] Үшбұрыштың ауданы 300 см2, ал іштей сызылған шеңбердің радиусы – 15 см. Үшбұрыштың периметр табыңыз.
-
[2 балл] МРК үшбұрышында МР = 15 см РК = 9 см, ??? ? = 0,4.К бұрышының синусын табыңыз.
-
[7 балл] АВС теңбүйірлі үшбұрышында, АВ қабырғасы 12 см, АС табанына қарсы жатқан бұрыш 1200 тең.Үшбұрышқа сырттай сызылған шеңбердің радиусын табыңыз.
-
[5 балл] Балхаш кӛлінің (АВ) енін және Сарышаган қаласынан (АС) демалыс орнына дейінгі ара-қашықты табыңыз, егер Балхаш қаласымен Сарышаган қаласының арақашықтығы (ВС) 143 км тең, ∠CAB = 500, ∠CBA = 1030бол

4 нұсқа
-
[4 балл] ] Үшбұрыштың қабырғаларымен түрлері арқылы сәйкестікті анықтаңыз. (бұрыштарының ӛлшемі бойынша)
|
Үшбұрыштың қабырғаларының ұзындығы |
Үшбұрыштың түрлері |
|
1. 5; 7; 8 |
A. сүйірбұрышты |
|
2. 10; 13; 18 |
B. тікбұрышты |
|
3. 8; 15; 17 |
C. доғалбұрышты |
|
4. 7; 10; 12 |
|
1. 2. 3. 4.
-
[2 балл] Үшбұрыштың ауданы 500 см2, іштей сызылған шеңбердің радиусы – 25 см.Үшбұрыштың периметрін табыңыз.
-
[2 балл] FDE үшбұрышында DE = 24 см, FD = 18 см, ??? E = 0,6болса.F бұрышының синусын табыңыз.
[7 балл] АВС теңбүйірлі үшбұрышында,табанына қарсы жатқан бұрышы 1200 тең. Бүйір қабырғасы ВС 14 см тең.Үшбұрышқа сырттай сызылған шеңбердің радиусын табыңыз.
-
[5 балл] Балхаш кӛлімен оған қарсы орналасқан демалыс орны (АВ)-ға дейін арақашықтығы 85 км, ал Сарышаган (ВС) қаласына дейінгі арақашықтық 143 км тең және
∠CAB = 500. Сарышаган қаласынан (АС) демалыс орнына дейінгі арақашықтықты табыңыз.

Балл қою кестесі
|
|
3 нұсқа |
4 нұсқа |
|
|
№ |
Жауабы |
Жауабы |
Балл |
|
1 |
1 – С |
1 – А |
1 |
|
2 – А |
2 – С |
1 |
|
|
3 – В |
3 – В |
1 |
|
|
4 – С |
4 – А |
1 |
|
|
2 |
? = ? = 300 = 20см ? 15 |
? = ? = 500 = 20см ? 25 |
1 |
|
Р = 2р = 40 см |
Р = 2р = 40 см |
1 |
|
|
3 |
9 15 = 0 |
18 24 = 0 |
1 |
|
2 ??? ? =
3 |
??? ? = 4 или ??? ? = 0,8 5 |
1 |
|
|
4 |
AC2 = AB2 + BC2 − 2AB · BC · ??? B = = 122 + 122 − 2 · 12 · 12 · ??? 1 200 |
AC2 = AB2 + BC2 − 2AB · BC · ??? B = = 142 + 142 − 2 · 14 · 14 · ??? 1 200 |
1 |
|
??? 1 200 = − ??? 6 00 = − 1 2 |
??? 1 200 = − ??? 6 00 = − 1 2 |
1 |
|
|
АС = 12√3см |
АС = 14√3см |
1 |
|
|
1 ???? = 2 ?? · ?? · ??? ? |
1 ???? = 2 ?? · ?? · ??? ? |
1 |
|
|
???? = 36√3см2 |
???? = 49√3см2 |
1 |
|
|
??? ? = 4 |
??? ? = 4 |
1 |
|
|
? = 12см |
? = 14см |
1 |
|
|
5 |
?? = ?? ; ?? = ??·??? ? ??? ? ??? ? ??? ? |
?? = ?? ; ??? ? = ??·??? ? ??? ? ??? ? ?? |
1 |
|
|
??? 1 030 = ??? 7 70 |
??? ? = 85·0,766 ≈ 0,4553; ∠? ≈ 270 1 |
1 |
|
|
?? = 143·0,9744 ≈ 182 км |
∠? = 1800 − (∠? + ∠?) = 1030 |
1 |
|
|
0,766 |
??? 1 030 = ??? 7 70 |
|
|
|
?? = ?? ; ?? = ??·??? ? ??? ? ??? ? ??? ? |
?? = ?? ; ?? = ??·??? ? ??? ? ??? ? ??? ? |
1 |
|
|
?? = 143·0,454 ≈ 85 км |
?? = 85·0,9744 ≈ 182км |
1 |
|
|
0,766 |
0,4553 |
|
|
Барлығы: |
20 |
||
4 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
|
Ұзақтылығы |
40 минут |
I нұсқа
-
1 балл Градустық ӛлшемі 36°тең доғаның ұзындығын табыңыз,егер шеңбердің радиусы 15 см болса.
-
3π
-
4π
-
6π
-
9π
-
15π
-
2 балл Дӛңес бесбұрыштың бұрыштарын табыңыз, егер олар 1, 3, 5, 7, 11 сандарына пропорционал болса.
-
3 балл Дӛңес кӛпбұрыштың бұрыштарының қосындысы оның сыртқы бұрыштарының қосындысынан 720қа
 артық.Осы кӛпбұрыштың қабырғалар санын табыңыз.
артық.Осы кӛпбұрыштың қабырғалар санын табыңыз.
-
 4 балл Правильный треугольник со стороной Қабырғасы 12√3 см болатын дұрыс үшбұрыш шеңберге іштей сызылған, ал дұрыс
алтыбұрыш бұл шеңберге сырттай сызылған. шестиугольник описан вокруг этой окружности.Осы дұрыс алтыбұрыштың қабырғасын
табыңыз.
4 балл Правильный треугольник со стороной Қабырғасы 12√3 см болатын дұрыс үшбұрыш шеңберге іштей сызылған, ал дұрыс
алтыбұрыш бұл шеңберге сырттай сызылған. шестиугольник описан вокруг этой окружности.Осы дұрыс алтыбұрыштың қабырғасын
табыңыз.
-
5 балл Үшбұрыштың ауданын табыңыз,егер оның екі медианасының ұзындықтары 6см және 9 см болса, ал медианалары перпендикуляр болса.
-
5 балл Суреттегі дӛңгелек сектордың центрі O және радиусы 12 см тең. ОР = 4 см, РКОК және РOК 45°. Боялған бӛліктің ауданын табыңыз.
Барлығы 20 балл.
II нұсқа
-
1 балл Градустық ӛлшемі 72°тең доғаның ұзындығын табыңыз,егер шеңбердің радиусы 20 см болса.
-
2π
-
4π
-
8π
-
12π
-
20π
-
-
2 балл Дӛңес алтыбұрыштың бұрыштарын табыңыз, егер олар 2, 4, 4, 6, 8, 12 сандарына пропорционал болса.
-
3 балл Дӛңес кӛпбұрыштың бұрыштарының қосындысы оның ішкі бұрыштарының қосындысынан 180қа кем. Осы кӛпбұрыштың қабырғалар санын табыңыз.
![]()
-
4 балл Қабырғасы 5√3 см болатын дұрыс алтыбұрыш шеңберге іштей сызылган, ал дұрыс үшбұрыш осы шеңберге сырттай сызылған.Дұрыс үшбұрыштың қабырғасын табыңыз.
-
5 балл APC үшбұрышының екі медианасы PK және AD, E-нүктесінде қиылысады. Егер P? = 6 cм; АD=12 см және АС=16 см болса, АРС үшбұрышының ауданын табыңыз.
-
5 балл Суреттегі дӛңгелек сектордың центрі O және радиусы 18 см тең. ОМ = ОН = 4 см және МOН 60°. Боялған бӛліктің ауданын табыңыз.

Барлығы 20 балл.
Балл қою кестесі
|
|
1 нұсқа |
2 нұсқа |
|
|
№ |
Жауабы |
Жауабы |
Балл |
|
1 |
А |
С |
1 |
|
2 |
1х+3х+5х+7х+11х=180°(5-2) |
2х+4х+4х+6х+8х+12х=180°(6-2) |
1 |
|
27х=540 х=20 20°; 60°; 100°; 140°; 220°. |
36х=720 х=20 40°; 80°; 80°; 120°; 160°; 240°. |
1 |
|
|
3 |
180°(n-2)=360°+720° |
180°(n-2)=360°+180° |
1 |
|
n-2=1080°: 180° или 180°n=1440° |
n-2=540°: 180° или 180°n=900° |
1 |
|
|
n=8 |
n=5 |
1 |
|
|
4 |
? = ?3 или ? = ?3√3 3 2???180° 3 3 3 |
? = ?6 или ? = ? 6 2???180° 6 6 6 |
1 |
|
?3 = 12 cм |
?6 = 5√3cм |
1 |
|
|
?3 = ?6 = 12 cм |
?6 = ?3 = 5√3 cм |
1 |
|
|
1 ?6 = 2 · ?6 · ?? 6 = 8√3(cм) |
? = 2 · ? · ?? 180° = 30(см) 3 |
1 |
|
|
5 |
?O = 2 A?= 6 (см) 3 |
?? = 2 A?= 8 (см) 3 |
1 |
|
CO = 2 MC= 4 (см) 3 |
?? = 1 ??= 2 (см) 3 |
1 |
|
|
?? ⊥ MC, АОС үшбұрышы- тікбұрышты |
? − AC − ортacы , A? = 8 cм. АЕК үшбұрышында: р = 8+8+2 = 2 9 (cм) |
1 |
|
|
1 ?∆?0? = ?? · ?? = 24(cм2) 2 |
?∆?E? = √9 · 1 · 1 · 7 = 3√7(cм2) |
1 |
|
|
???? = 3 · ?∆?0? = 3 · 24 = 72(cм2) |
??P? = 6 · ?∆?E? = 6 · 3√7 = 18√7(cм2) |
1 |
|
|
6 |
??2 ?cектор = 360° · ? |
??2 ?cектор = 360° · ? |
1 |
|
? · 122 ?cектор = 360° · 45° = 18? |
? · 182 ?cектор = 360° · 60° = 54? |
1 |
|
|
∆ ??? те бҮірлі тікбҮрыштыРОК= 45°, ОК=КР=?? · ???45° = 2√2 ( |
∆ ??? те бҮйірлі, O т беcіндегі бҮры болca, ондa ∆OMH те цaбырғaлы |
1 |
|
|
? = 1 ?? · ?P = 4(cм2) ∆ |
a2√3 ?∆OMH = = 16√3(cм2)
4 |
1 |
|
|
?фигурacы = ?cектор − ?∆?0? = 18? − 4(cм2) |
?фигурacы = ?cектор − ?∆?0?
= |
1 |
|
|
Барлығы: |
20 |
||
III вариант
-
1 балл Градустық ӛлшемі 80°тең доғаның ұзындығын табыңыз,егер шеңбердің радиусы 9 см болса.
-
3π
-
4π
-
6π
-
8π
-
9π
-
2 балл Дӛңес тӛртбұрыштың бұрыштарын табыңыз, егер олар 2, 2, 3, 5 сандарына пропорционал болса.
-
2 балл Дӛңес кӛпбұрыштың бұрыштарының қосындысы оның сыртқы бұрыштарының қосындысынан 2есе кем. Осы кӛпбұрыштың қабырғалар санын табыңыз.
-
4 балл Шаршыға іштей сызылған шеңбердің радиусы 1 дм.Шаршыға сырттай сызылған шеңбердің радиусын табыңыз
-
3 балл Периметрі 2м 16см болатын дұрыс алтыбұрыш шеңберге сырттай сызылған.Осы шеңбердің радиусын табыңыз.
-
4 балл AКC үшбұрышының екі медианасы KЕ және AВ, E-нүктесінде қиылысады. Егер ?∆??? = 6 cм2 болса АКС үшбұрышының ауданын табыңыз.
-
4 балл Суреттегі дӛңгелек сегменттің центрі O және радиусы 12 см тең. және АOК 150°.Сегменттің ауданын табыңыз.

Барлығы 20 балл
IV нұсқа
-
1 балл Градустық ӛлшемі 120°тең доғаның ұзындығын табыңыз,егер шеңбердің радиусы 12 см болса.
-
3π
-
4π
-
5π
-
8π
-
10π
-
-
2 балл Дӛңес тӛртбұрыштың бұрыштарын табыңыз, егер олар 3, 8, 9, 10 сандарына пропорционал болса.
3 . 2 балл Дӛңес п-бұрышты кӛпбұрыштың бұрыштарының қосындысы оның сыртқы бұрыштарының қосындысына тең. п-ды табыңыз.
-
4 балл Дұрыс үшбұрышқа іштей сызылған шеңбердің радиусы 6 см.Үшбұрышқа сырттай сызылған шеңбердің радиусын табыңыз
-
3 балл Радиусы 42см болатын шеңбер дұрыс алтыбұрышқа іштей сызылған.Дұрыс алтыбұрыштың периметрін табыңыз.
-
4 балл AКC үшбұрышының екі медианасы KЕ және AВ, E-нүктесінде қиылысады. Егер ?∆??? = 6 cм2 болса, СВЕ үшбұрышының ауданын табыңыз.
-
4 балл Суреттегі дӛңгелек сегменттің центрі O және радиусы 6 см тең. және ВOМ 120°.Сегменттің ауданын табыңыз.

Барлығы 20 балл.
Балл қою кестесі
|
|
3 нұсқа |
4 нұсқа |
|
|
№ |
Жауабы |
Жауабы |
Балл |
|
1 |
В |
D |
1 |
|
2 |
2х+2х+3х+5х=180°(4-2) |
3х+8х+9х+10х=180°(4-2) |
1 |
|
12х=360 х=30 60°; 60°; 90°; 150 |
30х=360 х=12 36°; 96°; 108°; 120° |
1 |
|
|
3 |
180°(n-2)2=360° |
180°(n-2)=360° |
1 |
|
n-2=360°: 360° n=3 |
n-2=360°: 180° n=4 |
1 |
|
|
4 |
1 ?4 = 2 · ?4 · ?? 4 |
1 ?3 = 2 · ?3 · ??? 3 |
1 |
|
a4 = 2 дм |
a3 = 6√3 ?м |
1 |
|
|
? = ?4 4 2???180° 4 |
? = ?3 3 2?g180° 3 |
1 |
|
|
2 ?4 = 2 = √2(дм) |
6√3 ?3 = = 3(cм) 2 |
1 |
|
|
5 |
216 : 6=36(см) |
?6 = a6 |
1 |
|
?6 = a6 |
a6 = 42 cм |
1 |
|
|
a6 = 36 cм |
426=252 (см) или 2 м 52 см |
1 |
|
|
6 |
Үшбұрыштың медианалары қиылысып, қиылысу нүктесінде1:2 қатынасындай бӛлінеді,тӛбесінен есептегенде |
Үшбұрыштың медианалары қиылысып, қиылысу нүктесінде1:2 қатынасындай бӛлінеді,тӛбесінен есептегенде |
1 |
|
∆HBE~∆HA?, Үцcacтыц коэффиценті ½ ; ?∆??E∶ ?∆?A? = 1∶ 4 |
∆CAE~∆CM?, Үцcacтыц коэффиценті ½ ; ?∆CAE∶ ?∆CM? = 1∶ 4 |
1 |
|
|
?∆??? = 6 · 4 = 24 (cм2) |
?∆??? = 48∶ 3 = 16(cм2) |
1 |
|
|
?∆A?C = 3 · 24 = 72(cм2) Балама тәсіл қабылданады |
?∆AEC = 16∶ 4 = 4 (cм2) Балама тәсіл қабылданады |
1 |
|
|
7 |
??2 ?cектор = 360° · ? |
??2 ?cектор = 360° · ? |
1 |
|
? · 122 ?cектор = 360° · 150° = 60? |
? · 62 ?cектор = 360° · 120° = 12? |
1 |
|
|
1
?∆A0? = ?? · AO · ???150° = 36(cм2) 2 |
1 ?∆BMO = 2 M? · BO · ???120°
= |
1 |
|
|
?cегментa = ?cекторa − ?∆A0? = 60? − 36 == 12(5? − 6)(cм2) |
?cегментa = ?cекторa − ?∆A0?
= 12? − 9√3 = = 3(4? − 3√3)(cм2) |
1 |
|
|
Барлығы : |
20 |
||

шағым қалдыра аласыз