
15
«Адам өміріндегі фигуралды сандар»
Орындаған: Рай Гаухар
Мазмұны
1.1. Фигуралы сандар тарихынан. 5
1.2. Фигуралы сандарды анықтау және оның түрлері. 6
1.3. Фигуралы сандардың қасиеттері 8
1.4. Сандық тізбектің өзара байланысы 9
1.5. Фигуралы сандардң адам өмірінде қолданылуы. 9
Аннотация
Жұмыстың мақсаты:
Математикалық ұғымдардың бірі ретіндегі фигуралы сандарды барынша терең зерттеу және оның өмірімізде алатын рөлін анықтау.
Зерттеу міндеттері:
-
Әртүрлі ғылыми және оқу-әдістемелік дереккөздерден аталған мәселе бойыша материалдарды жинақтау және талдау.
-
Фигуралы сандардың пайда болу тарихы мен олардың өмірінде қолданылуын қарастыру.
Зерттеу объектісі:
Фигуралы сандардың бірнеше түрі және олардың қасиеттері. Сонымен қатар, олардың өмірде қолданылуы.
Зерттеудің ғылыми жаңалығы:
Тіктөртбұрыштың ауданын есептеуде жазық сандардың, тікбұрышты параллелепипедтің көлемін септеуде денелік сандардың, өмірде әртүрлі жағдаяттарда басқа да фигуралы сандардың қолданылуы.
Annotation
Goal of research: to deeply investigate and prove an importance of figurate numbers in our life, which is one of the concepts of mathematics.
Tasks of research:
-
To collect and analyze materials about this topic from different scientific and educational-didactic sources.
-
To consider the discovery of figurate numbers and their application in the world.
Object of research:
Different types of figurate numbers and their properties. Also, their application in the life.
Novelty of the research:
The usage of figurate numbers: plane numbers in finding the area of a rectangle, bodily numbers in computing the volume of a parallelogram and other numbers’s application.
КІРІСПЕ
Өзімнің зерттеу жұмысымда мен фигуралы сандарды математикада ғана емес, қоршаған өмірде де қолдануға болатынын қарастырдым.
Қарапайым бөлшектер тақырыбын оқыған кезде мен математика оқулығындағы (авторы Виленкин Н.Я.) фигуралы сандар туралы шағын тарихи деректерге назар аудардым. Осы дереккөздегі мәліметтер тақырыпты зерттеуіме себеп болды және зерттеудегі мақсатым – фигуралы сандардың айналадағы өмірде де жиі кездесетінін, адамдар бұл сандарды көп жағдайда байқамайтынын көрсеткім келді. Осы мақсатқа қол жеткізу үшін мен қосымша әдебиеттер мен басқа да ресурстар, дереккөздерді зерделедім.
Маған мектеп оқушыларының фигуралы сандар туралы білетінін немесе білмейтінін анықтау мәселесі қызығушылық туғызды. Сондықтан 6-10-сыныптардағы оқушылар арасында сауалнама жүргіздім, сауалнамаға 86 оқушы қатысты.
Нәтижесінде, жауап берген оқушылардың фигуралы сандар туралы 34,4%-ы ғана білетіні анықталды. 19,8% -ы фигуралы сандар жазықтық сандары деп есептейді. 32,5 % - көлемдік фигуралар, 47,7 % - олардың жазықтық және көлемдік фигуралар түрінде бейнеленуі мүмкін деп жауап берген. 46,5 % оқушылар бұл сандарды Пифагор ойлап тапқан деп шешкен. Респонденттердің жартысы күнделікті тұрмыста фигуралы сандармен жиі кездесеміз деп белгілеген.
Жұмыстың мақсаты: Математикалық ұғымдардың бірі ретіндегі фигуралы сандарды барынша терең зерттеу және оның өмірімізде алатын рөлін анықтау.
Міндеттері:
-
Әртүрлі ғылыми және оқу-әдістемелік дереккөздерден аталған мәселе бойынша материалдарды жинақтау және оны талдау.
-
Фигуралы сандардың пайда болу тарихы мен олардың адам өмірінде қолданылуын қарастыру.
НЕГІЗГІ БӨЛІМ
1.1. Фигуралы сандар тарихынан.
«Сандар Пифагормен, ежелгі гректермен және пифагоршылармен есеп шығаратын тақта – абакада немесе құмда орналастырылған тастар түрінде ойша елестетілген. Сондықтан гректер нөл санын білмеген, оны «көру» мүмкін емес еді. Бір санының өзін де толыққанды сан ретінде есептемеген, гректер үшін бір саны- өзінен барлық сандар туындайтын қандай-да бір «сандық атом» ретінде қарастырылған. Пифагоршылар бірді «сандар мен бөліктер» немесе бүтін сандар мен бөлшектер арасындағы «шекара» деп атаған, сөйте тұра бір санында «дән мен мәңгі түбірді» де көрген. Сан бірліктерден тұратын көп сан ретінде анықталған. «Сандық атом» деп қабылданған бір саны өзінің ерекше жағдайына байланысты «геометриялық атом» деген атауы бар нүктемен жақындасты. Сондықтан Аристотель: «Нүкте орны бар бірлік, бірлік- орны жоқ нүкте» деп мазмұндаған. Сонымен, заманауи терминологиядағы пифагор сандары – ол натурал сандар [2, с.117]
Ежелгі заманда адамдар тастармен санау арқылы өздеріне көмектесе отыра, тастардан ретпен орналастыруға болатын дұрыс фигуралардың бар екенін байқаған. Тастарды бір қатарға жай ғана орналастыруға болады: бір, екі, үш және т.с. Егер оларды екі қатарға тік төртбұрыш болатындай етіп орналастырса, онда барлығы жұп сан болып шығады. Тастарды үш қатарға орналастыруға да болады: онда үшке бөлінетін сандар шығады және т.б.
Ежелгі гректер сандарды көбейту қажет болған жағдайда тік төртбұрыш суретін сызған; үшті беске көбейту үшін үш және бес жақты төртбұрышты бейнелеген. Бұл - тастар арқылы санаудың дамуы. Сандармен әрекеттесу негізінде пайда болған заңдылықтардың басым көпшілігі ежелгі гректермен сызбаларды зерделеу кезінде анықталған болатын. Осындай сәйкестіктердің шынайылығын дәлелдейтін тәсіл ретінде көптеген ғасырлар бойы тік төртбұрыштары, квадраттары, пирамидалары және кубтары бар геометриялық тәсіл саналып келді. Біздің эрамызға дейінгі 5-4 ғасырларда натурал сандарды араластыру арқылы ғалымдар олардан қызықты қатарлар
түзеген, олар қатарлардың элементтеріне белгілі бір геометриялық тұжырым беріп отырған. Солардың көмегімен дұрыс геометриялық фигураларды салуға болатын еді: үшбұрыштар, шаршылар, пирамидалар және т.б..
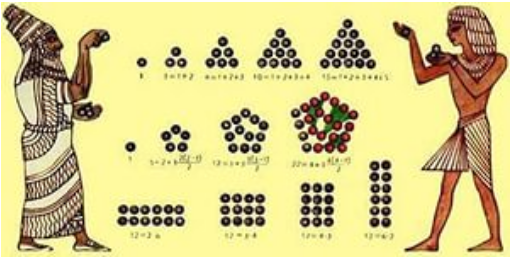
Блез Паскаль және Пьер Ферма бір-біріне тәуелсіз бола тұра, осындай сандарды табу мәселесімен қызығушылықпен айналысқан.
1.2. Фигуралы сандарды анықтау және оның түрлері.
Тастар - сандар дұрыс геометриялық фигуралар ретінде орналастырылған, осы фигуралар жіктелген. Бүгінгі күні фигуралы деп аталатын сандар осылайша пайда болған.
![]()
 Сызықтық
сандар (қарапайым)
– бірге және өзіне-өзі
бөлінетін сандар, бір сызықтың бойына бірізді нүктелер түрінде
орналасу арқылы бейнеленген.
Сызықтық
сандар (қарапайым)
– бірге және өзіне-өзі
бөлінетін сандар, бір сызықтың бойына бірізді нүктелер түрінде
орналасу арқылы бейнеленген.
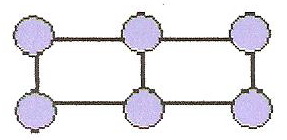
Жазықтық сандар – екі көбейткішті сандар көбейтіндісі ретінде көрінетін сандар (жазықтық саны 6=2∙3).
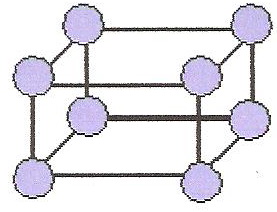
Денелік сандар, үш көбейткіштің сандар көбейтіндісі (денелік сан 8=2∙2∙2).
Ү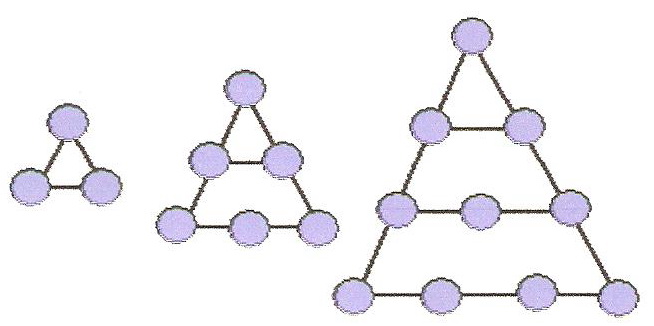 шбұрышты
сандар (3,
6, 10).
шбұрышты
сандар (3,
6, 10).
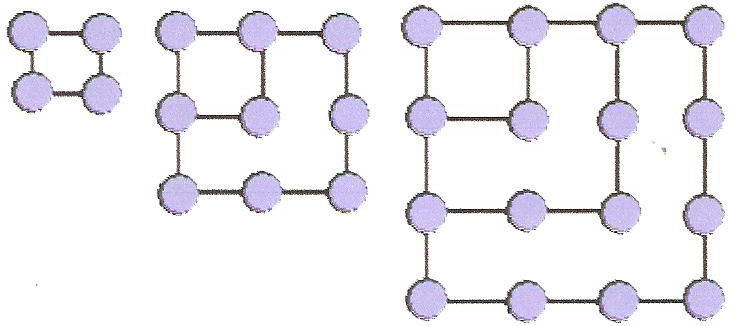
Квадратты (шаршылы) сандар (4,9,16).
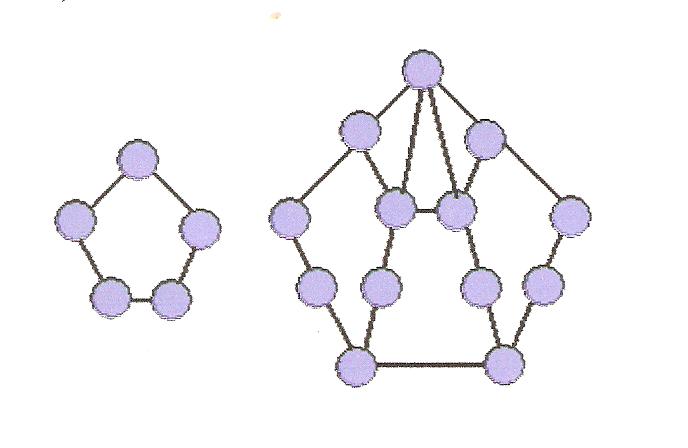
Бесбұрышты сандар (5, 12, 22)

«Квадратқа немесе кубқа өсіру» деген ұғым осы фигуралы сандардан пайда болған.
![]()
Дұрыс геометриялық фигуралар түрінде сандарды көрсету пифагоршыларға алуан түрлі сандық заңдылықтарды табуға ықпал етті. Мысалы, қандай-да бір үшбұрышты n- саны үшін n – натуралды сандар жиынтығы - 1+2+3+…+ n болып табылатын ортақ мәнін табу үшін, бұл санды тік төртбұрышты санға дейін толықтыру n(n+1) жеткілікті және
+2+3+…+ n
= ![]()
теңсіздігін байқауға (көзбен!) болады.
К вадратты
сандардың бірізділігін жазып алып, тағы да n жиынтығы үшін
1+3+5+…+(2 n-1) = n2
мәнін бірден байқауға (көруге)
болады.
вадратты
сандардың бірізділігін жазып алып, тағы да n жиынтығы үшін
1+3+5+…+(2 n-1) = n2
мәнін бірден байқауға (көруге)
болады.
1.3. Фигуралы сандардың қасиеттері
Үшбұрышты сандар:
-
Үшбұрышты сандар бірізділігі: 1, 3, 6, 10, 15, 21, 28...
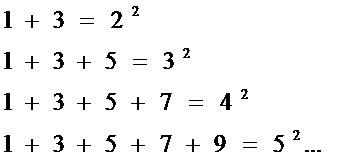
-
Қатар тұрған екі үшбұрышты санның қосындысы санның квадратын береді.
-
Тізбектегі элементтердің жұптығы немесе тақтығы 4-тік периодпен ауысады: тақ, тақ, жұп, жұп.
Квадратты сандар:
-
Кез келген жұп квадратты сан қатар орналасқан екі үшбұрышты санның қосындысын 4-ке көбейткенге тең. Мысалы: 36=4(3+6), 64=4(6+10).
-
Кез келген тақ квадратты сан сегіз еселенген үшбұрышты сан мен 1-дің қосындысына тең. Мысалы: 25=8*3+1



1.4. Сандық тізбектің өзара байланысы
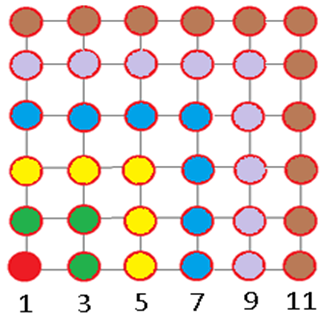
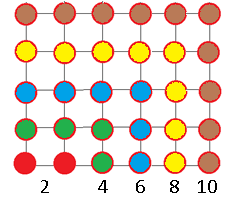
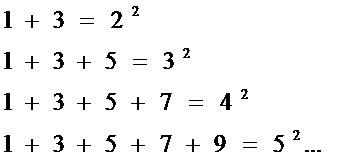
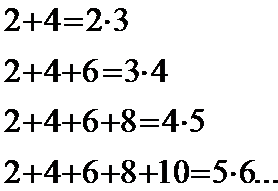
Фигуралы сандарға берілген есептер
-
Шарлар теңқабырғалы үшбұрыштар құрайтындай орналастырылды. Он бесінші үшбұрышта 120 шар болса, он алтыншы және он төртінші үшбұрыштарда қанша шар бар?
Шешуі: әрбір үшбұрышта 120/15=8 шар, он алтыншысында 16*8=128 шар, он төртіншіде 14*8=112 шар.
-
Үшбұрышты сандар тізбегінде жұп және тақ сандар қандай ретпен орналасқан? 17, 18, 19, 20, 60, 78, 35 нөмірлерде орналасқан сандардың жұп тақтығын анықтаңыз.
-
35-ші нөмірде тұрған үшбұрышты сан неге тең?
![]()
-
3
 5-ші нөмірде тұрған бесбұрышты
сан неге тең?
5-ші нөмірде тұрған бесбұрышты
сан неге тең?
-
35-ші нөмірде тұрған алтыбұрышты сан неге тең?
![]()
-
Шарларды 25 қатарлы теңқабырғалы үшбұрышқа орналастыру үшін барлығы неше шар керек?
-
Бірнеше шарларды теңқабырғалы үшбұрыш құрайтындай орналастырғанда, 3 шар артық қалды. Ал, қабырғасы бір шарға артық үшбұрышты құрастырғанда, 4 шар жетпей қалды. Сонда барлағы неше шар болған?
Жауабы: 295
ҚОРЫТЫНДЫ
Аталған мәселе бойынша зерттеу жұмысын жүргізуде мен бастапқыда қойған мақсатыма қол жеткіздім: математиканың бір ұғымы ретіндегі фигуралы сандарды зерттедім және зерделедім.
Жұмысымның қорытындысын шығаруда мен осы тақырыптың өзекті екеніне көз жеткіздім. Заманауи өмірді фигуралы сандарсыз елестету қиын, олар біздің айналамызда, біз олардың ортасында өмір сүреміз, олар бізге ауадай, күн сәулесіндей, судай қажет. Зерттеу нәтижесінде, мен фигуралы сандардың өмірде көптеген тұрмыс салаларында, атап айтқанда, дүкенде, әскери шерулерде, бөлме интерьерінде т.б. жерлерде кездестіруге болатынын білдім.
ӘДЕБИЕТ ТІЗІМІ
-
Виленкин Н.Я. Математика. 6 -сынып: жалпы білім беретін мекемелер үшін оқулық- М.: Мнемозина, 2015.
-
Волошинов А.В. Пифагор: шынайылық, мейірімділік және сұлулық одағы М..: Просвещение, 1993.
-
Жас математиктің энциклопедиялық сөздігі/ Құрастырушы А.П.Савин.
– М.: Педагогика, 1985
ҚОСЫМША
1
 -қосымша
-қосымша
 2-қосымша
2-қосымша

3-қосымша


4- қосымша


5-қосымша 6-қосымша
7-қосымша


8-қосымша
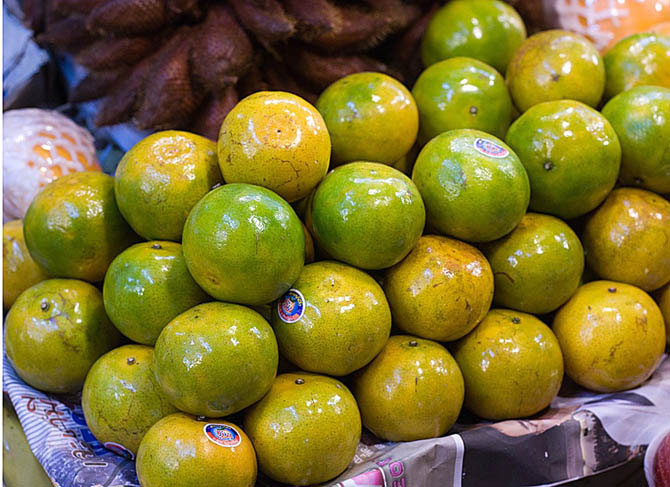


ПІКІР
Рай Гаухар математика курсында көп қарастырыла бермейтін фигуралы сандарды зерттеп, оның тарихымен, түрлерімен, өмірде алатын орнымен танысқан және өзі де үй жағдайында бөлменің интерьерін жасауда осы фигуралы сандарды қолданған.
Мектеп оқушыларының фигуралы сандар туралы қаншалықты білетінін білу мақсатында сауалнама жүргізген және соның нәтижесінде сыныптастарына фигуралы сандар туралы түсінік беріп, оның түрлерімен, өмірде кездесетін орындарымен таныстырған.
Жұмысты 5-8-ші сыныптар арасында таңдау курстарында, үйірме жұмыстарында қолдануға болады.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
«Адам өміріндегі фигуралды сандар»
«Адам өміріндегі фигуралды сандар»
15
«Адам өміріндегі фигуралды сандар»
Орындаған: Рай Гаухар
Мазмұны
1.1. Фигуралы сандар тарихынан. 5
1.2. Фигуралы сандарды анықтау және оның түрлері. 6
1.3. Фигуралы сандардың қасиеттері 8
1.4. Сандық тізбектің өзара байланысы 9
1.5. Фигуралы сандардң адам өмірінде қолданылуы. 9
Аннотация
Жұмыстың мақсаты:
Математикалық ұғымдардың бірі ретіндегі фигуралы сандарды барынша терең зерттеу және оның өмірімізде алатын рөлін анықтау.
Зерттеу міндеттері:
-
Әртүрлі ғылыми және оқу-әдістемелік дереккөздерден аталған мәселе бойыша материалдарды жинақтау және талдау.
-
Фигуралы сандардың пайда болу тарихы мен олардың өмірінде қолданылуын қарастыру.
Зерттеу объектісі:
Фигуралы сандардың бірнеше түрі және олардың қасиеттері. Сонымен қатар, олардың өмірде қолданылуы.
Зерттеудің ғылыми жаңалығы:
Тіктөртбұрыштың ауданын есептеуде жазық сандардың, тікбұрышты параллелепипедтің көлемін септеуде денелік сандардың, өмірде әртүрлі жағдаяттарда басқа да фигуралы сандардың қолданылуы.
Annotation
Goal of research: to deeply investigate and prove an importance of figurate numbers in our life, which is one of the concepts of mathematics.
Tasks of research:
-
To collect and analyze materials about this topic from different scientific and educational-didactic sources.
-
To consider the discovery of figurate numbers and their application in the world.
Object of research:
Different types of figurate numbers and their properties. Also, their application in the life.
Novelty of the research:
The usage of figurate numbers: plane numbers in finding the area of a rectangle, bodily numbers in computing the volume of a parallelogram and other numbers’s application.
КІРІСПЕ
Өзімнің зерттеу жұмысымда мен фигуралы сандарды математикада ғана емес, қоршаған өмірде де қолдануға болатынын қарастырдым.
Қарапайым бөлшектер тақырыбын оқыған кезде мен математика оқулығындағы (авторы Виленкин Н.Я.) фигуралы сандар туралы шағын тарихи деректерге назар аудардым. Осы дереккөздегі мәліметтер тақырыпты зерттеуіме себеп болды және зерттеудегі мақсатым – фигуралы сандардың айналадағы өмірде де жиі кездесетінін, адамдар бұл сандарды көп жағдайда байқамайтынын көрсеткім келді. Осы мақсатқа қол жеткізу үшін мен қосымша әдебиеттер мен басқа да ресурстар, дереккөздерді зерделедім.
Маған мектеп оқушыларының фигуралы сандар туралы білетінін немесе білмейтінін анықтау мәселесі қызығушылық туғызды. Сондықтан 6-10-сыныптардағы оқушылар арасында сауалнама жүргіздім, сауалнамаға 86 оқушы қатысты.
Нәтижесінде, жауап берген оқушылардың фигуралы сандар туралы 34,4%-ы ғана білетіні анықталды. 19,8% -ы фигуралы сандар жазықтық сандары деп есептейді. 32,5 % - көлемдік фигуралар, 47,7 % - олардың жазықтық және көлемдік фигуралар түрінде бейнеленуі мүмкін деп жауап берген. 46,5 % оқушылар бұл сандарды Пифагор ойлап тапқан деп шешкен. Респонденттердің жартысы күнделікті тұрмыста фигуралы сандармен жиі кездесеміз деп белгілеген.
Жұмыстың мақсаты: Математикалық ұғымдардың бірі ретіндегі фигуралы сандарды барынша терең зерттеу және оның өмірімізде алатын рөлін анықтау.
Міндеттері:
-
Әртүрлі ғылыми және оқу-әдістемелік дереккөздерден аталған мәселе бойынша материалдарды жинақтау және оны талдау.
-
Фигуралы сандардың пайда болу тарихы мен олардың адам өмірінде қолданылуын қарастыру.
НЕГІЗГІ БӨЛІМ
1.1. Фигуралы сандар тарихынан.
«Сандар Пифагормен, ежелгі гректермен және пифагоршылармен есеп шығаратын тақта – абакада немесе құмда орналастырылған тастар түрінде ойша елестетілген. Сондықтан гректер нөл санын білмеген, оны «көру» мүмкін емес еді. Бір санының өзін де толыққанды сан ретінде есептемеген, гректер үшін бір саны- өзінен барлық сандар туындайтын қандай-да бір «сандық атом» ретінде қарастырылған. Пифагоршылар бірді «сандар мен бөліктер» немесе бүтін сандар мен бөлшектер арасындағы «шекара» деп атаған, сөйте тұра бір санында «дән мен мәңгі түбірді» де көрген. Сан бірліктерден тұратын көп сан ретінде анықталған. «Сандық атом» деп қабылданған бір саны өзінің ерекше жағдайына байланысты «геометриялық атом» деген атауы бар нүктемен жақындасты. Сондықтан Аристотель: «Нүкте орны бар бірлік, бірлік- орны жоқ нүкте» деп мазмұндаған. Сонымен, заманауи терминологиядағы пифагор сандары – ол натурал сандар [2, с.117]
Ежелгі заманда адамдар тастармен санау арқылы өздеріне көмектесе отыра, тастардан ретпен орналастыруға болатын дұрыс фигуралардың бар екенін байқаған. Тастарды бір қатарға жай ғана орналастыруға болады: бір, екі, үш және т.с. Егер оларды екі қатарға тік төртбұрыш болатындай етіп орналастырса, онда барлығы жұп сан болып шығады. Тастарды үш қатарға орналастыруға да болады: онда үшке бөлінетін сандар шығады және т.б.
Ежелгі гректер сандарды көбейту қажет болған жағдайда тік төртбұрыш суретін сызған; үшті беске көбейту үшін үш және бес жақты төртбұрышты бейнелеген. Бұл - тастар арқылы санаудың дамуы. Сандармен әрекеттесу негізінде пайда болған заңдылықтардың басым көпшілігі ежелгі гректермен сызбаларды зерделеу кезінде анықталған болатын. Осындай сәйкестіктердің шынайылығын дәлелдейтін тәсіл ретінде көптеген ғасырлар бойы тік төртбұрыштары, квадраттары, пирамидалары және кубтары бар геометриялық тәсіл саналып келді. Біздің эрамызға дейінгі 5-4 ғасырларда натурал сандарды араластыру арқылы ғалымдар олардан қызықты қатарлар
түзеген, олар қатарлардың элементтеріне белгілі бір геометриялық тұжырым беріп отырған. Солардың көмегімен дұрыс геометриялық фигураларды салуға болатын еді: үшбұрыштар, шаршылар, пирамидалар және т.б..

Блез Паскаль және Пьер Ферма бір-біріне тәуелсіз бола тұра, осындай сандарды табу мәселесімен қызығушылықпен айналысқан.
1.2. Фигуралы сандарды анықтау және оның түрлері.
Тастар - сандар дұрыс геометриялық фигуралар ретінде орналастырылған, осы фигуралар жіктелген. Бүгінгі күні фигуралы деп аталатын сандар осылайша пайда болған.
![]()
 Сызықтық
сандар (қарапайым)
– бірге және өзіне-өзі
бөлінетін сандар, бір сызықтың бойына бірізді нүктелер түрінде
орналасу арқылы бейнеленген.
Сызықтық
сандар (қарапайым)
– бірге және өзіне-өзі
бөлінетін сандар, бір сызықтың бойына бірізді нүктелер түрінде
орналасу арқылы бейнеленген.
Жазықтық сандар – екі көбейткішті сандар көбейтіндісі ретінде көрінетін сандар (жазықтық саны 6=2∙3).

Денелік сандар, үш көбейткіштің сандар көбейтіндісі (денелік сан 8=2∙2∙2).
Ү шбұрышты
сандар (3,
6, 10).
шбұрышты
сандар (3,
6, 10).

Квадратты (шаршылы) сандар (4,9,16).

Бесбұрышты сандар (5, 12, 22)

«Квадратқа немесе кубқа өсіру» деген ұғым осы фигуралы сандардан пайда болған.
![]()
Дұрыс геометриялық фигуралар түрінде сандарды көрсету пифагоршыларға алуан түрлі сандық заңдылықтарды табуға ықпал етті. Мысалы, қандай-да бір үшбұрышты n- саны үшін n – натуралды сандар жиынтығы - 1+2+3+…+ n болып табылатын ортақ мәнін табу үшін, бұл санды тік төртбұрышты санға дейін толықтыру n(n+1) жеткілікті және
+2+3+…+ n
= ![]()
теңсіздігін байқауға (көзбен!) болады.
К вадратты
сандардың бірізділігін жазып алып, тағы да n жиынтығы үшін
1+3+5+…+(2 n-1) = n2
мәнін бірден байқауға (көруге)
болады.
вадратты
сандардың бірізділігін жазып алып, тағы да n жиынтығы үшін
1+3+5+…+(2 n-1) = n2
мәнін бірден байқауға (көруге)
болады.
1.3. Фигуралы сандардың қасиеттері
Үшбұрышты сандар:
-
Үшбұрышты сандар бірізділігі: 1, 3, 6, 10, 15, 21, 28...
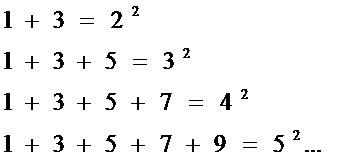
-
Қатар тұрған екі үшбұрышты санның қосындысы санның квадратын береді.
-
Тізбектегі элементтердің жұптығы немесе тақтығы 4-тік периодпен ауысады: тақ, тақ, жұп, жұп.
Квадратты сандар:
-
Кез келген жұп квадратты сан қатар орналасқан екі үшбұрышты санның қосындысын 4-ке көбейткенге тең. Мысалы: 36=4(3+6), 64=4(6+10).
-
Кез келген тақ квадратты сан сегіз еселенген үшбұрышты сан мен 1-дің қосындысына тең. Мысалы: 25=8*3+1



1.4. Сандық тізбектің өзара байланысы


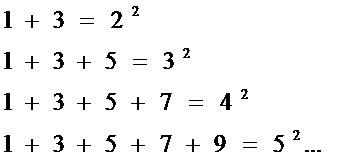
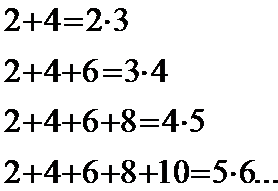
Фигуралы сандарға берілген есептер
-
Шарлар теңқабырғалы үшбұрыштар құрайтындай орналастырылды. Он бесінші үшбұрышта 120 шар болса, он алтыншы және он төртінші үшбұрыштарда қанша шар бар?
Шешуі: әрбір үшбұрышта 120/15=8 шар, он алтыншысында 16*8=128 шар, он төртіншіде 14*8=112 шар.
-
Үшбұрышты сандар тізбегінде жұп және тақ сандар қандай ретпен орналасқан? 17, 18, 19, 20, 60, 78, 35 нөмірлерде орналасқан сандардың жұп тақтығын анықтаңыз.
-
35-ші нөмірде тұрған үшбұрышты сан неге тең?
![]()
-
3
 5-ші нөмірде тұрған бесбұрышты
сан неге тең?
5-ші нөмірде тұрған бесбұрышты
сан неге тең?
-
35-ші нөмірде тұрған алтыбұрышты сан неге тең?
![]()
-
Шарларды 25 қатарлы теңқабырғалы үшбұрышқа орналастыру үшін барлығы неше шар керек?
-
Бірнеше шарларды теңқабырғалы үшбұрыш құрайтындай орналастырғанда, 3 шар артық қалды. Ал, қабырғасы бір шарға артық үшбұрышты құрастырғанда, 4 шар жетпей қалды. Сонда барлағы неше шар болған?
Жауабы: 295
ҚОРЫТЫНДЫ
Аталған мәселе бойынша зерттеу жұмысын жүргізуде мен бастапқыда қойған мақсатыма қол жеткіздім: математиканың бір ұғымы ретіндегі фигуралы сандарды зерттедім және зерделедім.
Жұмысымның қорытындысын шығаруда мен осы тақырыптың өзекті екеніне көз жеткіздім. Заманауи өмірді фигуралы сандарсыз елестету қиын, олар біздің айналамызда, біз олардың ортасында өмір сүреміз, олар бізге ауадай, күн сәулесіндей, судай қажет. Зерттеу нәтижесінде, мен фигуралы сандардың өмірде көптеген тұрмыс салаларында, атап айтқанда, дүкенде, әскери шерулерде, бөлме интерьерінде т.б. жерлерде кездестіруге болатынын білдім.
ӘДЕБИЕТ ТІЗІМІ
-
Виленкин Н.Я. Математика. 6 -сынып: жалпы білім беретін мекемелер үшін оқулық- М.: Мнемозина, 2015.
-
Волошинов А.В. Пифагор: шынайылық, мейірімділік және сұлулық одағы М..: Просвещение, 1993.
-
Жас математиктің энциклопедиялық сөздігі/ Құрастырушы А.П.Савин.
– М.: Педагогика, 1985
ҚОСЫМША
1
 -қосымша
-қосымша
 2-қосымша
2-қосымша

3-қосымша


4- қосымша


5-қосымша 6-қосымша
7-қосымша


8-қосымша
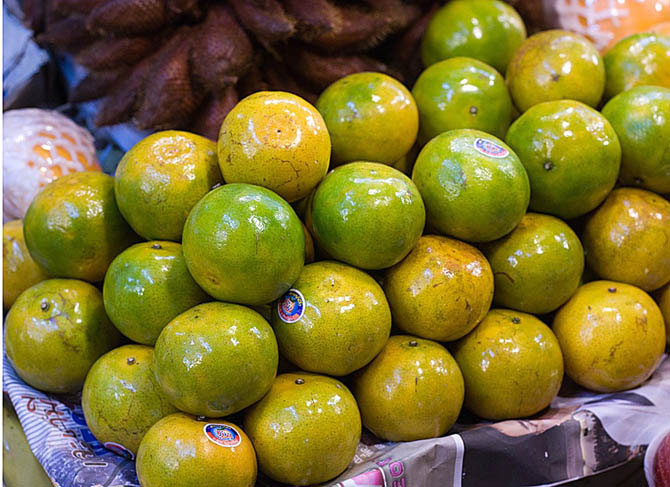


ПІКІР
Рай Гаухар математика курсында көп қарастырыла бермейтін фигуралы сандарды зерттеп, оның тарихымен, түрлерімен, өмірде алатын орнымен танысқан және өзі де үй жағдайында бөлменің интерьерін жасауда осы фигуралы сандарды қолданған.
Мектеп оқушыларының фигуралы сандар туралы қаншалықты білетінін білу мақсатында сауалнама жүргізген және соның нәтижесінде сыныптастарына фигуралы сандар туралы түсінік беріп, оның түрлерімен, өмірде кездесетін орындарымен таныстырған.
Жұмысты 5-8-ші сыныптар арасында таңдау курстарында, үйірме жұмыстарында қолдануға болады.

шағым қалдыра аласыз

















