
Айналу эллипсоиды
 эллипсоид ОУ осінен
айналып шыққан, айналу эллипс сызығының теңдеуін
жазыңыздар.
эллипсоид ОУ осінен
айналып шыққан, айналу эллипс сызығының теңдеуін
жазыңыздар.
Шешуі: Айналу бетінің теңдеуін
табу ережесіне сәйкес эллипс сызығының
теңдеуіндегі  Нәтижесінде берілген
эллипстің теңдеуіндегі х-тың орнына
Нәтижесінде берілген
эллипстің теңдеуіндегі х-тың орнына  қойылады.Сонда
қойылады.Сонда
 +
+ немесе
немесе  теңдеуіне
айналады.
теңдеуіне
айналады.
Демек,
 айналу эллипс
сызығының теңдеуі алынады. 39
айналу эллипс
сызығының теңдеуі алынады. 39
Жарты осьтері 5 пен 3 болатын эллипс, өзінің үлкен осіның бойына айналады. Үлкен осі ОУ осінде, ал эллипс центрі координаталары системасының бас нүктесінде орналасқан.Осы эллипстің ОУ осіне айналу кезіндегі бетінің теңдеуін табыңыздар.
Шешуі: Берілуі бойынша
в және
уо
және
уо жазықтығында жатыр. Оның
теңдеуі
жазықтығында жатыр. Оның
теңдеуі

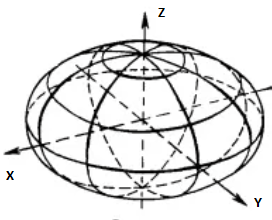
Берілгені бойынша қисықтың
теңдеуі уо жазықтығында жатыр.Ал
қисық ОУ осінен айналған кезде пайда болатын бетті алу
үшін
жазықтығында жатыр.Ал
қисық ОУ осінен айналған кезде пайда болатын бетті алу
үшін 
 Сонда қисықтың
теңдеуі
Сонда қисықтың
теңдеуі
 немесе
немесе  түрінде
жазылады.
түрінде
жазылады.
Демек,
алынған  ізделінді теңдеу
болады.
ізделінді теңдеу
болады.
х-2у ,
,
 айналғанда алынатын
айналу бетінің теңдеуін табыңыздар.
айналғанда алынатын
айналу бетінің теңдеуін табыңыздар.
Шешуі: М нүктесі сызығының
төбесі дейік. Оның координатасы (4; 0;0) болады. Осы конустың кез
келген А нүктесінің координатасы  десек, оның сәйкес
негізін В (х,у,о) нүктесі болады.А мен В ның координаталары А
(
десек, оның сәйкес
негізін В (х,у,о) нүктесі болады.А мен В ның координаталары А
( В(х,у,о) болады, сонда А
мен В координата нүктесінің әртүрлі нүктесі, ал В (х,у,о)
координатасында болады. Сонда
у2
В(х,у,о) болады, сонда А
мен В координата нүктесінің әртүрлі нүктесі, ал В (х,у,о)
координатасында болады. Сонда
у2 2. Ал бұдан
Х
2. Ал бұдан
Х у
у болады.
болады.
Сонда айналу бетінің ауданы
Х+ -4
-4
Х+ -4
-4
(
 )2
)2
4( 16+8
16+8 2
2
4( (
(
Демек,
4( (
( айналу беті болып
табылады.
айналу беті болып
табылады.
№5
.х2 теңдеуі қандай бетті
анықтайды?
теңдеуі қандай бетті
анықтайды?
Шешуі: Координаталық осьтерді
ОХ осінің айналасында  бұрышқа бұрайық. Мұнда
ОУ осінен ОХ осіне қажет нақты бағытта бұрылады. Сонда
х
бұрышқа бұрайық. Мұнда
ОУ осінен ОХ осіне қажет нақты бағытта бұрылады. Сонда
х 1,
у
1,
у 1
1  1
1 ,
,
 1
1 +
+ 1
1 .Сондықтан
.Сондықтан
 ,
онда
,
онда
х 1
,
у
1
,
у (
( 1-
1- 1),
1),
 (
( 1-
1- 1)
1)
Осы мәндерді беттің теңдеулеріне қоямыз, сонда
 -
- немесе
немесе  +
+ 0
0
Демек, конустың төбесі координаталар басында, ал координаталар осі болып табылады.
№6
 2) параболасы
о
2) параболасы
о осінің бойынан бұрылады
(вращается). Теңдеуді анықтаңыздар.
осінің бойынан бұрылады
(вращается). Теңдеуді анықтаңыздар.
Шешуі: Берілген мысал о*у
жазықтығында F(х,у )
) теңдеуімен берілген.
Парабола осінің бетінен айналады. Бұл жағдайда
х
теңдеуімен берілген.
Парабола осінің бетінен айналады. Бұл жағдайда
х 1,
у
1,
у теңдігінен және мына
теңдеулермен F(
теңдігінен және мына
теңдеулермен F( )
) болады. Осы теңдік
ізделінген теңдікті анықтайды.
болады. Осы теңдік
ізделінген теңдікті анықтайды.
№7
 -
- ОУ осі бойымен айналады.
Алынған екінші ретті беттің типін
анықтаңыздар.
ОУ осі бойымен айналады.
Алынған екінші ретті беттің типін
анықтаңыздар.
Шешуі: Берілген бет ОХУ
жазықтығында, ОУ осінің бойында айнала алады. Гипербола осінен
айналу кезінде у у
у теңдігі орындалады.
Айналған кезде
теңдігі орындалады.
Айналған кезде
F( )
) орындалады.
орындалады.
Берілген есептің шарты
бойынша 
яғни,
 -
- теңдеуі
алынады.
теңдеуі
алынады.
Сонда,
 -
- алынады. Демек, бұл
теңдеу бірқуысты гипербола. 42
алынады. Демек, бұл
теңдеу бірқуысты гипербола. 42
№9
х түзуі ОƵ осі бойымен
айналады. Айналу бетінің теңдеуін
табыңыздар.
түзуі ОƵ осі бойымен
айналады. Айналу бетінің теңдеуін
табыңыздар.
![]()
![]()


 900
900
![]()
![]()
Шешуі:
х түзуінің ОƵ осі бойымен
айналуын табайық. х
түзуінің ОƵ осі бойымен
айналуын табайық. х түзуі ХоƵ жазықтығында
ОƵ осі бойымен айналғанда Ƶ өзгеріссіз қалады.Себебі, ол ОƵ осіне
байланысты.Ал екінші айнымалысы Х айналған кезде оның таңбасы оң
және теріс болып қалған Х пен У –тен квадрат түбір табу керек, яғни
сонда
түзуі ХоƵ жазықтығында
ОƵ осі бойымен айналғанда Ƶ өзгеріссіз қалады.Себебі, ол ОƵ осіне
байланысты.Ал екінші айнымалысы Х айналған кезде оның таңбасы оң
және теріс болып қалған Х пен У –тен квадрат түбір табу керек, яғни
сонда  (1) түрінде жазуға
болады. Бұл теңдікті квадраттасақ, онда теңдеу
(1) түрінде жазуға
болады. Бұл теңдікті квадраттасақ, онда теңдеу
 немесе
немесе  түрінде
жазылады.
түрінде
жазылады.
Демек,
 конустың теңдеуі
болады. 43
конустың теңдеуі
болады. 43
№8
х түзуі ОƵ осін айналады.
Айналу бетінің теңдеуін табыңыздар.
түзуі ОƵ осін айналады.
Айналу бетінің теңдеуін табыңыздар.
Шешуі:
х жазықтықта Х пен Ƶ
теңдеуге енген. Берілген теңдеуде Ƶ айнымалысы өзгеріссіз қалады.
Есепте берілуі бойынша ОƵ осі бойымен айналу осі болып тұр. Ал
теңдеудегі екінші айнымалы Х-тің өзі
жазықтықта Х пен Ƶ
теңдеуге енген. Берілген теңдеуде Ƶ айнымалысы өзгеріссіз қалады.
Есепте берілуі бойынша ОƵ осі бойымен айналу осі болып тұр. Ал
теңдеудегі екінші айнымалы Х-тің өзі  айнымалысымен алмасып
жазылуы керек. Сонда берілген теңдеу мынадай түрінде
жазылады:
айнымалысымен алмасып
жазылуы керек. Сонда берілген теңдеу мынадай түрінде
жазылады:
Бұл теңдеудің екі жағын
квадраттау арқылы  теңдеуі алынады.
Теңдеуді
теңдеуі алынады.
Теңдеуді  түрінде жазуға болады.
Бұл кезде теңдеудің төбесі координаталар сақинасының бас
нүктесінде, ал Х
түрінде жазуға болады.
Бұл кезде теңдеудің төбесі координаталар сақинасының бас
нүктесінде, ал Х Ƶ теңдеуі Ƶ бұрышының
биссектрисасы болады. Мұндағы у
Ƶ теңдеуі Ƶ бұрышының
биссектрисасы болады. Мұндағы у дегеніміз конус.... тең
конустық биссектрисасы болады.
дегеніміз конус.... тең
конустық биссектрисасы болады.
Бұл конустың осі
6 болады.
болады.
Демек,
 айналу бетінің
теңдеуі, нәтижесінде конус алынады.
айналу бетінің
теңдеуі, нәтижесінде конус алынады.
№10
 теңдеуімен берілген
параболаның ОƵ осі бойымен айналуынан пайда болған беттің теңдеуін
табыңыз.
теңдеуімен берілген
параболаның ОƵ осі бойымен айналуынан пайда болған беттің теңдеуін
табыңыз.
Шешуі: ху бетті табу үшін
теңдеудегі х-тың орнына  табу
керек.
табу
керек.  . Бұл
түзуден
. Бұл
түзуден  4х2+4у2.
4х2+4у2.
Демек, ізделінде теңдеу
-  4х2+4у2
болады.
44
4х2+4у2
болады.
44
№11 Гиперболаның ОƵ осі бойымен айналуынан алынған бірқуысты гиперболоидтың теңдеуін құрыңыздар.
Шешуі: Гиперболаның жорамал осін айналу арқылы алынған гиперболоидты табу керек. Сонымен ОƵ осін гиперболаның осі болса, онда гиперболаның теңдеуі

болады. Осы теңдеуде
х-ті  -қа ауыстырсақ, онда
бірқуысты гиперболоидтың теңдеуі
-қа ауыстырсақ, онда
бірқуысты гиперболоидтың теңдеуі
 немесе
немесе  +
+ болады.
болады.
Демек, Гиперболаны ОƵ осі бойымен айналдырғанда, шыққан бірқуысты гиперболоидтың теңдеуі
 +
+ алынады.
45
алынады.
45
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Айналу эллипсоиды
Айналу эллипсоиды
Айналу эллипсоиды
 эллипсоид ОУ осінен
айналып шыққан, айналу эллипс сызығының теңдеуін
жазыңыздар.
эллипсоид ОУ осінен
айналып шыққан, айналу эллипс сызығының теңдеуін
жазыңыздар.
Шешуі: Айналу бетінің теңдеуін
табу ережесіне сәйкес эллипс сызығының
теңдеуіндегі  Нәтижесінде берілген
эллипстің теңдеуіндегі х-тың орнына
Нәтижесінде берілген
эллипстің теңдеуіндегі х-тың орнына  қойылады.Сонда
қойылады.Сонда
 +
+ немесе
немесе  теңдеуіне
айналады.
теңдеуіне
айналады.
Демек,
 айналу эллипс
сызығының теңдеуі алынады. 39
айналу эллипс
сызығының теңдеуі алынады. 39
Жарты осьтері 5 пен 3 болатын эллипс, өзінің үлкен осіның бойына айналады. Үлкен осі ОУ осінде, ал эллипс центрі координаталары системасының бас нүктесінде орналасқан.Осы эллипстің ОУ осіне айналу кезіндегі бетінің теңдеуін табыңыздар.
Шешуі: Берілуі бойынша
в және
уо
және
уо жазықтығында жатыр. Оның
теңдеуі
жазықтығында жатыр. Оның
теңдеуі


Берілгені бойынша қисықтың
теңдеуі уо жазықтығында жатыр.Ал
қисық ОУ осінен айналған кезде пайда болатын бетті алу
үшін
жазықтығында жатыр.Ал
қисық ОУ осінен айналған кезде пайда болатын бетті алу
үшін 
 Сонда қисықтың
теңдеуі
Сонда қисықтың
теңдеуі
 немесе
немесе  түрінде
жазылады.
түрінде
жазылады.
Демек,
алынған  ізделінді теңдеу
болады.
ізделінді теңдеу
болады.
х-2у ,
,
 айналғанда алынатын
айналу бетінің теңдеуін табыңыздар.
айналғанда алынатын
айналу бетінің теңдеуін табыңыздар.
Шешуі: М нүктесі сызығының
төбесі дейік. Оның координатасы (4; 0;0) болады. Осы конустың кез
келген А нүктесінің координатасы  десек, оның сәйкес
негізін В (х,у,о) нүктесі болады.А мен В ның координаталары А
(
десек, оның сәйкес
негізін В (х,у,о) нүктесі болады.А мен В ның координаталары А
( В(х,у,о) болады, сонда А
мен В координата нүктесінің әртүрлі нүктесі, ал В (х,у,о)
координатасында болады. Сонда
у2
В(х,у,о) болады, сонда А
мен В координата нүктесінің әртүрлі нүктесі, ал В (х,у,о)
координатасында болады. Сонда
у2 2. Ал бұдан
Х
2. Ал бұдан
Х у
у болады.
болады.
Сонда айналу бетінің ауданы
Х+ -4
-4
Х+ -4
-4
(
 )2
)2
4( 16+8
16+8 2
2
4( (
(
Демек,
4( (
( айналу беті болып
табылады.
айналу беті болып
табылады.
№5
.х2 теңдеуі қандай бетті
анықтайды?
теңдеуі қандай бетті
анықтайды?
Шешуі: Координаталық осьтерді
ОХ осінің айналасында  бұрышқа бұрайық. Мұнда
ОУ осінен ОХ осіне қажет нақты бағытта бұрылады. Сонда
х
бұрышқа бұрайық. Мұнда
ОУ осінен ОХ осіне қажет нақты бағытта бұрылады. Сонда
х 1,
у
1,
у 1
1  1
1 ,
,
 1
1 +
+ 1
1 .Сондықтан
.Сондықтан
 ,
онда
,
онда
х 1
,
у
1
,
у (
( 1-
1- 1),
1),
 (
( 1-
1- 1)
1)
Осы мәндерді беттің теңдеулеріне қоямыз, сонда
 -
- немесе
немесе  +
+ 0
0
Демек, конустың төбесі координаталар басында, ал координаталар осі болып табылады.
№6
 2) параболасы
о
2) параболасы
о осінің бойынан бұрылады
(вращается). Теңдеуді анықтаңыздар.
осінің бойынан бұрылады
(вращается). Теңдеуді анықтаңыздар.
Шешуі: Берілген мысал о*у
жазықтығында F(х,у )
) теңдеуімен берілген.
Парабола осінің бетінен айналады. Бұл жағдайда
х
теңдеуімен берілген.
Парабола осінің бетінен айналады. Бұл жағдайда
х 1,
у
1,
у теңдігінен және мына
теңдеулермен F(
теңдігінен және мына
теңдеулермен F( )
) болады. Осы теңдік
ізделінген теңдікті анықтайды.
болады. Осы теңдік
ізделінген теңдікті анықтайды.
№7
 -
- ОУ осі бойымен айналады.
Алынған екінші ретті беттің типін
анықтаңыздар.
ОУ осі бойымен айналады.
Алынған екінші ретті беттің типін
анықтаңыздар.
Шешуі: Берілген бет ОХУ
жазықтығында, ОУ осінің бойында айнала алады. Гипербола осінен
айналу кезінде у у
у теңдігі орындалады.
Айналған кезде
теңдігі орындалады.
Айналған кезде
F( )
) орындалады.
орындалады.
Берілген есептің шарты
бойынша 
яғни,
 -
- теңдеуі
алынады.
теңдеуі
алынады.
Сонда,
 -
- алынады. Демек, бұл
теңдеу бірқуысты гипербола. 42
алынады. Демек, бұл
теңдеу бірқуысты гипербола. 42
№9
х түзуі ОƵ осі бойымен
айналады. Айналу бетінің теңдеуін
табыңыздар.
түзуі ОƵ осі бойымен
айналады. Айналу бетінің теңдеуін
табыңыздар.
![]()
![]()


 900
900
![]()
![]()
Шешуі:
х түзуінің ОƵ осі бойымен
айналуын табайық. х
түзуінің ОƵ осі бойымен
айналуын табайық. х түзуі ХоƵ жазықтығында
ОƵ осі бойымен айналғанда Ƶ өзгеріссіз қалады.Себебі, ол ОƵ осіне
байланысты.Ал екінші айнымалысы Х айналған кезде оның таңбасы оң
және теріс болып қалған Х пен У –тен квадрат түбір табу керек, яғни
сонда
түзуі ХоƵ жазықтығында
ОƵ осі бойымен айналғанда Ƶ өзгеріссіз қалады.Себебі, ол ОƵ осіне
байланысты.Ал екінші айнымалысы Х айналған кезде оның таңбасы оң
және теріс болып қалған Х пен У –тен квадрат түбір табу керек, яғни
сонда  (1) түрінде жазуға
болады. Бұл теңдікті квадраттасақ, онда теңдеу
(1) түрінде жазуға
болады. Бұл теңдікті квадраттасақ, онда теңдеу
 немесе
немесе  түрінде
жазылады.
түрінде
жазылады.
Демек,
 конустың теңдеуі
болады. 43
конустың теңдеуі
болады. 43
№8
х түзуі ОƵ осін айналады.
Айналу бетінің теңдеуін табыңыздар.
түзуі ОƵ осін айналады.
Айналу бетінің теңдеуін табыңыздар.
Шешуі:
х жазықтықта Х пен Ƶ
теңдеуге енген. Берілген теңдеуде Ƶ айнымалысы өзгеріссіз қалады.
Есепте берілуі бойынша ОƵ осі бойымен айналу осі болып тұр. Ал
теңдеудегі екінші айнымалы Х-тің өзі
жазықтықта Х пен Ƶ
теңдеуге енген. Берілген теңдеуде Ƶ айнымалысы өзгеріссіз қалады.
Есепте берілуі бойынша ОƵ осі бойымен айналу осі болып тұр. Ал
теңдеудегі екінші айнымалы Х-тің өзі  айнымалысымен алмасып
жазылуы керек. Сонда берілген теңдеу мынадай түрінде
жазылады:
айнымалысымен алмасып
жазылуы керек. Сонда берілген теңдеу мынадай түрінде
жазылады:
Бұл теңдеудің екі жағын
квадраттау арқылы  теңдеуі алынады.
Теңдеуді
теңдеуі алынады.
Теңдеуді  түрінде жазуға болады.
Бұл кезде теңдеудің төбесі координаталар сақинасының бас
нүктесінде, ал Х
түрінде жазуға болады.
Бұл кезде теңдеудің төбесі координаталар сақинасының бас
нүктесінде, ал Х Ƶ теңдеуі Ƶ бұрышының
биссектрисасы болады. Мұндағы у
Ƶ теңдеуі Ƶ бұрышының
биссектрисасы болады. Мұндағы у дегеніміз конус.... тең
конустық биссектрисасы болады.
дегеніміз конус.... тең
конустық биссектрисасы болады.
Бұл конустың осі
6 болады.
болады.
Демек,
 айналу бетінің
теңдеуі, нәтижесінде конус алынады.
айналу бетінің
теңдеуі, нәтижесінде конус алынады.
№10
 теңдеуімен берілген
параболаның ОƵ осі бойымен айналуынан пайда болған беттің теңдеуін
табыңыз.
теңдеуімен берілген
параболаның ОƵ осі бойымен айналуынан пайда болған беттің теңдеуін
табыңыз.
Шешуі: ху бетті табу үшін
теңдеудегі х-тың орнына  табу
керек.
табу
керек.  . Бұл
түзуден
. Бұл
түзуден  4х2+4у2.
4х2+4у2.
Демек, ізделінде теңдеу
-  4х2+4у2
болады.
44
4х2+4у2
болады.
44
№11 Гиперболаның ОƵ осі бойымен айналуынан алынған бірқуысты гиперболоидтың теңдеуін құрыңыздар.
Шешуі: Гиперболаның жорамал осін айналу арқылы алынған гиперболоидты табу керек. Сонымен ОƵ осін гиперболаның осі болса, онда гиперболаның теңдеуі

болады. Осы теңдеуде
х-ті  -қа ауыстырсақ, онда
бірқуысты гиперболоидтың теңдеуі
-қа ауыстырсақ, онда
бірқуысты гиперболоидтың теңдеуі
 немесе
немесе  +
+ болады.
болады.
Демек, Гиперболаны ОƵ осі бойымен айналдырғанда, шыққан бірқуысты гиперболоидтың теңдеуі
 +
+ алынады.
45
алынады.
45

шағым қалдыра аласыз















