
Алгебралық теңсіздіктердің геометриялық мағынасы
Карыбаева Сауле Шешкеновна – «Қарақол орта мектеп-балабақшасы» КММ-нің
математика пәнінің мұғалімі, ҚР Білім беру ісінің үздігі
Екі айнымалысы бар F(x,y)=0 теңдеуінің графигі жазықтықта жатқан координаталары осы теңдеуді қанағаттандыратын (х,у) нүктелерінің жиыны болып табылады. у = f(х) функциясының графиктік кескінделуі—ең көрнекі тәсілге жатады. График сызығы жазықтықты бірнеше бөлікке бөледі. Олардың біреулерінде F(x,y)<0 болса; ал басқаларында F(x,y) >0 теңсіздігі орындалады.
Сонымен теңдеу, теңсіздік және олардың жүйелерінің геометриялық мағынасын сипаттау үшін оқушыларға қажет тірек білімдері:
-
Теңдеуіне қарай функция түрлерін анықтай білу (сызықтық, квадраттық, дәрежелік, кері пропорционалдық, т.б);
-
Функция қасиеттерін білу (анықталу облысы, мәндер облысы, жұптығы, тақтығы, т.б);
-
Графиктерді түрлендіре білу (параллель көшіру, созу, сығу, осьтік симметрия, т.б);
-
Шеңбер x2+y2=R2, (х-а)2+(у-в)2=R2, эллипс теңдеулерін
 білу;
білу; -
Теңдеуге сәйкес графиктерді сауатты сыза білу.
-
Жазықтықтағы нүктелер жиынының бір немесе екі айнымалысы бар теңсіздікпен берілуі
Жарты жазықтықтардың берілу жағдайына тоқталайық. Оу осінің нүктелер жиыны х=0 теңдеуімен беріледі. Егер абсциссасы оң, ординатасы кез келген сан десек, онда мұндай қасиетке ие нүктелер жиыны х>0 теңсіздігімен берілетін оң жақ ашық жарты жазықтықты (1– сурет), ал х<0 теңсіздігі сол жақ ашық жарты жазықтықты анықтайды.
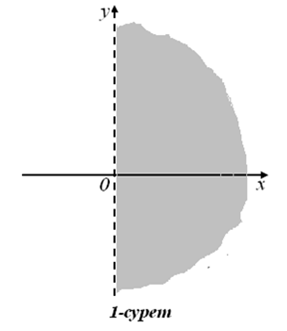
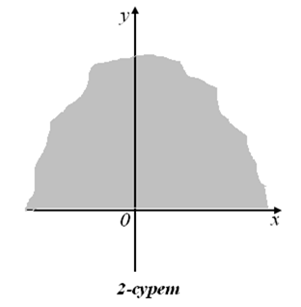
Екі жағдайда да шекаралық х=0 түзуінің нүктелер жиыны шешімге кірмейтіндіктен үзік сызықтармен сызылады. Дәл осылайша жоғарғы жәнетөменгі ашық жарты жазықтықтары сәйкесінше у>0 және у<0 теңсіздіктерімен беріледі. Егер тұйық жарты жазықтықты анықтау қажет болса, онда шекаралық түзудің нүктелерін енгізу арқылы у0 теңсіздігін аламыз (2–сурет).
Жаттығулар
Берілген теңсіздіктерді қанағаттандыра-тын жазықтық нүктелерінің жиынын тап.
а) х≤2 в) у≤1
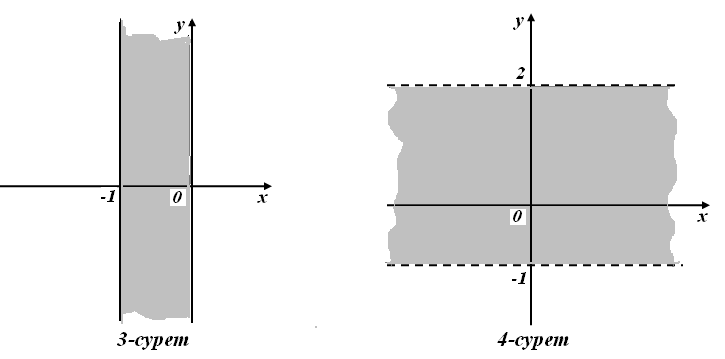
ә) у>–3 г) –1≤х≤0 (3–сурет)
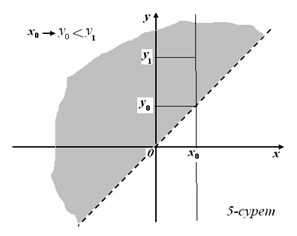
б) х>–4 д) –1< у< 2 (4–сурет)
г, д қос теңсіздіктері екі теңсіздіктен құралған жүйені береді
 ;
; 
у–х=0 сызықтық теңдеуін қарастырайық. Бұл у=х түзуі І және ІІІ ширектің биссектрисасы болып табылады. Сонда у>х теңсіздігінің шешімі жоғарғы ашық жарты жазықтықтың нүктелерінің жиыны болады (5-сурет).
Жаттығулар
Берілген теңсіздіктердің шешімдерін жазықтықта кескінде
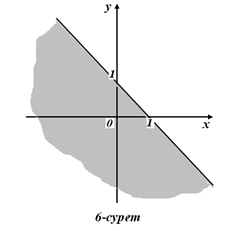
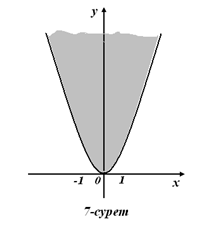
а) х+у–1≤0 ә) у х2
у≤ –х+1 (6-сурет) (7-сурет )
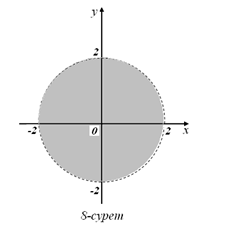
б)  в)
в) 
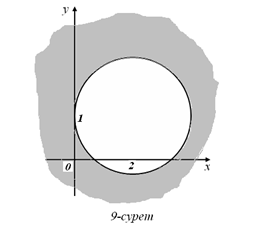 г)
г)  д)
д)

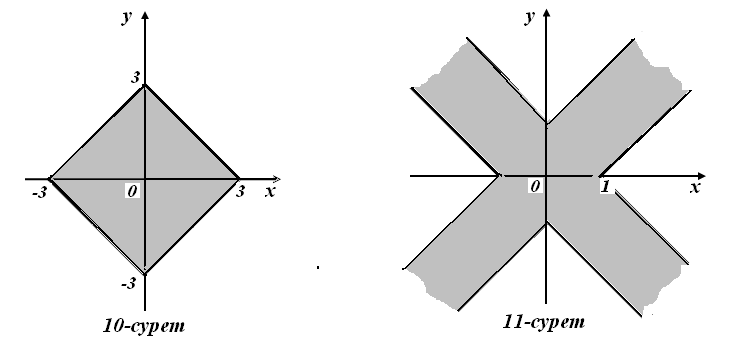
ІІ. Алгебралық теңсіздіктер жүйесінің геометриялық мағынасы
Жүйенің шешімі– жүйедегі теңсіздіктердің ортақ шешімі, яғни шешімдер жиынының қиылысуы болады. Мысалы

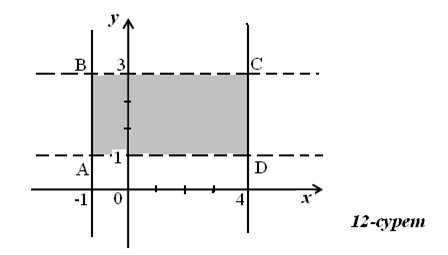
–1≤х≤4 тік жолақтың, ал 1<у<3 көлденең жолақтың нүктелер жиыны. Олардың қиылысуы АВСД тік төртбұрышы (12-сурет) берілген жүйеге шешім болады. Сонда АД және ВС кесінділері ұштарымен қоса алғанда шешімдер жиынына кірмейді,олар үзік сызықтармен сызылған.
Жаттығулар
а)  )
)
ә)

б) 
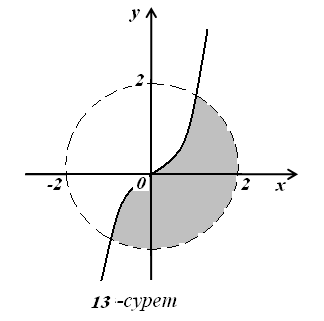
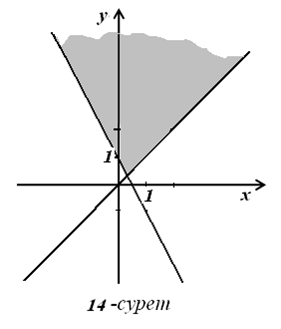
в) 
ІІІ. Қарақол орта мектебінің математиканы тереңдетіп оқитын 9«А» сыныбы оқушыларының құрған есептері
1) 
2) 
3)

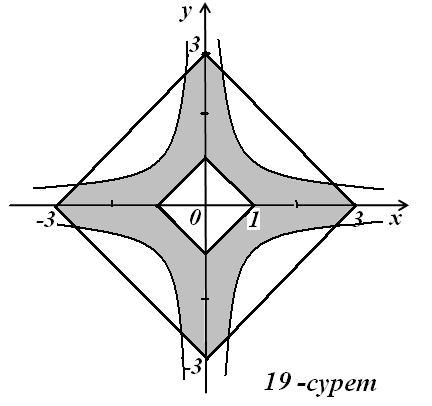
4) 
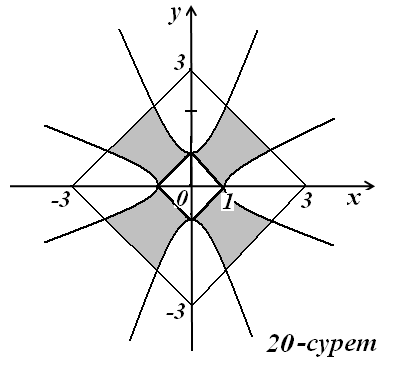
5) 
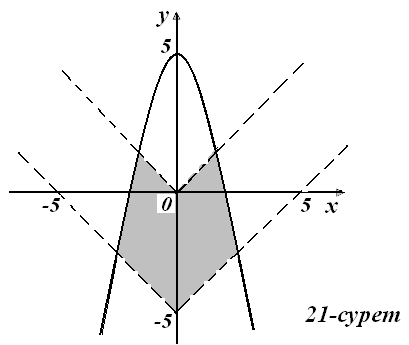
6) 
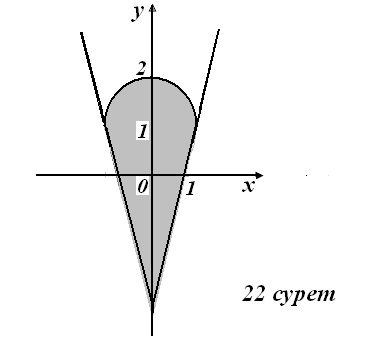
7) 
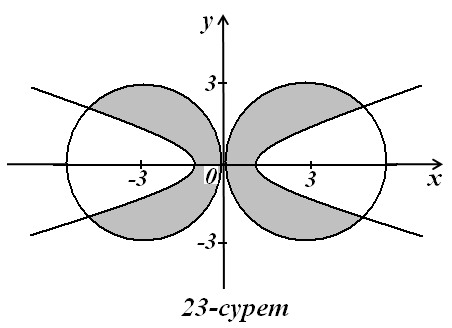
8)
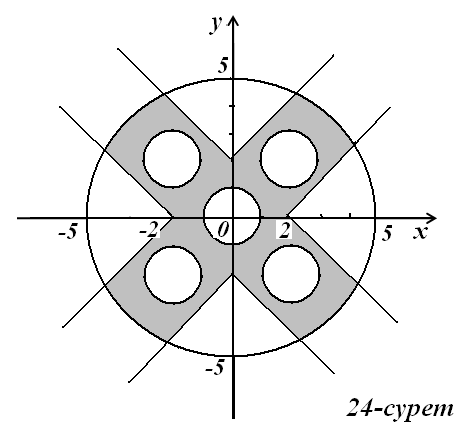
9) 
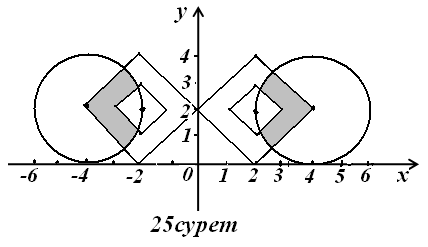
10) 
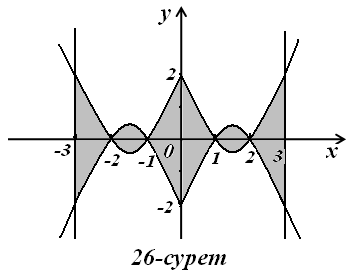
11) 
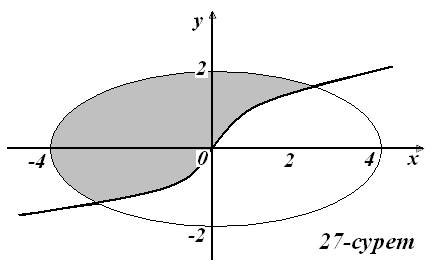
12) 
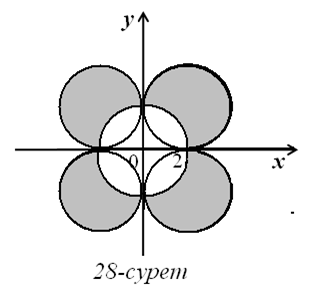
13)  Бұл жүйе келесі
жүйелер жиынымен мәндес
Бұл жүйе келесі
жүйелер жиынымен мәндес

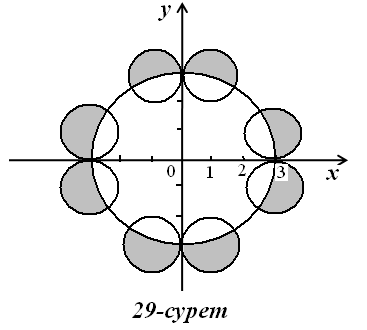
14)
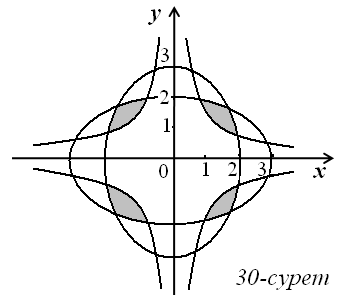
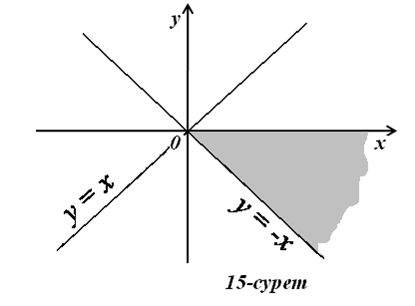
15) 
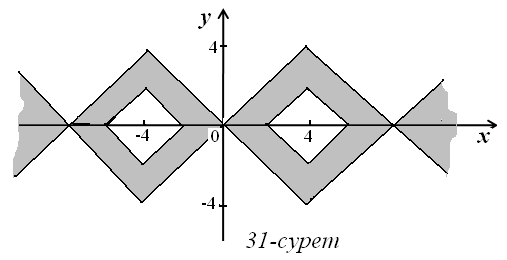
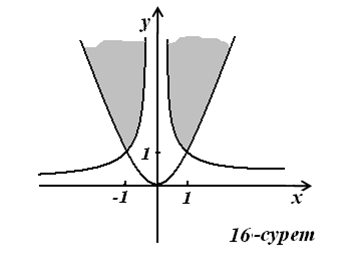
16) 
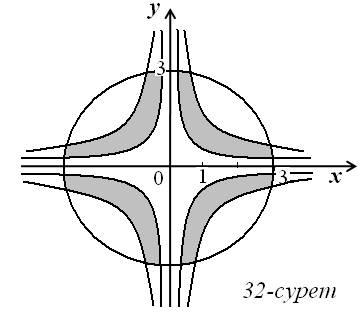
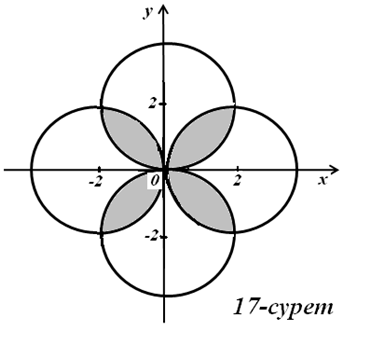
17) 
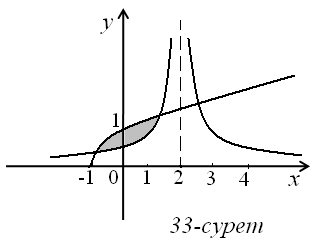
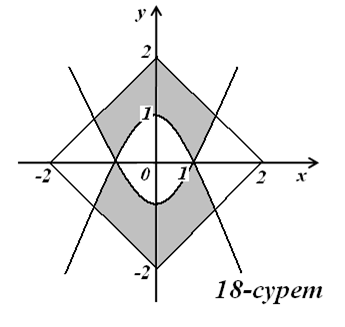
18) 
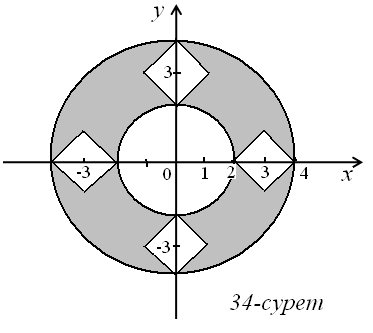
Қолданылған әдебиеттер:
1.Баймұханов Б, Алгебра–9 кл, Алматы, «Жазушы», 2005
7
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Алгебралық теңсіздіктердің геометриялық мағынасы
Алгебралық теңсіздіктердің геометриялық мағынасы
Алгебралық теңсіздіктердің геометриялық мағынасы
Карыбаева Сауле Шешкеновна – «Қарақол орта мектеп-балабақшасы» КММ-нің
математика пәнінің мұғалімі, ҚР Білім беру ісінің үздігі
Екі айнымалысы бар F(x,y)=0 теңдеуінің графигі жазықтықта жатқан координаталары осы теңдеуді қанағаттандыратын (х,у) нүктелерінің жиыны болып табылады. у = f(х) функциясының графиктік кескінделуі—ең көрнекі тәсілге жатады. График сызығы жазықтықты бірнеше бөлікке бөледі. Олардың біреулерінде F(x,y)<0 болса; ал басқаларында F(x,y) >0 теңсіздігі орындалады.
Сонымен теңдеу, теңсіздік және олардың жүйелерінің геометриялық мағынасын сипаттау үшін оқушыларға қажет тірек білімдері:
-
Теңдеуіне қарай функция түрлерін анықтай білу (сызықтық, квадраттық, дәрежелік, кері пропорционалдық, т.б);
-
Функция қасиеттерін білу (анықталу облысы, мәндер облысы, жұптығы, тақтығы, т.б);
-
Графиктерді түрлендіре білу (параллель көшіру, созу, сығу, осьтік симметрия, т.б);
-
Шеңбер x2+y2=R2, (х-а)2+(у-в)2=R2, эллипс теңдеулерін
 білу;
білу; -
Теңдеуге сәйкес графиктерді сауатты сыза білу.
-
Жазықтықтағы нүктелер жиынының бір немесе екі айнымалысы бар теңсіздікпен берілуі
Жарты жазықтықтардың берілу жағдайына тоқталайық. Оу осінің нүктелер жиыны х=0 теңдеуімен беріледі. Егер абсциссасы оң, ординатасы кез келген сан десек, онда мұндай қасиетке ие нүктелер жиыны х>0 теңсіздігімен берілетін оң жақ ашық жарты жазықтықты (1– сурет), ал х<0 теңсіздігі сол жақ ашық жарты жазықтықты анықтайды.


Екі жағдайда да шекаралық х=0 түзуінің нүктелер жиыны шешімге кірмейтіндіктен үзік сызықтармен сызылады. Дәл осылайша жоғарғы жәнетөменгі ашық жарты жазықтықтары сәйкесінше у>0 және у<0 теңсіздіктерімен беріледі. Егер тұйық жарты жазықтықты анықтау қажет болса, онда шекаралық түзудің нүктелерін енгізу арқылы у0 теңсіздігін аламыз (2–сурет).
Жаттығулар
Берілген теңсіздіктерді қанағаттандыра-тын жазықтық нүктелерінің жиынын тап.
а) х≤2 в) у≤1
ә) у>–3 г) –1≤х≤0 (3–сурет)
б) х>–4 д) –1< у< 2 (4–сурет)
г, д қос теңсіздіктері екі теңсіздіктен құралған жүйені береді
 ;
; 

у–х=0 сызықтық теңдеуін қарастырайық. Бұл у=х түзуі І және ІІІ ширектің биссектрисасы болып табылады. Сонда у>х теңсіздігінің шешімі жоғарғы ашық жарты жазықтықтың нүктелерінің жиыны болады (5-сурет).

Жаттығулар
Берілген теңсіздіктердің шешімдерін жазықтықта кескінде
а) х+у–1≤0 ә) у х2
у≤ –х+1 (6-сурет) (7-сурет )


б)  в)
в) 

 г)
г)  д)
д)


ІІ. Алгебралық теңсіздіктер жүйесінің геометриялық мағынасы
Жүйенің шешімі– жүйедегі теңсіздіктердің ортақ шешімі, яғни шешімдер жиынының қиылысуы болады. Мысалы


–1≤х≤4 тік жолақтың, ал 1<у<3 көлденең жолақтың нүктелер жиыны. Олардың қиылысуы АВСД тік төртбұрышы (12-сурет) берілген жүйеге шешім болады. Сонда АД және ВС кесінділері ұштарымен қоса алғанда шешімдер жиынына кірмейді,олар үзік сызықтармен сызылған.
Жаттығулар
а)  )
)
ә)

б) 



в) 

ІІІ. Қарақол орта мектебінің математиканы тереңдетіп оқитын 9«А» сыныбы оқушыларының құрған есептері
1) 

2) 

3)


4) 

5) 

6) 

7) 

8)

9) 

10) 

11) 

12) 

13)  Бұл жүйе келесі
жүйелер жиынымен мәндес
Бұл жүйе келесі
жүйелер жиынымен мәндес


14)

15) 

16) 

17) 

18) 

Қолданылған әдебиеттер:
1.Баймұханов Б, Алгебра–9 кл, Алматы, «Жазушы», 2005
7

шағым қалдыра аласыз















