
МАЗМҰНЫ
КІРІСПЕ................................................... ...................................................................3
І. ЖҮЙЕ ДИНАМИКАСЫНЫҢ ЖАЛПЫ ТЕОРЕМАЛАРЫ................................4
-
Жүйенің кинетикалық энергиясы................................................... ................4
1.2. Потенциалдық күш өрісі және күштік функция...............................................6
ІІ. АНАЛИТИКАЛЫҚ МЕХАНИКА................................................... ..................13
2.1. Динамикалық байланыстар................................................. .............................13
2.2. Жүйенің ықтимал орын ауыстыруы. Жүйенің еркіндік дәреже саны..........14
ҚОРЫТЫНДЫ .........................................................................................................22
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР.....................................................................23
І. ЖҮЙЕ ДИНАМИКАСЫНЫҢ ЖАЛПЫ ТЕОРЕМАЛАРЫ
-
Жүйенің кинетикалық энергиясы
Жүйенің кинетикалық энергиясы деп, оның барлық нүктелерінің кинетикалық энергияларының арифметиаклық қосындысына тең Т-скалярлық шаманы атаймыз:
![]()
Кинетикалық энергия
жүйенің ілгерілемелі де, айналма да қозғалыстарын сипаттайды, демек
сүрден қозғалыстарды да сипаттайды. Жүйенің қозғалыс мөлшері
![]() -менен
-менен ![]() - ден негізгі айырмашылығы Т
скаляр және оң сан. Сондықтан ол қозғалыстың бағытына байланысты
емес, оны анықтамайды да. Егер жүйе бірнеше денеден құралса,
онда
- ден негізгі айырмашылығы Т
скаляр және оң сан. Сондықтан ол қозғалыстың бағытына байланысты
емес, оны анықтамайды да. Егер жүйе бірнеше денеден құралса,
онда
![]()
Кинетикалық энергияны анықтайтын өрнектер қозғалыстың түріне байланысты болады.
1. Ілгерілемелі қозғалыс
Бұл қозғалыста
барлық нүктелер жүйенің бір жылдамдықпен қозғалады. Сол үшін (1)-ші
өрнекте ![]() деп алу
керек:
деп алу
керек:
![]()
Демек
![]()
2. Айналма қозғалыс
Егер дене бір өсті айнала қозғалса, кез келген М нүктенің
жылдамдығы ![]() Олай
болса,
Олай
болса,
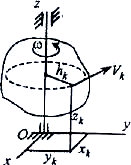
Демек, ![]()
![]() - дененің z өсіне
қатысты екпін
- дененің z өсіне
қатысты екпін
моменті
3. Жазық параллель қозғалыс
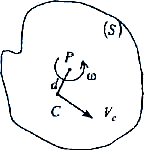 Мұндай қозғалысты (S) қима
Мұндай қозғалысты (S) қима
жазықтығына перпендикуляр
лездік жылдамдық Р центрінен
өтетін өсті айналу қозғалысы деп
қарастыруға болады.
Онда
![]()
![]() - дененің Р лездік
өске қатысты инерция
моменті.
- дененің Р лездік
өске қатысты инерция
моменті.
Бұл өрнекті С массалар центрінен өтетін өске қатысты жазайық.
![]() -Гюйгенс-Штейнер
теоремасы.
-Гюйгенс-Штейнер
теоремасы.
Онда 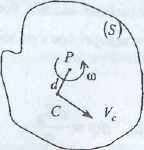
![]()
а) Дененің айнала қозғалысын тудыратын күш жұмысы.
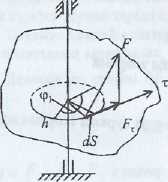
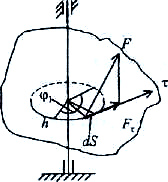 Кез
келген М нүктеде
Кез
келген М нүктеде
![]() күштің элементар
жұмысы
күштің элементар
жұмысы
![]()
Мұндағы ![]()
Яғни ![]()
![]() -
-![]() күштің Oz өсіне қатысты
моменті:
күштің Oz өсіне қатысты
моменті:
![]()
Демек,
![]()
Егерде ![]() шекті шама болса
шекті шама болса ![]() , онда дененің
, онда дененің ![]() күш әсерінен
шекті
күш әсерінен
шекті ![]() айналуындағы жұмысы
келесі интегралмен беріледі:
айналуындағы жұмысы
келесі интегралмен беріледі:

![]() - тұрақты
болса
- тұрақты
болса
![]()
Шекті жұмыс қуаты
![]()
б) Түзу бойымен сырғанамай домалайтын дөңгелекке түскен үйкеліс күш жұмысы.
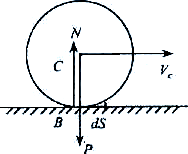
![]()
В нүкте дөңгелек үшін – лездік жылдамдықтар центрі:
![]() , демек
, демек ![]()
Олай болса
![]()
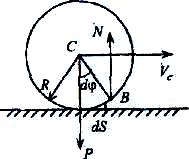 Егер дөңгелекпен
байланыс деформация алатын болса,
Егер дөңгелекпен
байланыс деформация алатын болса, ![]() қос күшке байланысты домалауға
кедергі қос күш пайда
болады:
қос күшке байланысты домалауға
кедергі қос күш пайда
болады:
![]()
![]()
![]()
![]()
![]() қос күш
момент
қос күш
момент
![]()
қос күштің шекті
жұмысы ![]()
 (13)
(13)
Жүйенің кинетикалық энергиясының өзгеруі туралы теорема
Жеке нүктенің
![]() кинетикалық энергиясының
өзгеруі туралы теорема жүйенің кез келген нүктесі үшін
әділ:
кинетикалық энергиясының
өзгеруі туралы теорема жүйенің кез келген нүктесі үшін
әділ:
![]()
Бұл теорема жүйе үшін оңай жазылады:

(14)-теореманың дифференциалдық түрін береді.
Жүйенің бастапқы
орнында кинетикалық энергия ![]() кез келген келесі орнындағы
кинетикалық энергиясы Т
болсын.
кез келген келесі орнындағы
кинетикалық энергиясы Т
болсын.
Соңғы теңдеудің екі жағынан интеграл алсақ,
![]()
(15)-теореманың шекті немесе интегралды түрін береді.
Теорема:
Жүйенің кез келген орын ауыстыруындағы кинетикалық энергияның өзгеруі сол орын ауыстырудағы сыртқы күштердің жұмыстарының қосындысына тең.
Жүйеге әсер ететін барлық күштерді берілген (актив) күштермен байланыс реакция күштеріне бөлуге болады.
![]()
Егер ![]() болса, жүйенің
байланыстарын идеалдық байланыстар деп
атаймыз.
болса, жүйенің
байланыстарын идеалдық байланыстар деп
атаймыз.
Байланыстар идеалдық байланыстар болса,
![]()
Механикалық жүйенің кинетикалық энергиясы мына өрнекпен берілсін:
![]()
Ілгерілемелі
қозғалыста ![]()
Айналма қозғалыста
![]()
Жазық-параллель
қозғалыста ![]()
1.2. Потенциалдық күш өрісі және күштік функция
Жүйе кинетикалық энергиясының өзгеру теоремасы арқылы есеп шығарғанда, жүйеге түскен сыртқы күштер жұмыстарын анықтау үшін қозғалыс заңын пайдаланбадық.
Төменде қандай күштерге қатысты дененің қозғалыс заңын пайдаланбай олардың жұмыстарын табуға болатынын анықтайық.
Дененің кез келген М
нүктесіне түскен ![]() күштің
күштің
![]() орын ауыстыруындағы
жұмысы .
орын ауыстыруындағы
жұмысы .

Мұндағы ![]() күштер нүктелердің
күштер нүктелердің ![]() орындары координаталарына тәуелді
болғанда ғана жоғарыдағы интегралды есептеуге болады. Мұндай
күштерді күштік өріс дейміз.
орындары координаталарына тәуелді
болғанда ғана жоғарыдағы интегралды есептеуге болады. Мұндай
күштерді күштік өріс дейміз.
Күштік өріс деп кеңістіктің кез келген бөлігінде нүктелер координаталарына тәуелді күштер жүйесін атаймыз.
Мысал ретінде планеталар мен Күннің тартылыс өрісін атауға болады. Сонымен күштік өріс
![]()
теңдеулермен
беріледі. ![]() - кез келген
функциялар.
- кез келген
функциялар.
Жалпы жағдайда (1)
интеграл астында бір айналымға көшу қажет, мысалы ![]() , демек, нүктенің траекториясы
белгілі болуы қажет.
, демек, нүктенің траекториясы
белгілі болуы қажет.
Бірақ, егер де
интегралдың астында (ішінде) тұрған элементар жұмыс ![]() айталық
айталық ![]() функциясының толық дифференциалы
болса, яғни
функциясының толық дифференциалы
болса, яғни
![]() немесе
немесе ![]()
онда ![]() жұмысты дене нүктесінің
траекториясымен білмей ақ анықтауға болады. Толық дифференциалы
элементар жұмысқа тең
жұмысты дене нүктесінің
траекториясымен білмей ақ анықтауға болады. Толық дифференциалы
элементар жұмысқа тең ![]() функцияны күштік фүнкция деп
атаймыз. Күштік функция сәйкес күштік өрісті (күштерді) потенциалды
күштік өріс, ал сол өрісте әсер ететін күшті потенциалды күштер деп
атаймыз.
функцияны күштік фүнкция деп
атаймыз. Күштік функция сәйкес күштік өрісті (күштерді) потенциалды
күштік өріс, ал сол өрісте әсер ететін күшті потенциалды күштер деп
атаймыз.
(1)-теңдікті қолданып, (2)-теңдеудің екі жағынан интеграл алайық.

![]() - күштік функцияның
- күштік функцияның
![]() нүктелердегі мәндері. Демек,
потенциалдық күштің жұмысы күштік функцияның бастапқы және соңғы
нүктелердегі мәндерінің айырымына тең, сонымен қатар нүктенің
траекториясына тәуелсіз.
нүктелердегі мәндері. Демек,
потенциалдық күштің жұмысы күштік функцияның бастапқы және соңғы
нүктелердегі мәндерінің айырымына тең, сонымен қатар нүктенің
траекториясына тәуелсіз.
Күштердің жұмысы (нүкте) траекториясының түріне немесе қозғалыс заңына тәуелді болса, ондай күштерді потенциалды емес күштер деп атаймыз. Ондай күштерге үйкеліс күші, орталардың кедергі күштері жатады.
Керісінше (2)-теңдеуден
![]()
Потенциалды күштерге ауырлық күші, серпімділік және тартылыс күштері жатады. Осы күштердің күштік функцияларын табайық.
1) ауырлық күш үшін
![]()

Демек,
![]()
2) серпімділік күш үшін
![]() . Бастапқы
шарт
. Бастапқы
шарт
![]() болсын.
Онда
болсын.
Онда
![]()
Егер де функция U белгілі болса, онда кез келген нүктеге әсер ететін күшті табуға болады. Шынында да, (3)-ші теңдеуден
![]()
Онда
![]()
(7)-мен анықталатын ![]() векорды
векорды ![]() функциясының градиенті деп
атайды.
функциясының градиенті деп
атайды.
Яғни ![]()
(7)-ден 
Демек,
![]()
Сонымен, күштер өрісінің күштік функциясы бар болса, күш (8)-ді қанағаттандыруы керек.
![]()
Потенциалдық энергия
Потенциалдық күштер үшін “потенциалды энергия” деген ұғымды ендіруге болады. Оны күштік өрістің белгілі нүктесінің “жұмыс қоры” деп қарастырамыз. “Жұмыс қорларын” өзара салыстыру үшін “жұмыс қоры” нөл болатын (нөлдік) нүкте таңдай алу қажет.
М нүктенің потенциалдық энергиясы деп күштердің М орыннан нөлдік орынға материялдық нүктенің орын ауыстыруындағы жұмысына тең П скалярлық шаманы атаймыз,
![]() .
.
![]() және
және ![]() функцияларының нөлдік нүктелері
бір деп есептейміз.
функцияларының нөлдік нүктелері
бір деп есептейміз.
Онда
![]()
![]() - күштік функцияның
М нүктедегі мәні.
- күштік функцияның
М нүктедегі мәні.
![]()
Потенциалдық энергия таңбамен алынған күштер функциясына тең. Мұнан шығатын қорытынды: потенциалдық күштер өрісінде күштер функциясының орнына потенциалды энергияны қарастыруға болады.
Мысалы: ![]() .
.
Механикалық энергияның сақталу заңы
Жүйеге әсер ететін барлық сыртқы және ішкі күштер потенциалы күштер болсын. Онда кез келген жүйе нүктесі үшін күштер жұмысы:
![]()
Онда жүйе үшін
![]()
Жүйе кинетикалық энергиясының өзгеруі туралы теорема төмендегідей жазылады.
![]()
немесе
![]() (11)
(11)
Демек, берілген потенциалдық күштер әсерінен қозғалысындағы кинетикалық және потенциалдық энергияларының қосындысы жүйенің кез келген орнында бірдей болады. Бұл заңды механикалық жүйенің сақталу заңы деп аталады.
Механикалық жүйе үшін Даламбер принципі. Дененің өзінің симметриялық жазықтығына перпендикуляр өсті айналуы
Еркін емес механикалық жүйенің қозғалысын қарастырған белгілі аксиомаға сүйеніп, жүйенің байланыстарын алып тастап, олардың әсерлерін реакцияларымен ауыстырып, еркін емес жүйені еркін деп қарастыруға болады. Демек, жүйеге реакциялар мен берілген күштерді түсіріп, еркін жүйе деп қарастырамыз.
Бір нүкте үшін
Даламбер принципі ![]() түрде
жазылады.
түрде
жазылады. ![]() -
екпін,
-
екпін, ![]() - реакция
күштері.
- реакция
күштері.
Еркін емес жүйе n материялық нүктелерден тұрады деп, оның әр нүктесіне Даламбер принципін қолдансақ,
![]()
Мұнда ![]() -
- ![]() нүктеге түскен берілген күштердің
тең әсерлі күші,
нүктеге түскен берілген күштердің
тең әсерлі күші, ![]() - сол нүктеге түскен
реакция күштерінің тең әсерлі күші,
- сол нүктеге түскен
реакция күштерінің тең әсерлі күші,
![]() нүктенің екпін
күші.
нүктенің екпін
күші.
Сонымен (1) теңдеуге
сәйкес жүйенің кез келген ![]() нүктесіне түскен берілген күштер
мен реакция күштерінің тең әсерлі күштері және инерция күшінің
геометриялық қосындысы кез келген уақытта нөлге
тең.
нүктесіне түскен берілген күштер
мен реакция күштерінің тең әсерлі күштері және инерция күшінің
геометриялық қосындысы кез келген уақытта нөлге
тең.
Бұл қағиданы еріксіз механикалық жүйеге қатысты Герман-Эйлер-Даламбер принципі деп атаймыз.
(1)-ден белгіленген n теңдеудің екі жағын өз-өзімен қоссақ,
![]()
болады.
Мұнда ![]() - берілген күштердің
бас векторы,
- берілген күштердің
бас векторы, ![]() - реакция күштерінің
бас векторы,
- реакция күштерінің
бас векторы, ![]() - инерция күштерінің
бас векторы. Демек,
- инерция күштерінің
бас векторы. Демек,
![]()
(3)-тен: еріксіз жүйеге түскен берілген, реакция және екпін күштерінің бас векторының геометриялық қосындысы кез келген уақытта нөлге тең.
Декарт тік бұрышты
санақ жүйесінің О бас нүктесінен ![]() нүктеге
нүктеге ![]() -радиус – вектор
жүргізейік.
-радиус – вектор
жүргізейік.
(1)-теңдеудің екі
жағын ![]() векторға
вектолық түрде көбейтсек,
векторға
вектолық түрде көбейтсек,
![]()
Теңдеулерді өз өзімен қосайық:
![]()
Мұнда ![]() - О центрге қатысты
берілген күштердің бас моменті,
- О центрге қатысты
берілген күштердің бас моменті, ![]() - О центрге қатысты
реакция күштерінің бас моменті,
- О центрге қатысты
реакция күштерінің бас моменті, ![]() - О центрге қатысты
екпін күштердің бас моменті.
- О центрге қатысты
екпін күштердің бас моменті.
Яғни
![]()
(5)-тен кез келген еріксіз жүйеге түскен берілген күштердің реакция және екпін күштерінің бас моменттерінің геометриялық қосындысы кез келген уақытта нөлге тең.
(3), (5) деп белгіленген теңдеулер механикалық жүйелердің динамикалық есептерін статикалық есептерге әкеледі.
Екпін күштер жүйесін
бір центрге көшіру үшін статикадағы Пуансо теоремасын пайдалануға
болады. Динамикада күштер көшіру центрі ретінде С массалар центрі
алынады. Қорытындыда екпін күштер жүйесі екпін күштер
бас ![]() векторымен бас
вектордың массалар центріне қатысты
векторымен бас
вектордың массалар центріне қатысты
![]() бас моментіне
келеді:
бас моментіне
келеді:
![]()
![]()
![]() - барлық нүктелерге
массалар центрінен
жүргізіледі.
- барлық нүктелерге
массалар центрінен
жүргізіледі.
Екпін бас векторын
анықтау үшін ![]() екенін еске
алайық. Бұл теңдікті екі жағынан уақыт бойынша бірінші туынды
алсақ,
екенін еске
алайық. Бұл теңдікті екі жағынан уақыт бойынша бірінші туынды
алсақ,
![]()
яғни ![]()
Екпін күштерінің бас векторы дененің қозғалысының түріне байланысты емес. Енді екпін күштердің бас моментін табайық. Бас моменттің өрнегі дененің қозғалысының түріне байланысты.
Екпін күштерінің бас векторы бас моменті.
Ілгерілемелі қозғалыс
Ілгерілемелі қозғалыста дененің барлық нүктелерінің үдеуі массалар центрінің үдеуіне тең.
Онда
![]()
![]() . Сол себептен
ілгерілемелі қозғалыста
. Сол себептен
ілгерілемелі қозғалыста
![]()
Демек, ілгерілемелі қозғалыста екпін күштері дененің массасы мен массалар центрінің үдеуінің көбейтіндісіне тең және массалар центріне түскен тең әсерлі күшке ғана келеді.
Дененің өзінің симметриялық жазықтығына перпендикуляр өсті айналуы
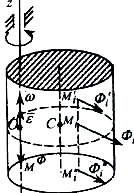 (S)
– дененің симметрия жазықтығы болсын. z
(S)
– дененің симметрия жазықтығы болсын. z
өсі (S) жазықтығына перпендикуляр. Мұндай
жағдайда z өсі - бас инерция өсі. Кез келген
![]() нүктеге (S)
жазықтыққа симметриялы
нүктеге (S)
жазықтыққа симметриялы
массасы ![]() нүктенің массасына тең
нүктенің массасына тең ![]()
нүкте табылады. Онда олардың инерция
күштері
![]()
өзара тең болады,
олардың тең әсерлі ![]() күші (S) жазықтықта
күші (S) жазықтықта ![]() нүктеде
жатады.
нүктеде
жатады.
Демек, ![]() ,
,![]() перпендикулярда жатқан барлық
нүктелердің екпін күштерінің тең әсерлі күші де
перпендикулярда жатқан барлық
нүктелердің екпін күштерінің тең әсерлі күші де ![]() нүктеге түседі. Онда дененің бас
екпін күші (S) жазықтықта жатқан барлық екпін күштердің
геометриялық қосындысына
тең.
нүктеге түседі. Онда дененің бас
екпін күші (S) жазықтықта жатқан барлық екпін күштердің
геометриялық қосындысына
тең.
Күштерді О бір нүктеге келтірсек, күштер жүйесі айналу О центріне түскен бір күшке және (S) жазықтықта жатқан бір қос күшке келеді.
Бас векторға тең күш
![]()
Оның модулі
![]()
Қос күш моментін
табу үшін әр нүктеге түскен екпін ![]() күшті жанама және нормаль
құраушыларына жіктейік
күшті жанама және нормаль
құраушыларына жіктейік
![]()
![]()
күштердің
бағыттары ![]() ,
, ![]() үдеулердің
бағыттарына қарама-қарсы.
үдеулердің
бағыттарына қарама-қарсы.
Нормаль құраушы күштер О айналу центрінен өтетін болғандықтан, ол күштердің моменттері нөлге тең.
Онда ![]()
![]() өсіне қатысты
дененің екпін моменті. Олай
болса
өсіне қатысты
дененің екпін моменті. Олай
болса
![]()
Вектор ![]() z өсінің бойымен
үдеу
z өсінің бойымен
үдеу ![]() векторына қарсы
бағытта жатады.
векторына қарсы
бағытта жатады.
![]() бас вектор мен
бас вектор мен
![]() бас моментін,
статикадағыдай, бір тең әсерлі
бас моментін,
статикадағыдай, бір тең әсерлі ![]() күшке келтіруге болады. Оның әсер
ету сызығы О келтіру нүктеден
күшке келтіруге болады. Оның әсер
ету сызығы О келтіру нүктеден ![]()
қашықтықта жатады.
Сонымен симметрия (S) жазықтығы бар дене сол жазықтыққа перпендикуляр өсті айнала қозғалса, дене нүктелерінің екпін бас моменті және бас екпін күші (S) жазықтықта жатқан Ф тең әсерлі күшке келеді. Оның модулі және бағыты (8)-ші өрнекпен анықталады. Өспен жазықтық қиылысу О нүктесінен h қашықтығы (10)–шы өрнекпен табылады.
Дененің симметриялық (S) қимасына перпендикуляр және оның массалар центрінен өтетін өсті айналуы.
Мұндай жағдайда айналма z өсі бас центрлік өсі болады. Массалар центрі айналма өсте жатқандықтан
![]()
Демек, екпін күштерінің бас векторы нөлге тең. Екпін күштердің бас моменті
![]()
Сонымен, егер қатты дене симметриялық (S) қимасына перпендикуляр және оның массалар центрінен өтетін өсті айналса, дене нүктелерінің екпін күштері симметриялық жазықтықта жататын бір қос күш келеді. Қос күш моменті (12)-ші өренктен
Симметрия жазықтығы дененің жазық қозғалысы
Мұндай қозғалыста дененің барлық нүктелерінің қозғалысы симметрия жазықтығына параллель болып қозғалады және екі қозғалыстан құралады. Ілгерілемелі қозғалыс – массалар центрінің қозғалысындай және сол центрден өтетін симметрия жазықтығына перпендикуляр өсті айналу қозғалысы.
Ілгерілемелі қозғалыста екпін күштері массалар центрінен өтетін бір
![]()
күшке, айналма қозғалыста симметрия жазықтығында жатқан, моменті
![]()
бір қос күшке келеді.
![]()
![]()
ІІ. АНАЛИТИКАЛЫҚ МЕХАНИКА
2.1. Динамикалық байланыстар
Механикалық жүйені еркін жүйе дейміз, егерде оның нүктелерінің қозғалуларына шектеулер қойылмаса. Қозғалысты шектейтін денелерді байланыстар деп атаймыз. Жүйенің қозғалысына шектеулер қойылса, жүйе еріксіз немесе ерікті емес жүйе деп аталады.
Егер дене кез келген
![]()
бетпенен қозғалса, бетті байланыс деп, беттің (1)–теңдеуін байланыс теңдеуі деп атаймыз.
Егер нүкте қисық сызықпен қозғалса, оны екі беттің қиылысы деп қарастыруға болады, қиылысу сызықтың
![]()
теңдеулерін
байланыстар теңдеулері деп, атаймыз.
Координаталары ![]() екі нүкте созылмайтын,
салмақсыз, ұзындығы
екі нүкте созылмайтын,
салмақсыз, ұзындығы ![]() сырықтың ұштарында бекітілсін. Онда
олардың байланысының теңдеуі былай
жазылады
сырықтың ұштарында бекітілсін. Онда
олардың байланысының теңдеуі былай
жазылады
![]()
Егер 2 нүкте
созылмайтын, ұзындығы ![]() жіптің екі ұшында бекітілсе,
байланыс
жіптің екі ұшында бекітілсе,
байланыс
![]()
теңсіздікпен беріледі.
Бір ұшы сфералық топсамен бекітілген сырықтың екінші ұшындағы материялық нүкте
![]()
теңдеуге сәйкес қозғалыста болады. (3) – байланыс теңдеуі
![]()
Егер байланыс теңдеуіне t уақыт енсе, мысалы,
![]()
ондай байланыстар стационарлы емес байланыстар деп аталады.
Теңдеулеріне t уақыт ашық кірмейтін байланыстарды стационарлы байланыстар деп атаймыз.
Теңдеулермен берілетін байланыстарды ұстай алатын байланыстар деп атаймыз. Байланыстар теңдеулері теңсіздікпен берілсе, ондай байланыстарды ұстай алмайтын байланыстар деп атаймыз.
Байланыс тек қана жүйе нүктелерінің координаталарын ғана шектесе, демек байланыс теңдеуі
![]()
түрде берілсе, ондай байланыстарды геометриялық немесе голономдық байланыстар деп атаймыз.
![]()
байланыстарды голономды байланыстар дейміз.
2.2. Жүйенің ықтимал орын ауыстыруы. Жүйенің еркіндік дәреже саны
Аналитикалық механикада дененің қозғалыс және тепе-теңдік шарттары қарастырылады. Алдымен дененің тыныштық күйіне тоқталайық. Бұрын статикада есеп шешуде денелердің тепе-теңдігін қарастырып, олардың байланыстар реакцияларын анықтаушы едік. Құрылма (конструкция) құрама болса, реакциялардың саны көбейіп, есептің шешілуі ұзаққа созылушы еді.
Аналитикалық механикада ықтимал орын ауыстыру принципін қолданып, кез келген механикалық жүйенің тепе-теңдік шарттарын жалпы түрде жазамыз.
Бұл принциптің
ерекшелігі байланыстар әсерлерін реакциялармен анықтамай, жүйені
ойша қозғалтып (жылжытып), байланыс әсерін орын алмастыруымен
анықтаймыз. Ондай орын ауыстыруды ықтимал орын ауыстрыруы деп
атаймыз. ![]() деп
белгілейміз.
деп
белгілейміз.
Ықтимал орын ауыстырулар біріншіден, шексіз аз болуы қажет, өйткені шекті орын алмастыруда жүйе басқа орынға көшіп, оның тепе–теңдік шарттары бұзылуы мүмкін.
Екіншіден, ![]() орын ауыстырулар жүйесінің
байланыстарын бұзбайлары, қиратпауы қажет, өйткені жүйенің түрі
өзгереді.
орын ауыстырулар жүйесінің
байланыстарын бұзбайлары, қиратпауы қажет, өйткені жүйенің түрі
өзгереді.
Сонымен ![]() ықтимал орын ауыстыру деп жүйенің
байланыстарын бұзбайтын, аз орын ауыстыруларды
атаймыз.
ықтимал орын ауыстыру деп жүйенің
байланыстарын бұзбайтын, аз орын ауыстыруларды
атаймыз.
Жалпы жағдайда
жүйенің ![]() орын алмастыруы
кез келген жиын болуы мүмкін. Бірақ, әр жүйе үшін байланыстардың
түріне тиісті, өзара тәуелсіз, анық санды
орын алмастыруы
кез келген жиын болуы мүмкін. Бірақ, әр жүйе үшін байланыстардың
түріне тиісті, өзара тәуелсіз, анық санды![]() орын алмастырулар
болады.
орын алмастырулар
болады.
Жүйенің өзара
тәуелсіз және бір мәнді анықталатын ![]() ықтимал орын алмастыру санын
жүйенің еркіндік дәреже саны деп
атаймыз.
ықтимал орын алмастыру санын
жүйенің еркіндік дәреже саны деп
атаймыз.
Мысалы, жазықтақтағы
нүктенің кез келген ![]() орын ауыстыруларын
орын ауыстыруларын ![]() екі орын алмастыру ретінде
қарастыруға болады. Демек, жазықтықта қозғалыстағы нүктенің
еркіндік дәреже саны 2
болады.
екі орын алмастыру ретінде
қарастыруға болады. Демек, жазықтықта қозғалыстағы нүктенің
еркіндік дәреже саны 2
болады.
Кеңістіктегі еркін нүктенің еркіндік дәреже саны 3.
Бір нүктесі бекітілген сфералық қозғалыстағы дененің еркіндік дәреже саны 3.
Жазық параллель қозғалытағы дененің еркіндік дәреже саны 3.
Кеңістіктегі еркін дене қозғалысының еркіндік дәреже саны 6.
Ықтимал орын алмастыру принципі
Ықтимал жұмысы деп
![]() орын алмастыруда
орындалатын
орын алмастыруда
орындалатын
![]()
жұмысты атаймыз
![]() актив және реакция күштері
үшін
актив және реакция күштері
үшін
![]()
Жүенің байланыстарын идеалдық байланыстар деп атаймыз, егер де
![]()
болса.
Жүенің
Мк
нүктесіне түскен, берілген
күштермен реакция күштірінің тең әсерлі күштерін ![]() деп белгілесек, нүкте тыныштықта
болса
деп белгілесек, нүкте тыныштықта
болса
![]()
Онда ол күштер үшін ықтимал күштер жұмыстарының қосындысы нөлге тең:
![]()
Жүйеге қатысты (6) былай жазылдады.
![]()
Егер жүйенің байланыстары идеалдық байланыстар болса,
![]() немесе
немесе ![]()
(8)- математикалық түрде ықтимал орын алмастыру принципін береді.
Егер жүенің байланыстары идеалдық байланыстар болса жүйе тыныштықта болу үшін барлық актив күштердің ықтимал жұмыстарының қосындысы нөлге тең болуы қажет.
Аналитикалық түрде принцип былай жазылады
![]()
Мұнда ![]() -тың
x,y,z
- өстеріне
проекциялары.
-тың
x,y,z
- өстеріне
проекциялары.
Даламбер – Лагранж принципі – динамиканың жалпы теңдеуі
Даламабер принципі динамиканың есептерін статиканың әдістеріне әкеледі. Жүйенің ықтимал орын ауыстыру принципі статиканың есептерінің шешуінің жалпы тәсілін береді. Сол себептен, осы екі принципті қатар пайдаланып, динамика есептері шешуінің жалпы тәсілін алуға болады.
Шынында да, егер
нүктеге әсер ететін ![]() күштерге
күштерге ![]() инерция күштерін қоссақ,
Даламбер принципі
инерция күштерін қоссақ,
Даламбер принципі ![]() бойынша
жүйе тыныштықта болады.
бойынша
жүйе тыныштықта болады.
Енді жүйенің байланыстарын идеалды деп аталған күштерге ықтимал орын ауыстыру принципін пайдалансақ,
![]()
яғни
![]()
Немесе
![]()
Даламбер–Лагранж принципі: идеалды байланысты жүйе қозғалысында барлық берілген және екпін күштерінің ықтимал жұмыстарының қосындысы кез келген уақытта нөлге тең.
Принциптің аналитикалық түрі
![]()
Жалпыланған координаталар, жалпыланған жылдамдықтар
Жүйенің еркіндік
дәреже саны өзара тәуелсіз ![]() ықтимал орын
ауыстырулардың санын атадық.
ықтимал орын
ауыстырулардың санын атадық.
Екінші жағынан жүйенің еркіндік дәреже саны әр уақытта жүйенің нүктелер саны, олардың байланыстарының саны және түрімен анықталады.
Төменде жүйенің геометриялық байланыстарын қарастырамыз. Геометриялық байланыстар деп жүйенің тек орнын шектейтін байланыстарды атаймыз.
Жүйенің еркіндік дәреже саны жүйенің геометриялық байланыстар теңдеулерінің санына кемиді.
Геометриялық байланысты жүйенің еркіндік дәреже саны өзара тәуелсіз кез келген координаталармен анықталады.
Ондай координаталар ретінде кез келген механикалык, физикалық, геометриялық параметрлерді алуға болады, мысалы: бұрышты, доғаны, ауданды, түзу сызықтың кесіндісін және т.б..
Кез келген өлшемді, өзара тәуелсіз, саны жүйенің еркіндік дәреже санына тең, әр уақытта жүйенің орнын бір мәнді анықтайтын параметрлерді жалпыланған координаталар деп атаймыз.
Оларды q әрпімен белгілейміз.
Еркін нүктенің еркіндік дәреже саны 3 болғандықтан, геометриялық байланыс теңдеулерінің саны к жүйенің еркіндік дәреже саны 8 былай аныкталады:
S = 3п-к (1)
Жүйенің кез келген уакыттағы орны
![]()
S жалпыланған координаталар санымен анықталады.
S
жалпыланған координаталар
өзара тәуелсіз болғандықтан,
олардың ![]()
өсімшелерінде тәуелсіз болады.
Тік бұрышты декарт санақ
жүйесінде нүктелердің X![]() ,Y
,Y![]() ,Z
,Z![]() координаталарын
q
координаталарын
q![]() жалпыланған кординаталары
арқылы анықтауға
болады:
жалпыланған кординаталары
арқылы анықтауға
болады:
![]()
![]() немесе
немесе ![]()
![]()
М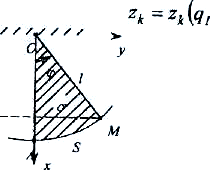 ысал: Жазық
математикалық маятниктің еркіндік дәреже саны
ысал: Жазық
математикалық маятниктің еркіндік дәреже саны ![]() .
Олай болса оның
орны
.
Олай болса оның
орны ![]() жалпыланған координатасымен
анықталады. Онда
жалпыланған координатасымен
анықталады. Онда ![]() ретінде 4 бұрышты, S доғаның
ұзындығын, ОАМ сектордың
ретінде 4 бұрышты, S доғаның
ұзындығын, ОАМ сектордың ![]() ауданын алуға болады. Бірақ
х координатасын алуға болмайды,
өйткені ол жүйенің орнын бір мәнді анықтамайды.
Егер
ауданын алуға болады. Бірақ
х координатасын алуға болмайды,
өйткені ол жүйенің орнын бір мәнді анықтамайды.
Егер ![]() ретінде
ретінде ![]() бүрышын алсақ,
онда
бүрышын алсақ,
онда
![]()
Жүйе қозғалысында
оның ![]() координаталары
уақытқа байланысты өзгеріп
отырады:
координаталары
уақытқа байланысты өзгеріп
отырады:
![]()
Бұлар жүйе қозғалысының жалпыланған координаталардағы кинематикалық теңдеулері деп аталады.
Уақыт бойынша жалпыланған координаталар туындылары.
![]() немесе
немесе ![]()
Шамаларды жалпыланған жылдамдықтар дейміз.
Олардың өлшемдері
![]() жалпыланған координаталардың
өлшемдерімен байланысты.
жалпыланған координаталардың
өлшемдерімен байланысты.
Мысалы q-бұрыш
болса, ![]() -бұрыштық
жылдамдық, егер q-аудан болса,
-бұрыштық
жылдамдық, егер q-аудан болса, ![]() -секторлық жылдамдық. Лагранж
теңдеулері жалпыланған
күштер
-секторлық жылдамдық. Лагранж
теңдеулері жалпыланған
күштер
n материалдық
нүктелерден тұратын механикалық жүйеге ![]() күштер түссін.
күштер түссін. ![]() номерлі нүктеге түскен күштердің
тең әсерлі күші.
номерлі нүктеге түскен күштердің
тең әсерлі күші.
Кез келген уақытта
кеңістіктегі жүйенің орны ![]() жалпыланған координаталармен
анықталсын. Жүйенің басқа координаталарына тәуелсіз
жалпыланған координаталармен
анықталсын. Жүйенің басқа координаталарына тәуелсіз ![]() координатасының
координатасының ![]() өсімше
алсын.
өсімше
алсын.
Басқа ![]() координаталар
өзгермесін.
координаталар
өзгермесін.
Онда ![]() алатын ықтимал орын
алмастыруы
алатын ықтимал орын
алмастыруы
![]()
Яғни ![]()
Күштердің ықтимал
жұмысы ![]() Демек,
Демек,

Содан кейін
![]() деп
белгілесек,
деп
белгілесек,

![]() жалпыланған
координатаға қатысты жалпыланған
күш,
жалпыланған
координатаға қатысты жалпыланған
күш,
![]() жалпыланған
координатаға қатысты жалпыланған
күш,
жалпыланған
координатаға қатысты жалпыланған
күш,
![]() жалпыланған
координатаға қатысты жалпыланған күш деп
атаймыз.
жалпыланған
координатаға қатысты жалпыланған күш деп
атаймыз.
Егер жүйе қозғалғанда барлық жалпыланған координаталар ықтимал орын алмастыру алса,
![]()
(6)-формуладан байқайтынымыз, жалпыланған күш ықтимал жұмыста ықтимал орын алмастырудың еселігі болады.
1) Есеп шығару үшін алдымен жүйенің еркіндік дәрежесін анықтау қажет.
2) Жалпыланған координаталарды таңдап алып, күштерді көрсету керек.
3) ![]() -ді табу үшін тек қана
-ді табу үшін тек қана ![]() -ді өзгерту
қажет.
-ді өзгерту
қажет.
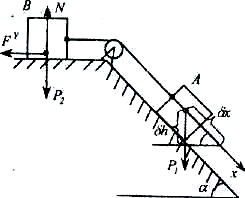 Есеп. Салмағы
Есеп. Салмағы
![]() дене А жылтыр көлбеу
жазықтықпен қозғалғанда, салмағы
дене А жылтыр көлбеу
жазықтықпен қозғалғанда, салмағы ![]() дене В кедір – бұдырлы, үйкеліс
коэффициенті
дене В кедір – бұдырлы, үйкеліс
коэффициенті ![]() , көлденең
жазықтықпен қозғалсын. Бұл жүйенің еркіндік дәреже саны - бір. Оның
орны
, көлденең
жазықтықпен қозғалсын. Бұл жүйенің еркіндік дәреже саны - бір. Оның
орны ![]() координатамен
беріледі.
координатамен
беріледі. ![]() -жалпыланған
күшті табу үшін жүйеге түскен күштердің ықтимал жұмысын
-жалпыланған
күшті табу үшін жүйеге түскен күштердің ықтимал жұмысын ![]() табуымыз керек. Жүйенің
табуымыз керек. Жүйенің ![]() орын алмастырудағы
орын алмастырудағы ![]() күштердің
жұмысы
күштердің
жұмысы

Жалпыланған координаталардағы механикалық жүйенің тепе–теңдік шарттары
Ықтимал орын ауыстыру принципіне байланысты механикалық жүйе тыныштық күйде болу үшін күштердің ықтимал жұмыстарының қосындысы нөлге тең болуы қажет, яғни
![]()
Жалпланған күштер үшін
![]()
немесе
![]()
Жалпыланған
![]() координаталардың өсімшелері.
Ықтимал орын ауыстырулар
координаталардың өсімшелері.
Ықтимал орын ауыстырулар ![]() өзара тәуелсіз болғандықтан,
олардың (7)-теңдеудегі еселіктері
өзара тәуелсіз болғандықтан,
олардың (7)-теңдеудегі еселіктері ![]() ,
, ![]() жеке-жеке нөлге тең болуы
қажет:
жеке-жеке нөлге тең болуы
қажет:
![]()
Шынында да, айталық,
![]() болсын. Ондай жүйе тыныштық
күйде болмайды. Денеге
болсын. Ондай жүйе тыныштық
күйде болмайды. Денеге ![]() ықтимал орын ауыстыру берсек (7)
орындалмайды.
ықтимал орын ауыстыру берсек (7)
орындалмайды.
Сонымен, механикалық
жүйе тепе-теңдік күйде болуы үшін, барлық ![]() жалпыланған координаталарға
қатысты жалпыланған
жалпыланған координаталарға
қатысты жалпыланған ![]() күштердің жеке-жеке нөлге тең
болуы қажетті және жеткілікті. Сол үшін статиканың есебін
шығарғанда ықтимал орын ауыстыру принципіне байланысты жалпыланған
күштерді тауып, нөлге теңестіру
қажет.
күштердің жеке-жеке нөлге тең
болуы қажетті және жеткілікті. Сол үшін статиканың есебін
шығарғанда ықтимал орын ауыстыру принципіне байланысты жалпыланған
күштерді тауып, нөлге теңестіру
қажет.
Егер жүйеге әсер
ететін күштер потенциалды күштер болса, ![]() онда
онда
![]()
яғни ![]()
Демек, күштер потенциалды күштер болса, механикалық жүйе тепе-теңдікте болуы үшін
![]()
болуы қажет.
Лагранж теңдеулері
Байланыстары геометриялық байланыстар механикалық жалпыланған координаталардағы қозғалысының теңдеулерін табу үшін динамиканың жалпы теңдеулерін қарастырамыз:

Төменде геометриялық
байланыстарды жалпы жағдайда идеалды байланыстар деп есептейміз.
Сол үшін бірінші суммаға берілген ![]() күштермен қатар
күштермен қатар ![]() кедергі күштер де
енеді.
кедергі күштер де
енеді.
Механикалық жүйенің еркіндік дәреже саны S болса, онда берілген күштердің ықтимал жұмысы.
![]()
Сол сияқты ![]() инерция күштердің ықтимал
жұмыстары
инерция күштердің ықтимал
жұмыстары
![]()
Мұнда ![]() -жалпыланған инерция күштері.
Яғни
-жалпыланған инерция күштері.
Яғни

(2) мен (3) еске алсақ, (1) былай жазылады.
![]()
![]() өзара тәуелсіз
болғандықтан
өзара тәуелсіз
болғандықтан ![]() шамалардың
еселіктері нөлге тең болуы
қажет:
шамалардың
еселіктері нөлге тең болуы
қажет:

Бұл теңдеулер көп жеңілдейді, егер жалпыланған инерция күштерін кинетикалық энергия арқылы анықтасақ
![]()
екені белгілі. Сонымен қатар
![]()
ал


![]()
(с) мен (d)-ны (b)-ға қойсақ.

Олай болса

Бұл теңдеулерді механикалық жүйенің қозғалысының жалпыланған координаталардағы қозғалыс теңдеулері немесе екінші текті Лагранж теңдеулері деп атаймыз.
Бұл теңдеулердің құндылы теңдеулер санына жүйе нүктелерінің саны немесе қозғалыстарының түрі әсер етпейді. Теңдеулер саны тек еркіндік дәреже санына байланысты.
Лагранж
теңдеулерінде ![]() жалпыланған
күштерді және есептің бастапқы шарттары белгілі болса, жүйенің
жалпыланған координаталардағы қозғалыс
заңын
жалпыланған
күштерді және есептің бастапқы шарттары белгілі болса, жүйенің
жалпыланған координаталардағы қозғалыс
заңын
![]()
табу оңай.
Лагранж теңдеулері
жалпыланған ![]() координаталардан екінші ретті
жай дифференциалдық теңдеулерін
береді.
координаталардан екінші ретті
жай дифференциалдық теңдеулерін
береді.
Егер күштер потенциалды болса,
![]()
немесе
![]()
![]() функциясы
кинетикалық потенциал не Лагранж функциясы деп
атаймыз.
функциясы
кинетикалық потенциал не Лагранж функциясы деп
атаймыз.
ҚОРЫТЫНДЫ
Жүйе кинетикалық энергиясының өзгеру теоремасы арқылы есеп шығарғанда, жүйеге түскен сыртқы күштер жұмыстарын анықтау үшін қозғалыс заңын пайдаланбадық.
Төменде қандай күштерге қатысты дененің қозғалыс заңын пайдаланбай олардың жұмыстарын табуға болатынын анықтайық.
Дененің кез келген М
нүктесіне түскен ![]() күштің
күштің
![]() орын ауыстыруындағы
жұмысы.
орын ауыстыруындағы
жұмысы.
Жүйенің кинетикалық энергиясы деп, оның барлық нүктелерінің кинетикалық энергияларының арифметиаклық қосындысына тең Т-скалярлышаманы атаймыз
Бұл теңдеулерді механикалық жүйенің қозғалысының жалпыланған координаталардағы қозғалыс теңдеулері немесе екінші текті Лагранж теңдеулері деп атаймыз.
Бұл теңдеулердің құндылы теңдеулер санына жүйе нүктелерінің саны немесе қозғалыстарының түрі әсер етпейді. Теңдеулер саны тек еркіндік дәреже санына байланысты.
Лагранж
теңдеулерінде ![]() жалпыланған
күштерді және есептің бастапқы шарттары белгілі болса, жүйенің
жалпыланған координаталардағы қозғалыс
заңын
жалпыланған
күштерді және есептің бастапқы шарттары белгілі болса, жүйенің
жалпыланған координаталардағы қозғалыс
заңын
![]()
табу оңай.
Лагранж теңдеулері
жалпыланған ![]() координаталардан екінші ретті
жай дифференциалдық теңдеулерін
береді.
координаталардан екінші ретті
жай дифференциалдық теңдеулерін
береді.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР
-
Н.Қожаспаев, С.Кешуов, И.Мухитов Электротехника /оқу құралы/ - Алматы. Республикалық баспа кабинеті, 1996 ж., 300 бет
-
Электротехника /Под ред- проф. В. Г. Герасимова.— М.: Высшая школа. 1935.
-
Волынский Б. А., Зейн Е. Н..Шатерников В. Е.Электротехника.— Москва.:Эпергоатомиздат, 1987.
-
Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н., Электротехника —Москва.:Эпергоатомиздат, 1985.
-
Касаткин А. С., Немцов М. В..Электротехника.— М.: Энерогоатомиздат. 1983.
-
Иванов И. И., Равдоник С. С. Электротехника.— М.: Высшее школа, 1984.
-
Электротехника. Программированное учебное пособие /Под ред. проф. В. Г. Герасимова.— М.: Высшая школа, 1983.
-
Основы промышленной электроники. /Под ред. проф. А Г. Герасимова.— М.:Высшая школа, 1986.
23
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
АНАЛИТИКАЛЫҚ МЕХАНИКА
АНАЛИТИКАЛЫҚ МЕХАНИКА
МАЗМҰНЫ
КІРІСПЕ................................................... ...................................................................3
І. ЖҮЙЕ ДИНАМИКАСЫНЫҢ ЖАЛПЫ ТЕОРЕМАЛАРЫ................................4
-
Жүйенің кинетикалық энергиясы................................................... ................4
1.2. Потенциалдық күш өрісі және күштік функция...............................................6
ІІ. АНАЛИТИКАЛЫҚ МЕХАНИКА................................................... ..................13
2.1. Динамикалық байланыстар................................................. .............................13
2.2. Жүйенің ықтимал орын ауыстыруы. Жүйенің еркіндік дәреже саны..........14
ҚОРЫТЫНДЫ .........................................................................................................22
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР.....................................................................23
І. ЖҮЙЕ ДИНАМИКАСЫНЫҢ ЖАЛПЫ ТЕОРЕМАЛАРЫ
-
Жүйенің кинетикалық энергиясы
Жүйенің кинетикалық энергиясы деп, оның барлық нүктелерінің кинетикалық энергияларының арифметиаклық қосындысына тең Т-скалярлық шаманы атаймыз:
![]()
Кинетикалық энергия
жүйенің ілгерілемелі де, айналма да қозғалыстарын сипаттайды, демек
сүрден қозғалыстарды да сипаттайды. Жүйенің қозғалыс мөлшері
![]() -менен
-менен ![]() - ден негізгі айырмашылығы Т
скаляр және оң сан. Сондықтан ол қозғалыстың бағытына байланысты
емес, оны анықтамайды да. Егер жүйе бірнеше денеден құралса,
онда
- ден негізгі айырмашылығы Т
скаляр және оң сан. Сондықтан ол қозғалыстың бағытына байланысты
емес, оны анықтамайды да. Егер жүйе бірнеше денеден құралса,
онда
![]()
Кинетикалық энергияны анықтайтын өрнектер қозғалыстың түріне байланысты болады.
1. Ілгерілемелі қозғалыс
Бұл қозғалыста
барлық нүктелер жүйенің бір жылдамдықпен қозғалады. Сол үшін (1)-ші
өрнекте ![]() деп алу
керек:
деп алу
керек:
![]()
Демек
![]()
2. Айналма қозғалыс
Егер дене бір өсті айнала қозғалса, кез келген М нүктенің
жылдамдығы ![]() Олай
болса,
Олай
болса,

Демек, ![]()
![]() - дененің z өсіне
қатысты екпін
- дененің z өсіне
қатысты екпін
моменті
3. Жазық параллель қозғалыс
 Мұндай қозғалысты (S) қима
Мұндай қозғалысты (S) қима
жазықтығына перпендикуляр
лездік жылдамдық Р центрінен
өтетін өсті айналу қозғалысы деп
қарастыруға болады.
Онда
![]()
![]() - дененің Р лездік
өске қатысты инерция
моменті.
- дененің Р лездік
өске қатысты инерция
моменті.
Бұл өрнекті С массалар центрінен өтетін өске қатысты жазайық.
![]() -Гюйгенс-Штейнер
теоремасы.
-Гюйгенс-Штейнер
теоремасы.
Онда 
![]()
а) Дененің айнала қозғалысын тудыратын күш жұмысы.

 Кез
келген М нүктеде
Кез
келген М нүктеде
![]() күштің элементар
жұмысы
күштің элементар
жұмысы
![]()
Мұндағы ![]()
Яғни ![]()
![]() -
-![]() күштің Oz өсіне қатысты
моменті:
күштің Oz өсіне қатысты
моменті:
![]()
Демек,
![]()
Егерде ![]() шекті шама болса
шекті шама болса ![]() , онда дененің
, онда дененің ![]() күш әсерінен
шекті
күш әсерінен
шекті ![]() айналуындағы жұмысы
келесі интегралмен беріледі:
айналуындағы жұмысы
келесі интегралмен беріледі:

![]() - тұрақты
болса
- тұрақты
болса
![]()
Шекті жұмыс қуаты
![]()
б) Түзу бойымен сырғанамай домалайтын дөңгелекке түскен үйкеліс күш жұмысы.

![]()
В нүкте дөңгелек үшін – лездік жылдамдықтар центрі:
![]() , демек
, демек ![]()
Олай болса
![]()
 Егер дөңгелекпен
байланыс деформация алатын болса,
Егер дөңгелекпен
байланыс деформация алатын болса, ![]() қос күшке байланысты домалауға
кедергі қос күш пайда
болады:
қос күшке байланысты домалауға
кедергі қос күш пайда
болады:
![]()
![]()
![]()
![]()
![]() қос күш
момент
қос күш
момент
![]()
қос күштің шекті
жұмысы ![]()
 (13)
(13)
Жүйенің кинетикалық энергиясының өзгеруі туралы теорема
Жеке нүктенің
![]() кинетикалық энергиясының
өзгеруі туралы теорема жүйенің кез келген нүктесі үшін
әділ:
кинетикалық энергиясының
өзгеруі туралы теорема жүйенің кез келген нүктесі үшін
әділ:
![]()
Бұл теорема жүйе үшін оңай жазылады:

(14)-теореманың дифференциалдық түрін береді.
Жүйенің бастапқы
орнында кинетикалық энергия ![]() кез келген келесі орнындағы
кинетикалық энергиясы Т
болсын.
кез келген келесі орнындағы
кинетикалық энергиясы Т
болсын.
Соңғы теңдеудің екі жағынан интеграл алсақ,
![]()
(15)-теореманың шекті немесе интегралды түрін береді.
Теорема:
Жүйенің кез келген орын ауыстыруындағы кинетикалық энергияның өзгеруі сол орын ауыстырудағы сыртқы күштердің жұмыстарының қосындысына тең.
Жүйеге әсер ететін барлық күштерді берілген (актив) күштермен байланыс реакция күштеріне бөлуге болады.
![]()
Егер ![]() болса, жүйенің
байланыстарын идеалдық байланыстар деп
атаймыз.
болса, жүйенің
байланыстарын идеалдық байланыстар деп
атаймыз.
Байланыстар идеалдық байланыстар болса,
![]()
Механикалық жүйенің кинетикалық энергиясы мына өрнекпен берілсін:
![]()
Ілгерілемелі
қозғалыста ![]()
Айналма қозғалыста
![]()
Жазық-параллель
қозғалыста ![]()
1.2. Потенциалдық күш өрісі және күштік функция
Жүйе кинетикалық энергиясының өзгеру теоремасы арқылы есеп шығарғанда, жүйеге түскен сыртқы күштер жұмыстарын анықтау үшін қозғалыс заңын пайдаланбадық.
Төменде қандай күштерге қатысты дененің қозғалыс заңын пайдаланбай олардың жұмыстарын табуға болатынын анықтайық.
Дененің кез келген М
нүктесіне түскен ![]() күштің
күштің
![]() орын ауыстыруындағы
жұмысы .
орын ауыстыруындағы
жұмысы .

Мұндағы ![]() күштер нүктелердің
күштер нүктелердің ![]() орындары координаталарына тәуелді
болғанда ғана жоғарыдағы интегралды есептеуге болады. Мұндай
күштерді күштік өріс дейміз.
орындары координаталарына тәуелді
болғанда ғана жоғарыдағы интегралды есептеуге болады. Мұндай
күштерді күштік өріс дейміз.
Күштік өріс деп кеңістіктің кез келген бөлігінде нүктелер координаталарына тәуелді күштер жүйесін атаймыз.
Мысал ретінде планеталар мен Күннің тартылыс өрісін атауға болады. Сонымен күштік өріс
![]()
теңдеулермен
беріледі. ![]() - кез келген
функциялар.
- кез келген
функциялар.
Жалпы жағдайда (1)
интеграл астында бір айналымға көшу қажет, мысалы ![]() , демек, нүктенің траекториясы
белгілі болуы қажет.
, демек, нүктенің траекториясы
белгілі болуы қажет.
Бірақ, егер де
интегралдың астында (ішінде) тұрған элементар жұмыс ![]() айталық
айталық ![]() функциясының толық дифференциалы
болса, яғни
функциясының толық дифференциалы
болса, яғни
![]() немесе
немесе ![]()
онда ![]() жұмысты дене нүктесінің
траекториясымен білмей ақ анықтауға болады. Толық дифференциалы
элементар жұмысқа тең
жұмысты дене нүктесінің
траекториясымен білмей ақ анықтауға болады. Толық дифференциалы
элементар жұмысқа тең ![]() функцияны күштік фүнкция деп
атаймыз. Күштік функция сәйкес күштік өрісті (күштерді) потенциалды
күштік өріс, ал сол өрісте әсер ететін күшті потенциалды күштер деп
атаймыз.
функцияны күштік фүнкция деп
атаймыз. Күштік функция сәйкес күштік өрісті (күштерді) потенциалды
күштік өріс, ал сол өрісте әсер ететін күшті потенциалды күштер деп
атаймыз.
(1)-теңдікті қолданып, (2)-теңдеудің екі жағынан интеграл алайық.

![]() - күштік функцияның
- күштік функцияның
![]() нүктелердегі мәндері. Демек,
потенциалдық күштің жұмысы күштік функцияның бастапқы және соңғы
нүктелердегі мәндерінің айырымына тең, сонымен қатар нүктенің
траекториясына тәуелсіз.
нүктелердегі мәндері. Демек,
потенциалдық күштің жұмысы күштік функцияның бастапқы және соңғы
нүктелердегі мәндерінің айырымына тең, сонымен қатар нүктенің
траекториясына тәуелсіз.
Күштердің жұмысы (нүкте) траекториясының түріне немесе қозғалыс заңына тәуелді болса, ондай күштерді потенциалды емес күштер деп атаймыз. Ондай күштерге үйкеліс күші, орталардың кедергі күштері жатады.
Керісінше (2)-теңдеуден
![]()
Потенциалды күштерге ауырлық күші, серпімділік және тартылыс күштері жатады. Осы күштердің күштік функцияларын табайық.
1) ауырлық күш үшін
![]()

Демек,
![]()
2) серпімділік күш үшін
![]() . Бастапқы
шарт
. Бастапқы
шарт
![]() болсын.
Онда
болсын.
Онда
![]()
Егер де функция U белгілі болса, онда кез келген нүктеге әсер ететін күшті табуға болады. Шынында да, (3)-ші теңдеуден
![]()
Онда
![]()
(7)-мен анықталатын ![]() векорды
векорды ![]() функциясының градиенті деп
атайды.
функциясының градиенті деп
атайды.
Яғни ![]()
(7)-ден 
Демек,
![]()
Сонымен, күштер өрісінің күштік функциясы бар болса, күш (8)-ді қанағаттандыруы керек.
![]()
Потенциалдық энергия
Потенциалдық күштер үшін “потенциалды энергия” деген ұғымды ендіруге болады. Оны күштік өрістің белгілі нүктесінің “жұмыс қоры” деп қарастырамыз. “Жұмыс қорларын” өзара салыстыру үшін “жұмыс қоры” нөл болатын (нөлдік) нүкте таңдай алу қажет.
М нүктенің потенциалдық энергиясы деп күштердің М орыннан нөлдік орынға материялдық нүктенің орын ауыстыруындағы жұмысына тең П скалярлық шаманы атаймыз,
![]() .
.
![]() және
және ![]() функцияларының нөлдік нүктелері
бір деп есептейміз.
функцияларының нөлдік нүктелері
бір деп есептейміз.
Онда
![]()
![]() - күштік функцияның
М нүктедегі мәні.
- күштік функцияның
М нүктедегі мәні.
![]()
Потенциалдық энергия таңбамен алынған күштер функциясына тең. Мұнан шығатын қорытынды: потенциалдық күштер өрісінде күштер функциясының орнына потенциалды энергияны қарастыруға болады.
Мысалы: ![]() .
.
Механикалық энергияның сақталу заңы
Жүйеге әсер ететін барлық сыртқы және ішкі күштер потенциалы күштер болсын. Онда кез келген жүйе нүктесі үшін күштер жұмысы:
![]()
Онда жүйе үшін
![]()
Жүйе кинетикалық энергиясының өзгеруі туралы теорема төмендегідей жазылады.
![]()
немесе
![]() (11)
(11)
Демек, берілген потенциалдық күштер әсерінен қозғалысындағы кинетикалық және потенциалдық энергияларының қосындысы жүйенің кез келген орнында бірдей болады. Бұл заңды механикалық жүйенің сақталу заңы деп аталады.
Механикалық жүйе үшін Даламбер принципі. Дененің өзінің симметриялық жазықтығына перпендикуляр өсті айналуы
Еркін емес механикалық жүйенің қозғалысын қарастырған белгілі аксиомаға сүйеніп, жүйенің байланыстарын алып тастап, олардың әсерлерін реакцияларымен ауыстырып, еркін емес жүйені еркін деп қарастыруға болады. Демек, жүйеге реакциялар мен берілген күштерді түсіріп, еркін жүйе деп қарастырамыз.
Бір нүкте үшін
Даламбер принципі ![]() түрде
жазылады.
түрде
жазылады. ![]() -
екпін,
-
екпін, ![]() - реакция
күштері.
- реакция
күштері.
Еркін емес жүйе n материялық нүктелерден тұрады деп, оның әр нүктесіне Даламбер принципін қолдансақ,
![]()
Мұнда ![]() -
- ![]() нүктеге түскен берілген күштердің
тең әсерлі күші,
нүктеге түскен берілген күштердің
тең әсерлі күші, ![]() - сол нүктеге түскен
реакция күштерінің тең әсерлі күші,
- сол нүктеге түскен
реакция күштерінің тең әсерлі күші,
![]() нүктенің екпін
күші.
нүктенің екпін
күші.
Сонымен (1) теңдеуге
сәйкес жүйенің кез келген ![]() нүктесіне түскен берілген күштер
мен реакция күштерінің тең әсерлі күштері және инерция күшінің
геометриялық қосындысы кез келген уақытта нөлге
тең.
нүктесіне түскен берілген күштер
мен реакция күштерінің тең әсерлі күштері және инерция күшінің
геометриялық қосындысы кез келген уақытта нөлге
тең.
Бұл қағиданы еріксіз механикалық жүйеге қатысты Герман-Эйлер-Даламбер принципі деп атаймыз.
(1)-ден белгіленген n теңдеудің екі жағын өз-өзімен қоссақ,
![]()
болады.
Мұнда ![]() - берілген күштердің
бас векторы,
- берілген күштердің
бас векторы, ![]() - реакция күштерінің
бас векторы,
- реакция күштерінің
бас векторы, ![]() - инерция күштерінің
бас векторы. Демек,
- инерция күштерінің
бас векторы. Демек,
![]()
(3)-тен: еріксіз жүйеге түскен берілген, реакция және екпін күштерінің бас векторының геометриялық қосындысы кез келген уақытта нөлге тең.
Декарт тік бұрышты
санақ жүйесінің О бас нүктесінен ![]() нүктеге
нүктеге ![]() -радиус – вектор
жүргізейік.
-радиус – вектор
жүргізейік.
(1)-теңдеудің екі
жағын ![]() векторға
вектолық түрде көбейтсек,
векторға
вектолық түрде көбейтсек,
![]()
Теңдеулерді өз өзімен қосайық:
![]()
Мұнда ![]() - О центрге қатысты
берілген күштердің бас моменті,
- О центрге қатысты
берілген күштердің бас моменті, ![]() - О центрге қатысты
реакция күштерінің бас моменті,
- О центрге қатысты
реакция күштерінің бас моменті, ![]() - О центрге қатысты
екпін күштердің бас моменті.
- О центрге қатысты
екпін күштердің бас моменті.
Яғни
![]()
(5)-тен кез келген еріксіз жүйеге түскен берілген күштердің реакция және екпін күштерінің бас моменттерінің геометриялық қосындысы кез келген уақытта нөлге тең.
(3), (5) деп белгіленген теңдеулер механикалық жүйелердің динамикалық есептерін статикалық есептерге әкеледі.
Екпін күштер жүйесін
бір центрге көшіру үшін статикадағы Пуансо теоремасын пайдалануға
болады. Динамикада күштер көшіру центрі ретінде С массалар центрі
алынады. Қорытындыда екпін күштер жүйесі екпін күштер
бас ![]() векторымен бас
вектордың массалар центріне қатысты
векторымен бас
вектордың массалар центріне қатысты
![]() бас моментіне
келеді:
бас моментіне
келеді:
![]()
![]()
![]() - барлық нүктелерге
массалар центрінен
жүргізіледі.
- барлық нүктелерге
массалар центрінен
жүргізіледі.
Екпін бас векторын
анықтау үшін ![]() екенін еске
алайық. Бұл теңдікті екі жағынан уақыт бойынша бірінші туынды
алсақ,
екенін еске
алайық. Бұл теңдікті екі жағынан уақыт бойынша бірінші туынды
алсақ,
![]()
яғни ![]()
Екпін күштерінің бас векторы дененің қозғалысының түріне байланысты емес. Енді екпін күштердің бас моментін табайық. Бас моменттің өрнегі дененің қозғалысының түріне байланысты.
Екпін күштерінің бас векторы бас моменті.
Ілгерілемелі қозғалыс
Ілгерілемелі қозғалыста дененің барлық нүктелерінің үдеуі массалар центрінің үдеуіне тең.
Онда
![]()
![]() . Сол себептен
ілгерілемелі қозғалыста
. Сол себептен
ілгерілемелі қозғалыста
![]()
Демек, ілгерілемелі қозғалыста екпін күштері дененің массасы мен массалар центрінің үдеуінің көбейтіндісіне тең және массалар центріне түскен тең әсерлі күшке ғана келеді.
Дененің өзінің симметриялық жазықтығына перпендикуляр өсті айналуы
 (S)
– дененің симметрия жазықтығы болсын. z
(S)
– дененің симметрия жазықтығы болсын. z
өсі (S) жазықтығына перпендикуляр. Мұндай
жағдайда z өсі - бас инерция өсі. Кез келген
![]() нүктеге (S)
жазықтыққа симметриялы
нүктеге (S)
жазықтыққа симметриялы
массасы ![]() нүктенің массасына тең
нүктенің массасына тең ![]()
нүкте табылады. Онда олардың инерция
күштері
![]()
өзара тең болады,
олардың тең әсерлі ![]() күші (S) жазықтықта
күші (S) жазықтықта ![]() нүктеде
жатады.
нүктеде
жатады.
Демек, ![]() ,
,![]() перпендикулярда жатқан барлық
нүктелердің екпін күштерінің тең әсерлі күші де
перпендикулярда жатқан барлық
нүктелердің екпін күштерінің тең әсерлі күші де ![]() нүктеге түседі. Онда дененің бас
екпін күші (S) жазықтықта жатқан барлық екпін күштердің
геометриялық қосындысына
тең.
нүктеге түседі. Онда дененің бас
екпін күші (S) жазықтықта жатқан барлық екпін күштердің
геометриялық қосындысына
тең.
Күштерді О бір нүктеге келтірсек, күштер жүйесі айналу О центріне түскен бір күшке және (S) жазықтықта жатқан бір қос күшке келеді.
Бас векторға тең күш
![]()
Оның модулі
![]()
Қос күш моментін
табу үшін әр нүктеге түскен екпін ![]() күшті жанама және нормаль
құраушыларына жіктейік
күшті жанама және нормаль
құраушыларына жіктейік
![]()
![]()
күштердің
бағыттары ![]() ,
, ![]() үдеулердің
бағыттарына қарама-қарсы.
үдеулердің
бағыттарына қарама-қарсы.
Нормаль құраушы күштер О айналу центрінен өтетін болғандықтан, ол күштердің моменттері нөлге тең.
Онда ![]()
![]() өсіне қатысты
дененің екпін моменті. Олай
болса
өсіне қатысты
дененің екпін моменті. Олай
болса
![]()
Вектор ![]() z өсінің бойымен
үдеу
z өсінің бойымен
үдеу ![]() векторына қарсы
бағытта жатады.
векторына қарсы
бағытта жатады.
![]() бас вектор мен
бас вектор мен
![]() бас моментін,
статикадағыдай, бір тең әсерлі
бас моментін,
статикадағыдай, бір тең әсерлі ![]() күшке келтіруге болады. Оның әсер
ету сызығы О келтіру нүктеден
күшке келтіруге болады. Оның әсер
ету сызығы О келтіру нүктеден ![]()
қашықтықта жатады.
Сонымен симметрия (S) жазықтығы бар дене сол жазықтыққа перпендикуляр өсті айнала қозғалса, дене нүктелерінің екпін бас моменті және бас екпін күші (S) жазықтықта жатқан Ф тең әсерлі күшке келеді. Оның модулі және бағыты (8)-ші өрнекпен анықталады. Өспен жазықтық қиылысу О нүктесінен h қашықтығы (10)–шы өрнекпен табылады.
Дененің симметриялық (S) қимасына перпендикуляр және оның массалар центрінен өтетін өсті айналуы.
Мұндай жағдайда айналма z өсі бас центрлік өсі болады. Массалар центрі айналма өсте жатқандықтан
![]()
Демек, екпін күштерінің бас векторы нөлге тең. Екпін күштердің бас моменті
![]()
Сонымен, егер қатты дене симметриялық (S) қимасына перпендикуляр және оның массалар центрінен өтетін өсті айналса, дене нүктелерінің екпін күштері симметриялық жазықтықта жататын бір қос күш келеді. Қос күш моменті (12)-ші өренктен
Симметрия жазықтығы дененің жазық қозғалысы
Мұндай қозғалыста дененің барлық нүктелерінің қозғалысы симметрия жазықтығына параллель болып қозғалады және екі қозғалыстан құралады. Ілгерілемелі қозғалыс – массалар центрінің қозғалысындай және сол центрден өтетін симметрия жазықтығына перпендикуляр өсті айналу қозғалысы.
Ілгерілемелі қозғалыста екпін күштері массалар центрінен өтетін бір
![]()
күшке, айналма қозғалыста симметрия жазықтығында жатқан, моменті
![]()
бір қос күшке келеді.
![]()
![]()
ІІ. АНАЛИТИКАЛЫҚ МЕХАНИКА
2.1. Динамикалық байланыстар
Механикалық жүйені еркін жүйе дейміз, егерде оның нүктелерінің қозғалуларына шектеулер қойылмаса. Қозғалысты шектейтін денелерді байланыстар деп атаймыз. Жүйенің қозғалысына шектеулер қойылса, жүйе еріксіз немесе ерікті емес жүйе деп аталады.
Егер дене кез келген
![]()
бетпенен қозғалса, бетті байланыс деп, беттің (1)–теңдеуін байланыс теңдеуі деп атаймыз.
Егер нүкте қисық сызықпен қозғалса, оны екі беттің қиылысы деп қарастыруға болады, қиылысу сызықтың
![]()
теңдеулерін
байланыстар теңдеулері деп, атаймыз.
Координаталары ![]() екі нүкте созылмайтын,
салмақсыз, ұзындығы
екі нүкте созылмайтын,
салмақсыз, ұзындығы ![]() сырықтың ұштарында бекітілсін. Онда
олардың байланысының теңдеуі былай
жазылады
сырықтың ұштарында бекітілсін. Онда
олардың байланысының теңдеуі былай
жазылады
![]()
Егер 2 нүкте
созылмайтын, ұзындығы ![]() жіптің екі ұшында бекітілсе,
байланыс
жіптің екі ұшында бекітілсе,
байланыс
![]()
теңсіздікпен беріледі.
Бір ұшы сфералық топсамен бекітілген сырықтың екінші ұшындағы материялық нүкте
![]()
теңдеуге сәйкес қозғалыста болады. (3) – байланыс теңдеуі
![]()
Егер байланыс теңдеуіне t уақыт енсе, мысалы,
![]()
ондай байланыстар стационарлы емес байланыстар деп аталады.
Теңдеулеріне t уақыт ашық кірмейтін байланыстарды стационарлы байланыстар деп атаймыз.
Теңдеулермен берілетін байланыстарды ұстай алатын байланыстар деп атаймыз. Байланыстар теңдеулері теңсіздікпен берілсе, ондай байланыстарды ұстай алмайтын байланыстар деп атаймыз.
Байланыс тек қана жүйе нүктелерінің координаталарын ғана шектесе, демек байланыс теңдеуі
![]()
түрде берілсе, ондай байланыстарды геометриялық немесе голономдық байланыстар деп атаймыз.
![]()
байланыстарды голономды байланыстар дейміз.
2.2. Жүйенің ықтимал орын ауыстыруы. Жүйенің еркіндік дәреже саны
Аналитикалық механикада дененің қозғалыс және тепе-теңдік шарттары қарастырылады. Алдымен дененің тыныштық күйіне тоқталайық. Бұрын статикада есеп шешуде денелердің тепе-теңдігін қарастырып, олардың байланыстар реакцияларын анықтаушы едік. Құрылма (конструкция) құрама болса, реакциялардың саны көбейіп, есептің шешілуі ұзаққа созылушы еді.
Аналитикалық механикада ықтимал орын ауыстыру принципін қолданып, кез келген механикалық жүйенің тепе-теңдік шарттарын жалпы түрде жазамыз.
Бұл принциптің
ерекшелігі байланыстар әсерлерін реакциялармен анықтамай, жүйені
ойша қозғалтып (жылжытып), байланыс әсерін орын алмастыруымен
анықтаймыз. Ондай орын ауыстыруды ықтимал орын ауыстрыруы деп
атаймыз. ![]() деп
белгілейміз.
деп
белгілейміз.
Ықтимал орын ауыстырулар біріншіден, шексіз аз болуы қажет, өйткені шекті орын алмастыруда жүйе басқа орынға көшіп, оның тепе–теңдік шарттары бұзылуы мүмкін.
Екіншіден, ![]() орын ауыстырулар жүйесінің
байланыстарын бұзбайлары, қиратпауы қажет, өйткені жүйенің түрі
өзгереді.
орын ауыстырулар жүйесінің
байланыстарын бұзбайлары, қиратпауы қажет, өйткені жүйенің түрі
өзгереді.
Сонымен ![]() ықтимал орын ауыстыру деп жүйенің
байланыстарын бұзбайтын, аз орын ауыстыруларды
атаймыз.
ықтимал орын ауыстыру деп жүйенің
байланыстарын бұзбайтын, аз орын ауыстыруларды
атаймыз.
Жалпы жағдайда
жүйенің ![]() орын алмастыруы
кез келген жиын болуы мүмкін. Бірақ, әр жүйе үшін байланыстардың
түріне тиісті, өзара тәуелсіз, анық санды
орын алмастыруы
кез келген жиын болуы мүмкін. Бірақ, әр жүйе үшін байланыстардың
түріне тиісті, өзара тәуелсіз, анық санды![]() орын алмастырулар
болады.
орын алмастырулар
болады.
Жүйенің өзара
тәуелсіз және бір мәнді анықталатын ![]() ықтимал орын алмастыру санын
жүйенің еркіндік дәреже саны деп
атаймыз.
ықтимал орын алмастыру санын
жүйенің еркіндік дәреже саны деп
атаймыз.
Мысалы, жазықтақтағы
нүктенің кез келген ![]() орын ауыстыруларын
орын ауыстыруларын ![]() екі орын алмастыру ретінде
қарастыруға болады. Демек, жазықтықта қозғалыстағы нүктенің
еркіндік дәреже саны 2
болады.
екі орын алмастыру ретінде
қарастыруға болады. Демек, жазықтықта қозғалыстағы нүктенің
еркіндік дәреже саны 2
болады.
Кеңістіктегі еркін нүктенің еркіндік дәреже саны 3.
Бір нүктесі бекітілген сфералық қозғалыстағы дененің еркіндік дәреже саны 3.
Жазық параллель қозғалытағы дененің еркіндік дәреже саны 3.
Кеңістіктегі еркін дене қозғалысының еркіндік дәреже саны 6.
Ықтимал орын алмастыру принципі
Ықтимал жұмысы деп
![]() орын алмастыруда
орындалатын
орын алмастыруда
орындалатын
![]()
жұмысты атаймыз
![]() актив және реакция күштері
үшін
актив және реакция күштері
үшін
![]()
Жүенің байланыстарын идеалдық байланыстар деп атаймыз, егер де
![]()
болса.
Жүенің
Мк
нүктесіне түскен, берілген
күштермен реакция күштірінің тең әсерлі күштерін ![]() деп белгілесек, нүкте тыныштықта
болса
деп белгілесек, нүкте тыныштықта
болса
![]()
Онда ол күштер үшін ықтимал күштер жұмыстарының қосындысы нөлге тең:
![]()
Жүйеге қатысты (6) былай жазылдады.
![]()
Егер жүйенің байланыстары идеалдық байланыстар болса,
![]() немесе
немесе ![]()
(8)- математикалық түрде ықтимал орын алмастыру принципін береді.
Егер жүенің байланыстары идеалдық байланыстар болса жүйе тыныштықта болу үшін барлық актив күштердің ықтимал жұмыстарының қосындысы нөлге тең болуы қажет.
Аналитикалық түрде принцип былай жазылады
![]()
Мұнда ![]() -тың
x,y,z
- өстеріне
проекциялары.
-тың
x,y,z
- өстеріне
проекциялары.
Даламбер – Лагранж принципі – динамиканың жалпы теңдеуі
Даламабер принципі динамиканың есептерін статиканың әдістеріне әкеледі. Жүйенің ықтимал орын ауыстыру принципі статиканың есептерінің шешуінің жалпы тәсілін береді. Сол себептен, осы екі принципті қатар пайдаланып, динамика есептері шешуінің жалпы тәсілін алуға болады.
Шынында да, егер
нүктеге әсер ететін ![]() күштерге
күштерге ![]() инерция күштерін қоссақ,
Даламбер принципі
инерция күштерін қоссақ,
Даламбер принципі ![]() бойынша
жүйе тыныштықта болады.
бойынша
жүйе тыныштықта болады.
Енді жүйенің байланыстарын идеалды деп аталған күштерге ықтимал орын ауыстыру принципін пайдалансақ,
![]()
яғни
![]()
Немесе
![]()
Даламбер–Лагранж принципі: идеалды байланысты жүйе қозғалысында барлық берілген және екпін күштерінің ықтимал жұмыстарының қосындысы кез келген уақытта нөлге тең.
Принциптің аналитикалық түрі
![]()
Жалпыланған координаталар, жалпыланған жылдамдықтар
Жүйенің еркіндік
дәреже саны өзара тәуелсіз ![]() ықтимал орын
ауыстырулардың санын атадық.
ықтимал орын
ауыстырулардың санын атадық.
Екінші жағынан жүйенің еркіндік дәреже саны әр уақытта жүйенің нүктелер саны, олардың байланыстарының саны және түрімен анықталады.
Төменде жүйенің геометриялық байланыстарын қарастырамыз. Геометриялық байланыстар деп жүйенің тек орнын шектейтін байланыстарды атаймыз.
Жүйенің еркіндік дәреже саны жүйенің геометриялық байланыстар теңдеулерінің санына кемиді.
Геометриялық байланысты жүйенің еркіндік дәреже саны өзара тәуелсіз кез келген координаталармен анықталады.
Ондай координаталар ретінде кез келген механикалык, физикалық, геометриялық параметрлерді алуға болады, мысалы: бұрышты, доғаны, ауданды, түзу сызықтың кесіндісін және т.б..
Кез келген өлшемді, өзара тәуелсіз, саны жүйенің еркіндік дәреже санына тең, әр уақытта жүйенің орнын бір мәнді анықтайтын параметрлерді жалпыланған координаталар деп атаймыз.
Оларды q әрпімен белгілейміз.
Еркін нүктенің еркіндік дәреже саны 3 болғандықтан, геометриялық байланыс теңдеулерінің саны к жүйенің еркіндік дәреже саны 8 былай аныкталады:
S = 3п-к (1)
Жүйенің кез келген уакыттағы орны
![]()
S жалпыланған координаталар санымен анықталады.
S
жалпыланған координаталар
өзара тәуелсіз болғандықтан,
олардың ![]()
өсімшелерінде тәуелсіз болады.
Тік бұрышты декарт санақ
жүйесінде нүктелердің X![]() ,Y
,Y![]() ,Z
,Z![]() координаталарын
q
координаталарын
q![]() жалпыланған кординаталары
арқылы анықтауға
болады:
жалпыланған кординаталары
арқылы анықтауға
болады:
![]()
![]() немесе
немесе ![]()
![]()
М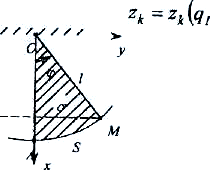 ысал: Жазық
математикалық маятниктің еркіндік дәреже саны
ысал: Жазық
математикалық маятниктің еркіндік дәреже саны ![]() .
Олай болса оның
орны
.
Олай болса оның
орны ![]() жалпыланған координатасымен
анықталады. Онда
жалпыланған координатасымен
анықталады. Онда ![]() ретінде 4 бұрышты, S доғаның
ұзындығын, ОАМ сектордың
ретінде 4 бұрышты, S доғаның
ұзындығын, ОАМ сектордың ![]() ауданын алуға болады. Бірақ
х координатасын алуға болмайды,
өйткені ол жүйенің орнын бір мәнді анықтамайды.
Егер
ауданын алуға болады. Бірақ
х координатасын алуға болмайды,
өйткені ол жүйенің орнын бір мәнді анықтамайды.
Егер ![]() ретінде
ретінде ![]() бүрышын алсақ,
онда
бүрышын алсақ,
онда
![]()
Жүйе қозғалысында
оның ![]() координаталары
уақытқа байланысты өзгеріп
отырады:
координаталары
уақытқа байланысты өзгеріп
отырады:
![]()
Бұлар жүйе қозғалысының жалпыланған координаталардағы кинематикалық теңдеулері деп аталады.
Уақыт бойынша жалпыланған координаталар туындылары.
![]() немесе
немесе ![]()
Шамаларды жалпыланған жылдамдықтар дейміз.
Олардың өлшемдері
![]() жалпыланған координаталардың
өлшемдерімен байланысты.
жалпыланған координаталардың
өлшемдерімен байланысты.
Мысалы q-бұрыш
болса, ![]() -бұрыштық
жылдамдық, егер q-аудан болса,
-бұрыштық
жылдамдық, егер q-аудан болса, ![]() -секторлық жылдамдық. Лагранж
теңдеулері жалпыланған
күштер
-секторлық жылдамдық. Лагранж
теңдеулері жалпыланған
күштер
n материалдық
нүктелерден тұратын механикалық жүйеге ![]() күштер түссін.
күштер түссін. ![]() номерлі нүктеге түскен күштердің
тең әсерлі күші.
номерлі нүктеге түскен күштердің
тең әсерлі күші.
Кез келген уақытта
кеңістіктегі жүйенің орны ![]() жалпыланған координаталармен
анықталсын. Жүйенің басқа координаталарына тәуелсіз
жалпыланған координаталармен
анықталсын. Жүйенің басқа координаталарына тәуелсіз ![]() координатасының
координатасының ![]() өсімше
алсын.
өсімше
алсын.
Басқа ![]() координаталар
өзгермесін.
координаталар
өзгермесін.
Онда ![]() алатын ықтимал орын
алмастыруы
алатын ықтимал орын
алмастыруы
![]()
Яғни ![]()
Күштердің ықтимал
жұмысы ![]() Демек,
Демек,

Содан кейін
![]() деп
белгілесек,
деп
белгілесек,

![]() жалпыланған
координатаға қатысты жалпыланған
күш,
жалпыланған
координатаға қатысты жалпыланған
күш,
![]() жалпыланған
координатаға қатысты жалпыланған
күш,
жалпыланған
координатаға қатысты жалпыланған
күш,
![]() жалпыланған
координатаға қатысты жалпыланған күш деп
атаймыз.
жалпыланған
координатаға қатысты жалпыланған күш деп
атаймыз.
Егер жүйе қозғалғанда барлық жалпыланған координаталар ықтимал орын алмастыру алса,
![]()
(6)-формуладан байқайтынымыз, жалпыланған күш ықтимал жұмыста ықтимал орын алмастырудың еселігі болады.
1) Есеп шығару үшін алдымен жүйенің еркіндік дәрежесін анықтау қажет.
2) Жалпыланған координаталарды таңдап алып, күштерді көрсету керек.
3) ![]() -ді табу үшін тек қана
-ді табу үшін тек қана ![]() -ді өзгерту
қажет.
-ді өзгерту
қажет.
 Есеп. Салмағы
Есеп. Салмағы
![]() дене А жылтыр көлбеу
жазықтықпен қозғалғанда, салмағы
дене А жылтыр көлбеу
жазықтықпен қозғалғанда, салмағы ![]() дене В кедір – бұдырлы, үйкеліс
коэффициенті
дене В кедір – бұдырлы, үйкеліс
коэффициенті ![]() , көлденең
жазықтықпен қозғалсын. Бұл жүйенің еркіндік дәреже саны - бір. Оның
орны
, көлденең
жазықтықпен қозғалсын. Бұл жүйенің еркіндік дәреже саны - бір. Оның
орны ![]() координатамен
беріледі.
координатамен
беріледі. ![]() -жалпыланған
күшті табу үшін жүйеге түскен күштердің ықтимал жұмысын
-жалпыланған
күшті табу үшін жүйеге түскен күштердің ықтимал жұмысын ![]() табуымыз керек. Жүйенің
табуымыз керек. Жүйенің ![]() орын алмастырудағы
орын алмастырудағы ![]() күштердің
жұмысы
күштердің
жұмысы

Жалпыланған координаталардағы механикалық жүйенің тепе–теңдік шарттары
Ықтимал орын ауыстыру принципіне байланысты механикалық жүйе тыныштық күйде болу үшін күштердің ықтимал жұмыстарының қосындысы нөлге тең болуы қажет, яғни
![]()
Жалпланған күштер үшін
![]()
немесе
![]()
Жалпыланған
![]() координаталардың өсімшелері.
Ықтимал орын ауыстырулар
координаталардың өсімшелері.
Ықтимал орын ауыстырулар ![]() өзара тәуелсіз болғандықтан,
олардың (7)-теңдеудегі еселіктері
өзара тәуелсіз болғандықтан,
олардың (7)-теңдеудегі еселіктері ![]() ,
, ![]() жеке-жеке нөлге тең болуы
қажет:
жеке-жеке нөлге тең болуы
қажет:
![]()
Шынында да, айталық,
![]() болсын. Ондай жүйе тыныштық
күйде болмайды. Денеге
болсын. Ондай жүйе тыныштық
күйде болмайды. Денеге ![]() ықтимал орын ауыстыру берсек (7)
орындалмайды.
ықтимал орын ауыстыру берсек (7)
орындалмайды.
Сонымен, механикалық
жүйе тепе-теңдік күйде болуы үшін, барлық ![]() жалпыланған координаталарға
қатысты жалпыланған
жалпыланған координаталарға
қатысты жалпыланған ![]() күштердің жеке-жеке нөлге тең
болуы қажетті және жеткілікті. Сол үшін статиканың есебін
шығарғанда ықтимал орын ауыстыру принципіне байланысты жалпыланған
күштерді тауып, нөлге теңестіру
қажет.
күштердің жеке-жеке нөлге тең
болуы қажетті және жеткілікті. Сол үшін статиканың есебін
шығарғанда ықтимал орын ауыстыру принципіне байланысты жалпыланған
күштерді тауып, нөлге теңестіру
қажет.
Егер жүйеге әсер
ететін күштер потенциалды күштер болса, ![]() онда
онда
![]()
яғни ![]()
Демек, күштер потенциалды күштер болса, механикалық жүйе тепе-теңдікте болуы үшін
![]()
болуы қажет.
Лагранж теңдеулері
Байланыстары геометриялық байланыстар механикалық жалпыланған координаталардағы қозғалысының теңдеулерін табу үшін динамиканың жалпы теңдеулерін қарастырамыз:

Төменде геометриялық
байланыстарды жалпы жағдайда идеалды байланыстар деп есептейміз.
Сол үшін бірінші суммаға берілген ![]() күштермен қатар
күштермен қатар ![]() кедергі күштер де
енеді.
кедергі күштер де
енеді.
Механикалық жүйенің еркіндік дәреже саны S болса, онда берілген күштердің ықтимал жұмысы.
![]()
Сол сияқты ![]() инерция күштердің ықтимал
жұмыстары
инерция күштердің ықтимал
жұмыстары
![]()
Мұнда ![]() -жалпыланған инерция күштері.
Яғни
-жалпыланған инерция күштері.
Яғни

(2) мен (3) еске алсақ, (1) былай жазылады.
![]()
![]() өзара тәуелсіз
болғандықтан
өзара тәуелсіз
болғандықтан ![]() шамалардың
еселіктері нөлге тең болуы
қажет:
шамалардың
еселіктері нөлге тең болуы
қажет:

Бұл теңдеулер көп жеңілдейді, егер жалпыланған инерция күштерін кинетикалық энергия арқылы анықтасақ
![]()
екені белгілі. Сонымен қатар
![]()
ал


![]()
(с) мен (d)-ны (b)-ға қойсақ.

Олай болса

Бұл теңдеулерді механикалық жүйенің қозғалысының жалпыланған координаталардағы қозғалыс теңдеулері немесе екінші текті Лагранж теңдеулері деп атаймыз.
Бұл теңдеулердің құндылы теңдеулер санына жүйе нүктелерінің саны немесе қозғалыстарының түрі әсер етпейді. Теңдеулер саны тек еркіндік дәреже санына байланысты.
Лагранж
теңдеулерінде ![]() жалпыланған
күштерді және есептің бастапқы шарттары белгілі болса, жүйенің
жалпыланған координаталардағы қозғалыс
заңын
жалпыланған
күштерді және есептің бастапқы шарттары белгілі болса, жүйенің
жалпыланған координаталардағы қозғалыс
заңын
![]()
табу оңай.
Лагранж теңдеулері
жалпыланған ![]() координаталардан екінші ретті
жай дифференциалдық теңдеулерін
береді.
координаталардан екінші ретті
жай дифференциалдық теңдеулерін
береді.
Егер күштер потенциалды болса,
![]()
немесе
![]()
![]() функциясы
кинетикалық потенциал не Лагранж функциясы деп
атаймыз.
функциясы
кинетикалық потенциал не Лагранж функциясы деп
атаймыз.
ҚОРЫТЫНДЫ
Жүйе кинетикалық энергиясының өзгеру теоремасы арқылы есеп шығарғанда, жүйеге түскен сыртқы күштер жұмыстарын анықтау үшін қозғалыс заңын пайдаланбадық.
Төменде қандай күштерге қатысты дененің қозғалыс заңын пайдаланбай олардың жұмыстарын табуға болатынын анықтайық.
Дененің кез келген М
нүктесіне түскен ![]() күштің
күштің
![]() орын ауыстыруындағы
жұмысы.
орын ауыстыруындағы
жұмысы.
Жүйенің кинетикалық энергиясы деп, оның барлық нүктелерінің кинетикалық энергияларының арифметиаклық қосындысына тең Т-скалярлышаманы атаймыз
Бұл теңдеулерді механикалық жүйенің қозғалысының жалпыланған координаталардағы қозғалыс теңдеулері немесе екінші текті Лагранж теңдеулері деп атаймыз.
Бұл теңдеулердің құндылы теңдеулер санына жүйе нүктелерінің саны немесе қозғалыстарының түрі әсер етпейді. Теңдеулер саны тек еркіндік дәреже санына байланысты.
Лагранж
теңдеулерінде ![]() жалпыланған
күштерді және есептің бастапқы шарттары белгілі болса, жүйенің
жалпыланған координаталардағы қозғалыс
заңын
жалпыланған
күштерді және есептің бастапқы шарттары белгілі болса, жүйенің
жалпыланған координаталардағы қозғалыс
заңын
![]()
табу оңай.
Лагранж теңдеулері
жалпыланған ![]() координаталардан екінші ретті
жай дифференциалдық теңдеулерін
береді.
координаталардан екінші ретті
жай дифференциалдық теңдеулерін
береді.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР
-
Н.Қожаспаев, С.Кешуов, И.Мухитов Электротехника /оқу құралы/ - Алматы. Республикалық баспа кабинеті, 1996 ж., 300 бет
-
Электротехника /Под ред- проф. В. Г. Герасимова.— М.: Высшая школа. 1935.
-
Волынский Б. А., Зейн Е. Н..Шатерников В. Е.Электротехника.— Москва.:Эпергоатомиздат, 1987.
-
Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н., Электротехника —Москва.:Эпергоатомиздат, 1985.
-
Касаткин А. С., Немцов М. В..Электротехника.— М.: Энерогоатомиздат. 1983.
-
Иванов И. И., Равдоник С. С. Электротехника.— М.: Высшее школа, 1984.
-
Электротехника. Программированное учебное пособие /Под ред. проф. В. Г. Герасимова.— М.: Высшая школа, 1983.
-
Основы промышленной электроники. /Под ред. проф. А Г. Герасимова.— М.:Высшая школа, 1986.
23

шағым қалдыра аласыз















