
«Ақ желкен» математикалық регатасы
9-сынып
№1.
 екені белгілі
болса,
екені белгілі
болса,  өрнегінің мәнін
табыңдар.
өрнегінің мәнін
табыңдар.
№2.
 екені
белгілі.
екені
белгілі.
Бір көбейткішті сызып
тастағаннан кейін қалған көбейтінді қандай да бір натурал санның
квадраты болатындай етіп  өрнектен бір көбейткішті
сызып тастаңыз.
өрнектен бір көбейткішті
сызып тастаңыз.
№3.
 болатын АВС үшбұрышы
берілген. АС,
ВС қабырғаларында
болатын АВС үшбұрышы
берілген. АС,
ВС қабырғаларында
 болатындай етіп
сәйкесінше Е
мен
D
нүктелері
салынған.
болатындай етіп
сәйкесінше Е
мен
D
нүктелері
салынған.  қатынасын
табыңыз.
қатынасын
табыңыз.
№4. Екі ыдыс берілген,
біріншісінде 1 л су бар, ал екінші ыдыс бос. Су бірінші ыдыстан
екінші ыдысқа, екінші ыдыстан бірінші ыдысқа және т.с.с.
кезектестіріп құйылады, бұл кезде құйылатын судың бөлігі суы
алынатын ыдыстағы судың кезектесе  және т.с.с. бөлігіне тең
болады. 2021 құюдан кейін ыдыстарда қанша су
болады?
және т.с.с. бөлігіне тең
болады. 2021 құюдан кейін ыдыстарда қанша су
болады?
Математическая регата «Ақ желкен»
9-класс
№1. Найдите значение
выражения  , если
известно что
, если
известно что
 .
.
№2. Известно,
что  .
.
Вычеркните один сомножитель из
произведения  , чтобы оставшееся
произведение стало квадратом некоторого натурального
числа.
, чтобы оставшееся
произведение стало квадратом некоторого натурального
числа.
№3. Дан
треугольник АВС, в
котором  . На
сторонах АС,
ВС выбраны
точки Е
и
D
соответственно, такие,
что
. На
сторонах АС,
ВС выбраны
точки Е
и
D
соответственно, такие,
что  . Найдите
отношение
. Найдите
отношение  .
.
№4. Имеются два сосуда, в
первом из них 1 л воды, второй сосуд пустой. Последовательно
проводятся переливания из первого сосуда во второй, из второго в
первый и т.д., причем доля отливаемой воды составляет
последовательно  и т.д. от количества
воды в сосуде, из которого вода отливается. Сколько воды будет в
сосудах после 2021 переливаний?
и т.д. от количества
воды в сосуде, из которого вода отливается. Сколько воды будет в
сосудах после 2021 переливаний?
«Ақ желкен» математикалық регатасы
10-сынып
№1. Әр түрлі он натурал санның арифметикалық ортасы 15-ке тең. Осы сандардың ең үлкенінің мүмкін болатын ең үлкен мәнін табыңыз.
№2.
Түбірі
 саны және
коэффициенттері бүтін сандар болатын көпмүшені
табыңыз.
саны және
коэффициенттері бүтін сандар болатын көпмүшені
табыңыз.
№3. Доғал бұрыштарының
қосындысы  болатын дөңес
көпбұрыштың қанша қабырғасы болуы мүмкін? (Мысалдар мен сызбаларды
көрсетудің қажеті жоқ)
болатын дөңес
көпбұрыштың қанша қабырғасы болуы мүмкін? (Мысалдар мен сызбаларды
көрсетудің қажеті жоқ)
№4. Қағаз парақты 5 бөлікке бөлді, осы бөліктердің кейбірін тағы 5 бөлікке бөлді және т.с.с. Бірнеше рет бөлгеннен кейін 2022 бөлік шығу мүмкін бе?
Математическая регата «Ақ желкен»
10-класс
№1. Среднее арифметическое десяти различных натуральных чисел равно 15. Найдите наибольшее значение наибольшего из этих чисел.
№2. Найдите многочлен с
целочисленными коэффициентами, корнем которого является
число  .
.
№3. Сколько сторон может иметь
выпуклый многоугольник, у которого сумма тупых углов
равна  ? (Примеры и чертежи
приводить не надо)
? (Примеры и чертежи
приводить не надо)
№4. Лист бумаги разрезали на 5 частей, некоторые из этих частей разрезали на 5 частей и т.д. Может ли за некоторое число разрезаний получиться 2022 листка бумаги?
«Ақ желкен» математикалық регатасы
11-сынып
№1. Егер
 болса, х
санына ең жақын болатын бүтін
санды табыңыз.
болса, х
санына ең жақын болатын бүтін
санды табыңыз.
№2.
Ғалымдар  деген жаңа операцияны
ойлап тапты, ол мынадай шарттарды
қанағаттандырады:
деген жаңа операцияны
ойлап тапты, ол мынадай шарттарды
қанағаттандырады:  және
және  (мұндағы «+» белгісі
қалыпты жағдайдағы қосу амалын білдіреді, ал жақшалар амалдар ретін
көрсетеді).
(мұндағы «+» белгісі
қалыпты жағдайдағы қосу амалын білдіреді, ал жақшалар амалдар ретін
көрсетеді).  есептеңіз.
есептеңіз.
№3. Табанының
радиусы R
және
биіктігі  болатын тік конусты
жазықтыққа қырынан жатқызып, төбесі қозғалмайтындай етіп дөңгелетіп
жіберді. Конус бастапқы қалыпқа келгенге дейін оның табаны қанша
айналым жасайды?
болатын тік конусты
жазықтыққа қырынан жатқызып, төбесі қозғалмайтындай етіп дөңгелетіп
жіберді. Конус бастапқы қалыпқа келгенге дейін оның табаны қанша
айналым жасайды?
№4. Бөлмеде алты отырғыш әр қатарда үш отырғыштан болатындай етіп екі қатарға қойылған. Екінші қатардағы отырғыштар бірінші қатардың дәл артында орналасқан. Бөлмеге бойлары әр түрлі алты адам келді. Бұл алты адамды алдыңғы қатарда отырған адамның бойы артында отырған адамның бойынан кіші болатындай етіп қанша тәсілмен отырғызуға болады?
Математическая регата «Ақ желкен»
11-класс
№1. Найдите ближайшее целое
число к числу х, если

№2. Ученые придумали новую
операцию  , которая удовлетворяет
условиям:
, которая удовлетворяет
условиям:
 и
и
 .
Вычислите
.
Вычислите  . (Знак «+» определяет
сложение в обычном смысле, скобки показывают порядок
действий.)
. (Знак «+» определяет
сложение в обычном смысле, скобки показывают порядок
действий.)
№3. Прямой круговой конус с
радиусом основания R
и высотой
 положили боком на
плоскость и покатили так, что его вершина осталась неподвижна.
Сколько оборотов сделает его основание до момента, когда конус
вернется в исходное положение?
положили боком на
плоскость и покатили так, что его вершина осталась неподвижна.
Сколько оборотов сделает его основание до момента, когда конус
вернется в исходное положение?
№4. В зале стоят шесть стульев в два ряда – по три стула в каждом, один ряд ровно за другим. В зал пришли шесть человек различного роста. Сколькими способами можно рассадить их так, чтобы каждый человек, сидящий в первом ряду, был ниже человека, сидящего за ним?
Шешуі мен жауаптары
9-сынып
№1.



Жауабы: 
№2.





Осылайша, алғашқы екі көбейткіш квадраттар екенін көреміз, сондықтан 10! сызып тастасақ, санның квадраты қалады. Басқа көбейткіштерді сызып тастаған кезде есептің шарты орындалмайтынын оңай көруге болады.
Жауабы: 10!
№3. Берілген
үшбұрышқа ВС
қабырғасына қатысты
симметриялы болатын  үшбұрышын
салайық.
үшбұрышын
салайық.  нүктелері бір түзудің
бойында жатыр, себебі
нүктелері бір түзудің
бойында жатыр, себебі
 .
Демек D
–
.
Демек D
–
 үшбұрышының
үшбұрышының  мен
СВ
медианаларының қиылысу нүктесі
және оларды төбесінен қарағанда 2:1 қатынаста
бөледі.
мен
СВ
медианаларының қиылысу нүктесі
және оларды төбесінен қарағанда 2:1 қатынаста
бөледі.
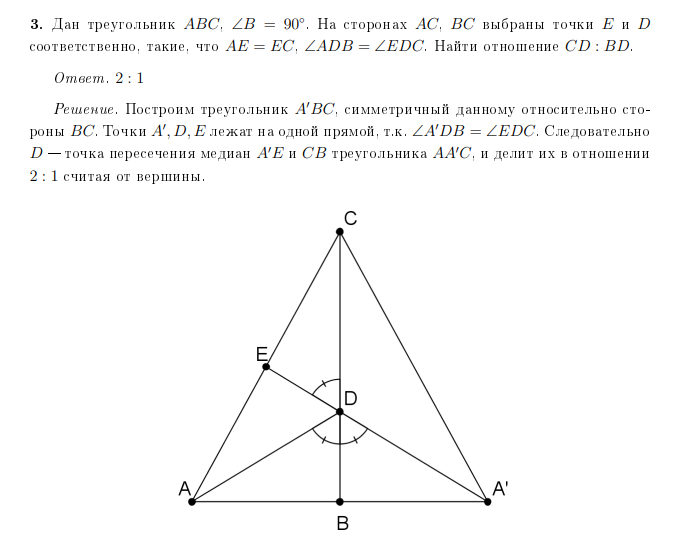
Жауабы: 2:1
№4. Алғашқы құюларды есептей
отырып, бірінші, үшінші, бесінші құюдан кейін
ыдыстарда  л су болатынын көруге
болады. Осы жағдай тақ нөмірлі кез келген құюдан кейін болатынын
дәлелдеу керек. Егер
л су болатынын көруге
болады. Осы жағдай тақ нөмірлі кез келген құюдан кейін болатынын
дәлелдеу керек. Егер  тақ нөмірлі құюдан кейін
ыдыстарда
тақ нөмірлі құюдан кейін
ыдыстарда  л су болса, онда келесі
құю кезінде екінші ыдыстан
л су болса, онда келесі
құю кезінде екінші ыдыстан  бөлік алынады да,
бірінші ыдыста
бөлік алынады да,
бірінші ыдыста  (л)
болады.
(л)
болады.  нөмірлі келесі құю
кезінде бірінші ыдыстан
нөмірлі келесі құю
кезінде бірінші ыдыстан  бөлік алынып, осы
ыдыста
бөлік алынып, осы
ыдыста  (л) қалады. Сондықтан
жетінші, тоғызыншы және кез келген тақ нөмірлі құюдан кейін әрбір
ыдыста
(л) қалады. Сондықтан
жетінші, тоғызыншы және кез келген тақ нөмірлі құюдан кейін әрбір
ыдыста  л су
болады.
л су
болады.
Жауабы: 2021 құюдан
кейін әрбір
ыдыста  л су
болады.
л су
болады.
Решения и ответы
9-класс
№1.



Ответ: 
№2.





Таким образом, мы видим, что первые два множителя – квадраты, поэтому если вычеркнуть 10!, то останется квадрат. Легко видеть, что вычеркивание других множителей, указанных в ответах, не дает желаемого результата.
Ответ: 10!
№3. Построим
треугольник  , симметричный данному
относительно стороны ВС. Точки
, симметричный данному
относительно стороны ВС. Точки
 лежат на одной
прямой, т.к.
лежат на одной
прямой, т.к.  .
Следовательно D
– точка пересечения
медиан
.
Следовательно D
– точка пересечения
медиан  и
СВ
треугольника
и
СВ
треугольника  , и делит их в отношении
2:1 считая от вершины.
, и делит их в отношении
2:1 считая от вершины.

Ответ: 2:1
№4. «Просчитав» несколько
первых переливаний, нетрудно обнаружить, что после первого,
третьего, пятого переливаний в обоих сосудах будет
по  л воды. Необходимо
доказать, что так будет после любого переливания с нечетным
номером. Если после переливания с нечетным
номером
л воды. Необходимо
доказать, что так будет после любого переливания с нечетным
номером. Если после переливания с нечетным
номером  в сосудах было
по
в сосудах было
по  л, то при следующем
переливании из второго сосуда берется
л, то при следующем
переливании из второго сосуда берется
 часть, так что в
первом сосуде оказывается
часть, так что в
первом сосуде оказывается  (л). При следующем
переливании, имеющем номер
(л). При следующем
переливании, имеющем номер  , из него
берется
, из него
берется  часть и
остается
часть и
остается  (л). Поэтому после
седьмого, девятого и вообще любого нечетного переливания в сосудах
будет по
(л). Поэтому после
седьмого, девятого и вообще любого нечетного переливания в сосудах
будет по  л
воды.
л
воды.
Ответ: после 2021
переливаний в сосудах будет
по  л
воды.
л
воды.
Шешуі мен жауаптары
10-сынып
№1. Есептің шарты бойынша
берілген сандардың қосындысы 150 болатыны белгілі. Қосылғыштардың
біреуі ең үлкен болу үшін қалған тоғыз қосылғыш ең кіші сандар болу
керек. Барлық қосылғыштар әр түрлі болу керек, сондықтан тоғыз
санның қосындысы  санынан аз бола алмайды.
Демек, берілген сандардың ең үлкені 105-тен артық болуы мүмкін
емес.
санынан аз бола алмайды.
Демек, берілген сандардың ең үлкені 105-тен артық болуы мүмкін
емес.
Жауабы: 105
№2.
 деп белгілейік.
Онда
деп белгілейік.
Онда  . Сонан
соң
. Сонан
соң  немесе
немесе  болады. Ал
ол
болады. Ал
ол  болады.
болады.
Сондықтан
а
саны
 көпмүшесінің түбірі
болады.
көпмүшесінің түбірі
болады.
Жауабы: 
№3. Дөңес көпбұрышта доғал емес
бұрыштардың саны үштен артық бола алмайды (егер ол тіктөртбұрыш
болмаса). Расында да, егер мұндай бұрыштар саны үштен көп болса,
онда олармен сыбайлас бұрыштар сүйір емес болады. Ал бұл тұжырым
дөңес көпбұрыштың сыртқы бұрыштарының қосындысы (әр төбесінен бір
бұрыштан алғанда)  -қа тең болады дегенге
қайшы келеді.
-қа тең болады дегенге
қайшы келеді.
Осылайша, берілген көпбұрыштың
бұрыштарының қосындысы  тең болады,
мұндағы
тең болады,
мұндағы  . Бұл
көпбұрышта п
қабырға болсын,
онда
. Бұл
көпбұрышта п
қабырға болсын,
онда
 ,
яғни
,
яғни  .
п
– натурал сан екенін ескере
отырып,
.
п
– натурал сан екенін ескере
отырып,  немесе
немесе  аламыз.
аламыз.
Жауабы: 19 немесе 20
№4. Әрбір қиған сайын бір
парақтан бес бөлік алынады, яғни бөліктер саны 4-ке артады. Демек,
бастапқы парақтан  ,
мұндағы
,
мұндағы  түріндегі бөліктер саны
алынуы мүмкін, яғни бұл санды 4-ке бөлгенде 1 қалдық қалады.
Бірақ
түріндегі бөліктер саны
алынуы мүмкін, яғни бұл санды 4-ке бөлгенде 1 қалдық қалады.
Бірақ
 . Демек, 2022
бөлік шығу мүмкін
емес.
. Демек, 2022
бөлік шығу мүмкін
емес.
Жауабы: 2022 бөлік шығу мүмкін емес.
Решения и ответы
10-класс
№1. Из условия задачи следует,
что сумма данных чисел равна 150. Для того, чтобы одно из слагаемых
было наибольшим, необходимо, чтобы остальные девять слагаемых были
как можно меньше. Так как все слагаемые должны быть различными, то
сумма девяти наименьших из них не может быть меньше,
чем  . Следовательно,
наибольшее из данных чисел не может быть больше, чем
105.
. Следовательно,
наибольшее из данных чисел не может быть больше, чем
105.
Ответ: 105
№2.
Обозначим  .
Тогда
.
Тогда  .
Затем
.
Затем  или
или
 , которое
равносильно
, которое
равносильно  .
.
А это означает,
что а
является корнем
многочлена  .
.
Ответ: 
№3. Заметим, что выпуклый
многоугольник не может иметь более трех не тупых углов (если это не
прямоугольник). Действительно, если таких углов больше, чем три, то
внешние углы, смежные с ними – не острые, а это противоречит тому,
что сумма внешних углов выпуклого многоугольника (взятых по одному
при каждой вершине) равна  .
.
Таким образом, сумма углов
данного многоугольника равна  ,
где
,
где
 . Пусть у
него п
сторон,
тогда
. Пусть у
него п
сторон,
тогда  , то
есть
, то
есть
 . Учитывая,
что п
– натуральное число,
получим:
. Учитывая,
что п
– натуральное число,
получим:
 или
или
 .
.
Ответ: 19 или 20
№4. Замечаем, что при каждом
разрезании из одного листка получаем пять, т.е. число листков
увеличивается на 4. Следовательно, из исходного листа может
получиться число листков вида  ,
где
,
где  , т.е. это число при
делении на 4 дает остаток 1. Но
, т.е. это число при
делении на 4 дает остаток 1. Но  . Следовательно, 2022
листков получиться не может.
. Следовательно, 2022
листков получиться не может.
Ответ: 2022 листков получиться не может
Шешуі мен жауаптары
11-сынып
№1.
Түрлендірейік:  .
.
 ,
ал
,
ал  болғандықтан,
болғандықтан,  болады. Демек, ізделінді
сан – бұл 2 саны.
болады. Демек, ізделінді
сан – бұл 2 саны.
Жауабы: 2
№2.




Жауабы: 1
№3. Табанындағы шеңбер
радиусы L
болатын шеңбер бойымен
қозғалады, мұндағы L
– конус жасаушысының ұзындығы.
Демек, ізделінді айналым саны
 болады.
болады.
Жауабы: 8
№4.
Бірінші
тәсіл. Алты адамды алты отырғышқа
отырғызу тәсілдерінің саны 6!. Кез келген ретте отырғызуды
қарастырайық. Егер бір-бірінің артында отырған адамдардың орнын
ауыстыратын болсақ, ол үшін  әр түрлі тәсіл бар және
олардың ішінен тек біреуі ғана есеп шартын қанағаттандырады. Демек,
ізделінді тәсілдер саны:
әр түрлі тәсіл бар және
олардың ішінен тек біреуі ғана есеп шартын қанағаттандырады. Демек,
ізделінді тәсілдер саны:  .
.
Екінші
тәсіл. Адамдарды бойларының өсуі
бойынша нөмірлеп, бірінші қатардағы адамдар солдан оңға реттеліп
отыратындай етіп тәсілдерді санайық. Сол жақ шетте үнемі нөмірі 1
болатын адам отырады, оның артына екінші қатарда қалған бесеуінің
кез келгені отыра алады. Екінші жұпта бірінші қатарға нөмірі ең аз
болатын адам отырады да, оның артына қалған үш адамның кез келген
біреуі отырады. Үшінші жұп қалған екі адамнан құралады және оларды
бір ғана тәсілмен отырғызуға болады.
Нәтижесінде  реттелген отырғызу
болады. Олардың әрқайсысы 6 әр түрлі тәсілді береді, өйткені
симметриялы отырғызуды да қарастыруымыз қажет. Сондықтан есеп
шартын қанағаттандыратын отырғызу тәсілдерінің ізделінді
саны
реттелген отырғызу
болады. Олардың әрқайсысы 6 әр түрлі тәсілді береді, өйткені
симметриялы отырғызуды да қарастыруымыз қажет. Сондықтан есеп
шартын қанағаттандыратын отырғызу тәсілдерінің ізделінді
саны  болады.
болады.
Жауабы: 90.
Решения и ответы
11-класс
№1.
Преобразуем:  .
.
Так как
 ,
а
,
а  ,
то
,
то  . Следовательно, искомое
число – это 2.
. Следовательно, искомое
число – это 2.
Ответ: 2
№2.




Ответ: 1
№3. Окружность основания
катится по окружности радиуса L, где
L
– длина образующей конуса.
Значит, искомое количество оборотов равно
 .
.
Ответ: 8
№4.
Первый
способ. Количество способов рассадить
шесть людей на шесть стульев 6!. Рассмотрим произвольную рассадку.
Если в ней менять местами людей, сидящих друг за другом, то для
этого есть  различных способов, из
которых ровно один удовлетворяет условию. Следовательно, искомых
способов:
различных способов, из
которых ровно один удовлетворяет условию. Следовательно, искомых
способов:  .
.
Второй
способ. Пронумеруем людей в порядке
возрастания роста и подсчитаем количество рассадок, в которых люди
в первом ряду упорядочены по номеру слева направо. Самым левым
всегда будет человек с номером 1, за ним во втором ряду может
сидеть любой из остальных. Во второй паре в первом ряду сядет
человек с наименьшим доступным номером, а за ним может сидеть любой
из троих оставшихся. Третья пара получается из оставшихся людей и
их можно усадить единственным образом. В итоге
получается  упорядоченных рассадок.
Каждая из них дает 6 разных рассадок, исходя из симметрии, поэтому
общее количество способов требуемой рассадки
равно
упорядоченных рассадок.
Каждая из них дает 6 разных рассадок, исходя из симметрии, поэтому
общее количество способов требуемой рассадки
равно  .
.
Ответ: 90.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
"Ақ желкен" математикалық регата тапсырмалары 9-11
"Ақ желкен" математикалық регата тапсырмалары 9-11
«Ақ желкен» математикалық регатасы
9-сынып
№1.
 екені белгілі
болса,
екені белгілі
болса,  өрнегінің мәнін
табыңдар.
өрнегінің мәнін
табыңдар.
№2.
 екені
белгілі.
екені
белгілі.
Бір көбейткішті сызып
тастағаннан кейін қалған көбейтінді қандай да бір натурал санның
квадраты болатындай етіп  өрнектен бір көбейткішті
сызып тастаңыз.
өрнектен бір көбейткішті
сызып тастаңыз.
№3.
 болатын АВС үшбұрышы
берілген. АС,
ВС қабырғаларында
болатын АВС үшбұрышы
берілген. АС,
ВС қабырғаларында
 болатындай етіп
сәйкесінше Е
мен
D
нүктелері
салынған.
болатындай етіп
сәйкесінше Е
мен
D
нүктелері
салынған.  қатынасын
табыңыз.
қатынасын
табыңыз.
№4. Екі ыдыс берілген,
біріншісінде 1 л су бар, ал екінші ыдыс бос. Су бірінші ыдыстан
екінші ыдысқа, екінші ыдыстан бірінші ыдысқа және т.с.с.
кезектестіріп құйылады, бұл кезде құйылатын судың бөлігі суы
алынатын ыдыстағы судың кезектесе  және т.с.с. бөлігіне тең
болады. 2021 құюдан кейін ыдыстарда қанша су
болады?
және т.с.с. бөлігіне тең
болады. 2021 құюдан кейін ыдыстарда қанша су
болады?
Математическая регата «Ақ желкен»
9-класс
№1. Найдите значение
выражения  , если
известно что
, если
известно что
 .
.
№2. Известно,
что  .
.
Вычеркните один сомножитель из
произведения  , чтобы оставшееся
произведение стало квадратом некоторого натурального
числа.
, чтобы оставшееся
произведение стало квадратом некоторого натурального
числа.
№3. Дан
треугольник АВС, в
котором  . На
сторонах АС,
ВС выбраны
точки Е
и
D
соответственно, такие,
что
. На
сторонах АС,
ВС выбраны
точки Е
и
D
соответственно, такие,
что  . Найдите
отношение
. Найдите
отношение  .
.
№4. Имеются два сосуда, в
первом из них 1 л воды, второй сосуд пустой. Последовательно
проводятся переливания из первого сосуда во второй, из второго в
первый и т.д., причем доля отливаемой воды составляет
последовательно  и т.д. от количества
воды в сосуде, из которого вода отливается. Сколько воды будет в
сосудах после 2021 переливаний?
и т.д. от количества
воды в сосуде, из которого вода отливается. Сколько воды будет в
сосудах после 2021 переливаний?
«Ақ желкен» математикалық регатасы
10-сынып
№1. Әр түрлі он натурал санның арифметикалық ортасы 15-ке тең. Осы сандардың ең үлкенінің мүмкін болатын ең үлкен мәнін табыңыз.
№2.
Түбірі
 саны және
коэффициенттері бүтін сандар болатын көпмүшені
табыңыз.
саны және
коэффициенттері бүтін сандар болатын көпмүшені
табыңыз.
№3. Доғал бұрыштарының
қосындысы  болатын дөңес
көпбұрыштың қанша қабырғасы болуы мүмкін? (Мысалдар мен сызбаларды
көрсетудің қажеті жоқ)
болатын дөңес
көпбұрыштың қанша қабырғасы болуы мүмкін? (Мысалдар мен сызбаларды
көрсетудің қажеті жоқ)
№4. Қағаз парақты 5 бөлікке бөлді, осы бөліктердің кейбірін тағы 5 бөлікке бөлді және т.с.с. Бірнеше рет бөлгеннен кейін 2022 бөлік шығу мүмкін бе?
Математическая регата «Ақ желкен»
10-класс
№1. Среднее арифметическое десяти различных натуральных чисел равно 15. Найдите наибольшее значение наибольшего из этих чисел.
№2. Найдите многочлен с
целочисленными коэффициентами, корнем которого является
число  .
.
№3. Сколько сторон может иметь
выпуклый многоугольник, у которого сумма тупых углов
равна  ? (Примеры и чертежи
приводить не надо)
? (Примеры и чертежи
приводить не надо)
№4. Лист бумаги разрезали на 5 частей, некоторые из этих частей разрезали на 5 частей и т.д. Может ли за некоторое число разрезаний получиться 2022 листка бумаги?
«Ақ желкен» математикалық регатасы
11-сынып
№1. Егер
 болса, х
санына ең жақын болатын бүтін
санды табыңыз.
болса, х
санына ең жақын болатын бүтін
санды табыңыз.
№2.
Ғалымдар  деген жаңа операцияны
ойлап тапты, ол мынадай шарттарды
қанағаттандырады:
деген жаңа операцияны
ойлап тапты, ол мынадай шарттарды
қанағаттандырады:  және
және  (мұндағы «+» белгісі
қалыпты жағдайдағы қосу амалын білдіреді, ал жақшалар амалдар ретін
көрсетеді).
(мұндағы «+» белгісі
қалыпты жағдайдағы қосу амалын білдіреді, ал жақшалар амалдар ретін
көрсетеді).  есептеңіз.
есептеңіз.
№3. Табанының
радиусы R
және
биіктігі  болатын тік конусты
жазықтыққа қырынан жатқызып, төбесі қозғалмайтындай етіп дөңгелетіп
жіберді. Конус бастапқы қалыпқа келгенге дейін оның табаны қанша
айналым жасайды?
болатын тік конусты
жазықтыққа қырынан жатқызып, төбесі қозғалмайтындай етіп дөңгелетіп
жіберді. Конус бастапқы қалыпқа келгенге дейін оның табаны қанша
айналым жасайды?
№4. Бөлмеде алты отырғыш әр қатарда үш отырғыштан болатындай етіп екі қатарға қойылған. Екінші қатардағы отырғыштар бірінші қатардың дәл артында орналасқан. Бөлмеге бойлары әр түрлі алты адам келді. Бұл алты адамды алдыңғы қатарда отырған адамның бойы артында отырған адамның бойынан кіші болатындай етіп қанша тәсілмен отырғызуға болады?
Математическая регата «Ақ желкен»
11-класс
№1. Найдите ближайшее целое
число к числу х, если

№2. Ученые придумали новую
операцию  , которая удовлетворяет
условиям:
, которая удовлетворяет
условиям:
 и
и
 .
Вычислите
.
Вычислите  . (Знак «+» определяет
сложение в обычном смысле, скобки показывают порядок
действий.)
. (Знак «+» определяет
сложение в обычном смысле, скобки показывают порядок
действий.)
№3. Прямой круговой конус с
радиусом основания R
и высотой
 положили боком на
плоскость и покатили так, что его вершина осталась неподвижна.
Сколько оборотов сделает его основание до момента, когда конус
вернется в исходное положение?
положили боком на
плоскость и покатили так, что его вершина осталась неподвижна.
Сколько оборотов сделает его основание до момента, когда конус
вернется в исходное положение?
№4. В зале стоят шесть стульев в два ряда – по три стула в каждом, один ряд ровно за другим. В зал пришли шесть человек различного роста. Сколькими способами можно рассадить их так, чтобы каждый человек, сидящий в первом ряду, был ниже человека, сидящего за ним?
Шешуі мен жауаптары
9-сынып
№1.



Жауабы: 
№2.





Осылайша, алғашқы екі көбейткіш квадраттар екенін көреміз, сондықтан 10! сызып тастасақ, санның квадраты қалады. Басқа көбейткіштерді сызып тастаған кезде есептің шарты орындалмайтынын оңай көруге болады.
Жауабы: 10!
№3. Берілген
үшбұрышқа ВС
қабырғасына қатысты
симметриялы болатын  үшбұрышын
салайық.
үшбұрышын
салайық.  нүктелері бір түзудің
бойында жатыр, себебі
нүктелері бір түзудің
бойында жатыр, себебі
 .
Демек D
–
.
Демек D
–
 үшбұрышының
үшбұрышының  мен
СВ
медианаларының қиылысу нүктесі
және оларды төбесінен қарағанда 2:1 қатынаста
бөледі.
мен
СВ
медианаларының қиылысу нүктесі
және оларды төбесінен қарағанда 2:1 қатынаста
бөледі.

Жауабы: 2:1
№4. Алғашқы құюларды есептей
отырып, бірінші, үшінші, бесінші құюдан кейін
ыдыстарда  л су болатынын көруге
болады. Осы жағдай тақ нөмірлі кез келген құюдан кейін болатынын
дәлелдеу керек. Егер
л су болатынын көруге
болады. Осы жағдай тақ нөмірлі кез келген құюдан кейін болатынын
дәлелдеу керек. Егер  тақ нөмірлі құюдан кейін
ыдыстарда
тақ нөмірлі құюдан кейін
ыдыстарда  л су болса, онда келесі
құю кезінде екінші ыдыстан
л су болса, онда келесі
құю кезінде екінші ыдыстан  бөлік алынады да,
бірінші ыдыста
бөлік алынады да,
бірінші ыдыста  (л)
болады.
(л)
болады.  нөмірлі келесі құю
кезінде бірінші ыдыстан
нөмірлі келесі құю
кезінде бірінші ыдыстан  бөлік алынып, осы
ыдыста
бөлік алынып, осы
ыдыста  (л) қалады. Сондықтан
жетінші, тоғызыншы және кез келген тақ нөмірлі құюдан кейін әрбір
ыдыста
(л) қалады. Сондықтан
жетінші, тоғызыншы және кез келген тақ нөмірлі құюдан кейін әрбір
ыдыста  л су
болады.
л су
болады.
Жауабы: 2021 құюдан
кейін әрбір
ыдыста  л су
болады.
л су
болады.
Решения и ответы
9-класс
№1.



Ответ: 
№2.





Таким образом, мы видим, что первые два множителя – квадраты, поэтому если вычеркнуть 10!, то останется квадрат. Легко видеть, что вычеркивание других множителей, указанных в ответах, не дает желаемого результата.
Ответ: 10!
№3. Построим
треугольник  , симметричный данному
относительно стороны ВС. Точки
, симметричный данному
относительно стороны ВС. Точки
 лежат на одной
прямой, т.к.
лежат на одной
прямой, т.к.  .
Следовательно D
– точка пересечения
медиан
.
Следовательно D
– точка пересечения
медиан  и
СВ
треугольника
и
СВ
треугольника  , и делит их в отношении
2:1 считая от вершины.
, и делит их в отношении
2:1 считая от вершины.

Ответ: 2:1
№4. «Просчитав» несколько
первых переливаний, нетрудно обнаружить, что после первого,
третьего, пятого переливаний в обоих сосудах будет
по  л воды. Необходимо
доказать, что так будет после любого переливания с нечетным
номером. Если после переливания с нечетным
номером
л воды. Необходимо
доказать, что так будет после любого переливания с нечетным
номером. Если после переливания с нечетным
номером  в сосудах было
по
в сосудах было
по  л, то при следующем
переливании из второго сосуда берется
л, то при следующем
переливании из второго сосуда берется
 часть, так что в
первом сосуде оказывается
часть, так что в
первом сосуде оказывается  (л). При следующем
переливании, имеющем номер
(л). При следующем
переливании, имеющем номер  , из него
берется
, из него
берется  часть и
остается
часть и
остается  (л). Поэтому после
седьмого, девятого и вообще любого нечетного переливания в сосудах
будет по
(л). Поэтому после
седьмого, девятого и вообще любого нечетного переливания в сосудах
будет по  л
воды.
л
воды.
Ответ: после 2021
переливаний в сосудах будет
по  л
воды.
л
воды.
Шешуі мен жауаптары
10-сынып
№1. Есептің шарты бойынша
берілген сандардың қосындысы 150 болатыны белгілі. Қосылғыштардың
біреуі ең үлкен болу үшін қалған тоғыз қосылғыш ең кіші сандар болу
керек. Барлық қосылғыштар әр түрлі болу керек, сондықтан тоғыз
санның қосындысы  санынан аз бола алмайды.
Демек, берілген сандардың ең үлкені 105-тен артық болуы мүмкін
емес.
санынан аз бола алмайды.
Демек, берілген сандардың ең үлкені 105-тен артық болуы мүмкін
емес.
Жауабы: 105
№2.
 деп белгілейік.
Онда
деп белгілейік.
Онда  . Сонан
соң
. Сонан
соң  немесе
немесе  болады. Ал
ол
болады. Ал
ол  болады.
болады.
Сондықтан
а
саны
 көпмүшесінің түбірі
болады.
көпмүшесінің түбірі
болады.
Жауабы: 
№3. Дөңес көпбұрышта доғал емес
бұрыштардың саны үштен артық бола алмайды (егер ол тіктөртбұрыш
болмаса). Расында да, егер мұндай бұрыштар саны үштен көп болса,
онда олармен сыбайлас бұрыштар сүйір емес болады. Ал бұл тұжырым
дөңес көпбұрыштың сыртқы бұрыштарының қосындысы (әр төбесінен бір
бұрыштан алғанда)  -қа тең болады дегенге
қайшы келеді.
-қа тең болады дегенге
қайшы келеді.
Осылайша, берілген көпбұрыштың
бұрыштарының қосындысы  тең болады,
мұндағы
тең болады,
мұндағы  . Бұл
көпбұрышта п
қабырға болсын,
онда
. Бұл
көпбұрышта п
қабырға болсын,
онда
 ,
яғни
,
яғни  .
п
– натурал сан екенін ескере
отырып,
.
п
– натурал сан екенін ескере
отырып,  немесе
немесе  аламыз.
аламыз.
Жауабы: 19 немесе 20
№4. Әрбір қиған сайын бір
парақтан бес бөлік алынады, яғни бөліктер саны 4-ке артады. Демек,
бастапқы парақтан  ,
мұндағы
,
мұндағы  түріндегі бөліктер саны
алынуы мүмкін, яғни бұл санды 4-ке бөлгенде 1 қалдық қалады.
Бірақ
түріндегі бөліктер саны
алынуы мүмкін, яғни бұл санды 4-ке бөлгенде 1 қалдық қалады.
Бірақ
 . Демек, 2022
бөлік шығу мүмкін
емес.
. Демек, 2022
бөлік шығу мүмкін
емес.
Жауабы: 2022 бөлік шығу мүмкін емес.
Решения и ответы
10-класс
№1. Из условия задачи следует,
что сумма данных чисел равна 150. Для того, чтобы одно из слагаемых
было наибольшим, необходимо, чтобы остальные девять слагаемых были
как можно меньше. Так как все слагаемые должны быть различными, то
сумма девяти наименьших из них не может быть меньше,
чем  . Следовательно,
наибольшее из данных чисел не может быть больше, чем
105.
. Следовательно,
наибольшее из данных чисел не может быть больше, чем
105.
Ответ: 105
№2.
Обозначим  .
Тогда
.
Тогда  .
Затем
.
Затем  или
или
 , которое
равносильно
, которое
равносильно  .
.
А это означает,
что а
является корнем
многочлена  .
.
Ответ: 
№3. Заметим, что выпуклый
многоугольник не может иметь более трех не тупых углов (если это не
прямоугольник). Действительно, если таких углов больше, чем три, то
внешние углы, смежные с ними – не острые, а это противоречит тому,
что сумма внешних углов выпуклого многоугольника (взятых по одному
при каждой вершине) равна  .
.
Таким образом, сумма углов
данного многоугольника равна  ,
где
,
где
 . Пусть у
него п
сторон,
тогда
. Пусть у
него п
сторон,
тогда  , то
есть
, то
есть
 . Учитывая,
что п
– натуральное число,
получим:
. Учитывая,
что п
– натуральное число,
получим:
 или
или
 .
.
Ответ: 19 или 20
№4. Замечаем, что при каждом
разрезании из одного листка получаем пять, т.е. число листков
увеличивается на 4. Следовательно, из исходного листа может
получиться число листков вида  ,
где
,
где  , т.е. это число при
делении на 4 дает остаток 1. Но
, т.е. это число при
делении на 4 дает остаток 1. Но  . Следовательно, 2022
листков получиться не может.
. Следовательно, 2022
листков получиться не может.
Ответ: 2022 листков получиться не может
Шешуі мен жауаптары
11-сынып
№1.
Түрлендірейік:  .
.
 ,
ал
,
ал  болғандықтан,
болғандықтан,  болады. Демек, ізделінді
сан – бұл 2 саны.
болады. Демек, ізделінді
сан – бұл 2 саны.
Жауабы: 2
№2.




Жауабы: 1
№3. Табанындағы шеңбер
радиусы L
болатын шеңбер бойымен
қозғалады, мұндағы L
– конус жасаушысының ұзындығы.
Демек, ізделінді айналым саны
 болады.
болады.
Жауабы: 8
№4.
Бірінші
тәсіл. Алты адамды алты отырғышқа
отырғызу тәсілдерінің саны 6!. Кез келген ретте отырғызуды
қарастырайық. Егер бір-бірінің артында отырған адамдардың орнын
ауыстыратын болсақ, ол үшін  әр түрлі тәсіл бар және
олардың ішінен тек біреуі ғана есеп шартын қанағаттандырады. Демек,
ізделінді тәсілдер саны:
әр түрлі тәсіл бар және
олардың ішінен тек біреуі ғана есеп шартын қанағаттандырады. Демек,
ізделінді тәсілдер саны:  .
.
Екінші
тәсіл. Адамдарды бойларының өсуі
бойынша нөмірлеп, бірінші қатардағы адамдар солдан оңға реттеліп
отыратындай етіп тәсілдерді санайық. Сол жақ шетте үнемі нөмірі 1
болатын адам отырады, оның артына екінші қатарда қалған бесеуінің
кез келгені отыра алады. Екінші жұпта бірінші қатарға нөмірі ең аз
болатын адам отырады да, оның артына қалған үш адамның кез келген
біреуі отырады. Үшінші жұп қалған екі адамнан құралады және оларды
бір ғана тәсілмен отырғызуға болады.
Нәтижесінде  реттелген отырғызу
болады. Олардың әрқайсысы 6 әр түрлі тәсілді береді, өйткені
симметриялы отырғызуды да қарастыруымыз қажет. Сондықтан есеп
шартын қанағаттандыратын отырғызу тәсілдерінің ізделінді
саны
реттелген отырғызу
болады. Олардың әрқайсысы 6 әр түрлі тәсілді береді, өйткені
симметриялы отырғызуды да қарастыруымыз қажет. Сондықтан есеп
шартын қанағаттандыратын отырғызу тәсілдерінің ізделінді
саны  болады.
болады.
Жауабы: 90.
Решения и ответы
11-класс
№1.
Преобразуем:  .
.
Так как
 ,
а
,
а  ,
то
,
то  . Следовательно, искомое
число – это 2.
. Следовательно, искомое
число – это 2.
Ответ: 2
№2.




Ответ: 1
№3. Окружность основания
катится по окружности радиуса L, где
L
– длина образующей конуса.
Значит, искомое количество оборотов равно
 .
.
Ответ: 8
№4.
Первый
способ. Количество способов рассадить
шесть людей на шесть стульев 6!. Рассмотрим произвольную рассадку.
Если в ней менять местами людей, сидящих друг за другом, то для
этого есть  различных способов, из
которых ровно один удовлетворяет условию. Следовательно, искомых
способов:
различных способов, из
которых ровно один удовлетворяет условию. Следовательно, искомых
способов:  .
.
Второй
способ. Пронумеруем людей в порядке
возрастания роста и подсчитаем количество рассадок, в которых люди
в первом ряду упорядочены по номеру слева направо. Самым левым
всегда будет человек с номером 1, за ним во втором ряду может
сидеть любой из остальных. Во второй паре в первом ряду сядет
человек с наименьшим доступным номером, а за ним может сидеть любой
из троих оставшихся. Третья пара получается из оставшихся людей и
их можно усадить единственным образом. В итоге
получается  упорядоченных рассадок.
Каждая из них дает 6 разных рассадок, исходя из симметрии, поэтому
общее количество способов требуемой рассадки
равно
упорядоченных рассадок.
Каждая из них дает 6 разных рассадок, исходя из симметрии, поэтому
общее количество способов требуемой рассадки
равно  .
.
Ответ: 90.

шағым қалдыра аласыз















