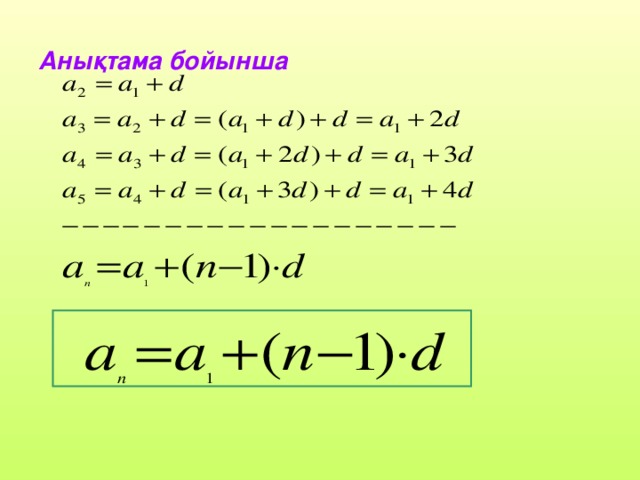|
Күні |
|
Мектеп: №51 орта мектеп №35 Арифметикалық прогрессия. Арифметикалық прогрессияның n-ші мүшесінің формуласы |
|
Сынып |
|
|
|
Оқушы саны |
|
|
|
Осы сабақта оқылатын оқу мақсаттары |
Арифметикалық прогрессия мен арифметикалық прогрессияның прогрессияның n-ші мүшесінің формуласымен танысады,біледі |
|
|
Күтілетін нәтижелер |
Арифметикалық прогрессия мен арифметикалық прогрессияның n-ші мүшесінің формуласы есептер шығаруда пайдаланады |
|
|
Тілдік мақсаттар |
Анықтамаларды, формулаларды айтады, түсіндіреді |
|
|
Оқылатын материал |
Арифметикалық прогрессия ,прогрессияның n-ші мүшесінің формуласы |
|
Жоспар
|
Сабақтын келісілген кестесі |
Жоспарланған іс-шаралар |
Ресурстар |
|
3-5 минут |
Сәлемдесу Оқушылардын зейіндерін сабаққа аудару Сергіту сәті |
|
|
Өткен сабақта:
|
Анықтама. Натурал аргументті функция сандар тізбегі, ал тізбекті құрайтын сандарды тізбектің мүшелері деп атайды. Тізбектің мүшелері сәйкес мүшелердің индексі (реттік нөмірі) көрсетілген әріппен белгіленеді. a1, a2, a3, …,an ,… сандар тізбегі әртүрлі тәсілдермен беріледі. І. Сандар тізбегінің баяндау тәсілмен берілуі. Баяндау тәсілінде сандар тізбегінің орналасу заңдылығы сөзбен беріледі. Мысалы: натурал сандар қатарының квадраттарынан тұратын тізбекті жаз. Шешуі. 1; 4 ; 9; 16; 25; 36; 49; ... ІІ.Сандар тізбегінің аналитикалық тәсілмен берілуі. Егер тізбек , n – ші мүшесінің формуласы арқылы берілсе, онда ол аналитикалық тәсіл болып табылады. Мысал. аn = 2n .берілген формула бойынша тізбектің кез келген мүшесін анықтауға болады. ІІІ. Сандар тізбегінің рекурренттік тәсілмен берілуі. Кейбір жағдайда тізбектің (n + 1) –ші мүшесі n – ші мүшесі арқылы есептелетін формула түрінде беріледі. Бұл жағдайда тізбектің бір немесе бірнеше алғашқы мүшелері қосымша беріледі. Тізбектің осылай берілуі рекурренттік тәсіл деп аталады. Мысалы. аn+1 = 4аn – 1 және а1 = 1. тізбектің бесінші мүшесін табу керек. ІV. Сандар тізбегінің графиктік тәсілмен берілуі. Оқулықтан 32-ші сурет. Енді тізбектің түрлеріне тоқталайық. Сантізбегі шекті және шексіз тізбекке бөлінеді. Тізбектің әрбір кейінгі мүшесінің алдыңғы мүшесіне қатысты орналасу ретіне қарай тізбек өспелі және кемімелі болып бөлінеді. Өспелі және кемімелі тізбектер бірсарынды тізбектер деп аталады. Бір ғана саннан құралған тізбек тұрақты тізбек деп аталады. |
|
|
Жаңа сабақта: |
Анықтама. Екінші мүшесінен бастап әрбір мүшесі алдыңғы мүшесіне қандайда бір тұрақты санды қосқанда шығатын сандар тізбегін арифметикалық прогрессия деп атайды. Қосылатын тұрақты сан, кез келген көршілес екі мүшесінің (алдыңғы және кейінгі ) айырымы екенін байқауға болады. Бұл санды арифметикалық прогрессияның айырымы деп атап, d әрпімен белгілейді.
бұл теңдік арифметикалық прогрессияның n-ші мүшесінің формуласы сандар тізбегі - натурал аргументті функция, ал арифметикалық прогрессия – сандар тізбегінің дербес түрі. арифметикалық прогрессия – натурал сандар жиынында берілген сызықты функция болып табылады. 1-ші теорема: a1, a2, a3, …,аn-1,an ,аn+1,... арифметикалық прогрессиясының екінші мүшесінен бастап әрбір мүшесі көршілес екі мүшенің арифметикалық ортасына тең. Яғни, кез келген n ≥ 2 үшін аn =(аn-1+ аn+1 )/2 |
|
|
Есептер шығару:
|
№165. 3; 7; 11; ... арифметикалық прогрессияның а) алтыншы; ә) отызыншы мүшесін табыңдар. а) а1 = 3; а2 = 7; а3 = 11 а6 = ? а6 =а1 + 5d d = a2 – а1 =7 – 3 = 4 а6 =3 + 5*4 = 23 ә) а1 = 3; а2 = 7; а3 = 11 а30 = ? а30 =а1 + 29d d = a2 – а1 =7 – 3 = 4 а30 =3 + 29*4 = 119 № 168. а) а1 = 17,6 ; d = – 0,4 {ап} арифметикалық прогрессияның жиырма бесінші мүшесін табыңдар. а25 = ? а25 =17,6 + 24*(-0,4) = 17,6 – 9,6 = 8 ә) с1 = -50 ; d = 1,2 {сп} арифметикалық прогрессияның қырық бесінші мүшесін табыңдар. с45 = ? а45 =-50 + 44*1,2 = -50 + 52,8 = 2,8
№169. а) 2 ; 4 ; 8 ; 16 ; 32 ; ... ә) 7 ; 7 ; 7 ; 7 ; 7 ; .... б) 1 ; 1/2 ; 1/3 ; 1/4 ; ... тізбектерінің қайсысы арифметикалық прогрессия болыптабылады ? а) және б) арифметикалық прогрессия болмайды, себебі арифметикалық прогрессияның қасиеттері орындалмайды. ә) болады , себебі (7+7)/2 = 7 №170. а) − 10,2 ; − 9,5 ; ... арифметикалық прогрессияның алғашқы оң таңбалы мүшесін табыңдар . d = − 9,5 – (− 10,2) = 0,7 − 10,2 + 0,7(n – 1) > 0 − 10,2 + 0,7n – 0,7 > 0 0,7n > 10,9 n > 109/7 демек 15 4/7 ден үлкен сан , 16 а16 = − 10,2 + 0,7(16 – 1) = 0,3 ә) 12,5 ; 11,2 ; ... арифметикалық прогрессияның алғашқы теріс таңбалы мүшесін табыңдар . d = 11,2 – 12,5 = − 1,3 12,5 – 1,3(n – 1) < 0 12,5 – 1,3n + 1,3 < 0 − 1,3n < − 13,8 n > − 138/(− 13) демек 10 8/13 тен үлкен сан, 11 а11 = 12,5 – 1,3(11 – 1) = − 0,5 |
|
|
Қорытынды |
Үйге тапсырма№171 есептер |
|
26.11.18________________
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Арифметикалық прогрессия. Арифметикалық прогрессияның n-ші мүшесінің формуласы
Арифметикалық прогрессия. Арифметикалық прогрессияның n-ші мүшесінің формуласы
|
Күні |
|
Мектеп: №51 орта мектеп №35 Арифметикалық прогрессия. Арифметикалық прогрессияның n-ші мүшесінің формуласы |
|
Сынып |
|
|
|
Оқушы саны |
|
|
|
Осы сабақта оқылатын оқу мақсаттары |
Арифметикалық прогрессия мен арифметикалық прогрессияның прогрессияның n-ші мүшесінің формуласымен танысады,біледі |
|
|
Күтілетін нәтижелер |
Арифметикалық прогрессия мен арифметикалық прогрессияның n-ші мүшесінің формуласы есептер шығаруда пайдаланады |
|
|
Тілдік мақсаттар |
Анықтамаларды, формулаларды айтады, түсіндіреді |
|
|
Оқылатын материал |
Арифметикалық прогрессия ,прогрессияның n-ші мүшесінің формуласы |
|
Жоспар
|
Сабақтын келісілген кестесі |
Жоспарланған іс-шаралар |
Ресурстар |
|
3-5 минут |
Сәлемдесу Оқушылардын зейіндерін сабаққа аудару Сергіту сәті |
|
|
Өткен сабақта:
|
Анықтама. Натурал аргументті функция сандар тізбегі, ал тізбекті құрайтын сандарды тізбектің мүшелері деп атайды. Тізбектің мүшелері сәйкес мүшелердің индексі (реттік нөмірі) көрсетілген әріппен белгіленеді. a1, a2, a3, …,an ,… сандар тізбегі әртүрлі тәсілдермен беріледі. І. Сандар тізбегінің баяндау тәсілмен берілуі. Баяндау тәсілінде сандар тізбегінің орналасу заңдылығы сөзбен беріледі. Мысалы: натурал сандар қатарының квадраттарынан тұратын тізбекті жаз. Шешуі. 1; 4 ; 9; 16; 25; 36; 49; ... ІІ.Сандар тізбегінің аналитикалық тәсілмен берілуі. Егер тізбек , n – ші мүшесінің формуласы арқылы берілсе, онда ол аналитикалық тәсіл болып табылады. Мысал. аn = 2n .берілген формула бойынша тізбектің кез келген мүшесін анықтауға болады. ІІІ. Сандар тізбегінің рекурренттік тәсілмен берілуі. Кейбір жағдайда тізбектің (n + 1) –ші мүшесі n – ші мүшесі арқылы есептелетін формула түрінде беріледі. Бұл жағдайда тізбектің бір немесе бірнеше алғашқы мүшелері қосымша беріледі. Тізбектің осылай берілуі рекурренттік тәсіл деп аталады. Мысалы. аn+1 = 4аn – 1 және а1 = 1. тізбектің бесінші мүшесін табу керек. ІV. Сандар тізбегінің графиктік тәсілмен берілуі. Оқулықтан 32-ші сурет. Енді тізбектің түрлеріне тоқталайық. Сантізбегі шекті және шексіз тізбекке бөлінеді. Тізбектің әрбір кейінгі мүшесінің алдыңғы мүшесіне қатысты орналасу ретіне қарай тізбек өспелі және кемімелі болып бөлінеді. Өспелі және кемімелі тізбектер бірсарынды тізбектер деп аталады. Бір ғана саннан құралған тізбек тұрақты тізбек деп аталады. |
|
|
Жаңа сабақта: |
Анықтама. Екінші мүшесінен бастап әрбір мүшесі алдыңғы мүшесіне қандайда бір тұрақты санды қосқанда шығатын сандар тізбегін арифметикалық прогрессия деп атайды. Қосылатын тұрақты сан, кез келген көршілес екі мүшесінің (алдыңғы және кейінгі ) айырымы екенін байқауға болады. Бұл санды арифметикалық прогрессияның айырымы деп атап, d әрпімен белгілейді.
бұл теңдік арифметикалық прогрессияның n-ші мүшесінің формуласы сандар тізбегі - натурал аргументті функция, ал арифметикалық прогрессия – сандар тізбегінің дербес түрі. арифметикалық прогрессия – натурал сандар жиынында берілген сызықты функция болып табылады. 1-ші теорема: a1, a2, a3, …,аn-1,an ,аn+1,... арифметикалық прогрессиясының екінші мүшесінен бастап әрбір мүшесі көршілес екі мүшенің арифметикалық ортасына тең. Яғни, кез келген n ≥ 2 үшін аn =(аn-1+ аn+1 )/2 |
|
|
Есептер шығару:
|
№165. 3; 7; 11; ... арифметикалық прогрессияның а) алтыншы; ә) отызыншы мүшесін табыңдар. а) а1 = 3; а2 = 7; а3 = 11 а6 = ? а6 =а1 + 5d d = a2 – а1 =7 – 3 = 4 а6 =3 + 5*4 = 23 ә) а1 = 3; а2 = 7; а3 = 11 а30 = ? а30 =а1 + 29d d = a2 – а1 =7 – 3 = 4 а30 =3 + 29*4 = 119 № 168. а) а1 = 17,6 ; d = – 0,4 {ап} арифметикалық прогрессияның жиырма бесінші мүшесін табыңдар. а25 = ? а25 =17,6 + 24*(-0,4) = 17,6 – 9,6 = 8 ә) с1 = -50 ; d = 1,2 {сп} арифметикалық прогрессияның қырық бесінші мүшесін табыңдар. с45 = ? а45 =-50 + 44*1,2 = -50 + 52,8 = 2,8
№169. а) 2 ; 4 ; 8 ; 16 ; 32 ; ... ә) 7 ; 7 ; 7 ; 7 ; 7 ; .... б) 1 ; 1/2 ; 1/3 ; 1/4 ; ... тізбектерінің қайсысы арифметикалық прогрессия болыптабылады ? а) және б) арифметикалық прогрессия болмайды, себебі арифметикалық прогрессияның қасиеттері орындалмайды. ә) болады , себебі (7+7)/2 = 7 №170. а) − 10,2 ; − 9,5 ; ... арифметикалық прогрессияның алғашқы оң таңбалы мүшесін табыңдар . d = − 9,5 – (− 10,2) = 0,7 − 10,2 + 0,7(n – 1) > 0 − 10,2 + 0,7n – 0,7 > 0 0,7n > 10,9 n > 109/7 демек 15 4/7 ден үлкен сан , 16 а16 = − 10,2 + 0,7(16 – 1) = 0,3 ә) 12,5 ; 11,2 ; ... арифметикалық прогрессияның алғашқы теріс таңбалы мүшесін табыңдар . d = 11,2 – 12,5 = − 1,3 12,5 – 1,3(n – 1) < 0 12,5 – 1,3n + 1,3 < 0 − 1,3n < − 13,8 n > − 138/(− 13) демек 10 8/13 тен үлкен сан, 11 а11 = 12,5 – 1,3(11 – 1) = − 0,5 |
|
|
Қорытынды |
Үйге тапсырма№171 есептер |
|
26.11.18________________

шағым қалдыра аласыз