
Ф-БЕ-06/9
ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ ОҚУ-АҒАРТУ МИНИСТРЛІГІ
ШЫМКЕНТ ҚАЛАСЫНЫҢ БІЛІМ БАСҚАРМАСЫ
ЖОЛ – КӨЛІК КОЛЛЕДЖІ
ӘДІСТЕМЕЛІК ТАЛДАУ
Ашық сабақ
Орындаған: Кожаева А.
Жалпыбілім және жалпы-
кәсіптік пәндер циклдік
комиссиясында қаралған.
Хаттама №____ «____» _____2025ж.
ЦК төрағасы: ________ Н.Сакбаева
Шымкент 2025ж.
Сабақтың тақырыбы: . Анықталған интегралдың көмегімен жазық фигуралардың ауданын есептеу
Сабақтың мақсаты мен міндеттері:
-Анықталған интегралдың геометриялық мағынасын түсіндіру
- Жазық фигура мен анықталған интеграл арасындағы байланысты ашу;
- Екі функция арасындағы аудан формуласын меңгерту және оларды есептер шығаруда қолдану;
-жасанды интеллектті тиімді пайдалануға баулу.
Күтілетін нәтижелер:
- Білім алушылар анықталған интегралдың аудан табудағы қолданылуын түсінеді; белгілі аралықтағы функция аудандарын есептей алады;Интегралдау нәтижесін практикалық есептерге қолдана біледі.
Сабақтың түрі: аралас сабақ
Сабақтың әдісі: тест тапсырмалары, талдау, іздену, кері байланыс.
Пән аралық байланыс: тарих, сызу, геометрия,физика
Қажетті ресурстар: тақырыптық плакат пен слайдтар, электронды оқулық, үлестірме материалдары,электронды оқулық.
Сабақтың барысы:
І. Ұйымдастыру кезеңі:
1. Сәлемдесу, журнал бойынша түгелдеу;
2. Сабаққа даярлықтарын тексеру;
3. Дәрісхана тазалығына назар аудару.
Психологиялық дайындық
1.Ынтымақтастық атмосферасы.

ІІ. Үй тапсырмасын сұрау
Өткен тақырыпқа шолу :
«Миға шабуыл » әдісі (Слайд 4-5) Жасанды интеллект платформасын қолдану арқылы.
-
Анықталған интеграл дегеніміз не ?
Жауап:Анықталған интеграл-функцияның белгілі бір аралықтағы қисық астындағы ауданын табуға арналған амал.
2.Интегралдың геометриялық мағынасы?
Жауап:Интеграл қисық пен ось арасындағы ауданның шамасын көрсетеді
3.Интегралдың төменгі және жоғарғы шектері нені білдіреді?
Жауап:Төменгі шек – есептеу басталатын нүкте(а),жоғарғы шек- есептеу аяқталатын нүкте (в)
4.Аудан теріс бола ма?
Аудан теріс болмайды,бірақ функция теріс болса,интеграл мәні теріс шығуы мүмкін.Сондықтан ауданды модульмен аламыз.
5.Қисықтар қиылысқан нүктелер не үшін қажет?
Жауап: олар интегралдың шектері
6.Анықталған интегралды қай формуламен есептейді?
Жауап:Ньютон-Лейбниц формуласымен
7.қисық сызықты трапеция дегеніміз не?
Жауап:Жоғарыдан функциямен,екі жағы түзулермен шектелген фигураны айтады.
ІІІ. Жаңа тақырыпты түсіндіру:
Барлық студенттер «Болжау» әдісі арқылы, көрсетілім материалдарын тамашалап, сабақтың тақырыбын табады.
1.Анықталған интегралдың геометриялық мағынасы.
 анықталған интегралы жоғарыдан
f(x) функциясының графигімен, төменгі жағынан Ox осіне
тиісті
анықталған интегралы жоғарыдан
f(x) функциясының графигімен, төменгі жағынан Ox осіне
тиісті  кесіндісімен, ал екі
жағынан x=a және x=b түзулерімен шектелген қисықсызықты трапецияның
ауданын беретіні белгілі.
кесіндісімен, ал екі
жағынан x=a және x=b түзулерімен шектелген қисықсызықты трапецияның
ауданын беретіні белгілі.
Кейбір жағдайларда жоғарыдан да, төменнен де әртүрлі функциялардың графиктерімен (әртүрлі қисықтармен) шектелген жазық фигураның ауданын табуға тура келеді (18-сурет).
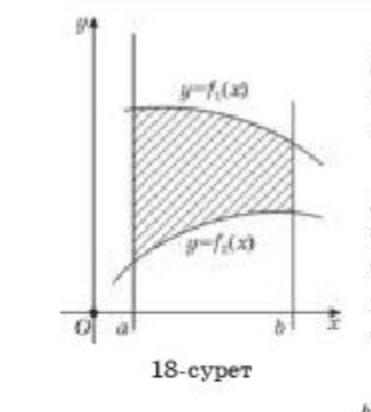
18-суретте кескіленген жазық
кескінделген жазық фигураның ауданын есептеу үшін
жоғарыдан  функциясының графигімен шектелген қисықсызықты трапецияның
ауданынан төменнен
функциясының графигімен шектелген қисықсызықты трапецияның
ауданынан төменнен  функциясының графигімен шектелген қисықсызықты трапецияның
ауданын азайту керек.
функциясының графигімен шектелген қисықсызықты трапецияның
ауданын азайту керек.
Сонда ізделінді ауданынды былай табамыз:

Немесе
 (1)
(1)
Кейбір дербес жағдайларда Ох осіне параллель у=с және у=d түзулерімен, х=0 түзуі және бір бүйір жағынан қисықпен (x=?(y) функциясының графигімен) шектелген фигуралардың ауданын есептеу қажет болады
(19-сурет)
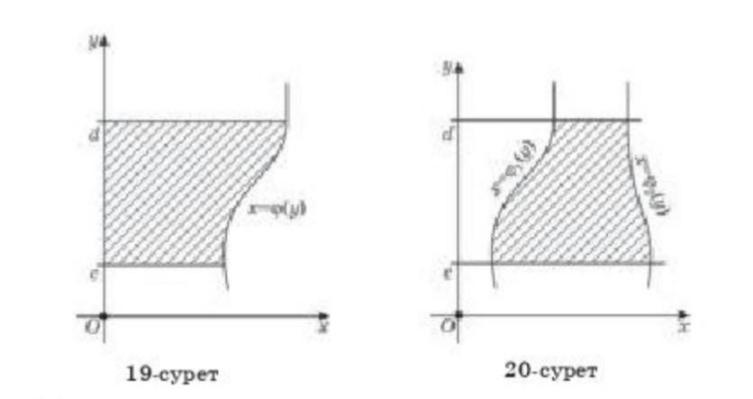
Мысал
-
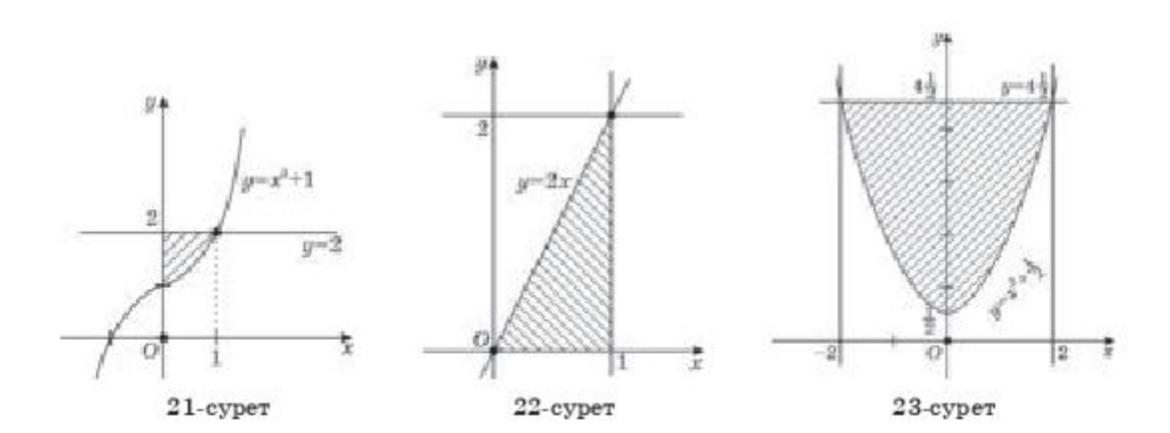
 қисығымен, у=2 түзуімен және
және Оу осімен шектелген фигураның ауданын табайық
(21-сурет)
қисығымен, у=2 түзуімен және
және Оу осімен шектелген фигураның ауданын табайық
(21-сурет)
Шешуі. 21-суретте берілген жазық фигураның ауданын (1)-формула бойынша есептейміз:

Жауабы:
 кв.
бірл.
кв.
бірл.
-
y=2x, x=1 түзулерімен және Ox осімен шектелген фигураның ауданын есептейік (22-сурет).
Шешуі. 22–суретте берілген
үшбұрыштың ауданын (1) формуланың көмегімен
табамыз:  .
.
Тура осындай қорытындыны
тікбұрышты үшбұрыштың ауданын есептеу
формуласы  арқылы да алуға болады.
Бұл жағдайда a=1, b=2.
Демек,
арқылы да алуға болады.
Бұл жағдайда a=1, b=2.
Демек,

Жауабы: 1 кв. бірл.
2.Екі функция арасындағы
аудан.  интегралы түрінде
берілген функцияның графигімен және
интегралы түрінде
берілген функцияның графигімен және  түзуімен шектелген
фигураның ауданын табайық.
түзуімен шектелген
фигураның ауданын табайық.
Шешуі. Алдымен интегралды табамыз:

Сонымен , есепті
шығару  параболасы
және
параболасы
және  түзуімен шектелген
фигураның ауданын табуға әкеледі (23-сурет).
түзуімен шектелген
фигураның ауданын табуға әкеледі (23-сурет).
Алдымен интегралдау шектерін
табайық. Ол үшін  теңдеуін шешеміз.
Теңдеудің түбірлері
теңдеуін шешеміз.
Теңдеудің түбірлері  және
және 
23-суретте берілген жазық
фигура Оу осіне қарағанда симметриялы. Сондықтан қисықсызықты
трапецияның ауданын  кесіндісінде есептеп,
екіге көбейтсе жеткілікті.
кесіндісінде есептеп,
екіге көбейтсе жеткілікті.

Жауабы:
 кв.
бірл.
кв.
бірл.
Практикалық қолдану. Анықталған интеграл арқылы тек матнматикалық фигуралардың емес,физикалық шамалардың дааудандарын,көлемдерін және жұмыс мөлшерлерін анықтауға болады.

Жұптық жұмыс. «Кім жылдам?» әдісі. Әр жұп бір-бірінің шешкен есебін тексереді.(20 минут)
№79 а) есепті бірінші топ ә) есепті екінші топ оқушылары шешеді .
Штрихталған фигураның ауданын табыңдар:


Білімді бекіту. «Есеп білгеннің есесі түгел»әдісі
(15 минут)
Есепті шешпей жауапты бірден көрсетеді және сол жауапты не үшін, қандай белгілеріне қарап таңдағаны туралы пікірін ортаға салады.
-
Штрихталған фигураның ауданын табыңдар


Сабақта ең оңай және қызықты болған есепті таңдау
-
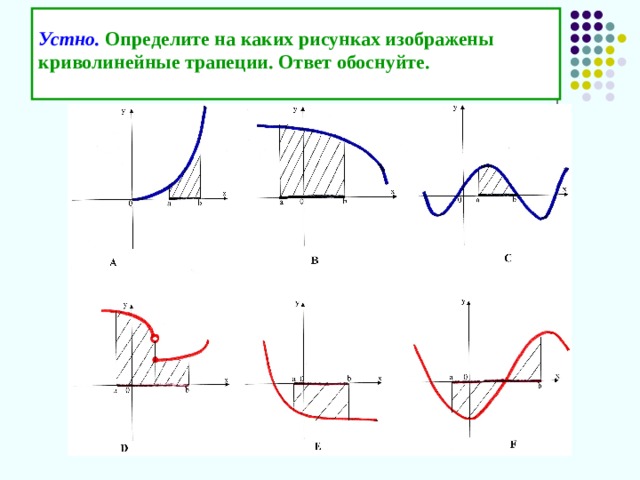
Ауызша қай суретте жазық фигураның ауданы көрсетілген? Жауаптарыңды негіздеңдер
![]()
![]() y
y

![]()
![]()
![]()
![]()
![]()
![]()
![]()
 y
y
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() o x
o
o x
o
ФС. Шығармашылық тапсырма: (10 минут) Өтілген тақырып бойынша теориялық, шығармашылық бағыттар бойынша тапсырмалар беріледі
Топтық, жұптық жұмыстар арқылы оқушылар өзара қолдау, көмек көрсетуді жүзеге асырады.
1)
 ; 2)
; 2) ;
3)
;
3) ;
4)
;
4)
 .
.
Жауабы:
1)
 2)
2) ;
3)
;
3) 4)
4) + cos x+
C.
+ cos x+
C.
1) 2)
2)  3)
3) 4)
4)
жауабы:
1) ;
2)
;
2)  ;
3)
;
3)  4)
4) 
1) +
5)dx; 2)
+
5)dx; 2) 3)
3) ;
4)
;
4)
жауабы: 1)
 2)
2)  3)
3)  4)
4)
ІV.Сабақты бекіту.
Тест. « Білімді бол » әдісі
|
Тапсырма |
Жауабы |
|
1)
Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
2) берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
3) Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
4) Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
Тапсырма |
Жауабы |
|
1) Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
2) Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
3) Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
4)
Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
Жауабы:
1)  кв.бірл.,
2)
кв.бірл.,
2) кв.бірл.,
3)
кв.бірл.,
3) кв.бірл.,
4)
кв.бірл.,
4)  кв.бірл.
кв.бірл.
V. Сабақты қорытындылау. Оқушылар стикерлерге өз ойларын қалдырып жазып қалдырып кетеді. Мен түсіндім… Мен білемін… Мен үшін әлі қиын… Әсіресе маған ұнағаны…
Жалпыұлттық идеяны өміршең ететін - Елдің бірлігі. Ауызбіршілік қашқан, алауыздық тасыған жерде ешқашан да жалпыұлттық идеялар жүзеге асқан емес. Қазақстанның шыққан шыңы мен бағындырған биіктерінің ең басты себебі - бірлік, берекесі. Біз тұрақтылықты бағалай білгеніміздің арқасында бүгінгі табыстарға жеттік. Ешкімді кемсітпей, ешкімнің тілі мен ділін мансұқтамай, барлық азаматтарға тең мүмкіндік беру арқылы тұрақтылықты нығайтып келеміз. Біздің кейінгі ұрпаққа аманаттар ең басты байлығымыз
- Ел бірлігі болуы керек. Осынау жалпыұлттық құндылықты біз әрбір жастың бойына сіңіре білуге тиіспіз», - деді Мемлекет басшысы.
1) 2)
2) 
3)
 +
sinx)dx; 4)
+
sinx)dx; 4)

Жауаптары:
1)  2) – 3 cosx
+
2) – 3 cosx
+  3)
3)  4) 5sinx
+
4) 5sinx
+ 
Еліңнің ұлы болсаң, еліңе жаның ашыса, азаматтық намысың болса, қазақтың ұлттық жалғыз мемлекетінің нығайып-көркеюі жолында жан теріңді сығып жүріп білім алып, еңбек ет. Жердің де, елдің де иесі өзің екендігін ұмытпа.
Рефлексия
«Синквейн» стратегиясы бойынша рефлексия өткізу. Оқушылар тақырыпқа байланысты:
-1-ші жол – бір сөз, тақырыптың аты, көп жағдайда кездесетін зат есім;
— 2-ші жол – екі сөз, сын есімдер
— 3-ші жол – үш сөз, етістік;
— 4-ші жол – төрт сөзден құрастырылған сөйлем
— 5-ші жол – синоним жазады.
VI.Оқушыларды бағалау (түсінік бере отырып)
VIІ.Үйге тапсырма:
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Ашық сабақ "Анықталған интегралдың көмегімен жазық фигуралардың ауданын есептеу
Ашық сабақ "Анықталған интегралдың көмегімен жазық фигуралардың ауданын есептеу
Ф-БЕ-06/9
ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ ОҚУ-АҒАРТУ МИНИСТРЛІГІ
ШЫМКЕНТ ҚАЛАСЫНЫҢ БІЛІМ БАСҚАРМАСЫ
ЖОЛ – КӨЛІК КОЛЛЕДЖІ
ӘДІСТЕМЕЛІК ТАЛДАУ
Ашық сабақ
Орындаған: Кожаева А.
Жалпыбілім және жалпы-
кәсіптік пәндер циклдік
комиссиясында қаралған.
Хаттама №____ «____» _____2025ж.
ЦК төрағасы: ________ Н.Сакбаева
Шымкент 2025ж.
Сабақтың тақырыбы: . Анықталған интегралдың көмегімен жазық фигуралардың ауданын есептеу
Сабақтың мақсаты мен міндеттері:
-Анықталған интегралдың геометриялық мағынасын түсіндіру
- Жазық фигура мен анықталған интеграл арасындағы байланысты ашу;
- Екі функция арасындағы аудан формуласын меңгерту және оларды есептер шығаруда қолдану;
-жасанды интеллектті тиімді пайдалануға баулу.
Күтілетін нәтижелер:
- Білім алушылар анықталған интегралдың аудан табудағы қолданылуын түсінеді; белгілі аралықтағы функция аудандарын есептей алады;Интегралдау нәтижесін практикалық есептерге қолдана біледі.
Сабақтың түрі: аралас сабақ
Сабақтың әдісі: тест тапсырмалары, талдау, іздену, кері байланыс.
Пән аралық байланыс: тарих, сызу, геометрия,физика
Қажетті ресурстар: тақырыптық плакат пен слайдтар, электронды оқулық, үлестірме материалдары,электронды оқулық.
Сабақтың барысы:
І. Ұйымдастыру кезеңі:
1. Сәлемдесу, журнал бойынша түгелдеу;
2. Сабаққа даярлықтарын тексеру;
3. Дәрісхана тазалығына назар аудару.
Психологиялық дайындық
1.Ынтымақтастық атмосферасы.

ІІ. Үй тапсырмасын сұрау
Өткен тақырыпқа шолу :
«Миға шабуыл » әдісі (Слайд 4-5) Жасанды интеллект платформасын қолдану арқылы.
-
Анықталған интеграл дегеніміз не ?
Жауап:Анықталған интеграл-функцияның белгілі бір аралықтағы қисық астындағы ауданын табуға арналған амал.
2.Интегралдың геометриялық мағынасы?
Жауап:Интеграл қисық пен ось арасындағы ауданның шамасын көрсетеді
3.Интегралдың төменгі және жоғарғы шектері нені білдіреді?
Жауап:Төменгі шек – есептеу басталатын нүкте(а),жоғарғы шек- есептеу аяқталатын нүкте (в)
4.Аудан теріс бола ма?
Аудан теріс болмайды,бірақ функция теріс болса,интеграл мәні теріс шығуы мүмкін.Сондықтан ауданды модульмен аламыз.
5.Қисықтар қиылысқан нүктелер не үшін қажет?
Жауап: олар интегралдың шектері
6.Анықталған интегралды қай формуламен есептейді?
Жауап:Ньютон-Лейбниц формуласымен
7.қисық сызықты трапеция дегеніміз не?
Жауап:Жоғарыдан функциямен,екі жағы түзулермен шектелген фигураны айтады.
ІІІ. Жаңа тақырыпты түсіндіру:
Барлық студенттер «Болжау» әдісі арқылы, көрсетілім материалдарын тамашалап, сабақтың тақырыбын табады.
1.Анықталған интегралдың геометриялық мағынасы.
 анықталған интегралы жоғарыдан
f(x) функциясының графигімен, төменгі жағынан Ox осіне
тиісті
анықталған интегралы жоғарыдан
f(x) функциясының графигімен, төменгі жағынан Ox осіне
тиісті  кесіндісімен, ал екі
жағынан x=a және x=b түзулерімен шектелген қисықсызықты трапецияның
ауданын беретіні белгілі.
кесіндісімен, ал екі
жағынан x=a және x=b түзулерімен шектелген қисықсызықты трапецияның
ауданын беретіні белгілі.
Кейбір жағдайларда жоғарыдан да, төменнен де әртүрлі функциялардың графиктерімен (әртүрлі қисықтармен) шектелген жазық фигураның ауданын табуға тура келеді (18-сурет).

18-суретте кескіленген жазық
кескінделген жазық фигураның ауданын есептеу үшін
жоғарыдан  функциясының графигімен шектелген қисықсызықты трапецияның
ауданынан төменнен
функциясының графигімен шектелген қисықсызықты трапецияның
ауданынан төменнен  функциясының графигімен шектелген қисықсызықты трапецияның
ауданын азайту керек.
функциясының графигімен шектелген қисықсызықты трапецияның
ауданын азайту керек.
Сонда ізделінді ауданынды былай табамыз:

Немесе
 (1)
(1)
Кейбір дербес жағдайларда Ох осіне параллель у=с және у=d түзулерімен, х=0 түзуі және бір бүйір жағынан қисықпен (x=?(y) функциясының графигімен) шектелген фигуралардың ауданын есептеу қажет болады
(19-сурет)

Мысал
-
 қисығымен, у=2 түзуімен және
және Оу осімен шектелген фигураның ауданын табайық
(21-сурет)
қисығымен, у=2 түзуімен және
және Оу осімен шектелген фигураның ауданын табайық
(21-сурет)
Шешуі. 21-суретте берілген жазық фигураның ауданын (1)-формула бойынша есептейміз:

Жауабы:
 кв.
бірл.
кв.
бірл.
-
y=2x, x=1 түзулерімен және Ox осімен шектелген фигураның ауданын есептейік (22-сурет).
Шешуі. 22–суретте берілген
үшбұрыштың ауданын (1) формуланың көмегімен
табамыз:  .
.
Тура осындай қорытындыны
тікбұрышты үшбұрыштың ауданын есептеу
формуласы  арқылы да алуға болады.
Бұл жағдайда a=1, b=2.
Демек,
арқылы да алуға болады.
Бұл жағдайда a=1, b=2.
Демек,

Жауабы: 1 кв. бірл.

2.Екі функция арасындағы
аудан.  интегралы түрінде
берілген функцияның графигімен және
интегралы түрінде
берілген функцияның графигімен және  түзуімен шектелген
фигураның ауданын табайық.
түзуімен шектелген
фигураның ауданын табайық.
Шешуі. Алдымен интегралды табамыз:

Сонымен , есепті
шығару  параболасы
және
параболасы
және  түзуімен шектелген
фигураның ауданын табуға әкеледі (23-сурет).
түзуімен шектелген
фигураның ауданын табуға әкеледі (23-сурет).
Алдымен интегралдау шектерін
табайық. Ол үшін  теңдеуін шешеміз.
Теңдеудің түбірлері
теңдеуін шешеміз.
Теңдеудің түбірлері  және
және 
23-суретте берілген жазық
фигура Оу осіне қарағанда симметриялы. Сондықтан қисықсызықты
трапецияның ауданын  кесіндісінде есептеп,
екіге көбейтсе жеткілікті.
кесіндісінде есептеп,
екіге көбейтсе жеткілікті.

Жауабы:
 кв.
бірл.
кв.
бірл.
Практикалық қолдану. Анықталған интеграл арқылы тек матнматикалық фигуралардың емес,физикалық шамалардың дааудандарын,көлемдерін және жұмыс мөлшерлерін анықтауға болады.


Жұптық жұмыс. «Кім жылдам?» әдісі. Әр жұп бір-бірінің шешкен есебін тексереді.(20 минут)
№79 а) есепті бірінші топ ә) есепті екінші топ оқушылары шешеді .
Штрихталған фигураның ауданын табыңдар:


Білімді бекіту. «Есеп білгеннің есесі түгел»әдісі
(15 минут)
Есепті шешпей жауапты бірден көрсетеді және сол жауапты не үшін, қандай белгілеріне қарап таңдағаны туралы пікірін ортаға салады.
-
Штрихталған фигураның ауданын табыңдар


Сабақта ең оңай және қызықты болған есепті таңдау
-
Ауызша қай суретте жазық фигураның ауданы көрсетілген? Жауаптарыңды негіздеңдер

![]()
![]() y
y

![]()
![]()
![]()
![]()
![]()
![]()
![]()
 y
y
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() o x
o
o x
o
ФС. Шығармашылық тапсырма: (10 минут) Өтілген тақырып бойынша теориялық, шығармашылық бағыттар бойынша тапсырмалар беріледі
Топтық, жұптық жұмыстар арқылы оқушылар өзара қолдау, көмек көрсетуді жүзеге асырады.
1)
 ; 2)
; 2) ;
3)
;
3) ;
4)
;
4)
 .
.
Жауабы:
1)
 2)
2) ;
3)
;
3) 4)
4) + cos x+
C.
+ cos x+
C.
1) 2)
2)  3)
3) 4)
4)
жауабы:
1) ;
2)
;
2)  ;
3)
;
3)  4)
4) 
1) +
5)dx; 2)
+
5)dx; 2) 3)
3) ;
4)
;
4)
жауабы: 1)
 2)
2)  3)
3)  4)
4)
ІV.Сабақты бекіту.
Тест. « Білімді бол » әдісі
|
Тапсырма |
Жауабы |
|
1)
Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
2) берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
3) Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
4) Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
Тапсырма |
Жауабы |
|
1) Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
2) Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
3) Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
|
4)
Берілген қисықтармен шектелген
қисықсызықты трапецияның ауданын табындар:
y
= |
|
Жауабы:
1)  кв.бірл.,
2)
кв.бірл.,
2) кв.бірл.,
3)
кв.бірл.,
3) кв.бірл.,
4)
кв.бірл.,
4)  кв.бірл.
кв.бірл.
V. Сабақты қорытындылау. Оқушылар стикерлерге өз ойларын қалдырып жазып қалдырып кетеді. Мен түсіндім… Мен білемін… Мен үшін әлі қиын… Әсіресе маған ұнағаны…
Жалпыұлттық идеяны өміршең ететін - Елдің бірлігі. Ауызбіршілік қашқан, алауыздық тасыған жерде ешқашан да жалпыұлттық идеялар жүзеге асқан емес. Қазақстанның шыққан шыңы мен бағындырған биіктерінің ең басты себебі - бірлік, берекесі. Біз тұрақтылықты бағалай білгеніміздің арқасында бүгінгі табыстарға жеттік. Ешкімді кемсітпей, ешкімнің тілі мен ділін мансұқтамай, барлық азаматтарға тең мүмкіндік беру арқылы тұрақтылықты нығайтып келеміз. Біздің кейінгі ұрпаққа аманаттар ең басты байлығымыз
- Ел бірлігі болуы керек. Осынау жалпыұлттық құндылықты біз әрбір жастың бойына сіңіре білуге тиіспіз», - деді Мемлекет басшысы.
1) 2)
2) 
3)
 +
sinx)dx; 4)
+
sinx)dx; 4)

Жауаптары:
1)  2) – 3 cosx
+
2) – 3 cosx
+  3)
3)  4) 5sinx
+
4) 5sinx
+ 
Еліңнің ұлы болсаң, еліңе жаның ашыса, азаматтық намысың болса, қазақтың ұлттық жалғыз мемлекетінің нығайып-көркеюі жолында жан теріңді сығып жүріп білім алып, еңбек ет. Жердің де, елдің де иесі өзің екендігін ұмытпа.
Рефлексия
«Синквейн» стратегиясы бойынша рефлексия өткізу. Оқушылар тақырыпқа байланысты:
-1-ші жол – бір сөз, тақырыптың аты, көп жағдайда кездесетін зат есім;
— 2-ші жол – екі сөз, сын есімдер
— 3-ші жол – үш сөз, етістік;
— 4-ші жол – төрт сөзден құрастырылған сөйлем
— 5-ші жол – синоним жазады.
VI.Оқушыларды бағалау (түсінік бере отырып)

VIІ.Үйге тапсырма:

шағым қалдыра аласыз



















