
Сабақ жоспары
Күні: 11.02.16ж
|
Сабақ жүргізген мұғалімнің аты-жөні |
Акенева Асем Жумагалиевна |
9 сынып |
Ж.Болғанбаев атындағы Самар орта мектебі |
|
|||||
|
Сабақтың атауы |
Дұрыс көпбұрыштарды салу |
|
|||||||
|
Сілтеме |
1.Мұғалімдерге арналған нұсқаулық 2.Оқыту әдістемесі 3.Оқулық, геометрия 9 сынып А.В. Погорелов |
|
|||||||
|
Жалпы мақсаты |
«Көпбұрыштар» тарауынан оқушылардың алған білімдерін тиянақтап, пысықтау, оларды салу жұмыстары кезінде пайдалана білуге үйрету. |
|
|||||||
|
Міндеттер |
1. Дұрыс көпбұрыштарды салу әдіс – тәсілін меңгереді; 2. Теориялық білімін практикада қолдана білу
және білім – білік дағдыларын қалыптастыру, оқушының танымын
кеңейту, ойлау қабілетін арттыру |
|
|||||||
|
Мұғалім үшін оқу нәтижелері |
|
|
|||||||
|
Күтілетін нәтиже |
-Өзінің құнды пікірін айтуға, барлық пікірдің құнды екенін үйренеді. - Қатынастың негізгі қасиетін меңгеру; -Екі санның қатынасын процент түрінде көрсетуге болады; -Бөлшек сандарды натурал сандардың қатынасы түрінде жазуға болады; -Алған теориялық білімдерін есеп қолдана білуге дағдыландыру; – пікір алмасуға үйренеді . -жұппен,топпен жұмыс жасай отырып, балалар сыни ойлауға қалыптасады. |
|
|||||||
|
Туындайтын идеялар |
Қатынасқа берілген есептерді практикалық жұмыс арқылы топпен, жұппен жұмыс жасау барысында талқылап, шығарып оқушылардың білімдері толыға түседі |
|
|||||||
|
Тапсырмалар |
І: Ұйымдастыру кезеңі 1. Қайталау сұрақтары.(Білу) 2. Топтық жұмыс .(Түсіну) ІІ: 3.Жұппен жұмыс. (Қолдану) ІІІ: 4. Жеке жұмыс. Постер жасау(Талдау) 5. Өздік жұмыс. Математикалық диктант (Жинақтау) 6.Тақырып бойынша сұраққа жауап беру. 7.Үйге тапсырма 8.Бағалау. Рефлексия(Бағалау) 9.Сабақты қорытындылау. |
-Топқа бөлінеді. -пысықтау сұрақтары бойынша сұрақтарға жауап береді. -топпен жұмыс -деңгейлік тапсырма -өздерін бағалау, бірін-бірі бағалау - рефлексия. |
|
||||||
|
Сабақтың түрі, әдіс тәсілдері |
АКТ, топпен жұмыс, оқыту мен оқудағы жаңа тәсілдер,диалогтық оқыту, Блум таксонономиясы, сұрақ-жауап, көшбасшылық, СТО, оқыту үшін бағалаужәне оқуды бағалау, жас ерекшеліктеріне байланысты тапсырмалар, талантты және дарынды балаларды оқыту. |
|
|||||||
|
Сабақтың көрнекілігі |
проектор, слайдтар, топтарға арналған тапсырма парақтары, үлестірме тапсырмалар, стикерлер,түрлі түсті кесінділер. |
|
|||||||
|
|
Сабақтың барысы |
||||||||
|
І.Оқушыларға психологиялық ахуал туғызу |
2. Мұғалімнің іс-әрекеті |
Оқушының іс-әрекеті |
|||||||
|
АКТ Оқытуды басқару және көшбасшылық |
Сыныпты топқа бөлу: «Шаттық шеңберінде» тұрады. /Топ басшыларын өздері тағайындайды, бағалау парағы таратылады./ Үй тапсырмасын сұрау № Қайталау сұрақтары 1.Дұрыс көпбұрыш дегеніміз не және ол қандай формуламен беріледі. Анықтама: Барлық қабырғалары және барлық бұрыштары тең дөңес көпбұрышты дұрыс көпбұрыш деп атайды. 2. Дұрыс көпбұрыштың ішкі бұрыштарының қосындысы неге тең ? /180˚(n – 2) / 3. Дұрыс көпбұрыштың әбір бұрышы қандай формуламен анықталады?
4. Көпбұрыштың сыртқы бұрыштарының қосындысы неге тең ? /360˚ / 5
6. Центрлік бұрыш дегеніміз не? Центрлік бұрыш деп төбесі шеңбердің центрінде жататын жазық бұрышты атайды. |
Топтарға бөлу Сұрақтарға жауап береді |
|||||||
|
Оқыту мен оқудағы жаңа тәсілдер |
ТҮСІНУ-3мин Диалогтық оқыту 2-тапсырма: Топпен жұмыс . Алгоритм бойынша тақырыпты өз беттерімен игеру. Алгоритм бойынша шеңберге іштей дұрыс көпбұрыш салу. Шеңберге іштей сызылған дұрыс көпбұрыш салу үшін, оның центрлік бұрышын салу жеткілікті. Дұрыс алтыбұрышты салу. 1. Центрлік бұрышын есепте. 2.Шеңбер бойынан қалауыңша А1 төбесін ал. 3.Осы нүктеден шеңбердің радиусына тең радиуспен белгі сал. Ол нүкте А2 төбесі. 4.Қалған төбелерді осыған ұқсас түрде сал. 5. А3, А4, А5, А6 төбелерін белгіле. 6.Төбелерді кесінділермен қос. Сырттай сызылған дұрыс алтыбұрышты салу үшін: 1. Іштей сызылған дұрыс көпбұрыштың төбелерінен шеңберге жанамалар жүргіз. 2.Жанмалардың қиылысу нүктелерін белгіле. Іштей сызылған дұрыс көпбұрыштың төбелерінен өтетін жанамалар сырттай сызылған дұрыс көпбұрыштың төбелері. |
Жеке жауап береді Әр оқушы өзіне берілген тақырыпты игеруге арналған тапсырмаға ұқсас тапсырмаларын орындайды. Жұпта талдайды, дұрыс не бұрыс екендігін айтады. Есептейді Дұрыс п-бұрышты салу үшін: 1.Шеңберде 3600/n-ге тең центрлік бұрышты санап алу 2.Шеңбер бойындағы нүктелерді белгілеу 3.Нүктелерді біріктіру Дұрыс 2n-бұрышты салу үшін: 1) Центрлік бұрыштардың биссектрисаны жүргізіп шеңбер бойында қиылысу нүктесін белгілеу 2) Шыққан нүктелерді n-бұрыштың төбелерімен біріктіру |
|||||||
|
Сыни ойлауын дамыту Оқыту үшін бағалау |
- ҚОЛДАНУ 7мин Сыни ойлауын дамыту Жұппен жұмыс №31 А.В. Погорелов. Шеңберге сырттай сегізбұрыш салыңдар |
Балалар тақтаға қарап назар аударып отырады. Постер жасайды. Бұл мәтінді тақтадан балалар кезектесіп оқып береді. Есептер шығарады. |
|||||||
|
Жас ерекшеліктеріне сай деңгейлік тапсырмалар |
ТАЛДАУ Дарындылық, жас ерекшеліктеріне сай деңгейлік тапсырмалар Жеке жұмыс А – деңгей Шеңберге іштей, сырттай дұрыс ұшбұрышты салу В – деңгей Шеңберге іштей, сырттай дұрыс төртбұрышты салу С – деңгей Шеңберге іштей, сырттай дұрыс бесбұрыш салу Алгоритм:1.AK⟘MN диаметрін жүргіз. 2.NL=LO 3. ⍵(L,A) шеңберін жүргіз 4.
⍵(L,A) 5.AF берілген шеңберге іштей сызылған бесбұрыштың қабырғасының ұзындығы 6.Осы ұзындықпен А нүктесінен бастап төрт рет өлшеп сал. Постер жасау Тақырыптың күнделікті өмірде қолданылуы ЖИНАҚТАУ-6мин Оқушыларға сұрақ қою және олардың жауаптарына қарай әрекет ету Оқушылар сабақ кезінде тапсырмалар орындайы. Өздік жұмыс І- вариант 1.Дұрыс 12-бұрыштың бұрыштарын тап. 2. Әрбір
бұрышы ІІ- вариант 1.Дұрыс 20-бұрыштың бұрыштарын тап. 2. Әрбір
бұрышы Математикалық диктант. 1.Кез келген дұрыс көпбұрышты тек сызғышпен салуға болады. /жоқ/ 2. Кез келген дөңес көпбұрыштың бұрыштары мен қабырғалары тең болады./Иә/ 3.Дұрыс көпбұрышты қағаз бүктеу арқылы кесіп алуға болады/ Иә/ 4.Дұрыс көпбұрыштың центрлік бұрышы 90°-қа тең болса, оның қабырғалар саны 4 /Иә/ 5.Дұрыс көпбұрыштың қабырғалар саны 8-ге тең болса, онда ол трапеция болады. /жоқ, сегіз қабырғалы болады/ БАҒАЛАУ — Шеңбер не үшін керек? Дұрыс көпбұрыштар салу үшін грек математигі Евклид 257 көпбұрыш салуды көрсеткен. Жетібұрыш пен тоғызбұрыш салынбайтынын дәлелдей алған жоқ. К.Гаусс неміс математигі жетібұрыш пен тоғызбұрыш салынбайтынын дәлелдеген. Рефлексия стикерлерге жазу. Кері байланыс Шығу парағын кубтың қырларына жапсырады, ондағы молекулалар топтасқан. Оқушылар оз ойларын оқып, жапсырады. Топ жетекшілері бағалау парғының қорытынды бағасын айтады. Үй жұмысы.Деңгейлік тапсырмалар. Тұсаукесер 11 Қорытынды жасау. Стикерлемен бағалау. |
Дарынды оқушы орнында жұмыс жасайды.
Дәптерлеріне есеп шығарады. Есептер шығарады. 1-жұп оқушылары кезектесіп сұрақтарды оқып, жауап береді. 2-жұп оқушылары кезектесіп сұрақтарды оқып, жауап береді. 3-жұп оқушылары кезектесіп сұрақтарды оқып, жауап береді. |
|||||||
|
Талантты және дарынды балаларды оқыту |
|||||||||
|
|
Бекіту 5 мин |
||||||||
|
|
3.Мұғалімнің іс-әрекеті |
Оқушының іс-әрекеті |
|||||||
|
|
Стикерге пікірлерін жазу. |
Оқушылар кестені толтырады. |
|||||||
|
|
Бағалау 3мин |
||||||||
|
|
4.Мұғалімнің іс-әрекеті |
Оқушының іс-әрекеті |
|||||||
|
|
Жұптардың бағаларын талдау, қорытынды бағаны шығару. |
Жұптағы оқушылар бірін-бірі бағалау критерийлері бойынша бағалайды |
|||||||
|
|
Үйге тапсырма 30 секунд |
||||||||
|
|
5.Мұғалімнің іс-әрекеті |
Оқушының іс-әрекеті |
|||||||
|
|
Үйге тапсырма: 213 бет, № 30 Дұрыс 12 бұрыш салу. |
Берілген тапсырманы күнделікке жазып алу |
|||||||
|
|
Рефлексия 30 секунд |
||||||||
|
|
Оқушыларға смайликтер таратамын. |
Оқушылар өздеріне сай смайликтерді таңдап дайын плакатқа жапсырады. |
|||||||
Тема. Построение правильных многоугольников.
Цели урока. Научить учащихся строить правильные многоугольники с помощью циркуля и линейки, познакомить их с отдельными областями применения правильных многоугольников в жизни.
Оборудование. Модели правильных многоугольников, технические детали, рисунки паркетов, коврики из лоскутков ткани, циркуль, линейка, карандаш, бумага.
Ход урока.
I. Организационный момент
II. Актуализация знаний учащихся
– Ребята, где вы могли видеть правильные многоугольники? (Паркеты, узоры, технические детали – болты, гайки…).
Чтобы все это сделать, необходимо уметь строить правильные многоугольники. Для получения паркета или узора необходимы лекало или шаблон, а для технических деталей – чертеж. (Демонстрируются болт, гайка и соответствующий чертеж; узор, паркет и соответствующий шаблон). Для построения правильных многоугольников будем использовать связь с окружностью. Научимся рисовать орнаменты с помощью циркуля.
III. Повторение пройденного материала.
1. Теоретический опрос.
Какой многоугольник называется правильным? (Выпуклый многоугольник называется правильным, если все его углы равны и все его стороны равны) [1]
Какой треугольник является правильным? Почему? (Равносторонний т.к. все его стороны равны и все его углы).
Является ли правильным четырехугольником прямоугольник, ромб, квадрат? Почему? (Хотя в прямоугольнике все углы равны, он не является правильным т.к. не все его стороны равны т.е. одно из условий правильного многоугольника не выполняется;
в ромбе все стороны равны, но не все углы равны;
квадрат – правильный многоугольник, т.к. все его стороны равны, все его углы равны).
2. Работа в группах.
Учащиеся делятся на группы по 3 – 4 ученика в каждой и решают тесты в течение 3 – 5 минут.
Тест для самостоятельной работы.
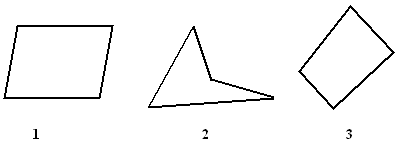
1. Какая из ломанных является многоугольником?
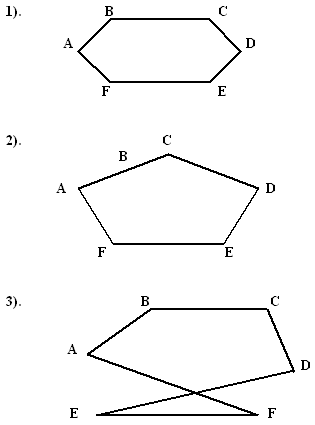
2.Какой многоугольник выпуклый?
3. Может ли пятиугольник иметь стороны длиной 3 см, 4 см, 8 см, 6см, 25 см?
1) да; 2) нет.
4. В правильном n-угольнике сумма внутренних углов равна 3600. Сколько сторон у этого многоугольника?
1) 4; 2) 3; 3) 5.
5. У правильного пятиугольника внешний угол равен:
1) 360; 2) 45 0; 3) 72 0.

2. Многоугольник является правильным, если все его ….
1) углы равны; 2) углы и стороны равны; 3) стороны равны.
IV. Объяснение новой темы.
– Ребята, где вы могли видеть правильные многоугольники? (Паркеты, узоры, технические детали – болты, гайки…).
Чтобы все это сделать, необходимо уметь строить правильные многоугольники. Для получения паркета или узора необходимы лекало или шаблон, а для технических деталей – чертеж. (Демонстрируются болт, гайка и соответствующий чертеж; узор, паркет и соответствующий шаблон).
Для построения правильных многоугольников будем использовать связь с окружностью.
Практическая работа.
Учащиеся выполняют работу на альбомных листах с помощью циркуля, линейки и карандаша.
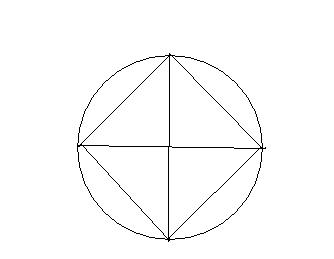
Проведите в окружности два перпендикулярных диаметра и соедините отрезками их концы. Докажите, что полученный четырехугольник правильный.
А теперь построим правильный пятиугольник.
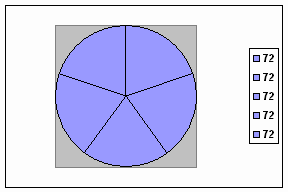
Радиусами ОА, ОВ, ОС, ОД, и ОЕ. Разобьем круг на пять сектаров с центральным углом, равным 3600/5=720 и соединим последовательно точки А,В,С,Д,Е. Получим многоугольник АВСДЕ. Докажите, что полученный пятиугольник правильный.
Можно построить правильный пятиугольник и другим способом.
Для деления окружности на пять равных частей поступают так:
-
Делят радиус ОА пополам;
-
Из полученной точки В радиусом ВС делают засечку на горизонтальном диаметре (точка Д);
-
Пользуясь отрезком СД, как стороной правильного пятиугольника, размечают его вершины;
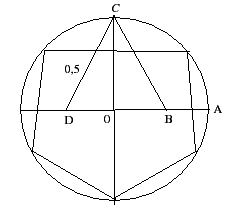
– Как связаны между собой радиус описанной окружности и сторона правильного шестиугольника? R = а.Поэтому для построения правильного шестиугольника в качестве вершины выберем произвольно точку окружности. Из нее, как из центра, циркулем сделаем засечки радиусом, равным радиусу окружности, – это остальные вершины. Все они последовательно соединяются отрезками.
Чтобы построить правильный вписанный треугольник, соединим через одну вершины правильного вписанного шестиугольника.
Зная как построить правильный n – угольник, легко можно построить 2n – угольник. (Проведя биссектрисы углов треугольника (?АОВ) рис 3. до пересечения с окружностью. Соединив эти точки на окружности получим 2n – угольник, из имеющегося n – угольника.
Разделив центральный угол пополам, получим сторону правильного десятиугольника.
Считалось, что если можно построить квадрат, правильный треугольник, пятиугольник, то легко построить правильный вписанный 2 n – угольник. И все. На этом ограничивались. Но в 1796 году немецкий математик Карл Гаусс еще юношей поразил весь математический мир разрешением проблемы построения правильного 17 –угольника. [2]
Этому открытию сам Гаусс придавал большое значение и даже завещал выгравировать на своем надгробии правильный 17-угольник, вписанный в круг. Хотя в современном мире компьютерной технике этим никого не удивишь.

V. Остановимся на отдельных областях применение правильных многоугольников.
Ребята, посмотрите на эти виды паркета. Какие они красивые. (Демонстрируются рисунки паркета, составленного из правильных многоугольников).
Где применить правильные многоугольники, человеку подсказка сама природа. Ребята, какими правильными многоугольниками можно заполнит плоскость так, чтобы не было пропусков, т.е. уложить их в виде паркета? Такими многоугольниками могут быть только правильные треугольники, квадраты или правильные шестиугольники. Ребята, вы все видели пчелиные соты. (Демонстрируются настоящие соты, если их нет, то рисунок). Из каких фигур они составлены? (Из правильных многоугольников).
Пчелы – удивительно творцы. Геометрические способности пчел проявляется при построение сот. Возникают вопросы: “Почему пчелы строят соты именно так? Почему они предпочли сеть правильных шестиугольников, а не правильных треугольников или квадратов, ведь их, казалось бы, гораздо проще сконструировать?”
Почему пчела выбрала правильный шестиугольник?
Во-первых, в каждой точке сходится не более трех шестиугольников. Во-вторых, при таком построение мало уходит воска. Поэтому, если мы хотим разбить поле на участки так, чтобы на ограждения пошло как можно меньше материала, то участкам нужно будет придавать форму правильных шестиугольников.
Подобные расчеты находят применение в обувной промышленности. Для изготовления обуви используют колодки определенных размеров. Для определения размера используют паркет, составленный из правильных шестиугольников.
В математике 6 является совершенном числом. Есть много примеров: в Древней Греции на 6 – м месте на званом перу возлежал самый уважаемый и самый знаменитый и почетный гость; в Древнем Вавилоне круг делили на 6 частей; в Библии утверждается, что мир создан за 6 дней. 6 – самое маленькое, самое первое совершенное число, не даром на него обратили внимание великие Пифагор и Евклид, Ферма и Эйлер.
Обратим внимание на один из видов народного ремесла. (Демонстрируются наволочки для диванных подушек). Этот древний вид искусства использовали разные народы. У тех, кто дома пользуется иголкой и ножницами, всегда остаются лоскутки тканей. Из них можно изготовить покрывала, наволочки, коврики. [3]
Предметы, сделанные своими руками, всегда принято использовать. В зависимости от вашей фантазии вы можете получить довольно оригинальные вещи.
Ребята, как вы думаете, в каких случаях и почему на практике чаще используют правильные многоугольники? (При изготовлении технических деталей, например, болтов, гаек, это удобно. А при составлении паркетов, узоров, это и красиво).
С помощью циркуля можно построить красивые узоры. Принципы построение узоров не сложны. Рисунки 1 – 7. [4]
Поэтому в качестве домашнего задания предлагаю вам:
-
Составить из правильных многоугольников рисунок красивого паркета или узора.
-
Решить задачу.
Для построенных правильных многоугольников вычислить длины сторон а3, а4, а5, а6, если R=4 см.
Цель: выработать у учащихся умение строить некоторые правильные многоугольники.
Ход урока
I. Проверка домашнего задания.
1. Проверить решение учащимися задач № 1087 и № 1088 по тетрадям.
2. Решить на доске часть заданий, вызвавших затруднения у учащихся.
II. Построение правильных многоугольников.
1. Рассмотреть решение задачи 1 пункта 109.
2. Построение правильного треугольника, вписанного в окружность.
3. Рассмотреть решение задачи 2 пункта 109.
4. Построение правильного двенадцатиугольника, вписанного в окружность (рис. 310).
5. Построение правильных четырехугольника, восьмиугольника, шестнадцатиугольника, вписанных в окружность.
6. Построение правильных шестиугольника, треугольника, описанных около окружности.
7. Построение правильных четырехугольника, восьмиугольника, описанных около окружности.
III. Итоги урока.
Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Оказывается, что не все правильные многоугольники допускают такое построение. Доказано, например, что правильный семиугольник не может быть построен при помощи циркуля и линейки.
Однако с помощью этих инструментов можно построить правильный семнадцатиугольник.
Домашнее задание: выполнить аналогичное задание на чертежных листах (построение правильных многоугольников, вписанных в окружность, и построение правильных многоугольников, описанных около окружности).
Учитель может указать количество сторон правильного многоугольника. Лучшие работы пойдут в методическую копилку.
Решить задачи №№ 1095, 1096, 1097.
|
абырғалар саны |
Сырттай сызылған шеңбер радиусы |
Іштей сызылған шеңбердің радиусы |
Аудан |
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
8 |
|
|
|
|
10 |
|
|
|
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Ашық сабақ "Дұрыс көпбұрыштарды салу" 9-сынып
Ашық сабақ "Дұрыс көпбұрыштарды салу" 9-сынып
Сабақ жоспары
Күні: 11.02.16ж
|
Сабақ жүргізген мұғалімнің аты-жөні |
Акенева Асем Жумагалиевна |
9 сынып |
Ж.Болғанбаев атындағы Самар орта мектебі |
|
|||||
|
Сабақтың атауы |
Дұрыс көпбұрыштарды салу |
|
|||||||
|
Сілтеме |
1.Мұғалімдерге арналған нұсқаулық 2.Оқыту әдістемесі 3.Оқулық, геометрия 9 сынып А.В. Погорелов |
|
|||||||
|
Жалпы мақсаты |
«Көпбұрыштар» тарауынан оқушылардың алған білімдерін тиянақтап, пысықтау, оларды салу жұмыстары кезінде пайдалана білуге үйрету. |
|
|||||||
|
Міндеттер |
1. Дұрыс көпбұрыштарды салу әдіс – тәсілін меңгереді; 2. Теориялық білімін практикада қолдана білу
және білім – білік дағдыларын қалыптастыру, оқушының танымын
кеңейту, ойлау қабілетін арттыру |
|
|||||||
|
Мұғалім үшін оқу нәтижелері |
|
|
|||||||
|
Күтілетін нәтиже |
-Өзінің құнды пікірін айтуға, барлық пікірдің құнды екенін үйренеді. - Қатынастың негізгі қасиетін меңгеру; -Екі санның қатынасын процент түрінде көрсетуге болады; -Бөлшек сандарды натурал сандардың қатынасы түрінде жазуға болады; -Алған теориялық білімдерін есеп қолдана білуге дағдыландыру; – пікір алмасуға үйренеді . -жұппен,топпен жұмыс жасай отырып, балалар сыни ойлауға қалыптасады. |
|
|||||||
|
Туындайтын идеялар |
Қатынасқа берілген есептерді практикалық жұмыс арқылы топпен, жұппен жұмыс жасау барысында талқылап, шығарып оқушылардың білімдері толыға түседі |
|
|||||||
|
Тапсырмалар |
І: Ұйымдастыру кезеңі 1. Қайталау сұрақтары.(Білу) 2. Топтық жұмыс .(Түсіну) ІІ: 3.Жұппен жұмыс. (Қолдану) ІІІ: 4. Жеке жұмыс. Постер жасау(Талдау) 5. Өздік жұмыс. Математикалық диктант (Жинақтау) 6.Тақырып бойынша сұраққа жауап беру. 7.Үйге тапсырма 8.Бағалау. Рефлексия(Бағалау) 9.Сабақты қорытындылау. |
-Топқа бөлінеді. -пысықтау сұрақтары бойынша сұрақтарға жауап береді. -топпен жұмыс -деңгейлік тапсырма -өздерін бағалау, бірін-бірі бағалау - рефлексия. |
|
||||||
|
Сабақтың түрі, әдіс тәсілдері |
АКТ, топпен жұмыс, оқыту мен оқудағы жаңа тәсілдер,диалогтық оқыту, Блум таксонономиясы, сұрақ-жауап, көшбасшылық, СТО, оқыту үшін бағалаужәне оқуды бағалау, жас ерекшеліктеріне байланысты тапсырмалар, талантты және дарынды балаларды оқыту. |
|
|||||||
|
Сабақтың көрнекілігі |
проектор, слайдтар, топтарға арналған тапсырма парақтары, үлестірме тапсырмалар, стикерлер,түрлі түсті кесінділер. |
|
|||||||
|
|
Сабақтың барысы |
||||||||
|
І.Оқушыларға психологиялық ахуал туғызу |
2. Мұғалімнің іс-әрекеті |
Оқушының іс-әрекеті |
|||||||
|
АКТ Оқытуды басқару және көшбасшылық |
Сыныпты топқа бөлу: «Шаттық шеңберінде» тұрады. /Топ басшыларын өздері тағайындайды, бағалау парағы таратылады./ Үй тапсырмасын сұрау № Қайталау сұрақтары 1.Дұрыс көпбұрыш дегеніміз не және ол қандай формуламен беріледі. Анықтама: Барлық қабырғалары және барлық бұрыштары тең дөңес көпбұрышты дұрыс көпбұрыш деп атайды. 2. Дұрыс көпбұрыштың ішкі бұрыштарының қосындысы неге тең ? /180˚(n – 2) / 3. Дұрыс көпбұрыштың әбір бұрышы қандай формуламен анықталады?
4. Көпбұрыштың сыртқы бұрыштарының қосындысы неге тең ? /360˚ / 5
6. Центрлік бұрыш дегеніміз не? Центрлік бұрыш деп төбесі шеңбердің центрінде жататын жазық бұрышты атайды. |
Топтарға бөлу Сұрақтарға жауап береді |
|||||||
|
Оқыту мен оқудағы жаңа тәсілдер |
ТҮСІНУ-3мин Диалогтық оқыту 2-тапсырма: Топпен жұмыс . Алгоритм бойынша тақырыпты өз беттерімен игеру. Алгоритм бойынша шеңберге іштей дұрыс көпбұрыш салу. Шеңберге іштей сызылған дұрыс көпбұрыш салу үшін, оның центрлік бұрышын салу жеткілікті. Дұрыс алтыбұрышты салу. 1. Центрлік бұрышын есепте. 2.Шеңбер бойынан қалауыңша А1 төбесін ал. 3.Осы нүктеден шеңбердің радиусына тең радиуспен белгі сал. Ол нүкте А2 төбесі. 4.Қалған төбелерді осыған ұқсас түрде сал. 5. А3, А4, А5, А6 төбелерін белгіле. 6.Төбелерді кесінділермен қос. Сырттай сызылған дұрыс алтыбұрышты салу үшін: 1. Іштей сызылған дұрыс көпбұрыштың төбелерінен шеңберге жанамалар жүргіз. 2.Жанмалардың қиылысу нүктелерін белгіле. Іштей сызылған дұрыс көпбұрыштың төбелерінен өтетін жанамалар сырттай сызылған дұрыс көпбұрыштың төбелері. |
Жеке жауап береді Әр оқушы өзіне берілген тақырыпты игеруге арналған тапсырмаға ұқсас тапсырмаларын орындайды. Жұпта талдайды, дұрыс не бұрыс екендігін айтады. Есептейді Дұрыс п-бұрышты салу үшін: 1.Шеңберде 3600/n-ге тең центрлік бұрышты санап алу 2.Шеңбер бойындағы нүктелерді белгілеу 3.Нүктелерді біріктіру Дұрыс 2n-бұрышты салу үшін: 1) Центрлік бұрыштардың биссектрисаны жүргізіп шеңбер бойында қиылысу нүктесін белгілеу 2) Шыққан нүктелерді n-бұрыштың төбелерімен біріктіру |
|||||||
|
Сыни ойлауын дамыту Оқыту үшін бағалау |
- ҚОЛДАНУ 7мин Сыни ойлауын дамыту Жұппен жұмыс №31 А.В. Погорелов. Шеңберге сырттай сегізбұрыш салыңдар |
Балалар тақтаға қарап назар аударып отырады. Постер жасайды. Бұл мәтінді тақтадан балалар кезектесіп оқып береді. Есептер шығарады. |
|||||||
|
Жас ерекшеліктеріне сай деңгейлік тапсырмалар |
ТАЛДАУ Дарындылық, жас ерекшеліктеріне сай деңгейлік тапсырмалар Жеке жұмыс А – деңгей Шеңберге іштей, сырттай дұрыс ұшбұрышты салу В – деңгей Шеңберге іштей, сырттай дұрыс төртбұрышты салу С – деңгей Шеңберге іштей, сырттай дұрыс бесбұрыш салу Алгоритм:1.AK⟘MN диаметрін жүргіз. 2.NL=LO 3. ⍵(L,A) шеңберін жүргіз 4.
⍵(L,A) 5.AF берілген шеңберге іштей сызылған бесбұрыштың қабырғасының ұзындығы 6.Осы ұзындықпен А нүктесінен бастап төрт рет өлшеп сал. Постер жасау Тақырыптың күнделікті өмірде қолданылуы ЖИНАҚТАУ-6мин Оқушыларға сұрақ қою және олардың жауаптарына қарай әрекет ету Оқушылар сабақ кезінде тапсырмалар орындайы. Өздік жұмыс І- вариант 1.Дұрыс 12-бұрыштың бұрыштарын тап. 2. Әрбір
бұрышы ІІ- вариант 1.Дұрыс 20-бұрыштың бұрыштарын тап. 2. Әрбір
бұрышы Математикалық диктант. 1.Кез келген дұрыс көпбұрышты тек сызғышпен салуға болады. /жоқ/ 2. Кез келген дөңес көпбұрыштың бұрыштары мен қабырғалары тең болады./Иә/ 3.Дұрыс көпбұрышты қағаз бүктеу арқылы кесіп алуға болады/ Иә/ 4.Дұрыс көпбұрыштың центрлік бұрышы 90°-қа тең болса, оның қабырғалар саны 4 /Иә/ 5.Дұрыс көпбұрыштың қабырғалар саны 8-ге тең болса, онда ол трапеция болады. /жоқ, сегіз қабырғалы болады/ БАҒАЛАУ — Шеңбер не үшін керек? Дұрыс көпбұрыштар салу үшін грек математигі Евклид 257 көпбұрыш салуды көрсеткен. Жетібұрыш пен тоғызбұрыш салынбайтынын дәлелдей алған жоқ. К.Гаусс неміс математигі жетібұрыш пен тоғызбұрыш салынбайтынын дәлелдеген. Рефлексия стикерлерге жазу. Кері байланыс Шығу парағын кубтың қырларына жапсырады, ондағы молекулалар топтасқан. Оқушылар оз ойларын оқып, жапсырады. Топ жетекшілері бағалау парғының қорытынды бағасын айтады. Үй жұмысы.Деңгейлік тапсырмалар. Тұсаукесер 11 Қорытынды жасау. Стикерлемен бағалау. |
Дарынды оқушы орнында жұмыс жасайды.
Дәптерлеріне есеп шығарады. Есептер шығарады. 1-жұп оқушылары кезектесіп сұрақтарды оқып, жауап береді. 2-жұп оқушылары кезектесіп сұрақтарды оқып, жауап береді. 3-жұп оқушылары кезектесіп сұрақтарды оқып, жауап береді. |
|||||||
|
Талантты және дарынды балаларды оқыту |
|||||||||
|
|
Бекіту 5 мин |
||||||||
|
|
3.Мұғалімнің іс-әрекеті |
Оқушының іс-әрекеті |
|||||||
|
|
Стикерге пікірлерін жазу. |
Оқушылар кестені толтырады. |
|||||||
|
|
Бағалау 3мин |
||||||||
|
|
4.Мұғалімнің іс-әрекеті |
Оқушының іс-әрекеті |
|||||||
|
|
Жұптардың бағаларын талдау, қорытынды бағаны шығару. |
Жұптағы оқушылар бірін-бірі бағалау критерийлері бойынша бағалайды |
|||||||
|
|
Үйге тапсырма 30 секунд |
||||||||
|
|
5.Мұғалімнің іс-әрекеті |
Оқушының іс-әрекеті |
|||||||
|
|
Үйге тапсырма: 213 бет, № 30 Дұрыс 12 бұрыш салу. |
Берілген тапсырманы күнделікке жазып алу |
|||||||
|
|
Рефлексия 30 секунд |
||||||||
|
|
Оқушыларға смайликтер таратамын. |
Оқушылар өздеріне сай смайликтерді таңдап дайын плакатқа жапсырады. |
|||||||
Тема. Построение правильных многоугольников.
Цели урока. Научить учащихся строить правильные многоугольники с помощью циркуля и линейки, познакомить их с отдельными областями применения правильных многоугольников в жизни.
Оборудование. Модели правильных многоугольников, технические детали, рисунки паркетов, коврики из лоскутков ткани, циркуль, линейка, карандаш, бумага.
Ход урока.
I. Организационный момент
II. Актуализация знаний учащихся
– Ребята, где вы могли видеть правильные многоугольники? (Паркеты, узоры, технические детали – болты, гайки…).
Чтобы все это сделать, необходимо уметь строить правильные многоугольники. Для получения паркета или узора необходимы лекало или шаблон, а для технических деталей – чертеж. (Демонстрируются болт, гайка и соответствующий чертеж; узор, паркет и соответствующий шаблон). Для построения правильных многоугольников будем использовать связь с окружностью. Научимся рисовать орнаменты с помощью циркуля.
III. Повторение пройденного материала.
1. Теоретический опрос.
Какой многоугольник называется правильным? (Выпуклый многоугольник называется правильным, если все его углы равны и все его стороны равны) [1]
Какой треугольник является правильным? Почему? (Равносторонний т.к. все его стороны равны и все его углы).
Является ли правильным четырехугольником прямоугольник, ромб, квадрат? Почему? (Хотя в прямоугольнике все углы равны, он не является правильным т.к. не все его стороны равны т.е. одно из условий правильного многоугольника не выполняется;
в ромбе все стороны равны, но не все углы равны;
квадрат – правильный многоугольник, т.к. все его стороны равны, все его углы равны).
2. Работа в группах.
Учащиеся делятся на группы по 3 – 4 ученика в каждой и решают тесты в течение 3 – 5 минут.
Тест для самостоятельной работы.
1. Какая из ломанных является многоугольником?

2.Какой многоугольник выпуклый?

3. Может ли пятиугольник иметь стороны длиной 3 см, 4 см, 8 см, 6см, 25 см?
1) да; 2) нет.
4. В правильном n-угольнике сумма внутренних углов равна 3600. Сколько сторон у этого многоугольника?
1) 4; 2) 3; 3) 5.
5. У правильного пятиугольника внешний угол равен:
1) 360; 2) 45 0; 3) 72 0.

2. Многоугольник является правильным, если все его ….
1) углы равны; 2) углы и стороны равны; 3) стороны равны.
IV. Объяснение новой темы.
– Ребята, где вы могли видеть правильные многоугольники? (Паркеты, узоры, технические детали – болты, гайки…).
Чтобы все это сделать, необходимо уметь строить правильные многоугольники. Для получения паркета или узора необходимы лекало или шаблон, а для технических деталей – чертеж. (Демонстрируются болт, гайка и соответствующий чертеж; узор, паркет и соответствующий шаблон).
Для построения правильных многоугольников будем использовать связь с окружностью.
Практическая работа.
Учащиеся выполняют работу на альбомных листах с помощью циркуля, линейки и карандаша.

Проведите в окружности два перпендикулярных диаметра и соедините отрезками их концы. Докажите, что полученный четырехугольник правильный.
А теперь построим правильный пятиугольник.

Радиусами ОА, ОВ, ОС, ОД, и ОЕ. Разобьем круг на пять сектаров с центральным углом, равным 3600/5=720 и соединим последовательно точки А,В,С,Д,Е. Получим многоугольник АВСДЕ. Докажите, что полученный пятиугольник правильный.
Можно построить правильный пятиугольник и другим способом.
Для деления окружности на пять равных частей поступают так:
-
Делят радиус ОА пополам;
-
Из полученной точки В радиусом ВС делают засечку на горизонтальном диаметре (точка Д);
-
Пользуясь отрезком СД, как стороной правильного пятиугольника, размечают его вершины;

– Как связаны между собой радиус описанной окружности и сторона правильного шестиугольника? R = а.Поэтому для построения правильного шестиугольника в качестве вершины выберем произвольно точку окружности. Из нее, как из центра, циркулем сделаем засечки радиусом, равным радиусу окружности, – это остальные вершины. Все они последовательно соединяются отрезками.
Чтобы построить правильный вписанный треугольник, соединим через одну вершины правильного вписанного шестиугольника.
Зная как построить правильный n – угольник, легко можно построить 2n – угольник. (Проведя биссектрисы углов треугольника (?АОВ) рис 3. до пересечения с окружностью. Соединив эти точки на окружности получим 2n – угольник, из имеющегося n – угольника.
Разделив центральный угол пополам, получим сторону правильного десятиугольника.
Считалось, что если можно построить квадрат, правильный треугольник, пятиугольник, то легко построить правильный вписанный 2 n – угольник. И все. На этом ограничивались. Но в 1796 году немецкий математик Карл Гаусс еще юношей поразил весь математический мир разрешением проблемы построения правильного 17 –угольника. [2]
Этому открытию сам Гаусс придавал большое значение и даже завещал выгравировать на своем надгробии правильный 17-угольник, вписанный в круг. Хотя в современном мире компьютерной технике этим никого не удивишь.

V. Остановимся на отдельных областях применение правильных многоугольников.
Ребята, посмотрите на эти виды паркета. Какие они красивые. (Демонстрируются рисунки паркета, составленного из правильных многоугольников).
Где применить правильные многоугольники, человеку подсказка сама природа. Ребята, какими правильными многоугольниками можно заполнит плоскость так, чтобы не было пропусков, т.е. уложить их в виде паркета? Такими многоугольниками могут быть только правильные треугольники, квадраты или правильные шестиугольники. Ребята, вы все видели пчелиные соты. (Демонстрируются настоящие соты, если их нет, то рисунок). Из каких фигур они составлены? (Из правильных многоугольников).
Пчелы – удивительно творцы. Геометрические способности пчел проявляется при построение сот. Возникают вопросы: “Почему пчелы строят соты именно так? Почему они предпочли сеть правильных шестиугольников, а не правильных треугольников или квадратов, ведь их, казалось бы, гораздо проще сконструировать?”
Почему пчела выбрала правильный шестиугольник?
Во-первых, в каждой точке сходится не более трех шестиугольников. Во-вторых, при таком построение мало уходит воска. Поэтому, если мы хотим разбить поле на участки так, чтобы на ограждения пошло как можно меньше материала, то участкам нужно будет придавать форму правильных шестиугольников.
Подобные расчеты находят применение в обувной промышленности. Для изготовления обуви используют колодки определенных размеров. Для определения размера используют паркет, составленный из правильных шестиугольников.
В математике 6 является совершенном числом. Есть много примеров: в Древней Греции на 6 – м месте на званом перу возлежал самый уважаемый и самый знаменитый и почетный гость; в Древнем Вавилоне круг делили на 6 частей; в Библии утверждается, что мир создан за 6 дней. 6 – самое маленькое, самое первое совершенное число, не даром на него обратили внимание великие Пифагор и Евклид, Ферма и Эйлер.
Обратим внимание на один из видов народного ремесла. (Демонстрируются наволочки для диванных подушек). Этот древний вид искусства использовали разные народы. У тех, кто дома пользуется иголкой и ножницами, всегда остаются лоскутки тканей. Из них можно изготовить покрывала, наволочки, коврики. [3]
Предметы, сделанные своими руками, всегда принято использовать. В зависимости от вашей фантазии вы можете получить довольно оригинальные вещи.
Ребята, как вы думаете, в каких случаях и почему на практике чаще используют правильные многоугольники? (При изготовлении технических деталей, например, болтов, гаек, это удобно. А при составлении паркетов, узоров, это и красиво).
С помощью циркуля можно построить красивые узоры. Принципы построение узоров не сложны. Рисунки 1 – 7. [4]
Поэтому в качестве домашнего задания предлагаю вам:
-
Составить из правильных многоугольников рисунок красивого паркета или узора.
-
Решить задачу.
Для построенных правильных многоугольников вычислить длины сторон а3, а4, а5, а6, если R=4 см.
Цель: выработать у учащихся умение строить некоторые правильные многоугольники.
Ход урока
I. Проверка домашнего задания.
1. Проверить решение учащимися задач № 1087 и № 1088 по тетрадям.
2. Решить на доске часть заданий, вызвавших затруднения у учащихся.
II. Построение правильных многоугольников.
1. Рассмотреть решение задачи 1 пункта 109.
2. Построение правильного треугольника, вписанного в окружность.
3. Рассмотреть решение задачи 2 пункта 109.
4. Построение правильного двенадцатиугольника, вписанного в окружность (рис. 310).
5. Построение правильных четырехугольника, восьмиугольника, шестнадцатиугольника, вписанных в окружность.
6. Построение правильных шестиугольника, треугольника, описанных около окружности.
7. Построение правильных четырехугольника, восьмиугольника, описанных около окружности.
III. Итоги урока.
Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Оказывается, что не все правильные многоугольники допускают такое построение. Доказано, например, что правильный семиугольник не может быть построен при помощи циркуля и линейки.
Однако с помощью этих инструментов можно построить правильный семнадцатиугольник.
Домашнее задание: выполнить аналогичное задание на чертежных листах (построение правильных многоугольников, вписанных в окружность, и построение правильных многоугольников, описанных около окружности).
Учитель может указать количество сторон правильного многоугольника. Лучшие работы пойдут в методическую копилку.
Решить задачи №№ 1095, 1096, 1097.
|
абырғалар саны |
Сырттай сызылған шеңбер радиусы |
Іштей сызылған шеңбердің радиусы |
Аудан |
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
8 |
|
|
|
|
10 |
|
|
|

шағым қалдыра аласыз



 .
.




































