
Краткосрочное планирование открытого урока
|
Раздел долгосрочного плана: Элементы комбинаторики и теории вероятностей Дата: 09.12.2021 Группа: 103 |
ФИО учителя: Куракбаева Т.Б. |
||||
|
Количество присутствующих: |
Количество отсутствующих: |
||||
|
Тема урока |
Правила сложения и умножения вероятностей. |
||||
|
Цели обучения, которые достигаются на данном уроке |
10.5.6.3 понимать и применять правила сложения и умножения вероятностей * P(A + B) = P(A) + P(B); * P(A +B) = P(A)+P(B)–P(A ∙ B); * P(A ∙ B) = P(A) ∙ P(B); |
||||
|
Цель урока |
Учащиеся узнают и применяют правила сложения и умножения вероятностей при решении задач. |
||||
|
Критерии оценивания |
Все учащиеся: понимают правила сложения и умножения вероятностей. Большинство учащихся: умеют применять их при решении задач. Некоторые учащиеся: анализируют выбор метода решения. |
||||
|
Навыки мышления |
Знание, понимание, использование, анализ, синтез, оценка |
||||
|
Языковые цели |
Предметная лексика и терминология: Предметная лексика и терминология:
|
||||
|
Привитие ценностей |
Умение учиться, повторять самостоятельно информацию, анализировать ситуацию, ставить проблемы и принимать решения, работать в команде, отвечать за качество своей работы, умение организовывать свое время. |
||||
|
Межпредметные связи |
У учащихся закладываются базовые знания в алгебре, теории вероятностей, исследования их. |
||||
|
Предварительные знания |
Понятие вероятности события и её свойства. |
||||
|
Ход урока |
|||||
|
Этапы урока |
Содержание урока |
Ресурсы |
|||
|
Орг. мом. 1 мин. Повтор. материала прошлого урока 3 мин. Целеполо-гание 1 мин Актуализация знаний 2 мин |
Приветствие, проверить готовность обучающихся к уроку. 1. «Вероятность» на трёх языках. (доп.задание Анищенко Дмитрий) 2. Викторина «Вероятность события и её свойства».Критерии оценивания: 0-3 правильных ответа – оценка 3 4-7 правильных ответа – оценка 4 8-9 правильных ответа – оценка 5 Обсуждение целей урока, цели обучения и критериев оценивания Учитель объявляет тему и цель урока. Цель урока и критерии разместить на видном месте на доске и сохранить записи до конца урока. Методика «Разместить на видном месте». Обратить внимание обучающихся на отличие совместных и несовместных событий, применяя примеры: Совместны ли события: а) на первом кубике выпало 1, а на втором – 2; б) Ербол пошёл в колледж, а завтра будет дождь; в) Студент сдал сессию на отлично, и провалил последний экзамен. Ответы:
|
программа Learningapps Презентация |
|||
|
Изучение нового материала 10 мин Закрепление изученного материала. 10 мин 5 мин
Подведение итогов урока. Рефлексия 2 мин Задание на дом: |
Совместная работа с классом. Предложить учащимся сравнить теоремы о сумме вероятностей несовместных и совместных событий. Теорема о сумме вероятностей несовместных событий: Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий. Р(А + В) = Р(А) + Р(В) Теорема о сумме вероятностей совместных событий: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления. Р(А + В) = Р(А) + Р(В) – Р(АВ). Пример 1 В ящике 30 мячиков одинаковых размеров: 10 красных, 5 синих и 15 белых. Вычислить вероятность того что, не глядя будет взят цветной (не белый) мячик. Решение.
Примем,
что событие А – «взят красный мячик», а
событие В – «взят синий мячик». Тогда
событие
и события В:
События А и В – взаимно несовместные, так как если взят один мячик, то нельзя взять мячики разных цветов. Поэтому используем сложение вероятностей:
Пример 2 Абитуриент подал заявления в два разных вуза по результатам ЕНТ (на бюджетной основе). Какова вероятность быть зачисленным абитуриенту хотя бы в один из вузов. Вероятность попасть в первый вуз Р1 = 0,5, во второй Р2 = 0,3. Решение. Анализируем, т.к. вероятность поступить в один и совместно в другой вуз не исключают друг друга, то решаем по формуле совместных событий: Р (А+В) = Р(А)+Р(В) – Р(АВ)= 0,5 + 0,3 – 0,5 ∙ 0,3=0,65 Теперь, рассмотрим произведение двух событий А и В состоящее в совместном появлении этих событий. Теорема о произведении вероятностей независимых событий Если случайные события А и В независимые, то вероятность совместного появления событий А и В равно произведению вероятностей этих событий. Р (А × В) = Р(А) × Р(В) Пример 3 Студент должен сдать два экзамена в сессию. Вероятность сдать первый экзамен Р1 =0,8. Вероятность сдать второй экзамен Р2 =0,7. Какова вероятность, что студент сдаст два экзамена в сессию. Решение. Событие А – сдать первый экзамен. Событие В – сдать второй экзамен. Оба события независимы. Событие А×В – сдать два экзамена. Вероятность сдать два экзамена вычисляется по формуле: Р(А × В) = Р(А)×Р(В) = Р1× Р2 = 0,7 × 0,8 = 0,56. |
Презентация Эл.учебник |
|||
|
Парная работа. Обучающиеся решают задачи в паре, проводят обсуждение и взаимопроверку. Учитель контролирует процесс решения и при необходимости оказывает поддержку. Критерии оценивания: понимают правила сложения и умножения - 2 балла анализируют выбор метода решения вероятностей – 4 балла умеют применять их при решении задач – 6 баллов Задача 1 В урне находится 30 шариков: 15 – красного цвета, 10 – синего и 5 – зеленого. Найдите вероятность того, что наугад извлеченный шарик окажется не зеленым. (событие А) Решение. Событие А наступит, если шарик б/т красный или синий, т.е. это сумма несовместимых событий В и С. Получим: Р(А) = Р(В)+ Р(С) = 15/30 + 10/30 = 5/6 Задача 2 Если бросить монету и игральную кость, то какова вероятность того, что монета упадёт гербом вверх и вместе с тем на кости выпадет пятёрка? Решение. 1/2 – выпадение герба, 1/6 – появление пятёрки. Совмещение двух независимых событий: Р(АВ)= Р(А)* Р(В)=1/2*1/6=1/12 Дополнительно: Задача 3 Монету бросают три раза подряд. Найти вероятность того, что все три раза выпадет герб.
Р
Индивидуальная работа Работа по карточкам «Пирамида» Критерии оценивания:
Выставление оценок Анкета Дом.задание 1. Повторить основные теоремы, формулы. 2. Задача: На автогонках при заезде на первой автомашине вероятность
победить Найти вероятность того, что победит хотя бы одна автомашина; |
Презентация |
||||
|
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? |
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? |
Здоровье и соблюдение техники безопасности |
|
|
Способные учащиеся помогают другим учащимся при выполнении заданий. |
Самооценивание, взаимооценивание |
На уроке используются здоровье сберегающие методики |
|
|
Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Общая оценка Какие два аспекта урока прошли хорошо (подумайте, как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: |
Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. |
||
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Ашық сабақ: Правила сложения и умножения вероятностей.
Ашық сабақ: Правила сложения и умножения вероятностей.
Краткосрочное планирование открытого урока
|
Раздел долгосрочного плана: Элементы комбинаторики и теории вероятностей Дата: 09.12.2021 Группа: 103 |
ФИО учителя: Куракбаева Т.Б. |
||||
|
Количество присутствующих: |
Количество отсутствующих: |
||||
|
Тема урока |
Правила сложения и умножения вероятностей. |
||||
|
Цели обучения, которые достигаются на данном уроке |
10.5.6.3 понимать и применять правила сложения и умножения вероятностей * P(A + B) = P(A) + P(B); * P(A +B) = P(A)+P(B)–P(A ∙ B); * P(A ∙ B) = P(A) ∙ P(B); |
||||
|
Цель урока |
Учащиеся узнают и применяют правила сложения и умножения вероятностей при решении задач. |
||||
|
Критерии оценивания |
Все учащиеся: понимают правила сложения и умножения вероятностей. Большинство учащихся: умеют применять их при решении задач. Некоторые учащиеся: анализируют выбор метода решения. |
||||
|
Навыки мышления |
Знание, понимание, использование, анализ, синтез, оценка |
||||
|
Языковые цели |
Предметная лексика и терминология: Предметная лексика и терминология:
|
||||
|
Привитие ценностей |
Умение учиться, повторять самостоятельно информацию, анализировать ситуацию, ставить проблемы и принимать решения, работать в команде, отвечать за качество своей работы, умение организовывать свое время. |
||||
|
Межпредметные связи |
У учащихся закладываются базовые знания в алгебре, теории вероятностей, исследования их. |
||||
|
Предварительные знания |
Понятие вероятности события и её свойства. |
||||
|
Ход урока |
|||||
|
Этапы урока |
Содержание урока |
Ресурсы |
|||
|
Орг. мом. 1 мин. Повтор. материала прошлого урока 3 мин. Целеполо-гание 1 мин Актуализация знаний 2 мин |
Приветствие, проверить готовность обучающихся к уроку. 1. «Вероятность» на трёх языках. (доп.задание Анищенко Дмитрий) 2. Викторина «Вероятность события и её свойства».Критерии оценивания: 0-3 правильных ответа – оценка 3 4-7 правильных ответа – оценка 4 8-9 правильных ответа – оценка 5 Обсуждение целей урока, цели обучения и критериев оценивания Учитель объявляет тему и цель урока. Цель урока и критерии разместить на видном месте на доске и сохранить записи до конца урока. Методика «Разместить на видном месте». Обратить внимание обучающихся на отличие совместных и несовместных событий, применяя примеры: Совместны ли события: а) на первом кубике выпало 1, а на втором – 2; б) Ербол пошёл в колледж, а завтра будет дождь; в) Студент сдал сессию на отлично, и провалил последний экзамен. Ответы:
|
программа Learningapps Презентация |
|||
|
Изучение нового материала 10 мин Закрепление изученного материала. 10 мин 5 мин
Подведение итогов урока. Рефлексия 2 мин Задание на дом: |
Совместная работа с классом. Предложить учащимся сравнить теоремы о сумме вероятностей несовместных и совместных событий. Теорема о сумме вероятностей несовместных событий: Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий. Р(А + В) = Р(А) + Р(В) Теорема о сумме вероятностей совместных событий: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления. Р(А + В) = Р(А) + Р(В) – Р(АВ). Пример 1 В ящике 30 мячиков одинаковых размеров: 10 красных, 5 синих и 15 белых. Вычислить вероятность того что, не глядя будет взят цветной (не белый) мячик. Решение.
Примем,
что событие А – «взят красный мячик», а
событие В – «взят синий мячик». Тогда
событие
и события В:
События А и В – взаимно несовместные, так как если взят один мячик, то нельзя взять мячики разных цветов. Поэтому используем сложение вероятностей:
Пример 2 Абитуриент подал заявления в два разных вуза по результатам ЕНТ (на бюджетной основе). Какова вероятность быть зачисленным абитуриенту хотя бы в один из вузов. Вероятность попасть в первый вуз Р1 = 0,5, во второй Р2 = 0,3. Решение. Анализируем, т.к. вероятность поступить в один и совместно в другой вуз не исключают друг друга, то решаем по формуле совместных событий: Р (А+В) = Р(А)+Р(В) – Р(АВ)= 0,5 + 0,3 – 0,5 ∙ 0,3=0,65 Теперь, рассмотрим произведение двух событий А и В состоящее в совместном появлении этих событий. Теорема о произведении вероятностей независимых событий Если случайные события А и В независимые, то вероятность совместного появления событий А и В равно произведению вероятностей этих событий. Р (А × В) = Р(А) × Р(В) Пример 3 Студент должен сдать два экзамена в сессию. Вероятность сдать первый экзамен Р1 =0,8. Вероятность сдать второй экзамен Р2 =0,7. Какова вероятность, что студент сдаст два экзамена в сессию. Решение. Событие А – сдать первый экзамен. Событие В – сдать второй экзамен. Оба события независимы. Событие А×В – сдать два экзамена. Вероятность сдать два экзамена вычисляется по формуле: Р(А × В) = Р(А)×Р(В) = Р1× Р2 = 0,7 × 0,8 = 0,56. |
Презентация Эл.учебник |
|||
|
Парная работа. Обучающиеся решают задачи в паре, проводят обсуждение и взаимопроверку. Учитель контролирует процесс решения и при необходимости оказывает поддержку. Критерии оценивания: понимают правила сложения и умножения - 2 балла анализируют выбор метода решения вероятностей – 4 балла умеют применять их при решении задач – 6 баллов Задача 1 В урне находится 30 шариков: 15 – красного цвета, 10 – синего и 5 – зеленого. Найдите вероятность того, что наугад извлеченный шарик окажется не зеленым. (событие А) Решение. Событие А наступит, если шарик б/т красный или синий, т.е. это сумма несовместимых событий В и С. Получим: Р(А) = Р(В)+ Р(С) = 15/30 + 10/30 = 5/6 Задача 2 Если бросить монету и игральную кость, то какова вероятность того, что монета упадёт гербом вверх и вместе с тем на кости выпадет пятёрка? Решение. 1/2 – выпадение герба, 1/6 – появление пятёрки. Совмещение двух независимых событий: Р(АВ)= Р(А)* Р(В)=1/2*1/6=1/12 Дополнительно: Задача 3 Монету бросают три раза подряд. Найти вероятность того, что все три раза выпадет герб.
Р
Индивидуальная работа Работа по карточкам «Пирамида» Критерии оценивания:
Выставление оценок Анкета Дом.задание 1. Повторить основные теоремы, формулы. 2. Задача: На автогонках при заезде на первой автомашине вероятность
победить Найти вероятность того, что победит хотя бы одна автомашина; |
Презентация |
||||
|
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? |
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? |
Здоровье и соблюдение техники безопасности |
|
|
Способные учащиеся помогают другим учащимся при выполнении заданий. |
Самооценивание, взаимооценивание |
На уроке используются здоровье сберегающие методики |
|
|
Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Общая оценка Какие два аспекта урока прошли хорошо (подумайте, как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: |
Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. |
||

шағым қалдыра аласыз


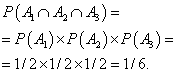 ешение.
ешение.












