Ғ.Мұратбаев атындағы Жетісай гуманитарлық-техникалық колледжі

Оқу сабағының жоспары

Сабақтың тақырыбы: Қисықсызықты трапеция және оның ауданы. Анықталған интеграл

Модуль /пән атауы: Математика
Педагог Сыздықова Бағила дайындады.

2024 жылғы «07» ақпан

1.Жалпы мәліметтер
Курс, топ: 1-курс, МБТ 23-9/2
Сабақ түрі: Аралас сабақ
2. Мақсаты, міндеттері:

- Қисықсызықты трапецияның анықтамасын беру және ауданын есептеуді үйрету;

-Анықталған интегралды есептеу тәсілдерін үйрету.

3. Күтілетін нәтижелер:

- қисықсызықты трапецияның анықтамасын біледі және ауданын есептейді;

- анықталған интеграл ұғымын біледі, анықталған интегралды есептейді.
4. Қажетті ресурстар:

5. Сабақтың барысы

І.Ұйымдастыру кезеңі (1-5 мин)

-Білім алушылармен сәлемдесу, түгелдеу.

-Білім алушылардың сабаққа дайындығын тексеру. Білім алушылардың назарын сабаққа аудару.

-Топқа бөлу, топ басшысын сайлау, бағалау парағын тарату.

Топты «Жұмыртқа аршу» әдісімен бөлу. Студенттер жұмыртқаны аршу арқылы ішінде жазылған топтың аты бойынша бөлінеді.

ІІ. Үйге берілген тапсырманы сұрау (5-15)

Формуланы сәйкестендіріңіз:

ІІІ.Жаңа сабақ (15-30)

Сабақтың тақырыбы: Қисықсызықты трапеция және оның ауданы. Анықталған интеграл

қисықтарымен шектелген фигура қисық сызықты трапеция деп аталады.

Мысалы төмендегі сызбаларда түрлі қисық сызықты трапециялар берілген.

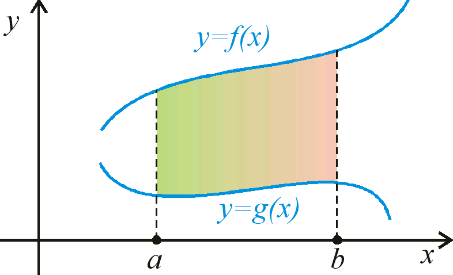
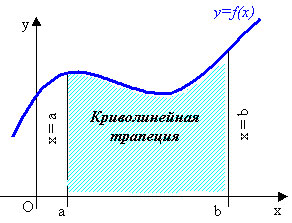
Қарапайым трапецияның ауданы екені белгілі

Қисық сызықты трапецияның ауданын интегралды қолдану арқылы есептейміз. Егер болса, аралығында берілген қисық сызықты трапецияның ауданы

формуласымен есептеледі.

Оқушыларға Ох осімен және y=x-3, x=4, x=7 түзулерімен шектелген трапеция ауданын есептеуді ұсыныңыз. Төмендегі суреттен:

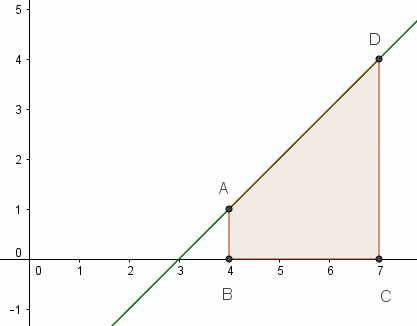
1-әдіс:

2-әдіс: F(x) - f(x) функциясының алғашқы функциясы екенін ескеріп , мұндағы .

1-ші және 2-әдістерден алынған нәтижелерді салыстырыңыз және сәйкес қорытындылар жасаңыз.

Егер f(x) функциясының графигі қисық сызық болса, онда жалпы жағдайда қисықсызықты трапеция деп, Ох осімен, x=a, x=b түзулерімен және f(x) функциясының графигімен шектелген фигураны айтады және ол келесі түрде болады:

Әрі қарай оқушыларға келесідей қисықсызықты трапецияларды бейнелеуді ұсыныңыз:

А деңгейі: f(x)=x², x=1, x=3,

В деңгейі: f(x)=sin(x), ,

IV. Сабақты бекіту (30-70 мин)

1-тапсырма QR код арқылы тапсырмаларды орындайды (топтық жұмыс)

1 - есеп:

сызықтарымен шектелген қисық сызықты трапецияның ауданын есептеңдер.

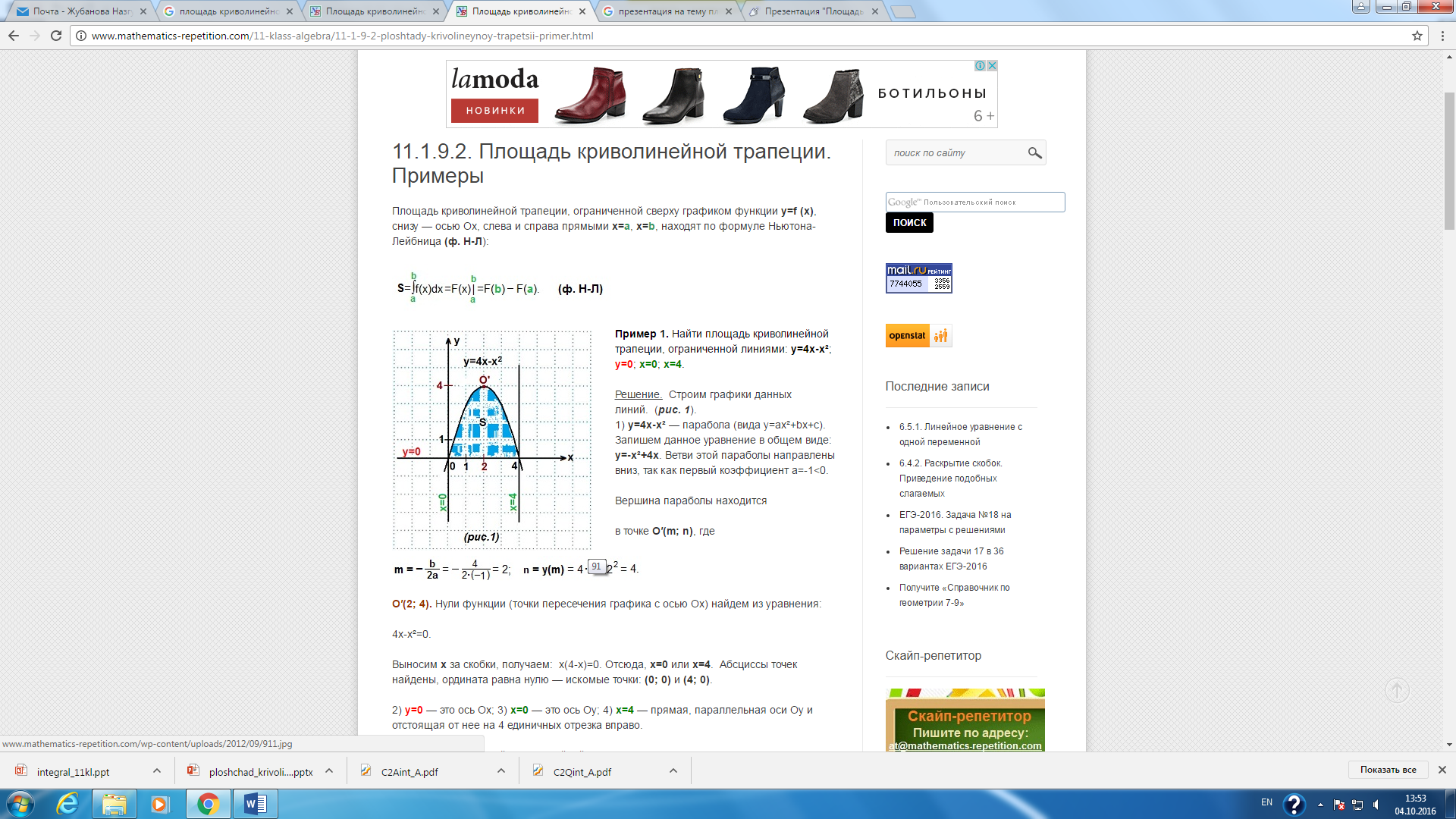
(кв.бірлік)

Жауабы:

2- есеп: сызықтарымен шектелген фигураның ауданын табыңдар.

Шектерін табу үшін екі функцияның қиылысу нүктелерін есептейміз.

Виет теоремасы бойынша

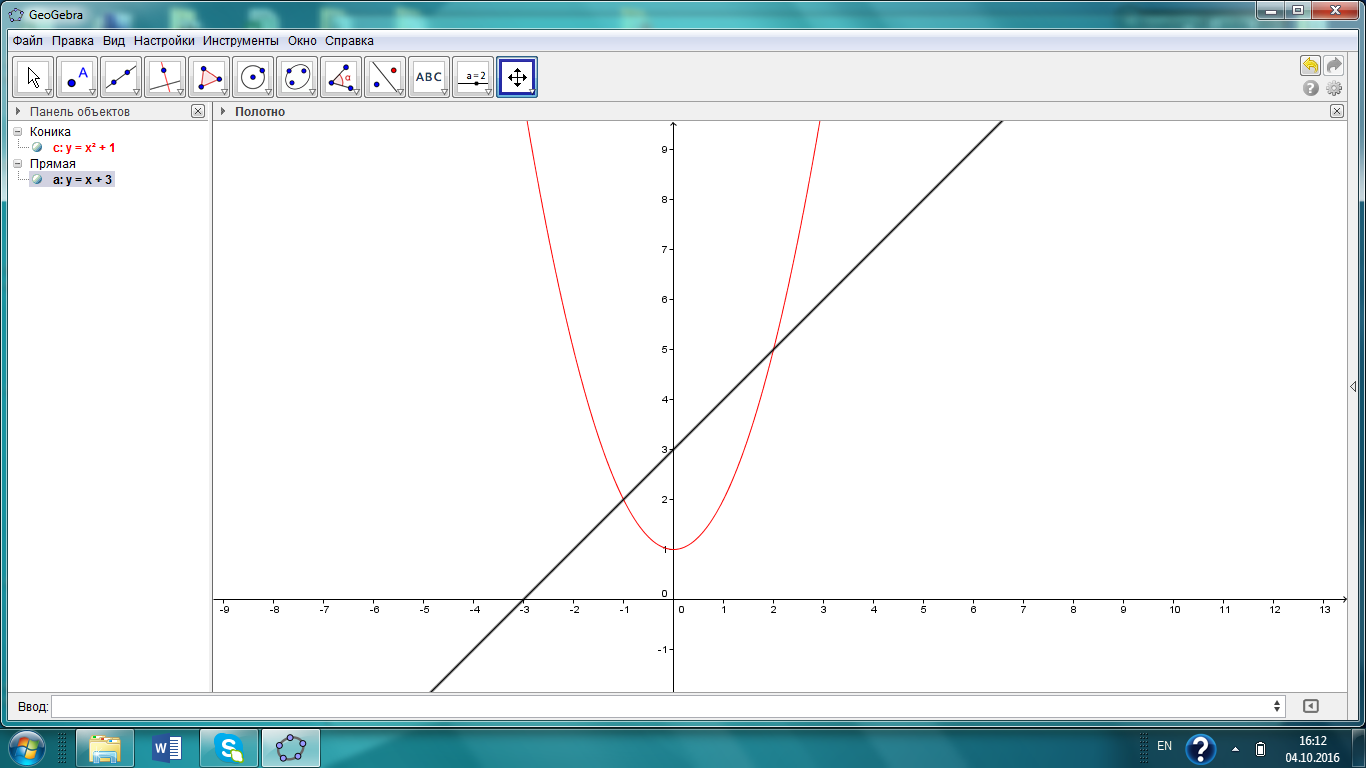
(кв.бірлік)

Жауабы:

3 –есеп :

сызықтарымен шектелген фигураның ауданын табыңдар.

(кв.бірлік)

Жауабы: S= 9

2-тапсырма ( Тақтамен жұмыс) Мұнда есепті шығару қадамдарын студенттер тақтаға кезекпен шығарады.

1-топқа

1) ; 2) ;

3) ; 4) .

Жауабы: 1) 2) ;

3) 4) + cos x+ C.

2-топқа

1) 2)

3) 4)

жауабы: 1) ; 2) ;

3) 4)

3-топқа

1) + 5)dx; 2)

3) ; 4)

жауабы: 1) 2)

3) 4)

Сергіту сәті

3-тапсырма

«Қол twister» әдісі арқылы ұяшықтағы жасырын тұрған сұрақтарға жауап береді.

1. Анықталған интегралдың анықталмаған интегралдан қандай айырмашылығы бар?

2. Ньютон - Лейбниц формуласымен ...................есептейді.

3. Берілген функция үшін алғашқы функцияның жалпы түрін жаз f(x) = 2.

4. формуласын толықтыр.

5. формуласын толықтыр.

6. есепті шығар

7. есепті шығар

8. есепті шығар

9. есепті шығар

V. Бағалау (75-80 мин)

Сабақ соңында әр тапсырманың бағалау критериилері бойынша жалпы баллдық жүйемен бағалау

Бағалау парағы.

р/с	Аты- жөні	Үй тапсырмасы 5-10 балл	1-тапсырма 15-25 балл	2- тапсырма 20-30 балл	3-тапсырма 20-35 балл	Ұпай саны	Бағасы
		Жүктеу ЖИ арқылы жасау ЖИ арқылы жасау Бөлісу 1 - айлық Материал тарифі -96% жеңілдік 00 05 00 ҚМЖ Ашық сабақ Тәрбие сағаты Презентация БЖБ, ТЖБ тесттер Көрнекіліктер Балабақшаға арнарлған құжаттар Мақала, Эссе Дидактикалық ойындар және тағы басқа 400 000 материал Барлық 400 000 материалдарды шексіз жүктеу мүмкіндігіне ие боласыз 1 990 ₸ 49 000₸ 1 айға қосылу Таңдау Материалға шағымдану Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз Жариялаған: Сыздикова Багила Болатовна 26 Ақпан 2024 621 Шағым жылдам қаралу үшін барынша толық ақпарат жіберіңіз Шағымды қалдыру Ашық сабақ: Қисықсызықты трапеция және оның ауданы. Анықталған интеграл Тақырып бойынша 11 материал табылды Ашық сабақ: Қисықсызықты трапеция және оның ауданы. Анықталған интеграл Материал туралы қысқаша түсінік Ашық сабақта әртүрлі әдіс-тәсілдер көрсетілген. Материалды жүктеу Материалдың қысқаша нұсқасы Ғ.Мұратбаев атындағы Жетісай гуманитарлық-техникалық колледжі Оқу сабағының жоспары Сабақтың тақырыбы: Қисықсызықты трапеция және оның ауданы. Анықталған интеграл Модуль /пән атауы: Математика Педагог Сыздықова Бағила дайындады. 2024 жылғы «07» ақпан 1.Жалпы мәліметтер Курс, топ: 1-курс, МБТ 23-9/2 Сабақ түрі: Аралас сабақ 2. Мақсаты, міндеттері: - Қисықсызықты трапецияның анықтамасын беру және ауданын есептеуді үйрету; -Анықталған интегралды есептеу тәсілдерін үйрету. 3. Күтілетін нәтижелер: - қисықсызықты трапецияның анықтамасын біледі және ауданын есептейді; - анықталған интеграл ұғымын біледі, анықталған интегралды есептейді. 4. Қажетті ресурстар: Алгебра және анализ бастамалары 11 сынып «Мектеп» баспасы, интерактивті панель, бағалау парағы, смартфон қағаздары, сәйкестендіру парағы. 5. Сабақтың барысы І.Ұйымдастыру кезеңі (1-5 мин) -Білім алушылармен сәлемдесу, түгелдеу. -Білім алушылардың сабаққа дайындығын тексеру. Білім алушылардың назарын сабаққа аудару. -Топқа бөлу, топ басшысын сайлау, бағалау парағын тарату. Топты «Жұмыртқа аршу» әдісімен бөлу. Студенттер жұмыртқаны аршу арқылы ішінде жазылған топтың аты бойынша бөлінеді. ІІ. Үйге берілген тапсырманы сұрау (5-15) Формуланы сәйкестендіріңіз: 1 А) sin x + C 2 Ә) tg x + C = Б) - ctg x + C В) 2 5 = Г ) 6 = Д) - cos x + C ІІІ.Жаңа сабақ (15-30) Сабақтың тақырыбы: Қисықсызықты трапеция және оның ауданы. Анықталған интеграл қисықтарымен шектелген фигура қисық сызықты трапеция деп аталады. Мысалы төмендегі сызбаларда түрлі қисық сызықты трапециялар берілген. Қарапайым трапецияның ауданы екені белгілі Қисық сызықты трапецияның ауданын интегралды қолдану арқылы есептейміз. Егер болса, аралығында берілген қисық сызықты трапецияның ауданы формуласымен есептеледі. Оқушыларға Ох осімен және y=x-3, x=4, x=7 түзулерімен шектелген трапеция ауданын есептеуді ұсыныңыз. Төмендегі суреттен: 1-әдіс: 2-әдіс: F(x) - f(x) функциясының алғашқы функциясы екенін ескеріп , мұндағы . 1-ші және 2-әдістерден алынған нәтижелерді салыстырыңыз және сәйкес қорытындылар жасаңыз. Егер f(x) функциясының графигі қисық сызық болса, онда жалпы жағдайда қисықсызықты трапеция деп, Ох осімен, x=a, x=b түзулерімен және f(x) функциясының графигімен шектелген фигураны айтады және ол келесі түрде болады: Әрі қарай оқушыларға келесідей қисықсызықты трапецияларды бейнелеуді ұсыныңыз: А деңгейі: f(x)=x2, x=1, x=3, В деңгейі: f(x)=sin(x), , IV. Сабақты бекіту (30-70 мин) 1-тапсырма QR код арқылы тапсырмаларды орындайды (топтық жұмыс) 1 - есеп: сызықтарымен шектелген қисық сызықты трапецияның ауданын есептеңдер. (кв.бірлік) Жауабы: 2- есеп: сызықтарымен шектелген фигураның ауданын табыңдар. Шектерін табу үшін екі функцияның қиылысу нүктелерін есептейміз. Виет теоремасы бойынша (кв.бірлік) Жауабы: 3 –есеп : сызықтарымен шектелген фигураның ауданын табыңдар. (кв.бірлік) Жауабы: S= 9 2-тапсырма ( Тақтамен жұмыс) Мұнда есепті шығару қадамдарын студенттер тақтаға кезекпен шығарады. 1-топқа 1) ; 2) ; 3) ; 4) . Жауабы: 1) 2) ; 3) 4) + cos x+ C. 2-топқа 1) 2) 3) 4) жауабы: 1) ; 2) ; 3) 4) 3-топқа 1) + 5)dx; 2) 3) ; 4) жауабы: 1) 2) 3) 4) Сергіту сәті 3-тапсырма «Қол twister» әдісі арқылы ұяшықтағы жасырын тұрған сұрақтарға жауап береді. 1. Анықталған интегралдың анықталмаған интегралдан қандай айырмашылығы бар? 2. Ньютон - Лейбниц формуласымен ...................есептейді. 3. Берілген функция үшін алғашқы функцияның жалпы түрін жаз f(x) = 2. 4. формуласын толықтыр. 5. формуласын толықтыр. 6. есепті шығар 7. есепті шығар 8. есепті шығар 9. есепті шығар V. Бағалау (75-80 мин) Сабақ соңында әр тапсырманың бағалау критериилері бойынша жалпы баллдық жүйемен бағалау Бағалау парағы. р/с Аты- жөні Үй тапсырмасы 5-10 балл 1-тапсырма 15-25 балл 2- тапсырма 20-30 балл 3-тапсырма 20-35 балл Ұпай саны Бағасы Материалды жүктеу Жүктеу Сақтау Бөлісу ЖИ арқылы жасау Файл форматы: docx Алгебра Ашық сабақ 11 сынып 26.02.2024 621 Жүктеу Сақтау ЖИ арқылы жасау Жариялаған: Сыздикова Багила Болатовна Бұл материалды қолданушы жариялаған. Ustaz Tilegi ақпаратты жеткізуші ғана болып табылады. Жарияланған материалдың мазмұны мен авторлық құқық толықтай автордың жауапкершілігінде. Егер материал авторлық құқықты бұзады немесе сайттан алынуы тиіс деп есептесеңіз, шағым қалдыра аласыз Қазақстандағы ең үлкен материалдар базасынан іздеу Сіз үшін 400 000 ұстаздардың еңбегі мен тәжірибесін біріктіріп, ең үлкен материалдар базасын жасадық. Төменде керек материалды іздеп, жүктеп алып сабағыңызға қолдана аласыз Іздеу Материал жариялап, аттестацияға 100% жарамды сертификатты тегін алыңыз! Ustaz tilegi журналы министірліктің тізіміне енген. Qr коды мен тіркеу номері беріледі. Материал жариялаған соң сертификат тегін бірден беріледі. Толығырақ Оқу-ағарту министірлігінің ресми жауабы Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз! Қазақстан Республикасының білім беру жүйесін дамытуға қосқан жеке үлесі үшін және де Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық материалыңызбен бөлісіп, белсенді болғаныңыз үшін алғыс білдіреміз! Жариялау Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз! Тәуелсіз Қазақстанның білім беру жүйесін дамытуға және білім беру сапасын арттыру мақсатында Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық жұмысын жариялағаны үшін марапатталасыз! Жариялау Министірлікпен келісілген курстар тізімі Химия пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Тарих пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Биология пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Ағылшын тілі пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ География пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Информатика пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Мектепке дейінгі білім беру бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ «Қазақ тілі» жəне «Қазақ əдебиеті» бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Дене шынықтыру пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Білім алушылардың білім сапасын арттыру мақсатында сабақта цифрлық технологияларды қолдану 80/108 сағат Толығырақ Инклюзивті білім беру жүйесінде ерекше білім беру қажеттілігі бар білім алушыға психологиялық-педагогикалық қолдау көрсету бойынша педагогтердің кәсіби және пәндік құзыреттіліктерін дамыту 80/108 сағат Толығырақ