
ГУ «Общеобразовательная школа №23»
Открытый урок
Решение задач на тему
«Теорема Пифагора».
8 «В» кл.
Сугурова А.Ж.
учитель математики.
2015-2016 г.г.
Тема урока: Обобщающий урок по теме «Теорема Пифагора»
Цели урока:
общеобразовательные: проверить теоретические знания учащихся (свойства прямоугольного треугольника, теорема Пифагора), умение использовать их при решении задач;
-
создав проблемную ситуацию, подвести учащихся к “открытию” обратной теоремы Пифагора.
развивающие: развитие умений применять теоретические знания на практике;
-
развитие умения формулировать выводы при наблюдениях;
-
развитие памяти, внимания, наблюдательности:
-
развитие мотивации учения через эмоциональное удовлетворение от открытий, через введение элементов истории развития математических понятий.
воспитательные: воспитывать устойчивый интерес к предмету через изучение жизнедеятельности Пифагора;
-
воспитание взаимопомощи и объективного оценивания знаний одноклассников через взаимопроверку.
Форма урока: повторительно-обобщающий.
План урока:
-
Организационный момент.
-
Проверка домашнего задания. Актуализация знаний.
-
Тестовые задания в программе «My TestХ».
-
Решение задач на практическое применение теоремы Пифагора
-
Самостоятельная работа (по индивидуальным карточкам с отгадыванием афоризмов Пифагора).
-
Домашнее задание.
-
Итоги урока.просмотр видеоролика о Пифагоре.
-
Оценка учащихся.
Ход урока.
Организационный момент.
Проверка домашнего задания. Актуализация знаний.
Учитель: Ответы домашнего задания: №240
Да- 1) 3) 4) 7)
Нет – 2) 5) 6)
Учитель: На доске записаны утверждения. Если вы согласны с ними на листочках напротив соответствующего номера вопроса поставьте “+”, если не согласны, то поставьте “–”.
На доске заранее написаны утверждения.
-
Гипотенуза больше катета.
-
Сумма острых углов прямоугольного треугольника равна 1800.
-
Теорема Пифагора верна для всех равнобедренных треугольников.
-
В прямоугольном треугольнике катет, лежащий напротив угла 300, равен половине гипотенузы.
-
Сумма квадратов катетов равна квадрату гипотенузы.
-
Квадрат катета равен разности квадратов гипотенузы и второго катета.
-
Сторона треугольника равна сумме двух других сторон.
Проверяются работы с помощью взаимопроверки. Утверждения, вызвавшие споры, – обсуждаются.
Ключ к теоретическим вопросам.
-
“+”
-
“-”
-
“–”
-
“+”
-
“+”
-
“+”
-
“–”
Учащиеся ставят друг другу оценки по следующей системе:
Тестовые задания в программе «My TestХ». Тест «Теорема Пифагора»
1. К каким треугольникам можно применить теорему Пифагора?
-
К любым;
-
К прямоугольным;
-
К равнобедренным;
-
Не знаю.
2. Верно ли, что в прямоугольном треугольнике любой из катетов меньше гипотенузы?
-
Нет;
-
Не знаю;
-
Да.
3. В прямоугольном треугольнике квадрат гипотенузы равен…
-
сумме катетов;
-
квадрату катета;
-
сумме квадратов катетов;
-
не знаю.
4. Сторона равностороннего треугольника равна 8 см. Найдите его медиану.
-
Диагонали ромба равны 12 см и 16 см. Найдите его сторону.
-
Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то эта сторона лежит напротив…
-
острого угла;
-
прямого угла;
-
тупого угла;
-
не знаю.
-
5 см;
-
4 см;
-
6 см;
-
8 см.
Решение практических задач с использованием теоремы Пифагора.
Учитель: предлагаю вам практические задачи с применением изучаемой теоремы. Побываем сначала в лесу, после бури, потом на загородном участке.
Задача 1. После бури сломалась ель. Высота оставшейся части 4,2 м. Расстояние от основания до упавшей макушки 5,6 м. Найти высоту ели до бури.
Задача 2. Высота дома 4,4 м Ширина газона вокруг дома 1,4 м. Какой длины надо изготовить лестницу, чтобы она не заступала на газон и доставала до крыши дома?
Самостоятельная работа (проводится по индивидуальным карточкам).
Карточки с заданиями І-уровень.
№1 №2
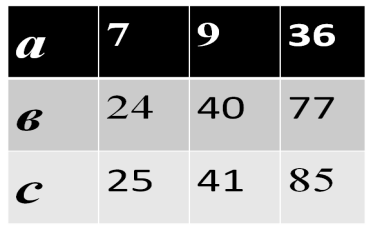
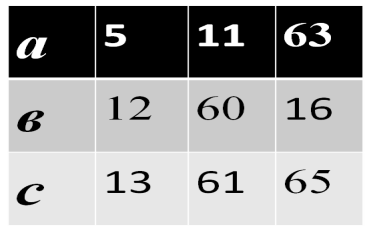
Учитель: Дома вы повторяли свойства ромба и прямоугольника. Перечислите их (идет беседа с классом). На прошлом уроке мы говорили о том, что Пифагор был разносторонней личностью. Он занимался и медициной, и музыкой, и астрономией, а так же был спортсменом и участвовал в олимпийских играх. А еще Пифагор был философом. Многие его афоризмы и сегодня актуальны для нас. Сейчас вы будете выполнять самостоятельную работу. К каждому заданию дано несколько вариантов ответов, рядом с которыми записаны фрагменты афоризмов Пифагора. Ваша задача – решив все задания, составить из полученных фрагментов высказывание и записать его.
Комментарии для учителя:
Эти карточки раздаются учащимся, из них они составляют афоризмы Пифагора следующим образом: к трем заданиям в карточке приведены варианты ответов и фрагменты высказываний. Ученик решает задачу, получает ответ, ищет его в нижней чести карточки и записывает соответствующую часть афоризма. Таким образом, решив все три задачи, ребенок собирает афоризм из трех частей. Чтобы дети не собирали их наугад – фрагменты афоризмов подобраны с очень близким по смыслу содержанием.
Карточка для B – I.
|
Катеты прямоугольного треугольника равны 10 и 24 см. Вычислите его гипотенузу. Диагонали прямоугольника ABCD пересекаются в точке О. СО = 10см, CD = 12 см. Вычислите сторону ВС. Является ли треугольник со сторонами 15, 39 и 36 см прямоугольным? Ответ обоснуйте. |
||
|
26 – не гоняйся за счастьем |
32 – оно присутствует |
“да” – в тебе самом |
|
676 – не бегай за счастьем |
16 – оно всегда находится |
“нет” – около тебя |
Ответ: Не гоняйся за счастьем, оно всегда находится в тебе самом.
Карточка для B – II.
|
Вычислите катет прямоугольного треугольника, если две другие его стороны равны 8 и 17 см. Диагонали ромба ABCD пересекаются в точке О. BD = 16см, ОС = 6см. Вычислите длину стороны ромба. Является ли треугольник со сторонами 15, 20 и 27 см прямоугольным? Ответ обоснуйте. |
||
|
225 – формулы |
10 – управляют |
“нет” – миром |
|
15 – числа |
14 – правят |
“да” – всем |
Ответ: Числа управляют миром.
Карточки для B – III
|
Вычислите катет прямоугольного треугольника, если две другие его стороны равны 15 и 17 см. В ромбе АBCD диагонали пересекаются в точке О. АС = 12см, ВО = 8см. Вычислите длину стороны ромба. Является ли треугольник со сторонами 18, 30 и 21 см прямоугольным? Ответ обоснуйте. |
||
|
8 – либо молчи |
10 – либо говори то |
“да” – что интересно всем |
|
64 – хочешь молчи |
14 – или говори о том |
“нет” – ценнее молчания |
Ответ: Либо молчи, либо говори то, что ценнее молчания.
Карточки для B – IV
|
Катеты прямоугольного треугольника равны 12 и 9 см. Вычислите его гипотенузу. В прямоугольнике ABCD диагонали пересекаются в точке О. АО = 10см, AD = 16см. Вычислите сторону АВ. Является ли треугольник со сторонами 14, 48 и 50 см прямоугольным? Ответ обоснуйте. |
||
|
15 – из двух спорящих |
26 – прав тот |
“да” – кто умнее |
|
225 – в споре |
12 – неправ тот |
“нет” – кто глупее |
Ответ: Из двух спорящих неправ тот, кто умнее.
Домашнее задание.
№ 245. №251.
Итоги урока.

Лист оценки. Фамилия и имя: ______________________________________
|
Домашнее задание |
О Пифагоре |
Устные вопросы |
Тест |
Решение задач |
Работа с карточками |
Итого |
|
|
|
|
|
|
|
|
Лист оценки. Фамилия и имя: ______________________________________
|
Домашнее задание |
О Пифагоре |
Устные вопросы |
Тест |
Решение задач |
Работа с карточками |
Итого |
|
|
|
|
|
|
|
|
Лист оценки. Фамилия и имя: ______________________________________
|
Домашнее задание |
О Пифагоре |
Устные вопросы |
Тест |
Решение задач |
Работа с карточками |
Итого |
|
|
|
|
|
|
|
|
Лист оценки. Фамилия и имя: ______________________________________
|
Домашнее задание |
О Пифагоре |
Устные вопросы |
Тест |
Решение задач |
Работа с карточками |
Итого |
|
|
|
|
|
|
|
|
Лист оценки. Фамилия и имя: ______________________________________
|
Домашнее задание |
О Пифагоре |
Устные вопросы |
Тест |
Решение задач |
Работа с карточками |
Итого |
|
|
|
|
|
|
|
|
Карточка для B – I.
|
Катеты прямоугольного треугольника равны 10 и 24 см. Вычислите его гипотенузу. Диагонали прямоугольника ABCD пересекаются в точке О. СО = 10см, CD = 12 см. Вычислите сторону ВС. Является ли треугольник со сторонами 15, 39 и 36 см прямоугольным? Ответ обоснуйте. |
||
|
26 – не гоняйся за счастьем |
32 – оно присутствует |
“да” – в тебе самом |
|
676 – не бегай за счастьем |
16 – оно всегда находится |
“нет” – около тебя |
Ответ: _____________________________________________________________________________
Карточка для B – II.
|
Вычислите катет прямоугольного треугольника, если две другие его стороны равны 8 и 17 см. Диагонали ромба ABCD пересекаются в точке О. BD = 16см, ОС = 6см. Вычислите длину стороны ромба. Является ли треугольник со сторонами 15, 20 и 27 см прямоугольным? Ответ обоснуйте. |
||
|
225 – формулы |
10 – управляют |
“нет” – миром |
|
15 – числа |
14 – правят |
“да” – всем |
Ответ: _______________________________________________________________________________
Карточки для B – III
|
Вычислите катет прямоугольного треугольника, если две другие его стороны равны 15 и 17 см. В ромбе АBCD диагонали пересекаются в точке О. АС = 12см, ВО = 8см. Вычислите длину стороны ромба. Является ли треугольник со сторонами 18, 30 и 21 см прямоугольным? Ответ обоснуйте. |
||
|
8 – либо молчи |
10 – либо говори то |
“да” – что интересно всем |
|
64 – хочешь-молчи |
14 – или говори о том |
“нет” – ценнее молчания |
Ответ: _______________________________________________________________________________
Карточки для B – IV
|
Катеты прямоугольного треугольника равны 12 и 9 см. Вычислите его гипотенузу. В прямоугольнике ABCD диагонали пересекаются в точке О. АО = 10см, AD = 16см. Вычислите сторону АВ. Является ли треугольник со сторонами 14, 48 и 50 см прямоугольным? Ответ обоснуйте. |
||
|
15 – из двух спорящих |
26 – прав тот |
“да” – кто умнее |
|
225 – в споре |
12 – неправ тот |
“нет” – кто глупее |
Ответ: ______________________________________________________________________
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Ашық сабақ "Теорема Пифагора" 8 сынып
Ашық сабақ "Теорема Пифагора" 8 сынып
ГУ «Общеобразовательная школа №23»
Открытый урок
Решение задач на тему
«Теорема Пифагора».
8 «В» кл.
Сугурова А.Ж.
учитель математики.
2015-2016 г.г.
Тема урока: Обобщающий урок по теме «Теорема Пифагора»
Цели урока:
общеобразовательные: проверить теоретические знания учащихся (свойства прямоугольного треугольника, теорема Пифагора), умение использовать их при решении задач;
-
создав проблемную ситуацию, подвести учащихся к “открытию” обратной теоремы Пифагора.
развивающие: развитие умений применять теоретические знания на практике;
-
развитие умения формулировать выводы при наблюдениях;
-
развитие памяти, внимания, наблюдательности:
-
развитие мотивации учения через эмоциональное удовлетворение от открытий, через введение элементов истории развития математических понятий.
воспитательные: воспитывать устойчивый интерес к предмету через изучение жизнедеятельности Пифагора;
-
воспитание взаимопомощи и объективного оценивания знаний одноклассников через взаимопроверку.
Форма урока: повторительно-обобщающий.
План урока:
-
Организационный момент.
-
Проверка домашнего задания. Актуализация знаний.
-
Тестовые задания в программе «My TestХ».
-
Решение задач на практическое применение теоремы Пифагора
-
Самостоятельная работа (по индивидуальным карточкам с отгадыванием афоризмов Пифагора).
-
Домашнее задание.
-
Итоги урока.просмотр видеоролика о Пифагоре.
-
Оценка учащихся.
Ход урока.
Организационный момент.
Проверка домашнего задания. Актуализация знаний.
Учитель: Ответы домашнего задания: №240
Да- 1) 3) 4) 7)
Нет – 2) 5) 6)
Учитель: На доске записаны утверждения. Если вы согласны с ними на листочках напротив соответствующего номера вопроса поставьте “+”, если не согласны, то поставьте “–”.
На доске заранее написаны утверждения.
-
Гипотенуза больше катета.
-
Сумма острых углов прямоугольного треугольника равна 1800.
-
Теорема Пифагора верна для всех равнобедренных треугольников.
-
В прямоугольном треугольнике катет, лежащий напротив угла 300, равен половине гипотенузы.
-
Сумма квадратов катетов равна квадрату гипотенузы.
-
Квадрат катета равен разности квадратов гипотенузы и второго катета.
-
Сторона треугольника равна сумме двух других сторон.
Проверяются работы с помощью взаимопроверки. Утверждения, вызвавшие споры, – обсуждаются.
Ключ к теоретическим вопросам.
-
“+”
-
“-”
-
“–”
-
“+”
-
“+”
-
“+”
-
“–”
Учащиеся ставят друг другу оценки по следующей системе:
Тестовые задания в программе «My TestХ». Тест «Теорема Пифагора»
1. К каким треугольникам можно применить теорему Пифагора?
-
К любым;
-
К прямоугольным;
-
К равнобедренным;
-
Не знаю.
2. Верно ли, что в прямоугольном треугольнике любой из катетов меньше гипотенузы?
-
Нет;
-
Не знаю;
-
Да.
3. В прямоугольном треугольнике квадрат гипотенузы равен…
-
сумме катетов;
-
квадрату катета;
-
сумме квадратов катетов;
-
не знаю.
4. Сторона равностороннего треугольника равна 8 см. Найдите его медиану.
-
Диагонали ромба равны 12 см и 16 см. Найдите его сторону.
-
Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то эта сторона лежит напротив…
-
острого угла;
-
прямого угла;
-
тупого угла;
-
не знаю.
-
5 см;
-
4 см;
-
6 см;
-
8 см.
Решение практических задач с использованием теоремы Пифагора.
Учитель: предлагаю вам практические задачи с применением изучаемой теоремы. Побываем сначала в лесу, после бури, потом на загородном участке.
Задача 1. После бури сломалась ель. Высота оставшейся части 4,2 м. Расстояние от основания до упавшей макушки 5,6 м. Найти высоту ели до бури.
Задача 2. Высота дома 4,4 м Ширина газона вокруг дома 1,4 м. Какой длины надо изготовить лестницу, чтобы она не заступала на газон и доставала до крыши дома?
Самостоятельная работа (проводится по индивидуальным карточкам).
Карточки с заданиями І-уровень.
№1 №2


Учитель: Дома вы повторяли свойства ромба и прямоугольника. Перечислите их (идет беседа с классом). На прошлом уроке мы говорили о том, что Пифагор был разносторонней личностью. Он занимался и медициной, и музыкой, и астрономией, а так же был спортсменом и участвовал в олимпийских играх. А еще Пифагор был философом. Многие его афоризмы и сегодня актуальны для нас. Сейчас вы будете выполнять самостоятельную работу. К каждому заданию дано несколько вариантов ответов, рядом с которыми записаны фрагменты афоризмов Пифагора. Ваша задача – решив все задания, составить из полученных фрагментов высказывание и записать его.
Комментарии для учителя:
Эти карточки раздаются учащимся, из них они составляют афоризмы Пифагора следующим образом: к трем заданиям в карточке приведены варианты ответов и фрагменты высказываний. Ученик решает задачу, получает ответ, ищет его в нижней чести карточки и записывает соответствующую часть афоризма. Таким образом, решив все три задачи, ребенок собирает афоризм из трех частей. Чтобы дети не собирали их наугад – фрагменты афоризмов подобраны с очень близким по смыслу содержанием.
Карточка для B – I.
|
Катеты прямоугольного треугольника равны 10 и 24 см. Вычислите его гипотенузу. Диагонали прямоугольника ABCD пересекаются в точке О. СО = 10см, CD = 12 см. Вычислите сторону ВС. Является ли треугольник со сторонами 15, 39 и 36 см прямоугольным? Ответ обоснуйте. |
||
|
26 – не гоняйся за счастьем |
32 – оно присутствует |
“да” – в тебе самом |
|
676 – не бегай за счастьем |
16 – оно всегда находится |
“нет” – около тебя |
Ответ: Не гоняйся за счастьем, оно всегда находится в тебе самом.
Карточка для B – II.
|
Вычислите катет прямоугольного треугольника, если две другие его стороны равны 8 и 17 см. Диагонали ромба ABCD пересекаются в точке О. BD = 16см, ОС = 6см. Вычислите длину стороны ромба. Является ли треугольник со сторонами 15, 20 и 27 см прямоугольным? Ответ обоснуйте. |
||
|
225 – формулы |
10 – управляют |
“нет” – миром |
|
15 – числа |
14 – правят |
“да” – всем |
Ответ: Числа управляют миром.
Карточки для B – III
|
Вычислите катет прямоугольного треугольника, если две другие его стороны равны 15 и 17 см. В ромбе АBCD диагонали пересекаются в точке О. АС = 12см, ВО = 8см. Вычислите длину стороны ромба. Является ли треугольник со сторонами 18, 30 и 21 см прямоугольным? Ответ обоснуйте. |
||
|
8 – либо молчи |
10 – либо говори то |
“да” – что интересно всем |
|
64 – хочешь молчи |
14 – или говори о том |
“нет” – ценнее молчания |
Ответ: Либо молчи, либо говори то, что ценнее молчания.
Карточки для B – IV
|
Катеты прямоугольного треугольника равны 12 и 9 см. Вычислите его гипотенузу. В прямоугольнике ABCD диагонали пересекаются в точке О. АО = 10см, AD = 16см. Вычислите сторону АВ. Является ли треугольник со сторонами 14, 48 и 50 см прямоугольным? Ответ обоснуйте. |
||
|
15 – из двух спорящих |
26 – прав тот |
“да” – кто умнее |
|
225 – в споре |
12 – неправ тот |
“нет” – кто глупее |
Ответ: Из двух спорящих неправ тот, кто умнее.
Домашнее задание.
№ 245. №251.
Итоги урока.

Лист оценки. Фамилия и имя: ______________________________________
|
Домашнее задание |
О Пифагоре |
Устные вопросы |
Тест |
Решение задач |
Работа с карточками |
Итого |
|
|
|
|
|
|
|
|
Лист оценки. Фамилия и имя: ______________________________________
|
Домашнее задание |
О Пифагоре |
Устные вопросы |
Тест |
Решение задач |
Работа с карточками |
Итого |
|
|
|
|
|
|
|
|
Лист оценки. Фамилия и имя: ______________________________________
|
Домашнее задание |
О Пифагоре |
Устные вопросы |
Тест |
Решение задач |
Работа с карточками |
Итого |
|
|
|
|
|
|
|
|
Лист оценки. Фамилия и имя: ______________________________________
|
Домашнее задание |
О Пифагоре |
Устные вопросы |
Тест |
Решение задач |
Работа с карточками |
Итого |
|
|
|
|
|
|
|
|
Лист оценки. Фамилия и имя: ______________________________________
|
Домашнее задание |
О Пифагоре |
Устные вопросы |
Тест |
Решение задач |
Работа с карточками |
Итого |
|
|
|
|
|
|
|
|
Карточка для B – I.
|
Катеты прямоугольного треугольника равны 10 и 24 см. Вычислите его гипотенузу. Диагонали прямоугольника ABCD пересекаются в точке О. СО = 10см, CD = 12 см. Вычислите сторону ВС. Является ли треугольник со сторонами 15, 39 и 36 см прямоугольным? Ответ обоснуйте. |
||
|
26 – не гоняйся за счастьем |
32 – оно присутствует |
“да” – в тебе самом |
|
676 – не бегай за счастьем |
16 – оно всегда находится |
“нет” – около тебя |
Ответ: _____________________________________________________________________________
Карточка для B – II.
|
Вычислите катет прямоугольного треугольника, если две другие его стороны равны 8 и 17 см. Диагонали ромба ABCD пересекаются в точке О. BD = 16см, ОС = 6см. Вычислите длину стороны ромба. Является ли треугольник со сторонами 15, 20 и 27 см прямоугольным? Ответ обоснуйте. |
||
|
225 – формулы |
10 – управляют |
“нет” – миром |
|
15 – числа |
14 – правят |
“да” – всем |
Ответ: _______________________________________________________________________________
Карточки для B – III
|
Вычислите катет прямоугольного треугольника, если две другие его стороны равны 15 и 17 см. В ромбе АBCD диагонали пересекаются в точке О. АС = 12см, ВО = 8см. Вычислите длину стороны ромба. Является ли треугольник со сторонами 18, 30 и 21 см прямоугольным? Ответ обоснуйте. |
||
|
8 – либо молчи |
10 – либо говори то |
“да” – что интересно всем |
|
64 – хочешь-молчи |
14 – или говори о том |
“нет” – ценнее молчания |
Ответ: _______________________________________________________________________________
Карточки для B – IV
|
Катеты прямоугольного треугольника равны 12 и 9 см. Вычислите его гипотенузу. В прямоугольнике ABCD диагонали пересекаются в точке О. АО = 10см, AD = 16см. Вычислите сторону АВ. Является ли треугольник со сторонами 14, 48 и 50 см прямоугольным? Ответ обоснуйте. |
||
|
15 – из двух спорящих |
26 – прав тот |
“да” – кто умнее |
|
225 – в споре |
12 – неправ тот |
“нет” – кто глупее |
Ответ: ______________________________________________________________________

шағым қалдыра аласыз















