
Математикадан ҰБТ-да кездесетін күрделі есептерді шығарудың тиімді әдістері
(Әдістемелік нұсқау)
Математикадан ҰБТ-да кездесетін күрделі есептерді шығарудың тиімді әдістері. Әдістемелік құрал
«Математикадан ҰБТ-да кездесетін күрделі есептерді шығарудың тиімді әдістері» әдістемелік құралында ҰБТ-да кездесетін әр түрлі есептер жинақталып, оларды шешудің оңтайлы әдістемесі көрсетілген.
Әдістемелік құралдың негізгі мақсаты – оқушыларға математикадан ұлттық бірыңғай тестілеу (ҰБТ) тапсырмаларында кездесетін көптеген шығару жолы қиын саналатын тапсырмаларды орындаудың тиімді әдістерін ұсыну және оқушыларға есептерді шешудің тиімді әдістемесін келтіру арқылы олардың ойлау қабілеті мен шығармашылық белсенділігінің дамуына ықпал ету, есептерді шығару дағдысын жетілдіре түсуге көмектесу болып табылады.
Әдістемелік құрал мұғалімдер мен мектеп оқушыларына, мектеп бітіруші түлектерге арналған.
Әдістемелік құрал білім басқармасы жанындағы эксперттік кеңестің шешімімен ұсынылды.
Кіріспе
«Математикадан ҰБТ тапсырмаларында кездесетін күрделі есептерді шығарудың тиімді әдістері» әдістемелік құралында оқушыларға математикадан ұлттық бірыңғай тестілеу (ҰБТ) тапсырмаларында кездесетін көптеген шығару жолы қиын саналатын тапсырмаларды орындаудың тиімді әдістері ұсынылған.
Әдістемелік құралда ұсынылған функция мәндерінің жиынын анықтау әдістемесі, тригонометриялық және кері тригонометриялық функциялары бар өрнектердің мәндерін табу әдістемесі, күрделі радикалдары бар өрнектерді ықшамдау әдістемесі, жай теңсіздіктер жүйесін шешу әдістемесі, аралас теңсіздіктер жүйесін шешу әдістемесі, анықталмаған сызықтық теңдеулерді шешу алгоритмі (авторлық тәсіл), қозғалысқа арналған есептерді графиктік тәсілмен шешу әдістемесі, функцияның ең кіші оң периодын табу әдістемесі, функцияның жұптылығы мен тақтылығын анықтау әдістемесі, сандардың ең кіші ортақ еселік (ЕКОЕ) пен ең үлкен ортақ бөлгішін (ЕҮОБ) Евклид алгоритімін пайдаланып анықтау әдістемесі берілген. Есептерді шығарудың мұндай әдістері мектеп оқулықтарында кездеспейтіндіктен, көрсетілген әдістеме ҰБТ кезінде оқушыларға үлкен көмек болатыны сөзсіз. Әдістемелік құралда кездесетін жай бөлшектерді Евклид алгоритмін пайдаланып қысқарту да кесте арқылы өте ұтымды орындалады. Сондықтан, осы тәсіл арқылы ЕКОЕ пен ЕҮОБ табу тапсырмаларын орындау, сандарды жай көбейткіштерге жіктеу тәсіліне қарағанда, оқушыларға еш қиындық келтірмейді.
-
Функция мәндерінің жиынын анықтау әдістемесі
 ,
,  және тағы басқа
түріндегі функциялардың мәндерінің жиынын анықтауға арналған
есептер мектеп бітірушілердің ұлттық бірыңғай тест (ҰБТ)
тапсырмаларында жиі кездеседі.
және тағы басқа
түріндегі функциялардың мәндерінің жиынын анықтауға арналған
есептер мектеп бітірушілердің ұлттық бірыңғай тест (ҰБТ)
тапсырмаларында жиі кездеседі.
Мектеп оқулықтарының бірде
бірінде мұндай есептер арнайы қарастырылмағандықтан, оқушылардың
көпшілігінің бұл есептерді шығара алмайды. Математикалық талдау
аппараттарын пайдалана отырып функцияны зерттеу, оның графигін салу
арқылы бұл тапсырмаларды орандауға болады. Бірақ ҰБТ кезінде мұндай
тапсырмаларды 1,5-2 минут ішінде орындау кез келген оқушының
қолынан келмейтіні белгілі. Функцияның мәндерінің жиынын табу көп
жағдайда теңдеудің шешімін табумен байланысты
болады.  саны
саны  функциясының мәндер
жиынына кіруүшін,
функциясының мәндер
жиынына кіруүшін,  теңдеуінің,
мұндағы
теңдеуінің,
мұндағы  , шешімінің болуы
қажетті және жеткілікті. Бұл теңдеудің
, шешімінің болуы
қажетті және жеткілікті. Бұл теңдеудің
 - дің мәніне
байланысты бір түбірі, бірнеше түбірі немесе түбірі болмауы да
мүмкін. Осындай есептерді шығарудың оңтайлы тәсілдерінің бірі
төменде келтірілген.
- дің мәніне
байланысты бір түбірі, бірнеше түбірі немесе түбірі болмауы да
мүмкін. Осындай есептерді шығарудың оңтайлы тәсілдерінің бірі
төменде келтірілген.
Ол үшін,
алдымен  (мұндағы
(мұндағы  ) түріндегі гиперболаны
қарастырайық. Бұл функцияның мәндер жиыны
) түріндегі гиперболаны
қарастырайық. Бұл функцияның мәндер жиыны
 екендігі
ақиқат.
екендігі
ақиқат.
1-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.  немесе
немесе  .
.
Жауабы:  .
.
2-мысал.
 функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.  сандары бөлшектің
бөлімінің нөлдері болғандықтан, бұл функция осы
нүктелерде анықталмайды. Ал,
сандары бөлшектің
бөлімінің нөлдері болғандықтан, бұл функция осы
нүктелерде анықталмайды. Ал,  саны алымы мен бөлімінің
ортақ нөлі. Сондықтан,
саны алымы мен бөлімінің
ортақ нөлі. Сондықтан,  болса,
онда
болса,
онда![]()
 функцияның
функцияның  нүктесіндегі
мәні
нүктесіндегі
мәні  , яғни,
берілген функцияның
мәні
, яғни,
берілген функцияның
мәні  -тің ешбір мәнінде 1-ге
тең бола алмайды, ендеше біріншіден
-тің ешбір мәнінде 1-ге
тең бола алмайды, ендеше біріншіден  .
Екіншіден,
.
Екіншіден,  гиперболасының мәндер
жиыны
гиперболасының мәндер
жиыны  екендігі
белгілі.
екендігі
белгілі.
Сондықтан, берілген функцияның
мәндер  .
.
Жауабы:
 .
.
3-мысал.
 функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі. Бөлшектің алымы мен
бөлімінің ортақ түбірі жоқ екендігі белгілі. Берілген
функцияны  немесе
немесе  түріне келтіреміз. Яғни,
функцияның мәндер жиынын табу үшін,
у
параметрдің қандай мәндерінде
соңғы квадрат теңдеудің шешімі болатындыған анықтау жеткілікті. Ол
үшін D
түріне келтіреміз. Яғни,
функцияның мәндер жиынын табу үшін,
у
параметрдің қандай мәндерінде
соңғы квадрат теңдеудің шешімі болатындыған анықтау жеткілікті. Ол
үшін D![]() 0 теңсіздігін құрып,
шешеміз:
0 теңсіздігін құрып,
шешеміз:  .
.
Соңғы теңсіздіктің
шешімі:  болатындығына көз
жеткізу қиын емес.
болатындығына көз
жеткізу қиын емес.
Жауабы:
4-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі. Мұндай есептерді квадрат
үшмүшенің толық квадратын айыру тәсілі және туынды арқылы
функцияның кризистік нүктесін анықтап, функцияның ең үлкен немесе
ең кіші мәндерін табу арқылы да шығаруға болады. Алайда, парабола
төбесінің ординатасының формуласын қолдану, тапсырманы тез және
дұрыс орындауға көмектеседі. Атап айтқанда,
 парабола төбесінің
ординатасының формуласы болғандықтан,
парабола төбесінің
ординатасының формуласы болғандықтан,
 болса,
онда
болса,
онда
 ,
ал
,
ал  болса,
онда
болса,
онда  болады.
болады.
Біздің
мысалда  ,
ал
,
ал  болғандықтан,
болғандықтан,  .
.
Жауабы:
 .
.
5-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі. Квадрат түбір
астындағы  квадрат үшмүшеліктің
мәндер жиыны
квадрат үшмүшеліктің
мәндер жиыны  )
болғандықтан,
)
болғандықтан,
 болатындығы
анық.
болатындығы
анық.
Жауабы:
 .
.
Ескерту: Сан аралығының «квадрат түбірін табу» амалының жазылуы ерсілеу көрінгенмен, оның дұрыстығы өрнектің монотондылығымен түсіндіріледі.
6-мысал.
 функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.  функциясының мәндер
жиыны:
функциясының мәндер
жиыны:
 болғандықтан,
болғандықтан,

 .
.
Жауабы: 
7-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.  .
.
Жауабы:  ].
].
8-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.
 .
.
Жауабы:  ].
].
9-мысал. у= функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.  функциясының мәндер
жиыны
функциясының мәндер
жиыны  ]
болғандықтан,
]
болғандықтан,  .
.
Жауабы:  ].
].
10-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.  (мұндағы a
(мұндағы a функциясының мәндер
жиыны
функциясының мәндер
жиыны  болғандықтан,
болғандықтан,  функциясының мәндер
жиыны:
функциясының мәндер
жиыны:
 .
.
Жауабы:  .
.
11-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі. 
![]()
 ⟺
⟺  .
Ал,
.
Ал,  теңдеуінің шешуі болу
үшін,
теңдеуінің шешуі болу
үшін,  шарты орындалуы қажет.
Сондықтан,
шарты орындалуы қажет.
Сондықтан,  .
.

![]()
 .
.
Жауабы: 
-
Тригонометриялық және кері тригонометриялық функциялары бар өрнектердің мәндерін табу әдістемесі.
12-мысал.  және
және  болса,
онда
болса,
онда  мәндерін
табыңыз.
мәндерін
табыңыз.
Шешуі. Көмекші тікбұрышты үшбұрышты пайдаланайық.
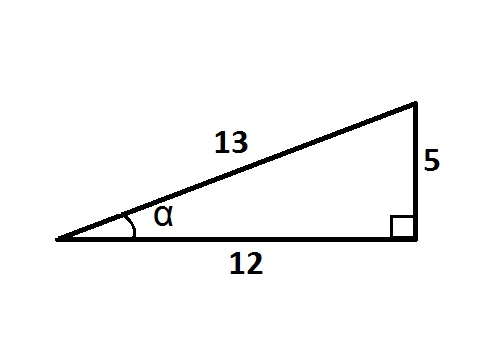
1-сурет.
 болғандықтан,
болғандықтан,  ,
ал,
,
ал,  шартын
ескерсек:
шартын
ескерсек:  .
.
Жауабы:  .
.
13-мысал.  есептеңіз.
есептеңіз.
Шешуі.  және
және  деп белгілесек, онда
анықтама бойынша
деп белгілесек, онда
анықтама бойынша  .
Ендеше,
.
Ендеше, 
 (12-мысал әдісімен).
Сондықтан
(12-мысал әдісімен).
Сондықтан

 .
.
Жүктеу
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Ашық сабақ: Туынды табу ережелері
Ашық сабақ: Туынды табу ережелері
Математикадан ҰБТ-да кездесетін күрделі есептерді шығарудың тиімді әдістері
(Әдістемелік нұсқау)
Математикадан ҰБТ-да кездесетін күрделі есептерді шығарудың тиімді әдістері. Әдістемелік құрал
«Математикадан ҰБТ-да кездесетін күрделі есептерді шығарудың тиімді әдістері» әдістемелік құралында ҰБТ-да кездесетін әр түрлі есептер жинақталып, оларды шешудің оңтайлы әдістемесі көрсетілген.
Әдістемелік құралдың негізгі мақсаты – оқушыларға математикадан ұлттық бірыңғай тестілеу (ҰБТ) тапсырмаларында кездесетін көптеген шығару жолы қиын саналатын тапсырмаларды орындаудың тиімді әдістерін ұсыну және оқушыларға есептерді шешудің тиімді әдістемесін келтіру арқылы олардың ойлау қабілеті мен шығармашылық белсенділігінің дамуына ықпал ету, есептерді шығару дағдысын жетілдіре түсуге көмектесу болып табылады.
Әдістемелік құрал мұғалімдер мен мектеп оқушыларына, мектеп бітіруші түлектерге арналған.
Әдістемелік құрал білім басқармасы жанындағы эксперттік кеңестің шешімімен ұсынылды.
Кіріспе
«Математикадан ҰБТ тапсырмаларында кездесетін күрделі есептерді шығарудың тиімді әдістері» әдістемелік құралында оқушыларға математикадан ұлттық бірыңғай тестілеу (ҰБТ) тапсырмаларында кездесетін көптеген шығару жолы қиын саналатын тапсырмаларды орындаудың тиімді әдістері ұсынылған.
Әдістемелік құралда ұсынылған функция мәндерінің жиынын анықтау әдістемесі, тригонометриялық және кері тригонометриялық функциялары бар өрнектердің мәндерін табу әдістемесі, күрделі радикалдары бар өрнектерді ықшамдау әдістемесі, жай теңсіздіктер жүйесін шешу әдістемесі, аралас теңсіздіктер жүйесін шешу әдістемесі, анықталмаған сызықтық теңдеулерді шешу алгоритмі (авторлық тәсіл), қозғалысқа арналған есептерді графиктік тәсілмен шешу әдістемесі, функцияның ең кіші оң периодын табу әдістемесі, функцияның жұптылығы мен тақтылығын анықтау әдістемесі, сандардың ең кіші ортақ еселік (ЕКОЕ) пен ең үлкен ортақ бөлгішін (ЕҮОБ) Евклид алгоритімін пайдаланып анықтау әдістемесі берілген. Есептерді шығарудың мұндай әдістері мектеп оқулықтарында кездеспейтіндіктен, көрсетілген әдістеме ҰБТ кезінде оқушыларға үлкен көмек болатыны сөзсіз. Әдістемелік құралда кездесетін жай бөлшектерді Евклид алгоритмін пайдаланып қысқарту да кесте арқылы өте ұтымды орындалады. Сондықтан, осы тәсіл арқылы ЕКОЕ пен ЕҮОБ табу тапсырмаларын орындау, сандарды жай көбейткіштерге жіктеу тәсіліне қарағанда, оқушыларға еш қиындық келтірмейді.
-
Функция мәндерінің жиынын анықтау әдістемесі
 ,
,  және тағы басқа
түріндегі функциялардың мәндерінің жиынын анықтауға арналған
есептер мектеп бітірушілердің ұлттық бірыңғай тест (ҰБТ)
тапсырмаларында жиі кездеседі.
және тағы басқа
түріндегі функциялардың мәндерінің жиынын анықтауға арналған
есептер мектеп бітірушілердің ұлттық бірыңғай тест (ҰБТ)
тапсырмаларында жиі кездеседі.
Мектеп оқулықтарының бірде
бірінде мұндай есептер арнайы қарастырылмағандықтан, оқушылардың
көпшілігінің бұл есептерді шығара алмайды. Математикалық талдау
аппараттарын пайдалана отырып функцияны зерттеу, оның графигін салу
арқылы бұл тапсырмаларды орандауға болады. Бірақ ҰБТ кезінде мұндай
тапсырмаларды 1,5-2 минут ішінде орындау кез келген оқушының
қолынан келмейтіні белгілі. Функцияның мәндерінің жиынын табу көп
жағдайда теңдеудің шешімін табумен байланысты
болады.  саны
саны  функциясының мәндер
жиынына кіруүшін,
функциясының мәндер
жиынына кіруүшін,  теңдеуінің,
мұндағы
теңдеуінің,
мұндағы  , шешімінің болуы
қажетті және жеткілікті. Бұл теңдеудің
, шешімінің болуы
қажетті және жеткілікті. Бұл теңдеудің
 - дің мәніне
байланысты бір түбірі, бірнеше түбірі немесе түбірі болмауы да
мүмкін. Осындай есептерді шығарудың оңтайлы тәсілдерінің бірі
төменде келтірілген.
- дің мәніне
байланысты бір түбірі, бірнеше түбірі немесе түбірі болмауы да
мүмкін. Осындай есептерді шығарудың оңтайлы тәсілдерінің бірі
төменде келтірілген.
Ол үшін,
алдымен  (мұндағы
(мұндағы  ) түріндегі гиперболаны
қарастырайық. Бұл функцияның мәндер жиыны
) түріндегі гиперболаны
қарастырайық. Бұл функцияның мәндер жиыны
 екендігі
ақиқат.
екендігі
ақиқат.
1-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.  немесе
немесе  .
.
Жауабы:  .
.
2-мысал.
 функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.  сандары бөлшектің
бөлімінің нөлдері болғандықтан, бұл функция осы
нүктелерде анықталмайды. Ал,
сандары бөлшектің
бөлімінің нөлдері болғандықтан, бұл функция осы
нүктелерде анықталмайды. Ал,  саны алымы мен бөлімінің
ортақ нөлі. Сондықтан,
саны алымы мен бөлімінің
ортақ нөлі. Сондықтан,  болса,
онда
болса,
онда![]()
 функцияның
функцияның  нүктесіндегі
мәні
нүктесіндегі
мәні  , яғни,
берілген функцияның
мәні
, яғни,
берілген функцияның
мәні  -тің ешбір мәнінде 1-ге
тең бола алмайды, ендеше біріншіден
-тің ешбір мәнінде 1-ге
тең бола алмайды, ендеше біріншіден  .
Екіншіден,
.
Екіншіден,  гиперболасының мәндер
жиыны
гиперболасының мәндер
жиыны  екендігі
белгілі.
екендігі
белгілі.
Сондықтан, берілген функцияның
мәндер  .
.
Жауабы:
 .
.
3-мысал.
 функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі. Бөлшектің алымы мен
бөлімінің ортақ түбірі жоқ екендігі белгілі. Берілген
функцияны  немесе
немесе  түріне келтіреміз. Яғни,
функцияның мәндер жиынын табу үшін,
у
параметрдің қандай мәндерінде
соңғы квадрат теңдеудің шешімі болатындыған анықтау жеткілікті. Ол
үшін D
түріне келтіреміз. Яғни,
функцияның мәндер жиынын табу үшін,
у
параметрдің қандай мәндерінде
соңғы квадрат теңдеудің шешімі болатындыған анықтау жеткілікті. Ол
үшін D![]() 0 теңсіздігін құрып,
шешеміз:
0 теңсіздігін құрып,
шешеміз:  .
.
Соңғы теңсіздіктің
шешімі:  болатындығына көз
жеткізу қиын емес.
болатындығына көз
жеткізу қиын емес.
Жауабы:
4-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі. Мұндай есептерді квадрат
үшмүшенің толық квадратын айыру тәсілі және туынды арқылы
функцияның кризистік нүктесін анықтап, функцияның ең үлкен немесе
ең кіші мәндерін табу арқылы да шығаруға болады. Алайда, парабола
төбесінің ординатасының формуласын қолдану, тапсырманы тез және
дұрыс орындауға көмектеседі. Атап айтқанда,
 парабола төбесінің
ординатасының формуласы болғандықтан,
парабола төбесінің
ординатасының формуласы болғандықтан,
 болса,
онда
болса,
онда
 ,
ал
,
ал  болса,
онда
болса,
онда  болады.
болады.
Біздің
мысалда  ,
ал
,
ал  болғандықтан,
болғандықтан,  .
.
Жауабы:
 .
.
5-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі. Квадрат түбір
астындағы  квадрат үшмүшеліктің
мәндер жиыны
квадрат үшмүшеліктің
мәндер жиыны  )
болғандықтан,
)
болғандықтан,
 болатындығы
анық.
болатындығы
анық.
Жауабы:
 .
.
Ескерту: Сан аралығының «квадрат түбірін табу» амалының жазылуы ерсілеу көрінгенмен, оның дұрыстығы өрнектің монотондылығымен түсіндіріледі.
6-мысал.
 функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.  функциясының мәндер
жиыны:
функциясының мәндер
жиыны:
 болғандықтан,
болғандықтан,

 .
.
Жауабы: 
7-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.  .
.
Жауабы:  ].
].
8-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.
 .
.
Жауабы:  ].
].
9-мысал. у= функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.  функциясының мәндер
жиыны
функциясының мәндер
жиыны  ]
болғандықтан,
]
болғандықтан,  .
.
Жауабы:  ].
].
10-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі.  (мұндағы a
(мұндағы a функциясының мәндер
жиыны
функциясының мәндер
жиыны  болғандықтан,
болғандықтан,  функциясының мәндер
жиыны:
функциясының мәндер
жиыны:
 .
.
Жауабы:  .
.
11-мысал.  функциясының мәндер
жиынын анықтаңыз.
функциясының мәндер
жиынын анықтаңыз.
Шешуі. 
![]()
 ⟺
⟺  .
Ал,
.
Ал,  теңдеуінің шешуі болу
үшін,
теңдеуінің шешуі болу
үшін,  шарты орындалуы қажет.
Сондықтан,
шарты орындалуы қажет.
Сондықтан,  .
.

![]()
 .
.
Жауабы: 
-
Тригонометриялық және кері тригонометриялық функциялары бар өрнектердің мәндерін табу әдістемесі.
12-мысал.  және
және  болса,
онда
болса,
онда  мәндерін
табыңыз.
мәндерін
табыңыз.
Шешуі. Көмекші тікбұрышты үшбұрышты пайдаланайық.

1-сурет.
 болғандықтан,
болғандықтан,  ,
ал,
,
ал,  шартын
ескерсек:
шартын
ескерсек:  .
.
Жауабы:  .
.
13-мысал.  есептеңіз.
есептеңіз.
Шешуі.  және
және  деп белгілесек, онда
анықтама бойынша
деп белгілесек, онда
анықтама бойынша  .
Ендеше,
.
Ендеше, 
 (12-мысал әдісімен).
Сондықтан
(12-мысал әдісімен).
Сондықтан

 .
.

шағым қалдыра аласыз















