Баспалдақты үшбұрыш

Қызылорда облысы

Жаңақорған ауданы Бесарық ауылы

№54 Ж. Қыдыров атындағы жалпы

орта мектеп математика

пәнінің мұғалімі

Күнтөреева Макира

Баспалдақты үшбұрыш

Мазмұны

1. Кіріспе

2. Баспалдақты үшбұрыш және оның қасиеттері

3. Баспалдақты үшбұрышқа қатысты теоремалар

4. Баспалдақты үшбұрыштың ауданын есептеу формулалары

5. Қорытынды

6. Қолданылған әдебиеттер тізімі

Кіріспе

«Геометрия» (грекше геометріа, ге – Жер және метрсо – өлшеймін) атауы дәл аударғанда «жер өлшеу» болады. Бұл ғылымның алғашқы нұсқалары Ежелгі Мысыр (Египет) елінде шыққан. Бұл жөнінде, біздің заманымыздан бұрынғы 4 ғасырда өмір сүрген грек математигі Евдем «Жер телімшелерін өлшеу нәтижесінде мысырлықтар геометрия ғылымын шығарды» деп жазған. Жер өлшеу өнерін мысырлықтардан үйренген ежелгі гректер оны алғашқы кезде өз тілінде «геометрия» деп атаған. Осы сөз кейін көптеген халықтардың тіліне еніп, ғылыми термин болып кеткен. Геометрия заңдылықтарын жер телімшелерін өлшеуде қолдануға әбден болады, бірақ геометрияның негізгі арнасы ол емес. Геометрияда қолданылатын мәселелер сан алуан. Геометрияда стреометрия есептерінің басым көпшілігі планиметрия есептеріне келіп тірелетіні белгілі. Планиметриядағы фигуралардың ішінде шеңбер мен үшбұрыштың алатын орны бөлек. Көп жағдайда үшбұрыштардың медианалары, биссектрисалары, биіктігі және олардың қасиеттері қарастырылып симедиана, антипараллель, үшбұрышқа сыртқары-іштей сызылған шеңбер ортоүшбұрыш т.с.с. тақырыптар, ұғымдар қарастырылмайды. Осы олқылықты толтыру мақсатында ғылыми жұмысымды қарастырыла бермейтін үшбұрыштардың қасиеттерін зерттеуге арнадым.

Оған себеп С.И.Зетельдің «Үшбұрыштар геометриясы» және Г. С. М. Коксетер мен С.Л.Грейтцердің (H.S.Coxeter and S.L. Greitzer) «Геометрияның көркемділігімен жүздесу» атты кітаптарындағы үшбұрыштың мектептегі геометрия пәнінде айтыла бермейтін тамаша қасиеттері және соңғы уақыттарда дәлелденген теоремалар себеп болды.

Жұмыстың бір тармағында баспалдақты үшбұрыштарды қарастырдым. Р нүктесі АВС үшбұрышының ішкі нүктесі болсын. Р нүктесінен АВС үшбұрышының АВ, ВС, СА қабырғаларына түсірілген биіктіктердің В₁, А₁, С₁ табандары төбелері болатын А₁В₁С₁ үшбұрышы бірінші баспалдақты үшбұрыш деп, ал Р нүктесі баспалдақ нүктесі деп аталады. Осы тармақта АВС үшбұрышы үшінші баспалдақты А₃В₃С₃ үшбұрышына ұқсас болатыны дәлелденді.

Өзектілігі: Соңғы 200 жылда математика ғылымы өте қатты қарқынмен дамыды, жаңа салалар пайда болды: математикалық талдау, топология, дифференциялды геометрия , эвклидті геометрия тағы басқа. Геометрия саласында көп қарастырылмайтын фигураларды зерттеу.

Жұмыстың көкейкестілігі.

Зерттеу обьектісі: ортоүшбұрыш, баспадақты үшбұрыш, шеңбер, өстері бірегей шеңбер және үшбұрыш.

1. Мақсаты: Мектептегі математика пәнінің бағдарламасында қарастырыла бермейтін фигураларды зерттеу. Баспалдақты үшбұрыш және оның қасиеттерін зерттеу.

2. Теориялық маңызы: Ұсынып отырған жұмысымды салу есептерін шағаруда қолдану.

3. Практикалық маңызы: «Шеңберге тиісті кез келген А₁, В₁, С₁ нүктелері берілген. Шеңберге іштей төбелерінен жүргізілген биіктіктер берілген А₁, В₁, С₁ нүктелерінен өтетіндей іштей үшбұрыш салу керек» есебін шығаруда пайдалану.

4. Ақпарат: Берілген тақырыпқа байланысты ғылыми мақалаларды, әдебиеттерді зерттеу.

Баспалдақты үшбұрыш

Р нүктесі АВС үшбұрышының ішкі нүктесі болсын, ал Р нүктесінен ВС, СА және АВ қабырғаларына түсірілген биіктіктердің табандарын В₁, С₁ және А₁ деп белгілейік. Осы А₁, В₁, С₁ болатын А₁В₁С₁ үшбұрышы АВС

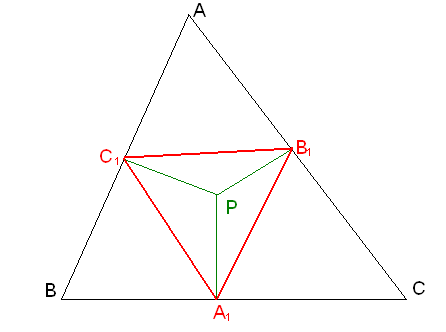
1-сурет

үшбұрышының Р нүктесіне қатысты баспалдақты үшбұрышы деп аталады. Егер Р нүктесі АВС үшбұрышының ортоцентрі болса, онда А₁В₁С₁ үшбұрышы ортоүшбұрыш болады, ал егер Р нүктесі АВС үшбұрышына сырттай сызылған шеңбердің центрі болса, онда А₁В₁С₁ үшбұрышы ортаүшбұрыш болатыны түсінікті. Р нүктесін баспалдақты А₁В₁С₁ үшбұрышының баспалдақ нүктесі деп айтамыз.

Осы баспалдақ үшбұрышты зерттейміз. В₁С₁ нүктелерінде Р, В, А, РВ, РСА бұрыштары тік болғандықтан А₁РС₁В төртбұрышына сырттай шеңбер сызуға болады. Басқаша айтқанда Р нүктесі А₁В₁С₁ үшбұрышына сырттай сызылған шеңбердің бойында жатады. Бұл А₁В₁С₁ үшбұрышына синустар теоремасын пайдаланамыз. Сонда:

Осы сияқты АВС үшбұрышына да шеңбер сызамыз.

Бұл теңдіктерден

Осы дәрежесі

және

Сонымен біз мынадай теореманы дәлелдедік.

Баспалдақты үшбұрышының қасиеттерi:

1. Егер үшбұрыштың төбелерiне баспалдақты нүктесiне қашықтық x, y, z болса, онда баспалдақты үшбұрышының қабырғаларының ұзындығы мынаған тең

Мұндағы сырттай сызылған шеңбердің радиусы.

Дәлелдеуі:

Әр алынған АС₁РВ₁, ВА₁РС₁, СВ₁РА₁ төртбұрыштарға сырттай шеңбер сызуға болады.

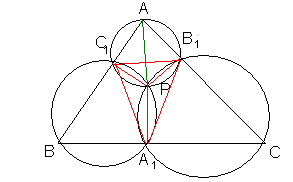
2-сурет

нүктесінен шыққан тік бұрыш сырттай сызылған шеңбердің диаметрінде орналасқан, басқаша айтқанда нүктесі үшбұрышына сырттай сызылған шеңберде орналасқан. Осы сияқты, нүктесі үшбұрышына сырттай сызылған шеңберде орналасқан. төртбұрышына сырттай шеңбер сызамыз, диаметрін . белгілей отырып, үшбұрышына синустар теоремасын қолданамыз:

үшбұрышына синустар теремасын қолдансақ, онда

(2)

Демек

Яғни

(3)

Мұндағы

Егер тең болса, онда баспалдақты үшбұрышының қабырғаларының ұзындығы мынаған тең.

Қасиет дәлелденді.

Ескерту: егер нүктесі сырттай сызылған шеңбердің центірі болса (x=y=z=R) суретте көрсетілген, онда баспалдақты үшбұрыштың қабырғаларының ұзындығы мынадай:

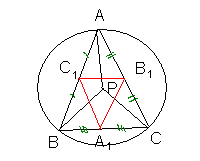
3-сурет

2. Үшбұрыштың төбелерінен қабырғасына түсірілген перпендикулярлардың табаны бір нүктенің бойында жатады, сонда тек сонда ғана егер бүл нүкте сырттай сызылған шеңберде жатса.

Бұл осы үшбұрыш туралы осы нүктенi Симсон түзуі ретінде белгілі. Оның геометриялық идеялары үшiн Симсон түзуі деп алаған. Тарихшыларға дегенмен оның ғалым жұмыстарында табудың сәтi түспедi. Шындықта Вильям Уоллесом 1797 жылда ашқан болатын.

Дәлелдеу:

нүктесін сырттай сызылған шеңбердің бойында жататын жағдайын қарастырайық.

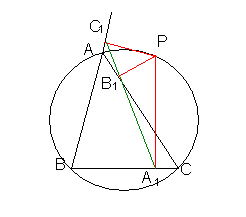4-сурет

Анықтаулар үшін нүктесін доғасында жатыр деп қарастырамыз, В нүктесіне тиісті емес. Қалған жағдайларда А, В, С бұрыштарын қою арқылы көреміз. бұрыштары тік болғандықтан, нүктесі үшбұрыштарына сырттай сызылған шеңберге тиісті. Сондықтан:

еспетесек, онда:

нүтелері шеңберде жатқандықтан:

А,В,С, Р нүктелері

шеңберде жақандықта:

Қорытындылай келгенде:

Бұл жерден нүктелері бір түзудің бойында жататынын көреміз..

Демек, қасиет дәлелденді.

Ескерту: Баспалдақты нүктесi нүкте тек қана бұл нүктеге (-шi сурет) АВС ты үшбұрыш айнала суреттеп айтылған шеңбер үстiнде жатыруға тыйым салып баяулату мүмкiн анықтау бойынша үшбұрыштың iшi болды тек қана бұл нүктеге (4-шi сурет) АВС үшбұрыш айнала суреттеп айтылған дөңгелекке үстiнде жатыруға тыйым салып баяулату мүмкiн үшiн талап.

5-сурет

Баспалдақты үшбұрыш үшін теоремалар.

Теорема 2.10: Үшбұрыштың L нүктесінен сәйкесінше қабырғасына ішкі перпендикулярлар l_a, l_b, l_с жүргізілсе, онда:

Дәлелдеу:

L нүктесін үшбұрыштың төбелерімен қосамыз. АВС үшбұрышы үш үшбұрышқа бөлінеді.

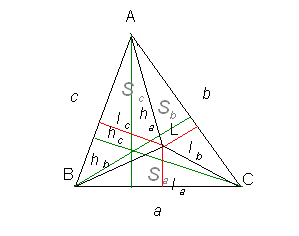6-сурет

Бұл үшбұрыштардың ауданын белгілейміз. Онда :

Теңдіктің оң және сол жағы біріктірсек, онда:

болғандықтан, онда .

Теорема дәлелденді.

Салдар : Теңқабырғалы үшбұрыштың кез келген нүктесінен оның қабырғасына дейінгі қашықтық тұрақты және үшбұрыштың биіктігіне тең.

Дәлелдеуі : Тең қабырғалы үшбұрыштың биіктіктері тең. Онда мына теңдіктерді қанағаттандырады:

Салдар дәлелденді.

Теорема 2.11: Үшбұрыштың кез келген нүктесінен қабырғасына түсірілген перпендикулярлар үшбұрышты алты жаққа бөліп, олардың үш қабырларының квадраттары қалған үш қабырғасының квадратына тең.

Дәлелдеуі: О нүктесінен сәйкесінше қабырғаларына түсірілген перпендикулярлар жүргіземіз.

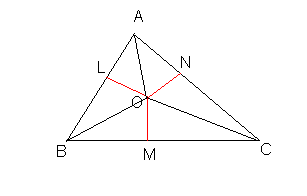7-сурет

Онда Пифагор теоремасы бойынша және үшбұрыштарынан алатынымыз:

Немесе

(51)

Ал және үшбұрыштарынан алатынымыз:

(52)

Онда және үшбұрыштарынан:

Теңдіктерді біріктірсек:

Немесе

Теоре