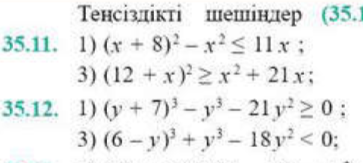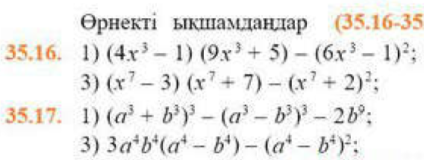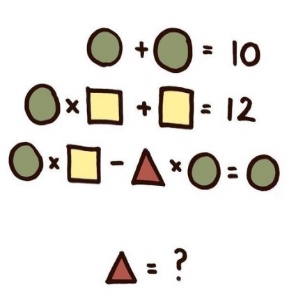Тексерілді: Г.Караманова
|
Бөлім: |
6.3В Бір айнымалысы бар сызықтық теңсіздіктер |
||
|
Педагогтің Т.А.Ә.(болған жағдайда |
Кужаева Г.К |
||
|
Күні: |
10.02.25ж |
||
|
Пән/Сынып: |
Математика, 6 «Б» сынып. |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Бір айнымалысы бар сызықтық теңсіздік. Бір айнымалысы бар сызықтық теңсіздіктерді шешу. |
||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары: |
6.2.2.10
6.2.2.11
алгебралық түрлендірулердің көмегімен теңсіздіктерді
|
||
|
Сабақтың мақсаты: |
алгебралық
түрлендірулердің көмегімен теңсіздіктерді ЕБҚ
мақсаты : |
||
|
Сабақтың құндылығы: |
«Жасампаздық пен жаңашылдық» Топпен, жұппен жұмыс орындау барысында ақпаратты талдау, жаңа идеяларды ұсыну, қазіргі заманғы цифрлық құралдар мен технологияларды игеру және идеяларды іске асыруда ресурстарды тиімді пайдалану |
||
Сабақтың барысы
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|||||||||||
|
5 минут |
Ұйым дастыру |
Сәлеметсіздерме! Бүгін, Бір айнымалысы бар сызықтық теңсіздік. Бір айнымалысы бар сызықтық теңсіздіктерді шешу.тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: - kx > b, kx ≥ b, kx < b, kx ≤ b түріндегі сызықтық теңсіздіктерді шешу алгоритмі. -kx > b, kx ≥ b, kx < b, kx ≤ b түріндегі сызықтық теңсіздіктерді шешу және теңсіздіктердің шешімдерін координаттық түзуде кескіндеу. Үй тапсырмасын тексеру. №932, №933. "Миға шабуыл" -Сан аралықтары дегеніміз не? -Сан аралығының қандай түрлерін білесіңдер? -Қатаң теңсіздіктің шешімдер жиыны координаталық түзуде қалай кескінделеді? -Қатаң емес теңсіздіктің сан аралығын жазу үшін қандай жақша қолданылады? -Неліктен кесіндіде координаталық түзуде көрсетілген сандар шешімдер жиынына кіреді? - деген жабық және ашық сұрақтар қоямын. |
Амандасады, үй тапсырмасына жауап береді. Сұрақтарға жауап береді |
|
Оқулық, жұмыс дәптері Тақта слайд |
|||||||||||
|
10 мин |
Жаңа сабақ |
Бір айнымалысы бар сызықтық теңсіздіктерді шешу І. Бір айнымалысы бар сызықтық теңсіздік. ах > b және ах < b (немесе ах b және ах b) түріндегі теңсіздіктер бір айнымалысы бар сызықтық теңсіздіктер деп аталады. Мұндағы a ≠ 0 және b – қандай да бір сандар, х – айнымалы (белгісіз). Айнымалының теңсіздікті тура санды теңсіздікке айналдыратын мәнін бір айнымалысы бар сызықтық теңсіздіктің шешімі деп атайды. Мысалы, x + 6 < 18. x-тің орнына 2 санын қойса, онда 2 + 6 < 18, 8 < 18 дұрыс теңсіздігі шығады. x – теңсіздіктің шешімі. Теңсіздікті шешу – оның барлық шешімін табу немесе шешімдері болмайтынын дәлелдеу.
Егер теңсіздіктің екі жақ бөлігі де бірдей теріс санға көбейтіліп не- месе бөлініп, сонымен бірге теңсіздік белгісі қарама-қарсы теңсіздік белгісіне өзгертілсе, берілген теңсіздік мәндес теңсіздікке түрленеді.
|
Тақырып бойынша ресурстарды қарап, танысады 1-мысал. 3х – 7 < х + 3 және 3х – х < 3 +7 – мәндес теңсіздіктер.
2. Егер теңсіздіктің екі жақ бөлігі де бірдей оң санға көбейтілсе не- месе бөлінсе, берілген теңсіздік мәндес теңсіздікке түрленеді.
|
|
Оқулық, жұмыс дәптері
Тақта слайд |
|||||||||||
|
25 минут
|
Бекіту тапсыр масы |
Топтық жұмыс. №1.
№2. Екі қаланың арақашықтығы 300 км-ден кем болатын. Пойыз бір қаладан шығып, екінші қалаға қарай 3 сағат жүргенде екінші қалаға дейін 45км қашықтық қалды. Пойыздың жылдамдығын бағалаңыз. №3. x-тің қандай мәндерінде өрнектің мәні теріс сан болады: 2x – 5; 1,4x – 7; 6 – x? «Кім жылдам» №1. Теңсіздікті шешіңіздер : а) 2х ≤ 10 д) у-4 ≥ 14 б) х+3 ≥ 7 е) −3у > −9 в) −4х < 8 ж) 13 < 8-х г) -х <5 |
Оқулықтан тақырыпқа қатысты есептерді шығарады.
Жауаптар: х < 3 х ≤5 х ≥ 4 х > −2 х ≥ 18 х < −5 х > −5 |
Дескриптор: - берілген бір айнымалысы бар сызықтық теңсіздіктерді шешеді.
«Басбармақ» әдісімен бағалау алады жүргізіледі |
Интернет ресурстары Жалпы білім беретін мектептің 6–сыныбына арналған оқулық. Оқулық авторлары: Т.А.Алдамұратова, Қ.С.Байшоланова, Е.С.Байшоланов Алматы «Атамұра» баспасы 2018 жыл |
|||||||||||
|
|
|
1-жұп: 1 2-жұп: 2 3-жұп: 3 3х - 7< х+1 2+х>8 – х 1 - х≤2х - 5 х<4 х>3 х≥2 (-∞; 4) (3; +∞) [2; +∞) 4-жұп: 4 5-жұп: 5 2x+1>x+6 4x+2>3x+1 x>5 x> - 1 (5; +∞) (-1; +∞) Өз бетімен жұмыс. Тест тапсырмасы
А) ашық сәуле Б) интервал В) кесінді Г) сәуле 2. Белгіленумен жаз: 1-ден 4-ке дейінгі кесінді А) (1;4) Б) [1;4] В) (1;4] Г) [1;4) 3. Белгіленуімен жаз: 1-ден 3-ке дейінгі 3 саны қоса алынған жартылай интервал А) (1;3] Б) [1;3] В) (1;3) Г) [1;3) 4. [4;9]сан аралығының аты: А) кесінді Б) сәуле В) ашық сәуле Г) интервал 5. Белгіленуімен жаз: 2-ден 7-ге дейінгі интервал А) [2;7] Б) (2;7] В) [2;7) Г) (2;7) c) [–0,5; 3,5] d) (–∞; 0,5] ∪ [3,5; +∞) |
Жауаптар: №1 а) х ≤5 б) х ≥ 4 в) х > −2 г) х > −5 №2
Оқулықтан тақырыпқа қатысты есептерді шығарады. Оқулықтан №1003, №1005. |
Дескриптор: Білім алушы: - интервалды жазады; - жарты интервалды жазады; - сәулені жазады; - кесіндіні жазады;
|
Интернет ресурстары
Жалпы білім беретін мектептің 6–сыныбына арналған оқулық. Оқулық авторлары: Т.А.Алдамұратова, Қ.С.Байшоланова, Е.С.Байшоланов Алматы «Атамұра» баспасы 2018 жыл |
|||||||||||
|
|
Жеке жұмыс |
№1. Кестеде теңсіздіктер және оның шешімдері берілген. Шешімі дұрыс көрсетілген болса «+», ал шешімі қате көрсетілген болса «-» қойыңыз.
|
Тапсырманы орындайды |
Дескриптор: -Теңсіздіктің шешімдерінің дұрыс, бұрыстығын тексереді. |
|
|||||||||||
|
5 минут
|
|
Кері байланыс
Үйге тапсырма. №940, №943. |
|
|
|
|||||||||||
Тексерілді: Г.Караманова
|
Педагогің Аты, Тегі; Әкесінің аты (бар болған жағдайда): |
Кужаева Г |
||||||||||||||||||||
|
Пән/Сынып: |
7 «А» сынып. Қатысқандар саны: Қатыспағандар саны: |
||||||||||||||||||||
|
Күні: |
10.02.25ж |
||||||||||||||||||||
|
Бөлім: |
Қысқаша көбейту формулалары |
||||||||||||||||||||
|
Сабақтың тақырыбы: |
Қысқаша көбейту формулаларының көмегімен өрнектерді түрлендіру |
||||||||||||||||||||
|
Оқу бағдарламасына сәйкес оқыту мақсаты: |
7. 1.2.14 тиімді есептеу үшін қысқаша көбейту формулаларын қолдану; |
||||||||||||||||||||
|
Сабақтың мақсаттары: |
- қысқаша көбейту формулаларын алгебралық өрнектерді ықшамдау кезінде қолдана алады |
||||||||||||||||||||
|
Сабақтың құндылығы |
«Жасампаздық пен жаңашылдық» құндылығына: Топпен, жұппен жұмыс орындау барысында ақпаратты талдау, жаңа идеяларды ұсыну, қазіргі заманғы цифрлық құралдар мен технологияларды игеру және идеяларды іске асыруда ресурстарды тиімді пайдалану |
||||||||||||||||||||
|
Сабақ барысы: |
|||||||||||||||||||||
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
||||||||||||||||
|
5 минут |
Ұйым дастыру |
Сәлеметсіздерме! Бүгін, Қысқаша көбейту формулаларының көмегімен өрнектерді түрлендіру тақырыбын қарастырамыз. Бүгінгі сабақта меңгеретініңіз: - Қысқаша көбейту формулаларын біледі және қолдана алады; - қысқаша көбейту формулаларын алгебралық өрнектерді ықшамдау кезінде қолдана алады -Қысқаша көбейту формулаларын өрнектерді көбейткіштерге жіктеу кезінде қолдана алады; Үй тапсырмасын тексеру. № |
Амандасады, сабаққа дайындалады. Сұрақтарға жауап береді |
«Бағдаршам» арқылы қалыптастыру шы бағалау |
Оқулық; оқу құралдары; тақта; слайд; |
||||||||||||||||
|
10 мин |
Жаңа сабақ |
1) Көпмүшені көбейткіштерге жіктеуді қалай түсінесіз? Көпмүшені көбейткіштерге жіктеу – көпмүшені екі немесе бірнеше көпмүшелердің көбейтіндісі түріне келтіру 2) Көпмүшені көбейткіштерге жіктеудің қандай түрлерін білесіз? (Ортақ көбейткішті жақшаның сыртына шығару, қысқаша көбейту формулаларын пайдалану, топтау тәсілі) 3) Көпмүшені көбейткіштерге жіктеу не үшін қажет? Көпмүшені көбейткіштерге жіктеу дағдысы өрнектерді түрлендіруде, алгебралық бөлшектерді қысқартуда, теңдеу мен теңсіздіктерді шешуде қажет. 4) Көбейткіштерге
жіктеңіз:
5) Көбейткіштерге жіктеуге есеп ойдан құрастырыңыз. 6) Топтау тәсілімен көбейткіштерге жіктеу тәсілін сипаттаңыз. Топтау тәсілімен көбейткіштерге жіктеу алгоритмі: 1. Көпмүшенің ортақ көбейткіштері бар мүшелерін бірыңғай топтарға бөлу; 2. Әр топтағы мүшелердің бірмүше түріндегі ортақ көбейткішін жақша сыртына шығару; 3. Әр топтағы мүшелердің бірмүше түріндегі ортақ көбейткішін жақша сыртына шығару; |
Тақырып бойынша ресурстарды қарап, танысады ⠀⠀ ⠀⠀ 2). Шешуі. Айырма кубының формуласын қолданып өрнекті түрлендір: (–x – 4y)3 = (–x)3 – 3 ∙ (–x)2 ∙ 4y + 3 ∙ (–x) ∙ (4y)2 – (4y)3 = –x3 – 12x2y – 48xy2 – 64y3. |
«Бағдаршам» арқылы қалыптастыру шы бағалау
|
Оқулық; оқу құралдары; тақта; слайд; Карточкалар;7 сыныпқа арналған оқулық Презентация |
||||||||||||||||
|
15 минут |
Бекіту тапсырмасы |
a) b)
Тапсырма. Төменгі әр теңдеу географиялық атаулармен аталған. Теңдеулердің жауабына әр географиялық атау туралы қосымша ақпарат сәйкес келеді. Берілген теңдеулерді шешіп, мәтіндегі түбірлердің орнына сәйкес географиялық атауды енгізе отырып, әрқайсысы туралы туралы ақпарат алыңыз. Әлемдегі ең үлкен
жанартау Әлемдегі ең биік тау
– Әлемдегі ең биік сарқырама
– Әлемдегі ең ұзын тау
– Әлемдегі жауын-шашын ең көп
түсетін жер – Әлемдегі ең үлкен тау асты
мұздығы -
Әр оқушы өзін дайын жауап бойынша тексереді. Әлемдегі ең биік тау – Гималай (Джомолунга, 8848 м) Әлемдегі ең ұзын тау – Анд (9000 км) Әлемдегі жауын-шашын ең көп түсетін жер – Черапунджи (жылына 12000 мм) Әлемдегі ең үлкен тау асты мұздығы - Хабборт (145 км) Әлемдегі ең биік сарқырама – Анхель (1054 м) Әлемдегі ең үлкен жанартау Гавайядағы Мауна-Лао (ені 10 км, тереңдігі 180 км)
Оқулықпен жұмыс. №5.128, №5.129. |
Оқушылар дескрипторға сәйкес тапсырмаларды орындайды.
Жазылуы бойынша формулаларды жалғастырады (1) ҚКФ ажырата алады (1) Формуланы ауызша тұжырымдай алады
Оқулықтан есептерді шығарады.
|
Дескриптор: Топтау тәсілін дұрыс қолдана алды; Ортақ көбейткішті жақша сыртына шығарады;
ҚБ:«Бас бармақ» әдісі
|
Презентация Слайд
Интернет ресурстары
Оқулық; оқу құралдары; тақта; слайд; Карточкалар;7 сыныпқа арналған оқулық Презентация |
||||||||||||||||
|
10 мин |
Оқулықпен жұмыс |
Оқулықтан есептер шығару:
|
Тапсырманы орындайды
|
Оқушының тақтадағы белсенділігіне байланысты ауызша бағалау |
Жалпы білім беретін мектептің 7–сыныбына арналған оқулық. Тақта Бор Кітап Дәптер
|
||||||||||||||||
|
5 минут
|
|
Бүгінгі сабақта:
- қысқаша көбейту формулаларын алгебралық өрнектерді ықшамдау кезінде қолдана алады -Қысқаша көбейту формулаларын өрнектерді көбейткіштерге жіктеу кезінде қолдана алады;
Үйге тапсырма.№ |
Тақырыпты меңгергенін анықтау |
Кері байланыс |
Оқулық; оқу құралдары; тақта; слайд;
|
||||||||||||||||
Тексерілді: Г.Караманова
|
Бөлім: |
8.3В Квадраттық функция |
||
|
Педагогтің Т.А.Ә.(болған жағдайда |
Кужаева Г.К |
||
|
Күні: |
07.02.2025ж |
||
|
Пән/Сынып: |
Алгебра, 8 “Ә” сынып. |
Қатысушылар саны: 24 |
Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Квадраттық функция және оның графигі |
||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары: |
8.4.1.4 аргументтің берілген мәндері бойынша функцияның мәндерін табу және функцияның мәні бойынша аргументтің мәнін табу; |
||
|
Сабақтың мақсаты: |
Аргументтің берілген мәндері бойынша функцияның мәндерін, және функцияның мәні бойынша аргументтің мәнін табуға дағдыландыру. |
||
|
Сабақтың құндылығы |
Жасампаздық және жаңашылдық - стандарттан тыс ойлау және әдеттегі әрекеттерінің шеңберінен шыға білу қабілеті; |
||
Сабақтың барысы
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
||||||
|
5 минут |
Ұйым дастыру |
Сәлеметсіздерме! Бүгін, Функцияның мәні бойынша аргументтің мәнін табу тақырыптарын қарастырамыз Бүгінгі сабақта меңгеретініңіз: - аргументтің берілген мәндері бойынша функцияның мәндерін табу және функцияның мәні бойынша аргументтің мәнін табу; |
Амандасу.Сыныпты түгендеу. Сабаққа дайындау, оқу құралдарын алу. Үй тапсырмасын айту. |
«Екі жұлдыз, бір тілек» |
Оқулық |
||||||
|
10мин |
Негізгі бөлім |
Тапсырма. №1. у=х2 функциясының графигін координаталық оське параллель жылжытып, әрбір жағдай үшін берілген функцияны жазыңдар. а) 3 бірлік оңға және 2 бірлік жоғары; у=(х-3)2+2 ә) 1 бірлік солға және 3 бірлік жоғары; у=(х+1)2+3 б) 5 бірлік оңға және 4 бірлік төмен у=(х-5)2-4 |
Сұрақтарға жауап береді. |
Дескриптор: - y = x2 функциясының анықтамасы мен қасиетін біледі - квадрат функцияның графигін салады -графиктерді түрлендірулерді орындайды |
Тақта Бор Кітап Дәптер Интерактивті тақта Бағалау парақтары |
||||||
|
25 мин |
Бекіту тапсырмасы |
Тапсырмалар. №1.
а - ның қандай
мәндерінде у=ах2 - 16х+1 параболасының симметрия осі х=4 түзуі
болады? Оқулықпен жұмыс. №14.18. Өз бетімен жұмыс. Квадраттық функция келесі формуламен берілген. Парабола төбесін анықтаңдар. 1) y = x2 -6 2) y = (x-5)2 3) y = (x-7)2 +4 4) y = (x+3)2 -1
Дескрипторлар:
|
Логикалық тапсырмалар. 1. Бес шырпы таяқшасынан екі үшбұрыш құру керек. Құраңдар. 2. Үш литрлік және бес литрлік банкамен 4 литр суды шелекке қалай алуға болады? Суды төгуге болмайды. Жауабы: 3+3=6 6-5=1 3+1=4л 3. Үшбұрыш қандай санға тең?
Жауабы: (0;-6) (5;0) (7;4) (-3;-1) |
Жеке жұмыс №1. Аргументтің -2;
3,5; №2. Аргументтің қандай
мәндерінде №4.
№5. №6.
|
Интернет ресурстары. |
||||||
|
|
Жеке жұмыс |
Тест 1..Берілген көпмүшелердің қайсысы квадрат үшмүше болады? А) 2х+3 В) х3 – х -7 С) х2-19х Д) 3х2 -9х -1 2. х2 -9х+8 квадрат үшмүшесін көбейткіштерге жіктеңдер: А)(х-1)(х-8) В) (х+1)(х –9) С) (х+1)(х+8) Д )жіктеуге болмайды. 3. y=(x+4)2-2 функцияның графигі қай ширекте орналасқан? А) екінші В) үшінші С) бірінші Д) төртінші 4. y=(x-5)2 функцияның графигін y=x2 функцияның графигінен қалай алуға болады? А) Ох осі бойымен 5 бірлік оңға В) Ох осі бойымен 5 бірлік солға С) Оу осі бойымен 5 бірлік төмен Д) Оу осі бойымен 5 бірлік жоғары жылжыту арқылы алуға болады. 5. Квадраттық функцияның графигі қалай аталады? А) түзу В) гипербола С) парабола Д) элипс |
Тапсырманы орындайды Тест кілті: 1-Д, 2-А, 3-В, 4-А, 5-С
|
Дескриптор: -Тест есептерінің шешімін дұрыс табады. |
Тақта Бор Кітап Дәптер Интерактивті тақта Бағалау парақтары |
||||||
|
5 мин |
|
Бүгінгі сабақта: -аргументтің берілген мәндері бойынша функцияның мәндерін табу және функцияның мәні бойынша аргументтің мәнін табу Рефлексия
|
Тақырыпты меңгергенін анықтау.
Үйге тапсырма. №14.19. Бағалау. |
Кері байланыс
|
|
Тексерілді: Г.Караманова
|
Бөлім: |
10.3В Функцияның шегі және үзіліссіздігі |
|||||||||||||||||||
|
Педагогтің Т.А.Ә.(болған жағдайда |
Кужаева Г |
|||||||||||||||||||
|
Күні: |
10.02.25ж |
|||||||||||||||||||
|
Пән/Сынып: |
Алгебра, 10 А сынып, ЖМБ. |
Қатысушылар саны: |
Қатыспағандар саны: |
|||||||||||||||||
|
Сабақтың тақырыбы: |
Сан тізбегінің шегі. |
|||||||||||||||||||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары: |
10.4.1.11 - функцияның шексіздіктегі шегінің қасиеттерін қолданып сан тізбектерінің шектерін табу; |
|||||||||||||||||||
|
Сабақтың мақсаты: |
Функцияның шексіздіктегі шегінің қасиеттерін қолданып сан тізбектерінің шектерін таба алады. |
|||||||||||||||||||
|
Сабақтың құндылығы |
«Жасампаздық пен жаңашылдық» құндылығына: Топпен, жұппен жұмыс орындау барысында ақпаратты талдау, жаңа идеяларды ұсыну, қазіргі заманғы цифрлық құралдар мен технологияларды игеру және идеяларды іске асыруда ресурстарды тиімді пайдалану |
|||||||||||||||||||
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|||||||||||||||
|
5 минут |
Ұйымдас тыру |
Сәлеметсіздерме! Бүгін, Сан тізбегінің шегі тақырыбын қарастырамыз. Бүгінгі сабақта меңгеретініңіз: - функцияның шексіздіктегі шегінің қасиеттерін қолданып сан тізбектерінің шектерін табу Ұйымдастыру. Үй жұмысын тексеру. |
Амандасады. Үй тапсырмасын айтады. |
|
Оқулық |
|||||||||||||||
|
10 мин |
Негізгі бөлім |
Жаңа сабақ Сандық тізбек х айнымалысының шегі туралы ұғымды қалыптастыру үшін оның қандай сандық жиынның мәндерінен құралатынын білу жеткіліксіз. Оған қосымша нақты қандай мәндер (оның ішінде қайталанатындары да болуы мүмкін) және оны қандай ретпен қабылдайтынын білу қажет, яғни айнымалы реттелген (бағытталған) болуы керек. Сандық тізбектің шегі Бізге натурал қатар 1, 2, 3, 4, …, n, … берілсе, бұл қатардағы әрбір натурал сан n-ді белгілі бір заңдылықпен xn нақты санымен ауыстырсақ, онда төмендегідей тізбек шығады (2.1): x={xn}=x1, x2, x3, …, xn,
бұл тізбектің мүшелері немесе элементтері өсу реті бойынша нөмірленіп орналасқан. 1-Анықтама. (2.1) тізбегі арқылы берілген Х айнымалысының мәндерін сандық қатар деп атайды. (2.1) қатары берілді деп есептеледі, егер оның кез келген мүшесін табуға болатын ереже белгілі болса.
2-Анықтама.
a санын X={Xn} тізбегінің шегі деп
атайды, егер кез келген барынша
аз
бұл фактіні былай жазады (2.3):
Бұл анықтаманы басқаша былай айтуға болады: a саны X={Xn} тізбегінің шегі болады, егер оның мәні белгілі бір орыннан бастап a санынан өте аз шамаға өзгешеленсе.
Мұндағы N
нөмірінің Егер а, а+ε , а-ε сандарын {xn} айнымалысының мәндерін нүктелер арқылы сандық жазықтыққа кескіндесек (2.1 – сурет), онда біз сан тізбегі шегінің айқын геометриялық ұғымын аламыз. Центрі a нүктесінде болатын қандай да бір өте аз (ұзындығы 2ε) кесіндісін алсақ та, xn -нің барлық нүктелері белгілі бір нөмірден бастап осы кесіндінің ішінде жатады (кесіндінің сыртында өте аз мөлшердегі нүктелер болуы мүмкін)
2.1 - сурет - Сан тізбегі |
Қосымша ақпарат көздерін пайдалана отырып түсінеді Тақырып бойынша ресурстарды қарап, танысады.
Сұрақтарға жауап береді.
|
«Екі жұлдыз бір ұсыныс» Дескриптор:
Дескриптор:
|
Оқулық |
|||||||||||||||
|
25 мин |
Бекіту тапсырма лары |
Тапсырмалар: №1. №2. №3. №4.
Оқулықтан №36.11, №36.15. Сергіту сәті. Логикалық тапсырмалар. |
Есептер шығарады Берілген тапсырма бойынша өз ойларын ортаға салып, пікірлерін білдіріп, топтық талдау жасайды. Талқылау нәтижесінде өзара бір келісімге келіп есепті орындайды. Өз бетімен жұмыс. №4. №6.
|
Дескриптор:
ҚБ «Екi жұлдыз бiр тiлек» әдiсi .Бiрiн-бiрi бағалау
Дескриптор:
|
Интернет ресурстары
Жалпы білім беретін мектептің 10–сыныбына арналған оқулық.
|
|||||||||||||||
|
|
Жеке жұмыс |
|
Тапсырмаларды орындайды. |
Парақша лар |
||||||||||||||||
|
5 минут
|
|
Бүгінгі сабақта: - функцияның шексіздіктегі шегінің қасиеттерін қолданып сан тізбектерінің шектерін таба алады. Кері байланыс:
|
Тақырыпты меңгергенін анықтау
Үйге тапсырма. №36.13. |
Кері байланыс |
|
|||||||||||||||
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Бір айнымалысы бар сызықтық теңсіздік. Бір айнымалысы бар сызықтық теңсіздіктерді шешу. 6сынып
Бір айнымалысы бар сызықтық теңсіздік. Бір айнымалысы бар сызықтық теңсіздіктерді шешу. 6сынып
Тексерілді: Г.Караманова
|
Бөлім: |
6.3В Бір айнымалысы бар сызықтық теңсіздіктер |
||
|
Педагогтің Т.А.Ә.(болған жағдайда |
Кужаева Г.К |
||
|
Күні: |
10.02.25ж |
||
|
Пән/Сынып: |
Математика, 6 «Б» сынып. |
Қатысушылар саны: |
Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Бір айнымалысы бар сызықтық теңсіздік. Бір айнымалысы бар сызықтық теңсіздіктерді шешу. |
||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары: |
6.2.2.10
6.2.2.11
алгебралық түрлендірулердің көмегімен теңсіздіктерді
|
||
|
Сабақтың мақсаты: |
алгебралық
түрлендірулердің көмегімен теңсіздіктерді ЕБҚ
мақсаты : |
||
|
Сабақтың құндылығы: |
«Жасампаздық пен жаңашылдық» Топпен, жұппен жұмыс орындау барысында ақпаратты талдау, жаңа идеяларды ұсыну, қазіргі заманғы цифрлық құралдар мен технологияларды игеру және идеяларды іске асыруда ресурстарды тиімді пайдалану |
||
Сабақтың барысы
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|||||||||||
|
5 минут |
Ұйым дастыру |
Сәлеметсіздерме! Бүгін, Бір айнымалысы бар сызықтық теңсіздік. Бір айнымалысы бар сызықтық теңсіздіктерді шешу.тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: - kx > b, kx ≥ b, kx < b, kx ≤ b түріндегі сызықтық теңсіздіктерді шешу алгоритмі. -kx > b, kx ≥ b, kx < b, kx ≤ b түріндегі сызықтық теңсіздіктерді шешу және теңсіздіктердің шешімдерін координаттық түзуде кескіндеу. Үй тапсырмасын тексеру. №932, №933. "Миға шабуыл" -Сан аралықтары дегеніміз не? -Сан аралығының қандай түрлерін білесіңдер? -Қатаң теңсіздіктің шешімдер жиыны координаталық түзуде қалай кескінделеді? -Қатаң емес теңсіздіктің сан аралығын жазу үшін қандай жақша қолданылады? -Неліктен кесіндіде координаталық түзуде көрсетілген сандар шешімдер жиынына кіреді? - деген жабық және ашық сұрақтар қоямын. |
Амандасады, үй тапсырмасына жауап береді. Сұрақтарға жауап береді |
|
Оқулық, жұмыс дәптері Тақта слайд |
|||||||||||
|
10 мин |
Жаңа сабақ |
Бір айнымалысы бар сызықтық теңсіздіктерді шешу І. Бір айнымалысы бар сызықтық теңсіздік. ах > b және ах < b (немесе ах b және ах b) түріндегі теңсіздіктер бір айнымалысы бар сызықтық теңсіздіктер деп аталады. Мұндағы a ≠ 0 және b – қандай да бір сандар, х – айнымалы (белгісіз). Айнымалының теңсіздікті тура санды теңсіздікке айналдыратын мәнін бір айнымалысы бар сызықтық теңсіздіктің шешімі деп атайды. Мысалы, x + 6 < 18. x-тің орнына 2 санын қойса, онда 2 + 6 < 18, 8 < 18 дұрыс теңсіздігі шығады. x – теңсіздіктің шешімі. Теңсіздікті шешу – оның барлық шешімін табу немесе шешімдері болмайтынын дәлелдеу.
Егер теңсіздіктің екі жақ бөлігі де бірдей теріс санға көбейтіліп не- месе бөлініп, сонымен бірге теңсіздік белгісі қарама-қарсы теңсіздік белгісіне өзгертілсе, берілген теңсіздік мәндес теңсіздікке түрленеді.
|
Тақырып бойынша ресурстарды қарап, танысады 1-мысал. 3х – 7 < х + 3 және 3х – х < 3 +7 – мәндес теңсіздіктер.
2. Егер теңсіздіктің екі жақ бөлігі де бірдей оң санға көбейтілсе не- месе бөлінсе, берілген теңсіздік мәндес теңсіздікке түрленеді.
|
|
Оқулық, жұмыс дәптері
Тақта слайд |
|||||||||||
|
25 минут
|
Бекіту тапсыр масы |
Топтық жұмыс. №1.
№2. Екі қаланың арақашықтығы 300 км-ден кем болатын. Пойыз бір қаладан шығып, екінші қалаға қарай 3 сағат жүргенде екінші қалаға дейін 45км қашықтық қалды. Пойыздың жылдамдығын бағалаңыз. №3. x-тің қандай мәндерінде өрнектің мәні теріс сан болады: 2x – 5; 1,4x – 7; 6 – x? «Кім жылдам» №1. Теңсіздікті шешіңіздер : а) 2х ≤ 10 д) у-4 ≥ 14 б) х+3 ≥ 7 е) −3у > −9 в) −4х < 8 ж) 13 < 8-х г) -х <5 |
Оқулықтан тақырыпқа қатысты есептерді шығарады.
Жауаптар: х < 3 х ≤5 х ≥ 4 х > −2 х ≥ 18 х < −5 х > −5 |
Дескриптор: - берілген бір айнымалысы бар сызықтық теңсіздіктерді шешеді.
«Басбармақ» әдісімен бағалау алады жүргізіледі |
Интернет ресурстары Жалпы білім беретін мектептің 6–сыныбына арналған оқулық. Оқулық авторлары: Т.А.Алдамұратова, Қ.С.Байшоланова, Е.С.Байшоланов Алматы «Атамұра» баспасы 2018 жыл |
|||||||||||
|
|
|
1-жұп: 1 2-жұп: 2 3-жұп: 3 3х - 7< х+1 2+х>8 – х 1 - х≤2х - 5 х<4 х>3 х≥2 (-∞; 4) (3; +∞) [2; +∞) 4-жұп: 4 5-жұп: 5 2x+1>x+6 4x+2>3x+1 x>5 x> - 1 (5; +∞) (-1; +∞) Өз бетімен жұмыс. Тест тапсырмасы
А) ашық сәуле Б) интервал В) кесінді Г) сәуле 2. Белгіленумен жаз: 1-ден 4-ке дейінгі кесінді А) (1;4) Б) [1;4] В) (1;4] Г) [1;4) 3. Белгіленуімен жаз: 1-ден 3-ке дейінгі 3 саны қоса алынған жартылай интервал А) (1;3] Б) [1;3] В) (1;3) Г) [1;3) 4. [4;9]сан аралығының аты: А) кесінді Б) сәуле В) ашық сәуле Г) интервал 5. Белгіленуімен жаз: 2-ден 7-ге дейінгі интервал А) [2;7] Б) (2;7] В) [2;7) Г) (2;7) c) [–0,5; 3,5] d) (–∞; 0,5] ∪ [3,5; +∞) |
Жауаптар: №1 а) х ≤5 б) х ≥ 4 в) х > −2 г) х > −5 №2
Оқулықтан тақырыпқа қатысты есептерді шығарады. Оқулықтан №1003, №1005. |
Дескриптор: Білім алушы: - интервалды жазады; - жарты интервалды жазады; - сәулені жазады; - кесіндіні жазады;
|
Интернет ресурстары
Жалпы білім беретін мектептің 6–сыныбына арналған оқулық. Оқулық авторлары: Т.А.Алдамұратова, Қ.С.Байшоланова, Е.С.Байшоланов Алматы «Атамұра» баспасы 2018 жыл |
|||||||||||
|
|
Жеке жұмыс |
№1. Кестеде теңсіздіктер және оның шешімдері берілген. Шешімі дұрыс көрсетілген болса «+», ал шешімі қате көрсетілген болса «-» қойыңыз.
|
Тапсырманы орындайды |
Дескриптор: -Теңсіздіктің шешімдерінің дұрыс, бұрыстығын тексереді. |
|
|||||||||||
|
5 минут
|
|
Кері байланыс
Үйге тапсырма. №940, №943. |
|
|
|
|||||||||||
Тексерілді: Г.Караманова
|
Педагогің Аты, Тегі; Әкесінің аты (бар болған жағдайда): |
Кужаева Г |
||||||||||||||||||||
|
Пән/Сынып: |
7 «А» сынып. Қатысқандар саны: Қатыспағандар саны: |
||||||||||||||||||||
|
Күні: |
10.02.25ж |
||||||||||||||||||||
|
Бөлім: |
Қысқаша көбейту формулалары |
||||||||||||||||||||
|
Сабақтың тақырыбы: |
Қысқаша көбейту формулаларының көмегімен өрнектерді түрлендіру |
||||||||||||||||||||
|
Оқу бағдарламасына сәйкес оқыту мақсаты: |
7. 1.2.14 тиімді есептеу үшін қысқаша көбейту формулаларын қолдану; |
||||||||||||||||||||
|
Сабақтың мақсаттары: |
- қысқаша көбейту формулаларын алгебралық өрнектерді ықшамдау кезінде қолдана алады |
||||||||||||||||||||
|
Сабақтың құндылығы |
«Жасампаздық пен жаңашылдық» құндылығына: Топпен, жұппен жұмыс орындау барысында ақпаратты талдау, жаңа идеяларды ұсыну, қазіргі заманғы цифрлық құралдар мен технологияларды игеру және идеяларды іске асыруда ресурстарды тиімді пайдалану |
||||||||||||||||||||
|
Сабақ барысы: |
|||||||||||||||||||||
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
||||||||||||||||
|
5 минут |
Ұйым дастыру |
Сәлеметсіздерме! Бүгін, Қысқаша көбейту формулаларының көмегімен өрнектерді түрлендіру тақырыбын қарастырамыз. Бүгінгі сабақта меңгеретініңіз: - Қысқаша көбейту формулаларын біледі және қолдана алады; - қысқаша көбейту формулаларын алгебралық өрнектерді ықшамдау кезінде қолдана алады -Қысқаша көбейту формулаларын өрнектерді көбейткіштерге жіктеу кезінде қолдана алады; Үй тапсырмасын тексеру. № |
Амандасады, сабаққа дайындалады. Сұрақтарға жауап береді |
«Бағдаршам» арқылы қалыптастыру шы бағалау |
Оқулық; оқу құралдары; тақта; слайд; |
||||||||||||||||
|
10 мин |
Жаңа сабақ |
1) Көпмүшені көбейткіштерге жіктеуді қалай түсінесіз? Көпмүшені көбейткіштерге жіктеу – көпмүшені екі немесе бірнеше көпмүшелердің көбейтіндісі түріне келтіру 2) Көпмүшені көбейткіштерге жіктеудің қандай түрлерін білесіз? (Ортақ көбейткішті жақшаның сыртына шығару, қысқаша көбейту формулаларын пайдалану, топтау тәсілі) 3) Көпмүшені көбейткіштерге жіктеу не үшін қажет? Көпмүшені көбейткіштерге жіктеу дағдысы өрнектерді түрлендіруде, алгебралық бөлшектерді қысқартуда, теңдеу мен теңсіздіктерді шешуде қажет. 4) Көбейткіштерге
жіктеңіз:
5) Көбейткіштерге жіктеуге есеп ойдан құрастырыңыз. 6) Топтау тәсілімен көбейткіштерге жіктеу тәсілін сипаттаңыз. Топтау тәсілімен көбейткіштерге жіктеу алгоритмі: 1. Көпмүшенің ортақ көбейткіштері бар мүшелерін бірыңғай топтарға бөлу; 2. Әр топтағы мүшелердің бірмүше түріндегі ортақ көбейткішін жақша сыртына шығару; 3. Әр топтағы мүшелердің бірмүше түріндегі ортақ көбейткішін жақша сыртына шығару; |
Тақырып бойынша ресурстарды қарап, танысады ⠀⠀ ⠀⠀ 2). Шешуі. Айырма кубының формуласын қолданып өрнекті түрлендір: (–x – 4y)3 = (–x)3 – 3 ∙ (–x)2 ∙ 4y + 3 ∙ (–x) ∙ (4y)2 – (4y)3 = –x3 – 12x2y – 48xy2 – 64y3. |
«Бағдаршам» арқылы қалыптастыру шы бағалау
|
Оқулық; оқу құралдары; тақта; слайд; Карточкалар;7 сыныпқа арналған оқулық Презентация |
||||||||||||||||
|
15 минут |
Бекіту тапсырмасы |
a) b)
Тапсырма. Төменгі әр теңдеу географиялық атаулармен аталған. Теңдеулердің жауабына әр географиялық атау туралы қосымша ақпарат сәйкес келеді. Берілген теңдеулерді шешіп, мәтіндегі түбірлердің орнына сәйкес географиялық атауды енгізе отырып, әрқайсысы туралы туралы ақпарат алыңыз. Әлемдегі ең үлкен
жанартау Әлемдегі ең биік тау
– Әлемдегі ең биік сарқырама
– Әлемдегі ең ұзын тау
– Әлемдегі жауын-шашын ең көп
түсетін жер – Әлемдегі ең үлкен тау асты
мұздығы -
Әр оқушы өзін дайын жауап бойынша тексереді. Әлемдегі ең биік тау – Гималай (Джомолунга, 8848 м) Әлемдегі ең ұзын тау – Анд (9000 км) Әлемдегі жауын-шашын ең көп түсетін жер – Черапунджи (жылына 12000 мм) Әлемдегі ең үлкен тау асты мұздығы - Хабборт (145 км) Әлемдегі ең биік сарқырама – Анхель (1054 м) Әлемдегі ең үлкен жанартау Гавайядағы Мауна-Лао (ені 10 км, тереңдігі 180 км)
Оқулықпен жұмыс. №5.128, №5.129. |
Оқушылар дескрипторға сәйкес тапсырмаларды орындайды.
Жазылуы бойынша формулаларды жалғастырады (1) ҚКФ ажырата алады (1) Формуланы ауызша тұжырымдай алады
Оқулықтан есептерді шығарады.
|
Дескриптор: Топтау тәсілін дұрыс қолдана алды; Ортақ көбейткішті жақша сыртына шығарады;
ҚБ:«Бас бармақ» әдісі
|
Презентация Слайд
Интернет ресурстары
Оқулық; оқу құралдары; тақта; слайд; Карточкалар;7 сыныпқа арналған оқулық Презентация |
||||||||||||||||
|
10 мин |
Оқулықпен жұмыс |
Оқулықтан есептер шығару:
|
Тапсырманы орындайды
|
Оқушының тақтадағы белсенділігіне байланысты ауызша бағалау |
Жалпы білім беретін мектептің 7–сыныбына арналған оқулық. Тақта Бор Кітап Дәптер
|
||||||||||||||||
|
5 минут
|
|
Бүгінгі сабақта:
- қысқаша көбейту формулаларын алгебралық өрнектерді ықшамдау кезінде қолдана алады -Қысқаша көбейту формулаларын өрнектерді көбейткіштерге жіктеу кезінде қолдана алады;
Үйге тапсырма.№ |
Тақырыпты меңгергенін анықтау |
Кері байланыс |
Оқулық; оқу құралдары; тақта; слайд;
|
||||||||||||||||
Тексерілді: Г.Караманова
|
Бөлім: |
8.3В Квадраттық функция |
||
|
Педагогтің Т.А.Ә.(болған жағдайда |
Кужаева Г.К |
||
|
Күні: |
07.02.2025ж |
||
|
Пән/Сынып: |
Алгебра, 8 “Ә” сынып. |
Қатысушылар саны: 24 |
Қатыспағандар саны: |
|
Сабақтың тақырыбы: |
Квадраттық функция және оның графигі |
||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары: |
8.4.1.4 аргументтің берілген мәндері бойынша функцияның мәндерін табу және функцияның мәні бойынша аргументтің мәнін табу; |
||
|
Сабақтың мақсаты: |
Аргументтің берілген мәндері бойынша функцияның мәндерін, және функцияның мәні бойынша аргументтің мәнін табуға дағдыландыру. |
||
|
Сабақтың құндылығы |
Жасампаздық және жаңашылдық - стандарттан тыс ойлау және әдеттегі әрекеттерінің шеңберінен шыға білу қабілеті; |
||
Сабақтың барысы
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
||||||
|
5 минут |
Ұйым дастыру |
Сәлеметсіздерме! Бүгін, Функцияның мәні бойынша аргументтің мәнін табу тақырыптарын қарастырамыз Бүгінгі сабақта меңгеретініңіз: - аргументтің берілген мәндері бойынша функцияның мәндерін табу және функцияның мәні бойынша аргументтің мәнін табу; |
Амандасу.Сыныпты түгендеу. Сабаққа дайындау, оқу құралдарын алу. Үй тапсырмасын айту. |
«Екі жұлдыз, бір тілек» |
Оқулық |
||||||
|
10мин |
Негізгі бөлім |
Тапсырма. №1. у=х2 функциясының графигін координаталық оське параллель жылжытып, әрбір жағдай үшін берілген функцияны жазыңдар. а) 3 бірлік оңға және 2 бірлік жоғары; у=(х-3)2+2 ә) 1 бірлік солға және 3 бірлік жоғары; у=(х+1)2+3 б) 5 бірлік оңға және 4 бірлік төмен у=(х-5)2-4 |
Сұрақтарға жауап береді. |
Дескриптор: - y = x2 функциясының анықтамасы мен қасиетін біледі - квадрат функцияның графигін салады -графиктерді түрлендірулерді орындайды |
Тақта Бор Кітап Дәптер Интерактивті тақта Бағалау парақтары |
||||||
|
25 мин |
Бекіту тапсырмасы |
Тапсырмалар. №1.
а - ның қандай
мәндерінде у=ах2 - 16х+1 параболасының симметрия осі х=4 түзуі
болады? Оқулықпен жұмыс. №14.18. Өз бетімен жұмыс. Квадраттық функция келесі формуламен берілген. Парабола төбесін анықтаңдар. 1) y = x2 -6 2) y = (x-5)2 3) y = (x-7)2 +4 4) y = (x+3)2 -1
Дескрипторлар:
|
Логикалық тапсырмалар. 1. Бес шырпы таяқшасынан екі үшбұрыш құру керек. Құраңдар. 2. Үш литрлік және бес литрлік банкамен 4 литр суды шелекке қалай алуға болады? Суды төгуге болмайды. Жауабы: 3+3=6 6-5=1 3+1=4л 3. Үшбұрыш қандай санға тең?
Жауабы: (0;-6) (5;0) (7;4) (-3;-1) |
Жеке жұмыс №1. Аргументтің -2;
3,5; №2. Аргументтің қандай
мәндерінде №4.
№5. №6.
|
Интернет ресурстары. |
||||||
|
|
Жеке жұмыс |
Тест 1..Берілген көпмүшелердің қайсысы квадрат үшмүше болады? А) 2х+3 В) х3 – х -7 С) х2-19х Д) 3х2 -9х -1 2. х2 -9х+8 квадрат үшмүшесін көбейткіштерге жіктеңдер: А)(х-1)(х-8) В) (х+1)(х –9) С) (х+1)(х+8) Д )жіктеуге болмайды. 3. y=(x+4)2-2 функцияның графигі қай ширекте орналасқан? А) екінші В) үшінші С) бірінші Д) төртінші 4. y=(x-5)2 функцияның графигін y=x2 функцияның графигінен қалай алуға болады? А) Ох осі бойымен 5 бірлік оңға В) Ох осі бойымен 5 бірлік солға С) Оу осі бойымен 5 бірлік төмен Д) Оу осі бойымен 5 бірлік жоғары жылжыту арқылы алуға болады. 5. Квадраттық функцияның графигі қалай аталады? А) түзу В) гипербола С) парабола Д) элипс |
Тапсырманы орындайды Тест кілті: 1-Д, 2-А, 3-В, 4-А, 5-С
|
Дескриптор: -Тест есептерінің шешімін дұрыс табады. |
Тақта Бор Кітап Дәптер Интерактивті тақта Бағалау парақтары |
||||||
|
5 мин |
|
Бүгінгі сабақта: -аргументтің берілген мәндері бойынша функцияның мәндерін табу және функцияның мәні бойынша аргументтің мәнін табу Рефлексия
|
Тақырыпты меңгергенін анықтау.
Үйге тапсырма. №14.19. Бағалау. |
Кері байланыс
|
|
Тексерілді: Г.Караманова
|
Бөлім: |
10.3В Функцияның шегі және үзіліссіздігі |
|||||||||||||||||||
|
Педагогтің Т.А.Ә.(болған жағдайда |
Кужаева Г |
|||||||||||||||||||
|
Күні: |
10.02.25ж |
|||||||||||||||||||
|
Пән/Сынып: |
Алгебра, 10 А сынып, ЖМБ. |
Қатысушылар саны: |
Қатыспағандар саны: |
|||||||||||||||||
|
Сабақтың тақырыбы: |
Сан тізбегінің шегі. |
|||||||||||||||||||
|
Оқу бағдарламасына сәйкес оқыту мақсаттары: |
10.4.1.11 - функцияның шексіздіктегі шегінің қасиеттерін қолданып сан тізбектерінің шектерін табу; |
|||||||||||||||||||
|
Сабақтың мақсаты: |
Функцияның шексіздіктегі шегінің қасиеттерін қолданып сан тізбектерінің шектерін таба алады. |
|||||||||||||||||||
|
Сабақтың құндылығы |
«Жасампаздық пен жаңашылдық» құндылығына: Топпен, жұппен жұмыс орындау барысында ақпаратты талдау, жаңа идеяларды ұсыну, қазіргі заманғы цифрлық құралдар мен технологияларды игеру және идеяларды іске асыруда ресурстарды тиімді пайдалану |
|||||||||||||||||||
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|||||||||||||||
|
5 минут |
Ұйымдас тыру |
Сәлеметсіздерме! Бүгін, Сан тізбегінің шегі тақырыбын қарастырамыз. Бүгінгі сабақта меңгеретініңіз: - функцияның шексіздіктегі шегінің қасиеттерін қолданып сан тізбектерінің шектерін табу Ұйымдастыру. Үй жұмысын тексеру. |
Амандасады. Үй тапсырмасын айтады. |
|
Оқулық |
|||||||||||||||
|
10 мин |
Негізгі бөлім |
Жаңа сабақ Сандық тізбек х айнымалысының шегі туралы ұғымды қалыптастыру үшін оның қандай сандық жиынның мәндерінен құралатынын білу жеткіліксіз. Оған қосымша нақты қандай мәндер (оның ішінде қайталанатындары да болуы мүмкін) және оны қандай ретпен қабылдайтынын білу қажет, яғни айнымалы реттелген (бағытталған) болуы керек. Сандық тізбектің шегі Бізге натурал қатар 1, 2, 3, 4, …, n, … берілсе, бұл қатардағы әрбір натурал сан n-ді белгілі бір заңдылықпен xn нақты санымен ауыстырсақ, онда төмендегідей тізбек шығады (2.1): x={xn}=x1, x2, x3, …, xn,
бұл тізбектің мүшелері немесе элементтері өсу реті бойынша нөмірленіп орналасқан. 1-Анықтама. (2.1) тізбегі арқылы берілген Х айнымалысының мәндерін сандық қатар деп атайды. (2.1) қатары берілді деп есептеледі, егер оның кез келген мүшесін табуға болатын ереже белгілі болса.
2-Анықтама.
a санын X={Xn} тізбегінің шегі деп
атайды, егер кез келген барынша
аз
бұл фактіні былай жазады (2.3):
Бұл анықтаманы басқаша былай айтуға болады: a саны X={Xn} тізбегінің шегі болады, егер оның мәні белгілі бір орыннан бастап a санынан өте аз шамаға өзгешеленсе.
Мұндағы N
нөмірінің Егер а, а+ε , а-ε сандарын {xn} айнымалысының мәндерін нүктелер арқылы сандық жазықтыққа кескіндесек (2.1 – сурет), онда біз сан тізбегі шегінің айқын геометриялық ұғымын аламыз. Центрі a нүктесінде болатын қандай да бір өте аз (ұзындығы 2ε) кесіндісін алсақ та, xn -нің барлық нүктелері белгілі бір нөмірден бастап осы кесіндінің ішінде жатады (кесіндінің сыртында өте аз мөлшердегі нүктелер болуы мүмкін)
2.1 - сурет - Сан тізбегі |
Қосымша ақпарат көздерін пайдалана отырып түсінеді Тақырып бойынша ресурстарды қарап, танысады.
Сұрақтарға жауап береді.
|
«Екі жұлдыз бір ұсыныс» Дескриптор:
Дескриптор:
|
Оқулық |
|||||||||||||||
|
25 мин |
Бекіту тапсырма лары |
Тапсырмалар: №1. №2. №3. №4.
Оқулықтан №36.11, №36.15. Сергіту сәті. Логикалық тапсырмалар. |
Есептер шығарады Берілген тапсырма бойынша өз ойларын ортаға салып, пікірлерін білдіріп, топтық талдау жасайды. Талқылау нәтижесінде өзара бір келісімге келіп есепті орындайды. Өз бетімен жұмыс. №4. №6.
|
Дескриптор:
ҚБ «Екi жұлдыз бiр тiлек» әдiсi .Бiрiн-бiрi бағалау
Дескриптор:
|
Интернет ресурстары
Жалпы білім беретін мектептің 10–сыныбына арналған оқулық.
|
|||||||||||||||
|
|
Жеке жұмыс |
|
Тапсырмаларды орындайды. |
Парақша лар |
||||||||||||||||
|
5 минут
|
|
Бүгінгі сабақта: - функцияның шексіздіктегі шегінің қасиеттерін қолданып сан тізбектерінің шектерін таба алады. Кері байланыс:
|
Тақырыпты меңгергенін анықтау
Үйге тапсырма. №36.13. |
Кері байланыс |
|
|||||||||||||||

шағым қалдыра аласыз