
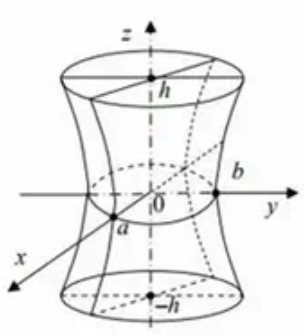
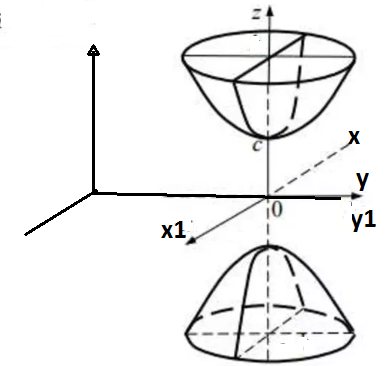
Бір қуысты гиперболоид
Бір қуысты гиперболоидтың канондық теңдеуі
 +
+
түзуінде жатады. Нақты осьтері абциссалар мен ординаталар осьтерінің координаталар осі жорамал беттерінде жатады. а, в,с - бір қуысты гиперболоидтың жарты осьтері деп аталады.
Бір қуысты гиперболоидтың координаталар жазықтықтарымен қиса, онда төменгі сызықтар пайда болады.
Егер ХОУ жазықтықтарымен
қиса,  онда
онда
 +
+ эллипсі
шығады.
эллипсі
шығады.
Егер ХОƵ жазықтықтарымен
қиса,  онда
онда
 +
+ гиперболасы
шығады.
гиперболасы
шығады.
Егер уоƵ жазықтықтарымен
қиса,  онда
онда
 +
+ гиперболасы пайда
болады.
гиперболасы пайда
болады.
Бір қуысты
гиперболоидты 
 және
және
 координаталар
жазықтықтарымен қиғанда
координаталар
жазықтықтарымен қиғанда
 ,
,
 ,
, 
теңдеулері алынады. 58
Гиперболоноид

теңдеуіндегі ОƵ осі бойымен айналдыра отырып гиперболоидтың теңдеуін құрыңыздар.
Шешуі: Гиперболоид теңдеуін түрлендірейік. Бірінші теңдеуінен х2 тауып, оны екінші теңдеудің квадратынан мына теңдеулер алынады.

алынады. Енді бұл теңдеуді мынадай
 -
- немесе
немесе 

 +
+
түрінде жазылған гиперболоидтың теңдеуі алынады.
Демек,


 +
+
бір қуысты гиперболоидтың теңдеуі болып табылады.
№12
х2+2у2+3 +2х+8у+18
+2х+8у+18 54
54 қандай теңдеу екенін
табыңдар
қандай теңдеу екенін
табыңдар
Шешуі: Теңдеудегі
х,у,  тердің толық
квадраттарын бөлсек, онда
тердің толық
квадраттарын бөлсек, онда
х2+2у2+3 +2х+8у+18
+2х+8у+18 54
54
(х2+2у2+1)-1+2(у2+4у+4)-8-3(
(х2+1)2+2(у+2)2-36 -3)2
-1-8+27-54
-3)2
-1-8+27-54
(х2+1)2+2(у+2)2-36 -3)2
-3)2

......... 36 –ға бөлсек, онда
 +
+
Бұл түзудің центрі (-1;-2; 5)
нүктесінде орналасқан. Енді тік бұрыштар координаталар
сақинасын  х+1,
х+1,  у-2,
у-2, 
 -3 формулалары арқылы
ауыстырсақ, онда
-3 формулалары арқылы
ауыстырсақ, онда  +
+ -
-
 болып, гиперболоидтың
теңдеуіне ауысады.
болып, гиперболоидтың
теңдеуіне ауысады.
Демек, берілген бет бір қуысты гиперболоидты анықтайды
М (-6; 2; 4) нүктелері арқылы өтетін және жазықтықтың


 +
+ түзу сызықты айналушысы
арқылы өтетін түзу сызықтарын жазыңыздар.
түзу сызықты айналушысы
арқылы өтетін түзу сызықтарын жазыңыздар.
Шешуі: (-6; 2; 4)нүктелері берілген жазықтықта жатсын делік, онда


 +
+ 4-1-4
4-1-4 

Бір қуысты гиперболоидтың әрбір нүктесі арқылы оның екі түзуі өтеді.
Бір қуысты гиперболоид түзуі үшін төмендегі теңдікті жазуға болады:


 немесе
немесе  +
+ -
- -
- +
+
Осыдан кейін екі системаны құрайық:


М нүктесі арқылы өтетіндіктен, k және l нүктелерін табамыз.
Алдымен k параметрін табамыз.

-6;
у
 мәндерін қойсақ,
онда
мәндерін қойсақ,
онда

-2+1
-2
k
Енді канон мәнін (2)-ге қойсақ, онда оның сол жағы

-2-1
-3
түрінде жазылады. Енді (1), (2)-ге қойсақ,
онда
 61
61
Ал бұдан
 алынады.
алынады.
Енді параметр l-ды табайық. Ол үшін (3)пен (4)-тен

Бұл теңдеуден
х,у,  мәндерін
қояйық.
мәндерін
қояйық.
Сонда

l -1 болады. Сондықтан
екінші схемасы мынадай болады:
-1 болады. Сондықтан
екінші схемасы мынадай болады:

Бұдан:

Демек, М (-6; 2; 4) нүктелерінен өтетін және гиперболоидтық түзусызықтың жолаушылары
 және
және  болады.
болады.


 теңдеуімен берілген
беттің А (6;2;8) нүктесінен болған беттің тіксызықты жасаушыларын
табыңыздар.
теңдеуімен берілген
беттің А (6;2;8) нүктесінен болған беттің тіксызықты жасаушыларын
табыңыздар.
Шешуі: Бір қуысты гиперболоидтың


 теңдеуі
берілген.
теңдеуі
берілген.
Ол бір қуысты гиперболоидтың тік түзуін жасаушылары.
 ,
,

деп анықталады,
мұнда 

 - кез келген нақты
сандар келтірілгенін пайдаланып, мынадай теңдеулер
жазамыз:
- кез келген нақты
сандар келтірілгенін пайдаланып, мынадай теңдеулер
жазамыз:
 ,
,

А нүктесінің координаталары (6; 2; 8)-де келтірілген системасының орнына қою арқылы
 ,
,

Бірінші
системадан  , екінші системадан
-
, екінші системадан
- болады.Осы
параллельдердің мәндерін қою арқылы келесі
системалар
болады.Осы
параллельдердің мәндерін қою арқылы келесі
системалар


шығады. Демек, бұлар беттің тіксызықты жасаушыларын анықтайды. 63
 -
- +
+ гиперболоидтың
координаталық жасаушыларын және
гиперболоидтың
координаталық жасаушыларын және  жазықтықтарының қиылысу
сызықтарын табыңыздар.
жазықтықтарының қиылысу
сызықтарын табыңыздар.
Шешуі: Берілген бір қуысты гиперболоидтың ХОУ координаталық жасаушыларының қиылысу сызығы
 -
- ,
,

ХОУ жазықтығындағы эллипс бетін табыңыз.
Бір қуысты гиперболоидтың УОƵ координаталық жазықтығының қиылысу сызығы
 -
-

жазықтығымен анықталады. Бұл теңдеулермен УОƵ жазықтығындағы гипербола анықталады.
ХОƵ координаталық жазықтығында бір қуысты гиперболоид
 -
- у
у
жазықтығымен анықталады. Бұл
ХОƵ координаталық жазықтығында гиперболаны анықтайды.
Гиперболамен  жазықтықтарының қиылысу
сызықтары
жазықтықтарының қиылысу
сызықтары

болады. Мұнда
эллипс  жазықтығында
жатады.
жазықтығында
жатады.
Бір қуысты гиперболоидпен
х жазықтығы
жазықтығы
 -
-

Мұнда
гипербола  жазықтығында жатады.
Егер бір қуысты гиперболоидтың координаталық
жазықтықтармен,
жазықтығында жатады.
Егер бір қуысты гиперболоидтың координаталық
жазықтықтармен,  және
және  жазықтықтарының қиылысу
сызықтары көрсетілген. 64
жазықтықтарының қиылысу
сызықтары көрсетілген. 64
............-16х-34у-2х- теңдеуі қандай бетті
анықтайды?
теңдеуі қандай бетті
анықтайды?
Шешуі: Теңдеуді түрлендірейік:
4х2-9у2+36 2-16х-54у-72
2-16х-54у-72 -65
-65
4(х2-4х+4)-9(у2+6у+9)+36( 2-27+1)-16+81-16-65
2-27+1)-16+81-16-65
4(х-4х)
2-9(у+3)2+36( 2
2

 -
- +
+ (1)
(1)
Енді
х-2 ;
у+3
;
у+3 ;
;

 алмастыруын жасасақ,
онда (1) теңдеуі
алмастыруын жасасақ,
онда (1) теңдеуі
 -
- +
+
теңдеуі пайда болады. Осындай бетті қию әдісімен қарастрайық.
Бетті ОХУ қимасымен қисақ, онда
 -
-
 гиперболасы
шығады.
гиперболасы
шығады.
Егер бетті ОУƵ жазықтықтарымен қиса, онда
 +
+
 ,
,
ОХ жазықтықтарымен қиса,
онда
жазықтықтарымен қиса,
онда
 +
+
 гиперболасы пайда
болады.
гиперболасы пайда
болады.
ОХУ жазықтығына параллель жазықтықпен қиса, онда гипербола болады.
 -
- -
- ,
,
 қияды.
қияды.
Ал
ОУ жазықтық
бойынша
жазықтық
бойынша
-
 +
+
 ,
,
 эллипспен
қияды.
эллипспен
қияды.
Ал
ОХ жазықтығы
жазықтығы
-
 +
+ +
+
 ,
,  эллипс бойынша
қияды.
эллипс бойынша
қияды.
Демек, берілген теңдеу бір қуысты гиперболаны анықтайды. 65
-
2х2-6у2+5
 -12
-12 -24у-24
-24у-24 теңдеуімен берілген бір
қуысты гиперболаны анықтаңыздар.
теңдеуімен берілген бір
қуысты гиперболаны анықтаңыздар.
Шешуі: Теңдеуді түрлендірейік:
2х2-6у2+5 -12
-12 -24у-24
-24у-24
2(х2-6 -18+24-48
-18+24-48
2(х+3)2-6(у-2)2-3( )2
)2 болады.
болады.
 +
+ +
+ теңдеуі
алынады.
теңдеуі
алынады.
Енді
х+3 ;
у-2
;
у-2 ;
;
 белгілеуін енгізсек,
онда
белгілеуін енгізсек,
онда
 -
- +
+
ОХУ қимасынан жүргізсек, онда гипербола
 -
-
 теңдеуі алынады. Егер
ОУ
теңдеуі алынады. Егер
ОУ қимасынан жүргізсек,
онда эллипс
қимасынан жүргізсек,
онда эллипс
- +
+
 теңдеуі
алынады.
теңдеуі
алынады.
ОХУ жазықтығына параллель жазықтық
 -
- -
- ,
,
 гиперболла бойынша,
ОУ
гиперболла бойынша,
ОУ жазықтығына параллель
жазықтық
жазықтығына параллель
жазықтық
-
 +
+
 ,
,
 гиперболла бойынша,
анықтайды.
гиперболла бойынша,
анықтайды.
Ал
ОХ жазықтығы
жазықтығы
-
 +
+ +
+
 ,
,  эллипс бойынша
қияды.
эллипс бойынша
қияды.
Демек, аталған эллипстерді қарастырып, берілген теңдеу бір қуысты гиперболаның теңдігін анықтайды. 66
 -1
-1 жазықтығы
жазықтығы  -
- +
+ бір қуысты гипербола
бойынша қияды.Гиперболаның жартысының төбелерін
анықтаңыздар.
бір қуысты гипербола
бойынша қияды.Гиперболаның жартысының төбелерін
анықтаңыздар.
Шешуі:
 -1
-1 теңдеуін
теңдеуін 
 -1 деп жазуға болады,
осы
-1 деп жазуға болады,
осы 
 -1 қиылысу сызығын табу
үшін,
-1 қиылысу сызығын табу
үшін, 
 -1 теңдеуіне ауыстырсақ,
онда
-1 теңдеуіне ауыстырсақ,
онда
 -
- ,
,
 -
- ,
,
 -
- теңдеуі шығады. Алынған
теңдеуде а2
теңдеуі шығады. Алынған
теңдеуде а2 а
а ,
в2
,
в2 9,
в
9,
в . Оның төбелері А(4; 0;
-1) және В(-4; 0, -1) нүктелерінде
орналасқан.
. Оның төбелері А(4; 0;
-1) және В(-4; 0, -1) нүктелерінде
орналасқан.
Демек, эллипстің жарты осьтері
а ,
в
,
в және төбелері А(4; 0;
-1), В(-4; 0, -1) нүктелерінде орналасқан.
және төбелері А(4; 0;
-1), В(-4; 0, -1) нүктелерінде орналасқан.
№9
 -
- ,
у
,
у гиперболаны
О
гиперболаны
О осіне бұру және
ОХ
осіне бұру және
ОХ жазықтығына бір мәнді
қылу арқылы
жазықтығына бір мәнді
қылу арқылы  -
- теңдеуімен анықталатын
бір қуысты гиперболоидты алу үшін қажетті басымдығын
дәлелдеңіздер.
теңдеуімен анықталатын
бір қуысты гиперболоидты алу үшін қажетті басымдығын
дәлелдеңіздер.
Шешуі: Гиперболаның
О осінен айналуынан шыққан
айналу бетінің мәні теңдеуімен
осінен айналуынан шыққан
айналу бетінің мәні теңдеуімен 
алынады.
ОХ жазықтығына сығылу
коэффициенті k=
жазықтығына сығылу
коэффициенті k= болса, онда беттің кез
келген М (Х,У,
болса, онда беттің кез
келген М (Х,У, М
(Х1,У1,
М
(Х1,У1, 1) нүктесіне көшеді. Бұл
жағдайда
1) нүктесіне көшеді. Бұл
жағдайда
 немесе
немесе 
болады. Алынған теңдеуді (1) ге қоссақ, онда


 алынады.
алынады.
Демек, берілген теңдеу бір қуысты гиперболаның теңдеуін анықтайды.
Егер бір қуысты гиперболаның
беті ОХУ жазықтығын кеседі, ал ОХ жазықтығын
жазықтығын 
 гипербола бойынша қияды. Сонда
бір қуысты гиперболаның канондық теңдеуін
табыңдар.
гипербола бойынша қияды. Сонда
бір қуысты гиперболаның канондық теңдеуін
табыңдар.
Шешуі: Бір қуысты гиперболаның теңдеуі



Егер бір қуысты гиперболоидты
ОХУ жазықтығы шеңбер бойымен есептеуі бойынша ,
яғни  9.
9.
Ал,
ОХ жазқтығымен қиылысу
сызығы
жазқтығымен қиылысу
сызығы


гипербола болады.Бұл есептің гиперболалық теңдеуі


түрінде берілген.
Мұнда 
 10
10
Демек, бір қуысты гиперболаның теңдеуі

 0 түрінде
жазылады.
0 түрінде
жазылады.

 ,
у
,
у 0 гиперболасының
О
0 гиперболасының
О осінен айналуынан
біртіндеп ОХ
осінен айналуынан
біртіндеп ОХ жазықтығына кеңістіктің
бір мәнді сығылу арқасында айқындалатынын
көрсетіңіздер.
жазықтығына кеңістіктің
бір мәнді сығылу арқасында айқындалатынын
көрсетіңіздер.
Шешуі:

 ,
у
,
у 0 гиперболасының
О
0 гиперболасының
О осінен айналғанда
мынадай теңдеумен
осінен айналғанда
мынадай теңдеумен

шығады.Осы формуланы пайдаланып, системаны былайша құрамыз.

 ,
,
 ,
,  68
68
Енді айналу беті
ОХ жазқтығына айналу
коэффициенті бойынша айналады. Осы ОХ
жазқтығына айналу
коэффициенті бойынша айналады. Осы ОХ жазықтығына айналу
бетінің М (Х,У,
жазықтығына айналу
бетінің М (Х,У, М
(Х1,У1,
М
(Х1,У1, 1) нүктесіне көшеді. Бұл
жағдайда
1) нүктесіне көшеді. Бұл
жағдайда
 немесе
немесе 
болады. Осы алынған теңдеуді (1) ге қоссақ,





 теңдеуі
алынады.
теңдеуі
алынады.
Демек, алынған теңдеу бір қуысты гиперболаның теңдеуі.
х2+2у2-4 -8
-8 теңдеуі тік бұрыштың
декарт координаталары айнымалысында қарастырып, екінші ретті беттік
теңдеуін қиылысатын әдіспен зерттеңіздер .
теңдеуі тік бұрыштың
декарт координаталары айнымалысында қарастырып, екінші ретті беттік
теңдеуін қиылысатын әдіспен зерттеңіздер .
Шешуі: Берілген теңдеудің толық квадратын бөліп жазсақ, онда
х2+2у2-4 -8
-8
 -
- 2
2
1. Осы
бетке  теңдеуін қойсақ,
онда
теңдеуін қойсақ,
онда

 +
+ 2
2
-тың орнына ху-тегі мәнін қойсақ, онда қисық
 теңдеуі пайда
болады.
теңдеуі пайда
болады.
2. Кеңістікті
х кесіндісімен қисақ,
онда
кесіндісімен қисақ,
онда
 +
+
 +
+ 2,
2,

 2
2
а)
 болса,
онда
болса,
онда 
 –
–
Бұл гипербола болады, мұнда
О нақты ось, ОУ-жанама
ось.
нақты ось, ОУ-жанама
ось.
б)
 болса,
онда
болса,
онда 
 –
–
Мұнда жалған нүкте анықталынады.
в)
 болса,
онда
болса,
онда 
 –
–
Мұндай жағдайда гипербола алынады,ОУ-нақты ось, ОУ-жанама ось.
3.Осы бетті
у  жазықтығымен қиысса,
онда
жазықтығымен қиысса,
онда
 2
2
анықталған жағдайлар екінші жағдайларға ұқсас. Демек, алынған бет
 2
2
теңдігін анықтайтын бір қуысты
гиперболоид,оның центрі (0;-0;-1) нүктесінде, ал осьтері
а в
в ,
с
,
с болады.
болады.
№13.
 бір қуысты
гиперболоидты, (0;-0;-1) нүктесінен оның жазықтығын қиған кезде
болатын қиманың теңдеуін табыңдар.
бір қуысты
гиперболоидты, (0;-0;-1) нүктесінен оның жазықтығын қиған кезде
болатын қиманың теңдеуін табыңдар.
Шешуі: (0;-0;-1) нүктесінен
өтетін жазықтықтың теңдеуі  болады.Осы теңдеуді бір
қуысты гиперболоидтың теңдеуіне қойсақ,
онда
болады.Осы теңдеуді бір
қуысты гиперболоидтың теңдеуіне қойсақ,
онда
 немесе
немесе 
Енді алынған
теңдеу  эллипсті анықтайды. Бір
қуысты гиперболоидтың (0;-0;-1) нүктесінен эллипс
өтеді.
эллипсті анықтайды. Бір
қуысты гиперболоидтың (0;-0;-1) нүктесінен эллипс
өтеді.
Демек, бір қуысты
гиперболоидтың түзуі мына  теңдеуге ауысады. Бұл
теңдеу эллипсті анықтайды. 70
теңдеуге ауысады. Бұл
теңдеу эллипсті анықтайды. 70
14.
 бір қуысты
гиперболоидтың қиындысының ОХУ жазықтығына пропорциясын
табыңдар.
бір қуысты
гиперболоидтың қиындысының ОХУ жазықтығына пропорциясын
табыңдар.
Шешуі: Бір қуысты
гиперболоидтың теңдеуіне х 2
2 теңдеуін
қосса,
теңдеуін
қосса,



х ,
,

Бұл теңдеуде
у у
у шешулері
болады.
шешулері
болады.
Демек,
у-4 у+4
у+4 жазықтықтары ОХУ
жазықтықтарындағы шешулері болады.
жазықтықтары ОХУ
жазықтықтарындағы шешулері болады.
№15 Бір қуысты гиперболоидтың
теңдеулері, егер ОХУ жазықтықтарында
х2+у шеңбер бойынша, ал ОХƵ
жазықтығын
шеңбер бойынша, ал ОХƵ
жазықтығын  жазықтығы бойынша қиса,
ол қандай канондық теңдеумен анықталатындығын
көрсетіңдер.
жазықтығы бойынша қиса,
ол қандай канондық теңдеумен анықталатындығын
көрсетіңдер.
Шешуі: Бір қуысты
гиперболоидтың теңдеулері  -
-
 түрінде жазылады.Сол
бойынша ОХУ қиылысында қимада шеңбер
х2+у2
түрінде жазылады.Сол
бойынша ОХУ қиылысында қимада шеңбер
х2+у2 Сонымен ОХУ теңдеуінен
қиған кезде гипербола нәтижесі
Сонымен ОХУ теңдеуінен
қиған кезде гипербола нәтижесі  -
-
 .Бұл теңдеуге
а
.Бұл теңдеуге
а қоссақ,
онда
қоссақ,
онда
 -
-

теңдеуі алынады. Бұдан
а2 2
2
Демек,
 -
- 
№16
 +
+  беттің тік сызықты
жасаушыларының ішінен (6;2;9) нүктесінен өтетінін
табыңыздар.
беттің тік сызықты
жасаушыларының ішінен (6;2;9) нүктесінен өтетінін
табыңыздар.
Шешуі: Беттің тік сызықты жасаушыларының теңдеуін жазсақ, онда
 (1)
(1)

Гипероидтың координаталарын
(6; 2;8) системалардың әрқайсысына қойсақ,
онда 
 алынады.
71
алынады.
71
Бірінші
системада  ал екінші
системада
ал екінші
системада  аламыз:
аламыз:

 ,
,
 шығады.
шығады.
Демек, есептің шарты системаны қанағаттандырады:
 ,
және
,
және 
 +
+
 теңдеуінен ОƵ осына
координаталар нақты , бір қуысты гиперболоидтың тік сызықты
жасаушыларын табыңыз.
теңдеуінен ОƵ осына
координаталар нақты , бір қуысты гиперболоидтың тік сызықты
жасаушыларын табыңыз.
Шешуі: Бір қуысты
гиперболоидтың  +
+
 теңдеуіне белгісіз
осы бір қуысты гиперболоидтың жасаушысының
теңдеуі
теңдеуіне белгісіз
осы бір қуысты гиперболоидтың жасаушысының
теңдеуі

теңдеуі шығады. Осы системаның ашып жазсақ, онда:

немесе

Берілген
жасаушының  бағыттаушы векторын
жазайық:
бағыттаушы векторын
жазайық:

Енді
 векторы ОХ осіне
перпендикуляр болуы тиіс, яғни
векторы ОХ осіне
перпендикуляр болуы тиіс, яғни
 =0
=0
Мұнда
 =
= . Осыдан 3
(
. Осыдан 3
( .
Сондықтан
.
Сондықтан  теңдеуі алынады.
Сонымен
теңдеуі алынады.
Сонымен  ,
,
 Осы мәндерді (1)
системаға қойсақ, онда
Осы мәндерді (1)
системаға қойсақ, онда
 (2)
(2)
 (3)
(3)
теңдеуі алынады. Осылай жазуымызға болады. Бұл жазықтықта екі түзу салынады. Сонымен, бірінші жазықтық екінші жазықтықта қиылысады.
у+6 жазықтығы гиперболоидтық
параболоидты
жазықтығы гиперболоидтық
параболоидты  -
-
 парабола бойынша
қиылысуын көрсетіңіздер.
парабола бойынша
қиылысуын көрсетіңіздер.
Оның периметрін және төбесін табыңыздар.
у+6 теңдеуін
у
теңдеуін
у -6 түрінде жазайық. Осы
мәнді
-6 түрінде жазайық. Осы
мәнді  -
-
 шықса, онда
бұдан
шықса, онда
бұдан  -
-
 ,
х2-45
,
х2-45 30
30 ,
х2
,
х2 +45,
х2
+45,
х2 +45) мәні алынады. Бұл
теңдеуде х2
+45) мәні алынады. Бұл
теңдеуде х2 +22,5). Мұнда
Р
+22,5). Мұнда
Р төбесі
.....
төбесі
.....
№..
 +1
+1 жазықтығы, бір қуысты
гиперболоидтың
жазықтығы, бір қуысты
гиперболоидтың  +
+
 гипербола бойынша
қиятындығын көрсетіңіздер. Оның жарты беттерін және төбесін
табыңыздар.
гипербола бойынша
қиятындығын көрсетіңіздер. Оның жарты беттерін және төбесін
табыңыздар.
Шешуі: Бір қуысты гиперболоидтың теңдеуімен жазықтықтың теңдеуінен схема құрайық.

шығады. Екінші теңдеуді біріншісіне қоссақ, онда
 ;
;
 ;
; 
Осындай гипербола болады. Бұл
гиперболаның теңдеуінде а тең екендігі шығады.
Бұдан А1(-4;0; -1),
А2(4;0; -1). Демек, гиперболаның
төбесі А1,
А2
нүктесінде, ал
тармақтары
тең екендігі шығады.
Бұдан А1(-4;0; -1),
А2(4;0; -1). Демек, гиперболаның
төбесі А1,
А2
нүктесінде, ал
тармақтары  гиперболамен
сәйкестенеді.
гиперболамен
сәйкестенеді.
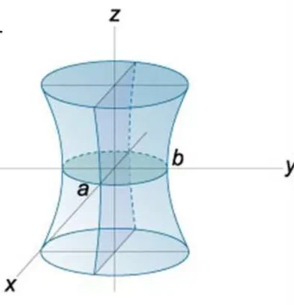
Екі қуысты гиперболоид.
Екі қуысты гиперболоидтың
канондық теңдеуі  -
-
 (1)
(1)
түрінде жазылады. Екі қуысты гиперболоидтың екі төбесі С1(0;0; -0), С1(0;0; -1) төбесі бар. Екі гиперболоидты ХОУ жазықтығымен қиса,

нағыз осі
О осінде, жанама осі ОХ
осінде жататын гипербола алынады, ал
уо
осінде, жанама осі ОХ
осінде жататын гипербола алынады, ал
уо жазықтығын
қиса,
жазықтығын
қиса,

нағыз осі
О осінде орналасқан,
жанама осі ОУ осінде жататын гипербола
алынады.
осінде орналасқан,
жанама осі ОУ осінде жататын гипербола
алынады.
Гипербола өзінің нақты осін айналатын болса, онда одан екі бөлек айналатын беттері алынады және оларды екі қуысты гиперболоид деп атайды.
-
 ,
у
,
у гиперболоиды ОХ осінен
алынған екі қуысты гиперболоидтың теңдеуін
алыңыздар.
гиперболоиды ОХ осінен
алынған екі қуысты гиперболоидтың теңдеуін
алыңыздар.
Шешуі: Гиперболаның
-  ,
у
,
у теңдеуінен мына
теңдеулерді
теңдеуінен мына
теңдеулерді
х2 а2(-1+
а2(-1+ ,
у2
,
у2
аламыз. Енді осыған екі
теңдеуді қоссақ, онда  (-1+
(-1+ . Осы
теңдеуден
. Осы
теңдеуден  -1+
-1+
 -1
-1
Демек,
 -1
-1
Теңдеу
о осінен айналғанда
алынатын екі қуысты гиперболоидтың теңдеуі болып
табылады.
осінен айналғанда
алынатын екі қуысты гиперболоидтың теңдеуі болып
табылады.
№2 Екі қуысты
гиперболоидтың  +
+

координаталық жазықтықтарына параллель жазықтықта теңдеуін табыңыздар.
Шешуі: Берілген екі қуысты
гиперболоидты уо ,
х
,
х жазықтықтарымен
қосқанда
жазықтықтарымен
қосқанда
![]()
 -
-
 немесе
немесе  +
+
 қисыны алынады.
Сондықтан, ХОУ жазықтығында осьтері
26
қисыны алынады.
Сондықтан, ХОУ жазықтығында осьтері
26 (нақты осі) және
2с
(нақты осі) және
2с (жанама осі) болатын
гиперболоиды алынады.
(жанама осі) болатын
гиперболоиды алынады.
Енді бетті ХоƵ,
у жазықтығымен қисақ,
онда
жазықтығымен қисақ,
онда
 +
+

алынады. Сондықтан, бұл қисық жорымал шеңбер болады. Мұнда нақты қисық жоқ.
Бетті енді
ХОУ,  жазықтықпен қисақ,
онда
жазықтықпен қисақ,
онда

 немесе
немесе


қисығы алынады. Бұл қисық ХОУ
жазықтығында осьтері 26 (нақты осі) және
2а
(нақты осі) және
2а (жанама осі) болатын
гиперболоиды анықтайды.
(жанама осі) болатын
гиперболоиды анықтайды.
Енді екі қуысты гиперболоидты
жазықтықтарына параллель, яғни  …………………
77
…………………
77
 +
+
 ,
, 
 ,
,
 -
-
 ,
,
 -
- 
Сонда

теңдеуі алынады. Мұнда
в1 ,
а1
,
а1 ,
,
2
в1 2
а1
2
а1 .
.
Есептің шартына сәйкес
2
в1 (2в) немесе
в1
(2в) немесе
в1 2в,
2а1
2в,
2а1 2 а немесе
а1
2 а немесе
а1
Енді а мен в орнына қойсақ, онда

Осы теңдеуді шеше
отырып,  ты
табайық:
ты
табайық:

 24,
24,



Табылған
 мәні
а1
мәні
а1 2 а болатындығын
көрсетеді:
2 а болатындығын
көрсетеді:
а1
Сонымен, хоу жазықтықтарына
параллель, теңдеулері  болатын екі жазықтық
бар. Берілген гиперболаны қиып өтетін, онда
уо
болатын екі жазықтық
бар. Берілген гиперболаны қиып өтетін, онда
уо жазықтықтарына параллель
жазықтықпен қиылысса, онда х
жазықтықтарына параллель
жазықтықпен қиылысса, онда х жазықтығын аламыз.
Сонымен
жазықтығын аламыз.
Сонымен
 +
+
 ,
,  -
-
 +1,
+1,  -
-

 -
-
 ,
,  -
-
 1
1
Нәтижесінде
 79
79
Жазықтықтағы теңдеуден
х у
у ........
........
- -
- +
+ немесе (-1)-ге көбейтсек,
-
немесе (-1)-ге көбейтсек,
- -
- -
-
теңдеуі алынады. Бұл теңдеу екі қуысты гиперболоидтың теңдеуі болып табылады.
Екі қуысты гиперболоидтың тік
бұрышты координаталар аймағында А (3;1;0),
В(2; 3) және
С(6;
3) және
С(6; ) нүктелері берілген.
Екі қуысты гиперболоидтың теңдеуін
табыңыздар.
) нүктелері берілген.
Екі қуысты гиперболоидтың теңдеуін
табыңыздар.
Шешуі: А нүктесі екі қуысты гиперболоидтың нүктесі болады. Сондықтан бұл нүктенің координаталарын екі қуысты гиперболоидтың нүктесіне қоссақ, онда
 +
+

Дәл осындай тәсілмен В мен С нүктелерінің координатасын қоссақ, онда

болады. Сонда

Егер бірінші теңдеуді 4-ке
көбейтіп, үшінші теңдеуді (-1)-көбейтіп алсақ,
онда 
Егер
 теңдеуді
теңдеуді  мен
мен
 ке қоссақ, онда
а2
ке қоссақ, онда
а2 в2
в2 ,
с2
,
с2 болады. Бұдан
х2+2х2-3
болады. Бұдан
х2+2х2-3 +1
+1 теңдеуі
алынады.
теңдеуі
алынады.
Демек, екі қуысты
гиперболоидтың теңдеуі х2+2х2-3 +1
+1 болады.
болады.
2
в11 ,
2
,
2 11
11
Есептің шартына сәйкес, 2
в11 немесе
в11
немесе
в11
2
с11 немесе
с11
немесе
с11
в11 мәндерін қойып, алынған
теңдеуді шешу арқылы в табылса, онда
мәндерін қойып, алынған
теңдеуді шешу арқылы в табылса, онда

 2
2 ,
,
 ,
12+
,
12+
 ,
,

 дің алынған
мәні
дің алынған
мәні  11
11 с теңдеуінде
қанағаттандырады, яғни
с теңдеуінде
қанағаттандырады, яғни  11
11
Дәл осындай әдіспен,
х теңдеуін
қанағаттандыратын екі жазықтықтарда бір мәнін көруге
болады.
теңдеуін
қанағаттандыратын екі жазықтықтарда бір мәнін көруге
болады.
Демек, есептің
х ,
,
 түбірлері
болады.
түбірлері
болады.
№3
3х2-4уу-6 2+24х+8ху-36
2+24х+8ху-36

Шешуі: Беттің теңдеуін түрлендірейік:
3х2-4у2-6 2+24х+8ху-36
2+24х+8ху-36
3(х2+8+16)-4(у2-2у-1)+6( 2-6
2-6 +9)-48+4-54+122
+9)-48+4-54+122
3(х2-4у2)-4(у-1)2+6( -3)2
-3)2
Теңдеудің екі жағын да 24-ке бөлсек, онда
 +
+
Егер мынадай белгілеулер

 ,
,

 ,
,
 енгізілсе, онда
мынадай теңдеу алынады:
енгізілсе, онда
мынадай теңдеу алынады:
 -
- +
+
Демек, бір түзу екі қуысты гиперболоидты анықтайды.
№4
х2-2у2+3 2-4х+4у-24
2-4х+4у-24 0 беттің канондық
теңдеуін анықтаңыздар.
0 беттің канондық
теңдеуін анықтаңыздар.
Шешуі: Беттің теңдеуін төмендегіше түрлендірсек, онда
-(х2+4х+4)+2(у2+2у) 0
0
-(х2+2х+4)+4+2(у2+2у+1)-2+3( 0
0
-(х2+2х)+2(у+1)2+3( -4)2+6
-4)2+6 0
0
-(х2-1)2+2(у+1)2+3( -4)2
-4)2 -6
-6
 +
+ 80
80
№5
4х2+4у2- 2-16у+20
2-16у+20 0 теңдеуінен берілген
екінші реттік беттің түрін анықтаңыздар. Оның кескінін
салыңыздар.
0 теңдеуінен берілген
екінші реттік беттің түрін анықтаңыздар. Оның кескінін
салыңыздар.
Шешуі: Берілген теңдеуді төмендегіше түрлендірсек, онда
4х2+4у2- 2-16у+20
2-16у+20 0
0
4х2+у+4у2
-16у- 2+20
2+20 0
0
4х2+4(у2-4у) 2+20
2+20 0
0
4х2+4(у-2) 2+4
2+4 0
0
4х2+(у-2)2 -1
-1
Координата сақинасының бас нүктесін 0(0;2;0) нүктесіне көшірсек, онда

Енді теңдеу мынадай түрге
 -1
-1
көшеді.Бұл теңдеу екі қуысты гиперболоид болады.

жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Бір қуысты гиперболоид
Бір қуысты гиперболоид
Бір қуысты гиперболоид
Бір қуысты гиперболоидтың канондық теңдеуі
 +
+
түзуінде жатады. Нақты осьтері абциссалар мен ординаталар осьтерінің координаталар осі жорамал беттерінде жатады. а, в,с - бір қуысты гиперболоидтың жарты осьтері деп аталады.
Бір қуысты гиперболоидтың координаталар жазықтықтарымен қиса, онда төменгі сызықтар пайда болады.
Егер ХОУ жазықтықтарымен
қиса,  онда
онда
 +
+ эллипсі
шығады.
эллипсі
шығады.
Егер ХОƵ жазықтықтарымен
қиса,  онда
онда
 +
+ гиперболасы
шығады.
гиперболасы
шығады.
Егер уоƵ жазықтықтарымен
қиса,  онда
онда
 +
+ гиперболасы пайда
болады.
гиперболасы пайда
болады.

Бір қуысты
гиперболоидты 
 және
және
 координаталар
жазықтықтарымен қиғанда
координаталар
жазықтықтарымен қиғанда
 ,
,
 ,
, 
теңдеулері алынады. 58
Гиперболоноид

теңдеуіндегі ОƵ осі бойымен айналдыра отырып гиперболоидтың теңдеуін құрыңыздар.
Шешуі: Гиперболоид теңдеуін түрлендірейік. Бірінші теңдеуінен х2 тауып, оны екінші теңдеудің квадратынан мына теңдеулер алынады.

алынады. Енді бұл теңдеуді мынадай
 -
- немесе
немесе 

 +
+
түрінде жазылған гиперболоидтың теңдеуі алынады.
Демек,


 +
+
бір қуысты гиперболоидтың теңдеуі болып табылады.
№12
х2+2у2+3 +2х+8у+18
+2х+8у+18 54
54 қандай теңдеу екенін
табыңдар
қандай теңдеу екенін
табыңдар
Шешуі: Теңдеудегі
х,у,  тердің толық
квадраттарын бөлсек, онда
тердің толық
квадраттарын бөлсек, онда
х2+2у2+3 +2х+8у+18
+2х+8у+18 54
54
(х2+2у2+1)-1+2(у2+4у+4)-8-3(
(х2+1)2+2(у+2)2-36 -3)2
-1-8+27-54
-3)2
-1-8+27-54
(х2+1)2+2(у+2)2-36 -3)2
-3)2

......... 36 –ға бөлсек, онда
 +
+
Бұл түзудің центрі (-1;-2; 5)
нүктесінде орналасқан. Енді тік бұрыштар координаталар
сақинасын  х+1,
х+1,  у-2,
у-2, 
 -3 формулалары арқылы
ауыстырсақ, онда
-3 формулалары арқылы
ауыстырсақ, онда  +
+ -
-
 болып, гиперболоидтың
теңдеуіне ауысады.
болып, гиперболоидтың
теңдеуіне ауысады.
Демек, берілген бет бір қуысты гиперболоидты анықтайды
М (-6; 2; 4) нүктелері арқылы өтетін және жазықтықтың


 +
+ түзу сызықты айналушысы
арқылы өтетін түзу сызықтарын жазыңыздар.
түзу сызықты айналушысы
арқылы өтетін түзу сызықтарын жазыңыздар.
Шешуі: (-6; 2; 4)нүктелері берілген жазықтықта жатсын делік, онда


 +
+ 4-1-4
4-1-4 

Бір қуысты гиперболоидтың әрбір нүктесі арқылы оның екі түзуі өтеді.
Бір қуысты гиперболоид түзуі үшін төмендегі теңдікті жазуға болады:


 немесе
немесе  +
+ -
- -
- +
+
Осыдан кейін екі системаны құрайық:


М нүктесі арқылы өтетіндіктен, k және l нүктелерін табамыз.
Алдымен k параметрін табамыз.

-6;
у
 мәндерін қойсақ,
онда
мәндерін қойсақ,
онда

-2+1
-2
k
Енді канон мәнін (2)-ге қойсақ, онда оның сол жағы

-2-1
-3
түрінде жазылады. Енді (1), (2)-ге қойсақ,
онда
 61
61
Ал бұдан
 алынады.
алынады.
Енді параметр l-ды табайық. Ол үшін (3)пен (4)-тен

Бұл теңдеуден
х,у,  мәндерін
қояйық.
мәндерін
қояйық.
Сонда

l -1 болады. Сондықтан
екінші схемасы мынадай болады:
-1 болады. Сондықтан
екінші схемасы мынадай болады:

Бұдан:

Демек, М (-6; 2; 4) нүктелерінен өтетін және гиперболоидтық түзусызықтың жолаушылары
 және
және  болады.
болады.


 теңдеуімен берілген
беттің А (6;2;8) нүктесінен болған беттің тіксызықты жасаушыларын
табыңыздар.
теңдеуімен берілген
беттің А (6;2;8) нүктесінен болған беттің тіксызықты жасаушыларын
табыңыздар.
Шешуі: Бір қуысты гиперболоидтың


 теңдеуі
берілген.
теңдеуі
берілген.
Ол бір қуысты гиперболоидтың тік түзуін жасаушылары.
 ,
,

деп анықталады,
мұнда 

 - кез келген нақты
сандар келтірілгенін пайдаланып, мынадай теңдеулер
жазамыз:
- кез келген нақты
сандар келтірілгенін пайдаланып, мынадай теңдеулер
жазамыз:
 ,
,

А нүктесінің координаталары (6; 2; 8)-де келтірілген системасының орнына қою арқылы
 ,
,

Бірінші
системадан  , екінші системадан
-
, екінші системадан
- болады.Осы
параллельдердің мәндерін қою арқылы келесі
системалар
болады.Осы
параллельдердің мәндерін қою арқылы келесі
системалар


шығады. Демек, бұлар беттің тіксызықты жасаушыларын анықтайды. 63
 -
- +
+ гиперболоидтың
координаталық жасаушыларын және
гиперболоидтың
координаталық жасаушыларын және  жазықтықтарының қиылысу
сызықтарын табыңыздар.
жазықтықтарының қиылысу
сызықтарын табыңыздар.
Шешуі: Берілген бір қуысты гиперболоидтың ХОУ координаталық жасаушыларының қиылысу сызығы
 -
- ,
,

ХОУ жазықтығындағы эллипс бетін табыңыз.
Бір қуысты гиперболоидтың УОƵ координаталық жазықтығының қиылысу сызығы
 -
-

жазықтығымен анықталады. Бұл теңдеулермен УОƵ жазықтығындағы гипербола анықталады.
ХОƵ координаталық жазықтығында бір қуысты гиперболоид
 -
- у
у
жазықтығымен анықталады. Бұл
ХОƵ координаталық жазықтығында гиперболаны анықтайды.
Гиперболамен  жазықтықтарының қиылысу
сызықтары
жазықтықтарының қиылысу
сызықтары

болады. Мұнда
эллипс  жазықтығында
жатады.
жазықтығында
жатады.
Бір қуысты гиперболоидпен
х жазықтығы
жазықтығы
 -
-

Мұнда
гипербола  жазықтығында жатады.
Егер бір қуысты гиперболоидтың координаталық
жазықтықтармен,
жазықтығында жатады.
Егер бір қуысты гиперболоидтың координаталық
жазықтықтармен,  және
және  жазықтықтарының қиылысу
сызықтары көрсетілген. 64
жазықтықтарының қиылысу
сызықтары көрсетілген. 64
............-16х-34у-2х- теңдеуі қандай бетті
анықтайды?
теңдеуі қандай бетті
анықтайды?
Шешуі: Теңдеуді түрлендірейік:
4х2-9у2+36 2-16х-54у-72
2-16х-54у-72 -65
-65
4(х2-4х+4)-9(у2+6у+9)+36( 2-27+1)-16+81-16-65
2-27+1)-16+81-16-65
4(х-4х)
2-9(у+3)2+36( 2
2

 -
- +
+ (1)
(1)
Енді
х-2 ;
у+3
;
у+3 ;
;

 алмастыруын жасасақ,
онда (1) теңдеуі
алмастыруын жасасақ,
онда (1) теңдеуі
 -
- +
+
теңдеуі пайда болады. Осындай бетті қию әдісімен қарастрайық.
Бетті ОХУ қимасымен қисақ, онда
 -
-
 гиперболасы
шығады.
гиперболасы
шығады.
Егер бетті ОУƵ жазықтықтарымен қиса, онда
 +
+
 ,
,
ОХ жазықтықтарымен қиса,
онда
жазықтықтарымен қиса,
онда
 +
+
 гиперболасы пайда
болады.
гиперболасы пайда
болады.
ОХУ жазықтығына параллель жазықтықпен қиса, онда гипербола болады.
 -
- -
- ,
,
 қияды.
қияды.
Ал
ОУ жазықтық
бойынша
жазықтық
бойынша
-
 +
+
 ,
,
 эллипспен
қияды.
эллипспен
қияды.
Ал
ОХ жазықтығы
жазықтығы
-
 +
+ +
+
 ,
,  эллипс бойынша
қияды.
эллипс бойынша
қияды.
Демек, берілген теңдеу бір қуысты гиперболаны анықтайды. 65
-
2х2-6у2+5
 -12
-12 -24у-24
-24у-24 теңдеуімен берілген бір
қуысты гиперболаны анықтаңыздар.
теңдеуімен берілген бір
қуысты гиперболаны анықтаңыздар.
Шешуі: Теңдеуді түрлендірейік:
2х2-6у2+5 -12
-12 -24у-24
-24у-24
2(х2-6 -18+24-48
-18+24-48
2(х+3)2-6(у-2)2-3( )2
)2 болады.
болады.
 +
+ +
+ теңдеуі
алынады.
теңдеуі
алынады.
Енді
х+3 ;
у-2
;
у-2 ;
;
 белгілеуін енгізсек,
онда
белгілеуін енгізсек,
онда
 -
- +
+
ОХУ қимасынан жүргізсек, онда гипербола
 -
-
 теңдеуі алынады. Егер
ОУ
теңдеуі алынады. Егер
ОУ қимасынан жүргізсек,
онда эллипс
қимасынан жүргізсек,
онда эллипс
- +
+
 теңдеуі
алынады.
теңдеуі
алынады.
ОХУ жазықтығына параллель жазықтық
 -
- -
- ,
,
 гиперболла бойынша,
ОУ
гиперболла бойынша,
ОУ жазықтығына параллель
жазықтық
жазықтығына параллель
жазықтық
-
 +
+
 ,
,
 гиперболла бойынша,
анықтайды.
гиперболла бойынша,
анықтайды.
Ал
ОХ жазықтығы
жазықтығы
-
 +
+ +
+
 ,
,  эллипс бойынша
қияды.
эллипс бойынша
қияды.
Демек, аталған эллипстерді қарастырып, берілген теңдеу бір қуысты гиперболаның теңдігін анықтайды. 66
 -1
-1 жазықтығы
жазықтығы  -
- +
+ бір қуысты гипербола
бойынша қияды.Гиперболаның жартысының төбелерін
анықтаңыздар.
бір қуысты гипербола
бойынша қияды.Гиперболаның жартысының төбелерін
анықтаңыздар.
Шешуі:
 -1
-1 теңдеуін
теңдеуін 
 -1 деп жазуға болады,
осы
-1 деп жазуға болады,
осы 
 -1 қиылысу сызығын табу
үшін,
-1 қиылысу сызығын табу
үшін, 
 -1 теңдеуіне ауыстырсақ,
онда
-1 теңдеуіне ауыстырсақ,
онда
 -
- ,
,
 -
- ,
,
 -
- теңдеуі шығады. Алынған
теңдеуде а2
теңдеуі шығады. Алынған
теңдеуде а2 а
а ,
в2
,
в2 9,
в
9,
в . Оның төбелері А(4; 0;
-1) және В(-4; 0, -1) нүктелерінде
орналасқан.
. Оның төбелері А(4; 0;
-1) және В(-4; 0, -1) нүктелерінде
орналасқан.
Демек, эллипстің жарты осьтері
а ,
в
,
в және төбелері А(4; 0;
-1), В(-4; 0, -1) нүктелерінде орналасқан.
және төбелері А(4; 0;
-1), В(-4; 0, -1) нүктелерінде орналасқан.
№9
 -
- ,
у
,
у гиперболаны
О
гиперболаны
О осіне бұру және
ОХ
осіне бұру және
ОХ жазықтығына бір мәнді
қылу арқылы
жазықтығына бір мәнді
қылу арқылы  -
- теңдеуімен анықталатын
бір қуысты гиперболоидты алу үшін қажетті басымдығын
дәлелдеңіздер.
теңдеуімен анықталатын
бір қуысты гиперболоидты алу үшін қажетті басымдығын
дәлелдеңіздер.
Шешуі: Гиперболаның
О осінен айналуынан шыққан
айналу бетінің мәні теңдеуімен
осінен айналуынан шыққан
айналу бетінің мәні теңдеуімен 
алынады.
ОХ жазықтығына сығылу
коэффициенті k=
жазықтығына сығылу
коэффициенті k= болса, онда беттің кез
келген М (Х,У,
болса, онда беттің кез
келген М (Х,У, М
(Х1,У1,
М
(Х1,У1, 1) нүктесіне көшеді. Бұл
жағдайда
1) нүктесіне көшеді. Бұл
жағдайда
 немесе
немесе 
болады. Алынған теңдеуді (1) ге қоссақ, онда


 алынады.
алынады.
Демек, берілген теңдеу бір қуысты гиперболаның теңдеуін анықтайды.
Егер бір қуысты гиперболаның
беті ОХУ жазықтығын кеседі, ал ОХ жазықтығын
жазықтығын 
 гипербола бойынша қияды. Сонда
бір қуысты гиперболаның канондық теңдеуін
табыңдар.
гипербола бойынша қияды. Сонда
бір қуысты гиперболаның канондық теңдеуін
табыңдар.
Шешуі: Бір қуысты гиперболаның теңдеуі



Егер бір қуысты гиперболоидты
ОХУ жазықтығы шеңбер бойымен есептеуі бойынша ,
яғни  9.
9.
Ал,
ОХ жазқтығымен қиылысу
сызығы
жазқтығымен қиылысу
сызығы


гипербола болады.Бұл есептің гиперболалық теңдеуі


түрінде берілген.
Мұнда 
 10
10
Демек, бір қуысты гиперболаның теңдеуі

 0 түрінде
жазылады.
0 түрінде
жазылады.

 ,
у
,
у 0 гиперболасының
О
0 гиперболасының
О осінен айналуынан
біртіндеп ОХ
осінен айналуынан
біртіндеп ОХ жазықтығына кеңістіктің
бір мәнді сығылу арқасында айқындалатынын
көрсетіңіздер.
жазықтығына кеңістіктің
бір мәнді сығылу арқасында айқындалатынын
көрсетіңіздер.
Шешуі:

 ,
у
,
у 0 гиперболасының
О
0 гиперболасының
О осінен айналғанда
мынадай теңдеумен
осінен айналғанда
мынадай теңдеумен

шығады.Осы формуланы пайдаланып, системаны былайша құрамыз.

 ,
,
 ,
,  68
68
Енді айналу беті
ОХ жазқтығына айналу
коэффициенті бойынша айналады. Осы ОХ
жазқтығына айналу
коэффициенті бойынша айналады. Осы ОХ жазықтығына айналу
бетінің М (Х,У,
жазықтығына айналу
бетінің М (Х,У, М
(Х1,У1,
М
(Х1,У1, 1) нүктесіне көшеді. Бұл
жағдайда
1) нүктесіне көшеді. Бұл
жағдайда
 немесе
немесе 
болады. Осы алынған теңдеуді (1) ге қоссақ,





 теңдеуі
алынады.
теңдеуі
алынады.
Демек, алынған теңдеу бір қуысты гиперболаның теңдеуі.
х2+2у2-4 -8
-8 теңдеуі тік бұрыштың
декарт координаталары айнымалысында қарастырып, екінші ретті беттік
теңдеуін қиылысатын әдіспен зерттеңіздер .
теңдеуі тік бұрыштың
декарт координаталары айнымалысында қарастырып, екінші ретті беттік
теңдеуін қиылысатын әдіспен зерттеңіздер .
Шешуі: Берілген теңдеудің толық квадратын бөліп жазсақ, онда
х2+2у2-4 -8
-8
 -
- 2
2
1. Осы
бетке  теңдеуін қойсақ,
онда
теңдеуін қойсақ,
онда

 +
+ 2
2
-тың орнына ху-тегі мәнін қойсақ, онда қисық
 теңдеуі пайда
болады.
теңдеуі пайда
болады.
2. Кеңістікті
х кесіндісімен қисақ,
онда
кесіндісімен қисақ,
онда
 +
+
 +
+ 2,
2,

 2
2
а)
 болса,
онда
болса,
онда 
 –
–
Бұл гипербола болады, мұнда
О нақты ось, ОУ-жанама
ось.
нақты ось, ОУ-жанама
ось.
б)
 болса,
онда
болса,
онда 
 –
–
Мұнда жалған нүкте анықталынады.
в)
 болса,
онда
болса,
онда 
 –
–
Мұндай жағдайда гипербола алынады,ОУ-нақты ось, ОУ-жанама ось.
3.Осы бетті
у  жазықтығымен қиысса,
онда
жазықтығымен қиысса,
онда
 2
2
анықталған жағдайлар екінші жағдайларға ұқсас. Демек, алынған бет
 2
2
теңдігін анықтайтын бір қуысты
гиперболоид,оның центрі (0;-0;-1) нүктесінде, ал осьтері
а в
в ,
с
,
с болады.
болады.
№13.
 бір қуысты
гиперболоидты, (0;-0;-1) нүктесінен оның жазықтығын қиған кезде
болатын қиманың теңдеуін табыңдар.
бір қуысты
гиперболоидты, (0;-0;-1) нүктесінен оның жазықтығын қиған кезде
болатын қиманың теңдеуін табыңдар.
Шешуі: (0;-0;-1) нүктесінен
өтетін жазықтықтың теңдеуі  болады.Осы теңдеуді бір
қуысты гиперболоидтың теңдеуіне қойсақ,
онда
болады.Осы теңдеуді бір
қуысты гиперболоидтың теңдеуіне қойсақ,
онда
 немесе
немесе 
Енді алынған
теңдеу  эллипсті анықтайды. Бір
қуысты гиперболоидтың (0;-0;-1) нүктесінен эллипс
өтеді.
эллипсті анықтайды. Бір
қуысты гиперболоидтың (0;-0;-1) нүктесінен эллипс
өтеді.
Демек, бір қуысты
гиперболоидтың түзуі мына  теңдеуге ауысады. Бұл
теңдеу эллипсті анықтайды. 70
теңдеуге ауысады. Бұл
теңдеу эллипсті анықтайды. 70
14.
 бір қуысты
гиперболоидтың қиындысының ОХУ жазықтығына пропорциясын
табыңдар.
бір қуысты
гиперболоидтың қиындысының ОХУ жазықтығына пропорциясын
табыңдар.
Шешуі: Бір қуысты
гиперболоидтың теңдеуіне х 2
2 теңдеуін
қосса,
теңдеуін
қосса,



х ,
,

Бұл теңдеуде
у у
у шешулері
болады.
шешулері
болады.
Демек,
у-4 у+4
у+4 жазықтықтары ОХУ
жазықтықтарындағы шешулері болады.
жазықтықтары ОХУ
жазықтықтарындағы шешулері болады.
№15 Бір қуысты гиперболоидтың
теңдеулері, егер ОХУ жазықтықтарында
х2+у шеңбер бойынша, ал ОХƵ
жазықтығын
шеңбер бойынша, ал ОХƵ
жазықтығын  жазықтығы бойынша қиса,
ол қандай канондық теңдеумен анықталатындығын
көрсетіңдер.
жазықтығы бойынша қиса,
ол қандай канондық теңдеумен анықталатындығын
көрсетіңдер.
Шешуі: Бір қуысты
гиперболоидтың теңдеулері  -
-
 түрінде жазылады.Сол
бойынша ОХУ қиылысында қимада шеңбер
х2+у2
түрінде жазылады.Сол
бойынша ОХУ қиылысында қимада шеңбер
х2+у2 Сонымен ОХУ теңдеуінен
қиған кезде гипербола нәтижесі
Сонымен ОХУ теңдеуінен
қиған кезде гипербола нәтижесі  -
-
 .Бұл теңдеуге
а
.Бұл теңдеуге
а қоссақ,
онда
қоссақ,
онда
 -
-

теңдеуі алынады. Бұдан
а2 2
2
Демек,
 -
- 
№16
 +
+  беттің тік сызықты
жасаушыларының ішінен (6;2;9) нүктесінен өтетінін
табыңыздар.
беттің тік сызықты
жасаушыларының ішінен (6;2;9) нүктесінен өтетінін
табыңыздар.
Шешуі: Беттің тік сызықты жасаушыларының теңдеуін жазсақ, онда
 (1)
(1)

Гипероидтың координаталарын
(6; 2;8) системалардың әрқайсысына қойсақ,
онда 
 алынады.
71
алынады.
71
Бірінші
системада  ал екінші
системада
ал екінші
системада  аламыз:
аламыз:

 ,
,
 шығады.
шығады.
Демек, есептің шарты системаны қанағаттандырады:
 ,
және
,
және 
 +
+
 теңдеуінен ОƵ осына
координаталар нақты , бір қуысты гиперболоидтың тік сызықты
жасаушыларын табыңыз.
теңдеуінен ОƵ осына
координаталар нақты , бір қуысты гиперболоидтың тік сызықты
жасаушыларын табыңыз.
Шешуі: Бір қуысты
гиперболоидтың  +
+
 теңдеуіне белгісіз
осы бір қуысты гиперболоидтың жасаушысының
теңдеуі
теңдеуіне белгісіз
осы бір қуысты гиперболоидтың жасаушысының
теңдеуі

теңдеуі шығады. Осы системаның ашып жазсақ, онда:

немесе

Берілген
жасаушының  бағыттаушы векторын
жазайық:
бағыттаушы векторын
жазайық:

Енді
 векторы ОХ осіне
перпендикуляр болуы тиіс, яғни
векторы ОХ осіне
перпендикуляр болуы тиіс, яғни
 =0
=0
Мұнда
 =
= . Осыдан 3
(
. Осыдан 3
( .
Сондықтан
.
Сондықтан  теңдеуі алынады.
Сонымен
теңдеуі алынады.
Сонымен  ,
,
 Осы мәндерді (1)
системаға қойсақ, онда
Осы мәндерді (1)
системаға қойсақ, онда
 (2)
(2)
 (3)
(3)
теңдеуі алынады. Осылай жазуымызға болады. Бұл жазықтықта екі түзу салынады. Сонымен, бірінші жазықтық екінші жазықтықта қиылысады.
у+6 жазықтығы гиперболоидтық
параболоидты
жазықтығы гиперболоидтық
параболоидты  -
-
 парабола бойынша
қиылысуын көрсетіңіздер.
парабола бойынша
қиылысуын көрсетіңіздер.
Оның периметрін және төбесін табыңыздар.
у+6 теңдеуін
у
теңдеуін
у -6 түрінде жазайық. Осы
мәнді
-6 түрінде жазайық. Осы
мәнді  -
-
 шықса, онда
бұдан
шықса, онда
бұдан  -
-
 ,
х2-45
,
х2-45 30
30 ,
х2
,
х2 +45,
х2
+45,
х2 +45) мәні алынады. Бұл
теңдеуде х2
+45) мәні алынады. Бұл
теңдеуде х2 +22,5). Мұнда
Р
+22,5). Мұнда
Р төбесі
.....
төбесі
.....
№..
 +1
+1 жазықтығы, бір қуысты
гиперболоидтың
жазықтығы, бір қуысты
гиперболоидтың  +
+
 гипербола бойынша
қиятындығын көрсетіңіздер. Оның жарты беттерін және төбесін
табыңыздар.
гипербола бойынша
қиятындығын көрсетіңіздер. Оның жарты беттерін және төбесін
табыңыздар.
Шешуі: Бір қуысты гиперболоидтың теңдеуімен жазықтықтың теңдеуінен схема құрайық.

шығады. Екінші теңдеуді біріншісіне қоссақ, онда
 ;
;
 ;
; 
Осындай гипербола болады. Бұл
гиперболаның теңдеуінде а тең екендігі шығады.
Бұдан А1(-4;0; -1),
А2(4;0; -1). Демек, гиперболаның
төбесі А1,
А2
нүктесінде, ал
тармақтары
тең екендігі шығады.
Бұдан А1(-4;0; -1),
А2(4;0; -1). Демек, гиперболаның
төбесі А1,
А2
нүктесінде, ал
тармақтары  гиперболамен
сәйкестенеді.
гиперболамен
сәйкестенеді.

Екі қуысты гиперболоид.
Екі қуысты гиперболоидтың
канондық теңдеуі  -
-
 (1)
(1)
түрінде жазылады. Екі қуысты гиперболоидтың екі төбесі С1(0;0; -0), С1(0;0; -1) төбесі бар. Екі гиперболоидты ХОУ жазықтығымен қиса,

нағыз осі
О осінде, жанама осі ОХ
осінде жататын гипербола алынады, ал
уо
осінде, жанама осі ОХ
осінде жататын гипербола алынады, ал
уо жазықтығын
қиса,
жазықтығын
қиса,

нағыз осі
О осінде орналасқан,
жанама осі ОУ осінде жататын гипербола
алынады.
осінде орналасқан,
жанама осі ОУ осінде жататын гипербола
алынады.
Гипербола өзінің нақты осін айналатын болса, онда одан екі бөлек айналатын беттері алынады және оларды екі қуысты гиперболоид деп атайды.

-
 ,
у
,
у гиперболоиды ОХ осінен
алынған екі қуысты гиперболоидтың теңдеуін
алыңыздар.
гиперболоиды ОХ осінен
алынған екі қуысты гиперболоидтың теңдеуін
алыңыздар.
Шешуі: Гиперболаның
-  ,
у
,
у теңдеуінен мына
теңдеулерді
теңдеуінен мына
теңдеулерді
х2 а2(-1+
а2(-1+ ,
у2
,
у2
аламыз. Енді осыған екі
теңдеуді қоссақ, онда  (-1+
(-1+ . Осы
теңдеуден
. Осы
теңдеуден  -1+
-1+
 -1
-1
Демек,
 -1
-1
Теңдеу
о осінен айналғанда
алынатын екі қуысты гиперболоидтың теңдеуі болып
табылады.
осінен айналғанда
алынатын екі қуысты гиперболоидтың теңдеуі болып
табылады.
№2 Екі қуысты
гиперболоидтың  +
+

координаталық жазықтықтарына параллель жазықтықта теңдеуін табыңыздар.
Шешуі: Берілген екі қуысты
гиперболоидты уо ,
х
,
х жазықтықтарымен
қосқанда
жазықтықтарымен
қосқанда

![]()
 -
-
 немесе
немесе  +
+
 қисыны алынады.
Сондықтан, ХОУ жазықтығында осьтері
26
қисыны алынады.
Сондықтан, ХОУ жазықтығында осьтері
26 (нақты осі) және
2с
(нақты осі) және
2с (жанама осі) болатын
гиперболоиды алынады.
(жанама осі) болатын
гиперболоиды алынады.
Енді бетті ХоƵ,
у жазықтығымен қисақ,
онда
жазықтығымен қисақ,
онда
 +
+

алынады. Сондықтан, бұл қисық жорымал шеңбер болады. Мұнда нақты қисық жоқ.
Бетті енді
ХОУ,  жазықтықпен қисақ,
онда
жазықтықпен қисақ,
онда

 немесе
немесе


қисығы алынады. Бұл қисық ХОУ
жазықтығында осьтері 26 (нақты осі) және
2а
(нақты осі) және
2а (жанама осі) болатын
гиперболоиды анықтайды.
(жанама осі) болатын
гиперболоиды анықтайды.
Енді екі қуысты гиперболоидты
жазықтықтарына параллель, яғни  …………………
77
…………………
77
 +
+
 ,
, 
 ,
,
 -
-
 ,
,
 -
- 
Сонда

теңдеуі алынады. Мұнда
в1 ,
а1
,
а1 ,
,
2
в1 2
а1
2
а1 .
.
Есептің шартына сәйкес
2
в1 (2в) немесе
в1
(2в) немесе
в1 2в,
2а1
2в,
2а1 2 а немесе
а1
2 а немесе
а1
Енді а мен в орнына қойсақ, онда

Осы теңдеуді шеше
отырып,  ты
табайық:
ты
табайық:

 24,
24,



Табылған
 мәні
а1
мәні
а1 2 а болатындығын
көрсетеді:
2 а болатындығын
көрсетеді:
а1
Сонымен, хоу жазықтықтарына
параллель, теңдеулері  болатын екі жазықтық
бар. Берілген гиперболаны қиып өтетін, онда
уо
болатын екі жазықтық
бар. Берілген гиперболаны қиып өтетін, онда
уо жазықтықтарына параллель
жазықтықпен қиылысса, онда х
жазықтықтарына параллель
жазықтықпен қиылысса, онда х жазықтығын аламыз.
Сонымен
жазықтығын аламыз.
Сонымен
 +
+
 ,
,  -
-
 +1,
+1,  -
-

 -
-
 ,
,  -
-
 1
1
Нәтижесінде
 79
79
Жазықтықтағы теңдеуден
х у
у ........
........
- -
- +
+ немесе (-1)-ге көбейтсек,
-
немесе (-1)-ге көбейтсек,
- -
- -
-
теңдеуі алынады. Бұл теңдеу екі қуысты гиперболоидтың теңдеуі болып табылады.
Екі қуысты гиперболоидтың тік
бұрышты координаталар аймағында А (3;1;0),
В(2; 3) және
С(6;
3) және
С(6; ) нүктелері берілген.
Екі қуысты гиперболоидтың теңдеуін
табыңыздар.
) нүктелері берілген.
Екі қуысты гиперболоидтың теңдеуін
табыңыздар.
Шешуі: А нүктесі екі қуысты гиперболоидтың нүктесі болады. Сондықтан бұл нүктенің координаталарын екі қуысты гиперболоидтың нүктесіне қоссақ, онда
 +
+

Дәл осындай тәсілмен В мен С нүктелерінің координатасын қоссақ, онда

болады. Сонда

Егер бірінші теңдеуді 4-ке
көбейтіп, үшінші теңдеуді (-1)-көбейтіп алсақ,
онда 
Егер
 теңдеуді
теңдеуді  мен
мен
 ке қоссақ, онда
а2
ке қоссақ, онда
а2 в2
в2 ,
с2
,
с2 болады. Бұдан
х2+2х2-3
болады. Бұдан
х2+2х2-3 +1
+1 теңдеуі
алынады.
теңдеуі
алынады.
Демек, екі қуысты
гиперболоидтың теңдеуі х2+2х2-3 +1
+1 болады.
болады.
2
в11 ,
2
,
2 11
11
Есептің шартына сәйкес, 2
в11 немесе
в11
немесе
в11
2
с11 немесе
с11
немесе
с11
в11 мәндерін қойып, алынған
теңдеуді шешу арқылы в табылса, онда
мәндерін қойып, алынған
теңдеуді шешу арқылы в табылса, онда

 2
2 ,
,
 ,
12+
,
12+
 ,
,

 дің алынған
мәні
дің алынған
мәні  11
11 с теңдеуінде
қанағаттандырады, яғни
с теңдеуінде
қанағаттандырады, яғни  11
11
Дәл осындай әдіспен,
х теңдеуін
қанағаттандыратын екі жазықтықтарда бір мәнін көруге
болады.
теңдеуін
қанағаттандыратын екі жазықтықтарда бір мәнін көруге
болады.
Демек, есептің
х ,
,
 түбірлері
болады.
түбірлері
болады.
№3
3х2-4уу-6 2+24х+8ху-36
2+24х+8ху-36

Шешуі: Беттің теңдеуін түрлендірейік:
3х2-4у2-6 2+24х+8ху-36
2+24х+8ху-36
3(х2+8+16)-4(у2-2у-1)+6( 2-6
2-6 +9)-48+4-54+122
+9)-48+4-54+122
3(х2-4у2)-4(у-1)2+6( -3)2
-3)2
Теңдеудің екі жағын да 24-ке бөлсек, онда
 +
+
Егер мынадай белгілеулер

 ,
,

 ,
,
 енгізілсе, онда
мынадай теңдеу алынады:
енгізілсе, онда
мынадай теңдеу алынады:
 -
- +
+
Демек, бір түзу екі қуысты гиперболоидты анықтайды.
№4
х2-2у2+3 2-4х+4у-24
2-4х+4у-24 0 беттің канондық
теңдеуін анықтаңыздар.
0 беттің канондық
теңдеуін анықтаңыздар.
Шешуі: Беттің теңдеуін төмендегіше түрлендірсек, онда
-(х2+4х+4)+2(у2+2у) 0
0
-(х2+2х+4)+4+2(у2+2у+1)-2+3( 0
0
-(х2+2х)+2(у+1)2+3( -4)2+6
-4)2+6 0
0
-(х2-1)2+2(у+1)2+3( -4)2
-4)2 -6
-6
 +
+ 80
80
№5
4х2+4у2- 2-16у+20
2-16у+20 0 теңдеуінен берілген
екінші реттік беттің түрін анықтаңыздар. Оның кескінін
салыңыздар.
0 теңдеуінен берілген
екінші реттік беттің түрін анықтаңыздар. Оның кескінін
салыңыздар.
Шешуі: Берілген теңдеуді төмендегіше түрлендірсек, онда
4х2+4у2- 2-16у+20
2-16у+20 0
0
4х2+у+4у2
-16у- 2+20
2+20 0
0
4х2+4(у2-4у) 2+20
2+20 0
0
4х2+4(у-2) 2+4
2+4 0
0
4х2+(у-2)2 -1
-1
Координата сақинасының бас нүктесін 0(0;2;0) нүктесіне көшірсек, онда

Енді теңдеу мынадай түрге
 -1
-1
көшеді.Бұл теңдеу екі қуысты гиперболоид болады.



шағым қалдыра аласыз















