
М А З М Ұ Н Ы
КІРІСПЕ..................................................................................................................3
-
ТЕОРИЯЛЫҚ БӨЛІМ
1.1. БИРЖА НАРЫҒЫНДАҒЫ КЕЗДЕЙСОҚ ОҚИҒАЛАР................4
-
Практикалық бөлім
2.1.БИРЖА НАРЫҒЫНЫҢ ОРТА ШАМАЛАРЫН ЕСЕПТЕУ....9
Қорытынды.................................................................................................19
Пайдаланылған әдебиеттер тізімі...........................................20
Зерттеу тақырыбының көкейкестігі. Зерттеу жұмысында қарастырылған мәселенің көкейкестігі қазіргі ғылым мен техниканы және экономиканы көтерудің күрделі мәселелерін шешу білім берудің жаңашылдық міндеті қоғамдық қатынастар мен құндылықтар жүйесіндегі өзгеріс талаптарына сәйкес мектептегі білім беру сапасын арттыру болып табылады.
Зерттеу мақсаты: биржадағы өзгерістерді математикалық модельдеу арқылы статистика элементтерінің практикалық қолданысын көрсету
Зерттеу болжамы: математикалық күтім, стандартты ауытқу мен бағанды диаграммаларды қолдану арқылы болжау.
Зерттеудің міндеттері:
Зерттеудің проблемасын шешу, болжамның дұрыстығына көз жеткізу және мақсатқа жету үшін келесі мәселелер орындалады:
-
осы тақырып бойынша бар ғылыми-зерттеу әдебиеттерді зерттеу;
-
заманауи оқу құралдарына осы тақырыптың баяндалуына логикалық талдау жүргізу;
-
алынған мәліметтерді жалпылау және жүйелеу;
-
жасалынған әдістемені пайдаланудың тиімділігін тәжірибеде тексеру;
Зерттеу әдістері:
Жұмыстың мақсатына жету, болжамды тексеру және жоғарыда қойылған мәселелерді шешу үшін келесі әдістер пайдаланылады:
-
мәліметтерді іздеу, жинақтау талдау;
-
әр түрлі ғылыми зерттеу жұмыстарын салыстырмалы талдау;
-
бақылау және бағалау;
-
уақытты үнемдеу мақсатында социометриялық әдісті де қолдану
Зерттеу объектісі: биржа математикасы
Зерттеудің теориялық және практикалық маңыздылығы:
Зерттеу жұмысы кіріспеден, 2 тараудан, қорытынды және қолданылған әдебиеттерден тұрады.
Кіріспе
"Сандардың көмегімен сіз бәрін дәлелдей аласыз"
Томас Карлайл, ағылшын публицисті, тарихшы
Статистикалық және математикалық әдістерді білу сізге көмектеседі:
- математикалық негізделген талдау жүргізу және баға динамикасына баға беру;;
- инвестициялардың нақты кірістілігі мен орташа нарықтық тәуекелін бағалау;
- әр түрлі активтер арасындағы өзара байланысты табу және олардың;
- түрлі оқиғалардың болу ықтималдығын бағалау;
- білікті тәуекел-менеджментті қолдау.
Ықтималдық процесі
Қаржы нарықтарындағы жұмыс болашақ оқиғаларды ықтималды бағалауды қамтиды. Бұл, ең алдымен, психологияға арналған тарауда ақпараттық "гололдың" қасиеттерін талдайтын адамдар жиі кездесетін ақпараттың жетіспеушілігінен туындайды және осы процестің математикалық сипаттамасына тоқталамыз. Мұндағы ең бастысы-қаржы нарықтарындағы сауда объектісі болып табылатын болашақты толық білмеуіміз. Сонымен, фьючерстік келісімшартты сатып ала отырып, біз фьючерстер жазылған тауар құнының өсуіне сенеміз. Егер сіз барлық 100 пайызға дұрыс нәрсені істеп жатқаныңызға сенімді болсаңыз, онда бұл жалған өзіне деген сенімділіктен артық емес. Өкінішке орай, нарықта ештеңеге сенімді болу мүмкін емес. Алайда, адам болашақты білмейді, бірақ көбінесе өткен туралы өте жаман және сенімсіз ақпаратқа ие.
Тек жақын өткен адамға ақпараттың толықтығы үшін қол жетімді, ал алыс құпия құпияның артында болашақтан гөрі жаман емес. Көп немесе аз адам қазіргі жағдайды түсінеді. Алайда, мұнда да ақпараттың көптігі адам өзінің айналасындағы шындықты біледі деп айтуға негіз бермейді. Осылайша, сіз қайда қарасаңыз да – өткенге, бүгінге немесе болашаққа – адам барлық жерде қабылдай алатын және талдай алатын, сондай-ақ оған қол жеткізе алатын ақпарат көлемімен шектеледі. Ақпараттың үнемі жетіспеушілігіне байланысты біз тек осы немесе басқа оқиғаның болу ықтималдығы туралы айтуымыз керек. Мен нарықтағы бағаның қозғалысы мүлдем кездейсоқ құбылыс деп айтпаймын, дегенмен бұл ықтималдық теориясын зерттеудің нысаны болып табылатын кездейсоқ оқиғалар.
1.1.БИРЖА НАРЫҒЫНДАҒЫ КЕЗДЕЙСОҚ ОҚИҒАЛАР
Кездейсоқ оқиға-тәжірибенің (жағдайдың) нәтижесіне байланысты әртүрлі мәндерді қабылдайтын және дәл болжау мүмкін емес оқиға.
Біздің білуімізше, ұзақ уақыт бойы баға динамикасын мүлдем жүз пайыз болжау әлі күнге дейін шешілмеген мәселе болып табылады. Жүреді ол бойынша жетілдірілмеуі себебі біздің түсіну немесе жеткіліксіз ақпарат, дерек мінез-құлық нарық қалады себепші болады. Непредсказуемостью ие және кездейсоқ оқиғалар. Бұл кездейсоқтық теориясы (кездейсоқ-walk theory) оның өмір сүруінің негізі ретінде қолданылады.
Мұнда қазіргі заманғы қаржылық шешімдердің негізін құрайтын негізгі теорияларға қысқаша шолу жасалуы керек. Оларға теорияларды жатқызуға болады:
- нарықтық тепе-теңдік,
- кездейсоқ кезбе;
- ойындар.
Нарықтық тепе-теңдік теориясы нарық сұраныс пен ұсыныс арасындағы тепе-теңдік жағдайына ұмтылады деген постулаттан туындайды. Бұл теория тепе-теңдік күйінен ауытқуларды жоққа шығармайды.
BCN тиімді нарық теориясына сәйкес жаңа ақпарат бірден нарықтық бағаларға енгізіледі. Осылайша, кез-келген ақпаратқа немесе өткен баға динамикасына, тиімді нарық теориясының қорытындыларына назар аудара отырып, пайда табу мүмкін емес:
- нарықтық бағалардың динамикасын ешкім болжай алмайды;
- барлық нарықтық бағалар осы активтер үшін жарамды, ал дұрыс бағаланбаған тауарлар жоқ.
Тиімді нарық теориясына қарсы қаржы нарықтарының тәжірибесі айтады. Біріншіден, ақпаратты әртүрлі адамдар әр түрлі қабылдайды, бұл туралы біз психологияға арналған тарауда айттық. Екіншіден, нарық алған ақпараттың жалған емес, шынайы екендігіне кепілдік қайда. Үшіншіден, уақыттың әртүрлі нүктелерінде бірдей ақпаратты әртүрлі жолмен түсіндіруге болады. Төртіншіден, нарықтық бағаның әр сәтте әділ немесе шынайы болуы екіталай. Бұл жерде нарықтық баға мезгіл-мезгіл әділ бағаны кесіп өтіп, көтерілген күйден оған қатысты төмендетілген бағаға ауысады және керісінше болады деп сенуге болады.
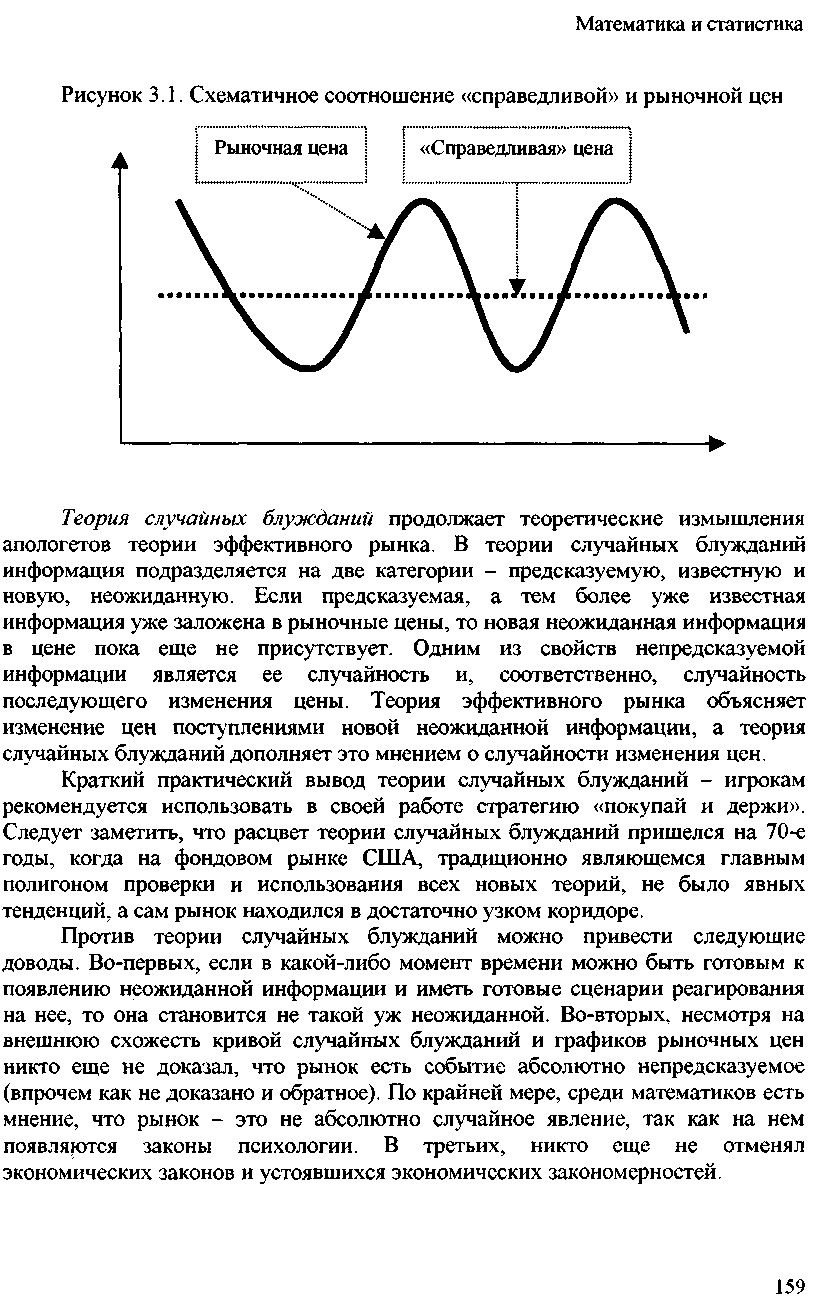
Сурет-1. Әділ мен нарықтық баға
Кездейсоқ серуендеу теориясы тиімді нарық теориясының кешірім сұрауын теориялық тұрғыдан жалғастыруда. кездейсоқ серуендеу теориясында ақпарат болжамды, белгілі және жаңа, күтпеген екі санатқа бөлінеді. Егер болжамды, тіпті одан да көп белгілі ақпарат нарықтық бағаларға енгізілген болса, онда бағада жаңа күтпеген ақпарат әлі жоқ. Болжанбайтын ақпараттың қасиеттерінің бірі оның кездейсоқтығы және сәйкесінше бағаның кейінгі өзгеруінің кездейсоқтығы болып табылады. Тиімді нарық теориясы бағаның өзгеруін жаңа күтпеген ақпараттың түсуімен түсіндіреді, ал кездейсоқ вагус теориясы мұны бағаның өзгеру мүмкіндігі туралы пікірмен толықтырады.Кездейсоқ серуендеу теориясының қысқаша практикалық тұжырымы ойыншыларға өз жұмысында "сатып алу және сақтау" стратегиясын қолдануға кеңес беріледі. Айта кету керек, кездейсоқ серуендеу теориясының өркендеуі 70-ші жылдары, АҚШ-тың қор нарығында, дәстүрлі түрде барлық теориялардың қолданылуын тексерудің негізгі жартысы болған кезде айқын тенденциялар болған жоқ, ал нарықтың өзі өте тар дәлізде болды.
Кездейсоқ серуендеу теориясына қарсы келесі дәлелдер келтіруге болады. Біріншіден, Егер сіз кез-келген уақытта күтпеген ақпараттың пайда болуына дайын болсаңыз және оған жауап берудің дайын сценарийлері болса, онда ол күтпеген жағдайға айналмайды. Екіншіден, кездейсоқ кезбе қисығының және нарықтық баға графигінің сыртқы ұқсастығына қарамастан, нарық мүлдем болжанбайтын оқиға екенін ешкім әлі дәлелдеген жоқ (дегенмен, керісінше дәлелденбеген). Кем дегенде, математиктердің арасында нарық мүлдем кездейсоқ құбылыс емес деген пікір бар, өйткені онда психология заңдары пайда болады. Үшіншіден, ол әлі де экономикалық заңдар мен қалыптасқан экономикалық заңдылықтарды жойды.
Джон Дж.Мерфи,
"...көбінесе кездейсоқтық Нести баға динамикасында жүйелі модельдер мен заңдылықтарды белгілеу ерекшелігі"
Ойынның ең қарапайым және кең таралған көрінісі-нәтиже матрицасын құру. Осы матрицаның әр элементі кез-келген ықтимал стратегия үшін белгілі бір ойыншы күткен нәтижені көрсетеді. Айта кету керек, ойын теориясы үшін ойыншы тек басқа ойыншылардың жағдайы мен әрекеттеріне әсер ете алатын белсенді қатысушы ретінде танылады. Тек нарықты ұстанатын пассивті қатысушылар, ойыншылар, олардың барлық қалауы бойынша. олар атала алмайды.
Мысалы. Төмендегі нәтижелер матрицасында екі қатысушы үшін нөлдік сомадағы а ойнатқышының нәтижелері көрсетілген:

Мұнда, егер А ойыншысы az стратегиясын, ал ойыншы стратегияны таңдаса . онда А ойыншысы үшін нәтиже -10, ал B + 10 ойыншысы үшін болады. Әр ойыншының міндеті-басқа ойыншының стратегиясын ескере отырып, қажетті нәтижені барынша арттыратын стратегияны таңдау. Сонымен, а ойыншысының көзқарасы бойынша в ойыншысының үш мүмкін стратегиясына ең жақсы реакция келесі жұптарды құрайды:), (b2, a1), (b3, A2). Ойыншы үшін А ойыншысының ықтимал стратегияларына ең жақсы реакция келесі жұптарды құрайды: (a1, b3), (a2. B3). (а3, b2). Мұндағы жалғыз қиылысатын стратегия-жұп (a, b). бұл екі ойыншының ең жақсы реакцияларында. Осылайша, А және В ойыншыларының 2-ші және 3-ші стратегияларын бір уақытта таңдау осы нәтиже матрицасының шешімі болады. Алайда, өмірлік тәжірибе көрсеткендей, бәрі бірдей қарапайым емес. Біріншіден, ойыншылар ережелердің басқа шешімдері негізінде шешім қабылдау арқылы ең жақсы таңдау туралы білмеуі мүмкін. Екіншіден, ойыншылардың әрекеттері өте сирек кездеседі, бұл ойыншылардың біріне артықшылық береді. Үшіншіден, стратегиялардың сансыз жиынтығы болуы мүмкін. Төртіншіден, өмірде нәтиже матрицалары жоғарыда келтірілген статикалық мысалдан айырмашылығы динамикалық жүйелер болып табылады.Дегенмен, маркетологтар (сөздің кең мағынасында) өз іс-әрекеттерін нақты және мүмкін болатын басқа қатысушылардың мінез-құлқымен, оның ішінде жалпы нарықтық массамен өлшеуге мәжбүр.Ойынның ең жақсы стратегиясын таңдаудағы басты мәселе-ақпараттың белгісіздігі. Бұл матрицаны шешу кезінде ықтималдық әдістерін қолдану қажеттілігін анықтайды.
Ойын теориясына нарық тек ірі ойыншылар келісе алатын ойыншылар қауымдастығы деген көзқараспен де жүгінуге болады. Тиісінше, олар тек ынтымақтастықтың пайдасын көре алады және кірістерін барынша арттыра алады. Қалғандары қатаң жалғыз әрекет етуге және бір-бірімен ірі ойыншылармен бәсекелесуге мәжбүр. Теорияға сәйкес, бір-бірімен ынтымақтастық жасамайтын ойыншылар сөзсіз бәсекелестіктен айырылады. Бұл дегеніміз, кішкентай ойыншылар үлкен ойыншылар олармен бөліскен кезде ғана жеңіске жетеді.
Ойын теориясының тәсілі, менің ойымша, кездейсоқ жүру теориясымен салыстырғанда қаржы нарықтарында қолдануға негізделген. Мұның себебі, менің ойымша, бұл тұрақты сериялардың барлық кейінгі сандары алдыңғы жолдармен жасалады, оларға кім және кім әсер етуге тырысса.
Ықтималдық теориясы
Алдыңғы абзацта айтылғандардың бәрі бізге нарықтық құбылыстарға кездейсоқ ретінде қарауға және сәйкесінше ықтималдық теориясын қолдануға негіз береді. Осылайша, ықтималдық теориясын түсінбестен, келесі қадамдарды жасаудың мағынасы жоқ.Ықтималдық - кез-келген кездейсоқ оқиғаның сандық өлшемі. Ықтималдық o-дан (мүмкін емес оқиға) 1-ге дейінгі аралықта (міндетті түрде болатын оқиға) болуы мүмкін. Кейде ықтималдық пайызбен сипатталады. Бұл жағдайда ықтималдық мәндерінің шекаралары сәйкесінше 0% және 100% болады.Кездейсоқ оқиғаның пайда болу ықтималдығын анықтаудың классикалық формуласы келесідей:
 ,мұндағы
(-1)
,мұндағы
(-1)
Nх - кездейсоқ оқиғаның болуы мүмкін нұсқалардың саны х;
N- ықтимал нәтижелердің жалпы саны
Мысалы. Ойынды лақтыру арқылы біз алты мүмкін нәтиже аламыз — алты жақтың біреуінің жоғалуы: 1, 2, 3, 4, 5 немесе 6. Осылайша, бетінің біреуінің құлау ықтималдығын анықтауға болады, мысалы, 3:
P(А)
= 0.1667
немесе
16.67%
0.1667
немесе
16.67%
Осылайша, ойнатқыштың бір бетінің құлау ықтималдығы (біздің мысалда 3) 16.67% құрайды.Сондай-ақ, екі беттің біреуінің құлау ықтималдығын анықтауға болады (мысалы, 2 немесе 3). Бұл жағдайда ықтималдылықты қосу ережесі қолданылады және ықтималдық келесідей есептеледі:
P(x немесе y) = p(x) + P (y) = 0.1667 +0.1667 = 0.3333 немесе 3-33%, мұндағы
P (x) – кездейсоқ оқиғаның басталу ықтималдығы х(біздің мысалда 2); P (u) — кездейсоқ оқиғаның пайда болу ықтималдығы у (3). Осылайша, 2 немесе 3 саны бар беттің түсу ықтималдығы 3-33% құрайды .
Ықтималдылықты қосу ережесі тәуелді оқиғалар үшін қолданылады, егер бір кездейсоқ оқиға басқа кездейсоқ оқиғаның басталуын жоққа шығармаса.
Егер бір уақытта екі немесе одан да көп кездейсоқ оқиғалардың пайда болу ықтималдығын табу қажет болса, ықтималдылықты көбейту ережесі қолданылады. Бұл жағдайда барлық оқиғалар бір-бірінен тәуелсіз болуы керек.
Мысалы. Екі ойнатқышты бір уақытта лақтырудың нәтижесінде біз 36 түрлі комбинацияны аламыз: 1-1, 1-2, 1-3, 14, 15, 16, 2-1, 2- 2, 2-3 және т. б. лақтыру нәтижесінде біз екі сүйектің бүйірлерінде бір-бірлеп аламыз деген ықтималдылықты анықтау үшін ықтималдылықты көбейту ережесін қолданамыз:
P (X және Y) = P(X) * P (y) = 0.1667*0.1667 = 0.0278 немесе 2.78%
Осылайша, 1 сандары бар беттердің сүйек сүйектерінің бір уақытта түсу ықтималдығы 2.78% құрайды.
2.1.БИРЖА НАРЫҒЫНЫҢ ОРТА ШАМАЛАРЫН ЕСЕПТЕУ
Арифметикалық орта
Баға динамикасын талдау, ең алдымен, бағалардың орташа деңгейін және олардың ауытқу аралықтарын анықтаудан тұрады. Талдау үшін орташа мән ең ықтимал деп айтуға болады. Объективті түрде, орташа мән мен мүмкін болатын мән арасында тең белгі қою дұрыс емес.Бағаның орташа деңгейі нарық үшін ең тартымды бағаны көрсетеді, ол белгілі бір уақытта нарықтың белсенді қатысушыларының инвестициялық артықшылықтарын көрсетеді.Арифметикалық орта-қатардың барлық мәндерінің қосындысының олардың санына қатынасы:
 мұндағы(-2)
мұндағы(-2)
хj — талданатын айнымалы;
n – айнымалы бақылаулар саны х.
Мысалы.
1999 жылғы қаңтардағы Dow Jones Industrial (DJI, close) индексі мәндерінің орташа арифметикалық қатарын ьтабу қажет:

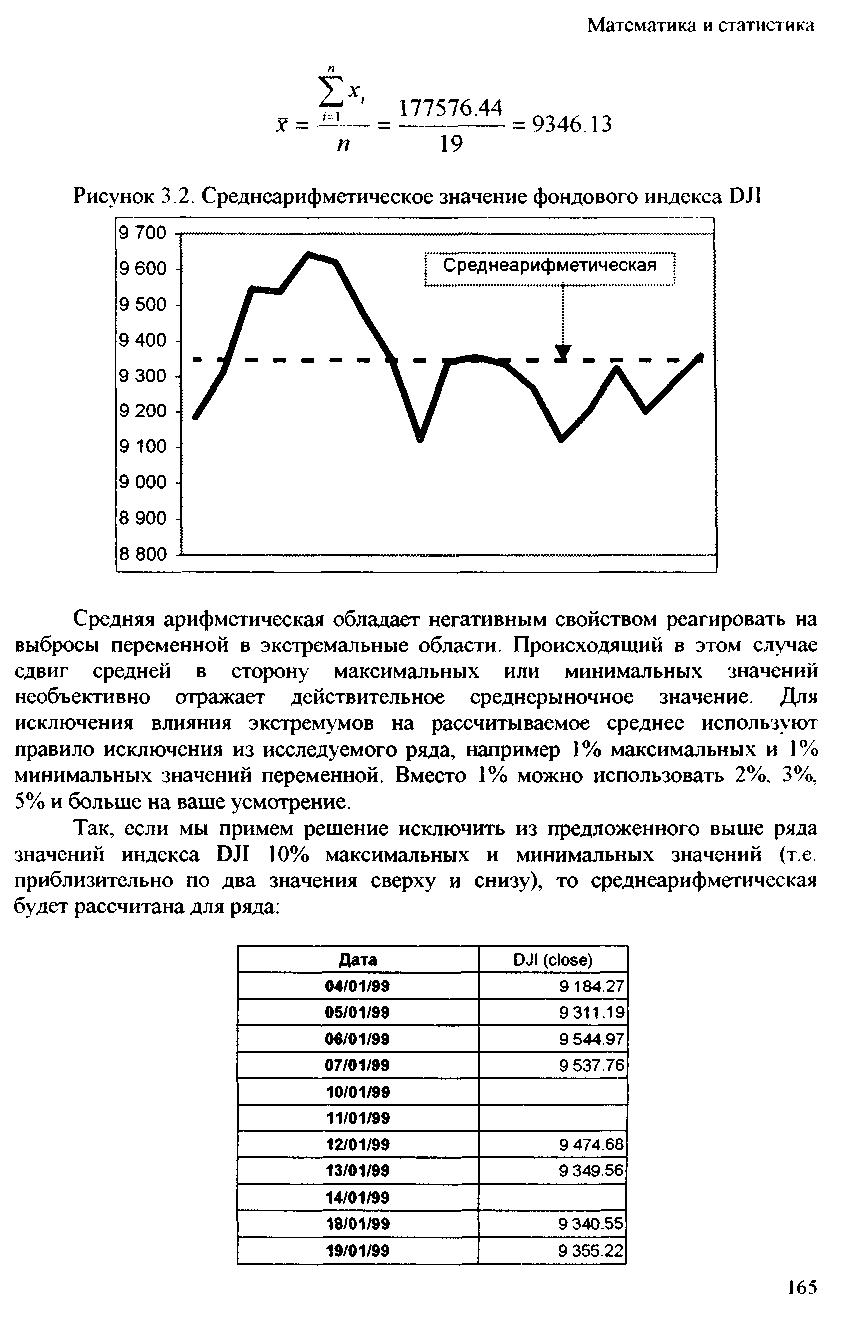
Арифметикалық орта айнымалылардың экстремалды облыстардағы шығарындыларына әсер етудің теріс қасиетіне ие. Бұл жағдайда орташа мәннің максималды минималды мәндерге қарай жылжуы нақты орташа нарықтық мәнді объективті түрде көрсетпейді. Экстремалардың есептелген орташа мәнге әсерін болдырмау үшін зерттелетін қатардан алып тастау ережесі қолданылады, мысалы, айнымалының ең жоғары мәндерінің 1% және ең төменгі мәндерінің 1%. 1% орнына 2%, 3% пайдалануға болады. 5% және одан да көп сіздің қалауыңыз бойынша.
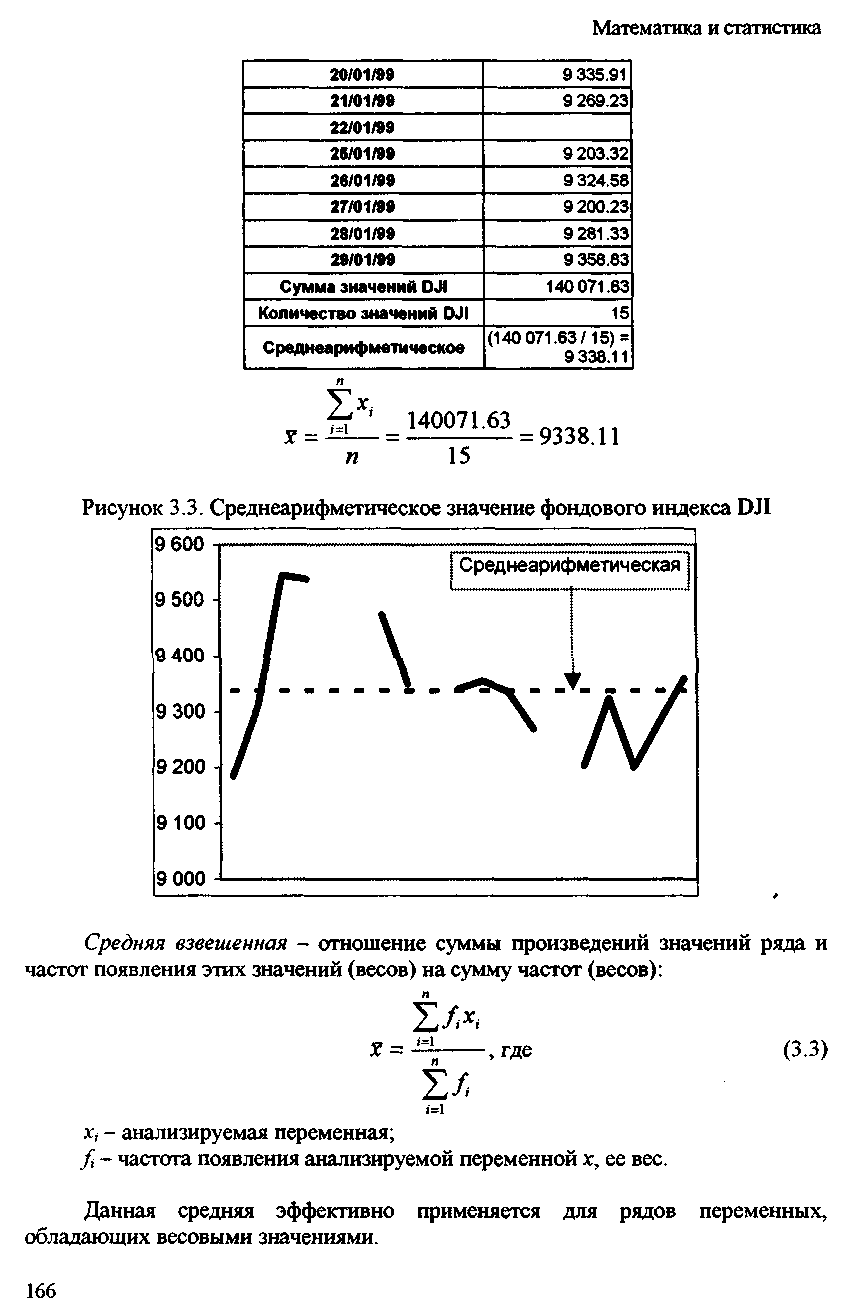
Сонымен, егер D индексінің 10% максималды және күдікті мәндерінің ұсынылған қатарынан алып тастау туралы шешім қабылдасақ (яғни, жоғарыдан және төменнен шамамен екі мән), онда орташа арифметикалық қатар үшін есептеледі:



Средняя взвешенная – отношение суммы произведений значений ряда и частот появления этих значений (весов) на сумму частот (весов):
 мұндағы(-3)
мұндағы(-3)
xi – талданатын айнымалы;
fi - талданатын айнымалы салмақтың пайда болу жиілігі.
Бұл орташа салмақ мәні бар айнымалылар қатарына тиімді қолданылады.
Мысалы. 1997 жылғы 26 маусымдағы топтастырылған GBP / USD валюталық индексі

Бұл серияның сәні 1.6660-тен 1,6665-ке дейінгі аралықта болады. Дәлірек айтқанда, талдаудың графикалық әдісі бізге сәнді анықтауға көмектеседі.
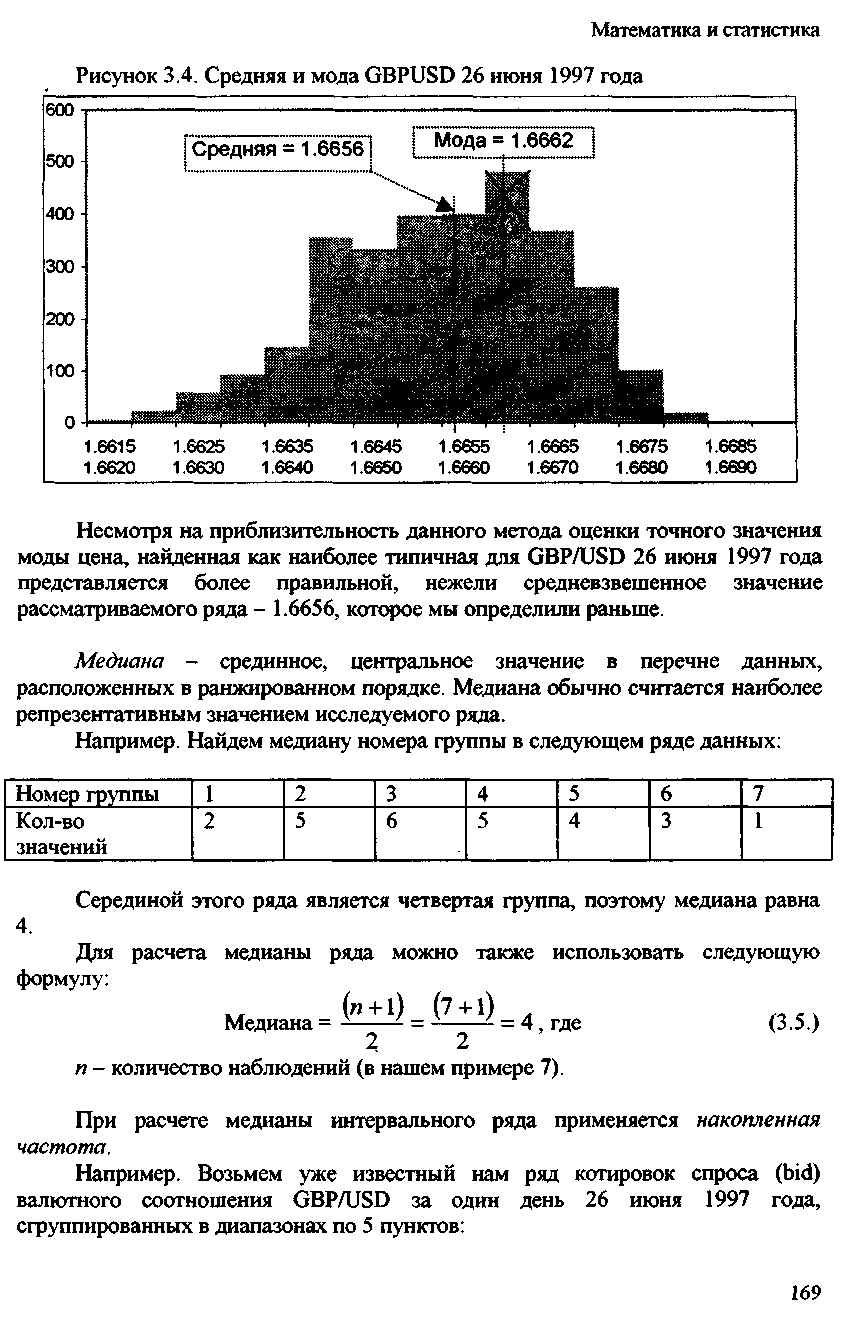
1997 жылғы 26 маусымда GBP/USD үшін ең тән баға ретінде табылған сәннің дәл мәнін бағалаудың осы әдісінің шамалығына қарамастан, біз бұрын анықтаған 1.6656 – қарастырылып отырған қатардың орташа өлшенген мәнінен гөрі дұрыс болып көрінеді.
Медиана-бұл орташа, рейтингте орналасқан мәліметтер тізіміндегі орталық мән. Медиана, әдетте, зерттелетін қатардың ең көрнекті мәні болып саналады.
Мысалы. Топ нөмірінің медианасын келесі деректер қатарынан табамыз:

Бұл қатардың ортасы-төртінші топ, сондықтан медианаға тең.
4. Сериялардың медианасын есептеу үшін келесі формуланы қолдануға болады:
Медиана =
 4,
(-5)
4,
(-5)
p-бақылаулар саны (біздің мысалда 7).
Аралық қатардың медианасын есептеу кезінде жинақталған жиілік қолданылады.
Мысалы. 1997 жылғы 26 маусымда 5 тармақтан тұратын диапазондарда топтастырылған, бізге белгілі GBP / USD валюталық арақатынасына сұраныстың (bid) бірқатар котировкаларын алайық:

Егер медиананы (-5) формула бойынша анықтасақ, онда оның мәні 1.6650-1.6655 және 1.6655-1.6660 аралықтары арасында орташа болады, яғни шамамен 1.6655. Енді біз медианды жинақталған жиілік әдісіне сәйкес есептейміз. Бастапқыда медиананы "іздеу" керек аралықты анықтау керек, ол үшін біз орташа жинақталған жиілікті есептейміз:
 = 1522, мұндағы
(-6)
= 1522, мұндағы
(-6)
fi - жалпы жинақталған жиілік (біздің мысалда 3043);
п – F айнымалысын бақылау саны (17).
Осылайша, меднаны орташа жинақталған жиілік болатын аралықта, атап айтқанда 1.6655-тен 1.6660-қа дейінгі аралықта "іздеу" керек, онда 1411-ден 1810-ға дейін бөлшектер (нақты мәндер) орналасқан. Бұл мәлімдеме 1.6615-тен 1.6655-ке дейінгі аралықта тек 1410 бөлшек бар, бұл 1522-ден аз. Дәлірек айтқанда, біз медиананы графикалық түрде табамыз.
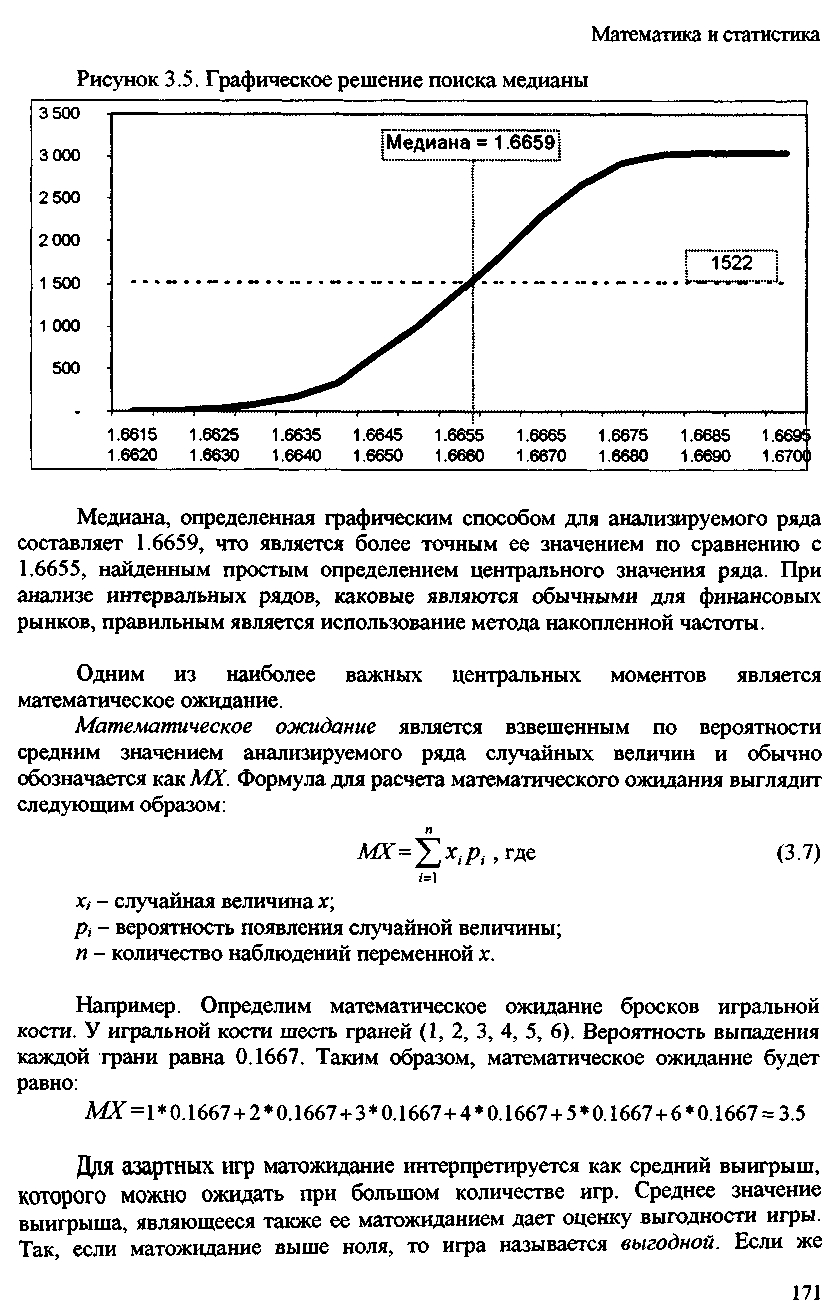
Талданған серия үшін графикалық әдіспен анықталған медиан 1.6639 құрайды, бұл серияның орталық мәнінің қарапайым анықтамасынан табылған 1.6655-ке қарағанда дәлірек мәні. Қаржы нарықтары үшін әдеттегідей аралық қатарларды талдау кезінде жинақталған жиілік әдісін қолдану дұрыс.
Ең маңызды орталық сәттердің бірі-математикалық күту.
Математикалық күту кездейсоқ шамалардың талданған қатарының орташа мәндерінің ықтималдығымен өлшенеді және әдетте мүк ретінде белгіленеді. Математикалық күтуді есептеу формуласы келесідей:
MX
= ,
мұндағы(-7)
,
мұндағы(-7)
xj – кездейсоқ шама х;
рi – кездейсоқ шаманың пайда болу ықтималдығы;
п – айнымалы бақылаулар саны х.
Мысалы. Біз лақтырудың математикалық күтуін анықтаймыз. Ойынның алты беті бар(1, 2, 3, 4, 5, 6). Әрбір транидің түсу ықтималдығы-0.1667. Осылайша, математикалық болжам тең болады:
MX =1*0.1667+2*0.1667+3*0.1667+4*0.1667+5*0.1667+6*0.1667 = -5
Құмар ойындар үшін күту көптеген ойындармен күтуге болатын орташа жеңіс ретінде түсіндіріледі. Ұтыстың орташа мәні, сонымен қатар оны күту ойынның пайдалылығын бағалайды. Сонымен, егер матожиданна нөлден жоғары болса, онда ойын тиімді деп аталады. Егер ойынды күту нөлден аз болса, онда мұндай ойын тиімсіз деп аталады. Зиянсыз ойын-бұл нөлдік күту ойыны. Көмегімен матожидання сондай-ақ артуға тиімділігі әр түрлі ойындар ақшалай ставкалар, бұл өте маңызды тәуекел-менеджмент. Мысалы. Сонымен, егер сіз тек "қызыл-қара"ойнайтын болсаңыз, рулетка ойынының математикалық күтуін есептейміз. Бұл тек 38 ойын өрісі - 36 Сан (18 қызыл және қара өрістер), сондай-ақ екі "нөл"екендігі анықталды. Осылайша, қызыл немесе қара ставка бойынша жеңіске жету ықтималдығы шамамен 0,4737 (18/38) құрайды. Ставканың оң нәтижесі болған жағдайда біз | таңбалауышты аламыз, ал сәтсіздікке ұшыраған жағдайда бір таңбалауышты жоғалтамыз. Демек, бізде теріс күту бар:
МХ =1*0.4737+(-1)*(1 – 0.4737) = -0.0526

Қаржы нарықтарында көптеген ойыншылардың нәтиженің белгісіздігі бар, мұндай жағдайлар үнемі қатысады. Сондықтан сізде осы "бұлтты суда" тепе-тең емес ставкаларды іздеуге мүмкіндік бар. Инсайдерлік ақпараттың болуы мұндай іздеуді айтарлықтай жеңілдетеді. Дәл осындай ақпарат сізге жеткілікті хабардар болуға және жеңіс пен жоғалу мүмкіндігін бағалау кезінде өзіндік тірек алуға мүмкіндік береді.
Сауда-саттыққа кіру бағасын есептеу кезінде оны математикалық пайдалану. Бұл жағдайда, әрине, уақыт өте келе өзгеруі мүмкін бірқатар болжамдар жасалады.
Мысалы. Егер мыналар белгілі болса, белгілі бір өнімді сатып алуға болатын бағаны есептейміз.
1. Біз осы өнім құнының өсу және төмендеу ықтималдығын 50-ден 50-ге дейін қарастырамыз.
2. Тауардың ағымдағы нарықтық бағасы 1,6250-55 (мұнда спрэд ескерілген). Осылайша, егер біз сатып алсақ, онда баға 1.6255, ал егер 1.6250 сатылса. Осы өнім үшін минималды көлемдегі стандартты спрэд 5 тармақты құрайтынын анықтаймыз.
- Біз бұрын сатып алынған тауарларды сатқымыз келетін қарсылық деңгейі (басқа баға белгілерін де қолдануға болады, олардың әрқайсысы қалаған пайда болады) 1.6350 құрайды. Бұл жағдайда нарық көрсетілген белгіге жетпеуі мүмкін екенін ескеру қажет. Сондықтан, біз нақты пайда алуды сәл төмендетеміз, мысалы, 10 тармаққа – 1.6340 дейін (1.6350 - 0.0010).
4. Қолдау деңгейі, оның өту кезінде біздің әрекет табу бойынша сатып алу тауарды деп танылады сәтсіз және тиісті шешім қабылданды шығу залалды мәміле құрайды 1,6130 (сондай-ақ пайдалануға болады, басқа да баға бағдарлары, олардың әрқайсысы ізделетін стоп-лоссом). Мұнда сәтсіздікті шешу үшін қолдау деңгейіне жету жеткіліксіз екенін түсіну керек. Нарықтық бағаның дю 1.6125 (1.6150 – 0,0025) қолдау деңгейінен 25 пунктке төмендеуі қолдау деңгейінен өтуге тағы бір жол беру қажеттілігі туындайды. Егер сіз әлі де тоқтату тақталарын орындау ережесін ескеретін болсаңыз, онда аяқтың нақты бағасы одан да төмен болуы мүмкін. Мысалы, 5 ұпай. Осылайша, тоқтатудың соңғы бағасы біз үшін 1.6120 (1.6125 - 0.0005) болады.
Осының бәрін біле отырып, біз нарыққа кіретін және өнімді сатып алатын бағаны есептейміз:
т р= т w *рl + т l *рw = 1.6340*0.5 +1.6120*0.5 = 1.6230, мұндағы
т р - қажетті баға;
т w — пайда пайда болатын баға,
т l — бағасы, пю оның орындалады стоп-люсс;
рw - стоп-юсстен бұрын пайда табу ықтималдығы;
pl – пайда табудан бұрын жоғалтуды тоқтату ықтималдығы.
Сурет -6. Қажетті бағаға байланысты әртүрлі баға деңгейлерінің арақатынасы

Егер сіз 50% - ға тең пайда алу ықтималдығына қанағаттанбасаңыз, онда сіз арақатынасты 50/50-ден басқасына өзгерте аласыз. Мысалы, 80/20. Бұл жағдайда сатып алу қажет болатын бағаны қайта есептеу қажет болады:
т р= т w *рl + т l *рw =1.6340*0.2+1.6120*0,8 = 1.6164
Қорытынды
Математиканы оқып – үйрену есеп шығаруды үйрену үшін ғана емес, кез – келген проблеманы шеше білу, өз қабілетіңізді жетілдіре алу үшін қажет.
Әр баланың мақсаты - өзінің білім деңгейін көтеру, сабаққа деген қызығушылығын арттыру, іздену. Осы мақсатты іске асыру барысындағы міндетім сол тақырыпты игерумен қатар, кең ауқымды есептерді шешуді зерттеу, ойлау қабілетімді машықтау.Бұны іске асырудың бір жолы қызықтыратын тапсырмалар таңдай білу. Математиканың сан алуан сырын, сандар әлемінің қызық құбылысын, ойлау элементтерімен өрнектеген зерттеу жұмысы қызықты, әрі ұтымды. Зерттеу барысында жүргізілетін жұмыстар қарапайымнан басталып, біртіндеп қиындап, танымдық қызметін белсендіруге назар аударылады. Зерттеу жұмыстарын жүргізу барысы менің зор ынтамды тудырды, білгенімді тереңдетіп, жаңа іс – қимылға жетеледі. Қорыта келгенде биржа математикасы және оның түрлері жан-жақты танылды. Сондықтан да бұл шығармашылық жұмыс келешекте менің өз білімдерін тереңдетуіне көмектесетініне сенімдімін.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
1. Белых Л.П. Основы финансового рынка. 13 тем: Учеб. пособие для вузов. – М.:
Финансы и статистика, ЮНИТИ, 1999. – 231 с.
2. Едронова В.Н., Мизиковский Е.А. Учет и анализ финансовых активов: акции,
облигации, векселя. – М.: Финансы и статистика, 1995. – 272 с.
3. Буренин А.Н. Форвардные, фьючерсные и опционные рынки. - М.: Тривола,
1995.- 240 с.
4. Буренин А.Н. Рынок ценных бумаг и производных финансовых инструментов.
– М.: 1 Федеративная Книготорговая Компания, 1998. – 352 с.
5. Меньшиков И.С. Финансовый анализ ценных бумаг: Курс лекций. – М.: Финан-
сы и статистика, 1998. – 360 с.
6. Тихонов В.И., Миронов М.А. Марковские процессы. М., Советское Радио,
1977. – 488 с.
7. Маршалл Дж.Ф., Бансал В.К. Финансовая инженерия: Полное руководство по
финансовым нововведениям: Пер. с англ. – М.: ИНФРА-М, 1998. – 784 с.
8. Hull J.C. Options, futures and other derivative securities.-2 ed. Englewood Cliff:
Prentice-Hall, Inc., 1993.-492 p.
Пікірі
Оқушы Әскер Дүйсенұлы ғылыми жоба істеу барысында көп ізденді.Яғни өзінің математика саласына қызығушылығымен қатар,қайтпас қайсар ізденпаздығын дәлелдеді.Әлем нарығында биржа математикасын зерттеу жас жеткіншектің болашаққа деген мақсатын айқындаумен қатар білімін шыңдай түсті.Биржа математикасына байланысты мәліметтерді жинаумен қатар зерттеу,талдау жүргізу оңайға соқпағаны рас.Бірақ алға қойған мақсатына жету талпынысының нәтиежесінде белгілі бір деңгейге жете білді. Ғылыми жоба зерттеу барысында оқушының жетекші ретінде бұл жобаның жас жеткіншектерге маңызы зор екенін түсіндім.Биржа математикасы тақырыбын болашақтада терең зерттеп,көптеген жаңа мәлімет нәтижелерге қол жеткізетініне сенімім зор.
Жетекшісі: Математика пәні мұғалімі Тілеуберді Алданышұлы
21
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Биржа математикасы ғылыми жоба
Биржа математикасы ғылыми жоба
М А З М Ұ Н Ы
КІРІСПЕ..................................................................................................................3
-
ТЕОРИЯЛЫҚ БӨЛІМ
1.1. БИРЖА НАРЫҒЫНДАҒЫ КЕЗДЕЙСОҚ ОҚИҒАЛАР................4
-
Практикалық бөлім
2.1.БИРЖА НАРЫҒЫНЫҢ ОРТА ШАМАЛАРЫН ЕСЕПТЕУ....9
Қорытынды.................................................................................................19
Пайдаланылған әдебиеттер тізімі...........................................20
Зерттеу тақырыбының көкейкестігі. Зерттеу жұмысында қарастырылған мәселенің көкейкестігі қазіргі ғылым мен техниканы және экономиканы көтерудің күрделі мәселелерін шешу білім берудің жаңашылдық міндеті қоғамдық қатынастар мен құндылықтар жүйесіндегі өзгеріс талаптарына сәйкес мектептегі білім беру сапасын арттыру болып табылады.
Зерттеу мақсаты: биржадағы өзгерістерді математикалық модельдеу арқылы статистика элементтерінің практикалық қолданысын көрсету
Зерттеу болжамы: математикалық күтім, стандартты ауытқу мен бағанды диаграммаларды қолдану арқылы болжау.
Зерттеудің міндеттері:
Зерттеудің проблемасын шешу, болжамның дұрыстығына көз жеткізу және мақсатқа жету үшін келесі мәселелер орындалады:
-
осы тақырып бойынша бар ғылыми-зерттеу әдебиеттерді зерттеу;
-
заманауи оқу құралдарына осы тақырыптың баяндалуына логикалық талдау жүргізу;
-
алынған мәліметтерді жалпылау және жүйелеу;
-
жасалынған әдістемені пайдаланудың тиімділігін тәжірибеде тексеру;
Зерттеу әдістері:
Жұмыстың мақсатына жету, болжамды тексеру және жоғарыда қойылған мәселелерді шешу үшін келесі әдістер пайдаланылады:
-
мәліметтерді іздеу, жинақтау талдау;
-
әр түрлі ғылыми зерттеу жұмыстарын салыстырмалы талдау;
-
бақылау және бағалау;
-
уақытты үнемдеу мақсатында социометриялық әдісті де қолдану
Зерттеу объектісі: биржа математикасы
Зерттеудің теориялық және практикалық маңыздылығы:
Зерттеу жұмысы кіріспеден, 2 тараудан, қорытынды және қолданылған әдебиеттерден тұрады.
Кіріспе
"Сандардың көмегімен сіз бәрін дәлелдей аласыз"
Томас Карлайл, ағылшын публицисті, тарихшы
Статистикалық және математикалық әдістерді білу сізге көмектеседі:
- математикалық негізделген талдау жүргізу және баға динамикасына баға беру;;
- инвестициялардың нақты кірістілігі мен орташа нарықтық тәуекелін бағалау;
- әр түрлі активтер арасындағы өзара байланысты табу және олардың;
- түрлі оқиғалардың болу ықтималдығын бағалау;
- білікті тәуекел-менеджментті қолдау.
Ықтималдық процесі
Қаржы нарықтарындағы жұмыс болашақ оқиғаларды ықтималды бағалауды қамтиды. Бұл, ең алдымен, психологияға арналған тарауда ақпараттық "гололдың" қасиеттерін талдайтын адамдар жиі кездесетін ақпараттың жетіспеушілігінен туындайды және осы процестің математикалық сипаттамасына тоқталамыз. Мұндағы ең бастысы-қаржы нарықтарындағы сауда объектісі болып табылатын болашақты толық білмеуіміз. Сонымен, фьючерстік келісімшартты сатып ала отырып, біз фьючерстер жазылған тауар құнының өсуіне сенеміз. Егер сіз барлық 100 пайызға дұрыс нәрсені істеп жатқаныңызға сенімді болсаңыз, онда бұл жалған өзіне деген сенімділіктен артық емес. Өкінішке орай, нарықта ештеңеге сенімді болу мүмкін емес. Алайда, адам болашақты білмейді, бірақ көбінесе өткен туралы өте жаман және сенімсіз ақпаратқа ие.
Тек жақын өткен адамға ақпараттың толықтығы үшін қол жетімді, ал алыс құпия құпияның артында болашақтан гөрі жаман емес. Көп немесе аз адам қазіргі жағдайды түсінеді. Алайда, мұнда да ақпараттың көптігі адам өзінің айналасындағы шындықты біледі деп айтуға негіз бермейді. Осылайша, сіз қайда қарасаңыз да – өткенге, бүгінге немесе болашаққа – адам барлық жерде қабылдай алатын және талдай алатын, сондай-ақ оған қол жеткізе алатын ақпарат көлемімен шектеледі. Ақпараттың үнемі жетіспеушілігіне байланысты біз тек осы немесе басқа оқиғаның болу ықтималдығы туралы айтуымыз керек. Мен нарықтағы бағаның қозғалысы мүлдем кездейсоқ құбылыс деп айтпаймын, дегенмен бұл ықтималдық теориясын зерттеудің нысаны болып табылатын кездейсоқ оқиғалар.
1.1.БИРЖА НАРЫҒЫНДАҒЫ КЕЗДЕЙСОҚ ОҚИҒАЛАР
Кездейсоқ оқиға-тәжірибенің (жағдайдың) нәтижесіне байланысты әртүрлі мәндерді қабылдайтын және дәл болжау мүмкін емес оқиға.
Біздің білуімізше, ұзақ уақыт бойы баға динамикасын мүлдем жүз пайыз болжау әлі күнге дейін шешілмеген мәселе болып табылады. Жүреді ол бойынша жетілдірілмеуі себебі біздің түсіну немесе жеткіліксіз ақпарат, дерек мінез-құлық нарық қалады себепші болады. Непредсказуемостью ие және кездейсоқ оқиғалар. Бұл кездейсоқтық теориясы (кездейсоқ-walk theory) оның өмір сүруінің негізі ретінде қолданылады.
Мұнда қазіргі заманғы қаржылық шешімдердің негізін құрайтын негізгі теорияларға қысқаша шолу жасалуы керек. Оларға теорияларды жатқызуға болады:
- нарықтық тепе-теңдік,
- кездейсоқ кезбе;
- ойындар.
Нарықтық тепе-теңдік теориясы нарық сұраныс пен ұсыныс арасындағы тепе-теңдік жағдайына ұмтылады деген постулаттан туындайды. Бұл теория тепе-теңдік күйінен ауытқуларды жоққа шығармайды.
BCN тиімді нарық теориясына сәйкес жаңа ақпарат бірден нарықтық бағаларға енгізіледі. Осылайша, кез-келген ақпаратқа немесе өткен баға динамикасына, тиімді нарық теориясының қорытындыларына назар аудара отырып, пайда табу мүмкін емес:
- нарықтық бағалардың динамикасын ешкім болжай алмайды;
- барлық нарықтық бағалар осы активтер үшін жарамды, ал дұрыс бағаланбаған тауарлар жоқ.
Тиімді нарық теориясына қарсы қаржы нарықтарының тәжірибесі айтады. Біріншіден, ақпаратты әртүрлі адамдар әр түрлі қабылдайды, бұл туралы біз психологияға арналған тарауда айттық. Екіншіден, нарық алған ақпараттың жалған емес, шынайы екендігіне кепілдік қайда. Үшіншіден, уақыттың әртүрлі нүктелерінде бірдей ақпаратты әртүрлі жолмен түсіндіруге болады. Төртіншіден, нарықтық бағаның әр сәтте әділ немесе шынайы болуы екіталай. Бұл жерде нарықтық баға мезгіл-мезгіл әділ бағаны кесіп өтіп, көтерілген күйден оған қатысты төмендетілген бағаға ауысады және керісінше болады деп сенуге болады.

Сурет-1. Әділ мен нарықтық баға
Кездейсоқ серуендеу теориясы тиімді нарық теориясының кешірім сұрауын теориялық тұрғыдан жалғастыруда. кездейсоқ серуендеу теориясында ақпарат болжамды, белгілі және жаңа, күтпеген екі санатқа бөлінеді. Егер болжамды, тіпті одан да көп белгілі ақпарат нарықтық бағаларға енгізілген болса, онда бағада жаңа күтпеген ақпарат әлі жоқ. Болжанбайтын ақпараттың қасиеттерінің бірі оның кездейсоқтығы және сәйкесінше бағаның кейінгі өзгеруінің кездейсоқтығы болып табылады. Тиімді нарық теориясы бағаның өзгеруін жаңа күтпеген ақпараттың түсуімен түсіндіреді, ал кездейсоқ вагус теориясы мұны бағаның өзгеру мүмкіндігі туралы пікірмен толықтырады.Кездейсоқ серуендеу теориясының қысқаша практикалық тұжырымы ойыншыларға өз жұмысында "сатып алу және сақтау" стратегиясын қолдануға кеңес беріледі. Айта кету керек, кездейсоқ серуендеу теориясының өркендеуі 70-ші жылдары, АҚШ-тың қор нарығында, дәстүрлі түрде барлық теориялардың қолданылуын тексерудің негізгі жартысы болған кезде айқын тенденциялар болған жоқ, ал нарықтың өзі өте тар дәлізде болды.
Кездейсоқ серуендеу теориясына қарсы келесі дәлелдер келтіруге болады. Біріншіден, Егер сіз кез-келген уақытта күтпеген ақпараттың пайда болуына дайын болсаңыз және оған жауап берудің дайын сценарийлері болса, онда ол күтпеген жағдайға айналмайды. Екіншіден, кездейсоқ кезбе қисығының және нарықтық баға графигінің сыртқы ұқсастығына қарамастан, нарық мүлдем болжанбайтын оқиға екенін ешкім әлі дәлелдеген жоқ (дегенмен, керісінше дәлелденбеген). Кем дегенде, математиктердің арасында нарық мүлдем кездейсоқ құбылыс емес деген пікір бар, өйткені онда психология заңдары пайда болады. Үшіншіден, ол әлі де экономикалық заңдар мен қалыптасқан экономикалық заңдылықтарды жойды.
Джон Дж.Мерфи,
"...көбінесе кездейсоқтық Нести баға динамикасында жүйелі модельдер мен заңдылықтарды белгілеу ерекшелігі"
Ойынның ең қарапайым және кең таралған көрінісі-нәтиже матрицасын құру. Осы матрицаның әр элементі кез-келген ықтимал стратегия үшін белгілі бір ойыншы күткен нәтижені көрсетеді. Айта кету керек, ойын теориясы үшін ойыншы тек басқа ойыншылардың жағдайы мен әрекеттеріне әсер ете алатын белсенді қатысушы ретінде танылады. Тек нарықты ұстанатын пассивті қатысушылар, ойыншылар, олардың барлық қалауы бойынша. олар атала алмайды.
Мысалы. Төмендегі нәтижелер матрицасында екі қатысушы үшін нөлдік сомадағы а ойнатқышының нәтижелері көрсетілген:

Мұнда, егер А ойыншысы az стратегиясын, ал ойыншы стратегияны таңдаса . онда А ойыншысы үшін нәтиже -10, ал B + 10 ойыншысы үшін болады. Әр ойыншының міндеті-басқа ойыншының стратегиясын ескере отырып, қажетті нәтижені барынша арттыратын стратегияны таңдау. Сонымен, а ойыншысының көзқарасы бойынша в ойыншысының үш мүмкін стратегиясына ең жақсы реакция келесі жұптарды құрайды:), (b2, a1), (b3, A2). Ойыншы үшін А ойыншысының ықтимал стратегияларына ең жақсы реакция келесі жұптарды құрайды: (a1, b3), (a2. B3). (а3, b2). Мұндағы жалғыз қиылысатын стратегия-жұп (a, b). бұл екі ойыншының ең жақсы реакцияларында. Осылайша, А және В ойыншыларының 2-ші және 3-ші стратегияларын бір уақытта таңдау осы нәтиже матрицасының шешімі болады. Алайда, өмірлік тәжірибе көрсеткендей, бәрі бірдей қарапайым емес. Біріншіден, ойыншылар ережелердің басқа шешімдері негізінде шешім қабылдау арқылы ең жақсы таңдау туралы білмеуі мүмкін. Екіншіден, ойыншылардың әрекеттері өте сирек кездеседі, бұл ойыншылардың біріне артықшылық береді. Үшіншіден, стратегиялардың сансыз жиынтығы болуы мүмкін. Төртіншіден, өмірде нәтиже матрицалары жоғарыда келтірілген статикалық мысалдан айырмашылығы динамикалық жүйелер болып табылады.Дегенмен, маркетологтар (сөздің кең мағынасында) өз іс-әрекеттерін нақты және мүмкін болатын басқа қатысушылардың мінез-құлқымен, оның ішінде жалпы нарықтық массамен өлшеуге мәжбүр.Ойынның ең жақсы стратегиясын таңдаудағы басты мәселе-ақпараттың белгісіздігі. Бұл матрицаны шешу кезінде ықтималдық әдістерін қолдану қажеттілігін анықтайды.
Ойын теориясына нарық тек ірі ойыншылар келісе алатын ойыншылар қауымдастығы деген көзқараспен де жүгінуге болады. Тиісінше, олар тек ынтымақтастықтың пайдасын көре алады және кірістерін барынша арттыра алады. Қалғандары қатаң жалғыз әрекет етуге және бір-бірімен ірі ойыншылармен бәсекелесуге мәжбүр. Теорияға сәйкес, бір-бірімен ынтымақтастық жасамайтын ойыншылар сөзсіз бәсекелестіктен айырылады. Бұл дегеніміз, кішкентай ойыншылар үлкен ойыншылар олармен бөліскен кезде ғана жеңіске жетеді.
Ойын теориясының тәсілі, менің ойымша, кездейсоқ жүру теориясымен салыстырғанда қаржы нарықтарында қолдануға негізделген. Мұның себебі, менің ойымша, бұл тұрақты сериялардың барлық кейінгі сандары алдыңғы жолдармен жасалады, оларға кім және кім әсер етуге тырысса.
Ықтималдық теориясы
Алдыңғы абзацта айтылғандардың бәрі бізге нарықтық құбылыстарға кездейсоқ ретінде қарауға және сәйкесінше ықтималдық теориясын қолдануға негіз береді. Осылайша, ықтималдық теориясын түсінбестен, келесі қадамдарды жасаудың мағынасы жоқ.Ықтималдық - кез-келген кездейсоқ оқиғаның сандық өлшемі. Ықтималдық o-дан (мүмкін емес оқиға) 1-ге дейінгі аралықта (міндетті түрде болатын оқиға) болуы мүмкін. Кейде ықтималдық пайызбен сипатталады. Бұл жағдайда ықтималдық мәндерінің шекаралары сәйкесінше 0% және 100% болады.Кездейсоқ оқиғаның пайда болу ықтималдығын анықтаудың классикалық формуласы келесідей:
 ,мұндағы
(-1)
,мұндағы
(-1)
Nх - кездейсоқ оқиғаның болуы мүмкін нұсқалардың саны х;
N- ықтимал нәтижелердің жалпы саны
Мысалы. Ойынды лақтыру арқылы біз алты мүмкін нәтиже аламыз — алты жақтың біреуінің жоғалуы: 1, 2, 3, 4, 5 немесе 6. Осылайша, бетінің біреуінің құлау ықтималдығын анықтауға болады, мысалы, 3:
P(А)
= 0.1667
немесе
16.67%
0.1667
немесе
16.67%
Осылайша, ойнатқыштың бір бетінің құлау ықтималдығы (біздің мысалда 3) 16.67% құрайды.Сондай-ақ, екі беттің біреуінің құлау ықтималдығын анықтауға болады (мысалы, 2 немесе 3). Бұл жағдайда ықтималдылықты қосу ережесі қолданылады және ықтималдық келесідей есептеледі:
P(x немесе y) = p(x) + P (y) = 0.1667 +0.1667 = 0.3333 немесе 3-33%, мұндағы
P (x) – кездейсоқ оқиғаның басталу ықтималдығы х(біздің мысалда 2); P (u) — кездейсоқ оқиғаның пайда болу ықтималдығы у (3). Осылайша, 2 немесе 3 саны бар беттің түсу ықтималдығы 3-33% құрайды .
Ықтималдылықты қосу ережесі тәуелді оқиғалар үшін қолданылады, егер бір кездейсоқ оқиға басқа кездейсоқ оқиғаның басталуын жоққа шығармаса.
Егер бір уақытта екі немесе одан да көп кездейсоқ оқиғалардың пайда болу ықтималдығын табу қажет болса, ықтималдылықты көбейту ережесі қолданылады. Бұл жағдайда барлық оқиғалар бір-бірінен тәуелсіз болуы керек.
Мысалы. Екі ойнатқышты бір уақытта лақтырудың нәтижесінде біз 36 түрлі комбинацияны аламыз: 1-1, 1-2, 1-3, 14, 15, 16, 2-1, 2- 2, 2-3 және т. б. лақтыру нәтижесінде біз екі сүйектің бүйірлерінде бір-бірлеп аламыз деген ықтималдылықты анықтау үшін ықтималдылықты көбейту ережесін қолданамыз:
P (X және Y) = P(X) * P (y) = 0.1667*0.1667 = 0.0278 немесе 2.78%
Осылайша, 1 сандары бар беттердің сүйек сүйектерінің бір уақытта түсу ықтималдығы 2.78% құрайды.
2.1.БИРЖА НАРЫҒЫНЫҢ ОРТА ШАМАЛАРЫН ЕСЕПТЕУ
Арифметикалық орта
Баға динамикасын талдау, ең алдымен, бағалардың орташа деңгейін және олардың ауытқу аралықтарын анықтаудан тұрады. Талдау үшін орташа мән ең ықтимал деп айтуға болады. Объективті түрде, орташа мән мен мүмкін болатын мән арасында тең белгі қою дұрыс емес.Бағаның орташа деңгейі нарық үшін ең тартымды бағаны көрсетеді, ол белгілі бір уақытта нарықтың белсенді қатысушыларының инвестициялық артықшылықтарын көрсетеді.Арифметикалық орта-қатардың барлық мәндерінің қосындысының олардың санына қатынасы:
 мұндағы(-2)
мұндағы(-2)
хj — талданатын айнымалы;
n – айнымалы бақылаулар саны х.
Мысалы.
1999 жылғы қаңтардағы Dow Jones Industrial (DJI, close) индексі мәндерінің орташа арифметикалық қатарын ьтабу қажет:


Арифметикалық орта айнымалылардың экстремалды облыстардағы шығарындыларына әсер етудің теріс қасиетіне ие. Бұл жағдайда орташа мәннің максималды минималды мәндерге қарай жылжуы нақты орташа нарықтық мәнді объективті түрде көрсетпейді. Экстремалардың есептелген орташа мәнге әсерін болдырмау үшін зерттелетін қатардан алып тастау ережесі қолданылады, мысалы, айнымалының ең жоғары мәндерінің 1% және ең төменгі мәндерінің 1%. 1% орнына 2%, 3% пайдалануға болады. 5% және одан да көп сіздің қалауыңыз бойынша.
Сонымен, егер D индексінің 10% максималды және күдікті мәндерінің ұсынылған қатарынан алып тастау туралы шешім қабылдасақ (яғни, жоғарыдан және төменнен шамамен екі мән), онда орташа арифметикалық қатар үшін есептеледі:




Средняя взвешенная – отношение суммы произведений значений ряда и частот появления этих значений (весов) на сумму частот (весов):
 мұндағы(-3)
мұндағы(-3)
xi – талданатын айнымалы;
fi - талданатын айнымалы салмақтың пайда болу жиілігі.
Бұл орташа салмақ мәні бар айнымалылар қатарына тиімді қолданылады.
Мысалы. 1997 жылғы 26 маусымдағы топтастырылған GBP / USD валюталық индексі

Бұл серияның сәні 1.6660-тен 1,6665-ке дейінгі аралықта болады. Дәлірек айтқанда, талдаудың графикалық әдісі бізге сәнді анықтауға көмектеседі.

1997 жылғы 26 маусымда GBP/USD үшін ең тән баға ретінде табылған сәннің дәл мәнін бағалаудың осы әдісінің шамалығына қарамастан, біз бұрын анықтаған 1.6656 – қарастырылып отырған қатардың орташа өлшенген мәнінен гөрі дұрыс болып көрінеді.
Медиана-бұл орташа, рейтингте орналасқан мәліметтер тізіміндегі орталық мән. Медиана, әдетте, зерттелетін қатардың ең көрнекті мәні болып саналады.
Мысалы. Топ нөмірінің медианасын келесі деректер қатарынан табамыз:

Бұл қатардың ортасы-төртінші топ, сондықтан медианаға тең.
4. Сериялардың медианасын есептеу үшін келесі формуланы қолдануға болады:
Медиана =
 4,
(-5)
4,
(-5)
p-бақылаулар саны (біздің мысалда 7).
Аралық қатардың медианасын есептеу кезінде жинақталған жиілік қолданылады.
Мысалы. 1997 жылғы 26 маусымда 5 тармақтан тұратын диапазондарда топтастырылған, бізге белгілі GBP / USD валюталық арақатынасына сұраныстың (bid) бірқатар котировкаларын алайық:

Егер медиананы (-5) формула бойынша анықтасақ, онда оның мәні 1.6650-1.6655 және 1.6655-1.6660 аралықтары арасында орташа болады, яғни шамамен 1.6655. Енді біз медианды жинақталған жиілік әдісіне сәйкес есептейміз. Бастапқыда медиананы "іздеу" керек аралықты анықтау керек, ол үшін біз орташа жинақталған жиілікті есептейміз:
 = 1522, мұндағы
(-6)
= 1522, мұндағы
(-6)
fi - жалпы жинақталған жиілік (біздің мысалда 3043);
п – F айнымалысын бақылау саны (17).
Осылайша, меднаны орташа жинақталған жиілік болатын аралықта, атап айтқанда 1.6655-тен 1.6660-қа дейінгі аралықта "іздеу" керек, онда 1411-ден 1810-ға дейін бөлшектер (нақты мәндер) орналасқан. Бұл мәлімдеме 1.6615-тен 1.6655-ке дейінгі аралықта тек 1410 бөлшек бар, бұл 1522-ден аз. Дәлірек айтқанда, біз медиананы графикалық түрде табамыз.

Талданған серия үшін графикалық әдіспен анықталған медиан 1.6639 құрайды, бұл серияның орталық мәнінің қарапайым анықтамасынан табылған 1.6655-ке қарағанда дәлірек мәні. Қаржы нарықтары үшін әдеттегідей аралық қатарларды талдау кезінде жинақталған жиілік әдісін қолдану дұрыс.
Ең маңызды орталық сәттердің бірі-математикалық күту.
Математикалық күту кездейсоқ шамалардың талданған қатарының орташа мәндерінің ықтималдығымен өлшенеді және әдетте мүк ретінде белгіленеді. Математикалық күтуді есептеу формуласы келесідей:
MX
= ,
мұндағы(-7)
,
мұндағы(-7)
xj – кездейсоқ шама х;
рi – кездейсоқ шаманың пайда болу ықтималдығы;
п – айнымалы бақылаулар саны х.
Мысалы. Біз лақтырудың математикалық күтуін анықтаймыз. Ойынның алты беті бар(1, 2, 3, 4, 5, 6). Әрбір транидің түсу ықтималдығы-0.1667. Осылайша, математикалық болжам тең болады:
MX =1*0.1667+2*0.1667+3*0.1667+4*0.1667+5*0.1667+6*0.1667 = -5
Құмар ойындар үшін күту көптеген ойындармен күтуге болатын орташа жеңіс ретінде түсіндіріледі. Ұтыстың орташа мәні, сонымен қатар оны күту ойынның пайдалылығын бағалайды. Сонымен, егер матожиданна нөлден жоғары болса, онда ойын тиімді деп аталады. Егер ойынды күту нөлден аз болса, онда мұндай ойын тиімсіз деп аталады. Зиянсыз ойын-бұл нөлдік күту ойыны. Көмегімен матожидання сондай-ақ артуға тиімділігі әр түрлі ойындар ақшалай ставкалар, бұл өте маңызды тәуекел-менеджмент. Мысалы. Сонымен, егер сіз тек "қызыл-қара"ойнайтын болсаңыз, рулетка ойынының математикалық күтуін есептейміз. Бұл тек 38 ойын өрісі - 36 Сан (18 қызыл және қара өрістер), сондай-ақ екі "нөл"екендігі анықталды. Осылайша, қызыл немесе қара ставка бойынша жеңіске жету ықтималдығы шамамен 0,4737 (18/38) құрайды. Ставканың оң нәтижесі болған жағдайда біз | таңбалауышты аламыз, ал сәтсіздікке ұшыраған жағдайда бір таңбалауышты жоғалтамыз. Демек, бізде теріс күту бар:
МХ =1*0.4737+(-1)*(1 – 0.4737) = -0.0526

Қаржы нарықтарында көптеген ойыншылардың нәтиженің белгісіздігі бар, мұндай жағдайлар үнемі қатысады. Сондықтан сізде осы "бұлтты суда" тепе-тең емес ставкаларды іздеуге мүмкіндік бар. Инсайдерлік ақпараттың болуы мұндай іздеуді айтарлықтай жеңілдетеді. Дәл осындай ақпарат сізге жеткілікті хабардар болуға және жеңіс пен жоғалу мүмкіндігін бағалау кезінде өзіндік тірек алуға мүмкіндік береді.
Сауда-саттыққа кіру бағасын есептеу кезінде оны математикалық пайдалану. Бұл жағдайда, әрине, уақыт өте келе өзгеруі мүмкін бірқатар болжамдар жасалады.
Мысалы. Егер мыналар белгілі болса, белгілі бір өнімді сатып алуға болатын бағаны есептейміз.
1. Біз осы өнім құнының өсу және төмендеу ықтималдығын 50-ден 50-ге дейін қарастырамыз.
2. Тауардың ағымдағы нарықтық бағасы 1,6250-55 (мұнда спрэд ескерілген). Осылайша, егер біз сатып алсақ, онда баға 1.6255, ал егер 1.6250 сатылса. Осы өнім үшін минималды көлемдегі стандартты спрэд 5 тармақты құрайтынын анықтаймыз.
- Біз бұрын сатып алынған тауарларды сатқымыз келетін қарсылық деңгейі (басқа баға белгілерін де қолдануға болады, олардың әрқайсысы қалаған пайда болады) 1.6350 құрайды. Бұл жағдайда нарық көрсетілген белгіге жетпеуі мүмкін екенін ескеру қажет. Сондықтан, біз нақты пайда алуды сәл төмендетеміз, мысалы, 10 тармаққа – 1.6340 дейін (1.6350 - 0.0010).
4. Қолдау деңгейі, оның өту кезінде біздің әрекет табу бойынша сатып алу тауарды деп танылады сәтсіз және тиісті шешім қабылданды шығу залалды мәміле құрайды 1,6130 (сондай-ақ пайдалануға болады, басқа да баға бағдарлары, олардың әрқайсысы ізделетін стоп-лоссом). Мұнда сәтсіздікті шешу үшін қолдау деңгейіне жету жеткіліксіз екенін түсіну керек. Нарықтық бағаның дю 1.6125 (1.6150 – 0,0025) қолдау деңгейінен 25 пунктке төмендеуі қолдау деңгейінен өтуге тағы бір жол беру қажеттілігі туындайды. Егер сіз әлі де тоқтату тақталарын орындау ережесін ескеретін болсаңыз, онда аяқтың нақты бағасы одан да төмен болуы мүмкін. Мысалы, 5 ұпай. Осылайша, тоқтатудың соңғы бағасы біз үшін 1.6120 (1.6125 - 0.0005) болады.
Осының бәрін біле отырып, біз нарыққа кіретін және өнімді сатып алатын бағаны есептейміз:
т р= т w *рl + т l *рw = 1.6340*0.5 +1.6120*0.5 = 1.6230, мұндағы
т р - қажетті баға;
т w — пайда пайда болатын баға,
т l — бағасы, пю оның орындалады стоп-люсс;
рw - стоп-юсстен бұрын пайда табу ықтималдығы;
pl – пайда табудан бұрын жоғалтуды тоқтату ықтималдығы.
Сурет -6. Қажетті бағаға байланысты әртүрлі баға деңгейлерінің арақатынасы

Егер сіз 50% - ға тең пайда алу ықтималдығына қанағаттанбасаңыз, онда сіз арақатынасты 50/50-ден басқасына өзгерте аласыз. Мысалы, 80/20. Бұл жағдайда сатып алу қажет болатын бағаны қайта есептеу қажет болады:
т р= т w *рl + т l *рw =1.6340*0.2+1.6120*0,8 = 1.6164
Қорытынды
Математиканы оқып – үйрену есеп шығаруды үйрену үшін ғана емес, кез – келген проблеманы шеше білу, өз қабілетіңізді жетілдіре алу үшін қажет.
Әр баланың мақсаты - өзінің білім деңгейін көтеру, сабаққа деген қызығушылығын арттыру, іздену. Осы мақсатты іске асыру барысындағы міндетім сол тақырыпты игерумен қатар, кең ауқымды есептерді шешуді зерттеу, ойлау қабілетімді машықтау.Бұны іске асырудың бір жолы қызықтыратын тапсырмалар таңдай білу. Математиканың сан алуан сырын, сандар әлемінің қызық құбылысын, ойлау элементтерімен өрнектеген зерттеу жұмысы қызықты, әрі ұтымды. Зерттеу барысында жүргізілетін жұмыстар қарапайымнан басталып, біртіндеп қиындап, танымдық қызметін белсендіруге назар аударылады. Зерттеу жұмыстарын жүргізу барысы менің зор ынтамды тудырды, білгенімді тереңдетіп, жаңа іс – қимылға жетеледі. Қорыта келгенде биржа математикасы және оның түрлері жан-жақты танылды. Сондықтан да бұл шығармашылық жұмыс келешекте менің өз білімдерін тереңдетуіне көмектесетініне сенімдімін.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
1. Белых Л.П. Основы финансового рынка. 13 тем: Учеб. пособие для вузов. – М.:
Финансы и статистика, ЮНИТИ, 1999. – 231 с.
2. Едронова В.Н., Мизиковский Е.А. Учет и анализ финансовых активов: акции,
облигации, векселя. – М.: Финансы и статистика, 1995. – 272 с.
3. Буренин А.Н. Форвардные, фьючерсные и опционные рынки. - М.: Тривола,
1995.- 240 с.
4. Буренин А.Н. Рынок ценных бумаг и производных финансовых инструментов.
– М.: 1 Федеративная Книготорговая Компания, 1998. – 352 с.
5. Меньшиков И.С. Финансовый анализ ценных бумаг: Курс лекций. – М.: Финан-
сы и статистика, 1998. – 360 с.
6. Тихонов В.И., Миронов М.А. Марковские процессы. М., Советское Радио,
1977. – 488 с.
7. Маршалл Дж.Ф., Бансал В.К. Финансовая инженерия: Полное руководство по
финансовым нововведениям: Пер. с англ. – М.: ИНФРА-М, 1998. – 784 с.
8. Hull J.C. Options, futures and other derivative securities.-2 ed. Englewood Cliff:
Prentice-Hall, Inc., 1993.-492 p.
Пікірі
Оқушы Әскер Дүйсенұлы ғылыми жоба істеу барысында көп ізденді.Яғни өзінің математика саласына қызығушылығымен қатар,қайтпас қайсар ізденпаздығын дәлелдеді.Әлем нарығында биржа математикасын зерттеу жас жеткіншектің болашаққа деген мақсатын айқындаумен қатар білімін шыңдай түсті.Биржа математикасына байланысты мәліметтерді жинаумен қатар зерттеу,талдау жүргізу оңайға соқпағаны рас.Бірақ алға қойған мақсатына жету талпынысының нәтиежесінде белгілі бір деңгейге жете білді. Ғылыми жоба зерттеу барысында оқушының жетекші ретінде бұл жобаның жас жеткіншектерге маңызы зор екенін түсіндім.Биржа математикасы тақырыбын болашақтада терең зерттеп,көптеген жаңа мәлімет нәтижелерге қол жеткізетініне сенімім зор.
Жетекшісі: Математика пәні мұғалімі Тілеуберді Алданышұлы
21

шағым қалдыра аласыз















