БӨЛШЕК.БӨЛШЕКТЕРДІҢ ТҮРЛЕРІ ЖӘНЕ ОЛАРҒА ҚОЛДАНАНЫЛАТЫН АМАЛДАР

ӘОЖ 511.13

БӨЛШЕК.БӨЛШЕКТЕРДІҢ ТҮРЛЕРІ ЖӘНЕ ОЛАРҒА ҚОЛДАНАНЫЛАТЫН АМАЛДАР

Аннотация:Бұл мақалада математикалық ұғымдардың бөлшек, бөлшектердің түрлері және оларға қолданылатын амалдары қарастырылады. Бөлшектердің түрлері және бөлшектерге тиімді амалдардың қолданылуы ашылып көрсетілген.

Кілт сөздер:бөлшек, дәреже, период, бөлгіш, бөлінгіш.

Арифметикада бөлшек деп бірліктің бір немесе бірнеше бөліктерінен (бөлшектері) тұратын санды айтады.

Жалпы тілмен айтқанда бөлшек сан 2 санның ( ) қатынасы болып табылады.Мұндағы -бөлгіш, -бөлінгіш.

Ең бірінші бөлшек сандар туралы ұғым Ежелгі Египет пен Вавилонда кездеседі.Бөлшек сандардың туындауы нақты және бөлінбестей адамдардың күнделікті өмірдегі қажеттіліктердің арқасында туған.Бөлшек ұғымы араб түбірлерін қамтиды және «бөлу,сындыру» деген мағынаны қамтиды. Қазіргі уақыттың өзінде бұл сөздің мағынасы ауысқан емес.Екі ел бөлшекті әртүрлі түсіндірген болатын.Алғашында енгізілген бөлшек болатын. Кейіннен бөлшектері және тағы басқа бөлшектер шыққан болатын.

Археологтардың айтуынша,бөлшек туралы ең бірінші ұғым шамамен 5 мың жыл бұрын пайда болған.

Египеттік бөлшектер қазіргі уақыттағы бөлшектермен салыстырғанмен айырмашылығы жоқ. Есептеу кезінде мысырлықтар бөлшек түрлерін бөлшек түрлерін термин түрінде жазуға тырысты және санның бөлшектерін жазу үшін кестелер енгізді.

Вавилонда бөлшек ұғымын қалыптастыруда қызықты жағдай туындады.Шумер 16-лық санау жүйесіне негізделген бөлшектің әрбір жаңа цифры 60-қа еселік болды.Бұл біздің заманымыздың уақыт жүйелері мен бұрыш өлшемдерінің пайда болуына серпін болды.

Егер санын бірдей санға бөлуге болатын болса, онда бөлшек бөлінеді.Егер біірдей санға бөлінбейтін болса, бөлшек бөлінбейді.Жоғарыда айтылған деректен бөлшектің негізгі қасиетін тұжырымдай аламыз: егер бірдей санға көбейтілсе немесе бөлінсе, мәні өзгермейді.

Бөлшектер болады:

1. Дұрыс бөлшектер:

2. Бұрыс бөлшектер:

Бөлшектердің түрлері:

1. Жай бөлшектер

Жай бөлшектер - түрінде жазылады. Мұндағы бүтін сан, ал натурал сан. Бөлінетін саны бөлшектің алымы, ал бөлгіш саны бөлшектің бөлімі деп аталады.

Мысалы: .

2. Дұрыс және бұрыс бөлшектер.

Бөлшек дұрыс бөлшек деп аталады, егер бөлшектің алымының модулі, бөлшектің бөліміндегі модульдан кіші болған жағдайда: .

Мысалы: және т.б. Бұрыс бөлшектер деп аталады, егер бөлшектің бөлімінің модулі, бөлшектің алымындағы санның модуліне тең немесе кіші болған жағдайда: . Мысалы: және т.б.

3. Аралас бөлшек сандар

Аралас бөлшек сандар, натурал сан және тұрақты бөлшек ретінде жазылған сан аралас сан (немесе аралас бөлшек) деп аталады және сол натурал сан мен бөлшектің қосындысы ретінде түсіндіріледі. Кез келген рационал санды аралас сан ретінде жазуға болады (теріс сандар үшін алдыңғы жағына «минус» белгісін қою арқылы). Аралас бөлшекке қарама-қарсы, тек алымы мен бөлімін қамтитын бөлшек жай деп аталады.

Мысалы:

4. Құрама бөлшектер

Құрама бөлшек бірнеше көлденең белгілері бар өрнек деп аталады.

Мысалы: және т.б.

5. Ондық бөлшектер

Ондық бөлшек бөлшектің позициялық жазбасы деп аталады, мұндағы бөлгіш нақты түрде берілмейді,бірақ бүтін сан ондық дәреже деп түсініледі (Мысалы:10,100,1000 және т.б.).

Теріс емес бөлшек жағдайында жазудың үтірге дейінгі бөлігі санның бүтін бөлігі,үтірден кейінгі бөлігі,ондық бөлшектің бөлігі болып табылады. Кез келген қарапайым бөлшекті ондық бөлшекке айналдыруға болады,бұндай жағдайда үтірден кейінгі бөлігі шекті саны болады немесе периодтық бөлшек болады.

Мысалы: ондық бөлшек, 2,1547896321 түріндегі қарапайым бөлшек .

Бірақ барлық ондық бөлшектердің шегі бола бермейді.Мысалы:

шексіз бөлшек екенін көрсетеді

Ондық бөлшектерді теріс көрсеткіштері бар экспоненциалды түрінде берілуі мүмкін.Мысалы: ,

Ондық бөлшектің тағы бір түрі өзімен бірге процент ұғымын қалыптастырады,% белгісімен белгіленеді және ондағы болжамды бөлгіш әрқашан 100 ге тең.Сонда мысалы ондық бөлшегіне тең.Егер алымындағы сан 4125 болса, түрінде жазылады және егер алымындағы сан теріс болатын болса,мысалы -25%= түрінде жазылады.

6. Бөлшек мәні және оның негізгі қасиеті

Бөлшек бұл тек санның жазбасы.Қарапайым бөлшектер мен ондық бөлшектердің әр түрлі бөлшектері бірдей санға келуі мүмкін.

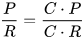
Бөлшектің мәні өзгеріссіз қалады,дегенмен бөлшектер өзгереді:

Бұл өрнекті керісінше,егер берілген бөлшектің алымы мен бөлімінде ортақ бөлгіш болса,онда екі бөлікті де оған бөлуге болады; мұндай процесс бөлшекті қысқарту деп аталады.

Мысалы: – мұнда бөлшектің алымы мен бөлімін 36 санына бөлдік.

Қысқармайтын бөлшек дегеніміз, аламы мен бөлімі өзара қарапайым және олардың ортақ бөлгіштері жоқ, тек .

Ондық бөлшектердің мәні әрдайым болады,тек нөлдер (оларды алып тастауға болады) немесе тек тоғыздар шексіз ретпен аяқталатын жағдайларды қоспағанда.

Мысалы: екі әртүрлі ондық бөлшектер тек 1 санға сәйкес келеді.

Бөлшектерге амалдар қолдану

Бұл бөлімде жай бөлшектер мен ондық бөлшектерге амалдар қолданылатын болады.

Ортақ бөлімге келтіру

Бөлшектерді салыстырып,ортақ бөлімге келтіру үшін түрлендіру қажет. Екі бөлшек берілсін делік . Орындалатын амалдар реті:

• Ең кіші ортақ бөлімін табамыз: .

• Бірінші бөлшектің алымы мен бөлімін көбейтеміз.

• Екінші бөлшектің алымы мен бөлімін көбейтеміз.

Осыдан соң екі бөлшекте бірдей тең болады М. Ең кіші ортақ еселіктің орнына қарапайым жағдайларда бөлшектердің бөлімін бір-біріне көбейтіп М санын алуға болады. Есептері салыстыру бөлімінде.

Салыстыру

Екі қарапайым бөлшекті салыстыру үшін, ек бөлшекті ортақ бөлімге келтіріп, алынған бөлшектердің сандарын салыстырамыз. Алымындағы саны үлкен болған бөлшек, екінші алымы кіші бөлшектен үлкен болады.

Мысалы:

; ;

Шығады: .

Бөлшектерді қосу және азайту

Бірдей бөлгіші бар қарапайым бөлшектердің қосындысы дегеніміз: бөлгіші бар және осы бөлшектердің алымдарының қосындысына тең тек алымы бар бөлшек.

Екі қарапайым бөлшекті қосу үшін оларды ортақ бөлім беру арқылы, бөлшектің бөлімдерін теңестіру қажет. Содан кейін бөлшектің алымын қосып, бөлімін өзгеріссіз қалдырамыз.

.Мысал:

Біздегі бөліміндегі сандар 2 мен 3. Екеуіне ортақ ең кіші сан 6. Ол үшін екі бөлшек санның бөлімдерін 3 ке көбейтеміз.

шығады. Енді алымдарын 2 мен 3 ке көбейтеміз. Өйткені бөлімдеріндегі санды 6 санына теңестірген соң, алымдарын ортақ бөлгіштің бөлінділеріне көбейтеміз. шығады.

Бөлшекті соңғы түріне келтіру үшін, оларды ортақ бөлгішке келтіріп, алымдарын қосып немесе алып, ал ортақ бөлімін өзгеріссіз қалдыру қажет.

Бұл жақтағы бөлшектердің бөлімі 2 мен 3 тең. Ең кіші ортақ -ға тең. Бөлшектерді ортақ бөлімге келетіріп, алымындағы сандарды есептейміз.

Енді бөлшектердің алымындардағы сандарды 3 пен 2 көбейтеміз.

Бөлшекті соңғы түріне келтіру үшін, оларды ортақ бөлгішке келтіріп, алымдарын қосып немесе алып, ал ортақ бөлімдерін өзгеріссіз қалдыру қажет.

2. Мысал:

Бөлшектерді көбейту және бөлі амалдары

Екі жай бөлшекті көбейту үшін алымы мен бөлімін 2-ші жай бөлшектің сәйкес алымы мен бөліміне көбейтеміз.

Егер де бөлшекті санға көбейтетін болсақ, бөлшектің алымы санға көбейтіледі.

Егер жай бөлшек санды өзара көбейтіп, нәтижесінде алымы мен бөлімі бірдей санға қысқаратын жағдай туындаса, онда жай бөлшекті бірдей қысқаратын санына бөлеміз.

Кері бөлшекті анықтап алу. Егер жай бөлшек пен сол жай бөлшектің қарама қарсы бөлшегін көбейткен кезде - ге тең болуы қажет.( )

Жай бөлшекті екінші жай бөлшекке бөлу үшін, бірінші бөлшекті екінші жай бөлшектің кері жай бөлшегіне көбейту қажет.

Мысалы:

Дәрежеге шығару және түбір алу

Бөлшектің дәрежесін шығару үшін, бөлшектің алымы мен бөлімін дәрежелейміз.

Мысалы:

Бөлшекті түбірдің астынан шығару үшін, бөлшектің алымы мен бөлімін жеке-жеке түбір астына жазамыз.

Мысалы:

Бөлшектерді әртүрлі жолдармен түрлендіру

Жай бөлшектерді ондық бөлшектерге айналдыру үшін алымын бөліміне бөлеміз, нәтижесінде шекті сан шығуы мүмкін, кейде шексіз периодты бөлшек шығуы да мүмкін.

- шексіз қайталанатын периодты бөлшекті жақша арқылы жазу қажет.

Шекті саны шығатын бөлшекті жай бөлшек түрінде жазу үшін, үтірден кейінгі бөлігін ондық бөлшек түрінде жазу қажет.Содан шыққан бөлігін аралас бөлшек түрінде жазу керек.Мысал:

Шексіз ондық бөлшек жай бөлшек түрінде ешқашан бола алмайды. Тек периодты ондық бөлшек түрінде жазылады.

Мысалы:

Шексіз периодты ондық бөлшекті жай бөлшекке түрлендіру. периодтық бөлшегін, жай бөлшек түріне келтіру.

Нәтижесінде: .

Пайдаланылған әдебиеттер тізімі:

Бөлшек арифметикалық / / математикалық энциклопедия (5 томдық). - Мәскеу: Кеңес Энциклопедиясы, 1982. - Т.2. — 389-390 ББ.

Математика: Оқу. 5 кл үшін. орташа. шк. / ред. Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. и. Шварцбурд. - 4-ші басылым. — Чебоксары: Сезім. кн. басылым, 1997. — 202-203 Б., 230.

Цыпкин А. Г. орта оқу орындарына арналған Математика анықтамалығы. - 3-ші басылым.. - Мәскеу: Ғылым, 1983. — Б. 51. - 480 б.

Ағылшын тілінде:

Berggren, J. Lennart. Medieval Islam-дағы математика / / Египеттің математикасы, Месопотамия, Қытай, Үндістан, және Ислам: a Sourcebook (ағылш.). — Princeton University Press, 2007. — P. 518. — ISBN 978-0-691-11485-9.

Jean-Claude Martzloff. A History of Chinese Mathematics. Springer (ағылш.). — 1997. — ISBN 3-540-33782-2.

William K. Simpson. An Additional Fragment from the "Hatnub" Stela // Journal of Near Eastern Studies. — 1961. - Қаңтар (т.20, № 1). — Б. 25-30.

Clagett, Marshall. Memoirs of the American Philosophical Society 232