|
Модуль/пән
атауы
|
Математика
|
|
Сабақтың
тақырыбы
|
Дифференциалдық
теңдеулер
|
|
Педагог
|
Төлебаева Жанерке
Мархабатқызы
|
|
Курс
|
1
|
|
Топ
|
|
|
|
|
|
|
Сабақтың өткізілетін
күні
|
|
|
|
|
|
|
Сабақтың
түрі
|
Теориялық
|
|
Сабақтың мақсаты немесе
оқыту
нәтижелері
|
Дифференциал теңдеу ұғымын және анықтамасын,
дифференциалдық теңдеудің ретін, жалпы және дербес шешімін,
айнымалылары бөліктенетін теңдеулерді шешу туралы жалпы
мағлұмат енгізу.
Дифференциал
теңдеулерге келтірілетін есептер
қарастыру.
|
|
Бағалау
критерийлері
|
Дифференциал теңдеудің
анықтамасын, дифференциал
теңдеу жалпы және дербес шешімін
білу. Дифференциал
теңдеу ретін анықтайды. Айнымалылары
бөліктенетін дифференциал
теңдеу жалпы шешімін таба
алады.
|
|
Оқу - әдістемелік құралдар,
әдебиеттер
|
Математика:Жалпы білім беретін
мектептің жаратылыстану-математика бағытындағы 11-сыныбына арналған
оқулық,1-2 бөлім, Алматы: «Мектеп»,
2019ж.
Деңгейлік саралау
технологиясы
|
|
Техникалық құралдар,
материалдар
|
Оқулықтар, үлестірме
материалдар, стикерлер,
плакаттар
|
|
Сабақ
барысы
|
|
Сабақ
кезеңдері
|
|
|
1.Ұйымдастыру кезеңі:
(5 минут)
|
а) сәлемдесу, оқушыларды
түгендеу;
б) сабақтың жүру жоспарын
түсіндіру.
|
|
2 Үй тапсырамасын тексеру
кезеңі
(20 минут)
|
«Миға шабуыл» әдісі бойынша
үйге берілген тапсырмаларды қайталап, еске
түсіру.
Кездейсоқ шаманың сандық
сипаттамаларын таңдамалар бойынша бағалау
тақырыбы бойынша
есептер:
10 сыныптың алгебра және анализ бастамалары
кітабының 185 бетіндегі 23.9 және 23.10
есептері
|
|
3. Жаңа материалды түсіндіруге дайындық кезеңі (жаңа тақырыпты
болжау) / Практикалық, зертханалық жұмысқа дайындық кезеңі (5
минут)
|
Дифференциалдық теңдеу, дифференциалдық
теңдеулер реті, ДТ дербес және жалпы шешімдері, айнымалысы
бөліктенетін теңдеулердің шешу
жолдары.
|
|
4. Жаңа материалды түсіндіру кезеңі (Практикалық,
зертханалық жұмысты орындау
кезеңі)
( 35 минут)
|
«Блум
таксономиясы» әдісі арқылы жаңа сабақты
түсіндіру.
Дифференциалдық теңдеулер —
ізделінетін функцияны оның әр түрлі
ретті туындыларымен (немесе дифференциалдарымен)
және тәуелсіз айнымалылармен байланыстыратын
теңдеулер.
Алгебралық теңдеулермен салыстырғанда, дифференциалдық
теңдеулерді шешу кезінде функция (функциялар отбасы) ізделінеді, ал
алгебралық теңдеулерді шешу нәтижесінде сан (бірнеше сан)
ізделінеді.
Біріншісінен жоғары ретті дифференциалдық теңдеуді бірінші
ретті теңдеулер жүйесіне айналдыруға болады. Бұл жүйесіне кіретін
теңдеулер саны бастапқы дифференциалдық теңдеудің ретіне
тең.
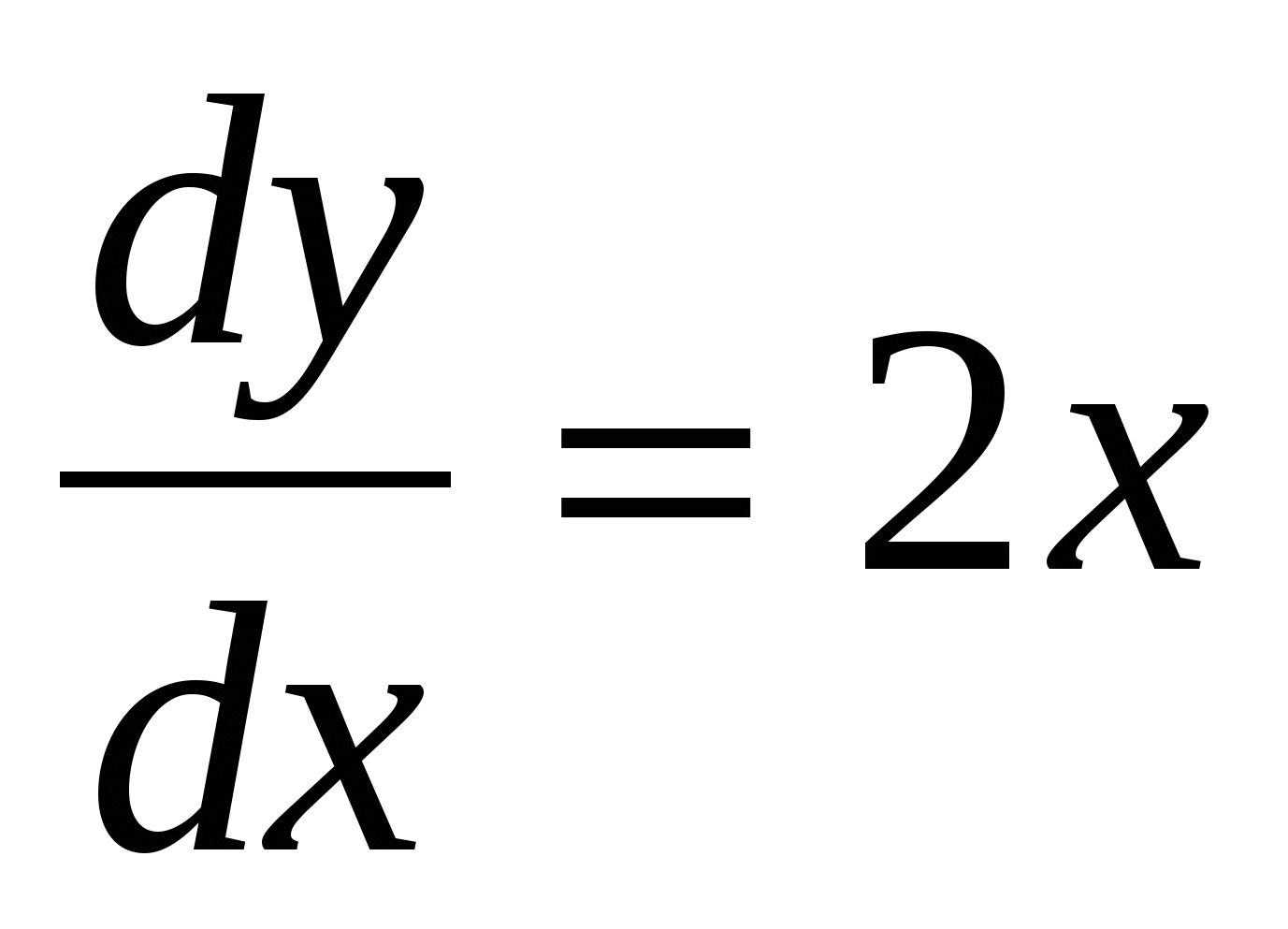 (1) (1)
Бұл (1) теңдеу дифференциалдық
теңдеу, өйткені оның құрамында ізделінді функцияның туындысы бар.
Оны 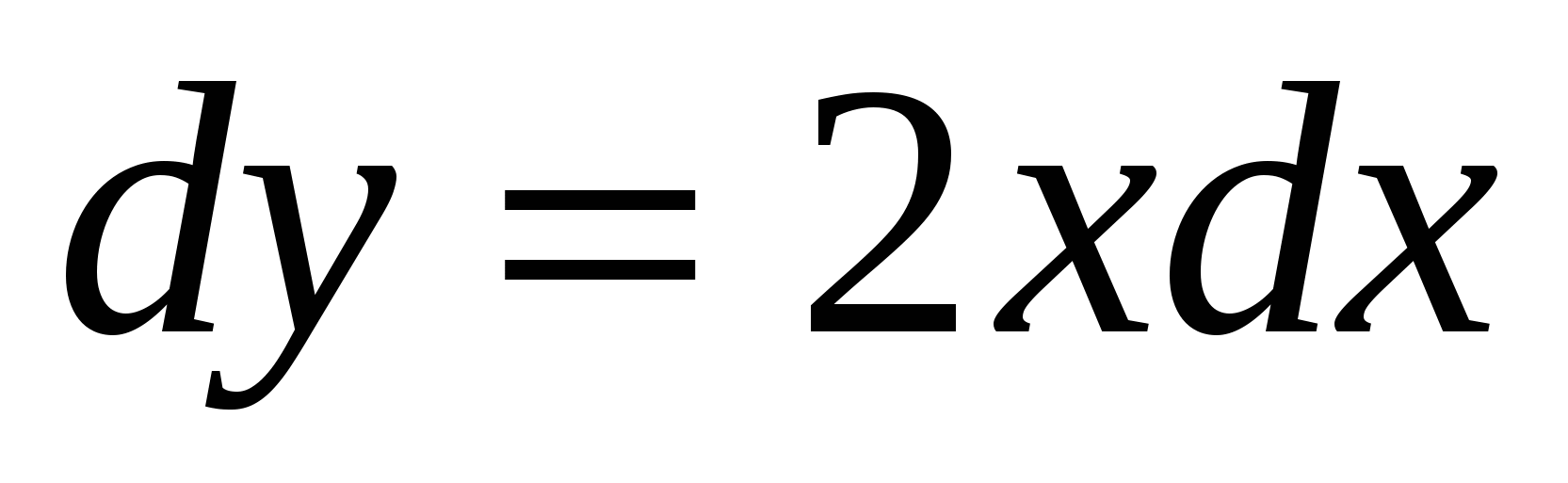 түрінде жазамыз. Бұдан
ізделінді функция 2х-тің алғашқы функциясы болады. түрінде жазамыз. Бұдан
ізделінді функция 2х-тің алғашқы функциясы болады.
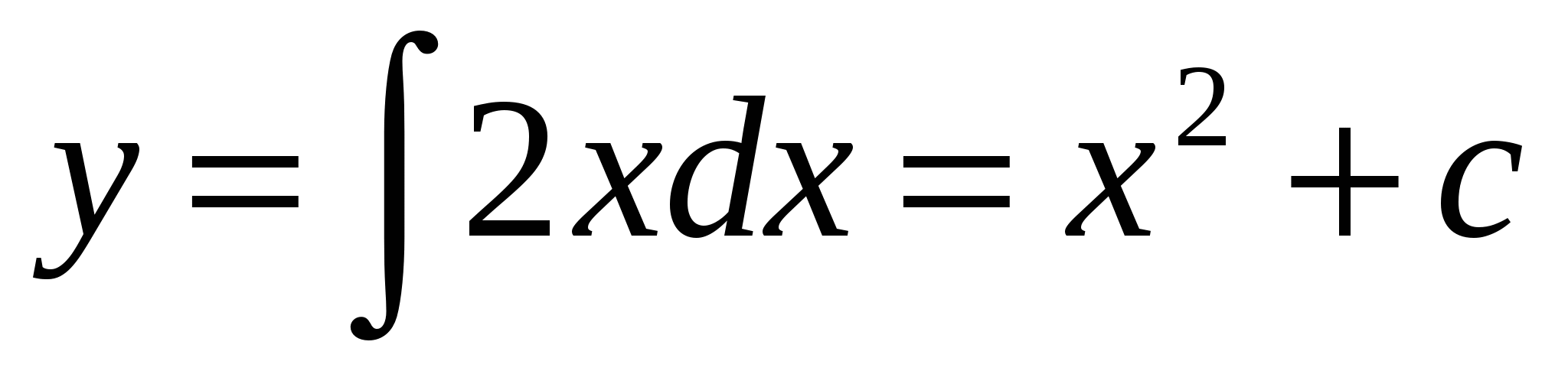 , , 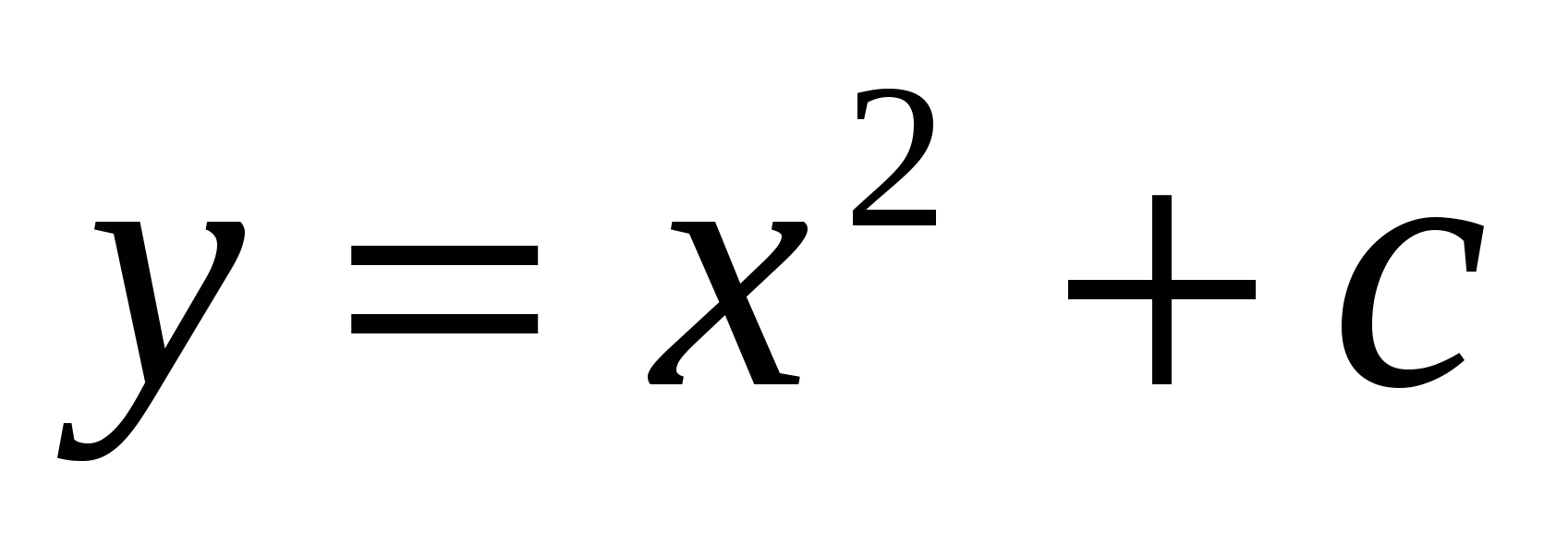 (2) (2)
(2)
теңдеуден (1) дифференциалдық теңдеудің шексіз көп шешімі бар
екенін көреміз, яғни (1) теңдеуді шексіз көп қисық – парабола
қанағаттандырады (1-сызба).
Осы
қисықтардың ішінен өзімізге қажеттісін таңдап алу үшін есептің
шартындағы ізделінді қисық О (0;0) нүктесі арқылы өтеді деген
шартты пайдаланамыз. Осы нүктенің координаталары (2) теңдеуді
қанағаттандыруы тиіс. Сонда 0 = 0 + c, яғни с = 0 болады. Сонымен, ізделінді
қисықтың теңдеуі 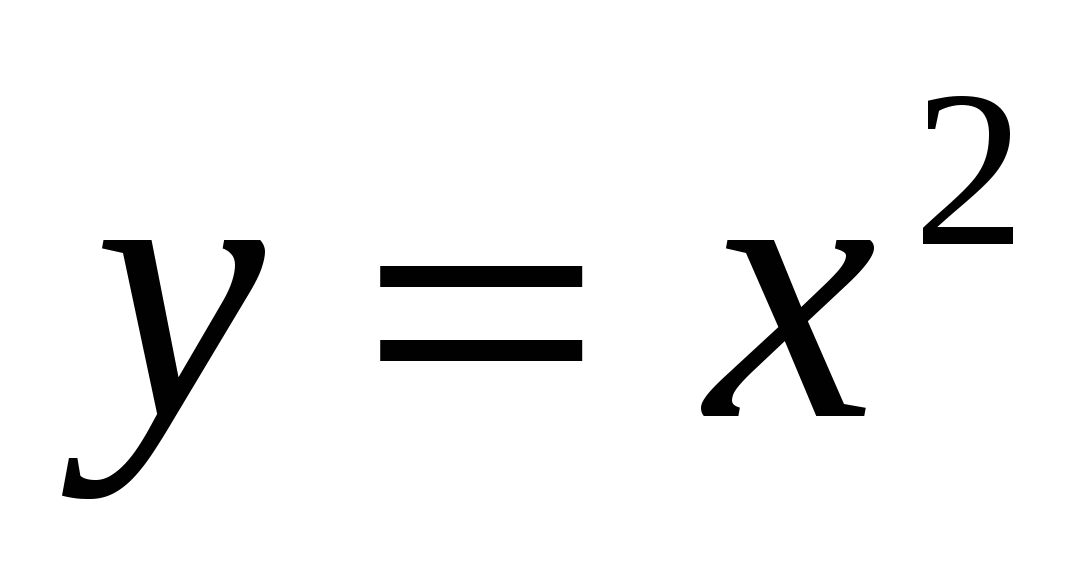 . .
Егер
ізділінді функция бір айнымалының функциясы болса, онда
оны қарапайым дифференциалдық
теңдеу деп атайды.
Оның
жалпы түрі
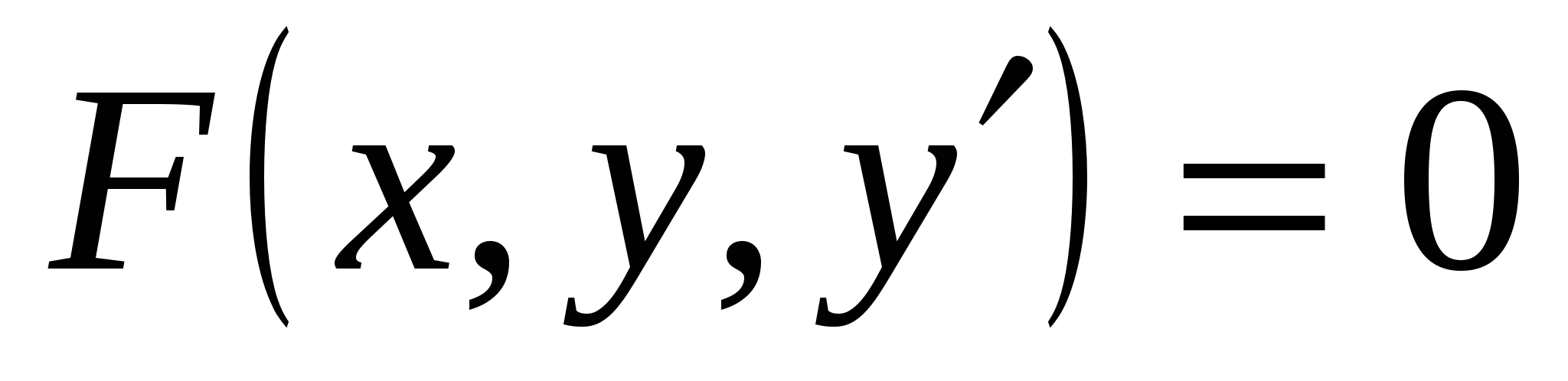 (3)
(3)
болады.
Дифференциалдық теңдеуге енетін функцияның туындысының ең жоғарғы
реті дифференциалдық
теңдеудің реті деп
аталады.
n-ші
ретті дифференциалдық теңдеудің жалпы түрі
мынандай:
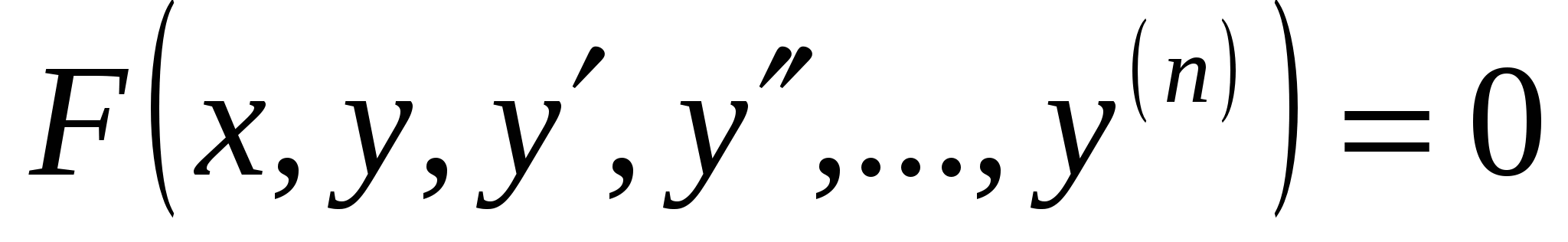 (4) (4)
Дербес жағдайда теңдеудің
құрамына х,у және n-нен төменгі туындылар кірмеуі мүмкін.
Мысалы, 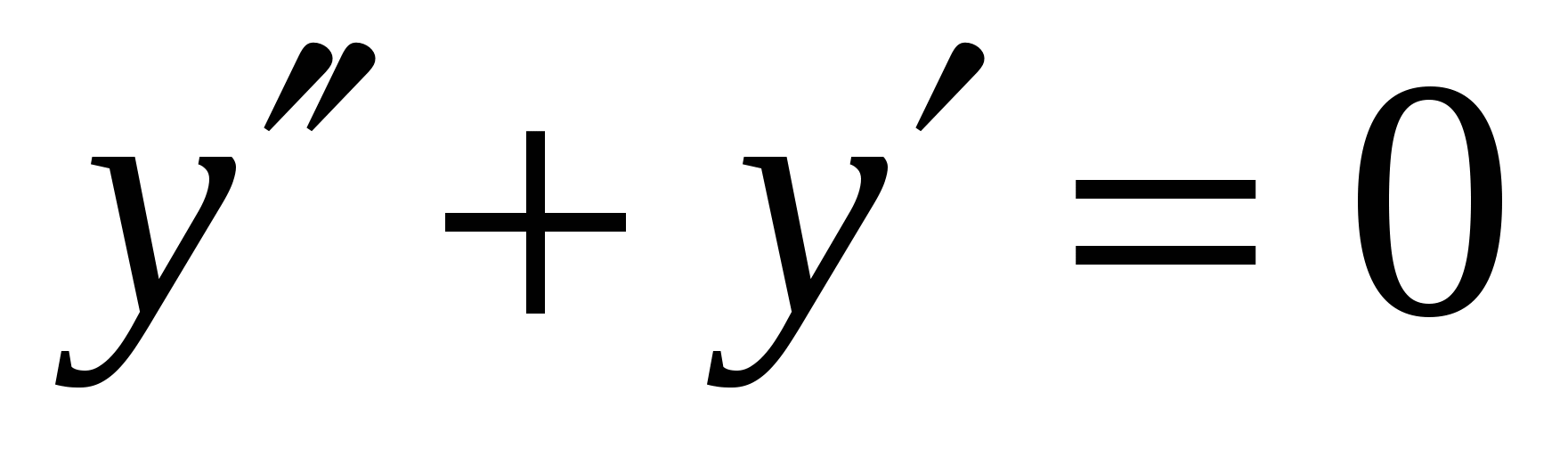 .
.
(4) теңдікті
қанағаттандыратын 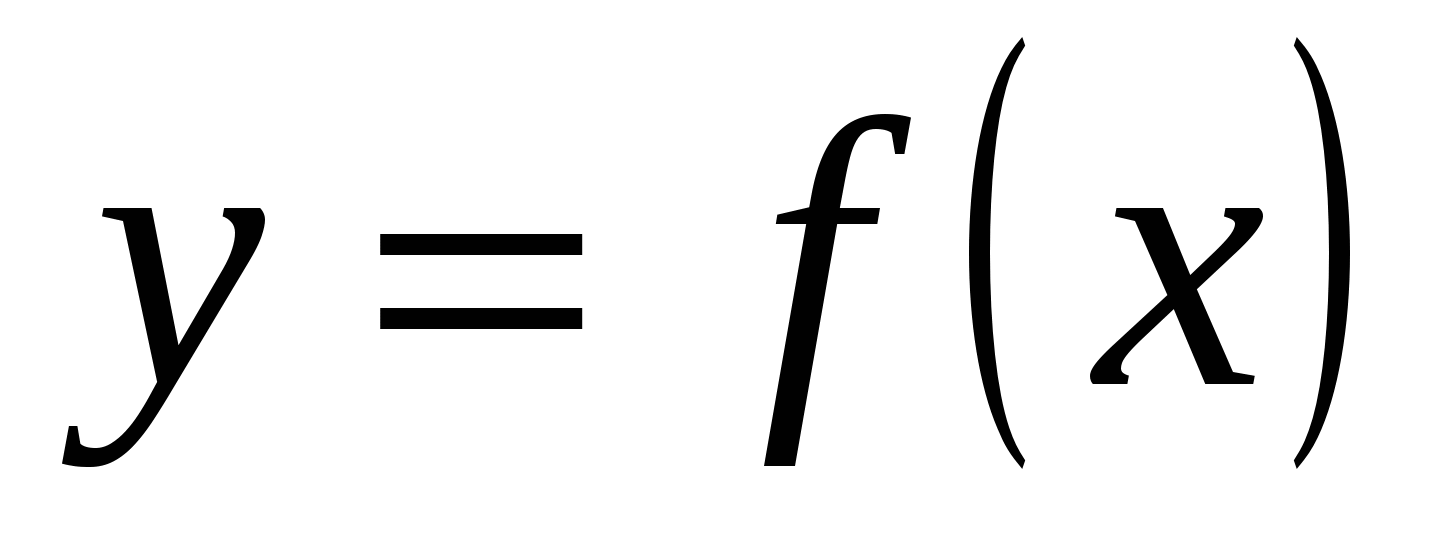 функциясы дифференциалдық
теңдеудің шешімі деп
аталады. функциясы дифференциалдық
теңдеудің шешімі деп
аталады.
|
|
5. Жаңа материалды бекіту кезеңі. (Практикалық, зертханалық
жұмысты тапсыру
кезеңі)
(15
минут)
|
«Серпілген
сауал» әдісі арқылы сабақты
қорытындылау мақсатында студенттерге өтілген тақырып бойынша
білімді меңгеруге арналған сұрақтар мен есептер
беру.
-
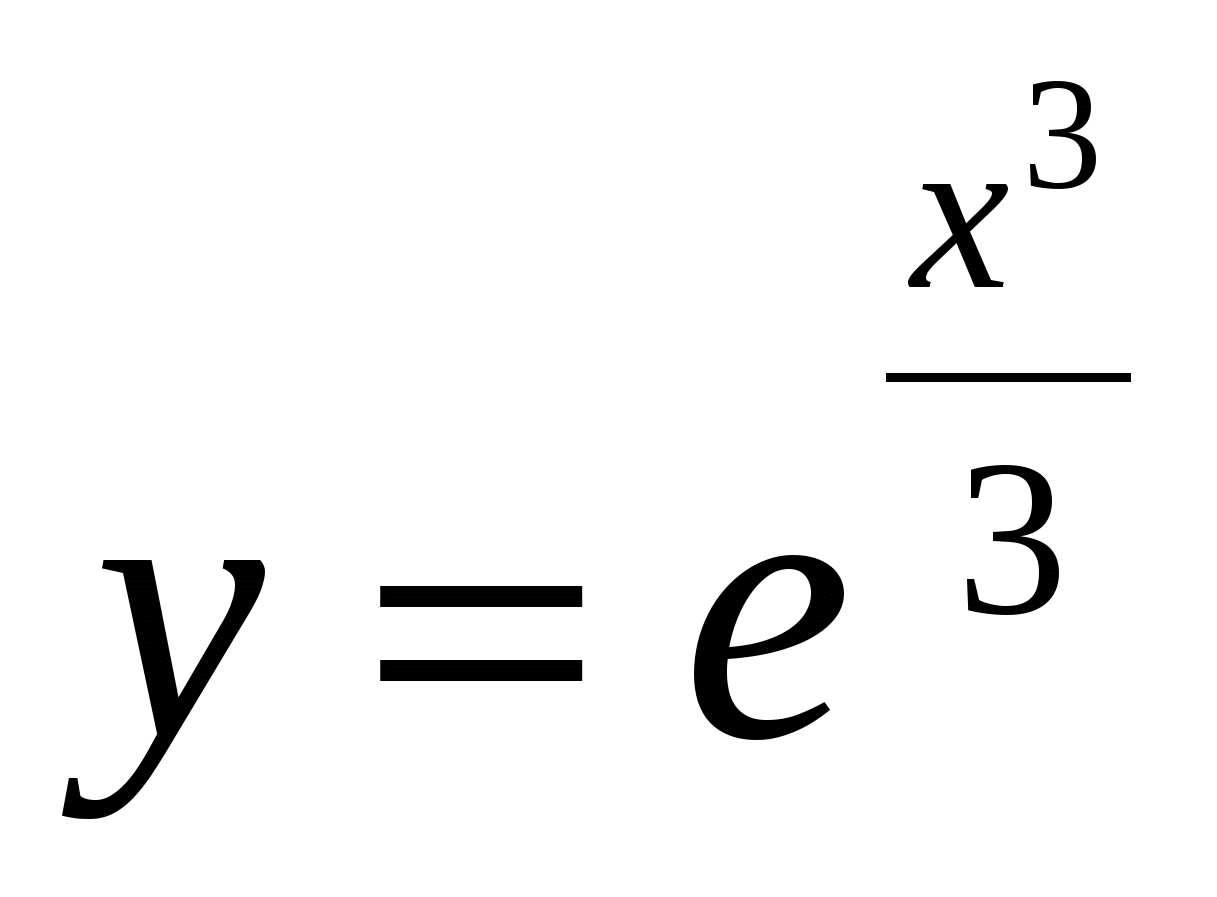 функциясы функциясы 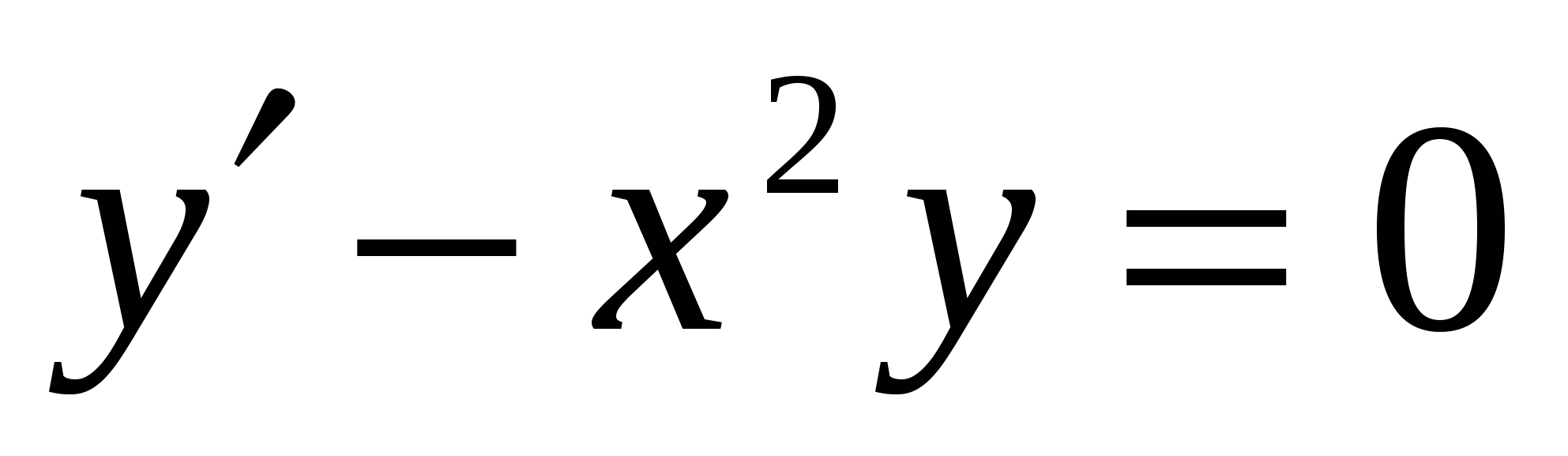 теңдеуінің шешімі
болатынын көрсету
керек. теңдеуінің шешімі
болатынын көрсету
керек.
-
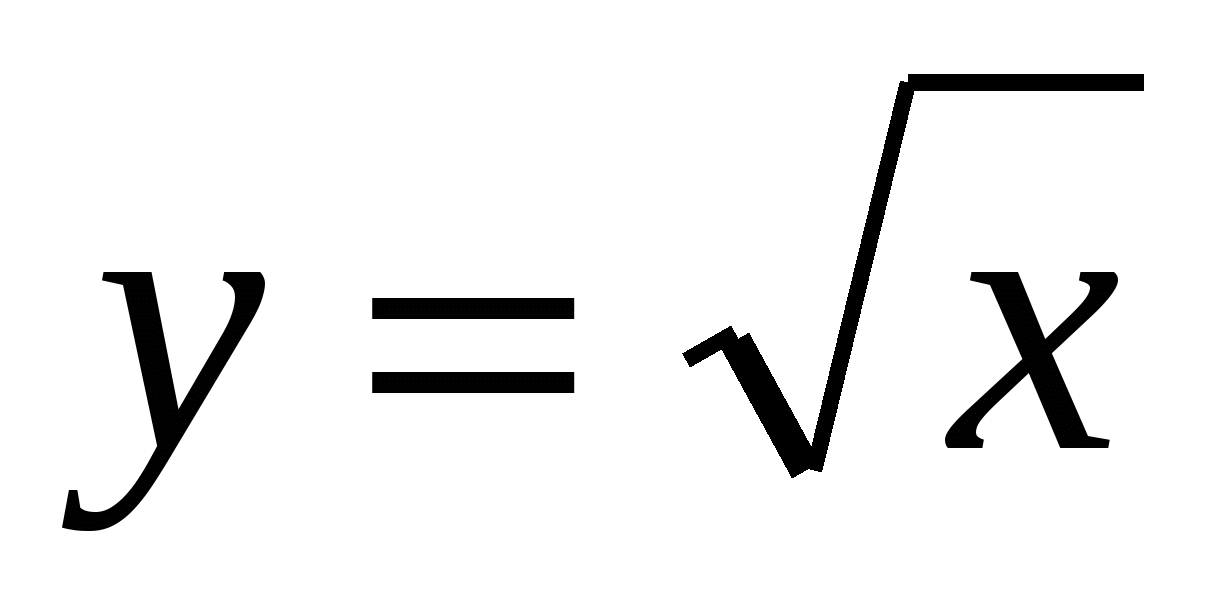 функциясы функциясы 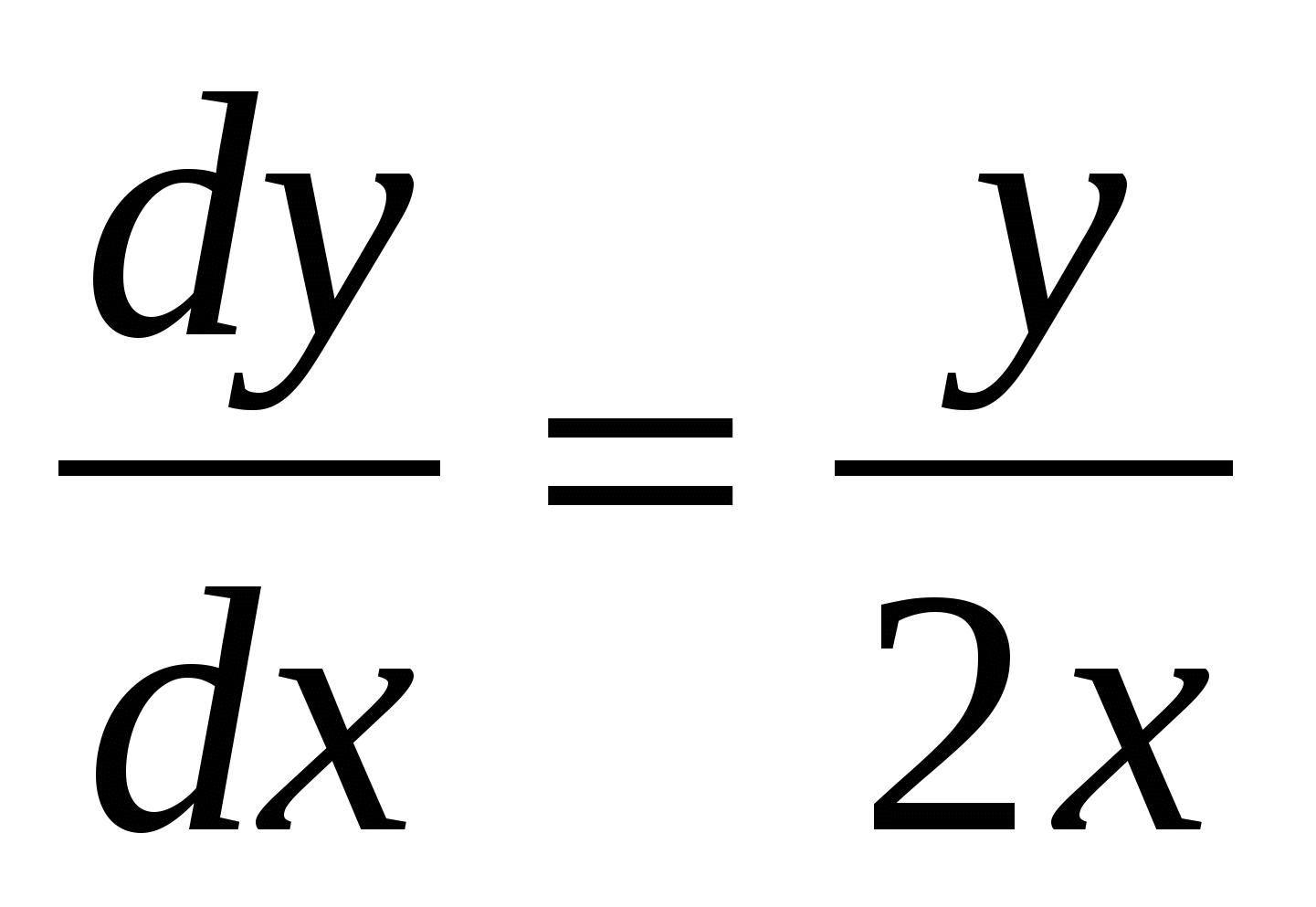 дифференциалдық
теңдеуінің шешімі болатынын көрсету
керек. дифференциалдық
теңдеуінің шешімі болатынын көрсету
керек.
-
Дифференциалдық тедеу
дегеніміз?
-
Дифференциалдық теңдеудің
жалпы шешімі?
|
|
6.Үй тапсырмасы туралы
ақпараттандыру кезеңі (3
минут)
|
Қарапайым тригонометриялық
теңдеулер тақырыбы бойынша
есептер:
10 сыныптың алгебра және анализ бастамалары
кітабының 184 бетіндегі 23.2 185 бетіндегі 23.5, 23.6
есептері
|
|
7.Сабақты қорытындылау және
рефлексия (7
минут)
|
Оқушыларды 100 балдық жүйе
арқылы бағалау
|
Нені
білдім?
|
Нені
үйрендім?
|
Нені білгім
келеді?
|
|
|
|
|
|


















