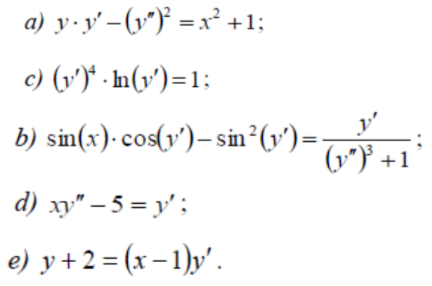М.ТЫНЫШПАЕВ АТЫНДАҒЫ ҚАЗАҚ КӨЛІК ЖӘНЕ КОММУНИКАЦИЯЛАР АКАДЕМИЯСЫНЫҢ
ШЫМКЕНТ КӨЛІК КОЛЛЕДЖІ
2023-2024 оқу жылы
Сабақ жоспары №64
|
Модуль/пән атауы |
Математика |
|||
|
Сабақтың тақырыбы |
Дифференциалдық теңдеулер туралы жалпы мағлұмат |
|||
|
Педагог |
Досан Б |
|||
|
Курс |
1 |
|||
|
Топ |
ОП-23-9 |
АТС-23-9 |
ДС-23-9 |
РэТ-23-9 |
|
Сабақтың өткізілетін күні |
|
|
|
|
|
Сабақтың түрі |
Жаңа білім беру сабағы |
|||
|
Сабақтың мақсаты немесе оқыту нәтижелері |
Дифференциалдық теңдеулерді шешу |
|||
|
Бағалау критерийлері |
1)Дифференциалдық теңдеулер ұғымын түсінеді; 2)Дифференциалдық теңдеулердің жалпы және дербес шешімдерін анықту. |
|||
|
Оқу - әдістемелік құралдар, әдебиеттер |
А.Е.Әбылқасымова, В.Е. Корчевский, З.Ә. Жұмағұлова, Алгебра және анализ бастамалары: Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 11-сыныбына арналған оқулық, Алматы: «Мектеп», 2019ж. |
|||
|
Техникалық құралдар, материалдар |
Оқулықтар,үлестірме материалдар,стикерлер,плакаттар |
|||
|
Сабақ барысы |
||||
|
Сабақ кезеңдері |
|
|||
|
1.Ұйымдастыру кезеңі:(10 минут) |
а) сәлемдесу, оқушыларды түгендеу; б) сабақтың жүру жоспарын түсіндіру |
|||
|
2. Үй тапсырамасын тексеру кезеңі (15 минут) |
Үй жұмысын тексеру. Үй жұмысына берілген тест тапсырмасын жұптық арқылы тексерту. |
|||
|
3. Жаңа материалды түсіндіруге дайындық кезеңі (жаңа тақырыпты болжау) / Практикалық, зертханалық жұмысқа дайындық кезеңі (5 минут) |
Бүгін,
Дифференциалдық теңдеулер
туралы жалпы мағлұмат тақырыбын
қарастырамыз.
|
|||
|
4. Жаңа материалды түсіндіру кезеңі (Практикалық, зертханалық жұмысты орындау кезеңі)
|
1.Қандай теңдеулер дифференциал теңдеулер деп аталады? 2.Айнымалыларын бөліктеу қалай орындалады? 3.Мысалдарды қарастырып дифференциалдық теңдеулерді шешу алгоритмін жазыңыз. Дифференциалдық теңдеулер — ізделінетін функцияны оның әр түрлі ретті туындыларымен (немесе дифференциалдарымен) және тәуелсіз айнымалылармен байланыстыратын теңдеулер. Алгебралық теңдеулермен салыстырғанда, дифференциалдық теңдеулерді шешу кезінде функция (функциялар отбасы) ізделінеді, ал алгебралық теңдеулерді шешу нәтижесінде сан (бірнеше сан) ізделінеді. Біріншісінен жоғары ретті дифференциалдық теңдеуді бірінші ретті теңдеулер жүйесіне айналдыруға болады. Бұл жүйесіне кіретін теңдеулер саны бастапқы дифференциалдық теңдеудің ретіне тең. Ізделінді функцияның ең жоғарғы туындысы (дифференциалы) теңдеудің реті деп аталады. Теңдеуді қанағаттандыратын, яғни тепе-теңдікке айналдыратын функция теңдеудің шешімі деп аталады. Тапсырма: 1.Дифференциалдық теңдеудің ретін анықтаңыз:
теңдеулерге 1) Егер
анықтауыш
алмастыруын енгіземіз,
мұндағы және
сандары-
Мысал. Шешуі.
Анықтауышты
есептейік: Нөлге тең емес болғандықтан келесі жүйені шешеміз:
Ендеше
алмастыруымыз
Айнымалыларды
алмастырайық: Жоғарғы теңдеуге қойсақ:
Айнымалыларды
ажыратайық:
Енді алғашқы функция у және айнымалы х-ке ораламыз:
|
|
5. Жаңа материалды бекіту кезеңі. (Практикалық, зертханалық жұмысты тапсыру кезеңі) 20 мин |
1) (x2 + y2 )dx − 2xydy = 0
2) у'
= 3) y − xy ' = y ln x
4) 3у '
=
|
|
6.Үй тапсырмасы туралы ақпараттандыру кезеңі (5 минут) |
Үйге тапсырма:
|
|
7.Сабақты қорытындылау және рефлексия (5 минут) |
Оқушыларды 100 баллдық жүйе арқылы бағалау. Сабақ соңында рефлексия жүргізу. |
Педагог: ___________________
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Дифференциялдық теңдеулерді шешу
Дифференциялдық теңдеулерді шешу
М.ТЫНЫШПАЕВ АТЫНДАҒЫ ҚАЗАҚ КӨЛІК ЖӘНЕ КОММУНИКАЦИЯЛАР АКАДЕМИЯСЫНЫҢ
ШЫМКЕНТ КӨЛІК КОЛЛЕДЖІ
2023-2024 оқу жылы
Сабақ жоспары №64
|
Модуль/пән атауы |
Математика |
|||
|
Сабақтың тақырыбы |
Дифференциалдық теңдеулер туралы жалпы мағлұмат |
|||
|
Педагог |
Досан Б |
|||
|
Курс |
1 |
|||
|
Топ |
ОП-23-9 |
АТС-23-9 |
ДС-23-9 |
РэТ-23-9 |
|
Сабақтың өткізілетін күні |
|
|
|
|
|
Сабақтың түрі |
Жаңа білім беру сабағы |
|||
|
Сабақтың мақсаты немесе оқыту нәтижелері |
Дифференциалдық теңдеулерді шешу |
|||
|
Бағалау критерийлері |
1)Дифференциалдық теңдеулер ұғымын түсінеді; 2)Дифференциалдық теңдеулердің жалпы және дербес шешімдерін анықту. |
|||
|
Оқу - әдістемелік құралдар, әдебиеттер |
А.Е.Әбылқасымова, В.Е. Корчевский, З.Ә. Жұмағұлова, Алгебра және анализ бастамалары: Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 11-сыныбына арналған оқулық, Алматы: «Мектеп», 2019ж. |
|||
|
Техникалық құралдар, материалдар |
Оқулықтар,үлестірме материалдар,стикерлер,плакаттар |
|||
|
Сабақ барысы |
||||
|
Сабақ кезеңдері |
|
|||
|
1.Ұйымдастыру кезеңі:(10 минут) |
а) сәлемдесу, оқушыларды түгендеу; б) сабақтың жүру жоспарын түсіндіру |
|||
|
2. Үй тапсырамасын тексеру кезеңі (15 минут) |
Үй жұмысын тексеру. Үй жұмысына берілген тест тапсырмасын жұптық арқылы тексерту. |
|||
|
3. Жаңа материалды түсіндіруге дайындық кезеңі (жаңа тақырыпты болжау) / Практикалық, зертханалық жұмысқа дайындық кезеңі (5 минут) |
Бүгін,
Дифференциалдық теңдеулер
туралы жалпы мағлұмат тақырыбын
қарастырамыз.
|
|||
|
4. Жаңа материалды түсіндіру кезеңі (Практикалық, зертханалық жұмысты орындау кезеңі)
|
1.Қандай теңдеулер дифференциал теңдеулер деп аталады? 2.Айнымалыларын бөліктеу қалай орындалады? 3.Мысалдарды қарастырып дифференциалдық теңдеулерді шешу алгоритмін жазыңыз. Дифференциалдық теңдеулер — ізделінетін функцияны оның әр түрлі ретті туындыларымен (немесе дифференциалдарымен) және тәуелсіз айнымалылармен байланыстыратын теңдеулер. Алгебралық теңдеулермен салыстырғанда, дифференциалдық теңдеулерді шешу кезінде функция (функциялар отбасы) ізделінеді, ал алгебралық теңдеулерді шешу нәтижесінде сан (бірнеше сан) ізделінеді. Біріншісінен жоғары ретті дифференциалдық теңдеуді бірінші ретті теңдеулер жүйесіне айналдыруға болады. Бұл жүйесіне кіретін теңдеулер саны бастапқы дифференциалдық теңдеудің ретіне тең. Ізделінді функцияның ең жоғарғы туындысы (дифференциалы) теңдеудің реті деп аталады. Теңдеуді қанағаттандыратын, яғни тепе-теңдікке айналдыратын функция теңдеудің шешімі деп аталады. Тапсырма: 1.Дифференциалдық теңдеудің ретін анықтаңыз:
теңдеулерге 1) Егер
анықтауыш
алмастыруын енгіземіз,
мұндағы және
сандары-
Мысал. Шешуі.
Анықтауышты
есептейік: Нөлге тең емес болғандықтан келесі жүйені шешеміз:
Ендеше
алмастыруымыз
Айнымалыларды
алмастырайық: Жоғарғы теңдеуге қойсақ:
Айнымалыларды
ажыратайық:
Енді алғашқы функция у және айнымалы х-ке ораламыз:
|
|
5. Жаңа материалды бекіту кезеңі. (Практикалық, зертханалық жұмысты тапсыру кезеңі) 20 мин |
1) (x2 + y2 )dx − 2xydy = 0
2) у'
= 3) y − xy ' = y ln x
4) 3у '
=
|
|
6.Үй тапсырмасы туралы ақпараттандыру кезеңі (5 минут) |
Үйге тапсырма:
|
|
7.Сабақты қорытындылау және рефлексия (5 минут) |
Оқушыларды 100 баллдық жүйе арқылы бағалау. Сабақ соңында рефлексия жүргізу. |
Педагог: ___________________

шағым қалдыра аласыз