
Мазмұны
1.1. Тәуелсіз айнымалы және функция 5
1.2. Функцияның берілу тәсілдері 10
1.3. Функциялар классификациясы 12
1.4. Функцияның графигі. Кері функциялар 13
1.7. Шексіз кіші және шексіз үлкен функциялар 26
2. Үздіксіз функциялардың екі негізгі теоремасы 32
2.1. Үздіксіздіктің анықтамасы 32
2.2. Үздіксіз функцияларға қолданылатын арифметикалық амалдар 34
2.3. Кейбір элементар функциялардың үздіксіздігі 35
2.5. Больцано теоремасының қолданылуы 39
2.6. Вейерштрасстың экстремалдық мәндер туралы теоремалары 43
2.7. Реттілік туралы теорема. Шағын жиындар 49
2.8. Функцияның біртекті үздіксіздігі ұғымы 51
2.9. Функцияның үздіксіздік модулі ұғымы 56
Пайдаланылған әдебиеттер тізімі 61
Кіріспе
Математикалық анализ курсын оқып үйренудің мақсаты – функцияларды оқып үйрену, сондай-ақ математиканың жалпы әдістерінің қолданбалы мәнін ашу болып табылады.
Функцияның қасиеттері мен оның графигін салуды үйрену математиканың тамаша қолданылуы болып табылады. Функцияны зерттеудің мұндай тәсілі бірнеше рет мұқият талдауға ұшыраған еді. Бұның басты себебі – математика қосымшаларының жаңа құбылыстарын зерттеу кезінде пайда болған бірінен-бірі күрделене түсетін функциялармен жұмыстану қажет болды. Математиканың құрастырылған ережелеріне бағынбайтын жағдайлар пайда болды.
Математикалық анализді оқып үйренудегі функциялық беру тәсілдерінің дамуы функциялардың үздіксіздігі мен үзіліс нүктелері жайында көрнекі мәліметтерді алуға, кез келген элементар функцияның қолданылу аясындағы үздіксіздігі туралы оқып үйрену, функциялардың графиктерін салуды үйренуге және негізгі элементар функциялар туралы мағлұматтарды тереңдетуге, сондай-ақ олардың қолданылу аясын анықтауға мүмкіндік береді.
Берілген тақырыптың өзектілігі. Қазіргі заманғы математикалық анализде үздіксіз функциялар және оларға қатысты теоремалар және оларды қолдану мәселесі әлі де ашық күйінде сақталып отыр. Алайда бұл бағыттағы мәлімет айтарлықтай көп жиналғандықтан, бұл мәліметтерді жинақтап, тізбектеп, жүйелеп, бөлек жұмыс ретінде жазу қажеттілігі туындап отыр.
Берілген дипломдық жұмыстың зерттеу объектісі – «Үздіксіз функциялардың екі негізгі теоремасы» тақырыбын оқып үйрену арқылы мектеп математика курсынан алған үздіксіз функция ұғымының кеңейтілуі.
Зерттеу пәні – үздіксіз функциялардың қасиеттері мен теоремалары.
Мақсаты – мектеп математика курсынан бастау алатын және жоғары математикада жалғасын табатын функция, соның ішінде үздіксіз функция туралы жалпы мәлімет алып, үздіксіз функциялардың екі негізгі теоремасы болып саналатын Больцано теоремасы мен Вейерштрасс теоремасымен танысып, олардың қолданылу аймағы туралы мәлімет алу.
Міндеттер:
-
үздіксіз функциялардың екі негізгі теоремасы туралы жалпы мағлұмат алу;
-
берілген тақырыпты кеңейту;
-
үздіксіз функциялардың екі негізгі теоремасының қолданылу аясын анықтау.
Зерттеу әдістері:
-
ғылыми, оқу әдебиеттерді талдау;
-
теориялық материалды жинақтау және жүйелеу;
-
тақырып бойынша білімді кеңейту.
Берілген жұмыстың құрамы:
-
Функция туралы жалпы мәлімет.
-
Үздіксіз функциялардың екі негізгі теоремасы.
Жұмыстың тәжірибелік маңыздылығы – жинақталған материал мұғалімнің басқаруымен немесе өз бетімен функция ұғымы және үздіксіз функцияның қасиеттері туралы білімді тереңдеткісі келетін жоғары сынып оқушылары мен ЖОО студенттеріне математикалық анализді оқып үйрену үрдісінде пайдалы болады.
1. Функция ұғымы
1.1. Тәуелсіз айнымалы және функция
Қазіргі заманғы математиканың маңызды бөлімдері функция ұғымының айналасында өрбиді. Бұл бөлімшеде біз функция ұғымын жүйелі анализдеумен айналысатын боламыз.
х-тің мәні берілмесе,

секілді өрнектердің белгілі бір сан мәні болмайды. Осындай өрнектің мәні х мәнінің функциясы деп айтады және

деп жазады. Мысалы,
егер  болса,
онда
болса,
онда  , яғни
, яғни
 . Осы
әдіспен х-тің кез келген бүтін, бөлшек,
иррационал, тіпті комплекс мәніндегі
. Осы
әдіспен х-тің кез келген бүтін, бөлшек,
иррационал, тіпті комплекс мәніндегі  функциясының мәнін табуға
болады.
функциясының мәнін табуға
болады.
п-нен кем жай сандардың саны
бүтін п
санының
 функциясы
болады. п
санының мәні берілген
жағдайда
функциясы
болады. п
санының мәні берілген
жағдайда  функциясының мәнін есептеудің
ешқандай алгебралық өрнегі берілмесе де,
функциясының мәнін есептеудің
ешқандай алгебралық өрнегі берілмесе де,
 функциясының мәні
анықталады. Үшбұрыштың ауданы оның үш қабырғасының ұзындықтарының
функциясы болады; функция қабырғалардың ұзындықтарымен бірге
өзгеріп тұрады және қабырғалардың ұзындықтары нақты берілген
жағдайда, функция да нақтыланады. Егер жазықтық проекцияланатын
болса немесе топологиялық түрлендірілсе, онда түрлендіруден кейінгі
нүктенің координаталары нүктенің бастапқы координаталарына тәуелді
болады, яғни олардың функциялары болып табылады. Шамалар
бір-бірімен қандай да бір физикалық қатынас арқылы байланысатын
жағдайлардың бәрінде «функция» ұғымы қолданылады. Цилиндрдің ішіне
енгізілген газдың көлемі поршеньге әсер ететін температура мен
қысымның функциясы болып табылады. Әуе шарына әсер ететін
атмосфералық қысым шардың теңіз деңгейіне қарағандағы биіктігінің
функциясы болатыны анықталды. Периодты құбылыстардың үлкен көлемі –
судың көтерілуінің қозғалысы, керілген сымның тербелісі,
қыздырылған сымның шығаратын жарық толқындарының таралуы
–
функциясының мәні
анықталады. Үшбұрыштың ауданы оның үш қабырғасының ұзындықтарының
функциясы болады; функция қабырғалардың ұзындықтарымен бірге
өзгеріп тұрады және қабырғалардың ұзындықтары нақты берілген
жағдайда, функция да нақтыланады. Егер жазықтық проекцияланатын
болса немесе топологиялық түрлендірілсе, онда түрлендіруден кейінгі
нүктенің координаталары нүктенің бастапқы координаталарына тәуелді
болады, яғни олардың функциялары болып табылады. Шамалар
бір-бірімен қандай да бір физикалық қатынас арқылы байланысатын
жағдайлардың бәрінде «функция» ұғымы қолданылады. Цилиндрдің ішіне
енгізілген газдың көлемі поршеньге әсер ететін температура мен
қысымның функциясы болып табылады. Әуе шарына әсер ететін
атмосфералық қысым шардың теңіз деңгейіне қарағандағы биіктігінің
функциясы болатыны анықталды. Периодты құбылыстардың үлкен көлемі –
судың көтерілуінің қозғалысы, керілген сымның тербелісі,
қыздырылған сымның шығаратын жарық толқындарының таралуы
–  және
және
 қарапайым
тригонометриялық функцияларымен
«реттеледі».
қарапайым
тригонометриялық функцияларымен
«реттеледі».
«Функция» ұғымын енгізген Лейбниц (1646-1716) үшін де, XVIII ғасырдағы математиктер үшін де функционалдық тәуелділік идеясы осы тәуелділікті нақты өрнектейтін қарапайым математикалық формуланың болуымен сипатталатын еді. Мұндай концепция математикалық физиканың қоятын талаптарына қатысты өте тар болып шықты, сондықтан «функция» ұғымы ұзақ уақыт бойына жалпылау мен өңдеуге ұшыраған болатын. [1]
Осы бөлімшеде аталған үрдістің қалай өткендігін жазатын боламын.
Анықтамалар мен мысалдар.
Көптеген жағдайларда қандай да бір S жиынтығынан (жиынынан) өзіміздің қалауымызбен еркін түрде таңдап алатын математикалық объектілермен жұмыстану қажет болады. Таңдалынған объект бұл жағдайда айнымалы деген атауға, ал S жиынтығы оның өзгеру аймағы деген атауға ие болады. Айнымалыларды алфавиттің соңғы әріптерімен белгілеу қабылданды. Мысалы, егер S әрпімен барлық бүтін сандардың жиыны белгіленген болса, онда S аймағынан алынған Х айнымалысы қандай да бір бүтін сан болады. «Х айнымалысы S жиынынан өтеді» деп айтады, ал оның астарында Х айнымалысын S жиынының кез келген элементімен теңдестіре аламыз деген ой жатады. Егер бүтін жиыннан еркімізше таңдап алатын элементтерге қатысты пікір айтқымыз келсе, айнымалы ұғымын пайдаланған ыңғайлы. Мысалы, S жоғарыда айтылғандай бүтін сандар жиыны, ал Х пен Y – S аймағынан алынған айнымалылар болса, онда

формуласы кез келген екі бүтін санның қосындысы қосылғыштардың орнына қатысты болмайды деген жайттың символдық түрдегі жеңіл өрнектелуін көрсетеді. Оның дербес жағдайы

тұрақты сандары бар теңдігімен өрнектеледі; бірақ барлық сандар жұбы үшін дұрыс орындалатын жалпы ережені көрсету үшін айнымалылардың мәнін қабылдайтын символдарды қолдану керек.
Х айнымалысының S өзгеру аймағының сандар жиыны болуының қажеттілігі жоқ. Мысалы, S жазықтықтағы барлық дөңгелектердің жиыны болуы мүмкін; онда Х айнымалысы кез келген бір дөңгелекті өрнектейтін болады. Немесе S жазықтықтағы барлық тұйық көпбұрыштардың жиыны болуы мүмкін, онда Х – кез келген көпбұрыш болады. Сондай-ақ айнымалының өзгеру аймағындағы элементтер санының шексіз болуы да міндетті емес. Мысалы, Х –белгілі бір уақыттағы берілген қаланың S тұрғындарының ішіндегі кез келген адамды сипаттауы мүмкін. Немесе Х – бүтін санды 5-ке бөлгендегі мүмкін болатын қалдықтардың біреуін өрнектеуі мүмкін; соңғы жағдайда S аймағы бес саннан тұратын болады: 0, 1, 2, 3, 4.
Сандық айнымалы жағдайы
маңызды болады; бұл жағдайда әдетте кішкентай
х
әрпі қолданылады – бұл
кезде S
өзгеру аймағы нақты сандар
осінің қандай да бір  интервалы (аралық) болады. Бұл
жағдайда х
– қарастырылып тұрған
интервалда үздіксіз (немесе
нақты)
айнымалы дейді. Үздіксіз айнымалының
өзгеру аймағы шексіздікке дейін де созылуы мүмкін.
Мысалы, S
барлық оң нақты сандар
жиыны
интервалы (аралық) болады. Бұл
жағдайда х
– қарастырылып тұрған
интервалда үздіксіз (немесе
нақты)
айнымалы дейді. Үздіксіз айнымалының
өзгеру аймағы шексіздікке дейін де созылуы мүмкін.
Мысалы, S
барлық оң нақты сандар
жиыны  болуы мүмкін немесе бірі
қалмастан барлық нақты сандар жиыны болуы
мүмкін. Осындай әдіспен жазықтықтың немесе тіктөртбұрыштың әлде
дөңгелектің қандай да бір ішкі аймағының нүктелерін
өрнектейтін Х
айнымалысын қарастыра аламыз.
Жазықтықтың әрбір нүктесі қандай да бір осьтер жұбына қатысты
алынған өзінің
болуы мүмкін немесе бірі
қалмастан барлық нақты сандар жиыны болуы
мүмкін. Осындай әдіспен жазықтықтың немесе тіктөртбұрыштың әлде
дөңгелектің қандай да бір ішкі аймағының нүктелерін
өрнектейтін Х
айнымалысын қарастыра аламыз.
Жазықтықтың әрбір нүктесі қандай да бір осьтер жұбына қатысты
алынған өзінің  екі координатасымен
анықталатындықтан, көп жағдайда х
және
у нақты (үздіксіз)
айнымалылардың жұбымен жұмыстанады
дейді.
екі координатасымен
анықталатындықтан, көп жағдайда х
және
у нақты (үздіксіз)
айнымалылардың жұбымен жұмыстанады
дейді.
Х-тің әрбір мәніне басқа
бір Y
айнымалысының белгілі бір
мәнін сәйкестендіретін жағдайлар болуы мүмкін.
Онда Y
айнымалысы Х
айнымалысының функциясы деп
аталады. Y
айнымалысы X-пен байланысатын
тәсіл  («тең
Х-тен
F-ке» деп оқылады) символымен
өрнектеледі. Егер Х
айнымалысы S
жиынынан өтсе,
онда Y
айнымалысы басқа бір жиынды
өтеді, оны Т
деп алайық. Мысалы,
егер S
–
жазықтықтағы Х
үшбұрыштардың жиыны болса,
онда
(«тең
Х-тен
F-ке» деп оқылады) символымен
өрнектеледі. Егер Х
айнымалысы S
жиынынан өтсе,
онда Y
айнымалысы басқа бір жиынды
өтеді, оны Т
деп алайық. Мысалы,
егер S
–
жазықтықтағы Х
үшбұрыштардың жиыны болса,
онда  функциясы ретінде қарастырылып
отырған Х
үшбұрышының периметрінің
ұзындығын алуға болады; яғни Т
– барлық оң сандар жиыны
болады. Әр түрлі
функциясы ретінде қарастырылып
отырған Х
үшбұрышының периметрінің
ұзындығын алуға болады; яғни Т
– барлық оң сандар жиыны
болады. Әр түрлі  мен
мен
 екі үшбұрыштың
периметрлері бірдей болуы мүмкін екенін атап кетейік,
яғни
екі үшбұрыштың
периметрлері бірдей болуы мүмкін екенін атап кетейік,
яғни  болса да
болса да
 теңдігі орындалуы
мүмкін. S
жазықтығын қандай да бір
басқа Т
жазықтығына проекциялық
түрлендіру S
жазықтығының
әрбір Х
нүктесіне
теңдігі орындалуы
мүмкін. S
жазықтығын қандай да бір
басқа Т
жазықтығына проекциялық
түрлендіру S
жазықтығының
әрбір Х
нүктесіне
 функционалдық символы
арқылы өрнектелетін белгілі бір ережеге сәйкес
Т
жазықтығының тек қана
бір Y
нүктесін сәйкестікке
қояды.Алдыңғы мысалға қарағанда соңғы мысалда ылғи
да
функционалдық символы
арқылы өрнектелетін белгілі бір ережеге сәйкес
Т
жазықтығының тек қана
бір Y
нүктесін сәйкестікке
қояды.Алдыңғы мысалға қарағанда соңғы мысалда ылғи
да  теңсіздігі орындалады,
егер
теңсіздігі орындалады,
егер  болса, осы
орайда S
жазықтығының Т
жазықтығына
бейнеленуі өзара
біртекті деп
айтамыз.
болса, осы
орайда S
жазықтығының Т
жазықтығына
бейнеленуі өзара
біртекті деп
айтамыз.
Үздіксіз айнымалының функциялары көп жағдайда алгебралық өрнектер арқылы анықталады. Мысал ретінде төмендегі функцияларды алуға болады:

Бұл өрнектердің біріншісі және
үшіншісінде х
барлық нақты сандар жиынында
өте алады, ал екінші мысалда х
0-ден басқа барлық нақты
сандар жиынында өте алады (0 мәні алынып тасталады,
себебі  символы сан бола
алмайды).
символы сан бола
алмайды).
п
санының жай
көбейткіштерінің  саны
п
функциясы болады
және п
натурал сандар жиынынан өтіп
шығады. Жалпы,
саны
п
функциясы болады
және п
натурал сандар жиынынан өтіп
шығады. Жалпы,  сандарының кез келген
реттілігін қандай да бір
сандарының кез келген
реттілігін қандай да бір  функциясының мәндерінің жиыны
деп қабылдауға болады және бұл жердегі тәуелсіз айнымалының өзгеру
аймағы натурал сандар жиыны болады. Жазуды қысқарту үшін
реттіліктің п-ші
мүшесін
функциясының мәндерінің жиыны
деп қабылдауға болады және бұл жердегі тәуелсіз айнымалының өзгеру
аймағы натурал сандар жиыны болады. Жазуды қысқарту үшін
реттіліктің п-ші
мүшесін  анығырақ функционалдық
белгілеуден гөрі
анығырақ функционалдық
белгілеуден гөрі  символымен белгілеу
қабылданған. Төмендегі өрнектер п
бүтін айнымалының функциялары
болып табылады:
символымен белгілеу
қабылданған. Төмендегі өрнектер п
бүтін айнымалының функциялары
болып табылады:



 қатынасы
берілсін; Х
айнымалысын тәуелсіз
айнымалы, ал
C
айнымалысының
мәні Х
мәніне тәуелді
болғандықтан C
айнымалысын тәуелді
айнымалы деп атау
келісілген.
қатынасы
берілсін; Х
айнымалысын тәуелсіз
айнымалы, ал
C
айнымалысының
мәні Х
мәніне тәуелді
болғандықтан C
айнымалысын тәуелді
айнымалы деп атау
келісілген.
Х айнымалысының барлық мәндеріне C айнымалысының бір ғана мәні сәйкес келетін, яғни Т жиыны бір ғана элементтен тұратын жағдай болып қалуы мүмкін. Онда біз дербес жағдаймен кездесеміз, бұл жағдайда C айнымалысы өзгермейді, яғни C – тұрақты мән болады (тұрақты немесе константа). Бұл жағдайды функцияның жалпы ұғымына қосып жібереміз.
Функционалды тәуелділік ұғымы тек қана «таза» математикада емес, сонымен қатар оның практикалық қосымшаларында да маңызды болып келеді. Физикалық заңдар кейбір шамалардың өзгеріске ұшыра алатын басқа шамаларға тәуелділігін өрнектейтін тәсіл болып табылады. Мысалы, тербелмелі сымның шығаратын дыбысының биіктігі сымның ұзындығына, салмағына және оның керілу дәрежесіне тәуелді; атмосфераның қысымы биіктікке тәуелді; оқтың энергиясы оның массасы мен жылдамдығына тәуелді. Физиканың міндеті осыған ұқсас тәуелділіктердің табиғатын дәл немесе жорамалдап анықтау болып табылады.
Функция ұғымы арқылы қозғалыстың математикалық тұрғыдан алғандағы дәл сипаттамасын беруге болады. Қозғалып келе жатқан бөлшек кеңістіктің x, y, z тікбұрышты координаталы қандай да бір нүктесінде шоғырланған және t айнымалысы уақытты өлшейді деп елестетіп көрсек, онда бөлшектің қозғалысы уақыт функциясы ретіндегі x, y, z координаталарымен толық анықталады:
 .
.
Бұның мысалы ретінде тек қана ауырлық күші әсер ететін бөлшектің тік еркін түсуін алуға болады: бұл жағдайда төмендегідей қатынастарды аламыз:

мұндағы g – ауырлық күшінің үдеуі. Егер бөлшек х, у жазықтығында бірлік шеңбер бойымен біртекті айналатын болса, онда оның қозғалысы

функцияларымен сипатталады, мұндағы ω – тұрақты сан (айналудың бұрыштық жылдамдығы).
Математикалық функцияны айнымалы шамалардың өзара тәуелділігін басқаратын заң ретінде ғана қабылдау керек. Функция ұғымы тәуелді және тәуелсіз айнымалылардың арасында «себеп пен салдарға» жақын байланыстың бар болуын тұспалдамайды. Бірақ күнделікті сөйлеуде «функционалды тәуелділік» термині осы соңғы мағынада қолданылып жүрсе де, ондай философиялық талдаудан ойымызды аулақ ұстаймын. Осылайша, мысалы, тұрақты температурада қандай да бір тұйық қабықта жинақталған газға қатысты Бойль заңы газдың р қысымы мен оның v көлемінің көбейтіндісі с-ға тең тұрақты шама болады деп пайымдайды (соңғы мән, өз кезегінде, температураға тәуелді):
 .
.
Бұл қатынасты р-ға қатысты да, v-ға қатысты да шешуге болады:
 немесе
немесе 
бұл жағдайда көлемнің өзгеруі қысымның өзгеруінің «себебі» деп немесе қысымның өзгеруі көлемнің өзгеруінің «себебі» деп қарастыруға болмайды. Математик үшін өз қарастырып отырған екі айнымалы шамалардың арасындағы қатынастың (байланыстың) түрі ғана маңызды болады. [2]
Функция ұғымына деген
көзқарастың математиктер мен физиктерде әр түрлі екенін айта кеткен
жөн. Математиктер әдетте қатынастың
заңына, тәуелді
u
айнымалысының мәнін табу үшін
тәуелсіз х
айнымалысына қолданатын
математикалық амалға көңіл аударады. Бұл
мәнмәтінде  символы –
математикалық
амалдың символы;
символы –
математикалық
амалдың символы;
 мәні
– х
санына
мәні
– х
санына
 амалын қолданудың
нәтижесі болады. Басқаша қарағанда, физик көп
жағдайда х
мәнінен
u
мәнін шығаратын математикалық
үрдіске емес, u шамасының
өзіне көңіл аударады. Мысалы,
дененің қозғалысына қатысты ауаның u
кедергісі
қозғалыстың v
жылдамдығына тәуелді болады
және u
мәнін есептеудің математикалық
формуласы берілу немесе берілмеуіне қарамастан, оны эксперименттік
түрде есептеп шығаруға болады. Физик үшін
арнайы
амалын қолданудың
нәтижесі болады. Басқаша қарағанда, физик көп
жағдайда х
мәнінен
u
мәнін шығаратын математикалық
үрдіске емес, u шамасының
өзіне көңіл аударады. Мысалы,
дененің қозғалысына қатысты ауаның u
кедергісі
қозғалыстың v
жылдамдығына тәуелді болады
және u
мәнін есептеудің математикалық
формуласы берілу немесе берілмеуіне қарамастан, оны эксперименттік
түрде есептеп шығаруға болады. Физик үшін
арнайы  математикалық формуласы емес,
іс жүзіндегі нақты кедергі маңыздырақ болады. Математиканы әдетте
физикаға немесе инженерлік іске қолданатын адамдардың көзқарасы осындай
болады. Математикалық анализдің кейбір жоғары бөлімдерінде
шатастырып алмау үшін
математикалық формуласы емес,
іс жүзіндегі нақты кедергі маңыздырақ болады. Математиканы әдетте
физикаға немесе инженерлік іске қолданатын адамдардың көзқарасы осындай
болады. Математикалық анализдің кейбір жоғары бөлімдерінде
шатастырып алмау үшін  символының
астарында u-дың мәнін алу
үшін х-ке
қолданылатын
символының
астарында u-дың мәнін алу
үшін х-ке
қолданылатын  амалы ма әлде басқа
бір z
айнымалысына басқаша түрде
тәуелді болып қарастырыла алатын u
шамасының өзі ме екенін
анықтап алу қажет. Мысалы, дөңгелектің
ауданы
амалы ма әлде басқа
бір z
айнымалысына басқаша түрде
тәуелді болып қарастырыла алатын u
шамасының өзі ме екенін
анықтап алу қажет. Мысалы, дөңгелектің
ауданы функциясымен беріледі,
мұндағы х
– дөңгелектің радиусы, бірақ
оны былай да жазуға болады:
функциясымен беріледі,
мұндағы х
– дөңгелектің радиусы, бірақ
оны былай да жазуға болады:  , мұндағы
z
– шеңбердің ұзындығы.
[3]
, мұндағы
z
– шеңбердің ұзындығы.
[3]
Бір тәуелсіз айнымалысы бар
математикалық функцияның ең жеңіл түрі ретінде
 тұрақты
«коэффициенттері» бар төмендегідей көпмүшелерді (полиномдарды) алуға
болады:
тұрақты
«коэффициенттері» бар төмендегідей көпмүшелерді (полиномдарды) алуға
болады:
 .
.
Одан кейін көпмүшелердің қатынасы болып табылатын төмендегідей рационал функцияларды:

ал олардан
кейін  жазықтығындағы бірлік шеңбер
арқылы жақсы анықталатын
жазықтығындағы бірлік шеңбер
арқылы жақсы анықталатын  және
және
 тригонометриялық
функцияларды жатқызуға болады.
Егер
тригонометриялық
функцияларды жатқызуға болады.
Егер  нүктесі осы шеңбер бойымен
қозғалса және егер х
– оң
таңбалы х
осін
ОР
радиусымен беттесетіндей етіп
бұру бұрышын анықтайтын бағытталған бұрыш болса,
онда
нүктесі осы шеңбер бойымен
қозғалса және егер х
– оң
таңбалы х
осін
ОР
радиусымен беттесетіндей етіп
бұру бұрышын анықтайтын бағытталған бұрыш болса,
онда  пен
пен
 Р нүктесінің координаталары
болады:
Р нүктесінің координаталары
болады:  . [4]
. [4]
1.2. Функцияның берілу тәсілдері
f
функциясын беру дегеніміз
– х
аргументінің әрбір мәніне оған
сәйкес  функциясының мәнін табудың
жолын көрсету. Функцияны берудің үш негізгі тәсілі
бар: аналитикалық,
кестелік және
графиктік.
функциясының мәнін табудың
жолын көрсету. Функцияны берудің үш негізгі тәсілі
бар: аналитикалық,
кестелік және
графиктік.
1) Аналитикалық тәсіл. Айнымалы шамалардың арасындағы тәуелділік аргументтің берілген мәніне сәйкес болатын функцияның мәнін алу үшін орындайтын іс-әрекеттерді көрсететін формула арқылы беріледі.
Мысалдар қарастырайық.
-
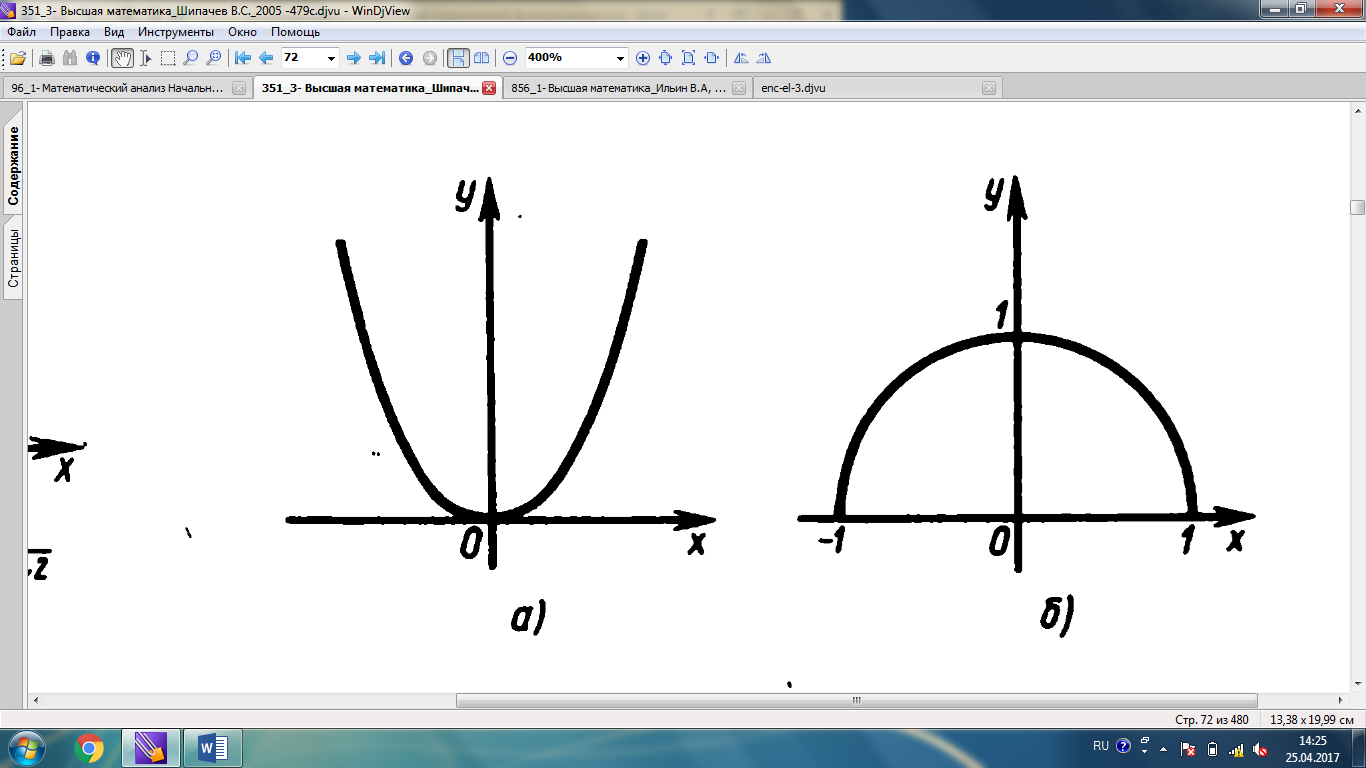
 формуласы анықталу
аймағы
формуласы анықталу
аймағы  сандық осі болатын, ал
мәндерінің жиыны
сандық осі болатын, ал
мәндерінің жиыны  жартытүзу болатын функцияны
береді (1-сурет).
жартытүзу болатын функцияны
береді (1-сурет). -
 формуласы анықталу
аймағы
формуласы анықталу
аймағы  кесіндісі болатын, ал
мәндерінің жиыны
кесіндісі болатын, ал
мәндерінің жиыны  кесіндісі болатын функцияны
береді (2-сурет).
кесіндісі болатын функцияны
береді (2-сурет). -

Бұл функция бірнеше формула
арқылы беріліп тұр. Ол сан осінің тұтас
бойында анықталады, ал оның мәндерінің
жиыны үш саннан тұрады: –1, 0 және +1
(3-сурет).
анықталады, ал оның мәндерінің
жиыны үш саннан тұрады: –1, 0 және +1
(3-сурет).
-
 формуласы
әрбір п
натурал санына (яғни бүтін оң
санға)
формуласы
әрбір п
натурал санына (яғни бүтін оң
санға)  санын сәйкестікке қояды.
Мысалы, егер
санын сәйкестікке қояды.
Мысалы, егер  болса,
онда
болса,
онда  болады.
Осылайша,
болады.
Осылайша,  формуласы анықталу
аймағы
формуласы анықталу
аймағы  болатын, ал мәндерінің
жиыны
болатын, ал мәндерінің
жиыны болатын функцияны береді
(4-сурет).
болатын функцияны береді
(4-сурет).
1-сурет 2-сурет 3-сурет

4-сурет
-
Дирихле функциясы

Бұл функция сан осінің тұтас
бойында  анықталады, ал мәндерінің
жиыны екі саннан тұрады: 0 және 1.
анықталады, ал мәндерінің
жиыны екі саннан тұрады: 0 және 1.
Дирихле функциясын графиктік түрде көрсету мүмкін емес екенін ескерте кетейік. [5]
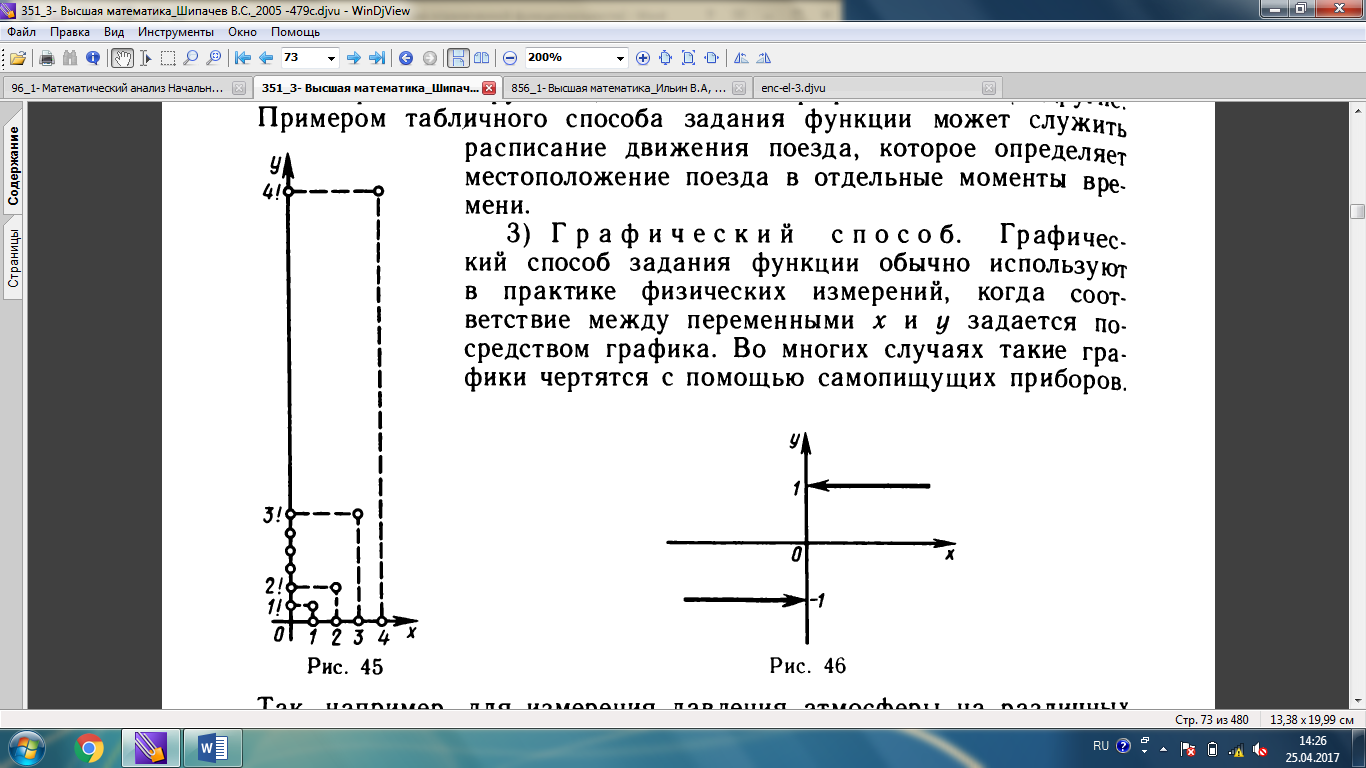
2) Кестелік тәсіл.Төмендегі кестені келтірейік:
|
х |
0 |
0,1 |
0,2 |
3 |
0,6 |
4 |
0,8 |
1,5 |
2 |
|
у |
–1 |
10 |
1 |
–2 |
–8 |
0,5 |
–2 |
5 |
7 |
Кестенің бірінші жолында тұрған әрбір х-ке оның астында тұрған кестенің екінші жолындағы у-тің мәнін сәйкестікке қойып, алынған функция кесте түрінде берілді деп айтамыз. Бұл функцияның анықталу облысы кестенің бірінші жолында тұрған тоғыз х санынан тұратын жиын болады, ал мәндерінің жиыны кестенің екінші жолында тұрған тоғыз у санынан тұратын жиын болады.
Функцияны кесте арқылы беру үшін аргументтің мәндерінің саны шекті болу керек. Кестелерді көп жағдайда функцияны беру үшін қолданады. Мысалы, тригонометриялық функциялардың кестелері, логарифмдер кестесі және т.б. Функцияны кесте арқылы берудің мысалы ретінде пойыздың жүру кестесін алуға болады, ол кесте пойыздың қандай да бір уақыт мезетіндегі орнын анықтайды.
3) Графиктік тәсіл. Функцияны графиктік тәсілмен беруді әдетте х пен у айнымалыларының сәйкестігі график арқылы көрсетілетін физикалық шамаларды өлшеу тәжірибесінде қолданады. Көп жағдайда мұндай графиктер өздігінен жазатын арнайы құрылғылар арқылы сызылады. Мысалы, атмосфераның әр түрлі биіктіктегі қысымын өлшеу үшін арнайы өздігінен жазатын құрылғы – барографты қолданады, бұл құрылғы биіктікке сәйкес қысымның өзгеруін жылжымалы таспаға қисық сызық түрінде салады. [6]
1.3. Функциялар классификациясы
 тұрақты
функциясы,
тұрақты
функциясы,  (α
– кез келген сан) дәрежелік
функциясы,
(α
– кез келген сан) дәрежелік
функциясы,  көрсеткіштік
функциясы,
көрсеткіштік
функциясы,  логарифмдік
функциясы,
логарифмдік
функциясы,  тригонометриялық функциялары
және
тригонометриялық функциялары
және  кері тригонометриялық
функциялары қарапайым элементар
функциялар деп
аталады.
кері тригонометриялық
функциялары қарапайым элементар
функциялар деп
аталады.
Элементар функцияларға саны шектеулі арифметикалық амалдарды орындау арқылы, сондай-ақ осы функциялардың суперпозициясы (немесе қабаттастыру) арқылы шығатын функциялар элементар функциялар класын құрайды. Элементар функциялардың мысалдары:

 т.с.с.
т.с.с.
Элементар функциялардың төмендегідей классификациясы бар:
1)
 – бүтін сан,
ал
– бүтін сан,
ал  –кез келген сандар –
коэффициенттер болатын
–кез келген сандар –
коэффициенттер болатын

түріндегі функция бүтін рационал функция немесе т дәрежелі алгебралық көпмүше деп аталады. Бірінші дәрежелі көпмүше сызықтық функция деп аталады.
2) Екі бүтін рационал функциялардың қатынасы түрінде берілген

функциясы бөлшек рационал функция деп аталады.
Бүтін рационал және бөлшек рационал функциялардың жиынтығы рационал функциялар класын құрайды.
3) Бүтін және бөлшек көрсеткішті дәрежелік функцияларға төрт арифметикалық амалдар мен саны шектеулі суперпозицияларды орындау арқылы алынған және рационал түрге жатпайтын функциялар иррационал функциялар деп аталады.
Мысалы,
 т.с.с.
т.с.с.
4) Рационал немесе иррационал
функцияға жатпайтын кез келген функция
трансценденттік
функция деп аталады. Олар,
мысалы, 
 және т.б. функциялары.
[7]
және т.б. функциялары.
[7]
1.4. Функцияның графигі. Кері функциялар
Көп жағдайда функцияның сипаты
қарапайым график арқылы түсінікті түрде көрсетіледі.
Егер  – өзара перпендикуляр екі
оське қатысты жазықтықтағы координаталар болса,
онда
– өзара перпендикуляр екі
оське қатысты жазықтықтағы координаталар болса,
онда

сызықтық функциялары түзу сызықтармен кескінделеді;

квадраттық функциялары – параболалармен;

функциясы – гиперболамен
кескінделеді және т.с.с. Қандай да бір
 функциясының графигі
функциясының графигі  координаталары
координаталары  теңдеуі арқылы байланысқан
жазықтықтың барлық нүктелерінен тұрады.
теңдеуі арқылы байланысқан
жазықтықтың барлық нүктелерінен тұрады.
 функциялары 5-суретте
және 6-суретте графиктік түрде көрсетілді. Бұл
графиктер х
өзгерген кезде функциялардың
қалай өсіп немесе кеміп тұрғанын көрнекі түрде көрсетіп
тұр.
функциялары 5-суретте
және 6-суретте графиктік түрде көрсетілді. Бұл
графиктер х
өзгерген кезде функциялардың
қалай өсіп немесе кеміп тұрғанын көрнекі түрде көрсетіп
тұр.
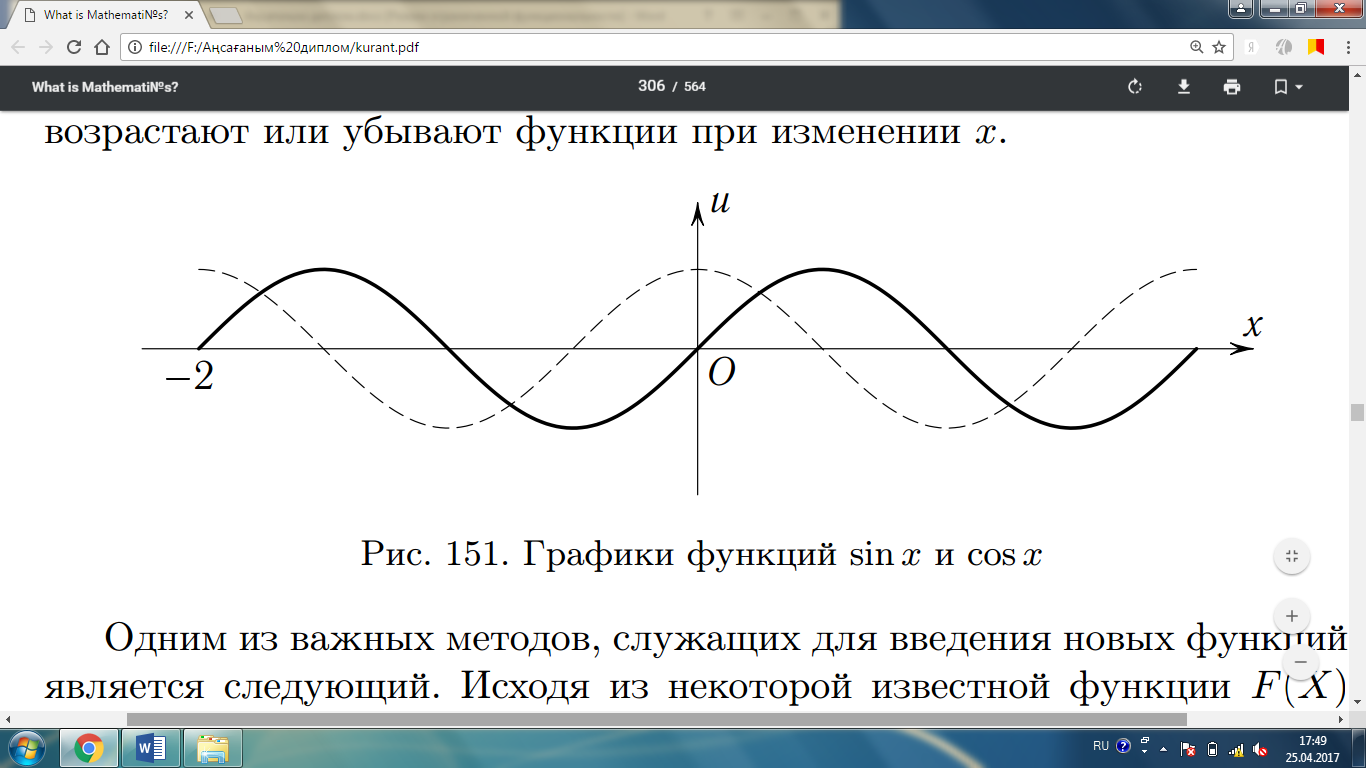
5-сурет.
 және
және  функцияларының
графиктері
функцияларының
графиктері
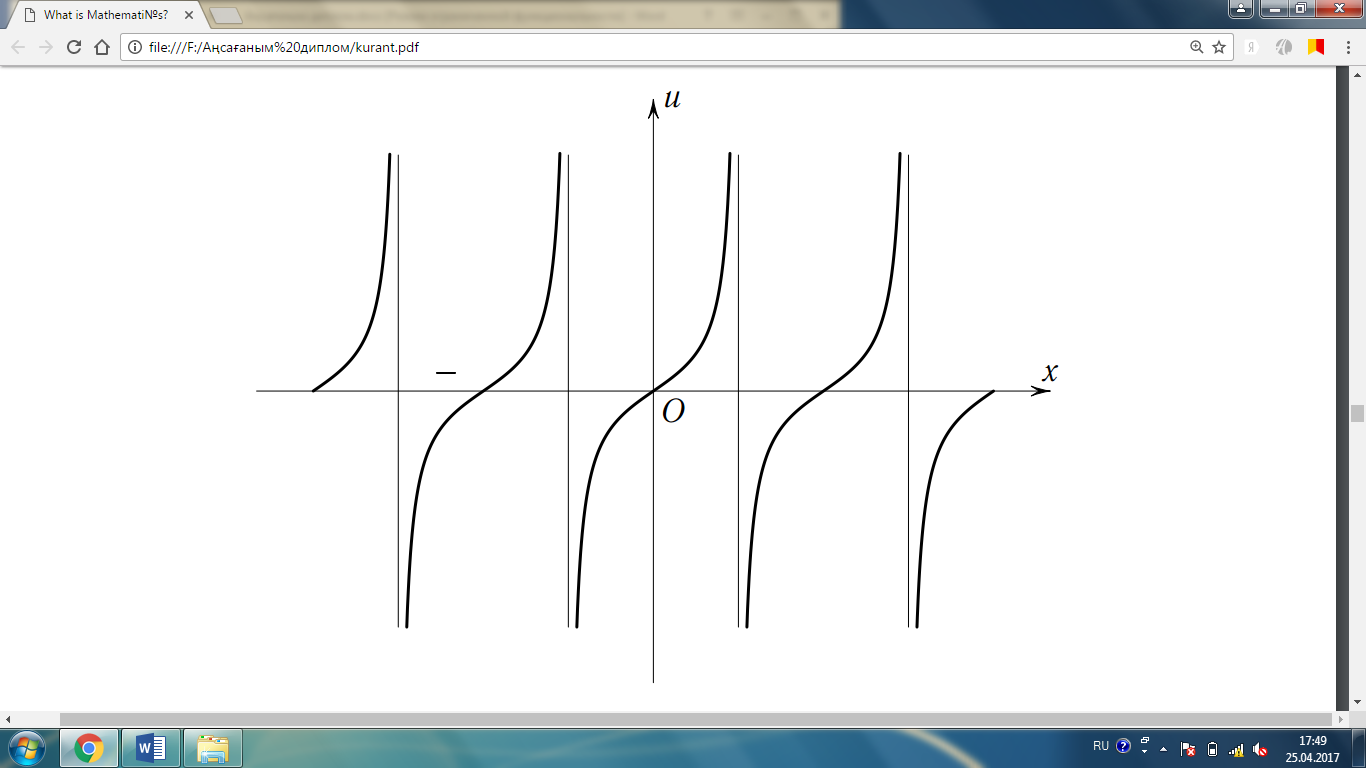
6-сурет.
 функциясының
графигі
функциясының
графигі
Жаңа функцияларды алудың
маңызды әдістердің бірі келесі әдіс болады. Қандай да бір
белгілі  функциясы
арқылы
функциясы
арқылы  теңдеуін
Х
айнымалысы Y-ке қатысты функция болатындай
етіп
теңдеуін
Х
айнымалысы Y-ке қатысты функция болатындай
етіп

деп өрнектеп шешіп көруге
болады. Онда  функциясы
функциясы
 функциясына
қатысты кері
функция деп аталады. Бұл үрдіс
егер
функциясына
қатысты кері
функция деп аталады. Бұл үрдіс
егер  функциясы
Х-тің өзгеру
аймағын Y-тің өзгеру аймағына өзара
бейнелейтін болса ғана, яғни
функциясы
Х-тің өзгеру
аймағын Y-тің өзгеру аймағына өзара
бейнелейтін болса ғана, яғни  теңсіздігі өзінің
артынан
теңсіздігі өзінің
артынан  теңсіздігін ала келетін болса
ғана нәтижеге алып келеді. Тек қана осы шарт
негізінде Y-тің әрбір
мәніне Х-тің бір ғана мәні сәйкес
келетін болады. Осы жерде жоғарыда келтірілген мысалды еске
түсіруге болады. Ол мысалда тәуелсіз
Х
айнымалысының рөлінде
жазықтықтағы кез келген үшбұрыш, ал
теңсіздігін ала келетін болса
ғана нәтижеге алып келеді. Тек қана осы шарт
негізінде Y-тің әрбір
мәніне Х-тің бір ғана мәні сәйкес
келетін болады. Осы жерде жоғарыда келтірілген мысалды еске
түсіруге болады. Ол мысалда тәуелсіз
Х
айнымалысының рөлінде
жазықтықтағы кез келген үшбұрыш, ал  функциясының рөлінде оның
периметрі болған еді. Үшбұрыштардың
S
жиынының оң
сандардың Т
жиынына бейнеленуі өзара дәл
емес екені айқын, себебі периметрі бірдей санға тең болатын
үшбұрыштардың шексіз көп саны бар. Сонымен, бұл
жағдайда
функциясының рөлінде оның
периметрі болған еді. Үшбұрыштардың
S
жиынының оң
сандардың Т
жиынына бейнеленуі өзара дәл
емес екені айқын, себебі периметрі бірдей санға тең болатын
үшбұрыштардың шексіз көп саны бар. Сонымен, бұл
жағдайда  қатынасы кері функцияны
анықтай алмайды. Басқа жағдайда, п
барлық бүтін
сандардың S
жиынынан өтетін,
ал т
оң
сандардың Т
жиынын
өтетін
қатынасы кері функцияны
анықтай алмайды. Басқа жағдайда, п
барлық бүтін
сандардың S
жиынынан өтетін,
ал т
оң
сандардың Т
жиынын
өтетін  функциясы екі жиынның арасында
дәл сәйкестікті анықтайды және
функциясы екі жиынның арасында
дәл сәйкестікті анықтайды және  кері функциясы анықталатын
болады. Берілген дәл сәйкестіктің басқа мысал
ретінде
кері функциясы анықталатын
болады. Берілген дәл сәйкестіктің басқа мысал
ретінде

функциясын келтірейік. х айнымалысы барлық нақты сандар жиынынан өтіп шыққанда у айнымалысы да барлық нақты сандар жиынынан әрбір мәнді бір рет және тек қана бір рет қабылдай отырып өтіп шығады. Бұл мысалда анықталған кері функция

түрінде болады.

функциясының жағдайында кері
функция дәл анықталмайды. Расында да,
 болғандықтан, у-тің әрбір оң
мәніне х-тің әр
түрлі екі мәні сәйкес келеді. Бірақ
егер
болғандықтан, у-тің әрбір оң
мәніне х-тің әр
түрлі екі мәні сәйкес келеді. Бірақ
егер  символының астында
квадраты х-ке тең
болатын оң
сан болады деп ойласақ (көп
жағдайда осылай болады), онда
символының астында
квадраты х-ке тең
болатын оң
сан болады деп ойласақ (көп
жағдайда осылай болады), онда

кері функциясы табылады, егер х пен у мәндерінің тек қана оң мәндерін қарастырамыз деп келісіп алсақ. [8]
Кері функцияның бар болуын
берілген функцияның графигіне қарап бірден анықтауға болады. кері
функция дәл анықталып табылады, егер
у-тің әрбір
мәніне х-тің бір ғана мәні сәйкес
келетін болса. Геометриялық тұрғыдан қарағанда алдыңғы сөйлем
графикті бір нүктеден көп жерде қиып өтетін
жәнех
осіне параллель болатын түзу
жоқ деген мағынаны білдіреді. Әрине мұндай жағдай мүмкін болады,
егер  функциясы монотонды, яғни
немесе барлық уақытта өспелі, немесе, керісінше, барлық уақытта
кемімелі (х
өскен кезде) болса. Мысалы,
егер
функциясы монотонды, яғни
немесе барлық уақытта өспелі, немесе, керісінше, барлық уақытта
кемімелі (х
өскен кезде) болса. Мысалы,
егер  функциясы барлық жерде өспелі
болса, онда
функциясы барлық жерде өспелі
болса, онда  болғанда барлық
уақытта
болғанда барлық
уақытта  болады.
Демек, у-тің берілген
мәніне
болады.
Демек, у-тің берілген
мәніне  болатындай х-тің бірден аспайтын мәні бар
және кері функция дәл анықталатын болады.
болатындай х-тің бірден аспайтын мәні бар
және кері функция дәл анықталатын болады.
 кері функциясының
графигі берілген графиктегі үзік сызыққа қатысты симметрия арқылы
алынады (7-сурет); бұл жағдайда х
және
у
осьтерінің орындары
ауыстырылады.
кері функциясының
графигі берілген графиктегі үзік сызыққа қатысты симметрия арқылы
алынады (7-сурет); бұл жағдайда х
және
у
осьтерінің орындары
ауыстырылады.
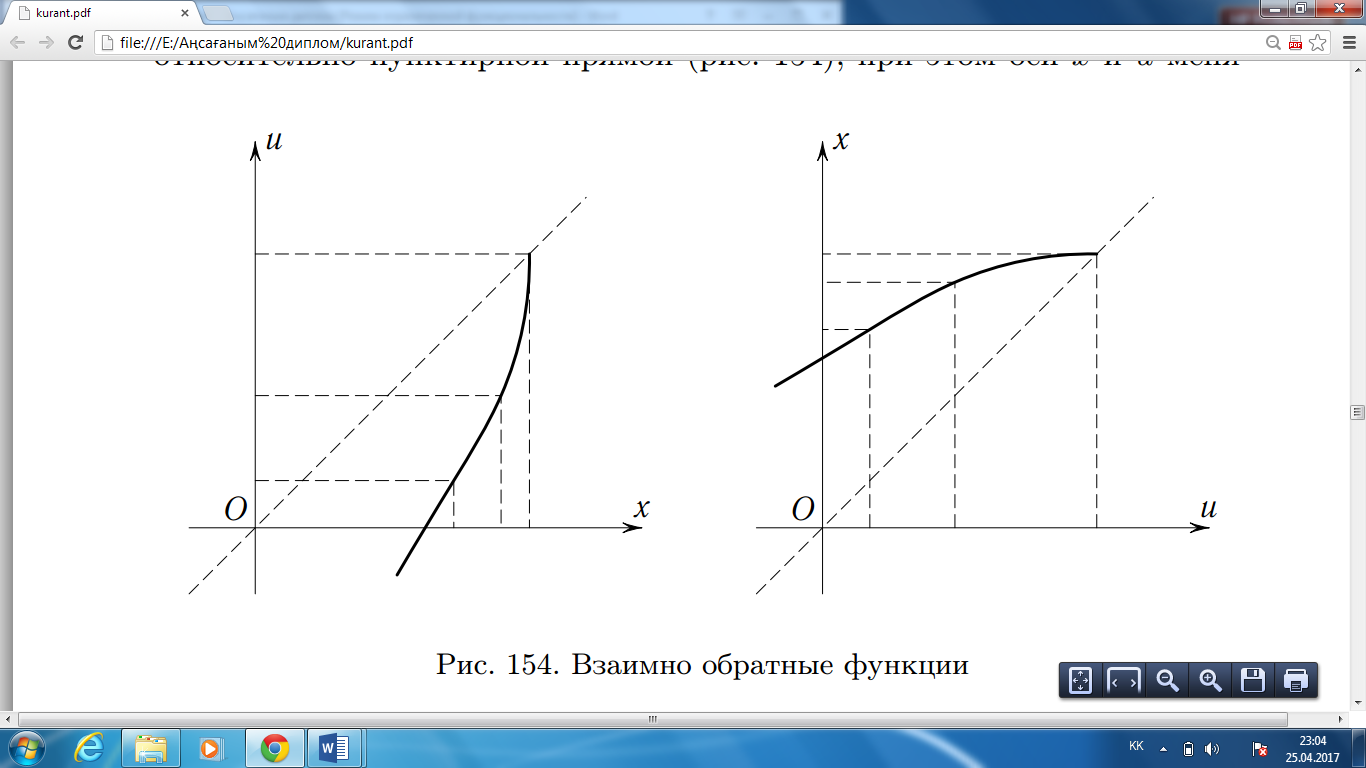
7-сурет. Өзара кері функциялар
Графиктің жаңа орналасуы х-ті у-ке қатысты функция ретінде кескіндейді. Негізгі орналасуында график у-тің мәнін көлденең орналасқан х осінен алғандағы биіктік деп көрсетеді, ал симметриядан кейін алынған график х-тің мәні көлденең орналасқан у осінен алғандағы биіктік деп көрсетеді.
Осы бөлімшедегі пайымдауларды

функциясы негізіндегі мысалда
кескіндеуге болады. бұл функция  аралығында монотонды болады (6-сурет): барлық
уақытта х-пен бірге
өсетін у-тің
мәндері
аралығында монотонды болады (6-сурет): барлық
уақытта х-пен бірге
өсетін у-тің
мәндері  -тен
-тен
 -ке дейін өзгереді;
бұдан
-ке дейін өзгереді;
бұдан

кері
функциясы у-тің барлық мәндері үшін
анықталатыны шығады. Мұндай функцияны
 деп белгілейді.
Осылайша,
деп белгілейді.
Осылайша,  болады,
себебі
болады,
себебі .
.
 графигі 8-суретте
көрсетілген. [9]
графигі 8-суретте
көрсетілген. [9]
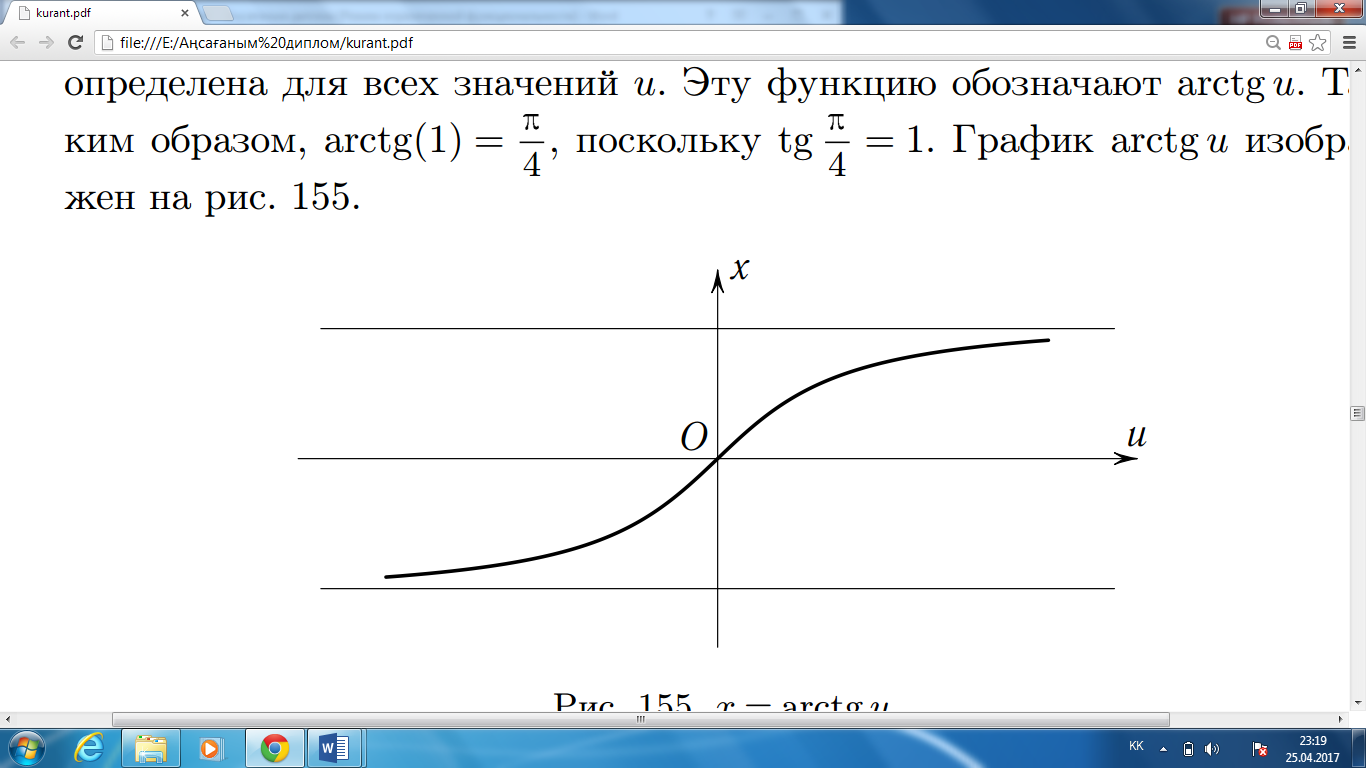
8-сурет.

1.5. Күрделі функциялар
Екі немесе одан да көп мәліметтерден жаңа функцияларды алудың екінші маңызды әдісі күрделі функцияларды құрастыру («композиция») әдісі болып табылады. Мысалы,

функциясын

екі жай функциясынан «құрастырып», мына түрде жазуға болады:

Дәл осылай,

функциясы

үш функциядан құрастырылады және оны

деп жазуға болады.

функциясы

екі функциядан
құрастырылды.  функциясы
функциясы
 болғанда анықталмайды,
себебі
болғанда анықталмайды,
себебі  мәнінде
мәнінде
 өрнегінің мәні жоқ. Бұл
тамаша функцияның графигі синустың графигімен байланысты болып
келеді.
өрнегінің мәні жоқ. Бұл
тамаша функцияның графигі синустың графигімен байланысты болып
келеді.  болғанда
болғанда
 болатынын білеміз,
мұндағы k
– кез келген оң немесе теріс
бүтін сан. Одан басқа,
болатынын білеміз,
мұндағы k
– кез келген оң немесе теріс
бүтін сан. Одан басқа,

мұндағы k – кез келген бүтін сан. Бұдан

шығады.
Егер  мәнін тізбектей қоя берсек,
бұл бөлшектердің бөлімі шексіз арта
береді.
мәнін тізбектей қоя берсек,
бұл бөлшектердің бөлімі шексіз арта
береді.
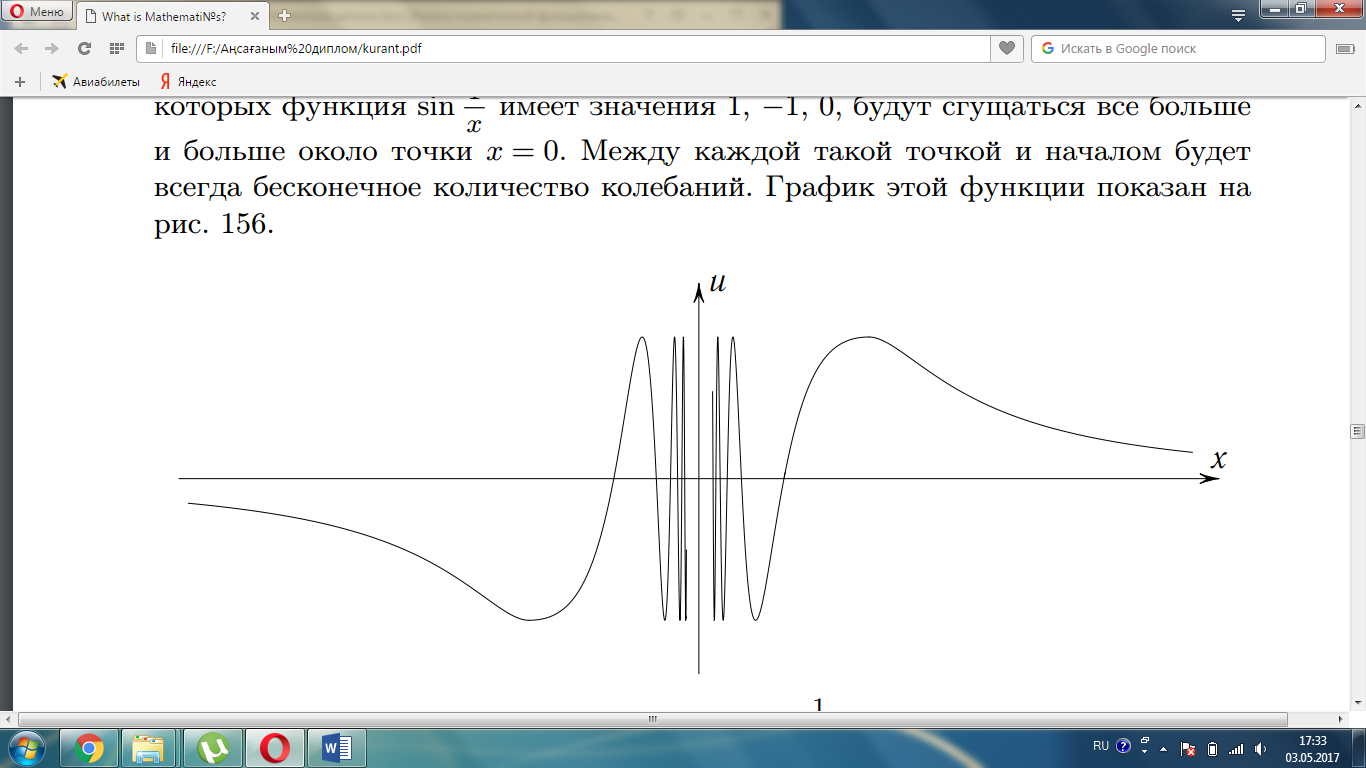
9-сурет.

Демек,
 функциясы 1, –1, 0
мәндеріне ие болатын х-тің
мәндері
функциясы 1, –1, 0
мәндеріне ие болатын х-тің
мәндері  нүктесінің айналасында
шоғырлана береді. Осындай әрбір нүкте мен басының арасында шексіз
көп тербелістер болады. Бұл функцияның графигі 9-суретте
көрсетілген. [10]
нүктесінің айналасында
шоғырлана береді. Осындай әрбір нүкте мен басының арасында шексіз
көп тербелістер болады. Бұл функцияның графигі 9-суретте
көрсетілген. [10]
1.6. Функцияның шегі
-
 болғандағы функцияның
шегі. Айталық,
болғандағы функцияның
шегі. Айталық, функциясы қандай да
бір Х
шексіз жиынында анықталған
болсын, ал
функциясы қандай да
бір Х
шексіз жиынында анықталған
болсын, ал  нүктесі –
шексіз
нүктесі –
шексіз  түзуінің нүктесі
және Х
жиынына тиісті болмайтын,
бірақ
түзуінің нүктесі
және Х
жиынына тиісті болмайтын,
бірақ  нүктесінің кез
келген δ
аймағында
Х
жиынының
нүктесінің кез
келген δ
аймағында
Х
жиынының
 нүктесінен өзге
нүктелері табылатын қасиетке ие болатын нүкте
болсын.
нүктесінен өзге
нүктелері табылатын қасиетке ие болатын нүкте
болсын.
Мысалы,
Х
жиыны
ретінде  интервалын алуға болады; бұл
жағдайда
интервалын алуға болады; бұл
жағдайда  нүктесі интервалдың шекаралық
нүктесі болғандықтан, интервал ішіне кірмейді,
бірақ
нүктесі интервалдың шекаралық
нүктесі болғандықтан, интервал ішіне кірмейді,
бірақ  нүктесінің кез
келген δ
аймағында берілген интервалдың
нүктелері табылады.
нүктесінің кез
келген δ
аймағында берілген интервалдың
нүктелері табылады.
 функциясы
берілген Х
жиынының басқа мысалы
ретінде
функциясы
берілген Х
жиынының басқа мысалы
ретінде  нүктесі алынып
тасталған
нүктесі алынып
тасталған  интервалына тиісті болатын
барлық рационал сандар жиынын алуға
болады.
интервалына тиісті болатын
барлық рационал сандар жиынын алуға
болады.
Кез
келген  үшін
үшін
 нүктесі алынып
тасталған
нүктесі алынып
тасталған  интервалын
интервалын  нүктесінің
тесілген δ
аймағы деп аталатынын ескерте
кетейік.
нүктесінің
тесілген δ
аймағы деп аталатынын ескерте
кетейік.
Х
жиынынан
 нүктесінен өзге
және
нүктесінен өзге
және  нүктесіне
шоғырланатын
нүктесіне
шоғырланатын

тізбегін алайық. Бұл тізбектің нүктелеріндегі функцияның мәндері де

сандық тізбекті құрайды және соңғы тізбектің шегінің бар болуы туралы сұрақ қоюға болады.
1-анықтама. А
саны  функциясының
функциясының  (немесе
(немесе  ) нүктесіндегі шегі деп
аталады, егер х аргументінің
) нүктесіндегі шегі деп
аталады, егер х аргументінің  нүктесінен
өзге
нүктесінен
өзге  нүктесіне шоғырланатын кез
келген
нүктесіне шоғырланатын кез
келген тізбегі үшін функцияның
сәйкес мәндерінің
тізбегі үшін функцияның
сәйкес мәндерінің  тізбегі А санына
жинақталатын болса.
тізбегі А санына
жинақталатын болса.
Символдық түрде ол былай
жазылады:  .
.
 функциясының
функциясының  нүктесінде тек бір ғана шегі
болады. Бұл ұйғарым
нүктесінде тек бір ғана шегі
болады. Бұл ұйғарым  тізбегінің тек бір ғана шегі
болады дегеннен шығады.
тізбегінің тек бір ғана шегі
болады дегеннен шығады.
Мысалдар қарастырайық.
-
 функциясының шегі сан
осінің кез келген
функциясының шегі сан
осінің кез келген  нүктесінде бар болады. Расында
да, егер
нүктесінде бар болады. Расында
да, егер  тізбегі –
тізбегі –
 нүктесіне шоғырланатын
кез келген тізбек болса, онда
нүктесіне шоғырланатын
кез келген тізбек болса, онда  тізбегі
тізбегі
 түрінде,
яғни
түрінде,
яғни  түрінде болады.
Бұдан
түрінде болады.
Бұдан  болғанда
болғанда
 немесе
немесе  болады деген қорытындыға
келеміз.
болады деген қорытындыға
келеміз. -
 функциясының шегі сан
осінің кез келген
функциясының шегі сан
осінің кез келген  нүктесінде
нүктесінде  -ге тең болады. Бұл
жағдайда
-ге тең болады. Бұл
жағдайда  және
және
 тізбектері тепе-тең,
яғни
тізбектері тепе-тең,
яғни  болады. Демек,
егер
болады. Демек,
егер  болса,
онда
болса,
онда  болғанда
болғанда
 немесе
немесе  болады.
болады. -
Барлық
 үшін
анықталған
үшін
анықталған  функциясының
(10-сурет)
функциясының
(10-сурет)  нүктесінде шегі болмайды.
Расында да, х
аргументі мәндерінің нөл
санына шоғырланатын екі тізбегін алайық:
нүктесінде шегі болмайды.
Расында да, х
аргументі мәндерінің нөл
санына шоғырланатын екі тізбегін алайық:
 және
және  .
.
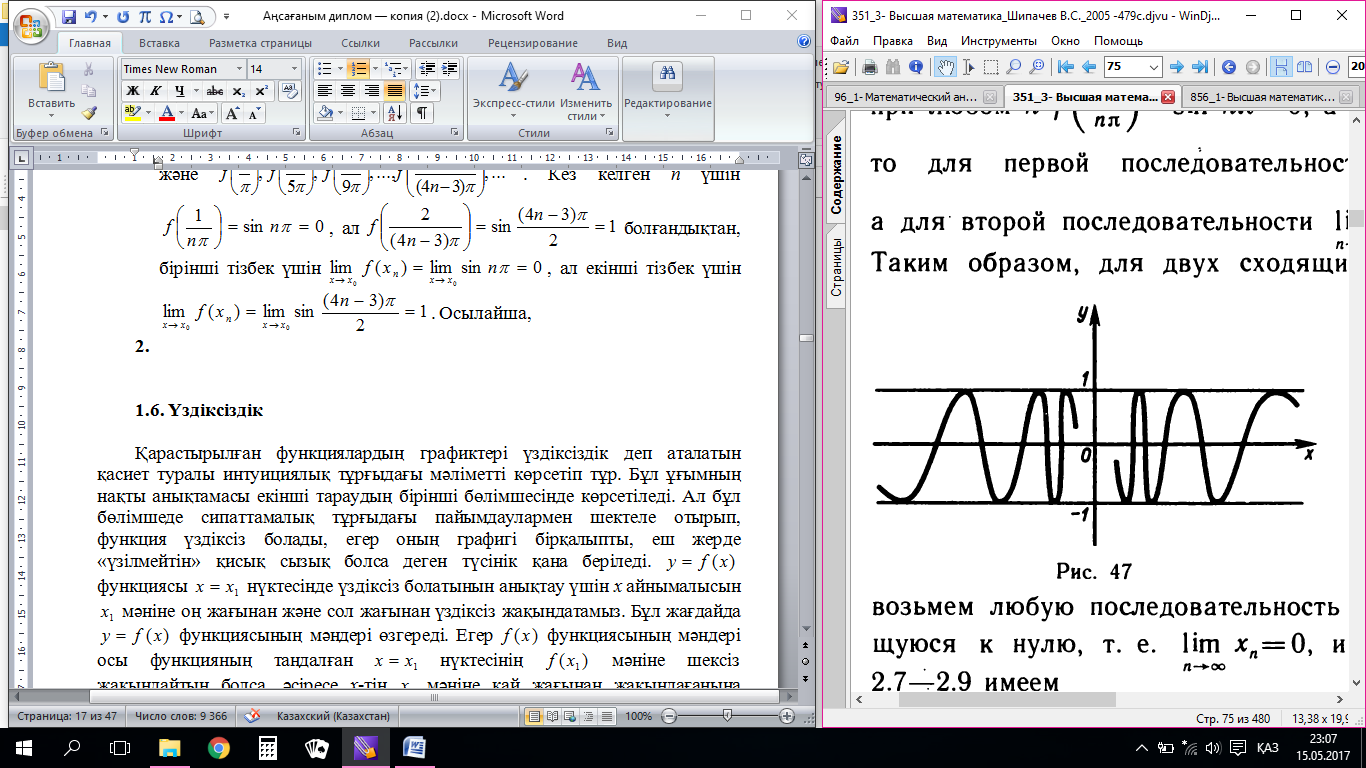
10-сурет
Олар үшін функцияның сәйкес
мәндерінің тізбегі мына түрде болады: және
және
 . Кез
келген п
үшін
. Кез
келген п
үшін
 ,
ал
,
ал  болғандықтан, бірінші тізбек
үшін
болғандықтан, бірінші тізбек
үшін  , ал екінші тізбек
үшін
, ал екінші тізбек
үшін  .
Осылайша, х
аргументі мәндерінің нөлге
шоғырланатын екі тізбегі үшін функция мәндерінің тізбектері әр
түрлі шектерге ие болады. Ал бұл ұйғарым функция шегінің
анықтамасына сәйкес
.
Осылайша, х
аргументі мәндерінің нөлге
шоғырланатын екі тізбегі үшін функция мәндерінің тізбектері әр
түрлі шектерге ие болады. Ал бұл ұйғарым функция шегінің
анықтамасына сәйкес  табылмайды дегенді
білдіреді.
табылмайды дегенді
білдіреді.
-
 функциясының
функциясының  нүктесінде шегі 1-ге тең
болады. Расында да, х
аргументі мәндерінің нөлге
шоғырланатын, яғни
нүктесінде шегі 1-ге тең
болады. Расында да, х
аргументі мәндерінің нөлге
шоғырланатын, яғни  және
және
 болатын кез келген
тізбегін алайық, онда
болатын кез келген
тізбегін алайық, онда
 .
.
Осылайша,
 табылады және ол нөлге
шоғырланатын
табылады және ол нөлге
шоғырланатын  тізбегін таңдаудан тәуелсіз
болғандықтан, функцияның шегі анықтамасы
негізінде
тізбегін таңдаудан тәуелсіз
болғандықтан, функцияның шегі анықтамасы
негізінде  болады деген шешімге
келеміз.
болады деген шешімге
келеміз.
-
Рационал нүктелердегі мәндері бірге, ал иррационал нүктелердегі мәндері нөлге тең болатын Дирихле функциясының сан осінің ешбір
 нүктесінде шегі болмайды.
Расында да, аргументтің
нүктесінде шегі болмайды.
Расында да, аргументтің  нүктесінде шоғырланатын
рационал мәндерінің тізбегі үшін функция мәндерінің сәйкес
тізбегінің шегі бірге тең, ал аргументтің
нүктесінде шоғырланатын
рационал мәндерінің тізбегі үшін функция мәндерінің сәйкес
тізбегінің шегі бірге тең, ал аргументтің
 нүктесінде шоғырланатын
иррационал мәндерінің тізбегі үшін функция мәндерінің сәйкес
тізбегінің шегі нөлге тең болады.
нүктесінде шоғырланатын
иррационал мәндерінің тізбегі үшін функция мәндерінің сәйкес
тізбегінің шегі нөлге тең болады.
Функция шегінің басқа да анықтамасы бар.
2-анықтама. А
саны  функциясының
функциясының  нүктесіндегі шегі деп
аталады, егер кез келген
нүктесіндегі шегі деп
аталады, егер кез келген  саны
үшін
саны
үшін  теңсіздігін
қанағаттандырғанда
теңсіздігін
қанағаттандырғанда  теңсіздігі орындалатын
барлық
теңсіздігі орындалатын
барлық  үшін
үшін  саны
табылса.
саны
табылса.
Логикалық символдарды қолдана отырып, 2-анықтаманы

түрінде жазуға
болады.  теңсіздіктерін
теңсіздіктерін  түрінде жазуға болатынын айта
кетейік.
түрінде жазуға болатынын айта
кетейік.
Бірінші анықтама сандық
тізбектің шегі ұғымына негізделген, сондықтан оны жиі «тізбектер
тіліндегі» анықтама деп атайды. Екінші анықтаманы
« тіліндегі» анықтама деп
атайды.
тіліндегі» анықтама деп
атайды.
1-теорема. Функцияның шегінің бірінші және екінші анықтамалары эквивалентті.
Дәлелдеу. 1)
Айталық, А
– бірінші анықтамаға
сәйкес, функциясының
функциясының  нүктесіндегі шегі
болсын. А
– екінші анықтамаға
сәйкес,
нүктесіндегі шегі
болсын. А
– екінші анықтамаға
сәйкес, функциясының шегі болатынын
көрсетейік. Кері жорамалдайық, яғни
А
– осы функцияның екінші
анықтамаға сәйкес шек болмайды деп пайымдайық. Демек, кез келген
емес
функциясының шегі болатынын
көрсетейік. Кері жорамалдайық, яғни
А
– осы функцияның екінші
анықтамаға сәйкес шек болмайды деп пайымдайық. Демек, кез келген
емес  үшін
үшін
 теңсіздігінен
теңсіздігінен  теңсіздігі
шығатындай
теңсіздігі
шығатындай  санын алуға болады, яғни
қандай да
санын алуға болады, яғни
қандай да  санын алмасақ
та,
санын алмасақ
та,  , бірақ
, бірақ
 болатындай ең болмағанда
бір
болатындай ең болмағанда
бір  нүктесі
табылатындай
нүктесі
табылатындай  саны бар
болады. δ
ретінде
кезектестіріп
саны бар
болады. δ
ретінде
кезектестіріп

сандарын таңдап аламыз. Онда
Х
жиынындағы  үшін
үшін
 ,
ал
,
ал  болатындай
болатындай  нүктесі
табылады;
нүктесі
табылады;
Х
жиынындағы  үшін
үшін
 ,
ал
,
ал  болатындай
болатындай  нүктесі
табылады;
нүктесі
табылады;
Х
жиынындағы  үшін
үшін
 ,
ал
,
ал  болатындай
болатындай  нүктесі
табылады;
нүктесі
табылады;
.....................................................................................................................
Х
жиынындағы  үшін
үшін
 ,
ал
,
ал  болатындай
болатындай  нүктесі
табылады;
нүктесі
табылады;
.....................................................................................................................
Нәтижесінде  нүктесінен өзге
және
нүктесінен өзге
және  үшін
үшін
 болғандықтан
болғандықтан нүктесіне
шоғырланатын
нүктесіне
шоғырланатын

нүктелерінің тізбегі шығады.
Сондықтан, функция шегінің бірінші анықтамасына сәйкес, функция
мәндерінің сәйкес  тізбегі
А
санына шоғырланады.
Демек,
тізбегі
А
санына шоғырланады.
Демек,  үшін
барлық
үшін
барлық  үшін
үшін
 теңсіздігі
орындалатын N
нөмірі табылады. Алынған
қарама-қайшылық А
саны – екінші анықтамаға
сәйкес,
теңсіздігі
орындалатын N
нөмірі табылады. Алынған
қарама-қайшылық А
саны – екінші анықтамаға
сәйкес,  функциясының
функциясының  нүктесіндегі шегі болатынын
дәлелдейді.
нүктесіндегі шегі болатынын
дәлелдейді.
2)
Айталық, А
саны – екінші анықтамаға
сәйкес,  функциясының
функциясының  нүктесіндегі шегі болсын.
Демек, кез келген
нүктесіндегі шегі болсын.
Демек, кез келген  үшін
үшін
 теңсіздігінен
теңсіздігінен  теңсіздігі
шығатындай
теңсіздігі
шығатындай  саны
табылады. А
– бірінші анықтамаға
сәйкес,
саны
табылады. А
– бірінші анықтамаға
сәйкес,  функциясының шегі болатынын
көрсетейік.
функциясының шегі болатынын
көрсетейік.  нүктесіне шоғырланатын кез
келген
нүктесіне шоғырланатын кез
келген

нүктелерінің тізбегін алайық.
Онда екінші анықтама бойынша ɛ-ге сәйкес
берілген  мәні үшін
мәні үшін
 үшін
үшін  теңсіздігі
орындалатын N
нөмірі табылады. Бірақ,
мұнымен қоса, екінші анықтамаға сәйкес,
теңсіздігі
орындалатын N
нөмірі табылады. Бірақ,
мұнымен қоса, екінші анықтамаға сәйкес,
 теңсіздігі де
орындалады. Ал ɛ
өз еркімізге сай
таңдалғандықтан,
теңсіздігі де
орындалады. Ал ɛ
өз еркімізге сай
таңдалғандықтан,  нүктесіне шоғырланатын кез
келген
нүктесіне шоғырланатын кез
келген  тізбегі
үшін
тізбегі
үшін  болады,
яғни А
саны – бірінші анықтамаға
сәйкес,
болады,
яғни А
саны – бірінші анықтамаға
сәйкес,  функциясының
функциясының  нүктесіндегі шегі болатынын
дәлелдейді. Теорема дәлелденді.
нүктесіндегі шегі болатынын
дәлелдейді. Теорема дәлелденді.
Сонымен, функцияның шегінің бірінші және екінші анықтамаларының эквиваленттілігі нақтыланды және олардың ішінен есепті шешуде тиімді болып табылатын кез келгенін қолдануға болады.
Функция шегінің «тізбектер
тіліндегі» анықтамасын функция шегінің Гейне (Гейне Генрих Эдуард
(1821-1881) – неміс математигі) анықтамасы деп, ал функция шегінің
« тіліндегі» анықтамасын функция
шегінің Коши (Коши Огюстен Луи (1789-1857) – француз математигі)
анықтамасы деп атайтынын айта кетейік.
тіліндегі» анықтамасын функция
шегінің Коши (Коши Огюстен Луи (1789-1857) – француз математигі)
анықтамасы деп атайтынын айта кетейік.
-
 және
және  болғандағы функцияның
шегі. Әрі қарай функцияның біржақты
шектері ұғымдары қолданылатын болады және олар былайша
анықталады.
болғандағы функцияның
шегі. Әрі қарай функцияның біржақты
шектері ұғымдары қолданылатын болады және олар былайша
анықталады.
3-анықтама. А
саны  функциясының
функциясының  нүктесіндегі оң жақты (сол
жақты) шегі деп аталады, егер
нүктесіндегі оң жақты (сол
жақты) шегі деп аталады, егер  нүктесіне шоғырланатын
және
нүктесіне шоғырланатын
және  элементтері
элементтері  нүктесінен артық (кем)
болатын кез келген
нүктесінен артық (кем)
болатын кез келген  тізбегі үшін
сәйкес
тізбегі үшін
сәйкес  тізбегі А санына
шоғырланатын болса.
тізбегі А санына
шоғырланатын болса.
Символдық
белгіленуі:  .
.
Мысал
ретінде  функциясын қарастырайық. Бұл
функцияның
функциясын қарастырайық. Бұл
функцияның  нүктесінде оң жақты және сол
жақты шектері бар:
нүктесінде оң жақты және сол
жақты шектері бар: 
 . Расында да,
егер
. Расында да,
егер  тізбегі – осы функция
аргументінің нөлге шоғырланатын және
тізбегі – осы функция
аргументінің нөлге шоғырланатын және  элементтері нөлден
үлкен
элементтері нөлден
үлкен  мәндерінің кез келген тізбегі
болса, онда
мәндерінің кез келген тізбегі
болса, онда  және
және
 болады.
Осыдан,
болады.
Осыдан,  . Дәл
осылайша
. Дәл
осылайша  анықталады.
анықталады.
Функцияның біржақты шектердің
анықтамасына теңкүшті болатын « тіліндегі» анықтамасын да
беріге болады: А
саны
тіліндегі» анықтамасын да
беріге болады: А
саны  функциясының
функциясының  нүктесіндегі оң жақты (сол
жақты) шегі деп аталады, егер кез келген
нүктесіндегі оң жақты (сол
жақты) шегі деп аталады, егер кез келген
 үшін барлық х
үшін
үшін барлық х
үшін  теңсіздігін
қанағаттандырғанда
теңсіздігін
қанағаттандырғанда  теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылса. Символдық
белгіленуі:
табылса. Символдық
белгіленуі:

Біржақты шектер мен функцияның шегі арасындағы байланысты төмендегі теорема орнатады.
2-теорема.  функциясының
функциясының  нүктесінде шегі болады
сонда және тек қана сонда, егер осы нүктеде оң жақты да, сол жақты
да шектері бар болса және олар өзара тең болса. Бұл жағдайда
функцияның шегі біржақты шекке тең
болады.
нүктесінде шегі болады
сонда және тек қана сонда, егер осы нүктеде оң жақты да, сол жақты
да шектері бар болса және олар өзара тең болса. Бұл жағдайда
функцияның шегі біржақты шекке тең
болады.
Дәлелдеу.  болсын. Онда функцияның оң
жақты және сол жақты шектері туралы анықтамаға сәйкес, кез
келген
болсын. Онда функцияның оң
жақты және сол жақты шектері туралы анықтамаға сәйкес, кез
келген  үшін
үшін
 теңсіздігін
қанағаттандыратын барлық х
үшін және
теңсіздігін
қанағаттандыратын барлық х
үшін және
 теңсіздігін
қанағаттандыратын барлық х
үшін
теңсіздігін
қанағаттандыратын барлық х
үшін
 теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  және
және
 табылады.
табылады.  алайық.
Онда
алайық.
Онда  теңсіздігін қанағаттандыратын
барлық х
үшін
теңсіздігін қанағаттандыратын
барлық х
үшін
 теңсіздігі орындалады.
Ал бұл ұйғарым, 2-анықтамаға сәйкес,
теңсіздігі орындалады.
Ал бұл ұйғарым, 2-анықтамаға сәйкес,  дегенді
білдіреді.
дегенді
білдіреді.
Керісінше,  болсын. Онда,
функцияның
болсын. Онда,
функцияның  нүктесінде шегі туралы
анықтамаға сәйкес, кез келген
нүктесінде шегі туралы
анықтамаға сәйкес, кез келген  үшін
үшін
 теңсіздігін
қанағаттандыратын барлық х
үшін
теңсіздігін
қанағаттандыратын барлық х
үшін
 теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылады.
Осылайша,
табылады.
Осылайша,  үшін де,
үшін де,
 үшін
де
үшін
де  теңсіздігі дұрыс болады. Ал бұ
л ұйғарым біржақты шектер турлы анықтамаға
сәйкес,
теңсіздігі дұрыс болады. Ал бұ
л ұйғарым біржақты шектер турлы анықтамаға
сәйкес,  болатынын көрсетеді. Теорема
дәлелденді.
болатынын көрсетеді. Теорема
дәлелденді.
-
 ,
,  және
және  болғандағы функцияның
шегі.
болғандағы функцияның
шегі.  болғандағы функцияның шегі мен
біржақты шектер ұғымдарынан басқа аргументтің шексіздікке
ұмтылғандағы функцияның шегі ұғымы бар.
болғандағы функцияның шегі мен
біржақты шектер ұғымдарынан басқа аргументтің шексіздікке
ұмтылғандағы функцияның шегі ұғымы бар.
4-анықтама. А
саны  функциясының
функциясының  болғандағы шегі деп
аталады, егер аргумент мәндерінің кез келген шексіз
үлкен
болғандағы шегі деп
аталады, егер аргумент мәндерінің кез келген шексіз
үлкен  тізбегі үшін
сәйкес
тізбегі үшін
сәйкес  тізбегі А санына
шоғырланатын болса.
тізбегі А санына
шоғырланатын болса.
Символдық
белгіленуі:  .
.
5-анықтама. А
саны  функциясының
функциясының  болғандағы шегі деп
аталады, егер
болғандағы шегі деп
аталады, егер  элементтері оң (теріс)
болатын аргумент мәндерінің кез келген шексіз
үлкен
элементтері оң (теріс)
болатын аргумент мәндерінің кез келген шексіз
үлкен  тізбегі үшін
сәйкес
тізбегі үшін
сәйкес  тізбегі А санына
шоғырланатын болса.
тізбегі А санына
шоғырланатын болса.
Символдық
белгіленуі:  .
.
Мысал
қарастырайық.  болсын. Бұл
функцияның
болсын. Бұл
функцияның  болғанда нөлге тең шегі бар.
Расында да, егер
болғанда нөлге тең шегі бар.
Расында да, егер  – аргумент мәндерінің шексіз
үлкен тізбегі болса, онда функция мәндерінің
сәйкес
– аргумент мәндерінің шексіз
үлкен тізбегі болса, онда функция мәндерінің
сәйкес  тізбегі шексіз аз тізбек болып
табылады, сондықтан нөлге тең шегі бар болады,
яғни
тізбегі шексіз аз тізбек болып
табылады, сондықтан нөлге тең шегі бар болады,
яғни  (11-сурет).
(11-сурет).
4-5-анықтамалары «тізбектер
тілінде» берілді. Оларға теңкүшті болатын
« тіліндегі» анықтамаларын
беріп, оларды логикалық символдар тілінде жазуға болады. Мысал
ретінде
тіліндегі» анықтамаларын
беріп, оларды логикалық символдар тілінде жазуға болады. Мысал
ретінде  болғандағы функцияның шегінің
анықтамасын келтірейік.
болғандағы функцияның шегінің
анықтамасын келтірейік.

11-сурет
6-анықтама. А
саны  функциясының
функциясының  болғандағы шегі деп
аталады, егер кез келген
болғандағы шегі деп
аталады, егер кез келген  үшін
үшін  теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  үшін
үшін  теңсіздігі орындалатындай δ
саны табылса. [11]
теңсіздігі орындалатындай δ
саны табылса. [11]
-
Функциялар шектері туралы теоремалар. Функция шегінің «тізбектер тіліндегі» анықтамасы функциядағы тізбектің шектері туралы жоғарыда дәлелденген теоремаларды өзгертуге мүмкіндік береді.
3-теорема.  және
және  функцияларының
функцияларының  нүктесіндегі В мен С
шектері бар болсын. Онда
нүктесіндегі В мен С
шектері бар болсын. Онда  функцияларының
функцияларының  нүктесіндегі шектері
сәйкесінше
нүктесіндегі шектері
сәйкесінше  болады.
болады.
Дәлелдеу.  –
–
 және
және  функцияларының аргумент
мәндерінің
функцияларының аргумент
мәндерінің  нүктесіне шоғырланатын тізбегі
болсын. Осы функциялардың сәйкесінше
нүктесіне шоғырланатын тізбегі
болсын. Осы функциялардың сәйкесінше  және
және
 мәндерінің тізбектерінің
шектері В
және
С
болады.
Онда
мәндерінің тізбектерінің
шектері В
және
С
болады.
Онда  тізбектері
сәйкесінше
тізбектері
сәйкесінше  шектеріне ие болады. Функция
шегінің 1-анықтамасына сәйкес,
шектеріне ие болады. Функция
шегінің 1-анықтамасына сәйкес,

болады. Теорема дәлелденді.
4-теорема.  ,
,
 және
және  функциялары
функциялары  нүктесін қоса алмаған
жағдайда
нүктесін қоса алмаған
жағдайда  нүктесінің қандай да бір
төңірегінде анықталған және
нүктесінің қандай да бір
төңірегінде анықталған және  ,
,
 функцияларының
функцияларының  нүктесінде А-ға тең шегі,
яғни
нүктесінде А-ға тең шегі,
яғни  болсын. Сонымен
қатар
болсын. Сонымен
қатар  теңсіздіктері орындалсын.
Онда
теңсіздіктері орындалсын.
Онда

Дәлелдеу.  –
–
 және
және  функцияларының аргумент
мәндерінің
функцияларының аргумент
мәндерінің  нүктесіне шоғырланатын тізбегі
болсын. Осы функциялардың сәйкесінше
нүктесіне шоғырланатын тізбегі
болсын. Осы функциялардың сәйкесінше  және
және
 мәндерінің тізбектерінің
шектері A-ға тең болады,
яғни
мәндерінің тізбектерінің
шектері A-ға тең болады,
яғни  болғандағы
болғандағы болады. Теореманың шартында
берілген теңсіздіктерді қолдана отырып, бұл
жерде
болады. Теореманың шартында
берілген теңсіздіктерді қолдана отырып, бұл
жерде

деп жазуға болады.
Бұдан  болатыны шығады. Функция
шегінің 1-анықтамасына сәйкес,
болатыны шығады. Функция
шегінің 1-анықтамасына сәйкес,

болатынын білдіреді.
1-ескерту. 3-теорема мен
4-теорема  -дің
орнында
-дің
орнында  символдарының біреуі тұратын
жағдайларда да дұрыс болады. [12]
символдарының біреуі тұратын
жағдайларда да дұрыс болады. [12]
1.7. Шексіз кіші және шексіз үлкен функциялар
1. Шексіз кіші
функциялар. 7-анықтама.  функциясы
функциясы  нүктесінде
(немесе
нүктесінде
(немесе  ) шекcіз кіші функция деп
аталады, егер
) шекcіз кіші функция деп
аталады, егер  болса.
болса.
 болғандағы шексіз кіші
функциялар да дәл осылай анықталады.
болғандағы шексіз кіші
функциялар да дәл осылай анықталады.
Шексіз кіші функцияның
теңкүшті анықтамасын « тілінде» беруге
болады:
тілінде» беруге
болады:  функциясы
функциясы  нүктесінде шекcіз кіші
функция деп аталады, егер кез келген
нүктесінде шекcіз кіші
функция деп аталады, егер кез келген
 үшін
үшін  теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  үшін
үшін  теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылса; немесе логикалық символдар
арқылы беруге болады:
табылса; немесе логикалық символдар
арқылы беруге болады:
 ;
;
немесе «тізбектер тілінде»
беруге болады:  функциясы
функциясы  нүктесінде шекcіз кіші
функция деп аталады, егер х аргументінің
нүктесінде шекcіз кіші
функция деп аталады, егер х аргументінің
 нүктесінен өзге
мәндерінің
нүктесінен өзге
мәндерінің  нүктесіне шоғырланатын кез
келген
нүктесіне шоғырланатын кез
келген  тізбегі үшін
сәйкес
тізбегі үшін
сәйкес  тізбегі шексіз кіші тізбек
болса.
тізбегі шексіз кіші тізбек
болса.
Келесі теорема орындалады.
5-теорема.  теңдігінің орындалуы
үшін
теңдігінің орындалуы
үшін  болғанда
болғанда

функциясының шексіз кіші болуы қажетті және жеткілікті.
Дәлелдеу. Қажеттілік.  болсын.
болсын.
 айырымын
қарастырып,
айырымын
қарастырып, 
 болғандағы шексіз кіші функция
болатынын көрсетейік. Расында да,
болғандағы шексіз кіші функция
болатынын көрсетейік. Расында да,  пен
А
функцияларының
әрқайсысының
пен
А
функцияларының
әрқайсысының  болғандағы
шегі А-ға тең, сондықтан 3-теоремаға
сәйкес,
болғандағы
шегі А-ға тең, сондықтан 3-теоремаға
сәйкес,

болады.
Жеткіліктік.  болсын,
мұндағы
болсын,
мұндағы  –
–
 болғандағы шексіз кіші
функция.
болғандағы шексіз кіші
функция.  екенін
көрсетейік.
екенін
көрсетейік.  болғандықтан,
болғандықтан,

болады. Теорема дәлелденді.
5-теоремадан  нүктесінде А-ға тең шегі болатын функция
үшін арнайы белгіленуді аламыз:
нүктесінде А-ға тең шегі болатын функция
үшін арнайы белгіленуді аламыз:
 ,
мұндағы
,
мұндағы  .
.
Бұл жерде,
әдетте,  функциясы
функциясы
 нүктесінің
аймағында А-дан шексіз кіші функцияға
өзгереді деп айтады.
нүктесінің
аймағында А-дан шексіз кіші функцияға
өзгереді деп айтады.
Шексіз кіші функциялардың қасиеттері шексіз кіші тізбектердің қасиеттерімен бірдей болады. Келесі теорема орындалады.
6-теорема.  болғандағы шексіз кіші
функциялардың алгебралық қосындысы мен көбейтіндісі, сондай-ақ
шексіз кіші функция мен шекті функцияның
көбейтіндісі
болғандағы шексіз кіші
функциялардың алгебралық қосындысы мен көбейтіндісі, сондай-ақ
шексіз кіші функция мен шекті функцияның
көбейтіндісі  болғандағы шексіз кіші
функцияға тең болады.
болғандағы шексіз кіші
функцияға тең болады.
 болғандағы шексіз кіші
функциялар туралы айтылғандардың барлығы
болғандағы шексіз кіші
функциялар туралы айтылғандардың барлығы
 болғандағы шексіз кіші
функциялар үшін де орындалады.
болғандағы шексіз кіші
функциялар үшін де орындалады.
2. Шексіз үлкен
функциялар. 8-анықтама.  функциясы
функциясы  нүктесінде
(немесе
нүктесінде
(немесе  ) шекcіз үлкен функция деп
аталады, егер кез келген
) шекcіз үлкен функция деп
аталады, егер кез келген  үшін
үшін  теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  үшін
үшін  теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылса.
табылса.
Бұл
жағдайда  деп жазады және
функция
деп жазады және
функция  болғанда шексіздікке ұмтылады
немесе функцияның
болғанда шексіздікке ұмтылады
немесе функцияның  нүктесінде шексіз шегі бар деп
айтады.
нүктесінде шексіз шегі бар деп
айтады.
Егер де
 теңсіздігі орындалса,
онда
теңсіздігі орындалса,
онда  деп жазады және
функция
деп жазады және
функция  нүктесінде
нүктесінде  -ге тең болатын шексіз шекке
ие болады деп айтады.
-ге тең болатын шексіз шекке
ие болады деп айтады.
Логикалық символдарды қолдана отырып, 8-анықтаманы

түрінде жазуға болады.
Шектеулі біржақты шектермен ұқсастығына қарай шексіз біржақты шектер де анықталады:

Осылайша,
мысалы,  деп жазады, егер кез
келген
деп жазады, егер кез
келген  үшін
үшін
 теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  үшін
үшін
 теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылса. Символдық
жазылуы:
табылса. Символдық
жазылуы:

«Тізбектер тілінде» бұл
анықтама  деп жазылады,
егер
деп жазылады,
егер  элементтері
элементтері  нүктесінен артық
болатындай х
аргументінің
мәндерінің
нүктесінен артық
болатындай х
аргументінің
мәндерінің  нүктесіне шоғырланатын кез
келген
нүктесіне шоғырланатын кез
келген  тізбегі үшін
сәйкес
тізбегі үшін
сәйкес  тізбегі оң таңбалы шексіз
үлкен тізбек болса.
тізбегі оң таңбалы шексіз
үлкен тізбек болса.
 болғандағы шексіз үлкен
функциялар да дәл осылай анықталады. Осылайша,
мысалы,
болғандағы шексіз үлкен
функциялар да дәл осылай анықталады. Осылайша,
мысалы,  функциясы
функциясы
 болғанда шексіз үлкен
функция деп аталады, егер кез келген
болғанда шексіз үлкен
функция деп аталады, егер кез келген  үшін
үшін
 теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  үшін
үшін
 теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылса. Бұл
жағдайда
табылса. Бұл
жағдайда  деп
жазады.
деп
жазады.
 болғандағы шексіз үлкен
функцияның символдық белгіленуі:
болғандағы шексіз үлкен
функцияның символдық белгіленуі:

Егер де
 теңсіздігі орындалса,
онда
теңсіздігі орындалса,
онда  деп
жазады.
деп
жазады.
Шексіз кіші және шексіз үлкен функциялардың арасындағы байланыс оларға сәйкес тізбектердің арасында болатын байланыспен бірдей болады, яғни шексіз кіші функцияға кері функция шексіз үлкен функция болып табылады және керісінше шексіз үлкен функцияға кері функция шексіз кіші функция болып табылады.
Расында
да,  болғанда
болғанда
 және
және  болсын.
болсын.
 екенін дәлелдейік.
Кездейсоқ
екенін дәлелдейік.
Кездейсоқ  алайық.
алайық.
 функциясы
–
функциясы
–  нүктесіндегі шексіз кіші
функция болғандықтан,
нүктесіндегі шексіз кіші
функция болғандықтан,  саны үшін
саны үшін
 теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  үшін
үшін
 теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылады.
Онда х
үшін
табылады.
Онда х
үшін
 теңсіздігі орындалады,
яғни
теңсіздігі орындалады,
яғни  функциясы
функциясы
 нүктесіндегі шексіз
үлкен функция болады. Дәлелдеу керегі осы.
[13]
нүктесіндегі шексіз
үлкен функция болады. Дәлелдеу керегі осы.
[13]
1.8. Үздіксіздік
Алдыңғы бөлімшелерде
қарастырылған функциялардың графиктері үздіксіздік деп аталатын
қасиет туралы интуициялық тұрғыдағы мәліметті көрсетіп тұр. Бұл
ұғымның нақты анықтамасы екінші тараудың бірінші бөлімшесінде
көрсетіледі. Ал бұл бөлімшеде сипаттамалық тұрғыдағы пайымдаулармен
шектеле отырып, функция үздіксіз болады, егер оның графигі
бірқалыпты, еш жерде «үзілмейтін» қисық сызық болса деген түсінік
қана беріледі.  функциясы
функциясы
 нүктесінде үздіксіз
болатынын анықтау үшін х
айнымалысын
нүктесінде үздіксіз
болатынын анықтау үшін х
айнымалысын  мәніне оң жағынан және сол
жағынан үздіксіз жақындатамыз. Бұл жағдайда
мәніне оң жағынан және сол
жағынан үздіксіз жақындатамыз. Бұл жағдайда
 функциясының мәндері
өзгереді. Егер
функциясының мәндері
өзгереді. Егер  функциясының мәндері осы
функцияның таңдалған
функциясының мәндері осы
функцияның таңдалған  нүктесінің
нүктесінің  мәніне шексіз жақындайтын
болса, әсіресе х-тің
мәніне шексіз жақындайтын
болса, әсіресе х-тің
 мәніне қай жағынан
жақындағанына қарамастан, онда
мәніне қай жағынан
жақындағанына қарамастан, онда  функциясы
функциясы
 нүктесінде үздіксіз деп айтады. Егер бұл жағдай
қандай да бір интервалдың әрбір
нүктесінде үздіксіз деп айтады. Егер бұл жағдай
қандай да бір интервалдың әрбір  нүктесінде орындалса, онда
функция берілген интервалда
үздіксіз деп
айтады.
нүктесінде орындалса, онда
функция берілген интервалда
үздіксіз деп
айтады.
Графигі бірқалыпты болатын әрбір функция үздіксіз болғанымен, барлық жерде үздіксіз болмайтын функцияларды анықтау өте оңай.
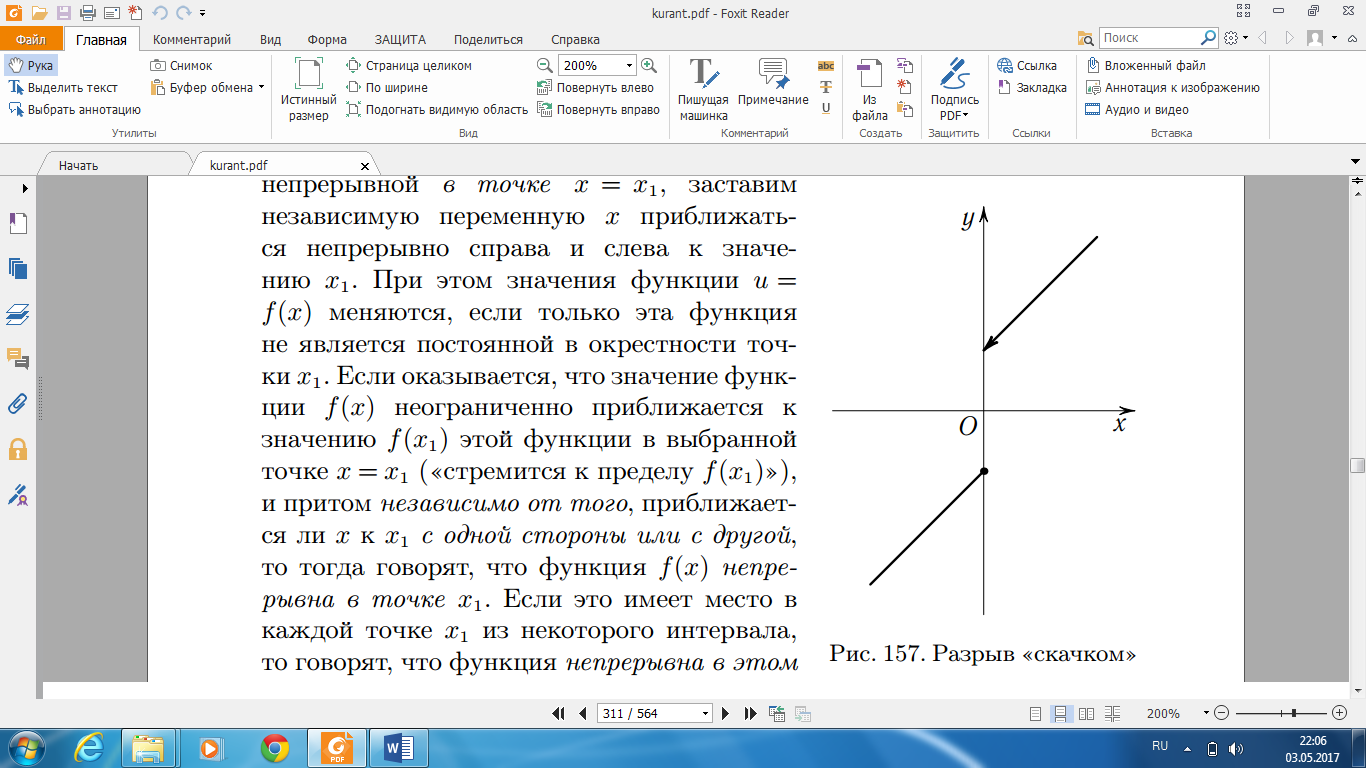
12-сурет. «Секіру» арқылы үзілу
Мысалы, 12-суретте берілген

формулалары
арқылы х-тің барлық мәндері үшін
анықталған функция  нүктесінде –1 мәніне ие болып,
осы нүктеде үзілісті болады. Егер берілген функцияның графигін
қарындашпен сызатын болсақ, осы нүктеде қарындашты қағаздан
алуымызға тура келеді.
нүктесінде –1 мәніне ие болып,
осы нүктеде үзілісті болады. Егер берілген функцияның графигін
қарындашпен сызатын болсақ, осы нүктеде қарындашты қағаздан
алуымызға тура келеді.  мәніне оң жағынан жақындаған
кезде
мәніне оң жағынан жақындаған
кезде  функциясы +1-ге ұмтылады.
Бірақ бұл мән функцияның дәл осы нүктедегі мәнінен, яғни –1-ден
өзгеше болады.
функциясы +1-ге ұмтылады.
Бірақ бұл мән функцияның дәл осы нүктедегі мәнінен, яғни –1-ден
өзгеше болады.
х
0-ге сол жағынан
ұмтылғандағы функциясының –1-ге ұмтылу
жағдайының өзі үздіксіздікті анықтау үшін жеткілікті
емес.
функциясының –1-ге ұмтылу
жағдайының өзі үздіксіздікті анықтау үшін жеткілікті
емес.
х-тің барлық мәндері үшін

формулаларымен
анықталған  функциясы
функциясы
 болғанда басқа түрде
үзіледі. Бұл жағдайда оң жағынан да, сол жағынан да шектері бар
және олар өзара тең, бірақ бұл жалпы шектік
мән
болғанда басқа түрде
үзіледі. Бұл жағдайда оң жағынан да, сол жағынан да шектері бар
және олар өзара тең, бірақ бұл жалпы шектік
мән  мәнінен өзге
болады.
мәнінен өзге
болады.  нүктесінде басқа түрде
үзілісті болатын
нүктесінде басқа түрде
үзілісті болатын

функциясының графигі
13-суретте көрсетіліп тұр. Егер х
0-ге кез келген жақтан
ұмтылатын болса, онда у
ылғи да шексіздікке ұмтылады,
бірақ функцияның графигі осы нүктеде «үзіледі» және
тәуелсіз х
айнымалысының  нүктесінің айналасындағы кіші
мәндеріне тәуелді у
айнымалысының өте үлкен
мәндері сәйкес келуі мүмкін. Басқаша айтқанда,
нүктесінің айналасындағы кіші
мәндеріне тәуелді у
айнымалысының өте үлкен
мәндері сәйкес келуі мүмкін. Басқаша айтқанда,
 болғандағы функцияның
мәні анықталмайды, себебі шексіздік сан деп қабылданбайды,
сондықтан
болғандағы функцияның
мәні анықталмайды, себебі шексіздік сан деп қабылданбайды,
сондықтан  болғанда
болғанда
 функциясы шексіздікке
тең деп айтуға болмайды. Демек, х
нөлге
жақындағанда
функциясы шексіздікке
тең деп айтуға болмайды. Демек, х
нөлге
жақындағанда  функциясы «шексіздікке
ұмтылады» деп айта аламыз.
функциясы «шексіздікке
ұмтылады» деп айта аламыз.
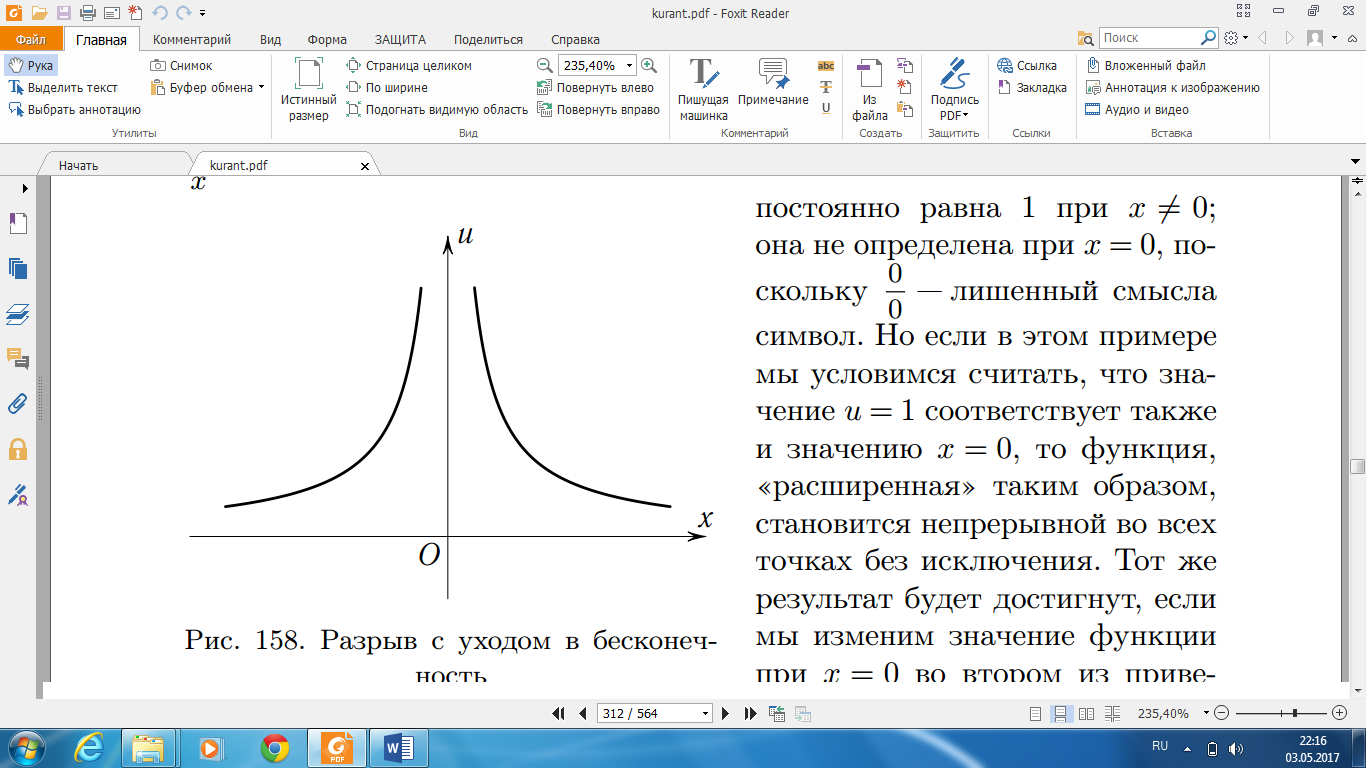
13-сурет. Шексіздікке бағытталу арқылы үзілу
Ал
 функциясының
функциясының  нүктесіндегі үзілуінің түрі
мүлдем басқаша (9-сурет).
нүктесіндегі үзілуінің түрі
мүлдем басқаша (9-сурет).
Келтірілген мысалдар қандай да
бір  нүктесінде функцияның
үздіксіздігі жойылатын бірнеше әр түрлі типтік жағдайларды
көрсетеді.
нүктесінде функцияның
үздіксіздігі жойылатын бірнеше әр түрлі типтік жағдайларды
көрсетеді.
-
Функцияның
 нүктесіндегі анықталған мәні
тиісті түрде анықталған немесе өзгертілгеннен кейін функция
үздіксіз болып қалуы мүмкін. Мысалы,
нүктесіндегі анықталған мәні
тиісті түрде анықталған немесе өзгертілгеннен кейін функция
үздіксіз болып қалуы мүмкін. Мысалы,  функциясы
функциясы
 кезде ылғи да 1-ге тең;
ол
кезде ылғи да 1-ге тең;
ол  болғанда анықталмайды,
себебі
болғанда анықталмайды,
себебі  – мағынасы жоқ символ. Бірақ
егер осы мысалда
– мағынасы жоқ символ. Бірақ
егер осы мысалда  мәні
мәні
 мәніне де сәйкес келеді
деп пайымдауға келісіп алсақ, онда осындай тәсілмен «кеңейтілген»
функция барлық нүктелерде үздіксіз болып өзгеріп кетеді. Дәл
осындай нәтижеге жетуге болады, егер жоғарыда көрсетілген
мысалдардың екіншісінде
мәніне де сәйкес келеді
деп пайымдауға келісіп алсақ, онда осындай тәсілмен «кеңейтілген»
функция барлық нүктелерде үздіксіз болып өзгеріп кетеді. Дәл
осындай нәтижеге жетуге болады, егер жоғарыда көрсетілген
мысалдардың екіншісінде  болғандағы функцияның мәнін
өзгертіп,
болғандағы функцияның мәнін
өзгертіп,  мәнінің
орнына
мәнінің
орнына  деп алсақ. Осындай түрдегі
үзілу жағдайлары жөнделетін деп
аталады.
деп алсақ. Осындай түрдегі
үзілу жағдайлары жөнделетін деп
аталады. -
х-тің х1 нүктесіне оң жағынан немесе сол жағынан жақындауына қарай функция әр түрлі шектерге ұмтылады (12-сурет).
-
Функцияның екі жағынан да шегі жоқ (9-сурет).
-
х-тің х1 нүктесіне жақындағанда функция шексіздікке ұмтылады (13-сурет).
Соңғы үш типті үзілу
жағдайлары маңызды немесе
жөнделмейтін деп аталады, себебі бір
ғана  нүктесінде функцияның мәнін
тиісті түрде анықтау арқылы өзгерту мүмкін емес.
[14]
нүктесінде функцияның мәнін
тиісті түрде анықтау арқылы өзгерту мүмкін емес.
[14]
2. Үздіксіз функциялардың екі негізгі теоремасы
2.1. Үздіксіздіктің анықтамасы
1-анықтама.  функциясы
функциясы
 нүктесінде үздіксіз деп
аталады, егер х
айнымалысы
нүктесінде үздіксіз деп
аталады, егер х
айнымалысы  -ге
ұмтылғанда
-ге
ұмтылғанда  шамасы тең болатын шекке
ұмтылатын болса. Егер бұл анықтама талдаудан өткізсек, онда ол
төмендегі екі шарттың орындалуын қажет ететіндігін
көреміз:
шамасы тең болатын шекке
ұмтылатын болса. Егер бұл анықтама талдаудан өткізсек, онда ол
төмендегі екі шарттың орындалуын қажет ететіндігін
көреміз:
а)
х
айнымалысы  -ге
ұмтылғанда
-ге
ұмтылғанда  функциясының а
шегі бар
болады;
функциясының а
шегі бар
болады;
ә) осы
а
шегі
 -ке тең болу
керек.
-ке тең болу
керек.
Егер шектің
анықтамасындағы а
шамасының орнына
оның  мәнін қойсақ, онда
үздіксіздіктің шарты мынадай түрде болады:
мәнін қойсақ, онда
үздіксіздіктің шарты мынадай түрде болады:
 үшін
үшін  функциясы үздіксіз болады,
егер оң ɛ саны қаншалықты аз болса,
функциясы үздіксіз болады,
егер оң ɛ саны қаншалықты аз болса,

теңсіздігі

шартын қанағаттандыратын барлық х үшін орындалатындай δ оң санын табуға болады.
Мысал
ретінде  функциясының
функциясының  нүктесіндегі үздіксіздігін
анықтайық. Сонда
нүктесіндегі үздіксіздігін
анықтайық. Сонда

болады. Енді аздаған
оң ɛ
санын таңдап алайық,
мысалы,  .
х
мәндерін
.
х
мәндерін
0-ге жақын сандармен шектеу арқылы  функциясының
0-ден
функциясының
0-ден  -ге кем болатын,
яғни
-ге кем болатын,
яғни  және
және
 аралығында жататын
сәйкес мәндерінің шығатынын көрсетуім керек.
Егер х-тің өзгеруін
0-ден
аралығында жататын
сәйкес мәндерінің шығатынын көрсетуім керек.
Егер х-тің өзгеруін
0-ден  -ге кем мәндерімен шектесек,
онда
-ге кем мәндерімен шектесек,
онда  мәндері жоғарыда көрсетілген
аралықтан аспайтынын көреміз; расында да егер
мәндері жоғарыда көрсетілген
аралықтан аспайтынын көреміз; расында да егер
 болса,
онда
болса,
онда  болады. Дәл
осылай
болады. Дәл
осылай  орнына кез келген
аздаған
орнына кез келген
аздаған  және т.б. мәнін ала
аламыз;
және т.б. мәнін ала
аламыз;  сандары біздің шартымызды
қанағаттандыратын болады, себебі
сандары біздің шартымызды
қанағаттандыратын болады, себебі  теңсіздігінен
теңсіздігінен  шығады.
шығады.
Үздіксіздіктің ɛ, δ арқылы жасалған анықтамасына сүйене отырып барлық полиномдар, рационал функциялар және тригонометриялық функциялар кез келген нүктеде үздіксіз екенін дәлелдеуге болады.
Үздіксіздіктің
анықтамасын  функциясының графигімен
байланыстыра отырып, оны келесідей геометриялық түрге келтіруге
болады. Қандай да бір оң ɛ
санын
таңдап, х
осіне параллель
болатын
функциясының графигімен
байланыстыра отырып, оны келесідей геометриялық түрге келтіруге
болады. Қандай да бір оң ɛ
санын
таңдап, х
осіне параллель
болатын  биіктікте
және х
осінен
төмен
биіктікте
және х
осінен
төмен  түзулерін жүргізейік. Онда
графиктің
түзулерін жүргізейік. Онда
графиктің  -дің қасында ені
2δ
болатын вертикаль жолақтың
ішінде жатқан бөлігі
-дің қасында ені
2δ
болатын вертикаль жолақтың
ішінде жатқан бөлігі  -тің қасында ені
2ɛ
болатын горизонталь жолақтың
ішінде де жататындай етіп оң δ
саны табылуы керек.
1-сурет
-тің қасында ені
2ɛ
болатын горизонталь жолақтың
ішінде де жататындай етіп оң δ
саны табылуы керек.
1-сурет  нүктесінде үздіксіз болатын
функцияны, ал
нүктесінде үздіксіз болатын
функцияны, ал
2-сурет осы нүктеде үзілетін функцияны
көрсетеді.
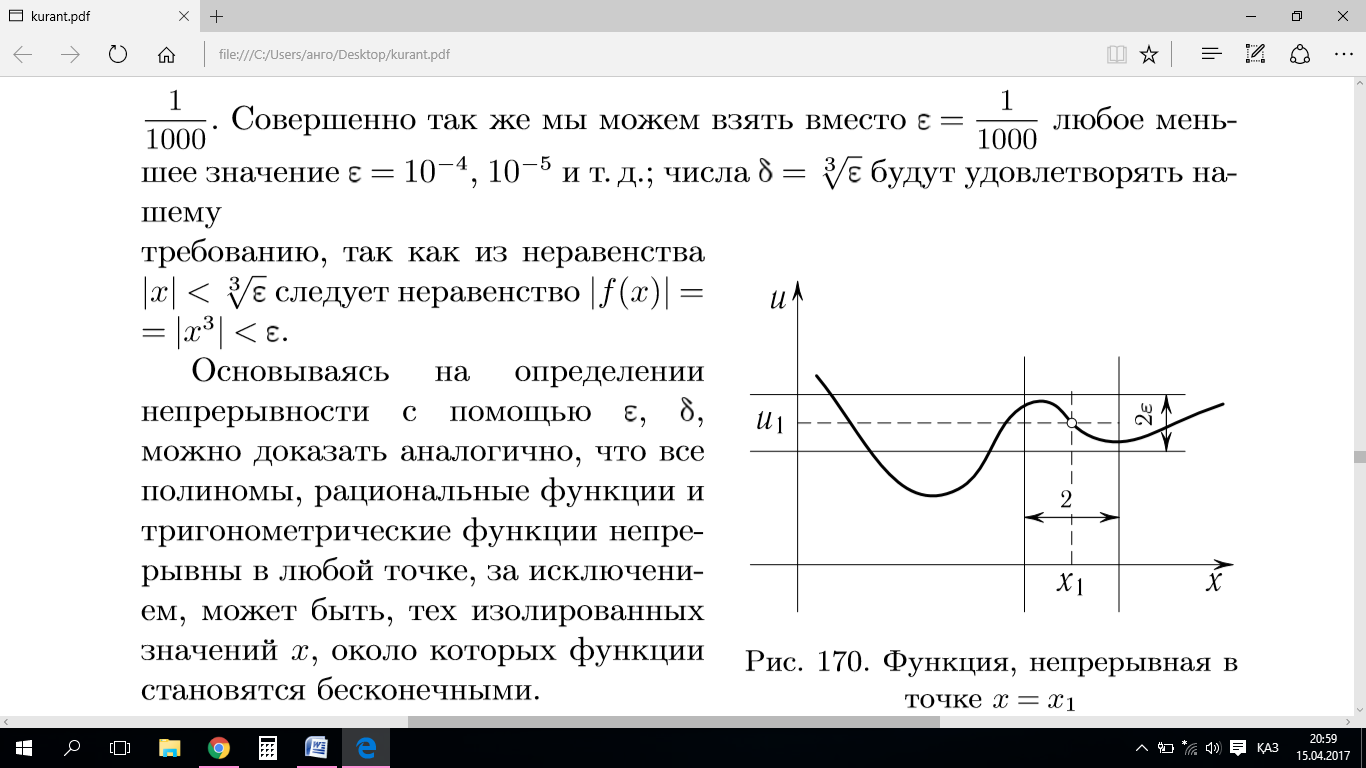
1-сурет.
 нүктесінде үздіксіз
функция
нүктесінде үздіксіз
функция

2-сурет.
Функцияның  нүктесінде үзіліс нүктесі
бар
нүктесінде үзіліс нүктесі
бар
Соңғы
жағдайда  -дің қасындағы вертикаль
жолақтың қаншалықты тар болса да, қашан да оның ішінде ені
2ɛ
болатын горизонталь жолақтың
ішінде жататын графиктің бөлігі жататын
болады.
-дің қасындағы вертикаль
жолақтың қаншалықты тар болса да, қашан да оның ішінде ені
2ɛ
болатын горизонталь жолақтың
ішінде жататын графиктің бөлігі жататын
болады.
Функция үздіксіздік қасиетіне ие болмайтын нүктелер үзіліс нүктелері деп аталады. [15]
Мысалдар қарастырайық.
-
 дәрежелік
функциясы
дәрежелік
функциясы  шексіз түзудің
әрбір а
нүктесінде үздіксіз болады,
мұндағы п
– натурал
сан.
шексіз түзудің
әрбір а
нүктесінде үздіксіз болады,
мұндағы п
– натурал
сан. -
Көпмүшелер және рационал бөлшектер берілген аймақтың әрбір нүктесінде дербес мәнге тең болатын шекті мәнге ие болады. Сондықтан олар берілген аймақтың әрбір нүктесінде үздіксіз функциялар болады.
-
 функциясы
функциясы  нүктесінде үзіледі және сан
осінің басқа нүктелерінде үздіксіз болады. Расында
да,
нүктесінде үзіледі және сан
осінің басқа нүктелерінде үздіксіз болады. Расында
да,  нүктесінде
нүктесінде функциясының оң жақтағы (+1-ге
тең) және сол жақтағы (–1-ге тең) шектері бар болады. Бұл біржақты
шектер өзара тең болмағандықтан,
функциясының оң жақтағы (+1-ге
тең) және сол жақтағы (–1-ге тең) шектері бар болады. Бұл біржақты
шектер өзара тең болмағандықтан,  функциясы 0 нүктесінде үзіледі
(үздіксіз болмайды). Сан осінің басқа нүктелерінде функцияның
дербес мәнге тең болатын шегі бар және осы нүктелерде функция
үздіксіз болады.
функциясы 0 нүктесінде үзіледі
(үздіксіз болмайды). Сан осінің басқа нүктелерінде функцияның
дербес мәнге тең болатын шегі бар және осы нүктелерде функция
үздіксіз болады. -
Дирихле функциясы (1.2 бөлімшені қара) сан осінің әрбір нүктесінде үзіледі, себебі функцияның ешбір нүктеде шегі жоқ. Алайда
 функциясы
функциясы  нүктесінде және шексіз түзудің
басқа нүктелерінде де үздіксіз болады, мұндағы
нүктесінде және шексіз түзудің
басқа нүктелерінде де үздіксіз болады, мұндағы
 – Дирихле
функциясы.
– Дирихле
функциясы.  функциясы
функциясы
 нүктесінде үздіксіз
болатынына көз жеткізейік.
нүктесінде үздіксіз
болатынына көз жеткізейік.  аргументінің мәндерінің шексіз
аз тізбегі үшін
аргументінің мәндерінің шексіз
аз тізбегі үшін  реттілігі шекті болады,
сондықтан
реттілігі шекті болады,
сондықтан  реттілігі шексіз аз болады,
яғни оның шегі
реттілігі шексіз аз болады,
яғни оның шегі  дербес мәніне тең нөл
болады.
дербес мәніне тең нөл
болады.
Функция  жиынында
үздіксіз деп айтамыз, егер функция осы
жиынның әрбір нүктесінде үздіксіз болса.
жиынында
үздіксіз деп айтамыз, егер функция осы
жиынның әрбір нүктесінде үздіксіз болса.
Мысалы, интервалдың әрбір нүктесінде үздіксіз болатын функция интервалдағы үздіксіз функция деп аталады.
Әсіресе
 функциясы
функциясы  сегментінде үздіксіз деп атауға келісейік, егер
функция осы сегменттің әрбір ішкі нүктесінде үзіксіз болса,
сондай-ақ а
нүктесінде оң жақтан үздіксіз
және b
нүктесінде сол жақтан үздіксіз
болса. [16]
сегментінде үздіксіз деп атауға келісейік, егер
функция осы сегменттің әрбір ішкі нүктесінде үзіксіз болса,
сондай-ақ а
нүктесінде оң жақтан үздіксіз
және b
нүктесінде сол жақтан үздіксіз
болса. [16]
2.2. Үздіксіз функцияларға қолданылатын арифметикалық амалдар
Үздіксіз функцияларға қолданылатын амалдар қайтадан үздіксіз функцияларға алып келетініне көз жеткізейік.
Келесі теорема орынды болады.
1-теорема. Бір
жиында  пен
пен
 функциялары берілсін
және бұл функциялар а
нүктесінде үздіксіз болсын.
Онда
функциялары берілсін
және бұл функциялар а
нүктесінде үздіксіз болсын.
Онда 
 және
және
 функциялары а
нүктесінде үздіксіз болады
(бөлімінің жағдайында қосымша
функциялары а
нүктесінде үздіксіз болады
(бөлімінің жағдайында қосымша  деген шарт қою
керек).
деген шарт қою
керек).
Дәлелдеу. а
нүктесінде
үздіксіз  пен
пен
 функциялардың а
нүктесінде
сәйкесінше
функциялардың а
нүктесінде
сәйкесінше  пен
пен
 шегі бар болатындықтан,
онда
шегі бар болатындықтан,
онда  және
және
 функцияларының шектері
табылады және сәйкесінше
функцияларының шектері
табылады және сәйкесінше  және
және
 мәндеріне тең болады. Ал
бұл мәндер берілген функциялардың а
нүктесіндегі дербес мәндерін
тең болады. Яғни берілген функциялар
а
нүктесінде үздіксіз болады.
Дәлелдеу керегі осы. [17]
мәндеріне тең болады. Ал
бұл мәндер берілген функциялардың а
нүктесіндегі дербес мәндерін
тең болады. Яғни берілген функциялар
а
нүктесінде үздіксіз болады.
Дәлелдеу керегі осы. [17]
2.3. Кейбір элементар функциялардың үздіксіздігі
Элементар функциялардың маңызды қасиеттерінің бірі – осы функциялар анықталу аймағының әрбір нүктесінде үздіксіз болуы. Кейбір функцияларға мысал келтіре отырып, функцияның үздіксіздік анықтамасы мен 1-теореманы қолдану арқылы аталған фактіні тексерейік.
-
Рационал функциялардың үздіксіздігі. Сан осінің кез келген
 нүктесінде үздіксіз болатын
функцияның қарапайым мысалы ретінде
нүктесінде үздіксіз болатын
функцияның қарапайым мысалы ретінде  тұрақты функцияны алуға
болады. Расында да, бұл жағдайда
тұрақты функцияны алуға
болады. Расында да, бұл жағдайда  болады, яғни тұрақты функция
сан осінің әрбір нүктесінде үздіксіз
болады.
болады, яғни тұрақты функция
сан осінің әрбір нүктесінде үздіксіз
болады.
Сан осінің кез
келген  нүктесінде
нүктесінде  функциясы да үздіксіз болады,
себебі
функциясы да үздіксіз болады,
себебі  , яғни
функцияның
, яғни
функцияның  нүктесіндегі шегі функцияның
осы нүктедегі мәніне тең. Айтылғанға және 1-теоремаға сәйкес кез
келген
нүктесіндегі шегі функцияның
осы нүктедегі мәніне тең. Айтылғанға және 1-теоремаға сәйкес кез
келген  нүктесінде
нүктесінде
 (п
– натурал сан) функциялары
үздіксіз болады. Белгілі болғандай,
(п
– натурал сан) функциялары
үздіксіз болады. Белгілі болғандай,  функциясы дәрежелік деп
аталады, ал
функциясы дәрежелік деп
аталады, ал

түріндегі функция алгебралық
көпмүше деп аталады, мұндағы  – бүтін
сан,
– бүтін
сан,  – кез келген
сандар.
– кез келген
сандар.
 қосылғыштарының
әрқайсысы екі үздіксіз функцияның (тұрақты және дәрежелік)
көбейтіндісі болады. 1-теоремаға сәйкес ол кез
келген х
нүктесінде үздіксіз.
Осылайша
қосылғыштарының
әрқайсысы екі үздіксіз функцияның (тұрақты және дәрежелік)
көбейтіндісі болады. 1-теоремаға сәйкес ол кез
келген х
нүктесінде үздіксіз.
Осылайша  көпмүшесі кез
келген х
нүктесінде үздіксіз болатын
функциялардың қосындысы болады және сәйкесінше кез
келген х
нүктесінде үздіксіз
болады.
көпмүшесі кез
келген х
нүктесінде үздіксіз болатын
функциялардың қосындысы болады және сәйкесінше кез
келген х
нүктесінде үздіксіз
болады.
Бөлшек-рационал функция, яғни

түріндегі функция бөлімі нөлге
тең болмайтын барлық х
нүктелерінде (яғни бөлімнің
түбірінен басқа барлық нүктелерде) үздіксіз болады,
мұндағы  мен
мен
 – алгебралық көпмүше.
Мысалы,
– алгебралық көпмүше.
Мысалы,  функциясы +1 мен –1
нүктелерінен басқа барлық х
нүктелерінде үздіксіз
болады.
функциясы +1 мен –1
нүктелерінен басқа барлық х
нүктелерінде үздіксіз
болады.
-
Тригонометриялық функциялардың үздіксіздігі.

 тригонометриялық функцияларды
қарастырайық.
тригонометриялық функцияларды
қарастырайық.  функциясының кез
келген х
нүктесінде үздіксіз болатынын
көрсетейік. Функцияның үздіксіздігінің анықтамасын
қолданайық. х
аргументіне
функциясының кез
келген х
нүктесінде үздіксіз болатынын
көрсетейік. Функцияның үздіксіздігінің анықтамасын
қолданайық. х
аргументіне  өсімшесін қою арқылы
функцияның
өсімшесін қою арқылы
функцияның
 немесе
немесе

өсімшесін
аламыз.  үшін теңдіктің оң және сол жақ
шектеріне ауысу арқылы
үшін теңдіктің оң және сол жақ
шектеріне ауысу арқылы

аламыз,
себебі  ,
,
 ,
,
ал шекті функция мен шексіз аз
санның көбейтіндісі шексіз аз сан болады.
Осылайша,  функциясының кез
келген х
нүктесінде үздіксіз
болады.
функциясының кез
келген х
нүктесінде үздіксіз
болады.
 функциясының кез
келген х
нүктесінде үздіксіз болуы дәл
осылай дәлелденеді.
функциясының кез
келген х
нүктесінде үздіксіз болуы дәл
осылай дәлелденеді.
1-теоремаға
сәйкес  пен
пен
 функцияларының
үздіксіздігінен
функцияларының
үздіксіздігінен  және
және
 функцияларының
функцияларының  нүктесінен басқа барлық
нүктелерде,
нүктесінен басқа барлық
нүктелерде,  және
және
 функцияларының
функцияларының  нүктесінен басқа барлық
нүктелерде үздіксіз болады.
нүктесінен басқа барлық
нүктелерде үздіксіз болады.
-
 функциясының
үздіксіздігі. 3-суретте графигі
сызылған
функциясының
үздіксіздігі. 3-суретте графигі
сызылған  функциясы сан осінің барлық
нүктелерінде анықталған және үздіксіз
болады.
функциясы сан осінің барлық
нүктелерінде анықталған және үздіксіз
болады.
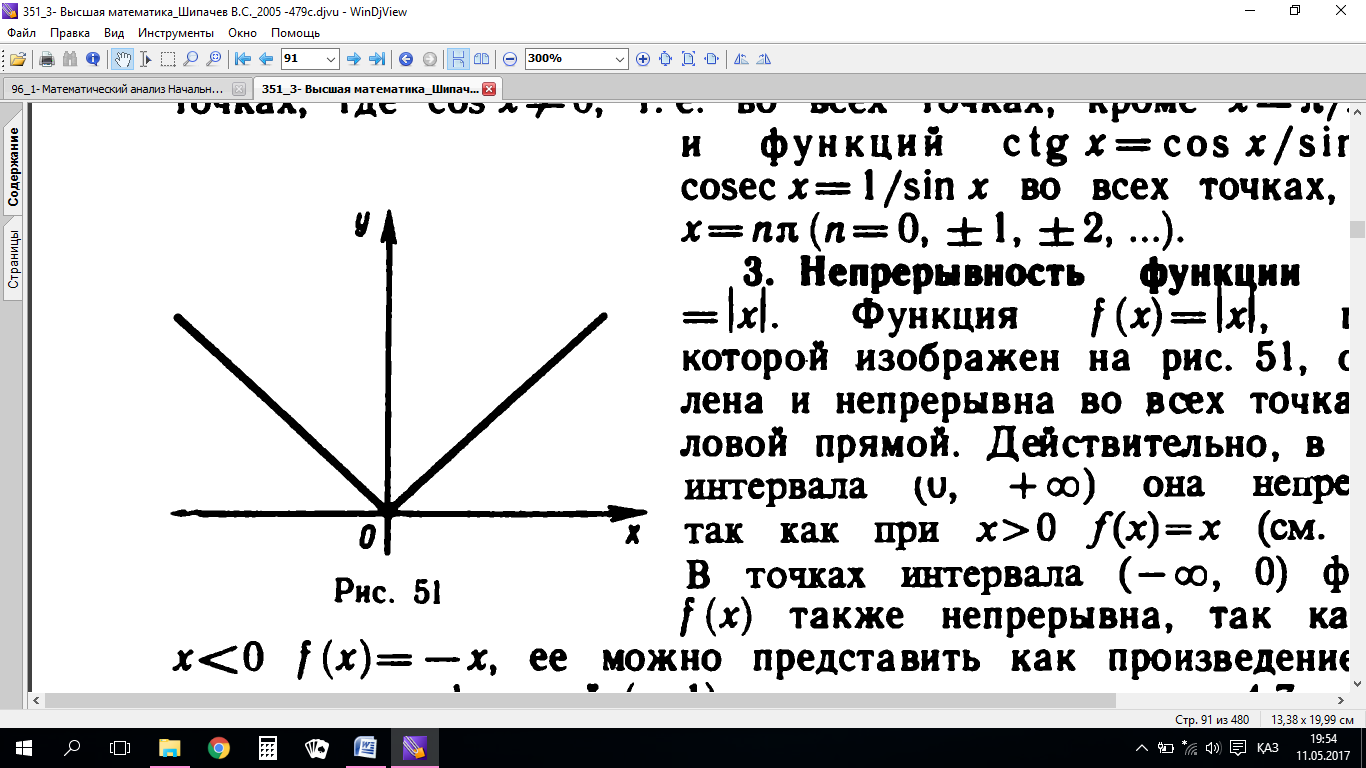
3-сурет.
 функциясы
функциясы
Расында
да,  интервалындағы нүктелерде бұл
функция үздіксіз, себебі
интервалындағы нүктелерде бұл
функция үздіксіз, себебі  болғанда,
болғанда,
 болады.
болады.  интервалындағы нүктелерде де
бұл функция үздіксіз, себебі
интервалындағы нүктелерде де
бұл функция үздіксіз, себебі  болғанда,
болғанда,
 болады және оны (–1)
мен х
екі үздіксіз функцияның
көбейтіндісі ретінде жазуға және көбейтіндінің үздіксіздігі туралы
1-теореманы қолдануға болады.
болады және оны (–1)
мен х
екі үздіксіз функцияның
көбейтіндісі ретінде жазуға және көбейтіндінің үздіксіздігі туралы
1-теореманы қолдануға болады.  функциясының
функциясының  нүктесіндегі үздіксіздігін
анықтау үшін функцияның осы нүктедегі біржақты шектерін
есептейік:
нүктесіндегі үздіксіздігін
анықтау үшін функцияның осы нүктедегі біржақты шектерін
есептейік:

Сонымен,
функцияның  нүктесіндегі оң жақты және сол
жақты шектері бір-біріне сәйкес келеді және функцияның осы
нүктедегі мәніне тең. Осыдан,
нүктесіндегі оң жақты және сол
жақты шектері бір-біріне сәйкес келеді және функцияның осы
нүктедегі мәніне тең. Осыдан,  функциясы
функциясы
 нүктесінде үздіксіз,
яғни сан осінің барлық нүктелерінде үздіксіз
болады.
нүктесінде үздіксіз,
яғни сан осінің барлық нүктелерінде үздіксіз
болады.
Осылайша, қарастырылған функциялардың барлығы анықталу аймағы шоғырланған әрбір нүктеде үздіксіз болады. Қосындының, айырманың, көбейтіндінің және бөліндінің үздіксіздігі туралы 1-теоремаға сәйкес саны шектеулі арифметикалық амалдар арқылы алынған функциялардың да анықталу аймағы шоғырланған әрбір нүктеде үздіксіз болатынын тұжырымдауға болады.
 функциясы
функциясы  интервалында үздіксіз деп
айтамыз, егер функция осы интервалдың әрбір нүктесінде үздіксіз
болса;
интервалында үздіксіз деп
айтамыз, егер функция осы интервалдың әрбір нүктесінде үздіксіз
болса;  кесіндісінде үздіксіз деп
айтамыз, егер функция
кесіндісінде үздіксіз деп
айтамыз, егер функция  интервалында үздіксіз болса.
[18]
интервалында үздіксіз болса.
[18]
2.4. Больцано теоремасы
Бернард Больцано (1781-1848) католикалық дін қызметшісі болған, схоластикалық философияның білгірі, математикалық анализге қазіргі заманғы қатаңдық ұғымын енгізгендердің бірі болды. Оның «Paradoxien des Unendlichen» атты керемет кітабы 1850 жылы шықты. Мұнда алғаш рет үздіксіз функцияларға қатысты көптеген қарапайым мәліметтер дәлелденуі керек деп қабылданды. Осының мысалы ретінде бір айнымалылы функциялар туралы келесідей теореманы алуға болады.
2-теорема.  үздіксіздік интервалында
х-тің қандай да бір мәнінде оң таңбаға ие болатын және х-тің басқа
бір мәнінде теріс таңбаға ие болатын х айнымалысына қатысты
үздіксіз функция х-тің қандай да бір аралық мәнінде нөлге айналуы
керек. Сонымен,
егер
үздіксіздік интервалында
х-тің қандай да бір мәнінде оң таңбаға ие болатын және х-тің басқа
бір мәнінде теріс таңбаға ие болатын х айнымалысына қатысты
үздіксіз функция х-тің қандай да бір аралық мәнінде нөлге айналуы
керек. Сонымен,
егер  функциясы
х-тің
а-дан
b-ға дейінгі барлық мәнінде
үздіксіз болса және
функциясы
х-тің
а-дан
b-ға дейінгі барлық мәнінде
үздіксіз болса және  болса,
онда х
айнымалысының
болса,
онда х
айнымалысының  болатындай α
мәні
табылады.
болатындай α
мәні
табылады.
Больцано теоремасы х осінің бір жағынан екінші жағына өту үшін қандай да бір нүктесінде міндетті түрде қиып өтетін үздіксіз қисық туралы ойларымызбен сәйкес келеді.
Дәлелдеу. Бұл теореманың қатаң
дәлелдеуін келтірейік. Егер Гаусс және басқа да ұлы математиктерге
сүйенсек, бұл фактіні дәлелдеусіз де алуға болады. Біздің
мақсатымыз бұл теореманы нақты сандар жүйесінің негізгі
қасиеттеріне, әсіресе Дедекинд-Кантордың керуші кесінділер туралы
постулатына негіздеу болып келеді. Ол үшін
берілген  функциясы
жататын
функциясы
жататын  болатын
I
кесіндісін қарастырайық және
оны
болатын
I
кесіндісін қарастырайық және
оны  орта нүктесі арқылы екі
бөлікке бөлейік. Егер осы орта нүктеде
орта нүктесі арқылы екі
бөлікке бөлейік. Егер осы орта нүктеде
 шықса, онда дәлелдейтін
ештеңе қалмайды. Егер, алайда,
шықса, онда дәлелдейтін
ештеңе қалмайды. Егер, алайда,  болса,
онда
болса,
онда  мәні нөлден үлкен немесе
нөлден кіші болу керек. Екі жағдайда да
I
кесіндісінің бөліктерінің бірі
оның екі шетіндегі
мәні нөлден үлкен немесе
нөлден кіші болу керек. Екі жағдайда да
I
кесіндісінің бөліктерінің бірі
оның екі шетіндегі  функциясының мәндерінің
таңбалары әр түрлі болады деген қасиетке тағы да ие
болады.
функциясының мәндерінің
таңбалары әр түрлі болады деген қасиетке тағы да ие
болады.
Бұл
кесіндіні  деп белгілейік. Бұл үрдісті
қайталай отырып
деп белгілейік. Бұл үрдісті
қайталай отырып  кесіндісін қақ бөлеміз;
онда
кесіндісін қақ бөлеміз;
онда  ортасында
ортасында
 болады немесе
біз
болады немесе
біз  кесіндісінің қандай да бір
жартысында функцияның мәндері әр түрлі болатын жартысын аламыз. Осы
үрдісті жалғастыра отырып, ең соңында кесіндіні бөлудің соңғы
қадамында
кесіндісінің қандай да бір
жартысында функцияның мәндері әр түрлі болатын жартысын аламыз. Осы
үрдісті жалғастыра отырып, ең соңында кесіндіні бөлудің соңғы
қадамында  болатындай нүктені табамыз
немесе
болатындай нүктені табамыз
немесе  керуші кесінділер қатарын
аламыз. Соңғы жағдайда Дедекинд-Кантордың постулаты
бастапқы I
кесіндісінде барлық
кесінділерге тиісті болатын α
нүктесінің табылатынын
қамтамасыз етеді.
керуші кесінділер қатарын
аламыз. Соңғы жағдайда Дедекинд-Кантордың постулаты
бастапқы I
кесіндісінде барлық
кесінділерге тиісті болатын α
нүктесінің табылатынын
қамтамасыз етеді.  , яғни
α
– дәлелдеуді қажет ететін сол
нүкте болады.
, яғни
α
– дәлелдеуді қажет ететін сол
нүкте болады.
Осыған
дейін  функциясының үздіксіздігі
туралы болжам қолданылған жоқ еді. Осы жерде оған сүйеніп,
теореманы кері болжау тәсілі арқылы дәлелдеу керек. Қарсы болжамды
қолданып, қарама-қайшылыққа келу арқылы
функциясының үздіксіздігі
туралы болжам қолданылған жоқ еді. Осы жерде оған сүйеніп,
теореманы кері болжау тәсілі арқылы дәлелдеу керек. Қарсы болжамды
қолданып, қарама-қайшылыққа келу арқылы
 екенін
дәлелдейміз.
екенін
дәлелдейміз.  деп болжайық:
мысалы,
деп болжайық:
мысалы,  болсын.
болсын.
 функциясы үздіксіз
болғандықтан,
функциясы үздіксіз
болғандықтан,  функциясының J
кесіндісіндегі
мәні
функциясының J
кесіндісіндегі
мәні  мәнінен
ɛ-ға аз болатындай
центрі α
нүктесі болатын ұзындығы
2δ-ға тең
J
кесіндісін аламыз. Сонан
соң
мәнінен
ɛ-ға аз болатындай
центрі α
нүктесі болатын ұзындығы
2δ-ға тең
J
кесіндісін аламыз. Сонан
соң  болғандықтан,
онда J
кесіндісінің әрбір
нүктесінде
болғандықтан,
онда J
кесіндісінің әрбір
нүктесінде  , яғни
J
кесіндісінде
, яғни
J
кесіндісінде  болады деп айта аламыз.
Бірақ J
кесіндісі – бекітілген
кесінді, және егер п
өте үлкен болса, онда
кіші
болады деп айта аламыз.
Бірақ J
кесіндісі – бекітілген
кесінді, және егер п
өте үлкен болса, онда
кіші  кесіндісі міндетті
түрде J
кесіндісінің ішінде болуы
керек, себебі
кесіндісі міндетті
түрде J
кесіндісінің ішінде болуы
керек, себебі  ұзындықтарының қатары нөлге
ұмтылады. Осы жерде қарама-қайшылық пайда
болды:
ұзындықтарының қатары нөлге
ұмтылады. Осы жерде қарама-қайшылық пайда
болды:  функциясы
функциясы
 кесіндісінің шеткі
нүктелерінде қарама-қарсы таңбаларға ие болады,
яғни
кесіндісінің шеткі
нүктелерінде қарама-қарсы таңбаларға ие болады,
яғни  функциясы
J
кесіндісінде теріс таңбаға ие
болады. Осыдан
функциясы
J
кесіндісінде теріс таңбаға ие
болады. Осыдан  сонымен қатар (дәл
осылайша)
сонымен қатар (дәл
осылайша)  болжамының қате екені шығады;
яғни
болжамының қате екені шығады;
яғни  екені дәлелденді.
[19]
екені дәлелденді.
[19]
2.5. Больцано теоремасының қолданылуы
Геометриялық қолданылуы. Жай және жалпы Больцано теоремасы арқылы алғашқыда жеңіл болып көрінбейтін кейбір пікірлерді дәлелдеуге болады. Әуелі мынаны енгізейік: егер А және В – жазықтықта берілген екі фигура болса, онда осы жазықтықта берілген үшбұрыштарды бір мезгілде теңөлшемді (ауданы бойынша) бөліктерге бөлетін түзу табылады. Мұндағы «Фигура» дегеніміз – жай қисық сызықпен шектелген жазықтықтың бөлігі.
Дәлелдеуді аталған жазықтықтан
кез келген шатты Р
нүктесін алудан бастап, осы
нүктеден шартты PR
сәулесін жүргізейік. Осы сәуле
арқылы бұрыштарды өлшеуді жүргізіп тұрамыз.
PR
сәулесімен х
бұрыш
жасайтын PS
сәулесі қандай болса
да, PS
сәулесіне параллель
және А фигурасын теңөлшемді
бөліктерге бөлетін бағытталған түзу табылады.
Расында да, PS
сәулесіне параллель болатын
және А
фигурасының бір жағында
орналасқан бағытталған түзулердің біреуін алып,
оны  деп
белгілейік.
деп
белгілейік.  түзуін нәтижесінде
(оны
түзуін нәтижесінде
(оны  деп
белгілейміз) А
фигурасы толықтай келесі
жағына өтетіндей етіп параллель көшіреміз (4-сурет). Бұл жағдайда
бағытталған түзудің оң жағында орналасқан
А
бөлігінің ауданы мен
бағытталған түзудің сол жағында орналасқан (егер түзу «солтүстікке»
бағытталған деп айтсақ, «оң жағында» – «шығыста», «сол жағында» –
«батыста») А
бөлігінің ауданының айырмасы
ретінде анықталатын функция
деп
белгілейміз) А
фигурасы толықтай келесі
жағына өтетіндей етіп параллель көшіреміз (4-сурет). Бұл жағдайда
бағытталған түзудің оң жағында орналасқан
А
бөлігінің ауданы мен
бағытталған түзудің сол жағында орналасқан (егер түзу «солтүстікке»
бағытталған деп айтсақ, «оң жағында» – «шығыста», «сол жағында» –
«батыста») А
бөлігінің ауданының айырмасы
ретінде анықталатын функция  түзуіне қатысты оң таңбалы
және
түзуіне қатысты оң таңбалы
және  түзуіне қатысты теріс таңбалы
болады. Бұл функция үздіксіз болғандықтан, онда Больцано теоремасы
бойынша ол
түзуіне қатысты теріс таңбалы
болады. Бұл функция үздіксіз болғандықтан, онда Больцано теоремасы
бойынша ол  белгісі арқылы белгіленетін
түзудің қандай да бір аралық орналасуында нөлге айналады және бұл
жағдайда А
фигурасы қақ бөлінеді.
Сонымен, х
қандай болса да
(
белгісі арқылы белгіленетін
түзудің қандай да бір аралық орналасуында нөлге айналады және бұл
жағдайда А
фигурасы қақ бөлінеді.
Сонымен, х
қандай болса да
( ),
А
фигурасын қақ
бөлетін
),
А
фигурасын қақ
бөлетін  түзуі
табылады.
түзуі
табылады.
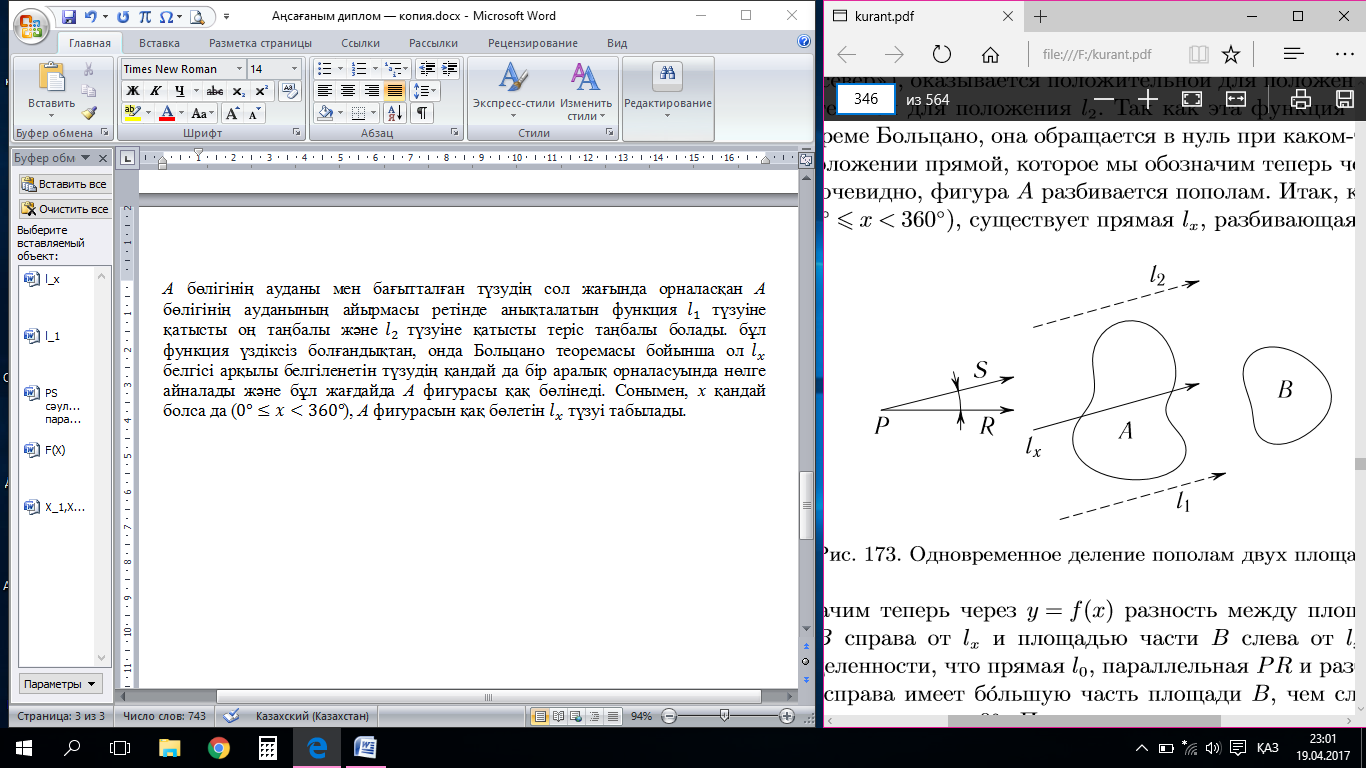
4-сурет. Екі ауданды бір мезгілде қақ бөлу
Енді
 түзуінің оң жағында
орналасқан В
фигурасының бір бөлігінің
ауданы мен
түзуінің оң жағында
орналасқан В
фигурасының бір бөлігінің
ауданы мен  түзуінің сол жағында
орналасқан В
фигурасының екінші бөлігінің
ауданының айырмасын
түзуінің сол жағында
орналасқан В
фигурасының екінші бөлігінің
ауданының айырмасын  деп белгілейік. Нақтылау
үшін PR
сәулесіне параллель
және А
фигурасын қақ
бөлетін
деп белгілейік. Нақтылау
үшін PR
сәулесіне параллель
және А
фигурасын қақ
бөлетін  түзуінің оң
жағында В
фигурасы ауданының басым
бөлігі орналасатынын атап кетейін; онда
у
оң таңбалы болады,
егер
түзуінің оң
жағында В
фигурасы ауданының басым
бөлігі орналасатынын атап кетейін; онда
у
оң таңбалы болады,
егер  болса.
Енді х
болса.
Енді х
 -қа дейін артсын;
онда PR
сәулесіне параллель
және А
фигурасын қақ
бөлетін
-қа дейін артсын;
онда PR
сәулесіне параллель
және А
фигурасын қақ
бөлетін  түзуі
түзуі
 түзуімен беттеседі
(бірақ қарама-қарсы бағытталады, ал «оң» және «сол» жақтары
жылжыды); осыдан
түзуімен беттеседі
(бірақ қарама-қарсы бағытталады, ал «оң» және «сол» жақтары
жылжыды); осыдан  болғандағы у-тің мәні
болғандағы у-тің мәні
 болғандағы мәнімен
сәйкес келетіні, бірақ қарама-қарсы таңбаға ие болатыны, яғни теріс
болатыны анық көрініп тұр. у
дегеніміз
болғандағы мәнімен
сәйкес келетіні, бірақ қарама-қарсы таңбаға ие болатыны, яғни теріс
болатыны анық көрініп тұр. у
дегеніміз
 болғандағы х-тің функциясы болғандықтан
(қиюшы түзудің бұрылуы кезінде аталған аудандардың айырымы үздіксіз
өзгеретіні айқын), онда у
функциясы нөлге
айналатындай
болғандағы х-тің функциясы болғандықтан
(қиюшы түзудің бұрылуы кезінде аталған аудандардың айырымы үздіксіз
өзгеретіні айқын), онда у
функциясы нөлге
айналатындай  мәні табылады. Бірақ
онда
мәні табылады. Бірақ
онда  түзуі
А
және
В
фигураларын бір мезгілде қақ
бөледі. Теорема дәлелденді.
түзуі
А
және
В
фигураларын бір мезгілде қақ
бөледі. Теорема дәлелденді.
Осы жерде біз жай ғана берілген қасиетке ие болатын түзудің табылатынын анықтадық, бірақ оны салудың белгілі бір жолын көрсетпедік: бұл – бар болуды дәлелдеудің «таза» математикалық әдісі.
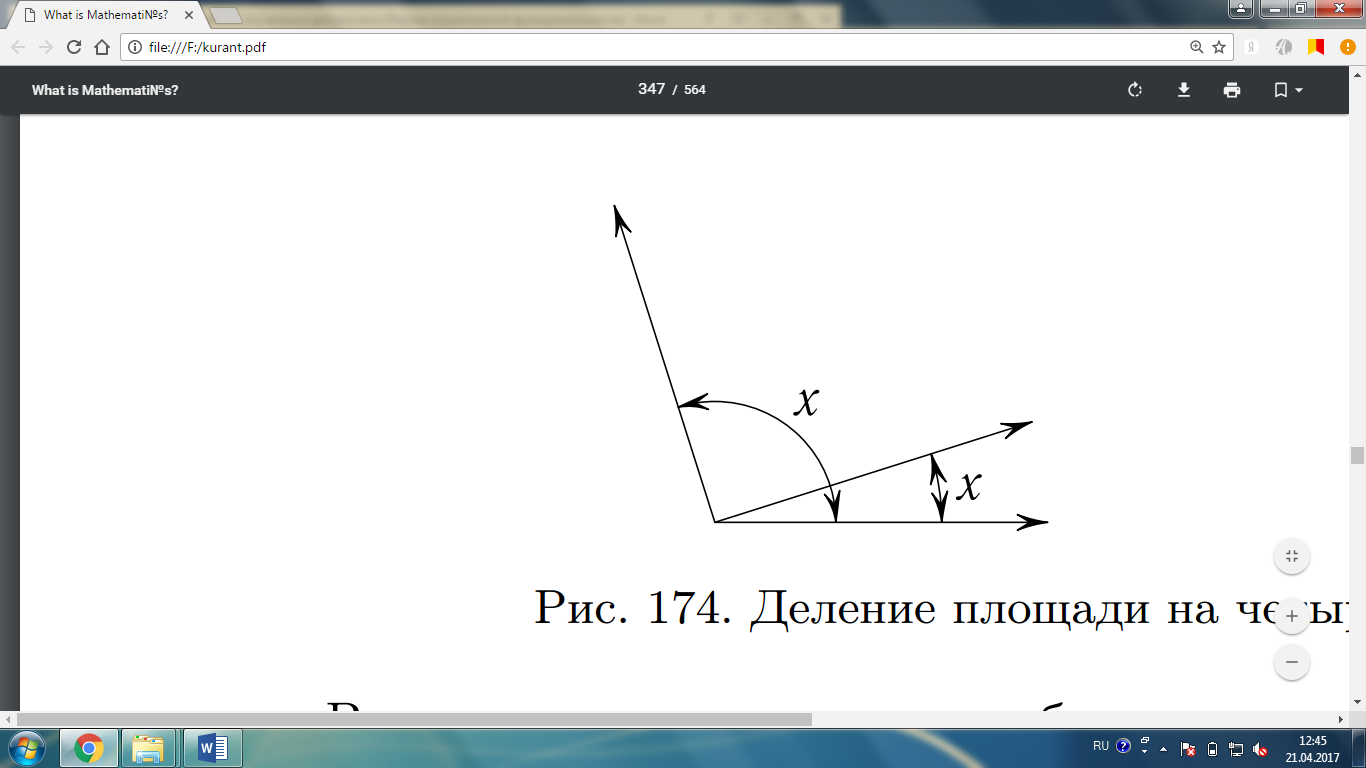
5-сурет. Ауданды тең төрт бөлікке бөлу
Осыған ұқсас басқа мәселе:
жазықтықта А
фигурасы беріліп тұр;
оны өзара перпендикуляр
екі түзумен
төрт теңөлшемді бөлікке бөлу керек.
Шешімнің бар болуын дәлелдеу үшін алдыңғы есептің
шешіміндегі  түзуі енгізіліп,
ал В
фигурасы әлі енгізілмеген
бөлімге оралайық.
түзуі енгізіліп,
ал В
фигурасы әлі енгізілмеген
бөлімге оралайық.  түзуіне перпендикуляр болатын
және А
фигурасын қақ
бөлетін
түзуіне перпендикуляр болатын
және А
фигурасын қақ
бөлетін  түзуін қарастырайық.
Егер А
фигурасының төрт бөлігін
5-суретте көрсетілгендей етіп нөмірлесек,
онда
түзуін қарастырайық.
Егер А
фигурасының төрт бөлігін
5-суретте көрсетілгендей етіп нөмірлесек,
онда

және

аламыз. Екі теңдікті бір-бірінен азайту арқылы

аламыз, яғни

болады, осыдан

болады.
Осылайша, мәселенің шешімінің
бар болуы дәлелденеді, егер  түзуі үшін берілген фигураның
екі бөлігінің
түзуі үшін берілген фигураның
екі бөлігінің

теңдігін
қанағаттандыратын α
бұрышының табылатынын
анықталатын болса, себебі бұдан төрт бөліктің де теңдігі шығады.
Енді функциясын
қарастырайық,
функциясын
қарастырайық,

мұндағы
 және
және  – берілген
фигураның
– берілген
фигураның  түзуіне сәйкес болатын
бөліктері.
түзуіне сәйкес болатын
бөліктері.  болғанда,
мысалы,
болғанда,
мысалы,  болсын.
Онда
болсын.
Онда  болғанда,
болғанда,
 болады.
Бірақ
болады.
Бірақ  – үздіксіз функция;
яғни
– үздіксіз функция;
яғни  мен
мен
 аралығындағы α-ның қандай да бір
мәнінде
аралығындағы α-ның қандай да бір
мәнінде  болады.
Онда
болады.
Онда  мен
мен
 түзулері фигураны
теңөлшемді төрт бөлікке бөледі.
түзулері фигураны
теңөлшемді төрт бөлікке бөледі.
Бұл мәселелер үшөлшемді немесе одан да көп болатын жағдайларда жалпыланады. Үшөлшемді жағдайда алғашқы мәселе былай пайымдалады: кеңістікте үш дене берілген; екі денені де бір мезгілде қақ бөлетін жазықтықты табу керек. Шешімнің бар болуын дәлелдеу үрдісі де Больцано теоремасына негізделеді. [20]
Бір механикалық мәселеге қолданылуы. Енді кезекте Больцано теоремасының бір механикалық мәселеде қолданылуын қарастыратын боламыз. Бұл мәселені Г.Уитни ұсынған болатын.
Айталық, бір пойыз қандай да
бір шектеулі уақыт бойына А
пунктінен
В
пунктіне түзусызықты қозғалып
келеді. Қозғалыс бірқалыпты жылдамдықпен немесе бірқалыпты үдеумен
жүреді деп мүлдем пайымдалмайды. Керісінше, пойыз қалағаны бойынша
жүре алады: жылдамдықты арттыра алады, кеміте алады; жол бойында
пойыздың тоқтауы да қарастырылуы мүмкін. Бірақ қалай болғанда да,
берілген уақыт аралығында пойыздың қозғалысы алдын ала белгілі
болады; басқаша айтқанда,  функциясы берілген деп
есептеледі, мұндағы s
–
пойыздың А
станциясынан қарағандағы
қашықтығы, ал t
– пойыздың қозғалыс
бастағаннан кезден есептелетін уақыт. Вагондардың біріндегі еденге
топса арқылы ауыр өзекше бекітілген, бұл өзекше вагондардың осіне
параллель бағытта өзінің осі бойынша үйкеліссіз алға және артқа
(еденнен еденге қарай) қозғала алады. (Еденге тигеннен кейін өзекше
келесі «секіруге» дейін еденде жатады деп ойлайық). Мәселе
мынада: пойыз қозғалған мезетте
барлық жол бойына пойыздың қозғалысы мен өзінің ауырлық күшінің
ықпалында болып, еденге тимейтіндей етіп өзекшені бастапқы қалыпта,
яғни қандай да бір көлбеу бұрышына қойып қоюға болады
ма?
функциясы берілген деп
есептеледі, мұндағы s
–
пойыздың А
станциясынан қарағандағы
қашықтығы, ал t
– пойыздың қозғалыс
бастағаннан кезден есептелетін уақыт. Вагондардың біріндегі еденге
топса арқылы ауыр өзекше бекітілген, бұл өзекше вагондардың осіне
параллель бағытта өзінің осі бойынша үйкеліссіз алға және артқа
(еденнен еденге қарай) қозғала алады. (Еденге тигеннен кейін өзекше
келесі «секіруге» дейін еденде жатады деп ойлайық). Мәселе
мынада: пойыз қозғалған мезетте
барлық жол бойына пойыздың қозғалысы мен өзінің ауырлық күшінің
ықпалында болып, еденге тимейтіндей етіп өзекшені бастапқы қалыпта,
яғни қандай да бір көлбеу бұрышына қойып қоюға болады
ма?
Алғашқы уақытта пойыздың қозғалыс сызбасын алдын ала біле отырып, ауырлық күші мен реакция күштерінің өзара әрекеттесуінің нәтижесінде өзекшенің берілген шартқа, яғни бастапқы қалыпты дұрыс таңдау шарына сәйкес қажетті тепе-теңдігін сақтауын қамтамасыз ету мүмкін емес болып көрінеді. Бірақ мұндай бастапқы қалыпты табу мүмкін болады дегенді дәлелдейміз.
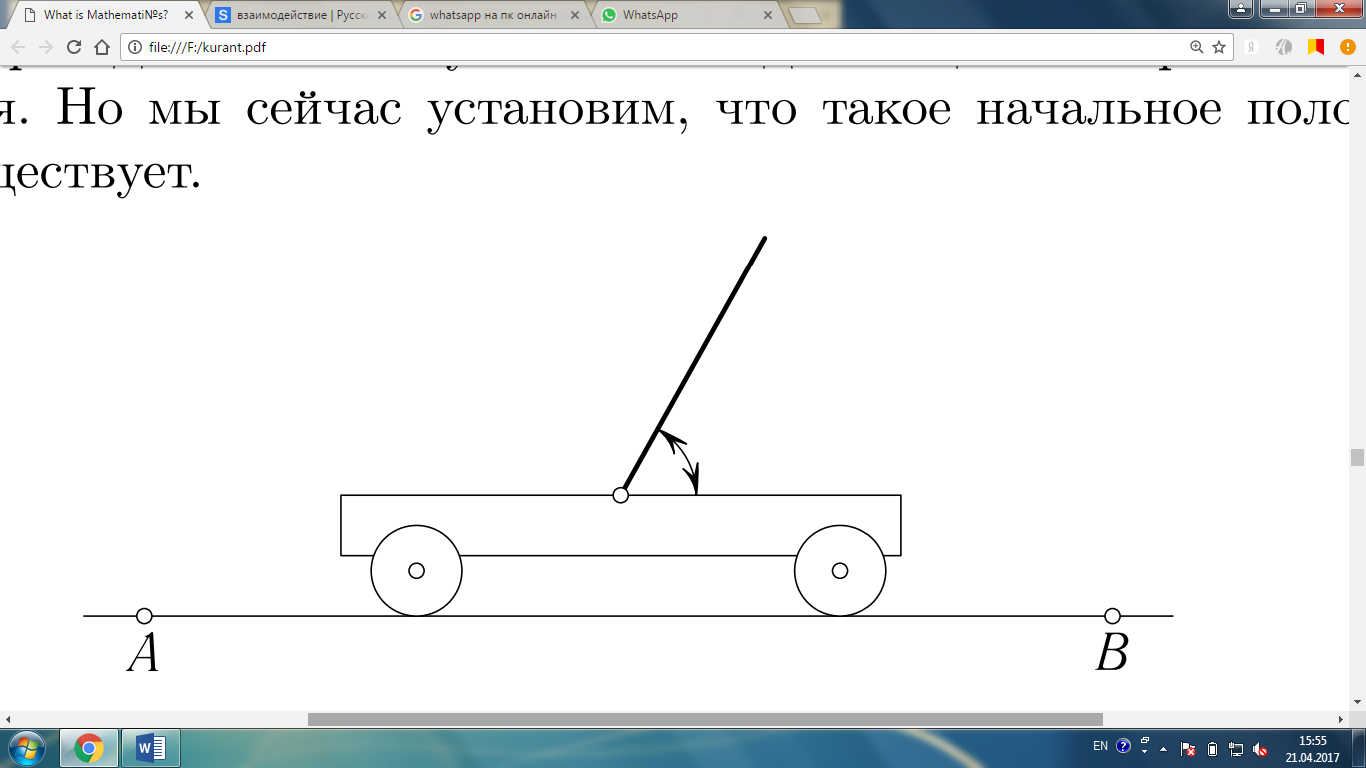
6-сурет. Уитни мәселесі
Бұл мәселені дәлелдеу динамиканың заңдарын білуді талап етпейді. (Бұл мәселені динамиканың заңдарына сүйене отырып дәлелдеу өте қиын болар еді). Физикалық мазмұндағы бір ғана жорамалды енгізу жеткілікті: өзекшенің келесі қозғалысы оның бастапқы қалыптағы күйіне үздіксіз байланысты болады; соның ішінде, пойыздың қозғалысы барысында берілген бастапқы қалыпта өзекше еденнің бір жағына құласа, онда берілген бастапқы қалыптан көп айырмашылығы жоқ кез келген бастапқы қалыпта өзекше еденнің қарама-қарсы жағына құламайды.
Енді кез келген уақыт
мезетінде өзекшенің қалыбы өзекшенің еденмен
жасайтын α
бұрышы арқылы сипатталатынына
назар аударайық.  және
және
 бұрыштарына екі
қарама-қарсы көлденең (жатқан) қалып сәйкес келеді. Өзекшенің
бастапқы қалыбындағы α
бұрышының
мәнін х
деп белгілейік. Берілген
мәселенің экзестенциалды болуы салдарынан оны дәлелдеу жанама түрде
болады. Айталық, барлық жағдайда, яғни өзекшенің кез
келген бастапқы қалыбында өзекше міндетті түрде бір жаққа немесе
екінші жаққа құлайды, яғни α
бұрышы
бұрыштарына екі
қарама-қарсы көлденең (жатқан) қалып сәйкес келеді. Өзекшенің
бастапқы қалыбындағы α
бұрышының
мәнін х
деп белгілейік. Берілген
мәселенің экзестенциалды болуы салдарынан оны дәлелдеу жанама түрде
болады. Айталық, барлық жағдайда, яғни өзекшенің кез
келген бастапқы қалыбында өзекше міндетті түрде бір жаққа немесе
екінші жаққа құлайды, яғни α
бұрышы
 немесе
немесе  мәнін қабылдайды.
Онда
мәнін қабылдайды.
Онда  функциясын
өзекше
функциясын
өзекше  немесе
немесе
 бұрышының мәніне сәйкес
еденнің бір жағына құлауына байланысты
бұрышының мәніне сәйкес
еденнің бір жағына құлауына байланысты
 немесе –1 деп
сипаттайық.
немесе –1 деп
сипаттайық.  функциясының қасиеттері
мынадай: ол
функциясының қасиеттері
мынадай: ол  интервалында берілген және бұл
интервалда үздіксіз, сондай-ақ
интервалында берілген және бұл
интервалда үздіксіз, сондай-ақ  . Осыдан, Больцано теоремасына
сәйкес х-тің қандай да бір аралық
мәнінде
. Осыдан, Больцано теоремасына
сәйкес х-тің қандай да бір аралық
мәнінде 
 теңдігі орындалу керек. Ал бұл
ұйғарым
теңдігі орындалу керек. Ал бұл
ұйғарым  функциясы тек қана +1 және –1
мәндерін қабылдау керек деген пікірге қайшы келеді. Сондықтан, кез
келген бастапқы қалыпқа қойылған өзекше пойыздың қозғалысы
барысында еденнің бір жағына құлайды деп алынған жорамалды теріс
деп қабылдап, одан бас тарту керек.
функциясы тек қана +1 және –1
мәндерін қабылдау керек деген пікірге қайшы келеді. Сондықтан, кез
келген бастапқы қалыпқа қойылған өзекше пойыздың қозғалысы
барысында еденнің бір жағына құлайды деп алынған жорамалды теріс
деп қабылдап, одан бас тарту керек.
Көрсетілген дәлелдеу тек қана
теориялық тұрғыдан қарастырылғаны анық, себебі дәлелдеу
қорытындысында өзекшенің бастапқы қалыбын анықтау бойынша ешқандай
нұсқаулар берілмейді. Сонымен қатар мұндай қалып теориялық тұрғыдан
алғанда абсолютті дәл есептелетін болған болса да, өзінің
тұрақсыздығы салдарынан практикалық жағынан еш пайдасыз болар еді.
Осылайша, мысалы, шекті жағдайда, егер пойыз «сапар» барысында
қозғалмайтын болса, шешімі анық болады:
 ; бірақ тегіс көлденең
беттің үстінде инені тік қалыбында тұрғызуға талпынған әрбір адам
бұл мәселені шешу практикалық тұрғыдан қарағанда мүмкін емес екенін
біледі. Алайда, математикалық тұрғыдан қарағанда келтірілген
дәлелдеу даусыз қызығушылық танытатыны рас.
[21]
; бірақ тегіс көлденең
беттің үстінде инені тік қалыбында тұрғызуға талпынған әрбір адам
бұл мәселені шешу практикалық тұрғыдан қарағанда мүмкін емес екенін
біледі. Алайда, математикалық тұрғыдан қарағанда келтірілген
дәлелдеу даусыз қызығушылық танытатыны рас.
[21]
2.6. Вейерштрасстың экстремалдық мәндер туралы теоремалары
Үздіксіз функцияларға қатысты өзге маңызды фактіні Карл Вейерштасс (1815-1897) тұжырымдаған болатын және бұл адам қазіргі кездегі математикалық анализдегі қатаңдыққа деген ұмтылыстың пайда болуына жауапты. Бұл теорема былайша пайымдалады:
3-теорема. Егер  функциясы шеткі a мен b
нүктелерін қоса алғандағы
функциясы шеткі a мен b
нүктелерін қоса алғандағы  , I интервалында үздіксіз
болса, онда I интервалында
, I интервалында үздіксіз
болса, онда I интервалында  функциясы ең үлкен М мәніне
ие болатын ең болмағанда бір нүкте және
функциясы ең үлкен М мәніне
ие болатын ең болмағанда бір нүкте және
 функциясы ең кіші т
мәніне ие болатын басқа нүкте табылады.
Басқаша
айтқанда
функциясы ең кіші т
мәніне ие болатын басқа нүкте табылады.
Басқаша
айтқанда  үздіксіз функцияның графигінде
ең болмағанда бір ең жоғарғы және бір ең кіші нүктелер болу
керек.
үздіксіз функцияның графигінде
ең болмағанда бір ең жоғарғы және бір ең кіші нүктелер болу
керек.
Егер
 функциясы I
интервалының шеткі
нүктелерінде үздіксіз болмаса, онда бұл тұжырым қате болуы мүмкін.
Мысалы,
функциясы I
интервалының шеткі
нүктелерінде үздіксіз болмаса, онда бұл тұжырым қате болуы мүмкін.
Мысалы,  функциясы
функциясы
 аралығының ішінде
үздіксіз болғанымен, оның бұл аралықтағы ең үлкен мәні жоқ. Сонымен
қатар үзілісті функция шектеулі болса да, ол ең үлкен және ең кіші
мәндеріне ие болмауы мүмкін. Мысалы, төмендегідей анықталатын
«төтенше» үзілісті
аралығының ішінде
үздіксіз болғанымен, оның бұл аралықтағы ең үлкен мәні жоқ. Сонымен
қатар үзілісті функция шектеулі болса да, ол ең үлкен және ең кіші
мәндеріне ие болмауы мүмкін. Мысалы, төмендегідей анықталатын
«төтенше» үзілісті  функциясын
қарастырайық:
функциясын
қарастырайық:  аралығында
аралығында
х
иррационал
болғанда,  ,
,
х
рационал
болғанда,  .
.
Бұл функцияның қабылдайтын
мәндерінің барлығы 0 мен 1-дің аралығында жатыр. Олардың ішінде 0
мен 1-ге өте жақын мәндер де бар: олар
х-ті иррационал және 0 немесе
1-ге өте жақын етіп таңдасақ шығады. Бірақ
 ешқашан 0-ге де, 1-ге де
тең бола алмайды, себебі рационал х
үшін
ешқашан 0-ге де, 1-ге де
тең бола алмайды, себебі рационал х
үшін
 , ал
иррационал х
үшін
, ал
иррационал х
үшін
 болады. Сонымен, 0 мен 1
мәндері ешбір нүктеде шықпайды.
болады. Сонымен, 0 мен 1
мәндері ешбір нүктеде шықпайды.
Дәлелдеу. Вейерштрасс теоремасы Больцано
теоремасы секілді дәлелденеді. I
интервалын екі жағынан
шектелген  пен
пен
 интервалдарына бөлейік
және назарымызды
интервалдарына бөлейік
және назарымызды  интервалына аударайық, бұл
интервалдан
интервалына аударайық, бұл
интервалдан  функциясының ең үлкен мәнін
іздейміз, егер
де
функциясының ең үлкен мәнін
іздейміз, егер
де  интервалында
интервалында  интервалындағы
интервалындағы  функциясының барлық
мәндерінен
функциясының барлық
мәндерінен  мәні үлкен болатын α
нүктесі табылмаса. Таңдап алынған
интервалды
мәні үлкен болатын α
нүктесі табылмаса. Таңдап алынған
интервалды  деп белгілейік.
Енді I
интервалында жасаған
амалдарды
деп белгілейік.
Енді I
интервалында жасаған
амалдарды  интервалында қайталап
орындайық; бұдан
интервалында қайталап
орындайық; бұдан  интервалын алайық және т.с.с.
Бұл үрдіс
интервалын алайық және т.с.с.
Бұл үрдіс  ішкі интервалдар қатарын
анықтайды, олардың барлығында қандай да бір
z
нүктесі болады. Осы нүктедегі
функцияның
ішкі интервалдар қатарын
анықтайды, олардың барлығында қандай да бір
z
нүктесі болады. Осы нүктедегі
функцияның  мәні
мәні
 функциясының бастапқы
интервалдағы барлық мәндерінің ішіндегі ең үлкені екенін
дәлелдейміз, яғни
функциясының бастапқы
интервалдағы барлық мәндерінің ішіндегі ең үлкені екенін
дәлелдейміз, яғни  болатындай s
нүктесінің табылуы мүмкін
еместігін көрсетеміз. Айталық,
болатындай s
нүктесінің табылуы мүмкін
еместігін көрсетеміз. Айталық,  шартын
қанағаттандыратын s
нүктесі табылды дейік,
мұндағы ɛ
– қандай да бір (мүмкін өте
аз) оң сан.
шартын
қанағаттандыратын s
нүктесі табылды дейік,
мұндағы ɛ
– қандай да бір (мүмкін өте
аз) оң сан.  функциясы үздіксіз
болғандықтан, z
нүктесін
s
нүктесін қоса алмайтындай етіп
кішкентай К
интервалымен шектей аламыз
және бұл К
интервалында
функциясы үздіксіз
болғандықтан, z
нүктесін
s
нүктесін қоса алмайтындай етіп
кішкентай К
интервалымен шектей аламыз
және бұл К
интервалында  функциясының
мәндері
функциясының
мәндері  мәнінен
ɛ-ға кем болады, сондықтан бұл
интервалдан міндетті түрде
мәнінен
ɛ-ға кем болады, сондықтан бұл
интервалдан міндетті түрде  іздейміз. Бірақ
үлкен п
мәндері
кезінде
іздейміз. Бірақ
үлкен п
мәндері
кезінде  интервалы
К
интервалының ішінде жатады,
сонымен қатар х
үшін
интервалы
К
интервалының ішінде жатады,
сонымен қатар х
үшін
 -тің
-тің  интервалынан тыс жатқан ешбір
мәні осы интервалдың құрамындағы х
нүктелеріндегі
интервалынан тыс жатқан ешбір
мәні осы интервалдың құрамындағы х
нүктелеріндегі  функциясының мәндерінен артық
бола алмайтындай етіп
функциясының мәндерінен артық
бола алмайтындай етіп  интервалы
анықталды.
интервалы
анықталды.
Бірақ
s
нүктесі
 интервалынан тысқары
жатады және ол интервалда
интервалынан тысқары
жатады және ол интервалда  болады,
ал К
интервалында, ал ол
арқылы
болады,
ал К
интервалында, ал ол
арқылы  интервалында
интервалында  болады. Осылайша, біз
қарама-қайшылыққа келдік.
болады. Осылайша, біз
қарама-қайшылыққа келдік.
Ең кіші
т
мәнінің ең болмағанда
біреуінің табылуы осы әдіспен дәлелденеді; ол алдыңғы дәлелдеудің
салдары болады, себебі  функциясының ең кіші
мәні
функциясының ең кіші
мәні  функциясының ең үлкен мәніне
сәйкес келеді.
функциясының ең үлкен мәніне
сәйкес келеді.
Вейерштрасс теоремасын дәлелдеу әдісі арқылы екі немесе одан да көп х, у, ... айнымалысы бар үздіксіз функцияларды да дәлелдеуге болады. Бұл жағдайда (шеткі нүктелері қоса алынған) шектелген интервалдардың орнына шектелген аймақтарды, алу керек, мысалы х, у жазықтығындағы тіктөртбұрыштар аймағы (контурды қоса алғанда). [22]
4-теорема. Егер  функциясы
функциясы  сегментінде үздіксіз болса,
онда функция осы сегментте шектелген
болады.
сегментінде үздіксіз болса,
онда функция осы сегментте шектелген
болады.
Дәлелдеу.  функциясы
функциясы
 сегментінде жоғарыдан
шектелгенін дәлелдейік (төменнен шектелгендігі осыған ұқсас
дәлелденеді).
сегментінде жоғарыдан
шектелгенін дәлелдейік (төменнен шектелгендігі осыған ұқсас
дәлелденеді).
Кері дәлелдеуді қолданамыз,
яғни  функциясы
функциясы
 сегментінде жоғарыдан
шектелмеген деп пайымдайық. Онда кез келген
натурал п
сегментінде жоғарыдан
шектелмеген деп пайымдайық. Онда кез келген
натурал п
 үшін
үшін  болатындай
болатындай  сегментінен ең болмағанда
бір
сегментінен ең болмағанда
бір  нүктесі табылады (қарсы
жағдайда
нүктесі табылады (қарсы
жағдайда  функциясы
функциясы
 сегментінде жоғарыдан
шектелген болар еді).
сегментінде жоғарыдан
шектелген болар еді).
Осылайша,
 сегментінен
сегментінен  функциясының сәйкес мәндерінің
тізбегі шексіз үлкен болатындай
функциясының сәйкес мәндерінің
тізбегі шексіз үлкен болатындай  мәндерінің тізбегін
көрсеттік.
мәндерінің тізбегін
көрсеттік.  тізбегінен қандай да
бір ξ
нүктесінде
шоғырланатын
тізбегінен қандай да
бір ξ
нүктесінде
шоғырланатын  ішкі тізбегін бөліп алуға
болады.
ішкі тізбегін бөліп алуға
болады.  ішкі тізбегінің барлық
элементтері
ішкі тізбегінің барлық
элементтері  сегментінде
орналасқандықтан, ξ
нүктесі
де
сегментінде
орналасқандықтан, ξ
нүктесі
де  сегментіне тиісті
болады.
сегментіне тиісті
болады.  функциясының ξ
нүктесіндегі үздіксіздігі
салдарынан
функциясының ξ
нүктесіндегі үздіксіздігі
салдарынан  функциясының сәйкес мәндерінің
ішкі тізбегі
функциясының сәйкес мәндерінің
ішкі тізбегі  -ке шоғырлануы керек. Бірақ
бұл ұйғарым
-ке шоғырлануы керек. Бірақ
бұл ұйғарым  шексіз үлкен тізбегінен
алынған
шексіз үлкен тізбегінен
алынған  ішкі тізбегінің өзі де шексіз
үлкен болады дегенге қарсы келеді. Шыққан қарама-қайшылық теореманы
дәлелдейді.
ішкі тізбегінің өзі де шексіз
үлкен болады дегенге қарсы келеді. Шыққан қарама-қайшылық теореманы
дәлелдейді.
1-ескерту. 4-теоремада айтылған ұйғарым
интервал үшін (немесе жартысегмент үшін) орындалмайды, яғни
функцияның интервалдағы (немесе жартысегменттегі) үздіксіздігі
ұйғарымынан функцияның осы жиындағы шектелгендігі туралы ұйғарым
шықпайды. Мысалы,  интервалындағы
(немесе
интервалындағы
(немесе  жартысегментіндегі)
жартысегментіндегі)  функциясын қарастырайық. Бұл
функция берілген жиында үздіксіз, бірақ шектелмеген болады. Расында
да,
функциясын қарастырайық. Бұл
функция берілген жиында үздіксіз, бірақ шектелмеген болады. Расында
да,  тізбегі берілген жиынға тиісті
болады, ал
тізбегі берілген жиынға тиісті
болады, ал  функциясының мәндерінің
тізбегі шексіз үлкен болып табылады.
функциясының мәндерінің
тізбегі шексіз үлкен болып табылады.
Берілген
 жиынында жоғарыдан
(төменнен) шектелген
жиынында жоғарыдан
(төменнен) шектелген  функциясын қарастырайық.
[23]
функциясын қарастырайық.
[23]
2-анықтама. М саны (т
саны)  функциясының
функциясының  жиынындағы дәл жоғарғы (дәл
төменгі) шекарасы деп аталады, егер екі шарт
орындалса: 1)
жиынындағы дәл жоғарғы (дәл
төменгі) шекарасы деп аталады, егер екі шарт
орындалса: 1)
 жиынының әрбір х мәні
үшін
жиынының әрбір х мәні
үшін  теңсіздігі
орындалады; 2)
кез
келген
теңсіздігі
орындалады; 2)
кез
келген  саны
үшін
саны
үшін  жиынында
жиынында  функциясының сәйкес
мәніне
функциясының сәйкес
мәніне

теңсіздігі орындалатындай х мәні табылады.
Берілген анықтамадағы 1)
шарт М
саны
(т
саны)
 функциясының
функциясының  жиынындағы жоғарғы (төменгі)
шекараларының бірі болады дегенді білдіреді, ал 2) шарт осы шекара
ең кіші (ең үлкен) мән болады және ол мән кішіреймейді (үлкеймейді)
дегенді білдіреді.
жиынындағы жоғарғы (төменгі)
шекараларының бірі болады дегенді білдіреді, ал 2) шарт осы шекара
ең кіші (ең үлкен) мән болады және ол мән кішіреймейді (үлкеймейді)
дегенді білдіреді.
 функциясының
функциясының  жиынындағы дәл
жоғарғы М
шекарасы
әдетте
жиынындағы дәл
жоғарғы М
шекарасы
әдетте

символымен,
ал  функциясының
функциясының  жиынындағы дәл
төменгі т
шекарасы
жиынындағы дәл
төменгі т
шекарасы

символымен белгіленеді.
Сонымен
қатар  функциясының
функциясының  сегментіндегі дәл жоғарғы
шекарасын төмендегі төрт символдың кез келгенімен белгілеуге
болады:
сегментіндегі дәл жоғарғы
шекарасын төмендегі төрт символдың кез келгенімен белгілеуге
болады:
 .
.
Сондай-ақ дәл төменгі шекарасын белгілеуге арналған төрт символ төмендегі түрде болады:
 .
.
Төмендегі ұйғарымдар дұрыс болады:
-
егер
 функциясы
функциясы  жиынында жоғарыдан
(төменнен) шектелген болса, онда осы жиында берілген функцияның дәл
жоғарғы шекарасы (дәл төменгі шекарасы)
болады;
жиынында жоғарыдан
(төменнен) шектелген болса, онда осы жиында берілген функцияның дәл
жоғарғы шекарасы (дәл төменгі шекарасы)
болады; -
егер
 функциясы
функциясы  жиынында шектелген болса
(екі жағынан), онда осы жиында берілген функцияның дәл жоғарғы да,
дәл төменгі де шекаралары болады.
жиынында шектелген болса
(екі жағынан), онда осы жиында берілген функцияның дәл жоғарғы да,
дәл төменгі де шекаралары болады.
Бұл ұйғарымдар негізінде
мынадай сұрақ туады:  жиынында
шектелген
жиынында
шектелген функциясының дәл жоғарғы (дәл
төменгі) шекарасы жетімді болады ма,
яғни
функциясының дәл жоғарғы (дәл
төменгі) шекарасы жетімді болады ма,
яғни  жиынында
функцияның
жиынында
функцияның  мәні
мәні
 жиынындағы
жиынындағы  функциясының дәл жоғарғы
(сәйкесінше дәл төменгі) шекарасына тең
болатындай
функциясының дәл жоғарғы
(сәйкесінше дәл төменгі) шекарасына тең
болатындай  нүктесі табылады
ма.
нүктесі табылады
ма.
Келесі мысал берілген жиында шектелген функцияның дәл шекаралары жалпы алғанда жетімді болмайтынын көрсетеді.
 сегментінде төмендегі
түрдегі
сегментінде төмендегі
түрдегі  функциясын қарастырайық
(7-сурет):
функциясын қарастырайық
(7-сурет):

Бұл
функция  сегментінде шектелген және осы
сегментте
сегментінде шектелген және осы
сегментте  дәл жоғарғы мәні
мен
дәл жоғарғы мәні
мен  дәл төменгі мәні болады.
Алайда бұл мәндер жетімді болмайды:
дәл төменгі мәні болады.
Алайда бұл мәндер жетімді болмайды:  сегментінің нүктелерінің
арасында функцияның мәндері нөлге немесе бірге тең болатын нүктелер
табылмайды.
сегментінің нүктелерінің
арасында функцияның мәндері нөлге немесе бірге тең болатын нүктелер
табылмайды.
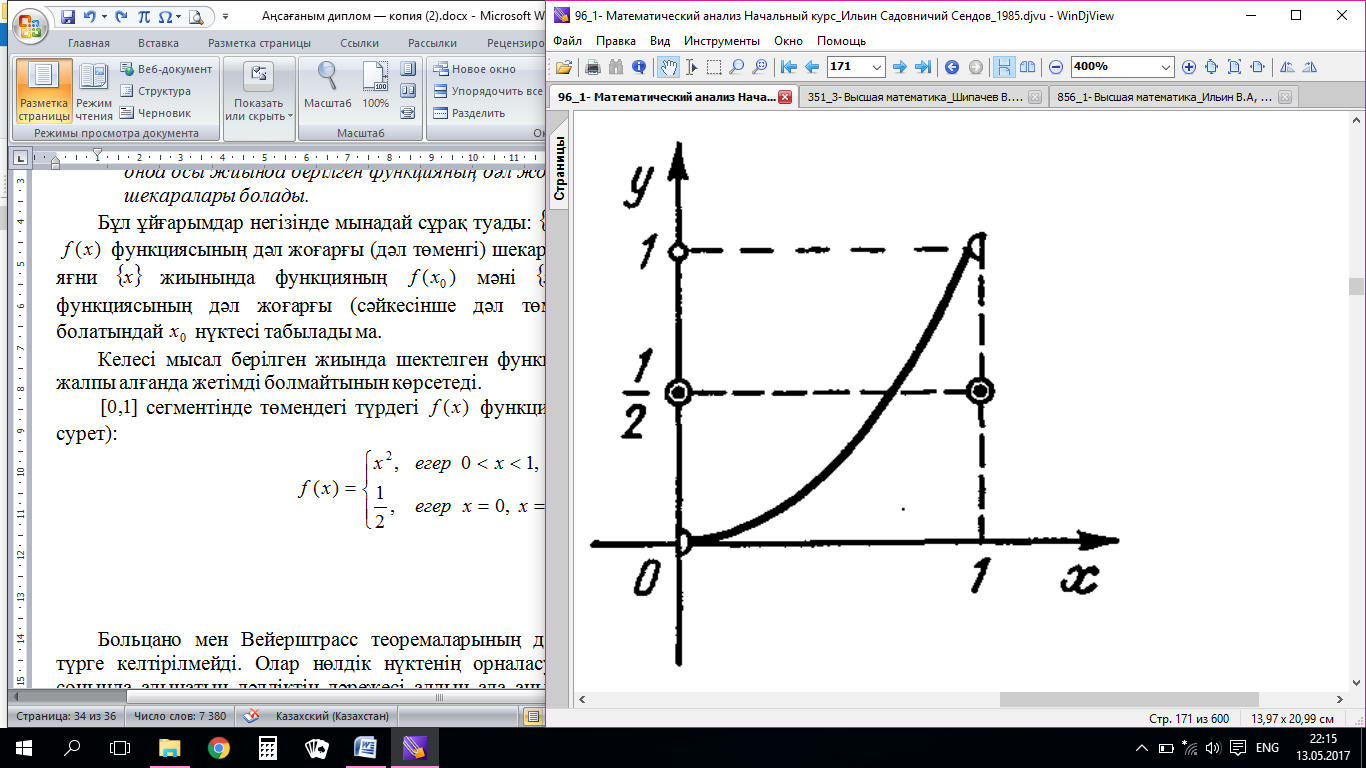
7-сурет
Қарастырылып
отырған  функциясы
функциясы
 сегментінде үздіксіз
болатынын ескере кетейік (функция
сегментінде үздіксіз
болатынын ескере кетейік (функция  және
және
 нүктелерінде үзілмейді).
[24] Бұл жағдай кездейсоқ емес, себебі төмендегі ұйғарым дұрыс
болады.
нүктелерінде үзілмейді).
[24] Бұл жағдай кездейсоқ емес, себебі төмендегі ұйғарым дұрыс
болады.
5-теорема. Егер  функциясы
функциясы  сегментінде үздіксіз болса,
онда ол осы сегментте өзінің дәл жоғарғы және дәл төменгі
шекараларына жетеді, яғни
сегментінде үздіксіз болса,
онда ол осы сегментте өзінің дәл жоғарғы және дәл төменгі
шекараларына жетеді, яғни  сегментінің нүктелерінің
ішінен
сегментінің нүктелерінің
ішінен  мәні
мәні  функциясының
функциясының  сегментіндегі дәл жоғарғы
шекарасына, ал
сегментіндегі дәл жоғарғы
шекарасына, ал  мәні
мәні  функциясының
функциясының  сегментіндегі дәл төменгі
шекарасына тең болатындай
сегментіндегі дәл төменгі
шекарасына тең болатындай  және
және  нүктелері
табылады.
нүктелері
табылады.
Дәлелдеу. 4-теоремаға
сәйкес  функциясы
функциясы
 сегментінде үздіксіз
болады, сондықтан функцияның осы сегментте
М
дәл жоғарғы шекарасы
мен т
дәл төменгі шекарасы бар
болады.
сегментінде үздіксіз
болады, сондықтан функцияның осы сегментте
М
дәл жоғарғы шекарасы
мен т
дәл төменгі шекарасы бар
болады.
М дәл жоғарғы мәніне жетуін дәлелдеуге тоқталайық, себебі т дәл төменгі мәніне жету осы жолмен дәлелденеді.
М
дәл жоғарғы мәні жетімсіз
болсын деп болжам жасайық, яғни  сегментінің барлық
нүктелерінде
сегментінің барлық
нүктелерінде  функциясы
М
мәнінен кем мәндерді
қабылдайды деп пайымдайық. Онда біз
функциясы
М
мәнінен кем мәндерді
қабылдайды деп пайымдайық. Онда біз

функциясын қарастыра аламыз.
Бөлшектің
 бөлімі
бөлімі  сегментінде үздіксіз және тек
қана оң таңбалы функция болып табылады.
Сондықтан
сегментінде үздіксіз және тек
қана оң таңбалы функция болып табылады.
Сондықтан  функциясы
функциясы
 сегментінде үздіксіз
болады. Демек, 4-теоремаға сәйкес
сегментінде үздіксіз
болады. Демек, 4-теоремаға сәйкес  функциясы
функциясы
 сегментінде шектелген
болады, яғни
сегментінде шектелген
болады, яғни  болатындай А
оң саны
табылады.
болатындай А
оң саны
табылады.  функциясы
функциясы
 сегментінде тек қана оң
таңбалы функция болғандықтан, соңғы теңсіздік
сегментінде тек қана оң
таңбалы функция болғандықтан, соңғы теңсіздік
 сегментінің
барлық х
үшін
сегментінің
барлық х
үшін
 теңсіздігіне
эквивалентті болады, ал бұл ұйғарым
М
саны – дәл жоғарғы шекарасы,
яғни
теңсіздігіне
эквивалентті болады, ал бұл ұйғарым
М
саны – дәл жоғарғы шекарасы,
яғни  функциясының
функциясының  сегментіндегі барлық жоғарғы
шекараларының ішіндегі ең кішісі деген ұйғарымға қарама-қайшы
болады.
сегментіндегі барлық жоғарғы
шекараларының ішіндегі ең кішісі деген ұйғарымға қарама-қайшы
болады.
Алынған қарама-қайшылық дәл жоғарғы шекараның жетімді болмайды деген болжамымыздың қате екенін дәлелдейді. [25]
2-ескерту.  сегментінде үздіксіз болатын
функцияның дәл жоғарғы және дәл төменгі мәндеріне жетуі дәлелденген
соң
сегментінде үздіксіз болатын
функцияның дәл жоғарғы және дәл төменгі мәндеріне жетуі дәлелденген
соң  функциясының
функциясының  сегментіндегі М
дәл жоғарғы
шекарасын максималды
мән деп, ал
т
дәл төменгі
шекарасын минималды
мән деп атай аламыз. 5-теореманы
басқаша түрде былай жазуға болады:
сегментіндегі М
дәл жоғарғы
шекарасын максималды
мән деп, ал
т
дәл төменгі
шекарасын минималды
мән деп атай аламыз. 5-теореманы
басқаша түрде былай жазуға болады:  сегментінде үздіксіз
болатын
сегментінде үздіксіз
болатын  функциясының осы сегментте
максималды және минималды мәндері
болады.
функциясының осы сегментте
максималды және минималды мәндері
болады.
 функциясының
функциясының  сегментіндегі максималды мәні
төмендегі символдардың бірімен
белгіленеді:
сегментіндегі максималды мәні
төмендегі символдардың бірімен
белгіленеді:
 .
.
 функциясының
функциясының  сегментіндегі минималды
мәндерінің символдары мынадай түрде
беріледі:
сегментіндегі минималды
мәндерінің символдары мынадай түрде
беріледі:
 .
.
3-ескерту. Берілген сегментте үздіксіз
болмайтын функциялар да осы сегментте өзінің дәл жоғарғы және дәл
төменгі мәндеріне ие бола алатынын ескере кетейік. Мысал ретінде
барлық иррационал х
үшін нөлге тең болатын және
барлық рационал х
үшін бірге тең
болатын  Дирихле функциясын қарастыруға
болады. Бұл функция
Дирихле функциясын қарастыруға
болады. Бұл функция  сегментінің әрбір нүктесінде
үзілісті болады, бірақ осы сегментте бірге тең болатын өзінің дәл
жоғарғы мәніне және нөлге тең болатын дәл төменгі мәніне жетеді.
[26]
сегментінің әрбір нүктесінде
үзілісті болады, бірақ осы сегментте бірге тең болатын өзінің дәл
жоғарғы мәніне және нөлге тең болатын дәл төменгі мәніне жетеді.
[26]
4-ескерту. 5-теоремадағы ұйғарым қате болады, егер оның жазылуындағы «сегмент» термині «интервал» немесе «жартысегмент» терминдерімен алмастырылатын болса.
Осылайша,
 функциясы
функциясы  интервалында
немесе
интервалында
немесе  жартысегментінде үздіксіз
болады, бірақ бұл функцияның берілген интервалдағы немесе
жартысегменттегі
жартысегментінде үздіксіз
болады, бірақ бұл функцияның берілген интервалдағы немесе
жартысегменттегі  дәл жоғарғы шекарасы бар
болады, алайда жетімді болмайды.
дәл жоғарғы шекарасы бар
болады, алайда жетімді болмайды.
Осыған қоса, интервалдағы немесе жартысегменттегі функцияның дәл шекаралары болмауы да мүмкін екенін айта кетейік, себебі мұндай функция берілген интервалда немесе жартысегментте шектеулі болмауы мүмкін (1-ескертуді қара).
Больцано мен Вейерштрасс теоремаларының дәлелдеуі конструктивтік түрге келтірілмейді. Олар нөлдік нүктенің орналасуын немесе үрдістердің соңында алынатын дәлдіктің дәрежесі алдын ала анықталған функцияның ең үлкен мен ең кіші мәнін табудың «тиімді» әдісін көрсетпейді. Олар тек қана аталған мәндердің барын немесе жоқтығын теріске шығарып дәлелдейді. [27]
2.7. Реттілік туралы теорема. Шағын жиындар
Айталық,
 әр түрлі немесе бірдей
сандардың
әр түрлі немесе бірдей
сандардың  кесіндісіндегі қандай да бір
шексіз реттілігі болсын. Реттілік шекке ұмтылуы немесе ұмтылмауы
мүмкін. Бірақ, қалай болғанда да, мұндай реттіліктен оның
кейбір мүшелерін шығарып тастау арқылы I кесіндісінде жататын шекке
ұмтылатын
кесіндісіндегі қандай да бір
шексіз реттілігі болсын. Реттілік шекке ұмтылуы немесе ұмтылмауы
мүмкін. Бірақ, қалай болғанда да, мұндай реттіліктен оның
кейбір мүшелерін шығарып тастау арқылы I кесіндісінде жататын шекке
ұмтылатын шексіз тізбекті қашанда
алуға болады.
шексіз тізбекті қашанда
алуға болады.
Бұл теореманы дәлелдеу
үшін I
интервалын  орта нүкте
арқылы
орта нүкте
арқылы  және
және
 шектелген екі кесіндіге
бөлейік:
шектелген екі кесіндіге
бөлейік:


Осы екі кесіндінің біреуінде
негізгі реттілікте тұрған  мүшелерінің шексіз саны
болады; оны
мүшелерінің шексіз саны
болады; оны  деп белгілейік.
Осы
деп белгілейік.
Осы  мүшелерінің ішінен біреуін
таңдап, оны
мүшелерінің ішінен біреуін
таңдап, оны  деп белгілейік. Осы
үрдісті
деп белгілейік. Осы
үрдісті  кесіндісінде
қаталаймыз.
кесіндісінде
қаталаймыз.  интервалында
интервалында  мүшелерінің шексіз саны
болғандықтан, олардың шексіз саны
мүшелерінің шексіз саны
болғандықтан, олардың шексіз саны  интервалының жартыларының
біреуінде де болу керек; бұл жарты интервалды
интервалының жартыларының
біреуінде де болу керек; бұл жарты интервалды
 деп
белгілейік.
деп
белгілейік.  кесіндісінде
кесіндісінде  болатындай
болатындай  мүшесін алып,
оны
мүшесін алып,
оны  деп белгілейміз. Осылайша
жалғастыра отырып п-нің мәні қандай болса
да
деп белгілейміз. Осылайша
жалғастыра отырып п-нің мәні қандай болса
да  интервалында жататын негізгі
реттілік мүшелерінің
интервалында жататын негізгі
реттілік мүшелерінің  тізбекшесін
және
тізбекшесін
және  ішкі кесінділерден тұратын
реттілікті аламыз. Интервалдардың мұндай реттілігі аралықтың қандай
да бір у
нүктесіне жиналады
және
ішкі кесінділерден тұратын
реттілікті аламыз. Интервалдардың мұндай реттілігі аралықтың қандай
да бір у
нүктесіне жиналады
және  реттілігінің
шегі у
болатыны белгілі болды.
Осылайша теорема дәлелденді. [28]
реттілігінің
шегі у
болатыны белгілі болды.
Осылайша теорема дәлелденді. [28]
Бұл пайымдаулар қазіргі
математикаға тән түрдегі жалпылауларды мүмкін етеді. Құрамында
«қашықтық» ұғымы белгілі бір түрде анықталатын қандай да
бір S
жиыннан
өтетін Х
айнымалысын
қарастырайық. S
жазықтықтағы немесе
кеңістіктегі нүктелер жиыны болуы мүмкін. Бірақ бұл міндетті емес;
мысалы, S
жазықтықтағы барлық
үшбұрыштардың жиыны да болуы мүмкін. Егер
Х
пен
Y
төбелері
А, В,
С және
 болатын үшбұрыштар
болса, онда үшбұрыштар арасындағы «қашықтық» ретінде,
мысалы
болатын үшбұрыштар
болса, онда үшбұрыштар арасындағы «қашықтық» ретінде,
мысалы

санын алуға болады,
мұндағы  дегеніміз
– A
мен
дегеніміз
– A
мен
 нүктелері арасындағы
әдеттегі қашықтық. Жиында «қашықтық» ұғымы енгізілгеннен
бастап S
жиынының мүшесі
болатын Х
шегіне
ұмтылатын
нүктелері арасындағы
әдеттегі қашықтық. Жиында «қашықтық» ұғымы енгізілгеннен
бастап S
жиынының мүшесі
болатын Х
шегіне
ұмтылатын  элементтерінің реттілігі
ұғымын анықтап алуға мүмкіндік туады. Бұл
арқылы
элементтерінің реттілігі
ұғымын анықтап алуға мүмкіндік туады. Бұл
арқылы  болғанда
болғанда
 болады демекпіз.
Енді S жиыны ықшамды болады деп
айтамыз, егер осы жиынның элементтері болатын
әрбір
болады демекпіз.
Енді S жиыны ықшамды болады деп
айтамыз, егер осы жиынның элементтері болатын
әрбір  реттілігінен S жиынына
тиісті қандай да бір Х шегіне ұмтылатын тізбекшені алуға болатын
болса. Алдыңғы бөлімшеде екі жағынан
шектелген
реттілігінен S жиынына
тиісті қандай да бір Х шегіне ұмтылатын тізбекшені алуға болатын
болса. Алдыңғы бөлімшеде екі жағынан
шектелген  аралығы берілген мәнмәтінде
ықшам екенін көрсеттік. [29] Осылайша, ықшамды жиын ұғымын сан
осіндегі шектелген
интервал ұғымының жалпыламасы деп алуға
болады. Сан осі өз алдына ықшамдалмаған, себебі 1, 2, 3, 4, 5, ...
бүтін сандар реттілігі ешбір шекке ұмтылмайды және бұл осьтің
құрамында қандай да бір шекке ұмтылатын ешбір реттілік жоқ.
Осылайша,
аралығы берілген мәнмәтінде
ықшам екенін көрсеттік. [29] Осылайша, ықшамды жиын ұғымын сан
осіндегі шектелген
интервал ұғымының жалпыламасы деп алуға
болады. Сан осі өз алдына ықшамдалмаған, себебі 1, 2, 3, 4, 5, ...
бүтін сандар реттілігі ешбір шекке ұмтылмайды және бұл осьтің
құрамында қандай да бір шекке ұмтылатын ешбір реттілік жоқ.
Осылайша,  ашық интервалы да
ықшамдалмаған болады; расында да
ашық интервалы да
ықшамдалмаған болады; расында да  реттілігі немесе оның кез
келген тізбекшесі 0 шегіне ұмтылады, алайда бұл шек қарастырылып
отырған ашық аралыққа тиісті емес. Осылайша қандай да бір
квадраттың немесе тіктөртбұрыштың ішкі нүктелерінен тұратын
жазықтықтың облысы ықшамдалмаған болады деп айта аламыз; бірақ ол
шеткі нүктелері анықталғаннан кейін ықшамды болып шығады. Төбелері
берілген шеңбердің бойында немесе ішінде жатқан барлық
үшбұрыштардың жиыны да ықшамды болатынына оңай көз жеткізуге
болады. [30]
реттілігі немесе оның кез
келген тізбекшесі 0 шегіне ұмтылады, алайда бұл шек қарастырылып
отырған ашық аралыққа тиісті емес. Осылайша қандай да бір
квадраттың немесе тіктөртбұрыштың ішкі нүктелерінен тұратын
жазықтықтың облысы ықшамдалмаған болады деп айта аламыз; бірақ ол
шеткі нүктелері анықталғаннан кейін ықшамды болып шығады. Төбелері
берілген шеңбердің бойында немесе ішінде жатқан барлық
үшбұрыштардың жиыны да ықшамды болатынына оңай көз жеткізуге
болады. [30]
Үздіксіздік
ұғымы Х
айнымалысы кез
келген S
жиынынан өтетін жағдайға
жалпыламаны мүмкін етеді, егер осы аталған
S
жиынында шекке ұмтылу ұғымы
алдын ала енгізілген болса.  функциясы
(мұндағы и
нақты сан болып
есептеледі) Х
элементінде үздіксіз деп
айтады, егер
функциясы
(мұндағы и
нақты сан болып
есептеледі) Х
элементінде үздіксіз деп
айтады, егер  элементтерінен құралған
реттіліктің шегі әркез Х, ал оған
сәйкес
элементтерінен құралған
реттіліктің шегі әркез Х, ал оған
сәйкес  сандар реттілігінің шегі
әркез
сандар реттілігінің шегі
әркез  болатын болса. Вейерштрасс
теоремасы жалпыланған үздіксіз
болатын болса. Вейерштрасс
теоремасы жалпыланған үздіксіз  функциясы үшін де
орындалатынына оңай көз жеткізуге болады, бұл функция қандай да бір
ықшамды жиында беріледі:
функциясы үшін де
орындалатынына оңай көз жеткізуге болады, бұл функция қандай да бір
ықшамды жиында беріледі:
Егер  ықшамды S жиынының барлық
элементтері үшін үздіксіз функция болса,
онда
ықшамды S жиынының барлық
элементтері үшін үздіксіз функция болса,
онда  функциясы ең үлкен мәнді
қабылдайтын S жиынының бір элементі
және
функциясы ең үлкен мәнді
қабылдайтын S жиынының бір элементі
және функциясы ең кіші мәнді
қабылдайтын S жиынының басқа бір элементі міндетті түрде
табылады.[31]
функциясы ең кіші мәнді
қабылдайтын S жиынының басқа бір элементі міндетті түрде
табылады.[31]
2.8. Функцияның біртекті үздіксіздігі ұғымы
Айталық,
 функциясы жиынның әрбір
нүктесі осы жиынның шекті нүктесі болатындай
функциясы жиынның әрбір
нүктесі осы жиынның шекті нүктесі болатындай
 жиынында берілсін.
Мұндай жиынның мысалы болып сегмент, интервал, жартысегмент,
жартытүзу, шексіз түзу, аталған жиындардың кез келгеніне тиісті
болатын барлық рационал нүктелердің жиыны бола
алады.
жиынында берілсін.
Мұндай жиынның мысалы болып сегмент, интервал, жартысегмент,
жартытүзу, шексіз түзу, аталған жиындардың кез келгеніне тиісті
болатын барлық рационал нүктелердің жиыны бола
алады.
3-анықтама.  функциясы
функциясы  жиынында біртекті үздіксіз
деп аталады, егер
жиынында біртекті үздіксіз
деп аталады, егер  жиынының
жиынының  шартын қанағаттандыратын
кез келген
шартын қанағаттандыратын
кез келген  және
және  екі нүктесі
үшін
екі нүктесі
үшін

теңсіздігі дұрыс болатындай кез келген оң таңбалы ɛ саны үшін оң таңбалы δ саны табылса. [32]
5-ескерту.  функциясы
функциясы
 жиынында біртекті
үздіксіз болса, онда ол
жиынында біртекті
үздіксіз болса, онда ол  жиынының
әрбір х
нүктесінде үздіксіз болатынын
бірден ескере кетейік. Расында да, жоғарыдағы
анықтамадағы
жиынының
әрбір х
нүктесінде үздіксіз болатынын
бірден ескере кетейік. Расында да, жоғарыдағы
анықтамадағы  орнына
орнына
 жиынының берілген
нақты
жиынының берілген
нақты  нүктесін,
ал
нүктесін,
ал  орнына
орнына
 жиынының кез келген
нүктесін алсақ, Коши бойынша
жиынының кез келген
нүктесін алсақ, Коши бойынша  функциясының
функциясының  нүктесіндегі үздіксіздігі
анықтамасына келеміз.
нүктесіндегі үздіксіздігі
анықтамасына келеміз.
6-ескерту. Біртекті үздіксіздіктің
жоғарыда келтірілген анықтамасының негізгі шарты – кез
келген  үшін
3-анықтамадағы
үшін
3-анықтамадағы жиынының
жиынының
 шартын қанағаттандыратын
барлық
шартын қанағаттандыратын
барлық  және
және
 нүктелеріне теңсіздіктің
орындалуын қамтамасыз ететін
нүктелеріне теңсіздіктің
орындалуын қамтамасыз ететін  әмбебап мәнінің табылуына
кепіл беретін шарт. [33]
әмбебап мәнінің табылуына
кепіл беретін шарт. [33]
Егер
 функциясының
функциясының  жиынындағы
әрбір
жиынындағы
әрбір  нүктесіндегі үздіксіздігін
талап етсек, онда кез келген
нүктесіндегі үздіксіздігін
талап етсек, онда кез келген  және
және
 жиынының кез
келген
жиынының кез
келген  нүктесі
үшін ɛ
санына ғана емес,
сондай-ақ
нүктесі
үшін ɛ
санына ғана емес,
сондай-ақ  нүктесіне тәуелді болатын
және
нүктесіне тәуелді болатын
және  жиынының
жиынының
 шартын қанағаттандыратын
барлық
шартын қанағаттандыратын
барлық  нүктесі
үшін
нүктесі
үшін  теңсіздігінің дұрыстығын
қамтамасыз ететін «өзіндік» оң
теңсіздігінің дұрыстығын
қамтамасыз ететін «өзіндік» оң  санының бар болуына кепіл
беруге болады. сонымен қоса, жалпы айтқанда,
санының бар болуына кепіл
беруге болады. сонымен қоса, жалпы айтқанда,
 жиынының
барлық
жиынының
барлық  нүктесі бойынша
көрсетілген
нүктесі бойынша
көрсетілген  сандарының оң дәл төменгі
шекарасы болмауы да мүмкін, яғни
сандарының оң дәл төменгі
шекарасы болмауы да мүмкін, яғни  функциясының
функциясының  жиынындағы біртекті
үздіксіздігі шықпайды.
жиынындағы біртекті
үздіксіздігі шықпайды.
7-ескерту. Біртекті үздіксіздіктің
жоғарыда көрсетілген анықтамасынан шығатыны:
егер  функциясы
функциясы
 жиынында біртекті
үздіксіз болса, онда бұл функция
жиынында біртекті
үздіксіз болса, онда бұл функция  жиынының кез келген ішкі
жиынында да біртекті үздіксіз болады. [34]
жиынының кез келген ішкі
жиынында да біртекті үздіксіз болады. [34]
Берілген
 жиынында біртекті
үздіксіздік қасиетіне ие болатын және ие болмайтын функциялардың
мысалдарын қарастырайық.
жиынында біртекті
үздіксіздік қасиетіне ие болатын және ие болмайтын функциялардың
мысалдарын қарастырайық.
-
 функциясы
функциясы  жартытүзуінде біртекті
үздіксіз екеніне көз жеткізейік. Расында да, берілген жартытүзуден
алынған кез келген
жартытүзуінде біртекті
үздіксіз екеніне көз жеткізейік. Расында да, берілген жартытүзуден
алынған кез келген  және
және
 екі нүкте үшін төмендегі
теңсіздік орындалады:
екі нүкте үшін төмендегі
теңсіздік орындалады:
 .
.
Сондықтан, кез
келген  үшін оң
таңбалы δ
санын
алсақ,
үшін оң
таңбалы δ
санын
алсақ,  жартытүзуінің
жартытүзуінің  шартын қанағаттандыратын кез
келген
шартын қанағаттандыратын кез
келген  және
және
 екі нүкте
үшін
екі нүкте
үшін  теңсіздігі орындалатынын
көреміз.
теңсіздігі орындалатынын
көреміз.
-
 функциясы
функциясы  интервалында біртекті үздіксіз
болмайды (бұл функция
интервалында біртекті үздіксіз
болмайды (бұл функция  интервалының әрбір нүктесінде
үздіксіз болса да). Бұған көз жеткізу үшін қандай да
бір
интервалының әрбір нүктесінде
үздіксіз болса да). Бұған көз жеткізу үшін қандай да
бір  және кез келген
аз
және кез келген
аз  үшін
үшін
 интервалында
интервалында
 бірақ
бірақ 
болатындай  және
және
 нүктелерінің ең
болмағанда бір жұбы табылатынын дәлелдесек
жеткілікті.
нүктелерінің ең
болмағанда бір жұбы табылатынын дәлелдесек
жеткілікті.
 интервалына тиісті
болатын
интервалына тиісті
болатын
 және
және 
элементтері
бар  және
және
 нүктелерінің екі
тізбегін қарастырайық.
нүктелерінің екі
тізбегін қарастырайық.
Бұл екі тізбек және олардың
айырымы шексіз аз болып табылады. Сондықтан кез келген
аз  үшін
үшін
 болатындай п
нөмірі табылады. Сонымен
қатар п-нің кез келген нөмірі
үшін
болатындай п
нөмірі табылады. Сонымен
қатар п-нің кез келген нөмірі
үшін

болады.
Сондықтан  және аз
және аз
 үшін
үшін  интервалынан
интервалынан  болғанымен
болғанымен  болатындай
болатындай  және
және
 нүктелерінің жұбы
табылады, бұл ұйғарым берілген функцияның
нүктелерінің жұбы
табылады, бұл ұйғарым берілген функцияның
 интервалында біртекті
үздіксіз болмайтынын көрсетеді.
интервалында біртекті
үздіксіз болмайтынын көрсетеді.
Осы
 функциясын
функциясын  интервалында
емес,
интервалында
емес,  интервалында қарастыратын
болсақ, онда жоғарыда келтірілген ұйғарымдар бұл жерде
орындалмайтынын айта кетейік, мұндағы
γ
–
интервалында қарастыратын
болсақ, онда жоғарыда келтірілген ұйғарымдар бұл жерде
орындалмайтынын айта кетейік, мұндағы
γ
–
 интервалының кез келген
саны. Бұл факт кездейсоқ емес, себебі төменде осы
функцияның
интервалының кез келген
саны. Бұл факт кездейсоқ емес, себебі төменде осы
функцияның  болғандағы
болғандағы  интервалында біртекті үздіксіз
екенін көрсетеміз. [35]
интервалында біртекті үздіксіз
екенін көрсетеміз. [35]
-
 функциясы
функциясы  жартытүзуінде біртекті
үздіксіз болмайтынына көз жеткізейік.
жартытүзуінде біртекті
үздіксіз болмайтынына көз жеткізейік.
 жартытүзуінің кез
келген
жартытүзуінің кез
келген  және
және
 екі нүктесі
үшін
екі нүктесі
үшін

теңсіздігі орындалатынын ескере кетейік.
Енді қандай да
бір  үшін ғана емес, сондай-ақ кез
келген
үшін ғана емес, сондай-ақ кез
келген  үшін де және кез келген
аз
үшін де және кез келген
аз  үшін де
үшін де
 жартытүзуінен
жартытүзуінен
 бірақ
бірақ 
болатындай  және
және
 нүктелер жұбы табылады
(Бұл ұйғарым
нүктелер жұбы табылады
(Бұл ұйғарым  функциясының қарастырылған
жартытүзуде біртекті үздіксіздік қасиетінің жоқтығын
білдіреді).
функциясының қарастырылған
жартытүзуде біртекті үздіксіздік қасиетінің жоқтығын
білдіреді).
Кез
келген  және
және
 сандарын
нақтылап,
сандарын
нақтылап,  ретінде бірден үлкен
және
ретінде бірден үлкен
және  болатын кез келген санды
алып,
болатын кез келген санды
алып,  деп пайымдайық.
Мұндай
деп пайымдайық.
Мұндай  және
және
 үшін
үшін  теңсіздігі орындалады. Басқа
жағынан, осы
теңсіздігі орындалады. Басқа
жағынан, осы  және
және
 үшін
үшін  теңсіздігіне
сәйкес
теңсіздігіне
сәйкес

басқа теңсіздігі де орындалады.
Осы
 функциясын
функциясын  жартытүзуінде емес, кез
келген
жартытүзуінде емес, кез
келген  сегментінде қарастыратын
болсақ, онда жоғарыда келтірілген ұйғарымдар бұл жерде
орындалмайтынын айта кетейік, мұндағы
b
– кез келген сан.
[36]
сегментінде қарастыратын
болсақ, онда жоғарыда келтірілген ұйғарымдар бұл жерде
орындалмайтынын айта кетейік, мұндағы
b
– кез келген сан.
[36]
Бұл факт төмендегі фундаменталь теоремаға сәйкес түсінікті болып шығады.
6-Негізгі
теорема. Егер  функциясы
функциясы  сегментінде үздіксіз болса,
онда функция осы сегментте біртекті үздіксіз де
болады.
сегментінде үздіксіз болса,
онда функция осы сегментте біртекті үздіксіз де
болады.
Дәлелдеу.  функциясы
функциясы
 сегментінде үздіксіз,
бірақ бұл сегментте біртекті үздіксіз емес деп
болжайық.
сегментінде үздіксіз,
бірақ бұл сегментте біртекті үздіксіз емес деп
болжайық.
Онда қандай да
бір  және кез келген
аз
және кез келген
аз  үшін
үшін
 сегментінің
сегментінің
 бірақ
бірақ 
болатындай  және
және
 нүктелері табылады. Оң
таңбалы
нүктелері табылады. Оң
таңбалы  сандарынан құралған шексіз аз
тізбекті алайық. Берілген
сандарынан құралған шексіз аз
тізбекті алайық. Берілген  үшін және кез
келген п
нөмірі
үшін
үшін және кез
келген п
нөмірі
үшін
 бірақ
бірақ 
болатындай  сегментінің
сегментінің  және
және
 екі нүктесі
табылады.
екі нүктесі
табылады.  тізбегі
тізбегі
 сегментінің нүктелерінен
құралатындықтан, онда ол шектелген болады және оның
ішінен
сегментінің нүктелерінен
құралатындықтан, онда ол шектелген болады және оның
ішінен  ішкі тізбегін шығарып алуға
болады. Берілген тізбектің ξ
шегі де
ішкі тізбегін шығарып алуға
болады. Берілген тізбектің ξ
шегі де
 сегментіне тиісті
болады.
сегментіне тиісті
болады.  теңсіздігіне
сәйкес
теңсіздігіне
сәйкес  ішкі тізбегі де дәл
осы ξ
нүктесіне
шоғырланады.
ішкі тізбегі де дәл
осы ξ
нүктесіне
шоғырланады.
 функциясы
функциясы  сегментінің әрбір нүктесінде
үздіксіз болғандықтан, ол ξ
нүктесінде де үздіксіз болады.
Бірақ онда функцияның сәйкес мәндерінің
сегментінің әрбір нүктесінде
үздіксіз болғандықтан, ол ξ
нүктесінде де үздіксіз болады.
Бірақ онда функцияның сәйкес мәндерінің
 және
және  екі ішкі тізбегі
де
екі ішкі тізбегі
де  айналасына шоғырлануы тиіс,
яғни көрсетілген ішкі тізбектерінің
айналасына шоғырлануы тиіс,
яғни көрсетілген ішкі тізбектерінің  айырымы шексіз аз болу керек.
Бұл ұйғарым барлық п
нөмірлеріне және
барлық
айырымы шексіз аз болу керек.
Бұл ұйғарым барлық п
нөмірлеріне және
барлық  нөмірлері үшін
орындалатын
нөмірлері үшін
орындалатын  теңсіздігіне қарама-қайшы
болады.
теңсіздігіне қарама-қайшы
болады.
Алынған қарама-қайшылық біз
пайымдап алған  сегментінде үздіксіз болатын
функция осы сегментте біртекті үздіксіз болмайды деген пікірдің
қате екенін көрсетеді. Теорема дәлелденді.
[37]
сегментінде үздіксіз болатын
функция осы сегментте біртекті үздіксіз болмайды деген пікірдің
қате екенін көрсетеді. Теорема дәлелденді.
[37]
Енді жоғарыда келтірілген
2-мысалға қайта оралып,  функциясы
функциясы
 интервалының кез
келген γ
саны үшін
интервалының кез
келген γ
саны үшін
 интервалында біртекті
үздіксіз екенін көрсетейік. Расында да, кез
келген γ
үшін ,
интервалында біртекті
үздіксіз екенін көрсетейік. Расында да, кез
келген γ
үшін ,
 функциясы
функциясы  сегментінде үздіксіз болады.
Демек, 6-теоремаға сәйкес
сегментінде үздіксіз болады.
Демек, 6-теоремаға сәйкес  функциясы
функциясы
 сегментінде біртекті
үздіксіз болады. Біртекті үздіксіздік анықтамасының 7-ескертуіне
сәйкес
сегментінде біртекті
үздіксіз болады. Біртекті үздіксіздік анықтамасының 7-ескертуіне
сәйкес  функциясы
функциясы
 сегментінің ішкі жиыны
болып табылатын
сегментінің ішкі жиыны
болып табылатын  интервалында біртекті үздіксіз
болады.
интервалында біртекті үздіксіз
болады.
6-теореманы берілген сегменттегі функцияның тербелісі терминдері арқылы басқа жазу ыңғайлы.
 функциясы
берілген
функциясы
берілген  сегментінде шектелген
болсын.
сегментінде шектелген
болсын.  функциясының
функциясының  сегментіндегі тербелісі
деп
сегментіндегі тербелісі
деп  функциясының осы
сегменттегі дәл жоғарғы шекарасы мен дәл төменгі шекарасы
арасындағы
функциясының осы
сегменттегі дәл жоғарғы шекарасы мен дәл төменгі шекарасы
арасындағы  айырымын
атайық.
айырымын
атайық.
 сегментінде
үздіксіз
сегментінде
үздіксіз  функциясы үшін тербеліс мәні
осы функцияның берілген сегменттегі максималды және минималды
мәндерінің айырымына тең. [38]
функциясы үшін тербеліс мәні
осы функцияның берілген сегменттегі максималды және минималды
мәндерінің айырымына тең. [38]
6-теоремадан тікелей келесі ұйғарымдар шығады:
6-теореманың
салдары. Егер  функциясы үздіксіз болса, онда кез
келген оң таңбалы ɛ саны үшін өзіне сәйкес келетін
және
функциясы үздіксіз болса, онда кез
келген оң таңбалы ɛ саны үшін өзіне сәйкес келетін
және  сегментіндегі ұзындығы δ
санынан кіші болатын ішкі
сегменттегі
сегментіндегі ұзындығы δ
санынан кіші болатын ішкі
сегменттегі функциясының тербелісі ɛ
санынан аз болатындай оң δ саны
табылады.
функциясының тербелісі ɛ
санынан аз болатындай оң δ саны
табылады.
8-ескерту. 4-теорема мен 5-теорема және
6-теоремалардың дәлелдеулерін талдай отырып осы үш
теоремадағы  сегментінің орнына төмендегі
шарттарды қанағаттандыратын кез келген
сегментінің орнына төмендегі
шарттарды қанағаттандыратын кез келген
 жиынын алуға болатынын
көруге болады: 1) бұл
жиынын алуға болатынын
көруге болады: 1) бұл  жиыны
шектеулі; 2)
бұл
жиыны
шектеулі; 2)
бұл  жиынының құрамында өзінің
кез келген шекті нүктесі болады
(мұндай
жиынды тұйық деп атауға келісіп
алайық).
жиынының құрамында өзінің
кез келген шекті нүктесі болады
(мұндай
жиынды тұйық деп атауға келісіп
алайық).
Көрсетілген екі шартты
қанағаттандыратын  жиынын
компакт
жиын деп
немесе компакт деп атауға келісейік.
Осылайша, аталған үш теорема сегментте үздіксіз функция үшін ғана
емес, сондай-ақ кез келген компактта үздіксіз функция үшін де дұрыс
болады. [39]
жиынын
компакт
жиын деп
немесе компакт деп атауға келісейік.
Осылайша, аталған үш теорема сегментте үздіксіз функция үшін ғана
емес, сондай-ақ кез келген компактта үздіксіз функция үшін де дұрыс
болады. [39]
2.9. Функцияның үздіксіздік модулі ұғымы
Айталық,
 функциясы әрбір нүктесі
шекті нүктесі болатын қандай да бір
функциясы әрбір нүктесі
шекті нүктесі болатын қандай да бір  жиынында анықталған және
үздіксіз болсын.
жиынында анықталған және
үздіксіз болсын.
4-анықтама. Кез
келген  үшін
үшін  жиынындағы
жиынындағы  функциясының үздіксіздік
модулі деп
функциясының үздіксіздік
модулі деп  жиынына тиісті
және
жиынына тиісті
және  теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  және
және  нүктелерінің
нүктелерінің  айырым модулінің дәл
жоғарғы шекарасын атаймыз.
айырым модулінің дәл
жоғарғы шекарасын атаймыз.
Көрсетілген дәл жоғарғы шекараны белгілеу үшін әдетте төмендегі символды қолданады:
 .
.
 жиынындағы
жиынындағы  функциясының үздіксіздік
модулінің өзін
функциясының үздіксіздік
модулінің өзін  символымен
белгілейді.
символымен
белгілейді.
Осылайша, анықтама бойынша

9-ескерту.  үздіксіздік модулінің
анықтамасындағы соңғы теңсіздіктің оң
жағындағы
үздіксіздік модулінің
анықтамасындағы соңғы теңсіздіктің оң
жағындағы  орнына модуль белгісін алып
тастап,
орнына модуль белгісін алып
тастап,  айырымын жазуға болар еді. Бұл
ұйғарым
айырымын жазуға болар еді. Бұл
ұйғарым  және
және
 нүктелерін орнымен
ауыстырып қоюға болады деген ұйғарымнан шығады (бұл
жерде
нүктелерін орнымен
ауыстырып қоюға болады деген ұйғарымнан шығады (бұл
жерде  айырымының таңбасы
қарама-қарсы таңбаға өзгереді, ал
айырымының таңбасы
қарама-қарсы таңбаға өзгереді, ал  шамасы
өзгермейді).
шамасы
өзгермейді).
 үздіксіздік модулінің
екі қасиетін келтірейік:
үздіксіздік модулінің
екі қасиетін келтірейік:
1º.
 үздіксіздік модулі
ылғи да теріс емес:
үздіксіздік модулі
ылғи да теріс емес:  .
.
Бұл қасиет үздіксіздік модулінен тікелей шығады.
2º.
 үздіксіздік
модулі
үздіксіздік
модулі  жартытүзуінде кемімейтін δ
функциясын құрайды.
жартытүзуінде кемімейтін δ
функциясын құрайды.
Расында да, δ кеміген кезде анықтамадағы супремум алынатын жиын сығылады, ал жиынның бөлігіндегі супремум түгел жиындағы супремумнен артық болмайды. [40]
Кейбір функциялардың үздіксіздік модулін есептейік.
-
 функциясының
функциясының  сегментіндегі үздіксіздік
модулін есептейік.
сегментіндегі үздіксіздік
модулін есептейік.  және
және
 нүктелері
–
нүктелері
–  болатындай
болатындай  сегментінің кез келген
нүктелері болсын, мұндағы
сегментінің кез келген
нүктелері болсын, мұндағы  .
Онда
.
Онда

болатыны көрініп тұр. Үздіксіздік модулінің анықтамасына қатысты ескертуді ескере отырып соңғы теңсіздіктен

екенін аламыз. Басқа
жағынан,  болатындай
болатындай  алып,
алып,

аламыз.
Демек,  (егер
(егер
 болса).
болса).
-
Енді
 функциясының
функциясының  интервалындағы үздіксіздік
модулін есептейік.
интервалындағы үздіксіздік
модулін есептейік.

болғандықтан,  болады. Басқа
жағынан,
болады. Басқа
жағынан,  интервалының
нүктелерінен
интервалының
нүктелерінен 
 түріндегі шексіз
аз
түріндегі шексіз
аз  және
және
 екі тізбекті алсақ, кез
келген
екі тізбекті алсақ, кез
келген  үшін
үшін
 және
және  болатындай п
нөмірін белгілей аламыз,
демек,
болатындай п
нөмірін белгілей аламыз,
демек,  және
және

болады.
Бұдан  шығады.
шығады.
-
Ендігі кезекте
 функциясының
функциясының  интервалындағы үздіксіздік
модулін есептейік. Бұл үздіксіздік модулі
интервалындағы үздіксіздік
модулін есептейік. Бұл үздіксіздік модулі
 -ке тең болатынына көз
жеткізейік.
-ке тең болатынына көз
жеткізейік.
Еркін
 нақтылап,
нақтылап,  болатындай
болатындай  қатынастарын
қанағаттандыратын
қатынастарын
қанағаттандыратын  және
және
 нүктелерін қарастырайық.
Бұдан
нүктелерін қарастырайық.
Бұдан

шығады. [41]
Ақырында
 функциясының
ағы үздіксіздік модулінің қасиеті
мен осы функцияның берілген жиындағы үздіксіздік модулінің
шамасының арасындағы байланысты орнататын теореманы
дәлелдейік.
функциясының
ағы үздіксіздік модулінің қасиеті
мен осы функцияның берілген жиындағы үздіксіздік модулінің
шамасының арасындағы байланысты орнататын теореманы
дәлелдейік.
7-теорема.  функциясы
функциясы жиынында біртекті үздіксіз
болуы үшін осы функцияның берілген
жиындағы
жиынында біртекті үздіксіз
болуы үшін осы функцияның берілген
жиындағы  үздіксіздік
модулі
үздіксіздік
модулі

қатынасын қанағаттандыруы қажетті және жеткілікті.
Дәлелдеу. 1)
Қажеттілік.  функциясы
функциясы
 жиынында біртекті
үздіксіз болсын. Теоремада берілген қатынастың дұрыстығын, яғни кез
келген
жиынында біртекті
үздіксіз болсын. Теоремада берілген қатынастың дұрыстығын, яғни кез
келген  үшін оған жауап беретін
және
үшін оған жауап беретін
және  шартын қанағаттандыратын
барлық δ
үшін
шартын қанағаттандыратын
барлық δ
үшін
 теңсіздігі
орындалатын
теңсіздігі
орындалатын  табылатынын дәлелдеу
керек.
табылатынын дәлелдеу
керек.
Біртекті үздіксіздіктің
анықтамасы бойынша кез келген  үшін оған жауап беретін
және
үшін оған жауап беретін
және  жиынында
жиынында
 шартын қанағаттандыратын
барлық
шартын қанағаттандыратын
барлық  және
және
 үшін
үшін  теңсіздігі
орындалатын
теңсіздігі
орындалатын  табылады. Бұл
ұйғарым
табылады. Бұл
ұйғарым  интервалының кез
келген δ
үшін
интервалының кез
келген δ
үшін

теңсіздігі орындалатынын көрсетіп тұр.
2)
Жеткіліктілік. 7-теоремадағы қатынас
орындалсын, яғни кез келген  үшін оған жауап беретін
және
үшін оған жауап беретін
және  шартын қанағаттандыратын
барлық δ
үшін
шартын қанағаттандыратын
барлық δ
үшін
 теңсіздігі
орындалатын
теңсіздігі
орындалатын  табылсын.
табылсын.
Үздіксіздік модулінің
анықтамасы бойынша  жиынында
жиынында
 шартын қанағаттандыратын
барлық
шартын қанағаттандыратын
барлық  және
және
 үшін
үшін  теңсіздігі орындалады, ал бұл
ұйғарым
теңсіздігі орындалады, ал бұл
ұйғарым  функциясының
функциясының  жиынында біртекті үздіксіз
екенін білдіреді. Теорема дәлелденді.
жиынында біртекті үздіксіз
екенін білдіреді. Теорема дәлелденді.
Жоғарыда біз үш функцияның
үздіксіз модулін есептеп шығардық:  сегментіндегі
сегментіндегі  функциясы
және
функциясы
және  интервалындағы
интервалындағы  және
және
 функциялары.
функциялары.
 болғандықтан, онда
7-теоремадан
болғандықтан, онда
7-теоремадан  функциясының
функциясының  сегментінде біртекті үздіксіз
екені, ал
сегментінде біртекті үздіксіз
екені, ал  және
және
 функциялары
функциялары  интервалында біртекті үзілісті
екені шығады. [42]
интервалында біртекті үзілісті
екені шығады. [42]
Қорытынды
Берілген дипломдық жұмыста көрсетілген мәліметтерді баяндауда кванторлар тілі минимумға жеткізіп, олар нақты сөздік түсіндірмелермен алмастырылды. Сонымен қатар жұмыстың өн бойында математикалық пайымдаудың нақты, көркем және логикалық мінсіз тіл қолданылды.
Әрбір бөлім мен бөлімшедегі материал осы бөлім немесе бөлімшені оқып үйренуді нақты түрде аяқтауды қамтамасыз ететіндей түрге жинақталып жазылды.
Дипломдық жұмысты жазудың тілі жеңілден күрделіге қарай дидактикалық принципіне сәйкес қолданылды. Осылайша, функция ұғымы әуелі сандар арқылы және геометриялық фигуралар арқылы баяндалып, мәселен, үшбұрыштың ауданы мен оның үш қабырғасының ұзындықтарының арасындағы байланыс негізінде функция ұғымы енгізіліп, шамалар бір-бірімен қандай да бір физикалық қатынас арқылы байланысатын жағдайлармен жалғасып, мәселені өрбіту күрделене беріп, математикалық анализдегі функция ұғымы толыққанды қарастырылды.
Бұл дипломдық жұмыстың алғашқы бөлімі тәуелсіз айнымалы және функция ұғымымен басталып, функцияның берілу тәсілдері, функциялардың классификациясы, функцияның графигі, кері функциялар, күрделі функциялар, функцияның шегі, үздіксіздік деген бөлімшелерді қамтиды.
Жұмыстың негізгі бөлімі үздіксіздіктің анықтамасынан басталып, үздіксіз функцияларға қолданылатын арифметикалық амалдар, кейбір элементар функциялардың үздіксіздігі туралы баяндалып, жұмыстың өзекті тақырыбы болып саналатын үздіксіз функцияларға қатысты Больцано және Вейерштрасс теоремаларымен жалғасады. Сонымен қатар осы теоремалардың қолданылуы туралы баяндалып, фунцияның біртекті үздіксіздігі және функцияның үздіксіздік модулі ұғымдарына жеке тоқталады.
Дипломдық жұмыста католикалық дін қызметшісі және схоластикалық философияның білгірі, математикалық анализге қазіргі заманғы қатаңдық ұғымын енгізгендердің бірі болып саналатын, «Paradoxien des Unendlichen» атты керемет кітабында үздіксіз функцияларға қатысты көптеген қарапайым мәліметтер дәлелденуі керек деген пікір білдірген Бернард Больцаноның теоремасы дәлелденіп, бұл теореманың геометриялық және бір механикалық мәселеге қолданылуы туралы баяндалады. Сонымен қатар Вейерштрасстың экстремалдық мәндер туралы теоремалары да келтіріліп, жан-жақты дәлелденді. Больцано мен Вейерштрасс теоремаларының дәлелдеуі конструктивтік түрге келтірілмейтіндігі, олар нөлдік нүктенің орналасуын немесе үрдістердің соңында алынатын дәлдіктің дәрежесі алдын ала анықталған функцияның ең үлкен және ең кіші мәнін табудың «тиімді» әдісін көрсетпейтіні, олар тек қана аталған мәндердің барын немесе жоқтығын теріске шығарып дәлелдейтіні аталып кетті.
Бұл жұмыста жинақталған материал мұғалімнің басқаруымен немесе өз бетімен функция ұғымы және үздіксіз функцияның қасиеттері туралы толыққанды оқып-үйренуге немесе білімді тереңдетуге ниеттеніп жүрген жоғары сынып оқушыларына, сондай-ақ әр түрлі мамандыққа даярлайтын факультеттердің студенттеріне, механиктер, физиктер және инженер-зерттеушілерге үздіксіз функциялар туралы анықтамалық ретінде қолдануға мүмкіндік береді.
Пайдаланылған әдебиеттер тізімі
-
Клини С.К., Введение в математику, М.: ИЛ, 1957.
-
Фихтенгольц Г.М., Основы математического анализа. Том 1. Наука, 1968.
-
Архипов Г.И., Садовничий В.А., Чубариков В.Н., Лекции по математическому анализу : учеб. для вузов, Дрофа, 2004.
-
Зорич В. А., Математический анализ. Часть I. М.: МЦНМО, 2002.
-
Камынин Л.И., Курс математического анализа. Том 1. М.: Изд-во МГУ, 2001.
-
Никольский С.М., Курс математического анализа., М.: Физматлит, 2001.
-
Кудрявцев Л.Д., Курс математического анализа (в двух томах), Том 1. М.: Высшая школа, 1981.
-
Бермант А.Ф., Курс математического анализа, Часть I. М.: Физматлит, 1959.
-
Берс Л., Математический анализ (в двух томах). Том 1. М.: Высшая Школа, 1975.
-
Франклин Ф., Математический анализ (в двух томах). Том 1. Иностранная Литература, 1950.
-
Кириллов А.А., Пределы. М.: Наука, 1968.
-
Гусак Г.М., Гусак Е.А., Функции и пределы, Минск: Вышэйш. Шк.,1987.
-
Валле-Пуссен Ш.-Ж., Курс анализа бесконечно малых, Том 1. 1922.
-
Рудин У., Основы математического анализа. М.: Мир, 1976.
-
Ландау Э., Основы анализа. Иностранная литература, 1947.
-
Немыцкий В., Слудская М., Черкасов А., Курс математического анализа. Изд. 3-е. ГИТТЛ, 1957.
-
Дороговцев А.Я., Математический анализ. Краткий курс в современном изложении (2-е издание). Киев: Факт, 2004.
-
Крейн С.Г., Ушакова В.Н., Математический анализ элементарных функций. Физматгиз, 1963.
-
Р.Курант, Г.Роббинс, Что такое математика? М.:МЦНМО, 2001.
-
Натанзон С.М., Краткий курс математического анализа. Изд-во МЦНМО, 2004.
-
Зельдович Я.Б., Высшая математика для начинающих и ее приложения к физике. М.: Наука, 1970.
-
Романовский П.И., Общий курс математического анализа в сжатом изложении. Физматгиз, 1962.
-
Фролов Н. А., Курс математического анализа. В 2-х частях. Ч. 1 - 1964 г.
-
Гельфанд И.М., Глаголева Е.Г., Шноль Э.Э., Функции и графики. М.: МЦНМО, 2001.
-
Ильин В.А., Куркина А.В., Высшая математика, М.: ООО «ТК Велби», 2002.
-
Шипачев В.С., Высшая математика: Учеб. для вузов. М.: Высшая школа, 2005.
-
Ильин В.А., Садовничий В.А., Сендов Бл.Х., Математический анализ, М.: изд-во МГУ, 1985.
-
Шведов И.А., Компактный курс математического анализа, ч. 1. Функции одной переменной: Учеб. пособие/ Новосиб. гос. ун-т. Ново- сибирск, 2001.
-
Понтрягин Л.С., Математический анализ для школьников. М.: Наука, 1988.
-
Морозова В.Д., Введение в анализ: Учебник для вузов / Под ред. В.С.Зарубина, А.П.Крищенко – М.: Изд-во МГТУ им. Н.Э.Баумана, 1996.
-
Уваров В.Б., Математический анализ: учеб. пособ. для вузов. М.: Высшая школа, 1984.
-
Шварц Л., Анализ / Пер. с франц. под ред. С.Г.Крейна: Том 1. М.: Мир, 1972.
-
Клейн Ф., Элементарная математика с точки зрения высшей. Том 1. Арифметика. Алгебра. Анализ / Пер. с нем. под ред. В.Г.Болтянского. М.: Наука, 1987.
-
Уиттекер Э.Т., Ватсон Дж.Н., Курс современного анализа. Часть 1. Основные операции анализа. М.: Физматлит, 1963.
-
Тарасов Л.В., Математический анализ: Беседы об основных понятиях. М.: Просвещение, 1979.
-
Шилов Г.Е., Математический анализ: специальный курс, М.: изд-во физико-математической литературы, 1961.
-
Смирнов В.И., Курс высшей математики, Том 1. М.: Наука, 1974.
-
Выгодский М.Я., Справочник по высшей математике. М.: Наука, 1977.
-
Дьедонне Ж., Основы современного анализа. М.: Мир, 1964.
-
Мышкис А.Д., Лекции по высшей математике, М.: Наука, 1973.
-
Свиридюк Г.А., Федоров В.Е., Математический анализ. Часть 1. Челябинск: ЧелГУ, 1999.
-
Толстов Г.П., Элементы математического анализа. Том 1. М.: Наука, 1974.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Дипломдық жұмыс, математика
Дипломдық жұмыс, математика
Мазмұны
1.1. Тәуелсіз айнымалы және функция 5
1.2. Функцияның берілу тәсілдері 10
1.3. Функциялар классификациясы 12
1.4. Функцияның графигі. Кері функциялар 13
1.7. Шексіз кіші және шексіз үлкен функциялар 26
2. Үздіксіз функциялардың екі негізгі теоремасы 32
2.1. Үздіксіздіктің анықтамасы 32
2.2. Үздіксіз функцияларға қолданылатын арифметикалық амалдар 34
2.3. Кейбір элементар функциялардың үздіксіздігі 35
2.5. Больцано теоремасының қолданылуы 39
2.6. Вейерштрасстың экстремалдық мәндер туралы теоремалары 43
2.7. Реттілік туралы теорема. Шағын жиындар 49
2.8. Функцияның біртекті үздіксіздігі ұғымы 51
2.9. Функцияның үздіксіздік модулі ұғымы 56
Пайдаланылған әдебиеттер тізімі 61
Кіріспе
Математикалық анализ курсын оқып үйренудің мақсаты – функцияларды оқып үйрену, сондай-ақ математиканың жалпы әдістерінің қолданбалы мәнін ашу болып табылады.
Функцияның қасиеттері мен оның графигін салуды үйрену математиканың тамаша қолданылуы болып табылады. Функцияны зерттеудің мұндай тәсілі бірнеше рет мұқият талдауға ұшыраған еді. Бұның басты себебі – математика қосымшаларының жаңа құбылыстарын зерттеу кезінде пайда болған бірінен-бірі күрделене түсетін функциялармен жұмыстану қажет болды. Математиканың құрастырылған ережелеріне бағынбайтын жағдайлар пайда болды.
Математикалық анализді оқып үйренудегі функциялық беру тәсілдерінің дамуы функциялардың үздіксіздігі мен үзіліс нүктелері жайында көрнекі мәліметтерді алуға, кез келген элементар функцияның қолданылу аясындағы үздіксіздігі туралы оқып үйрену, функциялардың графиктерін салуды үйренуге және негізгі элементар функциялар туралы мағлұматтарды тереңдетуге, сондай-ақ олардың қолданылу аясын анықтауға мүмкіндік береді.
Берілген тақырыптың өзектілігі. Қазіргі заманғы математикалық анализде үздіксіз функциялар және оларға қатысты теоремалар және оларды қолдану мәселесі әлі де ашық күйінде сақталып отыр. Алайда бұл бағыттағы мәлімет айтарлықтай көп жиналғандықтан, бұл мәліметтерді жинақтап, тізбектеп, жүйелеп, бөлек жұмыс ретінде жазу қажеттілігі туындап отыр.
Берілген дипломдық жұмыстың зерттеу объектісі – «Үздіксіз функциялардың екі негізгі теоремасы» тақырыбын оқып үйрену арқылы мектеп математика курсынан алған үздіксіз функция ұғымының кеңейтілуі.
Зерттеу пәні – үздіксіз функциялардың қасиеттері мен теоремалары.
Мақсаты – мектеп математика курсынан бастау алатын және жоғары математикада жалғасын табатын функция, соның ішінде үздіксіз функция туралы жалпы мәлімет алып, үздіксіз функциялардың екі негізгі теоремасы болып саналатын Больцано теоремасы мен Вейерштрасс теоремасымен танысып, олардың қолданылу аймағы туралы мәлімет алу.
Міндеттер:
-
үздіксіз функциялардың екі негізгі теоремасы туралы жалпы мағлұмат алу;
-
берілген тақырыпты кеңейту;
-
үздіксіз функциялардың екі негізгі теоремасының қолданылу аясын анықтау.
Зерттеу әдістері:
-
ғылыми, оқу әдебиеттерді талдау;
-
теориялық материалды жинақтау және жүйелеу;
-
тақырып бойынша білімді кеңейту.
Берілген жұмыстың құрамы:
-
Функция туралы жалпы мәлімет.
-
Үздіксіз функциялардың екі негізгі теоремасы.
Жұмыстың тәжірибелік маңыздылығы – жинақталған материал мұғалімнің басқаруымен немесе өз бетімен функция ұғымы және үздіксіз функцияның қасиеттері туралы білімді тереңдеткісі келетін жоғары сынып оқушылары мен ЖОО студенттеріне математикалық анализді оқып үйрену үрдісінде пайдалы болады.
1. Функция ұғымы
1.1. Тәуелсіз айнымалы және функция
Қазіргі заманғы математиканың маңызды бөлімдері функция ұғымының айналасында өрбиді. Бұл бөлімшеде біз функция ұғымын жүйелі анализдеумен айналысатын боламыз.
х-тің мәні берілмесе,

секілді өрнектердің белгілі бір сан мәні болмайды. Осындай өрнектің мәні х мәнінің функциясы деп айтады және

деп жазады. Мысалы,
егер  болса,
онда
болса,
онда  , яғни
, яғни
 . Осы
әдіспен х-тің кез келген бүтін, бөлшек,
иррационал, тіпті комплекс мәніндегі
. Осы
әдіспен х-тің кез келген бүтін, бөлшек,
иррационал, тіпті комплекс мәніндегі  функциясының мәнін табуға
болады.
функциясының мәнін табуға
болады.
п-нен кем жай сандардың саны
бүтін п
санының
 функциясы
болады. п
санының мәні берілген
жағдайда
функциясы
болады. п
санының мәні берілген
жағдайда  функциясының мәнін есептеудің
ешқандай алгебралық өрнегі берілмесе де,
функциясының мәнін есептеудің
ешқандай алгебралық өрнегі берілмесе де,
 функциясының мәні
анықталады. Үшбұрыштың ауданы оның үш қабырғасының ұзындықтарының
функциясы болады; функция қабырғалардың ұзындықтарымен бірге
өзгеріп тұрады және қабырғалардың ұзындықтары нақты берілген
жағдайда, функция да нақтыланады. Егер жазықтық проекцияланатын
болса немесе топологиялық түрлендірілсе, онда түрлендіруден кейінгі
нүктенің координаталары нүктенің бастапқы координаталарына тәуелді
болады, яғни олардың функциялары болып табылады. Шамалар
бір-бірімен қандай да бір физикалық қатынас арқылы байланысатын
жағдайлардың бәрінде «функция» ұғымы қолданылады. Цилиндрдің ішіне
енгізілген газдың көлемі поршеньге әсер ететін температура мен
қысымның функциясы болып табылады. Әуе шарына әсер ететін
атмосфералық қысым шардың теңіз деңгейіне қарағандағы биіктігінің
функциясы болатыны анықталды. Периодты құбылыстардың үлкен көлемі –
судың көтерілуінің қозғалысы, керілген сымның тербелісі,
қыздырылған сымның шығаратын жарық толқындарының таралуы
–
функциясының мәні
анықталады. Үшбұрыштың ауданы оның үш қабырғасының ұзындықтарының
функциясы болады; функция қабырғалардың ұзындықтарымен бірге
өзгеріп тұрады және қабырғалардың ұзындықтары нақты берілген
жағдайда, функция да нақтыланады. Егер жазықтық проекцияланатын
болса немесе топологиялық түрлендірілсе, онда түрлендіруден кейінгі
нүктенің координаталары нүктенің бастапқы координаталарына тәуелді
болады, яғни олардың функциялары болып табылады. Шамалар
бір-бірімен қандай да бір физикалық қатынас арқылы байланысатын
жағдайлардың бәрінде «функция» ұғымы қолданылады. Цилиндрдің ішіне
енгізілген газдың көлемі поршеньге әсер ететін температура мен
қысымның функциясы болып табылады. Әуе шарына әсер ететін
атмосфералық қысым шардың теңіз деңгейіне қарағандағы биіктігінің
функциясы болатыны анықталды. Периодты құбылыстардың үлкен көлемі –
судың көтерілуінің қозғалысы, керілген сымның тербелісі,
қыздырылған сымның шығаратын жарық толқындарының таралуы
–  және
және
 қарапайым
тригонометриялық функцияларымен
«реттеледі».
қарапайым
тригонометриялық функцияларымен
«реттеледі».
«Функция» ұғымын енгізген Лейбниц (1646-1716) үшін де, XVIII ғасырдағы математиктер үшін де функционалдық тәуелділік идеясы осы тәуелділікті нақты өрнектейтін қарапайым математикалық формуланың болуымен сипатталатын еді. Мұндай концепция математикалық физиканың қоятын талаптарына қатысты өте тар болып шықты, сондықтан «функция» ұғымы ұзақ уақыт бойына жалпылау мен өңдеуге ұшыраған болатын. [1]
Осы бөлімшеде аталған үрдістің қалай өткендігін жазатын боламын.
Анықтамалар мен мысалдар.
Көптеген жағдайларда қандай да бір S жиынтығынан (жиынынан) өзіміздің қалауымызбен еркін түрде таңдап алатын математикалық объектілермен жұмыстану қажет болады. Таңдалынған объект бұл жағдайда айнымалы деген атауға, ал S жиынтығы оның өзгеру аймағы деген атауға ие болады. Айнымалыларды алфавиттің соңғы әріптерімен белгілеу қабылданды. Мысалы, егер S әрпімен барлық бүтін сандардың жиыны белгіленген болса, онда S аймағынан алынған Х айнымалысы қандай да бір бүтін сан болады. «Х айнымалысы S жиынынан өтеді» деп айтады, ал оның астарында Х айнымалысын S жиынының кез келген элементімен теңдестіре аламыз деген ой жатады. Егер бүтін жиыннан еркімізше таңдап алатын элементтерге қатысты пікір айтқымыз келсе, айнымалы ұғымын пайдаланған ыңғайлы. Мысалы, S жоғарыда айтылғандай бүтін сандар жиыны, ал Х пен Y – S аймағынан алынған айнымалылар болса, онда

формуласы кез келген екі бүтін санның қосындысы қосылғыштардың орнына қатысты болмайды деген жайттың символдық түрдегі жеңіл өрнектелуін көрсетеді. Оның дербес жағдайы

тұрақты сандары бар теңдігімен өрнектеледі; бірақ барлық сандар жұбы үшін дұрыс орындалатын жалпы ережені көрсету үшін айнымалылардың мәнін қабылдайтын символдарды қолдану керек.
Х айнымалысының S өзгеру аймағының сандар жиыны болуының қажеттілігі жоқ. Мысалы, S жазықтықтағы барлық дөңгелектердің жиыны болуы мүмкін; онда Х айнымалысы кез келген бір дөңгелекті өрнектейтін болады. Немесе S жазықтықтағы барлық тұйық көпбұрыштардың жиыны болуы мүмкін, онда Х – кез келген көпбұрыш болады. Сондай-ақ айнымалының өзгеру аймағындағы элементтер санының шексіз болуы да міндетті емес. Мысалы, Х –белгілі бір уақыттағы берілген қаланың S тұрғындарының ішіндегі кез келген адамды сипаттауы мүмкін. Немесе Х – бүтін санды 5-ке бөлгендегі мүмкін болатын қалдықтардың біреуін өрнектеуі мүмкін; соңғы жағдайда S аймағы бес саннан тұратын болады: 0, 1, 2, 3, 4.
Сандық айнымалы жағдайы
маңызды болады; бұл жағдайда әдетте кішкентай
х
әрпі қолданылады – бұл
кезде S
өзгеру аймағы нақты сандар
осінің қандай да бір  интервалы (аралық) болады. Бұл
жағдайда х
– қарастырылып тұрған
интервалда үздіксіз (немесе
нақты)
айнымалы дейді. Үздіксіз айнымалының
өзгеру аймағы шексіздікке дейін де созылуы мүмкін.
Мысалы, S
барлық оң нақты сандар
жиыны
интервалы (аралық) болады. Бұл
жағдайда х
– қарастырылып тұрған
интервалда үздіксіз (немесе
нақты)
айнымалы дейді. Үздіксіз айнымалының
өзгеру аймағы шексіздікке дейін де созылуы мүмкін.
Мысалы, S
барлық оң нақты сандар
жиыны  болуы мүмкін немесе бірі
қалмастан барлық нақты сандар жиыны болуы
мүмкін. Осындай әдіспен жазықтықтың немесе тіктөртбұрыштың әлде
дөңгелектің қандай да бір ішкі аймағының нүктелерін
өрнектейтін Х
айнымалысын қарастыра аламыз.
Жазықтықтың әрбір нүктесі қандай да бір осьтер жұбына қатысты
алынған өзінің
болуы мүмкін немесе бірі
қалмастан барлық нақты сандар жиыны болуы
мүмкін. Осындай әдіспен жазықтықтың немесе тіктөртбұрыштың әлде
дөңгелектің қандай да бір ішкі аймағының нүктелерін
өрнектейтін Х
айнымалысын қарастыра аламыз.
Жазықтықтың әрбір нүктесі қандай да бір осьтер жұбына қатысты
алынған өзінің  екі координатасымен
анықталатындықтан, көп жағдайда х
және
у нақты (үздіксіз)
айнымалылардың жұбымен жұмыстанады
дейді.
екі координатасымен
анықталатындықтан, көп жағдайда х
және
у нақты (үздіксіз)
айнымалылардың жұбымен жұмыстанады
дейді.
Х-тің әрбір мәніне басқа
бір Y
айнымалысының белгілі бір
мәнін сәйкестендіретін жағдайлар болуы мүмкін.
Онда Y
айнымалысы Х
айнымалысының функциясы деп
аталады. Y
айнымалысы X-пен байланысатын
тәсіл  («тең
Х-тен
F-ке» деп оқылады) символымен
өрнектеледі. Егер Х
айнымалысы S
жиынынан өтсе,
онда Y
айнымалысы басқа бір жиынды
өтеді, оны Т
деп алайық. Мысалы,
егер S
–
жазықтықтағы Х
үшбұрыштардың жиыны болса,
онда
(«тең
Х-тен
F-ке» деп оқылады) символымен
өрнектеледі. Егер Х
айнымалысы S
жиынынан өтсе,
онда Y
айнымалысы басқа бір жиынды
өтеді, оны Т
деп алайық. Мысалы,
егер S
–
жазықтықтағы Х
үшбұрыштардың жиыны болса,
онда  функциясы ретінде қарастырылып
отырған Х
үшбұрышының периметрінің
ұзындығын алуға болады; яғни Т
– барлық оң сандар жиыны
болады. Әр түрлі
функциясы ретінде қарастырылып
отырған Х
үшбұрышының периметрінің
ұзындығын алуға болады; яғни Т
– барлық оң сандар жиыны
болады. Әр түрлі  мен
мен
 екі үшбұрыштың
периметрлері бірдей болуы мүмкін екенін атап кетейік,
яғни
екі үшбұрыштың
периметрлері бірдей болуы мүмкін екенін атап кетейік,
яғни  болса да
болса да
 теңдігі орындалуы
мүмкін. S
жазықтығын қандай да бір
басқа Т
жазықтығына проекциялық
түрлендіру S
жазықтығының
әрбір Х
нүктесіне
теңдігі орындалуы
мүмкін. S
жазықтығын қандай да бір
басқа Т
жазықтығына проекциялық
түрлендіру S
жазықтығының
әрбір Х
нүктесіне
 функционалдық символы
арқылы өрнектелетін белгілі бір ережеге сәйкес
Т
жазықтығының тек қана
бір Y
нүктесін сәйкестікке
қояды.Алдыңғы мысалға қарағанда соңғы мысалда ылғи
да
функционалдық символы
арқылы өрнектелетін белгілі бір ережеге сәйкес
Т
жазықтығының тек қана
бір Y
нүктесін сәйкестікке
қояды.Алдыңғы мысалға қарағанда соңғы мысалда ылғи
да  теңсіздігі орындалады,
егер
теңсіздігі орындалады,
егер  болса, осы
орайда S
жазықтығының Т
жазықтығына
бейнеленуі өзара
біртекті деп
айтамыз.
болса, осы
орайда S
жазықтығының Т
жазықтығына
бейнеленуі өзара
біртекті деп
айтамыз.
Үздіксіз айнымалының функциялары көп жағдайда алгебралық өрнектер арқылы анықталады. Мысал ретінде төмендегі функцияларды алуға болады:

Бұл өрнектердің біріншісі және
үшіншісінде х
барлық нақты сандар жиынында
өте алады, ал екінші мысалда х
0-ден басқа барлық нақты
сандар жиынында өте алады (0 мәні алынып тасталады,
себебі  символы сан бола
алмайды).
символы сан бола
алмайды).
п
санының жай
көбейткіштерінің  саны
п
функциясы болады
және п
натурал сандар жиынынан өтіп
шығады. Жалпы,
саны
п
функциясы болады
және п
натурал сандар жиынынан өтіп
шығады. Жалпы,  сандарының кез келген
реттілігін қандай да бір
сандарының кез келген
реттілігін қандай да бір  функциясының мәндерінің жиыны
деп қабылдауға болады және бұл жердегі тәуелсіз айнымалының өзгеру
аймағы натурал сандар жиыны болады. Жазуды қысқарту үшін
реттіліктің п-ші
мүшесін
функциясының мәндерінің жиыны
деп қабылдауға болады және бұл жердегі тәуелсіз айнымалының өзгеру
аймағы натурал сандар жиыны болады. Жазуды қысқарту үшін
реттіліктің п-ші
мүшесін  анығырақ функционалдық
белгілеуден гөрі
анығырақ функционалдық
белгілеуден гөрі  символымен белгілеу
қабылданған. Төмендегі өрнектер п
бүтін айнымалының функциялары
болып табылады:
символымен белгілеу
қабылданған. Төмендегі өрнектер п
бүтін айнымалының функциялары
болып табылады:



 қатынасы
берілсін; Х
айнымалысын тәуелсіз
айнымалы, ал
C
айнымалысының
мәні Х
мәніне тәуелді
болғандықтан C
айнымалысын тәуелді
айнымалы деп атау
келісілген.
қатынасы
берілсін; Х
айнымалысын тәуелсіз
айнымалы, ал
C
айнымалысының
мәні Х
мәніне тәуелді
болғандықтан C
айнымалысын тәуелді
айнымалы деп атау
келісілген.
Х айнымалысының барлық мәндеріне C айнымалысының бір ғана мәні сәйкес келетін, яғни Т жиыны бір ғана элементтен тұратын жағдай болып қалуы мүмкін. Онда біз дербес жағдаймен кездесеміз, бұл жағдайда C айнымалысы өзгермейді, яғни C – тұрақты мән болады (тұрақты немесе константа). Бұл жағдайды функцияның жалпы ұғымына қосып жібереміз.
Функционалды тәуелділік ұғымы тек қана «таза» математикада емес, сонымен қатар оның практикалық қосымшаларында да маңызды болып келеді. Физикалық заңдар кейбір шамалардың өзгеріске ұшыра алатын басқа шамаларға тәуелділігін өрнектейтін тәсіл болып табылады. Мысалы, тербелмелі сымның шығаратын дыбысының биіктігі сымның ұзындығына, салмағына және оның керілу дәрежесіне тәуелді; атмосфераның қысымы биіктікке тәуелді; оқтың энергиясы оның массасы мен жылдамдығына тәуелді. Физиканың міндеті осыған ұқсас тәуелділіктердің табиғатын дәл немесе жорамалдап анықтау болып табылады.
Функция ұғымы арқылы қозғалыстың математикалық тұрғыдан алғандағы дәл сипаттамасын беруге болады. Қозғалып келе жатқан бөлшек кеңістіктің x, y, z тікбұрышты координаталы қандай да бір нүктесінде шоғырланған және t айнымалысы уақытты өлшейді деп елестетіп көрсек, онда бөлшектің қозғалысы уақыт функциясы ретіндегі x, y, z координаталарымен толық анықталады:
 .
.
Бұның мысалы ретінде тек қана ауырлық күші әсер ететін бөлшектің тік еркін түсуін алуға болады: бұл жағдайда төмендегідей қатынастарды аламыз:

мұндағы g – ауырлық күшінің үдеуі. Егер бөлшек х, у жазықтығында бірлік шеңбер бойымен біртекті айналатын болса, онда оның қозғалысы

функцияларымен сипатталады, мұндағы ω – тұрақты сан (айналудың бұрыштық жылдамдығы).
Математикалық функцияны айнымалы шамалардың өзара тәуелділігін басқаратын заң ретінде ғана қабылдау керек. Функция ұғымы тәуелді және тәуелсіз айнымалылардың арасында «себеп пен салдарға» жақын байланыстың бар болуын тұспалдамайды. Бірақ күнделікті сөйлеуде «функционалды тәуелділік» термині осы соңғы мағынада қолданылып жүрсе де, ондай философиялық талдаудан ойымызды аулақ ұстаймын. Осылайша, мысалы, тұрақты температурада қандай да бір тұйық қабықта жинақталған газға қатысты Бойль заңы газдың р қысымы мен оның v көлемінің көбейтіндісі с-ға тең тұрақты шама болады деп пайымдайды (соңғы мән, өз кезегінде, температураға тәуелді):
 .
.
Бұл қатынасты р-ға қатысты да, v-ға қатысты да шешуге болады:
 немесе
немесе 
бұл жағдайда көлемнің өзгеруі қысымның өзгеруінің «себебі» деп немесе қысымның өзгеруі көлемнің өзгеруінің «себебі» деп қарастыруға болмайды. Математик үшін өз қарастырып отырған екі айнымалы шамалардың арасындағы қатынастың (байланыстың) түрі ғана маңызды болады. [2]
Функция ұғымына деген
көзқарастың математиктер мен физиктерде әр түрлі екенін айта кеткен
жөн. Математиктер әдетте қатынастың
заңына, тәуелді
u
айнымалысының мәнін табу үшін
тәуелсіз х
айнымалысына қолданатын
математикалық амалға көңіл аударады. Бұл
мәнмәтінде  символы –
математикалық
амалдың символы;
символы –
математикалық
амалдың символы;
 мәні
– х
санына
мәні
– х
санына
 амалын қолданудың
нәтижесі болады. Басқаша қарағанда, физик көп
жағдайда х
мәнінен
u
мәнін шығаратын математикалық
үрдіске емес, u шамасының
өзіне көңіл аударады. Мысалы,
дененің қозғалысына қатысты ауаның u
кедергісі
қозғалыстың v
жылдамдығына тәуелді болады
және u
мәнін есептеудің математикалық
формуласы берілу немесе берілмеуіне қарамастан, оны эксперименттік
түрде есептеп шығаруға болады. Физик үшін
арнайы
амалын қолданудың
нәтижесі болады. Басқаша қарағанда, физик көп
жағдайда х
мәнінен
u
мәнін шығаратын математикалық
үрдіске емес, u шамасының
өзіне көңіл аударады. Мысалы,
дененің қозғалысына қатысты ауаның u
кедергісі
қозғалыстың v
жылдамдығына тәуелді болады
және u
мәнін есептеудің математикалық
формуласы берілу немесе берілмеуіне қарамастан, оны эксперименттік
түрде есептеп шығаруға болады. Физик үшін
арнайы  математикалық формуласы емес,
іс жүзіндегі нақты кедергі маңыздырақ болады. Математиканы әдетте
физикаға немесе инженерлік іске қолданатын адамдардың көзқарасы осындай
болады. Математикалық анализдің кейбір жоғары бөлімдерінде
шатастырып алмау үшін
математикалық формуласы емес,
іс жүзіндегі нақты кедергі маңыздырақ болады. Математиканы әдетте
физикаға немесе инженерлік іске қолданатын адамдардың көзқарасы осындай
болады. Математикалық анализдің кейбір жоғары бөлімдерінде
шатастырып алмау үшін  символының
астарында u-дың мәнін алу
үшін х-ке
қолданылатын
символының
астарында u-дың мәнін алу
үшін х-ке
қолданылатын  амалы ма әлде басқа
бір z
айнымалысына басқаша түрде
тәуелді болып қарастырыла алатын u
шамасының өзі ме екенін
анықтап алу қажет. Мысалы, дөңгелектің
ауданы
амалы ма әлде басқа
бір z
айнымалысына басқаша түрде
тәуелді болып қарастырыла алатын u
шамасының өзі ме екенін
анықтап алу қажет. Мысалы, дөңгелектің
ауданы функциясымен беріледі,
мұндағы х
– дөңгелектің радиусы, бірақ
оны былай да жазуға болады:
функциясымен беріледі,
мұндағы х
– дөңгелектің радиусы, бірақ
оны былай да жазуға болады:  , мұндағы
z
– шеңбердің ұзындығы.
[3]
, мұндағы
z
– шеңбердің ұзындығы.
[3]
Бір тәуелсіз айнымалысы бар
математикалық функцияның ең жеңіл түрі ретінде
 тұрақты
«коэффициенттері» бар төмендегідей көпмүшелерді (полиномдарды) алуға
болады:
тұрақты
«коэффициенттері» бар төмендегідей көпмүшелерді (полиномдарды) алуға
болады:
 .
.
Одан кейін көпмүшелердің қатынасы болып табылатын төмендегідей рационал функцияларды:

ал олардан
кейін  жазықтығындағы бірлік шеңбер
арқылы жақсы анықталатын
жазықтығындағы бірлік шеңбер
арқылы жақсы анықталатын  және
және
 тригонометриялық
функцияларды жатқызуға болады.
Егер
тригонометриялық
функцияларды жатқызуға болады.
Егер  нүктесі осы шеңбер бойымен
қозғалса және егер х
– оң
таңбалы х
осін
ОР
радиусымен беттесетіндей етіп
бұру бұрышын анықтайтын бағытталған бұрыш болса,
онда
нүктесі осы шеңбер бойымен
қозғалса және егер х
– оң
таңбалы х
осін
ОР
радиусымен беттесетіндей етіп
бұру бұрышын анықтайтын бағытталған бұрыш болса,
онда  пен
пен
 Р нүктесінің координаталары
болады:
Р нүктесінің координаталары
болады:  . [4]
. [4]
1.2. Функцияның берілу тәсілдері
f
функциясын беру дегеніміз
– х
аргументінің әрбір мәніне оған
сәйкес  функциясының мәнін табудың
жолын көрсету. Функцияны берудің үш негізгі тәсілі
бар: аналитикалық,
кестелік және
графиктік.
функциясының мәнін табудың
жолын көрсету. Функцияны берудің үш негізгі тәсілі
бар: аналитикалық,
кестелік және
графиктік.
1) Аналитикалық тәсіл. Айнымалы шамалардың арасындағы тәуелділік аргументтің берілген мәніне сәйкес болатын функцияның мәнін алу үшін орындайтын іс-әрекеттерді көрсететін формула арқылы беріледі.
Мысалдар қарастырайық.
-
 формуласы анықталу
аймағы
формуласы анықталу
аймағы  сандық осі болатын, ал
мәндерінің жиыны
сандық осі болатын, ал
мәндерінің жиыны  жартытүзу болатын функцияны
береді (1-сурет).
жартытүзу болатын функцияны
береді (1-сурет). -
 формуласы анықталу
аймағы
формуласы анықталу
аймағы  кесіндісі болатын, ал
мәндерінің жиыны
кесіндісі болатын, ал
мәндерінің жиыны  кесіндісі болатын функцияны
береді (2-сурет).
кесіндісі болатын функцияны
береді (2-сурет). -

Бұл функция бірнеше формула
арқылы беріліп тұр. Ол сан осінің тұтас
бойында анықталады, ал оның мәндерінің
жиыны үш саннан тұрады: –1, 0 және +1
(3-сурет).
анықталады, ал оның мәндерінің
жиыны үш саннан тұрады: –1, 0 және +1
(3-сурет).
-
 формуласы
әрбір п
натурал санына (яғни бүтін оң
санға)
формуласы
әрбір п
натурал санына (яғни бүтін оң
санға)  санын сәйкестікке қояды.
Мысалы, егер
санын сәйкестікке қояды.
Мысалы, егер  болса,
онда
болса,
онда  болады.
Осылайша,
болады.
Осылайша,  формуласы анықталу
аймағы
формуласы анықталу
аймағы  болатын, ал мәндерінің
жиыны
болатын, ал мәндерінің
жиыны болатын функцияны береді
(4-сурет).
болатын функцияны береді
(4-сурет).


1-сурет 2-сурет 3-сурет

4-сурет
-
Дирихле функциясы

Бұл функция сан осінің тұтас
бойында  анықталады, ал мәндерінің
жиыны екі саннан тұрады: 0 және 1.
анықталады, ал мәндерінің
жиыны екі саннан тұрады: 0 және 1.
Дирихле функциясын графиктік түрде көрсету мүмкін емес екенін ескерте кетейік. [5]
2) Кестелік тәсіл.Төмендегі кестені келтірейік:
|
х |
0 |
0,1 |
0,2 |
3 |
0,6 |
4 |
0,8 |
1,5 |
2 |
|
у |
–1 |
10 |
1 |
–2 |
–8 |
0,5 |
–2 |
5 |
7 |
Кестенің бірінші жолында тұрған әрбір х-ке оның астында тұрған кестенің екінші жолындағы у-тің мәнін сәйкестікке қойып, алынған функция кесте түрінде берілді деп айтамыз. Бұл функцияның анықталу облысы кестенің бірінші жолында тұрған тоғыз х санынан тұратын жиын болады, ал мәндерінің жиыны кестенің екінші жолында тұрған тоғыз у санынан тұратын жиын болады.
Функцияны кесте арқылы беру үшін аргументтің мәндерінің саны шекті болу керек. Кестелерді көп жағдайда функцияны беру үшін қолданады. Мысалы, тригонометриялық функциялардың кестелері, логарифмдер кестесі және т.б. Функцияны кесте арқылы берудің мысалы ретінде пойыздың жүру кестесін алуға болады, ол кесте пойыздың қандай да бір уақыт мезетіндегі орнын анықтайды.
3) Графиктік тәсіл. Функцияны графиктік тәсілмен беруді әдетте х пен у айнымалыларының сәйкестігі график арқылы көрсетілетін физикалық шамаларды өлшеу тәжірибесінде қолданады. Көп жағдайда мұндай графиктер өздігінен жазатын арнайы құрылғылар арқылы сызылады. Мысалы, атмосфераның әр түрлі биіктіктегі қысымын өлшеу үшін арнайы өздігінен жазатын құрылғы – барографты қолданады, бұл құрылғы биіктікке сәйкес қысымның өзгеруін жылжымалы таспаға қисық сызық түрінде салады. [6]
1.3. Функциялар классификациясы
 тұрақты
функциясы,
тұрақты
функциясы,  (α
– кез келген сан) дәрежелік
функциясы,
(α
– кез келген сан) дәрежелік
функциясы,  көрсеткіштік
функциясы,
көрсеткіштік
функциясы,  логарифмдік
функциясы,
логарифмдік
функциясы,  тригонометриялық функциялары
және
тригонометриялық функциялары
және  кері тригонометриялық
функциялары қарапайым элементар
функциялар деп
аталады.
кері тригонометриялық
функциялары қарапайым элементар
функциялар деп
аталады.
Элементар функцияларға саны шектеулі арифметикалық амалдарды орындау арқылы, сондай-ақ осы функциялардың суперпозициясы (немесе қабаттастыру) арқылы шығатын функциялар элементар функциялар класын құрайды. Элементар функциялардың мысалдары:

 т.с.с.
т.с.с.
Элементар функциялардың төмендегідей классификациясы бар:
1)
 – бүтін сан,
ал
– бүтін сан,
ал  –кез келген сандар –
коэффициенттер болатын
–кез келген сандар –
коэффициенттер болатын

түріндегі функция бүтін рационал функция немесе т дәрежелі алгебралық көпмүше деп аталады. Бірінші дәрежелі көпмүше сызықтық функция деп аталады.
2) Екі бүтін рационал функциялардың қатынасы түрінде берілген

функциясы бөлшек рационал функция деп аталады.
Бүтін рационал және бөлшек рационал функциялардың жиынтығы рационал функциялар класын құрайды.
3) Бүтін және бөлшек көрсеткішті дәрежелік функцияларға төрт арифметикалық амалдар мен саны шектеулі суперпозицияларды орындау арқылы алынған және рационал түрге жатпайтын функциялар иррационал функциялар деп аталады.
Мысалы,
 т.с.с.
т.с.с.
4) Рационал немесе иррационал
функцияға жатпайтын кез келген функция
трансценденттік
функция деп аталады. Олар,
мысалы, 
 және т.б. функциялары.
[7]
және т.б. функциялары.
[7]
1.4. Функцияның графигі. Кері функциялар
Көп жағдайда функцияның сипаты
қарапайым график арқылы түсінікті түрде көрсетіледі.
Егер  – өзара перпендикуляр екі
оське қатысты жазықтықтағы координаталар болса,
онда
– өзара перпендикуляр екі
оське қатысты жазықтықтағы координаталар болса,
онда

сызықтық функциялары түзу сызықтармен кескінделеді;

квадраттық функциялары – параболалармен;

функциясы – гиперболамен
кескінделеді және т.с.с. Қандай да бір
 функциясының графигі
функциясының графигі  координаталары
координаталары  теңдеуі арқылы байланысқан
жазықтықтың барлық нүктелерінен тұрады.
теңдеуі арқылы байланысқан
жазықтықтың барлық нүктелерінен тұрады.
 функциялары 5-суретте
және 6-суретте графиктік түрде көрсетілді. Бұл
графиктер х
өзгерген кезде функциялардың
қалай өсіп немесе кеміп тұрғанын көрнекі түрде көрсетіп
тұр.
функциялары 5-суретте
және 6-суретте графиктік түрде көрсетілді. Бұл
графиктер х
өзгерген кезде функциялардың
қалай өсіп немесе кеміп тұрғанын көрнекі түрде көрсетіп
тұр.

5-сурет.
 және
және  функцияларының
графиктері
функцияларының
графиктері

6-сурет.
 функциясының
графигі
функциясының
графигі
Жаңа функцияларды алудың
маңызды әдістердің бірі келесі әдіс болады. Қандай да бір
белгілі  функциясы
арқылы
функциясы
арқылы  теңдеуін
Х
айнымалысы Y-ке қатысты функция болатындай
етіп
теңдеуін
Х
айнымалысы Y-ке қатысты функция болатындай
етіп

деп өрнектеп шешіп көруге
болады. Онда  функциясы
функциясы
 функциясына
қатысты кері
функция деп аталады. Бұл үрдіс
егер
функциясына
қатысты кері
функция деп аталады. Бұл үрдіс
егер  функциясы
Х-тің өзгеру
аймағын Y-тің өзгеру аймағына өзара
бейнелейтін болса ғана, яғни
функциясы
Х-тің өзгеру
аймағын Y-тің өзгеру аймағына өзара
бейнелейтін болса ғана, яғни  теңсіздігі өзінің
артынан
теңсіздігі өзінің
артынан  теңсіздігін ала келетін болса
ғана нәтижеге алып келеді. Тек қана осы шарт
негізінде Y-тің әрбір
мәніне Х-тің бір ғана мәні сәйкес
келетін болады. Осы жерде жоғарыда келтірілген мысалды еске
түсіруге болады. Ол мысалда тәуелсіз
Х
айнымалысының рөлінде
жазықтықтағы кез келген үшбұрыш, ал
теңсіздігін ала келетін болса
ғана нәтижеге алып келеді. Тек қана осы шарт
негізінде Y-тің әрбір
мәніне Х-тің бір ғана мәні сәйкес
келетін болады. Осы жерде жоғарыда келтірілген мысалды еске
түсіруге болады. Ол мысалда тәуелсіз
Х
айнымалысының рөлінде
жазықтықтағы кез келген үшбұрыш, ал  функциясының рөлінде оның
периметрі болған еді. Үшбұрыштардың
S
жиынының оң
сандардың Т
жиынына бейнеленуі өзара дәл
емес екені айқын, себебі периметрі бірдей санға тең болатын
үшбұрыштардың шексіз көп саны бар. Сонымен, бұл
жағдайда
функциясының рөлінде оның
периметрі болған еді. Үшбұрыштардың
S
жиынының оң
сандардың Т
жиынына бейнеленуі өзара дәл
емес екені айқын, себебі периметрі бірдей санға тең болатын
үшбұрыштардың шексіз көп саны бар. Сонымен, бұл
жағдайда  қатынасы кері функцияны
анықтай алмайды. Басқа жағдайда, п
барлық бүтін
сандардың S
жиынынан өтетін,
ал т
оң
сандардың Т
жиынын
өтетін
қатынасы кері функцияны
анықтай алмайды. Басқа жағдайда, п
барлық бүтін
сандардың S
жиынынан өтетін,
ал т
оң
сандардың Т
жиынын
өтетін  функциясы екі жиынның арасында
дәл сәйкестікті анықтайды және
функциясы екі жиынның арасында
дәл сәйкестікті анықтайды және  кері функциясы анықталатын
болады. Берілген дәл сәйкестіктің басқа мысал
ретінде
кері функциясы анықталатын
болады. Берілген дәл сәйкестіктің басқа мысал
ретінде

функциясын келтірейік. х айнымалысы барлық нақты сандар жиынынан өтіп шыққанда у айнымалысы да барлық нақты сандар жиынынан әрбір мәнді бір рет және тек қана бір рет қабылдай отырып өтіп шығады. Бұл мысалда анықталған кері функция

түрінде болады.

функциясының жағдайында кері
функция дәл анықталмайды. Расында да,
 болғандықтан, у-тің әрбір оң
мәніне х-тің әр
түрлі екі мәні сәйкес келеді. Бірақ
егер
болғандықтан, у-тің әрбір оң
мәніне х-тің әр
түрлі екі мәні сәйкес келеді. Бірақ
егер  символының астында
квадраты х-ке тең
болатын оң
сан болады деп ойласақ (көп
жағдайда осылай болады), онда
символының астында
квадраты х-ке тең
болатын оң
сан болады деп ойласақ (көп
жағдайда осылай болады), онда

кері функциясы табылады, егер х пен у мәндерінің тек қана оң мәндерін қарастырамыз деп келісіп алсақ. [8]
Кері функцияның бар болуын
берілген функцияның графигіне қарап бірден анықтауға болады. кері
функция дәл анықталып табылады, егер
у-тің әрбір
мәніне х-тің бір ғана мәні сәйкес
келетін болса. Геометриялық тұрғыдан қарағанда алдыңғы сөйлем
графикті бір нүктеден көп жерде қиып өтетін
жәнех
осіне параллель болатын түзу
жоқ деген мағынаны білдіреді. Әрине мұндай жағдай мүмкін болады,
егер  функциясы монотонды, яғни
немесе барлық уақытта өспелі, немесе, керісінше, барлық уақытта
кемімелі (х
өскен кезде) болса. Мысалы,
егер
функциясы монотонды, яғни
немесе барлық уақытта өспелі, немесе, керісінше, барлық уақытта
кемімелі (х
өскен кезде) болса. Мысалы,
егер  функциясы барлық жерде өспелі
болса, онда
функциясы барлық жерде өспелі
болса, онда  болғанда барлық
уақытта
болғанда барлық
уақытта  болады.
Демек, у-тің берілген
мәніне
болады.
Демек, у-тің берілген
мәніне  болатындай х-тің бірден аспайтын мәні бар
және кері функция дәл анықталатын болады.
болатындай х-тің бірден аспайтын мәні бар
және кері функция дәл анықталатын болады.
 кері функциясының
графигі берілген графиктегі үзік сызыққа қатысты симметрия арқылы
алынады (7-сурет); бұл жағдайда х
және
у
осьтерінің орындары
ауыстырылады.
кері функциясының
графигі берілген графиктегі үзік сызыққа қатысты симметрия арқылы
алынады (7-сурет); бұл жағдайда х
және
у
осьтерінің орындары
ауыстырылады.

7-сурет. Өзара кері функциялар
Графиктің жаңа орналасуы х-ті у-ке қатысты функция ретінде кескіндейді. Негізгі орналасуында график у-тің мәнін көлденең орналасқан х осінен алғандағы биіктік деп көрсетеді, ал симметриядан кейін алынған график х-тің мәні көлденең орналасқан у осінен алғандағы биіктік деп көрсетеді.
Осы бөлімшедегі пайымдауларды

функциясы негізіндегі мысалда
кескіндеуге болады. бұл функция  аралығында монотонды болады (6-сурет): барлық
уақытта х-пен бірге
өсетін у-тің
мәндері
аралығында монотонды болады (6-сурет): барлық
уақытта х-пен бірге
өсетін у-тің
мәндері  -тен
-тен
 -ке дейін өзгереді;
бұдан
-ке дейін өзгереді;
бұдан

кері
функциясы у-тің барлық мәндері үшін
анықталатыны шығады. Мұндай функцияны
 деп белгілейді.
Осылайша,
деп белгілейді.
Осылайша,  болады,
себебі
болады,
себебі .
.
 графигі 8-суретте
көрсетілген. [9]
графигі 8-суретте
көрсетілген. [9]

8-сурет.

1.5. Күрделі функциялар
Екі немесе одан да көп мәліметтерден жаңа функцияларды алудың екінші маңызды әдісі күрделі функцияларды құрастыру («композиция») әдісі болып табылады. Мысалы,

функциясын

екі жай функциясынан «құрастырып», мына түрде жазуға болады:

Дәл осылай,

функциясы

үш функциядан құрастырылады және оны

деп жазуға болады.

функциясы

екі функциядан
құрастырылды.  функциясы
функциясы
 болғанда анықталмайды,
себебі
болғанда анықталмайды,
себебі  мәнінде
мәнінде
 өрнегінің мәні жоқ. Бұл
тамаша функцияның графигі синустың графигімен байланысты болып
келеді.
өрнегінің мәні жоқ. Бұл
тамаша функцияның графигі синустың графигімен байланысты болып
келеді.  болғанда
болғанда
 болатынын білеміз,
мұндағы k
– кез келген оң немесе теріс
бүтін сан. Одан басқа,
болатынын білеміз,
мұндағы k
– кез келген оң немесе теріс
бүтін сан. Одан басқа,

мұндағы k – кез келген бүтін сан. Бұдан

шығады.
Егер  мәнін тізбектей қоя берсек,
бұл бөлшектердің бөлімі шексіз арта
береді.
мәнін тізбектей қоя берсек,
бұл бөлшектердің бөлімі шексіз арта
береді.

9-сурет.

Демек,
 функциясы 1, –1, 0
мәндеріне ие болатын х-тің
мәндері
функциясы 1, –1, 0
мәндеріне ие болатын х-тің
мәндері  нүктесінің айналасында
шоғырлана береді. Осындай әрбір нүкте мен басының арасында шексіз
көп тербелістер болады. Бұл функцияның графигі 9-суретте
көрсетілген. [10]
нүктесінің айналасында
шоғырлана береді. Осындай әрбір нүкте мен басының арасында шексіз
көп тербелістер болады. Бұл функцияның графигі 9-суретте
көрсетілген. [10]
1.6. Функцияның шегі
-
 болғандағы функцияның
шегі. Айталық,
болғандағы функцияның
шегі. Айталық, функциясы қандай да
бір Х
шексіз жиынында анықталған
болсын, ал
функциясы қандай да
бір Х
шексіз жиынында анықталған
болсын, ал  нүктесі –
шексіз
нүктесі –
шексіз  түзуінің нүктесі
және Х
жиынына тиісті болмайтын,
бірақ
түзуінің нүктесі
және Х
жиынына тиісті болмайтын,
бірақ  нүктесінің кез
келген δ
аймағында
Х
жиынының
нүктесінің кез
келген δ
аймағында
Х
жиынының
 нүктесінен өзге
нүктелері табылатын қасиетке ие болатын нүкте
болсын.
нүктесінен өзге
нүктелері табылатын қасиетке ие болатын нүкте
болсын.
Мысалы,
Х
жиыны
ретінде  интервалын алуға болады; бұл
жағдайда
интервалын алуға болады; бұл
жағдайда  нүктесі интервалдың шекаралық
нүктесі болғандықтан, интервал ішіне кірмейді,
бірақ
нүктесі интервалдың шекаралық
нүктесі болғандықтан, интервал ішіне кірмейді,
бірақ  нүктесінің кез
келген δ
аймағында берілген интервалдың
нүктелері табылады.
нүктесінің кез
келген δ
аймағында берілген интервалдың
нүктелері табылады.
 функциясы
берілген Х
жиынының басқа мысалы
ретінде
функциясы
берілген Х
жиынының басқа мысалы
ретінде  нүктесі алынып
тасталған
нүктесі алынып
тасталған  интервалына тиісті болатын
барлық рационал сандар жиынын алуға
болады.
интервалына тиісті болатын
барлық рационал сандар жиынын алуға
болады.
Кез
келген  үшін
үшін
 нүктесі алынып
тасталған
нүктесі алынып
тасталған  интервалын
интервалын  нүктесінің
тесілген δ
аймағы деп аталатынын ескерте
кетейік.
нүктесінің
тесілген δ
аймағы деп аталатынын ескерте
кетейік.
Х
жиынынан
 нүктесінен өзге
және
нүктесінен өзге
және  нүктесіне
шоғырланатын
нүктесіне
шоғырланатын

тізбегін алайық. Бұл тізбектің нүктелеріндегі функцияның мәндері де

сандық тізбекті құрайды және соңғы тізбектің шегінің бар болуы туралы сұрақ қоюға болады.
1-анықтама. А
саны  функциясының
функциясының  (немесе
(немесе  ) нүктесіндегі шегі деп
аталады, егер х аргументінің
) нүктесіндегі шегі деп
аталады, егер х аргументінің  нүктесінен
өзге
нүктесінен
өзге  нүктесіне шоғырланатын кез
келген
нүктесіне шоғырланатын кез
келген тізбегі үшін функцияның
сәйкес мәндерінің
тізбегі үшін функцияның
сәйкес мәндерінің  тізбегі А санына
жинақталатын болса.
тізбегі А санына
жинақталатын болса.
Символдық түрде ол былай
жазылады:  .
.
 функциясының
функциясының  нүктесінде тек бір ғана шегі
болады. Бұл ұйғарым
нүктесінде тек бір ғана шегі
болады. Бұл ұйғарым  тізбегінің тек бір ғана шегі
болады дегеннен шығады.
тізбегінің тек бір ғана шегі
болады дегеннен шығады.
Мысалдар қарастырайық.
-
 функциясының шегі сан
осінің кез келген
функциясының шегі сан
осінің кез келген  нүктесінде бар болады. Расында
да, егер
нүктесінде бар болады. Расында
да, егер  тізбегі –
тізбегі –
 нүктесіне шоғырланатын
кез келген тізбек болса, онда
нүктесіне шоғырланатын
кез келген тізбек болса, онда  тізбегі
тізбегі
 түрінде,
яғни
түрінде,
яғни  түрінде болады.
Бұдан
түрінде болады.
Бұдан  болғанда
болғанда
 немесе
немесе  болады деген қорытындыға
келеміз.
болады деген қорытындыға
келеміз. -
 функциясының шегі сан
осінің кез келген
функциясының шегі сан
осінің кез келген  нүктесінде
нүктесінде  -ге тең болады. Бұл
жағдайда
-ге тең болады. Бұл
жағдайда  және
және
 тізбектері тепе-тең,
яғни
тізбектері тепе-тең,
яғни  болады. Демек,
егер
болады. Демек,
егер  болса,
онда
болса,
онда  болғанда
болғанда
 немесе
немесе  болады.
болады. -
Барлық
 үшін
анықталған
үшін
анықталған  функциясының
(10-сурет)
функциясының
(10-сурет)  нүктесінде шегі болмайды.
Расында да, х
аргументі мәндерінің нөл
санына шоғырланатын екі тізбегін алайық:
нүктесінде шегі болмайды.
Расында да, х
аргументі мәндерінің нөл
санына шоғырланатын екі тізбегін алайық:
 және
және  .
.

10-сурет
Олар үшін функцияның сәйкес
мәндерінің тізбегі мына түрде болады: және
және
 . Кез
келген п
үшін
. Кез
келген п
үшін
 ,
ал
,
ал  болғандықтан, бірінші тізбек
үшін
болғандықтан, бірінші тізбек
үшін  , ал екінші тізбек
үшін
, ал екінші тізбек
үшін  .
Осылайша, х
аргументі мәндерінің нөлге
шоғырланатын екі тізбегі үшін функция мәндерінің тізбектері әр
түрлі шектерге ие болады. Ал бұл ұйғарым функция шегінің
анықтамасына сәйкес
.
Осылайша, х
аргументі мәндерінің нөлге
шоғырланатын екі тізбегі үшін функция мәндерінің тізбектері әр
түрлі шектерге ие болады. Ал бұл ұйғарым функция шегінің
анықтамасына сәйкес  табылмайды дегенді
білдіреді.
табылмайды дегенді
білдіреді.
-
 функциясының
функциясының  нүктесінде шегі 1-ге тең
болады. Расында да, х
аргументі мәндерінің нөлге
шоғырланатын, яғни
нүктесінде шегі 1-ге тең
болады. Расында да, х
аргументі мәндерінің нөлге
шоғырланатын, яғни  және
және
 болатын кез келген
тізбегін алайық, онда
болатын кез келген
тізбегін алайық, онда
 .
.
Осылайша,
 табылады және ол нөлге
шоғырланатын
табылады және ол нөлге
шоғырланатын  тізбегін таңдаудан тәуелсіз
болғандықтан, функцияның шегі анықтамасы
негізінде
тізбегін таңдаудан тәуелсіз
болғандықтан, функцияның шегі анықтамасы
негізінде  болады деген шешімге
келеміз.
болады деген шешімге
келеміз.
-
Рационал нүктелердегі мәндері бірге, ал иррационал нүктелердегі мәндері нөлге тең болатын Дирихле функциясының сан осінің ешбір
 нүктесінде шегі болмайды.
Расында да, аргументтің
нүктесінде шегі болмайды.
Расында да, аргументтің  нүктесінде шоғырланатын
рационал мәндерінің тізбегі үшін функция мәндерінің сәйкес
тізбегінің шегі бірге тең, ал аргументтің
нүктесінде шоғырланатын
рационал мәндерінің тізбегі үшін функция мәндерінің сәйкес
тізбегінің шегі бірге тең, ал аргументтің
 нүктесінде шоғырланатын
иррационал мәндерінің тізбегі үшін функция мәндерінің сәйкес
тізбегінің шегі нөлге тең болады.
нүктесінде шоғырланатын
иррационал мәндерінің тізбегі үшін функция мәндерінің сәйкес
тізбегінің шегі нөлге тең болады.
Функция шегінің басқа да анықтамасы бар.
2-анықтама. А
саны  функциясының
функциясының  нүктесіндегі шегі деп
аталады, егер кез келген
нүктесіндегі шегі деп
аталады, егер кез келген  саны
үшін
саны
үшін  теңсіздігін
қанағаттандырғанда
теңсіздігін
қанағаттандырғанда  теңсіздігі орындалатын
барлық
теңсіздігі орындалатын
барлық  үшін
үшін  саны
табылса.
саны
табылса.
Логикалық символдарды қолдана отырып, 2-анықтаманы

түрінде жазуға
болады.  теңсіздіктерін
теңсіздіктерін  түрінде жазуға болатынын айта
кетейік.
түрінде жазуға болатынын айта
кетейік.
Бірінші анықтама сандық
тізбектің шегі ұғымына негізделген, сондықтан оны жиі «тізбектер
тіліндегі» анықтама деп атайды. Екінші анықтаманы
« тіліндегі» анықтама деп
атайды.
тіліндегі» анықтама деп
атайды.
1-теорема. Функцияның шегінің бірінші және екінші анықтамалары эквивалентті.
Дәлелдеу. 1)
Айталық, А
– бірінші анықтамаға
сәйкес, функциясының
функциясының  нүктесіндегі шегі
болсын. А
– екінші анықтамаға
сәйкес,
нүктесіндегі шегі
болсын. А
– екінші анықтамаға
сәйкес, функциясының шегі болатынын
көрсетейік. Кері жорамалдайық, яғни
А
– осы функцияның екінші
анықтамаға сәйкес шек болмайды деп пайымдайық. Демек, кез келген
емес
функциясының шегі болатынын
көрсетейік. Кері жорамалдайық, яғни
А
– осы функцияның екінші
анықтамаға сәйкес шек болмайды деп пайымдайық. Демек, кез келген
емес  үшін
үшін
 теңсіздігінен
теңсіздігінен  теңсіздігі
шығатындай
теңсіздігі
шығатындай  санын алуға болады, яғни
қандай да
санын алуға болады, яғни
қандай да  санын алмасақ
та,
санын алмасақ
та,  , бірақ
, бірақ
 болатындай ең болмағанда
бір
болатындай ең болмағанда
бір  нүктесі
табылатындай
нүктесі
табылатындай  саны бар
болады. δ
ретінде
кезектестіріп
саны бар
болады. δ
ретінде
кезектестіріп

сандарын таңдап аламыз. Онда
Х
жиынындағы  үшін
үшін
 ,
ал
,
ал  болатындай
болатындай  нүктесі
табылады;
нүктесі
табылады;
Х
жиынындағы  үшін
үшін
 ,
ал
,
ал  болатындай
болатындай  нүктесі
табылады;
нүктесі
табылады;
Х
жиынындағы  үшін
үшін
 ,
ал
,
ал  болатындай
болатындай  нүктесі
табылады;
нүктесі
табылады;
.....................................................................................................................
Х
жиынындағы  үшін
үшін
 ,
ал
,
ал  болатындай
болатындай  нүктесі
табылады;
нүктесі
табылады;
.....................................................................................................................
Нәтижесінде  нүктесінен өзге
және
нүктесінен өзге
және  үшін
үшін
 болғандықтан
болғандықтан нүктесіне
шоғырланатын
нүктесіне
шоғырланатын

нүктелерінің тізбегі шығады.
Сондықтан, функция шегінің бірінші анықтамасына сәйкес, функция
мәндерінің сәйкес  тізбегі
А
санына шоғырланады.
Демек,
тізбегі
А
санына шоғырланады.
Демек,  үшін
барлық
үшін
барлық  үшін
үшін
 теңсіздігі
орындалатын N
нөмірі табылады. Алынған
қарама-қайшылық А
саны – екінші анықтамаға
сәйкес,
теңсіздігі
орындалатын N
нөмірі табылады. Алынған
қарама-қайшылық А
саны – екінші анықтамаға
сәйкес,  функциясының
функциясының  нүктесіндегі шегі болатынын
дәлелдейді.
нүктесіндегі шегі болатынын
дәлелдейді.
2)
Айталық, А
саны – екінші анықтамаға
сәйкес,  функциясының
функциясының  нүктесіндегі шегі болсын.
Демек, кез келген
нүктесіндегі шегі болсын.
Демек, кез келген  үшін
үшін
 теңсіздігінен
теңсіздігінен  теңсіздігі
шығатындай
теңсіздігі
шығатындай  саны
табылады. А
– бірінші анықтамаға
сәйкес,
саны
табылады. А
– бірінші анықтамаға
сәйкес,  функциясының шегі болатынын
көрсетейік.
функциясының шегі болатынын
көрсетейік.  нүктесіне шоғырланатын кез
келген
нүктесіне шоғырланатын кез
келген

нүктелерінің тізбегін алайық.
Онда екінші анықтама бойынша ɛ-ге сәйкес
берілген  мәні үшін
мәні үшін
 үшін
үшін  теңсіздігі
орындалатын N
нөмірі табылады. Бірақ,
мұнымен қоса, екінші анықтамаға сәйкес,
теңсіздігі
орындалатын N
нөмірі табылады. Бірақ,
мұнымен қоса, екінші анықтамаға сәйкес,
 теңсіздігі де
орындалады. Ал ɛ
өз еркімізге сай
таңдалғандықтан,
теңсіздігі де
орындалады. Ал ɛ
өз еркімізге сай
таңдалғандықтан,  нүктесіне шоғырланатын кез
келген
нүктесіне шоғырланатын кез
келген  тізбегі
үшін
тізбегі
үшін  болады,
яғни А
саны – бірінші анықтамаға
сәйкес,
болады,
яғни А
саны – бірінші анықтамаға
сәйкес,  функциясының
функциясының  нүктесіндегі шегі болатынын
дәлелдейді. Теорема дәлелденді.
нүктесіндегі шегі болатынын
дәлелдейді. Теорема дәлелденді.
Сонымен, функцияның шегінің бірінші және екінші анықтамаларының эквиваленттілігі нақтыланды және олардың ішінен есепті шешуде тиімді болып табылатын кез келгенін қолдануға болады.
Функция шегінің «тізбектер
тіліндегі» анықтамасын функция шегінің Гейне (Гейне Генрих Эдуард
(1821-1881) – неміс математигі) анықтамасы деп, ал функция шегінің
« тіліндегі» анықтамасын функция
шегінің Коши (Коши Огюстен Луи (1789-1857) – француз математигі)
анықтамасы деп атайтынын айта кетейік.
тіліндегі» анықтамасын функция
шегінің Коши (Коши Огюстен Луи (1789-1857) – француз математигі)
анықтамасы деп атайтынын айта кетейік.
-
 және
және  болғандағы функцияның
шегі. Әрі қарай функцияның біржақты
шектері ұғымдары қолданылатын болады және олар былайша
анықталады.
болғандағы функцияның
шегі. Әрі қарай функцияның біржақты
шектері ұғымдары қолданылатын болады және олар былайша
анықталады.
3-анықтама. А
саны  функциясының
функциясының  нүктесіндегі оң жақты (сол
жақты) шегі деп аталады, егер
нүктесіндегі оң жақты (сол
жақты) шегі деп аталады, егер  нүктесіне шоғырланатын
және
нүктесіне шоғырланатын
және  элементтері
элементтері  нүктесінен артық (кем)
болатын кез келген
нүктесінен артық (кем)
болатын кез келген  тізбегі үшін
сәйкес
тізбегі үшін
сәйкес  тізбегі А санына
шоғырланатын болса.
тізбегі А санына
шоғырланатын болса.
Символдық
белгіленуі:  .
.
Мысал
ретінде  функциясын қарастырайық. Бұл
функцияның
функциясын қарастырайық. Бұл
функцияның  нүктесінде оң жақты және сол
жақты шектері бар:
нүктесінде оң жақты және сол
жақты шектері бар: 
 . Расында да,
егер
. Расында да,
егер  тізбегі – осы функция
аргументінің нөлге шоғырланатын және
тізбегі – осы функция
аргументінің нөлге шоғырланатын және  элементтері нөлден
үлкен
элементтері нөлден
үлкен  мәндерінің кез келген тізбегі
болса, онда
мәндерінің кез келген тізбегі
болса, онда  және
және
 болады.
Осыдан,
болады.
Осыдан,  . Дәл
осылайша
. Дәл
осылайша  анықталады.
анықталады.
Функцияның біржақты шектердің
анықтамасына теңкүшті болатын « тіліндегі» анықтамасын да
беріге болады: А
саны
тіліндегі» анықтамасын да
беріге болады: А
саны  функциясының
функциясының  нүктесіндегі оң жақты (сол
жақты) шегі деп аталады, егер кез келген
нүктесіндегі оң жақты (сол
жақты) шегі деп аталады, егер кез келген
 үшін барлық х
үшін
үшін барлық х
үшін  теңсіздігін
қанағаттандырғанда
теңсіздігін
қанағаттандырғанда  теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылса. Символдық
белгіленуі:
табылса. Символдық
белгіленуі:

Біржақты шектер мен функцияның шегі арасындағы байланысты төмендегі теорема орнатады.
2-теорема.  функциясының
функциясының  нүктесінде шегі болады
сонда және тек қана сонда, егер осы нүктеде оң жақты да, сол жақты
да шектері бар болса және олар өзара тең болса. Бұл жағдайда
функцияның шегі біржақты шекке тең
болады.
нүктесінде шегі болады
сонда және тек қана сонда, егер осы нүктеде оң жақты да, сол жақты
да шектері бар болса және олар өзара тең болса. Бұл жағдайда
функцияның шегі біржақты шекке тең
болады.
Дәлелдеу.  болсын. Онда функцияның оң
жақты және сол жақты шектері туралы анықтамаға сәйкес, кез
келген
болсын. Онда функцияның оң
жақты және сол жақты шектері туралы анықтамаға сәйкес, кез
келген  үшін
үшін
 теңсіздігін
қанағаттандыратын барлық х
үшін және
теңсіздігін
қанағаттандыратын барлық х
үшін және
 теңсіздігін
қанағаттандыратын барлық х
үшін
теңсіздігін
қанағаттандыратын барлық х
үшін
 теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  және
және
 табылады.
табылады.  алайық.
Онда
алайық.
Онда  теңсіздігін қанағаттандыратын
барлық х
үшін
теңсіздігін қанағаттандыратын
барлық х
үшін
 теңсіздігі орындалады.
Ал бұл ұйғарым, 2-анықтамаға сәйкес,
теңсіздігі орындалады.
Ал бұл ұйғарым, 2-анықтамаға сәйкес,  дегенді
білдіреді.
дегенді
білдіреді.
Керісінше,  болсын. Онда,
функцияның
болсын. Онда,
функцияның  нүктесінде шегі туралы
анықтамаға сәйкес, кез келген
нүктесінде шегі туралы
анықтамаға сәйкес, кез келген  үшін
үшін
 теңсіздігін
қанағаттандыратын барлық х
үшін
теңсіздігін
қанағаттандыратын барлық х
үшін
 теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылады.
Осылайша,
табылады.
Осылайша,  үшін де,
үшін де,
 үшін
де
үшін
де  теңсіздігі дұрыс болады. Ал бұ
л ұйғарым біржақты шектер турлы анықтамаға
сәйкес,
теңсіздігі дұрыс болады. Ал бұ
л ұйғарым біржақты шектер турлы анықтамаға
сәйкес,  болатынын көрсетеді. Теорема
дәлелденді.
болатынын көрсетеді. Теорема
дәлелденді.
-
 ,
,  және
және  болғандағы функцияның
шегі.
болғандағы функцияның
шегі.  болғандағы функцияның шегі мен
біржақты шектер ұғымдарынан басқа аргументтің шексіздікке
ұмтылғандағы функцияның шегі ұғымы бар.
болғандағы функцияның шегі мен
біржақты шектер ұғымдарынан басқа аргументтің шексіздікке
ұмтылғандағы функцияның шегі ұғымы бар.
4-анықтама. А
саны  функциясының
функциясының  болғандағы шегі деп
аталады, егер аргумент мәндерінің кез келген шексіз
үлкен
болғандағы шегі деп
аталады, егер аргумент мәндерінің кез келген шексіз
үлкен  тізбегі үшін
сәйкес
тізбегі үшін
сәйкес  тізбегі А санына
шоғырланатын болса.
тізбегі А санына
шоғырланатын болса.
Символдық
белгіленуі:  .
.
5-анықтама. А
саны  функциясының
функциясының  болғандағы шегі деп
аталады, егер
болғандағы шегі деп
аталады, егер  элементтері оң (теріс)
болатын аргумент мәндерінің кез келген шексіз
үлкен
элементтері оң (теріс)
болатын аргумент мәндерінің кез келген шексіз
үлкен  тізбегі үшін
сәйкес
тізбегі үшін
сәйкес  тізбегі А санына
шоғырланатын болса.
тізбегі А санына
шоғырланатын болса.
Символдық
белгіленуі:  .
.
Мысал
қарастырайық.  болсын. Бұл
функцияның
болсын. Бұл
функцияның  болғанда нөлге тең шегі бар.
Расында да, егер
болғанда нөлге тең шегі бар.
Расында да, егер  – аргумент мәндерінің шексіз
үлкен тізбегі болса, онда функция мәндерінің
сәйкес
– аргумент мәндерінің шексіз
үлкен тізбегі болса, онда функция мәндерінің
сәйкес  тізбегі шексіз аз тізбек болып
табылады, сондықтан нөлге тең шегі бар болады,
яғни
тізбегі шексіз аз тізбек болып
табылады, сондықтан нөлге тең шегі бар болады,
яғни  (11-сурет).
(11-сурет).
4-5-анықтамалары «тізбектер
тілінде» берілді. Оларға теңкүшті болатын
« тіліндегі» анықтамаларын
беріп, оларды логикалық символдар тілінде жазуға болады. Мысал
ретінде
тіліндегі» анықтамаларын
беріп, оларды логикалық символдар тілінде жазуға болады. Мысал
ретінде  болғандағы функцияның шегінің
анықтамасын келтірейік.
болғандағы функцияның шегінің
анықтамасын келтірейік.

11-сурет
6-анықтама. А
саны  функциясының
функциясының  болғандағы шегі деп
аталады, егер кез келген
болғандағы шегі деп
аталады, егер кез келген  үшін
үшін  теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  үшін
үшін  теңсіздігі орындалатындай δ
саны табылса. [11]
теңсіздігі орындалатындай δ
саны табылса. [11]
-
Функциялар шектері туралы теоремалар. Функция шегінің «тізбектер тіліндегі» анықтамасы функциядағы тізбектің шектері туралы жоғарыда дәлелденген теоремаларды өзгертуге мүмкіндік береді.
3-теорема.  және
және  функцияларының
функцияларының  нүктесіндегі В мен С
шектері бар болсын. Онда
нүктесіндегі В мен С
шектері бар болсын. Онда  функцияларының
функцияларының  нүктесіндегі шектері
сәйкесінше
нүктесіндегі шектері
сәйкесінше  болады.
болады.
Дәлелдеу.  –
–
 және
және  функцияларының аргумент
мәндерінің
функцияларының аргумент
мәндерінің  нүктесіне шоғырланатын тізбегі
болсын. Осы функциялардың сәйкесінше
нүктесіне шоғырланатын тізбегі
болсын. Осы функциялардың сәйкесінше  және
және
 мәндерінің тізбектерінің
шектері В
және
С
болады.
Онда
мәндерінің тізбектерінің
шектері В
және
С
болады.
Онда  тізбектері
сәйкесінше
тізбектері
сәйкесінше  шектеріне ие болады. Функция
шегінің 1-анықтамасына сәйкес,
шектеріне ие болады. Функция
шегінің 1-анықтамасына сәйкес,

болады. Теорема дәлелденді.
4-теорема.  ,
,
 және
және  функциялары
функциялары  нүктесін қоса алмаған
жағдайда
нүктесін қоса алмаған
жағдайда  нүктесінің қандай да бір
төңірегінде анықталған және
нүктесінің қандай да бір
төңірегінде анықталған және  ,
,
 функцияларының
функцияларының  нүктесінде А-ға тең шегі,
яғни
нүктесінде А-ға тең шегі,
яғни  болсын. Сонымен
қатар
болсын. Сонымен
қатар  теңсіздіктері орындалсын.
Онда
теңсіздіктері орындалсын.
Онда

Дәлелдеу.  –
–
 және
және  функцияларының аргумент
мәндерінің
функцияларының аргумент
мәндерінің  нүктесіне шоғырланатын тізбегі
болсын. Осы функциялардың сәйкесінше
нүктесіне шоғырланатын тізбегі
болсын. Осы функциялардың сәйкесінше  және
және
 мәндерінің тізбектерінің
шектері A-ға тең болады,
яғни
мәндерінің тізбектерінің
шектері A-ға тең болады,
яғни  болғандағы
болғандағы болады. Теореманың шартында
берілген теңсіздіктерді қолдана отырып, бұл
жерде
болады. Теореманың шартында
берілген теңсіздіктерді қолдана отырып, бұл
жерде

деп жазуға болады.
Бұдан  болатыны шығады. Функция
шегінің 1-анықтамасына сәйкес,
болатыны шығады. Функция
шегінің 1-анықтамасына сәйкес,

болатынын білдіреді.
1-ескерту. 3-теорема мен
4-теорема  -дің
орнында
-дің
орнында  символдарының біреуі тұратын
жағдайларда да дұрыс болады. [12]
символдарының біреуі тұратын
жағдайларда да дұрыс болады. [12]
1.7. Шексіз кіші және шексіз үлкен функциялар
1. Шексіз кіші
функциялар. 7-анықтама.  функциясы
функциясы  нүктесінде
(немесе
нүктесінде
(немесе  ) шекcіз кіші функция деп
аталады, егер
) шекcіз кіші функция деп
аталады, егер  болса.
болса.
 болғандағы шексіз кіші
функциялар да дәл осылай анықталады.
болғандағы шексіз кіші
функциялар да дәл осылай анықталады.
Шексіз кіші функцияның
теңкүшті анықтамасын « тілінде» беруге
болады:
тілінде» беруге
болады:  функциясы
функциясы  нүктесінде шекcіз кіші
функция деп аталады, егер кез келген
нүктесінде шекcіз кіші
функция деп аталады, егер кез келген
 үшін
үшін  теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  үшін
үшін  теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылса; немесе логикалық символдар
арқылы беруге болады:
табылса; немесе логикалық символдар
арқылы беруге болады:
 ;
;
немесе «тізбектер тілінде»
беруге болады:  функциясы
функциясы  нүктесінде шекcіз кіші
функция деп аталады, егер х аргументінің
нүктесінде шекcіз кіші
функция деп аталады, егер х аргументінің
 нүктесінен өзге
мәндерінің
нүктесінен өзге
мәндерінің  нүктесіне шоғырланатын кез
келген
нүктесіне шоғырланатын кез
келген  тізбегі үшін
сәйкес
тізбегі үшін
сәйкес  тізбегі шексіз кіші тізбек
болса.
тізбегі шексіз кіші тізбек
болса.
Келесі теорема орындалады.
5-теорема.  теңдігінің орындалуы
үшін
теңдігінің орындалуы
үшін  болғанда
болғанда

функциясының шексіз кіші болуы қажетті және жеткілікті.
Дәлелдеу. Қажеттілік.  болсын.
болсын.
 айырымын
қарастырып,
айырымын
қарастырып, 
 болғандағы шексіз кіші функция
болатынын көрсетейік. Расында да,
болғандағы шексіз кіші функция
болатынын көрсетейік. Расында да,  пен
А
функцияларының
әрқайсысының
пен
А
функцияларының
әрқайсысының  болғандағы
шегі А-ға тең, сондықтан 3-теоремаға
сәйкес,
болғандағы
шегі А-ға тең, сондықтан 3-теоремаға
сәйкес,

болады.
Жеткіліктік.  болсын,
мұндағы
болсын,
мұндағы  –
–
 болғандағы шексіз кіші
функция.
болғандағы шексіз кіші
функция.  екенін
көрсетейік.
екенін
көрсетейік.  болғандықтан,
болғандықтан,

болады. Теорема дәлелденді.
5-теоремадан  нүктесінде А-ға тең шегі болатын функция
үшін арнайы белгіленуді аламыз:
нүктесінде А-ға тең шегі болатын функция
үшін арнайы белгіленуді аламыз:
 ,
мұндағы
,
мұндағы  .
.
Бұл жерде,
әдетте,  функциясы
функциясы
 нүктесінің
аймағында А-дан шексіз кіші функцияға
өзгереді деп айтады.
нүктесінің
аймағында А-дан шексіз кіші функцияға
өзгереді деп айтады.
Шексіз кіші функциялардың қасиеттері шексіз кіші тізбектердің қасиеттерімен бірдей болады. Келесі теорема орындалады.
6-теорема.  болғандағы шексіз кіші
функциялардың алгебралық қосындысы мен көбейтіндісі, сондай-ақ
шексіз кіші функция мен шекті функцияның
көбейтіндісі
болғандағы шексіз кіші
функциялардың алгебралық қосындысы мен көбейтіндісі, сондай-ақ
шексіз кіші функция мен шекті функцияның
көбейтіндісі  болғандағы шексіз кіші
функцияға тең болады.
болғандағы шексіз кіші
функцияға тең болады.
 болғандағы шексіз кіші
функциялар туралы айтылғандардың барлығы
болғандағы шексіз кіші
функциялар туралы айтылғандардың барлығы
 болғандағы шексіз кіші
функциялар үшін де орындалады.
болғандағы шексіз кіші
функциялар үшін де орындалады.
2. Шексіз үлкен
функциялар. 8-анықтама.  функциясы
функциясы  нүктесінде
(немесе
нүктесінде
(немесе  ) шекcіз үлкен функция деп
аталады, егер кез келген
) шекcіз үлкен функция деп
аталады, егер кез келген  үшін
үшін  теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  үшін
үшін  теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылса.
табылса.
Бұл
жағдайда  деп жазады және
функция
деп жазады және
функция  болғанда шексіздікке ұмтылады
немесе функцияның
болғанда шексіздікке ұмтылады
немесе функцияның  нүктесінде шексіз шегі бар деп
айтады.
нүктесінде шексіз шегі бар деп
айтады.
Егер де
 теңсіздігі орындалса,
онда
теңсіздігі орындалса,
онда  деп жазады және
функция
деп жазады және
функция  нүктесінде
нүктесінде  -ге тең болатын шексіз шекке
ие болады деп айтады.
-ге тең болатын шексіз шекке
ие болады деп айтады.
Логикалық символдарды қолдана отырып, 8-анықтаманы

түрінде жазуға болады.
Шектеулі біржақты шектермен ұқсастығына қарай шексіз біржақты шектер де анықталады:

Осылайша,
мысалы,  деп жазады, егер кез
келген
деп жазады, егер кез
келген  үшін
үшін
 теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  үшін
үшін
 теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылса. Символдық
жазылуы:
табылса. Символдық
жазылуы:

«Тізбектер тілінде» бұл
анықтама  деп жазылады,
егер
деп жазылады,
егер  элементтері
элементтері  нүктесінен артық
болатындай х
аргументінің
мәндерінің
нүктесінен артық
болатындай х
аргументінің
мәндерінің  нүктесіне шоғырланатын кез
келген
нүктесіне шоғырланатын кез
келген  тізбегі үшін
сәйкес
тізбегі үшін
сәйкес  тізбегі оң таңбалы шексіз
үлкен тізбек болса.
тізбегі оң таңбалы шексіз
үлкен тізбек болса.
 болғандағы шексіз үлкен
функциялар да дәл осылай анықталады. Осылайша,
мысалы,
болғандағы шексіз үлкен
функциялар да дәл осылай анықталады. Осылайша,
мысалы,  функциясы
функциясы
 болғанда шексіз үлкен
функция деп аталады, егер кез келген
болғанда шексіз үлкен
функция деп аталады, егер кез келген  үшін
үшін
 теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  үшін
үшін
 теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылса. Бұл
жағдайда
табылса. Бұл
жағдайда  деп
жазады.
деп
жазады.
 болғандағы шексіз үлкен
функцияның символдық белгіленуі:
болғандағы шексіз үлкен
функцияның символдық белгіленуі:

Егер де
 теңсіздігі орындалса,
онда
теңсіздігі орындалса,
онда  деп
жазады.
деп
жазады.
Шексіз кіші және шексіз үлкен функциялардың арасындағы байланыс оларға сәйкес тізбектердің арасында болатын байланыспен бірдей болады, яғни шексіз кіші функцияға кері функция шексіз үлкен функция болып табылады және керісінше шексіз үлкен функцияға кері функция шексіз кіші функция болып табылады.
Расында
да,  болғанда
болғанда
 және
және  болсын.
болсын.
 екенін дәлелдейік.
Кездейсоқ
екенін дәлелдейік.
Кездейсоқ  алайық.
алайық.
 функциясы
–
функциясы
–  нүктесіндегі шексіз кіші
функция болғандықтан,
нүктесіндегі шексіз кіші
функция болғандықтан,  саны үшін
саны үшін
 теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  үшін
үшін
 теңсіздігі
орындалатындай
теңсіздігі
орындалатындай  табылады.
Онда х
үшін
табылады.
Онда х
үшін
 теңсіздігі орындалады,
яғни
теңсіздігі орындалады,
яғни  функциясы
функциясы
 нүктесіндегі шексіз
үлкен функция болады. Дәлелдеу керегі осы.
[13]
нүктесіндегі шексіз
үлкен функция болады. Дәлелдеу керегі осы.
[13]
1.8. Үздіксіздік
Алдыңғы бөлімшелерде
қарастырылған функциялардың графиктері үздіксіздік деп аталатын
қасиет туралы интуициялық тұрғыдағы мәліметті көрсетіп тұр. Бұл
ұғымның нақты анықтамасы екінші тараудың бірінші бөлімшесінде
көрсетіледі. Ал бұл бөлімшеде сипаттамалық тұрғыдағы пайымдаулармен
шектеле отырып, функция үздіксіз болады, егер оның графигі
бірқалыпты, еш жерде «үзілмейтін» қисық сызық болса деген түсінік
қана беріледі.  функциясы
функциясы
 нүктесінде үздіксіз
болатынын анықтау үшін х
айнымалысын
нүктесінде үздіксіз
болатынын анықтау үшін х
айнымалысын  мәніне оң жағынан және сол
жағынан үздіксіз жақындатамыз. Бұл жағдайда
мәніне оң жағынан және сол
жағынан үздіксіз жақындатамыз. Бұл жағдайда
 функциясының мәндері
өзгереді. Егер
функциясының мәндері
өзгереді. Егер  функциясының мәндері осы
функцияның таңдалған
функциясының мәндері осы
функцияның таңдалған  нүктесінің
нүктесінің  мәніне шексіз жақындайтын
болса, әсіресе х-тің
мәніне шексіз жақындайтын
болса, әсіресе х-тің
 мәніне қай жағынан
жақындағанына қарамастан, онда
мәніне қай жағынан
жақындағанына қарамастан, онда  функциясы
функциясы
 нүктесінде үздіксіз деп айтады. Егер бұл жағдай
қандай да бір интервалдың әрбір
нүктесінде үздіксіз деп айтады. Егер бұл жағдай
қандай да бір интервалдың әрбір  нүктесінде орындалса, онда
функция берілген интервалда
үздіксіз деп
айтады.
нүктесінде орындалса, онда
функция берілген интервалда
үздіксіз деп
айтады.
Графигі бірқалыпты болатын әрбір функция үздіксіз болғанымен, барлық жерде үздіксіз болмайтын функцияларды анықтау өте оңай.

12-сурет. «Секіру» арқылы үзілу
Мысалы, 12-суретте берілген

формулалары
арқылы х-тің барлық мәндері үшін
анықталған функция  нүктесінде –1 мәніне ие болып,
осы нүктеде үзілісті болады. Егер берілген функцияның графигін
қарындашпен сызатын болсақ, осы нүктеде қарындашты қағаздан
алуымызға тура келеді.
нүктесінде –1 мәніне ие болып,
осы нүктеде үзілісті болады. Егер берілген функцияның графигін
қарындашпен сызатын болсақ, осы нүктеде қарындашты қағаздан
алуымызға тура келеді.  мәніне оң жағынан жақындаған
кезде
мәніне оң жағынан жақындаған
кезде  функциясы +1-ге ұмтылады.
Бірақ бұл мән функцияның дәл осы нүктедегі мәнінен, яғни –1-ден
өзгеше болады.
функциясы +1-ге ұмтылады.
Бірақ бұл мән функцияның дәл осы нүктедегі мәнінен, яғни –1-ден
өзгеше болады.
х
0-ге сол жағынан
ұмтылғандағы функциясының –1-ге ұмтылу
жағдайының өзі үздіксіздікті анықтау үшін жеткілікті
емес.
функциясының –1-ге ұмтылу
жағдайының өзі үздіксіздікті анықтау үшін жеткілікті
емес.
х-тің барлық мәндері үшін

формулаларымен
анықталған  функциясы
функциясы
 болғанда басқа түрде
үзіледі. Бұл жағдайда оң жағынан да, сол жағынан да шектері бар
және олар өзара тең, бірақ бұл жалпы шектік
мән
болғанда басқа түрде
үзіледі. Бұл жағдайда оң жағынан да, сол жағынан да шектері бар
және олар өзара тең, бірақ бұл жалпы шектік
мән  мәнінен өзге
болады.
мәнінен өзге
болады.  нүктесінде басқа түрде
үзілісті болатын
нүктесінде басқа түрде
үзілісті болатын

функциясының графигі
13-суретте көрсетіліп тұр. Егер х
0-ге кез келген жақтан
ұмтылатын болса, онда у
ылғи да шексіздікке ұмтылады,
бірақ функцияның графигі осы нүктеде «үзіледі» және
тәуелсіз х
айнымалысының  нүктесінің айналасындағы кіші
мәндеріне тәуелді у
айнымалысының өте үлкен
мәндері сәйкес келуі мүмкін. Басқаша айтқанда,
нүктесінің айналасындағы кіші
мәндеріне тәуелді у
айнымалысының өте үлкен
мәндері сәйкес келуі мүмкін. Басқаша айтқанда,
 болғандағы функцияның
мәні анықталмайды, себебі шексіздік сан деп қабылданбайды,
сондықтан
болғандағы функцияның
мәні анықталмайды, себебі шексіздік сан деп қабылданбайды,
сондықтан  болғанда
болғанда
 функциясы шексіздікке
тең деп айтуға болмайды. Демек, х
нөлге
жақындағанда
функциясы шексіздікке
тең деп айтуға болмайды. Демек, х
нөлге
жақындағанда  функциясы «шексіздікке
ұмтылады» деп айта аламыз.
функциясы «шексіздікке
ұмтылады» деп айта аламыз.

13-сурет. Шексіздікке бағытталу арқылы үзілу
Ал
 функциясының
функциясының  нүктесіндегі үзілуінің түрі
мүлдем басқаша (9-сурет).
нүктесіндегі үзілуінің түрі
мүлдем басқаша (9-сурет).
Келтірілген мысалдар қандай да
бір  нүктесінде функцияның
үздіксіздігі жойылатын бірнеше әр түрлі типтік жағдайларды
көрсетеді.
нүктесінде функцияның
үздіксіздігі жойылатын бірнеше әр түрлі типтік жағдайларды
көрсетеді.
-
Функцияның
 нүктесіндегі анықталған мәні
тиісті түрде анықталған немесе өзгертілгеннен кейін функция
үздіксіз болып қалуы мүмкін. Мысалы,
нүктесіндегі анықталған мәні
тиісті түрде анықталған немесе өзгертілгеннен кейін функция
үздіксіз болып қалуы мүмкін. Мысалы,  функциясы
функциясы
 кезде ылғи да 1-ге тең;
ол
кезде ылғи да 1-ге тең;
ол  болғанда анықталмайды,
себебі
болғанда анықталмайды,
себебі  – мағынасы жоқ символ. Бірақ
егер осы мысалда
– мағынасы жоқ символ. Бірақ
егер осы мысалда  мәні
мәні
 мәніне де сәйкес келеді
деп пайымдауға келісіп алсақ, онда осындай тәсілмен «кеңейтілген»
функция барлық нүктелерде үздіксіз болып өзгеріп кетеді. Дәл
осындай нәтижеге жетуге болады, егер жоғарыда көрсетілген
мысалдардың екіншісінде
мәніне де сәйкес келеді
деп пайымдауға келісіп алсақ, онда осындай тәсілмен «кеңейтілген»
функция барлық нүктелерде үздіксіз болып өзгеріп кетеді. Дәл
осындай нәтижеге жетуге болады, егер жоғарыда көрсетілген
мысалдардың екіншісінде  болғандағы функцияның мәнін
өзгертіп,
болғандағы функцияның мәнін
өзгертіп,  мәнінің
орнына
мәнінің
орнына  деп алсақ. Осындай түрдегі
үзілу жағдайлары жөнделетін деп
аталады.
деп алсақ. Осындай түрдегі
үзілу жағдайлары жөнделетін деп
аталады. -
х-тің х1 нүктесіне оң жағынан немесе сол жағынан жақындауына қарай функция әр түрлі шектерге ұмтылады (12-сурет).
-
Функцияның екі жағынан да шегі жоқ (9-сурет).
-
х-тің х1 нүктесіне жақындағанда функция шексіздікке ұмтылады (13-сурет).
Соңғы үш типті үзілу
жағдайлары маңызды немесе
жөнделмейтін деп аталады, себебі бір
ғана  нүктесінде функцияның мәнін
тиісті түрде анықтау арқылы өзгерту мүмкін емес.
[14]
нүктесінде функцияның мәнін
тиісті түрде анықтау арқылы өзгерту мүмкін емес.
[14]
2. Үздіксіз функциялардың екі негізгі теоремасы
2.1. Үздіксіздіктің анықтамасы
1-анықтама.  функциясы
функциясы
 нүктесінде үздіксіз деп
аталады, егер х
айнымалысы
нүктесінде үздіксіз деп
аталады, егер х
айнымалысы  -ге
ұмтылғанда
-ге
ұмтылғанда  шамасы тең болатын шекке
ұмтылатын болса. Егер бұл анықтама талдаудан өткізсек, онда ол
төмендегі екі шарттың орындалуын қажет ететіндігін
көреміз:
шамасы тең болатын шекке
ұмтылатын болса. Егер бұл анықтама талдаудан өткізсек, онда ол
төмендегі екі шарттың орындалуын қажет ететіндігін
көреміз:
а)
х
айнымалысы  -ге
ұмтылғанда
-ге
ұмтылғанда  функциясының а
шегі бар
болады;
функциясының а
шегі бар
болады;
ә) осы
а
шегі
 -ке тең болу
керек.
-ке тең болу
керек.
Егер шектің
анықтамасындағы а
шамасының орнына
оның  мәнін қойсақ, онда
үздіксіздіктің шарты мынадай түрде болады:
мәнін қойсақ, онда
үздіксіздіктің шарты мынадай түрде болады:
 үшін
үшін  функциясы үздіксіз болады,
егер оң ɛ саны қаншалықты аз болса,
функциясы үздіксіз болады,
егер оң ɛ саны қаншалықты аз болса,

теңсіздігі

шартын қанағаттандыратын барлық х үшін орындалатындай δ оң санын табуға болады.
Мысал
ретінде  функциясының
функциясының  нүктесіндегі үздіксіздігін
анықтайық. Сонда
нүктесіндегі үздіксіздігін
анықтайық. Сонда

болады. Енді аздаған
оң ɛ
санын таңдап алайық,
мысалы,  .
х
мәндерін
.
х
мәндерін
0-ге жақын сандармен шектеу арқылы  функциясының
0-ден
функциясының
0-ден  -ге кем болатын,
яғни
-ге кем болатын,
яғни  және
және
 аралығында жататын
сәйкес мәндерінің шығатынын көрсетуім керек.
Егер х-тің өзгеруін
0-ден
аралығында жататын
сәйкес мәндерінің шығатынын көрсетуім керек.
Егер х-тің өзгеруін
0-ден  -ге кем мәндерімен шектесек,
онда
-ге кем мәндерімен шектесек,
онда  мәндері жоғарыда көрсетілген
аралықтан аспайтынын көреміз; расында да егер
мәндері жоғарыда көрсетілген
аралықтан аспайтынын көреміз; расында да егер
 болса,
онда
болса,
онда  болады. Дәл
осылай
болады. Дәл
осылай  орнына кез келген
аздаған
орнына кез келген
аздаған  және т.б. мәнін ала
аламыз;
және т.б. мәнін ала
аламыз;  сандары біздің шартымызды
қанағаттандыратын болады, себебі
сандары біздің шартымызды
қанағаттандыратын болады, себебі  теңсіздігінен
теңсіздігінен  шығады.
шығады.
Үздіксіздіктің ɛ, δ арқылы жасалған анықтамасына сүйене отырып барлық полиномдар, рационал функциялар және тригонометриялық функциялар кез келген нүктеде үздіксіз екенін дәлелдеуге болады.
Үздіксіздіктің
анықтамасын  функциясының графигімен
байланыстыра отырып, оны келесідей геометриялық түрге келтіруге
болады. Қандай да бір оң ɛ
санын
таңдап, х
осіне параллель
болатын
функциясының графигімен
байланыстыра отырып, оны келесідей геометриялық түрге келтіруге
болады. Қандай да бір оң ɛ
санын
таңдап, х
осіне параллель
болатын  биіктікте
және х
осінен
төмен
биіктікте
және х
осінен
төмен  түзулерін жүргізейік. Онда
графиктің
түзулерін жүргізейік. Онда
графиктің  -дің қасында ені
2δ
болатын вертикаль жолақтың
ішінде жатқан бөлігі
-дің қасында ені
2δ
болатын вертикаль жолақтың
ішінде жатқан бөлігі  -тің қасында ені
2ɛ
болатын горизонталь жолақтың
ішінде де жататындай етіп оң δ
саны табылуы керек.
1-сурет
-тің қасында ені
2ɛ
болатын горизонталь жолақтың
ішінде де жататындай етіп оң δ
саны табылуы керек.
1-сурет  нүктесінде үздіксіз болатын
функцияны, ал
нүктесінде үздіксіз болатын
функцияны, ал
2-сурет осы нүктеде үзілетін функцияны
көрсетеді.

1-сурет.
 нүктесінде үздіксіз
функция
нүктесінде үздіксіз
функция

2-сурет.
Функцияның  нүктесінде үзіліс нүктесі
бар
нүктесінде үзіліс нүктесі
бар
Соңғы
жағдайда  -дің қасындағы вертикаль
жолақтың қаншалықты тар болса да, қашан да оның ішінде ені
2ɛ
болатын горизонталь жолақтың
ішінде жататын графиктің бөлігі жататын
болады.
-дің қасындағы вертикаль
жолақтың қаншалықты тар болса да, қашан да оның ішінде ені
2ɛ
болатын горизонталь жолақтың
ішінде жататын графиктің бөлігі жататын
болады.
Функция үздіксіздік қасиетіне ие болмайтын нүктелер үзіліс нүктелері деп аталады. [15]
Мысалдар қарастырайық.
-
 дәрежелік
функциясы
дәрежелік
функциясы  шексіз түзудің
әрбір а
нүктесінде үздіксіз болады,
мұндағы п
– натурал
сан.
шексіз түзудің
әрбір а
нүктесінде үздіксіз болады,
мұндағы п
– натурал
сан. -
Көпмүшелер және рационал бөлшектер берілген аймақтың әрбір нүктесінде дербес мәнге тең болатын шекті мәнге ие болады. Сондықтан олар берілген аймақтың әрбір нүктесінде үздіксіз функциялар болады.
-
 функциясы
функциясы  нүктесінде үзіледі және сан
осінің басқа нүктелерінде үздіксіз болады. Расында
да,
нүктесінде үзіледі және сан
осінің басқа нүктелерінде үздіксіз болады. Расында
да,  нүктесінде
нүктесінде функциясының оң жақтағы (+1-ге
тең) және сол жақтағы (–1-ге тең) шектері бар болады. Бұл біржақты
шектер өзара тең болмағандықтан,
функциясының оң жақтағы (+1-ге
тең) және сол жақтағы (–1-ге тең) шектері бар болады. Бұл біржақты
шектер өзара тең болмағандықтан,  функциясы 0 нүктесінде үзіледі
(үздіксіз болмайды). Сан осінің басқа нүктелерінде функцияның
дербес мәнге тең болатын шегі бар және осы нүктелерде функция
үздіксіз болады.
функциясы 0 нүктесінде үзіледі
(үздіксіз болмайды). Сан осінің басқа нүктелерінде функцияның
дербес мәнге тең болатын шегі бар және осы нүктелерде функция
үздіксіз болады. -
Дирихле функциясы (1.2 бөлімшені қара) сан осінің әрбір нүктесінде үзіледі, себебі функцияның ешбір нүктеде шегі жоқ. Алайда
 функциясы
функциясы  нүктесінде және шексіз түзудің
басқа нүктелерінде де үздіксіз болады, мұндағы
нүктесінде және шексіз түзудің
басқа нүктелерінде де үздіксіз болады, мұндағы
 – Дирихле
функциясы.
– Дирихле
функциясы.  функциясы
функциясы
 нүктесінде үздіксіз
болатынына көз жеткізейік.
нүктесінде үздіксіз
болатынына көз жеткізейік.  аргументінің мәндерінің шексіз
аз тізбегі үшін
аргументінің мәндерінің шексіз
аз тізбегі үшін  реттілігі шекті болады,
сондықтан
реттілігі шекті болады,
сондықтан  реттілігі шексіз аз болады,
яғни оның шегі
реттілігі шексіз аз болады,
яғни оның шегі  дербес мәніне тең нөл
болады.
дербес мәніне тең нөл
болады.
Функция  жиынында
үздіксіз деп айтамыз, егер функция осы
жиынның әрбір нүктесінде үздіксіз болса.
жиынында
үздіксіз деп айтамыз, егер функция осы
жиынның әрбір нүктесінде үздіксіз болса.
Мысалы, интервалдың әрбір нүктесінде үздіксіз болатын функция интервалдағы үздіксіз функция деп аталады.
Әсіресе
 функциясы
функциясы  сегментінде үздіксіз деп атауға келісейік, егер
функция осы сегменттің әрбір ішкі нүктесінде үзіксіз болса,
сондай-ақ а
нүктесінде оң жақтан үздіксіз
және b
нүктесінде сол жақтан үздіксіз
болса. [16]
сегментінде үздіксіз деп атауға келісейік, егер
функция осы сегменттің әрбір ішкі нүктесінде үзіксіз болса,
сондай-ақ а
нүктесінде оң жақтан үздіксіз
және b
нүктесінде сол жақтан үздіксіз
болса. [16]
2.2. Үздіксіз функцияларға қолданылатын арифметикалық амалдар
Үздіксіз функцияларға қолданылатын амалдар қайтадан үздіксіз функцияларға алып келетініне көз жеткізейік.
Келесі теорема орынды болады.
1-теорема. Бір
жиында  пен
пен
 функциялары берілсін
және бұл функциялар а
нүктесінде үздіксіз болсын.
Онда
функциялары берілсін
және бұл функциялар а
нүктесінде үздіксіз болсын.
Онда 
 және
және
 функциялары а
нүктесінде үздіксіз болады
(бөлімінің жағдайында қосымша
функциялары а
нүктесінде үздіксіз болады
(бөлімінің жағдайында қосымша  деген шарт қою
керек).
деген шарт қою
керек).
Дәлелдеу. а
нүктесінде
үздіксіз  пен
пен
 функциялардың а
нүктесінде
сәйкесінше
функциялардың а
нүктесінде
сәйкесінше  пен
пен
 шегі бар болатындықтан,
онда
шегі бар болатындықтан,
онда  және
және
 функцияларының шектері
табылады және сәйкесінше
функцияларының шектері
табылады және сәйкесінше  және
және
 мәндеріне тең болады. Ал
бұл мәндер берілген функциялардың а
нүктесіндегі дербес мәндерін
тең болады. Яғни берілген функциялар
а
нүктесінде үздіксіз болады.
Дәлелдеу керегі осы. [17]
мәндеріне тең болады. Ал
бұл мәндер берілген функциялардың а
нүктесіндегі дербес мәндерін
тең болады. Яғни берілген функциялар
а
нүктесінде үздіксіз болады.
Дәлелдеу керегі осы. [17]
2.3. Кейбір элементар функциялардың үздіксіздігі
Элементар функциялардың маңызды қасиеттерінің бірі – осы функциялар анықталу аймағының әрбір нүктесінде үздіксіз болуы. Кейбір функцияларға мысал келтіре отырып, функцияның үздіксіздік анықтамасы мен 1-теореманы қолдану арқылы аталған фактіні тексерейік.
-
Рационал функциялардың үздіксіздігі. Сан осінің кез келген
 нүктесінде үздіксіз болатын
функцияның қарапайым мысалы ретінде
нүктесінде үздіксіз болатын
функцияның қарапайым мысалы ретінде  тұрақты функцияны алуға
болады. Расында да, бұл жағдайда
тұрақты функцияны алуға
болады. Расында да, бұл жағдайда  болады, яғни тұрақты функция
сан осінің әрбір нүктесінде үздіксіз
болады.
болады, яғни тұрақты функция
сан осінің әрбір нүктесінде үздіксіз
болады.
Сан осінің кез
келген  нүктесінде
нүктесінде  функциясы да үздіксіз болады,
себебі
функциясы да үздіксіз болады,
себебі  , яғни
функцияның
, яғни
функцияның  нүктесіндегі шегі функцияның
осы нүктедегі мәніне тең. Айтылғанға және 1-теоремаға сәйкес кез
келген
нүктесіндегі шегі функцияның
осы нүктедегі мәніне тең. Айтылғанға және 1-теоремаға сәйкес кез
келген  нүктесінде
нүктесінде
 (п
– натурал сан) функциялары
үздіксіз болады. Белгілі болғандай,
(п
– натурал сан) функциялары
үздіксіз болады. Белгілі болғандай,  функциясы дәрежелік деп
аталады, ал
функциясы дәрежелік деп
аталады, ал

түріндегі функция алгебралық
көпмүше деп аталады, мұндағы  – бүтін
сан,
– бүтін
сан,  – кез келген
сандар.
– кез келген
сандар.
 қосылғыштарының
әрқайсысы екі үздіксіз функцияның (тұрақты және дәрежелік)
көбейтіндісі болады. 1-теоремаға сәйкес ол кез
келген х
нүктесінде үздіксіз.
Осылайша
қосылғыштарының
әрқайсысы екі үздіксіз функцияның (тұрақты және дәрежелік)
көбейтіндісі болады. 1-теоремаға сәйкес ол кез
келген х
нүктесінде үздіксіз.
Осылайша  көпмүшесі кез
келген х
нүктесінде үздіксіз болатын
функциялардың қосындысы болады және сәйкесінше кез
келген х
нүктесінде үздіксіз
болады.
көпмүшесі кез
келген х
нүктесінде үздіксіз болатын
функциялардың қосындысы болады және сәйкесінше кез
келген х
нүктесінде үздіксіз
болады.
Бөлшек-рационал функция, яғни

түріндегі функция бөлімі нөлге
тең болмайтын барлық х
нүктелерінде (яғни бөлімнің
түбірінен басқа барлық нүктелерде) үздіксіз болады,
мұндағы  мен
мен
 – алгебралық көпмүше.
Мысалы,
– алгебралық көпмүше.
Мысалы,  функциясы +1 мен –1
нүктелерінен басқа барлық х
нүктелерінде үздіксіз
болады.
функциясы +1 мен –1
нүктелерінен басқа барлық х
нүктелерінде үздіксіз
болады.
-
Тригонометриялық функциялардың үздіксіздігі.

 тригонометриялық функцияларды
қарастырайық.
тригонометриялық функцияларды
қарастырайық.  функциясының кез
келген х
нүктесінде үздіксіз болатынын
көрсетейік. Функцияның үздіксіздігінің анықтамасын
қолданайық. х
аргументіне
функциясының кез
келген х
нүктесінде үздіксіз болатынын
көрсетейік. Функцияның үздіксіздігінің анықтамасын
қолданайық. х
аргументіне  өсімшесін қою арқылы
функцияның
өсімшесін қою арқылы
функцияның
 немесе
немесе

өсімшесін
аламыз.  үшін теңдіктің оң және сол жақ
шектеріне ауысу арқылы
үшін теңдіктің оң және сол жақ
шектеріне ауысу арқылы

аламыз,
себебі  ,
,
 ,
,
ал шекті функция мен шексіз аз
санның көбейтіндісі шексіз аз сан болады.
Осылайша,  функциясының кез
келген х
нүктесінде үздіксіз
болады.
функциясының кез
келген х
нүктесінде үздіксіз
болады.
 функциясының кез
келген х
нүктесінде үздіксіз болуы дәл
осылай дәлелденеді.
функциясының кез
келген х
нүктесінде үздіксіз болуы дәл
осылай дәлелденеді.
1-теоремаға
сәйкес  пен
пен
 функцияларының
үздіксіздігінен
функцияларының
үздіксіздігінен  және
және
 функцияларының
функцияларының  нүктесінен басқа барлық
нүктелерде,
нүктесінен басқа барлық
нүктелерде,  және
және
 функцияларының
функцияларының  нүктесінен басқа барлық
нүктелерде үздіксіз болады.
нүктесінен басқа барлық
нүктелерде үздіксіз болады.
-
 функциясының
үздіксіздігі. 3-суретте графигі
сызылған
функциясының
үздіксіздігі. 3-суретте графигі
сызылған  функциясы сан осінің барлық
нүктелерінде анықталған және үздіксіз
болады.
функциясы сан осінің барлық
нүктелерінде анықталған және үздіксіз
болады.

3-сурет.
 функциясы
функциясы
Расында
да,  интервалындағы нүктелерде бұл
функция үздіксіз, себебі
интервалындағы нүктелерде бұл
функция үздіксіз, себебі  болғанда,
болғанда,
 болады.
болады.  интервалындағы нүктелерде де
бұл функция үздіксіз, себебі
интервалындағы нүктелерде де
бұл функция үздіксіз, себебі  болғанда,
болғанда,
 болады және оны (–1)
мен х
екі үздіксіз функцияның
көбейтіндісі ретінде жазуға және көбейтіндінің үздіксіздігі туралы
1-теореманы қолдануға болады.
болады және оны (–1)
мен х
екі үздіксіз функцияның
көбейтіндісі ретінде жазуға және көбейтіндінің үздіксіздігі туралы
1-теореманы қолдануға болады.  функциясының
функциясының  нүктесіндегі үздіксіздігін
анықтау үшін функцияның осы нүктедегі біржақты шектерін
есептейік:
нүктесіндегі үздіксіздігін
анықтау үшін функцияның осы нүктедегі біржақты шектерін
есептейік:

Сонымен,
функцияның  нүктесіндегі оң жақты және сол
жақты шектері бір-біріне сәйкес келеді және функцияның осы
нүктедегі мәніне тең. Осыдан,
нүктесіндегі оң жақты және сол
жақты шектері бір-біріне сәйкес келеді және функцияның осы
нүктедегі мәніне тең. Осыдан,  функциясы
функциясы
 нүктесінде үздіксіз,
яғни сан осінің барлық нүктелерінде үздіксіз
болады.
нүктесінде үздіксіз,
яғни сан осінің барлық нүктелерінде үздіксіз
болады.
Осылайша, қарастырылған функциялардың барлығы анықталу аймағы шоғырланған әрбір нүктеде үздіксіз болады. Қосындының, айырманың, көбейтіндінің және бөліндінің үздіксіздігі туралы 1-теоремаға сәйкес саны шектеулі арифметикалық амалдар арқылы алынған функциялардың да анықталу аймағы шоғырланған әрбір нүктеде үздіксіз болатынын тұжырымдауға болады.
 функциясы
функциясы  интервалында үздіксіз деп
айтамыз, егер функция осы интервалдың әрбір нүктесінде үздіксіз
болса;
интервалында үздіксіз деп
айтамыз, егер функция осы интервалдың әрбір нүктесінде үздіксіз
болса;  кесіндісінде үздіксіз деп
айтамыз, егер функция
кесіндісінде үздіксіз деп
айтамыз, егер функция  интервалында үздіксіз болса.
[18]
интервалында үздіксіз болса.
[18]
2.4. Больцано теоремасы
Бернард Больцано (1781-1848) католикалық дін қызметшісі болған, схоластикалық философияның білгірі, математикалық анализге қазіргі заманғы қатаңдық ұғымын енгізгендердің бірі болды. Оның «Paradoxien des Unendlichen» атты керемет кітабы 1850 жылы шықты. Мұнда алғаш рет үздіксіз функцияларға қатысты көптеген қарапайым мәліметтер дәлелденуі керек деп қабылданды. Осының мысалы ретінде бір айнымалылы функциялар туралы келесідей теореманы алуға болады.
2-теорема.  үздіксіздік интервалында
х-тің қандай да бір мәнінде оң таңбаға ие болатын және х-тің басқа
бір мәнінде теріс таңбаға ие болатын х айнымалысына қатысты
үздіксіз функция х-тің қандай да бір аралық мәнінде нөлге айналуы
керек. Сонымен,
егер
үздіксіздік интервалында
х-тің қандай да бір мәнінде оң таңбаға ие болатын және х-тің басқа
бір мәнінде теріс таңбаға ие болатын х айнымалысына қатысты
үздіксіз функция х-тің қандай да бір аралық мәнінде нөлге айналуы
керек. Сонымен,
егер  функциясы
х-тің
а-дан
b-ға дейінгі барлық мәнінде
үздіксіз болса және
функциясы
х-тің
а-дан
b-ға дейінгі барлық мәнінде
үздіксіз болса және  болса,
онда х
айнымалысының
болса,
онда х
айнымалысының  болатындай α
мәні
табылады.
болатындай α
мәні
табылады.
Больцано теоремасы х осінің бір жағынан екінші жағына өту үшін қандай да бір нүктесінде міндетті түрде қиып өтетін үздіксіз қисық туралы ойларымызбен сәйкес келеді.
Дәлелдеу. Бұл теореманың қатаң
дәлелдеуін келтірейік. Егер Гаусс және басқа да ұлы математиктерге
сүйенсек, бұл фактіні дәлелдеусіз де алуға болады. Біздің
мақсатымыз бұл теореманы нақты сандар жүйесінің негізгі
қасиеттеріне, әсіресе Дедекинд-Кантордың керуші кесінділер туралы
постулатына негіздеу болып келеді. Ол үшін
берілген  функциясы
жататын
функциясы
жататын  болатын
I
кесіндісін қарастырайық және
оны
болатын
I
кесіндісін қарастырайық және
оны  орта нүктесі арқылы екі
бөлікке бөлейік. Егер осы орта нүктеде
орта нүктесі арқылы екі
бөлікке бөлейік. Егер осы орта нүктеде
 шықса, онда дәлелдейтін
ештеңе қалмайды. Егер, алайда,
шықса, онда дәлелдейтін
ештеңе қалмайды. Егер, алайда,  болса,
онда
болса,
онда  мәні нөлден үлкен немесе
нөлден кіші болу керек. Екі жағдайда да
I
кесіндісінің бөліктерінің бірі
оның екі шетіндегі
мәні нөлден үлкен немесе
нөлден кіші болу керек. Екі жағдайда да
I
кесіндісінің бөліктерінің бірі
оның екі шетіндегі  функциясының мәндерінің
таңбалары әр түрлі болады деген қасиетке тағы да ие
болады.
функциясының мәндерінің
таңбалары әр түрлі болады деген қасиетке тағы да ие
болады.
Бұл
кесіндіні  деп белгілейік. Бұл үрдісті
қайталай отырып
деп белгілейік. Бұл үрдісті
қайталай отырып  кесіндісін қақ бөлеміз;
онда
кесіндісін қақ бөлеміз;
онда  ортасында
ортасында
 болады немесе
біз
болады немесе
біз  кесіндісінің қандай да бір
жартысында функцияның мәндері әр түрлі болатын жартысын аламыз. Осы
үрдісті жалғастыра отырып, ең соңында кесіндіні бөлудің соңғы
қадамында
кесіндісінің қандай да бір
жартысында функцияның мәндері әр түрлі болатын жартысын аламыз. Осы
үрдісті жалғастыра отырып, ең соңында кесіндіні бөлудің соңғы
қадамында  болатындай нүктені табамыз
немесе
болатындай нүктені табамыз
немесе  керуші кесінділер қатарын
аламыз. Соңғы жағдайда Дедекинд-Кантордың постулаты
бастапқы I
кесіндісінде барлық
кесінділерге тиісті болатын α
нүктесінің табылатынын
қамтамасыз етеді.
керуші кесінділер қатарын
аламыз. Соңғы жағдайда Дедекинд-Кантордың постулаты
бастапқы I
кесіндісінде барлық
кесінділерге тиісті болатын α
нүктесінің табылатынын
қамтамасыз етеді.  , яғни
α
– дәлелдеуді қажет ететін сол
нүкте болады.
, яғни
α
– дәлелдеуді қажет ететін сол
нүкте болады.
Осыған
дейін  функциясының үздіксіздігі
туралы болжам қолданылған жоқ еді. Осы жерде оған сүйеніп,
теореманы кері болжау тәсілі арқылы дәлелдеу керек. Қарсы болжамды
қолданып, қарама-қайшылыққа келу арқылы
функциясының үздіксіздігі
туралы болжам қолданылған жоқ еді. Осы жерде оған сүйеніп,
теореманы кері болжау тәсілі арқылы дәлелдеу керек. Қарсы болжамды
қолданып, қарама-қайшылыққа келу арқылы
 екенін
дәлелдейміз.
екенін
дәлелдейміз.  деп болжайық:
мысалы,
деп болжайық:
мысалы,  болсын.
болсын.
 функциясы үздіксіз
болғандықтан,
функциясы үздіксіз
болғандықтан,  функциясының J
кесіндісіндегі
мәні
функциясының J
кесіндісіндегі
мәні  мәнінен
ɛ-ға аз болатындай
центрі α
нүктесі болатын ұзындығы
2δ-ға тең
J
кесіндісін аламыз. Сонан
соң
мәнінен
ɛ-ға аз болатындай
центрі α
нүктесі болатын ұзындығы
2δ-ға тең
J
кесіндісін аламыз. Сонан
соң  болғандықтан,
онда J
кесіндісінің әрбір
нүктесінде
болғандықтан,
онда J
кесіндісінің әрбір
нүктесінде  , яғни
J
кесіндісінде
, яғни
J
кесіндісінде  болады деп айта аламыз.
Бірақ J
кесіндісі – бекітілген
кесінді, және егер п
өте үлкен болса, онда
кіші
болады деп айта аламыз.
Бірақ J
кесіндісі – бекітілген
кесінді, және егер п
өте үлкен болса, онда
кіші  кесіндісі міндетті
түрде J
кесіндісінің ішінде болуы
керек, себебі
кесіндісі міндетті
түрде J
кесіндісінің ішінде болуы
керек, себебі  ұзындықтарының қатары нөлге
ұмтылады. Осы жерде қарама-қайшылық пайда
болды:
ұзындықтарының қатары нөлге
ұмтылады. Осы жерде қарама-қайшылық пайда
болды:  функциясы
функциясы
 кесіндісінің шеткі
нүктелерінде қарама-қарсы таңбаларға ие болады,
яғни
кесіндісінің шеткі
нүктелерінде қарама-қарсы таңбаларға ие болады,
яғни  функциясы
J
кесіндісінде теріс таңбаға ие
болады. Осыдан
функциясы
J
кесіндісінде теріс таңбаға ие
болады. Осыдан  сонымен қатар (дәл
осылайша)
сонымен қатар (дәл
осылайша)  болжамының қате екені шығады;
яғни
болжамының қате екені шығады;
яғни  екені дәлелденді.
[19]
екені дәлелденді.
[19]
2.5. Больцано теоремасының қолданылуы
Геометриялық қолданылуы. Жай және жалпы Больцано теоремасы арқылы алғашқыда жеңіл болып көрінбейтін кейбір пікірлерді дәлелдеуге болады. Әуелі мынаны енгізейік: егер А және В – жазықтықта берілген екі фигура болса, онда осы жазықтықта берілген үшбұрыштарды бір мезгілде теңөлшемді (ауданы бойынша) бөліктерге бөлетін түзу табылады. Мұндағы «Фигура» дегеніміз – жай қисық сызықпен шектелген жазықтықтың бөлігі.
Дәлелдеуді аталған жазықтықтан
кез келген шатты Р
нүктесін алудан бастап, осы
нүктеден шартты PR
сәулесін жүргізейік. Осы сәуле
арқылы бұрыштарды өлшеуді жүргізіп тұрамыз.
PR
сәулесімен х
бұрыш
жасайтын PS
сәулесі қандай болса
да, PS
сәулесіне параллель
және А фигурасын теңөлшемді
бөліктерге бөлетін бағытталған түзу табылады.
Расында да, PS
сәулесіне параллель болатын
және А
фигурасының бір жағында
орналасқан бағытталған түзулердің біреуін алып,
оны  деп
белгілейік.
деп
белгілейік.  түзуін нәтижесінде
(оны
түзуін нәтижесінде
(оны  деп
белгілейміз) А
фигурасы толықтай келесі
жағына өтетіндей етіп параллель көшіреміз (4-сурет). Бұл жағдайда
бағытталған түзудің оң жағында орналасқан
А
бөлігінің ауданы мен
бағытталған түзудің сол жағында орналасқан (егер түзу «солтүстікке»
бағытталған деп айтсақ, «оң жағында» – «шығыста», «сол жағында» –
«батыста») А
бөлігінің ауданының айырмасы
ретінде анықталатын функция
деп
белгілейміз) А
фигурасы толықтай келесі
жағына өтетіндей етіп параллель көшіреміз (4-сурет). Бұл жағдайда
бағытталған түзудің оң жағында орналасқан
А
бөлігінің ауданы мен
бағытталған түзудің сол жағында орналасқан (егер түзу «солтүстікке»
бағытталған деп айтсақ, «оң жағында» – «шығыста», «сол жағында» –
«батыста») А
бөлігінің ауданының айырмасы
ретінде анықталатын функция  түзуіне қатысты оң таңбалы
және
түзуіне қатысты оң таңбалы
және  түзуіне қатысты теріс таңбалы
болады. Бұл функция үздіксіз болғандықтан, онда Больцано теоремасы
бойынша ол
түзуіне қатысты теріс таңбалы
болады. Бұл функция үздіксіз болғандықтан, онда Больцано теоремасы
бойынша ол  белгісі арқылы белгіленетін
түзудің қандай да бір аралық орналасуында нөлге айналады және бұл
жағдайда А
фигурасы қақ бөлінеді.
Сонымен, х
қандай болса да
(
белгісі арқылы белгіленетін
түзудің қандай да бір аралық орналасуында нөлге айналады және бұл
жағдайда А
фигурасы қақ бөлінеді.
Сонымен, х
қандай болса да
( ),
А
фигурасын қақ
бөлетін
),
А
фигурасын қақ
бөлетін  түзуі
табылады.
түзуі
табылады.

4-сурет. Екі ауданды бір мезгілде қақ бөлу
Енді
 түзуінің оң жағында
орналасқан В
фигурасының бір бөлігінің
ауданы мен
түзуінің оң жағында
орналасқан В
фигурасының бір бөлігінің
ауданы мен  түзуінің сол жағында
орналасқан В
фигурасының екінші бөлігінің
ауданының айырмасын
түзуінің сол жағында
орналасқан В
фигурасының екінші бөлігінің
ауданының айырмасын  деп белгілейік. Нақтылау
үшін PR
сәулесіне параллель
және А
фигурасын қақ
бөлетін
деп белгілейік. Нақтылау
үшін PR
сәулесіне параллель
және А
фигурасын қақ
бөлетін  түзуінің оң
жағында В
фигурасы ауданының басым
бөлігі орналасатынын атап кетейін; онда
у
оң таңбалы болады,
егер
түзуінің оң
жағында В
фигурасы ауданының басым
бөлігі орналасатынын атап кетейін; онда
у
оң таңбалы болады,
егер  болса.
Енді х
болса.
Енді х
 -қа дейін артсын;
онда PR
сәулесіне параллель
және А
фигурасын қақ
бөлетін
-қа дейін артсын;
онда PR
сәулесіне параллель
және А
фигурасын қақ
бөлетін  түзуі
түзуі
 түзуімен беттеседі
(бірақ қарама-қарсы бағытталады, ал «оң» және «сол» жақтары
жылжыды); осыдан
түзуімен беттеседі
(бірақ қарама-қарсы бағытталады, ал «оң» және «сол» жақтары
жылжыды); осыдан  болғандағы у-тің мәні
болғандағы у-тің мәні
 болғандағы мәнімен
сәйкес келетіні, бірақ қарама-қарсы таңбаға ие болатыны, яғни теріс
болатыны анық көрініп тұр. у
дегеніміз
болғандағы мәнімен
сәйкес келетіні, бірақ қарама-қарсы таңбаға ие болатыны, яғни теріс
болатыны анық көрініп тұр. у
дегеніміз
 болғандағы х-тің функциясы болғандықтан
(қиюшы түзудің бұрылуы кезінде аталған аудандардың айырымы үздіксіз
өзгеретіні айқын), онда у
функциясы нөлге
айналатындай
болғандағы х-тің функциясы болғандықтан
(қиюшы түзудің бұрылуы кезінде аталған аудандардың айырымы үздіксіз
өзгеретіні айқын), онда у
функциясы нөлге
айналатындай  мәні табылады. Бірақ
онда
мәні табылады. Бірақ
онда  түзуі
А
және
В
фигураларын бір мезгілде қақ
бөледі. Теорема дәлелденді.
түзуі
А
және
В
фигураларын бір мезгілде қақ
бөледі. Теорема дәлелденді.
Осы жерде біз жай ғана берілген қасиетке ие болатын түзудің табылатынын анықтадық, бірақ оны салудың белгілі бір жолын көрсетпедік: бұл – бар болуды дәлелдеудің «таза» математикалық әдісі.

5-сурет. Ауданды тең төрт бөлікке бөлу
Осыған ұқсас басқа мәселе:
жазықтықта А
фигурасы беріліп тұр;
оны өзара перпендикуляр
екі түзумен
төрт теңөлшемді бөлікке бөлу керек.
Шешімнің бар болуын дәлелдеу үшін алдыңғы есептің
шешіміндегі  түзуі енгізіліп,
ал В
фигурасы әлі енгізілмеген
бөлімге оралайық.
түзуі енгізіліп,
ал В
фигурасы әлі енгізілмеген
бөлімге оралайық.  түзуіне перпендикуляр болатын
және А
фигурасын қақ
бөлетін
түзуіне перпендикуляр болатын
және А
фигурасын қақ
бөлетін  түзуін қарастырайық.
Егер А
фигурасының төрт бөлігін
5-суретте көрсетілгендей етіп нөмірлесек,
онда
түзуін қарастырайық.
Егер А
фигурасының төрт бөлігін
5-суретте көрсетілгендей етіп нөмірлесек,
онда

және

аламыз. Екі теңдікті бір-бірінен азайту арқылы

аламыз, яғни

болады, осыдан

болады.
Осылайша, мәселенің шешімінің
бар болуы дәлелденеді, егер  түзуі үшін берілген фигураның
екі бөлігінің
түзуі үшін берілген фигураның
екі бөлігінің

теңдігін
қанағаттандыратын α
бұрышының табылатынын
анықталатын болса, себебі бұдан төрт бөліктің де теңдігі шығады.
Енді функциясын
қарастырайық,
функциясын
қарастырайық,

мұндағы
 және
және  – берілген
фигураның
– берілген
фигураның  түзуіне сәйкес болатын
бөліктері.
түзуіне сәйкес болатын
бөліктері.  болғанда,
мысалы,
болғанда,
мысалы,  болсын.
Онда
болсын.
Онда  болғанда,
болғанда,
 болады.
Бірақ
болады.
Бірақ  – үздіксіз функция;
яғни
– үздіксіз функция;
яғни  мен
мен
 аралығындағы α-ның қандай да бір
мәнінде
аралығындағы α-ның қандай да бір
мәнінде  болады.
Онда
болады.
Онда  мен
мен
 түзулері фигураны
теңөлшемді төрт бөлікке бөледі.
түзулері фигураны
теңөлшемді төрт бөлікке бөледі.
Бұл мәселелер үшөлшемді немесе одан да көп болатын жағдайларда жалпыланады. Үшөлшемді жағдайда алғашқы мәселе былай пайымдалады: кеңістікте үш дене берілген; екі денені де бір мезгілде қақ бөлетін жазықтықты табу керек. Шешімнің бар болуын дәлелдеу үрдісі де Больцано теоремасына негізделеді. [20]
Бір механикалық мәселеге қолданылуы. Енді кезекте Больцано теоремасының бір механикалық мәселеде қолданылуын қарастыратын боламыз. Бұл мәселені Г.Уитни ұсынған болатын.
Айталық, бір пойыз қандай да
бір шектеулі уақыт бойына А
пунктінен
В
пунктіне түзусызықты қозғалып
келеді. Қозғалыс бірқалыпты жылдамдықпен немесе бірқалыпты үдеумен
жүреді деп мүлдем пайымдалмайды. Керісінше, пойыз қалағаны бойынша
жүре алады: жылдамдықты арттыра алады, кеміте алады; жол бойында
пойыздың тоқтауы да қарастырылуы мүмкін. Бірақ қалай болғанда да,
берілген уақыт аралығында пойыздың қозғалысы алдын ала белгілі
болады; басқаша айтқанда,  функциясы берілген деп
есептеледі, мұндағы s
–
пойыздың А
станциясынан қарағандағы
қашықтығы, ал t
– пойыздың қозғалыс
бастағаннан кезден есептелетін уақыт. Вагондардың біріндегі еденге
топса арқылы ауыр өзекше бекітілген, бұл өзекше вагондардың осіне
параллель бағытта өзінің осі бойынша үйкеліссіз алға және артқа
(еденнен еденге қарай) қозғала алады. (Еденге тигеннен кейін өзекше
келесі «секіруге» дейін еденде жатады деп ойлайық). Мәселе
мынада: пойыз қозғалған мезетте
барлық жол бойына пойыздың қозғалысы мен өзінің ауырлық күшінің
ықпалында болып, еденге тимейтіндей етіп өзекшені бастапқы қалыпта,
яғни қандай да бір көлбеу бұрышына қойып қоюға болады
ма?
функциясы берілген деп
есептеледі, мұндағы s
–
пойыздың А
станциясынан қарағандағы
қашықтығы, ал t
– пойыздың қозғалыс
бастағаннан кезден есептелетін уақыт. Вагондардың біріндегі еденге
топса арқылы ауыр өзекше бекітілген, бұл өзекше вагондардың осіне
параллель бағытта өзінің осі бойынша үйкеліссіз алға және артқа
(еденнен еденге қарай) қозғала алады. (Еденге тигеннен кейін өзекше
келесі «секіруге» дейін еденде жатады деп ойлайық). Мәселе
мынада: пойыз қозғалған мезетте
барлық жол бойына пойыздың қозғалысы мен өзінің ауырлық күшінің
ықпалында болып, еденге тимейтіндей етіп өзекшені бастапқы қалыпта,
яғни қандай да бір көлбеу бұрышына қойып қоюға болады
ма?
Алғашқы уақытта пойыздың қозғалыс сызбасын алдын ала біле отырып, ауырлық күші мен реакция күштерінің өзара әрекеттесуінің нәтижесінде өзекшенің берілген шартқа, яғни бастапқы қалыпты дұрыс таңдау шарына сәйкес қажетті тепе-теңдігін сақтауын қамтамасыз ету мүмкін емес болып көрінеді. Бірақ мұндай бастапқы қалыпты табу мүмкін болады дегенді дәлелдейміз.

6-сурет. Уитни мәселесі
Бұл мәселені дәлелдеу динамиканың заңдарын білуді талап етпейді. (Бұл мәселені динамиканың заңдарына сүйене отырып дәлелдеу өте қиын болар еді). Физикалық мазмұндағы бір ғана жорамалды енгізу жеткілікті: өзекшенің келесі қозғалысы оның бастапқы қалыптағы күйіне үздіксіз байланысты болады; соның ішінде, пойыздың қозғалысы барысында берілген бастапқы қалыпта өзекше еденнің бір жағына құласа, онда берілген бастапқы қалыптан көп айырмашылығы жоқ кез келген бастапқы қалыпта өзекше еденнің қарама-қарсы жағына құламайды.
Енді кез келген уақыт
мезетінде өзекшенің қалыбы өзекшенің еденмен
жасайтын α
бұрышы арқылы сипатталатынына
назар аударайық.  және
және
 бұрыштарына екі
қарама-қарсы көлденең (жатқан) қалып сәйкес келеді. Өзекшенің
бастапқы қалыбындағы α
бұрышының
мәнін х
деп белгілейік. Берілген
мәселенің экзестенциалды болуы салдарынан оны дәлелдеу жанама түрде
болады. Айталық, барлық жағдайда, яғни өзекшенің кез
келген бастапқы қалыбында өзекше міндетті түрде бір жаққа немесе
екінші жаққа құлайды, яғни α
бұрышы
бұрыштарына екі
қарама-қарсы көлденең (жатқан) қалып сәйкес келеді. Өзекшенің
бастапқы қалыбындағы α
бұрышының
мәнін х
деп белгілейік. Берілген
мәселенің экзестенциалды болуы салдарынан оны дәлелдеу жанама түрде
болады. Айталық, барлық жағдайда, яғни өзекшенің кез
келген бастапқы қалыбында өзекше міндетті түрде бір жаққа немесе
екінші жаққа құлайды, яғни α
бұрышы
 немесе
немесе  мәнін қабылдайды.
Онда
мәнін қабылдайды.
Онда  функциясын
өзекше
функциясын
өзекше  немесе
немесе
 бұрышының мәніне сәйкес
еденнің бір жағына құлауына байланысты
бұрышының мәніне сәйкес
еденнің бір жағына құлауына байланысты
 немесе –1 деп
сипаттайық.
немесе –1 деп
сипаттайық.  функциясының қасиеттері
мынадай: ол
функциясының қасиеттері
мынадай: ол  интервалында берілген және бұл
интервалда үздіксіз, сондай-ақ
интервалында берілген және бұл
интервалда үздіксіз, сондай-ақ  . Осыдан, Больцано теоремасына
сәйкес х-тің қандай да бір аралық
мәнінде
. Осыдан, Больцано теоремасына
сәйкес х-тің қандай да бір аралық
мәнінде 
 теңдігі орындалу керек. Ал бұл
ұйғарым
теңдігі орындалу керек. Ал бұл
ұйғарым  функциясы тек қана +1 және –1
мәндерін қабылдау керек деген пікірге қайшы келеді. Сондықтан, кез
келген бастапқы қалыпқа қойылған өзекше пойыздың қозғалысы
барысында еденнің бір жағына құлайды деп алынған жорамалды теріс
деп қабылдап, одан бас тарту керек.
функциясы тек қана +1 және –1
мәндерін қабылдау керек деген пікірге қайшы келеді. Сондықтан, кез
келген бастапқы қалыпқа қойылған өзекше пойыздың қозғалысы
барысында еденнің бір жағына құлайды деп алынған жорамалды теріс
деп қабылдап, одан бас тарту керек.
Көрсетілген дәлелдеу тек қана
теориялық тұрғыдан қарастырылғаны анық, себебі дәлелдеу
қорытындысында өзекшенің бастапқы қалыбын анықтау бойынша ешқандай
нұсқаулар берілмейді. Сонымен қатар мұндай қалып теориялық тұрғыдан
алғанда абсолютті дәл есептелетін болған болса да, өзінің
тұрақсыздығы салдарынан практикалық жағынан еш пайдасыз болар еді.
Осылайша, мысалы, шекті жағдайда, егер пойыз «сапар» барысында
қозғалмайтын болса, шешімі анық болады:
 ; бірақ тегіс көлденең
беттің үстінде инені тік қалыбында тұрғызуға талпынған әрбір адам
бұл мәселені шешу практикалық тұрғыдан қарағанда мүмкін емес екенін
біледі. Алайда, математикалық тұрғыдан қарағанда келтірілген
дәлелдеу даусыз қызығушылық танытатыны рас.
[21]
; бірақ тегіс көлденең
беттің үстінде инені тік қалыбында тұрғызуға талпынған әрбір адам
бұл мәселені шешу практикалық тұрғыдан қарағанда мүмкін емес екенін
біледі. Алайда, математикалық тұрғыдан қарағанда келтірілген
дәлелдеу даусыз қызығушылық танытатыны рас.
[21]
2.6. Вейерштрасстың экстремалдық мәндер туралы теоремалары
Үздіксіз функцияларға қатысты өзге маңызды фактіні Карл Вейерштасс (1815-1897) тұжырымдаған болатын және бұл адам қазіргі кездегі математикалық анализдегі қатаңдыққа деген ұмтылыстың пайда болуына жауапты. Бұл теорема былайша пайымдалады:
3-теорема. Егер  функциясы шеткі a мен b
нүктелерін қоса алғандағы
функциясы шеткі a мен b
нүктелерін қоса алғандағы  , I интервалында үздіксіз
болса, онда I интервалында
, I интервалында үздіксіз
болса, онда I интервалында  функциясы ең үлкен М мәніне
ие болатын ең болмағанда бір нүкте және
функциясы ең үлкен М мәніне
ие болатын ең болмағанда бір нүкте және
 функциясы ең кіші т
мәніне ие болатын басқа нүкте табылады.
Басқаша
айтқанда
функциясы ең кіші т
мәніне ие болатын басқа нүкте табылады.
Басқаша
айтқанда  үздіксіз функцияның графигінде
ең болмағанда бір ең жоғарғы және бір ең кіші нүктелер болу
керек.
үздіксіз функцияның графигінде
ең болмағанда бір ең жоғарғы және бір ең кіші нүктелер болу
керек.
Егер
 функциясы I
интервалының шеткі
нүктелерінде үздіксіз болмаса, онда бұл тұжырым қате болуы мүмкін.
Мысалы,
функциясы I
интервалының шеткі
нүктелерінде үздіксіз болмаса, онда бұл тұжырым қате болуы мүмкін.
Мысалы,  функциясы
функциясы
 аралығының ішінде
үздіксіз болғанымен, оның бұл аралықтағы ең үлкен мәні жоқ. Сонымен
қатар үзілісті функция шектеулі болса да, ол ең үлкен және ең кіші
мәндеріне ие болмауы мүмкін. Мысалы, төмендегідей анықталатын
«төтенше» үзілісті
аралығының ішінде
үздіксіз болғанымен, оның бұл аралықтағы ең үлкен мәні жоқ. Сонымен
қатар үзілісті функция шектеулі болса да, ол ең үлкен және ең кіші
мәндеріне ие болмауы мүмкін. Мысалы, төмендегідей анықталатын
«төтенше» үзілісті  функциясын
қарастырайық:
функциясын
қарастырайық:  аралығында
аралығында
х
иррационал
болғанда,  ,
,
х
рационал
болғанда,  .
.
Бұл функцияның қабылдайтын
мәндерінің барлығы 0 мен 1-дің аралығында жатыр. Олардың ішінде 0
мен 1-ге өте жақын мәндер де бар: олар
х-ті иррационал және 0 немесе
1-ге өте жақын етіп таңдасақ шығады. Бірақ
 ешқашан 0-ге де, 1-ге де
тең бола алмайды, себебі рационал х
үшін
ешқашан 0-ге де, 1-ге де
тең бола алмайды, себебі рационал х
үшін
 , ал
иррационал х
үшін
, ал
иррационал х
үшін
 болады. Сонымен, 0 мен 1
мәндері ешбір нүктеде шықпайды.
болады. Сонымен, 0 мен 1
мәндері ешбір нүктеде шықпайды.
Дәлелдеу. Вейерштрасс теоремасы Больцано
теоремасы секілді дәлелденеді. I
интервалын екі жағынан
шектелген  пен
пен
 интервалдарына бөлейік
және назарымызды
интервалдарына бөлейік
және назарымызды  интервалына аударайық, бұл
интервалдан
интервалына аударайық, бұл
интервалдан  функциясының ең үлкен мәнін
іздейміз, егер
де
функциясының ең үлкен мәнін
іздейміз, егер
де  интервалында
интервалында  интервалындағы
интервалындағы  функциясының барлық
мәндерінен
функциясының барлық
мәндерінен  мәні үлкен болатын α
нүктесі табылмаса. Таңдап алынған
интервалды
мәні үлкен болатын α
нүктесі табылмаса. Таңдап алынған
интервалды  деп белгілейік.
Енді I
интервалында жасаған
амалдарды
деп белгілейік.
Енді I
интервалында жасаған
амалдарды  интервалында қайталап
орындайық; бұдан
интервалында қайталап
орындайық; бұдан  интервалын алайық және т.с.с.
Бұл үрдіс
интервалын алайық және т.с.с.
Бұл үрдіс  ішкі интервалдар қатарын
анықтайды, олардың барлығында қандай да бір
z
нүктесі болады. Осы нүктедегі
функцияның
ішкі интервалдар қатарын
анықтайды, олардың барлығында қандай да бір
z
нүктесі болады. Осы нүктедегі
функцияның  мәні
мәні
 функциясының бастапқы
интервалдағы барлық мәндерінің ішіндегі ең үлкені екенін
дәлелдейміз, яғни
функциясының бастапқы
интервалдағы барлық мәндерінің ішіндегі ең үлкені екенін
дәлелдейміз, яғни  болатындай s
нүктесінің табылуы мүмкін
еместігін көрсетеміз. Айталық,
болатындай s
нүктесінің табылуы мүмкін
еместігін көрсетеміз. Айталық,  шартын
қанағаттандыратын s
нүктесі табылды дейік,
мұндағы ɛ
– қандай да бір (мүмкін өте
аз) оң сан.
шартын
қанағаттандыратын s
нүктесі табылды дейік,
мұндағы ɛ
– қандай да бір (мүмкін өте
аз) оң сан.  функциясы үздіксіз
болғандықтан, z
нүктесін
s
нүктесін қоса алмайтындай етіп
кішкентай К
интервалымен шектей аламыз
және бұл К
интервалында
функциясы үздіксіз
болғандықтан, z
нүктесін
s
нүктесін қоса алмайтындай етіп
кішкентай К
интервалымен шектей аламыз
және бұл К
интервалында  функциясының
мәндері
функциясының
мәндері  мәнінен
ɛ-ға кем болады, сондықтан бұл
интервалдан міндетті түрде
мәнінен
ɛ-ға кем болады, сондықтан бұл
интервалдан міндетті түрде  іздейміз. Бірақ
үлкен п
мәндері
кезінде
іздейміз. Бірақ
үлкен п
мәндері
кезінде  интервалы
К
интервалының ішінде жатады,
сонымен қатар х
үшін
интервалы
К
интервалының ішінде жатады,
сонымен қатар х
үшін
 -тің
-тің  интервалынан тыс жатқан ешбір
мәні осы интервалдың құрамындағы х
нүктелеріндегі
интервалынан тыс жатқан ешбір
мәні осы интервалдың құрамындағы х
нүктелеріндегі  функциясының мәндерінен артық
бола алмайтындай етіп
функциясының мәндерінен артық
бола алмайтындай етіп  интервалы
анықталды.
интервалы
анықталды.
Бірақ
s
нүктесі
 интервалынан тысқары
жатады және ол интервалда
интервалынан тысқары
жатады және ол интервалда  болады,
ал К
интервалында, ал ол
арқылы
болады,
ал К
интервалында, ал ол
арқылы  интервалында
интервалында  болады. Осылайша, біз
қарама-қайшылыққа келдік.
болады. Осылайша, біз
қарама-қайшылыққа келдік.
Ең кіші
т
мәнінің ең болмағанда
біреуінің табылуы осы әдіспен дәлелденеді; ол алдыңғы дәлелдеудің
салдары болады, себебі  функциясының ең кіші
мәні
функциясының ең кіші
мәні  функциясының ең үлкен мәніне
сәйкес келеді.
функциясының ең үлкен мәніне
сәйкес келеді.
Вейерштрасс теоремасын дәлелдеу әдісі арқылы екі немесе одан да көп х, у, ... айнымалысы бар үздіксіз функцияларды да дәлелдеуге болады. Бұл жағдайда (шеткі нүктелері қоса алынған) шектелген интервалдардың орнына шектелген аймақтарды, алу керек, мысалы х, у жазықтығындағы тіктөртбұрыштар аймағы (контурды қоса алғанда). [22]
4-теорема. Егер  функциясы
функциясы  сегментінде үздіксіз болса,
онда функция осы сегментте шектелген
болады.
сегментінде үздіксіз болса,
онда функция осы сегментте шектелген
болады.
Дәлелдеу.  функциясы
функциясы
 сегментінде жоғарыдан
шектелгенін дәлелдейік (төменнен шектелгендігі осыған ұқсас
дәлелденеді).
сегментінде жоғарыдан
шектелгенін дәлелдейік (төменнен шектелгендігі осыған ұқсас
дәлелденеді).
Кері дәлелдеуді қолданамыз,
яғни  функциясы
функциясы
 сегментінде жоғарыдан
шектелмеген деп пайымдайық. Онда кез келген
натурал п
сегментінде жоғарыдан
шектелмеген деп пайымдайық. Онда кез келген
натурал п
 үшін
үшін  болатындай
болатындай  сегментінен ең болмағанда
бір
сегментінен ең болмағанда
бір  нүктесі табылады (қарсы
жағдайда
нүктесі табылады (қарсы
жағдайда  функциясы
функциясы
 сегментінде жоғарыдан
шектелген болар еді).
сегментінде жоғарыдан
шектелген болар еді).
Осылайша,
 сегментінен
сегментінен  функциясының сәйкес мәндерінің
тізбегі шексіз үлкен болатындай
функциясының сәйкес мәндерінің
тізбегі шексіз үлкен болатындай  мәндерінің тізбегін
көрсеттік.
мәндерінің тізбегін
көрсеттік.  тізбегінен қандай да
бір ξ
нүктесінде
шоғырланатын
тізбегінен қандай да
бір ξ
нүктесінде
шоғырланатын  ішкі тізбегін бөліп алуға
болады.
ішкі тізбегін бөліп алуға
болады.  ішкі тізбегінің барлық
элементтері
ішкі тізбегінің барлық
элементтері  сегментінде
орналасқандықтан, ξ
нүктесі
де
сегментінде
орналасқандықтан, ξ
нүктесі
де  сегментіне тиісті
болады.
сегментіне тиісті
болады.  функциясының ξ
нүктесіндегі үздіксіздігі
салдарынан
функциясының ξ
нүктесіндегі үздіксіздігі
салдарынан  функциясының сәйкес мәндерінің
ішкі тізбегі
функциясының сәйкес мәндерінің
ішкі тізбегі  -ке шоғырлануы керек. Бірақ
бұл ұйғарым
-ке шоғырлануы керек. Бірақ
бұл ұйғарым  шексіз үлкен тізбегінен
алынған
шексіз үлкен тізбегінен
алынған  ішкі тізбегінің өзі де шексіз
үлкен болады дегенге қарсы келеді. Шыққан қарама-қайшылық теореманы
дәлелдейді.
ішкі тізбегінің өзі де шексіз
үлкен болады дегенге қарсы келеді. Шыққан қарама-қайшылық теореманы
дәлелдейді.
1-ескерту. 4-теоремада айтылған ұйғарым
интервал үшін (немесе жартысегмент үшін) орындалмайды, яғни
функцияның интервалдағы (немесе жартысегменттегі) үздіксіздігі
ұйғарымынан функцияның осы жиындағы шектелгендігі туралы ұйғарым
шықпайды. Мысалы,  интервалындағы
(немесе
интервалындағы
(немесе  жартысегментіндегі)
жартысегментіндегі)  функциясын қарастырайық. Бұл
функция берілген жиында үздіксіз, бірақ шектелмеген болады. Расында
да,
функциясын қарастырайық. Бұл
функция берілген жиында үздіксіз, бірақ шектелмеген болады. Расында
да,  тізбегі берілген жиынға тиісті
болады, ал
тізбегі берілген жиынға тиісті
болады, ал  функциясының мәндерінің
тізбегі шексіз үлкен болып табылады.
функциясының мәндерінің
тізбегі шексіз үлкен болып табылады.
Берілген
 жиынында жоғарыдан
(төменнен) шектелген
жиынында жоғарыдан
(төменнен) шектелген  функциясын қарастырайық.
[23]
функциясын қарастырайық.
[23]
2-анықтама. М саны (т
саны)  функциясының
функциясының  жиынындағы дәл жоғарғы (дәл
төменгі) шекарасы деп аталады, егер екі шарт
орындалса: 1)
жиынындағы дәл жоғарғы (дәл
төменгі) шекарасы деп аталады, егер екі шарт
орындалса: 1)
 жиынының әрбір х мәні
үшін
жиынының әрбір х мәні
үшін  теңсіздігі
орындалады; 2)
кез
келген
теңсіздігі
орындалады; 2)
кез
келген  саны
үшін
саны
үшін  жиынында
жиынында  функциясының сәйкес
мәніне
функциясының сәйкес
мәніне

теңсіздігі орындалатындай х мәні табылады.
Берілген анықтамадағы 1)
шарт М
саны
(т
саны)
 функциясының
функциясының  жиынындағы жоғарғы (төменгі)
шекараларының бірі болады дегенді білдіреді, ал 2) шарт осы шекара
ең кіші (ең үлкен) мән болады және ол мән кішіреймейді (үлкеймейді)
дегенді білдіреді.
жиынындағы жоғарғы (төменгі)
шекараларының бірі болады дегенді білдіреді, ал 2) шарт осы шекара
ең кіші (ең үлкен) мән болады және ол мән кішіреймейді (үлкеймейді)
дегенді білдіреді.
 функциясының
функциясының  жиынындағы дәл
жоғарғы М
шекарасы
әдетте
жиынындағы дәл
жоғарғы М
шекарасы
әдетте

символымен,
ал  функциясының
функциясының  жиынындағы дәл
төменгі т
шекарасы
жиынындағы дәл
төменгі т
шекарасы

символымен белгіленеді.
Сонымен
қатар  функциясының
функциясының  сегментіндегі дәл жоғарғы
шекарасын төмендегі төрт символдың кез келгенімен белгілеуге
болады:
сегментіндегі дәл жоғарғы
шекарасын төмендегі төрт символдың кез келгенімен белгілеуге
болады:
 .
.
Сондай-ақ дәл төменгі шекарасын белгілеуге арналған төрт символ төмендегі түрде болады:
 .
.
Төмендегі ұйғарымдар дұрыс болады:
-
егер
 функциясы
функциясы  жиынында жоғарыдан
(төменнен) шектелген болса, онда осы жиында берілген функцияның дәл
жоғарғы шекарасы (дәл төменгі шекарасы)
болады;
жиынында жоғарыдан
(төменнен) шектелген болса, онда осы жиында берілген функцияның дәл
жоғарғы шекарасы (дәл төменгі шекарасы)
болады; -
егер
 функциясы
функциясы  жиынында шектелген болса
(екі жағынан), онда осы жиында берілген функцияның дәл жоғарғы да,
дәл төменгі де шекаралары болады.
жиынында шектелген болса
(екі жағынан), онда осы жиында берілген функцияның дәл жоғарғы да,
дәл төменгі де шекаралары болады.
Бұл ұйғарымдар негізінде
мынадай сұрақ туады:  жиынында
шектелген
жиынында
шектелген функциясының дәл жоғарғы (дәл
төменгі) шекарасы жетімді болады ма,
яғни
функциясының дәл жоғарғы (дәл
төменгі) шекарасы жетімді болады ма,
яғни  жиынында
функцияның
жиынында
функцияның  мәні
мәні
 жиынындағы
жиынындағы  функциясының дәл жоғарғы
(сәйкесінше дәл төменгі) шекарасына тең
болатындай
функциясының дәл жоғарғы
(сәйкесінше дәл төменгі) шекарасына тең
болатындай  нүктесі табылады
ма.
нүктесі табылады
ма.
Келесі мысал берілген жиында шектелген функцияның дәл шекаралары жалпы алғанда жетімді болмайтынын көрсетеді.
 сегментінде төмендегі
түрдегі
сегментінде төмендегі
түрдегі  функциясын қарастырайық
(7-сурет):
функциясын қарастырайық
(7-сурет):

Бұл
функция  сегментінде шектелген және осы
сегментте
сегментінде шектелген және осы
сегментте  дәл жоғарғы мәні
мен
дәл жоғарғы мәні
мен  дәл төменгі мәні болады.
Алайда бұл мәндер жетімді болмайды:
дәл төменгі мәні болады.
Алайда бұл мәндер жетімді болмайды:  сегментінің нүктелерінің
арасында функцияның мәндері нөлге немесе бірге тең болатын нүктелер
табылмайды.
сегментінің нүктелерінің
арасында функцияның мәндері нөлге немесе бірге тең болатын нүктелер
табылмайды.

7-сурет
Қарастырылып
отырған  функциясы
функциясы
 сегментінде үздіксіз
болатынын ескере кетейік (функция
сегментінде үздіксіз
болатынын ескере кетейік (функция  және
және
 нүктелерінде үзілмейді).
[24] Бұл жағдай кездейсоқ емес, себебі төмендегі ұйғарым дұрыс
болады.
нүктелерінде үзілмейді).
[24] Бұл жағдай кездейсоқ емес, себебі төмендегі ұйғарым дұрыс
болады.
5-теорема. Егер  функциясы
функциясы  сегментінде үздіксіз болса,
онда ол осы сегментте өзінің дәл жоғарғы және дәл төменгі
шекараларына жетеді, яғни
сегментінде үздіксіз болса,
онда ол осы сегментте өзінің дәл жоғарғы және дәл төменгі
шекараларына жетеді, яғни  сегментінің нүктелерінің
ішінен
сегментінің нүктелерінің
ішінен  мәні
мәні  функциясының
функциясының  сегментіндегі дәл жоғарғы
шекарасына, ал
сегментіндегі дәл жоғарғы
шекарасына, ал  мәні
мәні  функциясының
функциясының  сегментіндегі дәл төменгі
шекарасына тең болатындай
сегментіндегі дәл төменгі
шекарасына тең болатындай  және
және  нүктелері
табылады.
нүктелері
табылады.
Дәлелдеу. 4-теоремаға
сәйкес  функциясы
функциясы
 сегментінде үздіксіз
болады, сондықтан функцияның осы сегментте
М
дәл жоғарғы шекарасы
мен т
дәл төменгі шекарасы бар
болады.
сегментінде үздіксіз
болады, сондықтан функцияның осы сегментте
М
дәл жоғарғы шекарасы
мен т
дәл төменгі шекарасы бар
болады.
М дәл жоғарғы мәніне жетуін дәлелдеуге тоқталайық, себебі т дәл төменгі мәніне жету осы жолмен дәлелденеді.
М
дәл жоғарғы мәні жетімсіз
болсын деп болжам жасайық, яғни  сегментінің барлық
нүктелерінде
сегментінің барлық
нүктелерінде  функциясы
М
мәнінен кем мәндерді
қабылдайды деп пайымдайық. Онда біз
функциясы
М
мәнінен кем мәндерді
қабылдайды деп пайымдайық. Онда біз

функциясын қарастыра аламыз.
Бөлшектің
 бөлімі
бөлімі  сегментінде үздіксіз және тек
қана оң таңбалы функция болып табылады.
Сондықтан
сегментінде үздіксіз және тек
қана оң таңбалы функция болып табылады.
Сондықтан  функциясы
функциясы
 сегментінде үздіксіз
болады. Демек, 4-теоремаға сәйкес
сегментінде үздіксіз
болады. Демек, 4-теоремаға сәйкес  функциясы
функциясы
 сегментінде шектелген
болады, яғни
сегментінде шектелген
болады, яғни  болатындай А
оң саны
табылады.
болатындай А
оң саны
табылады.  функциясы
функциясы
 сегментінде тек қана оң
таңбалы функция болғандықтан, соңғы теңсіздік
сегментінде тек қана оң
таңбалы функция болғандықтан, соңғы теңсіздік
 сегментінің
барлық х
үшін
сегментінің
барлық х
үшін
 теңсіздігіне
эквивалентті болады, ал бұл ұйғарым
М
саны – дәл жоғарғы шекарасы,
яғни
теңсіздігіне
эквивалентті болады, ал бұл ұйғарым
М
саны – дәл жоғарғы шекарасы,
яғни  функциясының
функциясының  сегментіндегі барлық жоғарғы
шекараларының ішіндегі ең кішісі деген ұйғарымға қарама-қайшы
болады.
сегментіндегі барлық жоғарғы
шекараларының ішіндегі ең кішісі деген ұйғарымға қарама-қайшы
болады.
Алынған қарама-қайшылық дәл жоғарғы шекараның жетімді болмайды деген болжамымыздың қате екенін дәлелдейді. [25]
2-ескерту.  сегментінде үздіксіз болатын
функцияның дәл жоғарғы және дәл төменгі мәндеріне жетуі дәлелденген
соң
сегментінде үздіксіз болатын
функцияның дәл жоғарғы және дәл төменгі мәндеріне жетуі дәлелденген
соң  функциясының
функциясының  сегментіндегі М
дәл жоғарғы
шекарасын максималды
мән деп, ал
т
дәл төменгі
шекарасын минималды
мән деп атай аламыз. 5-теореманы
басқаша түрде былай жазуға болады:
сегментіндегі М
дәл жоғарғы
шекарасын максималды
мән деп, ал
т
дәл төменгі
шекарасын минималды
мән деп атай аламыз. 5-теореманы
басқаша түрде былай жазуға болады:  сегментінде үздіксіз
болатын
сегментінде үздіксіз
болатын  функциясының осы сегментте
максималды және минималды мәндері
болады.
функциясының осы сегментте
максималды және минималды мәндері
болады.
 функциясының
функциясының  сегментіндегі максималды мәні
төмендегі символдардың бірімен
белгіленеді:
сегментіндегі максималды мәні
төмендегі символдардың бірімен
белгіленеді:
 .
.
 функциясының
функциясының  сегментіндегі минималды
мәндерінің символдары мынадай түрде
беріледі:
сегментіндегі минималды
мәндерінің символдары мынадай түрде
беріледі:
 .
.
3-ескерту. Берілген сегментте үздіксіз
болмайтын функциялар да осы сегментте өзінің дәл жоғарғы және дәл
төменгі мәндеріне ие бола алатынын ескере кетейік. Мысал ретінде
барлық иррационал х
үшін нөлге тең болатын және
барлық рационал х
үшін бірге тең
болатын  Дирихле функциясын қарастыруға
болады. Бұл функция
Дирихле функциясын қарастыруға
болады. Бұл функция  сегментінің әрбір нүктесінде
үзілісті болады, бірақ осы сегментте бірге тең болатын өзінің дәл
жоғарғы мәніне және нөлге тең болатын дәл төменгі мәніне жетеді.
[26]
сегментінің әрбір нүктесінде
үзілісті болады, бірақ осы сегментте бірге тең болатын өзінің дәл
жоғарғы мәніне және нөлге тең болатын дәл төменгі мәніне жетеді.
[26]
4-ескерту. 5-теоремадағы ұйғарым қате болады, егер оның жазылуындағы «сегмент» термині «интервал» немесе «жартысегмент» терминдерімен алмастырылатын болса.
Осылайша,
 функциясы
функциясы  интервалында
немесе
интервалында
немесе  жартысегментінде үздіксіз
болады, бірақ бұл функцияның берілген интервалдағы немесе
жартысегменттегі
жартысегментінде үздіксіз
болады, бірақ бұл функцияның берілген интервалдағы немесе
жартысегменттегі  дәл жоғарғы шекарасы бар
болады, алайда жетімді болмайды.
дәл жоғарғы шекарасы бар
болады, алайда жетімді болмайды.
Осыған қоса, интервалдағы немесе жартысегменттегі функцияның дәл шекаралары болмауы да мүмкін екенін айта кетейік, себебі мұндай функция берілген интервалда немесе жартысегментте шектеулі болмауы мүмкін (1-ескертуді қара).
Больцано мен Вейерштрасс теоремаларының дәлелдеуі конструктивтік түрге келтірілмейді. Олар нөлдік нүктенің орналасуын немесе үрдістердің соңында алынатын дәлдіктің дәрежесі алдын ала анықталған функцияның ең үлкен мен ең кіші мәнін табудың «тиімді» әдісін көрсетпейді. Олар тек қана аталған мәндердің барын немесе жоқтығын теріске шығарып дәлелдейді. [27]
2.7. Реттілік туралы теорема. Шағын жиындар
Айталық,
 әр түрлі немесе бірдей
сандардың
әр түрлі немесе бірдей
сандардың  кесіндісіндегі қандай да бір
шексіз реттілігі болсын. Реттілік шекке ұмтылуы немесе ұмтылмауы
мүмкін. Бірақ, қалай болғанда да, мұндай реттіліктен оның
кейбір мүшелерін шығарып тастау арқылы I кесіндісінде жататын шекке
ұмтылатын
кесіндісіндегі қандай да бір
шексіз реттілігі болсын. Реттілік шекке ұмтылуы немесе ұмтылмауы
мүмкін. Бірақ, қалай болғанда да, мұндай реттіліктен оның
кейбір мүшелерін шығарып тастау арқылы I кесіндісінде жататын шекке
ұмтылатын шексіз тізбекті қашанда
алуға болады.
шексіз тізбекті қашанда
алуға болады.
Бұл теореманы дәлелдеу
үшін I
интервалын  орта нүкте
арқылы
орта нүкте
арқылы  және
және
 шектелген екі кесіндіге
бөлейік:
шектелген екі кесіндіге
бөлейік:


Осы екі кесіндінің біреуінде
негізгі реттілікте тұрған  мүшелерінің шексіз саны
болады; оны
мүшелерінің шексіз саны
болады; оны  деп белгілейік.
Осы
деп белгілейік.
Осы  мүшелерінің ішінен біреуін
таңдап, оны
мүшелерінің ішінен біреуін
таңдап, оны  деп белгілейік. Осы
үрдісті
деп белгілейік. Осы
үрдісті  кесіндісінде
қаталаймыз.
кесіндісінде
қаталаймыз.  интервалында
интервалында  мүшелерінің шексіз саны
болғандықтан, олардың шексіз саны
мүшелерінің шексіз саны
болғандықтан, олардың шексіз саны  интервалының жартыларының
біреуінде де болу керек; бұл жарты интервалды
интервалының жартыларының
біреуінде де болу керек; бұл жарты интервалды
 деп
белгілейік.
деп
белгілейік.  кесіндісінде
кесіндісінде  болатындай
болатындай  мүшесін алып,
оны
мүшесін алып,
оны  деп белгілейміз. Осылайша
жалғастыра отырып п-нің мәні қандай болса
да
деп белгілейміз. Осылайша
жалғастыра отырып п-нің мәні қандай болса
да  интервалында жататын негізгі
реттілік мүшелерінің
интервалында жататын негізгі
реттілік мүшелерінің  тізбекшесін
және
тізбекшесін
және  ішкі кесінділерден тұратын
реттілікті аламыз. Интервалдардың мұндай реттілігі аралықтың қандай
да бір у
нүктесіне жиналады
және
ішкі кесінділерден тұратын
реттілікті аламыз. Интервалдардың мұндай реттілігі аралықтың қандай
да бір у
нүктесіне жиналады
және  реттілігінің
шегі у
болатыны белгілі болды.
Осылайша теорема дәлелденді. [28]
реттілігінің
шегі у
болатыны белгілі болды.
Осылайша теорема дәлелденді. [28]
Бұл пайымдаулар қазіргі
математикаға тән түрдегі жалпылауларды мүмкін етеді. Құрамында
«қашықтық» ұғымы белгілі бір түрде анықталатын қандай да
бір S
жиыннан
өтетін Х
айнымалысын
қарастырайық. S
жазықтықтағы немесе
кеңістіктегі нүктелер жиыны болуы мүмкін. Бірақ бұл міндетті емес;
мысалы, S
жазықтықтағы барлық
үшбұрыштардың жиыны да болуы мүмкін. Егер
Х
пен
Y
төбелері
А, В,
С және
 болатын үшбұрыштар
болса, онда үшбұрыштар арасындағы «қашықтық» ретінде,
мысалы
болатын үшбұрыштар
болса, онда үшбұрыштар арасындағы «қашықтық» ретінде,
мысалы

санын алуға болады,
мұндағы  дегеніміз
– A
мен
дегеніміз
– A
мен
 нүктелері арасындағы
әдеттегі қашықтық. Жиында «қашықтық» ұғымы енгізілгеннен
бастап S
жиынының мүшесі
болатын Х
шегіне
ұмтылатын
нүктелері арасындағы
әдеттегі қашықтық. Жиында «қашықтық» ұғымы енгізілгеннен
бастап S
жиынының мүшесі
болатын Х
шегіне
ұмтылатын  элементтерінің реттілігі
ұғымын анықтап алуға мүмкіндік туады. Бұл
арқылы
элементтерінің реттілігі
ұғымын анықтап алуға мүмкіндік туады. Бұл
арқылы  болғанда
болғанда
 болады демекпіз.
Енді S жиыны ықшамды болады деп
айтамыз, егер осы жиынның элементтері болатын
әрбір
болады демекпіз.
Енді S жиыны ықшамды болады деп
айтамыз, егер осы жиынның элементтері болатын
әрбір  реттілігінен S жиынына
тиісті қандай да бір Х шегіне ұмтылатын тізбекшені алуға болатын
болса. Алдыңғы бөлімшеде екі жағынан
шектелген
реттілігінен S жиынына
тиісті қандай да бір Х шегіне ұмтылатын тізбекшені алуға болатын
болса. Алдыңғы бөлімшеде екі жағынан
шектелген  аралығы берілген мәнмәтінде
ықшам екенін көрсеттік. [29] Осылайша, ықшамды жиын ұғымын сан
осіндегі шектелген
интервал ұғымының жалпыламасы деп алуға
болады. Сан осі өз алдына ықшамдалмаған, себебі 1, 2, 3, 4, 5, ...
бүтін сандар реттілігі ешбір шекке ұмтылмайды және бұл осьтің
құрамында қандай да бір шекке ұмтылатын ешбір реттілік жоқ.
Осылайша,
аралығы берілген мәнмәтінде
ықшам екенін көрсеттік. [29] Осылайша, ықшамды жиын ұғымын сан
осіндегі шектелген
интервал ұғымының жалпыламасы деп алуға
болады. Сан осі өз алдына ықшамдалмаған, себебі 1, 2, 3, 4, 5, ...
бүтін сандар реттілігі ешбір шекке ұмтылмайды және бұл осьтің
құрамында қандай да бір шекке ұмтылатын ешбір реттілік жоқ.
Осылайша,  ашық интервалы да
ықшамдалмаған болады; расында да
ашық интервалы да
ықшамдалмаған болады; расында да  реттілігі немесе оның кез
келген тізбекшесі 0 шегіне ұмтылады, алайда бұл шек қарастырылып
отырған ашық аралыққа тиісті емес. Осылайша қандай да бір
квадраттың немесе тіктөртбұрыштың ішкі нүктелерінен тұратын
жазықтықтың облысы ықшамдалмаған болады деп айта аламыз; бірақ ол
шеткі нүктелері анықталғаннан кейін ықшамды болып шығады. Төбелері
берілген шеңбердің бойында немесе ішінде жатқан барлық
үшбұрыштардың жиыны да ықшамды болатынына оңай көз жеткізуге
болады. [30]
реттілігі немесе оның кез
келген тізбекшесі 0 шегіне ұмтылады, алайда бұл шек қарастырылып
отырған ашық аралыққа тиісті емес. Осылайша қандай да бір
квадраттың немесе тіктөртбұрыштың ішкі нүктелерінен тұратын
жазықтықтың облысы ықшамдалмаған болады деп айта аламыз; бірақ ол
шеткі нүктелері анықталғаннан кейін ықшамды болып шығады. Төбелері
берілген шеңбердің бойында немесе ішінде жатқан барлық
үшбұрыштардың жиыны да ықшамды болатынына оңай көз жеткізуге
болады. [30]
Үздіксіздік
ұғымы Х
айнымалысы кез
келген S
жиынынан өтетін жағдайға
жалпыламаны мүмкін етеді, егер осы аталған
S
жиынында шекке ұмтылу ұғымы
алдын ала енгізілген болса.  функциясы
(мұндағы и
нақты сан болып
есептеледі) Х
элементінде үздіксіз деп
айтады, егер
функциясы
(мұндағы и
нақты сан болып
есептеледі) Х
элементінде үздіксіз деп
айтады, егер  элементтерінен құралған
реттіліктің шегі әркез Х, ал оған
сәйкес
элементтерінен құралған
реттіліктің шегі әркез Х, ал оған
сәйкес  сандар реттілігінің шегі
әркез
сандар реттілігінің шегі
әркез  болатын болса. Вейерштрасс
теоремасы жалпыланған үздіксіз
болатын болса. Вейерштрасс
теоремасы жалпыланған үздіксіз  функциясы үшін де
орындалатынына оңай көз жеткізуге болады, бұл функция қандай да бір
ықшамды жиында беріледі:
функциясы үшін де
орындалатынына оңай көз жеткізуге болады, бұл функция қандай да бір
ықшамды жиында беріледі:
Егер  ықшамды S жиынының барлық
элементтері үшін үздіксіз функция болса,
онда
ықшамды S жиынының барлық
элементтері үшін үздіксіз функция болса,
онда  функциясы ең үлкен мәнді
қабылдайтын S жиынының бір элементі
және
функциясы ең үлкен мәнді
қабылдайтын S жиынының бір элементі
және функциясы ең кіші мәнді
қабылдайтын S жиынының басқа бір элементі міндетті түрде
табылады.[31]
функциясы ең кіші мәнді
қабылдайтын S жиынының басқа бір элементі міндетті түрде
табылады.[31]
2.8. Функцияның біртекті үздіксіздігі ұғымы
Айталық,
 функциясы жиынның әрбір
нүктесі осы жиынның шекті нүктесі болатындай
функциясы жиынның әрбір
нүктесі осы жиынның шекті нүктесі болатындай
 жиынында берілсін.
Мұндай жиынның мысалы болып сегмент, интервал, жартысегмент,
жартытүзу, шексіз түзу, аталған жиындардың кез келгеніне тиісті
болатын барлық рационал нүктелердің жиыны бола
алады.
жиынында берілсін.
Мұндай жиынның мысалы болып сегмент, интервал, жартысегмент,
жартытүзу, шексіз түзу, аталған жиындардың кез келгеніне тиісті
болатын барлық рационал нүктелердің жиыны бола
алады.
3-анықтама.  функциясы
функциясы  жиынында біртекті үздіксіз
деп аталады, егер
жиынында біртекті үздіксіз
деп аталады, егер  жиынының
жиынының  шартын қанағаттандыратын
кез келген
шартын қанағаттандыратын
кез келген  және
және  екі нүктесі
үшін
екі нүктесі
үшін

теңсіздігі дұрыс болатындай кез келген оң таңбалы ɛ саны үшін оң таңбалы δ саны табылса. [32]
5-ескерту.  функциясы
функциясы
 жиынында біртекті
үздіксіз болса, онда ол
жиынында біртекті
үздіксіз болса, онда ол  жиынының
әрбір х
нүктесінде үздіксіз болатынын
бірден ескере кетейік. Расында да, жоғарыдағы
анықтамадағы
жиынының
әрбір х
нүктесінде үздіксіз болатынын
бірден ескере кетейік. Расында да, жоғарыдағы
анықтамадағы  орнына
орнына
 жиынының берілген
нақты
жиынының берілген
нақты  нүктесін,
ал
нүктесін,
ал  орнына
орнына
 жиынының кез келген
нүктесін алсақ, Коши бойынша
жиынының кез келген
нүктесін алсақ, Коши бойынша  функциясының
функциясының  нүктесіндегі үздіксіздігі
анықтамасына келеміз.
нүктесіндегі үздіксіздігі
анықтамасына келеміз.
6-ескерту. Біртекті үздіксіздіктің
жоғарыда келтірілген анықтамасының негізгі шарты – кез
келген  үшін
3-анықтамадағы
үшін
3-анықтамадағы жиынының
жиынының
 шартын қанағаттандыратын
барлық
шартын қанағаттандыратын
барлық  және
және
 нүктелеріне теңсіздіктің
орындалуын қамтамасыз ететін
нүктелеріне теңсіздіктің
орындалуын қамтамасыз ететін  әмбебап мәнінің табылуына
кепіл беретін шарт. [33]
әмбебап мәнінің табылуына
кепіл беретін шарт. [33]
Егер
 функциясының
функциясының  жиынындағы
әрбір
жиынындағы
әрбір  нүктесіндегі үздіксіздігін
талап етсек, онда кез келген
нүктесіндегі үздіксіздігін
талап етсек, онда кез келген  және
және
 жиынының кез
келген
жиынының кез
келген  нүктесі
үшін ɛ
санына ғана емес,
сондай-ақ
нүктесі
үшін ɛ
санына ғана емес,
сондай-ақ  нүктесіне тәуелді болатын
және
нүктесіне тәуелді болатын
және  жиынының
жиынының
 шартын қанағаттандыратын
барлық
шартын қанағаттандыратын
барлық  нүктесі
үшін
нүктесі
үшін  теңсіздігінің дұрыстығын
қамтамасыз ететін «өзіндік» оң
теңсіздігінің дұрыстығын
қамтамасыз ететін «өзіндік» оң  санының бар болуына кепіл
беруге болады. сонымен қоса, жалпы айтқанда,
санының бар болуына кепіл
беруге болады. сонымен қоса, жалпы айтқанда,
 жиынының
барлық
жиынының
барлық  нүктесі бойынша
көрсетілген
нүктесі бойынша
көрсетілген  сандарының оң дәл төменгі
шекарасы болмауы да мүмкін, яғни
сандарының оң дәл төменгі
шекарасы болмауы да мүмкін, яғни  функциясының
функциясының  жиынындағы біртекті
үздіксіздігі шықпайды.
жиынындағы біртекті
үздіксіздігі шықпайды.
7-ескерту. Біртекті үздіксіздіктің
жоғарыда көрсетілген анықтамасынан шығатыны:
егер  функциясы
функциясы
 жиынында біртекті
үздіксіз болса, онда бұл функция
жиынында біртекті
үздіксіз болса, онда бұл функция  жиынының кез келген ішкі
жиынында да біртекті үздіксіз болады. [34]
жиынының кез келген ішкі
жиынында да біртекті үздіксіз болады. [34]
Берілген
 жиынында біртекті
үздіксіздік қасиетіне ие болатын және ие болмайтын функциялардың
мысалдарын қарастырайық.
жиынында біртекті
үздіксіздік қасиетіне ие болатын және ие болмайтын функциялардың
мысалдарын қарастырайық.
-
 функциясы
функциясы  жартытүзуінде біртекті
үздіксіз екеніне көз жеткізейік. Расында да, берілген жартытүзуден
алынған кез келген
жартытүзуінде біртекті
үздіксіз екеніне көз жеткізейік. Расында да, берілген жартытүзуден
алынған кез келген  және
және
 екі нүкте үшін төмендегі
теңсіздік орындалады:
екі нүкте үшін төмендегі
теңсіздік орындалады:
 .
.
Сондықтан, кез
келген  үшін оң
таңбалы δ
санын
алсақ,
үшін оң
таңбалы δ
санын
алсақ,  жартытүзуінің
жартытүзуінің  шартын қанағаттандыратын кез
келген
шартын қанағаттандыратын кез
келген  және
және
 екі нүкте
үшін
екі нүкте
үшін  теңсіздігі орындалатынын
көреміз.
теңсіздігі орындалатынын
көреміз.
-
 функциясы
функциясы  интервалында біртекті үздіксіз
болмайды (бұл функция
интервалында біртекті үздіксіз
болмайды (бұл функция  интервалының әрбір нүктесінде
үздіксіз болса да). Бұған көз жеткізу үшін қандай да
бір
интервалының әрбір нүктесінде
үздіксіз болса да). Бұған көз жеткізу үшін қандай да
бір  және кез келген
аз
және кез келген
аз  үшін
үшін
 интервалында
интервалында
 бірақ
бірақ 
болатындай  және
және
 нүктелерінің ең
болмағанда бір жұбы табылатынын дәлелдесек
жеткілікті.
нүктелерінің ең
болмағанда бір жұбы табылатынын дәлелдесек
жеткілікті.
 интервалына тиісті
болатын
интервалына тиісті
болатын
 және
және 
элементтері
бар  және
және
 нүктелерінің екі
тізбегін қарастырайық.
нүктелерінің екі
тізбегін қарастырайық.
Бұл екі тізбек және олардың
айырымы шексіз аз болып табылады. Сондықтан кез келген
аз  үшін
үшін
 болатындай п
нөмірі табылады. Сонымен
қатар п-нің кез келген нөмірі
үшін
болатындай п
нөмірі табылады. Сонымен
қатар п-нің кез келген нөмірі
үшін

болады.
Сондықтан  және аз
және аз
 үшін
үшін  интервалынан
интервалынан  болғанымен
болғанымен  болатындай
болатындай  және
және
 нүктелерінің жұбы
табылады, бұл ұйғарым берілген функцияның
нүктелерінің жұбы
табылады, бұл ұйғарым берілген функцияның
 интервалында біртекті
үздіксіз болмайтынын көрсетеді.
интервалында біртекті
үздіксіз болмайтынын көрсетеді.
Осы
 функциясын
функциясын  интервалында
емес,
интервалында
емес,  интервалында қарастыратын
болсақ, онда жоғарыда келтірілген ұйғарымдар бұл жерде
орындалмайтынын айта кетейік, мұндағы
γ
–
интервалында қарастыратын
болсақ, онда жоғарыда келтірілген ұйғарымдар бұл жерде
орындалмайтынын айта кетейік, мұндағы
γ
–
 интервалының кез келген
саны. Бұл факт кездейсоқ емес, себебі төменде осы
функцияның
интервалының кез келген
саны. Бұл факт кездейсоқ емес, себебі төменде осы
функцияның  болғандағы
болғандағы  интервалында біртекті үздіксіз
екенін көрсетеміз. [35]
интервалында біртекті үздіксіз
екенін көрсетеміз. [35]
-
 функциясы
функциясы  жартытүзуінде біртекті
үздіксіз болмайтынына көз жеткізейік.
жартытүзуінде біртекті
үздіксіз болмайтынына көз жеткізейік.
 жартытүзуінің кез
келген
жартытүзуінің кез
келген  және
және
 екі нүктесі
үшін
екі нүктесі
үшін

теңсіздігі орындалатынын ескере кетейік.
Енді қандай да
бір  үшін ғана емес, сондай-ақ кез
келген
үшін ғана емес, сондай-ақ кез
келген  үшін де және кез келген
аз
үшін де және кез келген
аз  үшін де
үшін де
 жартытүзуінен
жартытүзуінен
 бірақ
бірақ 
болатындай  және
және
 нүктелер жұбы табылады
(Бұл ұйғарым
нүктелер жұбы табылады
(Бұл ұйғарым  функциясының қарастырылған
жартытүзуде біртекті үздіксіздік қасиетінің жоқтығын
білдіреді).
функциясының қарастырылған
жартытүзуде біртекті үздіксіздік қасиетінің жоқтығын
білдіреді).
Кез
келген  және
және
 сандарын
нақтылап,
сандарын
нақтылап,  ретінде бірден үлкен
және
ретінде бірден үлкен
және  болатын кез келген санды
алып,
болатын кез келген санды
алып,  деп пайымдайық.
Мұндай
деп пайымдайық.
Мұндай  және
және
 үшін
үшін  теңсіздігі орындалады. Басқа
жағынан, осы
теңсіздігі орындалады. Басқа
жағынан, осы  және
және
 үшін
үшін  теңсіздігіне
сәйкес
теңсіздігіне
сәйкес

басқа теңсіздігі де орындалады.
Осы
 функциясын
функциясын  жартытүзуінде емес, кез
келген
жартытүзуінде емес, кез
келген  сегментінде қарастыратын
болсақ, онда жоғарыда келтірілген ұйғарымдар бұл жерде
орындалмайтынын айта кетейік, мұндағы
b
– кез келген сан.
[36]
сегментінде қарастыратын
болсақ, онда жоғарыда келтірілген ұйғарымдар бұл жерде
орындалмайтынын айта кетейік, мұндағы
b
– кез келген сан.
[36]
Бұл факт төмендегі фундаменталь теоремаға сәйкес түсінікті болып шығады.
6-Негізгі
теорема. Егер  функциясы
функциясы  сегментінде үздіксіз болса,
онда функция осы сегментте біртекті үздіксіз де
болады.
сегментінде үздіксіз болса,
онда функция осы сегментте біртекті үздіксіз де
болады.
Дәлелдеу.  функциясы
функциясы
 сегментінде үздіксіз,
бірақ бұл сегментте біртекті үздіксіз емес деп
болжайық.
сегментінде үздіксіз,
бірақ бұл сегментте біртекті үздіксіз емес деп
болжайық.
Онда қандай да
бір  және кез келген
аз
және кез келген
аз  үшін
үшін
 сегментінің
сегментінің
 бірақ
бірақ 
болатындай  және
және
 нүктелері табылады. Оң
таңбалы
нүктелері табылады. Оң
таңбалы  сандарынан құралған шексіз аз
тізбекті алайық. Берілген
сандарынан құралған шексіз аз
тізбекті алайық. Берілген  үшін және кез
келген п
нөмірі
үшін
үшін және кез
келген п
нөмірі
үшін
 бірақ
бірақ 
болатындай  сегментінің
сегментінің  және
және
 екі нүктесі
табылады.
екі нүктесі
табылады.  тізбегі
тізбегі
 сегментінің нүктелерінен
құралатындықтан, онда ол шектелген болады және оның
ішінен
сегментінің нүктелерінен
құралатындықтан, онда ол шектелген болады және оның
ішінен  ішкі тізбегін шығарып алуға
болады. Берілген тізбектің ξ
шегі де
ішкі тізбегін шығарып алуға
болады. Берілген тізбектің ξ
шегі де
 сегментіне тиісті
болады.
сегментіне тиісті
болады.  теңсіздігіне
сәйкес
теңсіздігіне
сәйкес  ішкі тізбегі де дәл
осы ξ
нүктесіне
шоғырланады.
ішкі тізбегі де дәл
осы ξ
нүктесіне
шоғырланады.
 функциясы
функциясы  сегментінің әрбір нүктесінде
үздіксіз болғандықтан, ол ξ
нүктесінде де үздіксіз болады.
Бірақ онда функцияның сәйкес мәндерінің
сегментінің әрбір нүктесінде
үздіксіз болғандықтан, ол ξ
нүктесінде де үздіксіз болады.
Бірақ онда функцияның сәйкес мәндерінің
 және
және  екі ішкі тізбегі
де
екі ішкі тізбегі
де  айналасына шоғырлануы тиіс,
яғни көрсетілген ішкі тізбектерінің
айналасына шоғырлануы тиіс,
яғни көрсетілген ішкі тізбектерінің  айырымы шексіз аз болу керек.
Бұл ұйғарым барлық п
нөмірлеріне және
барлық
айырымы шексіз аз болу керек.
Бұл ұйғарым барлық п
нөмірлеріне және
барлық  нөмірлері үшін
орындалатын
нөмірлері үшін
орындалатын  теңсіздігіне қарама-қайшы
болады.
теңсіздігіне қарама-қайшы
болады.
Алынған қарама-қайшылық біз
пайымдап алған  сегментінде үздіксіз болатын
функция осы сегментте біртекті үздіксіз болмайды деген пікірдің
қате екенін көрсетеді. Теорема дәлелденді.
[37]
сегментінде үздіксіз болатын
функция осы сегментте біртекті үздіксіз болмайды деген пікірдің
қате екенін көрсетеді. Теорема дәлелденді.
[37]
Енді жоғарыда келтірілген
2-мысалға қайта оралып,  функциясы
функциясы
 интервалының кез
келген γ
саны үшін
интервалының кез
келген γ
саны үшін
 интервалында біртекті
үздіксіз екенін көрсетейік. Расында да, кез
келген γ
үшін ,
интервалында біртекті
үздіксіз екенін көрсетейік. Расында да, кез
келген γ
үшін ,
 функциясы
функциясы  сегментінде үздіксіз болады.
Демек, 6-теоремаға сәйкес
сегментінде үздіксіз болады.
Демек, 6-теоремаға сәйкес  функциясы
функциясы
 сегментінде біртекті
үздіксіз болады. Біртекті үздіксіздік анықтамасының 7-ескертуіне
сәйкес
сегментінде біртекті
үздіксіз болады. Біртекті үздіксіздік анықтамасының 7-ескертуіне
сәйкес  функциясы
функциясы
 сегментінің ішкі жиыны
болып табылатын
сегментінің ішкі жиыны
болып табылатын  интервалында біртекті үздіксіз
болады.
интервалында біртекті үздіксіз
болады.
6-теореманы берілген сегменттегі функцияның тербелісі терминдері арқылы басқа жазу ыңғайлы.
 функциясы
берілген
функциясы
берілген  сегментінде шектелген
болсын.
сегментінде шектелген
болсын.  функциясының
функциясының  сегментіндегі тербелісі
деп
сегментіндегі тербелісі
деп  функциясының осы
сегменттегі дәл жоғарғы шекарасы мен дәл төменгі шекарасы
арасындағы
функциясының осы
сегменттегі дәл жоғарғы шекарасы мен дәл төменгі шекарасы
арасындағы  айырымын
атайық.
айырымын
атайық.
 сегментінде
үздіксіз
сегментінде
үздіксіз  функциясы үшін тербеліс мәні
осы функцияның берілген сегменттегі максималды және минималды
мәндерінің айырымына тең. [38]
функциясы үшін тербеліс мәні
осы функцияның берілген сегменттегі максималды және минималды
мәндерінің айырымына тең. [38]
6-теоремадан тікелей келесі ұйғарымдар шығады:
6-теореманың
салдары. Егер  функциясы үздіксіз болса, онда кез
келген оң таңбалы ɛ саны үшін өзіне сәйкес келетін
және
функциясы үздіксіз болса, онда кез
келген оң таңбалы ɛ саны үшін өзіне сәйкес келетін
және  сегментіндегі ұзындығы δ
санынан кіші болатын ішкі
сегменттегі
сегментіндегі ұзындығы δ
санынан кіші болатын ішкі
сегменттегі функциясының тербелісі ɛ
санынан аз болатындай оң δ саны
табылады.
функциясының тербелісі ɛ
санынан аз болатындай оң δ саны
табылады.
8-ескерту. 4-теорема мен 5-теорема және
6-теоремалардың дәлелдеулерін талдай отырып осы үш
теоремадағы  сегментінің орнына төмендегі
шарттарды қанағаттандыратын кез келген
сегментінің орнына төмендегі
шарттарды қанағаттандыратын кез келген
 жиынын алуға болатынын
көруге болады: 1) бұл
жиынын алуға болатынын
көруге болады: 1) бұл  жиыны
шектеулі; 2)
бұл
жиыны
шектеулі; 2)
бұл  жиынының құрамында өзінің
кез келген шекті нүктесі болады
(мұндай
жиынды тұйық деп атауға келісіп
алайық).
жиынының құрамында өзінің
кез келген шекті нүктесі болады
(мұндай
жиынды тұйық деп атауға келісіп
алайық).
Көрсетілген екі шартты
қанағаттандыратын  жиынын
компакт
жиын деп
немесе компакт деп атауға келісейік.
Осылайша, аталған үш теорема сегментте үздіксіз функция үшін ғана
емес, сондай-ақ кез келген компактта үздіксіз функция үшін де дұрыс
болады. [39]
жиынын
компакт
жиын деп
немесе компакт деп атауға келісейік.
Осылайша, аталған үш теорема сегментте үздіксіз функция үшін ғана
емес, сондай-ақ кез келген компактта үздіксіз функция үшін де дұрыс
болады. [39]
2.9. Функцияның үздіксіздік модулі ұғымы
Айталық,
 функциясы әрбір нүктесі
шекті нүктесі болатын қандай да бір
функциясы әрбір нүктесі
шекті нүктесі болатын қандай да бір  жиынында анықталған және
үздіксіз болсын.
жиынында анықталған және
үздіксіз болсын.
4-анықтама. Кез
келген  үшін
үшін  жиынындағы
жиынындағы  функциясының үздіксіздік
модулі деп
функциясының үздіксіздік
модулі деп  жиынына тиісті
және
жиынына тиісті
және  теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық  және
және  нүктелерінің
нүктелерінің  айырым модулінің дәл
жоғарғы шекарасын атаймыз.
айырым модулінің дәл
жоғарғы шекарасын атаймыз.
Көрсетілген дәл жоғарғы шекараны белгілеу үшін әдетте төмендегі символды қолданады:
 .
.
 жиынындағы
жиынындағы  функциясының үздіксіздік
модулінің өзін
функциясының үздіксіздік
модулінің өзін  символымен
белгілейді.
символымен
белгілейді.
Осылайша, анықтама бойынша

9-ескерту.  үздіксіздік модулінің
анықтамасындағы соңғы теңсіздіктің оң
жағындағы
үздіксіздік модулінің
анықтамасындағы соңғы теңсіздіктің оң
жағындағы  орнына модуль белгісін алып
тастап,
орнына модуль белгісін алып
тастап,  айырымын жазуға болар еді. Бұл
ұйғарым
айырымын жазуға болар еді. Бұл
ұйғарым  және
және
 нүктелерін орнымен
ауыстырып қоюға болады деген ұйғарымнан шығады (бұл
жерде
нүктелерін орнымен
ауыстырып қоюға болады деген ұйғарымнан шығады (бұл
жерде  айырымының таңбасы
қарама-қарсы таңбаға өзгереді, ал
айырымының таңбасы
қарама-қарсы таңбаға өзгереді, ал  шамасы
өзгермейді).
шамасы
өзгермейді).
 үздіксіздік модулінің
екі қасиетін келтірейік:
үздіксіздік модулінің
екі қасиетін келтірейік:
1º.
 үздіксіздік модулі
ылғи да теріс емес:
үздіксіздік модулі
ылғи да теріс емес:  .
.
Бұл қасиет үздіксіздік модулінен тікелей шығады.
2º.
 үздіксіздік
модулі
үздіксіздік
модулі  жартытүзуінде кемімейтін δ
функциясын құрайды.
жартытүзуінде кемімейтін δ
функциясын құрайды.
Расында да, δ кеміген кезде анықтамадағы супремум алынатын жиын сығылады, ал жиынның бөлігіндегі супремум түгел жиындағы супремумнен артық болмайды. [40]
Кейбір функциялардың үздіксіздік модулін есептейік.
-
 функциясының
функциясының  сегментіндегі үздіксіздік
модулін есептейік.
сегментіндегі үздіксіздік
модулін есептейік.  және
және
 нүктелері
–
нүктелері
–  болатындай
болатындай  сегментінің кез келген
нүктелері болсын, мұндағы
сегментінің кез келген
нүктелері болсын, мұндағы  .
Онда
.
Онда

болатыны көрініп тұр. Үздіксіздік модулінің анықтамасына қатысты ескертуді ескере отырып соңғы теңсіздіктен

екенін аламыз. Басқа
жағынан,  болатындай
болатындай  алып,
алып,

аламыз.
Демек,  (егер
(егер
 болса).
болса).
-
Енді
 функциясының
функциясының  интервалындағы үздіксіздік
модулін есептейік.
интервалындағы үздіксіздік
модулін есептейік.

болғандықтан,  болады. Басқа
жағынан,
болады. Басқа
жағынан,  интервалының
нүктелерінен
интервалының
нүктелерінен 
 түріндегі шексіз
аз
түріндегі шексіз
аз  және
және
 екі тізбекті алсақ, кез
келген
екі тізбекті алсақ, кез
келген  үшін
үшін
 және
және  болатындай п
нөмірін белгілей аламыз,
демек,
болатындай п
нөмірін белгілей аламыз,
демек,  және
және

болады.
Бұдан  шығады.
шығады.
-
Ендігі кезекте
 функциясының
функциясының  интервалындағы үздіксіздік
модулін есептейік. Бұл үздіксіздік модулі
интервалындағы үздіксіздік
модулін есептейік. Бұл үздіксіздік модулі
 -ке тең болатынына көз
жеткізейік.
-ке тең болатынына көз
жеткізейік.
Еркін
 нақтылап,
нақтылап,  болатындай
болатындай  қатынастарын
қанағаттандыратын
қатынастарын
қанағаттандыратын  және
және
 нүктелерін қарастырайық.
Бұдан
нүктелерін қарастырайық.
Бұдан

шығады. [41]
Ақырында
 функциясының
ағы үздіксіздік модулінің қасиеті
мен осы функцияның берілген жиындағы үздіксіздік модулінің
шамасының арасындағы байланысты орнататын теореманы
дәлелдейік.
функциясының
ағы үздіксіздік модулінің қасиеті
мен осы функцияның берілген жиындағы үздіксіздік модулінің
шамасының арасындағы байланысты орнататын теореманы
дәлелдейік.
7-теорема.  функциясы
функциясы жиынында біртекті үздіксіз
болуы үшін осы функцияның берілген
жиындағы
жиынында біртекті үздіксіз
болуы үшін осы функцияның берілген
жиындағы  үздіксіздік
модулі
үздіксіздік
модулі

қатынасын қанағаттандыруы қажетті және жеткілікті.
Дәлелдеу. 1)
Қажеттілік.  функциясы
функциясы
 жиынында біртекті
үздіксіз болсын. Теоремада берілген қатынастың дұрыстығын, яғни кез
келген
жиынында біртекті
үздіксіз болсын. Теоремада берілген қатынастың дұрыстығын, яғни кез
келген  үшін оған жауап беретін
және
үшін оған жауап беретін
және  шартын қанағаттандыратын
барлық δ
үшін
шартын қанағаттандыратын
барлық δ
үшін
 теңсіздігі
орындалатын
теңсіздігі
орындалатын  табылатынын дәлелдеу
керек.
табылатынын дәлелдеу
керек.
Біртекті үздіксіздіктің
анықтамасы бойынша кез келген  үшін оған жауап беретін
және
үшін оған жауап беретін
және  жиынында
жиынында
 шартын қанағаттандыратын
барлық
шартын қанағаттандыратын
барлық  және
және
 үшін
үшін  теңсіздігі
орындалатын
теңсіздігі
орындалатын  табылады. Бұл
ұйғарым
табылады. Бұл
ұйғарым  интервалының кез
келген δ
үшін
интервалының кез
келген δ
үшін

теңсіздігі орындалатынын көрсетіп тұр.
2)
Жеткіліктілік. 7-теоремадағы қатынас
орындалсын, яғни кез келген  үшін оған жауап беретін
және
үшін оған жауап беретін
және  шартын қанағаттандыратын
барлық δ
үшін
шартын қанағаттандыратын
барлық δ
үшін
 теңсіздігі
орындалатын
теңсіздігі
орындалатын  табылсын.
табылсын.
Үздіксіздік модулінің
анықтамасы бойынша  жиынында
жиынында
 шартын қанағаттандыратын
барлық
шартын қанағаттандыратын
барлық  және
және
 үшін
үшін  теңсіздігі орындалады, ал бұл
ұйғарым
теңсіздігі орындалады, ал бұл
ұйғарым  функциясының
функциясының  жиынында біртекті үздіксіз
екенін білдіреді. Теорема дәлелденді.
жиынында біртекті үздіксіз
екенін білдіреді. Теорема дәлелденді.
Жоғарыда біз үш функцияның
үздіксіз модулін есептеп шығардық:  сегментіндегі
сегментіндегі  функциясы
және
функциясы
және  интервалындағы
интервалындағы  және
және
 функциялары.
функциялары.
 болғандықтан, онда
7-теоремадан
болғандықтан, онда
7-теоремадан  функциясының
функциясының  сегментінде біртекті үздіксіз
екені, ал
сегментінде біртекті үздіксіз
екені, ал  және
және
 функциялары
функциялары  интервалында біртекті үзілісті
екені шығады. [42]
интервалында біртекті үзілісті
екені шығады. [42]
Қорытынды
Берілген дипломдық жұмыста көрсетілген мәліметтерді баяндауда кванторлар тілі минимумға жеткізіп, олар нақты сөздік түсіндірмелермен алмастырылды. Сонымен қатар жұмыстың өн бойында математикалық пайымдаудың нақты, көркем және логикалық мінсіз тіл қолданылды.
Әрбір бөлім мен бөлімшедегі материал осы бөлім немесе бөлімшені оқып үйренуді нақты түрде аяқтауды қамтамасыз ететіндей түрге жинақталып жазылды.
Дипломдық жұмысты жазудың тілі жеңілден күрделіге қарай дидактикалық принципіне сәйкес қолданылды. Осылайша, функция ұғымы әуелі сандар арқылы және геометриялық фигуралар арқылы баяндалып, мәселен, үшбұрыштың ауданы мен оның үш қабырғасының ұзындықтарының арасындағы байланыс негізінде функция ұғымы енгізіліп, шамалар бір-бірімен қандай да бір физикалық қатынас арқылы байланысатын жағдайлармен жалғасып, мәселені өрбіту күрделене беріп, математикалық анализдегі функция ұғымы толыққанды қарастырылды.
Бұл дипломдық жұмыстың алғашқы бөлімі тәуелсіз айнымалы және функция ұғымымен басталып, функцияның берілу тәсілдері, функциялардың классификациясы, функцияның графигі, кері функциялар, күрделі функциялар, функцияның шегі, үздіксіздік деген бөлімшелерді қамтиды.
Жұмыстың негізгі бөлімі үздіксіздіктің анықтамасынан басталып, үздіксіз функцияларға қолданылатын арифметикалық амалдар, кейбір элементар функциялардың үздіксіздігі туралы баяндалып, жұмыстың өзекті тақырыбы болып саналатын үздіксіз функцияларға қатысты Больцано және Вейерштрасс теоремаларымен жалғасады. Сонымен қатар осы теоремалардың қолданылуы туралы баяндалып, фунцияның біртекті үздіксіздігі және функцияның үздіксіздік модулі ұғымдарына жеке тоқталады.
Дипломдық жұмыста католикалық дін қызметшісі және схоластикалық философияның білгірі, математикалық анализге қазіргі заманғы қатаңдық ұғымын енгізгендердің бірі болып саналатын, «Paradoxien des Unendlichen» атты керемет кітабында үздіксіз функцияларға қатысты көптеген қарапайым мәліметтер дәлелденуі керек деген пікір білдірген Бернард Больцаноның теоремасы дәлелденіп, бұл теореманың геометриялық және бір механикалық мәселеге қолданылуы туралы баяндалады. Сонымен қатар Вейерштрасстың экстремалдық мәндер туралы теоремалары да келтіріліп, жан-жақты дәлелденді. Больцано мен Вейерштрасс теоремаларының дәлелдеуі конструктивтік түрге келтірілмейтіндігі, олар нөлдік нүктенің орналасуын немесе үрдістердің соңында алынатын дәлдіктің дәрежесі алдын ала анықталған функцияның ең үлкен және ең кіші мәнін табудың «тиімді» әдісін көрсетпейтіні, олар тек қана аталған мәндердің барын немесе жоқтығын теріске шығарып дәлелдейтіні аталып кетті.
Бұл жұмыста жинақталған материал мұғалімнің басқаруымен немесе өз бетімен функция ұғымы және үздіксіз функцияның қасиеттері туралы толыққанды оқып-үйренуге немесе білімді тереңдетуге ниеттеніп жүрген жоғары сынып оқушыларына, сондай-ақ әр түрлі мамандыққа даярлайтын факультеттердің студенттеріне, механиктер, физиктер және инженер-зерттеушілерге үздіксіз функциялар туралы анықтамалық ретінде қолдануға мүмкіндік береді.
Пайдаланылған әдебиеттер тізімі
-
Клини С.К., Введение в математику, М.: ИЛ, 1957.
-
Фихтенгольц Г.М., Основы математического анализа. Том 1. Наука, 1968.
-
Архипов Г.И., Садовничий В.А., Чубариков В.Н., Лекции по математическому анализу : учеб. для вузов, Дрофа, 2004.
-
Зорич В. А., Математический анализ. Часть I. М.: МЦНМО, 2002.
-
Камынин Л.И., Курс математического анализа. Том 1. М.: Изд-во МГУ, 2001.
-
Никольский С.М., Курс математического анализа., М.: Физматлит, 2001.
-
Кудрявцев Л.Д., Курс математического анализа (в двух томах), Том 1. М.: Высшая школа, 1981.
-
Бермант А.Ф., Курс математического анализа, Часть I. М.: Физматлит, 1959.
-
Берс Л., Математический анализ (в двух томах). Том 1. М.: Высшая Школа, 1975.
-
Франклин Ф., Математический анализ (в двух томах). Том 1. Иностранная Литература, 1950.
-
Кириллов А.А., Пределы. М.: Наука, 1968.
-
Гусак Г.М., Гусак Е.А., Функции и пределы, Минск: Вышэйш. Шк.,1987.
-
Валле-Пуссен Ш.-Ж., Курс анализа бесконечно малых, Том 1. 1922.
-
Рудин У., Основы математического анализа. М.: Мир, 1976.
-
Ландау Э., Основы анализа. Иностранная литература, 1947.
-
Немыцкий В., Слудская М., Черкасов А., Курс математического анализа. Изд. 3-е. ГИТТЛ, 1957.
-
Дороговцев А.Я., Математический анализ. Краткий курс в современном изложении (2-е издание). Киев: Факт, 2004.
-
Крейн С.Г., Ушакова В.Н., Математический анализ элементарных функций. Физматгиз, 1963.
-
Р.Курант, Г.Роббинс, Что такое математика? М.:МЦНМО, 2001.
-
Натанзон С.М., Краткий курс математического анализа. Изд-во МЦНМО, 2004.
-
Зельдович Я.Б., Высшая математика для начинающих и ее приложения к физике. М.: Наука, 1970.
-
Романовский П.И., Общий курс математического анализа в сжатом изложении. Физматгиз, 1962.
-
Фролов Н. А., Курс математического анализа. В 2-х частях. Ч. 1 - 1964 г.
-
Гельфанд И.М., Глаголева Е.Г., Шноль Э.Э., Функции и графики. М.: МЦНМО, 2001.
-
Ильин В.А., Куркина А.В., Высшая математика, М.: ООО «ТК Велби», 2002.
-
Шипачев В.С., Высшая математика: Учеб. для вузов. М.: Высшая школа, 2005.
-
Ильин В.А., Садовничий В.А., Сендов Бл.Х., Математический анализ, М.: изд-во МГУ, 1985.
-
Шведов И.А., Компактный курс математического анализа, ч. 1. Функции одной переменной: Учеб. пособие/ Новосиб. гос. ун-т. Ново- сибирск, 2001.
-
Понтрягин Л.С., Математический анализ для школьников. М.: Наука, 1988.
-
Морозова В.Д., Введение в анализ: Учебник для вузов / Под ред. В.С.Зарубина, А.П.Крищенко – М.: Изд-во МГТУ им. Н.Э.Баумана, 1996.
-
Уваров В.Б., Математический анализ: учеб. пособ. для вузов. М.: Высшая школа, 1984.
-
Шварц Л., Анализ / Пер. с франц. под ред. С.Г.Крейна: Том 1. М.: Мир, 1972.
-
Клейн Ф., Элементарная математика с точки зрения высшей. Том 1. Арифметика. Алгебра. Анализ / Пер. с нем. под ред. В.Г.Болтянского. М.: Наука, 1987.
-
Уиттекер Э.Т., Ватсон Дж.Н., Курс современного анализа. Часть 1. Основные операции анализа. М.: Физматлит, 1963.
-
Тарасов Л.В., Математический анализ: Беседы об основных понятиях. М.: Просвещение, 1979.
-
Шилов Г.Е., Математический анализ: специальный курс, М.: изд-во физико-математической литературы, 1961.
-
Смирнов В.И., Курс высшей математики, Том 1. М.: Наука, 1974.
-
Выгодский М.Я., Справочник по высшей математике. М.: Наука, 1977.
-
Дьедонне Ж., Основы современного анализа. М.: Мир, 1964.
-
Мышкис А.Д., Лекции по высшей математике, М.: Наука, 1973.
-
Свиридюк Г.А., Федоров В.Е., Математический анализ. Часть 1. Челябинск: ЧелГУ, 1999.
-
Толстов Г.П., Элементы математического анализа. Том 1. М.: Наука, 1974.

шағым қалдыра аласыз















