Мазмұны
1. Теңсіздіктің теориялық аспектілері 5
1.2. Теңсіздіктер туралы ілімнің негізгі аксиомалары 7
1.3. Теріс көбейткіштері бар көбейтінділер 11
2. Математиканың негізгі теңсіздіктері 12
2.3. Анализ және Лагранжтың көбейткіштері 18
2.4. Функционалдық теңдеулер 19
2.5. Мажорлау – Бордың дәлелдеуі 21
2.8.  орталары және
орталары және  қосындылары 24
қосындылары 24
2.9. Классикалық теңсіздіктерді жалпылау 27
2.13. Минковский–Малер теңсіздігі 44
2.16. Карамат теңсіздігінің дәлелдеуі 46
2.17. Островский теңсіздігі 47
2.19. Симметриялы функциялар 48
2.21. Уайтлидің кейбір қорытындылары 51
2.22. Гиперболалық көпмүшелер 52
2.24. Гиперболалық көпмүшелердің мысалдары 54
2.28. Фавар–Бервальд жалпыламасы 61
2.29. Коши теоремасының басқа түрлері 63
2.30. Коши–Буняковский–Шварц теңсіздіктерін нақтылау 64
2.31. Ескі теңсіздіктен жаңа теңсіздіктерді шығару 65
2.32. Стеффенсен теңсіздігі 67
Қорытынды 70
Кіріспе
Теңсіздіктер қазіргі заманғы математиканың көптеген бөлімдерінде фундаменталды рөлге ие, теңсіздіктерсіз физика да, математикалық статистика да, экономика да әрекет ете алмайды. Алайда қазіргі кезде жалпы «теңсіздіктер теориясына» қатысты жақсы ұйымдастырылып жазылған жұмыс жоқ, бірақ теңсіздіктердің жекелеген бөлімдерін анықтау үшін шағын теория жасалды.
Қай түрде болса да теңсіздіктер математиканың классикалық бөлімдерінде де (геометрия, дифференциал және интегралды есептеулерде, сандар теориясында), қазіргі заманғы бөлімдерінде де (автоматтар теориясы, кодтау теориясы) кездеседі.
Өкінішке орай мектептегі математиканың негізгі курсында классикалық теңсіздіктер деп аталатын нағыз математикалық байлық туралы ештеңе айтылмайды. Екі теріс емес нақты сандардың арифметикалық және геометриялық орталары арасындағы қатынасты ғана мектеп оқулықтарының беттерінен табуға болады.
Қандай да бір нәтижеге алғашқы болып жеткен ғалымдарды атап, олардың еңбегін елеп кету керек. Алайда нәтижелердің көбісі геометрияның, астрономияның немесе физиканың қандай да бір жұмысының кейбір көмекші құралы ретінде пайда болып қолданып, бірнеше жылдан кейін қайтадан жаңалық ретінде ашылды. Бұл жағдайдың салдары ретінде көптеген тамаша теңсіздіктердің аттарының сақталмауын алуға болады. Әр түрлі елдерде және әр түрлі математика мектептерінде бір теңсіздікті әр түрлі атайды және оның ашылуын әр түрлі математик ғалымдарға жазып қояды, алайда көп жағдайда бұл теңсіздік одан да жалпылама болатын теңсіздіктің дербес жағдайы болып шығады.
Көптеген нәтижелердің авторсыз
қалуының басқа да себебі бар. Мысалы, кез келген нақты санның
квадраты қашанда теріс емес, яғни кез келген
нақты a
және
b
сандары
үшін  қатынасы орындалады,
яғни
қатынасы орындалады,
яғни  , бұдан кез келген нақты теріс
емес
, бұдан кез келген нақты теріс
емес  және
және
 сандары үшін әйгілі
«мектептік» арифметикалық
сандары үшін әйгілі
«мектептік» арифметикалық  ортасы мен
геометриялық
ортасы мен
геометриялық  ортасы
арасындағы
ортасы
арасындағы  қатынасы шығады деген
фундаменталды фактын алғаш ашқан ғалымды қалай табуға
болады.
қатынасы шығады деген
фундаменталды фактын алғаш ашқан ғалымды қалай табуға
болады.
Алайда, бұл дипломдық жұмыста көптеген теңсіздіктердің авторларын атап, олардың атымен аталған теңсіздіктердің түрлері қарастырылады.
Берілген тақырыптың өзектілігі – классикалық теңсіздіктерді қолданбай шешуін табу қиын немесе шешуі мүлдем шықпайтын есептер оқушыларға арналған математикалық олимпиадаларда жиі кездеседі, сондықтан қандай да бір математикалық сайысқа қатысатын оқушыға аса танымал және жиі қолданылатын тамаша теңсіздіктерді білу қажет. Көптеген математикалық олимпиадаларда айнымалысы бар теңсіздіктерді дәлелдеу тапсырмалары жиі кездеседі. Осы тапсырмаларды шешу жолы көбіне жалпыға танымал (бірақ мектеп математика курсында қарастырылмайтын) фактілерге сүйенеді немесе бұл есептерді шешу тәсілі мектеп математика курсында берілген материал көлемінен шықпайтын қарапайым пайымдаулардың қатарына сүйенеді, бірақ осы элементар пайымдаулардың қатарын құрудың логикасы мен идеясы мектеп математика курсының әдістер мен тәсілдерінің шегінен шығып кетеді.
Берілген дипломдық жұмыстың зерттеу объектісі – «Математиканың негізгі теңсіздіктері» тақырыбын оқып үйрену арқылы мектеп математика курсынан алған теңсіздіктер ұғымын кеңейтілуі.
Зерттеу пәні – математиканың негізгі теңсіздіктерінің топталуы.
Мақсаты – математикалық олимпиадаларға қатысатын оқушылардың мектеп математика курсынан белгілі теңсіздіктер туралы білімді кеңейту.
Міндеттер:
-
теңсіздік туралы жалпы мағлұмат алу;
-
берілген тақырыпты кеңейту;
-
математикалық олимпиадаларға қатысатын оқушыларға көмек көрсету.
Зерттеу әдістері:
-
ғылыми, оқу әдебиеттерді талдау;
-
теориялық материалды жинақтау және жүйелеу;
-
әдістемелік жоспарларды жинақтау.
Берілген жұмыстың құрамы:
-
Теңсіздіктер туралы жалпы мәлімет.
-
Математиканың негізгі теңсіздіктерін жалпылау, талдау.
Жұмыстың тәжірибелік маңыздылығы – жинақталған материал мұғалімнің басқаруымен немесе өз бетімен кейбір классикалық теңсіздіктермен танысқысы келетін жоғары сынып оқушылары мен ЖОО студенттеріне математиканың негізгі теңсіздіктерін оқып үйрену үрдісінде пайдалы болады.
1. Теңсіздіктің теориялық аспектілері
1.1. «Артық» қатынасы
« > » белгісі «артық» деген
мағынаны білдіретінін еске түсірейік. Онда біз мына сұраққа жауап
бере аламыз:  екені дұрыс па? Әрине,
дұрыс.
екені дұрыс па? Әрине,
дұрыс.
Бірақ
 екені дұрыс па? Бұл
жағдайда –3 саны –2 санына қарағанда «артық теріс сан» деп айтуға
болады. бірақ бұл ұйғарым берілген сұрақтың жауабы болмайды. Егер
нақты сандар (оң және теріс, рационал және иррационал сандар,
сондай-ақ нөл) 1-суретте көрсетілгендей, геометриялық әдіс арқылы
оңға бағытталған сан осіндегі нүктелер түрінде белгіленген болса,
онда сан осінде солдан оңға қарай қозғалу барысында сандар өсу
ретімен шыға береді. –2 санын бейнелейтін нүкте –3 санын
бейнелейтін нүктенің оң жағында орналасады;
сондықтан
екені дұрыс па? Бұл
жағдайда –3 саны –2 санына қарағанда «артық теріс сан» деп айтуға
болады. бірақ бұл ұйғарым берілген сұрақтың жауабы болмайды. Егер
нақты сандар (оң және теріс, рационал және иррационал сандар,
сондай-ақ нөл) 1-суретте көрсетілгендей, геометриялық әдіс арқылы
оңға бағытталған сан осіндегі нүктелер түрінде белгіленген болса,
онда сан осінде солдан оңға қарай қозғалу барысында сандар өсу
ретімен шыға береді. –2 санын бейнелейтін нүкте –3 санын
бейнелейтін нүктенің оң жағында орналасады;
сондықтан  деп есептеу керек. Дәл
осылай,
деп есептеу керек. Дәл
осылай,
 (1.1.1)
(1.1.1)

1-сурет
Осылайша, теңсіздікті анықтайтын төмендегідей геометриялық ереже аламыз:
a және b – оңнан соңға
бағытталған сан осінде нүктелер арқылы белгіленген қандай да бір
нақты сандар болсын. Онда  болады сонда және тек қана
сонда, егер а санын бейнелейтін нүкте b санын бейнелейтін нүктенің
оң жағында жатса.
болады сонда және тек қана
сонда, егер а санын бейнелейтін нүкте b санын бейнелейтін нүктенің
оң жағында жатса.
Сондықтан
 немесе
немесе  деп айтсақ, ол жоғарыда
берілген ережеге қарсы болар еді, яғни дұрыс болмас еді
[1].
деп айтсақ, ол жоғарыда
берілген ережеге қарсы болар еді, яғни дұрыс болмас еді
[1].
Теңсіздіктермен жұмыстану барысында көп жағдайда графикалық түрде емес, алгебралық түрде әрекет ету керек. Егер негізгі ұғым ретінде оң сан ұғымын алатын болсақ, онда жоғарыда көрсетілген геометриялық ережені төмендегідей алгебралық ережемен алмастыруға болады:
Анықтама. a және b – қандай да бір
нақты сандар болсын. Онда  болады сонда және тек қана
сонда, егер
болады сонда және тек қана
сонда, егер  оң
болса.
оң
болса.
Яғни егер
 ,
ал
,
ал  болса,
онда
болса,
онда  айырмасы оң болады. Сондықтан
жоғарыда қарастырылған геометриялық ұйғарым
бойынша
айырмасы оң болады. Сондықтан
жоғарыда қарастырылған геометриялық ұйғарым
бойынша  болады.
(1.1.1) теңсіздіктерді сандардың
айырмасын табуға негізделген осы алгебралық әдіс арқылы тексеруге
болады, сондай-ақ төмендегі теңсіздіктерді геометриялық та,
алгебралық та әдістер арқылы нақтылауға
болады:
болады.
(1.1.1) теңсіздіктерді сандардың
айырмасын табуға негізделген осы алгебралық әдіс арқылы тексеруге
болады, сондай-ақ төмендегі теңсіздіктерді геометриялық та,
алгебралық та әдістер арқылы нақтылауға
болады:
 .
.
Жоғарыда
 теңсіздігін оң сан ұғымы
арқылы анықтадық. Барлық Р
оң сандар жиыны және оған
сәйкес барлық N
теріс сандар жиыны және жалғыз
ғана 0 саны бар О
жиыны теңсіздіктерді оқып
үйренуде үлкен рөл ойнайды. Расында да, нақты сандар жиынының
жалпыға таныс коммутативтік, ассоциативтік және дистрибутивтік
қасиеттері секілді алгебралық қасиеттерін пайдалана отырып мынадай
қорытындыға келеміз: нақты сандар жиынында
орындалатын реттіліктің қатынастарының негізі ретінде Р оң сандар
жиынына қатысты болатын екі аксиома
алынады. Бұл аксиомалар келесі
бөлімшеде беріледі.
теңсіздігін оң сан ұғымы
арқылы анықтадық. Барлық Р
оң сандар жиыны және оған
сәйкес барлық N
теріс сандар жиыны және жалғыз
ғана 0 саны бар О
жиыны теңсіздіктерді оқып
үйренуде үлкен рөл ойнайды. Расында да, нақты сандар жиынының
жалпыға таныс коммутативтік, ассоциативтік және дистрибутивтік
қасиеттері секілді алгебралық қасиеттерін пайдалана отырып мынадай
қорытындыға келеміз: нақты сандар жиынында
орындалатын реттіліктің қатынастарының негізі ретінде Р оң сандар
жиынына қатысты болатын екі аксиома
алынады. Бұл аксиомалар келесі
бөлімшеде беріледі.
«а оң саны» ұйғарымын
символдық түрде « » деп жазады, бұл жазу
«Р
жиынының
а
элементі» немесе
«а
Р
жиынына тиісті» деп оқылады.
Осылайша,
» деп жазады, бұл жазу
«Р
жиынының
а
элементі» немесе
«а
Р
жиынына тиісті» деп оқылады.
Осылайша,  .
.
P, N, O жиындары және олардың элементтері жөнінде сөз қозғайық.
Нөл саны әрине О жиынының жалғыз 0 элементі болып табылады; оның кез келген нақты а саны үшін орындалатын

қасиеті бар.
N
теріс сандар жиынына көше
отырып, теріс сан ұғымы қарама-қарсы саны ұғымынан өзгеше екенін
ескерте кетейік. а
санына қарама-қарсы сан
төмендегі теңдікті қанағаттандырады және
 деп
анықталады
деп
анықталады

Яғни егер
 болса, онда
қарама-қарсы а
саны
болса, онда
қарама-қарсы а
саны
 болады,
себебі
болады,
себебі  Дәл осылай,
егер
Дәл осылай,
егер  болса,
онда
болса,
онда  , себебі
, себебі

Теріс
сан оң санға қарама-қарсы сан
ретінде анықталады. Осылайша  сандары
Р
оң сандар жиынының элементтері
екенін білеміз; сондықтан
сандары
Р
оң сандар жиынының элементтері
екенін білеміз; сондықтан  сандары
N
теріс сандар жиынының
элементтері болады [2].
сандары
N
теріс сандар жиынының
элементтері болады [2].
Негізгі ұғым – оң сан ұғымын анықтамай-ақ екі негізгі аксиома негізінде осы сандардың сипаттамасына көшейік.
Енді І және ІІ Аксиомалардың күшіне көзімізді жеткізейік. Бұл аксиомалар арқылы нөлге тең емес нақты сандардың қайсысы Р оң сандар жиынына тиісті екенін және қайсысы N теріс сандар жиынына тиісті екенін білуге болады.
Оны көрсету үшін сәйкес сандардың сипаттамасы туралы ақпарат бізге алдын ала белгілі болмай, аксиомалардан алынды деген мағынаны білдіретіндей етіп «оң» және «теріс» сөздерін тырнақшаға алып жазамыз.
 санынан
бастайық.
санынан
бастайық.  болғандықтан,
болғандықтан,  екені шығады.
Осылайша,
екені шығады.
Осылайша,  «оң» болады.
Бірақ
«оң» болады.
Бірақ

яғни 1 – «оң» сан.
Ары қарай
 . 1 – «оң» сан екенін
жаңа анықтағандықтан және
. 1 – «оң» сан екенін
жаңа анықтағандықтан және 
болатындықтан, онда екі «оң» санның қосындысы «оң» сан болатынын
көрсеткен ІІ Аксиомаға сәйкес 2 – «оң» сан
болады.
Енді
 болсын.
Онда
болсын.
Онда  болады; осылайша, «оң» 2
санының және a
санының көбейтіндісі – «оң» 1
саны болады. Бірақ егер а
«теріс» сан болған болса, онда
2 мен а-ның көбейтіндісі «теріс»
болар еді. Сондықтан
болады; осылайша, «оң» 2
санының және a
санының көбейтіндісі – «оң» 1
саны болады. Бірақ егер а
«теріс» сан болған болса, онда
2 мен а-ның көбейтіндісі «теріс»
болар еді. Сондықтан  «оң» болу
керек.
«оң» болу
керек.
Осылайша,
 сандары «оң» болады және
сәйкесінше 1-кестеге сәйкес
сандары «оң» болады және
сәйкесінше 1-кестеге сәйкес  сандары «теріс»
болады.
сандары «теріс»
болады.
Жалғастыра отырып 3, 4 және
т.б. бүтін сандар,  және т.б. бөлшектер
және
және т.б. бөлшектер
және  және т.б. бөлшектер «оң»
болатынын және сәйкесінше
және т.б. бөлшектер «оң»
болатынын және сәйкесінше  және т.б. «теріс» болатынын
көрсете аламыз. Яғни нөлге тең емес кез келген рационал санның «оң»
немесе «теріс» болатынын анықтай аламыз.
және т.б. «теріс» болатынын
көрсете аламыз. Яғни нөлге тең емес кез келген рационал санның «оң»
немесе «теріс» болатынын анықтай аламыз.
Иррационал сандарды анықтауда қолданылатын шекті ауысуларды рационал сандардың қайсысы «оң» және қайсысы «теріс» болатын ақпаратқа сүйене отырып нақты сандардың реттелген өрісіне тиісті болатын берілген иррационал санның «оң» немесе «теріс» екенін анықтау үшін пайдалануға болады. Осы жұмыста біз иррационал сандарды қарастырмаймыз.
1.2. Теңсіздіктер туралы ілімнің негізгі аксиомалары
Р оң сандар жиынына қатысты төменде келтірілетін сөйлемдер дәлелденбейді; сондықтан олар аксиомалар деп аталады. Теңсіздіктер теориясы жалғыз ғана осы сөйлемдер негізінде (нақты сандар жиынының алгебралық қасиеттерімен қатар) дамитыны өте қызықты факт екенін байқау керек.
Аксиома
І. Егер а – нақты сан болса,
онда төменде келтірілген ұйғарымдардың ішінен жалғыз және тек қана
жалғыз ұйғарым орындалады:
а – О жиынының жалғыз 0 элементі; а – Р оң сандар жиынының
элементі; – a – Р жиынының элементі.
Аксиома
ІІ. Егер a және b – Р оң сандар
жиынының элементтері болса, онда олардың
 қосындысы және
олардың
қосындысы және
олардың  көбейтіндісі Р жиынының
элементі болады.
көбейтіндісі Р жиынының
элементі болады.
І Аксиомада көрсетілген
бір-бірін өзара жоққа шығаратын мүмкіндіктер кез
келген а
нақты саны мен оған
қарама-қарсы –
a саны арасында төмендегідей
қатынастар орнатады: егер а
нөл болса, онда
да нөл болады;
егер а
оң
сан болса,
онда –
a саны жоғарыда келтірілген
анықтама негізінде теріс сан болады; ал
егер –
a оң
сан болса,
онда  теріс сан анықтамасы
негізінде теріс болу керек. Осылайша,
қарама-қарсы а
және
–
a сандарының
жұбы P,
N және
О
жиындары бойынша 1-кестеде
көрсетілгендей орналасады.
теріс сан анықтамасы
негізінде теріс болу керек. Осылайша,
қарама-қарсы а
және
–
a сандарының
жұбы P,
N және
О
жиындары бойынша 1-кестеде
көрсетілгендей орналасады.
1-кесте. Өзара қарама-қарсы сандар
жұптарын орналастыру
|
Сан |
Жиын |
|
a |
P N O |
|
– a |
N P O |
Сандарды геометриялық түрде кескіндеуде (1-сурет) а және – a сандарын бейнелейтін нүктелер немесе нөл нүктесін бейнелейтін нүктемен беттеседі, немесе бұл нүктенің екі жағында орналасады [3].
І Аксиома
Р
оң сандар жиынына қатысты
болады; басқа жағынан қарағанда  теңсіздігі Р
жиынының терминдері негізінде
анықталған болатын. Енді осы аксиоманы теңсіздіктер тілінде
жазайық.
теңсіздігі Р
жиынының терминдері негізінде
анықталған болатын. Енді осы аксиоманы теңсіздіктер тілінде
жазайық.
Егер
a
және
b
– кез келген нақты сандар
болса, онда олардың  айырымы да нақты сан болады;
сондықтан І Аксиоманы
айырымы да нақты сан болады;
сондықтан І Аксиоманы  айырымына да қолдануға болады.
Осылайша, немесе
айырымына да қолдануға болады.
Осылайша, немесе  (яғни
(яғни
 ),
немесе
),
немесе 
(яғни  ), немесе
), немесе
 (яғни
(яғни  ) және осы үш мүмкіндік
бір-бірін өзара жоққа шығарады. Осылайша, келесі ұйғарым
) және осы үш мүмкіндік
бір-бірін өзара жоққа шығарады. Осылайша, келесі ұйғарым
І Аксиоманың салдары болып табылады:
Аксиома І'. Егер a және b – нақты сандар болса, онда төмендегі қатынастардың жалғыз және жалғыз ғана қатынас орындалады:

 болғандағы арнаулы
жағдайда І' Аксиома егер а
– нақты сан болса, онда
бір-бірін өзара жоққа шығаратын үш жағдайдың жалғыз және жалғыз
жағдайы орындалады деп пайымдайды:
болғандағы арнаулы
жағдайда І' Аксиома егер а
– нақты сан болса, онда
бір-бірін өзара жоққа шығаратын үш жағдайдың жалғыз және жалғыз
жағдайы орындалады деп пайымдайды:  (яғни
(яғни
 );
);
 (яғни
(яғни  );
);
 (яғни
(яғни  ). Яғни І Аксиома І'
Аксиомадан шығарылады.
). Яғни І Аксиома І'
Аксиомадан шығарылады.
Егер S ұйғарымын Т ұйғарымынан шығаруға болатын болса (яғни оның салдары болса), «Т-дан S шығады» деп айтады. І Аксиомадан І' Аксиома шығатынын, сондай-ақ І' Аксиомадан І Аксиома шығатынын көрдік. Егер екі ұйғарымның әрқайсысы екіншісінен шығатын болса, онда олар бір-біріне теңкүшті немесе эквивалентті деп айтады. Осылайша, І және І' Аксиомалар өзара эквивалентті.
І және І' Аксиомаларды
суреттеу үшін  сандарын
қарастырайық.
сандарын
қарастырайық.
І Аксиоманы суреттеу
барысында  екенін ескертейік;
сондай-ақ
екенін ескертейік;
сондай-ақ  («
(« О
жиынының элементі емес» деп
оқылады) және
О
жиынының элементі емес» деп
оқылады) және  және т.б. екенін
ескертейік.
және т.б. екенін
ескертейік.
І' Аксиоманы суреттеу үшін

екенін көрсетеміз.
Осылайша, осы төрт жағдайдың әрқайсысында І' Аксиомадағы үш қатынастың ішінен жалғыз және тек қана жалғыз қатынас орындалатынын көреміз.
 теңсіздігінің
орнына
теңсіздігінің
орнына  деп жаза аламыз және ол
«а
b-дан кем» деп оқылады. Бұл екі
теңсіздік толықтай эквивалентті және олардың ешқайсысының
екіншісінен артықшылығы жоқ. Жоғарыда көрсетілген І' Аксиоманы
суреттеуде мазмұндаудың біртекті болуы үшін барлық жерде «>»
белгісін қолдандық. Бірақ біртектілік мақсатында барлық
жағдайларда а-ны
b-ның алдына жазуға болар еді.
Ол жағдайда
деп жаза аламыз және ол
«а
b-дан кем» деп оқылады. Бұл екі
теңсіздік толықтай эквивалентті және олардың ешқайсысының
екіншісінен артықшылығы жоқ. Жоғарыда көрсетілген І' Аксиоманы
суреттеуде мазмұндаудың біртекті болуы үшін барлық жерде «>»
белгісін қолдандық. Бірақ біртектілік мақсатында барлық
жағдайларда а-ны
b-ның алдына жазуға болар еді.
Ол жағдайда
 (1.2.1)
(1.2.1)
болар еді.
Дәл осылай

« > » және « < » белгілері қатаң теңсіздіктерді өрнектейді.
Теңсіздіктерді оқып үйрену
кезіндегі басқа екі қатынас – қатаң
емес  және
және
 теңсіздіктері, олар
сәйкесінше «а
b-дан кем емес» және
«а
b-дан артық емес» деген
мағынаны білдіреді. Олардың алғашқысы
теңсіздіктері, олар
сәйкесінше «а
b-дан кем емес» және
«а
b-дан артық емес» деген
мағынаны білдіреді. Олардың алғашқысы
 теңсіздігі
немесе
теңсіздігі
немесе  екенін,
немесе
екенін,
немесе  екенін білдіреді;
мысалы,
екенін білдіреді;
мысалы,  және
және
сондай-ақ  болады.
Екіншісі
болады.
Екіншісі  теңсіздігі
немесе
теңсіздігі
немесе  екенін,
немесе
екенін,
немесе  екенін білдіреді;
мысалы,
екенін білдіреді;
мысалы,  және
және
 .
.
(1.2.1) жағдайда І' Аксиомада көрсетілген үш қатынастың біреуі ғана орындалатыны айтылып тұр. Ал аксиома осы қатынастардың ішінен тек қана біреуі орындалатынын айтады. Сондықтан І' Аксиоманы сипаттауды аяқтау үшін келесідей ұйғарымдарды қосуымыз керек:
 (1.2.2)
(1.2.2)
бұл ұйғарымдар
« -ден кем емес және тең емес»
және т.б. мағынаны береді.
-ден кем емес және тең емес»
және т.б. мағынаны береді.
(1.2.2) көрсетілген теріс ұйғарымдар бұл жерде артық екенін көруге болады, расында да оларды (1.2.1) көрсетілген ақпаратты толықтыру үшін жазуды ешкім талап етпейді. Бұл І немесе І' Аксиомалардағы «жалғыз тек қана жалғыз» сөздерімен сипатталатын теңсіздіктердің үйлесімсіздік принципі өз алдына белгілі екендігімен түсіндіріледі.
Осыдан, теңсіздіктердің үйлесімсіздік принципі негізінде (1.2.1) және (1.2.2) бір-біріне жауап беретін қатынастар өзара теңкүшті екені, яғни олардың әрқайсысы екіншісінен шығатыны белгілі болды. Дегенмен, теңсіздікті терістеу көп жағдайда маңызды ұғым болып табылады [4].
Егер сіз « > » және « <
» белгілерін шатастырып алудан қорықсаңыз,
 немесе
немесе  секілді дұрыс теңсіздіктерде
теңсіздік белгісінің кең (ашық) ұшы үлкен санға қарап тұрғанын, ал
тар (ұшталған) ұшы кіші санға қарап тұрғанын байқап
алыңыз.
секілді дұрыс теңсіздіктерде
теңсіздік белгісінің кең (ашық) ұшы үлкен санға қарап тұрғанын, ал
тар (ұшталған) ұшы кіші санға қарап тұрғанын байқап
алыңыз.
Теңсіздіктердің негізгі қасиеттері:
-
Егер
 болса,
онда
болса,
онда  болады; немесе
егер
болады; немесе
егер  болса,
онда
болса,
онда  болады.
болады. -
Егер
 болса,
онда
болса,
онда  ; немесе
егер
; немесе
егер  болса,
онда
болса,
онда  болады.
Яғни теңсіздіктің екі жағына
бірдей санды қосуға (азайтуға) болады.
болады.
Яғни теңсіздіктің екі жағына
бірдей санды қосуға (азайтуға) болады. -
Егер
 және
және  болса,
онда
болса,
онда  болады.
Яғни бірдей
мағыналы (бірдей > немесе <
таңбалы) теңсіздіктерді бір-біріне
мүшелеп қосуға болады. Бірдей мағыналы теңсіздіктерді бір-бірінен
мүшелеп азайтуға болмайтынын ескертейік. Себебі нәтижесі
қате болуы мүмкін.
болады.
Яғни бірдей
мағыналы (бірдей > немесе <
таңбалы) теңсіздіктерді бір-біріне
мүшелеп қосуға болады. Бірдей мағыналы теңсіздіктерді бір-бірінен
мүшелеп азайтуға болмайтынын ескертейік. Себебі нәтижесі
қате болуы мүмкін. -
Егер
 және
және  болса,
онда
болса,
онда  болады. Немесе
егер
болады. Немесе
егер  және
және
 болса,
онда
болса,
онда  болады.
Яғни қарама-қарсы мағыналы
теңсіздіктерді бір-бірінен мүшелеп азайтуға болады және
теңсіздіктің азаятын белгісін алу
керек.
болады.
Яғни қарама-қарсы мағыналы
теңсіздіктерді бір-бірінен мүшелеп азайтуға болады және
теңсіздіктің азаятын белгісін алу
керек. -
Егер
 және
және  болса,
онда
болса,
онда  және
және
 болады.
Яғни теңсіздіктің екі жағын да
бірдей оң таңбалы санға көбейтуге немесе бөлуге болады. Бұл
жағдайда теңсіздік өз таңбасын
сақтайды.
болады.
Яғни теңсіздіктің екі жағын да
бірдей оң таңбалы санға көбейтуге немесе бөлуге болады. Бұл
жағдайда теңсіздік өз таңбасын
сақтайды. -
Егер
 және
және  болса,
онда
болса,
онда  және
және  болады.
Яғни теңсіздіктің екі жағын да
бірдей теріс таңбалы санға көбейтуге немесе бөлуге болады. Бұл
жағдайда теңсіздік өз таңбасын қарама-қарсы таңбаға
ауыстырады [5].
болады.
Яғни теңсіздіктің екі жағын да
бірдей теріс таңбалы санға көбейтуге немесе бөлуге болады. Бұл
жағдайда теңсіздік өз таңбасын қарама-қарсы таңбаға
ауыстырады [5].
1.3. Теріс көбейткіштері бар көбейтінділер
Оң сан мен теріс санның көбейтіндісі сандардың қай түріне жатады? Немесе екі теріс санның көбейтіндісі? Бұл сұрақтарға жауап алу үшін І мен І' Аксиомаларын және олардың кейбір салдарларын қолдануға болады.
Егер
 және
және  болса, онда 1-кестеге
сәйкес
болса, онда 1-кестеге
сәйкес  болады, осыдан ІІ Аксиомаға
сәйкес олардың көбейтіндісі
болады, осыдан ІІ Аксиомаға
сәйкес олардың көбейтіндісі  болады. Бұдан теріс санның
анықтамасына сәйкес
болады. Бұдан теріс санның
анықтамасына сәйкес  болады;
бірақ
болады;
бірақ  болады,
себебі
болады,
себебі

минус таңбасын жақшаның
сыртына шығарудың белгілі ережесі бар.
Сондықтан  . Осылайша, төмендегідей
нәтижеге келдік:
. Осылайша, төмендегідей
нәтижеге келдік:
1-Теорема. Оң а саны мен теріс b санының ab көбейтіндісі теріс сан болады.
Дәл осылай, егер
Егер  және
және
 болса, онда 1-кестеге
сәйкес
болса, онда 1-кестеге
сәйкес  және
және
 болады. Осыдан ІІ
Аксиомаға сәйкес олардың көбейтіндісі
болады. Осыдан ІІ
Аксиомаға сәйкес олардың көбейтіндісі
 болады. Осылайша,
төмендегідей нәтижеге келдік:
болады. Осылайша,
төмендегідей нәтижеге келдік:
2-Теорема. Теріс a мен b екі
санның  көбейтіндісі оң сан
болады.
көбейтіндісі оң сан
болады.
Соңғы нәтиже мен ІІ Аксиома
негізінде нөлден өзге кез келген нақты санның квадраты оң сан
болады деген ұйғарым шығады. Әрине  .
.
Осылайша, теңсіздіктер теориясының ең жеңіл әрі пайдалы нәтиже шығады.
3-Теорема. Кез келген нақты а
саны  теңсіздігін
қанағаттандырады. Теңдік белгісі орындалады сонда тек қана сонда,
егер
теңсіздігін
қанағаттандырады. Теңдік белгісі орындалады сонда тек қана сонда,
егер  болса [3].
болса [3].
Жоғарыда көрсетілген бастапқы мәліметтерді пайдалана отырып математиканың негізгі теңсіздіктерін қарастыруға көшеміз.
2. Математиканың негізгі теңсіздіктері
2.1. Коши теңсіздігі
Кез келген нақты санның
квадратының теріс еместігін өрнектейтін теңсіздік ең негізгі
фундаменталды теңсіздік болып табылады. Бұл ұйғарымды тиімді
пайдалану үшін оны  айырмасына қолданайық,
мұндағы
айырмасына қолданайық,
мұндағы  және
және
 – нақты сандар.
Онда
– нақты сандар.
Онда  теңсіздігі төмендегі ұйғарымға
сай болады:
теңсіздігі төмендегі ұйғарымға
сай болады:
 (2.1.1)
(2.1.1)
Теңдік орындалады сонда және
тек қана сонда, егер  болса. Бұл – арифметикалық
және геометриялық орталарды байланыстыратын теңсіздіктің ең
қарапайым түрі. Ендігі жерде жалпы нәтиже Кошиге сәйкес осы дербес
жағдайға сүйене отырып дәлелденетін
болады.
болса. Бұл – арифметикалық
және геометриялық орталарды байланыстыратын теңсіздіктің ең
қарапайым түрі. Ендігі жерде жалпы нәтиже Кошиге сәйкес осы дербес
жағдайға сүйене отырып дәлелденетін
болады.
Квадраттардың теріс еместігін бұдан да тиімдірек қолдануға болады, ол үшін құрамындағы шамалар нақты болатын төмендегі қосындыны қолдану керек:
 (2.1.2)
(2.1.2)
u және v үшін алынған квадраттық өрнек u және v барлық нақты мәндері үшін теріс емес болғандықтан, оның дискриминанты теріс емес болу керек, бұл ұйғарым Коши теңсіздігін береді [6]:
 (2.1.3)
(2.1.3)
Бұл теңсіздікті кез келген
санмен өрнектелетін евклидтік кеңістікте бұрыш косинусының
абсолюттік шамасы бірден артық болмайды деген фактінің ұйғарымы деп
қарастыруға болады. Теңдік орындалады сонда және тек қана сонда,
егер  және
және
 сандарының жүйелері
өзара пропорционал болса, яғни сонда және тек қана сонда, егер
нөлге тең емес және төмендегі шартты
қанағаттандыратын λ
мен
μ
сандары бар
болса:
сандарының жүйелері
өзара пропорционал болса, яғни сонда және тек қана сонда, егер
нөлге тең емес және төмендегі шартты
қанағаттандыратын λ
мен
μ
сандары бар
болса:

Егер алдыңғы ұйғарымды жай
ғана п-өлшемді евклидтік кеңістікке
емес, ал кез келген екі х
және
у
элементтері үшін төмендегідей
қасиеттері бар  скаляр көбейтіндісі
анықталған S
жалпы сызықтық кеңістікке
қолданатын болса, бұдан да жалпы нәтижелерді алуға
болады:
скаляр көбейтіндісі
анықталған S
жалпы сызықтық кеңістікке
қолданатын болса, бұдан да жалпы нәтижелерді алуға
болады:
(![]() а) кез
келген
а) кез
келген  үшін
үшін

(ә)
 (2.1.4)
(2.1.4)
(б) кез келген нақты скаляр u және v үшін

Бұл қасиеттерден u және v үшін квадраттық өрнек
 (2.1.5)
(2.1.5)
барлық нақты u және v үшін теріс емес болатынын пайымдауға болады.
Бұдан, жоғарыдағыдай,
 (2.1.6)
(2.1.6)
теңсіздігін аламыз, бұл теңсіздік, өз кезегінде, одан да жалпы теңсіздіктердің дербес жағдайы болады.
Енді
бұдан S
пен
 скаляр көбейтіндісін
таңдап, теңсіздіктердің бұдан да көп санын шығаруға болады.
Осылайша,
скаляр көбейтіндісін
таңдап, теңсіздіктердің бұдан да көп санын шығаруға болады.
Осылайша,
 (2.1.7)
(2.1.7)
мұндағы интеграл Стильтьес
мағынасында қабылданады және  үшін
үшін
 кемімейді
немесе
кемімейді
немесе
 (2.1.8)
(2.1.8)
мұндағы
 – оң таңбалы матрица
және т.с.с.
– оң таңбалы матрица
және т.с.с.
Арифметикалық және геометриялық орталарының арасындағы теңсіздік.
Кең нәтижелерді қарастыру ең маңызды және теңсіздіктер теориясының негізі болып табылатын бір теңсіздіктен – арифметикалық және геометриялық орталарының арасындағы теңсіздіктен басталады. Бұл ерекше әдемі теңсіздік келесідей етіп тұжырымдалады.
1-Теорема.  –
теріс емес сандар
және
–
теріс емес сандар
және  болсын.
Онда
болсын.
Онда
 (2.1.9)
(2.1.9)
болады. Бұл жерде қатаң теңсіздік
орындалады, тек барлық өзара тең
болмаса.
өзара тең
болмаса.
3-9 бөлімшелерінде осы фундаменталды теңсіздіктің әр түрлі принциптерге негізделген немесе әр түрлі әдістерді қамтитын он екі дәлелдеуі көрсетіледі. (2.1.9) теңсіздіктің өлшенген орталарға жататын жалпылаулары бар. Олар осы теңсіздіктің және оның шекті жағдайларының дербес жағдайлары болып табылатынын ескерте кету керек.
Жоғары және төмен бағытталған индукция.
1-теореманың дәлелдеуінің
классикалық түрі Кошиға тиесілі. (2.1.1) теңсіздікте көрсетілгендей,
кез келген  және
және
 үшін
үшін
 (2.1.10)
(2.1.10)
орындалады.  деп алып,
(2.1.10) теңсіздіктен
деп алып,
(2.1.10) теңсіздіктен
 (2.1.11)
(2.1.11)
аламыз,
мұндағы  және
және
 – кез келген теріс емес
сандар. (2.1.1) теңсіздіктен белгілі
болғандай, (2.1.11) теңсіздікте теңдік орындалады
сонда және тек қана сонда, егер
– кез келген теріс емес
сандар. (2.1.1) теңсіздіктен белгілі
болғандай, (2.1.11) теңсіздікте теңдік орындалады
сонда және тек қана сонда, егер  болса.
болса.
Енді
 орнына
орнына  және
және
 орнына
орнына  жаңа айнымалыларын қойсақ,
онда екі рет қолданылған (2.1.11) теңсіздіктен
жаңа айнымалыларын қойсақ,
онда екі рет қолданылған (2.1.11) теңсіздіктен

 (2.1.12)
(2.1.12)
Осылайша жалғастыра
отырып, (2.1.9) теңсіздік
 үшін және 2-нің дәрежесі
болатын кез келген п
үшін орындалатынын көреміз.
Бұл – жоғары бағытталған
индукция.
үшін және 2-нің дәрежесі
болатын кез келген п
үшін орындалатынын көреміз.
Бұл – жоғары бағытталған
индукция.
Енді төмен бағытталған
индукцияны қолданайық. Егер теңсіздік
п
үшін орындалса, онда
ол  үшін де орындалатынын
көрсетейік. (2.1.9) теңсіздікте
үшін де орындалатынын
көрсетейік. (2.1.9) теңсіздікте  орнына
орнына
 (2.1.13)
(2.1.13)
жаңа айнымалы қоямыз,
мұндағы  , ал
басқа
, ал
басқа  өзгеріссіз қалдырамыз.
Онда (2.1.9) теңсіздік
бойынша
өзгеріссіз қалдырамыз.
Онда (2.1.9) теңсіздік
бойынша

 (2.1.14)
(2.1.14)
аламыз немесе
 (2.1.15)
(2.1.15)
ықшамдап, ізделінді теңсіздікті аламыз:
 (2.1.16)
(2.1.16)
2-нің дәрежесі үшін алынған нәтижесімен байланыстыра отырып, теореманың индукциялық дәлелдемесін аламыз.
Жоғарыға және төменге бағытталған индукциямен дәлелденетін басқа қызықты теңсіздік ретінде Фань Цзыдың жарияланбаған келесідей теңсіздігін алуға болады:
егер
 үшін
үшін  болса,
онда
болса,
онда
 (2.1.17)
(2.1.17)
болады, теңдік орындалады
сонда және тек қана сонда, егер барлық
 өзара тең
болса.
өзара тең
болса.
Гаусстың арифметикалық-геометриялық ортасы. Элементар симметриялық функциялар.
 – оң сандар
және
– оң сандар
және  болсын.
болсын.
 тізбектерінің келесі
мүшелерін
тізбектерінің келесі
мүшелерін
 (2.1.18)
(2.1.18)
қатынастар арқылы анықтайық.
 (2.1.19)
(2.1.19)
екенін көруге болады
және  мен
мен
 тізбектерінің
тізбектерінің  ортақ шегі болатынын
дәлелдеуге болады. Бұл
ортақ шегі болатынын
дәлелдеуге болады. Бұл  функциясын алғашқы рет Гаусс
зерттеген болатын [7]. Ол эллипстік функциялар теориясында маңызды
рөл атқарады; сонымен қатар Гаусс бұл теория толығымен осы
функцияға негізделетінін көрсеткен еді.
функциясын алғашқы рет Гаусс
зерттеген болатын [7]. Ол эллипстік функциялар теориясында маңызды
рөл атқарады; сонымен қатар Гаусс бұл теория толығымен осы
функцияға негізделетінін көрсеткен еді.
Жоғарыдағы  мен
мен
 тізбектерінің
үйлесімділігі туралы ұйығарым көптеген жалпылаулардың шығуына
мүмкіндік береді. Мысалы, егер
тізбектерінің
үйлесімділігі туралы ұйығарым көптеген жалпылаулардың шығуына
мүмкіндік береді. Мысалы, егер  және
және

 (2.1.20)
(2.1.20)
болса, онда
 (2.1.21)
(2.1.21)
болатынын оңай көруге болады.
Симметриялық орталардың нәтижелерін дәлелдеудің бір тәсілі ретінде п нақты айнымалысы бар элементар симметриялық функциялар арасындағы кейбір қызықты теңсіздіктерді қолдануға болады. Арифметикалық және геометриялық орталардың арасындағы теңсіздік дәл осындай теңсіздіктер тізбегінің бір бөлігі болып табылады екен.
Ролль теоремасына негізделген дәлелдеу әдісін қолданайық. Бұл әдіс берілген көпмүшенің нақты түбірлері болмайды деген фактіден ғана емес, сонымен қатар көпмүшенің барлық түбірлері нақты сан болады деген фактіден де пайдалы салдарларды алуға болатынын (бұл туралы жоғарыда баяндалды) көрсетеді.
Бізге қажетті нәтиже Ролль теоремасының тікелей салдары болып табылады; ол келесідей болады.
1-Лемма. Егер
 (2.1.22)
(2.1.22)
теңдеуінің
барлық  түріндегі түбірлері нақты
сандар болса, онда (2.1.22) тепе-теңдігін х және у
бойынша дифференциалдау арқылы алынған теңдеулердің барлық
түбірлері де нақты сандар болады.
түріндегі түбірлері нақты
сандар болса, онда (2.1.22) тепе-теңдігін х және у
бойынша дифференциалдау арқылы алынған теңдеулердің барлық
түбірлері де нақты сандар болады.
Бұл лемманы
 (2.1.23)
(2.1.23)
көпмүшесіне қолданайық,
мұндағы  – нақты
сандар.
– нақты
сандар.
 (2.1.24)
(2.1.24)
болатынын ескере отырып, мұндағы
 (2.1.25)
(2.1.25)
 және
және  сандарына қатысты симметриялық
функция. Осыдан
сандарына қатысты симметриялық
функция. Осыдан  теңдеуін екінші рет
дифференциалдаудан шығатын
теңдеуін екінші рет
дифференциалдаудан шығатын
 (2.1.26)
(2.1.26)
теңдеуінің екі нақты түбірі болатыны шығады. Осылайша,
 (2.1.27)
(2.1.27)
болады. Теңсіздік кез келген
оң, теріс немесе нөлге тең  сандары үшін орындалатынын
ескере кетейік.
сандары үшін орындалатынын
ескере кетейік.
Енді
(2.1.27) теңсіздігінен Маклоренге
тиесілі бір нәтижені шығарайық [8]. Ол үшін
барлық  сандары оң деп пайымдайық.
Онда (2.1.27) бойынша
сандары оң деп пайымдайық.
Онда (2.1.27) бойынша
 (2.1.28)
(2.1.28)
немесе
 (2.1.29)
(2.1.29)
теңсіздіктері орындалады.
(2.1.29) теңсіздіктен

шығады, яғни арифметикалық және геометриялық орталардың арасындағы теңсіздікті аламыз.
Якобсталь дәлелдеуі.
Арифметикалық және геометриялық орталардың арасындағы теңсіздіктің осы орталардың алгебралық қатынастарына негізделетін бірнеше дәлелдеуі бар. Олардың ішіндегі ең қызықтысы төмендегі дәлелдеу болып табылады [9].
Әуелі
 (2.1.30)
(2.1.30)
тепе-теңдігінен бастаймыз, мұндағы

Сонан соң
 және
және  үшін
орындалатын
үшін
орындалатын
 (2.1.31)
(2.1.31)
теңсіздігін қолданамыз. п-нің бүтін мәндері үшін (2.1.31) теңсіздігі

тепе-теңдігінен шығады. Егер

деп белгілесек, онда (2.1.30) теңдіктен
 (2.1.32)
(2.1.32)
немесе
 (2.1.33)
(2.1.33)
Индукция бойынша ізделінді жалпы нәтижені табамыз:
 .
.
2.2. Лагранж тепе-теңдігі
Кез келген берілген белгілі теңсіздікті айқын етіп көрсететін тепе-теңдік арқылы дәлелдеу үрдісі көптеген оқыс тармақталулары бар өте қызықты және қиын тапсырма болып табылады. (2.1.3) теңсіздік
 (2.2.1)
(2.2.1)
тепе-теңдігінен шығады, бұл тепе-теңдік бұдан да жалпы тепе-теңдіктің дербес жағдайы болып табылады.
2.3. Анализ және Лагранжтың көбейткіштері
Енді арифметикалық және
геометриялық орталары арасындағы теңсіздікті анализдің есебі
ретінде қарастырайық. Бізге  функциясының теріс емес және
төменде көрсетілген нормалау шартын
қанағаттандыратын
функциясының теріс емес және
төменде көрсетілген нормалау шартын
қанағаттандыратын  облысындағы ең кіші мәнін табу
керек
облысындағы ең кіші мәнін табу
керек
 (2.3.1)
(2.3.1)
Ізделінді ең кіші мән шекті нүктеден алынуы мүмкін еместігі белгілі болғандықтан, локальды минимумды анықтау үшін Лагранж көбейткіштері әдісін қолдануға болады.
 (2.3.2)
(2.3.2)
функциясы үшін экстремумнің қажетті шарттары
 (2.3.3)
(2.3.3)
түрінде болады,
осыдан  болу керек. Бұдан локалды
минимумның бір ғана нүктесі
болу керек. Бұдан локалды
минимумның бір ғана нүктесі  болады,
яғни
болады,
яғни  болады, ал
ол (2.1.9) теңсіздікке пара-пар келеді
деген қорытындыға келеміз.
болады, ал
ол (2.1.9) теңсіздікке пара-пар келеді
деген қорытындыға келеміз.
2.4. Функционалдық теңдеулер
1-теорема динамикалық
бағдарламалаудың функционалдық теңдеулер әдісімен де дәлелденеді
[10].  сандарының төмендегі шарттарды
қанағаттандыратындай ең үлкен мәнін табудан
бастаймыз:
сандарының төмендегі шарттарды
қанағаттандыратындай ең үлкен мәнін табудан
бастаймыз:

Осы ең үлкен
мәнді  деп
белгілейік.
деп
белгілейік.  мен
мен
 арасында рекурентті
қатынасты алу үшін белгіленген
арасында рекурентті
қатынасты алу үшін белгіленген  таңдау кезінде төмендегі
шарттарға бағынатын және
таңдау кезінде төмендегі
шарттарға бағынатын және  көбейтіндісі ең үлкен мәнге ие
болатындай
көбейтіндісі ең үлкен мәнге ие
болатындай  таңдау мәселесі қалатынын
ескере кету керек:
таңдау мәселесі қалатынын
ескере кету керек:
 (2.4.1)
(2.4.1)
Осыдан,
 үшін
үшін
 (2.4.2)
(2.4.2)
болатыны шығады.
 айнымалыларды
алмастырып,
айнымалыларды
алмастырып,
 (2.4.3)
(2.4.3)
аламыз. Осы алмастыруды (2.4.2) теңдікке қойып,
 (2.4.4)
(2.4.4)
 болғандықтан,
болғандықтан,  болады,
бұл (2.1.9)
теңсіздікке пара-пар
келеді.
болады,
бұл (2.1.9)
теңсіздікке пара-пар
келеді.
Ойыстық.
Енді 1-теореманың дәлелдеуін
геометриялық пайымдауларға негізделген түрде келтірейік [11].
1-суретте  қисығы көрсетілген.
Дифференциалдау тұрғысынан қарағанда бұл қисық ойыс орналасқан және
оның кез келген екі нүктесін қосатын хорда қисықтың астында
орналасады. Яғни
қисығы көрсетілген.
Дифференциалдау тұрғысынан қарағанда бұл қисық ойыс орналасқан және
оның кез келген екі нүктесін қосатын хорда қисықтың астында
орналасады. Яғни  үшін
үшін
 (2.4.5)
(2.4.5)
болады және теңдік орындалады
сонда және тек қана сонда, егер  .
.
Бұл нәтиже
 (2.4.6)
(2.4.6)
теңсіздігіне пара-пар келеді.
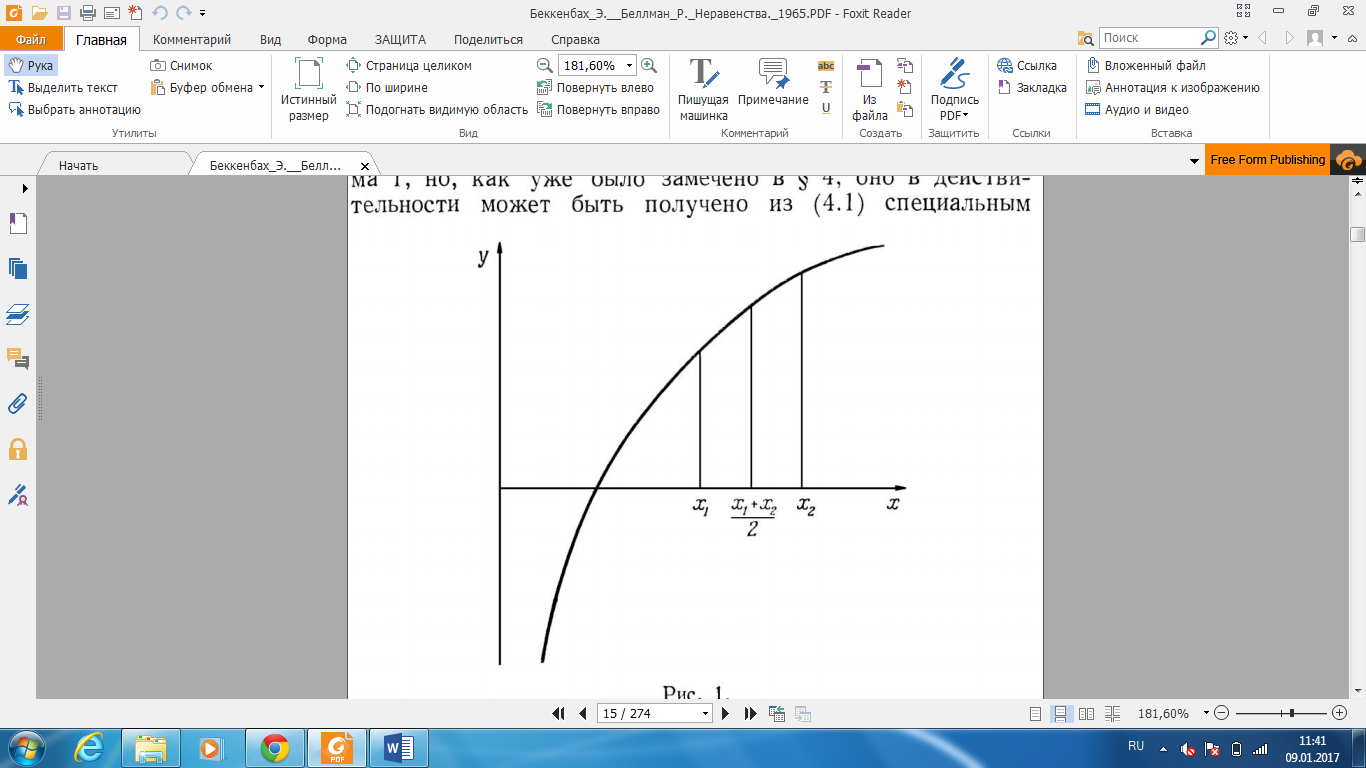
1-сурет
Дәл осындай
пайымдау  үшін
үшін
 (2.4.7)
(2.4.7)
болатынын және кез
келген  мен
мен
 үшін
үшін
 (2.4.8)
(2.4.8)
болатынын көрсетеді.
Жоғарыда айтылғандай бұл
теңсіздік 1-теоремаға қарағанда күштірек болып көрінеді,
ол (2.1.9) теңсіздіктен  мәндерін арнайы таңдаудан және
шекті ауысудан алынады.
мәндерін арнайы таңдаудан және
шекті ауысудан алынады.
Элерс дәлелдеуі.
Енді 1-теореманы

теңдігінен

теңсіздігі шығатынын анықтау арқылы дәлелдейміз.
Бұл теңсіздік п үшін орындалатынын және

болады
делік.  және
және
 сандары
–
сандары
–  , ал
, ал
 болатындай
болатындай  сандарының ішіндегі екі сан
болсын. Онда
сандарының ішіндегі екі сан
болсын. Онда  немесе
немесе
 (2.4.9)
(2.4.9)
болады.
Бұдан  мәндерінің п
саны үшін теңсіздік
негізінде
мәндерінің п
саны үшін теңсіздік
негізінде
 (2.4.10)
(2.4.10)
болатыны шығады. Сонан соң
нәтиже  үшін де дұрыс болады, осылайша
1-теорема дәлелденді.
үшін де дұрыс болады, осылайша
1-теорема дәлелденді.
2.5. Мажорлау – Бордың дәлелдеуі
1-теореманы тамаша дәлелдеулерінің бірі Г.Борға тиесілі [12].
Әуелі мажорлау ұғымын
енгізейік.  және
және
 – екі формалды дәрежелік
қатар болсын:
– екі формалды дәрежелік
қатар болсын:
 (2.5.1)
(2.5.1)
мұндағы
 үшін
үшін 
Егер
 үшін
үшін  болса,
онда
болса,
онда
 (2.5.2)
(2.5.2)
деп жазылады.
Егер  және
және
 болса,
онда
болса,
онда  болатыны
айқын.
болатыны
айқын.
 және
және  үшін
үшін
 (2.5.3)
(2.5.3)
түріндегі жай мажорлаудан бастап,
 (2.5.4)
(2.5.4)
екенін анықталады.
Осыдан,  алдындағы коэффициенттерін
салыстырып, барлық оң таңбалы бүтін
N
үшін
алдындағы коэффициенттерін
салыстырып, барлық оң таңбалы бүтін
N
үшін
 (2.5.5)
(2.5.5)
немесе
 (2.5.6)
(2.5.6)
теңсіздіктерін аламыз.
Стирлинг формуласына
сәйкес  үшін
үшін
 (2.5.7)
(2.5.7)
болғандықтан,
 (2.5.8)
(2.5.8)
болады. (2.5.6) пен (2.5.8) өрнектерден 1-теорема шығады. Бұл – келтірілген дәлелдеулердің ішіндегі теңдік белгісі орындалатын шарттарды қарастыруға мүмкіндік бермейтін жалғыз дәлелдеу.
2.6. Гурвиц дәлелдеуі
Енді Гурвицтің қызықты дәлелдеуіне көшейік [13]. Ол 1891 жылы оның топтар бойынша интегралдау арқылы инварианттарды табу туралы еңбегінен 6 жыл бұрын жарияланған болатын [14], бірақ бұл еңбекке кейінгі еңбектерінде дамытылған кейбір мәселелер салынған еді.
 нақты сандар жиынындағы
айнымалылар үшін п
функциясы
берілсін.
нақты сандар жиынындағы
айнымалылар үшін п
функциясы
берілсін.  аргументтерін
барлық
аргументтерін
барлық  алмастырулары
бойынша f
қосындысын
алмастырулары
бойынша f
қосындысын  деп белгілейік. Осылайша,
мысалы,
деп белгілейік. Осылайша,
мысалы,
 (2.6.1)
(2.6.1)
Төмендегідей әдіспен
алынатын  функцияларын
қарастырайық:
функцияларын
қарастырайық:
 (2.6.2)
(2.6.2)
Осыдан,
 (2.6.3)
(2.6.3)
шығатынын көреміз.
Дәл осылай
 (2.6.4)
(2.6.4)
Өрнектерді бір-біріне қосу арқылы
 (2.6.5)
(2.6.5)
аламыз. Бірақ (2.6.1) өрнекке сәйкес
 (2.6.6)
(2.6.6)
болады.
 функцияларының
әрқайсысы
функцияларының
әрқайсысы  үшін теріс емес екендігі айқын
көрініп тұр, себебі
үшін теріс емес екендігі айқын
көрініп тұр, себебі
 (2.6.7)
(2.6.7)
Осылайша, (2.1.6) тепе-теңдіктің сол жағындағы айырма теріс емес болады, ал бұл ұйғарым 1-теореманың дәлелдеуі болады. Бұл дәлелдеу – (2.1.9) теңсіздікті тепе-теңдікке айналдыратын жалғыз ғана дәлелдеу.
2.7. Юнг теңсіздігі
Айталық,
 функциясы
– х-ке қатысты үзіліссіз қатаң
өспелі функция болсын,
функциясы
– х-ке қатысты үзіліссіз қатаң
өспелі функция болсын,  және
және
 (2-сурет қара). Сәйкес
интегралдармен берілген аудандарды
қарастырып,
(2-сурет қара). Сәйкес
интегралдармен берілген аудандарды
қарастырып,
 (2.7.1)
(2.7.1)
екеніне көз жеткіземіз,
мұндағы  функциясы
функциясы
 функциясына кері
функция. Бұл жерде теңдік тек қана
функциясына кері
функция. Бұл жерде теңдік тек қана  болғанда орындалатынын байқау
қиын емес. Бұл теңсіздік Юнг теңсіздігі деп аталады
[15].
болғанда орындалатынын байқау
қиын емес. Бұл теңсіздік Юнг теңсіздігі деп аталады
[15].
φ үшін әр түрлі фукнцияларды таңдай отырып, бірқатар қызықты нәтижелер аламыз.
 болғанда (2.7.1)
теңсіздік
болғанда (2.7.1)
теңсіздік
 (2.7.2)
(2.7.2)
түріне келеді.
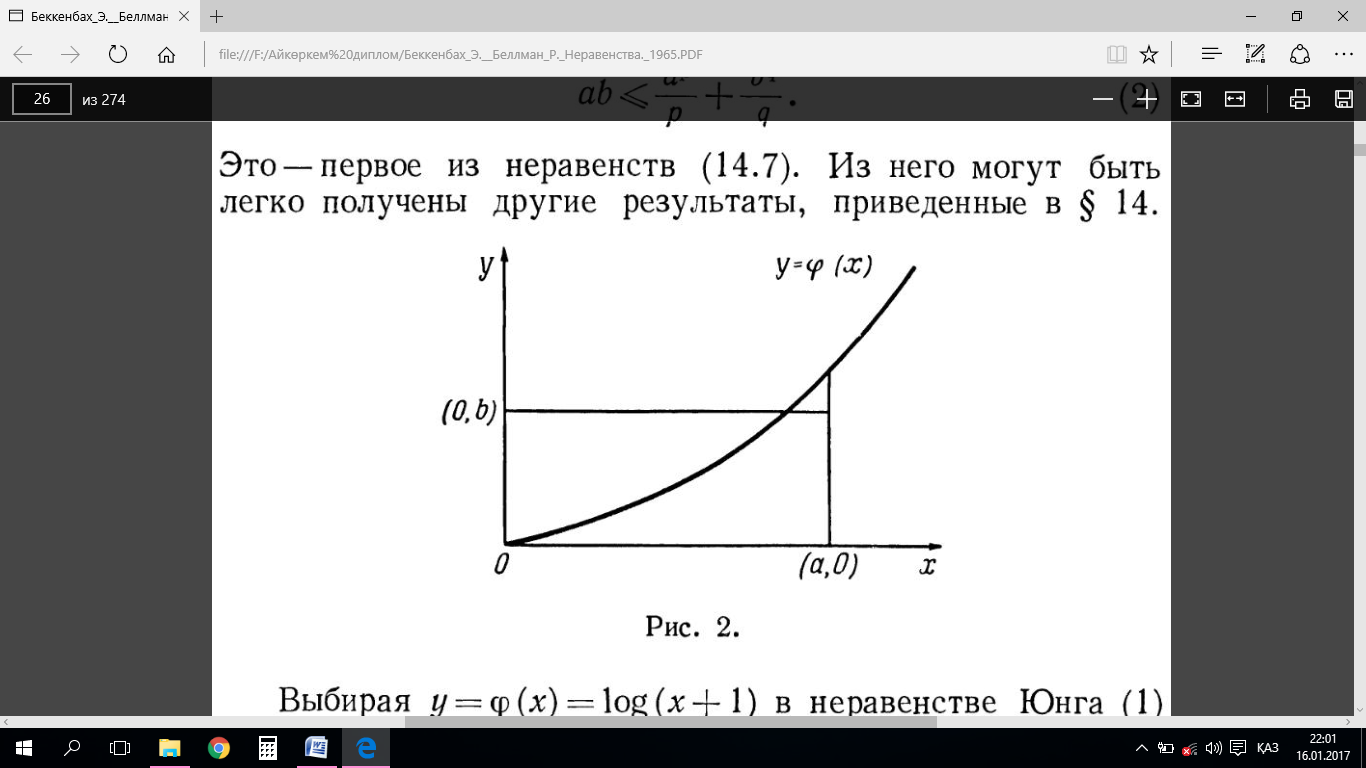
2-сурет
(2.7.1) Юнг
теңсіздігінде  таңдап
және а-ны
таңдап
және а-ны
 -ге алмастырып, басқа
бір қызықты нәтижені, яғни
-ге алмастырып, басқа
бір қызықты нәтижені, яғни

теңсіздігін аламыз. Бұл теңсіздік Фурье қатарлары теориясында жиі қолданылады.
2.1 бөлімшеде арифметикалық және геометриялық орталарының арасындағы теңсіздік элементар симметриялы функциялар қанағаттандыратын теңсіздіктер тізбегінің бірі екенін көрдік. Енді осы орталардың орталар мәндерінің үзіліссіз толық иерархиясына жататынын көрсетейік. Осында қарастырылатын теңсіздіктер үшін элементар дәлелдеулер бар болғанына қарамастан, негізінен дифференциалдық санауды қолданамыз. Біздің басты қаруымыз дөңес функциялар теориясы болады; әсіресе осы бөлімшеде 2.4 бөлімшеде көрсетілген геометриялық ұйғарымдардың аналитикалық негізін көрсетеміз. Дөңес функциялардың және олардың қосымшаларының жалпы теориясы Беккенбах пен Гриннің еңбектерінде қарастырылады.
Кез келген оң таңбалы

мәндері үшін және оң

үшін және кез келген
нақты  үшін
t ретінің
ортасын немесе
t-норманы анықтаймыз:
үшін
t ретінің
ортасын немесе
t-норманы анықтаймыз:

Соның ішінде, –1, 1 және 2 реттерінің орталары сәйкесінше гармоникалық, арифметикалық және квадраттық орталар.
Лопиталь ережесінің көмегімен
 (2.8.1)
(2.8.1)
болатынын, яғни геометриялық
ортаға тең болатыны оңай анықталады. Содан кейін
егер  болса, онда,
сірә,
болса, онда,
сірә,  үшін
үшін

болады, бұдан
 (2.8.2)
(2.8.2)
болады. Бірақ

қатынасынан енді
 (2.8.3)
(2.8.3)
болатыны шығады. Осының негізінде



болады.
Егер
 -ге қатысты оның теріс
емес екені және олардың әйтеуір біреуі нөлге тең екені
жорамалданатын болса, онда
-ге қатысты оның теріс
емес екені және олардың әйтеуір біреуі нөлге тең екені
жорамалданатын болса, онда  үшін
үшін
 ортасы нөлге тең болады
деп ұйғарылады. Алайда біз тек қана оң таңбалы
ортасы нөлге тең болады
деп ұйғарылады. Алайда біз тек қана оң таңбалы
 қарастырамыз.
қарастырамыз.
Енді
оң
таңбалы  үшін
үшін  ортасы t-ға
қатысты
ортасы t-ға
қатысты  үшін кемімейтін функция
болатынын және де егер
үшін кемімейтін функция
болатынын және де егер  -дің арасында бір-біріне
тең емес
-дің арасында бір-біріне
тең емес  мәндері табылса,
онда
мәндері табылса,
онда  қатаң өсетін
болатынын көрсетейік. Арифметикалық және
геометриялық орталардың арасындағы теңсіздік бұл ұйғарымның дербес
жағдайы болып табылады.
қатаң өсетін
болатынын көрсетейік. Арифметикалық және
геометриялық орталардың арасындағы теңсіздік бұл ұйғарымның дербес
жағдайы болып табылады.
Осы жалпылама фактіні негіздеу
үшін әуелі дөңес функцияларға қатысты бір ескерту енгізейік.
Егер  функциясының
функциясының  үшін
үшін
 (2.8.4)
(2.8.4)
теңсіздігін қанағаттандыратын
екінші туындысы бар болса, онда  графигі осы интервалда дөңес
доға түрінде болады. Егер
графигі осы интервалда дөңес
доға түрінде болады. Егер

мәндері
 интервалында жатса,
ал
интервалында жатса,
ал

болса,
онда  та
та
 интервалында жатады және
Тейлор формуласы бойынша
интервалында жатады және
Тейлор формуласы бойынша

болады. Бұл
теңсіздіктерді  -ге көбейтіп және
қосып,
-ге көбейтіп және
қосып,

аламыз, ал бұдан (2.8.4) сәйкес
 (2.8.5)
(2.8.5)
болады және де теңдік тек қана х-тің барлығы өзара тең болғанда орындалады.
Демек,

функциясы үшін

аламыз, осыдан (2.8.5) теңсіздікке сәйкес х-тің оң мәндері үшін
 (2.8.6)
(2.8.6)
теңсіздігі дұрыс болады,
теңдік тек қана барлық  өзара тең болғанда
орындалады.
өзара тең болғанда
орындалады.
Осы жерде

болатынын тексеру қиын емес
және  мәндеріне
қолданылған (2.8.6) теңсіздік
мәндеріне
қолданылған (2.8.6) теңсіздік

екенін көрсетеді, теңдік тек
қана барлық  өзара тең болғанда
орындалады.
өзара тең болғанда
орындалады.
Осылайша, егер
барлық  өзара тең болмаса,
онда
өзара тең болмаса,
онда  функциясы
t-ға қатысты өспелі функция
болады және оның графигінде екі тік асимптота болады. Осының
негізінде
функциясы
t-ға қатысты өспелі функция
болады және оның графигінде екі тік асимптота болады. Осының
негізінде  функциясының графигі тек қана
бір нүктеде майысады, яғни бір ойыс және бір дөңес бөлігі бар деп
жорамалдауға болады. Бірақ бұл жорамал әр уақытта да дұрыс бола
бермейді [16], алайда
функциясының графигі тек қана
бір нүктеде майысады, яғни бір ойыс және бір дөңес бөлігі бар деп
жорамалдауға болады. Бірақ бұл жорамал әр уақытта да дұрыс бола
бермейді [16], алайда  функциясы
t-ға қатысты дөңес функция
болатынын көрсету қиын емес (ол үшін дифференциалдаудан кейін Коши
теңсіздігін қолдану керек). Демек, (2.8.5) теңсіздікке
сәйкес
функциясы
t-ға қатысты дөңес функция
болатынын көрсету қиын емес (ол үшін дифференциалдаудан кейін Коши
теңсіздігін қолдану керек). Демек, (2.8.5) теңсіздікке
сәйкес  функциясы кез
келген
функциясы кез
келген  үшін
үшін
 (2.8.7)
(2.8.7)
теңсіздігін қанағаттандырады және
 (2.8.8)
(2.8.8)
t ретінің қосындысы

t-ға қатысты функция ретінде
басқаша болады. – ∞-тен 0-ге дейін артатын
t
үшін ол
 -тен 0-ге дейін
бірсарынды кемиді, ал 0-ден +∞-ге дейін
артатын t
үшін ол
∞-тен
-тен 0-ге дейін
бірсарынды кемиді, ал 0-ден +∞-ге дейін
артатын t
үшін ол
∞-тен  -ке дейін бірсарынды
кемиді.
-ке дейін бірсарынды
кемиді.

теңсіздігін кейде Иенсен теңсіздігі деп атайды [17], екінші ретті туындысы оң мән қабылдайтын функциялар үшін ғана емес, сондай-ақ кез келген үздіксіз дөңес функциялар үшін орындалатын (2.8.5) теңсіздікті де солай атайды.
 функциясы t-ға қатысты дөңес функция
болғандықтан,
функциясы t-ға қатысты дөңес функция
болғандықтан,  функциясы
да t-ға қатысты дөңес функция
болатыны оңай шығады. Сондықтан (2.8.7) теңсіздік
M-нің
орнында S
болғанда да
орындалады.
функциясы
да t-ға қатысты дөңес функция
болатыны оңай шығады. Сондықтан (2.8.7) теңсіздік
M-нің
орнында S
болғанда да
орындалады.
 функциясы
функциясы  үшін міндетті түрде ойыс
болмайды [18]; бірақ
үшін міндетті түрде ойыс
болмайды [18]; бірақ
 үшін әркез дөңес болады.
Сәйкесінше,
үшін әркез дөңес болады.
Сәйкесінше,  (2.8.8) шарттарға бағынатын кез
келген
(2.8.8) шарттарға бағынатын кез
келген  және
T
мен
және
T
мен
 үшін
үшін

теңсіздігін қанағаттандырады.
Бұдан басқа,  функциясы
t-ға
қатысты
функциясы
t-ға
қатысты  үшін дөңес функция болады
деген ұйғарым бар, сондықтан (2.8.5) сәйкес
үшін дөңес функция болады
деген ұйғарым бар, сондықтан (2.8.5) сәйкес

болады.
2.9. Классикалық теңсіздіктерді жалпылау
Жоғарыда қарастырылған теңсіздіктерді көптеген бағытта жалпылап нәтижелеуге болады. Бұл бөлімшеде осы нәтижелердің ішіндегі маңыздыларына тоқталып өтейік.
Гёльдер мен Минковскийдің теңсіздіктерінің нәтижелеріне математикалық индукцияның қолданылуын көрсетейік.
Егер  мен
мен  үшін
үшін  және
егер
және
егер

болғанда  болса,
онда
болса,
онда
 (2.9.1)
(2.9.1)
болады; теңдік орындалады
сонда және тек қана сонда, егер  сандарының т жүйелері өзара
пропорционал болса, яғни сонда және тек қана сонда, егер барлығы
бір мезгілде нөлге тең емес және
сандарының т жүйелері өзара
пропорционал болса, яғни сонда және тек қана сонда, егер барлығы
бір мезгілде нөлге тең емес және

болатын  сандары бар
болса.
сандары бар
болса.
Егер  мен
мен  үшін
үшін  және
егер
және
егер  болса,
онда
болса,
онда
 (2.9.2)
(2.9.2)
болады. Теңсіздік белгісі
кері белгіге ауысады, егер  болса.
(
болса.
( үшін
үшін  болады деп жорамалдау
керек). Осы жағдайлардың әрқайсысында теңдік орындалады сонда және
тек қана сонда, егер
болады деп жорамалдау
керек). Осы жағдайлардың әрқайсысында теңдік орындалады сонда және
тек қана сонда, егер  сандарының т жүйелері өзара
пропорционал болса.
сандарының т жүйелері өзара
пропорционал болса.
Сонымен қатар, осы теңсіздіктердің шекті және шексіз қосындыларға қатысты нәтижелері де бар. Шек үрдісін қолданған кезде теңдіктің орындалуы мүмкін жағдайларды көрсету ерекше назарда болу керек.
Алдыңғы теңсіздіктер «Σ-ге қатысты біртекті» болғандықтан, орталар үшін де аналогтары болады. (2.9.1) теңсіздіктің осындай аналогы

теңсіздігі
болады. (2.9.2) теңсіздікте де дәл
осылай  және
және
 көбейткіштерін немесе
олардың біреуін сәйкес орындарға қоюға
болады.
көбейткіштерін немесе
олардың біреуін сәйкес орындарға қоюға
болады.
Σ-ге қатысты біртекті
теңсіздіктердің интегралдық аналогтары болады. Осылайша, Гёльдер
мен Минковскийдің теңсіздіктері келесідей теңсіздіктерге алып
келеді (Коши теңсіздігі  болғандағы Гёльдердің
дискреттік теңсіздігінің дербес жағдайы болады; оның интегралды
аналогы Коши-Шварц теңсіздігі немесе жай ғана Шварц теңсіздігі,
немесе Буняковский–Шварц теңсіздігі деп
аталады).
болғандағы Гёльдердің
дискреттік теңсіздігінің дербес жағдайы болады; оның интегралды
аналогы Коши-Шварц теңсіздігі немесе жай ғана Шварц теңсіздігі,
немесе Буняковский–Шварц теңсіздігі деп
аталады).
2-Теорема.  және
және  функциялары – қандай да бір
R облысында анықталған функциялар болсын және dV – осы облыс
көлемінің элементі болсын. Осылайша, төменде келтірілген
теңсіздіктердің оң жағындағы интегралдар бар болса, онда сәйкес
теңсіздіктің сол жағындағы интегралдар да бар болады және бұл
теңсіздіктер орындалады:
функциялары – қандай да бір
R облысында анықталған функциялар болсын және dV – осы облыс
көлемінің элементі болсын. Осылайша, төменде келтірілген
теңсіздіктердің оң жағындағы интегралдар бар болса, онда сәйкес
теңсіздіктің сол жағындағы интегралдар да бар болады және бұл
теңсіздіктер орындалады:
 (2.9.3)
(2.9.3)
(Буняковский–Шварц);
 (2.9.4)
(2.9.4)
(Гёльдер);
 (2.9.5)
(2.9.5)
(Минковский).
(2.9.3), (2.9.4), (2.9.5) теңсіздіктерде теңдік орындалады сонда және тек қана сонда, егер f және g функциялары өзара оң таңбалы пропорционал болса.
Минковский теңсіздігі (2.9.5) теңсіздіктегі қосындыны төмендегі интегралдармен алмастыру арқылы бұдан да кеңірек қорытындыланады:
 (2.9.6)
(2.9.6)
(2.9.2) теңсіздікте j-ге қатысты қосындыларды ғана
интегралдармен алмастыруға болады. Әрбір жағдайда теңсіздік белгісі
кері белгіге ауысады, егер  болса,
бірақ
болса,
бірақ  болғанда функциялар нөлге тең
болмайды деген ұйғарым жасауымыз керек.
болғанда функциялар нөлге тең
болмайды деген ұйғарым жасауымыз керек.
Осындай интегралдық теңсіздіктерді дәлелдеудің бірнеше жолы бар. Оларды дискреттік теңсіздіктердің шекті жағдайлары ретінде шығара аламыз, сондай-ақ дискреттік аналогтарды дәлелдеудегі әдістерді қолдана отырып дәлелдей аламыз.
Аталған жолдардың біріншісін көрсету үшін
 (2.9.7)
(2.9.7)
теңсіздігінің дәлелдеуін
қарастырамыз. Айталық, f
және
g
функциялары үзіліссіз
функциялар болсын. Онда (2.9.7) теңсіздік
 болатын
шекте
болатын
шекте
 (2.9.8)
(2.9.8)
Коши теңсіздігі болып табылатын дискреттік теңсіздігінен шығады.
(2.9.7) теңсіздікті толығымен алу үшін
Лебег бойынша интегралданатын функциялар
 -нормада көпмүшелер
арқылы аппроксимирлана алады деген ұйғарымды пайдалану керек.
Дәлелдеудің бұл жолы ыңғайсыз екені және егер ол теңсіздік еселі
интегралдарға қатысты теңсіздік болатын болса, онда бұл жол үлкен
қиындықтарға алып келетіні көрініп тұр.
-нормада көпмүшелер
арқылы аппроксимирлана алады деген ұйғарымды пайдалану керек.
Дәлелдеудің бұл жолы ыңғайсыз екені және егер ол теңсіздік еселі
интегралдарға қатысты теңсіздік болатын болса, онда бұл жол үлкен
қиындықтарға алып келетіні көрініп тұр.
Енді кез келген R облыстары үшін (2.9.7) теңсіздікті дәлелдеудің тік жолын көрсетейік. Кез келген нақты u және v үшін
 (2.9.9)
(2.9.9)
теңсіздігін қарастырамыз.
u және v-ны Р-ға қатысты функциялар деп қарастырып және R бойынша интегралдап,
 (2.9.10)
(2.9.10)
теңсіздігін аламыз.
Енді u-дың орынына

ал v-ның орнына

жаңа айнымалыларын енгізейік. Онда (2.9.10) теңсіздіктен
 (2.9.11)
(2.9.11)
шығады және бұл теңсіздік (2.9.7) теңсіздікті кез келген R облысы үшін дәлелдейді.
Буняковский–Шварцтың теңсіздіктерін Бохердің кітабынан [19] және Огурдың еңбегінен табуға болады. Геометриялық талдау, функционалдық кеңістіктердегі теңсіздіктерге арналған Огурдың мәліметтері Бохердің евклидтік кеңістіктегі талдаудың аналогтары болып табылады.
Гёльдер мен Минковский теңсіздігінің ∑-ге қатысты біртектілігінің салдарынан орталар үшін аналогтар мен интегралды аналогтар табылуы мүмкін. Осы себеппен орталар үшін интегралды аналогтар да табылады. Ол үшін бар болғаны барлық жердегі

белгісін

етіп ауыстыру керек.
2.9 бөлімшеде қарастырылған, шекті қосындыларға жататын
 немесе
немесе 
теңсіздігі ∑-ге қатысты біртекті емес және оның интегралды аналог жоқ. Бірақ орталардың арасында жататын оған кері

теңсіздігі ∑-ге қатысты біртекті емес болғанымен, интегралды аналогы бар:

Бұл
жердегі  және
және
 орнына сәйкесінше бар
болатын минимум мен максимумды (яғни жоғарғы және төменгі
шектерді), ал
орнына сәйкесінше бар
болатын минимум мен максимумды (яғни жоғарғы және төменгі
шектерді), ал  орына
орына

геометриялық ортасын ойлауымыз керек.
Бір фундаменталды қатынас.
 үшін
орындалатын
үшін
орындалатын
 немесе
немесе  (2.9.12)
(2.9.12)
 (2.9.13)
(2.9.13)
тамаша теңсіздіктері жалпы теория үшін фундаменталды болып табылады, себебі олардан арифметикалық және геометриялық орталардың арасындағы теңсіздік, сондай-ақ Гёльдер мен Минковскийдің негізгі теңсіздіктері шығады.
(2.9.12) және
(2.9.13) теңсіздіктері дифференциалдық
есептеу арқылы оңай дәлелденеді. Теңсіздік тек
қана  болғанда ғана
орындалады.
болғанда ғана
орындалады.
Осы теңсіздіктерді бұдан
күрделірек, бірақ бұдан элементар болатын дәлелдеу үрдісі
төмендегілерді қамтиды:  және
және
 үшін
үшін

тепе-теңдігі

болатынын көрсетеді және
теңдік тек қана  болғанда орындалады. Осыдан,
кез келген бүтін
болғанда орындалады. Осыдан,
кез келген бүтін  үшін
үшін

болады,
бұдан  үшін
үшін

теңсіздігі шығады, бұл
теңсіздік  мәндерінде (2.9.12) теңсіздікпен сәйкес келеді,
дәлірек айтқанда,
мәндерінде (2.9.12) теңсіздікпен сәйкес келеді,
дәлірек айтқанда,
 (2.9.14)
(2.9.14)
және теңдік тек
қана  болғанда
орындалады.
болғанда
орындалады.
(2.9.12) теңсіздік
иррационал  үшін
(2.9.14) теңсіздіктен
үшін
(2.9.14) теңсіздіктен  болғанда шығады, бірақ шекті
ауысу кезінде
болғанда шығады, бірақ шекті
ауысу кезінде  үшін қатаң теңсіздік жоғалады.
Оны қайтару үшін
үшін қатаң теңсіздік жоғалады.
Оны қайтару үшін  деп аламыз,
мұндағы
деп аламыз,
мұндағы  және
және
 ,
бірақ r
– рационал сан.
Онда
,
бірақ r
– рационал сан.
Онда

болады және бұл
өрнек  үшін
(2.9.12) теңсіздікті дәлелдеу үрдісін
аяқтайды.
үшін
(2.9.12) теңсіздікті дәлелдеу үрдісін
аяқтайды.
(2.9.12) теңсіздікте

алмастыруын орындап, оны

түріндегі теңсіздікке
келтіреміз, осы жерде (2.9.12) теңсіздік
 болғанда да орындалатын
болады. Дәл осындай
болғанда да орындалатын
болады. Дәл осындай

алмастыруы  болғанда
(2.9.13) теңсіздіктің орындалатынын
көрсетеді. Бұрынғыдай
болғанда
(2.9.13) теңсіздіктің орындалатынын
көрсетеді. Бұрынғыдай  болғанда
(2.9.12) теңсіздікте
және
болғанда
(2.9.12) теңсіздікте
және  болғанда
(2.9.13) теңсіздікте теңдік тек
қана
болғанда
(2.9.13) теңсіздікте теңдік тек
қана  болғанда
орындалады.
болғанда
орындалады.  және
және
 шекті жағдайларында
теңсіздік барлық
шекті жағдайларында
теңсіздік барлық  үшін
орындалады:
үшін
орындалады:
 егер
егер  немесе
немесе

Енді арифметикалық және
геометриялық орталардың арасындағы теңсіздікті шығарып алу
үшін  үшін
(2.9.13) теңсіздікке
үшін
(2.9.13) теңсіздікке

алмастырып қою үрдісі

теңсіздігіне алып келеді, бұл теңсіздіктен

болатыны шығады, ал бұл кез
келген  және кез келген оң
мәнді α
мен
және кез келген оң
мәнді α
мен
 үшін ізделінді теңсіздік
болады. Теңдік тек қана
үшін ізделінді теңсіздік
болады. Теңдік тек қана  болғанда
орындалады.
болғанда
орындалады.
Жалпы нәтиже
 (2.9.15)
(2.9.15)
 (2.9.16)
(2.9.16)
болғанда индукция бойынша оңай
алынады. Бұл нәтижеге (2.9.15) теңсіздіктегі теңдік
барлық  үшін тек
қана
үшін тек
қана  болғанда орындалады деген
тұжырым кіреді. Расында да, егер (2.9.15) теңсіздік
п
үшін орындалатын болса,
онда
болғанда орындалады деген
тұжырым кіреді. Расында да, егер (2.9.15) теңсіздік
п
үшін орындалатын болса,
онда

үшін де

және

болады.

болатыны айқын және осыдан индукциялық пайымдау бойынша

болады және егер
барлық  өзара тең болған барлық
жағдайда ғана теңдік орындалады.
өзара тең болған барлық
жағдайда ғана теңдік орындалады.
Осылайша, тағы
да (2.9.15) теңсіздікті (2.9.16) шартты қанағаттандыратын кез
келген  үшін дәлелденді; бірақ кез
келген нақты (рационал болуы міндетті емес)
үшін дәлелденді; бірақ кез
келген нақты (рационал болуы міндетті емес)
 үшін бұл дәледеу өте
элементарлы болып тұр.
үшін бұл дәледеу өте
элементарлы болып тұр.
Егер
 және
және

алмастыруларын енгізсе, онда (2.9.12) және (2.9.13) теңсіздіктерді симметриялы түрде жазуға болады. Онда
 (2.9.17)
(2.9.17)
болады.
 немесе
немесе  болатынына
қарай (2.9.12) және
(2.9.13) теңсіздіктері
болатынына
қарай (2.9.12) және
(2.9.13) теңсіздіктері
 немесе
немесе  (2.9.18)
(2.9.18)
түрінде
жазылады. (2.9.18) теңсіздіктегі теңдік тек
қана  болғанда
орындалады.
болғанда
орындалады.  үшін
(2.9.18) екінші теңсіздігі қандай да
бір
үшін
(2.9.18) екінші теңсіздігі қандай да
бір  жалпылама ұйғарымдарда
орындалатынын оңай байқауға болады.
жалпылама ұйғарымдарда
орындалатынын оңай байқауға болады.
Гёльдер мен Минковскийдің теңсіздіктері.
(2.9.18) теңсіздіктерге сәйкес егер

болса, онда
 (2.9.19)
(2.9.19)
болады және
егер  болса,
онда
болса,
онда

болады.
Егер осы
жерде  болғанда
болғанда

болады деп жорамалдап, осы
теңсіздіктерді бір-біріне қоссақ, онда
 үшін
орындалатын
үшін
орындалатын
 (2.9.20)
(2.9.20)
теңсіздігін және үшін кері
теңсіздікті аламыз. Теңдік орындалады сонда және тек қана сонда,
егер  және
және
 өзара пропорционал
болса. Осылайша, Гёльдердің классикалық теңсіздігін дәлелденді
[20].
өзара пропорционал
болса. Осылайша, Гёльдердің классикалық теңсіздігін дәлелденді
[20].
3-Теорема. Егер  болса,
онда
болса,
онда
 (2.9.21)
(2.9.21)
болады. Теңсіздік белгісі
қарама-қарсы белгісіне өзгереді, егер
 болса.
(
болса.
( үшін
үшін  болады деп жорамалдау
керек). Осы жағдайлардың әрқайсысында теңдік орындалады сонда және
тек қана сонда, егер
болады деп жорамалдау
керек). Осы жағдайлардың әрқайсысында теңдік орындалады сонда және
тек қана сонда, егер  және
және
 өзара пропорционал
болса.
өзара пропорционал
болса.
Классикалық теңсіздіктер қатарын аяқтау үшін Минковскийдің теңсіздігін де келтірейік [21].
4-Теорема. Егер  болса,
онда
болса,
онда
 (2.9.22)
(2.9.22)
болады. Теңсіздік белгісі
қарама-қарсы белгісіне өзгереді, егер
 болса.
(
болса.
( үшін
үшін  болады деп жорамалдау
керек). Осы жағдайлардың әрқайсысында теңдік орындалады сонда және
тек қана сонда, егер (x)
және (y)
өзара пропорционал
болса.
болады деп жорамалдау
керек). Осы жағдайлардың әрқайсысында теңдік орындалады сонда және
тек қана сонда, егер (x)
және (y)
өзара пропорционал
болса.
Әуелі осы теореманың шағын дәлелдеуін ұсынамыз, ал кейіннен, Минковскийдің теңсіздігін квазисызықтандыру арқылы шығарамыз.
 (2.9.23)
(2.9.23)
теңдігінің оң жағындағы әрбір қосындыға p және q дәрежелері бар Гёльдер теңсіздігін қолданайық, нәтижесінде (2.9.22) теңсіздікке пара-пар келетін

теңсіздігін аламыз. Теңсіздік
белгісі қарама-қарсы белгісіне өзгереді,
егер
 болса. Теңдік орындалады сонда
және тек қана сонда, егер
болса. Теңдік орындалады сонда
және тек қана сонда, егер  және
және
 -ға пропорционал болса
немесе (x)
және
(y)
өзара пропорционал
болса.
-ға пропорционал болса
немесе (x)
және
(y)
өзара пропорционал
болса.
(2.9.22) теңсіздік кейде «үшбұрыш
теңсіздігі» деп те аталады, себебі  үшін ол геометриялық тұрғыдан
алғанда п-өлшемді евклидтік кеңістікте
түрлендірілуі мүмкін, бұл жағдай ол үшбұрыштың екі қабырғасының
ұзындықтарының қосындысы үшінші қабырғаның ұзындығынан кем болмайды
деген мағынаны береді. Бұл жағдайда теңсіздік
үшін ол геометриялық тұрғыдан
алғанда п-өлшемді евклидтік кеңістікте
түрлендірілуі мүмкін, бұл жағдай ол үшбұрыштың екі қабырғасының
ұзындықтарының қосындысы үшінші қабырғаның ұзындығынан кем болмайды
деген мағынаны береді. Бұл жағдайда теңсіздік
 -дің барлық нақты
мәндері (оң болуы шарт емес) үшін орындалады және теңдіктің
орындалуының шарты ретінде (x)
және
(y) өзара пропорционалдығының оң
мән болуы, яғни әйтеуір біреу нөлден өзге болатын
және
-дің барлық нақты
мәндері (оң болуы шарт емес) үшін орындалады және теңдіктің
орындалуының шарты ретінде (x)
және
(y) өзара пропорционалдығының оң
мән болуы, яғни әйтеуір біреу нөлден өзге болатын
және

болатындай  және
және
 сандарының бар болуы
алынады.
сандарының бар болуы
алынады.
Минковский теңсіздігі.
Бұл типті ұйғарымдардың алғашқы мысалы ретінде жоғарыда дәлелденген Минковский теңсіздігінің жаңа дәлелдеуін келтірейік.
5-Теорема.  үшін
үшін
 (2.9.24)
(2.9.24)
болады.
Дәлелдеу. Гёльдер теңсіздігіне сәйкес
 (2.9.25)
(2.9.25)
болғандықтан,

болатынын табамыз,
мұндағы  –
–

қатынасымен анықталатын облыс. Дәлелдеу керегі осы.
Гёльдер теңсіздігіндегі
теңдіктің орындалу шартын қолдана отырып,
(2.9.24) теңсіздіктегі теңдік белгісі
орындалады сонда және тек қана сонда, егер
немесе  болса, немесе
(x)
пен
(y) өзара пропорционал болса
екенін көрсету қиын емес.
болса, немесе
(x)
пен
(y) өзара пропорционал болса
екенін көрсету қиын емес.
Минковскийдің өзге теңсіздігі.
Квазисызықтандыру әдісін қолдана отырып, 2.20 және 2.21 бөлімшелерінде пайдаланылатын тағы бір теңсіздікті енгізейік.
6-Теорема.  үшін
үшін
 (2.9.26)
(2.9.26)
болады.
Дәлелдеу. Арифметикалық және геометриялық орталардың арасындағы теңсіздік
 (2.9.27)
(2.9.27)
болатынын көрсетті,
мұндағы  –
–
 (2.9.28)
(2.9.28)
қатынасымен анықталатын облыс. (2.9.27) теңдіктен ізделінді теңсіздікті төмендегідей етіп табамыз:
 (2.9.29)
(2.9.29)
 үшін Минковский
теңсіздігі.
үшін Минковский
теңсіздігі.
Квазисызықтандыруды тағы да қолдана отырып келесідей қорытынды шығарамыз.
7-Теорема. Егер  болса,
онда
болса,
онда
 (2.9.30)
(2.9.30)
болады.
Дәлелдеу. Айталық,
 болсын. Бұл белгілеулер
арқылы
болсын. Бұл белгілеулер
арқылы
 (2.9.31)
(2.9.31)
болатынын дәлелдегіміз келіп
тұр.  үшін
үшін
 (2.9.32)
(2.9.32)
болатындықтан, онда

болады,
мұндағы  функциясы
функциясы
 қатынастарымен
анықталады. Дәлелдеу керегі осы.
қатынастарымен
анықталады. Дәлелдеу керегі осы.
2.10. Квазисызықтандыру
Квазисызықтандыру әдісін
қарастыруды мынадай ескертпеден бастайық:
 үшін Гёльдер
теңсіздігінің дискреттік нұсқасын төмендегідей ұйғарымдауға
болады:
үшін Гёльдер
теңсіздігінің дискреттік нұсқасын төмендегідей ұйғарымдауға
болады:
8-Теорема.  үшін
үшін
 (2.10.1)
(2.10.1)
ұғымды аламыз,
мұндағы  –
–
 (2.10.2)
(2.10.2)
қатынастармен анықталатын облыс.
Бұл ұғымның маңыздылығы (2.10.1) теңсіздіктің сол жағында тұрған сызықтық емес функцияны сызықтық функциялардың жанаспа қисығы түрінде көрсете алуымызда. Яғни сызықтық емес функцияның кейбір тривиал емес қасиеттерін

сызықтық функцияның тривиал қасиеттерінің қарапайым салдарлары түрінде орната аламыз. Бұл ойдың жалғасы төмендегі 2.13 бөлімшеде қарастырылатын болады.
Енді квазисызықтандыру ұғымы туралы бірнеше алдын ала пайымдауларды қарастырайық.
Айталық,
 функциясы
– х
және
у
екі айнымалысы бар функция
болсын, мұндағы х
және
у
–
R
және
S
нормаланған кеңістіктерінің
элементтері.
функциясы
– х
және
у
екі айнымалысы бар функция
болсын, мұндағы х
және
у
–
R
және
S
нормаланған кеңістіктерінің
элементтері.  –
–
 элементінің нормасының
белгіленуі болсын; х
аргументіне
элементінің нормасының
белгіленуі болсын; х
аргументіне
 (2.10.3)
(2.10.3)
қатынаста қатысты
болатын  жаңа функциясын
анықтайық.
жаңа функциясын
анықтайық.
х-ке
қатысты функциясының кез
келген у
үшін орындалатын оң
таңбалылық, сызықтылық және дөңестік секілді қарапайым
қасиеттері  функциясының сәйкес
қасиеттерінің орындалуына себепші болады. Көптеген
жағдайларда
функциясының сәйкес
қасиеттерінің орындалуына себепші болады. Көптеген
жағдайларда  функциясының сәйкес
қасиеттерін орнатудан гөрі бұл қасиеттерді
функциясының сәйкес
қасиеттерін орнатудан гөрі бұл қасиеттерді
 функциясынан табу
оңайырақ болып келеді.
функциясынан табу
оңайырақ болып келеді.
Алғашқы және ең маңызды
жағдайлардың бірі – кез келген у
үшін
х-ке
қатысты  функциясы сызықтық болу
жағдайы, яғни
функциясы сызықтық болу
жағдайы, яғни
 (2.10.4)
(2.10.4)
Бұдан
 (2.10.5)
(2.10.5)
шығады. Бұл – «үшбұрыш
теңіздігі» немесе  үшін
«субаддитивтік».
үшін
«субаддитивтік».
Келесі маңызды жағдай бұл –
 (2.10.6)
(2.10.6)
Мұндағы
 , интегралдау
үрдісі z
кеңістігінің қандай да бір
облысы бойынша өтеді және
, интегралдау
үрдісі z
кеңістігінің қандай да бір
облысы бойынша өтеді және  функциясы кез
келген у
пен
z
үшін
х-ке қатысты сызықты функция
болады.
функциясы кез
келген у
пен
z
үшін
х-ке қатысты сызықты функция
болады.
Онда
 үшін
үшін
 (2.10.7)
(2.10.7)
болады.
 көрсеткіштері бар
Гёльдер теңсіздігін қолданып, одан
көрсеткіштері бар
Гёльдер теңсіздігін қолданып, одан
 (2.10.8)
(2.10.8)
қатынасын аламыз. Логарифмдеу
арқылы  функциясы кез
келген у
үшін
х-ке қатысты дөңес функция
болатынын көреміз.
функциясы кез
келген у
үшін
х-ке қатысты дөңес функция
болатынын көреміз.
Беллман, Гликсберг және Гросстың кітабында вариациялық санаудың классикалық емес есептеріне қатысты
 (2.10.9)
(2.10.9)
формуласының кейбір қосымшалары берілген [22]. Квазисызықтандыру әдісін Фурье қатарлары теориясында Зигмунд кеңінен қолданған болатын [23].
Дөңес және ойыс функцияларды квазисызықтандыру.
Дөңес және ойыс функциялар мен
функционалдарға қолдануға болатын квазисызықтандыруды қарастырайық.
Бірөлшемді жағдайдан бастайық.  – барлық
u
үшін
u-ға қатысты
және
– барлық
u
үшін
u-ға қатысты
және  болатын қатаң дөңес функция
болсын. Онда
болатын қатаң дөңес функция
болсын. Онда
 (2.10.10)
(2.10.10)
болатынын және жалғыз ғана
максимум  болғанда орындалатынын оңай
көруге болады. Осылайша қатаң ойыс функция үшін
де
болғанда орындалатынын оңай
көруге болады. Осылайша қатаң ойыс функция үшін
де
 (2.10.11)
(2.10.11)
аламыз. Жалпы нәтиже төмендегідей болады.
9-Теорема. Айталық,  функциясы – барлық х үшін
х-ке қатысты қатаң дөңес функция болсын,
онда
функциясы – барлық х үшін
х-ке қатысты қатаң дөңес функция болсын,
онда
 (2.10.12)
(2.10.12)
мұндағы  функциясы
–
функциясы
–  функциясының градиенті.
Жалғыз ғана максимум
функциясының градиенті.
Жалғыз ғана максимум  болғанда ғана
орындалады.
болғанда ғана
орындалады.
Квазисызықтандырудың бұл түрін функционалдық теңдеулерді және оларды шешудің ұқсас әдістерін зерттеуде Беллман [24] және Калаба кеңінен қолданды [25].
Квазисызықтандырудың басқа түрі.
Кездейсоқ айнымалыларды қолдану арқылы квазисызықтандыру әдісін Зигмунд және Марцинкевич қолданды [26].
10-Теорема.  дегеніміз
дегеніміз  құрамына кіретін функциялар
тобы болсын және Т – әрбір i үшін
құрамына кіретін функциялар
тобы болсын және Т – әрбір i үшін
 секілді қасиетке ие
болатын сызықтық түрлендіру болсын. Егер сондай-ақ барлық i
үшін
секілді қасиетке ие
болатын сызықтық түрлендіру болсын. Егер сондай-ақ барлық i
үшін
 (2.10.13)
(2.10.13)
болатындай т тұрақтысы бар
болса, онда S-тың кез келген  функциялар жүйесі
үшін
функциялар жүйесі
үшін
 (2.10.14)
(2.10.14)
болады.
2.11. Беккенбах теңсіздігі
Енді төмендегі нәтижені дәлелдейік [27]:
11-Теорема. Айталық,  және
және  үшін
үшін  болсын.
Онда
болсын.
Онда
 (2.11.1)
(2.11.1)
Дәлелдеу.  үшін теңсіздік тривиалды болып
келеді.
үшін теңсіздік тривиалды болып
келеді.  үшін 2.10
бөлімшедегідей
үшін 2.10
бөлімшедегідей
 (2.11.2)
(2.11.2)
болады. Сондықтан
барлық  үшін
үшін
 (2.11.3)
(2.11.3)
болатынын көрсету жеткілікті
болады (мұндағы  –
–
 қатынастарымен
анықталатын облыс екенін ескерте кетейік).
қатынастарымен
анықталатын облыс екенін ескерте кетейік).
(2.11.3) теңсіздікте кездесетін өрнектерді ықшамдау үшін жаңа айнымалы енгізейік:
 (2.11.4)
(2.11.4)
Бұдан
 және
және  қосындыларын тауып, оларды
ізделінді (2.11.3) теңсіздікке қоя отырып, оны
төмендегідей өзіне пара-пар түрге
келтіреміз:
қосындыларын тауып, оларды
ізделінді (2.11.3) теңсіздікке қоя отырып, оны
төмендегідей өзіне пара-пар түрге
келтіреміз:
 (2.11.5)
(2.11.5)
(2.11.5) теңсіздіктің орындалуын
дәлелдеу үшін сол жағындағы бөлшектің алымына
 үшін Гёльдер теңсіздігін
қолданып,
үшін Гёльдер теңсіздігін
қолданып,
 (2.11.6)
(2.11.6)
аламыз. Осылайша, (2.11.5) теңсіздік орындалады, егер
 (2.11.7)
(2.11.7)
теңсіздігі бар болса. Бірақ
бұл –  , яғни
, яғни
![]() үшін орындалатын Минковский
теңсіздігі.
үшін орындалатын Минковский
теңсіздігі. ![]() үшін
(2.11.7) теңсіздік тривиалды
болады.
үшін
(2.11.7) теңсіздік тривиалды
болады.
![]() үшін
(2.11.1) теңсіздіктегі теңсіздік
белгісі кері белгіге ауыстырылу керек.
үшін
(2.11.1) теңсіздіктегі теңсіздік
белгісі кері белгіге ауыстырылу керек.
2.12. Дрешер теңсіздігі
Беккенбахтың теңсіздігін Дрешер жалпылаған болатын [28]. Оны дәлелдеу үшін Дрешер моменттер әдісін қолданды.
12-Теорема. Егер  болса,
онда
болса,
онда
 (2.12.1)
(2.12.1)
болады.
Бұл нәтижені 2.11 бөлімшеде көрсетілген квазисызықтандыру әдісі арқылы да алуға болады. (2.12.1) теңсіздікті Гёльдер мен Минковскийдің теңсіздіктерін қиыстыру арқылы Данскин де дәлелдеген болатын [29].
2.13. Минковский–Малер теңсіздігі
Теңсіздіктерді дәлелдеудің
2.10-2.12 бөлімшелерде қолданған әдісі Минковскийдің бір идеясына
негізделген болатын [30]. Айталық,  – төмендегі қасиеттерге ие
болатын функция болсын:
– төмендегі қасиеттерге ие
болатын функция болсын:
(![]() а)
а)  үшін
үшін

(ә)
 үшін
үшін  (2.13.1)
(2.13.1)
(б)

 функциясы жалпыланған
қашықтық (координаталар басынан) немесе
функциясы жалпыланған
қашықтық (координаталар басынан) немесе
п-өлшемді
х
векторының
жалпыланған нормасы екені
белгілі.
Егер жоғарыда көрсетілген
қасиеттерге ие болатын функция берілсе, онда
біз поляр
функция деп аталатын және төмендегі
қатынаспен анықталатын  жаңа функциясын шығарып ала
аламыз:
жаңа функциясын шығарып ала
аламыз:
 (2.13.2)
(2.13.2)
Дөңес денелер
теориясында  функциясы «тірек функциясы»
деп аталады. Геометриялық тұрғыдан ол кері
полярларды
функциясы «тірек функциясы»
деп аталады. Геометриялық тұрғыдан ол кері
полярларды  сферасына қатысты түрлендіру
арқылы анықталады. Осы негізде төмендегі екілік қатынас орындалу
керек деген ұйғарымға келуге болады:
сферасына қатысты түрлендіру
арқылы анықталады. Осы негізде төмендегі екілік қатынас орындалу
керек деген ұйғарымға келуге болады:
 (2.13.3)
(2.13.3)
Бұл теңсіздікті расында да Минковский дәлелдеген болатын. Осыдан
 (2.13.4)
(2.13.4)
екені шығады. Бұл теңсіздік алғашқы рет сандардың геометриялық теориясында Малер көрсетті [31].
Кейбір полюс–поляр қатынастарының маңызды жалпыламаларын Л.Юнг қарастырды [32].
Бұл идеяларды кең түрде Лорх зерттеген болатын [33]. Оның еңбектерінде теңсіздіктер, дөңестік және Минковскийдің «аралас көлем» ұғымы арасындағы тығыз байланысты ашатын көптеген маңызды нәтижелерді табуға болады.
2.14. Карамат теңсіздігі
9-Теореманың функциясын көрсетудің мысалы ретінде Островскийге тиесілі болатын [34] және Караматтың келесі теоремасының жалпыламасы болып табылатын бір нәтижені дәлелдейміз [35].
13-Теорема. Айталық, төмендегі
шарттарды қанағаттандыратын  сандарының 2п саны
берілсін:
сандарының 2п саны
берілсін:
(а)

(![]() ә)
ә) 
 (2.14.1)
(2.14.1)
Онда кез келген үзіліссіз
дөңес  функциясы
үшін
функциясы
үшін
 (2.14.2)
(2.14.2)
теңсіздігін аламыз.
Теореманың шарттары өте жасанды болып көрінгенімен, бұндай түрдегі теңсіздіктер көптеген әр түрлі сұрақтарда пайда болатыны анықталды [36].
2.15. Шур түрлендіруі
Алдыңғы бөлімшедегі теореманы өзі жеке дара қызығушылық танытатын келесі теореманың негізінде Карамат дәлелдеген болатын.
14-Теорема.  2п
саны (2.14.1) теңсіздіктерді
қанағаттандырудың қажетті және жеткілікті шарты олардың арасында
төмендегідей қатынастардың орындалуы болып
табылады:
2п
саны (2.14.1) теңсіздіктерді
қанағаттандырудың қажетті және жеткілікті шарты олардың арасында
төмендегідей қатынастардың орындалуы болып
табылады:
 (2.15.1)
(2.15.1)
мұндағы
 (2.15.2)
(2.15.2)
(2.15.1) түрдегі түрлендірулерді
алғашқы рет Шур қарастырды [37]; Островскийдің пікірі бойынша біз
оларды Шур
түрлендірулері деп атайтын боламыз. Соңғы
кездері элементтері (2.15.2) шарттарды
қанағаттандыратын  матрицаларды екі түрлі
стохастикалық деп атайды. Олар кейбір
комбинаторикалық есептерде маңызды рөл
атқарады.
матрицаларды екі түрлі
стохастикалық деп атайды. Олар кейбір
комбинаторикалық есептерде маңызды рөл
атқарады.
2.16. Карамат теңсіздігінің дәлелдеуі
Осы бөлімшеде 13-Теореманы дәлелдеуде квазисызықтандыру әдісін қолдануды көрсетеміз. Бастапқы мәлімет ретінде
 (2.16.1)
(2.16.1)
теңдігін аламыз және
мұндағы  әзірше қатаң дөңес функция деп
пайымдайық.
әзірше қатаң дөңес функция деп
пайымдайық.
Максимум
мәні  , ал
, ал
 болғанда орындалады, біз
(z) мәнінің өзгеріс
облысын
болғанда орындалады, біз
(z) мәнінің өзгеріс
облысын
 (2.16.2)
(2.16.2)
теңсіздіктерімен шектей аламыз.
Ізделінді теңсіздікті дәлелдеу
үшін (2.14.1) шарттарды қанағаттандыратын
барлық  үшін және
(2.16.2) шартты қанағаттандыратын
барлық
үшін және
(2.16.2) шартты қанағаттандыратын
барлық  үшін
үшін
 (2.16.3)
(2.16.3)
Бұл теңсіздік бөліп-бөліп қосудан шығады (Абель–Бруначчи формуласы):
 (2.16.4)
(2.16.4)
теңсіздігі орындалады,
мұндағы  .
.
 болғандықтан,
болғандықтан,  болатынын көреміз. Сонымен
қатар
болатынын көреміз. Сонымен
қатар  болғандықтан, (2.16.3) теңдік расында да
орындалады.
болғандықтан, (2.16.3) теңдік расында да
орындалады.
2.17. Островский теңсіздігі
Функциялардың бұдан да кеңірек
тобына сәйкес теңсіздікті орнату үшін қатаң
дөңес  функциясын
қарастырамыз:
функциясын
қарастырамыз:
 (2.17.1)
(2.17.1)
Максимум мәні
 (2.17.2)
(2.17.2)
облысы бойынша алынады деп
есептей аламыз, себебі біз осындай түрде
реттелген  мәндерін қарастыруды мақсат
етіп отырмыз. Алдыңғы бөлімдегі ұйғарымдар бұл
бөлімдегі
мәндерін қарастыруды мақсат
етіп отырмыз. Алдыңғы бөлімдегі ұйғарымдар бұл
бөлімдегі  бөлшегіне қатысты кейбір
шарттардың орындалуында ғана пайдаланылады.
Әсіресе
бөлшегіне қатысты кейбір
шарттардың орындалуында ғана пайдаланылады.
Әсіресе
 (2.17.3)
(2.17.3)
теңсіздігінің орындалуын талап
ету дұрыс болады. Бұл талап  үшін
үшін
 шартының жалпыламасы.
Егер F
берілген шартты
қанағаттандыратын болса, онда F
Шур шартына қанағаттандырады
деп айтамыз.
шартының жалпыламасы.
Егер F
берілген шартты
қанағаттандыратын болса, онда F
Шур шартына қанағаттандырады
деп айтамыз.
Бұл шарт негізінде алдыңғы бөлімшедегі дәлелдеу толығымен өтіп, біз келесідей теореманы ұйғара аламыз.
15-Теорема. Егер F Шур шартын
қанағаттандыратын болса және  (2.14.1) шарттарын қанағаттандыратын
болса, онда
(2.14.1) шарттарын қанағаттандыратын
болса, онда
 (2.17.4)
(2.17.4)
болады.
Бұл теореманы басқа идея негізінде Л.Фукс дәлелдеген болатын [38]. Оған жақын нәтижелерді Татаркевич пен Бисак көрсетті [39].
2.18. Континуал аналогтар
2.14-2.17 бөлімшелердегі теоремалардың континуал аналогтарын Фан мен Лоренц тапты [40].
 (2.18.1)
(2.18.1)
деп жазамыз, егер
 (2.18.2)
(2.18.2)
және
 (2.18.3)
(2.18.3)
болса. Жоғарыда көрсетілген
жұмыста  функциясына қатысты қажетті
және жеткілікті шарттар келтірілген. Бұл шарттар
негізінде
функциясына қатысты қажетті
және жеткілікті шарттар келтірілген. Бұл шарттар
негізінде  қатынастарын қанағаттандыратын
шектелген және кемімелі
қатынастарын қанағаттандыратын
шектелген және кемімелі  және
және
 функцияларының кез
келген жүйесі үшін
функцияларының кез
келген жүйесі үшін
 (2.18.4)
(2.18.4)
болады.
2.19. Симметриялы функциялар
Енді Маркус пен Лопестің
кейбір қызықты теңсіздіктеріне көшейік [41].
 – теріс емес сандар
болсын;
– теріс емес сандар
болсын;  арқылы осы сандар үшін
құрылған r-ші элементар симметриялы
функцияны белгілейік, яғни
арқылы осы сандар үшін
құрылған r-ші элементар симметриялы
функцияны белгілейік, яғни
 (2.19.1)
(2.19.1)
Айталық,
 болсын.
Нәтижесінде
болсын.
Нәтижесінде  ~
~
 деп жазамыз,
егер
деп жазамыз,
егер
 (2.19.2)
(2.19.2)
болатындай λ саны табылса.
Біз дәлелдейтін бірінші ұйғарым төмендегідей болады.
16-Теорема.  үшін
үшін
 (2.19.3)
(2.19.3)
теңсіздігі орындалады,
егер  -дің
және
-дің
және  -дің кейбіреулері нөлге тең
болмаса. Теңдік орындалады, егер
-дің кейбіреулері нөлге тең
болмаса. Теңдік орындалады, егер  болса
немесе
болса
немесе  ~
~ болса
және
болса
және  -дің
және
-дің
және
 -дің ең болмағанда r саны
оң болса.
-дің ең болмағанда r саны
оң болса.
Дәлелдеу.  үшін
теңсіздік
үшін
теңсіздік
 (2.19.4)
(2.19.4)
тепе-теңдігінен шығады.
Енді  және
және

 деп
пайымдайық.
деп
пайымдайық.  өрнегін
өрнегін
 сандар жүйесі арқылы
белгілейік. Енді бізде екі тепе-теңдік
бар:
сандар жүйесі арқылы
белгілейік. Енді бізде екі тепе-теңдік
бар:
 (2.19.5)
(2.19.5)
Олардың екіншісін i арқылы қосып,
 (2.19.6)
(2.19.6)
аламыз, бұдан біріншісі бойынша
 (2.19.7)
(2.19.7)
шығады.
 (2.19.8)
(2.19.8)
болғандықтан,
 (2.19.9)
(2.19.9)
немесе
 (2.19.10)
(2.19.10)
қатынасын табамыз.
Бұдан  және
барлық х
үшін төмендегі тепе-теңдік бар
болады деген қорытынды шығады:
және
барлық х
үшін төмендегі тепе-теңдік бар
болады деген қорытынды шығады:
 (2.19.11)
(2.19.11)
мұндағы
 .
.
Енді теоремадағы
ұйғарым  үшін орындалады,
яғни
үшін орындалады,
яғни
 (2.19.12)
(2.19.12)
болады деп жорамалдайық.
Теоремадағы ұйғарым орындалмайды, егер
(2.19.12) теңсіздікте теңдік белгісі
тұрғанда қатынасы бар болса. Онда 
 болғанда қандай да
бір i
үшін
болғанда қандай да
бір i
үшін
 (2.19.13)
(2.19.13)
Осылайша, ізделінді
теңсіздік r
үшін де орындалады, егер
қандай да бір i
үшін

 болса. Егер де
әрбір i
үшін
болса. Егер де
әрбір i
үшін

 болса, онда
әрбір i
үшін
болса, онда
әрбір i
үшін
 болады және
онда
болады және
онда
 (2.19.14)
(2.19.14)
Бірақ
 , себебі шарт
бойынша
, себебі шарт
бойынша  сандарының r
саны оң болады.
Сондықтан
сандарының r
саны оң болады.
Сондықтан  болғанда
(2.19.12) теңсіздіктің бірінші
теңсіздігі теңдікпен алмастырылуы керек,
(2.19.13) теңдіктен
(2.19.12) теңсіздіктің ортаңғы
мүшесі
болғанда
(2.19.12) теңсіздіктің бірінші
теңсіздігі теңдікпен алмастырылуы керек,
(2.19.13) теңдіктен
(2.19.12) теңсіздіктің ортаңғы
мүшесі 
 шарты кезінде оң мәнді
қабылдайды, себебі осы шарттан және әрбір
i
үшін
шарты кезінде оң мәнді
қабылдайды, себебі осы шарттан және әрбір
i
үшін


 барлық
i
үшін мүмкін емес екені
шығады.
барлық
i
үшін мүмкін емес екені
шығады.
2.20. Тағы бір теңсіздік
Симметриялы функцияларға жататын тағы бір нәтиже төмендегідей болады.
17-Теорема. Егер  және
және  п оң таңбалы айнымалылары
бар жүйелері болса, онда
п оң таңбалы айнымалылары
бар жүйелері болса, онда
 (2.20.1)
(2.20.1)
болады.
Бұдан да күшті нәтиже теңдік белгісінің орындалу жағдайларын зерттеу жұмысы Лопес пен Маркустың еңбегінде көрсетілген. Біз тек қана ұйғарымдалған теоремамен шектелеміз.
Теореманың дәлелдеуі 6-Теорема мен 16-Теореманың бірігуіне негізделеді. Бұл теоремалар бойынша

 (2.20.2)
(2.20.2)
болады.
2.21. Уайтлидің кейбір қорытындылары
Осыған ұқсас және кеңірек нәтижелерді Уайтли алды. Айталық,
 (2.21.1)
(2.21.1)
болсын,
мұндағы  – оң сандар.
Онда
– оң сандар.
Онда  үшін
үшін
 (2.21.2)
(2.21.2)
теңсіздігі орындалады,
ал  болғанда 17-Теореманың
теңсіздігі орындалады.
болғанда 17-Теореманың
теңсіздігі орындалады.
(2.21.2) теңсіздіктегі жаңа нәтиже
интегралды түрлендірулер әдісі арқылы оңай алынады, бұл әдісті біз
келесі бөлімшеде кеңірек қарастырамыз. Кіші
 және
және  үшін
үшін
 (2.21.3)
(2.21.3)
шығады, бұдан

 (2.21.4)
(2.21.4)
болады. Осыдан
 (2.21.5)
(2.21.5)
шығады, мұндағы
 (2.21.6)
(2.21.6)
(2.21.2) теңсіздік енді Минковский теңсіздігінің салдары болып шықты.
2.22. Гиперболалық көпмүшелер
Осы бөлімшеде Гординг енгізген
маңызды ұғым – гиперболалық
көпмүше ұғымына тоқталып өтеміз
[42].  –
–
 -ге
қатысты т
дәрежелі біртекті көпмүше
және
-ге
қатысты т
дәрежелі біртекті көпмүше
және  – нақты сандар жүйесі болсын.
Егер s-ке
қатысты
– нақты сандар жүйесі болсын.
Егер s-ке
қатысты

теңдеуінің барлық
нақты  үшін
т
нақты түбірі болса,
онда
үшін
т
нақты түбірі болса,
онда  –
а-ға қатысты гиперболалық
көпмүше деп айтамыз. Осыған ұқсас анықтама төмендегідей
болады:
–
а-ға қатысты гиперболалық
көпмүше деп айтамыз. Осыған ұқсас анықтама төмендегідей
болады:
 (2.22.1)
(2.22.1)
мұндағы
 және
және  нақты
х
үшін нақты сан
болады.
нақты
х
үшін нақты сан
болады.
Көріп отырғанымыздай, бұл ұғымның осы тараудың бірнеше нәтижелеріне тікелей қатысы бар және ол матрицалар теориясында маңызды рөлге ие болады.
Бір гиперболалық көпмүше негізінде төмендегі лемма арқылы жаңа гиперболалық көпмүшелерді шығарып алуға болады.
2-Лемма. Егер а
мен  қатысты
қатысты  көпмүшесі гиперболалық
көпмүше болса, онда
көпмүшесі гиперболалық
көпмүше болса, онда
 (2.22.2)
(2.22.2)
көпмүшесі де а-ға қатысты гиперболалық көпмүше болады.
Дәлелдеу 2.1 бөлімшедегідей, Ролль теоремасынан шығады. Осы лемманы екінші рет қолдану
 (2.22.3)
(2.22.3)
теңдігімен
анықталған  көпмүшелері де гиперболалық
екенін көрсетеді.
көпмүшелері де гиперболалық
екенін көрсетеді.
2.23. Гординг теңсіздігі
 –
–  көпмүшесінің толық поляр түрі
болсын, мұндағы
көпмүшесінің толық поляр түрі
болсын, мұндағы  мүшесі –
мүшесі –
 п-өлшемді
вектор:
п-өлшемді
вектор:
 (2.23.1)
(2.23.1)
18-Теорема.  көпмүшесі а-ға қатысты гиперболалық
көпмүше болсын,
көпмүшесі а-ға қатысты гиперболалық
көпмүше болсын,  және М – Р-ның толық поляр
түрі болсын. Осыдан кейін
және М – Р-ның толық поляр
түрі болсын. Осыдан кейін  –
–
 -дің жүйесі
және
-дің жүйесі
және  үшін
үшін  болады.
Сонда
болады.
Сонда
 (2.23.2)
(2.23.2)
Бұл теореманың теңдік белгісін қарастыру арқылы дәлелдеуі толық түсіндіруді талап ететіндіктен, біз Гординг еңбегін қарауды ұсынамыз.
2.24. Гиперболалық көпмүшелердің мысалдары
Екі қызықты мысал
болып  болғандағы а-ға
қатысты
болғандағы а-ға
қатысты
 (2.24.1)
(2.24.1)
гиперболалық көпмүше (бұл
квадраттық түрді 2.25 бөлімшеде қарастырамыз)
және  болғандағы а-ға
қатысты
болғандағы а-ға
қатысты
 (2.24.2)
(2.24.2)
гиперболалық көпмүше
болады. (2.24.2) функция
үшін  болғандағы
болғандағы
 (2.24.3)
(2.24.3)
қатынасы бар
болғандықтан,  – элементар симметриялы
функциялар – (1,1,…,1) қатысты гиперболалық
болады.
– элементар симметриялы
функциялар – (1,1,…,1) қатысты гиперболалық
болады.
Гординг мынаны байқаған
болатын: егер  көпмүшедегі а-ға қатысты гиперболалық
көпмүше болса, онда
көпмүшедегі а-ға қатысты гиперболалық
көпмүше болса, онда  гипербеттері
гипербеттері  үшін
үшін
 болатын
болатын  -дан
тұратын х
облысында дөңес болады. Бұдан
2.19 және 2.20 бөлімшелердегі кейбір нәтижелер шығарылуы
мүмкін.
-дан
тұратын х
облысында дөңес болады. Бұдан
2.19 және 2.20 бөлімшелердегі кейбір нәтижелер шығарылуы
мүмкін.
2.25. Лоренц кеңістіктері
Осы бөлімшеде анықталмаған түрлер үшін кейбір нәтижелерді алу тәсілдерін қарастырамыз. Келесі теореманы дәлелдейік.
19-Теорема. Айталық,
 (2.25.1)
(2.25.1)
функциясы R облысындағы
барлық  үшін
және
үшін
және
 (2.25.2)
(2.25.2)
қатынастарымен анықталған
функция болсын. Онда  үшін
үшін
 (2.25.3)
(2.25.3)
болады.
Дәлелдеу. Жоғарыда түсіндірілген квазисызықтандыру әдісін қолданамыз.
 (2.25.4)
(2.25.4)
болатынын көрсетейік,
мұндағы  – төмендегі қатынастармен
анықталған облыс:
– төмендегі қатынастармен
анықталған облыс:
 (2.25.2)
(2.25.2)
Гёльдер теңсіздігін қолданып,
 (2.25.6)
(2.25.6)
аламыз. Соңғы өрнектің
минимумы  -ге қатысты функция
ретінде (2.25.2) пен
(2.25.5) шарттары
негізінде
-ге қатысты функция
ретінде (2.25.2) пен
(2.25.5) шарттары
негізінде

нүктеде болады
және  тең болады. Бұл
жерден (2.25.4) өрнек шығады. Бұл өрнектен
теорема шығады. Көрсетілген дәлелдеу Беллманға тиесілі
[43].
тең болады. Бұл
жерден (2.25.4) өрнек шығады. Бұл өрнектен
теорема шығады. Көрсетілген дәлелдеу Беллманға тиесілі
[43].
Осындай түрдегі теңсіздіктер туралы ұйғарымдарды Мурнаганнан да көруге болады.
Бұл нәтижелерді басқа жолмен де табуға болады, ол үшін Бохнерге тиесілі өрнекті қолдану керек [44].
 квадраттық түрі
салыстырмалылық теориясында маңызды рөл
атқарады. (2.25.3) теңсіздік әйгілі «егіздер
парадоксына» қатысатынын айта кеткен жөн.
квадраттық түрі
салыстырмалылық теориясында маңызды рөл
атқарады. (2.25.3) теңсіздік әйгілі «егіздер
парадоксына» қатысатынын айта кеткен жөн.
Бұл теңсіздіктердің евклидтік емес геометрия тұрғысынан қарағандағы түрлендіруі Ацел мен Варгтың жұмысында қамтылады.
2.26. Кері теңсіздіктер
Алдыңғы 2.9 бөлімшеде Буняковский–Шварц теңсіздігін және оның жалпыламасы – Гёльдер теңсіздігін қарастырған болатынбыз.
 (2.26.1)
(2.26.1)
түріндегі
теңсіздік  кеңістігінен алынған
барлық u
және
v
үшін ешбір оң
абсолют k
тұрақтысы үшін орындала
алмайды. Алайда мұндай теңсіздік орындалады,
егер u
және
v
кейбір
кеңістігінен алынған
барлық u
және
v
үшін ешбір оң
абсолют k
тұрақтысы үшін орындала
алмайды. Алайда мұндай теңсіздік орындалады,
егер u
және
v
кейбір
 кеңістігіне тиісті
болса.
кеңістігіне тиісті
болса.
Мұндай есептерді Франк пен Пи, Бляшке мен Пик, Бюкнер, Фавар, Бервальд, Кнезер мен Беллман қарастырды. Бұл есептерді моменттер теориясы мен дөңес теңсіздіктер теориясының әдістері арқылы жүйелі қарастыру болатындықтан және Фавар мен Бервальд әдістерімен жалпылауға болатындықтан, осы бөлімшеде Беллманның дәлелдеу әдістері бойынша жүреміз [45], себебі бұл әдістер арқылы нәтижелер дәлдігінің аздығы арқылы басқа бағыттағы жалпыламаларды алуға мүмкіндік береді.
Алғашқы нәтиже мынадай болмақ.
20-Теорема. Айталық,  және
және  функциялары
функциялары  үшін х-ке қатысты төмендегі
шарттар бойынша нормаланған ойыс функциялар
болсын:
үшін х-ке қатысты төмендегі
шарттар бойынша нормаланған ойыс функциялар
болсын:
 (2.26.2)
(2.26.2)
Онда
 (2.26.3)
(2.26.3)
болады.  минималды
мәні
минималды
мәні
 (2.26.4)
(2.26.4)
үшін болады.
Дәлелдеу.  функциясы
функциясы
 үшін ойыс және
анықталған және осы кесіндінің шектерінде нөлге тең болатын
функциялар класына тиісті болсын. Екінші туындысы оң емес болатын
функциялар класының тармағын қарастырайық:
үшін ойыс және
анықталған және осы кесіндінің шектерінде нөлге тең болатын
функциялар класына тиісті болсын. Екінші туындысы оң емес болатын
функциялар класының тармағын қарастырайық:
 (2.26.5)
(2.26.5)
Бұдан да кең кластың функцияларының минимумдары (2.26.5) шартты қанағаттандыратын функциялар класының төменгі шегін нақты табу үрдісіне эквивалентті болады.
 функциясы
– (2.26.5) көрсетілген шекті шарттары
бар
функциясы
– (2.26.5) көрсетілген шекті шарттары
бар  операторы үшін Грин функциясы
болсын, яғни
операторы үшін Грин функциясы
болсын, яғни
 (2.26.6)
(2.26.6)
Онда
 функциясын
функциясын
 (2.26.7)
(2.26.7)
түрінде жазуға болады.
Осы жазуды қолданып,
көрсетілген нормасы бар барлық  ойыс функциялар
үшін
ойыс функциялар
үшін
 (2.26.8)
(2.26.8)
сызықтық функционалдың
минимумын анықтайық, мұндағы  – берілген теріс емес
функция.
– берілген теріс емес
функция.
 (2.26.9)
(2.26.9)
функциясының
 (2.26.10)
(2.26.10)
шартын қанағаттандыратын
барлық  үшін төменгі шектің нақты
мәнін табуымыз керек, мұндағы
үшін төменгі шектің нақты
мәнін табуымыз керек, мұндағы
 (2.26.11)
(2.26.11)
Жоғарыда көрсетілген жағдайға
ұқсас аналогпен пайымдай отырып,  бойынша нақты төменгі шек,
яғни u
бойынша нақты төменгі
шек
бойынша нақты төменгі шек,
яғни u
бойынша нақты төменгі
шек
 (2.26.12)
(2.26.12)
формуласымен анықталатыны көрініп тұр.
Бұл ұйғарымның дәлелдеуін осы
бөлімшеде келтірмейміз, себебі 2.27 бөлімшеде
 үшін жалпы жағдайда
келтіретін боламыз.
үшін жалпы жағдайда
келтіретін боламыз.
Осы нәтижеден 20-Теорема шығады. Бізге
 (2.26.13)
(2.26.13)
белгілі.
 теріс емес функциясына
және
теріс емес функциясына
және  ойыс функция үшін осы
теңсіздікті қолдана отырып, төмендегідей соңғы нәтижені
аламыз:
ойыс функция үшін осы
теңсіздікті қолдана отырып, төмендегідей соңғы нәтижені
аламыз:
 (2.26.14)
(2.26.14)
Енді теңсіздікті тривиал емес
екенін көрсету керек. Гросс қолданған тікелей есептеу әдісі
минимумның  болғанда
және
болғанда
және  симметриялық нүктеде шығатынын
және
симметриялық нүктеде шығатынын
және  -ге тең болатынын көрсетеді.
Эсктремал функциялар жоғарыда көрсетілген
болатын.
-ге тең болатынын көрсетеді.
Эсктремал функциялар жоғарыда көрсетілген
болатын.
2.27.  кеңістігі
кеңістігі
20-Теореманың  -жалпыламасын дәлелдейік
((2.26.7) қара). Біз көрсететін
дәлелдеуді Вейнбергер тапты.
-жалпыламасын дәлелдейік
((2.26.7) қара). Біз көрсететін
дәлелдеуді Вейнбергер тапты.
21-Теорема.  және
және  функциялары – төмендегі
шарттармен нормаланған ойыс функциялар
болсын:
функциялары – төмендегі
шарттармен нормаланған ойыс функциялар
болсын:
 (2.27.1)
(2.27.1)
Онда
 (2.27.2)
(2.27.2)
болады.
Оң жағының
максимумы  болғанда шығатыны көрініп
тұр.
болғанда шығатыны көрініп
тұр.
Дәлелдеу. Жоғарыдағыдай пайымдайық:
 (2.27.3)
(2.27.3)
Онда
 (2.27.4)
(2.27.4)
мұндағы
 (2.27.5)
(2.27.5)
Барлық интегралдар 0 мен 1 аралығында алынады. Гёльдер теңсіздігін қолданып,
 (2.27.6)
(2.27.6)
Дәл осылай
 (2.27.7)
(2.27.7)
(2.27.6) және (2.27.7) теңсіздіктер (2.27.4) өрнекпен бірге
 (2.27.8)
(2.27.8)
екенін көрсетеді.
Есептеу үрдісі (2.27.2) теңсіздіктің оң жағындағы өрнекке алып келеді. Бұл есептеуді Гросс шығарған еді.
Көпөлшемді жағдай.
2.26 бөлімшеде көрсетілген пайымдауларға ұқсас етіп төмендегі жалпы нәтижені дәлелдеуге болады.
22-Теорема.  және
және  қандай да бір R облысына
тиісті Р нүктелері үшін анықталған және төмендегі үш шартты
қанағаттандыратын болсын:
қандай да бір R облысына
тиісті Р нүктелері үшін анықталған және төмендегі үш шартты
қанағаттандыратын болсын:
(![]() а)
а) 
(ә)
R
шегі
В
нүктесінде  (2.27.9)
(2.27.9)
(б)

 функциясы – R облысы
үшін Грин функциясы болсын және
функциясы – R облысы
үшін Грин функциясы болсын және
 (2.27.11)
(2.27.11)
онда
 (2.27.11)
(2.27.11)
болады.
Бұл нәтиженің тривиал емес екенін (яғни теңсіздіктің оң жағы оң таңбалы болатынын) анықтау оңай болмайды. Облыстардың әр түрлі типтері үшін осы минимумды анықтау да қиын мәселе болып тұр.
Мор мен Нолль теоремасы.

теңсіздігінің нақты алуын Мор мен Нолль берген болатын.
23-Теорема. Егер  функциясының
функциясының  кесіндісінде үзіліссіз п-ші
туындысы бар болса, онда
кесіндісінде үзіліссіз п-ші
туындысы бар болса, онда
 (2.27.12)
(2.27.12)
мұндағы
 (2.27.13)
(2.27.13)
 үзіліссіз екені оның
басқа бір өрнектелуінен шығады:
үзіліссіз екені оның
басқа бір өрнектелуінен шығады:
 (2.27.14)
(2.27.14)
мұндағы интегралдау
 (2.27.15)
(2.27.15)
облысы бойынша жүргізіледі.
Егер

сызықты дифференциал теңдеуімен байланысатын кері операторларды қолдансақ бұдан да кеңірек нәтижелер алуға болады.
2.28. Фавар–Бервальд жалпыламасы
2.26 бөлімшеде айтылған Франк–Пик нәтижесінің жалпыламалары Фавар мен Бервальдке тиесілі теңсіздіктердің дербес жағдайлары ретінде алынуы мүмкін.
Фаварға төмендегі теорема тиесілі.
24-Теорема.  функциясы
–
функциясы
–  кесіндісінде теріс емес
үзіліссіз ойыс және тепе-тең нөлден өзге функция болсын.
Айталық
кесіндісінде теріс емес
үзіліссіз ойыс және тепе-тең нөлден өзге функция болсын.
Айталық
 (2.28.1)
(2.28.1)
болсын.  функциясы –
функциясы –
 және
және

үшін шектелген кемімейтін функция болсын. Онда
 (2.28.2)
(2.28.2)
болады.
Фавар бірнеше айнымалысы бар функцияларға қатысты сәйкес теоремаларды дәлелдеді және (2.28.2) теңсіздіктегі теңдік белгісінің орындалу шарттарын көрсетті. 24-Теореманың жалпыламасы болып Бервальд теоремасы алынады.
25-Теорема.  функциясы
–
функциясы
–  кесіндісінде теріс емес
үзіліссіз ойыс және тепе-тең нөлден өзге функция
болсын.
кесіндісінде теріс емес
үзіліссіз ойыс және тепе-тең нөлден өзге функция
болсын.  функциясы
–
функциясы
–  кесіндісінде қатаң
монотонды және үзіліссіз болсын, мұндағы
кесіндісінде қатаң
монотонды және үзіліссіз болсын, мұндағы
 – өте үлкен сан.
Онда
– өте үлкен сан.
Онда
 (2.28.3)
(2.28.3)
теңдеуінің тек қана бір оң
түбірі болады:  .
.
 функциясы
–
функциясы
–  үшін шектелген және
монотонды болсын; айталық
үшін шектелген және
монотонды болсын; айталық
 (2.28.4)
(2.28.4)
(Стильтьес интегралы) болсын. Онда
 (2.28.5)
(2.28.5)
болады,
егер  және
және  функциялары бірдей мағынада
монотонды және
функциялары бірдей мағынада
монотонды және
 (2.28.6)
(2.28.6)
болады, егер бұл функциялар қарама-қарсы мағынада монотонды болса.
Бервальд мұнымен қоса теңдіктің орындалу жағдайларын да анықтап берді.
25-Теореманың бірінші қосымшасы ретінде
 (2.28.7)
(2.28.7)
аламыз. Онда
 (2.28.8)
(2.28.8)
мұндағы
 (2.28.9)
(2.28.9)
Онда (2.28.5) теңсіздіктен
 (2.28.10)
(2.28.10)
табамыз.
 болғанда Франк–Пик
теңсіздігін аламыз, ал
болғанда Франк–Пик
теңсіздігін аламыз, ал  болғанда Фавар теңсіздігін
аламыз:
болғанда Фавар теңсіздігін
аламыз:
 (2.28.11)
(2.28.11)
Басқа дербес жағдайлары ретінде төмендегі теңсіздіктерді алуға болады:
 (2.28.12)
(2.28.12)
және
 (2.28.13)
(2.28.13)
бұл теңсіздіктер сәйкесінше
Фавар мен Бервальдқа тиесілі. Соңғы екі теңсіздік жоғарыда
көрсетілген  -ке қатысты пайымдауларда
орындалады.
-ке қатысты пайымдауларда
орындалады.
Фавар мен Бервальдтың аталған еңбектерінде басқа да көптеген нәтижелер бар, оның ішінде көпөлшемді жағдайлардың жалпыламалары да қамтылған.
2.29. Коши теоремасының басқа түрлері
2.26 – 2.28 бөлімшелерде Коши теңсіздігінің бір түрін қарастырдық. Енді Швейцер мен Пойа–Сегё берген осы теңсіздіктің басқа түрін қарастырайық және дәлелдейік [46].
26-Теорема. Егер  болса,
онда
болса,
онда
 (2.29.1)
(2.29.1)
болады.
Сонымен қатар континуалды аналог та бар болады.
Дрешер көрсеткендей, Коши мен Гёльдердің классикалық теңсіздіктерді моменттер теориясы теоремаларының салдарлары ретінде шығарып алуға болады. 26-Теорема осы типке жатады және осылай дәлелденеді. Көпөлшемді жағдайға қатысты жалпыламаларды Маданский берді.
(2.29.1) теңсіздікті Уотсон жақсартқан болатын, ал дәлелдеуін Касселс берді.
27-Теорема.  болсын,
бірақ
болсын,
бірақ  -дің барлығы бірдей нөлге
тең емес. Онда
-дің барлығы бірдей нөлге
тең емес. Онда
 (2.29.2)
(2.29.2)
болады.
Осы бағыттағы тағы бір нәтиже Фань Цзы мен Тоддқа тиесілі [47].
28-Теорема.  – нақты сандар болсын
және
– нақты сандар болсын
және  болсын.
Онда
болсын.
Онда

Бұл теңсіздік Хассанның бұрынғы нәтиженің жалпыламасы болып табылады [48].
2.30. Коши–Буняковский–Шварц теңсіздіктерін нақтылау
 (2.30.1)
(2.30.1)
функционалының теріс еместігін анықтап, оның төменгі шегінің дәл шығуына мүдделіміз. Егер қарастырып отырған функциялар немесе функционалдар төмендегі мағынада квадрат түрде болса ғана оның төменгі шегін таба аламыз.
Скаляр көбейтінді ұғымын қолданып, барлық u және v үшін теріс емес болатын төмендегі функционалды қарастырайық:
 (2.30.2)
(2.30.2)
u
айнымалысын  айнымалысына алмастырамыз,
мұндағы r
және
s
– скалярлар.
Онда
айнымалысына алмастырамыз,
мұндағы r
және
s
– скалярлар.
Онда  шартына сәйкес төмендегі
теңсіздікті аламыз:
шартына сәйкес төмендегі
теңсіздікті аламыз:
 (2.30.3)
(2.30.3)
Ал бұл теңсіздік, өз кезегінде, төмендегі теңсіздікке алып келеді:
 (2.30.4)
(2.30.4)
Бұл теңсіздік төмендегідей пайымдалады: нақтыланған v және кез келген f пен g екі элементтері үшін анықталған
 (2.30.5)
(2.30.5)
жаңа скаляр
көбейтінді  ескі скаляр көбейтіндінің
қанағаттандыратын
ескі скаляр көбейтіндінің
қанағаттандыратын
 (2.30.6)
(2.30.6)
шартын қанағаттандырады.
Бұл үрдісті қайталауға болады және қайталау арқылы әрбір келесісі алдыңғысынан күштірек болатын теңсіздіктер қатарын аламыз.
2.31. Ескі теңсіздіктен жаңа теңсіздіктерді шығару
(2.30.4) теңсіздігі жүйелеу арқылы алынатын басқа кеңірек теңсіздіктердің дербес жағдайы болып табылады.
 (2.31.1)
(2.31.1)
теңсіздігі теңдік белгісі
орындалады сонда тек қана сонда, егер
 болса деген қасиетке
ие. (2.31.1) теңсіздіктен
болса деген қасиетке
ие. (2.31.1) теңсіздіктен
 (2.31.2)
(2.31.2)
алмастыру арқылы шығатын
ұйытқыған теңсіздікті қарастырайық, мұндағы
 элементтері
– u
мен
v
элементтерімен бірдей,
ал r
және
s
– скаляр
шамалар. F
өрнегін
элементтері
– u
мен
v
элементтерімен бірдей,
ал r
және
s
– скаляр
шамалар. F
өрнегін
 нүктесінің айналасында
дәрежелік қатарға жіктеп, төмендегі қатынасты
аламыз:
нүктесінің айналасында
дәрежелік қатарға жіктеп, төмендегі қатынасты
аламыз:
 (2.31.3)
(2.31.3)
r және s мәндерін өте кіші етіп алып, бұдан барлық r және s үшін
 (2.31.4)
(2.31.4)
теңсіздігі шығатынын көреміз, яғни
 (2.31.5)
(2.31.5)
болу керек.
Бұл ұйғарым Буняковский–Шварц теңсіздігін шығару кезінде қолданылды. Басқа да қызықты теңсіздіктер осы әдіспен Гёльдер теңсіздігінен және арифметикалық және геометриялық орталардың арасындағы теңсіздіктен шығаруға болады.
Арифметикалық және геометриялық орталар арасындағы теңсіздіктерді нақтылау.
Белгілі болғандай, бұл
теңсіздікте әрқашан қатаң теңдік белгісі орындалады,
егер  элементтерінің барлығы өзара
тең болмаса. Алгебралық сандар теориясына
сәйкес
элементтерінің барлығы өзара
тең болмаса. Алгебралық сандар теориясына
сәйкес  «шашырауын»
«шашырауын»
 (2.31.6)
(2.31.6)
дискриминантпен өлшеу арқылы
 (2.31.7)
(2.31.7)
қатынасының  арқылы өрнектелетін төменгі
шегін табу қызықтырады. Бұл типтің нәтижелерін алғашқы рет Шур
алған болатын; бұл сұрақтың одан арғы зерттеуімен Зигель, Кобер мен
Дингхас айналысты.
арқылы өрнектелетін төменгі
шегін табу қызықтырады. Бұл типтің нәтижелерін алғашқы рет Шур
алған болатын; бұл сұрақтың одан арғы зерттеуімен Зигель, Кобер мен
Дингхас айналысты.
Таңбалары кезектесетін теңсіздіктер.
Келесі нәтижені Сегё алды.
29-Теорема.  және
және  функциясы
–
функциясы
–  кесіндісінде дөңес функция
болсын. Онда
кесіндісінде дөңес функция
болсын. Онда
 (2.31.8)
(2.31.8)
болады.
Осыған ұқсас нәтижені аудандарды салыстыру арқылы Беллман алды.
30-Теорема.  және
және  функциясы
–
функциясы
–  кесіндісінде дөңес функция
болсын. Онда егер
кесіндісінде дөңес функция
болсын. Онда егер  болса,
онда
болса,
онда
 (2.31.9)
(2.31.9)
болады.
 дербес жағдайы Вейнберг
тәуелсіз анықтаған болатын.
дербес жағдайы Вейнберг
тәуелсіз анықтаған болатын.
Бұл екі теорема төмендегі Олкин теоремасының дербес жағдайлары болып табылады.
31-Теорема.  және
және  функциясы
–
функциясы
–  кесіндісінде дөңес функция
болсын. Онда
кесіндісінде дөңес функция
болсын. Онда
 (2.31.10)
(2.31.10)
Бұл теореманы Олкин секілді дәлелдеудің орнына, құрамында Олкин теңсіздігі бар басқа теореманы дәлелдейміз, 2.32 бөлімшені қара.
Брунктың еңбегінде Олкиннің бірнеше теңсіздігі қамтылды және олардың бұдан да жалпы нәтижелері берілді. Олар жоғарыдағы 2.14-2.18 бөлімшелерде дәлелденген теоремалармен ұқсас болып келеді.
2.32. Стеффенсен теңсіздігі
Стеффенсенге тиесілі келесі теңсіздікті дәлелдейік. Дәлелдеуді Беллманның жолымен жасаймыз [49].
32-Теорема. Айталық,
(![]() а)
а)  функциясы теріс емес
және
функциясы теріс емес
және  кесіндісінде
кесіндісінде
монотонды кемімелі,
(ә)
 функциясы
функциясы  шарттарын
(2.32.1)
шарттарын
(2.32.1)
қанағаттандырады
болсын. Онда
 (2.32.2)
(2.32.2)
болады, мұндағы
 (2.32.3)
(2.32.3)
Дәлелдеу.  функциясын
функциясын
 (2.32.4)
(2.32.4)
қатынасымен
анықтайық. f
және g,
 функцияларына салынған
шарттардың негізінде
функцияларына салынған
шарттардың негізінде  функциясы
s
a-дан
b-ға дейін өскенде үзіліссіз
және монотонды өспелі және
функциясы
s
a-дан
b-ға дейін өскенде үзіліссіз
және монотонды өспелі және  болатыны көрініп тұр.
Дифференциалдау арқылы
болатыны көрініп тұр.
Дифференциалдау арқылы
 (2.32.5)
(2.32.5)
болатынын табамыз, бұдан
 (2.32.6)
(2.32.6)
шығады. Осыдан,
 (2.32.7)
(2.32.7)
болады және осы арқылы (2.32.2) қос теңсіздіктің оң жақ теңсіздігі дәлелденді. Осылайша сол жақ теңсіздік те дәлелденеді.
Брунк–Олкин теңсіздігі.
(2.31.10) Олкин теңсіздігін алу үшін
(бұл жерде f-ты
h-қа алмастырып),
32-Теоремадан
 (2.32.8)
(2.32.8)
аламыз, мұндағы
 т.с.с. (2.32.9)
т.с.с. (2.32.9)
және
 . Онда біз 31-Теоремадан
да кұштірек нәтиже аламыз.
. Онда біз 31-Теоремадан
да кұштірек нәтиже аламыз.
Стеффенсен теңсіздігінің жалпыламасы.
Осындай жолмен басқа да көптеген теңсіздікті дәлелдеуге болады. мысалы, Стеффенсен теңсіздігінің төмендегідей жалпыламасы орындалады.
33-Теорема. Айталық,
(![]() а)
а)  функциясы теріс
және
функциясы теріс
және  кесіндісінде
кесіндісінде
монотонды кемімелі,
(ә)
 (2.32.10)
(2.32.10)
(б)

мұндағы

Онда
 (2.32.11)
(2.32.11)
мұндағы
 (2.32.12)
(2.32.12)
болады.
Қорытынды
Берілген дипломдық жұмыста көрсетілген теңсіздіктерді шынайы түрде тамаша теңсіздіктер деп атауға болады. Себебі олар математикалық тұрғыдан қарағанда сондай тамаша және қолданбалы ғылыми пәндерде өте кең қолданылады. Негізгі теңсіздіктер арқылы көптеген жағдайда бірнеше функцияны олардың туындысын таппай-ақ (әсіресе зерттелетін кейбір функцияның туындысы болмай қалуы да мүмкін), максимум және минимумға зерттеуге болады. Негізгі теңсіздіктер теңдеуді шешуге және бірнеше (көп жағдайда – екеу) нақты сандардың ішінен «Қайсысы артық?» деген сұраққа жауап беруге, тіпті банктік салымның мүмкін болатын пайдасын есептеуге көмектесе алады.
Бұл дипломдық жұмыстың негізгі бөлімі ХХ ғасырдың ортасында анықталған және математиканың әр түрлі бөлімдеріне (матрицалық алгебра, операторлар теориясы және т.б.) жататын теңсіздіктерді қамтиды. Теңсіздіктерді іздеу және дәлелдеудің жаңа функционалды-аналитикалық әдістерді сипаттау ерекше қызықтырады.
Дипломдық жұмыста теңсіздіктер теориясының негізгі нәтижелері және олардың дәлелдеулері келтірілді. Жұмыстың негізгі бөлімі Коши теңсіздігі мен Лагранж тепе-теңдігінен басталып, сонан соң бір монографияға лайықты болатын п теріс емес сандардың арифметикалық және геометриялық орталары сұрағы қарастырылды. Бұл фундаменталды теңсіздіктің он екі дәлелдеуі келтірілді. Бұл дәлелдеулер алгебра мен анализде қолданылатын теңсіздіктерді шешу әдістерінің көп түрлігін көрсетуге мүмкіндік береді. Әсіресе Коши, Гурвица және Бора дәлелдеулері аса қызықты болып табылады. Келесі болып Гельдер мен Минковскийдің теңсіздіктері қарастырылды. Сонан соң бір-біріне ұқсас, бірақ қиындау болып табылатын Беккебах пен Дрешердің нәтижелері көрсетілді. Бұл жерде алғашқы рет Минковский, кейіннен Малер қолданған квазисызықтандырудың маңызды әдісі пайдаланылады. Бұл әдісті үлкен жетістікпен Юнг, Зигмунд және Беллман қолданған еді. Сондай-ақ екі түрлі стохастикалық матрицаларды түрлендірудің Шура әдісі және Карамат, Островский мен Харди, Литтлвуд пен Пойаның мажорланған реттілік қатарына жататын кейбір нәтижелері көрсетілді және Фано мен Лоренцтің континуалды аналог туралы айтылып, Уайтлиге тиесілі нәтижелер туралы баяндалды. Сонан соң классикалық теңсіздіктерді ұсыну және нақтылаудың өте қызықты сұрақтары қарастырылды. Бұл жерде Бляшка мен Пиктің немесе Бюкнердің әдістерінің орнына дифференциалданған теңдеулерге негізделген кері теңсіздіктерді алудың Беллман әдісін қолданылады. Тараудың соңғы бөлімшесі Вейнбергер, Сегё, Олкин, Беллман және тағы басқалары қарастырған таңбалары кезектесіп тұратын мүшелері бар қосындыларға қатысты болатын теңсіздіктерге арналды. Бұл барлық теңсіздіктер Стеффенсеннің жаңа теңсіздігінің дербес жағдайлары болып табылады.
Баяндаудың жүйелілігі және нақты материалмен толықтығы дипломдық жұмысты математикалық олимпиадаларға қатысуға ниеттеніп жүрген жоғары сынып оқушыларына, сондай-ақ әр түрлі мамандыққа даярлайтын факультеттердің студенттеріне, механиктер, физиктер және инженер-зерттеушілерге математиканың негізгі теңсіздіктерінің анықтамалығы ретінде қолдануға мүмкіндік береді.
Бұл жұмыс мектептегі бейінді сыныптардың жоғары сынып оқушыларына, университеттердің педагогикалық институттардың, техникалық ЖОО-ның математикалық және физикалық факультеттердің студенттеріне, аспиранттарына, мұғалімдеріне, сонымен қатар есептеуіш орталықтардың қызметкерлеріне пайдалы болады.
Пайдаланылған әдебиеттер тізімі
-
А.Колмогоров, О языке математических знаков // Математика – наука и профессия. – М.: Наука, 1988. – 166-173 б.
-
Э.Беккенбах, Р.Беллман, Введение в неравенства. – М.: Мир, 1965.
-
С.Гомонов, Замечательные неравенства: способы получения и примеры применения., учебное пособие. – М.: Дрофа, 2006.
-
П.Коровкин, Неравенства. – М.: Наука, 1966.
-
Г.Харди, Д.Литтльвуд, Г.Полиа, Неравенства. – М.: Ин. Лит., 1948.
-
Коши (Cauchy A.L.), Cours d’Analyse de l’Ecole Royale Polytechnique, Ire partie, Analyse algebrique, Pfris, Debure, 1821, Oeuvres completes, IIe serie, III.
-
Гаусс (Gauss C.F.), Werke, 10, 1, 172-292. Leipzig, Teubher, 1917.
-
Маклорен (Maclaurin C.), A second letter to Mfrtin Folges, Esq.; concerning the roots of education with the demonstration of other rules in algebra, Phil. Trans., 1729, 5996.
-
Якобсталь (Jacobsthal E.), Uber das arithmetische und geometriscche Mittel, Norske Vid. Selsk. Forh. (Trondheim), 1951, 122.
-
Беллман (Bellman R.), Dynamic programming, Princeton, N.J., Princeton University Press, 1957. Русский перевод: Динамическое программирование, ИЛ, М., 1960.
-
Боннесен, Фенхель (Bonnesen T., Fenchel W.), Thorie der konvexen Korper, Berlin, Springer, 1951.
-
Бор (Bohr H.), The arithmetic and geometric means, J. London Math. Soc., 1935, 114.
-
Гурвиц (Hurwitz A.), Uber den Vergleich der arithmetischen und des geometrischen Mittels, Math. Werke, 505-507, Basel, Birkhauser, 1933.
-
Гурвиц (Hurwitz A.), Uber den Erzeugung der Invarianten druch Integration, Math. Werke, 546-564, Basel, Birkhauser, 1933.
-
Юнг (Young W.H.), On classes of summable functions and their Fourier series, Proc. Roy. Soc. (A), 1912, 225-229.
-
Шнайад (Shniad H.), On the convexity of mean value functions, Bull. Am. Math. Soc., 1948, 770-776.
-
Иенсен (Jensen J.L.W.V.), Sur les fonctions convexes et les inequalities entre les valeurs moyennes, Acta Math., 1906, 175-193.
-
Беккенбах (Beckenbach E.F.), An inequality of Jensen, Am. Math. Monthly, 1946, 501-505.
-
Бохер (Bocher M.), Introduction to higher algebra, New York, Macmillan, 1907.
-
Гёльдер (Holder O.), Uber einen Mittelwertsatz, Gotting. Nachr., 1889, 38-47.
-
Минковский (Minkowski H.), Geometrie der Zahlen, I, Leipziq, Teubner, 1896.
-
Беллман, Гликсберг, Гросс (Bellman R., Glicksberg I., Gross O., Some aspects of the mathematical theory of control processes, Santa Monica, Calif., The Rand Corporation, Report R-313, 1958. Русский перевод: Некоторые вопросы математической теории процессов регулирования, ИЛ, М., 1962.
-
Зигмунд (Zygmund A.), On certain integrals, Trans. Am. Math. Soc., 1944, 170-204.
-
Беллман (Bellman R.), Functional equations in the theory of dynamic programming, V, Positivity and quasi-linearity, Proc. Nat. Acad. Sci. USA, 1955, 843-846.
-
Калаба (Kalaba R.), On nonlinear differential equations, the maximum operation, and monotonic convergence, J. Math. and Mech., 1959, 519-574.
-
Марцинкевич, Зигмунд (Marcienkiewicz J., Zygmund A.), Quelques inegalites pour les operations lineaires, Fund. Math., 1939, 115-121.
-
Беккенбах (Beckenbach E.F.), A class ofmeanvalue functions, Am. Math. Monthly, 1950, 1-6.
-
Дрешер (Dresher M.), Moment spaces and intequalities, Duke Math. J., 1953, 261-271.
-
Данскин (Danskin J.M.), Dresher’s inequality, Am. Math. Monthly, 1952, 687-688.
-
Минковский (Minkowski H.), Thorie der konvexen Korper, Berlin, Springer, 1951.
-
Малер (Mahler K.), Ein Ubertragungsprinzip fur konvexe Korper, Casopis Mat. Fysik, 1939, 93-102.
-
Юнг (Young W.H.), On an inequality of Mfrcel Riesz, Ann. of Math., 1939, 567-574.
-
Лорх (Lorch E.R.), On the volume of smooth convex bodies in Hilbert space, Math. Z., 1955, 391-407.
-
Островский (Ostrowski A.), Sur quelques applications des fonctions convexes et concaves au sens de I. Schur., J. Math. Pure Appl., 1952, 253-292.
-
Карамата (Karamata J.), Sur une inegalite relative aux fonctions convexes, Publ. Math. Univ. Belgrade, 1932, 145-148.
-
Блекуэлл (Blackwell D.), Comparison of experiments, Proc. Second Berkeley Symposium on Mathematical Statistics and Probability, 1950, 93-102, Berkeley, Calif., University of California Press, 1951.
-
Шур (Schur I.), Uber eine Klasse von Mittelbildungen mit Anwendungen auf die Determinantentheorie, Sitzber. Berl. Math. Ges., 1923, 9-20.
-
Фукс (Fuchs L.), A new proof of an inequality of Hardy – Littlewood – Polya, Mat. Tidskr., 1947,53-54.
-
Бисак (Beesack P.R.), A hote on an integral inequality, Proc. Am. Math. Soc., 1957, 875-879.
-
Фань-Цзыб Лорентц (Fan K., Lorentz G.G.), An integral inequality. Am. Math. Monthly, 1954, 626-631.
-
Маркус, Лопес (Marcus M., Lopes L.), Inequalities for symmetric functions and Hermitian matrices, Canad. J. Math., 1956, 524-531.
-
Гординг (Garding L.), An inequality for hyperbolic polynomials, J. Math. and Mech., 1959, 957-966.
-
Беллман (Bellman R.), On an inequality concerning an indefinite form, Am. Math. Monthly, 1957, 108-109.
-
Бохнер (Bochner S.), Group invariance of Cauchy’s formula in several variables, Ann. of Math., 1944, 686-707.
-
Беллман (Bellman R.), Converses of Schwarz’s inequality, Duke Math. J., 1956, 429-434.
-
Пойа, Сегё (Polya G., Szego G.,, Aufgaben und Lehrsatze aus der Analysis, I, 57, Berlin, Springer, 1925. Русский перевод: Задачи и теоремы анализа, часть І, Физматгиз, М., 1956.
-
Фань Цзы, Тодд (Fan K., Todd J.), A determinantal inequality, J. London Math. Soc., 1955, 58-64.
-
Хассан (Chassan J.B.), A statistical derivation of a pair of trigonometrical inequalities, Am. Math. Monthly, 1955, 353-356.
-
Беллман (Bellman R.), On inequalities with alternating signs, Proc. Am. Math. Soc., 1959, 807-809.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Дипломдық жұмыс, математика
Дипломдық жұмыс, математика
Мазмұны
1. Теңсіздіктің теориялық аспектілері 5
1.2. Теңсіздіктер туралы ілімнің негізгі аксиомалары 7
1.3. Теріс көбейткіштері бар көбейтінділер 11
2. Математиканың негізгі теңсіздіктері 12
2.3. Анализ және Лагранжтың көбейткіштері 18
2.4. Функционалдық теңдеулер 19
2.5. Мажорлау – Бордың дәлелдеуі 21
2.8.  орталары және
орталары және  қосындылары 24
қосындылары 24
2.9. Классикалық теңсіздіктерді жалпылау 27
2.13. Минковский–Малер теңсіздігі 44
2.16. Карамат теңсіздігінің дәлелдеуі 46
2.17. Островский теңсіздігі 47
2.19. Симметриялы функциялар 48
2.21. Уайтлидің кейбір қорытындылары 51
2.22. Гиперболалық көпмүшелер 52
2.24. Гиперболалық көпмүшелердің мысалдары 54
2.28. Фавар–Бервальд жалпыламасы 61
2.29. Коши теоремасының басқа түрлері 63
2.30. Коши–Буняковский–Шварц теңсіздіктерін нақтылау 64
2.31. Ескі теңсіздіктен жаңа теңсіздіктерді шығару 65
2.32. Стеффенсен теңсіздігі 67
Қорытынды 70
Кіріспе
Теңсіздіктер қазіргі заманғы математиканың көптеген бөлімдерінде фундаменталды рөлге ие, теңсіздіктерсіз физика да, математикалық статистика да, экономика да әрекет ете алмайды. Алайда қазіргі кезде жалпы «теңсіздіктер теориясына» қатысты жақсы ұйымдастырылып жазылған жұмыс жоқ, бірақ теңсіздіктердің жекелеген бөлімдерін анықтау үшін шағын теория жасалды.
Қай түрде болса да теңсіздіктер математиканың классикалық бөлімдерінде де (геометрия, дифференциал және интегралды есептеулерде, сандар теориясында), қазіргі заманғы бөлімдерінде де (автоматтар теориясы, кодтау теориясы) кездеседі.
Өкінішке орай мектептегі математиканың негізгі курсында классикалық теңсіздіктер деп аталатын нағыз математикалық байлық туралы ештеңе айтылмайды. Екі теріс емес нақты сандардың арифметикалық және геометриялық орталары арасындағы қатынасты ғана мектеп оқулықтарының беттерінен табуға болады.
Қандай да бір нәтижеге алғашқы болып жеткен ғалымдарды атап, олардың еңбегін елеп кету керек. Алайда нәтижелердің көбісі геометрияның, астрономияның немесе физиканың қандай да бір жұмысының кейбір көмекші құралы ретінде пайда болып қолданып, бірнеше жылдан кейін қайтадан жаңалық ретінде ашылды. Бұл жағдайдың салдары ретінде көптеген тамаша теңсіздіктердің аттарының сақталмауын алуға болады. Әр түрлі елдерде және әр түрлі математика мектептерінде бір теңсіздікті әр түрлі атайды және оның ашылуын әр түрлі математик ғалымдарға жазып қояды, алайда көп жағдайда бұл теңсіздік одан да жалпылама болатын теңсіздіктің дербес жағдайы болып шығады.
Көптеген нәтижелердің авторсыз
қалуының басқа да себебі бар. Мысалы, кез келген нақты санның
квадраты қашанда теріс емес, яғни кез келген
нақты a
және
b
сандары
үшін  қатынасы орындалады,
яғни
қатынасы орындалады,
яғни  , бұдан кез келген нақты теріс
емес
, бұдан кез келген нақты теріс
емес  және
және
 сандары үшін әйгілі
«мектептік» арифметикалық
сандары үшін әйгілі
«мектептік» арифметикалық  ортасы мен
геометриялық
ортасы мен
геометриялық  ортасы
арасындағы
ортасы
арасындағы  қатынасы шығады деген
фундаменталды фактын алғаш ашқан ғалымды қалай табуға
болады.
қатынасы шығады деген
фундаменталды фактын алғаш ашқан ғалымды қалай табуға
болады.
Алайда, бұл дипломдық жұмыста көптеген теңсіздіктердің авторларын атап, олардың атымен аталған теңсіздіктердің түрлері қарастырылады.
Берілген тақырыптың өзектілігі – классикалық теңсіздіктерді қолданбай шешуін табу қиын немесе шешуі мүлдем шықпайтын есептер оқушыларға арналған математикалық олимпиадаларда жиі кездеседі, сондықтан қандай да бір математикалық сайысқа қатысатын оқушыға аса танымал және жиі қолданылатын тамаша теңсіздіктерді білу қажет. Көптеген математикалық олимпиадаларда айнымалысы бар теңсіздіктерді дәлелдеу тапсырмалары жиі кездеседі. Осы тапсырмаларды шешу жолы көбіне жалпыға танымал (бірақ мектеп математика курсында қарастырылмайтын) фактілерге сүйенеді немесе бұл есептерді шешу тәсілі мектеп математика курсында берілген материал көлемінен шықпайтын қарапайым пайымдаулардың қатарына сүйенеді, бірақ осы элементар пайымдаулардың қатарын құрудың логикасы мен идеясы мектеп математика курсының әдістер мен тәсілдерінің шегінен шығып кетеді.
Берілген дипломдық жұмыстың зерттеу объектісі – «Математиканың негізгі теңсіздіктері» тақырыбын оқып үйрену арқылы мектеп математика курсынан алған теңсіздіктер ұғымын кеңейтілуі.
Зерттеу пәні – математиканың негізгі теңсіздіктерінің топталуы.
Мақсаты – математикалық олимпиадаларға қатысатын оқушылардың мектеп математика курсынан белгілі теңсіздіктер туралы білімді кеңейту.
Міндеттер:
-
теңсіздік туралы жалпы мағлұмат алу;
-
берілген тақырыпты кеңейту;
-
математикалық олимпиадаларға қатысатын оқушыларға көмек көрсету.
Зерттеу әдістері:
-
ғылыми, оқу әдебиеттерді талдау;
-
теориялық материалды жинақтау және жүйелеу;
-
әдістемелік жоспарларды жинақтау.
Берілген жұмыстың құрамы:
-
Теңсіздіктер туралы жалпы мәлімет.
-
Математиканың негізгі теңсіздіктерін жалпылау, талдау.
Жұмыстың тәжірибелік маңыздылығы – жинақталған материал мұғалімнің басқаруымен немесе өз бетімен кейбір классикалық теңсіздіктермен танысқысы келетін жоғары сынып оқушылары мен ЖОО студенттеріне математиканың негізгі теңсіздіктерін оқып үйрену үрдісінде пайдалы болады.
1. Теңсіздіктің теориялық аспектілері
1.1. «Артық» қатынасы
« > » белгісі «артық» деген
мағынаны білдіретінін еске түсірейік. Онда біз мына сұраққа жауап
бере аламыз:  екені дұрыс па? Әрине,
дұрыс.
екені дұрыс па? Әрине,
дұрыс.
Бірақ
 екені дұрыс па? Бұл
жағдайда –3 саны –2 санына қарағанда «артық теріс сан» деп айтуға
болады. бірақ бұл ұйғарым берілген сұрақтың жауабы болмайды. Егер
нақты сандар (оң және теріс, рационал және иррационал сандар,
сондай-ақ нөл) 1-суретте көрсетілгендей, геометриялық әдіс арқылы
оңға бағытталған сан осіндегі нүктелер түрінде белгіленген болса,
онда сан осінде солдан оңға қарай қозғалу барысында сандар өсу
ретімен шыға береді. –2 санын бейнелейтін нүкте –3 санын
бейнелейтін нүктенің оң жағында орналасады;
сондықтан
екені дұрыс па? Бұл
жағдайда –3 саны –2 санына қарағанда «артық теріс сан» деп айтуға
болады. бірақ бұл ұйғарым берілген сұрақтың жауабы болмайды. Егер
нақты сандар (оң және теріс, рационал және иррационал сандар,
сондай-ақ нөл) 1-суретте көрсетілгендей, геометриялық әдіс арқылы
оңға бағытталған сан осіндегі нүктелер түрінде белгіленген болса,
онда сан осінде солдан оңға қарай қозғалу барысында сандар өсу
ретімен шыға береді. –2 санын бейнелейтін нүкте –3 санын
бейнелейтін нүктенің оң жағында орналасады;
сондықтан  деп есептеу керек. Дәл
осылай,
деп есептеу керек. Дәл
осылай,
 (1.1.1)
(1.1.1)

1-сурет
Осылайша, теңсіздікті анықтайтын төмендегідей геометриялық ереже аламыз:
a және b – оңнан соңға
бағытталған сан осінде нүктелер арқылы белгіленген қандай да бір
нақты сандар болсын. Онда  болады сонда және тек қана
сонда, егер а санын бейнелейтін нүкте b санын бейнелейтін нүктенің
оң жағында жатса.
болады сонда және тек қана
сонда, егер а санын бейнелейтін нүкте b санын бейнелейтін нүктенің
оң жағында жатса.
Сондықтан
 немесе
немесе  деп айтсақ, ол жоғарыда
берілген ережеге қарсы болар еді, яғни дұрыс болмас еді
[1].
деп айтсақ, ол жоғарыда
берілген ережеге қарсы болар еді, яғни дұрыс болмас еді
[1].
Теңсіздіктермен жұмыстану барысында көп жағдайда графикалық түрде емес, алгебралық түрде әрекет ету керек. Егер негізгі ұғым ретінде оң сан ұғымын алатын болсақ, онда жоғарыда көрсетілген геометриялық ережені төмендегідей алгебралық ережемен алмастыруға болады:
Анықтама. a және b – қандай да бір
нақты сандар болсын. Онда  болады сонда және тек қана
сонда, егер
болады сонда және тек қана
сонда, егер  оң
болса.
оң
болса.
Яғни егер
 ,
ал
,
ал  болса,
онда
болса,
онда  айырмасы оң болады. Сондықтан
жоғарыда қарастырылған геометриялық ұйғарым
бойынша
айырмасы оң болады. Сондықтан
жоғарыда қарастырылған геометриялық ұйғарым
бойынша  болады.
(1.1.1) теңсіздіктерді сандардың
айырмасын табуға негізделген осы алгебралық әдіс арқылы тексеруге
болады, сондай-ақ төмендегі теңсіздіктерді геометриялық та,
алгебралық та әдістер арқылы нақтылауға
болады:
болады.
(1.1.1) теңсіздіктерді сандардың
айырмасын табуға негізделген осы алгебралық әдіс арқылы тексеруге
болады, сондай-ақ төмендегі теңсіздіктерді геометриялық та,
алгебралық та әдістер арқылы нақтылауға
болады:
 .
.
Жоғарыда
 теңсіздігін оң сан ұғымы
арқылы анықтадық. Барлық Р
оң сандар жиыны және оған
сәйкес барлық N
теріс сандар жиыны және жалғыз
ғана 0 саны бар О
жиыны теңсіздіктерді оқып
үйренуде үлкен рөл ойнайды. Расында да, нақты сандар жиынының
жалпыға таныс коммутативтік, ассоциативтік және дистрибутивтік
қасиеттері секілді алгебралық қасиеттерін пайдалана отырып мынадай
қорытындыға келеміз: нақты сандар жиынында
орындалатын реттіліктің қатынастарының негізі ретінде Р оң сандар
жиынына қатысты болатын екі аксиома
алынады. Бұл аксиомалар келесі
бөлімшеде беріледі.
теңсіздігін оң сан ұғымы
арқылы анықтадық. Барлық Р
оң сандар жиыны және оған
сәйкес барлық N
теріс сандар жиыны және жалғыз
ғана 0 саны бар О
жиыны теңсіздіктерді оқып
үйренуде үлкен рөл ойнайды. Расында да, нақты сандар жиынының
жалпыға таныс коммутативтік, ассоциативтік және дистрибутивтік
қасиеттері секілді алгебралық қасиеттерін пайдалана отырып мынадай
қорытындыға келеміз: нақты сандар жиынында
орындалатын реттіліктің қатынастарының негізі ретінде Р оң сандар
жиынына қатысты болатын екі аксиома
алынады. Бұл аксиомалар келесі
бөлімшеде беріледі.
«а оң саны» ұйғарымын
символдық түрде « » деп жазады, бұл жазу
«Р
жиынының
а
элементі» немесе
«а
Р
жиынына тиісті» деп оқылады.
Осылайша,
» деп жазады, бұл жазу
«Р
жиынының
а
элементі» немесе
«а
Р
жиынына тиісті» деп оқылады.
Осылайша,  .
.
P, N, O жиындары және олардың элементтері жөнінде сөз қозғайық.
Нөл саны әрине О жиынының жалғыз 0 элементі болып табылады; оның кез келген нақты а саны үшін орындалатын

қасиеті бар.
N
теріс сандар жиынына көше
отырып, теріс сан ұғымы қарама-қарсы саны ұғымынан өзгеше екенін
ескерте кетейік. а
санына қарама-қарсы сан
төмендегі теңдікті қанағаттандырады және
 деп
анықталады
деп
анықталады

Яғни егер
 болса, онда
қарама-қарсы а
саны
болса, онда
қарама-қарсы а
саны
 болады,
себебі
болады,
себебі  Дәл осылай,
егер
Дәл осылай,
егер  болса,
онда
болса,
онда  , себебі
, себебі

Теріс
сан оң санға қарама-қарсы сан
ретінде анықталады. Осылайша  сандары
Р
оң сандар жиынының элементтері
екенін білеміз; сондықтан
сандары
Р
оң сандар жиынының элементтері
екенін білеміз; сондықтан  сандары
N
теріс сандар жиынының
элементтері болады [2].
сандары
N
теріс сандар жиынының
элементтері болады [2].
Негізгі ұғым – оң сан ұғымын анықтамай-ақ екі негізгі аксиома негізінде осы сандардың сипаттамасына көшейік.
Енді І және ІІ Аксиомалардың күшіне көзімізді жеткізейік. Бұл аксиомалар арқылы нөлге тең емес нақты сандардың қайсысы Р оң сандар жиынына тиісті екенін және қайсысы N теріс сандар жиынына тиісті екенін білуге болады.
Оны көрсету үшін сәйкес сандардың сипаттамасы туралы ақпарат бізге алдын ала белгілі болмай, аксиомалардан алынды деген мағынаны білдіретіндей етіп «оң» және «теріс» сөздерін тырнақшаға алып жазамыз.
 санынан
бастайық.
санынан
бастайық.  болғандықтан,
болғандықтан,  екені шығады.
Осылайша,
екені шығады.
Осылайша,  «оң» болады.
Бірақ
«оң» болады.
Бірақ

яғни 1 – «оң» сан.
Ары қарай
 . 1 – «оң» сан екенін
жаңа анықтағандықтан және
. 1 – «оң» сан екенін
жаңа анықтағандықтан және 
болатындықтан, онда екі «оң» санның қосындысы «оң» сан болатынын
көрсеткен ІІ Аксиомаға сәйкес 2 – «оң» сан
болады.
Енді
 болсын.
Онда
болсын.
Онда  болады; осылайша, «оң» 2
санының және a
санының көбейтіндісі – «оң» 1
саны болады. Бірақ егер а
«теріс» сан болған болса, онда
2 мен а-ның көбейтіндісі «теріс»
болар еді. Сондықтан
болады; осылайша, «оң» 2
санының және a
санының көбейтіндісі – «оң» 1
саны болады. Бірақ егер а
«теріс» сан болған болса, онда
2 мен а-ның көбейтіндісі «теріс»
болар еді. Сондықтан  «оң» болу
керек.
«оң» болу
керек.
Осылайша,
 сандары «оң» болады және
сәйкесінше 1-кестеге сәйкес
сандары «оң» болады және
сәйкесінше 1-кестеге сәйкес  сандары «теріс»
болады.
сандары «теріс»
болады.
Жалғастыра отырып 3, 4 және
т.б. бүтін сандар,  және т.б. бөлшектер
және
және т.б. бөлшектер
және  және т.б. бөлшектер «оң»
болатынын және сәйкесінше
және т.б. бөлшектер «оң»
болатынын және сәйкесінше  және т.б. «теріс» болатынын
көрсете аламыз. Яғни нөлге тең емес кез келген рационал санның «оң»
немесе «теріс» болатынын анықтай аламыз.
және т.б. «теріс» болатынын
көрсете аламыз. Яғни нөлге тең емес кез келген рационал санның «оң»
немесе «теріс» болатынын анықтай аламыз.
Иррационал сандарды анықтауда қолданылатын шекті ауысуларды рационал сандардың қайсысы «оң» және қайсысы «теріс» болатын ақпаратқа сүйене отырып нақты сандардың реттелген өрісіне тиісті болатын берілген иррационал санның «оң» немесе «теріс» екенін анықтау үшін пайдалануға болады. Осы жұмыста біз иррационал сандарды қарастырмаймыз.
1.2. Теңсіздіктер туралы ілімнің негізгі аксиомалары
Р оң сандар жиынына қатысты төменде келтірілетін сөйлемдер дәлелденбейді; сондықтан олар аксиомалар деп аталады. Теңсіздіктер теориясы жалғыз ғана осы сөйлемдер негізінде (нақты сандар жиынының алгебралық қасиеттерімен қатар) дамитыны өте қызықты факт екенін байқау керек.
Аксиома
І. Егер а – нақты сан болса,
онда төменде келтірілген ұйғарымдардың ішінен жалғыз және тек қана
жалғыз ұйғарым орындалады:
а – О жиынының жалғыз 0 элементі; а – Р оң сандар жиынының
элементі; – a – Р жиынының элементі.
Аксиома
ІІ. Егер a және b – Р оң сандар
жиынының элементтері болса, онда олардың
 қосындысы және
олардың
қосындысы және
олардың  көбейтіндісі Р жиынының
элементі болады.
көбейтіндісі Р жиынының
элементі болады.
І Аксиомада көрсетілген
бір-бірін өзара жоққа шығаратын мүмкіндіктер кез
келген а
нақты саны мен оған
қарама-қарсы –
a саны арасында төмендегідей
қатынастар орнатады: егер а
нөл болса, онда
да нөл болады;
егер а
оң
сан болса,
онда –
a саны жоғарыда келтірілген
анықтама негізінде теріс сан болады; ал
егер –
a оң
сан болса,
онда  теріс сан анықтамасы
негізінде теріс болу керек. Осылайша,
қарама-қарсы а
және
–
a сандарының
жұбы P,
N және
О
жиындары бойынша 1-кестеде
көрсетілгендей орналасады.
теріс сан анықтамасы
негізінде теріс болу керек. Осылайша,
қарама-қарсы а
және
–
a сандарының
жұбы P,
N және
О
жиындары бойынша 1-кестеде
көрсетілгендей орналасады.
1-кесте. Өзара қарама-қарсы сандар
жұптарын орналастыру
|
Сан |
Жиын |
|
a |
P N O |
|
– a |
N P O |
Сандарды геометриялық түрде кескіндеуде (1-сурет) а және – a сандарын бейнелейтін нүктелер немесе нөл нүктесін бейнелейтін нүктемен беттеседі, немесе бұл нүктенің екі жағында орналасады [3].
І Аксиома
Р
оң сандар жиынына қатысты
болады; басқа жағынан қарағанда  теңсіздігі Р
жиынының терминдері негізінде
анықталған болатын. Енді осы аксиоманы теңсіздіктер тілінде
жазайық.
теңсіздігі Р
жиынының терминдері негізінде
анықталған болатын. Енді осы аксиоманы теңсіздіктер тілінде
жазайық.
Егер
a
және
b
– кез келген нақты сандар
болса, онда олардың  айырымы да нақты сан болады;
сондықтан І Аксиоманы
айырымы да нақты сан болады;
сондықтан І Аксиоманы  айырымына да қолдануға болады.
Осылайша, немесе
айырымына да қолдануға болады.
Осылайша, немесе  (яғни
(яғни
 ),
немесе
),
немесе 
(яғни  ), немесе
), немесе
 (яғни
(яғни  ) және осы үш мүмкіндік
бір-бірін өзара жоққа шығарады. Осылайша, келесі ұйғарым
) және осы үш мүмкіндік
бір-бірін өзара жоққа шығарады. Осылайша, келесі ұйғарым
І Аксиоманың салдары болып табылады:
Аксиома І'. Егер a және b – нақты сандар болса, онда төмендегі қатынастардың жалғыз және жалғыз ғана қатынас орындалады:

 болғандағы арнаулы
жағдайда І' Аксиома егер а
– нақты сан болса, онда
бір-бірін өзара жоққа шығаратын үш жағдайдың жалғыз және жалғыз
жағдайы орындалады деп пайымдайды:
болғандағы арнаулы
жағдайда І' Аксиома егер а
– нақты сан болса, онда
бір-бірін өзара жоққа шығаратын үш жағдайдың жалғыз және жалғыз
жағдайы орындалады деп пайымдайды:  (яғни
(яғни
 );
);
 (яғни
(яғни  );
);
 (яғни
(яғни  ). Яғни І Аксиома І'
Аксиомадан шығарылады.
). Яғни І Аксиома І'
Аксиомадан шығарылады.
Егер S ұйғарымын Т ұйғарымынан шығаруға болатын болса (яғни оның салдары болса), «Т-дан S шығады» деп айтады. І Аксиомадан І' Аксиома шығатынын, сондай-ақ І' Аксиомадан І Аксиома шығатынын көрдік. Егер екі ұйғарымның әрқайсысы екіншісінен шығатын болса, онда олар бір-біріне теңкүшті немесе эквивалентті деп айтады. Осылайша, І және І' Аксиомалар өзара эквивалентті.
І және І' Аксиомаларды
суреттеу үшін  сандарын
қарастырайық.
сандарын
қарастырайық.
І Аксиоманы суреттеу
барысында  екенін ескертейік;
сондай-ақ
екенін ескертейік;
сондай-ақ  («
(« О
жиынының элементі емес» деп
оқылады) және
О
жиынының элементі емес» деп
оқылады) және  және т.б. екенін
ескертейік.
және т.б. екенін
ескертейік.
І' Аксиоманы суреттеу үшін

екенін көрсетеміз.
Осылайша, осы төрт жағдайдың әрқайсысында І' Аксиомадағы үш қатынастың ішінен жалғыз және тек қана жалғыз қатынас орындалатынын көреміз.
 теңсіздігінің
орнына
теңсіздігінің
орнына  деп жаза аламыз және ол
«а
b-дан кем» деп оқылады. Бұл екі
теңсіздік толықтай эквивалентті және олардың ешқайсысының
екіншісінен артықшылығы жоқ. Жоғарыда көрсетілген І' Аксиоманы
суреттеуде мазмұндаудың біртекті болуы үшін барлық жерде «>»
белгісін қолдандық. Бірақ біртектілік мақсатында барлық
жағдайларда а-ны
b-ның алдына жазуға болар еді.
Ол жағдайда
деп жаза аламыз және ол
«а
b-дан кем» деп оқылады. Бұл екі
теңсіздік толықтай эквивалентті және олардың ешқайсысының
екіншісінен артықшылығы жоқ. Жоғарыда көрсетілген І' Аксиоманы
суреттеуде мазмұндаудың біртекті болуы үшін барлық жерде «>»
белгісін қолдандық. Бірақ біртектілік мақсатында барлық
жағдайларда а-ны
b-ның алдына жазуға болар еді.
Ол жағдайда
 (1.2.1)
(1.2.1)
болар еді.
Дәл осылай

« > » және « < » белгілері қатаң теңсіздіктерді өрнектейді.
Теңсіздіктерді оқып үйрену
кезіндегі басқа екі қатынас – қатаң
емес  және
және
 теңсіздіктері, олар
сәйкесінше «а
b-дан кем емес» және
«а
b-дан артық емес» деген
мағынаны білдіреді. Олардың алғашқысы
теңсіздіктері, олар
сәйкесінше «а
b-дан кем емес» және
«а
b-дан артық емес» деген
мағынаны білдіреді. Олардың алғашқысы
 теңсіздігі
немесе
теңсіздігі
немесе  екенін,
немесе
екенін,
немесе  екенін білдіреді;
мысалы,
екенін білдіреді;
мысалы,  және
және
сондай-ақ  болады.
Екіншісі
болады.
Екіншісі  теңсіздігі
немесе
теңсіздігі
немесе  екенін,
немесе
екенін,
немесе  екенін білдіреді;
мысалы,
екенін білдіреді;
мысалы,  және
және
 .
.
(1.2.1) жағдайда І' Аксиомада көрсетілген үш қатынастың біреуі ғана орындалатыны айтылып тұр. Ал аксиома осы қатынастардың ішінен тек қана біреуі орындалатынын айтады. Сондықтан І' Аксиоманы сипаттауды аяқтау үшін келесідей ұйғарымдарды қосуымыз керек:
 (1.2.2)
(1.2.2)
бұл ұйғарымдар
« -ден кем емес және тең емес»
және т.б. мағынаны береді.
-ден кем емес және тең емес»
және т.б. мағынаны береді.
(1.2.2) көрсетілген теріс ұйғарымдар бұл жерде артық екенін көруге болады, расында да оларды (1.2.1) көрсетілген ақпаратты толықтыру үшін жазуды ешкім талап етпейді. Бұл І немесе І' Аксиомалардағы «жалғыз тек қана жалғыз» сөздерімен сипатталатын теңсіздіктердің үйлесімсіздік принципі өз алдына белгілі екендігімен түсіндіріледі.
Осыдан, теңсіздіктердің үйлесімсіздік принципі негізінде (1.2.1) және (1.2.2) бір-біріне жауап беретін қатынастар өзара теңкүшті екені, яғни олардың әрқайсысы екіншісінен шығатыны белгілі болды. Дегенмен, теңсіздікті терістеу көп жағдайда маңызды ұғым болып табылады [4].
Егер сіз « > » және « <
» белгілерін шатастырып алудан қорықсаңыз,
 немесе
немесе  секілді дұрыс теңсіздіктерде
теңсіздік белгісінің кең (ашық) ұшы үлкен санға қарап тұрғанын, ал
тар (ұшталған) ұшы кіші санға қарап тұрғанын байқап
алыңыз.
секілді дұрыс теңсіздіктерде
теңсіздік белгісінің кең (ашық) ұшы үлкен санға қарап тұрғанын, ал
тар (ұшталған) ұшы кіші санға қарап тұрғанын байқап
алыңыз.
Теңсіздіктердің негізгі қасиеттері:
-
Егер
 болса,
онда
болса,
онда  болады; немесе
егер
болады; немесе
егер  болса,
онда
болса,
онда  болады.
болады. -
Егер
 болса,
онда
болса,
онда  ; немесе
егер
; немесе
егер  болса,
онда
болса,
онда  болады.
Яғни теңсіздіктің екі жағына
бірдей санды қосуға (азайтуға) болады.
болады.
Яғни теңсіздіктің екі жағына
бірдей санды қосуға (азайтуға) болады. -
Егер
 және
және  болса,
онда
болса,
онда  болады.
Яғни бірдей
мағыналы (бірдей > немесе <
таңбалы) теңсіздіктерді бір-біріне
мүшелеп қосуға болады. Бірдей мағыналы теңсіздіктерді бір-бірінен
мүшелеп азайтуға болмайтынын ескертейік. Себебі нәтижесі
қате болуы мүмкін.
болады.
Яғни бірдей
мағыналы (бірдей > немесе <
таңбалы) теңсіздіктерді бір-біріне
мүшелеп қосуға болады. Бірдей мағыналы теңсіздіктерді бір-бірінен
мүшелеп азайтуға болмайтынын ескертейік. Себебі нәтижесі
қате болуы мүмкін. -
Егер
 және
және  болса,
онда
болса,
онда  болады. Немесе
егер
болады. Немесе
егер  және
және
 болса,
онда
болса,
онда  болады.
Яғни қарама-қарсы мағыналы
теңсіздіктерді бір-бірінен мүшелеп азайтуға болады және
теңсіздіктің азаятын белгісін алу
керек.
болады.
Яғни қарама-қарсы мағыналы
теңсіздіктерді бір-бірінен мүшелеп азайтуға болады және
теңсіздіктің азаятын белгісін алу
керек. -
Егер
 және
және  болса,
онда
болса,
онда  және
және
 болады.
Яғни теңсіздіктің екі жағын да
бірдей оң таңбалы санға көбейтуге немесе бөлуге болады. Бұл
жағдайда теңсіздік өз таңбасын
сақтайды.
болады.
Яғни теңсіздіктің екі жағын да
бірдей оң таңбалы санға көбейтуге немесе бөлуге болады. Бұл
жағдайда теңсіздік өз таңбасын
сақтайды. -
Егер
 және
және  болса,
онда
болса,
онда  және
және  болады.
Яғни теңсіздіктің екі жағын да
бірдей теріс таңбалы санға көбейтуге немесе бөлуге болады. Бұл
жағдайда теңсіздік өз таңбасын қарама-қарсы таңбаға
ауыстырады [5].
болады.
Яғни теңсіздіктің екі жағын да
бірдей теріс таңбалы санға көбейтуге немесе бөлуге болады. Бұл
жағдайда теңсіздік өз таңбасын қарама-қарсы таңбаға
ауыстырады [5].
1.3. Теріс көбейткіштері бар көбейтінділер
Оң сан мен теріс санның көбейтіндісі сандардың қай түріне жатады? Немесе екі теріс санның көбейтіндісі? Бұл сұрақтарға жауап алу үшін І мен І' Аксиомаларын және олардың кейбір салдарларын қолдануға болады.
Егер
 және
және  болса, онда 1-кестеге
сәйкес
болса, онда 1-кестеге
сәйкес  болады, осыдан ІІ Аксиомаға
сәйкес олардың көбейтіндісі
болады, осыдан ІІ Аксиомаға
сәйкес олардың көбейтіндісі  болады. Бұдан теріс санның
анықтамасына сәйкес
болады. Бұдан теріс санның
анықтамасына сәйкес  болады;
бірақ
болады;
бірақ  болады,
себебі
болады,
себебі

минус таңбасын жақшаның
сыртына шығарудың белгілі ережесі бар.
Сондықтан  . Осылайша, төмендегідей
нәтижеге келдік:
. Осылайша, төмендегідей
нәтижеге келдік:
1-Теорема. Оң а саны мен теріс b санының ab көбейтіндісі теріс сан болады.
Дәл осылай, егер
Егер  және
және
 болса, онда 1-кестеге
сәйкес
болса, онда 1-кестеге
сәйкес  және
және
 болады. Осыдан ІІ
Аксиомаға сәйкес олардың көбейтіндісі
болады. Осыдан ІІ
Аксиомаға сәйкес олардың көбейтіндісі
 болады. Осылайша,
төмендегідей нәтижеге келдік:
болады. Осылайша,
төмендегідей нәтижеге келдік:
2-Теорема. Теріс a мен b екі
санның  көбейтіндісі оң сан
болады.
көбейтіндісі оң сан
болады.
Соңғы нәтиже мен ІІ Аксиома
негізінде нөлден өзге кез келген нақты санның квадраты оң сан
болады деген ұйғарым шығады. Әрине  .
.
Осылайша, теңсіздіктер теориясының ең жеңіл әрі пайдалы нәтиже шығады.
3-Теорема. Кез келген нақты а
саны  теңсіздігін
қанағаттандырады. Теңдік белгісі орындалады сонда тек қана сонда,
егер
теңсіздігін
қанағаттандырады. Теңдік белгісі орындалады сонда тек қана сонда,
егер  болса [3].
болса [3].
Жоғарыда көрсетілген бастапқы мәліметтерді пайдалана отырып математиканың негізгі теңсіздіктерін қарастыруға көшеміз.
2. Математиканың негізгі теңсіздіктері
2.1. Коши теңсіздігі
Кез келген нақты санның
квадратының теріс еместігін өрнектейтін теңсіздік ең негізгі
фундаменталды теңсіздік болып табылады. Бұл ұйғарымды тиімді
пайдалану үшін оны  айырмасына қолданайық,
мұндағы
айырмасына қолданайық,
мұндағы  және
және
 – нақты сандар.
Онда
– нақты сандар.
Онда  теңсіздігі төмендегі ұйғарымға
сай болады:
теңсіздігі төмендегі ұйғарымға
сай болады:
 (2.1.1)
(2.1.1)
Теңдік орындалады сонда және
тек қана сонда, егер  болса. Бұл – арифметикалық
және геометриялық орталарды байланыстыратын теңсіздіктің ең
қарапайым түрі. Ендігі жерде жалпы нәтиже Кошиге сәйкес осы дербес
жағдайға сүйене отырып дәлелденетін
болады.
болса. Бұл – арифметикалық
және геометриялық орталарды байланыстыратын теңсіздіктің ең
қарапайым түрі. Ендігі жерде жалпы нәтиже Кошиге сәйкес осы дербес
жағдайға сүйене отырып дәлелденетін
болады.
Квадраттардың теріс еместігін бұдан да тиімдірек қолдануға болады, ол үшін құрамындағы шамалар нақты болатын төмендегі қосындыны қолдану керек:
 (2.1.2)
(2.1.2)
u және v үшін алынған квадраттық өрнек u және v барлық нақты мәндері үшін теріс емес болғандықтан, оның дискриминанты теріс емес болу керек, бұл ұйғарым Коши теңсіздігін береді [6]:
 (2.1.3)
(2.1.3)
Бұл теңсіздікті кез келген
санмен өрнектелетін евклидтік кеңістікте бұрыш косинусының
абсолюттік шамасы бірден артық болмайды деген фактінің ұйғарымы деп
қарастыруға болады. Теңдік орындалады сонда және тек қана сонда,
егер  және
және
 сандарының жүйелері
өзара пропорционал болса, яғни сонда және тек қана сонда, егер
нөлге тең емес және төмендегі шартты
қанағаттандыратын λ
мен
μ
сандары бар
болса:
сандарының жүйелері
өзара пропорционал болса, яғни сонда және тек қана сонда, егер
нөлге тең емес және төмендегі шартты
қанағаттандыратын λ
мен
μ
сандары бар
болса:

Егер алдыңғы ұйғарымды жай
ғана п-өлшемді евклидтік кеңістікке
емес, ал кез келген екі х
және
у
элементтері үшін төмендегідей
қасиеттері бар  скаляр көбейтіндісі
анықталған S
жалпы сызықтық кеңістікке
қолданатын болса, бұдан да жалпы нәтижелерді алуға
болады:
скаляр көбейтіндісі
анықталған S
жалпы сызықтық кеңістікке
қолданатын болса, бұдан да жалпы нәтижелерді алуға
болады:
(![]() а) кез
келген
а) кез
келген  үшін
үшін

(ә)
 (2.1.4)
(2.1.4)
(б) кез келген нақты скаляр u және v үшін

Бұл қасиеттерден u және v үшін квадраттық өрнек
 (2.1.5)
(2.1.5)
барлық нақты u және v үшін теріс емес болатынын пайымдауға болады.
Бұдан, жоғарыдағыдай,
 (2.1.6)
(2.1.6)
теңсіздігін аламыз, бұл теңсіздік, өз кезегінде, одан да жалпы теңсіздіктердің дербес жағдайы болады.
Енді
бұдан S
пен
 скаляр көбейтіндісін
таңдап, теңсіздіктердің бұдан да көп санын шығаруға болады.
Осылайша,
скаляр көбейтіндісін
таңдап, теңсіздіктердің бұдан да көп санын шығаруға болады.
Осылайша,
 (2.1.7)
(2.1.7)
мұндағы интеграл Стильтьес
мағынасында қабылданады және  үшін
үшін
 кемімейді
немесе
кемімейді
немесе
 (2.1.8)
(2.1.8)
мұндағы
 – оң таңбалы матрица
және т.с.с.
– оң таңбалы матрица
және т.с.с.
Арифметикалық және геометриялық орталарының арасындағы теңсіздік.
Кең нәтижелерді қарастыру ең маңызды және теңсіздіктер теориясының негізі болып табылатын бір теңсіздіктен – арифметикалық және геометриялық орталарының арасындағы теңсіздіктен басталады. Бұл ерекше әдемі теңсіздік келесідей етіп тұжырымдалады.
1-Теорема.  –
теріс емес сандар
және
–
теріс емес сандар
және  болсын.
Онда
болсын.
Онда
 (2.1.9)
(2.1.9)
болады. Бұл жерде қатаң теңсіздік
орындалады, тек барлық өзара тең
болмаса.
өзара тең
болмаса.
3-9 бөлімшелерінде осы фундаменталды теңсіздіктің әр түрлі принциптерге негізделген немесе әр түрлі әдістерді қамтитын он екі дәлелдеуі көрсетіледі. (2.1.9) теңсіздіктің өлшенген орталарға жататын жалпылаулары бар. Олар осы теңсіздіктің және оның шекті жағдайларының дербес жағдайлары болып табылатынын ескерте кету керек.
Жоғары және төмен бағытталған индукция.
1-теореманың дәлелдеуінің
классикалық түрі Кошиға тиесілі. (2.1.1) теңсіздікте көрсетілгендей,
кез келген  және
және
 үшін
үшін
 (2.1.10)
(2.1.10)
орындалады.  деп алып,
(2.1.10) теңсіздіктен
деп алып,
(2.1.10) теңсіздіктен
 (2.1.11)
(2.1.11)
аламыз,
мұндағы  және
және
 – кез келген теріс емес
сандар. (2.1.1) теңсіздіктен белгілі
болғандай, (2.1.11) теңсіздікте теңдік орындалады
сонда және тек қана сонда, егер
– кез келген теріс емес
сандар. (2.1.1) теңсіздіктен белгілі
болғандай, (2.1.11) теңсіздікте теңдік орындалады
сонда және тек қана сонда, егер  болса.
болса.
Енді
 орнына
орнына  және
және
 орнына
орнына  жаңа айнымалыларын қойсақ,
онда екі рет қолданылған (2.1.11) теңсіздіктен
жаңа айнымалыларын қойсақ,
онда екі рет қолданылған (2.1.11) теңсіздіктен

 (2.1.12)
(2.1.12)
Осылайша жалғастыра
отырып, (2.1.9) теңсіздік
 үшін және 2-нің дәрежесі
болатын кез келген п
үшін орындалатынын көреміз.
Бұл – жоғары бағытталған
индукция.
үшін және 2-нің дәрежесі
болатын кез келген п
үшін орындалатынын көреміз.
Бұл – жоғары бағытталған
индукция.
Енді төмен бағытталған
индукцияны қолданайық. Егер теңсіздік
п
үшін орындалса, онда
ол  үшін де орындалатынын
көрсетейік. (2.1.9) теңсіздікте
үшін де орындалатынын
көрсетейік. (2.1.9) теңсіздікте  орнына
орнына
 (2.1.13)
(2.1.13)
жаңа айнымалы қоямыз,
мұндағы  , ал
басқа
, ал
басқа  өзгеріссіз қалдырамыз.
Онда (2.1.9) теңсіздік
бойынша
өзгеріссіз қалдырамыз.
Онда (2.1.9) теңсіздік
бойынша

 (2.1.14)
(2.1.14)
аламыз немесе
 (2.1.15)
(2.1.15)
ықшамдап, ізделінді теңсіздікті аламыз:
 (2.1.16)
(2.1.16)
2-нің дәрежесі үшін алынған нәтижесімен байланыстыра отырып, теореманың индукциялық дәлелдемесін аламыз.
Жоғарыға және төменге бағытталған индукциямен дәлелденетін басқа қызықты теңсіздік ретінде Фань Цзыдың жарияланбаған келесідей теңсіздігін алуға болады:
егер
 үшін
үшін  болса,
онда
болса,
онда
 (2.1.17)
(2.1.17)
болады, теңдік орындалады
сонда және тек қана сонда, егер барлық
 өзара тең
болса.
өзара тең
болса.
Гаусстың арифметикалық-геометриялық ортасы. Элементар симметриялық функциялар.
 – оң сандар
және
– оң сандар
және  болсын.
болсын.
 тізбектерінің келесі
мүшелерін
тізбектерінің келесі
мүшелерін
 (2.1.18)
(2.1.18)
қатынастар арқылы анықтайық.
 (2.1.19)
(2.1.19)
екенін көруге болады
және  мен
мен
 тізбектерінің
тізбектерінің  ортақ шегі болатынын
дәлелдеуге болады. Бұл
ортақ шегі болатынын
дәлелдеуге болады. Бұл  функциясын алғашқы рет Гаусс
зерттеген болатын [7]. Ол эллипстік функциялар теориясында маңызды
рөл атқарады; сонымен қатар Гаусс бұл теория толығымен осы
функцияға негізделетінін көрсеткен еді.
функциясын алғашқы рет Гаусс
зерттеген болатын [7]. Ол эллипстік функциялар теориясында маңызды
рөл атқарады; сонымен қатар Гаусс бұл теория толығымен осы
функцияға негізделетінін көрсеткен еді.
Жоғарыдағы  мен
мен
 тізбектерінің
үйлесімділігі туралы ұйығарым көптеген жалпылаулардың шығуына
мүмкіндік береді. Мысалы, егер
тізбектерінің
үйлесімділігі туралы ұйығарым көптеген жалпылаулардың шығуына
мүмкіндік береді. Мысалы, егер  және
және

 (2.1.20)
(2.1.20)
болса, онда
 (2.1.21)
(2.1.21)
болатынын оңай көруге болады.
Симметриялық орталардың нәтижелерін дәлелдеудің бір тәсілі ретінде п нақты айнымалысы бар элементар симметриялық функциялар арасындағы кейбір қызықты теңсіздіктерді қолдануға болады. Арифметикалық және геометриялық орталардың арасындағы теңсіздік дәл осындай теңсіздіктер тізбегінің бір бөлігі болып табылады екен.
Ролль теоремасына негізделген дәлелдеу әдісін қолданайық. Бұл әдіс берілген көпмүшенің нақты түбірлері болмайды деген фактіден ғана емес, сонымен қатар көпмүшенің барлық түбірлері нақты сан болады деген фактіден де пайдалы салдарларды алуға болатынын (бұл туралы жоғарыда баяндалды) көрсетеді.
Бізге қажетті нәтиже Ролль теоремасының тікелей салдары болып табылады; ол келесідей болады.
1-Лемма. Егер
 (2.1.22)
(2.1.22)
теңдеуінің
барлық  түріндегі түбірлері нақты
сандар болса, онда (2.1.22) тепе-теңдігін х және у
бойынша дифференциалдау арқылы алынған теңдеулердің барлық
түбірлері де нақты сандар болады.
түріндегі түбірлері нақты
сандар болса, онда (2.1.22) тепе-теңдігін х және у
бойынша дифференциалдау арқылы алынған теңдеулердің барлық
түбірлері де нақты сандар болады.
Бұл лемманы
 (2.1.23)
(2.1.23)
көпмүшесіне қолданайық,
мұндағы  – нақты
сандар.
– нақты
сандар.
 (2.1.24)
(2.1.24)
болатынын ескере отырып, мұндағы
 (2.1.25)
(2.1.25)
 және
және  сандарына қатысты симметриялық
функция. Осыдан
сандарына қатысты симметриялық
функция. Осыдан  теңдеуін екінші рет
дифференциалдаудан шығатын
теңдеуін екінші рет
дифференциалдаудан шығатын
 (2.1.26)
(2.1.26)
теңдеуінің екі нақты түбірі болатыны шығады. Осылайша,
 (2.1.27)
(2.1.27)
болады. Теңсіздік кез келген
оң, теріс немесе нөлге тең  сандары үшін орындалатынын
ескере кетейік.
сандары үшін орындалатынын
ескере кетейік.
Енді
(2.1.27) теңсіздігінен Маклоренге
тиесілі бір нәтижені шығарайық [8]. Ол үшін
барлық  сандары оң деп пайымдайық.
Онда (2.1.27) бойынша
сандары оң деп пайымдайық.
Онда (2.1.27) бойынша
 (2.1.28)
(2.1.28)
немесе
 (2.1.29)
(2.1.29)
теңсіздіктері орындалады.
(2.1.29) теңсіздіктен

шығады, яғни арифметикалық және геометриялық орталардың арасындағы теңсіздікті аламыз.
Якобсталь дәлелдеуі.
Арифметикалық және геометриялық орталардың арасындағы теңсіздіктің осы орталардың алгебралық қатынастарына негізделетін бірнеше дәлелдеуі бар. Олардың ішіндегі ең қызықтысы төмендегі дәлелдеу болып табылады [9].
Әуелі
 (2.1.30)
(2.1.30)
тепе-теңдігінен бастаймыз, мұндағы

Сонан соң
 және
және  үшін
орындалатын
үшін
орындалатын
 (2.1.31)
(2.1.31)
теңсіздігін қолданамыз. п-нің бүтін мәндері үшін (2.1.31) теңсіздігі

тепе-теңдігінен шығады. Егер

деп белгілесек, онда (2.1.30) теңдіктен
 (2.1.32)
(2.1.32)
немесе
 (2.1.33)
(2.1.33)
Индукция бойынша ізделінді жалпы нәтижені табамыз:
 .
.
2.2. Лагранж тепе-теңдігі
Кез келген берілген белгілі теңсіздікті айқын етіп көрсететін тепе-теңдік арқылы дәлелдеу үрдісі көптеген оқыс тармақталулары бар өте қызықты және қиын тапсырма болып табылады. (2.1.3) теңсіздік
 (2.2.1)
(2.2.1)
тепе-теңдігінен шығады, бұл тепе-теңдік бұдан да жалпы тепе-теңдіктің дербес жағдайы болып табылады.
2.3. Анализ және Лагранжтың көбейткіштері
Енді арифметикалық және
геометриялық орталары арасындағы теңсіздікті анализдің есебі
ретінде қарастырайық. Бізге  функциясының теріс емес және
төменде көрсетілген нормалау шартын
қанағаттандыратын
функциясының теріс емес және
төменде көрсетілген нормалау шартын
қанағаттандыратын  облысындағы ең кіші мәнін табу
керек
облысындағы ең кіші мәнін табу
керек
 (2.3.1)
(2.3.1)
Ізделінді ең кіші мән шекті нүктеден алынуы мүмкін еместігі белгілі болғандықтан, локальды минимумды анықтау үшін Лагранж көбейткіштері әдісін қолдануға болады.
 (2.3.2)
(2.3.2)
функциясы үшін экстремумнің қажетті шарттары
 (2.3.3)
(2.3.3)
түрінде болады,
осыдан  болу керек. Бұдан локалды
минимумның бір ғана нүктесі
болу керек. Бұдан локалды
минимумның бір ғана нүктесі  болады,
яғни
болады,
яғни  болады, ал
ол (2.1.9) теңсіздікке пара-пар келеді
деген қорытындыға келеміз.
болады, ал
ол (2.1.9) теңсіздікке пара-пар келеді
деген қорытындыға келеміз.
2.4. Функционалдық теңдеулер
1-теорема динамикалық
бағдарламалаудың функционалдық теңдеулер әдісімен де дәлелденеді
[10].  сандарының төмендегі шарттарды
қанағаттандыратындай ең үлкен мәнін табудан
бастаймыз:
сандарының төмендегі шарттарды
қанағаттандыратындай ең үлкен мәнін табудан
бастаймыз:

Осы ең үлкен
мәнді  деп
белгілейік.
деп
белгілейік.  мен
мен
 арасында рекурентті
қатынасты алу үшін белгіленген
арасында рекурентті
қатынасты алу үшін белгіленген  таңдау кезінде төмендегі
шарттарға бағынатын және
таңдау кезінде төмендегі
шарттарға бағынатын және  көбейтіндісі ең үлкен мәнге ие
болатындай
көбейтіндісі ең үлкен мәнге ие
болатындай  таңдау мәселесі қалатынын
ескере кету керек:
таңдау мәселесі қалатынын
ескере кету керек:
 (2.4.1)
(2.4.1)
Осыдан,
 үшін
үшін
 (2.4.2)
(2.4.2)
болатыны шығады.
 айнымалыларды
алмастырып,
айнымалыларды
алмастырып,
 (2.4.3)
(2.4.3)
аламыз. Осы алмастыруды (2.4.2) теңдікке қойып,
 (2.4.4)
(2.4.4)
 болғандықтан,
болғандықтан,  болады,
бұл (2.1.9)
теңсіздікке пара-пар
келеді.
болады,
бұл (2.1.9)
теңсіздікке пара-пар
келеді.
Ойыстық.
Енді 1-теореманың дәлелдеуін
геометриялық пайымдауларға негізделген түрде келтірейік [11].
1-суретте  қисығы көрсетілген.
Дифференциалдау тұрғысынан қарағанда бұл қисық ойыс орналасқан және
оның кез келген екі нүктесін қосатын хорда қисықтың астында
орналасады. Яғни
қисығы көрсетілген.
Дифференциалдау тұрғысынан қарағанда бұл қисық ойыс орналасқан және
оның кез келген екі нүктесін қосатын хорда қисықтың астында
орналасады. Яғни  үшін
үшін
 (2.4.5)
(2.4.5)
болады және теңдік орындалады
сонда және тек қана сонда, егер  .
.
Бұл нәтиже
 (2.4.6)
(2.4.6)
теңсіздігіне пара-пар келеді.

1-сурет
Дәл осындай
пайымдау  үшін
үшін
 (2.4.7)
(2.4.7)
болатынын және кез
келген  мен
мен
 үшін
үшін
 (2.4.8)
(2.4.8)
болатынын көрсетеді.
Жоғарыда айтылғандай бұл
теңсіздік 1-теоремаға қарағанда күштірек болып көрінеді,
ол (2.1.9) теңсіздіктен  мәндерін арнайы таңдаудан және
шекті ауысудан алынады.
мәндерін арнайы таңдаудан және
шекті ауысудан алынады.
Элерс дәлелдеуі.
Енді 1-теореманы

теңдігінен

теңсіздігі шығатынын анықтау арқылы дәлелдейміз.
Бұл теңсіздік п үшін орындалатынын және

болады
делік.  және
және
 сандары
–
сандары
–  , ал
, ал
 болатындай
болатындай  сандарының ішіндегі екі сан
болсын. Онда
сандарының ішіндегі екі сан
болсын. Онда  немесе
немесе
 (2.4.9)
(2.4.9)
болады.
Бұдан  мәндерінің п
саны үшін теңсіздік
негізінде
мәндерінің п
саны үшін теңсіздік
негізінде
 (2.4.10)
(2.4.10)
болатыны шығады. Сонан соң
нәтиже  үшін де дұрыс болады, осылайша
1-теорема дәлелденді.
үшін де дұрыс болады, осылайша
1-теорема дәлелденді.
2.5. Мажорлау – Бордың дәлелдеуі
1-теореманы тамаша дәлелдеулерінің бірі Г.Борға тиесілі [12].
Әуелі мажорлау ұғымын
енгізейік.  және
және
 – екі формалды дәрежелік
қатар болсын:
– екі формалды дәрежелік
қатар болсын:
 (2.5.1)
(2.5.1)
мұндағы
 үшін
үшін 
Егер
 үшін
үшін  болса,
онда
болса,
онда
 (2.5.2)
(2.5.2)
деп жазылады.
Егер  және
және
 болса,
онда
болса,
онда  болатыны
айқын.
болатыны
айқын.
 және
және  үшін
үшін
 (2.5.3)
(2.5.3)
түріндегі жай мажорлаудан бастап,
 (2.5.4)
(2.5.4)
екенін анықталады.
Осыдан,  алдындағы коэффициенттерін
салыстырып, барлық оң таңбалы бүтін
N
үшін
алдындағы коэффициенттерін
салыстырып, барлық оң таңбалы бүтін
N
үшін
 (2.5.5)
(2.5.5)
немесе
 (2.5.6)
(2.5.6)
теңсіздіктерін аламыз.
Стирлинг формуласына
сәйкес  үшін
үшін
 (2.5.7)
(2.5.7)
болғандықтан,
 (2.5.8)
(2.5.8)
болады. (2.5.6) пен (2.5.8) өрнектерден 1-теорема шығады. Бұл – келтірілген дәлелдеулердің ішіндегі теңдік белгісі орындалатын шарттарды қарастыруға мүмкіндік бермейтін жалғыз дәлелдеу.
2.6. Гурвиц дәлелдеуі
Енді Гурвицтің қызықты дәлелдеуіне көшейік [13]. Ол 1891 жылы оның топтар бойынша интегралдау арқылы инварианттарды табу туралы еңбегінен 6 жыл бұрын жарияланған болатын [14], бірақ бұл еңбекке кейінгі еңбектерінде дамытылған кейбір мәселелер салынған еді.
 нақты сандар жиынындағы
айнымалылар үшін п
функциясы
берілсін.
нақты сандар жиынындағы
айнымалылар үшін п
функциясы
берілсін.  аргументтерін
барлық
аргументтерін
барлық  алмастырулары
бойынша f
қосындысын
алмастырулары
бойынша f
қосындысын  деп белгілейік. Осылайша,
мысалы,
деп белгілейік. Осылайша,
мысалы,
 (2.6.1)
(2.6.1)
Төмендегідей әдіспен
алынатын  функцияларын
қарастырайық:
функцияларын
қарастырайық:
 (2.6.2)
(2.6.2)
Осыдан,
 (2.6.3)
(2.6.3)
шығатынын көреміз.
Дәл осылай
 (2.6.4)
(2.6.4)
Өрнектерді бір-біріне қосу арқылы
 (2.6.5)
(2.6.5)
аламыз. Бірақ (2.6.1) өрнекке сәйкес
 (2.6.6)
(2.6.6)
болады.
 функцияларының
әрқайсысы
функцияларының
әрқайсысы  үшін теріс емес екендігі айқын
көрініп тұр, себебі
үшін теріс емес екендігі айқын
көрініп тұр, себебі
 (2.6.7)
(2.6.7)
Осылайша, (2.1.6) тепе-теңдіктің сол жағындағы айырма теріс емес болады, ал бұл ұйғарым 1-теореманың дәлелдеуі болады. Бұл дәлелдеу – (2.1.9) теңсіздікті тепе-теңдікке айналдыратын жалғыз ғана дәлелдеу.
2.7. Юнг теңсіздігі
Айталық,
 функциясы
– х-ке қатысты үзіліссіз қатаң
өспелі функция болсын,
функциясы
– х-ке қатысты үзіліссіз қатаң
өспелі функция болсын,  және
және
 (2-сурет қара). Сәйкес
интегралдармен берілген аудандарды
қарастырып,
(2-сурет қара). Сәйкес
интегралдармен берілген аудандарды
қарастырып,
 (2.7.1)
(2.7.1)
екеніне көз жеткіземіз,
мұндағы  функциясы
функциясы
 функциясына кері
функция. Бұл жерде теңдік тек қана
функциясына кері
функция. Бұл жерде теңдік тек қана  болғанда орындалатынын байқау
қиын емес. Бұл теңсіздік Юнг теңсіздігі деп аталады
[15].
болғанда орындалатынын байқау
қиын емес. Бұл теңсіздік Юнг теңсіздігі деп аталады
[15].
φ үшін әр түрлі фукнцияларды таңдай отырып, бірқатар қызықты нәтижелер аламыз.
 болғанда (2.7.1)
теңсіздік
болғанда (2.7.1)
теңсіздік
 (2.7.2)
(2.7.2)
түріне келеді.

2-сурет
(2.7.1) Юнг
теңсіздігінде  таңдап
және а-ны
таңдап
және а-ны
 -ге алмастырып, басқа
бір қызықты нәтижені, яғни
-ге алмастырып, басқа
бір қызықты нәтижені, яғни

теңсіздігін аламыз. Бұл теңсіздік Фурье қатарлары теориясында жиі қолданылады.
2.1 бөлімшеде арифметикалық және геометриялық орталарының арасындағы теңсіздік элементар симметриялы функциялар қанағаттандыратын теңсіздіктер тізбегінің бірі екенін көрдік. Енді осы орталардың орталар мәндерінің үзіліссіз толық иерархиясына жататынын көрсетейік. Осында қарастырылатын теңсіздіктер үшін элементар дәлелдеулер бар болғанына қарамастан, негізінен дифференциалдық санауды қолданамыз. Біздің басты қаруымыз дөңес функциялар теориясы болады; әсіресе осы бөлімшеде 2.4 бөлімшеде көрсетілген геометриялық ұйғарымдардың аналитикалық негізін көрсетеміз. Дөңес функциялардың және олардың қосымшаларының жалпы теориясы Беккенбах пен Гриннің еңбектерінде қарастырылады.
Кез келген оң таңбалы

мәндері үшін және оң

үшін және кез келген
нақты  үшін
t ретінің
ортасын немесе
t-норманы анықтаймыз:
үшін
t ретінің
ортасын немесе
t-норманы анықтаймыз:

Соның ішінде, –1, 1 және 2 реттерінің орталары сәйкесінше гармоникалық, арифметикалық және квадраттық орталар.
Лопиталь ережесінің көмегімен
 (2.8.1)
(2.8.1)
болатынын, яғни геометриялық
ортаға тең болатыны оңай анықталады. Содан кейін
егер  болса, онда,
сірә,
болса, онда,
сірә,  үшін
үшін

болады, бұдан
 (2.8.2)
(2.8.2)
болады. Бірақ

қатынасынан енді
 (2.8.3)
(2.8.3)
болатыны шығады. Осының негізінде



болады.
Егер
 -ге қатысты оның теріс
емес екені және олардың әйтеуір біреуі нөлге тең екені
жорамалданатын болса, онда
-ге қатысты оның теріс
емес екені және олардың әйтеуір біреуі нөлге тең екені
жорамалданатын болса, онда  үшін
үшін
 ортасы нөлге тең болады
деп ұйғарылады. Алайда біз тек қана оң таңбалы
ортасы нөлге тең болады
деп ұйғарылады. Алайда біз тек қана оң таңбалы
 қарастырамыз.
қарастырамыз.
Енді
оң
таңбалы  үшін
үшін  ортасы t-ға
қатысты
ортасы t-ға
қатысты  үшін кемімейтін функция
болатынын және де егер
үшін кемімейтін функция
болатынын және де егер  -дің арасында бір-біріне
тең емес
-дің арасында бір-біріне
тең емес  мәндері табылса,
онда
мәндері табылса,
онда  қатаң өсетін
болатынын көрсетейік. Арифметикалық және
геометриялық орталардың арасындағы теңсіздік бұл ұйғарымның дербес
жағдайы болып табылады.
қатаң өсетін
болатынын көрсетейік. Арифметикалық және
геометриялық орталардың арасындағы теңсіздік бұл ұйғарымның дербес
жағдайы болып табылады.
Осы жалпылама фактіні негіздеу
үшін әуелі дөңес функцияларға қатысты бір ескерту енгізейік.
Егер  функциясының
функциясының  үшін
үшін
 (2.8.4)
(2.8.4)
теңсіздігін қанағаттандыратын
екінші туындысы бар болса, онда  графигі осы интервалда дөңес
доға түрінде болады. Егер
графигі осы интервалда дөңес
доға түрінде болады. Егер

мәндері
 интервалында жатса,
ал
интервалында жатса,
ал

болса,
онда  та
та
 интервалында жатады және
Тейлор формуласы бойынша
интервалында жатады және
Тейлор формуласы бойынша

болады. Бұл
теңсіздіктерді  -ге көбейтіп және
қосып,
-ге көбейтіп және
қосып,

аламыз, ал бұдан (2.8.4) сәйкес
 (2.8.5)
(2.8.5)
болады және де теңдік тек қана х-тің барлығы өзара тең болғанда орындалады.
Демек,

функциясы үшін

аламыз, осыдан (2.8.5) теңсіздікке сәйкес х-тің оң мәндері үшін
 (2.8.6)
(2.8.6)
теңсіздігі дұрыс болады,
теңдік тек қана барлық  өзара тең болғанда
орындалады.
өзара тең болғанда
орындалады.
Осы жерде

болатынын тексеру қиын емес
және  мәндеріне
қолданылған (2.8.6) теңсіздік
мәндеріне
қолданылған (2.8.6) теңсіздік

екенін көрсетеді, теңдік тек
қана барлық  өзара тең болғанда
орындалады.
өзара тең болғанда
орындалады.
Осылайша, егер
барлық  өзара тең болмаса,
онда
өзара тең болмаса,
онда  функциясы
t-ға қатысты өспелі функция
болады және оның графигінде екі тік асимптота болады. Осының
негізінде
функциясы
t-ға қатысты өспелі функция
болады және оның графигінде екі тік асимптота болады. Осының
негізінде  функциясының графигі тек қана
бір нүктеде майысады, яғни бір ойыс және бір дөңес бөлігі бар деп
жорамалдауға болады. Бірақ бұл жорамал әр уақытта да дұрыс бола
бермейді [16], алайда
функциясының графигі тек қана
бір нүктеде майысады, яғни бір ойыс және бір дөңес бөлігі бар деп
жорамалдауға болады. Бірақ бұл жорамал әр уақытта да дұрыс бола
бермейді [16], алайда  функциясы
t-ға қатысты дөңес функция
болатынын көрсету қиын емес (ол үшін дифференциалдаудан кейін Коши
теңсіздігін қолдану керек). Демек, (2.8.5) теңсіздікке
сәйкес
функциясы
t-ға қатысты дөңес функция
болатынын көрсету қиын емес (ол үшін дифференциалдаудан кейін Коши
теңсіздігін қолдану керек). Демек, (2.8.5) теңсіздікке
сәйкес  функциясы кез
келген
функциясы кез
келген  үшін
үшін
 (2.8.7)
(2.8.7)
теңсіздігін қанағаттандырады және
 (2.8.8)
(2.8.8)
t ретінің қосындысы

t-ға қатысты функция ретінде
басқаша болады. – ∞-тен 0-ге дейін артатын
t
үшін ол
 -тен 0-ге дейін
бірсарынды кемиді, ал 0-ден +∞-ге дейін
артатын t
үшін ол
∞-тен
-тен 0-ге дейін
бірсарынды кемиді, ал 0-ден +∞-ге дейін
артатын t
үшін ол
∞-тен  -ке дейін бірсарынды
кемиді.
-ке дейін бірсарынды
кемиді.

теңсіздігін кейде Иенсен теңсіздігі деп атайды [17], екінші ретті туындысы оң мән қабылдайтын функциялар үшін ғана емес, сондай-ақ кез келген үздіксіз дөңес функциялар үшін орындалатын (2.8.5) теңсіздікті де солай атайды.
 функциясы t-ға қатысты дөңес функция
болғандықтан,
функциясы t-ға қатысты дөңес функция
болғандықтан,  функциясы
да t-ға қатысты дөңес функция
болатыны оңай шығады. Сондықтан (2.8.7) теңсіздік
M-нің
орнында S
болғанда да
орындалады.
функциясы
да t-ға қатысты дөңес функция
болатыны оңай шығады. Сондықтан (2.8.7) теңсіздік
M-нің
орнында S
болғанда да
орындалады.
 функциясы
функциясы  үшін міндетті түрде ойыс
болмайды [18]; бірақ
үшін міндетті түрде ойыс
болмайды [18]; бірақ
 үшін әркез дөңес болады.
Сәйкесінше,
үшін әркез дөңес болады.
Сәйкесінше,  (2.8.8) шарттарға бағынатын кез
келген
(2.8.8) шарттарға бағынатын кез
келген  және
T
мен
және
T
мен
 үшін
үшін

теңсіздігін қанағаттандырады.
Бұдан басқа,  функциясы
t-ға
қатысты
функциясы
t-ға
қатысты  үшін дөңес функция болады
деген ұйғарым бар, сондықтан (2.8.5) сәйкес
үшін дөңес функция болады
деген ұйғарым бар, сондықтан (2.8.5) сәйкес

болады.
2.9. Классикалық теңсіздіктерді жалпылау
Жоғарыда қарастырылған теңсіздіктерді көптеген бағытта жалпылап нәтижелеуге болады. Бұл бөлімшеде осы нәтижелердің ішіндегі маңыздыларына тоқталып өтейік.
Гёльдер мен Минковскийдің теңсіздіктерінің нәтижелеріне математикалық индукцияның қолданылуын көрсетейік.
Егер  мен
мен  үшін
үшін  және
егер
және
егер

болғанда  болса,
онда
болса,
онда
 (2.9.1)
(2.9.1)
болады; теңдік орындалады
сонда және тек қана сонда, егер  сандарының т жүйелері өзара
пропорционал болса, яғни сонда және тек қана сонда, егер барлығы
бір мезгілде нөлге тең емес және
сандарының т жүйелері өзара
пропорционал болса, яғни сонда және тек қана сонда, егер барлығы
бір мезгілде нөлге тең емес және

болатын  сандары бар
болса.
сандары бар
болса.
Егер  мен
мен  үшін
үшін  және
егер
және
егер  болса,
онда
болса,
онда
 (2.9.2)
(2.9.2)
болады. Теңсіздік белгісі
кері белгіге ауысады, егер  болса.
(
болса.
( үшін
үшін  болады деп жорамалдау
керек). Осы жағдайлардың әрқайсысында теңдік орындалады сонда және
тек қана сонда, егер
болады деп жорамалдау
керек). Осы жағдайлардың әрқайсысында теңдік орындалады сонда және
тек қана сонда, егер  сандарының т жүйелері өзара
пропорционал болса.
сандарының т жүйелері өзара
пропорционал болса.
Сонымен қатар, осы теңсіздіктердің шекті және шексіз қосындыларға қатысты нәтижелері де бар. Шек үрдісін қолданған кезде теңдіктің орындалуы мүмкін жағдайларды көрсету ерекше назарда болу керек.
Алдыңғы теңсіздіктер «Σ-ге қатысты біртекті» болғандықтан, орталар үшін де аналогтары болады. (2.9.1) теңсіздіктің осындай аналогы

теңсіздігі
болады. (2.9.2) теңсіздікте де дәл
осылай  және
және
 көбейткіштерін немесе
олардың біреуін сәйкес орындарға қоюға
болады.
көбейткіштерін немесе
олардың біреуін сәйкес орындарға қоюға
болады.
Σ-ге қатысты біртекті
теңсіздіктердің интегралдық аналогтары болады. Осылайша, Гёльдер
мен Минковскийдің теңсіздіктері келесідей теңсіздіктерге алып
келеді (Коши теңсіздігі  болғандағы Гёльдердің
дискреттік теңсіздігінің дербес жағдайы болады; оның интегралды
аналогы Коши-Шварц теңсіздігі немесе жай ғана Шварц теңсіздігі,
немесе Буняковский–Шварц теңсіздігі деп
аталады).
болғандағы Гёльдердің
дискреттік теңсіздігінің дербес жағдайы болады; оның интегралды
аналогы Коши-Шварц теңсіздігі немесе жай ғана Шварц теңсіздігі,
немесе Буняковский–Шварц теңсіздігі деп
аталады).
2-Теорема.  және
және  функциялары – қандай да бір
R облысында анықталған функциялар болсын және dV – осы облыс
көлемінің элементі болсын. Осылайша, төменде келтірілген
теңсіздіктердің оң жағындағы интегралдар бар болса, онда сәйкес
теңсіздіктің сол жағындағы интегралдар да бар болады және бұл
теңсіздіктер орындалады:
функциялары – қандай да бір
R облысында анықталған функциялар болсын және dV – осы облыс
көлемінің элементі болсын. Осылайша, төменде келтірілген
теңсіздіктердің оң жағындағы интегралдар бар болса, онда сәйкес
теңсіздіктің сол жағындағы интегралдар да бар болады және бұл
теңсіздіктер орындалады:
 (2.9.3)
(2.9.3)
(Буняковский–Шварц);
 (2.9.4)
(2.9.4)
(Гёльдер);
 (2.9.5)
(2.9.5)
(Минковский).
(2.9.3), (2.9.4), (2.9.5) теңсіздіктерде теңдік орындалады сонда және тек қана сонда, егер f және g функциялары өзара оң таңбалы пропорционал болса.
Минковский теңсіздігі (2.9.5) теңсіздіктегі қосындыны төмендегі интегралдармен алмастыру арқылы бұдан да кеңірек қорытындыланады:
 (2.9.6)
(2.9.6)
(2.9.2) теңсіздікте j-ге қатысты қосындыларды ғана
интегралдармен алмастыруға болады. Әрбір жағдайда теңсіздік белгісі
кері белгіге ауысады, егер  болса,
бірақ
болса,
бірақ  болғанда функциялар нөлге тең
болмайды деген ұйғарым жасауымыз керек.
болғанда функциялар нөлге тең
болмайды деген ұйғарым жасауымыз керек.
Осындай интегралдық теңсіздіктерді дәлелдеудің бірнеше жолы бар. Оларды дискреттік теңсіздіктердің шекті жағдайлары ретінде шығара аламыз, сондай-ақ дискреттік аналогтарды дәлелдеудегі әдістерді қолдана отырып дәлелдей аламыз.
Аталған жолдардың біріншісін көрсету үшін
 (2.9.7)
(2.9.7)
теңсіздігінің дәлелдеуін
қарастырамыз. Айталық, f
және
g
функциялары үзіліссіз
функциялар болсын. Онда (2.9.7) теңсіздік
 болатын
шекте
болатын
шекте
 (2.9.8)
(2.9.8)
Коши теңсіздігі болып табылатын дискреттік теңсіздігінен шығады.
(2.9.7) теңсіздікті толығымен алу үшін
Лебег бойынша интегралданатын функциялар
 -нормада көпмүшелер
арқылы аппроксимирлана алады деген ұйғарымды пайдалану керек.
Дәлелдеудің бұл жолы ыңғайсыз екені және егер ол теңсіздік еселі
интегралдарға қатысты теңсіздік болатын болса, онда бұл жол үлкен
қиындықтарға алып келетіні көрініп тұр.
-нормада көпмүшелер
арқылы аппроксимирлана алады деген ұйғарымды пайдалану керек.
Дәлелдеудің бұл жолы ыңғайсыз екені және егер ол теңсіздік еселі
интегралдарға қатысты теңсіздік болатын болса, онда бұл жол үлкен
қиындықтарға алып келетіні көрініп тұр.
Енді кез келген R облыстары үшін (2.9.7) теңсіздікті дәлелдеудің тік жолын көрсетейік. Кез келген нақты u және v үшін
 (2.9.9)
(2.9.9)
теңсіздігін қарастырамыз.
u және v-ны Р-ға қатысты функциялар деп қарастырып және R бойынша интегралдап,
 (2.9.10)
(2.9.10)
теңсіздігін аламыз.
Енді u-дың орынына

ал v-ның орнына

жаңа айнымалыларын енгізейік. Онда (2.9.10) теңсіздіктен
 (2.9.11)
(2.9.11)
шығады және бұл теңсіздік (2.9.7) теңсіздікті кез келген R облысы үшін дәлелдейді.
Буняковский–Шварцтың теңсіздіктерін Бохердің кітабынан [19] және Огурдың еңбегінен табуға болады. Геометриялық талдау, функционалдық кеңістіктердегі теңсіздіктерге арналған Огурдың мәліметтері Бохердің евклидтік кеңістіктегі талдаудың аналогтары болып табылады.
Гёльдер мен Минковский теңсіздігінің ∑-ге қатысты біртектілігінің салдарынан орталар үшін аналогтар мен интегралды аналогтар табылуы мүмкін. Осы себеппен орталар үшін интегралды аналогтар да табылады. Ол үшін бар болғаны барлық жердегі

белгісін

етіп ауыстыру керек.
2.9 бөлімшеде қарастырылған, шекті қосындыларға жататын
 немесе
немесе 
теңсіздігі ∑-ге қатысты біртекті емес және оның интегралды аналог жоқ. Бірақ орталардың арасында жататын оған кері

теңсіздігі ∑-ге қатысты біртекті емес болғанымен, интегралды аналогы бар:

Бұл
жердегі  және
және
 орнына сәйкесінше бар
болатын минимум мен максимумды (яғни жоғарғы және төменгі
шектерді), ал
орнына сәйкесінше бар
болатын минимум мен максимумды (яғни жоғарғы және төменгі
шектерді), ал  орына
орына

геометриялық ортасын ойлауымыз керек.
Бір фундаменталды қатынас.
 үшін
орындалатын
үшін
орындалатын
 немесе
немесе  (2.9.12)
(2.9.12)
 (2.9.13)
(2.9.13)
тамаша теңсіздіктері жалпы теория үшін фундаменталды болып табылады, себебі олардан арифметикалық және геометриялық орталардың арасындағы теңсіздік, сондай-ақ Гёльдер мен Минковскийдің негізгі теңсіздіктері шығады.
(2.9.12) және
(2.9.13) теңсіздіктері дифференциалдық
есептеу арқылы оңай дәлелденеді. Теңсіздік тек
қана  болғанда ғана
орындалады.
болғанда ғана
орындалады.
Осы теңсіздіктерді бұдан
күрделірек, бірақ бұдан элементар болатын дәлелдеу үрдісі
төмендегілерді қамтиды:  және
және
 үшін
үшін

тепе-теңдігі

болатынын көрсетеді және
теңдік тек қана  болғанда орындалады. Осыдан,
кез келген бүтін
болғанда орындалады. Осыдан,
кез келген бүтін  үшін
үшін

болады,
бұдан  үшін
үшін

теңсіздігі шығады, бұл
теңсіздік  мәндерінде (2.9.12) теңсіздікпен сәйкес келеді,
дәлірек айтқанда,
мәндерінде (2.9.12) теңсіздікпен сәйкес келеді,
дәлірек айтқанда,
 (2.9.14)
(2.9.14)
және теңдік тек
қана  болғанда
орындалады.
болғанда
орындалады.
(2.9.12) теңсіздік
иррационал  үшін
(2.9.14) теңсіздіктен
үшін
(2.9.14) теңсіздіктен  болғанда шығады, бірақ шекті
ауысу кезінде
болғанда шығады, бірақ шекті
ауысу кезінде  үшін қатаң теңсіздік жоғалады.
Оны қайтару үшін
үшін қатаң теңсіздік жоғалады.
Оны қайтару үшін  деп аламыз,
мұндағы
деп аламыз,
мұндағы  және
және
 ,
бірақ r
– рационал сан.
Онда
,
бірақ r
– рационал сан.
Онда

болады және бұл
өрнек  үшін
(2.9.12) теңсіздікті дәлелдеу үрдісін
аяқтайды.
үшін
(2.9.12) теңсіздікті дәлелдеу үрдісін
аяқтайды.
(2.9.12) теңсіздікте

алмастыруын орындап, оны

түріндегі теңсіздікке
келтіреміз, осы жерде (2.9.12) теңсіздік
 болғанда да орындалатын
болады. Дәл осындай
болғанда да орындалатын
болады. Дәл осындай

алмастыруы  болғанда
(2.9.13) теңсіздіктің орындалатынын
көрсетеді. Бұрынғыдай
болғанда
(2.9.13) теңсіздіктің орындалатынын
көрсетеді. Бұрынғыдай  болғанда
(2.9.12) теңсіздікте
және
болғанда
(2.9.12) теңсіздікте
және  болғанда
(2.9.13) теңсіздікте теңдік тек
қана
болғанда
(2.9.13) теңсіздікте теңдік тек
қана  болғанда
орындалады.
болғанда
орындалады.  және
және
 шекті жағдайларында
теңсіздік барлық
шекті жағдайларында
теңсіздік барлық  үшін
орындалады:
үшін
орындалады:
 егер
егер  немесе
немесе

Енді арифметикалық және
геометриялық орталардың арасындағы теңсіздікті шығарып алу
үшін  үшін
(2.9.13) теңсіздікке
үшін
(2.9.13) теңсіздікке

алмастырып қою үрдісі

теңсіздігіне алып келеді, бұл теңсіздіктен

болатыны шығады, ал бұл кез
келген  және кез келген оң
мәнді α
мен
және кез келген оң
мәнді α
мен
 үшін ізделінді теңсіздік
болады. Теңдік тек қана
үшін ізделінді теңсіздік
болады. Теңдік тек қана  болғанда
орындалады.
болғанда
орындалады.
Жалпы нәтиже
 (2.9.15)
(2.9.15)
 (2.9.16)
(2.9.16)
болғанда индукция бойынша оңай
алынады. Бұл нәтижеге (2.9.15) теңсіздіктегі теңдік
барлық  үшін тек
қана
үшін тек
қана  болғанда орындалады деген
тұжырым кіреді. Расында да, егер (2.9.15) теңсіздік
п
үшін орындалатын болса,
онда
болғанда орындалады деген
тұжырым кіреді. Расында да, егер (2.9.15) теңсіздік
п
үшін орындалатын болса,
онда

үшін де

және

болады.

болатыны айқын және осыдан индукциялық пайымдау бойынша

болады және егер
барлық  өзара тең болған барлық
жағдайда ғана теңдік орындалады.
өзара тең болған барлық
жағдайда ғана теңдік орындалады.
Осылайша, тағы
да (2.9.15) теңсіздікті (2.9.16) шартты қанағаттандыратын кез
келген  үшін дәлелденді; бірақ кез
келген нақты (рационал болуы міндетті емес)
үшін дәлелденді; бірақ кез
келген нақты (рационал болуы міндетті емес)
 үшін бұл дәледеу өте
элементарлы болып тұр.
үшін бұл дәледеу өте
элементарлы болып тұр.
Егер
 және
және

алмастыруларын енгізсе, онда (2.9.12) және (2.9.13) теңсіздіктерді симметриялы түрде жазуға болады. Онда
 (2.9.17)
(2.9.17)
болады.
 немесе
немесе  болатынына
қарай (2.9.12) және
(2.9.13) теңсіздіктері
болатынына
қарай (2.9.12) және
(2.9.13) теңсіздіктері
 немесе
немесе  (2.9.18)
(2.9.18)
түрінде
жазылады. (2.9.18) теңсіздіктегі теңдік тек
қана  болғанда
орындалады.
болғанда
орындалады.  үшін
(2.9.18) екінші теңсіздігі қандай да
бір
үшін
(2.9.18) екінші теңсіздігі қандай да
бір  жалпылама ұйғарымдарда
орындалатынын оңай байқауға болады.
жалпылама ұйғарымдарда
орындалатынын оңай байқауға болады.
Гёльдер мен Минковскийдің теңсіздіктері.
(2.9.18) теңсіздіктерге сәйкес егер

болса, онда
 (2.9.19)
(2.9.19)
болады және
егер  болса,
онда
болса,
онда

болады.
Егер осы
жерде  болғанда
болғанда

болады деп жорамалдап, осы
теңсіздіктерді бір-біріне қоссақ, онда
 үшін
орындалатын
үшін
орындалатын
 (2.9.20)
(2.9.20)
теңсіздігін және үшін кері
теңсіздікті аламыз. Теңдік орындалады сонда және тек қана сонда,
егер  және
және
 өзара пропорционал
болса. Осылайша, Гёльдердің классикалық теңсіздігін дәлелденді
[20].
өзара пропорционал
болса. Осылайша, Гёльдердің классикалық теңсіздігін дәлелденді
[20].
3-Теорема. Егер  болса,
онда
болса,
онда
 (2.9.21)
(2.9.21)
болады. Теңсіздік белгісі
қарама-қарсы белгісіне өзгереді, егер
 болса.
(
болса.
( үшін
үшін  болады деп жорамалдау
керек). Осы жағдайлардың әрқайсысында теңдік орындалады сонда және
тек қана сонда, егер
болады деп жорамалдау
керек). Осы жағдайлардың әрқайсысында теңдік орындалады сонда және
тек қана сонда, егер  және
және
 өзара пропорционал
болса.
өзара пропорционал
болса.
Классикалық теңсіздіктер қатарын аяқтау үшін Минковскийдің теңсіздігін де келтірейік [21].
4-Теорема. Егер  болса,
онда
болса,
онда
 (2.9.22)
(2.9.22)
болады. Теңсіздік белгісі
қарама-қарсы белгісіне өзгереді, егер
 болса.
(
болса.
( үшін
үшін  болады деп жорамалдау
керек). Осы жағдайлардың әрқайсысында теңдік орындалады сонда және
тек қана сонда, егер (x)
және (y)
өзара пропорционал
болса.
болады деп жорамалдау
керек). Осы жағдайлардың әрқайсысында теңдік орындалады сонда және
тек қана сонда, егер (x)
және (y)
өзара пропорционал
болса.
Әуелі осы теореманың шағын дәлелдеуін ұсынамыз, ал кейіннен, Минковскийдің теңсіздігін квазисызықтандыру арқылы шығарамыз.
 (2.9.23)
(2.9.23)
теңдігінің оң жағындағы әрбір қосындыға p және q дәрежелері бар Гёльдер теңсіздігін қолданайық, нәтижесінде (2.9.22) теңсіздікке пара-пар келетін

теңсіздігін аламыз. Теңсіздік
белгісі қарама-қарсы белгісіне өзгереді,
егер
 болса. Теңдік орындалады сонда
және тек қана сонда, егер
болса. Теңдік орындалады сонда
және тек қана сонда, егер  және
және
 -ға пропорционал болса
немесе (x)
және
(y)
өзара пропорционал
болса.
-ға пропорционал болса
немесе (x)
және
(y)
өзара пропорционал
болса.
(2.9.22) теңсіздік кейде «үшбұрыш
теңсіздігі» деп те аталады, себебі  үшін ол геометриялық тұрғыдан
алғанда п-өлшемді евклидтік кеңістікте
түрлендірілуі мүмкін, бұл жағдай ол үшбұрыштың екі қабырғасының
ұзындықтарының қосындысы үшінші қабырғаның ұзындығынан кем болмайды
деген мағынаны береді. Бұл жағдайда теңсіздік
үшін ол геометриялық тұрғыдан
алғанда п-өлшемді евклидтік кеңістікте
түрлендірілуі мүмкін, бұл жағдай ол үшбұрыштың екі қабырғасының
ұзындықтарының қосындысы үшінші қабырғаның ұзындығынан кем болмайды
деген мағынаны береді. Бұл жағдайда теңсіздік
 -дің барлық нақты
мәндері (оң болуы шарт емес) үшін орындалады және теңдіктің
орындалуының шарты ретінде (x)
және
(y) өзара пропорционалдығының оң
мән болуы, яғни әйтеуір біреу нөлден өзге болатын
және
-дің барлық нақты
мәндері (оң болуы шарт емес) үшін орындалады және теңдіктің
орындалуының шарты ретінде (x)
және
(y) өзара пропорционалдығының оң
мән болуы, яғни әйтеуір біреу нөлден өзге болатын
және

болатындай  және
және
 сандарының бар болуы
алынады.
сандарының бар болуы
алынады.
Минковский теңсіздігі.
Бұл типті ұйғарымдардың алғашқы мысалы ретінде жоғарыда дәлелденген Минковский теңсіздігінің жаңа дәлелдеуін келтірейік.
5-Теорема.  үшін
үшін
 (2.9.24)
(2.9.24)
болады.
Дәлелдеу. Гёльдер теңсіздігіне сәйкес
 (2.9.25)
(2.9.25)
болғандықтан,

болатынын табамыз,
мұндағы  –
–

қатынасымен анықталатын облыс. Дәлелдеу керегі осы.
Гёльдер теңсіздігіндегі
теңдіктің орындалу шартын қолдана отырып,
(2.9.24) теңсіздіктегі теңдік белгісі
орындалады сонда және тек қана сонда, егер
немесе  болса, немесе
(x)
пен
(y) өзара пропорционал болса
екенін көрсету қиын емес.
болса, немесе
(x)
пен
(y) өзара пропорционал болса
екенін көрсету қиын емес.
Минковскийдің өзге теңсіздігі.
Квазисызықтандыру әдісін қолдана отырып, 2.20 және 2.21 бөлімшелерінде пайдаланылатын тағы бір теңсіздікті енгізейік.
6-Теорема.  үшін
үшін
 (2.9.26)
(2.9.26)
болады.
Дәлелдеу. Арифметикалық және геометриялық орталардың арасындағы теңсіздік
 (2.9.27)
(2.9.27)
болатынын көрсетті,
мұндағы  –
–
 (2.9.28)
(2.9.28)
қатынасымен анықталатын облыс. (2.9.27) теңдіктен ізделінді теңсіздікті төмендегідей етіп табамыз:
 (2.9.29)
(2.9.29)
 үшін Минковский
теңсіздігі.
үшін Минковский
теңсіздігі.
Квазисызықтандыруды тағы да қолдана отырып келесідей қорытынды шығарамыз.
7-Теорема. Егер  болса,
онда
болса,
онда
 (2.9.30)
(2.9.30)
болады.
Дәлелдеу. Айталық,
 болсын. Бұл белгілеулер
арқылы
болсын. Бұл белгілеулер
арқылы
 (2.9.31)
(2.9.31)
болатынын дәлелдегіміз келіп
тұр.  үшін
үшін
 (2.9.32)
(2.9.32)
болатындықтан, онда

болады,
мұндағы  функциясы
функциясы
 қатынастарымен
анықталады. Дәлелдеу керегі осы.
қатынастарымен
анықталады. Дәлелдеу керегі осы.
2.10. Квазисызықтандыру
Квазисызықтандыру әдісін
қарастыруды мынадай ескертпеден бастайық:
 үшін Гёльдер
теңсіздігінің дискреттік нұсқасын төмендегідей ұйғарымдауға
болады:
үшін Гёльдер
теңсіздігінің дискреттік нұсқасын төмендегідей ұйғарымдауға
болады:
8-Теорема.  үшін
үшін
 (2.10.1)
(2.10.1)
ұғымды аламыз,
мұндағы  –
–
 (2.10.2)
(2.10.2)
қатынастармен анықталатын облыс.
Бұл ұғымның маңыздылығы (2.10.1) теңсіздіктің сол жағында тұрған сызықтық емес функцияны сызықтық функциялардың жанаспа қисығы түрінде көрсете алуымызда. Яғни сызықтық емес функцияның кейбір тривиал емес қасиеттерін

сызықтық функцияның тривиал қасиеттерінің қарапайым салдарлары түрінде орната аламыз. Бұл ойдың жалғасы төмендегі 2.13 бөлімшеде қарастырылатын болады.
Енді квазисызықтандыру ұғымы туралы бірнеше алдын ала пайымдауларды қарастырайық.
Айталық,
 функциясы
– х
және
у
екі айнымалысы бар функция
болсын, мұндағы х
және
у
–
R
және
S
нормаланған кеңістіктерінің
элементтері.
функциясы
– х
және
у
екі айнымалысы бар функция
болсын, мұндағы х
және
у
–
R
және
S
нормаланған кеңістіктерінің
элементтері.  –
–
 элементінің нормасының
белгіленуі болсын; х
аргументіне
элементінің нормасының
белгіленуі болсын; х
аргументіне
 (2.10.3)
(2.10.3)
қатынаста қатысты
болатын  жаңа функциясын
анықтайық.
жаңа функциясын
анықтайық.
х-ке
қатысты функциясының кез
келген у
үшін орындалатын оң
таңбалылық, сызықтылық және дөңестік секілді қарапайым
қасиеттері  функциясының сәйкес
қасиеттерінің орындалуына себепші болады. Көптеген
жағдайларда
функциясының сәйкес
қасиеттерінің орындалуына себепші болады. Көптеген
жағдайларда  функциясының сәйкес
қасиеттерін орнатудан гөрі бұл қасиеттерді
функциясының сәйкес
қасиеттерін орнатудан гөрі бұл қасиеттерді
 функциясынан табу
оңайырақ болып келеді.
функциясынан табу
оңайырақ болып келеді.
Алғашқы және ең маңызды
жағдайлардың бірі – кез келген у
үшін
х-ке
қатысты  функциясы сызықтық болу
жағдайы, яғни
функциясы сызықтық болу
жағдайы, яғни
 (2.10.4)
(2.10.4)
Бұдан
 (2.10.5)
(2.10.5)
шығады. Бұл – «үшбұрыш
теңіздігі» немесе  үшін
«субаддитивтік».
үшін
«субаддитивтік».
Келесі маңызды жағдай бұл –
 (2.10.6)
(2.10.6)
Мұндағы
 , интегралдау
үрдісі z
кеңістігінің қандай да бір
облысы бойынша өтеді және
, интегралдау
үрдісі z
кеңістігінің қандай да бір
облысы бойынша өтеді және  функциясы кез
келген у
пен
z
үшін
х-ке қатысты сызықты функция
болады.
функциясы кез
келген у
пен
z
үшін
х-ке қатысты сызықты функция
болады.
Онда
 үшін
үшін
 (2.10.7)
(2.10.7)
болады.
 көрсеткіштері бар
Гёльдер теңсіздігін қолданып, одан
көрсеткіштері бар
Гёльдер теңсіздігін қолданып, одан
 (2.10.8)
(2.10.8)
қатынасын аламыз. Логарифмдеу
арқылы  функциясы кез
келген у
үшін
х-ке қатысты дөңес функция
болатынын көреміз.
функциясы кез
келген у
үшін
х-ке қатысты дөңес функция
болатынын көреміз.
Беллман, Гликсберг және Гросстың кітабында вариациялық санаудың классикалық емес есептеріне қатысты
 (2.10.9)
(2.10.9)
формуласының кейбір қосымшалары берілген [22]. Квазисызықтандыру әдісін Фурье қатарлары теориясында Зигмунд кеңінен қолданған болатын [23].
Дөңес және ойыс функцияларды квазисызықтандыру.
Дөңес және ойыс функциялар мен
функционалдарға қолдануға болатын квазисызықтандыруды қарастырайық.
Бірөлшемді жағдайдан бастайық.  – барлық
u
үшін
u-ға қатысты
және
– барлық
u
үшін
u-ға қатысты
және  болатын қатаң дөңес функция
болсын. Онда
болатын қатаң дөңес функция
болсын. Онда
 (2.10.10)
(2.10.10)
болатынын және жалғыз ғана
максимум  болғанда орындалатынын оңай
көруге болады. Осылайша қатаң ойыс функция үшін
де
болғанда орындалатынын оңай
көруге болады. Осылайша қатаң ойыс функция үшін
де
 (2.10.11)
(2.10.11)
аламыз. Жалпы нәтиже төмендегідей болады.
9-Теорема. Айталық,  функциясы – барлық х үшін
х-ке қатысты қатаң дөңес функция болсын,
онда
функциясы – барлық х үшін
х-ке қатысты қатаң дөңес функция болсын,
онда
 (2.10.12)
(2.10.12)
мұндағы  функциясы
–
функциясы
–  функциясының градиенті.
Жалғыз ғана максимум
функциясының градиенті.
Жалғыз ғана максимум  болғанда ғана
орындалады.
болғанда ғана
орындалады.
Квазисызықтандырудың бұл түрін функционалдық теңдеулерді және оларды шешудің ұқсас әдістерін зерттеуде Беллман [24] және Калаба кеңінен қолданды [25].
Квазисызықтандырудың басқа түрі.
Кездейсоқ айнымалыларды қолдану арқылы квазисызықтандыру әдісін Зигмунд және Марцинкевич қолданды [26].
10-Теорема.  дегеніміз
дегеніміз  құрамына кіретін функциялар
тобы болсын және Т – әрбір i үшін
құрамына кіретін функциялар
тобы болсын және Т – әрбір i үшін
 секілді қасиетке ие
болатын сызықтық түрлендіру болсын. Егер сондай-ақ барлық i
үшін
секілді қасиетке ие
болатын сызықтық түрлендіру болсын. Егер сондай-ақ барлық i
үшін
 (2.10.13)
(2.10.13)
болатындай т тұрақтысы бар
болса, онда S-тың кез келген  функциялар жүйесі
үшін
функциялар жүйесі
үшін
 (2.10.14)
(2.10.14)
болады.
2.11. Беккенбах теңсіздігі
Енді төмендегі нәтижені дәлелдейік [27]:
11-Теорема. Айталық,  және
және  үшін
үшін  болсын.
Онда
болсын.
Онда
 (2.11.1)
(2.11.1)
Дәлелдеу.  үшін теңсіздік тривиалды болып
келеді.
үшін теңсіздік тривиалды болып
келеді.  үшін 2.10
бөлімшедегідей
үшін 2.10
бөлімшедегідей
 (2.11.2)
(2.11.2)
болады. Сондықтан
барлық  үшін
үшін
 (2.11.3)
(2.11.3)
болатынын көрсету жеткілікті
болады (мұндағы  –
–
 қатынастарымен
анықталатын облыс екенін ескерте кетейік).
қатынастарымен
анықталатын облыс екенін ескерте кетейік).
(2.11.3) теңсіздікте кездесетін өрнектерді ықшамдау үшін жаңа айнымалы енгізейік:
 (2.11.4)
(2.11.4)
Бұдан
 және
және  қосындыларын тауып, оларды
ізделінді (2.11.3) теңсіздікке қоя отырып, оны
төмендегідей өзіне пара-пар түрге
келтіреміз:
қосындыларын тауып, оларды
ізделінді (2.11.3) теңсіздікке қоя отырып, оны
төмендегідей өзіне пара-пар түрге
келтіреміз:
 (2.11.5)
(2.11.5)
(2.11.5) теңсіздіктің орындалуын
дәлелдеу үшін сол жағындағы бөлшектің алымына
 үшін Гёльдер теңсіздігін
қолданып,
үшін Гёльдер теңсіздігін
қолданып,
 (2.11.6)
(2.11.6)
аламыз. Осылайша, (2.11.5) теңсіздік орындалады, егер
 (2.11.7)
(2.11.7)
теңсіздігі бар болса. Бірақ
бұл –  , яғни
, яғни
![]() үшін орындалатын Минковский
теңсіздігі.
үшін орындалатын Минковский
теңсіздігі. ![]() үшін
(2.11.7) теңсіздік тривиалды
болады.
үшін
(2.11.7) теңсіздік тривиалды
болады.
![]() үшін
(2.11.1) теңсіздіктегі теңсіздік
белгісі кері белгіге ауыстырылу керек.
үшін
(2.11.1) теңсіздіктегі теңсіздік
белгісі кері белгіге ауыстырылу керек.
2.12. Дрешер теңсіздігі
Беккенбахтың теңсіздігін Дрешер жалпылаған болатын [28]. Оны дәлелдеу үшін Дрешер моменттер әдісін қолданды.
12-Теорема. Егер  болса,
онда
болса,
онда
 (2.12.1)
(2.12.1)
болады.
Бұл нәтижені 2.11 бөлімшеде көрсетілген квазисызықтандыру әдісі арқылы да алуға болады. (2.12.1) теңсіздікті Гёльдер мен Минковскийдің теңсіздіктерін қиыстыру арқылы Данскин де дәлелдеген болатын [29].
2.13. Минковский–Малер теңсіздігі
Теңсіздіктерді дәлелдеудің
2.10-2.12 бөлімшелерде қолданған әдісі Минковскийдің бір идеясына
негізделген болатын [30]. Айталық,  – төмендегі қасиеттерге ие
болатын функция болсын:
– төмендегі қасиеттерге ие
болатын функция болсын:
(![]() а)
а)  үшін
үшін

(ә)
 үшін
үшін  (2.13.1)
(2.13.1)
(б)

 функциясы жалпыланған
қашықтық (координаталар басынан) немесе
функциясы жалпыланған
қашықтық (координаталар басынан) немесе
п-өлшемді
х
векторының
жалпыланған нормасы екені
белгілі.
Егер жоғарыда көрсетілген
қасиеттерге ие болатын функция берілсе, онда
біз поляр
функция деп аталатын және төмендегі
қатынаспен анықталатын  жаңа функциясын шығарып ала
аламыз:
жаңа функциясын шығарып ала
аламыз:
 (2.13.2)
(2.13.2)
Дөңес денелер
теориясында  функциясы «тірек функциясы»
деп аталады. Геометриялық тұрғыдан ол кері
полярларды
функциясы «тірек функциясы»
деп аталады. Геометриялық тұрғыдан ол кері
полярларды  сферасына қатысты түрлендіру
арқылы анықталады. Осы негізде төмендегі екілік қатынас орындалу
керек деген ұйғарымға келуге болады:
сферасына қатысты түрлендіру
арқылы анықталады. Осы негізде төмендегі екілік қатынас орындалу
керек деген ұйғарымға келуге болады:
 (2.13.3)
(2.13.3)
Бұл теңсіздікті расында да Минковский дәлелдеген болатын. Осыдан
 (2.13.4)
(2.13.4)
екені шығады. Бұл теңсіздік алғашқы рет сандардың геометриялық теориясында Малер көрсетті [31].
Кейбір полюс–поляр қатынастарының маңызды жалпыламаларын Л.Юнг қарастырды [32].
Бұл идеяларды кең түрде Лорх зерттеген болатын [33]. Оның еңбектерінде теңсіздіктер, дөңестік және Минковскийдің «аралас көлем» ұғымы арасындағы тығыз байланысты ашатын көптеген маңызды нәтижелерді табуға болады.
2.14. Карамат теңсіздігі
9-Теореманың функциясын көрсетудің мысалы ретінде Островскийге тиесілі болатын [34] және Караматтың келесі теоремасының жалпыламасы болып табылатын бір нәтижені дәлелдейміз [35].
13-Теорема. Айталық, төмендегі
шарттарды қанағаттандыратын  сандарының 2п саны
берілсін:
сандарының 2п саны
берілсін:
(а)

(![]() ә)
ә) 
 (2.14.1)
(2.14.1)
Онда кез келген үзіліссіз
дөңес  функциясы
үшін
функциясы
үшін
 (2.14.2)
(2.14.2)
теңсіздігін аламыз.
Теореманың шарттары өте жасанды болып көрінгенімен, бұндай түрдегі теңсіздіктер көптеген әр түрлі сұрақтарда пайда болатыны анықталды [36].
2.15. Шур түрлендіруі
Алдыңғы бөлімшедегі теореманы өзі жеке дара қызығушылық танытатын келесі теореманың негізінде Карамат дәлелдеген болатын.
14-Теорема.  2п
саны (2.14.1) теңсіздіктерді
қанағаттандырудың қажетті және жеткілікті шарты олардың арасында
төмендегідей қатынастардың орындалуы болып
табылады:
2п
саны (2.14.1) теңсіздіктерді
қанағаттандырудың қажетті және жеткілікті шарты олардың арасында
төмендегідей қатынастардың орындалуы болып
табылады:
 (2.15.1)
(2.15.1)
мұндағы
 (2.15.2)
(2.15.2)
(2.15.1) түрдегі түрлендірулерді
алғашқы рет Шур қарастырды [37]; Островскийдің пікірі бойынша біз
оларды Шур
түрлендірулері деп атайтын боламыз. Соңғы
кездері элементтері (2.15.2) шарттарды
қанағаттандыратын  матрицаларды екі түрлі
стохастикалық деп атайды. Олар кейбір
комбинаторикалық есептерде маңызды рөл
атқарады.
матрицаларды екі түрлі
стохастикалық деп атайды. Олар кейбір
комбинаторикалық есептерде маңызды рөл
атқарады.
2.16. Карамат теңсіздігінің дәлелдеуі
Осы бөлімшеде 13-Теореманы дәлелдеуде квазисызықтандыру әдісін қолдануды көрсетеміз. Бастапқы мәлімет ретінде
 (2.16.1)
(2.16.1)
теңдігін аламыз және
мұндағы  әзірше қатаң дөңес функция деп
пайымдайық.
әзірше қатаң дөңес функция деп
пайымдайық.
Максимум
мәні  , ал
, ал
 болғанда орындалады, біз
(z) мәнінің өзгеріс
облысын
болғанда орындалады, біз
(z) мәнінің өзгеріс
облысын
 (2.16.2)
(2.16.2)
теңсіздіктерімен шектей аламыз.
Ізделінді теңсіздікті дәлелдеу
үшін (2.14.1) шарттарды қанағаттандыратын
барлық  үшін және
(2.16.2) шартты қанағаттандыратын
барлық
үшін және
(2.16.2) шартты қанағаттандыратын
барлық  үшін
үшін
 (2.16.3)
(2.16.3)
Бұл теңсіздік бөліп-бөліп қосудан шығады (Абель–Бруначчи формуласы):
 (2.16.4)
(2.16.4)
теңсіздігі орындалады,
мұндағы  .
.
 болғандықтан,
болғандықтан,  болатынын көреміз. Сонымен
қатар
болатынын көреміз. Сонымен
қатар  болғандықтан, (2.16.3) теңдік расында да
орындалады.
болғандықтан, (2.16.3) теңдік расында да
орындалады.
2.17. Островский теңсіздігі
Функциялардың бұдан да кеңірек
тобына сәйкес теңсіздікті орнату үшін қатаң
дөңес  функциясын
қарастырамыз:
функциясын
қарастырамыз:
 (2.17.1)
(2.17.1)
Максимум мәні
 (2.17.2)
(2.17.2)
облысы бойынша алынады деп
есептей аламыз, себебі біз осындай түрде
реттелген  мәндерін қарастыруды мақсат
етіп отырмыз. Алдыңғы бөлімдегі ұйғарымдар бұл
бөлімдегі
мәндерін қарастыруды мақсат
етіп отырмыз. Алдыңғы бөлімдегі ұйғарымдар бұл
бөлімдегі  бөлшегіне қатысты кейбір
шарттардың орындалуында ғана пайдаланылады.
Әсіресе
бөлшегіне қатысты кейбір
шарттардың орындалуында ғана пайдаланылады.
Әсіресе
 (2.17.3)
(2.17.3)
теңсіздігінің орындалуын талап
ету дұрыс болады. Бұл талап  үшін
үшін
 шартының жалпыламасы.
Егер F
берілген шартты
қанағаттандыратын болса, онда F
Шур шартына қанағаттандырады
деп айтамыз.
шартының жалпыламасы.
Егер F
берілген шартты
қанағаттандыратын болса, онда F
Шур шартына қанағаттандырады
деп айтамыз.
Бұл шарт негізінде алдыңғы бөлімшедегі дәлелдеу толығымен өтіп, біз келесідей теореманы ұйғара аламыз.
15-Теорема. Егер F Шур шартын
қанағаттандыратын болса және  (2.14.1) шарттарын қанағаттандыратын
болса, онда
(2.14.1) шарттарын қанағаттандыратын
болса, онда
 (2.17.4)
(2.17.4)
болады.
Бұл теореманы басқа идея негізінде Л.Фукс дәлелдеген болатын [38]. Оған жақын нәтижелерді Татаркевич пен Бисак көрсетті [39].
2.18. Континуал аналогтар
2.14-2.17 бөлімшелердегі теоремалардың континуал аналогтарын Фан мен Лоренц тапты [40].
 (2.18.1)
(2.18.1)
деп жазамыз, егер
 (2.18.2)
(2.18.2)
және
 (2.18.3)
(2.18.3)
болса. Жоғарыда көрсетілген
жұмыста  функциясына қатысты қажетті
және жеткілікті шарттар келтірілген. Бұл шарттар
негізінде
функциясына қатысты қажетті
және жеткілікті шарттар келтірілген. Бұл шарттар
негізінде  қатынастарын қанағаттандыратын
шектелген және кемімелі
қатынастарын қанағаттандыратын
шектелген және кемімелі  және
және
 функцияларының кез
келген жүйесі үшін
функцияларының кез
келген жүйесі үшін
 (2.18.4)
(2.18.4)
болады.
2.19. Симметриялы функциялар
Енді Маркус пен Лопестің
кейбір қызықты теңсіздіктеріне көшейік [41].
 – теріс емес сандар
болсын;
– теріс емес сандар
болсын;  арқылы осы сандар үшін
құрылған r-ші элементар симметриялы
функцияны белгілейік, яғни
арқылы осы сандар үшін
құрылған r-ші элементар симметриялы
функцияны белгілейік, яғни
 (2.19.1)
(2.19.1)
Айталық,
 болсын.
Нәтижесінде
болсын.
Нәтижесінде  ~
~
 деп жазамыз,
егер
деп жазамыз,
егер
 (2.19.2)
(2.19.2)
болатындай λ саны табылса.
Біз дәлелдейтін бірінші ұйғарым төмендегідей болады.
16-Теорема.  үшін
үшін
 (2.19.3)
(2.19.3)
теңсіздігі орындалады,
егер  -дің
және
-дің
және  -дің кейбіреулері нөлге тең
болмаса. Теңдік орындалады, егер
-дің кейбіреулері нөлге тең
болмаса. Теңдік орындалады, егер  болса
немесе
болса
немесе  ~
~ болса
және
болса
және  -дің
және
-дің
және
 -дің ең болмағанда r саны
оң болса.
-дің ең болмағанда r саны
оң болса.
Дәлелдеу.  үшін
теңсіздік
үшін
теңсіздік
 (2.19.4)
(2.19.4)
тепе-теңдігінен шығады.
Енді  және
және

 деп
пайымдайық.
деп
пайымдайық.  өрнегін
өрнегін
 сандар жүйесі арқылы
белгілейік. Енді бізде екі тепе-теңдік
бар:
сандар жүйесі арқылы
белгілейік. Енді бізде екі тепе-теңдік
бар:
 (2.19.5)
(2.19.5)
Олардың екіншісін i арқылы қосып,
 (2.19.6)
(2.19.6)
аламыз, бұдан біріншісі бойынша
 (2.19.7)
(2.19.7)
шығады.
 (2.19.8)
(2.19.8)
болғандықтан,
 (2.19.9)
(2.19.9)
немесе
 (2.19.10)
(2.19.10)
қатынасын табамыз.
Бұдан  және
барлық х
үшін төмендегі тепе-теңдік бар
болады деген қорытынды шығады:
және
барлық х
үшін төмендегі тепе-теңдік бар
болады деген қорытынды шығады:
 (2.19.11)
(2.19.11)
мұндағы
 .
.
Енді теоремадағы
ұйғарым  үшін орындалады,
яғни
үшін орындалады,
яғни
 (2.19.12)
(2.19.12)
болады деп жорамалдайық.
Теоремадағы ұйғарым орындалмайды, егер
(2.19.12) теңсіздікте теңдік белгісі
тұрғанда қатынасы бар болса. Онда 
 болғанда қандай да
бір i
үшін
болғанда қандай да
бір i
үшін
 (2.19.13)
(2.19.13)
Осылайша, ізделінді
теңсіздік r
үшін де орындалады, егер
қандай да бір i
үшін

 болса. Егер де
әрбір i
үшін
болса. Егер де
әрбір i
үшін

 болса, онда
әрбір i
үшін
болса, онда
әрбір i
үшін
 болады және
онда
болады және
онда
 (2.19.14)
(2.19.14)
Бірақ
 , себебі шарт
бойынша
, себебі шарт
бойынша  сандарының r
саны оң болады.
Сондықтан
сандарының r
саны оң болады.
Сондықтан  болғанда
(2.19.12) теңсіздіктің бірінші
теңсіздігі теңдікпен алмастырылуы керек,
(2.19.13) теңдіктен
(2.19.12) теңсіздіктің ортаңғы
мүшесі
болғанда
(2.19.12) теңсіздіктің бірінші
теңсіздігі теңдікпен алмастырылуы керек,
(2.19.13) теңдіктен
(2.19.12) теңсіздіктің ортаңғы
мүшесі 
 шарты кезінде оң мәнді
қабылдайды, себебі осы шарттан және әрбір
i
үшін
шарты кезінде оң мәнді
қабылдайды, себебі осы шарттан және әрбір
i
үшін


 барлық
i
үшін мүмкін емес екені
шығады.
барлық
i
үшін мүмкін емес екені
шығады.
2.20. Тағы бір теңсіздік
Симметриялы функцияларға жататын тағы бір нәтиже төмендегідей болады.
17-Теорема. Егер  және
және  п оң таңбалы айнымалылары
бар жүйелері болса, онда
п оң таңбалы айнымалылары
бар жүйелері болса, онда
 (2.20.1)
(2.20.1)
болады.
Бұдан да күшті нәтиже теңдік белгісінің орындалу жағдайларын зерттеу жұмысы Лопес пен Маркустың еңбегінде көрсетілген. Біз тек қана ұйғарымдалған теоремамен шектелеміз.
Теореманың дәлелдеуі 6-Теорема мен 16-Теореманың бірігуіне негізделеді. Бұл теоремалар бойынша

 (2.20.2)
(2.20.2)
болады.
2.21. Уайтлидің кейбір қорытындылары
Осыған ұқсас және кеңірек нәтижелерді Уайтли алды. Айталық,
 (2.21.1)
(2.21.1)
болсын,
мұндағы  – оң сандар.
Онда
– оң сандар.
Онда  үшін
үшін
 (2.21.2)
(2.21.2)
теңсіздігі орындалады,
ал  болғанда 17-Теореманың
теңсіздігі орындалады.
болғанда 17-Теореманың
теңсіздігі орындалады.
(2.21.2) теңсіздіктегі жаңа нәтиже
интегралды түрлендірулер әдісі арқылы оңай алынады, бұл әдісті біз
келесі бөлімшеде кеңірек қарастырамыз. Кіші
 және
және  үшін
үшін
 (2.21.3)
(2.21.3)
шығады, бұдан

 (2.21.4)
(2.21.4)
болады. Осыдан
 (2.21.5)
(2.21.5)
шығады, мұндағы
 (2.21.6)
(2.21.6)
(2.21.2) теңсіздік енді Минковский теңсіздігінің салдары болып шықты.
2.22. Гиперболалық көпмүшелер
Осы бөлімшеде Гординг енгізген
маңызды ұғым – гиперболалық
көпмүше ұғымына тоқталып өтеміз
[42].  –
–
 -ге
қатысты т
дәрежелі біртекті көпмүше
және
-ге
қатысты т
дәрежелі біртекті көпмүше
және  – нақты сандар жүйесі болсын.
Егер s-ке
қатысты
– нақты сандар жүйесі болсын.
Егер s-ке
қатысты

теңдеуінің барлық
нақты  үшін
т
нақты түбірі болса,
онда
үшін
т
нақты түбірі болса,
онда  –
а-ға қатысты гиперболалық
көпмүше деп айтамыз. Осыған ұқсас анықтама төмендегідей
болады:
–
а-ға қатысты гиперболалық
көпмүше деп айтамыз. Осыған ұқсас анықтама төмендегідей
болады:
 (2.22.1)
(2.22.1)
мұндағы
 және
және  нақты
х
үшін нақты сан
болады.
нақты
х
үшін нақты сан
болады.
Көріп отырғанымыздай, бұл ұғымның осы тараудың бірнеше нәтижелеріне тікелей қатысы бар және ол матрицалар теориясында маңызды рөлге ие болады.
Бір гиперболалық көпмүше негізінде төмендегі лемма арқылы жаңа гиперболалық көпмүшелерді шығарып алуға болады.
2-Лемма. Егер а
мен  қатысты
қатысты  көпмүшесі гиперболалық
көпмүше болса, онда
көпмүшесі гиперболалық
көпмүше болса, онда
 (2.22.2)
(2.22.2)
көпмүшесі де а-ға қатысты гиперболалық көпмүше болады.
Дәлелдеу 2.1 бөлімшедегідей, Ролль теоремасынан шығады. Осы лемманы екінші рет қолдану
 (2.22.3)
(2.22.3)
теңдігімен
анықталған  көпмүшелері де гиперболалық
екенін көрсетеді.
көпмүшелері де гиперболалық
екенін көрсетеді.
2.23. Гординг теңсіздігі
 –
–  көпмүшесінің толық поляр түрі
болсын, мұндағы
көпмүшесінің толық поляр түрі
болсын, мұндағы  мүшесі –
мүшесі –
 п-өлшемді
вектор:
п-өлшемді
вектор:
 (2.23.1)
(2.23.1)
18-Теорема.  көпмүшесі а-ға қатысты гиперболалық
көпмүше болсын,
көпмүшесі а-ға қатысты гиперболалық
көпмүше болсын,  және М – Р-ның толық поляр
түрі болсын. Осыдан кейін
және М – Р-ның толық поляр
түрі болсын. Осыдан кейін  –
–
 -дің жүйесі
және
-дің жүйесі
және  үшін
үшін  болады.
Сонда
болады.
Сонда
 (2.23.2)
(2.23.2)
Бұл теореманың теңдік белгісін қарастыру арқылы дәлелдеуі толық түсіндіруді талап ететіндіктен, біз Гординг еңбегін қарауды ұсынамыз.
2.24. Гиперболалық көпмүшелердің мысалдары
Екі қызықты мысал
болып  болғандағы а-ға
қатысты
болғандағы а-ға
қатысты
 (2.24.1)
(2.24.1)
гиперболалық көпмүше (бұл
квадраттық түрді 2.25 бөлімшеде қарастырамыз)
және  болғандағы а-ға
қатысты
болғандағы а-ға
қатысты
 (2.24.2)
(2.24.2)
гиперболалық көпмүше
болады. (2.24.2) функция
үшін  болғандағы
болғандағы
 (2.24.3)
(2.24.3)
қатынасы бар
болғандықтан,  – элементар симметриялы
функциялар – (1,1,…,1) қатысты гиперболалық
болады.
– элементар симметриялы
функциялар – (1,1,…,1) қатысты гиперболалық
болады.
Гординг мынаны байқаған
болатын: егер  көпмүшедегі а-ға қатысты гиперболалық
көпмүше болса, онда
көпмүшедегі а-ға қатысты гиперболалық
көпмүше болса, онда  гипербеттері
гипербеттері  үшін
үшін
 болатын
болатын  -дан
тұратын х
облысында дөңес болады. Бұдан
2.19 және 2.20 бөлімшелердегі кейбір нәтижелер шығарылуы
мүмкін.
-дан
тұратын х
облысында дөңес болады. Бұдан
2.19 және 2.20 бөлімшелердегі кейбір нәтижелер шығарылуы
мүмкін.
2.25. Лоренц кеңістіктері
Осы бөлімшеде анықталмаған түрлер үшін кейбір нәтижелерді алу тәсілдерін қарастырамыз. Келесі теореманы дәлелдейік.
19-Теорема. Айталық,
 (2.25.1)
(2.25.1)
функциясы R облысындағы
барлық  үшін
және
үшін
және
 (2.25.2)
(2.25.2)
қатынастарымен анықталған
функция болсын. Онда  үшін
үшін
 (2.25.3)
(2.25.3)
болады.
Дәлелдеу. Жоғарыда түсіндірілген квазисызықтандыру әдісін қолданамыз.
 (2.25.4)
(2.25.4)
болатынын көрсетейік,
мұндағы  – төмендегі қатынастармен
анықталған облыс:
– төмендегі қатынастармен
анықталған облыс:
 (2.25.2)
(2.25.2)
Гёльдер теңсіздігін қолданып,
 (2.25.6)
(2.25.6)
аламыз. Соңғы өрнектің
минимумы  -ге қатысты функция
ретінде (2.25.2) пен
(2.25.5) шарттары
негізінде
-ге қатысты функция
ретінде (2.25.2) пен
(2.25.5) шарттары
негізінде

нүктеде болады
және  тең болады. Бұл
жерден (2.25.4) өрнек шығады. Бұл өрнектен
теорема шығады. Көрсетілген дәлелдеу Беллманға тиесілі
[43].
тең болады. Бұл
жерден (2.25.4) өрнек шығады. Бұл өрнектен
теорема шығады. Көрсетілген дәлелдеу Беллманға тиесілі
[43].
Осындай түрдегі теңсіздіктер туралы ұйғарымдарды Мурнаганнан да көруге болады.
Бұл нәтижелерді басқа жолмен де табуға болады, ол үшін Бохнерге тиесілі өрнекті қолдану керек [44].
 квадраттық түрі
салыстырмалылық теориясында маңызды рөл
атқарады. (2.25.3) теңсіздік әйгілі «егіздер
парадоксына» қатысатынын айта кеткен жөн.
квадраттық түрі
салыстырмалылық теориясында маңызды рөл
атқарады. (2.25.3) теңсіздік әйгілі «егіздер
парадоксына» қатысатынын айта кеткен жөн.
Бұл теңсіздіктердің евклидтік емес геометрия тұрғысынан қарағандағы түрлендіруі Ацел мен Варгтың жұмысында қамтылады.
2.26. Кері теңсіздіктер
Алдыңғы 2.9 бөлімшеде Буняковский–Шварц теңсіздігін және оның жалпыламасы – Гёльдер теңсіздігін қарастырған болатынбыз.
 (2.26.1)
(2.26.1)
түріндегі
теңсіздік  кеңістігінен алынған
барлық u
және
v
үшін ешбір оң
абсолют k
тұрақтысы үшін орындала
алмайды. Алайда мұндай теңсіздік орындалады,
егер u
және
v
кейбір
кеңістігінен алынған
барлық u
және
v
үшін ешбір оң
абсолют k
тұрақтысы үшін орындала
алмайды. Алайда мұндай теңсіздік орындалады,
егер u
және
v
кейбір
 кеңістігіне тиісті
болса.
кеңістігіне тиісті
болса.
Мұндай есептерді Франк пен Пи, Бляшке мен Пик, Бюкнер, Фавар, Бервальд, Кнезер мен Беллман қарастырды. Бұл есептерді моменттер теориясы мен дөңес теңсіздіктер теориясының әдістері арқылы жүйелі қарастыру болатындықтан және Фавар мен Бервальд әдістерімен жалпылауға болатындықтан, осы бөлімшеде Беллманның дәлелдеу әдістері бойынша жүреміз [45], себебі бұл әдістер арқылы нәтижелер дәлдігінің аздығы арқылы басқа бағыттағы жалпыламаларды алуға мүмкіндік береді.
Алғашқы нәтиже мынадай болмақ.
20-Теорема. Айталық,  және
және  функциялары
функциялары  үшін х-ке қатысты төмендегі
шарттар бойынша нормаланған ойыс функциялар
болсын:
үшін х-ке қатысты төмендегі
шарттар бойынша нормаланған ойыс функциялар
болсын:
 (2.26.2)
(2.26.2)
Онда
 (2.26.3)
(2.26.3)
болады.  минималды
мәні
минималды
мәні
 (2.26.4)
(2.26.4)
үшін болады.
Дәлелдеу.  функциясы
функциясы
 үшін ойыс және
анықталған және осы кесіндінің шектерінде нөлге тең болатын
функциялар класына тиісті болсын. Екінші туындысы оң емес болатын
функциялар класының тармағын қарастырайық:
үшін ойыс және
анықталған және осы кесіндінің шектерінде нөлге тең болатын
функциялар класына тиісті болсын. Екінші туындысы оң емес болатын
функциялар класының тармағын қарастырайық:
 (2.26.5)
(2.26.5)
Бұдан да кең кластың функцияларының минимумдары (2.26.5) шартты қанағаттандыратын функциялар класының төменгі шегін нақты табу үрдісіне эквивалентті болады.
 функциясы
– (2.26.5) көрсетілген шекті шарттары
бар
функциясы
– (2.26.5) көрсетілген шекті шарттары
бар  операторы үшін Грин функциясы
болсын, яғни
операторы үшін Грин функциясы
болсын, яғни
 (2.26.6)
(2.26.6)
Онда
 функциясын
функциясын
 (2.26.7)
(2.26.7)
түрінде жазуға болады.
Осы жазуды қолданып,
көрсетілген нормасы бар барлық  ойыс функциялар
үшін
ойыс функциялар
үшін
 (2.26.8)
(2.26.8)
сызықтық функционалдың
минимумын анықтайық, мұндағы  – берілген теріс емес
функция.
– берілген теріс емес
функция.
 (2.26.9)
(2.26.9)
функциясының
 (2.26.10)
(2.26.10)
шартын қанағаттандыратын
барлық  үшін төменгі шектің нақты
мәнін табуымыз керек, мұндағы
үшін төменгі шектің нақты
мәнін табуымыз керек, мұндағы
 (2.26.11)
(2.26.11)
Жоғарыда көрсетілген жағдайға
ұқсас аналогпен пайымдай отырып,  бойынша нақты төменгі шек,
яғни u
бойынша нақты төменгі
шек
бойынша нақты төменгі шек,
яғни u
бойынша нақты төменгі
шек
 (2.26.12)
(2.26.12)
формуласымен анықталатыны көрініп тұр.
Бұл ұйғарымның дәлелдеуін осы
бөлімшеде келтірмейміз, себебі 2.27 бөлімшеде
 үшін жалпы жағдайда
келтіретін боламыз.
үшін жалпы жағдайда
келтіретін боламыз.
Осы нәтижеден 20-Теорема шығады. Бізге
 (2.26.13)
(2.26.13)
белгілі.
 теріс емес функциясына
және
теріс емес функциясына
және  ойыс функция үшін осы
теңсіздікті қолдана отырып, төмендегідей соңғы нәтижені
аламыз:
ойыс функция үшін осы
теңсіздікті қолдана отырып, төмендегідей соңғы нәтижені
аламыз:
 (2.26.14)
(2.26.14)
Енді теңсіздікті тривиал емес
екенін көрсету керек. Гросс қолданған тікелей есептеу әдісі
минимумның  болғанда
және
болғанда
және  симметриялық нүктеде шығатынын
және
симметриялық нүктеде шығатынын
және  -ге тең болатынын көрсетеді.
Эсктремал функциялар жоғарыда көрсетілген
болатын.
-ге тең болатынын көрсетеді.
Эсктремал функциялар жоғарыда көрсетілген
болатын.
2.27.  кеңістігі
кеңістігі
20-Теореманың  -жалпыламасын дәлелдейік
((2.26.7) қара). Біз көрсететін
дәлелдеуді Вейнбергер тапты.
-жалпыламасын дәлелдейік
((2.26.7) қара). Біз көрсететін
дәлелдеуді Вейнбергер тапты.
21-Теорема.  және
және  функциялары – төмендегі
шарттармен нормаланған ойыс функциялар
болсын:
функциялары – төмендегі
шарттармен нормаланған ойыс функциялар
болсын:
 (2.27.1)
(2.27.1)
Онда
 (2.27.2)
(2.27.2)
болады.
Оң жағының
максимумы  болғанда шығатыны көрініп
тұр.
болғанда шығатыны көрініп
тұр.
Дәлелдеу. Жоғарыдағыдай пайымдайық:
 (2.27.3)
(2.27.3)
Онда
 (2.27.4)
(2.27.4)
мұндағы
 (2.27.5)
(2.27.5)
Барлық интегралдар 0 мен 1 аралығында алынады. Гёльдер теңсіздігін қолданып,
 (2.27.6)
(2.27.6)
Дәл осылай
 (2.27.7)
(2.27.7)
(2.27.6) және (2.27.7) теңсіздіктер (2.27.4) өрнекпен бірге
 (2.27.8)
(2.27.8)
екенін көрсетеді.
Есептеу үрдісі (2.27.2) теңсіздіктің оң жағындағы өрнекке алып келеді. Бұл есептеуді Гросс шығарған еді.
Көпөлшемді жағдай.
2.26 бөлімшеде көрсетілген пайымдауларға ұқсас етіп төмендегі жалпы нәтижені дәлелдеуге болады.
22-Теорема.  және
және  қандай да бір R облысына
тиісті Р нүктелері үшін анықталған және төмендегі үш шартты
қанағаттандыратын болсын:
қандай да бір R облысына
тиісті Р нүктелері үшін анықталған және төмендегі үш шартты
қанағаттандыратын болсын:
(![]() а)
а) 
(ә)
R
шегі
В
нүктесінде  (2.27.9)
(2.27.9)
(б)

 функциясы – R облысы
үшін Грин функциясы болсын және
функциясы – R облысы
үшін Грин функциясы болсын және
 (2.27.11)
(2.27.11)
онда
 (2.27.11)
(2.27.11)
болады.
Бұл нәтиженің тривиал емес екенін (яғни теңсіздіктің оң жағы оң таңбалы болатынын) анықтау оңай болмайды. Облыстардың әр түрлі типтері үшін осы минимумды анықтау да қиын мәселе болып тұр.
Мор мен Нолль теоремасы.

теңсіздігінің нақты алуын Мор мен Нолль берген болатын.
23-Теорема. Егер  функциясының
функциясының  кесіндісінде үзіліссіз п-ші
туындысы бар болса, онда
кесіндісінде үзіліссіз п-ші
туындысы бар болса, онда
 (2.27.12)
(2.27.12)
мұндағы
 (2.27.13)
(2.27.13)
 үзіліссіз екені оның
басқа бір өрнектелуінен шығады:
үзіліссіз екені оның
басқа бір өрнектелуінен шығады:
 (2.27.14)
(2.27.14)
мұндағы интегралдау
 (2.27.15)
(2.27.15)
облысы бойынша жүргізіледі.
Егер

сызықты дифференциал теңдеуімен байланысатын кері операторларды қолдансақ бұдан да кеңірек нәтижелер алуға болады.
2.28. Фавар–Бервальд жалпыламасы
2.26 бөлімшеде айтылған Франк–Пик нәтижесінің жалпыламалары Фавар мен Бервальдке тиесілі теңсіздіктердің дербес жағдайлары ретінде алынуы мүмкін.
Фаварға төмендегі теорема тиесілі.
24-Теорема.  функциясы
–
функциясы
–  кесіндісінде теріс емес
үзіліссіз ойыс және тепе-тең нөлден өзге функция болсын.
Айталық
кесіндісінде теріс емес
үзіліссіз ойыс және тепе-тең нөлден өзге функция болсын.
Айталық
 (2.28.1)
(2.28.1)
болсын.  функциясы –
функциясы –
 және
және

үшін шектелген кемімейтін функция болсын. Онда
 (2.28.2)
(2.28.2)
болады.
Фавар бірнеше айнымалысы бар функцияларға қатысты сәйкес теоремаларды дәлелдеді және (2.28.2) теңсіздіктегі теңдік белгісінің орындалу шарттарын көрсетті. 24-Теореманың жалпыламасы болып Бервальд теоремасы алынады.
25-Теорема.  функциясы
–
функциясы
–  кесіндісінде теріс емес
үзіліссіз ойыс және тепе-тең нөлден өзге функция
болсын.
кесіндісінде теріс емес
үзіліссіз ойыс және тепе-тең нөлден өзге функция
болсын.  функциясы
–
функциясы
–  кесіндісінде қатаң
монотонды және үзіліссіз болсын, мұндағы
кесіндісінде қатаң
монотонды және үзіліссіз болсын, мұндағы
 – өте үлкен сан.
Онда
– өте үлкен сан.
Онда
 (2.28.3)
(2.28.3)
теңдеуінің тек қана бір оң
түбірі болады:  .
.
 функциясы
–
функциясы
–  үшін шектелген және
монотонды болсын; айталық
үшін шектелген және
монотонды болсын; айталық
 (2.28.4)
(2.28.4)
(Стильтьес интегралы) болсын. Онда
 (2.28.5)
(2.28.5)
болады,
егер  және
және  функциялары бірдей мағынада
монотонды және
функциялары бірдей мағынада
монотонды және
 (2.28.6)
(2.28.6)
болады, егер бұл функциялар қарама-қарсы мағынада монотонды болса.
Бервальд мұнымен қоса теңдіктің орындалу жағдайларын да анықтап берді.
25-Теореманың бірінші қосымшасы ретінде
 (2.28.7)
(2.28.7)
аламыз. Онда
 (2.28.8)
(2.28.8)
мұндағы
 (2.28.9)
(2.28.9)
Онда (2.28.5) теңсіздіктен
 (2.28.10)
(2.28.10)
табамыз.
 болғанда Франк–Пик
теңсіздігін аламыз, ал
болғанда Франк–Пик
теңсіздігін аламыз, ал  болғанда Фавар теңсіздігін
аламыз:
болғанда Фавар теңсіздігін
аламыз:
 (2.28.11)
(2.28.11)
Басқа дербес жағдайлары ретінде төмендегі теңсіздіктерді алуға болады:
 (2.28.12)
(2.28.12)
және
 (2.28.13)
(2.28.13)
бұл теңсіздіктер сәйкесінше
Фавар мен Бервальдқа тиесілі. Соңғы екі теңсіздік жоғарыда
көрсетілген  -ке қатысты пайымдауларда
орындалады.
-ке қатысты пайымдауларда
орындалады.
Фавар мен Бервальдтың аталған еңбектерінде басқа да көптеген нәтижелер бар, оның ішінде көпөлшемді жағдайлардың жалпыламалары да қамтылған.
2.29. Коши теоремасының басқа түрлері
2.26 – 2.28 бөлімшелерде Коши теңсіздігінің бір түрін қарастырдық. Енді Швейцер мен Пойа–Сегё берген осы теңсіздіктің басқа түрін қарастырайық және дәлелдейік [46].
26-Теорема. Егер  болса,
онда
болса,
онда
 (2.29.1)
(2.29.1)
болады.
Сонымен қатар континуалды аналог та бар болады.
Дрешер көрсеткендей, Коши мен Гёльдердің классикалық теңсіздіктерді моменттер теориясы теоремаларының салдарлары ретінде шығарып алуға болады. 26-Теорема осы типке жатады және осылай дәлелденеді. Көпөлшемді жағдайға қатысты жалпыламаларды Маданский берді.
(2.29.1) теңсіздікті Уотсон жақсартқан болатын, ал дәлелдеуін Касселс берді.
27-Теорема.  болсын,
бірақ
болсын,
бірақ  -дің барлығы бірдей нөлге
тең емес. Онда
-дің барлығы бірдей нөлге
тең емес. Онда
 (2.29.2)
(2.29.2)
болады.
Осы бағыттағы тағы бір нәтиже Фань Цзы мен Тоддқа тиесілі [47].
28-Теорема.  – нақты сандар болсын
және
– нақты сандар болсын
және  болсын.
Онда
болсын.
Онда

Бұл теңсіздік Хассанның бұрынғы нәтиженің жалпыламасы болып табылады [48].
2.30. Коши–Буняковский–Шварц теңсіздіктерін нақтылау
 (2.30.1)
(2.30.1)
функционалының теріс еместігін анықтап, оның төменгі шегінің дәл шығуына мүдделіміз. Егер қарастырып отырған функциялар немесе функционалдар төмендегі мағынада квадрат түрде болса ғана оның төменгі шегін таба аламыз.
Скаляр көбейтінді ұғымын қолданып, барлық u және v үшін теріс емес болатын төмендегі функционалды қарастырайық:
 (2.30.2)
(2.30.2)
u
айнымалысын  айнымалысына алмастырамыз,
мұндағы r
және
s
– скалярлар.
Онда
айнымалысына алмастырамыз,
мұндағы r
және
s
– скалярлар.
Онда  шартына сәйкес төмендегі
теңсіздікті аламыз:
шартына сәйкес төмендегі
теңсіздікті аламыз:
 (2.30.3)
(2.30.3)
Ал бұл теңсіздік, өз кезегінде, төмендегі теңсіздікке алып келеді:
 (2.30.4)
(2.30.4)
Бұл теңсіздік төмендегідей пайымдалады: нақтыланған v және кез келген f пен g екі элементтері үшін анықталған
 (2.30.5)
(2.30.5)
жаңа скаляр
көбейтінді  ескі скаляр көбейтіндінің
қанағаттандыратын
ескі скаляр көбейтіндінің
қанағаттандыратын
 (2.30.6)
(2.30.6)
шартын қанағаттандырады.
Бұл үрдісті қайталауға болады және қайталау арқылы әрбір келесісі алдыңғысынан күштірек болатын теңсіздіктер қатарын аламыз.
2.31. Ескі теңсіздіктен жаңа теңсіздіктерді шығару
(2.30.4) теңсіздігі жүйелеу арқылы алынатын басқа кеңірек теңсіздіктердің дербес жағдайы болып табылады.
 (2.31.1)
(2.31.1)
теңсіздігі теңдік белгісі
орындалады сонда тек қана сонда, егер
 болса деген қасиетке
ие. (2.31.1) теңсіздіктен
болса деген қасиетке
ие. (2.31.1) теңсіздіктен
 (2.31.2)
(2.31.2)
алмастыру арқылы шығатын
ұйытқыған теңсіздікті қарастырайық, мұндағы
 элементтері
– u
мен
v
элементтерімен бірдей,
ал r
және
s
– скаляр
шамалар. F
өрнегін
элементтері
– u
мен
v
элементтерімен бірдей,
ал r
және
s
– скаляр
шамалар. F
өрнегін
 нүктесінің айналасында
дәрежелік қатарға жіктеп, төмендегі қатынасты
аламыз:
нүктесінің айналасында
дәрежелік қатарға жіктеп, төмендегі қатынасты
аламыз:
 (2.31.3)
(2.31.3)
r және s мәндерін өте кіші етіп алып, бұдан барлық r және s үшін
 (2.31.4)
(2.31.4)
теңсіздігі шығатынын көреміз, яғни
 (2.31.5)
(2.31.5)
болу керек.
Бұл ұйғарым Буняковский–Шварц теңсіздігін шығару кезінде қолданылды. Басқа да қызықты теңсіздіктер осы әдіспен Гёльдер теңсіздігінен және арифметикалық және геометриялық орталардың арасындағы теңсіздіктен шығаруға болады.
Арифметикалық және геометриялық орталар арасындағы теңсіздіктерді нақтылау.
Белгілі болғандай, бұл
теңсіздікте әрқашан қатаң теңдік белгісі орындалады,
егер  элементтерінің барлығы өзара
тең болмаса. Алгебралық сандар теориясына
сәйкес
элементтерінің барлығы өзара
тең болмаса. Алгебралық сандар теориясына
сәйкес  «шашырауын»
«шашырауын»
 (2.31.6)
(2.31.6)
дискриминантпен өлшеу арқылы
 (2.31.7)
(2.31.7)
қатынасының  арқылы өрнектелетін төменгі
шегін табу қызықтырады. Бұл типтің нәтижелерін алғашқы рет Шур
алған болатын; бұл сұрақтың одан арғы зерттеуімен Зигель, Кобер мен
Дингхас айналысты.
арқылы өрнектелетін төменгі
шегін табу қызықтырады. Бұл типтің нәтижелерін алғашқы рет Шур
алған болатын; бұл сұрақтың одан арғы зерттеуімен Зигель, Кобер мен
Дингхас айналысты.
Таңбалары кезектесетін теңсіздіктер.
Келесі нәтижені Сегё алды.
29-Теорема.  және
және  функциясы
–
функциясы
–  кесіндісінде дөңес функция
болсын. Онда
кесіндісінде дөңес функция
болсын. Онда
 (2.31.8)
(2.31.8)
болады.
Осыған ұқсас нәтижені аудандарды салыстыру арқылы Беллман алды.
30-Теорема.  және
және  функциясы
–
функциясы
–  кесіндісінде дөңес функция
болсын. Онда егер
кесіндісінде дөңес функция
болсын. Онда егер  болса,
онда
болса,
онда
 (2.31.9)
(2.31.9)
болады.
 дербес жағдайы Вейнберг
тәуелсіз анықтаған болатын.
дербес жағдайы Вейнберг
тәуелсіз анықтаған болатын.
Бұл екі теорема төмендегі Олкин теоремасының дербес жағдайлары болып табылады.
31-Теорема.  және
және  функциясы
–
функциясы
–  кесіндісінде дөңес функция
болсын. Онда
кесіндісінде дөңес функция
болсын. Онда
 (2.31.10)
(2.31.10)
Бұл теореманы Олкин секілді дәлелдеудің орнына, құрамында Олкин теңсіздігі бар басқа теореманы дәлелдейміз, 2.32 бөлімшені қара.
Брунктың еңбегінде Олкиннің бірнеше теңсіздігі қамтылды және олардың бұдан да жалпы нәтижелері берілді. Олар жоғарыдағы 2.14-2.18 бөлімшелерде дәлелденген теоремалармен ұқсас болып келеді.
2.32. Стеффенсен теңсіздігі
Стеффенсенге тиесілі келесі теңсіздікті дәлелдейік. Дәлелдеуді Беллманның жолымен жасаймыз [49].
32-Теорема. Айталық,
(![]() а)
а)  функциясы теріс емес
және
функциясы теріс емес
және  кесіндісінде
кесіндісінде
монотонды кемімелі,
(ә)
 функциясы
функциясы  шарттарын
(2.32.1)
шарттарын
(2.32.1)
қанағаттандырады
болсын. Онда
 (2.32.2)
(2.32.2)
болады, мұндағы
 (2.32.3)
(2.32.3)
Дәлелдеу.  функциясын
функциясын
 (2.32.4)
(2.32.4)
қатынасымен
анықтайық. f
және g,
 функцияларына салынған
шарттардың негізінде
функцияларына салынған
шарттардың негізінде  функциясы
s
a-дан
b-ға дейін өскенде үзіліссіз
және монотонды өспелі және
функциясы
s
a-дан
b-ға дейін өскенде үзіліссіз
және монотонды өспелі және  болатыны көрініп тұр.
Дифференциалдау арқылы
болатыны көрініп тұр.
Дифференциалдау арқылы
 (2.32.5)
(2.32.5)
болатынын табамыз, бұдан
 (2.32.6)
(2.32.6)
шығады. Осыдан,
 (2.32.7)
(2.32.7)
болады және осы арқылы (2.32.2) қос теңсіздіктің оң жақ теңсіздігі дәлелденді. Осылайша сол жақ теңсіздік те дәлелденеді.
Брунк–Олкин теңсіздігі.
(2.31.10) Олкин теңсіздігін алу үшін
(бұл жерде f-ты
h-қа алмастырып),
32-Теоремадан
 (2.32.8)
(2.32.8)
аламыз, мұндағы
 т.с.с. (2.32.9)
т.с.с. (2.32.9)
және
 . Онда біз 31-Теоремадан
да кұштірек нәтиже аламыз.
. Онда біз 31-Теоремадан
да кұштірек нәтиже аламыз.
Стеффенсен теңсіздігінің жалпыламасы.
Осындай жолмен басқа да көптеген теңсіздікті дәлелдеуге болады. мысалы, Стеффенсен теңсіздігінің төмендегідей жалпыламасы орындалады.
33-Теорема. Айталық,
(![]() а)
а)  функциясы теріс
және
функциясы теріс
және  кесіндісінде
кесіндісінде
монотонды кемімелі,
(ә)
 (2.32.10)
(2.32.10)
(б)

мұндағы

Онда
 (2.32.11)
(2.32.11)
мұндағы
 (2.32.12)
(2.32.12)
болады.
Қорытынды
Берілген дипломдық жұмыста көрсетілген теңсіздіктерді шынайы түрде тамаша теңсіздіктер деп атауға болады. Себебі олар математикалық тұрғыдан қарағанда сондай тамаша және қолданбалы ғылыми пәндерде өте кең қолданылады. Негізгі теңсіздіктер арқылы көптеген жағдайда бірнеше функцияны олардың туындысын таппай-ақ (әсіресе зерттелетін кейбір функцияның туындысы болмай қалуы да мүмкін), максимум және минимумға зерттеуге болады. Негізгі теңсіздіктер теңдеуді шешуге және бірнеше (көп жағдайда – екеу) нақты сандардың ішінен «Қайсысы артық?» деген сұраққа жауап беруге, тіпті банктік салымның мүмкін болатын пайдасын есептеуге көмектесе алады.
Бұл дипломдық жұмыстың негізгі бөлімі ХХ ғасырдың ортасында анықталған және математиканың әр түрлі бөлімдеріне (матрицалық алгебра, операторлар теориясы және т.б.) жататын теңсіздіктерді қамтиды. Теңсіздіктерді іздеу және дәлелдеудің жаңа функционалды-аналитикалық әдістерді сипаттау ерекше қызықтырады.
Дипломдық жұмыста теңсіздіктер теориясының негізгі нәтижелері және олардың дәлелдеулері келтірілді. Жұмыстың негізгі бөлімі Коши теңсіздігі мен Лагранж тепе-теңдігінен басталып, сонан соң бір монографияға лайықты болатын п теріс емес сандардың арифметикалық және геометриялық орталары сұрағы қарастырылды. Бұл фундаменталды теңсіздіктің он екі дәлелдеуі келтірілді. Бұл дәлелдеулер алгебра мен анализде қолданылатын теңсіздіктерді шешу әдістерінің көп түрлігін көрсетуге мүмкіндік береді. Әсіресе Коши, Гурвица және Бора дәлелдеулері аса қызықты болып табылады. Келесі болып Гельдер мен Минковскийдің теңсіздіктері қарастырылды. Сонан соң бір-біріне ұқсас, бірақ қиындау болып табылатын Беккебах пен Дрешердің нәтижелері көрсетілді. Бұл жерде алғашқы рет Минковский, кейіннен Малер қолданған квазисызықтандырудың маңызды әдісі пайдаланылады. Бұл әдісті үлкен жетістікпен Юнг, Зигмунд және Беллман қолданған еді. Сондай-ақ екі түрлі стохастикалық матрицаларды түрлендірудің Шура әдісі және Карамат, Островский мен Харди, Литтлвуд пен Пойаның мажорланған реттілік қатарына жататын кейбір нәтижелері көрсетілді және Фано мен Лоренцтің континуалды аналог туралы айтылып, Уайтлиге тиесілі нәтижелер туралы баяндалды. Сонан соң классикалық теңсіздіктерді ұсыну және нақтылаудың өте қызықты сұрақтары қарастырылды. Бұл жерде Бляшка мен Пиктің немесе Бюкнердің әдістерінің орнына дифференциалданған теңдеулерге негізделген кері теңсіздіктерді алудың Беллман әдісін қолданылады. Тараудың соңғы бөлімшесі Вейнбергер, Сегё, Олкин, Беллман және тағы басқалары қарастырған таңбалары кезектесіп тұратын мүшелері бар қосындыларға қатысты болатын теңсіздіктерге арналды. Бұл барлық теңсіздіктер Стеффенсеннің жаңа теңсіздігінің дербес жағдайлары болып табылады.
Баяндаудың жүйелілігі және нақты материалмен толықтығы дипломдық жұмысты математикалық олимпиадаларға қатысуға ниеттеніп жүрген жоғары сынып оқушыларына, сондай-ақ әр түрлі мамандыққа даярлайтын факультеттердің студенттеріне, механиктер, физиктер және инженер-зерттеушілерге математиканың негізгі теңсіздіктерінің анықтамалығы ретінде қолдануға мүмкіндік береді.
Бұл жұмыс мектептегі бейінді сыныптардың жоғары сынып оқушыларына, университеттердің педагогикалық институттардың, техникалық ЖОО-ның математикалық және физикалық факультеттердің студенттеріне, аспиранттарына, мұғалімдеріне, сонымен қатар есептеуіш орталықтардың қызметкерлеріне пайдалы болады.
Пайдаланылған әдебиеттер тізімі
-
А.Колмогоров, О языке математических знаков // Математика – наука и профессия. – М.: Наука, 1988. – 166-173 б.
-
Э.Беккенбах, Р.Беллман, Введение в неравенства. – М.: Мир, 1965.
-
С.Гомонов, Замечательные неравенства: способы получения и примеры применения., учебное пособие. – М.: Дрофа, 2006.
-
П.Коровкин, Неравенства. – М.: Наука, 1966.
-
Г.Харди, Д.Литтльвуд, Г.Полиа, Неравенства. – М.: Ин. Лит., 1948.
-
Коши (Cauchy A.L.), Cours d’Analyse de l’Ecole Royale Polytechnique, Ire partie, Analyse algebrique, Pfris, Debure, 1821, Oeuvres completes, IIe serie, III.
-
Гаусс (Gauss C.F.), Werke, 10, 1, 172-292. Leipzig, Teubher, 1917.
-
Маклорен (Maclaurin C.), A second letter to Mfrtin Folges, Esq.; concerning the roots of education with the demonstration of other rules in algebra, Phil. Trans., 1729, 5996.
-
Якобсталь (Jacobsthal E.), Uber das arithmetische und geometriscche Mittel, Norske Vid. Selsk. Forh. (Trondheim), 1951, 122.
-
Беллман (Bellman R.), Dynamic programming, Princeton, N.J., Princeton University Press, 1957. Русский перевод: Динамическое программирование, ИЛ, М., 1960.
-
Боннесен, Фенхель (Bonnesen T., Fenchel W.), Thorie der konvexen Korper, Berlin, Springer, 1951.
-
Бор (Bohr H.), The arithmetic and geometric means, J. London Math. Soc., 1935, 114.
-
Гурвиц (Hurwitz A.), Uber den Vergleich der arithmetischen und des geometrischen Mittels, Math. Werke, 505-507, Basel, Birkhauser, 1933.
-
Гурвиц (Hurwitz A.), Uber den Erzeugung der Invarianten druch Integration, Math. Werke, 546-564, Basel, Birkhauser, 1933.
-
Юнг (Young W.H.), On classes of summable functions and their Fourier series, Proc. Roy. Soc. (A), 1912, 225-229.
-
Шнайад (Shniad H.), On the convexity of mean value functions, Bull. Am. Math. Soc., 1948, 770-776.
-
Иенсен (Jensen J.L.W.V.), Sur les fonctions convexes et les inequalities entre les valeurs moyennes, Acta Math., 1906, 175-193.
-
Беккенбах (Beckenbach E.F.), An inequality of Jensen, Am. Math. Monthly, 1946, 501-505.
-
Бохер (Bocher M.), Introduction to higher algebra, New York, Macmillan, 1907.
-
Гёльдер (Holder O.), Uber einen Mittelwertsatz, Gotting. Nachr., 1889, 38-47.
-
Минковский (Minkowski H.), Geometrie der Zahlen, I, Leipziq, Teubner, 1896.
-
Беллман, Гликсберг, Гросс (Bellman R., Glicksberg I., Gross O., Some aspects of the mathematical theory of control processes, Santa Monica, Calif., The Rand Corporation, Report R-313, 1958. Русский перевод: Некоторые вопросы математической теории процессов регулирования, ИЛ, М., 1962.
-
Зигмунд (Zygmund A.), On certain integrals, Trans. Am. Math. Soc., 1944, 170-204.
-
Беллман (Bellman R.), Functional equations in the theory of dynamic programming, V, Positivity and quasi-linearity, Proc. Nat. Acad. Sci. USA, 1955, 843-846.
-
Калаба (Kalaba R.), On nonlinear differential equations, the maximum operation, and monotonic convergence, J. Math. and Mech., 1959, 519-574.
-
Марцинкевич, Зигмунд (Marcienkiewicz J., Zygmund A.), Quelques inegalites pour les operations lineaires, Fund. Math., 1939, 115-121.
-
Беккенбах (Beckenbach E.F.), A class ofmeanvalue functions, Am. Math. Monthly, 1950, 1-6.
-
Дрешер (Dresher M.), Moment spaces and intequalities, Duke Math. J., 1953, 261-271.
-
Данскин (Danskin J.M.), Dresher’s inequality, Am. Math. Monthly, 1952, 687-688.
-
Минковский (Minkowski H.), Thorie der konvexen Korper, Berlin, Springer, 1951.
-
Малер (Mahler K.), Ein Ubertragungsprinzip fur konvexe Korper, Casopis Mat. Fysik, 1939, 93-102.
-
Юнг (Young W.H.), On an inequality of Mfrcel Riesz, Ann. of Math., 1939, 567-574.
-
Лорх (Lorch E.R.), On the volume of smooth convex bodies in Hilbert space, Math. Z., 1955, 391-407.
-
Островский (Ostrowski A.), Sur quelques applications des fonctions convexes et concaves au sens de I. Schur., J. Math. Pure Appl., 1952, 253-292.
-
Карамата (Karamata J.), Sur une inegalite relative aux fonctions convexes, Publ. Math. Univ. Belgrade, 1932, 145-148.
-
Блекуэлл (Blackwell D.), Comparison of experiments, Proc. Second Berkeley Symposium on Mathematical Statistics and Probability, 1950, 93-102, Berkeley, Calif., University of California Press, 1951.
-
Шур (Schur I.), Uber eine Klasse von Mittelbildungen mit Anwendungen auf die Determinantentheorie, Sitzber. Berl. Math. Ges., 1923, 9-20.
-
Фукс (Fuchs L.), A new proof of an inequality of Hardy – Littlewood – Polya, Mat. Tidskr., 1947,53-54.
-
Бисак (Beesack P.R.), A hote on an integral inequality, Proc. Am. Math. Soc., 1957, 875-879.
-
Фань-Цзыб Лорентц (Fan K., Lorentz G.G.), An integral inequality. Am. Math. Monthly, 1954, 626-631.
-
Маркус, Лопес (Marcus M., Lopes L.), Inequalities for symmetric functions and Hermitian matrices, Canad. J. Math., 1956, 524-531.
-
Гординг (Garding L.), An inequality for hyperbolic polynomials, J. Math. and Mech., 1959, 957-966.
-
Беллман (Bellman R.), On an inequality concerning an indefinite form, Am. Math. Monthly, 1957, 108-109.
-
Бохнер (Bochner S.), Group invariance of Cauchy’s formula in several variables, Ann. of Math., 1944, 686-707.
-
Беллман (Bellman R.), Converses of Schwarz’s inequality, Duke Math. J., 1956, 429-434.
-
Пойа, Сегё (Polya G., Szego G.,, Aufgaben und Lehrsatze aus der Analysis, I, 57, Berlin, Springer, 1925. Русский перевод: Задачи и теоремы анализа, часть І, Физматгиз, М., 1956.
-
Фань Цзы, Тодд (Fan K., Todd J.), A determinantal inequality, J. London Math. Soc., 1955, 58-64.
-
Хассан (Chassan J.B.), A statistical derivation of a pair of trigonometrical inequalities, Am. Math. Monthly, 1955, 353-356.
-
Беллман (Bellman R.), On inequalities with alternating signs, Proc. Am. Math. Soc., 1959, 807-809.

шағым қалдыра аласыз