
Өзін-өзі тексеру
Өзара тексеру
Сырттай тексеру
өзін-өзі тексеру
- өзі жасаған қателерінің пайда болу себептерін анықтау
- өзін-өзі тексеру
қателердің алдын алу
- мұғалімнің оқушылардың әрекетін тексеруі
- оқушылардың бір-бірін тексеруі
оқушылардың мұғалімнің әрекетін тексеруі
- өзін-өзі тексеруге деген қажеттіліктің қалыптасуы
- өзін-өзі тексеру тәсілдерінің мәнін түсіну
өзін-өзі тексеруді өткізу бойынша нұсқаулық
өзін-өзі басқарудың тікелей дамуы
өзін-өзі тексерудің жанама түрде дамуы
оқушыларды өзін-өзі тексеруге түрткі болу
Сырттай тексеру
МазмұныКіріспе
1. «Көпмүшелер» тақырыбының теориялық аспектілері
1.1 Көпмүшелер түсінігі
1.2 Бір айнымалысы бар көпмүшелер
1.3 Көпмүшелердің бөлінгіштік қасиеттері
1.4 Анықталмаған коэффициенттер әдісі
1.5 Көпмүшені көпмүшеге «бағандап» (немесе «бұрыштап») бөлу
1.6 Безу теоремасы және оның салдарлары
1.7 Көпмүшенің түбірлері туралы тұжырымдар
1.8 Көпмүшені көбейткіштерге жіктеу
1.9 Көпмүше сақинасы ұғымы
1.10 Көпмүшелерге қолданылатын амалдар
1.11 Көпмүшенің дәрежесі
1.12  екімүшесіне бөлу және көпмүшенің
түбірлері
екімүшесіне бөлу және көпмүшенің
түбірлері
1.13 Көпмүшенің бүтіндік аймағынан тыс түбірлерінің максимальды саны
1.14 Көпмүшелердің алгебралық және функционалдық теңдігі
1.15 Евклид алгоритмі. Екі көпмүшенің ЕҮОБ
1.16 Ең кіші ортақ еселік
1.17 Көпмүшенің формальды туындысы. Көпмүшенің келтірілмейтін еселіктері
1.18 Туындылардың қасиеттері
2. «Көпмүшелер» тақырыбын оқып үйрену кезіндегі әдістемелік және психологиялық-педагогикалық аспектілері
2.1 Тақырыпты оқып үйрену кезіндегі логикалық ойлауды дамыту
2.2 Тақырыпты оқыту кезіндегі қолданылатын әдістер
2.3 Практикалық сабақтарды өткізуге арналған әдістемелік ұсыныстар
2.4 Көпмүшелердің бөлінгіштік қасиеттерін қолдану
2.5 Безу теоремасы мен оның салдарларын оқып үйренудің әдістемесі
2.6 Көпмүшенің түбірлері туралы тұжырымды қолдану
2.7 Көпмүшені көбейткіштерге жіктеу әдістері
Қорытынды
Пайдаланылған әдебиеттер тізімі
Қосымшалар
Кіріспе
Математика пәнінен өтетін факультативтік сабақтардың басты мақсаты оқушылардың білімін тереңдету, пәнге деген қызығушылықтарын арттыру, математикалық қабілеттерін дамыту, математикамен өз бетімен шұғылдануға қызығушылықтарын нығайту, шығармашылықтарын дамыту болып табылады.
Орта мектепке арналған математика пәнінің негізгі курсының бағдарламасы мен математикадан факультативтік сабақтардың бағдарламасы берілген сынып оқушыларына арналған математика пәні бойынша жоғары деңгейдің бағдарламасын құрайды.
Математикадан факультативтік сабақтардың бағдарламасы математиканың негізгі курсымен қатар оқытуға болатындай етіп құрастырылған. Берілген сыныпта математиканың негізгі курсын бір мұғалім, ал факультативтік сабақтарды басқа мұғалім жүргізген жағдайда факультативтік курстың сабақтарын негізгі курс бағдарламасына тәуелсіз өткізуге болады (бұл жағдайда факультативтік курстың тақырыптарын негізгі курстың бағдарламасына қарағанда кейінірек өткізуге болады). Математика пәнінен өткізілетін факультативтік сабақтар нәтижелі болу үшін оларды төмендегідей жағдайлар жасалу керек:
-
жоғары білікті мұғалімдер немесе сабақтарды ғылыми-әдістемелік деңгейде өткізе алатын басқа мамандардың болуы;
-
берілген факультативтік курсты оқып үйренуге қызығушылығы бар 15-тен кем емес оқушы болуы.
Егер мектепте толымдылығы аз сыныптар болса (әсіресе ауылдық мектептерде), онда факультативтік сабақтарға қатысатын оқушылар тобын параллель сыныптардың оқушыларынан немесе көршілес сыныптардың (IX-X сыныптар, X-XI сыныптар, т.б.) оқушыларынан құрауға болады.
Факультативтік курсқа қатысатын оқушыларды қызығушылықтарына сай өз еріктерімен жазу керек. Оқушыларды міндетті түрде факультативтік сабақтарға қатысуға мәжбүрлемеу керек. Әсіресе математиканы оқып үйренуде қиындықтарға кезігетін оқушыларды немесе мектептен тыс уақытта басқа сабақтарға (спорт, музыка, сурет, т.б.) қатысатын оқушыларды мәжбүрлеуге болмайды.
Факультативтік курсты аяқтағаннан кейін оқушылар аттестатқа жазылатын сынақ тапсырады.
Математика пәнінің мұғалімі факультативтік сабақтардың сапасы үшін толық жауапкершілікті алады; факультативтік сабақтар сабақ кестесіне енгізіліп, мұғалімге еңбекақысы төленеді.
Математика пәнінен факультативтік сабақтарды өткізуде сыныптан тыс шаралардың басқа түрлерінен (математикалық үйірмелер, кештер, олимпиадалар, т.б.) бас тартуға болмайды. Бұл шаралар математикаға қызығушылығы бар оқушылармен жасалатын жұмыстарды толықтырып тұру керек.
Математикаға қызығушылығы мен қабілеттері бар оқушылармен аптасына қосымша 1-2 сағат жұмыстану үрдісі математиканы оқытудың жаңаша түрлерінің бірі – саралап оқытудың бір көрінісі. Факультативтік сабақтар шын мәнінде саралап оқытудың айрықша динамикалық түрі болып табылады.
Математикадан факультативтік сабақтарды өткізудің қандай түрі мен әдістері таңдалса да, сабақтар оқушыларға қызықты, тартымды болатындай етіп ұйымдастырылуы керек. Өз пәніңізге деген тұрақты қызығушылықты қалыптастыру үшін оқушының білім алуға деген табиғи құмарлығын пайдалану керек. Әйгілі француз физигі Луи де Бройль заманауи ғылым туралы «ғылымның үздіксіз дамуын қамтамасыз ететін үнемі жасырын қозғаушы күштері болып табылатын таңырқау мен әуестіктің қызы»деп жазды.
Қазіргі таңда математикадан факультативтік сабақтарды өткізудің негізгі түрлері ретінде факультативтік курстың түйінді сұрақтарын мұғалімнің түсіндіруі (дәріс әдісі), семинарлар, тілдесу (пікірталас), есептер шығару, оқушылардың рефераттары (теория және есептер шығару бойынша), математикалық шығармалар, оқушылардың баяндамалары, т.б. алуға болады.
Бірақ мұғалімге аталған әдістердің тек қана біреуін таңдап алуға болмайды. Алайда факультативтік сабақтарда басты назар оқушылардың өз бетімен жұмысына аударылуы керек екенін есте сақтай отырып, сабақтарды әр түрлі пікірталас, семинарлар, ғылыми-көпшілік әдебиеттерді оқу және т.б. түрлерінде де өткізуге болады.
Математика пәнінен факультативтік сабақтарды өткізудің бір тәсілі ретінде әрбір сабақты екі бөлімге бөліп өткізуге болады. Бірінші бөлім жаңа тақырыпты меңгеруге және оқушылардың теориялық, практикалық бағыттағы өзіндік жұмыстарына арналады. Сабақтың бірінші бөлімін аяқтағаннан кейін оқушыларға теория мен оның қосымшаларын оқуға бағытталған үй тапсырмасы беріледі. Әрбір сабақтың екінші бөлімі қиындығы жоғары есептерді шығаруға және мұндай аса күрделі есептерді талдауға арналады. Факультативтік сабақтарды өткізудің осындай түрі мектепте оқытудың түрлері мен әдістерінен жоғары оқу орындарындағы оқытудың түрлері мен әдістеріне сәтті түрде көшуге көмектеседі.
Факультативтік сабақтарды өткізуде математиканы оқып үйренудің (оқытудың емес) әдістерін, сонымен қатар проблемалық оқыту түрін қолдануға болады.
Проблемалық оқыту әдісін факультативтік курсты бірізді белгіленген міндеттердің жиыны ретінде ұсыну арқылы қолдануға болады. «Барлық міндеттерді өз бетімен немесе мұғалімнің аздаған көмегімен орындау арқылы оқушылар белсенділік пен дербестікті көрсете отырып және математикалық ойлау техникасын меңгере отырып берілген курсты өзінің тікелей қатысуымен оқып үйренеді. Теоремалар есеп түрінде беріледі. Егер оқушыларға дәлелдеуге берілген теорема үлкен немесе қиын болса, онда бұл теорема алдыңғы есептің шешімі келесі есепті шешуге көмектесетіндей етіп бірнеше есептерге бөлінеді. Анықтамаларды мұғалім есептің мәтініне қосады немесе бөлек айтылады. Қажет болған жағдайда мұғалім алдын ала кеңес өткізеді. Баспа құралы арқылы көбейтілген тапсырмалар жазылған парақтар әрбір сабақта барлық оқушыларға таратылады».
Сонымен қатар проблемалық есептерді шешу де пайдалы болады.
Қазіргі уақытта математикадан факультативтік сабақтарда екі негізгі бағытта өткізіледі:
а) «Математика курсының қосымша тараулары мен сұрақтары» бағдарламасы бойынша курстарды оқып үйрену;
б) арнайы математикалық курстарды оқып үйрену.
«Математика курсының қосымша тараулары мен сұрақтары» бағдарламасының мазмұны бағдарламаның материалын шығаруға және тереңдетіп оқуға, оқушыларды қазіргі заманғы математикалық идеялармен таныстыруға, мұғалімге жаңа бағдарламамен жұмыстануға дайындалуға мүмкіндік береді.
Берілген тақырыптың өзектілігі – ұғымдар мен формулалардың көптігінен және әр түрлі символдар арқылы белгіленулердің себебінен оқушыларға оқып үйренетін материалды түсіну қиындық туғызатыны. Бұның барлығы материалдың дұрыс меңгерілмеуіне әкеліп соғады. Сонымен қатар материалды меңгеруге бұл тақырыпқа бөлінген сағат саны да әсер етеді. Негізгі басымдық берілген материалды жан-жақты және терең оқып үйрену үшін сыныптан тыс, жеке және топтық сабақтарға беріледі.
Берілген дипломдық жұмыстың зерттеу объектісі – «Көпмүшелер» тақырыбын оқып үйренудің ұйымдастырылуы.
Зерттеу пәні – 10, 11-сыныптарда көпмүшелерді оқыту әдістемесі.
Мақсаты – берілген тақырыпты оқып үйренуге әдістемелік ұсыныстар.
Міндеттер:
-
10, 11-сыныптарда көпмүшелерді қолдануды зерттеу;
-
берілген тақырып бойынша өткізілетін сабақтарға әдістемелік ұсыныстар беру.
Зерттеу әдістері:
-
ғылыми, оқу әдебиеттерді талдау;
-
теориялық материалды жинақтау және жүйелеу;
-
әдістемелік жоспарларды жинақтау.
Берілген жұмыстың құрамы:
-
10-11 сыныптардағы алгебра және анализ бастамалары курсындағы «Көпмүшелер» тақырыбы бойынша теориялық мәліметтер.
-
Берілген тақырып аясында сыныптар тыс шараларды өткізу бойынша әдістемелік ұсыныстар.
Жұмыстың тәжірибелік маңыздылығы – жинақталған материал жас мұғалімдерге оқу үрдісін ұйымдастыруда, сонымен қатар педагогикалық ЖОО студенттеріне педагогикалық тәжірибеден өту кезінде қосымша, жеке және топтық сабақтарды ұйымдастыру мен өткізуде, математиканы оқытудың теориясы мен әдістемесін оқып үйрену үрдісінде пайдалы болады.
1. «Көпмүшелер» тақырыбының теориялық аспектілері
-
Көпмүшелер түсінігі
Бірмүше деп сандары мен әріптері тек қана екі амалмен – көбейту мен натурал дәрежеге шығару арқылы байланысқан алгебралық өрнек аталады.
Мысалы, төменде берілген әрбір алгебралық өрнек бірмүше болып табылады:
 .
.
Егер бірмүшенің құрамындағы барлық сандардың көбейтіндісін әріптердің алдынан, ал әрбір әріптің көбейтіндісі мен оның дәрежелерін осы әріптің натурал дәрежесі ретінде жазсақ, онда мұндай өзгертулерден кейін бірмүше стандарт түрде жазылды деп есептелінеді, ал оның сандық көбейтіндісі бірмүшенің коэффициенті деп аталады.
Бірмүшелерді көбейту үшін олардың коэффициенттерін көбейтіп, негізі бірдей дәрежелерді көбейту керек.
Бірмүшені дәрежеге шығару үшін оның коэффициентін осы дәрежеге шығарып, әрбір әріптің дәреже көрсеткішін бірмүшенің дәреже көрсеткішіне көбейту керек.
Көпмүше деп бірнеше бірмүшелердің алгебралық қосындысын айтады.
Көпмүшенің құрамындағы бірмүшелер көпмүшенің мүшелері деп аталады. Бірмүше дегеніміз көпмүшенің дербес түрі.
Стандарт түрде жазылған бірмүшелер бір-біріне сәйкес келетін немесе коэффициентімен ғана ерекшеленетін болса, онда мұндай бірмүшелер ұқсас бірмүшелер деп аталады.
Мысалы,
 – ұқсас
көпмүшелер.
– ұқсас
көпмүшелер.
Көпмүшенің ұқсас мүшелерін коэффициенттерін қосу арқылы біріктіруге болады; мұндай алмастыру ұқсас мүшелерді біріктіру деп аталады.
Алдына плюс таңбасы қойылған жақшаға алынған көпмүшені оның бірмүшелерінің алдында тұрған таңбаларын сақтай отырып жақшасыз жазуға болады.
Мысалы,
 .
.
Алдына минус таңбасы қойылған жақшаға алынған көпмүшені оның бірмүшелерінің алдында тұрған таңбаларын қарама-қарсы таңбаға ауыстыра отырып жақшасыз жазуға болады.
Мысалы,
 .
.
Екі көпмүшенің
қосындысы (айырмасы) деп коэффициенттері берілген
көпмүшелердің ұқсас мүшелерінің коэффициенттерінің қосындысына
(айырмасына) тең болатын көпмүшені айтады. Мысалы,
 және
және  көпмүшелерінің айырмасы
көпмүшелерінің айырмасы  күпмүшесі болады.
күпмүшесі болады.
Көпмүшелердің қосындысы мен айырмасын табу кезінде жоғарыда аталған жақшаларды ашу ережесін тәжірибеде жиі қолданады.
Көпмүшені бірмүшеге көбейту үшін көпмүшенің әрбір мүшесін бірмүшеге көбейтіп, шыққан бірмүшелерді қосу керек.
Көпмүшені көпмүшеге көбейту үшін бірінші көпмүшенің әрбір мүшесін екінші көпмүшенің әрбір мүшесіне көбейтіп, шыққан бірмүшелерді қосу керек.
Мысалы,
 .
.
Көпмүшелерге арналған дәрежесінің қасиеттері сандарға арналған дәреженің қасиеттерімен сәйкес келеді.
Мысалы,
 егер
егер  .
.
Көпмүшені екі немесе бірнеше көпмүшелердің көбейтіндісі ретінде жазу көпмүшені көбейткіштерге жіктеу деп аталады. Көпмүшені көбейткіштерге жіктеу үшін әр түрлі әдістер қолданылады: қысқаша көбейту формулалары, ортақ көбейткішті жақшаның сыртына шығару, топтау әдісі және т.б.
Көбейткіштерге жіктеу үшін қандай да бір әріпке (немесе өрнекке) қатысты төменде көрсетілген формула арқылы толық квадратты айыру әдісін қолдану тиімді болады:

Мысалы,
а)

б)

1.2 Бір айнымалысы бар көпмүшелер
х айнымалысына қатысты

түріндегі
 көпмүшесі
х-тің
дәрежесінің азаюы бойынша орналастырылған көпмүше
деп
аталады, мұндағы
көпмүшесі
х-тің
дәрежесінің азаюы бойынша орналастырылған көпмүше
деп
аталады, мұндағы  – нақты сандар және
– нақты сандар және  .
.
 сандары – оның
коэффициенттері,
сандары – оның
коэффициенттері,  бірмүшесі – үлкен
мүшесі, ал п саны көпмүшенің дәрежесі деп
аталады.
бірмүшесі – үлкен
мүшесі, ал п саны көпмүшенің дәрежесі деп
аталады.
Егер канондық түрде берілген көпмүшеде х-тің қандай да бір дәрежесі болмаса, онда сәйкес бірмүшенің коэффициенті нөлге тең болады.
Канондық түрде берілген екі көпмүшенің дәрежелері және х-тің бірдей дәрежелеріндегі коэффициенттер тең болса, онда мұндай көпмүшелер тепе-тең көпмүшелер деп аталады.
Мысал.  екімүшесінің кубы болатын
екімүшесінің кубы болатын  көпмүше берілген.
көпмүше берілген.  сандарын табыңдар.
сандарын табыңдар.
Шешуі. Екі көпмүшенің тепе-теңдігінің анықтамасын қолдана отырып, төмендегі жүйені аламыз:
 , бұдан
, бұдан
 .
.
Егер
 көпмүшелері
көпмүшелері

тепе-теңдігі
орындалатындай болса, онда  және
және  көпмүшелерінің әрқайсысы
көпмүшелерінің әрқайсысы  көпмүшесінің бөлгіші
деп
айтады. Мұнымен қоса
көпмүшесінің бөлгіші
деп
айтады. Мұнымен қоса  көпмүшесі
көпмүшесі  (немесе
(немесе  ) көпмүшесіне бөлінеді
(қалдықсыз) бөлінеді, сонда
) көпмүшесіне бөлінеді
(қалдықсыз) бөлінеді, сонда
 көпмүшесін
(сәйкесінше
көпмүшесін
(сәйкесінше  )
)  көпмүшесі
көпмүшесі  көпмүшесіне бөлгендегі бөлінді деп
айтады.
көпмүшесіне бөлгендегі бөлінді деп
айтады.
п
дәрежелі
көпмүше т
дәрежелі
көпмүшеге бөлінсе, онда бөлінді  дәрежелі көпмүше болады және бұл көпмүше жалғыз болады
деген дәлел бар.
дәрежелі көпмүше болады және бұл көпмүше жалғыз болады
деген дәлел бар.
Бұдан егер
п дәрежелі
 көпмүшесі
п дәрежелі
көпмүшесі
п дәрежелі
 көпмүшесіне бөлінетін болса,
онда
көпмүшесіне бөлінетін болса,
онда  , мұндағы
, мұндағы  , яғни бұл көпмүшелердің коэффициенттері пропорционал екені
шығады, мысалы, егер
, яғни бұл көпмүшелердің коэффициенттері пропорционал екені
шығады, мысалы, егер  көпмүшесі
көпмүшесі  көпмүшесіне бөлінетіні белгілі болса, онда
көпмүшесіне бөлінетіні белгілі болса, онда
 болады.
болады.
1.3 Көпмүшелердің бөлінгіштік қасиеттері
-
Егер
 көпмүшесі
көпмүшесі
 көпмүшесіне, ал
көпмүшесіне, ал
 көпмүшесі
көпмүшесі
 көпмүшесіне бөлінетін болса,
онда
көпмүшесіне бөлінетін болса,
онда  көпмүшесі
көпмүшесі  көпмүшесіне бөлінеді.
көпмүшесіне бөлінеді.
Мысалы,
 көпмүшесі
көпмүшесі
 көпмүшесіне бөлінеді,
сондықтан
көпмүшесіне бөлінеді,
сондықтан
 көпмүшесі
көпмүшесі  көпмүшесіне де бөлінеді.
көпмүшесіне де бөлінеді.
-
Егер
 және
және  көпмүшелері
көпмүшелері  көпмүшесіне бөлінсе, онда
көпмүшесіне бөлінсе, онда  және
және  көпмүшелері
көпмүшелері  көпмүшесіне бөлінеді, ал
көпмүшесіне бөлінеді, ал  көпмүшесі
көпмүшесі  көпмүшесіне бөлінеді.
көпмүшесіне бөлінеді.
Мысалы,
 және
және  көпмүшелерінің әрқайсысы
көпмүшелерінің әрқайсысы  көпмүшесіне бөлінеді, сондықтан
көпмүшесіне бөлінеді, сондықтан  және
және  көпмүшелерінің қосындысына тең
көпмүшелерінің қосындысына тең  көпмүшесі және айырмасына тең
көпмүшесі және айырмасына тең  көпмүшесі
көпмүшесі  көпмүшесіне бөлінеді, ал
көпмүшесіне бөлінеді, ал  және
және  көпмүшелерінің көбейтіндісіне тең
көпмүшелерінің көбейтіндісіне тең  көпмүшесі
көпмүшесі  көпмүшесіне бөлінеді.
көпмүшесіне бөлінеді.
-
Егер
 көпмүшесі
көпмүшесі
 көпмүшесіне бөлінсе,
онда
көпмүшесіне бөлінсе,
онда  көпмүшесінің кез келген
көпмүшесінің кез келген  көпмүшесіне көбейтіндісі
көпмүшесіне көбейтіндісі  көпмүшесіне бөлінеді.
көпмүшесіне бөлінеді.
Мысалы,
 көпмүшесі
көпмүшесі
 көпмүшесіне бөлінеді,
сондықтан
көпмүшесіне бөлінеді,
сондықтан  және
және  көпмүшелерінің көбетіндісіне тең
көпмүшелерінің көбетіндісіне тең  көбейтіндісі
көбейтіндісі  көпмүшесіне бөлінеді.
көпмүшесіне бөлінеді.
-
 және
және  көпмүшелері сонда және тек қана сонда бір-біріне бөлінеді,
егер
көпмүшелері сонда және тек қана сонда бір-біріне бөлінеді,
егер
 , мұндағы
, мұндағы
 болса.
болса.
Мысал.  көпмүшесі мен
көпмүшесі мен  көпмүшесі бір-біріне бөлінетіндігі және
көпмүшесі бір-біріне бөлінетіндігі және
 екені белгілі.
екені белгілі.
 көпмүшесін табу
керек.
көпмүшесін табу
керек.
Шешуі. 4-қасиет бойынша
 екені шығады.
екені шығады.
 болғандықтан,
болғандықтан,
 болады. Яғни
болады. Яғни
 .
.
-
Егер
 көпмүшесі
көпмүшесі
 екімүшесіне бөлінсе,
онда
екімүшесіне бөлінсе,
онда  және
және  көпмүшелерінің ең болмағанда біреуі
көпмүшелерінің ең болмағанда біреуі  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
Мысалы,
 көпмүшесі
көпмүшесі
 екімүшесіне бөлінетіндіктен
және
екімүшесіне бөлінетіндіктен
және
 болатындықтан,
болатындықтан,  көпмүшесі
көпмүшесі  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
 көпмүшесін
көпмүшесін
 көпмүшесіне
(
көпмүшесіне
( ) қалдықпен бөлу
дегеніміз
) қалдықпен бөлу
дегеніміз
 , мұндағы
, мұндағы

тепе-теңдігі
орындалатындай етіп  және
және  көпмүшелерін табуды айтады. Мұндағы
көпмүшелерін табуды айтады. Мұндағы  көпмүшесі – бөлінді, ал
көпмүшесі – бөлінді, ал  көпмүшесі қалдық деп
аталады.
көпмүшесі қалдық деп
аталады.
 көпмүшесі
көпмүшесі
 көпмүшесіне қалдықпен бөлінсе,
онда
көпмүшесіне қалдықпен бөлінсе,
онда
 орындалатындай
орындалатындай  және
және  көпмүшелерінің тек қана бір жұбы бар болады
және
көпмүшелерінің тек қана бір жұбы бар болады
және  .
.
Кез келген
 көпмүшесі
көпмүшесі
 көпмүшесіне
(
көпмүшесіне
( ) қалдықсыз немесе қалдықпен
бөлінеді. Бірінші жағдайда (қалдықсыз бөлуде) бөліндіні, ал екінші
жағдайда (қалдықпен бөлуде) бөлінді мен қалдықты
анықталмаған коэффициенттер әдісі
арқылы
табуға болады.
) қалдықсыз немесе қалдықпен
бөлінеді. Бірінші жағдайда (қалдықсыз бөлуде) бөліндіні, ал екінші
жағдайда (қалдықпен бөлуде) бөлінді мен қалдықты
анықталмаған коэффициенттер әдісі
арқылы
табуға болады.
1.4 Анықталмаған коэффициенттер әдісі
п
дәрежелі  көпмүшесі және т дәрежелі
көпмүшесі және т дәрежелі
 көпмүшесі (
көпмүшесі ( ) берілген.
) берілген.
Айталық,  (1) бөліндісі және
(1) бөліндісі және
 (2), мұндағы
(2), мұндағы  ,
,  және
және  сандары белгісіз
болсын.
сандары белгісіз
болсын.
Тепе-теңдікті жазайық:
 (3)
(3)
 және
және  көпмүшелерін көбейтіп, ұқсас
мүшелерді біріктіріп, (3)
тепе-теңдіктің оң жағында канондық түрде
жазылған п-ші дәрежелі көпмүше аламыз. Осы көпмүшенің және
көпмүшелерін көбейтіп, ұқсас
мүшелерді біріктіріп, (3)
тепе-теңдіктің оң жағында канондық түрде
жазылған п-ші дәрежелі көпмүше аламыз. Осы көпмүшенің және
 көпмүшесінің
х-тің бірдей
дәрежелеріндегі коэффициенттерді теңестіріп, п теңдеулер жүйесін
аламыз, осы жүйені шеше отырып
көпмүшесінің
х-тің бірдей
дәрежелеріндегі коэффициенттерді теңестіріп, п теңдеулер жүйесін
аламыз, осы жүйені шеше отырып  сандарын табамыз.
сандарын табамыз.
Егер  сандарының барлығы нөлге тең болып
шықса, онда
сандарының барлығы нөлге тең болып
шықса, онда  көпмүшесі
көпмүшесі  көпмүшесіне қалдықсыз бөлінетін
болады. Егер
көпмүшесіне қалдықсыз бөлінетін
болады. Егер  коэффициенттерінің ең болмағанда
біреуі нөлден өзге сан болса, онда
коэффициенттерінің ең болмағанда
біреуі нөлден өзге сан болса, онда  көпмүшесі
көпмүшесі  көпмүшесіне қалдықпен бөлінеді, бұл
жағдайда қалдықтың дәрежесі (2) теңдіктің оң жағындағы
коэффициенті нөлге тең емес х-ке қатысты бірмүшенің ең
үлкен дәрежесіне тең болады.
көпмүшесіне қалдықпен бөлінеді, бұл
жағдайда қалдықтың дәрежесі (2) теңдіктің оң жағындағы
коэффициенті нөлге тең емес х-ке қатысты бірмүшенің ең
үлкен дәрежесіне тең болады.
Мысал.  көпмүшесін
көпмүшесін  көпмүшесіне бөлу.
көпмүшесіне бөлу.
Шешуі.  көпмүшесі түріндегі бөліндіні
және
көпмүшесі түріндегі бөліндіні
және
 көпмүшесі
түрінде болатын қалдықты іздейміз.
көпмүшесі
түрінде болатын қалдықты іздейміз.
 тепе-теңдігі белгілі болады.
Жақшаларды ашып және ұқсас мүшелерді біріктіру арқылы
тепе-теңдігі белгілі болады.
Жақшаларды ашып және ұқсас мүшелерді біріктіру арқылы
 аламыз. х-тің бірдей дәрежелері
бар коэффициенттерді теңестіру арқылы төмендегі жүйені
аламыз:
аламыз. х-тің бірдей дәрежелері
бар коэффициенттерді теңестіру арқылы төмендегі жүйені
аламыз:
 , бұдан
, бұдан  .
.
Осыдан  , ал
, ал  , яғни
, яғни  .
.
Мысал.  көпмүшесін
көпмүшесін  көпмүшесіне бөлу.
көпмүшесіне бөлу.
Шешуі.  көпмүшесі түріндегі бөліндіні
және
көпмүшесі түріндегі бөліндіні
және  көпмүшесі түрінде
болатын қалдықты іздейміз.
көпмүшесі түрінде
болатын қалдықты іздейміз.  немесе
немесе  аламыз. х-тің бірдей дәрежелері
бар коэффициенттерді теңестіру арқылы төмендегі жүйені
аламыз:
аламыз. х-тің бірдей дәрежелері
бар коэффициенттерді теңестіру арқылы төмендегі жүйені
аламыз:
 , бұдан
, бұдан  .
.
Осыдан  , ал
, ал  , яғни
, яғни
 көпмүшесі
көпмүшесі  көпмүшесіне қалдықсыз бөлінеді
және
көпмүшесіне қалдықсыз бөлінеді
және  болады.
болады.
1.5 Көпмүшені көпмүшеге «бағандап» (немесе «бұрыштап») бөлу
Бұл әдісті
 көпмүшесін
көпмүшесін  көпмүшесіне бөлу мысалында
қарастырайық:
көпмүшесіне бөлу мысалында
қарастырайық:

 көпмүшесін
көпмүшесін
 көпмүшесіне
көпмүшесіне
 «бағандап» бөлудің жалпы
жағдайында
«бағандап» бөлудің жалпы
жағдайында  және
және  көпмүшелері х-тің кемімелі дәрежелері
түрінде орналасады. Сонан соң
көпмүшелері х-тің кемімелі дәрежелері
түрінде орналасады. Сонан соң  көпмүшесінің үлкен мүшесін
көпмүшесінің үлкен мүшесін  көпмүшесінің үлкен мүшесіне бөледі де,
көпмүшесінің үлкен мүшесіне бөледі де,
 бөлінді-көпмүшесінің үлкен
мүшесін алады, содан кейін
бөлінді-көпмүшесінің үлкен
мүшесін алады, содан кейін  бөлінді-көпмүшесінің үлкен мүшесін
бөлінді-көпмүшесінің үлкен мүшесін 
бөлгіш-көпмүшесіне көбейтіп, шыққан көпмүшені
 көпмүшесінен азайтады.
Азайтудың нәтижесінде дәрежесі п-нен кіші болатын белгілі
бір
көпмүшесінен азайтады.
Азайтудың нәтижесінде дәрежесі п-нен кіші болатын белгілі
бір  көпмүшесі
шығады.
көпмүшесі
шығады.
Егер
 көпмүшесінің
дәрежесі т-нен кіші болса, онда бөлу
үрдісі аяқталады да, бұл жағдайда
көпмүшесінің
дәрежесі т-нен кіші болса, онда бөлу
үрдісі аяқталады да, бұл жағдайда  көпмүшесі қалдық болады. Егер
көпмүшесі қалдық болады. Егер  көпмүшесінің дәрежесі т-нен артық
немесе т-ге тең болса, онда
көрсетілген бөлу үрдісі
көпмүшесінің дәрежесі т-нен артық
немесе т-ге тең болса, онда
көрсетілген бөлу үрдісі  көпмүшесі үшін жалғасады, яғни
көпмүшесі үшін жалғасады, яғни  көпмүшесінің үлкен мүшесін
көпмүшесінің үлкен мүшесін  көпмүшесінің үлкен мүшесіне бөледі және шыққан
көпмүшені
көпмүшесінің үлкен мүшесіне бөледі және шыққан
көпмүшені  көпмүшесінен азайтады. Азайтудың нәтижесінде
дәрежесі
көпмүшесінен азайтады. Азайтудың нәтижесінде
дәрежесі  -нен кіші болатын
-нен кіші болатын  көпмүшесі шығады. Егер
көпмүшесі шығады. Егер  көпмүшесінің дәрежесі т-нен кіші болса, онда бөлу
үрдісі аяқталады да, бұл жағдайда
көпмүшесінің дәрежесі т-нен кіші болса, онда бөлу
үрдісі аяқталады да, бұл жағдайда  көпмүшесі қалдық болады. Егер
көпмүшесі қалдық болады. Егер  көпмүшесінің дәрежесі т-нен артық
немесе т-ге тең болса, онда
көрсетілген бөлу үрдісі
көпмүшесінің дәрежесі т-нен артық
немесе т-ге тең болса, онда
көрсетілген бөлу үрдісі  көпмүшесі үшін жалғасады. Бұл үрдіс
k қадамда
шыққан
көпмүшесі үшін жалғасады. Бұл үрдіс
k қадамда
шыққан көпмүшесінің дәрежесі
көпмүшесінің дәрежесі  көпмүшесінің т
дәрежесінен кем болғанша жалғасады. Бұл
жағдайда
көпмүшесінің т
дәрежесінен кем болғанша жалғасады. Бұл
жағдайда  көпмүшесі қалдық болады.
көпмүшесі қалдық болады.

х-тің кемімелі дәрежелері
бойынша орналасқан  көпмүшесін
көпмүшесін  екімүшесіне бөлген кезде Горнер
схемасы деп аталатын қысқаша бөлу
әдісі қолданылады. Бұл әдіс анықталмаған коэффициенттер әдісінің
тікелей салдары болып табылады. п
дәрежелі
екімүшесіне бөлген кезде Горнер
схемасы деп аталатын қысқаша бөлу
әдісі қолданылады. Бұл әдіс анықталмаған коэффициенттер әдісінің
тікелей салдары болып табылады. п
дәрежелі  көпмүшесін
көпмүшесін  екімүшесіне бөлу кезінде бөліндіде
екімүшесіне бөлу кезінде бөліндіде  дәрежелі
дәрежелі
 көпмүшесі, ал қалдықта сан (әсіресе нөл) шығады.
Анықталмаған коэффициенттер әдісі арқылы төмендегідей теңдіктерді
аламыз:
көпмүшесі, ал қалдықта сан (әсіресе нөл) шығады.
Анықталмаған коэффициенттер әдісі арқылы төмендегідей теңдіктерді
аламыз:

 ,
яғни
,
яғни


 (4)
(4)
(4) теңдіктің оң және сол жақтарындағы бірдей дәрежелердің коэффициенттерін теңестіре отырып, төмендегі жүйені аламыз:

Бұл жүйеден
бөліндінің  коэффициенттерін және r
қалдықты
табудың рекурентті формулаларын
аламыз:
коэффициенттерін және r
қалдықты
табудың рекурентті формулаларын
аламыз:


…………………..


 бөліндісінің коэффициенттерін
және r
қалдығын
есептеу үрдісі төмендегідей схема (Горнер схемасы) бойынша
жүргізіледі:
бөліндісінің коэффициенттерін
және r
қалдығын
есептеу үрдісі төмендегідей схема (Горнер схемасы) бойынша
жүргізіледі:

Бұл
схемада  коэффициентінен бастап үшінші жолдың әрбір саны алдыңғы
жолдың санын α
санына
көбейтіп, шыққан нәтижеге бірінші жолдың сәйкес санын қосқанда
шығады.
коэффициентінен бастап үшінші жолдың әрбір саны алдыңғы
жолдың санын α
санына
көбейтіп, шыққан нәтижеге бірінші жолдың сәйкес санын қосқанда
шығады.
 көпмүшесін
көпмүшесін
 екімүшесіне бөлгенде төмендегі
тепе-теңдік шығады:
екімүшесіне бөлгенде төмендегі
тепе-теңдік шығады:

Бұл
тепе-теңдік , яғни
, яғни  болғанда дұрыс болады.
болғанда дұрыс болады.
Келесі теорема арқылы көпмүшені екімүшеге бөлгендегі бөліндіні таппай, қалдықты табуға болады.
1.6 Безу теоремасы және оның салдарлары
 көпмүшесін
көпмүшесін
 екімүшесіне бөлгендегі
қалық
екімүшесіне бөлгендегі
қалық  болғандағы
болғандағы  көпмүшесінің мәніне, яғни
көпмүшесінің мәніне, яғни  тең болады.
тең болады.
α
саны  көпмүшесінің түбірі деп аталады, егер
көпмүшесінің түбірі деп аталады, егер
 болғанда көпмүшенің сандық
мәні нөлге тең болса, яғни
болғанда көпмүшенің сандық
мәні нөлге тең болса, яғни  болса.
болса.
Ескерту:
 көпмүшесін
көпмүшесін
 түріндегі екімүшеге бөлгенде
берілген көпмүшенің
түріндегі екімүшеге бөлгенде
берілген көпмүшенің  болғандағы мәніне, яғни
болғандағы мәніне, яғни  тең болады.
тең болады.
Салдарлар.
-
 көпмүшесі
көпмүшесі
 екімүшесіне сонда және тек
қана сонда бөлінеді, егер α
саны
екімүшесіне сонда және тек
қана сонда бөлінеді, егер α
саны  көпмүшесінің түбірі болса.
көпмүшесінің түбірі болса. -
 көпмүшесі
көпмүшесі
 екімүшесіне
п саны кез келген натурал сан
болғанда бөлінеді және
екімүшесіне
п саны кез келген натурал сан
болғанда бөлінеді және

-
 көпмүшесі
көпмүшесі
 екімүшесіне
п саны кез келген натурал сан
болғанда бөлінеді және
екімүшесіне
п саны кез келген натурал сан
болғанда бөлінеді және

-
 көпмүшесі
көпмүшесі
 екімүшесіне
п саны кез келген натурал сан
болғанда бөлінеді және
екімүшесіне
п саны кез келген натурал сан
болғанда бөлінеді және

Кез келген
 көпмүшесі үшін
көпмүшесі үшін
 көпмүшесі қалдықсыз
бөлінетін
көпмүшесі қалдықсыз
бөлінетін  екімүшесі табылады. Осы айтылғанның мысалы
ретінде
екімүшесі табылады. Осы айтылғанның мысалы
ретінде
 болғандағы
болғандағы  түріндегі екі дәрежелі көпмүшені алуға
болады.
түріндегі екі дәрежелі көпмүшені алуға
болады.
 түріндегі көпмүше квадрат
үшмүше деп аталады.
түріндегі көпмүше квадрат
үшмүше деп аталады.
Квадрат үшмүшені толық квадратты айыру әдісі арқылы түрлендірейік:


 өрнегі квадрат үшмүшенің
дискриминанты деп аталады және D
әрпімен
белгіленеді, яғни анықтама бойынша
өрнегі квадрат үшмүшенің
дискриминанты деп аталады және D
әрпімен
белгіленеді, яғни анықтама бойынша  . Егер
. Егер  болса, онда квадрат үшмүше төмендегідей түрде
болады:
болса, онда квадрат үшмүше төмендегідей түрде
болады:


яғни бұл жағдайда квадрат үшмүше екі сызықтық көбейткіштерге жіктеледі, ал
 және
және

сандарының әрқайсысы квадрат үшмүшенің түбірі болады.
Егер
 болса, онда квадрат үшмүше
төмендегідей түрде болады:
болса, онда квадрат үшмүше
төмендегідей түрде болады:

яғни екі бірдей сызықтық
көбейткіштерге жіктеледі және  болғанда нөлге айналады.
болғанда нөлге айналады.
 болғанда квадрат үшмүше
сызықтық көбейткіштерге жіктелмейді және оның нақты түбірлері
болмайды.
болғанда квадрат үшмүше
сызықтық көбейткіштерге жіктелмейді және оның нақты түбірлері
болмайды.
Мысал. Квадрат үшмүшені көбейткіштерге жіктеу:
Шешуі.
-
 болғандықтан,
болғандықтан,
 , яғни
, яғни  .
. -
 болғандықтан,
болғандықтан,
 және
және  , яғни
, яғни
 .
. -
 болғандықтан,
болғандықтан,
 квадрат үшмүшесінің нақты
түбірлері жоқ және ол сызықтық көбейткіштерге
жіктелмейді.
квадрат үшмүшесінің нақты
түбірлері жоқ және ол сызықтық көбейткіштерге
жіктелмейді.
Егер
 болса, онда
болса, онда
 квадрат
үшмүшесінің
квадрат
үшмүшесінің  және
және  түбірлері үшін төмендегі тепе-теңдіктер
(Виет теоремасы) дұрыс
болады:
түбірлері үшін төмендегі тепе-теңдіктер
(Виет теоремасы) дұрыс
болады:
 және
және
 .
.
Қарама-қарсы тұжырым да
дұрыс: егер  және
және  болатындай α
және β
сандары
бар болса, онда олар
болатындай α
және β
сандары
бар болса, онда олар  квадрат үшмүшенің түбірлері
болады.
квадрат үшмүшенің түбірлері
болады.
 түріндегі келтірілген квадрат
үшмүше берілген жағдайда көбейтіндісі q
бос
мүшесіне, ал қосындысы қарама-қарсы таңбамен алынған екінші
коэффициентке, яғни
түріндегі келтірілген квадрат
үшмүше берілген жағдайда көбейтіндісі q
бос
мүшесіне, ал қосындысы қарама-қарсы таңбамен алынған екінші
коэффициентке, яғни  -ға тең болатын екі сан оңай табуға болады. Виет
теоремасына сәйкес, осы табылған сандар
-ға тең болатын екі сан оңай табуға болады. Виет
теоремасына сәйкес, осы табылған сандар  түріндегі келтірілген квадрат үшмүшенің түбірлері
болады.
түріндегі келтірілген квадрат үшмүшенің түбірлері
болады.
Дәрежесі 2-ден артық кез келген көпмүше қалдықсыз бөлінетіндей квадрат үшмүше табылатыны дәлелденеді.
 үшінші дәрежелі көпмүше үшін
екі түрлі жағдай болу мүмкін: немесе ол екімүшелердің
көбейтіндісіне жіктеледі, яғни
үшінші дәрежелі көпмүше үшін
екі түрлі жағдай болу мүмкін: немесе ол екімүшелердің
көбейтіндісіне жіктеледі, яғни

мұндағы
 сандары бірдей болуы мүмкін,
немесе ол екімүше мен квадрат үшмүшенің көбейтіндісіне жіктеледі,
яғни
сандары бірдей болуы мүмкін,
немесе ол екімүше мен квадрат үшмүшенің көбейтіндісіне жіктеледі,
яғни

1.7 Көпмүшенің түбірлері туралы тұжырымдар
-
п-ші дәрежелі көпмүшенің нақты түбірлерінің саны п-нен артық болмайды.
-
Тақ дәрежелі көпмүшенің ең болмағанда бір нақты түбірі болады.
-
(Виет теоремасы). Егер
 сандары
сандары
 көпмүшесінің нақты түбірлері
болса, онда төмендегідей теңдіктер
орындалады:
көпмүшесінің нақты түбірлері
болса, онда төмендегідей теңдіктер
орындалады:





-
Егер
 болса, онда
болса, онда
 көпмүшесінің әрбір
түбірі
көпмүшесінің әрбір
түбірі  және
және  көпмүшелерінің біреуінің түбірі болады, ал
көпмүшелерінің біреуінің түбірі болады, ал
 көпмүшесінің әрбір түбірі
және
көпмүшесінің әрбір түбірі
және  көпмүшесінің әрбір түбірі
көпмүшесінің әрбір түбірі  көпмүшесінің түбірі болады.
көпмүшесінің түбірі болады. -
Егер α саны
 көпмүшесінің түбірі болса, онда
көпмүшесінің түбірі болса, онда
 , мұндағы
, мұндағы  – (
– ( ) дәрежелі белгілі бір
көпмүше.
) дәрежелі белгілі бір
көпмүше.
Көпмүшенің түбірлерін
табу үрдісі жалпы жағдайда оңай тапсырма емес, алайда
 көпмүшесі әрқайсысының
дәрежесі 2-ден артық емес көпмүшелердің көбейтіндісі ретінде
берілген жағдайларда бұл тапсырманы толықтай орындауға болады,
себебі 4-қасиет бойынша
көпмүшесі әрқайсысының
дәрежесі 2-ден артық емес көпмүшелердің көбейтіндісі ретінде
берілген жағдайларда бұл тапсырманы толықтай орындауға болады,
себебі 4-қасиет бойынша  көпмүшесінің түбірлерінің жиыны оның бөлгіштерінің
түбірлерінің жиынымен сәйкес
келеді.
көпмүшесінің түбірлерінің жиыны оның бөлгіштерінің
түбірлерінің жиынымен сәйкес
келеді.
Қысқартылмайтын  (p
– бүтін
сан, q
– натурал
сан) бөлшегі
(p
– бүтін
сан, q
– натурал
сан) бөлшегі

көпмүшенің бүтін санды
коэффициенттері бар түбірі болуы үшін р
саны  бос мүшенің бөлгіші болуы керек, ал
q саны
бос мүшенің бөлгіші болуы керек, ал
q саны  үлкен коэффициентінің бөлгіші болуы
керек.
үлкен коэффициентінің бөлгіші болуы
керек.
Егер
 көпмүшесінде бүтін
коэффициенттер және
көпмүшесінде бүтін
коэффициенттер және  болса, онда мұндай көпмүшенің рационал түбірлері тек
қана
болса, онда мұндай көпмүшенің рационал түбірлері тек
қана  бос мүшенің бөлгіштері болатын бүтін сандар
болады.
бос мүшенің бөлгіштері болатын бүтін сандар
болады.
Мысал.  көпмүшенің түбірлерін табу.
көпмүшенің түбірлерін табу.
Шешуі. Берілген көпмүшенің түбірі
рационал сан болатынын немесе болмайтынын анықтайық.
Қысқартылмайтын  бөлшегі берілген көпмүшенің түбірі болсын, онда жоғарыда
келтірілген тұжырым бойынша р
саны
бөлшегі берілген көпмүшенің түбірі болсын, онда жоғарыда
келтірілген тұжырым бойынша р
саны  мәндеріне ие бола алады, ал q
саны 1, 2
мәндеріне ие бола алады. Осылайша, берілген көпмүшенің рационал
түбірлері ретінде тек қана мына сандар болуы мүмкін:
мәндеріне ие бола алады, ал q
саны 1, 2
мәндеріне ие бола алады. Осылайша, берілген көпмүшенің рационал
түбірлері ретінде тек қана мына сандар болуы мүмкін:

Берілген көпмүшеге осы сандарды жеке-жеке қоя отырып,

екенін аламыз.
Осыдан,
 берілген
берілген
 көпмүшенің түбірі болады
және
көпмүшенің түбірі болады
және
 .
.
Горнер схемасын
қолданып, түбірлері  және
және  сандары болатын
сандары болатын  өрнегін аламыз. Сондықтан берілген көпмүшенің
түбірлері
өрнегін аламыз. Сондықтан берілген көпмүшенің
түбірлері
 болады.
болады.
Мысал.  көпмүшесін көбейткіштерге
жіктеу.
көпмүшесін көбейткіштерге
жіктеу.
Шешуі. Көпмүшенің түбірі рационал сан
болатынын немесе болмайтынын анықтайық.
Қысқартылмайтын  бөлшегі берілген көпмүшенің түбірі болсын,
онда р
саны
бөлшегі берілген көпмүшенің түбірі болсын,
онда р
саны  мәндеріне ие бола алады, ал q
саны 1
және 2 мәндеріне ие бола алады. Осылайша, берілген көпмүшенің
рационал түбірлері ретінде тек қана мына сандар болуы
мүмкін:
мәндеріне ие бола алады, ал q
саны 1
және 2 мәндеріне ие бола алады. Осылайша, берілген көпмүшенің
рационал түбірлері ретінде тек қана мына сандар болуы
мүмкін: 
Берілген көпмүшеге осы сандарды жеке-жеке қоя отырып,

екенін аламыз.
 болғандықтан,
болғандықтан,
 және
және  сандары берілген көпмүшенің түбірі болады,
яғни
сандары берілген көпмүшенің түбірі болады,
яғни  .
.
 көпмүшесін
көпмүшесін
 көпмүшесін
көпмүшесін
 көпмүшесіне «бағандап» бөлу
арқылы немесе Горнер схемасына сәйкес
көпмүшесіне «бағандап» бөлу
арқылы немесе Горнер схемасына сәйкес  көпмүшесін
көпмүшесін  көпмүшесіне бөліп, шыққан бөліндіні
көпмүшесіне бөліп, шыққан бөліндіні  көпмүшесіне бөлу арқылы, немесе анықталмаған коэффициенттер
әдісі арқылы табуға болады.
көпмүшесіне бөлу арқылы, немесе анықталмаған коэффициенттер
әдісі арқылы табуға болады.
 көпмүшесін анықталмаған
коэффициенттер әдісі арқылы
табайық.
көпмүшесін анықталмаған
коэффициенттер әдісі арқылы
табайық.
 тепе-теңдігінде теңдіктің сол
жағындағы көпмүшенің бос мүшесі
тепе-теңдігінде теңдіктің сол
жағындағы көпмүшенің бос мүшесі  -ге тең, ал теңдіктің оң жағындағы көпмүшенің бос
мүшесі
-ге тең, ал теңдіктің оң жағындағы көпмүшенің бос
мүшесі  -ге тең болғандықтан,
-ге тең болғандықтан,  болады. Тепе-теңдіктегі с-ның орнына 4 санын,
ал х-тің орнына 1 санын
қойып, b-ның мәнін
табамыз:
болады. Тепе-теңдіктегі с-ның орнына 4 санын,
ал х-тің орнына 1 санын
қойып, b-ның мәнін
табамыз:

бұдан  .
.
Сонымен,
 .
.
 көпмүшесінің нақты түбірлері
жоқ және көбейткіштерге жіктелмейді. Сондықтан есептің шартында
берілген көпмүше көбейткіштерге келесідей жіктеледі:
көпмүшесінің нақты түбірлері
жоқ және көбейткіштерге жіктелмейді. Сондықтан есептің шартында
берілген көпмүше көбейткіштерге келесідей жіктеледі:
 .
.
1.8 Көпмүшені көбейткіштерге жіктеу
-
Ортақ көбейткішті жақшаның сыртына шығару және топтау тәсілі. Кейбір жағдайларда кейбір мүшелерді ұқсас мүшелердің қосындысына (айырмасына) түрлендірген немесе өзара жойылатын мүшелерді енгізген жөн.
-
Қысқаша көбейту формулаларын қолдану. Кей жағдайларда көбейткішті жақшаның сыртына шығаруға, мүшелерді топтауға, толық квадратты, ал одан кейін кубтардың қосындысын, квадраттардың айырмасын немесе кубтардың айырмасын көбейткіштер түрінде жазу керек болады.
-
Безу теоремасын және анықталмаған коэффициенттер әдісін қолдану.
Мысал. Көбейткіштерге
жіктеу:  .
.
 болғандықтан,
болғандықтан,
 көпмүшесі
көпмүшесі
 -ке бөлінеді. Анықталмаған
коэффициенттер әдісі арқылы
-ке бөлінеді. Анықталмаған
коэффициенттер әдісі арқылы  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі бөлгішті
табамыз.
екімүшесіне бөлгендегі бөлгішті
табамыз.
Айталық,
бөлінді  көпмүшесі болсын.
көпмүшесі болсын.  болғандықтан, төмендегі жүйе
шығады:
болғандықтан, төмендегі жүйе
шығады:

Бұдан  . Яғни
. Яғни  .
.
 болғандықтан,
онда
болғандықтан,
онда  .
.
-
Безу теоремасын және «бағандап» бөлуді қолдану.
Мысал. Көбейткіштерге
жіктеу:  .
.
Шешуі.  болғандықтан, онда
болғандықтан, онда  көпмүшесі
көпмүшесі  -ге бөлінеді. «Бағандап» бөлу арқылы бөліндіні
табамыз:
-ге бөлінеді. «Бағандап» бөлу арқылы бөліндіні
табамыз:
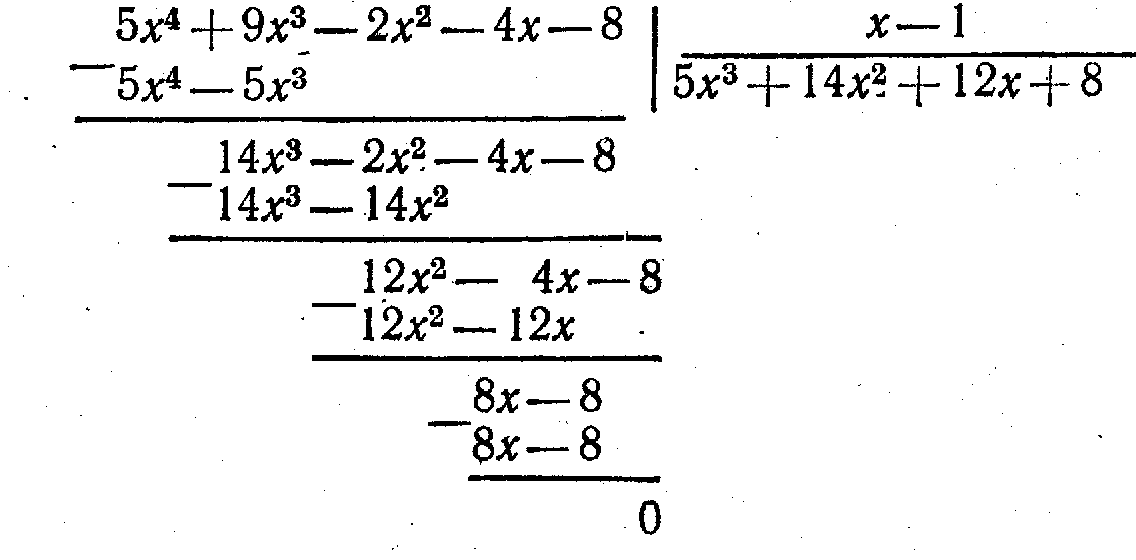
Яғни
 .
.
 болғандықтан,
болғандықтан,
 көпмүшесі
көпмүшесі
 -ге
бөлінеді.
-ге
бөлінеді.
«Бағандап» бөлу арқылы
бөлгішін тапқаннан кейін  шығады.
шығады.
 квадрат үшмүшенің
дискриминанты
квадрат үшмүшенің
дискриминанты  болғандықтан, бұл квадрат үшмүше сызықтық көбейткіштерге
жіктелмейді.
болғандықтан, бұл квадрат үшмүше сызықтық көбейткіштерге
жіктелмейді.
Сонымен,
 .
.
-
Безу теоремасын және Горнер схемасын қолдану. Бұл тәсілдер арқылы табылған бөлінгішті осы тәсілмен немесе кез келген басқа әдіспен көбейткіштерге жіктеуге болады.
Мысал. Көбейткіштерге
жіктеу:  .
.
Шешуі. Берілген көпмүшенің рационал
түбірлері бар болса, онда олар тек қана  сандарының арасында болуы
мүмкін.
сандарының арасында болуы
мүмкін.
Берілген көпмүшенің түбірін табу үшін төмендегідей тұжырымды пайдаланайық:
Егер белгілі
бір  кесіндісінің шеттерінде көпмүшенің мәндері әр түрлі
таңбаға ие болса, онда
кесіндісінің шеттерінде көпмүшенің мәндері әр түрлі
таңбаға ие болса, онда  аралығында бұл көпмүшенің ең болмағанда бір түбірі
болады.
аралығында бұл көпмүшенің ең болмағанда бір түбірі
болады.
Берілген көпмүше
үшін  . Яғни
. Яғни  аралығында берілген көпмүшенің ең болмағанда бір түбірі
бар. Сондықтан жоғарыда жазылған 24 сандардың арасынан
әуелі
аралығында берілген көпмүшенің ең болмағанда бір түбірі
бар. Сондықтан жоғарыда жазылған 24 сандардың арасынан
әуелі  аралығына жататын сандарды тексеріп алған жөн. Бұл
сандардың ішінен тек қана
аралығына жататын сандарды тексеріп алған жөн. Бұл
сандардың ішінен тек қана  саны осы аралыққа тиісті.
саны осы аралыққа тиісті.
 болғандағы
болғандағы
 мәнін тек орнына қою арқылы
ғана емес, сондай-ақ басқа да әдістермен табуға болады, мысалы,
Горнер схемасы арқылы, өйткені
мәнін тек орнына қою арқылы
ғана емес, сондай-ақ басқа да әдістермен табуға болады, мысалы,
Горнер схемасы арқылы, өйткені  саны
саны  көпмүшесін
көпмүшесін  -ға бөлгендегі қалдыққа тең. Онымен қоса, көптеген
есептерде бұл әдіс тиімдірек, себебі сол кезде бөлінгіштің
коэффициенттері де табылады.
-ға бөлгендегі қалдыққа тең. Онымен қоса, көптеген
есептерде бұл әдіс тиімдірек, себебі сол кезде бөлінгіштің
коэффициенттері де табылады.
Берілген мысал үшін Горнер схемасына сәйкес:
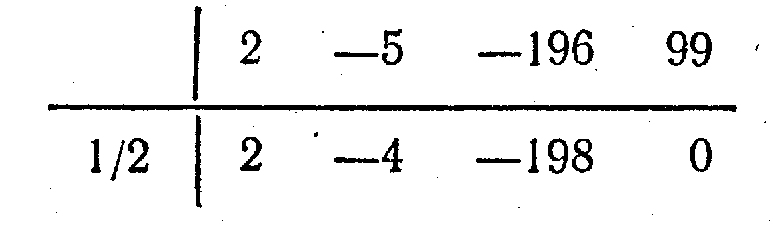
 болғандықтан,
болғандықтан,
 саны
саны  көпмүшесінің түбірі болады және
көпмүшесінің түбірі болады және  көпмүшесі
көпмүшесі  -ге бөлінеді, яғни
-ге бөлінеді, яғни  .
.

 болғандықтан,
болғандықтан,  .
.
1.9 Көпмүше сақинасы ұғымы
Айталық, K және L коммутатив сақиналар болсын.
Анықтама
1: L
сақинасы К
сақинасының х
элементтері арқылы жасалған жай кеңейтілім деп аталады
және  деп белгіленеді егер:
деп белгіленеді егер:
-
 сақинаның ішкі
сақинасы
сақинаның ішкі
сақинасы -

 негізгі жиынын
негізгі жиынын
 символдарымен
белгілейді.
символдарымен
белгілейді.
Анықтама
2: К
сақинасының х
элементтері арқылы жасалған  жай кеңейтілім х
арқылы
жасалған К
сақинасының жай трансценденттік кеңейтілім болады егер
төмендегі шарттар орындалса:
жай кеңейтілім х
арқылы
жасалған К
сақинасының жай трансценденттік кеңейтілім болады егер
төмендегі шарттар орындалса:
-
 сақинаның ішкі
сақинасы
сақинаның ішкі
сақинасы -

-
 егер
егер  болса, онда
болса, онда
 .
.
Анықтама
3: х
элементі К
сақинасынан тыс трансценденттік деп аталады, егер мына шарт
орындалса:  егер
егер  болса, онда
болса, онда  .
.
Ұсыныс.  жай трансценденттік кеңейтілім болсын. Егер
жай трансценденттік кеңейтілім болсын. Егер
 және
және  болатын
болатын  болса, онда
болса, онда  болады.
болады.
Дәлелдеуі. Шарт
бойынша  ,
,  . Бірінші өрнектен екінші өрнекті азайтып,
. Бірінші өрнектен екінші өрнекті азайтып,
 аламыз.
х элементі
К-дан тыс трансценденттік
болғандықтан, Анықтама 3 бойынша
аламыз.
х элементі
К-дан тыс трансценденттік
болғандықтан, Анықтама 3 бойынша  шығады.
шығады.
Қорытынды. х элементі арқылы жасалған К коммутатив сақинасының жай трансценденттік кеңейтілімнің кез келген нөлге тең емес элементі х элементінің теріс емес бүтін дәрежелерінің сызықтық комбинациясы түрінде бір ғана жазылуын жасайды.
Анықтама 4: Нөлге тең емес К сақинасынан тыс белгісіз х арқылы жасалған көпмүше сақинасы деп х элементі арқылы жасалған нөлге тең емес коммутатив К сақинасының жай трансценденттік кеңейтілімді айтады.
Теорема
1. Нөлге тең емес кез келген
коммутатив К
сақинасы
үшін х
элементі
арқылы жасалған  жай трансценденттік кеңейтілім бар
болады.
жай трансценденттік кеңейтілім бар
болады.
1.10 Көпмүшелерге қолданылатын амалдар
Айталық,
 – нөлге тең емес кез келген
коммутатив К
сақинасының сақинасы
болсын.
– нөлге тең емес кез келген
коммутатив К
сақинасының сақинасы
болсын.
Анықтама
5:  сақинасының f
және g
көпмүшелері тең болады және
сақинасының f
және g
көпмүшелері тең болады және
 деп белгіленеді, егер f
және g
көпмүшелерінің белгісіз х-тің бірдей дәрежелеріндегі
барлық коэффициенттері өзара тең
болса.
деп белгіленеді, егер f
және g
көпмүшелерінің белгісіз х-тің бірдей дәрежелеріндегі
барлық коэффициенттері өзара тең
болса.
Салдар 1. Көпмүшенің жазылуында қосылғыштардың орналасу реті маңызды емес. Көпмүшенің жазылуында коэффициенті нөлге тең қосылғыштарды жазуға немесе алып тастауға болады.
 g
g болсын.
болсын.
Анықтама
6: f
және g
көпмүшелерінің қосындысы деп төмендегідей теңдікпен
анықталатын  көпмүшесін атаймыз:
көпмүшесін атаймыз:

мұндағы
 .
.
Анықтама 7: f және g көпмүшелерінің көбейтіндісі (fg) деп белгіленіп, төмендегі ереже бойынша есептеледі:

мұндағы
 .
.
1.11 Көпмүшенің дәрежесі
Айталық,
 коммутатив сақина
болсын.
коммутатив сақина
болсын.  – К
өрісінен
тыс көпмүшелер сақинасы
– К
өрісінен
тыс көпмүшелер сақинасы  .
.
Анықтама
8:  – кез келген көпмүше болсын. Егер
– кез келген көпмүше болсын. Егер  болса, онда теріс емес бүтін п
саны
– f көпмүшелерінің дәрежесі. Бұл
жағдайда
болса, онда теріс емес бүтін п
саны
– f көпмүшелерінің дәрежесі. Бұл
жағдайда  деп жазады.
деп жазады.
 сандары
– үлкен
коэффициенті
сандары
– үлкен
коэффициенті  болатын көпмүшенің
коэффициенттері.
болатын көпмүшенің
коэффициенттері.
Егер
 болса,
f – тұрақты. Нөлге тең
көпмүшенің дәрежесі анықталмаған.
болса,
f – тұрақты. Нөлге тең
көпмүшенің дәрежесі анықталмаған.
Көпмүше дәрежесінің қасиеттері:
1.
 және
және  .
.
2.
 және
және  және
және 
3.
К – бүтіндік
аймағы 
Дәлелдеуі.  болғандықтан,
болғандықтан,  болады. К
–
бүтіндік аймағы
болады. К
–
бүтіндік аймағы  .
.
Салдар
2: К
(бүтіндік
аймағы) өрісінен тыс  өз кезегінде бүтіндік аймағы болып табылады. Кез келген
бүтіндік аймағы үшін бүтіндік аймағы бар
болады.
өз кезегінде бүтіндік аймағы болып табылады. Кез келген
бүтіндік аймағы үшін бүтіндік аймағы бар
болады.
Салдар
3: Кез келген
 үшін К бүтіндік аймағынан тыс
бөлінгіштер өрісі болады.
үшін К бүтіндік аймағынан тыс
бөлінгіштер өрісі болады.
1.12
 екімүшесіне бөлу және
көпмүшенің түбірлері
екімүшесіне бөлу және
көпмүшенің түбірлері
Айталық,
 болсын,
болсын,
 элементі
f көпмүшесінің
элементі
f көпмүшесінің
 аргументінен табылған мәні деп
аталады.
аргументінен табылған мәні деп
аталады.
Безу
теоремасы: Кез келген
 көпмүшесі және
көпмүшесі және
 үшін
үшін
 элементі бар
болады.
элементі бар
болады.
Дәлелдеуі.  – кез келген көпмүше болсын.
– кез келген көпмүше болсын.  .
.




Салдар
4:  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдық
екімүшесіне бөлгендегі қалдық  болады.
болады.
Анықтама
9:  элементі f
көпмүшесінің түбірі болады, егер
элементі f
көпмүшесінің түбірі болады, егер
 болса.
болса.
Теорема
2:  элементі f
көпмүшесінің түбірі болады сонда және тек қана сонда
егер f
көпмүшесі
элементі f
көпмүшесінің түбірі болады сонда және тек қана сонда
егер f
көпмүшесі  екімүшесіне бөлінетін болса
екімүшесіне бөлінетін болса  .
.
Дәлелдеуі:
-
Қажеттілік шарты. Айталық
 болсын. Безу теоремасынан
болсын. Безу теоремасынан  шығады, бөлінгіштік қасиеті бойынша
шығады, бөлінгіштік қасиеті бойынша  болады.
болады. -
Жеткіліктік шарты. Айталық,
 болсын, онда
болсын, онда
 . Д.К.О.
. Д.К.О.
1.13 Көпмүшенің бүтіндік аймағынан тыс түбірлерінің максималды саны
Теорема
3: k– бүтіндік аймағы болсын. f
көпмүшесінің k
бүтіндік
аймағындағы түбірлер саны f
көпмүшесінің п
дәреже
көрсеткішінен аспайды.
бүтіндік аймағы болсын. f
көпмүшесінің k
бүтіндік
аймағындағы түбірлер саны f
көпмүшесінің п
дәреже
көрсеткішінен аспайды.
Дәлелдеуі:
-
Көпмүше дәрежесінің индукциясы бойынша.
 болсын. Бұдан
f көпмүшесінің нөл түбірі бар
және олардың саны
болсын. Бұдан
f көпмүшесінің нөл түбірі бар
және олардың саны  аспайды.
аспайды.
-
Теорема кез келген
 үшін дәлелденген болсын.
үшін дәлелденген болсын. -
Бөлімше 2-ден көпмүшелерге арналған теоремадағы тұжырымының
 дұрыстығы шығатынын
көрсетейік.
дұрыстығы шығатынын
көрсетейік.
Айталық,
 және
және  . Екі жағдай болу мүмкін:
. Екі жағдай болу мүмкін:
А) f көпмүшесінің түбірлері жоқ, яғни теоремадағы тұжырым дұрыс.
Б)
f көпмүшесінің ең
болмағанда  түбірі бар, Безу теоремасы бойынша
түбірі бар, Безу теоремасы бойынша  , k
–
бүтіндік аймағы болғандықтан, Қасиет 3 (көпмүшенің дәрежелері)
бойынша
, k
–
бүтіндік аймағы болғандықтан, Қасиет 3 (көпмүшенің дәрежелері)
бойынша  екені шығады.
екені шығады.
 және
және  болсын.
болсын.
 және k – бүтіндік аймағы
болғандықтан,
және k – бүтіндік аймағы
болғандықтан,
 .
.
Осылайша,
 болғандықтан,
болғандықтан,
 көпмүшесінің барлық
түбірлері g
көпмүшесінің түбірлері де болады, индукциялық болжам
бойынша g
көпмүшесінің барлық түбірлерінің саны
п-нен аспайды,
яғни f
көпмүшесінің түбірлерінің саны
көпмүшесінің барлық
түбірлері g
көпмүшесінің түбірлері де болады, индукциялық болжам
бойынша g
көпмүшесінің барлық түбірлерінің саны
п-нен аспайды,
яғни f
көпмүшесінің түбірлерінің саны  -ден аспайды.
-ден аспайды.
Салдар
5: k
–
бүтіндік аймағы болсын, егер f
көпмүшесінің түбірлерінің саны п
санынан
артық және  болса, онда f
– нөлдік
көпмүше.
болса, онда f
– нөлдік
көпмүше.
1.14 Көпмүшелердің алгебралық және функционалдық теңдігі
 қандай да бір көпмүше болсын,
ол белгілі бір
қандай да бір көпмүше болсын,
ол белгілі бір  функциясын жалпы жағдайда сипаттайды, кез келген көпмүше
бір функцияны сипаттай алады.
функциясын жалпы жағдайда сипаттайды, кез келген көпмүше
бір функцияны сипаттай алады.
Теорема
4:  – бүтіндік аймағы болсын, сонда f және
– бүтіндік аймағы болсын, сонда f және  көпмүшелерінің теңдігі
көпмүшелерінің теңдігі  және
және  функцияларымен сипатталатын теңдікке (тепе-теңдікке (≡))
пара-пар келеді.
функцияларымен сипатталатын теңдікке (тепе-теңдікке (≡))
пара-пар келеді.
Дәлелдеуі:
-
Қажеттілік шарты. f және
 – ∞ бүтіндік аймағы,
– ∞ бүтіндік аймағы,  болсын.
болсын.  болсын, яғни
болсын, яғни
 .
. -
Жеткіліктік шарты. Айталық,
 .
.
 қарастырайық,
қарастырайық,
 бүтіндік аймағы
болғандықтан, h
көпмүшесінің ∞ түбірлері бар, онда Салдар 5
бойынша h
– нөлдік
көпмүше. Осылайша,
бүтіндік аймағы
болғандықтан, h
көпмүшесінің ∞ түбірлері бар, онда Салдар 5
бойынша h
– нөлдік
көпмүше. Осылайша,  . Д.К.О.
. Д.К.О.
Қалдықпен бөлу туралы теорема
Анықтама
10: Евклидтік
К сақинасы деп
 жиынында төмендегі шартты
қанағаттандыратын және теріс емес бүтін мәндерді
қабылдайтын h
функциясы
анықталатын k
бүтіндік
аймағы аталады:
жиынында төмендегі шартты
қанағаттандыратын және теріс емес бүтін мәндерді
қабылдайтын h
функциясы
анықталатын k
бүтіндік
аймағы аталады:
 және
және
 немесе
немесе  .
.
Берілген
 элементтері үшін
элементтері үшін
 элементтерін табу үрдісі
қалдықпен бөлу деп аталады, мұндағы q
– толық
емес бөлінді, r
–
элементтерін табу үрдісі
қалдықпен бөлу деп аталады, мұндағы q
– толық
емес бөлінді, r
–  бөліндісінің қалдығы.
бөліндісінің қалдығы.
Теорема 5
(қалдықпен бөлу туралы):  – F
өрісінен
тыс көпмүшелер сақинасы және
– F
өрісінен
тыс көпмүшелер сақинасы және  көпмүшесі болсын.
көпмүшесі болсын.  болатын және
болатын және  немесе
немесе  шарты орындалатын
шарты орындалатын  көпмүшелерінің жалғыз жұбы бар
болады.
көпмүшелерінің жалғыз жұбы бар
болады.
 немесе
немесе
 .
.
Дәлелдеуі: Көпмүшенің бар
болуы.  , яғни
, яғни  болсын. Егер f
– нөлдік
көпмүше немесе
болсын. Егер f
– нөлдік
көпмүше немесе
 болса, теорема дұрыс екені көрінеді, себебі
болса, теорема дұрыс екені көрінеді, себебі
 немесе
немесе  .
.
 болғандағы теореманы
дәлелдейік. Дәлелдеуді f
көпмүшенің дәрежесінің индукциясы бойынша
жүргіземіз.
болғандағы теореманы
дәлелдейік. Дәлелдеуді f
көпмүшенің дәрежесінің индукциясы бойынша
жүргіземіз.  көпмүшесі үшін теорема дәлелденді деп болжайық. Бұл
жағдайда теоремадағы тұжырым
көпмүшесі үшін теорема дәлелденді деп болжайық. Бұл
жағдайда теоремадағы тұжырым
 үшін орындалғанын көрсетейік. Расында да,
үшін орындалғанын көрсетейік. Расында да,
 – f
көпмүшесінің үлкен коэффициенті болсын,
осыдан
– f
көпмүшесінің үлкен коэффициенті болсын,
осыдан  көпмүшесінің үлкен коэффициенті мен дәрежесі
f көпмүшесіндегі үлкен
коэффициенті мен дәрежесіне тең болатыны шығады,
осылайша
көпмүшесінің үлкен коэффициенті мен дәрежесі
f көпмүшесіндегі үлкен
коэффициенті мен дәрежесіне тең болатыны шығады,
осылайша
 көпмүшесінде
көпмүшесінде  болады немесе ол нөлдік көпмүше болады. Егер
болады немесе ол нөлдік көпмүше болады. Егер
 болса, онда
болса, онда
 , бұдан
, бұдан
 және
және  болғандағы
болғандағы
 шығады. Егер
шығады. Егер  болса, онда индукциялық болжам бойынша
болса, онда индукциялық болжам бойынша
 болады, бұдан
болады, бұдан
 , яғни
, яғни
 болғанда
болғанда
 немесе
немесе  шығады. Көпмүшенің бар болатыны
дәлелденді.
шығады. Көпмүшенің бар болатыны
дәлелденді.
Көпмүшелердің мұндай жұбы жалғыз болатынын дәлелдейік.
 немесе
немесе  бар болсын, екі теңдікті бір-бірінен
азайтайық:
бар болсын, екі теңдікті бір-бірінен
азайтайық:  . Екі жағдай болу мүмкін:
. Екі жағдай болу мүмкін:  немесе
немесе  .
.
 болсын.
болсын.
Басқа жағынан, дәрежелер
шарты бойынша  немесе
немесе  ,
,  немесе
немесе  .
.
Егер
 болса, онда қарама-қайшылық
пайда болады да,
болса, онда қарама-қайшылық
пайда болады да,  . Жалғыздық
дәлелденді.
. Жалғыздық
дәлелденді.
Салдар
6: F
өрісінен
тыс  көпмүшелер сақинасы Евклид
кеңістігі деп аталады.
көпмүшелер сақинасы Евклид
кеңістігі деп аталады.
Салдар
7: F
өрісінен
тыс  көпмүшелер сақинасы басты
идеалдар (кез келген идеалдың бір ғана құраушысы болады) сақинасы
болып табылады.
көпмүшелер сақинасы басты
идеалдар (кез келген идеалдың бір ғана құраушысы болады) сақинасы
болып табылады.
Кез келген Евклид
сақинасы факториалды: F
өрісінен
тыс  көпмүшелер сақинасы факториал
сақинасы деп аталады.
көпмүшелер сақинасы факториал
сақинасы деп аталады.
1.15 Евклид алгоритмі. Екі көпмүшенің ЕҮОБ
 – F
өрісінен
тыс көпмүшелер сақинасы болсын.
– F
өрісінен
тыс көпмүшелер сақинасы болсын.
Анықтама
11: f
және  болсын. Егер
болсын. Егер  көпмүшесі бар болса, онда
көпмүшесі бар болса, онда  бөліндісінің қалдығы нөлге тең болады, g –
f көпмүшесінің бөлгіші болады
және
бөліндісінің қалдығы нөлге тең болады, g –
f көпмүшесінің бөлгіші болады
және  деп
белгіленеді.
деп
белгіленеді.
Анықтама 12: f және g көпмүшелерінің ең үлкен ортақ бөлгіші h көпмүшесі болады:
-
 және
және  (h
– f
және g
көпмүшелерінің ортақ бөлгіші).
(h
– f
және g
көпмүшелерінің ортақ бөлгіші). -
 (
( f және g көпмүшелерінің кез
келген ортақ бөлгішіне).
f және g көпмүшелерінің кез
келген ортақ бөлгішіне).
f
және g
көпмүшелерінің ең үлкен ортақ бөлгіші
ЕҮОБ(f;g) деп белгіленеді. Кез
келген көпмүшелердің ортақ бөлгіштерінің қатарына
 , яғни нөлге тең
емес F
өрісі
ішіндегі дәрежесі нөлге тең барлық көпмүшелер жатады. Берілген
екі f
және g
көпмүшелерінің нөлдік көпмүше емес ортақ бөлгіштері болмайтын
жағдай орын алуы мүмкін.
, яғни нөлге тең
емес F
өрісі
ішіндегі дәрежесі нөлге тең барлық көпмүшелер жатады. Берілген
екі f
және g
көпмүшелерінің нөлдік көпмүше емес ортақ бөлгіштері болмайтын
жағдай орын алуы мүмкін.
Анықтама 13: Егер f және g көпмүшелерінің дәрежесі нөлге тең көпмүше емес ортақ бөлгіштері болмаса, онда олар өзара жай көпмүшелер деп аталады.
Лемма: Егер  – F
өрісінен
тыс х-ке қатысты көпмүшелер
болса және
– F
өрісінен
тыс х-ке қатысты көпмүшелер
болса және  теңдігі орындалса, f
және g
көпмүшелерінің ең үлкен ортақ бөлгіші q
және r
көпмүшелерінің ең үлкен ортақ бөлгішімен
ассоциацияланады.
теңдігі орындалса, f
және g
көпмүшелерінің ең үлкен ортақ бөлгіші q
және r
көпмүшелерінің ең үлкен ортақ бөлгішімен
ассоциацияланады.  .
.
 жазуы
жазуы  дегенді білдіреді.
дегенді білдіреді.
Дәлелдеуі: және
және  болсын.
болсын.
-
 , бұдан
, бұдан
 және
және
 шығады, яғни
d – q
және r
көпмүшелерінің ортақ бөлгіші болады
шығады, яғни
d – q
және r
көпмүшелерінің ортақ бөлгіші болады  .
. -
 .
. -
 .
.
Евклид алгоритмі
 – F
өрісінен
тыс
– F
өрісінен
тыс  сақинасының көпмүшелері
болсын.
сақинасының көпмүшелері
болсын.  табудың Евклид алгоритмінің мәні тізбектей бөлу әдісі
арқылы
табудың Евклид алгоритмінің мәні тізбектей бөлу әдісі
арқылы
 және
және  көпмүшелерінің ең үлкен ортақ бөлгішін табу үрдісі кіші
дәрежелі екі көпмүшенің ең үлкен ортақ бөлгішін табу үрдісіне
әкеліп соғатынында болып тұр.
көпмүшелерінің ең үлкен ортақ бөлгішін табу үрдісі кіші
дәрежелі екі көпмүшенің ең үлкен ортақ бөлгішін табу үрдісіне
әкеліп соғатынында болып тұр.
 болсын, қалдықпен бөлу
теоремасы бойынша
болсын, қалдықпен бөлу
теоремасы бойынша  көпмүшелері бар болады және екі жағдай болуы
мүмкін:
көпмүшелері бар болады және екі жағдай болуы
мүмкін:
-

-
 , қалдықпен бөлу теоремасы
бойынша
, қалдықпен бөлу теоремасы
бойынша  , бұл жағдайда
, бұл жағдайда  -ді
-ді  -ге қалдықпен бөлеміз:
-ге қалдықпен бөлеміз:  .
.
 деп болжайық. Қалдықта нөл шыққанша берілген схемамен
бөлуді жалғастырамыз. Бөлудің төмендегідей тізбегін
аламыз:
деп болжайық. Қалдықта нөл шыққанша берілген схемамен
бөлуді жалғастырамыз. Бөлудің төмендегідей тізбегін
аламыз:
 және
және 
 және
және 
..................................................................
 және
және 

Бөлудің тізбегі
аяқталды, себебі  , бұл ретте
, бұл ретте  – теріс емес бүтін сан, бөлудегі қалдықтың
дәрежесі
– теріс емес бүтін сан, бөлудегі қалдықтың
дәрежесі  дәрежесінен кем болатын теріс емес бүтін сандардың соңғы
саны бар болады. Лемма 1 бойынша:
дәрежесінен кем болатын теріс емес бүтін сандардың соңғы
саны бар болады. Лемма 1 бойынша:

Осылайша, Евклид
алгоритмі арқылы тізбектей бөлу кезінде  .
.
1.16 Ең кіші ортақ еселік
 – F
өрісінен
тыс көпмүшелер сақинасы болсын.
– F
өрісінен
тыс көпмүшелер сақинасы болсын.
Анықтама
14:  көпмүшесі f
және
көпмүшесі f
және  көпмүшелерінің ең кіші ортақ еселігі деп аталады, егер мына
шарттар орындалса:
көпмүшелерінің ең кіші ортақ еселігі деп аталады, егер мына
шарттар орындалса:
-
 (h
– f
және g
көпмүшелерінің ортақ еселігі).
(h
– f
және g
көпмүшелерінің ортақ еселігі). -
 (h
– f
және g
көпмүшелерінің ортақ еселіктерінің ең
кішісі).
(h
– f
және g
көпмүшелерінің ортақ еселіктерінің ең
кішісі).
Келесідей белгілеулерді
енгізейік:  – кез келген кесінді. f
және g
көпмүшелерінің ең кіші ортақ еселігі – үйлестірілген мән. ЕКОЕ
символымен үйлестірілген ең кіші ортақ еселік
белгіленеді.
– кез келген кесінді. f
және g
көпмүшелерінің ең кіші ортақ еселігі – үйлестірілген мән. ЕКОЕ
символымен үйлестірілген ең кіші ортақ еселік
белгіленеді.
Ескерту. Кез
келген f
және  көпмүшелері үшін
көпмүшелері үшін
 (басты идеалдар қиылысуы) бар
болады.
(басты идеалдар қиылысуы) бар
болады.



Теорема 6 (ЕҮОБ
мен ЕКОЕ арасындағы байланыс): f
және  көпмүшелері F
өрісінен
тыс х-ке қатысты көпмүшелер
болсын, осылайша, мына қатынас бар болады:
көпмүшелері F
өрісінен
тыс х-ке қатысты көпмүшелер
болсын, осылайша, мына қатынас бар болады:  .
.
Дәлелдеуі:  белгілеулерін енгізейік.
белгілеулерін енгізейік.
 көпмүшесін қарастырайық.
көпмүшесін қарастырайық.
-
 , осылайша,
, осылайша,
 болатындай
болатындай
 және
және  көпмүшелері бар болады, мұндағы
көпмүшелері бар болады, мұндағы  .
. -
 көпмүшесін қарастырайық,
сонда
көпмүшесін қарастырайық,
сонда  , осылайша,
, осылайша,  .
. -
 шығады.
Д.К.О.
шығады.
Д.К.О.
Мысал.  .
.  табу керек.
табу керек.
Ш![]() ешуі.
ешуі.














0

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Осылайша,



Жауабы: 
1.17 Көпмүшенің формальды туындысы. Көпмүшенің келтірілмейтін еселіктері
 – F
өрісінен
тыс
– F
өрісінен
тыс  құрайтын көпмүшелер сақинасы
болсын.
құрайтын көпмүшелер сақинасы
болсын.  – у
арқылы
жасалған жай трансценденттік кеңейтілім
болсын.
– у
арқылы
жасалған жай трансценденттік кеңейтілім
болсын.
 .
.  элементі – коэффициенті F
өрісінен
тыс х-тен жасалған көпмүше
болатын у
айнымалысынан жасалған көпмүше. Егер
элементі – коэффициенті F
өрісінен
тыс х-тен жасалған көпмүше
болатын у
айнымалысынан жасалған көпмүше. Егер
 болса және
х-ке тәуелді болса,
онда
болса және
х-ке тәуелді болса,
онда  деп жазады.
деп жазады.
 ,
,

Мынадай белгілеу енгізейік:

Осылайша,

Анықтама
15:  болсын. f
көпмүшесінің формальды туындысы деп төмендегідей көпмүше
аталады:
болсын. f
көпмүшесінің формальды туындысы деп төмендегідей көпмүше
аталады:

Формальды туынды
 немесе
немесе  деп белгіленеді.
деп белгіленеді.
1.18 Туындылардың қасиеттері
Кез келген
f және  көпмүшелері үшін:
көпмүшелері үшін:




 дәлелдеу:
дәлелдеу:

Осылайша,
 Д.К.О.
Д.К.О.
 дәлелдеу:
дәлелдеу:
 ,
,

 Д.К.О.
Д.К.О.
 дәлелдеуі
дәлелдеуі
 болғандағы
болғандағы
 қасиеттен
шығады.
қасиеттен
шығады.
 дәлелдеуі
дәлелдеуі
 болғандағы
болғандағы
 қасиеттен
п дәреженің индукциясы бойынша
шығады.
қасиеттен
п дәреженің индукциясы бойынша
шығады.
2. «Көпмүшелер» тақырыбын оқып үйрену кезіндегі әдістемелік және психологиялық-педагогикалық аспектілері
2.1 Тақырыпты оқып үйрену кезіндегі логикалық ойлауды дамыту
Қоршаған ортамен танысу түйсіктен, қабылдаудан, сезімдерден басталып, ойлауға ауысады. Ойлаудың функциясы – белгілі түйсіктің шегінен шығып танымның шектерін кеңейту. Ойлау түйсік арқылы аша алмайтын нәрсені немесе құбылысты ақыл қорытындысы арқылы ашуға мүмкіндік береді.
Ойлаудың міндеті – заттар арасындағы қатынасты ашу, байланыстарды анықтау және оларды кездейсоқ сәйкестіктерден ажырату. Ойлау ұғымдарды пайдаланады және жалпылау мен жоспарлау функцияларын орындайды. Ойлау– түйсінетін объектілердің арасындағы байланысты орнататын психикалық бейнелеудің айрықша жалпыланған және жанамаланған түрі.
Қоғам дамыған сайын ойлау да бірте-бірте дамып келеді және ұғымдардағы жалпылама, теориялық ойлауға көшіп бара жатыр. Санның, кеңістіктің және уақыттың абстракциялары пайда болып, дамып келеді. Сонымен қатар ешқандай ұғым болып қалыптаспаған ұғымдарға сүйенуге әкеліп соғады.
Сондықтан баланың ойлау қабілетінің дамуы бірте-бірте жүреді. Алғашқыда ол заттарды мәнсіз қозғаудың дамуымен анықталады, сонан соң ойлау бағытталған объектімен анықталып, мәні бар құбылысқа айналады.
Баланың интеллектуалды дамуы оның іс-әрекетінің, қарым-қатынас жасаудың, қоғамдық тәжірибені меңгерудің барысында жүзеге асады.
Интеллектуалды дамудың тізбектелген сатылары – бұл көрнекі-әрекеттік және тілдік-логикалық ойлау. Сондай-ақ ойлаудың дамуына көптеген ұғымдардың пайда болуын қамтамасыз ететін дамытушы сөйлеу әрекеті үлкен ықпал етеді.
Сөздерді қабылдау (сенсорлы сөйлеу) әрекеті баланы объектіні және оның сипаттамаларын дұрыс түсінуге ықпал ететінін айта кету керек. Заттың немесе құбылыстың бір жақтарын ғана ерекшелеп, ал басқаларына назар аударуға баулитын қарапайым абстракция алғашқы қарапайым жалпылауға алып келеді.
Осылайша, бақылау – баланың ойлау әрекетінің негізгі болып табылады. Мысалы, көпмүшелер тақырыбын оқып үйрену барысында мүмкіндігінше көрнекі құралдарды пайдаланған жөн. Оның нәтижесінде ойлау әрекеті сәйкестендіру мен салыстыруда көрініс табады. Бұл ретте зат және заттың қасиеті ұғымдарының арасындағы айырмашылықтар меңгеріледі. Оның нәтижесінде бала заңдылық туралы қорытынды жасауды үйренеді. Бұл ретте практикалық әрекеттермен ойлау байланысы сақталса да, ол бұрынғыдай тығыз, түзу және тікелей болмайды. Бірқатар жағдайларда объектімен практикалық қимыл-әрекет жасау қажет болмайды, бірақ барлық жағдайда оны нақты қабылдау және көрнекі көрсету қажет. Себебі балалардың бейнелік ойлауы әлі тікелей жүзеге асады, сондықтан олар қарастырылып тұрған объектінің айқын көзге түсетін қасиеттерінен ұғымдар арқылы абстракциялана алмайды.
Ойлау қалыптасу барысында екі сатыдан өтеді: ұғымға дейінгі және ұғымдық.
Сонымен, ойлау нақты бір бейнеден сөзбен белгіленген әрекетке қарай дамиды. Түйсіну заттар мен құбылыстардағы ұқсас, өзгермейтін қасиеттерді бейнелейді.
Безу теоремасын және оның салдарын оқып үйрену барысында баланың интеллектуалды дамуындағы елеулі өзгерістер көпмүшелердің қасиеттерін оқуда, ол үшін қажетті ойлау амалдарының қалыптасуында, танымдық әрекеттің жаңа түрткілерінің пайда болуында байқалады.
Осының нәтижесінде бұдан да қиын танымдық міндеттер қолжетімді болады. Оларды шешу барысында ойлау амалдары жалпыланады, рәсімделеді және бұлар арқылы жаңа жағдайларда қолдану ауқымы кеңейеді. Өзара байланысқан, жалпыланған амалдардың жүйесі қалыптасады. Пайымдау, өзінің ойын дәлелдеу, пайымдау үрдісін түсіну және бақылау, оның жалпы әдістерін үйрену, пайымдаудың кеңейтілген түрлерінен қысқа түрлеріне ауысып тұру қабілеті дамиды. Нақты ұғымдық ойлаудан абстрактылы ұғымдық ойлауға ауысу орындалады.
Баланың интеллектуалды дамуы алдыңғысы келесісін дайындайтын сатылардың заңды түрде ауысуымен сипатталады. Ойлаудың жаңа түрлерінің пайда болуымен қатар ескі түрлері жойылмайды, керісінше, сақталады және дамиды.
Әрбір ойлау үрдісі ұғымдарды жалпылауда өтеді, алайда әдетте оның құрылымына ұғымдармен қатар бейнелер де кіреді. Мұндай үрдістің бастапқы кезеңі проблемалық жағдайды түсіну болып табылады. Проблеманы қоюдың өзі ойлаудың әрекеті болып табылады, көп жағдайда ол үлкен ойлау жұмысты талап етеді.
Ойланатын адамның бірінші белгісі – проблеманы дер кезінде көре білу. Сұрақтардың пайда болуы ой жұмысы дамуының белгісі болып табылады. Адамның білімі неғұрлым кең болса, соғұрлым ол көп проблема көре алады.
Проблеманы түсінуден кейін ой ол проблеманы шешуге ауысады. Есепті шешу әр түрлі тәсілдермен жүзеге асады. Ерекше есептер болады, оларды шешу үшін белгілі мәліметтерді жаңаша сәйкестендіріп, жағдайды қайта ойлау ғана қажет болады.
Көптеген жағдайда есепті шешу үшін теориялық жалпылама білімнің негізі керек болады. Есепті шешу үрдісі белгілі білімді есепті шешудің әдісі мен тәсілі ретінде қолдануды қажет етеді.
Есепті шешудің ережесін қолдану үрдісі екі ойлау амалын қамтиды:
-
есепті шешу үшін қандай «ережені» қолдану керектігін анықтау;
-
жалпы ережені есептің жеке шарттарына қолдану.
Мұндай есептерді шешуде ойлау дағдыларының рөлі білімнің жалпылама жүйесі бар бағыттарда аса жоғары болатынын ескерте кетейік.
Өте қиын проблеманы шешу кезінде әдетте болжам болып ұғынатын шешу жолы белгіленеді. Болжамды ұғыну тексеру жүргізуге деген қажеттілікті туындатады. Тексеру аяқталғаннан кейін ойлау үрдісі соңғы саты – берілген сұрақты талдау сатысына көшеді.
Осылайша, ойлау үрдісі – бастапқы жағдайды (есептің шартын) ұғынудан басталатын, саналы және мақсатты, ұғымдар мен бейнелерді пайдаланатын және белгілі бір нәтижемен аяқталатын үрдіс.
Проблеманы шешудің 4 сатысы бар:
-
дайындық;
-
шешімнің нақтылануы;
-
шабыт;
-
табылған шешімді тексеру.
Проблеманы шешудегі ойлау үрдісінің құрылымы:
-
Түрткі (проблеманы шешуге деген ықылас);
-
Проблеманы талдау («берілгенді», «табу керекті», жетпейтін немесе артық мәліметтерді және т.б. анықтау);
-
Шешу жолын іздеу:
-
Белгілі алгоритм негізінде есепті шешу жолын іздеу (ынталанған ойлау);
-
Көптеген белгілі алгоритмдердің ішінен тиімді нұсқасын таңдау арқылы есептің шешімін іздеу;
-
Әр түрлі алгоритмдердің жекелеген бөліктерін үйлестіру арқылы есепті шешу;
-
Есепті шешудің жаңаша түрін табу (шығармашылық ойлау):
-
Терең логикалық пайымдаулар (талдау, салыстыру, синтез, топтастыру, ақыл қорытындысы және т.б.) негізінде;
-
Ұқсастықтарды қолдану негізінде;
-
Эвристикалық амалдарды қолдану негізінде;
-
Сынау және қателесудің қарапайым әдістерін қолдану негізінде;
-
-
Қателескен жағдайда:
-
Ашулану, басқа әрекетке ауысып кету, «инкубациялық демалу» - «ойдың пісуі», нұрға бөлену, шабыттану, инсайд, белгілі бір проблеманы шешу жолын сол мезетте ұғыну (интуитивтік ойлау);
«Нұрға бөленуге» көмектесетін факторлар:
а) проблемаға деген үлкен қызығушылық;
ә) жетістікке, проблеманың шешілуіне деген сенімділік;
б) проблема туралы көп ақпаратты білу, жиналған тәжірибе;
в) мидың үлкен ассоциациялық әрекеті (ұйықтаған кезде, дене қызуы жоғарылағанда, безгек кезінде, жағымды эмоциялық түрткі кезінде);
-
Есепті шешудің табылған жолын логикалық түрде дәлелдеу, шешімнің дұрыстығының логикалық дәлелдеуі;
-
Шешімді іске асыру;
-
Табылған шешімді тексеру;
-
Түзету (қажет болған жағдайда 2-кезеңге қайта оралу).
Ойлау әрекеті саналы деңгейде де, санасыз деңгейде де жүзеге асады, күрделі ауысулар және бұл кезеңдердің өзара байланысымен сипатталады. Сәтті (мақсатты) әрекет нәтижесінде алдын ала мақсатқа сәйкес келетін нәтиже шығады.
Осылайша, ойлауды дамыту кезінде жеке-жеке іске аспайтын, бір-бірімен байланысатын амалдардың көптүрлілігі қажет.
2.2 Тақырыпты оқыту кезіндегі қолданылатын әдістер
Оқыту әдістері дегеніміз – оқу материалын анықтап алу арқылы белгілі бір мақсатқа жетуге бағытталған мұғалім мен оқушылар арасындағы өзара әрекетті тізбектеп алмастыру. «Әдіс» (грек тілінен – «бірдеңеге жету жолы») – мақсатқа жету тәсілі, білімді алу тәсілі. Педагогикалық әдебиеттерде «оқыту әдісі» ұғымына анықтама мен оның рөлі жөнінде бірыңғай пікір жоқ. Мысалы, Ю.К.Бабанский «оқыту әдісі» деген – білім берудің міндеттерін орындаудағы мұғалім мен оқушылардың арасындағы бірыңғай реттелген байланыс әрекеті деп есептейді. Т.А.Ильина оқыту әдістерін «оқушылардың танымдық іс-әрекетін ұйымдастырудың тәсілі» деп түсіндіреді.
Дидактика тарихында оқыту әдістерінің әр түрлі топтары бар. Әдістердің көп таралған тобы мазмұнды жеткізудің түрлеріне негізделеді. Бұл сөздік, практикалық және көрнекі әдістер:
-
Сөздік әдістер: әңгімелеу, баяндау;
-
Практикалық әдістер: жаттығу, машықтану;
-
Көрнекі әдістер: көрнекіліктерді, плакаттарды көрсету.
Әдістердің тағы бір тобы жеке тұлғаны қалыптастыру негізінде құрылған:
-
Сананы қалыптастыру әдістері: әңгімелеу, баяндау, нұсқама, көрсету, көрнекілеу;
-
Іс-әрекетті қалыптастыру әдістері: жаттығу, машықтану, өзін-өзі басқару;
-
Сезімдерді қалыптастыру әдістері (түрткі беру): мадақтау, бақылау.
Кесте 1
Оқушылардың әрекет түрлеріне қарай бөлінетін әдістер тобы
|
Әдіс |
Әрекет түрі |
Оқушының ой әрекетінің деңгейлері |
Білімнің деңгейлері |
Мазмұн |
Жақсарту |
|
1. Түсіндір-мелі көрнекі |
Мұғалім-нің көмегімен |
І – тану |
ІІ – тану білімі |
Дәстүрлі оқыту – белгілі дайын білімді беру үрдісі |
Бағдарламалы оқыту |
|
2. Репродук-тивті |
Оқушы-ның өзі |
ІІ – жаңғырту |
ІІ – тану білімі |
1-кестенің жалғасы
|
3. Пробле-малық оқыту |
Мұғалімнің көмегімен |
ІІІ – қолдану |
ІІІ – қолдану білімі |
Проблема-лық оқыту– белсенді ізденістің және оқушылар-дың жаңа білімді ашу үрдісі |
Іскерлік ойындар |
|
4. Жарты-лай ізден-гіш |
Мұғалімнің бақылауы-мен |
ІІІ – қолдану IV – шығарма-шылық |
ІІІ – қолдану білімі IV – өзгерту білімі |
||
|
5. Зерттеу-шілік |
Мұғалімнің көмегінсіз |
IV – шығарма-шылық |
IV – өзгерту білімі |
Сонымен қатар әдістердің монологтық (ақпараттық-хабарламалық) тобы да бар, мысалы: әңгіме, лекция, түсіндіру және оқу материалын диалогтік түрде айту (әңгімелесу, проблемалық оқыту, диспут).
Оқушылардың әрекет түрлеріне (өз бетімен жұмыстану және шығармашылық деңгейлері) қарай бөлінетін әдістер тобының тағы біреуіне тоқталайық. Бұл өнімді топты 1965 ж И.Я.Лернер мен М.Н.Скаткин ұсынған болатын. Олар оқыту әдістеріне деген бұрынғы көзқарастар әдістердің сыртқы құрылымының немесе дереккөздерінің әр түрлілігіне сүйеніп жасалғанын айтты. Оқытудың жетістігі оқушылардың белсенділігін мен бағытына, әрекет түрлеріне байланысты болғандықтан, осы аталған әрекет түрі, өз бетімен жұмыстану және шығармашылық деңгей әдісті таңдаудың маңызды критерийлері болуы керек. И.Я.Лернер мен М.Н.Скаткин оқыту әдістерінің бес түрін бөлуді ұсынды және бұл топтағы әрбір келесі әдісті қолдануда оқушылардың белсенділігі мен өз бетімен жұмыстану деңгейі арта береді.
-
Оқытудың түсіндірмелі-көрнекі әдісі (мұғалім түсіндіреді, оқу материалын көрнекі түрде көрсетеді) –лекция, әңгіме, тәжірибелерді көрсету, экскурсия және т.б. түрінде өткізіледі. Оқушының қызметі ақпаратты алуға, тануға бағытталады, нәтижесінде «тану білімі» қалыптасады.
-
Репродуктивті әдіс – мұғалім оқушылар алған білімін пайдалануға, қызмет тәсілдерін, есепті шешу, тәжірибелерді еске түсіруге бағытталған тапсырмалар әзірлейді, бұл арқылы оқушы өз бетімен белсенді түрде оқу материалын пайдаланады: сұрақтарға жауап береді, есептерді шешеді және т.б.; нәтижесінде «көшірме білім» қалыптасады.
-
Проблемалық оқыту әдісі. Әр түрлі дереккөздер мен тәсілдерді қолдана отырып мұғалім материалды берместен бұрын проблемалық сұрақ қояды, танымдық есепті береді, сонан соң дәлелдер жүйесін ашып, әр түрлі көзқарастарды салыстыра отырып, берілген есепті шешу тәсілін көрсетеді. Оқушылар өздерін ғылыми ізденістің куәсі болғандай сезінеді. Бұрынғы кезде де, қазіргі кезде бұл әдіс кеңінен қолданылады.
-
Жартылай ізденгіш немесе эвристикалық әдіс. Оқыту барысында берілген (немесе өз бетімен жасалған) танымдық есепті шешудің жолдарын мұғалімнің басшылығы немесе эвристикалық бағдарламалар мен нұсқаулар арқылы белсенді түрде іздеуді ұйымдастыруға негізделеді. Ойлау үрдісі өнімді түрде болады, бірақ бағдарламалармен (соның ішінде компьютерлік бағдарламалар) және оқу әдебиеттерімен жұмыстану арқылы мұғалім немесе оқушылардың өздері ойлау кезеңдерін бағыттайды және бақылайды. Түрлерінің бірі эвристикалық әңгімелесу болатын мұндай әдіс семинарлар мен коллоквиумдарда ойлауды жандандырудың танымдық әрекетке қызығушылықты арттырудың тиімді тәсілі болып табылады.
-
Зерттеушілік әдіс. Материалды талдау, проблеманы қою және ауызша немесе жазбаша қысқаша нұсқаулықпен танысқаннан кейін оқушылар өз бетімен әдебиеттермен, дереккөздермен танысады, бақылау жүргізеді және басқа да іздену жұмыстарын атқарады. Зерттеу әрекеті кезінде ықылас, ынта, өз бетімен жұмыс, шығармашылық ізденіс толық көрініс табады. Оқу жұмысының әдістері ғылыми зерттеу әдістеріне еріксіз айналып кетеді.
Оқыту үрдісінде әдіс белгілі бір оқу-тәрбиелік мақсаттарға жетудің мұғалім мен оқушылардың байланысқан қызметінің ыңғайластырылған тәсілі ретінде және оқушылардың оқу-танымдық іс-әрекеттерін ұйымдастырудың тәсілі ретінде қарастырылады.
Түсіндірмелі-көрнекі және репродуктивті әдістері – оқушылардың дайын белгілі білімді жеткізу үрдісі болып табылатын дәстүрлі оқытудың әдістері.
Дәстүрлі оқытудың кемшіліктері:
-
материалды оқудың жалпы орташа жылдамдығы;
-
оқушыларға берілетін білімнің бірыңғай орташа көлемі;
-
өзіндік жұмыстар қарастырылмаған мұғалім арқылы дайын түрде алынатын білімнің үлкен көлемі, оның нәтижесінде оқушы «ойлануды ұмытады»;
-
айтылған білімді оқушылардың түсінгенінен немесе түсінбегенінен мұғалімнің хабарсыз болуы;
-
материалды берудің сөздік әдістерінің көп болуы, ол зейіннің шашыраңқы болуына әкеледі;
-
оқу материалының бөлініп берілмеуінің салдарынан оқушылардың оқулықпен өз бетімен жұмыстана алмауы;
-
оқушылардың еске сақтауына үлкен ауырлық, себебі оқу материалын еске сақтап айту керек; кімнің еске сақтауы жақсы – сол жақсы айтып береді.
Бірақ болашақтағы кәсіптік қызметте ақпаратты жаттап алуды мен нақты айтып берудің мұндай әдістері қажет болмайды және қолданылмайды, сондықтан, басқа жағынан қарағанда, оқушы кәсіби қызметте кездесетін жұмыстың түрлеріне (өндірістік мәселені шешу үшін қажетті ақпаратты табу, күрделі жағдайларда шығармашылық шешімді таба білу біліктігі) дайын болмайды. Осылайша, дәстүрлі оқыту кезінде адамға оқу үрдісінде қойылатын талаптар мен кәсіптік қызметте қойылатын талаптар арасында қажетті сәйкестік байқалмайды.
Дәстүрлі оқытудың кейбір кемшіліктері 60-жылдары педагогика, психология және кибернетиканың тоғысында пайда болған бағдарламаланған оқыту арқылы түзетіледі. Бағдарламаланған оқыту негізінде оқыту туралы үш ой жатыр: 1) басқару үрдісі ретінде, 2) ақпараттық үрдіс ретінде және 3) жекелеген үрдіс ретінде.
Бағдарламаланған оқыту негізінде 1) оқу бағдарламасы; 2) оқу бағдарламасын меңгеру бойынша оқушының іс-әрекеті; 3) меңгеруді бақылау түрлері жүйеленген оқыту бағдарламасы бар.
Оқу материалы көлемі аз логикалық аяқталған шағын бөлімдерге бөлінеді, әрбір бөлімді меңгергеннен кейін мұғалім-программист алдын ала әзірлеген бірнеше жауаптың ішінен оқушы дұрыс жауабын таңдау арқылы бақылау сұрақтарына жауап береді немесе берілген символдар, әріптер, цифрлар арқылы жауапты өзі айтады. Егер дұрыс жауап берілсе, келесі оқу бөлімі беріледі. Қате жауап берілген болса, оқу бөлімін тағы бір қайталап, сұраққа тағы да жауап беру қажеттілігі туады.
Бейімделген бағдарламалар бағдарламаның оңай немесе қиын бөлімдеріне өтуге мүмкіндік береді және бұл ауысу оқушының алдыңғы жауаптары мен қателерін ескеру негізінде жүргізіледі. Бейімделген оқу бағдарламасына оқушылардың жауаптарын талдау схемасы, сондай-ақ оқушының жеке ерекшеліктеріне және жауаптарына қарай ақпаратты беру тәсілін, қиындық деңгейін, оқу материалының тереңдігі мен көлемін, сұрақтардың түрлерін және т.б. өзгерту мүмкіндігі қарастырылған параллельді ішкі бағдарламалар топтамасы енгізіледі.
Құрастырылған оқу бағдарламасы техникалық құрал – компьютер арқылы немесе «шатастырылған беттер» түрінде жасалған (берген жауабына сәйкес оқушы оқулықтың белгілі бір бетіне ауысады) бағдарламаланған оқулықтар арқылы жүзеге асырылуы мүмкін.
Бағдарламаланған оқытудың негізгі принциптері мен артықшылықтары:
-
оқу материалының мөлшерлі түрде болуы;
-
оқушының белсенді түрде өз бетімен жұмыстануы;
-
меңгеруді тұрақты бақылануы;
-
оқыту жылдамдығын, оқу материалының көлемін дараландыру;
-
оқытудың автоматтандырылған техникалық құралдарын қолдану мүмкіндігі.
Бағдарламаланған оқыту нақты материалға және біркелкі, нақты формулалары мен алгоритмдері бар қайталанатын іс-әрекеттерге негізделген пәндерді оқытуда пайдалы болмақ. Бағдарламаланған оқыту басты міндеті – автоматтандырылған дағды, берік біркелкі білім мен білікті қалыптастыру.
Бағдарламаланған оқыту оқытудың техникалық тәсілдерін қолдануға және дамытуға ықпал етті. Оқытудың техникалық тәсілдеріне (ОТТ) оқу үрдісінің тиімділігін арттыру мақсатында қолданылатын оқу-дидактикалық материалдармен қатар пайдаланылатын әр түрлі құрылғылар, машиналар және жүйелер жатады. Олар: 1) ақпараттық ОТТ – ақпаратты ұсынудың техникалық құралдары, 2) бақылаушы ОТТ, 3) оқытуды басқарудың тұйықталған циклын қамтамасыз ететін бағдарламаланған оқытуды орындайтын оқыту ОТТ деп бөлінеді.
2.3 Практикалық сабақтарды өткізуге арналған әдістемелік ұсыныстар
Сабақты бастау
Істі жаңадан бастау қиын, сабақты бастау да қиын болады. Себебі сабақтың бірінші минутынан-ақ мұғалім мен оқушылардың белгіленген мақсатқа жетудегі бірлескен қызметі жемісті болу үшін қажетті жағдай жасалуы керек. Бұл кезде туындаған қиындықтар төмендегі мәселелерді шешумен байланысты болады:
-
ұйымдастырушылық;
-
мазмұндық;
-
этикалық.
Ұйымдастырушылық мәселелерді шешу қажеттілігі мұғалім қоңырау соғылғаннан кейін сыныпқа кіргеннен-ақ басталады. Оның алғашқысы – мұғалім мен оқушының бір-бірімен амандасуы.
Егер бұл үрдіс оқушыларда қалыптаспаған болса, онда бұл жағдайды әдетте бір-екі сабақта өзгерту мүмкін болмайды. Бұл жағдайда шыдамдылық пен табандылық танытып, оқушылардан берілген әрекетті орындауларын, соның ішінде мұғаліммен амандасудан кейін жұмыс орындарына отыруларын талап ету керек.
Оқыту кезінде сабақтың басында әдетте ұйымдастырушылық мәселелерді шешу проблемасы болмайды: оқушылар сабақ басталысымен сабаққа кірісіп кетеді және мұғалімнің бастамасы мен ынтасын сақтай отырып, оқитын материалымен ғана шұғылданады. Шын мәнінде бұның артында оқушылардың бойында сабақ басындағы қажетті дағдыларды қалыптастырудағы мұғалімнің ұзақ және тыңғылықты жұмысы тұрады.
Кей кездері жоспарланған жұмысқа оқушылардың назарын аударту қажеттілігі туады. Бұл үшін оқушыларға «Назар аударыңдар, сабақты бастаймыз» деп айту жеткілікті болады. Егер оқушылар аса қозғалғыш күйде болса, онда мұндай үндеу нәтижесін болады. Мұндай жағдайлар бақылау жұмыстарынан кейін, сыныптағы жеке кикілжің жағдайлардан кейін болады. Бұл кезде сабақты оқылған материал негізінде құрылған қызықты тапсырмаларды қолдану арқылы бастаған жөн. Сонда оларды орындау үрдісінің өзі, әсіресе жазбаша жұмысты орындау үрдісі, қозғалғыш күйді төмендетуге және оқушыларды қалыпты жағдайға түсіріп, сабақты бастауға мүмкіндік береді. Көп жағдайда бұл уақытта үй тапсырмасын орындауды тексеру үрдісі жүргізіледі.
Сабақтың басында мазмұнды тапсырмаларды беру және шешу үрдісі бірнеше тәсілмен жүзеге асуы мүмкін. Олар кімнің және қалай таңдауына, жасауына және беруіне қарай топталады:
-
тек қана мұғаліммен (жаңа материалды оқып үйренуде қолданылады, басты рөл мұғалімге беріледі);
-
оқушылар және мұғаліммен (мұғалім өз ойын әдейі аяқтамайды да, оқушылардан аяқтауды сұрайды). Осылайша, оқушылар мысалдың соңын табу үшін логикалық ойланады, яғни шешу жолын ұсынады.
-
оқушылардың өздерімен.
Оқыту кезінде сабақтағы алдын ала жасалатын мазмұндық жұмыс көп жағдайда тек қана мұғаліммен ұйымдастырылады. Бұл жұмыс оқушылардың жаңа материалды оқып үйренуге, бұрыннан бар білімді пайдалануға, жаңа біліктерді меңгеруге дайындайды. Бұл мақсатта сабақтың басында математикалық диктанттар, ойын түріндегі тапсырмалар, заңдылықты анықтауға арналған тапсырмалар, берілген есепті шешудің тиімді жолын табуға арналған тапсырмалар беріледі. Алайда, тек бір ғана тапсырманы қайталап өткізе беруге болмайды. Қолданылатын тапсырмаларды әрдайым түрлендіру кенеттік және жаңашылдық элементтерін енгізеді, яғни оқушылардың сабаққа деген қызығушылығын бірінші минуттан оятуға көмектеседі.
Оқыту кезінде сабақтағы алдын ала жасалатын мазмұндық жұмысты түрлендіруге оқушыларды да тартуға болады. Бұл жерде тек оқушылардың қызығушылығын арттыру ғана емес, сонымен қатар олардың көмегінің қажет екенін көрсету арқылы сенімдерін арттыруға болады. Ол үшін оқушыларға математикалық сөзжұмбақ құрастыруды тапсыруға болады.
Әрине, алғашқы уақытта оқушылардың дайындаған жұмыстарында мұғалімнің жұмыстарынан көп айырмашылық болмайды. Бірақ, оқушыларды мадақтау және ынталандыру қажет, бұл олардың өз-өзін реттеу үрдісін жақсартады. Сол кезде оқушылар өз идеяларын терең ойлап, қосымша әдебиеттермен таныса бастайды. Бұл уақытта оқушылар мұғалімнің өзі де шеше алмайтын тапсырма алып келеді деп қорықпау керек. Мұндай жағдайларда оқушылардың өздері есептің шешімін көрсетіп, жақсы баға алуларына болады. Әрине, мұғалім осындай рөлде өте сирек болуы керек, ал ол үшін мұғалімнің өзі де ұдайы ізденісте болу керек.
Осылайша, сабақтағы алдын ала жасалатын мазмұндық жұмысты түрлендірудің тәсілдерін кешенді түрде жүзеге асыру арқылы әр сабақты бірдей әрекеттермен бастау мүмкін болмайды. Бұл жерде оқушылар «сабақтағы қызметтің біркелкі болуынан шаршайды, ал жаңа бастама қызықты болған жағдайда сабақтың басқа бөлігі дәстүрлі түрде ұйымдастырылған болса да, шаршаудан аулақ болуға көмектесетінін» ескерту орынды болады.
Сабақтың сәтті өтуіне оның бастамасынан оқушылар үшін жағымды эмоциялық климат орнатудың да маңызы зор.
Мұғалімнің жағымды құлшынысы, атқарып жатқан іспен әуестенуі, сабақты жақсы көңіл-күймен бастау және өткізу іскерлігі оқушылар тарапынан жоғары бағаланады. Сабақ кезінде өзіңнің жайсыздығыңызды, сабырсыздығыңызды, дөрекілігіңізді, ашық ызаңызды, жұмысқа деген немқұрайлығыңызды көрсетуге болмайды.
Мұғалім өзінің тілінің сауаттылығына назар аудару керек, қажет емесе дыбыстар мен сөздерден құтылып, негізгі ойды айту кезінде қысқа, нақты және логикалық түрде дұрыс айтып, тілді «ал», «қысқасы», «жаңағы» және т.б. тәрізді паразит сөздерден тазарту керек. Оқушыларды біркелкі тыныш немесе қатты дауыс ашуландыратындықтан, сыныптағы жағдайға байланысты дауыстың күші мен үнін өзгертіп отыру керек.
Сабақтың басында жоғарыда көрсетілген мәселелердің барлығын шешу іскерлігі сабақтың ары қарай өтуіне әсер етеді: ол сабақтың қажетті қарқынын, эмоциялық климатты, мұғалім мен оқушылардың өнімді жұмысын анықтайды.
Жаңа материалды оқып үйрену бойынша әдістемелік ұсыныстар
Сабақтың құрылымындағы басты мәселе – жаңа материалды оқып үйрену. Сабақтың барысындағы сұрақтар жаңа тақырыпқа негізделе отырып немесе байланыса отырып шешіледі. Математиканы оқыту кезінде ол көбіне математикалық ұғымдарды, сөйлемдерді, теоремаларды оқып үйренуге саяды. Бұл жағдайда үш негізгі кезеңді бөлуге болады: қабылдауға дайындық, кіріспе және жаңа материалды алғашқы ұғыну.
Жаңа материалды қабылдауға дайындық кезеңі тірек ұғымдардың қалыптасуымен байланысты. Оқушылардың жаңа білімді меңгеруге дайындығын қамтамасыз етуге бағытталады. Мұндай білім беру жаңаны меңгеруді немесе тірек білімді өзектендіруді ынталандыруға тиісті назар аудармауда байқалады.
-
Негізгі белгілерді анықтау мен тірек білімді өзектендіру арқылы оқып үйренуге дайындау алдын ала практикалық есептерді шешу, көрнекі материалдарды көрсету, тарихи мәліметтерді қысқаша баяндау үрдісі кезінде жүзеге асыруға болады. Расында да, қандай да бір математикалық ұғымды дәйектеуде оны одан да кең ұғымға, ал ол кең ұғымды одан да үлкен ұғымға әкелуге болады.
-
Оқушыларды көпмүшелердің қасиеттерін сипаттайтын теоремаларды, ұғынуға дайындау барысында теоремаларды, аксиомаларды, математикалық сөйлемдерді дәлелдеусіз алуға болады.
Оқушыларға теоремалардың тұжырымдамасын ұғынуды жеңілдету үшін болжамды ұсынуда бірлесіп жұмыстануды ұйымдастыруға болады. Ол үшін оқушыларда белгіленген өрнектерді жазу, оқу, орналастыру бойынша дағдылардың қалыптасуына бағытталған жоспарлы түрде бірнеше тізбектелген сабақтарда белгілі бір жаттығуларды орындау қажет.
Жаңа материалды оқып үйрену кезінде оқушылардың қызметін басқару психологиялық-дидактикалық заңдылықтарды ескеру арқылы жүргізілу керек. Бұл кезде оқушы сабаққа енжарлықпен қатысса, көптеген мәліметтерді ұқпай қалатынын есте сақтау қажет. Материалды толық ұғыну үшін төмендегідей шарттарды орындаған кезде мәліметтермен танысу барысында ұлғая беретін белсенді ой қызметі жүзеге асырылу қажет:
-
оқушылар материалмен танысу барысында берілген материалды терең түсінуге көмектесетін белгілі бір тапсырманы орындайды;
-
бұл тапсырма оқушының күшін ой қызметінің белгілі бір тәсілін қолдануға бағыттайды;
-
оқушының берілген тапсырманы орындауға қажет болатын білімі бар;
-
материал аса жеңіл емес.
Жұмыстың соңында жаңа материалдың ұғынуға тиісті негізгі мазмұнын және онымен жұмыстанудың тәсілдерін бекіту арқылы қол жеткізілетін «таңбаны» ерекшелеу керек.
Әрине, жаңа материалды оқып үйрену кезінде оны ұғыну, түсіну, еске сақтау, қолдану білігі тәрізді сұрақтар жаңадан шешіле бастайды. Аталған үрдістер оқып үйренген материалды бекіту кезінде дамиды, ал бекітуді келесі бөлімде жекелеп қарастырамыз.
Оқып үйренгенді бекіту бойынша әдістемелік ұсыныстар
Оқып үйренгенді бекіту кезінде оқушылардың оқу материалын меңгеруінің бағдарламаның шарттарына сай келетін деңгейде болуы қамтамасыз етіледі.
Белгілі болғандай, білім тек қана онымен өз бетімен тиісті деңгейде жұмыстануда меңгеріледі. Сондықтан мұғалім тарапынан барысы мен алынатын нәтижелерді бақылау мүмкіндігі болатындай оқушылардың өз бетімен жұмыстануды ұйымдастыруға назар аударылу керек. Мұндай іс-әрекет біртіндеп сыртқы бақылауды өткізумен аяқталып, бұл әрекеттерді ойша орындауға көшумен жалғасу керек.
Бекіту барысында оқу материалын есте сақтауды және есептер шығару кезінде қолдану білігін қалыптастыруды қамтамасыз етуге болады.
Әрине, оқып үйрену кезінде оқушыға көптеген мәліметті әдейі жаттауға тура келеді. Бұл кезде ол өзіне мақсат қою керек – өзі немесе мұғалім белгілеген материалды барынша толық, нақты және берік есте сақтау. Мұнда мұғалім оқушыларға осы тақырып бойынша бақылау жұмысын жазасыңдар деген уәж өткізу керек.
Әлбетте, оқушы материалды дұрыс түсінбеген жағдайда, оны есте сақтау қиындайды. Үлкен көлемді материалды оқып үйрену кезінде де мұндай қиындық кездеседі. Жалпы айтқанда, оқушылар белсенді ой қызметімен айналысқан жағдайда ғана берілген материалды терең түсініп, жақсы есте сақтайды.
Оқу материалын жаттау кезінде оны дауыстап немесе іштен оқумен ғана шектелмеу керек. Сондай-ақ оны еске түсіріп қайта жаңғырту арқылы жазбаша орындау керек. Сондықтан тақырыпты түсіндіруге қатысты мәселелер айтылғанды дәптерге түсіру арқылы беріледі. Бұл жағдайда материал берік есте сақталады, себебі көзден миға баратын жүйке талшықтары құлақтан миға баратын жүйке талшықтарынан жиырма бес есе қалың болады.
Есте сақтауға қарама-қарсы үрдіс ұмыту болып табылады. Ол адамның ағзасына биологиялық тұрғыдан алғанда абзал. Ұмытудың қарқындылығы жаттағаннан кейінгі алғашқы уақытта көп болады. Мәнсіз материалды ұмыту (оқығаннан кейінгі сегіз сағат ішінде келесі отыз күнге қарағанда көп ұмытылады) мәні терең материалды ұмытуға қарағанда тез жүргізілсе де, бұл заңдылық жалпы заңдылық болып табылады.
Ұмытудың алдын алудың бірден бір тәсілі оқығанды қайталау және оны жаңа есептерді шығаруға қосу болып табылады. Біртектес есептерді шығару арқылы біркелкі түрде қайталаудың нәтижелілігі өте аз. Бірақ бұл біртектес есептерден бас тарту керек дегенді білдірмейді. Бұл кезде мұндай қайталауды жиі өткізуге болмайтынын, біртектес есептердің санын үштен көп болмауын қадағалау керектігін ескеру керек.
Осылайша, сабақта өтілген материалды нәтижелі түрде қайталау және бекіту үшін тексеру жұмыстары және өзіндік жұмыстар қарастырылады. Сыныпта өткізілетін мұндай жұмыстардың мазмұны, түрі, ұзақтығы сабақтың қойылған мақсаттарына сай болу керек. Кей кездері олар те бірнеше минутта, ал кей кездері сабақтың өн бойында өтуі мүмкін.
Білім мен біліктің диагностикасы
Қазіргі заманғы мұғалім мен оқушылардың бағдарламалық материалды меңгеру қызметінің негізгі бөлімдері: бағыттаушылық, орындаушылық және тексерушілік. Тексерушілік бөлімде «Мұғалім – оқушы» жүйесінде кері байланыс орнатылады, кері байланыс оқушылардың оқу материалын меңгеру сапасын анықтауға, уақтылы диагностикалауға және олардың білімі мен біліктерді түзетуге арналған ақпаратты үнемі алып тұруға мүмкіндік береді. Басқаша айтқанда, тексеру кезінде оқушылардың білімі мен біліктері анықталып, бағаланады және оқушылардың оқуын, тәрбиесі мен дамуын ауызша басқару үшін қажетті ақпаратты алуға және жинақтауға мүмкіндік береді.
Осы орайда тексеруді үш түрге жіктейді:

Сырттай тексеру оқушыларды оқу жұмысын сапалы және жүйелі орындауға үйретеді, жұмысты одан да жақсы етіп істеуге деген құлшынысты арттырады, ал мақсатқа бағытталған жұмыс барысында мұғалімдер өзара тексеру мен өзін-өзі тексерудің дамуына ықпал етеді.
Өзін-өзі тексеру кезінде оқушының өзі жасаған әрекеттердің дұрыстығын сезінеді және болашақта қате жасамауға тырысатын болады.
Өзін-өзі тексеру сызбасын келтірейік:

Берілген сызбаны дәлелдейтін бірнеше мысал келтірейік.
-
Өзін-өзі тексеруге деген қажеттіліктің қалыптасуын тапсырмаларды өз бетімен орындау кезінде ұйымдастыруға болады. Мысалы, оқушылардың біреуіне «Горнер схемасы» тақырыбы бойынша тапсырмалар беріледі, оқушы оны орындағаннан кейін шығару жолын тақтада көрсетіп, шешу жолын түсіндіреді.
-
Оқушылардың мұғалімнің қызметін тексеруге ерекше назар аудару керек. Тақырыпты түсіндіру кезінде мұғалім әдейілеп қате жіберуі мүмкін. Егер оқушылар қатені бірден байқап қалмаса, онда мұғалім «жетекші» сұрақтар арқылы оқушыларды қажеттісіне алып келеді.
-
Оқушылардың бір-бірін өзара тексеруін келесідей ұйымдастыруға болады. 10 минутқа арналған тексеру жұмысын жүргізу керек. Сабақтың соңына қарай (2 минутқа таман) есептеуді тоқтату және «ал енді парақтарды көршілеріңмен ауыстырып, көршіңіздің жұмысын тексеріңдер. Тексеріп болғаннан кейін, көршіңіздің жұмысына сіздің ойыңызша лайық бағаны қойыңдар» деп айту керек.
Жалпы алғанда, тексеру мақсатты, объективті, жанжақты, жүйелі және жеке болу керек. Оның нәтижелілігі оқушының білімі мен білігінің бағдарламаның шарттарымен сәйкестік деңгейін сипаттайтын бағамен өрнектеледі. Бұл нормаларға сәйкестік белгі деп аталатын бағаны жазудың сандық немесе басқа да символдық түрде болуы мүмкін.
-
Көпмүшелердің бөлінгіштік қасиеттерін қолдану
Бұл тақырыпты оқып үйрену үшін оқушылардың бастапқы білімдерін және көпмүшелердің бөлінгіштік белгілері туралы теореманы қайталап алу керек. Оқушылардың қарастырылып отырған теореманың тұжырымы мен мәнін дұрыс түсінуін тексеріп алу керек. Оны төменде көрсетілген мысалдар арқылы тексеруге болады:
Оқушыларға «Оқып кеткен теореманы бекіту үшін мысалды қарастырайық» деген ұсыныс беру керек.
Оқушылардың біреуін тақтаға шақырып, қайталаған материалды қолдана отырып берілген мысалды шешуді сұрау керек. Бұл кезде басқа оқушылар осы мысалды орындарында өз беттерімен шығарып бастайды, тек тақтада шығарып жатқан оқушының есебімен әлсін-әлсін салыстырып отырады. Тақтадағы шығару жолы мұғалімнің бақылауымен жүргізілуі керек.
Мысал
1.  көпмүшесі
көпмүшесі  көпмүшесіне бөлінетіндігі белгілі. Бөліндіні
табыңдар.
көпмүшесіне бөлінетіндігі белгілі. Бөліндіні
табыңдар.
Шешу жолын анықтап алғаннан кейін, тақтада тұрған оқушыдан шығару жолын түсіндіріп тұруын сұрау ету керек. Бұл әрекет материалдың меңгерілуін тағы да бекітуге мүмкіндік береді.
Шешуі. Төртінші дәрежелі көпмүшені
екінші дәрежелі көпмүшеге бөлгендегі бөлінді екінші дәрежелі
көпмүше болады. Төртінші дәрежелі көпмүшені екінші дәрежелі
көпмүшеге бөлгендегі бөлінді болатын көпмүшені табу үшін жаңа
айнымалыны енгізу қажет. Ізделінді көпмүше  болсын. Онда мына теңдік дұрыс
болады:
болсын. Онда мына теңдік дұрыс
болады:

 көпмүшесіне тең
болатын
көпмүшесіне тең
болатын  көпмүшені қарастырамыз. Екі көпмүшеде де
х-тің дәрежелері бірдей, бірақ
коэффициенттері әр түрлі екені көрініп тұр.
х-тің бірдей дәрежелеріндегі
коэффициенттерді теңестіру арқылы, төмендегі жүйені
аламыз:
көпмүшені қарастырамыз. Екі көпмүшеде де
х-тің дәрежелері бірдей, бірақ
коэффициенттері әр түрлі екені көрініп тұр.
х-тің бірдей дәрежелеріндегі
коэффициенттерді теңестіру арқылы, төмендегі жүйені
аламыз:
 , бұдан
, бұдан
 .
.
Жаңа айнымалы болып
енгізілген  қайтып келеміз, құрылған және шешілген
жүйеден
қайтып келеміз, құрылған және шешілген
жүйеден  болады. Сонымен,
болады. Сонымен,  көпмүшесін
көпмүшесін  көпмүшесіне бөлгендегі бөлінді
көпмүшесіне бөлгендегі бөлінді  болады.
болады.
-
Безу теоремасы мен оның салдарларын оқып үйренудің әдістемесі
Осы тақырыпты оқып үйрену сабағын ұзақтығы 30 минуттан аспайтын лекция түрінде өткізуге болады.
Бұл әдісті педагогикалық әдебиеттерде түсіндірмелі-көрнекілік әдіс деп, әдістемелік әдебиеттерде – мектептік лекция деп аталады. Мұнда лекциялық әдістің негізгі ерекшеліктерін ерекшелеу үшін«жауаптың үлгісі» деген өзінше атау берілді.
Қарастырылып тұрған әдіске қойылатын негізгі талап – мұғалімнің түсіндіруін (қысқаша немесе ұзақ) жауаптың үлгілері ретінде қарастыру керек. Бұл жерде теориялық сұрақтарды баяндау үлгілері ғана емес, сондай-ақ, ең бастысы, есепті шығару үлгілері қарастырылу керек.
Есепті шығарудағы жауаптың үлгісі – байланысқан түрдегі әңгімелеудің маңызды тәсілдерінің бірі. Орындап жатқан тапсырманы жүйелі әңгіме ретінде мүлтіксіз баяндау және түсіндіру біліктерінің қалыптасуы мұғалімнің түсіндіруінен басталады. Мұғалім жаңа типті тапсырманы қалай орындалу керектігін, жазбаларды қалай орналастыру керектігін, орындап жатқан амалдарды қай уақытта және қалай түсіндіру керектігін көрсетеді.
Мұғалімнің баяндауымен беріліп тұрған жауап үлгісі – жүйелі әңгімелеуге үйретудегі қажетті кезең. Себебі мұғалімнің жаңа типтегі жаттығуды орындау үлгісінде (егер де бұл үлгі жоғарыда көрсетілген шарттарға сай болса) мазмұндық элементтер (қалай орындау қажет?) ғана емес, сонымен қатар дәл әдістемелік компоненттер (қалай түсіндіру керек, жазбаларды қалай орналастыру керек, сызбаларды қалай көрсету керек? және т.б.) болады. Жауап үлгісінің аталған дәл әдістемелік компоненттерін алғаш рет мұғалім беруі мүмкін.
Лекция сабағын өткізудегі ең бастысы – оқушылардың белсенді ойлау қабілеттеріне қол жеткізу. Мұғалімнің тәжірибесінде оқушылардың әңгімелеу барысында белсенді ойлауына қол жеткізуге көмектесетін тәсілдері көп болуы керек.
Түсіндіруге кіріспестен бұрын мұғалім сыныпқа жаңа материалды түсуге бағыттайтын нақты тапсырма береді. Мұғалімнің әңгімелеуі барысында бұл тапсырманың орындалуы оқушылардың ойлау қызметін жандандырады.
Оқыту тәсілдерін қарастырайық.
Мұғалім жаңа материалды түсіндірген кезде әдейі қате жіберетінін, ал оқушылар мұқият тыңдап, сол қатені табу керектігін оқушыларға хабарлайды. Бұл тәсілдің артықшылықтарын білу үшін мұғалім оны екі-үш рет қолданып, оқушылардың қатені табуға құлшынатындықтарын және сабаққа белсенді араласатынын көру керек.
Мысал
2. Теореманың тұжырымын мынадай
түрде беру керек: « көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі бөлінді
екімүшесіне бөлгендегі бөлінді  болғандағы
болғандағы  көпмүшесінің мәніне тең болады, яғни
көпмүшесінің мәніне тең болады, яғни
 ». Оқушылардан тұжырымды оқып,
ойланып, қатесін табуды сұрау
керек.
». Оқушылардан тұжырымды оқып,
ойланып, қатесін табуды сұрау
керек.
Теореманы түсіндіруді бастамастан бұрын мұғалім оны дәлелдеудің жоспарын береді. Жоспар дәлелдеу идеясын түсінуге көмектеседі. Нәтижесінде есте сақтауға деген нұсқау терең түсінуге мүмкіндік туғызады. Мұғалімнің түсіндіруін тыңдай отырып, оқушылар оның пайымдауларын берілген жоспармен сәйкестендіреді, материалдың бір логикалық бөлімінен екінші бөліміне өтуді жеңіл түйсінеді, олардың арасындағы байланысты орнатады. Оқытудың мұндай тәсілін қолданған уақытта оқушылар материалды жақсы меңгереді сондай-ақ, ең бастысы, тыңдауды, жоспарды қолдануды және болашақта мұғалімнің түсіндіруі кезінде жоспарды құруға үйренеді.
Берілген тарауды жақсы меңгеру үшін оқушылар баяндаушының айтқан сөзі мен ойын конспектілеу керек, себебі бұл кезде тек көру және есту арқылы есте сақтау ғана емес, сонымен қатар механикалық есте сақтау да жұмыс істейді.
Горнер схемасы
Горнер схемасын да лекцияға қосуға болады.
Келесідей мысалдарды қарастырып талдаған жөн:
Мысал
3.  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдықты
табыңдар.
екімүшесіне бөлгендегі қалдықты
табыңдар.
Шешуі.  теңдеуін қарастырайық, бұдан
теңдеуін қарастырайық, бұдан  болады. Безу теоремасына сәйкес
болады. Безу теоремасына сәйкес  мәнін
мәнін  көпмүшесіне қойып,
көпмүшесіне қойып,  аламыз. Осылайша,
аламыз. Осылайша,  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдық нөлінші дәрежелі 9 көпмүшесі
болады.
екімүшесіне бөлгендегі қалдық нөлінші дәрежелі 9 көпмүшесі
болады.
Мысал
4.  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдықты
табыңдар.
екімүшесіне бөлгендегі қалдықты
табыңдар.
Шешуі.  теңдеуін қарастырайық, бұдан
теңдеуін қарастырайық, бұдан  болады. Безу теоремасына сәйкес
болады. Безу теоремасына сәйкес  мәнін
мәнін  көпмүшесіне қойып,
көпмүшесіне қойып,
 аламыз.
аламыз.  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдық нөлінші
дәрежелі
екімүшесіне бөлгендегі қалдық нөлінші
дәрежелі  көпмүшесі болады.
көпмүшесі болады.
Мысал
5.  көпмүшесі а)
көпмүшесі а)  екімүшесіне;
екімүшесіне;
ә)  екімүшесіне бөлінеді
ме?
екімүшесіне бөлінеді
ме?
Шешуі. а)  болғандықтан
болғандықтан  екені шығады. Безу теоремасы бойынша:
екені шығады. Безу теоремасы бойынша:
 болады. Көпмүшелерді
бөлгендегі қалдық
болады. Көпмүшелерді
бөлгендегі қалдық  болғандықтан, берілген көпмүше
болғандықтан, берілген көпмүше  екімүшесіне қалдықсыз
бөлінбейді;
екімүшесіне қалдықсыз
бөлінбейді;
ә)
 болғандықтан
болғандықтан
 екені шығады. Безу теоремасы
бойынша:
екені шығады. Безу теоремасы
бойынша:  болады. Көпмүшелерді бөлгенде қалдық болмайтындықтан,
берілген көпмүше
болады. Көпмүшелерді бөлгенде қалдық болмайтындықтан,
берілген көпмүше  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
Мысал
6.  көпмүшесі
көпмүшесі  екімүшесіне бөлінетіндігін
дәлелдеңдер.
екімүшесіне бөлінетіндігін
дәлелдеңдер.
Шешуі.  теңдеуін қарастырайық, бұдан
теңдеуін қарастырайық, бұдан  болады. Безу теоремасына сәйкес:
болады. Безу теоремасына сәйкес:  шығады, яғни
шығады, яғни  көпмүшесі
көпмүшесі  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
Мысал
7.  көпмүшесін
көпмүшесін  екімүшесіне бөліңдер.
екімүшесіне бөліңдер.
Шешуі.  болғандықтан, Салдар 2 бойынша
болғандықтан, Салдар 2 бойынша
 көпмүшесі
көпмүшесі  екімүшесіне бөлінеді және
екімүшесіне бөлінеді және

Мысал
8. Горнер схемасын қолдана
отырып  көпмүшесін
көпмүшесін  екімүшесіне бөліңдер.
екімүшесіне бөліңдер.
Шешуі. Жеңіл және көрнекі болу үшін
бөлінгішті канондық түрде жазайық, яғни  түрінде жазамыз.
түрінде жазамыз.
Горнер схемасын қолданып,

аламыз.
 теңдеуін қарастырайық,
бұдан
теңдеуін қарастырайық,
бұдан  болады. Бұл санды Горнер схемасының сол жақ төменгі
бұрышына жазамыз. Горнер схемасы бойынша есептеудің алгоритмін
қолданамыз.
болады. Бұл санды Горнер схемасының сол жақ төменгі
бұрышына жазамыз. Горнер схемасы бойынша есептеудің алгоритмін
қолданамыз.
Алынған
 сандары
сандары
 көпмүшесін
көпмүшесін
 екімүшесіне бөлгендегі бөлінді
болып табылатын көпмүшенің коэффициенттері
болады.
екімүшесіне бөлгендегі бөлінді
болып табылатын көпмүшенің коэффициенттері
болады.
Сонымен,
бөлінді  және қалдық
және қалдық  болады.
болады.
Яғни
 .
.
Безу теоремасын оқып үйрену
Өткен білімді қайталау, берілген теореманың және салдардың тұжырымын беру, оқушылардың дұрыс түсінуін тексеру. Келесідей мысалды шешуді ұсыну. Мұғалім бұл есепті өз бетінше немесе тақтаға бір оқушыны шақыру арқылы шығаруға болады.
Мысал
9.  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдықты
табыңдар.
екімүшесіне бөлгендегі қалдықты
табыңдар.
Шешуі.  теңдеуін қарастырайық, бұдан
теңдеуін қарастырайық, бұдан  болады. Безу теоремасына сәйкес
болады. Безу теоремасына сәйкес  мәнін
мәнін  көпмүшесіне қойып,
көпмүшесіне қойып,  аламыз. Осылайша,
аламыз. Осылайша,  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдық нөлінші дәрежелі 9 көпмүшесі
болады.
екімүшесіне бөлгендегі қалдық нөлінші дәрежелі 9 көпмүшесі
болады.
Келесі мысалды өз беттерімен дәптерге шығаруды ұсынуға болады, содан соң оқушылар дәптерлерін көршілерімен алмастырып, бір-бірінің қателерін тексеріп, кейіннен дұрыс жауапты айту керек.
Мысал
10.  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдықты
табыңдар.
екімүшесіне бөлгендегі қалдықты
табыңдар.
Шешуі.  теңдеуін қарастырайық, бұдан
теңдеуін қарастырайық, бұдан  болады. Безу теоремасына сәйкес
болады. Безу теоремасына сәйкес  мәнін
мәнін  көпмүшесіне қойып,
көпмүшесіне қойып,  аламыз.
аламыз.  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдық нөлінші
дәрежелі
екімүшесіне бөлгендегі қалдық нөлінші
дәрежелі  көпмүшесі болады.
көпмүшесі болады.
Мысал
11.  көпмүшесі а)
көпмүшесі а)  екімүшесіне;
екімүшесіне;
ә)  екімүшесіне бөлінеді
ме?
екімүшесіне бөлінеді
ме?
Шешуі. а)  болғаннан
болғаннан  екені шығады. Безу теоремасы бойынша:
екені шығады. Безу теоремасы бойынша:
 болады. Көпмүшелерді
бөлгендегі қалдық
болады. Көпмүшелерді
бөлгендегі қалдық  болғандықтан, берілген көпмүше
болғандықтан, берілген көпмүше  екімүшесіне қалдықсыз
бөлінбейді;
екімүшесіне қалдықсыз
бөлінбейді;
ә)
 болғаннан
болғаннан
 екені шығады. Безу теоремасы
бойынша:
екені шығады. Безу теоремасы
бойынша:  болады. Көпмүшелерді бөлгенде қалдық болмайтындықтан,
берілген көпмүше
болады. Көпмүшелерді бөлгенде қалдық болмайтындықтан,
берілген көпмүше  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
Безу теоремасының салдарын қолдану
Теореманы дұрыс түсінген оқушылар төмендегі мысалдарды өз бетінше шығара алады.
Мысал
12.  көпмүшесі
көпмүшесі  екімүшесіне бөлінетіндігін
дәлелдеңдер.
екімүшесіне бөлінетіндігін
дәлелдеңдер.
Шешуі.  теңдеуін қарастырайық, бұдан
теңдеуін қарастырайық, бұдан  болады. Безу теоремасына сәйкес:
болады. Безу теоремасына сәйкес:  шығады, яғни
шығады, яғни  көпмүшесі
көпмүшесі  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
Мысал
13.  көпмүшесін
көпмүшесін  екімүшесіне бөліңдер.
екімүшесіне бөліңдер.
Шешуі.  болғандықтан, Салдар 2 бойынша
болғандықтан, Салдар 2 бойынша
 көпмүшесі
көпмүшесі  екімүшесіне бөлінеді және
екімүшесіне бөлінеді және

Безу теоремасы мен Горнер схемасын қолдану
Өтілген материалды бекіту үшін оқушыларға 10-15 минутқа арналған шағын өзіндік жұмыс беруге болады. Одан кейін оқушылар бір-бірінің жұмысын тексере алады. Өзіндік жұмыс оқушылардың есеп шығару дағдысын нығайту үшін жүргізіледі.
Өзіндік жұмыс 2 нұсқада ұсынылады: 1-нұсқа а) және б) есептерін, 2-нұсқа ә) және в) есептерін орындайды.
Мысал 14. Көбейткіштерге жіктеңдер:
а)

ә)

б)

в)

Шешуі.
а) үлкен дәреженің
коэффициенті 1-ге тең, сондықтан  көпмүшесінің түбірлері бола алатын бүтін сандар бос мүше
12-нің бөлгіштері болады. бұл сандарды теріп жазайық:
көпмүшесінің түбірлері бола алатын бүтін сандар бос мүше
12-нің бөлгіштері болады. бұл сандарды теріп жазайық:
 . Әр санды берілген көпмүшеге
қою арқылы
. Әр санды берілген көпмүшеге
қою арқылы  аламыз.
аламыз.  болғандықтан,
болғандықтан,  саны
саны  көпмүшесінің түбірі болады, сондықтан
көпмүшесінің түбірі болады, сондықтан
 көпмүшесі
көпмүшесі
 екімүшесіне бөлінеді. Горнер
схемасы бойынша
екімүшесіне бөлінеді. Горнер
схемасы бойынша  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі бөліндінің коэффициенттерін табамыз.
(Мұнда және әрі қарай Горнер схемасы қысқартылған түрде беріледі):
осылайша,
екімүшесіне бөлгендегі бөліндінің коэффициенттерін табамыз.
(Мұнда және әрі қарай Горнер схемасы қысқартылған түрде беріледі):
осылайша,  .
.
 болғандықтан,
болғандықтан,
 болады.
болады.
ә) Егер
 көпмүшесінің
көпмүшесінің
 рационал түбірі бар болса,
онда р
саны (+1)
бос мүшенің бөлгіші болады, ал q
саны 2
коэффициентінің бөлгіші болады, сондықтан барлық рационал сандардың
ішінен тек қана
рационал түбірі бар болса,
онда р
саны (+1)
бос мүшенің бөлгіші болады, ал q
саны 2
коэффициентінің бөлгіші болады, сондықтан барлық рационал сандардың
ішінен тек қана  сандары түбірлер бола алады. Берілгенге табылған мәндерді
қою арқылы
сандары түбірлер бола алады. Берілгенге табылған мәндерді
қою арқылы  аламыз.
аламыз.
 болғандықтан,
болғандықтан,
 саны
саны  көпмүшесінің түбірі болады, сондықтан
көпмүшесінің түбірі болады, сондықтан
 көпмүшесі
көпмүшесі
 екімүшесіне
бөлінеді.
екімүшесіне
бөлінеді.
Осылайша,
 .
.  квадрат үшмүшенің дискриминантын табайық.
квадрат үшмүшенің дискриминантын табайық.
 болғандықтан,
онда
болғандықтан,
онда  және
және  сандары осы үшмүшенің түбірлері болады;
сондықтан
сандары осы үшмүшенің түбірлері болады;
сондықтан  .
.
Сонымен,
 .
.
б) Егер берілген
көпмүшенің түбірлерінің арасында бүтін сандар бар болса, онда бұл
сандар 1 немесе  болады.
болады.  табайық:
табайық:  .
.
 болғандықтан
болғандықтан
 саны
саны  көпмүшесінің түбірі болады, сондықтан
көпмүшесінің түбірі болады, сондықтан
 көпмүшесі
көпмүшесі
 екімүшесіне бөлінеді. Горнер
схемасы бойынша
екімүшесіне бөлінеді. Горнер
схемасы бойынша  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі бөліндінің коэффициенттерін
табамыз:
екімүшесіне бөлгендегі бөліндінің коэффициенттерін
табамыз:
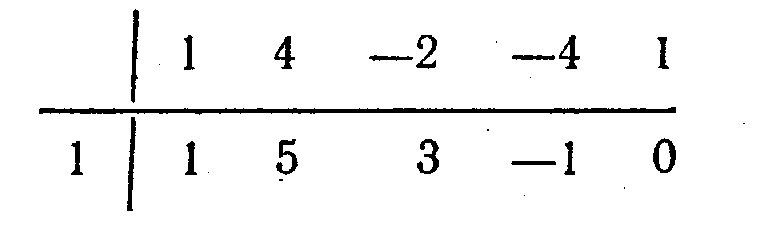
Осылайша,
 .
.
 көпмүшесі
көпмүшесі
 болғанда нөлге тең болады;
сондықтан ол
болғанда нөлге тең болады;
сондықтан ол  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
Горнер схемасы
бойынша  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі бөліндінің коэффициенттерін
табамыз.
екімүшесіне бөлгендегі бөліндінің коэффициенттерін
табамыз.
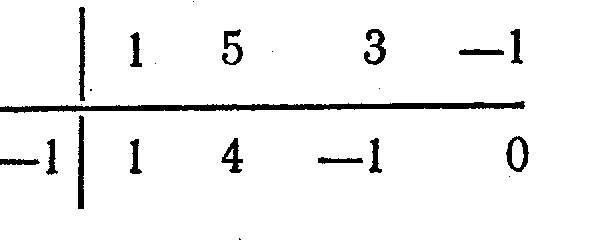
Осыдан
 шығады.
шығады.
 болғандықтан,
онда
болғандықтан,
онда  болады.
болады.
в)
 болғандықтан, онда Горнер
схемасына сәйкес мынаны аламыз:
болғандықтан, онда Горнер
схемасына сәйкес мынаны аламыз:
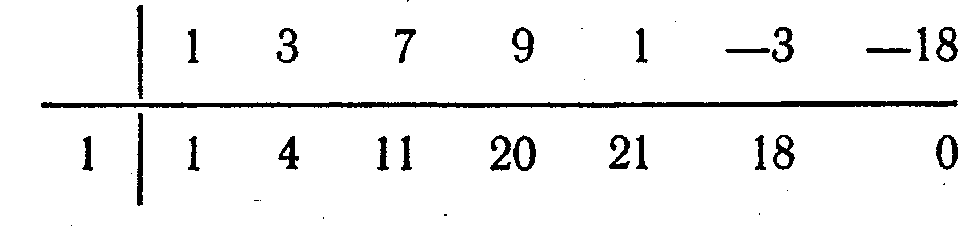
Бұдан

Горнер схемасын қолдана
отырып,  көпмүшесі
көпмүшесі  екімүшесіне бөлінетініне көз
жеткіземіз:
екімүшесіне бөлінетініне көз
жеткіземіз:
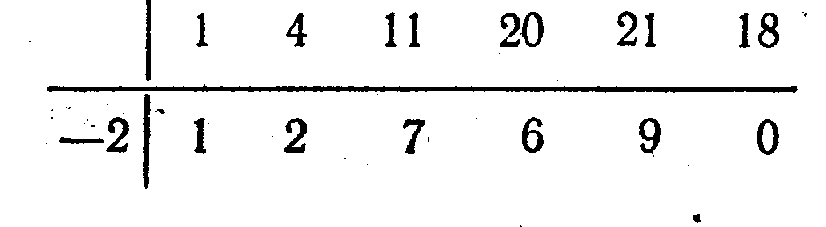
Осыдан,
 болады.
болады.
Топтастырып және толық квадратты шығарып, төмендегідей теңдікті аламыз:

 квадрат үшмүшенің
дискриминанты нөлден кем болғандықтан, бұл үшмүше сызықтық
көбейткіштерге жіктелмейді.
квадрат үшмүшенің
дискриминанты нөлден кем болғандықтан, бұл үшмүше сызықтық
көбейткіштерге жіктелмейді.
Сонымен,
 болады.
болады.
-
Көпмүшенің түбірлері туралы тұжырымды қолдану
Бұл тақырып оқушыларға бұрыннан таныс және олар осы бөлімнің мәнін өз бетімен аша алады. Бірнеше оқушыға бұл тақырыпты дайындап келіп, оны сабақта баяндама түрінде түсіндіруді тапсыруға болады. Бекіту үшін оқушыларға келесідей мысалдарды өз бетімен шығаруға ұсынуға болады. Оқушылардың барлық әрекеттері мұғалім тарапынан ұдайы тексеріліп тұруы керек, түсіндіру барысында мұғалімге баяндаушыны түзетуге және оқушылар тарапынан баяндамашыға қойылған қиын сұрақтарға жауап беруге болады.
Мысал
15.  көпмүшенің түбірлерін
табыңдар.
көпмүшенің түбірлерін
табыңдар.
Шешуі. Берілген көпмүшенің
түбірлерінің арасында рационал сан болатынын немесе болмайтынын
анықтайық. Айталық,  қысқартылмайтын бөлшегі берілген көпмүшенің түбірі болсын,
онда жоғарыда көрсетілген тұжырым бойынша р саны
қысқартылмайтын бөлшегі берілген көпмүшенің түбірі болсын,
онда жоғарыда көрсетілген тұжырым бойынша р саны  мәндеріне, ал q
саны
мәндеріне, ал q
саны  мәндеріне ие бола алады. Осылайша, берілген көпмүшенің
рационал түбірлері ретінде тек қана келесідей сандар болуы
мүмкін:
мәндеріне ие бола алады. Осылайша, берілген көпмүшенің
рационал түбірлері ретінде тек қана келесідей сандар болуы
мүмкін:  .
.
Осы сандардың әрқайсысын
берілген көпмүшеге қою арқылы  аламыз.
аламыз.
Осыдан,
 саны берілген
саны берілген
 көпмүшесінің түбірі болады
және
көпмүшесінің түбірі болады
және  .
.
Горнер схемасын қолдана
отырып, түбірлері  және
және  сандары болатын
сандары болатын  өрнегін табамыз. Сондықтан берілген көпмүшенің
түбірлері
өрнегін табамыз. Сондықтан берілген көпмүшенің
түбірлері  сандары болады.
сандары болады.
Мысал
16.  көпмүшесін көбейткіштерге
жіктеңдер.
көпмүшесін көбейткіштерге
жіктеңдер.
Шешуі. Берілген көпмүшенің
түбірлерінің арасында рационал сан болатынын немесе болмайтынын
анықтайық. Айталық,  қысқартылмайтын бөлшегі берілген көпмүшенің түбірі болсын,
онда жоғарыда көрсетілген тұжырым бойынша р саны
қысқартылмайтын бөлшегі берілген көпмүшенің түбірі болсын,
онда жоғарыда көрсетілген тұжырым бойынша р саны  мәндеріне, ал q
саны
мәндеріне, ал q
саны  мәндеріне ие бола алады. Осылайша, берілген көпмүшенің
рационал түбірлері ретінде тек қана келесідей сандар болуы
мүмкін:
мәндеріне ие бола алады. Осылайша, берілген көпмүшенің
рационал түбірлері ретінде тек қана келесідей сандар болуы
мүмкін:  .
.
Осы сандардың әрқайсысын
берілген көпмүшеге қою арқылы  аламыз.
аламыз.
 болғандықтан,
болғандықтан,
 және
және  сандары берілген
сандары берілген  көпмүшесінің түбірі болады, яғни
көпмүшесінің түбірі болады, яғни  .
.
 көпмүшесін
көпмүшесін
 көпмүшесін
көпмүшесін
 көпмүшесіне «бағандап» бөлу
арқылы немесе Горнер схемасы бойынша
көпмүшесіне «бағандап» бөлу
арқылы немесе Горнер схемасы бойынша  көпмүшесін
көпмүшесін  екімүшесіне, сонан соң шыққан бөліндіні
екімүшесіне, сонан соң шыққан бөліндіні
 екімүшесіне бөлу арқылы немесе
анықталмаған коэффициенттер әдісі арқылы табуға
болады.
екімүшесіне бөлу арқылы немесе
анықталмаған коэффициенттер әдісі арқылы табуға
болады.
 көпмүшесін анықталмаған
коэффициенттер әдісі арқылы
табайық.
көпмүшесін анықталмаған
коэффициенттер әдісі арқылы
табайық.
 тепе-теңдігі орындалатындықтан
және сол жақта тұрған көпмүшенің бос мүшесі
тепе-теңдігі орындалатындықтан
және сол жақта тұрған көпмүшенің бос мүшесі  -ге, ал оң жақта тұрған көпмүшенің бос мүшесі
-ге, ал оң жақта тұрған көпмүшенің бос мүшесі
 -ге тең
болғандықтан,
-ге тең
болғандықтан,  болады. Тепе-теңдіктегі с-ның орнына 4
санын, х-тің орнына 1-ді
қойып, b-ны
табамыз:
болады. Тепе-теңдіктегі с-ның орнына 4
санын, х-тің орнына 1-ді
қойып, b-ны
табамыз:

Бұдан  болады.
болады.
Сонымен,
 .
.
 көпмүшесінің нақты түбірлері
болмайды және ол көбейткіштерге жіктелмейді. Сондықтан есептің
шартында берілген көпмүше көбейткіштерге былай
жіктеледі:
көпмүшесінің нақты түбірлері
болмайды және ол көбейткіштерге жіктелмейді. Сондықтан есептің
шартында берілген көпмүше көбейткіштерге былай
жіктеледі:  .
.
-
Көпмүшені көбейткіштерге жіктеу әдістері
Бұл жұмысты оқушыларға қайталау сабағы ретінде ұсынуға болады. Оқушыларды тақтаға шақырып, мысалдарды шешуге болады. Мұндай есептерді шығару үшін оқушыларда қажетті білімнің барлығы бар. Басқа оқушылар орындарынан өз бетінше шығарады, басқаларынан «алға» шыққан оқушылар қосымша тапсырмалар алады және соларды орындайды.
Мысал 17. Көпмүшені көбейткіштерге жіктеңдер:
а)
ә)

Шешуі.
а)
 теңдеуін шешіп,
көбейтіндісі
теңдеуін шешіп,
көбейтіндісі  бос мүшеге, ал қосындысы
бос мүшеге, ал қосындысы  -ке тең болатын 2 және 3 сандарын аламыз, бұл
сандар
-ке тең болатын 2 және 3 сандарын аламыз, бұл
сандар
 көпмүшесінің түбірлері болады, яғни
көпмүшесінің түбірлері болады, яғни  көпмүшесі
көпмүшесі
 болып көбейткіштерге
жіктеледі;
болып көбейткіштерге
жіктеледі;
ә)
 теңдеуін шешіп,
теңдеуін шешіп,
 және
және
 болатындай
болатындай
 және
және  сандарын аламыз, бұл сандар
сандарын аламыз, бұл сандар
 көпмүшесінің түбірлері болады, яғни
көпмүшесінің түбірлері болады, яғни  көпмүшесін
көпмүшесін  болып көбейткіштерге жіктеуге
болады.
болып көбейткіштерге жіктеуге
болады.
Мысал 18. Көбейткіштерге жіктеңдер:
1)

2)
 .
.
Шешуі.
1)
 болғандықтан,
болғандықтан,
 көпмүшесі
көпмүшесі
 екімүшесіне бөлінеді.
Анықталмаған коэффициенттер әдісі арқылы
екімүшесіне бөлінеді.
Анықталмаған коэффициенттер әдісі арқылы  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі бөліндіні
табамыз.
екімүшесіне бөлгендегі бөліндіні
табамыз.
Бөлінді
 көпмүшесі
болсын.
көпмүшесі
болсын.  болғандықтан, төмендегі жүйені
аламыз:
болғандықтан, төмендегі жүйені
аламыз:

Бұдан
 болады. Яғни
болады. Яғни
 болады.
болады.
 болғандықтан,
болғандықтан,
 болады.
болады.
2)
 болғандықтан,
болғандықтан,
 көпмүшесі
көпмүшесі
 екімүшесіне бөлінеді.
Анықталмаған коэффициенттер әдісін қолдана отырып,
екімүшесіне бөлінеді.
Анықталмаған коэффициенттер әдісін қолдана отырып,
 бөліндіні
табамыз.
бөліндіні
табамыз.
 болғандықтан, төмендегі жүйені
аламыз:
болғандықтан, төмендегі жүйені
аламыз:

Бұдан
 болады. Яғни
болады. Яғни
 болады.
болады.
Оң жақтағы көпмүшені көбейткіштерге жіктейміз:

 квадрат үшмүшенің
дискриминантын табайық.
квадрат үшмүшенің
дискриминантын табайық.
 болғандықтан,
болғандықтан,
 және
және  сандары бұл үшмүшенің түбірлері болады.
Сондықтан
сандары бұл үшмүшенің түбірлері болады.
Сондықтан  болады.
болады.
Сонымен,
 .
.
Қорытынды
Дипломдық жұмыстың нәтижесі – «Көпмүшелер» тақырыбын оқып үйренуге арналған әдістеменің әзірленуі. Қазіргі уақытта білімнің жоғары бағалануына орай берілген тақырып бойынша білімді алу және тереңдету қажеттілігі туып отыр. Ал осы тақырыпты оқып үйрену кезінде оқушыларда ғылыми-зерттеу қызметіне деген қабілеті артады.
Анықтамаларды, теоремаларды және салдарларды дұрыс түсінуді жақсарту үшін оларды аналитикалық әдіс арқылы енгізу керек. Оның жүзеге асыру жолдары осы жұмыста көрсетілген. Сонымен қатар білімді толық меңгеруге көмектесетін әдістемелік ережелер жобаланып әзірленген.
Осы дипломдық жұмысын орындауда қол жеткізген жетістіктер:
-
«Көпмүшелер» тақырыбы бойынша материал жинақталып, жүйеленді;
-
әдістемелік нұсқаулар жобаланып, әзірленді;
-
тақырыпты оқып үйрену бойынша психологиялық-педагогикалық бөлім әзірленіп, жасалды.
Зерттеу жұмысында берілген материалды орта мектептің және математика бағытында мамандандырылған мектептердің мұғалімдеріне қолдануға болады. Сонымен қатар орта мектептердің, мектеп-лицейлерінің, мектеп-гимназияларының жоғары сынып оқушыларына, қорытынды емтихан мен жоғары оқу орнына түсуге арналған емтиханға дайындығын тереңдеткісі келетін оқушыларға, сонымен қатар педагогикалық институттар мен университеттердің физика-математика факультеттерінің студенттеріне ұсынылады.
Пайдаланылған әдебиеттер тізімі
-
«Математика» Большой справочник для школьников и поступающих в вузы – Дрофа 1998, 864 бет.
-
«Математика» Задачи М. И. Сканави с решениями – Минск 1996, 448 бет.
-
Бугров Я.С. Высшая математика.- Ростов-на-Дону 1997.
-
Винберг В.А. Алгебра.- Москва 1995.
-
Выгодский М.Я. Справочник по элементарной математике.- Москва 1997.
-
Зив Б.Г. Математика, 11. Уроки повторения. — СПб.: Мир и семья-95, 1998.
-
Кузнецова Г.Н. Миндюк Н.Г. «Программа» (Тематическое планирование к учебникам федерального комплекта «Математика») – М.:2002г 320 бет.
-
Курош А.Г. Курс высшей алгебры.- Наука 1973.
-
Мордкович А.Г. Алгебра және анализ бастамалары, 10-11. Оқулық, есептер жинағы.
-
Сборник задач по математике с решениями / под ред. М. И. Сканави –М.: Издательский дом Оникс 1999, 624 бет.
-
Фрижман Л.М., Турецкий Е.Н. «Как научиться решать задачи»: Просвещение 1984, 175 бет.
-
Шлярский Д.О., Ченцов Н.Н., Яглом И.М. "Избранные задачи и теоремы элементарной математики" Том 1 Арифметика и алгебра.-С-Петербург 1998, 328 бет.
Қосымшалар
Бұл бөлімде факультативтік сабақтарда қарастыруға арналған кейбір есептер келтіріледі. (*) таңбасымен берілген есептер – қиындығы жоғары тапсырмалар. Бұл есептерді үй немесе жеке жұмысқа беру ұсынылады.
1.
 өрнегінде жақшаларды ашып,
ұқсас мүшелерді біріктіргеннен кейін шығатын көпмүшенің
коэффициенттерінің қосындысын
табыңдар.
өрнегінде жақшаларды ашып,
ұқсас мүшелерді біріктіргеннен кейін шығатын көпмүшенің
коэффициенттерінің қосындысын
табыңдар.
Айталық, берілген
өрнекті х-тің дәрежелері арқылы
жіктеу  түрінде болады делік, мұндағы
түрінде болады делік, мұндағы  – қосындысын табуды қажет ететін анықталмаған
коэффициенттер, ал n
–
берілген өрнектің дәрежесі (ол оңай табылады және
– қосындысын табуды қажет ететін анықталмаған
коэффициенттер, ал n
–
берілген өрнектің дәрежесі (ол оңай табылады және
 болады). Егер бұл
теңдікте
болады). Егер бұл
теңдікте  болса, онда
болса, онда
 шығады.
шығады.
Осылайша, ізделінді қосынды 1-ге тең болады.
2. Қайсысында жақшаларды
ашып, ұқсас мүшелерді біріктіргеннен кейін  алдындағы коэффициент артық
болады?
алдындағы коэффициент артық
болады?
Екі өрнектің жақшаларын
ашып, ұқсас мүшелерді біріктіргеннен кейін
х-ке қатысты екі көпмүше
аламыз. Енді берілген өрнектердегі х-ті  -ке ауыстырайық. Сондай-ақ алынған көпмүшелерде
де х-ті
-ке ауыстырайық. Сондай-ақ алынған көпмүшелерде
де х-ті  -ке алмастырамыз, яғни олардың әрқайсысында
х-тің жұп дәрежелеріндегі
коэффициенттерді өзгертпей, х-тің тақ дәрежелеріндегі
коэффициенттердің таңбаларын ауыстырамыз. Әсіресе
-ке алмастырамыз, яғни олардың әрқайсысында
х-тің жұп дәрежелеріндегі
коэффициенттерді өзгертпей, х-тің тақ дәрежелеріндегі
коэффициенттердің таңбаларын ауыстырамыз. Әсіресе
 коэффициенттер өзгермейді.
Осылайша, алынған екі көпмүшедегі
коэффициенттер өзгермейді.
Осылайша, алынған екі көпмүшедегі  коэффициенттер
коэффициенттер  және
және  өрнектерінің жақшаларын ашып, ұқсас мүшелерді
біріктіргеннен кейін шығатын көпмүшелердегі
өрнектерінің жақшаларын ашып, ұқсас мүшелерді
біріктіргеннен кейін шығатын көпмүшелердегі  коэффициенттер тең екенін
көреміз.
коэффициенттер тең екенін
көреміз.
Бірақ, жаңа
көпмүшелердің біріншісінде коэффициенті ең үлкен болатыны анық. Расында да, бірінші
өрнекте жақшаларды ашқаннан кейін х-тің әр түрлі дәрежелерінде тек
қана оң таңбалы коэффициенттер шығады және ұқсас мүшелерді
біріктірген кезде осы коэффициенттер қосылады. Екінші өрнекте
жақшаларды ашқаннан кейін х-тің әр түрлі дәрежелерінде әр
түрлі таңбалы коэффициенттер шығады және ұқсас мүшелерді
біріктірген кезде осы коэффициенттер
азаяды.
коэффициенті ең үлкен болатыны анық. Расында да, бірінші
өрнекте жақшаларды ашқаннан кейін х-тің әр түрлі дәрежелерінде тек
қана оң таңбалы коэффициенттер шығады және ұқсас мүшелерді
біріктірген кезде осы коэффициенттер қосылады. Екінші өрнекте
жақшаларды ашқаннан кейін х-тің әр түрлі дәрежелерінде әр
түрлі таңбалы коэффициенттер шығады және ұқсас мүшелерді
біріктірген кезде осы коэффициенттер
азаяды.
Сонымен,
 және
және  өрнектерінің жақшаларын ашып, ұқсас мүшелерді
біріктіргеннен кейін бірінші өрнектегі
өрнектерінің жақшаларын ашып, ұқсас мүшелерді
біріктіргеннен кейін бірінші өрнектегі  коэффициенті екіншісіне қарағанда артық
болады.
коэффициенті екіншісіне қарағанда артық
болады.
3.
 көбейтіндісінде жақшаларды
ашып, ұқсас мүшелерді біріктіргеннен кейін
х-тің қандай да бір дәрежелерін
қамтитын мүшелер қалмайтынын дәлелдеу
керек.
көбейтіндісінде жақшаларды
ашып, ұқсас мүшелерді біріктіргеннен кейін
х-тің қандай да бір дәрежелерін
қамтитын мүшелер қалмайтынын дәлелдеу
керек.
Есептің тұжырымы төмендегідей түрлендіруден шығады:

 .
.
Төмендегі өрнектерде
жақшаларды ашып, ұқсас мүшелерді біріктіргеннен кейін
 коэффициентін табу:
а)
коэффициентін табу:
а)  ; ә)
; ә)  .
.
а) геометриялық прогрессияның қосындысының формуласына және Ньютон формуласына сәйкес:


Осылайша, ізделінді
коэффициент  болады.
болады.
ә) Берілген
өрнекті  деп белгілейік. Онда:
деп белгілейік. Онда:
 .
.
Бұдан
 .
.
Осылайша, ізделінді
коэффициент  болады.
болады.
4.
* (п
рет)
өрнегіндегі жақшаларды ашып, ұқсас мүшелерді біріктіргеннен кейін
шыққан
(п
рет)
өрнегіндегі жақшаларды ашып, ұқсас мүшелерді біріктіргеннен кейін
шыққан  алдындағы коэффициентті
анықтаңдар.
алдындағы коэффициентті
анықтаңдар.
Алдымен
 өрнегінде жақшаларды ашып,
ұқсас мүшелерді біріктіргеннен кейін шығатын бос мүшені табайық.
Ол
өрнегінде жақшаларды ашып,
ұқсас мүшелерді біріктіргеннен кейін шығатын бос мүшені табайық.
Ол  болғандағы осы өрнектің мәніне
тең, яғни
болғандағы осы өрнектің мәніне
тең, яғни

Келесі
кезекте х-тің
коэффициентін  деп,
деп,  -тың коэффициентін
-тың коэффициентін  деп,
деп,
х-тің жоғары дәрежелеріндегі
коэффициенттердің қосындысын  деп белгілейік. Онда
деп белгілейік. Онда  аламыз.
аламыз.
Басқаша алғанда,



Бұдан
 .
.
 болғандықтан,
болғандықтан,
 болады. Яғни
болады. Яғни
 болады. Енді
болады. Енді
 есептейік:
есептейік:

 .
.
Осы
өрнекке  қойып,
қойып,



5.
 көпмүшесін а)
көпмүшесін а)
 -ге; ә)
-ге; ә)
 -ге бөлгендегі қалдықты
табыңдар.
-ге бөлгендегі қалдықты
табыңдар.
а) Бірінші тәсілі. Кез
келген бүтін k
үшін  екімүшесі
екімүшесі  -ге бөлінетіндіктен,
-ге бөлінетіндіктен,  өрнегін
өрнегін  -ге бөлгенде 6 қалдық
қалады.
-ге бөлгенде 6 қалдық
қалады.
Екінші
тәсілі.  көпмүшесін
көпмүшесін  -ге бөлгендегі бөліндіні
-ге бөлгендегі бөліндіні  , ал қалдықты r
деп
белгілейік. Онда
, ал қалдықты r
деп
белгілейік. Онда  .
.
Осы
теңдікте  деп аламыз, сонда қалдықта 6
шығады.
деп аламыз, сонда қалдықта 6
шығады.
ә) Алдыңғы есептің
екінші тәсіліне сәйкес берілген көпмүшені  -ге бөлгендегі бөліндіні
-ге бөлгендегі бөліндіні  , ал қалдықты
, ал қалдықты  деп белгілейік (көпмүшені квадрат үшмүшеге бөлгендегі
қалдық бірінші дәрежелі екімүше
болады):
деп белгілейік (көпмүшені квадрат үшмүшеге бөлгендегі
қалдық бірінші дәрежелі екімүше
болады):
 , бұдан
, бұдан
 .
.
Осылайша, ізделінді
қалдық  -ке тең.
-ке тең.
6. Белгісіз
көпмүшені  -ге бөлгенде 2 қалдық, ал
-ге бөлгенде 2 қалдық, ал  -ге бөлгенде 1 қалдық қалады. Осы көпмүшені
-ге бөлгенде 1 қалдық қалады. Осы көпмүшені
 -ге бөлгенде қанша қалдық
қалады?
-ге бөлгенде қанша қалдық
қалады?
Айталық,
 – белгісіз
көпмүше,
– белгісіз
көпмүше,  – осы көпмүшені
– осы көпмүшені  -ге бөлгендегі бөлінді, ал
-ге бөлгендегі бөлінді, ал  – ізделінді қалдық болсын.
Онда
– ізделінді қалдық болсын.
Онда
 (*)
(*)
Есептің шарты
бойынша  , бұдан
, бұдан  ;
;
 , бұдан
, бұдан  болады.
болады.
 және
және  сандарын (*) теңдікке қойып,
сандарын (*) теңдікке қойып,  шығады, бұдан
шығады, бұдан  . Осылайша, ізделінді қалдық
. Осылайша, ізделінді қалдық  болады.
болады.
7.
 көпмүшесін
көпмүшесін
 -ге бөлгенде бөлінді мен
қалдық шығады. Бөліндідегі
-ге бөлгенде бөлінді мен
қалдық шығады. Бөліндідегі  коэффициентін табу.
коэффициентін табу.
 көпмүшесін көбейткіштерге
жіктеуге болады, ол
көпмүшесін көбейткіштерге
жіктеуге болады, ол  болады. Осы көпмүше
болады. Осы көпмүше  көпмүшесінің бөлгіші болатыны көрініп тұр.
Яғни
көпмүшесінің бөлгіші болатыны көрініп тұр.
Яғни

 көпмүшесін
көпмүшесін
 -ге бөлу
-ге бөлу
 көпмүшесін
көпмүшесін
 -ге бөліп,
нәтижесін
-ге бөліп,
нәтижесін  -ге көбейткенмен бірдей
болады.
-ге көбейткенмен бірдей
болады.
 екенін оңай көруге болады, ол
үшін берілген көпмүшелерді «бұрыштап» бөлуге немесе
екенін оңай көруге болады, ол
үшін берілген көпмүшелерді «бұрыштап» бөлуге немесе
 екенін байқап, жұп дәрежелі
екі бірмүшенің айырмасын дәреже негізінің айырмасына бөлу
формуласын қолдануға болады. Осыдан, ізделінді
коэффициент
екенін байқап, жұп дәрежелі
екі бірмүшенің айырмасын дәреже негізінің айырмасына бөлу
формуласын қолдануға болады. Осыдан, ізделінді
коэффициент  көбейтіндісіндегі
көбейтіндісіндегі  коэффициенті болатын
коэффициенті болатын  -ге тең болатыны шығады.
-ге тең болатыны шығады.
8.
 тепе-теңдігі орындалатын
барлық
тепе-теңдігі орындалатын
барлық  көпмүшелерін табу.
көпмүшелерін табу.
Есептің шартында
берілген тепе-теңдіктен ізделінді  (мұндағы п
–
көпмүшенің дәрежесі) көпмүшесі х-ке бөлінетіндігі шығады,
яғни
(мұндағы п
–
көпмүшенің дәрежесі) көпмүшесі х-ке бөлінетіндігі шығады,
яғни
 , мұндағы
, мұндағы  –
–  дәрежелі қандай да бір жаңа көпмүше.
Сондықтан
дәрежелі қандай да бір жаңа көпмүше.
Сондықтан  және
және  болады, осыдан
болады, осыдан  көпмүшесі
көпмүшесі  -ге бөлінеді, яғни
-ге бөлінеді, яғни  (
( -ге
-ге  бөлінеді). Онда
бөлінеді). Онда  болады және
болады және  шығады, бұдан
шығады, бұдан  көпмүшесі
көпмүшесі  -ге де бөлінетіндігі шығады (яғни
-ге де бөлінетіндігі шығады (яғни  көпмүшесі
көпмүшесі  -ге бөлінеді), яғни
-ге бөлінеді), яғни  . Осы
. Осы  мәнін берілген қатынасқа қою арқылы
мәнін берілген қатынасқа қою арқылы  көпмүшесінің
көпмүшесінің  -ке де бөлінетіндігін көреміз, яғни
-ке де бөлінетіндігін көреміз, яғни  болады және т.с.с.
болады және т.с.с.
Осы әдісті жалғастыра
берсек, соңында  көпмүшесінің келесідей түріне
келеміз:
көпмүшесінің келесідей түріне
келеміз:

Берілген
тепе-теңдікке  көпмүшесінің осы өрнегін қою
арқылы
көпмүшесінің осы өрнегін қою
арқылы

аламыз,
бұдан  дәрежелі
дәрежелі  көпмүшесі үшін
көпмүшесі үшін
 (*)
(*)
Егер  – дәрежесі нөлге тең көпмүше (сан!) болса, онда (*)
тепе-теңдігі орындалады; ол тек бір ғана жағдайда орындалатынын
көрсетейік. Расында да, егер
– дәрежесі нөлге тең көпмүше (сан!) болса, онда (*)
тепе-теңдігі орындалады; ол тек бір ғана жағдайда орындалатынын
көрсетейік. Расында да, егер  болса, онда (*) тепе-теңдігінің
болса, онда (*) тепе-теңдігінің  екі жағындағы
екі жағындағы  коэффициенттерін теңестіре отырып, Ньютон биномы
бойынша
коэффициенттерін теңестіре отырып, Ньютон биномы
бойынша  немесе
немесе  аламыз,
аламыз,  саны
саны  ұйғарымына қайшы келеді. Осылайша,
ұйғарымына қайшы келеді. Осылайша,  және
және
 – 26-шы дәрежелі көпмүше.
– 26-шы дәрежелі көпмүше.
9.  а) натурал
а) натурал  коэффициенттері бар; ә) бүтін
коэффициенттері бар; ә) бүтін  коэффициенттері бар көпмүшесі берілген;
коэффициенттері бар көпмүшесі берілген;
 санының цифрларының
қосындысын
санының цифрларының
қосындысын  деп белгілейік.
деп белгілейік.  тізбегінде шексіз көп сан болса, онда оның құрамында шексіз
көп бірдей сандар болатынын дәлелдеу
керек.
тізбегінде шексіз көп сан болса, онда оның құрамында шексіз
көп бірдей сандар болатынын дәлелдеу
керек.
а)  көпмүшесінің коэффициенттерінің барлығы теріс емес сандар
болса, онда
көпмүшесінің коэффициенттерінің барлығы теріс емес сандар
болса, онда  сандарының барлығы бар болады. Онның
сандарының барлығы бар болады. Онның
 түріндегі дәрежесін
қарастырайық, мұндағы N
–
түріндегі дәрежесін
қарастырайық, мұндағы N
–  көпмүшесінің
көпмүшесінің  коэффициенттерінен артық сан. Онда көпмүшенің
коэффициенттерінен артық сан. Онда көпмүшенің
 коэффициенті қандай цифрлармен
жазылса,
коэффициенті қандай цифрлармен
жазылса,  саны сол цифрлардан басталады; сонан соң (мүмкін бірнеше
нөлден кейін)
саны сол цифрлардан басталады; сонан соң (мүмкін бірнеше
нөлден кейін)  санының цифрлары жазылады; сонан соң (мүмкін тағы да
бірнеше нөлден кейін) –
санының цифрлары жазылады; сонан соң (мүмкін тағы да
бірнеше нөлден кейін) –  санының цифрлар және
санының цифрлар және  санына дейін т.с.с. жалғасады; сондықтан
санына дейін т.с.с. жалғасады; сондықтан
 саны
саны  сандарының барлық цифрларының қосындысына тең болады.
Осы S
санына
сандарының барлық цифрларының қосындысына тең болады.
Осы S
санына  шамалары да тең болады, осыдан
шамалары да тең болады, осыдан  тізбегінде S
саны
шексіз көп рет кездеседі деген қорытынды
шығады.
тізбегінде S
саны
шексіз көп рет кездеседі деген қорытынды
шығады.
ә)  көпмүшесінің ең үлкен коэффициенті теріс сан болса,
онда
көпмүшесінің ең үлкен коэффициенті теріс сан болса,
онда  сандарының арасында тек қана теріс сандар болатыны анық.
Олай болса, тек қана
сандарының арасында тек қана теріс сандар болатыны анық.
Олай болса, тек қана  жағдайын қарастыру қалды. Бірақ бұл жағдайда
жағдайын қарастыру қалды. Бірақ бұл жағдайда
 саны бар болады,
егер
саны бар болады,
егер  «жылжытылған» көпмүшенің коэффициенттерінің барлығы оң сан
болса. Осыдан
«жылжытылған» көпмүшенің коэффициенттерінің барлығы оң сан
болса. Осыдан  сандарының цифрларының қосындысынан тұратын
сандарының цифрларының қосындысынан тұратын
 тізбегінде шексіз көп бірдей
сандар болады және
тізбегінде шексіз көп бірдей
сандар болады және  болатындықтан,
болатындықтан,  тізбегінде де шексіз көп бірдей сандар болады деген
қорытынды шығады.
тізбегінде де шексіз көп бірдей сандар болады деген
қорытынды шығады.
Енді, жоғарыда жазылған
ұйғарымды дәлелдеу керек. Бірақ егер  боса, онда Ньютон биномы бойынша
боса, онда Ньютон биномы бойынша  болады. Осылайша,
болады. Осылайша,  ең үлкен коэффициенті
ең үлкен коэффициенті  болатын М-ге қатысты
болатын М-ге қатысты
 дәрежелі көпмүше түрінде
болады; сондықтан барлық
дәрежелі көпмүше түрінде
болады; сондықтан барлық  (мұндағы
(мұндағы  және
және  ) М-нің үлкен мәнінде оң мәнге ие
болады, дәлелдеу керегі осы.
) М-нің үлкен мәнінде оң мәнге ие
болады, дәлелдеу керегі осы.
10.  көпмүшесін
көпмүшесін  көбейтіндісі болатындай х
айнымалысы және у
айнымалысынан құралған екі көпмүше арқылы өрнектеуге
болмайтынын дәлелдеу керек.
көбейтіндісі болатындай х
айнымалысы және у
айнымалысынан құралған екі көпмүше арқылы өрнектеуге
болмайтынын дәлелдеу керек.
 және
және
 көпмүшелерінің
көпмүшелерінің
 (яғни
(яғни  ) және
) және  бос мүшелері болсын. Айталық,
бос мүшелері болсын. Айталық,  тепе-теңдігінде х
айнымалысы 0-ге тең болсын, онда
тепе-теңдігінде х
айнымалысы 0-ге тең болсын, онда  болады, яғни
болады, яғни  ; осылайша,
; осылайша,  барлық у
үшін
барлық у
үшін  -ге тең болады, яғни
-ге тең болады, яғни  тұрақты сан болады (нөлінші дәрежелі көпмүше). Дәл
осылайша
тұрақты сан болады (нөлінші дәрежелі көпмүше). Дәл
осылайша  екені оңай дәлелденеді, яғни
екені оңай дәлелденеді, яғни  . Алынған қарама-қайшылық есептің ұйғарымын
дәлелдейді.
. Алынған қарама-қайшылық есептің ұйғарымын
дәлелдейді.
11.  теңдеуінің (нақты) түбірлері болмайтындай
етіп
теңдеуінің (нақты) түбірлері болмайтындай
етіп  квадрат үшмүше берілген.
квадрат үшмүше берілген.  теңдеуінің де нақты түбірлері болмайтынын
дәлелдеңдер.
теңдеуінің де нақты түбірлері болмайтынын
дәлелдеңдер.
 (квадрат) теңдеуінің
нақты түбірлері болмайтындықтан,
(квадрат) теңдеуінің
нақты түбірлері болмайтындықтан,  квадрат үшмүше х-тің барлық мәнінде бірдей
таңбаның мәніне ие болады. Бірақ мұндай жағдайда кез
келген
квадрат үшмүше х-тің барлық мәнінде бірдей
таңбаның мәніне ие болады. Бірақ мұндай жағдайда кез
келген  үшін
үшін  , яғни
, яғни  болады және ұйғарым бойынша
болады және ұйғарым бойынша  , яғни
, яғни  болғандықтан,
болғандықтан,
 болады, осыдан
болады, осыдан  саны
саны  (4-ші дәрежелі) теңдеудің түбірі бола алмайды деген
қорытынды шығады.
(4-ші дәрежелі) теңдеудің түбірі бола алмайды деген
қорытынды шығады.
 деп есептейік, олай
болмаса,
деп есептейік, олай
болмаса,  көпмүшесін (берілген шарттарды
қанағаттандыратын)
көпмүшесін (берілген шарттарды
қанағаттандыратын)  көпмүшесіне алмастырамыз. Дәл солай
көпмүшесіне алмастырамыз. Дәл солай  деп есептейік, олай болмаса,
деп есептейік, олай болмаса,  көпмүшесін (берілген шарттарды
қанағаттандыратын)
көпмүшесін (берілген шарттарды
қанағаттандыратын)  көпмүшесіне алмастырамыз. Енді
көпмүшесіне алмастырамыз. Енді  мәндерін
мәндерін  теңсіздігіне қойып,
теңсіздігіне қойып,  аламыз, яғни
аламыз, яғни  болады. Сонан соң егер
болады. Сонан соң егер  болса, онда (
болса, онда ( болғанда)
болғанда)
 болады, осыдан
болады, осыдан  және
және  , бұдан
, бұдан
 шығады. Дәл осылай
шығады. Дәл осылай  үшін
үшін  болғанда
болғанда  және
және  , бұдан
, бұдан  шығады.
шығады.
12. Егер
 саны –
саны –  теңдеуінің түбірі, ал
теңдеуінің түбірі, ал  саны
саны  теңдеуінің түбірі болса, онда олардың арасында жататын,
яғни
теңдеуінің түбірі болса, онда олардың арасында жататын,
яғни
 немесе
немесе  және
және  теңдеуінің түбірі болатын
теңдеуінің түбірі болатын  саны табылатынын дәлелдеу
керек.
саны табылатынын дәлелдеу
керек.
Берілген үш теңдеу де бірінші
дәрежелі теңдеу болып шығатын, яғни бір-бірімен сәйкес келетін
бірдей түбірі (мұнда  ) бар болатын
) бар болатын  болатын жағдайды және
болатын жағдайды және  болып, үш теңдеудің түбірлері
болып, үш теңдеудің түбірлері  болатын жағдайды
қарастырмаймыз.
болатын жағдайды
қарастырмаймыз.
Егер  болса, онда
болса, онда  болады, осылайша егер
болады, осылайша егер  болса, онда
болса, онда  болады.
болады.
Осыдан,
 және
және  шамаларының таңбалары әр түрлі болады. Яғни
шамаларының таңбалары әр түрлі болады. Яғни
 параболасының
параболасының
 және
және  нүктелері х
өсінің
екі жағында орналасады, бұдан параболада осы екі нүктенің арасында
жататын және х
өсін осы
нүктеде қиып өтетін, сондай-ақ үшінші теңдеудің ізделінді түбірі
болатын
нүктелері х
өсінің
екі жағында орналасады, бұдан параболада осы екі нүктенің арасында
жататын және х
өсін осы
нүктеде қиып өтетін, сондай-ақ үшінші теңдеудің ізделінді түбірі
болатын  нүктесі табылады деген қорытынды
шығады.
нүктесі табылады деген қорытынды
шығады.
13.  және
және  сандары
сандары  теңдеуінің түбірлері, ал
теңдеуінің түбірлері, ал  және
және  сандары
сандары  теңдеуінің түбірлері болсын.
теңдеуінің түбірлері болсын.  көбейтіндісін берілген теңдеулердің коэффициенттері арқылы
өрнектеу керек.
көбейтіндісін берілген теңдеулердің коэффициенттері арқылы
өрнектеу керек.
Егер  және
және  сандары
сандары  теңдеуінің түбірлері болса, онда
теңдеуінің түбірлері болса, онда  . Яғни
. Яғни  .
.
Бірақ  , яғни
, яғни

14. а)  өрнегі b
және с
бүтін
сандары бар
өрнегі b
және с
бүтін
сандары бар
 көбейтіндісіне жіктелетіндей а
санын
табу керек; ә) коэффициенттері бүтін сандар болатын төртінші
дәрежелі
көбейтіндісіне жіктелетіндей а
санын
табу керек; ә) коэффициенттері бүтін сандар болатын төртінші
дәрежелі  көпмүшесін коэффициенттері бүтін сандар болатын екі
көпмүшенің көбейтіндісі түрінде жазуға болатындай бір-біріне тең
болмайтын нөлден өзге a, b, c
бүтін
сандарын табу керек.
көпмүшесін коэффициенттері бүтін сандар болатын екі
көпмүшенің көбейтіндісі түрінде жазуға болатындай бір-біріне тең
болмайтын нөлден өзге a, b, c
бүтін
сандарын табу керек.
а) Айталық,
 болсын. Теңдіктің екі
жағында
болсын. Теңдіктің екі
жағында  деп алып,
деп алып,  теңдігін аламыз. Бұдан
теңдігін аламыз. Бұдан  .
.
а
және b
– бүтін
сандар болғандықтан,  және
және  да – бүтін сандар болады. Бірақ
да – бүтін сандар болады. Бірақ  саны екі бүтін санның көбейтіндісі ретінде тек қана бір
әдіспен жазылады:
саны екі бүтін санның көбейтіндісі ретінде тек қана бір
әдіспен жазылады:  . Сондықтан тек қана екі жағдай болуы
мүмкін:
. Сондықтан тек қана екі жағдай болуы
мүмкін:
-
 ; онда
; онда  , яғни
, яғни  :
:
 .
. -
 ; онда
; онда  , яғни
, яғни  :
:
 .
.
ә) Төртінші дәрежелі көпмүшені бірінші дәрежелі көпмүше мен үшінші дәрежелі көпмүшенің көбейтіндісі түрінде немесе екінші дәрежелі екі көпмүшенің көбейтіндісі түрінде өрнектеуге болады, сондықтан бізге екі жағдайды қарастыру керек:
А)  (*) (теңдіктің оң жағындағы бірінші
көбейткіштегі х-ке қатысты коэффициенттер
және екінші көбейткіштегі
(*) (теңдіктің оң жағындағы бірінші
көбейткіштегі х-ке қатысты коэффициенттер
және екінші көбейткіштегі  -ке қатысты коэффициенттер екеуі де 1-ге
немесе
-ке қатысты коэффициенттер екеуі де 1-ге
немесе  -ге тең болады, себебі бұл көбейткіштердің көбейтіндісі
болатын өрнектегі
-ге тең болады, себебі бұл көбейткіштердің көбейтіндісі
болатын өрнектегі  коэффициенті
коэффициенті  өрнегіндегі
өрнегіндегі  коэффициентіне, яғни 1-ге тең болу керек; ал
коэффициентіне, яғни 1-ге тең болу керек; ал
 теңдігін оң
жағын
теңдігін оң
жағын  -ге көбейту арқылы (*) түріне келтіруге
болады).
-ге көбейту арқылы (*) түріне келтіруге
болады).
(*) теңдігіне
тізбектеп  қойып және 1 саны көбейткіштерге тек қана екі түрлі әдіспен
көбейткіштерге жіктелетінін, яғни
қойып және 1 саны көбейткіштерге тек қана екі түрлі әдіспен
көбейткіштерге жіктелетінін, яғни
 екенін ескере отырып, әр түрлі
екенін ескере отырып, әр түрлі  төрт сан (0, a, b, c
сандары
әр түрлі екенін еске саламыз) тек қана екі мәнге ие бола
алады:
төрт сан (0, a, b, c
сандары
әр түрлі екенін еске саламыз) тек қана екі мәнге ие бола
алады:  және
және  , ал бұл мүмкін емес.
, ал бұл мүмкін емес.
Ә)  . Бұдан, жоғарыдағы әдіспен
. Бұдан, жоғарыдағы әдіспен  қойғанда
қойғанда  және
және
 көпмүшелері 1 немесе
көпмүшелері 1 немесе  мәндеріне ие болады. Бірақ
мәндеріне ие болады. Бірақ  квадрат үшмүше х-тің әр түрлі үш мәнінде
бірдей
квадрат үшмүше х-тің әр түрлі үш мәнінде
бірдей  мәніне ие бола алмайды (әйтпесе,
мәніне ие бола алмайды (әйтпесе,  квадрат теңдеуінің әр түрлі үш түбірі болар еді),
бұдан
квадрат теңдеуінің әр түрлі үш түбірі болар еді),
бұдан  төрт мәннің ішінен екеуінде бұл үшмүше 1 санының мәнін, ал
басқа екеуінде
төрт мәннің ішінен екеуінде бұл үшмүше 1 санының мәнін, ал
басқа екеуінде  санының мәнін қабылдайды.
санының мәнін қабылдайды.  және
және  мәні
мәні мәндерінің ішінен бұл үшмүше 1 санының мәнін қабылдайтын
дәл сол болсын; бұл жағдайда
мәндерінің ішінен бұл үшмүше 1 санының мәнін қабылдайтын
дәл сол болсын; бұл жағдайда  және
және  мәндерінде бұл үшмүше
мәндерінде бұл үшмүше  санының мәнін қабылдайды.
Сонымен:
санының мәнін қабылдайды.
Сонымен:

 теңдігінен
теңдігінен
 екені шығады (себебі ұйығарым
бойынша
екені шығады (себебі ұйығарым
бойынша  ). Осылайша, соңғы екі теңдік
). Осылайша, соңғы екі теңдік  түріне келеді. Бірінші теңдіктен екінші теңдікті
азайтып,
түріне келеді. Бірінші теңдіктен екінші теңдікті
азайтып,  аламыз, бұдан
аламыз, бұдан  болғандықтан,
болғандықтан,  аламыз. Енді
аламыз. Енді  теңдігінен b,c
және а
үшін
мынадай мәндер табылады:
теңдігінен b,c
және а
үшін
мынадай мәндер табылады:




Осыған ұқсас,
егер  үшмүшесі
үшмүшесі  және
және  мәндерінде
мәндерінде  мәніне,
мәніне,  және
және  мәндерінде
мәндерінде  мәніне ие болса, онда:
мәніне ие болса, онда:
 ,
бұдан
,
бұдан


Осылайша, a, b, c үшін мүмкін болатын тағы екі жүйе аламыз:




15. Бір-бірінен әр түрлі
қандай  бүтін сандары үшін
бүтін сандары үшін
а)  ; ә)
; ә)  көпмүшелері басқа көпмүшелердің көбейтіндісіне жіктеледі
ме?
көпмүшелері басқа көпмүшелердің көбейтіндісіне жіктеледі
ме?
а)  деп алайық, мұндағы
деп алайық, мұндағы  пен
пен  – дәрежелерінің қосындысы п-ге тең бүтін коэффициенттері
бар көпмүшелер; осы екі көпмүшенің ең үлкен коэффициенті
– дәрежелерінің қосындысы п-ге тең бүтін коэффициенттері
бар көпмүшелер; осы екі көпмүшенің ең үлкен коэффициенті
1-ге тең деп есептейміз (алдыңғы есеппен салыстырыңдар). Осы
теңдікке
 мәндерін қойып және
мәндерін қойып және  саны екі бүтін көбейткіштерге бір ғана тәсілмен
жіктелетінін:
саны екі бүтін көбейткіштерге бір ғана тәсілмен
жіктелетінін:  ескере отырып,
ескере отырып,  аламыз. Осылайша,
аламыз. Осылайша,  қосындысы
қосындысы
 үшін нөлге тең екенін көреміз. Сонымен,
үшін нөлге тең екенін көреміз. Сонымен,
 теңдеуінің
түбірлері
теңдеуінің
түбірлері  болады, бұдан
болады, бұдан
 көпмүшесі
көпмүшесі  бөлінеді, яғни
бөлінеді, яғни
 көбейтіндісіне де бөлінетіндігі шығады. Бірақ
көбейтіндісіне де бөлінетіндігі шығады. Бірақ
 теңдеуінің
дәрежесі
теңдеуінің
дәрежесі  көпмүшелерінің ең үлкен дәрежесіне тең және
п-нен кем
(п саны –
көпмүшелерінің ең үлкен дәрежесіне тең және
п-нен кем
(п саны –  өрнегінің дәрежесі). Осыдан
өрнегінің дәрежесі). Осыдан  қосындысы
қосындысы  көбейтіндісіне жіктелмейтіні шығады, яғни біз ұйғарған
көбейткіштерге жіктеу мүмкін емес.
көбейтіндісіне жіктелмейтіні шығады, яғни біз ұйғарған
көбейткіштерге жіктеу мүмкін емес.
ә)  деп алайық, мұндағы
деп алайық, мұндағы  пен
пен  – ең үлкен дәрежелері 1-ге тең бүтін коэффициенттері бар
көпмүшелер. Осы теңдікке
– ең үлкен дәрежелері 1-ге тең бүтін коэффициенттері бар
көпмүшелер. Осы теңдікке  мәндерін қойып, әрбір қарастырған жағдайда
мәндерін қойып, әрбір қарастырған жағдайда
 немесе
немесе
 болатынын көреміз.
Осылайша,
болатынын көреміз.
Осылайша,  айырмасы
айырмасы
х-тің әр түрлі мәндерінде нөлге
айналатынын көреміз. Осыдан, біріншіден,  , екіншіден, п
саны –
жұп:
, екіншіден, п
саны –
жұп:  , мұндағы
, мұндағы
k
–  көпмүшелерінің әрқайсысының дәрежесі. Енді
теңдікті
көпмүшелерінің әрқайсысының дәрежесі. Енді
теңдікті
 немесе
немесе  түрінде жазайық.
түрінде жазайық.
Сонымен,
 және
және  көпмүшелерінің көбейтіндісі
көпмүшелерінің көбейтіндісі  кезінде нөлге айналады. Яғни х-тің әрбір мәнінде
көбейткіштердің ең болмағанда біреуі нөлге айналады,
бұдан
кезінде нөлге айналады. Яғни х-тің әрбір мәнінде
көбейткіштердің ең болмағанда біреуі нөлге айналады,
бұдан  немесе
немесе  көпмүшелерінің біреуі
көпмүшелерінің біреуі  екімүшесіне бөлінеді немесе
екімүшесіне бөлінеді немесе  немесе
немесе  көпмүшелерінің біреуі
көпмүшелерінің біреуі  екімүшесіне бөлінеді т.с.с. деген қорытынды
шығады. k
дәрежелі
көпмүше
екімүшесіне бөлінеді т.с.с. деген қорытынды
шығады. k
дәрежелі
көпмүше  түріндегі әр түрлі өрнектердің
түріндегі әр түрлі өрнектердің
k санынан артық көбейтіндісіне
бөлінбейтіндіктен және ең үлкен коэффициенті 1-ге тең
k дәрежелі көпмүше
 түріндегі
өрнектің k
санына
бөлінетіндіктен,
түріндегі
өрнектің k
санына
бөлінетіндіктен,  көпмүшесі соңғы теңдіктің сол жағындағы
2k көбейткіштердің
k көбейтіндісіне,
ал
көпмүшесі соңғы теңдіктің сол жағындағы
2k көбейткіштердің
k көбейтіндісіне,
ал  көпмүшесі қалған
k көбейтіндісіне тең
болады.
көпмүшесі қалған
k көбейтіндісіне тең
болады.
Айталық,
 деп алайық. Бірінші теңдіктен
екінші теңдікті азайтып,
деп алайық. Бірінші теңдіктен
екінші теңдікті азайтып,  . Осы теңдікке
. Осы теңдікке  қойып, 2 санының k
бүтін
көбейткішке жіктелуін аламыз:
қойып, 2 санының k
бүтін
көбейткішке жіктелуін аламыз:  .
.
2 санын әр түрлі үш
көбейткіштен артық көбейткіштерге жіктеу мүмкін емес,
сондықтан  екені белгілі болады. Бірақ
екені белгілі болады. Бірақ  болған жағдай да келесідей себеп үшін мүмкін емес. 2 саны
әр түрлі үш көбейткішке тек қана бір тәсілмен
жіктеледі:
болған жағдай да келесідей себеп үшін мүмкін емес. 2 саны
әр түрлі үш көбейткішке тек қана бір тәсілмен
жіктеледі:  .
.  деп алайық. Онда
деп алайық. Онда  , мұндағы
, мұндағы  және сәйкесінше
және сәйкесінше  .
.  мәнін
мәнін
 формуласына қойып, 2 санының басқа үш көбейткішке жіктелуін
аламыз:
формуласына қойып, 2 санының басқа үш көбейткішке жіктелуін
аламыз:  , мұндағы
, мұндағы  . Бұдан
. Бұдан  болады, яғни
болады, яғни  , ал ол есептің шартына қайшы
келеді.
, ал ол есептің шартына қайшы
келеді.
Сонымен, екі жағдай ғана болуы
мүмкін:  .
.
 . Егер
. Егер
 болса, онда:
болса, онда:
 , бұдан
, бұдан
 және
және  -ді а
арқылы
өрнектеп,
-ді а
арқылы
өрнектеп,  .
.
 . Егер
. Егер
 болса, онда:
болса, онда:
 болады, мұндағы
болады, мұндағы
 . Соңғы теңдікке
. Соңғы теңдікке
 және
және  қойып,
қойып,

 аламыз.
аламыз.
Бірақ 2 санын кему ретімен
орналасқан екі көбейткішке тек қана екі тәсілмен жіктеуге
болады:  және
және  . Сонымен қатар
. Сонымен қатар
 , сондықтан
, сондықтан  болады, бұдан
болады, бұдан  -ді а
арқылы
өрнектеп,
-ді а
арқылы
өрнектеп,  және
және  аламыз.
аламыз.
16. * Әр түрлі
 бүтін сандары
үшін
бүтін сандары
үшін  көпмүшесі бүтін коэффициенттері бар екі әр түрлі
көпмүшелердің көбейтіндісіне жіктелетінін
дәлелдеу.
көпмүшесі бүтін коэффициенттері бар екі әр түрлі
көпмүшелердің көбейтіндісіне жіктелетінін
дәлелдеу.
Алдыңғы есептің шешуіне
сәйкес  (*) ұйғарымынан
(*) ұйғарымынан  үшін
үшін
 немесе
немесе  болады, мұндағы
болады, мұндағы  – бүтін коэффициенттері бар қандай да бір
көпмүшелер.
– бүтін коэффициенттері бар қандай да бір
көпмүшелер.  көпмүшесі (әрине
көпмүшесі (әрине  көпмүшесі де)
көпмүшесі де)  барлық мәндерінде 1-ге тең болатынын немесе
барлық мәндерінде 1-ге тең болатынын немесе
 -ге тең болатынын
көрсетейік.
-ге тең болатынын
көрсетейік.
Расында да, егер
де  көпмүшесі
көпмүшесі
 мәнінде 1-ге тең,
ал
мәнінде 1-ге тең,
ал  мәнінде
мәнінде
 -ге тең болса,
онда
-ге тең болса,
онда  мен
мен  аралығындағы х-тің қандай да бір мәнінде
нөлге айналар еді (егер
аралығындағы х-тің қандай да бір мәнінде
нөлге айналар еді (егер  функциясының графигі
функциясының графигі  кезінде Ох
өсінен
жоғары, ал
кезінде Ох
өсінен
жоғары, ал  кезінде Ох
өсінен
төмен орналасатын болса, онда
кезінде Ох
өсінен
төмен орналасатын болса, онда  үзіліссіз қисығы Ох
өсін
үзіліссіз қисығы Ох
өсін  мен
мен  арасында қиып өтеді), ал бұл мүмкін емес, себебі (*)
теңдігінің сол жағы ылғи да 1-ге тең немесе 1-ден артық
болғандықтан нөлге айналмайды.
арасында қиып өтеді), ал бұл мүмкін емес, себебі (*)
теңдігінің сол жағы ылғи да 1-ге тең немесе 1-ден артық
болғандықтан нөлге айналмайды.
 те,
те,
 те
те  мәндерінде 1-ге тең болады делік. Бұл
жағдайда
мәндерінде 1-ге тең болады делік. Бұл
жағдайда  де,
де,  де
де  мәндерінде нөлге айналады, яғни
мәндерінде нөлге айналады, яғни  және
және  көпмүшелері
көпмүшелері  -ге бөлінеді.
-ге бөлінеді.  және
және  көпмүшелерінің дәрежелерінің қосындысы
көпмүшелерінің дәрежелерінің қосындысы
 дәрежесіне, яғни
дәрежесіне, яғни
 -ге тең
болғандықтан,
-ге тең
болғандықтан,  және
және  болады (алдыңғы есептің шешуімен
салыстырыңдар).
болады (алдыңғы есептің шешуімен
салыстырыңдар).
Осылайша,
 , бұдан
, бұдан
 болады, ал ол мүмкін
емес.
болады, ал ол мүмкін
емес.  және
және  көпмүшелері
көпмүшелері  нүктелерінде
нүктелерінде  мәнін қабылдай алмайды (бұл жағдайда
мәнін қабылдай алмайды (бұл жағдайда шығар еді).
шығар еді).
Сонымен,
 өрнегін коэффициенттері бүтін
сан болатын екі көпмүшенің көбейтіндісіне жіктеу мүмкін емес екенін
көреміз.
өрнегін коэффициенттері бүтін
сан болатын екі көпмүшенің көбейтіндісіне жіктеу мүмкін емес екенін
көреміз.
17. Коэффициенттері бүтін сан
болатын  көпмүшесі х-тің жұп мәндерінде 7-ге тең
болса, х-тің ешбір бүтін мәнінде 14-ке
тең бола алмайтынын дәлелдеу керек.
көпмүшесі х-тің жұп мәндерінде 7-ге тең
болса, х-тің ешбір бүтін мәнінде 14-ке
тең бола алмайтынын дәлелдеу керек.
 көпмүшесі
көпмүшесі
 мәндерінде 7-ге тең болсын.
Олай болса,
мәндерінде 7-ге тең болсын.
Олай болса,  теңдеуінің төрт бүтін түбірі бар:
теңдеуінің төрт бүтін түбірі бар:  . Бұдан
. Бұдан  көпмүшесі
көпмүшесі  -ға бөлінетіндігі шығады, яғни
-ға бөлінетіндігі шығады, яғни  болады, мұндағы
болады, мұндағы  мәні 1-ге тең бола алады.
мәні 1-ге тең бола алады.
Ендігі кезекте
 көпмүшесі
көпмүшесі
 бүтін мәнінде 14-ке тең болады
делік.
бүтін мәнінде 14-ке тең болады
делік.  мәнін соңғы теңдікке қойып,
мәнін соңғы теңдікке қойып,  аламыз, ал бұл мүмкін емес, себебі
аламыз, ал бұл мүмкін емес, себебі  бүтін сандарының барлығы әр түрлі, ал 7 санын ең болмағанда
төртеуі бір-біріне тең болмайтын әр түрлі бес санның көбейтіндісі
ретінде жіктеуге болмайды.
бүтін сандарының барлығы әр түрлі, ал 7 санын ең болмағанда
төртеуі бір-біріне тең болмайтын әр түрлі бес санның көбейтіндісі
ретінде жіктеуге болмайды.
18. Бүтін коэффициенттері
бар  көпмүшесі
х-тің 7 бүтін
мәнінде
көпмүшесі
х-тің 7 бүтін
мәнінде  және
және  мәндеріне тең болса, онда оны бүтін коэффициенттері бар екі
көпмүшенің көбейтіндісі ретінде жіктеуге болмайтынын дәлелдеу
керек.
мәндеріне тең болса, онда оны бүтін коэффициенттері бар екі
көпмүшенің көбейтіндісі ретінде жіктеуге болмайтынын дәлелдеу
керек.
Егер жетінші
дәрежелі  көпмүшесі бүтін коэффициентті
көпмүшесі бүтін коэффициентті  және
және  екі көпмүшенің көбейтіндісіне жіктелсе, онда
көбейткіштерінің біреуінің дәрежесі 3-тен артық болмайды; мұндай
көбейткіш
екі көпмүшенің көбейтіндісіне жіктелсе, онда
көбейткіштерінің біреуінің дәрежесі 3-тен артық болмайды; мұндай
көбейткіш  болсын. Егер
болсын. Егер  х-тің 7 бүтін
мәнінде
х-тің 7 бүтін
мәнінде  және
және  мәндеріне тең болса, онда
мәндеріне тең болса, онда  та х-тің 7 бүтін
мәнінде
та х-тің 7 бүтін
мәнінде  және
және  мәндеріне тең болады (себебі
мәндеріне тең болады (себебі  ).
). 
 мәніне тең
болатын х-тің бүтін жеті мәнінің
ішінен
мәніне тең
болатын х-тің бүтін жеті мәнінің
ішінен  1 санының мәніне тең болатындай төрт сан
немесе
1 санының мәніне тең болатындай төрт сан
немесе 
 санының мәніне тең болатындай
төрт сан табылады. Бірінші жағдайда үшінші дәрежелі
санының мәніне тең болатындай
төрт сан табылады. Бірінші жағдайда үшінші дәрежелі
 теңдеуінің төрт түбірі болады,
екінші жағдайда
теңдеуінің төрт түбірі болады,
екінші жағдайда  теңдеуінің төрт түбірі болады. Бірінші жағдай да, екінші
жағдай да орындалмайды, себебі бірінші жағдайда
теңдеуінің төрт түбірі болады. Бірінші жағдай да, екінші
жағдай да орындалмайды, себебі бірінші жағдайда
 төртінші дәрежелі көпмүшеге
бөліну керек еді.
төртінші дәрежелі көпмүшеге
бөліну керек еді.
19. Бүтін
коэффициентті  көпмүшесі
көпмүшесі  және
және  үшін тақ мәнге тең болса,
үшін тақ мәнге тең болса,  теңдеуінің a
рационал
түбірі болса, онда
теңдеуінің a
рационал
түбірі болса, онда  өрнегі 1 немесе 2-ге тең және
өрнегі 1 немесе 2-ге тең және  болатынын дәлелдеу керек.
болатынын дәлелдеу керек.
p
және q
– бір
мезгілде жұп немесе тақ екі бүтін сан болсын. Онда
 айырмасы жұп болады. Расында
да,
айырмасы жұп болады. Расында
да,  өрнегі
өрнегі  жұп өрнегіне бөлінеді.
жұп өрнегіне бөлінеді.
p
– жұп сан
болғанда,  жұп болады. Бірақ есептің шарты бойынша
жұп болады. Бірақ есептің шарты бойынша
 – тақ сан, яғни
– тақ сан, яғни
 да тақ сан болады, себебі
есептің шарты бойынша
да тақ сан болады, себебі
есептің шарты бойынша  тақ сан, осыдан
тақ сан, осыдан  екені шығады.
екені шығады.
Осылайша,
 көпмұшесі
х-тің ешбір бүтін мәнінде (жұп
болсын, тақ болсын) нөлге айнала алмайды, яғни
көпмұшесі
х-тің ешбір бүтін мәнінде (жұп
болсын, тақ болсын) нөлге айнала алмайды, яғни
 көпмүшесінің бүтін түбірлері
болмайды.
көпмүшесінің бүтін түбірлері
болмайды.
Айталық,
 теңдеуінің
теңдеуінің
 рационал түбірі болсын,
яғни
рационал түбірі болсын,
яғни
 .
.  көпмүшесін
көпмүшесін  дәрежелері бойынша жіктейік, яғни оны
дәрежелері бойынша жіктейік, яғни оны
 түрінде жазайық,
мұндағы
түрінде жазайық,
мұндағы  –
–  мәндері белгілі болған жағдайда оғай табылатын қандай да
бір сандар (
мәндері белгілі болған жағдайда оғай табылатын қандай да
бір сандар ( мәні
мәні  көпмүшесінің ең үлкен коэффициенті
көпмүшесінің ең үлкен коэффициенті  -ге тең,
-ге тең,  мәні
мәні  көпмүшесінің ең үлкен коэффициенті
көпмүшесінің ең үлкен коэффициенті  -ге тең,
-ге тең,  мәні
мәні  көпмүшесінің ең үлкен коэффициенті
көпмүшесінің ең үлкен коэффициенті  -ге тең, т.с.с.).
-ге тең, т.с.с.).  мәнін
мәнін  көпмүшесінің соңғы өрнегіне қойып,
көпмүшесінің соңғы өрнегіне қойып,  аламыз. Осы өрнекке
аламыз. Осы өрнекке  мәнін қойып, нәтижесін
мәнін қойып, нәтижесін  -не көбейтіп:
-не көбейтіп:

аламыз, бұдан
егер  болса, онда
болса, онда  бүтін сан болады. Бірақ
бүтін сан болады. Бірақ  көбейтіндісі l-ға бөлінетіндіктен,
ал k мен l – өзара жай сандар
болғандықтан (әйтпесе
көбейтіндісі l-ға бөлінетіндіктен,
ал k мен l – өзара жай сандар
болғандықтан (әйтпесе  бөлшегін қысқартуға болар еді), онда
бөлшегін қысқартуға болар еді), онда
 мен l – өзара жай сандар болады,
бұдан
мен l – өзара жай сандар болады,
бұдан  мен
мен  – өзара жай сандар болады деген қорытынды шығады.
Осыдан
– өзара жай сандар болады деген қорытынды шығады.
Осыдан  болған жағдайда ғана
болған жағдайда ғана  бүтін сан бола алатындығы
шығады.
бүтін сан бола алатындығы
шығады.
Дәл осылайша
 екенін
дәлелдейміз.
екенін
дәлелдейміз.
Енді  теңдігінен
теңдігінен  теңдігін азайтып,
теңдігін азайтып,  немесе
немесе  аламыз. Бірақ
аламыз. Бірақ  және
және  болғандықтан,
болғандықтан,
 болады, осыдан
болады, осыдан  .
.
Сонымен, егер
 болса, онда
болса, онда
 теңдеуінің рационал түбірлері
болмайды. Егер
теңдеуінің рационал түбірлері
болмайды. Егер  немесе
немесе  болса, онда
болса, онда  рационал түбірі бар болуы мүмкін. Осы жерде
рационал түбірі бар болуы мүмкін. Осы жерде
 теңдіктерін
қосып,
теңдіктерін
қосып,  аламыз. Дәлелдеу керегі
осы.
аламыз. Дәлелдеу керегі
осы.
3
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Дипломдық жұмыс, математика. "Көпмүшелер"
Дипломдық жұмыс, математика. "Көпмүшелер"
Өзін-өзі тексеру
Өзара тексеру
Сырттай тексеру
өзін-өзі тексеру
- өзі жасаған қателерінің пайда болу себептерін анықтау
- өзін-өзі тексеру
қателердің алдын алу
- мұғалімнің оқушылардың әрекетін тексеруі
- оқушылардың бір-бірін тексеруі
оқушылардың мұғалімнің әрекетін тексеруі
- өзін-өзі тексеруге деген қажеттіліктің қалыптасуы
- өзін-өзі тексеру тәсілдерінің мәнін түсіну
өзін-өзі тексеруді өткізу бойынша нұсқаулық
өзін-өзі басқарудың тікелей дамуы
өзін-өзі тексерудің жанама түрде дамуы
оқушыларды өзін-өзі тексеруге түрткі болу
Сырттай тексеру
МазмұныКіріспе
1. «Көпмүшелер» тақырыбының теориялық аспектілері
1.1 Көпмүшелер түсінігі
1.2 Бір айнымалысы бар көпмүшелер
1.3 Көпмүшелердің бөлінгіштік қасиеттері
1.4 Анықталмаған коэффициенттер әдісі
1.5 Көпмүшені көпмүшеге «бағандап» (немесе «бұрыштап») бөлу
1.6 Безу теоремасы және оның салдарлары
1.7 Көпмүшенің түбірлері туралы тұжырымдар
1.8 Көпмүшені көбейткіштерге жіктеу
1.9 Көпмүше сақинасы ұғымы
1.10 Көпмүшелерге қолданылатын амалдар
1.11 Көпмүшенің дәрежесі
1.12  екімүшесіне бөлу және көпмүшенің
түбірлері
екімүшесіне бөлу және көпмүшенің
түбірлері
1.13 Көпмүшенің бүтіндік аймағынан тыс түбірлерінің максимальды саны
1.14 Көпмүшелердің алгебралық және функционалдық теңдігі
1.15 Евклид алгоритмі. Екі көпмүшенің ЕҮОБ
1.16 Ең кіші ортақ еселік
1.17 Көпмүшенің формальды туындысы. Көпмүшенің келтірілмейтін еселіктері
1.18 Туындылардың қасиеттері
2. «Көпмүшелер» тақырыбын оқып үйрену кезіндегі әдістемелік және психологиялық-педагогикалық аспектілері
2.1 Тақырыпты оқып үйрену кезіндегі логикалық ойлауды дамыту
2.2 Тақырыпты оқыту кезіндегі қолданылатын әдістер
2.3 Практикалық сабақтарды өткізуге арналған әдістемелік ұсыныстар
2.4 Көпмүшелердің бөлінгіштік қасиеттерін қолдану
2.5 Безу теоремасы мен оның салдарларын оқып үйренудің әдістемесі
2.6 Көпмүшенің түбірлері туралы тұжырымды қолдану
2.7 Көпмүшені көбейткіштерге жіктеу әдістері
Қорытынды
Пайдаланылған әдебиеттер тізімі
Қосымшалар
Кіріспе
Математика пәнінен өтетін факультативтік сабақтардың басты мақсаты оқушылардың білімін тереңдету, пәнге деген қызығушылықтарын арттыру, математикалық қабілеттерін дамыту, математикамен өз бетімен шұғылдануға қызығушылықтарын нығайту, шығармашылықтарын дамыту болып табылады.
Орта мектепке арналған математика пәнінің негізгі курсының бағдарламасы мен математикадан факультативтік сабақтардың бағдарламасы берілген сынып оқушыларына арналған математика пәні бойынша жоғары деңгейдің бағдарламасын құрайды.
Математикадан факультативтік сабақтардың бағдарламасы математиканың негізгі курсымен қатар оқытуға болатындай етіп құрастырылған. Берілген сыныпта математиканың негізгі курсын бір мұғалім, ал факультативтік сабақтарды басқа мұғалім жүргізген жағдайда факультативтік курстың сабақтарын негізгі курс бағдарламасына тәуелсіз өткізуге болады (бұл жағдайда факультативтік курстың тақырыптарын негізгі курстың бағдарламасына қарағанда кейінірек өткізуге болады). Математика пәнінен өткізілетін факультативтік сабақтар нәтижелі болу үшін оларды төмендегідей жағдайлар жасалу керек:
-
жоғары білікті мұғалімдер немесе сабақтарды ғылыми-әдістемелік деңгейде өткізе алатын басқа мамандардың болуы;
-
берілген факультативтік курсты оқып үйренуге қызығушылығы бар 15-тен кем емес оқушы болуы.
Егер мектепте толымдылығы аз сыныптар болса (әсіресе ауылдық мектептерде), онда факультативтік сабақтарға қатысатын оқушылар тобын параллель сыныптардың оқушыларынан немесе көршілес сыныптардың (IX-X сыныптар, X-XI сыныптар, т.б.) оқушыларынан құрауға болады.
Факультативтік курсқа қатысатын оқушыларды қызығушылықтарына сай өз еріктерімен жазу керек. Оқушыларды міндетті түрде факультативтік сабақтарға қатысуға мәжбүрлемеу керек. Әсіресе математиканы оқып үйренуде қиындықтарға кезігетін оқушыларды немесе мектептен тыс уақытта басқа сабақтарға (спорт, музыка, сурет, т.б.) қатысатын оқушыларды мәжбүрлеуге болмайды.
Факультативтік курсты аяқтағаннан кейін оқушылар аттестатқа жазылатын сынақ тапсырады.
Математика пәнінің мұғалімі факультативтік сабақтардың сапасы үшін толық жауапкершілікті алады; факультативтік сабақтар сабақ кестесіне енгізіліп, мұғалімге еңбекақысы төленеді.
Математика пәнінен факультативтік сабақтарды өткізуде сыныптан тыс шаралардың басқа түрлерінен (математикалық үйірмелер, кештер, олимпиадалар, т.б.) бас тартуға болмайды. Бұл шаралар математикаға қызығушылығы бар оқушылармен жасалатын жұмыстарды толықтырып тұру керек.
Математикаға қызығушылығы мен қабілеттері бар оқушылармен аптасына қосымша 1-2 сағат жұмыстану үрдісі математиканы оқытудың жаңаша түрлерінің бірі – саралап оқытудың бір көрінісі. Факультативтік сабақтар шын мәнінде саралап оқытудың айрықша динамикалық түрі болып табылады.
Математикадан факультативтік сабақтарды өткізудің қандай түрі мен әдістері таңдалса да, сабақтар оқушыларға қызықты, тартымды болатындай етіп ұйымдастырылуы керек. Өз пәніңізге деген тұрақты қызығушылықты қалыптастыру үшін оқушының білім алуға деген табиғи құмарлығын пайдалану керек. Әйгілі француз физигі Луи де Бройль заманауи ғылым туралы «ғылымның үздіксіз дамуын қамтамасыз ететін үнемі жасырын қозғаушы күштері болып табылатын таңырқау мен әуестіктің қызы»деп жазды.
Қазіргі таңда математикадан факультативтік сабақтарды өткізудің негізгі түрлері ретінде факультативтік курстың түйінді сұрақтарын мұғалімнің түсіндіруі (дәріс әдісі), семинарлар, тілдесу (пікірталас), есептер шығару, оқушылардың рефераттары (теория және есептер шығару бойынша), математикалық шығармалар, оқушылардың баяндамалары, т.б. алуға болады.
Бірақ мұғалімге аталған әдістердің тек қана біреуін таңдап алуға болмайды. Алайда факультативтік сабақтарда басты назар оқушылардың өз бетімен жұмысына аударылуы керек екенін есте сақтай отырып, сабақтарды әр түрлі пікірталас, семинарлар, ғылыми-көпшілік әдебиеттерді оқу және т.б. түрлерінде де өткізуге болады.
Математика пәнінен факультативтік сабақтарды өткізудің бір тәсілі ретінде әрбір сабақты екі бөлімге бөліп өткізуге болады. Бірінші бөлім жаңа тақырыпты меңгеруге және оқушылардың теориялық, практикалық бағыттағы өзіндік жұмыстарына арналады. Сабақтың бірінші бөлімін аяқтағаннан кейін оқушыларға теория мен оның қосымшаларын оқуға бағытталған үй тапсырмасы беріледі. Әрбір сабақтың екінші бөлімі қиындығы жоғары есептерді шығаруға және мұндай аса күрделі есептерді талдауға арналады. Факультативтік сабақтарды өткізудің осындай түрі мектепте оқытудың түрлері мен әдістерінен жоғары оқу орындарындағы оқытудың түрлері мен әдістеріне сәтті түрде көшуге көмектеседі.
Факультативтік сабақтарды өткізуде математиканы оқып үйренудің (оқытудың емес) әдістерін, сонымен қатар проблемалық оқыту түрін қолдануға болады.
Проблемалық оқыту әдісін факультативтік курсты бірізді белгіленген міндеттердің жиыны ретінде ұсыну арқылы қолдануға болады. «Барлық міндеттерді өз бетімен немесе мұғалімнің аздаған көмегімен орындау арқылы оқушылар белсенділік пен дербестікті көрсете отырып және математикалық ойлау техникасын меңгере отырып берілген курсты өзінің тікелей қатысуымен оқып үйренеді. Теоремалар есеп түрінде беріледі. Егер оқушыларға дәлелдеуге берілген теорема үлкен немесе қиын болса, онда бұл теорема алдыңғы есептің шешімі келесі есепті шешуге көмектесетіндей етіп бірнеше есептерге бөлінеді. Анықтамаларды мұғалім есептің мәтініне қосады немесе бөлек айтылады. Қажет болған жағдайда мұғалім алдын ала кеңес өткізеді. Баспа құралы арқылы көбейтілген тапсырмалар жазылған парақтар әрбір сабақта барлық оқушыларға таратылады».
Сонымен қатар проблемалық есептерді шешу де пайдалы болады.
Қазіргі уақытта математикадан факультативтік сабақтарда екі негізгі бағытта өткізіледі:
а) «Математика курсының қосымша тараулары мен сұрақтары» бағдарламасы бойынша курстарды оқып үйрену;
б) арнайы математикалық курстарды оқып үйрену.
«Математика курсының қосымша тараулары мен сұрақтары» бағдарламасының мазмұны бағдарламаның материалын шығаруға және тереңдетіп оқуға, оқушыларды қазіргі заманғы математикалық идеялармен таныстыруға, мұғалімге жаңа бағдарламамен жұмыстануға дайындалуға мүмкіндік береді.
Берілген тақырыптың өзектілігі – ұғымдар мен формулалардың көптігінен және әр түрлі символдар арқылы белгіленулердің себебінен оқушыларға оқып үйренетін материалды түсіну қиындық туғызатыны. Бұның барлығы материалдың дұрыс меңгерілмеуіне әкеліп соғады. Сонымен қатар материалды меңгеруге бұл тақырыпқа бөлінген сағат саны да әсер етеді. Негізгі басымдық берілген материалды жан-жақты және терең оқып үйрену үшін сыныптан тыс, жеке және топтық сабақтарға беріледі.
Берілген дипломдық жұмыстың зерттеу объектісі – «Көпмүшелер» тақырыбын оқып үйренудің ұйымдастырылуы.
Зерттеу пәні – 10, 11-сыныптарда көпмүшелерді оқыту әдістемесі.
Мақсаты – берілген тақырыпты оқып үйренуге әдістемелік ұсыныстар.
Міндеттер:
-
10, 11-сыныптарда көпмүшелерді қолдануды зерттеу;
-
берілген тақырып бойынша өткізілетін сабақтарға әдістемелік ұсыныстар беру.
Зерттеу әдістері:
-
ғылыми, оқу әдебиеттерді талдау;
-
теориялық материалды жинақтау және жүйелеу;
-
әдістемелік жоспарларды жинақтау.
Берілген жұмыстың құрамы:
-
10-11 сыныптардағы алгебра және анализ бастамалары курсындағы «Көпмүшелер» тақырыбы бойынша теориялық мәліметтер.
-
Берілген тақырып аясында сыныптар тыс шараларды өткізу бойынша әдістемелік ұсыныстар.
Жұмыстың тәжірибелік маңыздылығы – жинақталған материал жас мұғалімдерге оқу үрдісін ұйымдастыруда, сонымен қатар педагогикалық ЖОО студенттеріне педагогикалық тәжірибеден өту кезінде қосымша, жеке және топтық сабақтарды ұйымдастыру мен өткізуде, математиканы оқытудың теориясы мен әдістемесін оқып үйрену үрдісінде пайдалы болады.
1. «Көпмүшелер» тақырыбының теориялық аспектілері
-
Көпмүшелер түсінігі
Бірмүше деп сандары мен әріптері тек қана екі амалмен – көбейту мен натурал дәрежеге шығару арқылы байланысқан алгебралық өрнек аталады.
Мысалы, төменде берілген әрбір алгебралық өрнек бірмүше болып табылады:
 .
.
Егер бірмүшенің құрамындағы барлық сандардың көбейтіндісін әріптердің алдынан, ал әрбір әріптің көбейтіндісі мен оның дәрежелерін осы әріптің натурал дәрежесі ретінде жазсақ, онда мұндай өзгертулерден кейін бірмүше стандарт түрде жазылды деп есептелінеді, ал оның сандық көбейтіндісі бірмүшенің коэффициенті деп аталады.
Бірмүшелерді көбейту үшін олардың коэффициенттерін көбейтіп, негізі бірдей дәрежелерді көбейту керек.
Бірмүшені дәрежеге шығару үшін оның коэффициентін осы дәрежеге шығарып, әрбір әріптің дәреже көрсеткішін бірмүшенің дәреже көрсеткішіне көбейту керек.
Көпмүше деп бірнеше бірмүшелердің алгебралық қосындысын айтады.
Көпмүшенің құрамындағы бірмүшелер көпмүшенің мүшелері деп аталады. Бірмүше дегеніміз көпмүшенің дербес түрі.
Стандарт түрде жазылған бірмүшелер бір-біріне сәйкес келетін немесе коэффициентімен ғана ерекшеленетін болса, онда мұндай бірмүшелер ұқсас бірмүшелер деп аталады.
Мысалы,
 – ұқсас
көпмүшелер.
– ұқсас
көпмүшелер.
Көпмүшенің ұқсас мүшелерін коэффициенттерін қосу арқылы біріктіруге болады; мұндай алмастыру ұқсас мүшелерді біріктіру деп аталады.
Алдына плюс таңбасы қойылған жақшаға алынған көпмүшені оның бірмүшелерінің алдында тұрған таңбаларын сақтай отырып жақшасыз жазуға болады.
Мысалы,
 .
.
Алдына минус таңбасы қойылған жақшаға алынған көпмүшені оның бірмүшелерінің алдында тұрған таңбаларын қарама-қарсы таңбаға ауыстыра отырып жақшасыз жазуға болады.
Мысалы,
 .
.
Екі көпмүшенің
қосындысы (айырмасы) деп коэффициенттері берілген
көпмүшелердің ұқсас мүшелерінің коэффициенттерінің қосындысына
(айырмасына) тең болатын көпмүшені айтады. Мысалы,
 және
және  көпмүшелерінің айырмасы
көпмүшелерінің айырмасы  күпмүшесі болады.
күпмүшесі болады.
Көпмүшелердің қосындысы мен айырмасын табу кезінде жоғарыда аталған жақшаларды ашу ережесін тәжірибеде жиі қолданады.
Көпмүшені бірмүшеге көбейту үшін көпмүшенің әрбір мүшесін бірмүшеге көбейтіп, шыққан бірмүшелерді қосу керек.
Көпмүшені көпмүшеге көбейту үшін бірінші көпмүшенің әрбір мүшесін екінші көпмүшенің әрбір мүшесіне көбейтіп, шыққан бірмүшелерді қосу керек.
Мысалы,
 .
.
Көпмүшелерге арналған дәрежесінің қасиеттері сандарға арналған дәреженің қасиеттерімен сәйкес келеді.
Мысалы,
 егер
егер  .
.
Көпмүшені екі немесе бірнеше көпмүшелердің көбейтіндісі ретінде жазу көпмүшені көбейткіштерге жіктеу деп аталады. Көпмүшені көбейткіштерге жіктеу үшін әр түрлі әдістер қолданылады: қысқаша көбейту формулалары, ортақ көбейткішті жақшаның сыртына шығару, топтау әдісі және т.б.
Көбейткіштерге жіктеу үшін қандай да бір әріпке (немесе өрнекке) қатысты төменде көрсетілген формула арқылы толық квадратты айыру әдісін қолдану тиімді болады:

Мысалы,
а)

б)

1.2 Бір айнымалысы бар көпмүшелер
х айнымалысына қатысты

түріндегі
 көпмүшесі
х-тің
дәрежесінің азаюы бойынша орналастырылған көпмүше
деп
аталады, мұндағы
көпмүшесі
х-тің
дәрежесінің азаюы бойынша орналастырылған көпмүше
деп
аталады, мұндағы  – нақты сандар және
– нақты сандар және  .
.
 сандары – оның
коэффициенттері,
сандары – оның
коэффициенттері,  бірмүшесі – үлкен
мүшесі, ал п саны көпмүшенің дәрежесі деп
аталады.
бірмүшесі – үлкен
мүшесі, ал п саны көпмүшенің дәрежесі деп
аталады.
Егер канондық түрде берілген көпмүшеде х-тің қандай да бір дәрежесі болмаса, онда сәйкес бірмүшенің коэффициенті нөлге тең болады.
Канондық түрде берілген екі көпмүшенің дәрежелері және х-тің бірдей дәрежелеріндегі коэффициенттер тең болса, онда мұндай көпмүшелер тепе-тең көпмүшелер деп аталады.
Мысал.  екімүшесінің кубы болатын
екімүшесінің кубы болатын  көпмүше берілген.
көпмүше берілген.  сандарын табыңдар.
сандарын табыңдар.
Шешуі. Екі көпмүшенің тепе-теңдігінің анықтамасын қолдана отырып, төмендегі жүйені аламыз:
 , бұдан
, бұдан
 .
.
Егер
 көпмүшелері
көпмүшелері

тепе-теңдігі
орындалатындай болса, онда  және
және  көпмүшелерінің әрқайсысы
көпмүшелерінің әрқайсысы  көпмүшесінің бөлгіші
деп
айтады. Мұнымен қоса
көпмүшесінің бөлгіші
деп
айтады. Мұнымен қоса  көпмүшесі
көпмүшесі  (немесе
(немесе  ) көпмүшесіне бөлінеді
(қалдықсыз) бөлінеді, сонда
) көпмүшесіне бөлінеді
(қалдықсыз) бөлінеді, сонда
 көпмүшесін
(сәйкесінше
көпмүшесін
(сәйкесінше  )
)  көпмүшесі
көпмүшесі  көпмүшесіне бөлгендегі бөлінді деп
айтады.
көпмүшесіне бөлгендегі бөлінді деп
айтады.
п
дәрежелі
көпмүше т
дәрежелі
көпмүшеге бөлінсе, онда бөлінді  дәрежелі көпмүше болады және бұл көпмүше жалғыз болады
деген дәлел бар.
дәрежелі көпмүше болады және бұл көпмүше жалғыз болады
деген дәлел бар.
Бұдан егер
п дәрежелі
 көпмүшесі
п дәрежелі
көпмүшесі
п дәрежелі
 көпмүшесіне бөлінетін болса,
онда
көпмүшесіне бөлінетін болса,
онда  , мұндағы
, мұндағы  , яғни бұл көпмүшелердің коэффициенттері пропорционал екені
шығады, мысалы, егер
, яғни бұл көпмүшелердің коэффициенттері пропорционал екені
шығады, мысалы, егер  көпмүшесі
көпмүшесі  көпмүшесіне бөлінетіні белгілі болса, онда
көпмүшесіне бөлінетіні белгілі болса, онда
 болады.
болады.
1.3 Көпмүшелердің бөлінгіштік қасиеттері
-
Егер
 көпмүшесі
көпмүшесі
 көпмүшесіне, ал
көпмүшесіне, ал
 көпмүшесі
көпмүшесі
 көпмүшесіне бөлінетін болса,
онда
көпмүшесіне бөлінетін болса,
онда  көпмүшесі
көпмүшесі  көпмүшесіне бөлінеді.
көпмүшесіне бөлінеді.
Мысалы,
 көпмүшесі
көпмүшесі
 көпмүшесіне бөлінеді,
сондықтан
көпмүшесіне бөлінеді,
сондықтан
 көпмүшесі
көпмүшесі  көпмүшесіне де бөлінеді.
көпмүшесіне де бөлінеді.
-
Егер
 және
және  көпмүшелері
көпмүшелері  көпмүшесіне бөлінсе, онда
көпмүшесіне бөлінсе, онда  және
және  көпмүшелері
көпмүшелері  көпмүшесіне бөлінеді, ал
көпмүшесіне бөлінеді, ал  көпмүшесі
көпмүшесі  көпмүшесіне бөлінеді.
көпмүшесіне бөлінеді.
Мысалы,
 және
және  көпмүшелерінің әрқайсысы
көпмүшелерінің әрқайсысы  көпмүшесіне бөлінеді, сондықтан
көпмүшесіне бөлінеді, сондықтан  және
және  көпмүшелерінің қосындысына тең
көпмүшелерінің қосындысына тең  көпмүшесі және айырмасына тең
көпмүшесі және айырмасына тең  көпмүшесі
көпмүшесі  көпмүшесіне бөлінеді, ал
көпмүшесіне бөлінеді, ал  және
және  көпмүшелерінің көбейтіндісіне тең
көпмүшелерінің көбейтіндісіне тең  көпмүшесі
көпмүшесі  көпмүшесіне бөлінеді.
көпмүшесіне бөлінеді.
-
Егер
 көпмүшесі
көпмүшесі
 көпмүшесіне бөлінсе,
онда
көпмүшесіне бөлінсе,
онда  көпмүшесінің кез келген
көпмүшесінің кез келген  көпмүшесіне көбейтіндісі
көпмүшесіне көбейтіндісі  көпмүшесіне бөлінеді.
көпмүшесіне бөлінеді.
Мысалы,
 көпмүшесі
көпмүшесі
 көпмүшесіне бөлінеді,
сондықтан
көпмүшесіне бөлінеді,
сондықтан  және
және  көпмүшелерінің көбетіндісіне тең
көпмүшелерінің көбетіндісіне тең  көбейтіндісі
көбейтіндісі  көпмүшесіне бөлінеді.
көпмүшесіне бөлінеді.
-
 және
және  көпмүшелері сонда және тек қана сонда бір-біріне бөлінеді,
егер
көпмүшелері сонда және тек қана сонда бір-біріне бөлінеді,
егер
 , мұндағы
, мұндағы
 болса.
болса.
Мысал.  көпмүшесі мен
көпмүшесі мен  көпмүшесі бір-біріне бөлінетіндігі және
көпмүшесі бір-біріне бөлінетіндігі және
 екені белгілі.
екені белгілі.
 көпмүшесін табу
керек.
көпмүшесін табу
керек.
Шешуі. 4-қасиет бойынша
 екені шығады.
екені шығады.
 болғандықтан,
болғандықтан,
 болады. Яғни
болады. Яғни
 .
.
-
Егер
 көпмүшесі
көпмүшесі
 екімүшесіне бөлінсе,
онда
екімүшесіне бөлінсе,
онда  және
және  көпмүшелерінің ең болмағанда біреуі
көпмүшелерінің ең болмағанда біреуі  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
Мысалы,
 көпмүшесі
көпмүшесі
 екімүшесіне бөлінетіндіктен
және
екімүшесіне бөлінетіндіктен
және
 болатындықтан,
болатындықтан,  көпмүшесі
көпмүшесі  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
 көпмүшесін
көпмүшесін
 көпмүшесіне
(
көпмүшесіне
( ) қалдықпен бөлу
дегеніміз
) қалдықпен бөлу
дегеніміз
 , мұндағы
, мұндағы

тепе-теңдігі
орындалатындай етіп  және
және  көпмүшелерін табуды айтады. Мұндағы
көпмүшелерін табуды айтады. Мұндағы  көпмүшесі – бөлінді, ал
көпмүшесі – бөлінді, ал  көпмүшесі қалдық деп
аталады.
көпмүшесі қалдық деп
аталады.
 көпмүшесі
көпмүшесі
 көпмүшесіне қалдықпен бөлінсе,
онда
көпмүшесіне қалдықпен бөлінсе,
онда
 орындалатындай
орындалатындай  және
және  көпмүшелерінің тек қана бір жұбы бар болады
және
көпмүшелерінің тек қана бір жұбы бар болады
және  .
.
Кез келген
 көпмүшесі
көпмүшесі
 көпмүшесіне
(
көпмүшесіне
( ) қалдықсыз немесе қалдықпен
бөлінеді. Бірінші жағдайда (қалдықсыз бөлуде) бөліндіні, ал екінші
жағдайда (қалдықпен бөлуде) бөлінді мен қалдықты
анықталмаған коэффициенттер әдісі
арқылы
табуға болады.
) қалдықсыз немесе қалдықпен
бөлінеді. Бірінші жағдайда (қалдықсыз бөлуде) бөліндіні, ал екінші
жағдайда (қалдықпен бөлуде) бөлінді мен қалдықты
анықталмаған коэффициенттер әдісі
арқылы
табуға болады.
1.4 Анықталмаған коэффициенттер әдісі
п
дәрежелі  көпмүшесі және т дәрежелі
көпмүшесі және т дәрежелі
 көпмүшесі (
көпмүшесі ( ) берілген.
) берілген.
Айталық,  (1) бөліндісі және
(1) бөліндісі және
 (2), мұндағы
(2), мұндағы  ,
,  және
және  сандары белгісіз
болсын.
сандары белгісіз
болсын.
Тепе-теңдікті жазайық:
 (3)
(3)
 және
және  көпмүшелерін көбейтіп, ұқсас
мүшелерді біріктіріп, (3)
тепе-теңдіктің оң жағында канондық түрде
жазылған п-ші дәрежелі көпмүше аламыз. Осы көпмүшенің және
көпмүшелерін көбейтіп, ұқсас
мүшелерді біріктіріп, (3)
тепе-теңдіктің оң жағында канондық түрде
жазылған п-ші дәрежелі көпмүше аламыз. Осы көпмүшенің және
 көпмүшесінің
х-тің бірдей
дәрежелеріндегі коэффициенттерді теңестіріп, п теңдеулер жүйесін
аламыз, осы жүйені шеше отырып
көпмүшесінің
х-тің бірдей
дәрежелеріндегі коэффициенттерді теңестіріп, п теңдеулер жүйесін
аламыз, осы жүйені шеше отырып  сандарын табамыз.
сандарын табамыз.
Егер  сандарының барлығы нөлге тең болып
шықса, онда
сандарының барлығы нөлге тең болып
шықса, онда  көпмүшесі
көпмүшесі  көпмүшесіне қалдықсыз бөлінетін
болады. Егер
көпмүшесіне қалдықсыз бөлінетін
болады. Егер  коэффициенттерінің ең болмағанда
біреуі нөлден өзге сан болса, онда
коэффициенттерінің ең болмағанда
біреуі нөлден өзге сан болса, онда  көпмүшесі
көпмүшесі  көпмүшесіне қалдықпен бөлінеді, бұл
жағдайда қалдықтың дәрежесі (2) теңдіктің оң жағындағы
коэффициенті нөлге тең емес х-ке қатысты бірмүшенің ең
үлкен дәрежесіне тең болады.
көпмүшесіне қалдықпен бөлінеді, бұл
жағдайда қалдықтың дәрежесі (2) теңдіктің оң жағындағы
коэффициенті нөлге тең емес х-ке қатысты бірмүшенің ең
үлкен дәрежесіне тең болады.
Мысал.  көпмүшесін
көпмүшесін  көпмүшесіне бөлу.
көпмүшесіне бөлу.
Шешуі.  көпмүшесі түріндегі бөліндіні
және
көпмүшесі түріндегі бөліндіні
және
 көпмүшесі
түрінде болатын қалдықты іздейміз.
көпмүшесі
түрінде болатын қалдықты іздейміз.
 тепе-теңдігі белгілі болады.
Жақшаларды ашып және ұқсас мүшелерді біріктіру арқылы
тепе-теңдігі белгілі болады.
Жақшаларды ашып және ұқсас мүшелерді біріктіру арқылы
 аламыз. х-тің бірдей дәрежелері
бар коэффициенттерді теңестіру арқылы төмендегі жүйені
аламыз:
аламыз. х-тің бірдей дәрежелері
бар коэффициенттерді теңестіру арқылы төмендегі жүйені
аламыз:
 , бұдан
, бұдан  .
.
Осыдан  , ал
, ал  , яғни
, яғни  .
.
Мысал.  көпмүшесін
көпмүшесін  көпмүшесіне бөлу.
көпмүшесіне бөлу.
Шешуі.  көпмүшесі түріндегі бөліндіні
және
көпмүшесі түріндегі бөліндіні
және  көпмүшесі түрінде
болатын қалдықты іздейміз.
көпмүшесі түрінде
болатын қалдықты іздейміз.  немесе
немесе  аламыз. х-тің бірдей дәрежелері
бар коэффициенттерді теңестіру арқылы төмендегі жүйені
аламыз:
аламыз. х-тің бірдей дәрежелері
бар коэффициенттерді теңестіру арқылы төмендегі жүйені
аламыз:
 , бұдан
, бұдан  .
.
Осыдан  , ал
, ал  , яғни
, яғни
 көпмүшесі
көпмүшесі  көпмүшесіне қалдықсыз бөлінеді
және
көпмүшесіне қалдықсыз бөлінеді
және  болады.
болады.
1.5 Көпмүшені көпмүшеге «бағандап» (немесе «бұрыштап») бөлу
Бұл әдісті
 көпмүшесін
көпмүшесін  көпмүшесіне бөлу мысалында
қарастырайық:
көпмүшесіне бөлу мысалында
қарастырайық:

 көпмүшесін
көпмүшесін
 көпмүшесіне
көпмүшесіне
 «бағандап» бөлудің жалпы
жағдайында
«бағандап» бөлудің жалпы
жағдайында  және
және  көпмүшелері х-тің кемімелі дәрежелері
түрінде орналасады. Сонан соң
көпмүшелері х-тің кемімелі дәрежелері
түрінде орналасады. Сонан соң  көпмүшесінің үлкен мүшесін
көпмүшесінің үлкен мүшесін  көпмүшесінің үлкен мүшесіне бөледі де,
көпмүшесінің үлкен мүшесіне бөледі де,
 бөлінді-көпмүшесінің үлкен
мүшесін алады, содан кейін
бөлінді-көпмүшесінің үлкен
мүшесін алады, содан кейін  бөлінді-көпмүшесінің үлкен мүшесін
бөлінді-көпмүшесінің үлкен мүшесін 
бөлгіш-көпмүшесіне көбейтіп, шыққан көпмүшені
 көпмүшесінен азайтады.
Азайтудың нәтижесінде дәрежесі п-нен кіші болатын белгілі
бір
көпмүшесінен азайтады.
Азайтудың нәтижесінде дәрежесі п-нен кіші болатын белгілі
бір  көпмүшесі
шығады.
көпмүшесі
шығады.
Егер
 көпмүшесінің
дәрежесі т-нен кіші болса, онда бөлу
үрдісі аяқталады да, бұл жағдайда
көпмүшесінің
дәрежесі т-нен кіші болса, онда бөлу
үрдісі аяқталады да, бұл жағдайда  көпмүшесі қалдық болады. Егер
көпмүшесі қалдық болады. Егер  көпмүшесінің дәрежесі т-нен артық
немесе т-ге тең болса, онда
көрсетілген бөлу үрдісі
көпмүшесінің дәрежесі т-нен артық
немесе т-ге тең болса, онда
көрсетілген бөлу үрдісі  көпмүшесі үшін жалғасады, яғни
көпмүшесі үшін жалғасады, яғни  көпмүшесінің үлкен мүшесін
көпмүшесінің үлкен мүшесін  көпмүшесінің үлкен мүшесіне бөледі және шыққан
көпмүшені
көпмүшесінің үлкен мүшесіне бөледі және шыққан
көпмүшені  көпмүшесінен азайтады. Азайтудың нәтижесінде
дәрежесі
көпмүшесінен азайтады. Азайтудың нәтижесінде
дәрежесі  -нен кіші болатын
-нен кіші болатын  көпмүшесі шығады. Егер
көпмүшесі шығады. Егер  көпмүшесінің дәрежесі т-нен кіші болса, онда бөлу
үрдісі аяқталады да, бұл жағдайда
көпмүшесінің дәрежесі т-нен кіші болса, онда бөлу
үрдісі аяқталады да, бұл жағдайда  көпмүшесі қалдық болады. Егер
көпмүшесі қалдық болады. Егер  көпмүшесінің дәрежесі т-нен артық
немесе т-ге тең болса, онда
көрсетілген бөлу үрдісі
көпмүшесінің дәрежесі т-нен артық
немесе т-ге тең болса, онда
көрсетілген бөлу үрдісі  көпмүшесі үшін жалғасады. Бұл үрдіс
k қадамда
шыққан
көпмүшесі үшін жалғасады. Бұл үрдіс
k қадамда
шыққан көпмүшесінің дәрежесі
көпмүшесінің дәрежесі  көпмүшесінің т
дәрежесінен кем болғанша жалғасады. Бұл
жағдайда
көпмүшесінің т
дәрежесінен кем болғанша жалғасады. Бұл
жағдайда  көпмүшесі қалдық болады.
көпмүшесі қалдық болады.

х-тің кемімелі дәрежелері
бойынша орналасқан  көпмүшесін
көпмүшесін  екімүшесіне бөлген кезде Горнер
схемасы деп аталатын қысқаша бөлу
әдісі қолданылады. Бұл әдіс анықталмаған коэффициенттер әдісінің
тікелей салдары болып табылады. п
дәрежелі
екімүшесіне бөлген кезде Горнер
схемасы деп аталатын қысқаша бөлу
әдісі қолданылады. Бұл әдіс анықталмаған коэффициенттер әдісінің
тікелей салдары болып табылады. п
дәрежелі  көпмүшесін
көпмүшесін  екімүшесіне бөлу кезінде бөліндіде
екімүшесіне бөлу кезінде бөліндіде  дәрежелі
дәрежелі
 көпмүшесі, ал қалдықта сан (әсіресе нөл) шығады.
Анықталмаған коэффициенттер әдісі арқылы төмендегідей теңдіктерді
аламыз:
көпмүшесі, ал қалдықта сан (әсіресе нөл) шығады.
Анықталмаған коэффициенттер әдісі арқылы төмендегідей теңдіктерді
аламыз:

 ,
яғни
,
яғни


 (4)
(4)
(4) теңдіктің оң және сол жақтарындағы бірдей дәрежелердің коэффициенттерін теңестіре отырып, төмендегі жүйені аламыз:

Бұл жүйеден
бөліндінің  коэффициенттерін және r
қалдықты
табудың рекурентті формулаларын
аламыз:
коэффициенттерін және r
қалдықты
табудың рекурентті формулаларын
аламыз:


…………………..


 бөліндісінің коэффициенттерін
және r
қалдығын
есептеу үрдісі төмендегідей схема (Горнер схемасы) бойынша
жүргізіледі:
бөліндісінің коэффициенттерін
және r
қалдығын
есептеу үрдісі төмендегідей схема (Горнер схемасы) бойынша
жүргізіледі:

Бұл
схемада  коэффициентінен бастап үшінші жолдың әрбір саны алдыңғы
жолдың санын α
санына
көбейтіп, шыққан нәтижеге бірінші жолдың сәйкес санын қосқанда
шығады.
коэффициентінен бастап үшінші жолдың әрбір саны алдыңғы
жолдың санын α
санына
көбейтіп, шыққан нәтижеге бірінші жолдың сәйкес санын қосқанда
шығады.
 көпмүшесін
көпмүшесін
 екімүшесіне бөлгенде төмендегі
тепе-теңдік шығады:
екімүшесіне бөлгенде төмендегі
тепе-теңдік шығады:

Бұл
тепе-теңдік , яғни
, яғни  болғанда дұрыс болады.
болғанда дұрыс болады.
Келесі теорема арқылы көпмүшені екімүшеге бөлгендегі бөліндіні таппай, қалдықты табуға болады.
1.6 Безу теоремасы және оның салдарлары
 көпмүшесін
көпмүшесін
 екімүшесіне бөлгендегі
қалық
екімүшесіне бөлгендегі
қалық  болғандағы
болғандағы  көпмүшесінің мәніне, яғни
көпмүшесінің мәніне, яғни  тең болады.
тең болады.
α
саны  көпмүшесінің түбірі деп аталады, егер
көпмүшесінің түбірі деп аталады, егер
 болғанда көпмүшенің сандық
мәні нөлге тең болса, яғни
болғанда көпмүшенің сандық
мәні нөлге тең болса, яғни  болса.
болса.
Ескерту:
 көпмүшесін
көпмүшесін
 түріндегі екімүшеге бөлгенде
берілген көпмүшенің
түріндегі екімүшеге бөлгенде
берілген көпмүшенің  болғандағы мәніне, яғни
болғандағы мәніне, яғни  тең болады.
тең болады.
Салдарлар.
-
 көпмүшесі
көпмүшесі
 екімүшесіне сонда және тек
қана сонда бөлінеді, егер α
саны
екімүшесіне сонда және тек
қана сонда бөлінеді, егер α
саны  көпмүшесінің түбірі болса.
көпмүшесінің түбірі болса. -
 көпмүшесі
көпмүшесі
 екімүшесіне
п саны кез келген натурал сан
болғанда бөлінеді және
екімүшесіне
п саны кез келген натурал сан
болғанда бөлінеді және

-
 көпмүшесі
көпмүшесі
 екімүшесіне
п саны кез келген натурал сан
болғанда бөлінеді және
екімүшесіне
п саны кез келген натурал сан
болғанда бөлінеді және

-
 көпмүшесі
көпмүшесі
 екімүшесіне
п саны кез келген натурал сан
болғанда бөлінеді және
екімүшесіне
п саны кез келген натурал сан
болғанда бөлінеді және

Кез келген
 көпмүшесі үшін
көпмүшесі үшін
 көпмүшесі қалдықсыз
бөлінетін
көпмүшесі қалдықсыз
бөлінетін  екімүшесі табылады. Осы айтылғанның мысалы
ретінде
екімүшесі табылады. Осы айтылғанның мысалы
ретінде
 болғандағы
болғандағы  түріндегі екі дәрежелі көпмүшені алуға
болады.
түріндегі екі дәрежелі көпмүшені алуға
болады.
 түріндегі көпмүше квадрат
үшмүше деп аталады.
түріндегі көпмүше квадрат
үшмүше деп аталады.
Квадрат үшмүшені толық квадратты айыру әдісі арқылы түрлендірейік:


 өрнегі квадрат үшмүшенің
дискриминанты деп аталады және D
әрпімен
белгіленеді, яғни анықтама бойынша
өрнегі квадрат үшмүшенің
дискриминанты деп аталады және D
әрпімен
белгіленеді, яғни анықтама бойынша  . Егер
. Егер  болса, онда квадрат үшмүше төмендегідей түрде
болады:
болса, онда квадрат үшмүше төмендегідей түрде
болады:


яғни бұл жағдайда квадрат үшмүше екі сызықтық көбейткіштерге жіктеледі, ал
 және
және

сандарының әрқайсысы квадрат үшмүшенің түбірі болады.
Егер
 болса, онда квадрат үшмүше
төмендегідей түрде болады:
болса, онда квадрат үшмүше
төмендегідей түрде болады:

яғни екі бірдей сызықтық
көбейткіштерге жіктеледі және  болғанда нөлге айналады.
болғанда нөлге айналады.
 болғанда квадрат үшмүше
сызықтық көбейткіштерге жіктелмейді және оның нақты түбірлері
болмайды.
болғанда квадрат үшмүше
сызықтық көбейткіштерге жіктелмейді және оның нақты түбірлері
болмайды.
Мысал. Квадрат үшмүшені көбейткіштерге жіктеу:
Шешуі.
-
 болғандықтан,
болғандықтан,
 , яғни
, яғни  .
. -
 болғандықтан,
болғандықтан,
 және
және  , яғни
, яғни
 .
. -
 болғандықтан,
болғандықтан,
 квадрат үшмүшесінің нақты
түбірлері жоқ және ол сызықтық көбейткіштерге
жіктелмейді.
квадрат үшмүшесінің нақты
түбірлері жоқ және ол сызықтық көбейткіштерге
жіктелмейді.
Егер
 болса, онда
болса, онда
 квадрат
үшмүшесінің
квадрат
үшмүшесінің  және
және  түбірлері үшін төмендегі тепе-теңдіктер
(Виет теоремасы) дұрыс
болады:
түбірлері үшін төмендегі тепе-теңдіктер
(Виет теоремасы) дұрыс
болады:
 және
және
 .
.
Қарама-қарсы тұжырым да
дұрыс: егер  және
және  болатындай α
және β
сандары
бар болса, онда олар
болатындай α
және β
сандары
бар болса, онда олар  квадрат үшмүшенің түбірлері
болады.
квадрат үшмүшенің түбірлері
болады.
 түріндегі келтірілген квадрат
үшмүше берілген жағдайда көбейтіндісі q
бос
мүшесіне, ал қосындысы қарама-қарсы таңбамен алынған екінші
коэффициентке, яғни
түріндегі келтірілген квадрат
үшмүше берілген жағдайда көбейтіндісі q
бос
мүшесіне, ал қосындысы қарама-қарсы таңбамен алынған екінші
коэффициентке, яғни  -ға тең болатын екі сан оңай табуға болады. Виет
теоремасына сәйкес, осы табылған сандар
-ға тең болатын екі сан оңай табуға болады. Виет
теоремасына сәйкес, осы табылған сандар  түріндегі келтірілген квадрат үшмүшенің түбірлері
болады.
түріндегі келтірілген квадрат үшмүшенің түбірлері
болады.
Дәрежесі 2-ден артық кез келген көпмүше қалдықсыз бөлінетіндей квадрат үшмүше табылатыны дәлелденеді.
 үшінші дәрежелі көпмүше үшін
екі түрлі жағдай болу мүмкін: немесе ол екімүшелердің
көбейтіндісіне жіктеледі, яғни
үшінші дәрежелі көпмүше үшін
екі түрлі жағдай болу мүмкін: немесе ол екімүшелердің
көбейтіндісіне жіктеледі, яғни

мұндағы
 сандары бірдей болуы мүмкін,
немесе ол екімүше мен квадрат үшмүшенің көбейтіндісіне жіктеледі,
яғни
сандары бірдей болуы мүмкін,
немесе ол екімүше мен квадрат үшмүшенің көбейтіндісіне жіктеледі,
яғни

1.7 Көпмүшенің түбірлері туралы тұжырымдар
-
п-ші дәрежелі көпмүшенің нақты түбірлерінің саны п-нен артық болмайды.
-
Тақ дәрежелі көпмүшенің ең болмағанда бір нақты түбірі болады.
-
(Виет теоремасы). Егер
 сандары
сандары
 көпмүшесінің нақты түбірлері
болса, онда төмендегідей теңдіктер
орындалады:
көпмүшесінің нақты түбірлері
болса, онда төмендегідей теңдіктер
орындалады:





-
Егер
 болса, онда
болса, онда
 көпмүшесінің әрбір
түбірі
көпмүшесінің әрбір
түбірі  және
және  көпмүшелерінің біреуінің түбірі болады, ал
көпмүшелерінің біреуінің түбірі болады, ал
 көпмүшесінің әрбір түбірі
және
көпмүшесінің әрбір түбірі
және  көпмүшесінің әрбір түбірі
көпмүшесінің әрбір түбірі  көпмүшесінің түбірі болады.
көпмүшесінің түбірі болады. -
Егер α саны
 көпмүшесінің түбірі болса, онда
көпмүшесінің түбірі болса, онда
 , мұндағы
, мұндағы  – (
– ( ) дәрежелі белгілі бір
көпмүше.
) дәрежелі белгілі бір
көпмүше.
Көпмүшенің түбірлерін
табу үрдісі жалпы жағдайда оңай тапсырма емес, алайда
 көпмүшесі әрқайсысының
дәрежесі 2-ден артық емес көпмүшелердің көбейтіндісі ретінде
берілген жағдайларда бұл тапсырманы толықтай орындауға болады,
себебі 4-қасиет бойынша
көпмүшесі әрқайсысының
дәрежесі 2-ден артық емес көпмүшелердің көбейтіндісі ретінде
берілген жағдайларда бұл тапсырманы толықтай орындауға болады,
себебі 4-қасиет бойынша  көпмүшесінің түбірлерінің жиыны оның бөлгіштерінің
түбірлерінің жиынымен сәйкес
келеді.
көпмүшесінің түбірлерінің жиыны оның бөлгіштерінің
түбірлерінің жиынымен сәйкес
келеді.
Қысқартылмайтын  (p
– бүтін
сан, q
– натурал
сан) бөлшегі
(p
– бүтін
сан, q
– натурал
сан) бөлшегі

көпмүшенің бүтін санды
коэффициенттері бар түбірі болуы үшін р
саны  бос мүшенің бөлгіші болуы керек, ал
q саны
бос мүшенің бөлгіші болуы керек, ал
q саны  үлкен коэффициентінің бөлгіші болуы
керек.
үлкен коэффициентінің бөлгіші болуы
керек.
Егер
 көпмүшесінде бүтін
коэффициенттер және
көпмүшесінде бүтін
коэффициенттер және  болса, онда мұндай көпмүшенің рационал түбірлері тек
қана
болса, онда мұндай көпмүшенің рационал түбірлері тек
қана  бос мүшенің бөлгіштері болатын бүтін сандар
болады.
бос мүшенің бөлгіштері болатын бүтін сандар
болады.
Мысал.  көпмүшенің түбірлерін табу.
көпмүшенің түбірлерін табу.
Шешуі. Берілген көпмүшенің түбірі
рационал сан болатынын немесе болмайтынын анықтайық.
Қысқартылмайтын  бөлшегі берілген көпмүшенің түбірі болсын, онда жоғарыда
келтірілген тұжырым бойынша р
саны
бөлшегі берілген көпмүшенің түбірі болсын, онда жоғарыда
келтірілген тұжырым бойынша р
саны  мәндеріне ие бола алады, ал q
саны 1, 2
мәндеріне ие бола алады. Осылайша, берілген көпмүшенің рационал
түбірлері ретінде тек қана мына сандар болуы мүмкін:
мәндеріне ие бола алады, ал q
саны 1, 2
мәндеріне ие бола алады. Осылайша, берілген көпмүшенің рационал
түбірлері ретінде тек қана мына сандар болуы мүмкін:

Берілген көпмүшеге осы сандарды жеке-жеке қоя отырып,

екенін аламыз.
Осыдан,
 берілген
берілген
 көпмүшенің түбірі болады
және
көпмүшенің түбірі болады
және
 .
.
Горнер схемасын
қолданып, түбірлері  және
және  сандары болатын
сандары болатын  өрнегін аламыз. Сондықтан берілген көпмүшенің
түбірлері
өрнегін аламыз. Сондықтан берілген көпмүшенің
түбірлері
 болады.
болады.
Мысал.  көпмүшесін көбейткіштерге
жіктеу.
көпмүшесін көбейткіштерге
жіктеу.
Шешуі. Көпмүшенің түбірі рационал сан
болатынын немесе болмайтынын анықтайық.
Қысқартылмайтын  бөлшегі берілген көпмүшенің түбірі болсын,
онда р
саны
бөлшегі берілген көпмүшенің түбірі болсын,
онда р
саны  мәндеріне ие бола алады, ал q
саны 1
және 2 мәндеріне ие бола алады. Осылайша, берілген көпмүшенің
рационал түбірлері ретінде тек қана мына сандар болуы
мүмкін:
мәндеріне ие бола алады, ал q
саны 1
және 2 мәндеріне ие бола алады. Осылайша, берілген көпмүшенің
рационал түбірлері ретінде тек қана мына сандар болуы
мүмкін: 
Берілген көпмүшеге осы сандарды жеке-жеке қоя отырып,

екенін аламыз.
 болғандықтан,
болғандықтан,
 және
және  сандары берілген көпмүшенің түбірі болады,
яғни
сандары берілген көпмүшенің түбірі болады,
яғни  .
.
 көпмүшесін
көпмүшесін
 көпмүшесін
көпмүшесін
 көпмүшесіне «бағандап» бөлу
арқылы немесе Горнер схемасына сәйкес
көпмүшесіне «бағандап» бөлу
арқылы немесе Горнер схемасына сәйкес  көпмүшесін
көпмүшесін  көпмүшесіне бөліп, шыққан бөліндіні
көпмүшесіне бөліп, шыққан бөліндіні  көпмүшесіне бөлу арқылы, немесе анықталмаған коэффициенттер
әдісі арқылы табуға болады.
көпмүшесіне бөлу арқылы, немесе анықталмаған коэффициенттер
әдісі арқылы табуға болады.
 көпмүшесін анықталмаған
коэффициенттер әдісі арқылы
табайық.
көпмүшесін анықталмаған
коэффициенттер әдісі арқылы
табайық.
 тепе-теңдігінде теңдіктің сол
жағындағы көпмүшенің бос мүшесі
тепе-теңдігінде теңдіктің сол
жағындағы көпмүшенің бос мүшесі  -ге тең, ал теңдіктің оң жағындағы көпмүшенің бос
мүшесі
-ге тең, ал теңдіктің оң жағындағы көпмүшенің бос
мүшесі  -ге тең болғандықтан,
-ге тең болғандықтан,  болады. Тепе-теңдіктегі с-ның орнына 4 санын,
ал х-тің орнына 1 санын
қойып, b-ның мәнін
табамыз:
болады. Тепе-теңдіктегі с-ның орнына 4 санын,
ал х-тің орнына 1 санын
қойып, b-ның мәнін
табамыз:

бұдан  .
.
Сонымен,
 .
.
 көпмүшесінің нақты түбірлері
жоқ және көбейткіштерге жіктелмейді. Сондықтан есептің шартында
берілген көпмүше көбейткіштерге келесідей жіктеледі:
көпмүшесінің нақты түбірлері
жоқ және көбейткіштерге жіктелмейді. Сондықтан есептің шартында
берілген көпмүше көбейткіштерге келесідей жіктеледі:
 .
.
1.8 Көпмүшені көбейткіштерге жіктеу
-
Ортақ көбейткішті жақшаның сыртына шығару және топтау тәсілі. Кейбір жағдайларда кейбір мүшелерді ұқсас мүшелердің қосындысына (айырмасына) түрлендірген немесе өзара жойылатын мүшелерді енгізген жөн.
-
Қысқаша көбейту формулаларын қолдану. Кей жағдайларда көбейткішті жақшаның сыртына шығаруға, мүшелерді топтауға, толық квадратты, ал одан кейін кубтардың қосындысын, квадраттардың айырмасын немесе кубтардың айырмасын көбейткіштер түрінде жазу керек болады.
-
Безу теоремасын және анықталмаған коэффициенттер әдісін қолдану.
Мысал. Көбейткіштерге
жіктеу:  .
.
 болғандықтан,
болғандықтан,
 көпмүшесі
көпмүшесі
 -ке бөлінеді. Анықталмаған
коэффициенттер әдісі арқылы
-ке бөлінеді. Анықталмаған
коэффициенттер әдісі арқылы  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі бөлгішті
табамыз.
екімүшесіне бөлгендегі бөлгішті
табамыз.
Айталық,
бөлінді  көпмүшесі болсын.
көпмүшесі болсын.  болғандықтан, төмендегі жүйе
шығады:
болғандықтан, төмендегі жүйе
шығады:

Бұдан  . Яғни
. Яғни  .
.
 болғандықтан,
онда
болғандықтан,
онда  .
.
-
Безу теоремасын және «бағандап» бөлуді қолдану.
Мысал. Көбейткіштерге
жіктеу:  .
.
Шешуі.  болғандықтан, онда
болғандықтан, онда  көпмүшесі
көпмүшесі  -ге бөлінеді. «Бағандап» бөлу арқылы бөліндіні
табамыз:
-ге бөлінеді. «Бағандап» бөлу арқылы бөліндіні
табамыз:
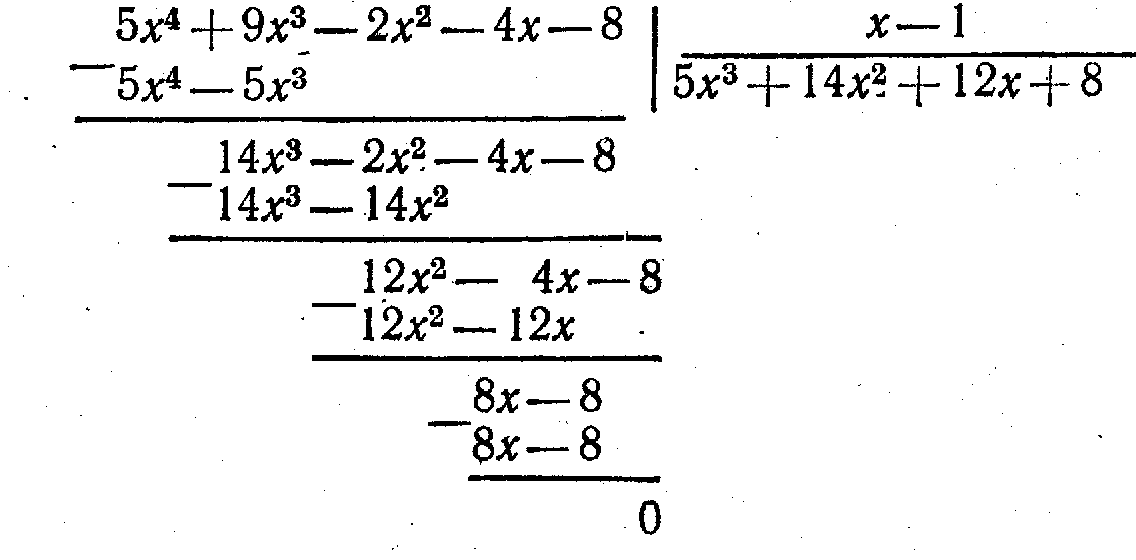
Яғни
 .
.
 болғандықтан,
болғандықтан,
 көпмүшесі
көпмүшесі
 -ге
бөлінеді.
-ге
бөлінеді.
«Бағандап» бөлу арқылы
бөлгішін тапқаннан кейін  шығады.
шығады.
 квадрат үшмүшенің
дискриминанты
квадрат үшмүшенің
дискриминанты  болғандықтан, бұл квадрат үшмүше сызықтық көбейткіштерге
жіктелмейді.
болғандықтан, бұл квадрат үшмүше сызықтық көбейткіштерге
жіктелмейді.
Сонымен,
 .
.
-
Безу теоремасын және Горнер схемасын қолдану. Бұл тәсілдер арқылы табылған бөлінгішті осы тәсілмен немесе кез келген басқа әдіспен көбейткіштерге жіктеуге болады.
Мысал. Көбейткіштерге
жіктеу:  .
.
Шешуі. Берілген көпмүшенің рационал
түбірлері бар болса, онда олар тек қана  сандарының арасында болуы
мүмкін.
сандарының арасында болуы
мүмкін.
Берілген көпмүшенің түбірін табу үшін төмендегідей тұжырымды пайдаланайық:
Егер белгілі
бір  кесіндісінің шеттерінде көпмүшенің мәндері әр түрлі
таңбаға ие болса, онда
кесіндісінің шеттерінде көпмүшенің мәндері әр түрлі
таңбаға ие болса, онда  аралығында бұл көпмүшенің ең болмағанда бір түбірі
болады.
аралығында бұл көпмүшенің ең болмағанда бір түбірі
болады.
Берілген көпмүше
үшін  . Яғни
. Яғни  аралығында берілген көпмүшенің ең болмағанда бір түбірі
бар. Сондықтан жоғарыда жазылған 24 сандардың арасынан
әуелі
аралығында берілген көпмүшенің ең болмағанда бір түбірі
бар. Сондықтан жоғарыда жазылған 24 сандардың арасынан
әуелі  аралығына жататын сандарды тексеріп алған жөн. Бұл
сандардың ішінен тек қана
аралығына жататын сандарды тексеріп алған жөн. Бұл
сандардың ішінен тек қана  саны осы аралыққа тиісті.
саны осы аралыққа тиісті.
 болғандағы
болғандағы
 мәнін тек орнына қою арқылы
ғана емес, сондай-ақ басқа да әдістермен табуға болады, мысалы,
Горнер схемасы арқылы, өйткені
мәнін тек орнына қою арқылы
ғана емес, сондай-ақ басқа да әдістермен табуға болады, мысалы,
Горнер схемасы арқылы, өйткені  саны
саны  көпмүшесін
көпмүшесін  -ға бөлгендегі қалдыққа тең. Онымен қоса, көптеген
есептерде бұл әдіс тиімдірек, себебі сол кезде бөлінгіштің
коэффициенттері де табылады.
-ға бөлгендегі қалдыққа тең. Онымен қоса, көптеген
есептерде бұл әдіс тиімдірек, себебі сол кезде бөлінгіштің
коэффициенттері де табылады.
Берілген мысал үшін Горнер схемасына сәйкес:

 болғандықтан,
болғандықтан,
 саны
саны  көпмүшесінің түбірі болады және
көпмүшесінің түбірі болады және  көпмүшесі
көпмүшесі  -ге бөлінеді, яғни
-ге бөлінеді, яғни  .
.

 болғандықтан,
болғандықтан,  .
.
1.9 Көпмүше сақинасы ұғымы
Айталық, K және L коммутатив сақиналар болсын.
Анықтама
1: L
сақинасы К
сақинасының х
элементтері арқылы жасалған жай кеңейтілім деп аталады
және  деп белгіленеді егер:
деп белгіленеді егер:
-
 сақинаның ішкі
сақинасы
сақинаның ішкі
сақинасы -

 негізгі жиынын
негізгі жиынын
 символдарымен
белгілейді.
символдарымен
белгілейді.
Анықтама
2: К
сақинасының х
элементтері арқылы жасалған  жай кеңейтілім х
арқылы
жасалған К
сақинасының жай трансценденттік кеңейтілім болады егер
төмендегі шарттар орындалса:
жай кеңейтілім х
арқылы
жасалған К
сақинасының жай трансценденттік кеңейтілім болады егер
төмендегі шарттар орындалса:
-
 сақинаның ішкі
сақинасы
сақинаның ішкі
сақинасы -

-
 егер
егер  болса, онда
болса, онда
 .
.
Анықтама
3: х
элементі К
сақинасынан тыс трансценденттік деп аталады, егер мына шарт
орындалса:  егер
егер  болса, онда
болса, онда  .
.
Ұсыныс.  жай трансценденттік кеңейтілім болсын. Егер
жай трансценденттік кеңейтілім болсын. Егер
 және
және  болатын
болатын  болса, онда
болса, онда  болады.
болады.
Дәлелдеуі. Шарт
бойынша  ,
,  . Бірінші өрнектен екінші өрнекті азайтып,
. Бірінші өрнектен екінші өрнекті азайтып,
 аламыз.
х элементі
К-дан тыс трансценденттік
болғандықтан, Анықтама 3 бойынша
аламыз.
х элементі
К-дан тыс трансценденттік
болғандықтан, Анықтама 3 бойынша  шығады.
шығады.
Қорытынды. х элементі арқылы жасалған К коммутатив сақинасының жай трансценденттік кеңейтілімнің кез келген нөлге тең емес элементі х элементінің теріс емес бүтін дәрежелерінің сызықтық комбинациясы түрінде бір ғана жазылуын жасайды.
Анықтама 4: Нөлге тең емес К сақинасынан тыс белгісіз х арқылы жасалған көпмүше сақинасы деп х элементі арқылы жасалған нөлге тең емес коммутатив К сақинасының жай трансценденттік кеңейтілімді айтады.
Теорема
1. Нөлге тең емес кез келген
коммутатив К
сақинасы
үшін х
элементі
арқылы жасалған  жай трансценденттік кеңейтілім бар
болады.
жай трансценденттік кеңейтілім бар
болады.
1.10 Көпмүшелерге қолданылатын амалдар
Айталық,
 – нөлге тең емес кез келген
коммутатив К
сақинасының сақинасы
болсын.
– нөлге тең емес кез келген
коммутатив К
сақинасының сақинасы
болсын.
Анықтама
5:  сақинасының f
және g
көпмүшелері тең болады және
сақинасының f
және g
көпмүшелері тең болады және
 деп белгіленеді, егер f
және g
көпмүшелерінің белгісіз х-тің бірдей дәрежелеріндегі
барлық коэффициенттері өзара тең
болса.
деп белгіленеді, егер f
және g
көпмүшелерінің белгісіз х-тің бірдей дәрежелеріндегі
барлық коэффициенттері өзара тең
болса.
Салдар 1. Көпмүшенің жазылуында қосылғыштардың орналасу реті маңызды емес. Көпмүшенің жазылуында коэффициенті нөлге тең қосылғыштарды жазуға немесе алып тастауға болады.
 g
g болсын.
болсын.
Анықтама
6: f
және g
көпмүшелерінің қосындысы деп төмендегідей теңдікпен
анықталатын  көпмүшесін атаймыз:
көпмүшесін атаймыз:

мұндағы
 .
.
Анықтама 7: f және g көпмүшелерінің көбейтіндісі (fg) деп белгіленіп, төмендегі ереже бойынша есептеледі:

мұндағы
 .
.
1.11 Көпмүшенің дәрежесі
Айталық,
 коммутатив сақина
болсын.
коммутатив сақина
болсын.  – К
өрісінен
тыс көпмүшелер сақинасы
– К
өрісінен
тыс көпмүшелер сақинасы  .
.
Анықтама
8:  – кез келген көпмүше болсын. Егер
– кез келген көпмүше болсын. Егер  болса, онда теріс емес бүтін п
саны
– f көпмүшелерінің дәрежесі. Бұл
жағдайда
болса, онда теріс емес бүтін п
саны
– f көпмүшелерінің дәрежесі. Бұл
жағдайда  деп жазады.
деп жазады.
 сандары
– үлкен
коэффициенті
сандары
– үлкен
коэффициенті  болатын көпмүшенің
коэффициенттері.
болатын көпмүшенің
коэффициенттері.
Егер
 болса,
f – тұрақты. Нөлге тең
көпмүшенің дәрежесі анықталмаған.
болса,
f – тұрақты. Нөлге тең
көпмүшенің дәрежесі анықталмаған.
Көпмүше дәрежесінің қасиеттері:
1.
 және
және  .
.
2.
 және
және  және
және 
3.
К – бүтіндік
аймағы 
Дәлелдеуі.  болғандықтан,
болғандықтан,  болады. К
–
бүтіндік аймағы
болады. К
–
бүтіндік аймағы  .
.
Салдар
2: К
(бүтіндік
аймағы) өрісінен тыс  өз кезегінде бүтіндік аймағы болып табылады. Кез келген
бүтіндік аймағы үшін бүтіндік аймағы бар
болады.
өз кезегінде бүтіндік аймағы болып табылады. Кез келген
бүтіндік аймағы үшін бүтіндік аймағы бар
болады.
Салдар
3: Кез келген
 үшін К бүтіндік аймағынан тыс
бөлінгіштер өрісі болады.
үшін К бүтіндік аймағынан тыс
бөлінгіштер өрісі болады.
1.12
 екімүшесіне бөлу және
көпмүшенің түбірлері
екімүшесіне бөлу және
көпмүшенің түбірлері
Айталық,
 болсын,
болсын,
 элементі
f көпмүшесінің
элементі
f көпмүшесінің
 аргументінен табылған мәні деп
аталады.
аргументінен табылған мәні деп
аталады.
Безу
теоремасы: Кез келген
 көпмүшесі және
көпмүшесі және
 үшін
үшін
 элементі бар
болады.
элементі бар
болады.
Дәлелдеуі.  – кез келген көпмүше болсын.
– кез келген көпмүше болсын.  .
.




Салдар
4:  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдық
екімүшесіне бөлгендегі қалдық  болады.
болады.
Анықтама
9:  элементі f
көпмүшесінің түбірі болады, егер
элементі f
көпмүшесінің түбірі болады, егер
 болса.
болса.
Теорема
2:  элементі f
көпмүшесінің түбірі болады сонда және тек қана сонда
егер f
көпмүшесі
элементі f
көпмүшесінің түбірі болады сонда және тек қана сонда
егер f
көпмүшесі  екімүшесіне бөлінетін болса
екімүшесіне бөлінетін болса  .
.
Дәлелдеуі:
-
Қажеттілік шарты. Айталық
 болсын. Безу теоремасынан
болсын. Безу теоремасынан  шығады, бөлінгіштік қасиеті бойынша
шығады, бөлінгіштік қасиеті бойынша  болады.
болады. -
Жеткіліктік шарты. Айталық,
 болсын, онда
болсын, онда
 . Д.К.О.
. Д.К.О.
1.13 Көпмүшенің бүтіндік аймағынан тыс түбірлерінің максималды саны
Теорема
3: k– бүтіндік аймағы болсын. f
көпмүшесінің k
бүтіндік
аймағындағы түбірлер саны f
көпмүшесінің п
дәреже
көрсеткішінен аспайды.
бүтіндік аймағы болсын. f
көпмүшесінің k
бүтіндік
аймағындағы түбірлер саны f
көпмүшесінің п
дәреже
көрсеткішінен аспайды.
Дәлелдеуі:
-
Көпмүше дәрежесінің индукциясы бойынша.
 болсын. Бұдан
f көпмүшесінің нөл түбірі бар
және олардың саны
болсын. Бұдан
f көпмүшесінің нөл түбірі бар
және олардың саны  аспайды.
аспайды.
-
Теорема кез келген
 үшін дәлелденген болсын.
үшін дәлелденген болсын. -
Бөлімше 2-ден көпмүшелерге арналған теоремадағы тұжырымының
 дұрыстығы шығатынын
көрсетейік.
дұрыстығы шығатынын
көрсетейік.
Айталық,
 және
және  . Екі жағдай болу мүмкін:
. Екі жағдай болу мүмкін:
А) f көпмүшесінің түбірлері жоқ, яғни теоремадағы тұжырым дұрыс.
Б)
f көпмүшесінің ең
болмағанда  түбірі бар, Безу теоремасы бойынша
түбірі бар, Безу теоремасы бойынша  , k
–
бүтіндік аймағы болғандықтан, Қасиет 3 (көпмүшенің дәрежелері)
бойынша
, k
–
бүтіндік аймағы болғандықтан, Қасиет 3 (көпмүшенің дәрежелері)
бойынша  екені шығады.
екені шығады.
 және
және  болсын.
болсын.
 және k – бүтіндік аймағы
болғандықтан,
және k – бүтіндік аймағы
болғандықтан,
 .
.
Осылайша,
 болғандықтан,
болғандықтан,
 көпмүшесінің барлық
түбірлері g
көпмүшесінің түбірлері де болады, индукциялық болжам
бойынша g
көпмүшесінің барлық түбірлерінің саны
п-нен аспайды,
яғни f
көпмүшесінің түбірлерінің саны
көпмүшесінің барлық
түбірлері g
көпмүшесінің түбірлері де болады, индукциялық болжам
бойынша g
көпмүшесінің барлық түбірлерінің саны
п-нен аспайды,
яғни f
көпмүшесінің түбірлерінің саны  -ден аспайды.
-ден аспайды.
Салдар
5: k
–
бүтіндік аймағы болсын, егер f
көпмүшесінің түбірлерінің саны п
санынан
артық және  болса, онда f
– нөлдік
көпмүше.
болса, онда f
– нөлдік
көпмүше.
1.14 Көпмүшелердің алгебралық және функционалдық теңдігі
 қандай да бір көпмүше болсын,
ол белгілі бір
қандай да бір көпмүше болсын,
ол белгілі бір  функциясын жалпы жағдайда сипаттайды, кез келген көпмүше
бір функцияны сипаттай алады.
функциясын жалпы жағдайда сипаттайды, кез келген көпмүше
бір функцияны сипаттай алады.
Теорема
4:  – бүтіндік аймағы болсын, сонда f және
– бүтіндік аймағы болсын, сонда f және  көпмүшелерінің теңдігі
көпмүшелерінің теңдігі  және
және  функцияларымен сипатталатын теңдікке (тепе-теңдікке (≡))
пара-пар келеді.
функцияларымен сипатталатын теңдікке (тепе-теңдікке (≡))
пара-пар келеді.
Дәлелдеуі:
-
Қажеттілік шарты. f және
 – ∞ бүтіндік аймағы,
– ∞ бүтіндік аймағы,  болсын.
болсын.  болсын, яғни
болсын, яғни
 .
. -
Жеткіліктік шарты. Айталық,
 .
.
 қарастырайық,
қарастырайық,
 бүтіндік аймағы
болғандықтан, h
көпмүшесінің ∞ түбірлері бар, онда Салдар 5
бойынша h
– нөлдік
көпмүше. Осылайша,
бүтіндік аймағы
болғандықтан, h
көпмүшесінің ∞ түбірлері бар, онда Салдар 5
бойынша h
– нөлдік
көпмүше. Осылайша,  . Д.К.О.
. Д.К.О.
Қалдықпен бөлу туралы теорема
Анықтама
10: Евклидтік
К сақинасы деп
 жиынында төмендегі шартты
қанағаттандыратын және теріс емес бүтін мәндерді
қабылдайтын h
функциясы
анықталатын k
бүтіндік
аймағы аталады:
жиынында төмендегі шартты
қанағаттандыратын және теріс емес бүтін мәндерді
қабылдайтын h
функциясы
анықталатын k
бүтіндік
аймағы аталады:
 және
және
 немесе
немесе  .
.
Берілген
 элементтері үшін
элементтері үшін
 элементтерін табу үрдісі
қалдықпен бөлу деп аталады, мұндағы q
– толық
емес бөлінді, r
–
элементтерін табу үрдісі
қалдықпен бөлу деп аталады, мұндағы q
– толық
емес бөлінді, r
–  бөліндісінің қалдығы.
бөліндісінің қалдығы.
Теорема 5
(қалдықпен бөлу туралы):  – F
өрісінен
тыс көпмүшелер сақинасы және
– F
өрісінен
тыс көпмүшелер сақинасы және  көпмүшесі болсын.
көпмүшесі болсын.  болатын және
болатын және  немесе
немесе  шарты орындалатын
шарты орындалатын  көпмүшелерінің жалғыз жұбы бар
болады.
көпмүшелерінің жалғыз жұбы бар
болады.
 немесе
немесе
 .
.
Дәлелдеуі: Көпмүшенің бар
болуы.  , яғни
, яғни  болсын. Егер f
– нөлдік
көпмүше немесе
болсын. Егер f
– нөлдік
көпмүше немесе
 болса, теорема дұрыс екені көрінеді, себебі
болса, теорема дұрыс екені көрінеді, себебі
 немесе
немесе  .
.
 болғандағы теореманы
дәлелдейік. Дәлелдеуді f
көпмүшенің дәрежесінің индукциясы бойынша
жүргіземіз.
болғандағы теореманы
дәлелдейік. Дәлелдеуді f
көпмүшенің дәрежесінің индукциясы бойынша
жүргіземіз.  көпмүшесі үшін теорема дәлелденді деп болжайық. Бұл
жағдайда теоремадағы тұжырым
көпмүшесі үшін теорема дәлелденді деп болжайық. Бұл
жағдайда теоремадағы тұжырым
 үшін орындалғанын көрсетейік. Расында да,
үшін орындалғанын көрсетейік. Расында да,
 – f
көпмүшесінің үлкен коэффициенті болсын,
осыдан
– f
көпмүшесінің үлкен коэффициенті болсын,
осыдан  көпмүшесінің үлкен коэффициенті мен дәрежесі
f көпмүшесіндегі үлкен
коэффициенті мен дәрежесіне тең болатыны шығады,
осылайша
көпмүшесінің үлкен коэффициенті мен дәрежесі
f көпмүшесіндегі үлкен
коэффициенті мен дәрежесіне тең болатыны шығады,
осылайша
 көпмүшесінде
көпмүшесінде  болады немесе ол нөлдік көпмүше болады. Егер
болады немесе ол нөлдік көпмүше болады. Егер
 болса, онда
болса, онда
 , бұдан
, бұдан
 және
және  болғандағы
болғандағы
 шығады. Егер
шығады. Егер  болса, онда индукциялық болжам бойынша
болса, онда индукциялық болжам бойынша
 болады, бұдан
болады, бұдан
 , яғни
, яғни
 болғанда
болғанда
 немесе
немесе  шығады. Көпмүшенің бар болатыны
дәлелденді.
шығады. Көпмүшенің бар болатыны
дәлелденді.
Көпмүшелердің мұндай жұбы жалғыз болатынын дәлелдейік.
 немесе
немесе  бар болсын, екі теңдікті бір-бірінен
азайтайық:
бар болсын, екі теңдікті бір-бірінен
азайтайық:  . Екі жағдай болу мүмкін:
. Екі жағдай болу мүмкін:  немесе
немесе  .
.
 болсын.
болсын.
Басқа жағынан, дәрежелер
шарты бойынша  немесе
немесе  ,
,  немесе
немесе  .
.
Егер
 болса, онда қарама-қайшылық
пайда болады да,
болса, онда қарама-қайшылық
пайда болады да,  . Жалғыздық
дәлелденді.
. Жалғыздық
дәлелденді.
Салдар
6: F
өрісінен
тыс  көпмүшелер сақинасы Евклид
кеңістігі деп аталады.
көпмүшелер сақинасы Евклид
кеңістігі деп аталады.
Салдар
7: F
өрісінен
тыс  көпмүшелер сақинасы басты
идеалдар (кез келген идеалдың бір ғана құраушысы болады) сақинасы
болып табылады.
көпмүшелер сақинасы басты
идеалдар (кез келген идеалдың бір ғана құраушысы болады) сақинасы
болып табылады.
Кез келген Евклид
сақинасы факториалды: F
өрісінен
тыс  көпмүшелер сақинасы факториал
сақинасы деп аталады.
көпмүшелер сақинасы факториал
сақинасы деп аталады.
1.15 Евклид алгоритмі. Екі көпмүшенің ЕҮОБ
 – F
өрісінен
тыс көпмүшелер сақинасы болсын.
– F
өрісінен
тыс көпмүшелер сақинасы болсын.
Анықтама
11: f
және  болсын. Егер
болсын. Егер  көпмүшесі бар болса, онда
көпмүшесі бар болса, онда  бөліндісінің қалдығы нөлге тең болады, g –
f көпмүшесінің бөлгіші болады
және
бөліндісінің қалдығы нөлге тең болады, g –
f көпмүшесінің бөлгіші болады
және  деп
белгіленеді.
деп
белгіленеді.
Анықтама 12: f және g көпмүшелерінің ең үлкен ортақ бөлгіші h көпмүшесі болады:
-
 және
және  (h
– f
және g
көпмүшелерінің ортақ бөлгіші).
(h
– f
және g
көпмүшелерінің ортақ бөлгіші). -
 (
( f және g көпмүшелерінің кез
келген ортақ бөлгішіне).
f және g көпмүшелерінің кез
келген ортақ бөлгішіне).
f
және g
көпмүшелерінің ең үлкен ортақ бөлгіші
ЕҮОБ(f;g) деп белгіленеді. Кез
келген көпмүшелердің ортақ бөлгіштерінің қатарына
 , яғни нөлге тең
емес F
өрісі
ішіндегі дәрежесі нөлге тең барлық көпмүшелер жатады. Берілген
екі f
және g
көпмүшелерінің нөлдік көпмүше емес ортақ бөлгіштері болмайтын
жағдай орын алуы мүмкін.
, яғни нөлге тең
емес F
өрісі
ішіндегі дәрежесі нөлге тең барлық көпмүшелер жатады. Берілген
екі f
және g
көпмүшелерінің нөлдік көпмүше емес ортақ бөлгіштері болмайтын
жағдай орын алуы мүмкін.
Анықтама 13: Егер f және g көпмүшелерінің дәрежесі нөлге тең көпмүше емес ортақ бөлгіштері болмаса, онда олар өзара жай көпмүшелер деп аталады.
Лемма: Егер  – F
өрісінен
тыс х-ке қатысты көпмүшелер
болса және
– F
өрісінен
тыс х-ке қатысты көпмүшелер
болса және  теңдігі орындалса, f
және g
көпмүшелерінің ең үлкен ортақ бөлгіші q
және r
көпмүшелерінің ең үлкен ортақ бөлгішімен
ассоциацияланады.
теңдігі орындалса, f
және g
көпмүшелерінің ең үлкен ортақ бөлгіші q
және r
көпмүшелерінің ең үлкен ортақ бөлгішімен
ассоциацияланады.  .
.
 жазуы
жазуы  дегенді білдіреді.
дегенді білдіреді.
Дәлелдеуі: және
және  болсын.
болсын.
-
 , бұдан
, бұдан
 және
және
 шығады, яғни
d – q
және r
көпмүшелерінің ортақ бөлгіші болады
шығады, яғни
d – q
және r
көпмүшелерінің ортақ бөлгіші болады  .
. -
 .
. -
 .
.
Евклид алгоритмі
 – F
өрісінен
тыс
– F
өрісінен
тыс  сақинасының көпмүшелері
болсын.
сақинасының көпмүшелері
болсын.  табудың Евклид алгоритмінің мәні тізбектей бөлу әдісі
арқылы
табудың Евклид алгоритмінің мәні тізбектей бөлу әдісі
арқылы
 және
және  көпмүшелерінің ең үлкен ортақ бөлгішін табу үрдісі кіші
дәрежелі екі көпмүшенің ең үлкен ортақ бөлгішін табу үрдісіне
әкеліп соғатынында болып тұр.
көпмүшелерінің ең үлкен ортақ бөлгішін табу үрдісі кіші
дәрежелі екі көпмүшенің ең үлкен ортақ бөлгішін табу үрдісіне
әкеліп соғатынында болып тұр.
 болсын, қалдықпен бөлу
теоремасы бойынша
болсын, қалдықпен бөлу
теоремасы бойынша  көпмүшелері бар болады және екі жағдай болуы
мүмкін:
көпмүшелері бар болады және екі жағдай болуы
мүмкін:
-

-
 , қалдықпен бөлу теоремасы
бойынша
, қалдықпен бөлу теоремасы
бойынша  , бұл жағдайда
, бұл жағдайда  -ді
-ді  -ге қалдықпен бөлеміз:
-ге қалдықпен бөлеміз:  .
.
 деп болжайық. Қалдықта нөл шыққанша берілген схемамен
бөлуді жалғастырамыз. Бөлудің төмендегідей тізбегін
аламыз:
деп болжайық. Қалдықта нөл шыққанша берілген схемамен
бөлуді жалғастырамыз. Бөлудің төмендегідей тізбегін
аламыз:
 және
және 
 және
және 
..................................................................
 және
және 

Бөлудің тізбегі
аяқталды, себебі  , бұл ретте
, бұл ретте  – теріс емес бүтін сан, бөлудегі қалдықтың
дәрежесі
– теріс емес бүтін сан, бөлудегі қалдықтың
дәрежесі  дәрежесінен кем болатын теріс емес бүтін сандардың соңғы
саны бар болады. Лемма 1 бойынша:
дәрежесінен кем болатын теріс емес бүтін сандардың соңғы
саны бар болады. Лемма 1 бойынша:

Осылайша, Евклид
алгоритмі арқылы тізбектей бөлу кезінде  .
.
1.16 Ең кіші ортақ еселік
 – F
өрісінен
тыс көпмүшелер сақинасы болсын.
– F
өрісінен
тыс көпмүшелер сақинасы болсын.
Анықтама
14:  көпмүшесі f
және
көпмүшесі f
және  көпмүшелерінің ең кіші ортақ еселігі деп аталады, егер мына
шарттар орындалса:
көпмүшелерінің ең кіші ортақ еселігі деп аталады, егер мына
шарттар орындалса:
-
 (h
– f
және g
көпмүшелерінің ортақ еселігі).
(h
– f
және g
көпмүшелерінің ортақ еселігі). -
 (h
– f
және g
көпмүшелерінің ортақ еселіктерінің ең
кішісі).
(h
– f
және g
көпмүшелерінің ортақ еселіктерінің ең
кішісі).
Келесідей белгілеулерді
енгізейік:  – кез келген кесінді. f
және g
көпмүшелерінің ең кіші ортақ еселігі – үйлестірілген мән. ЕКОЕ
символымен үйлестірілген ең кіші ортақ еселік
белгіленеді.
– кез келген кесінді. f
және g
көпмүшелерінің ең кіші ортақ еселігі – үйлестірілген мән. ЕКОЕ
символымен үйлестірілген ең кіші ортақ еселік
белгіленеді.
Ескерту. Кез
келген f
және  көпмүшелері үшін
көпмүшелері үшін
 (басты идеалдар қиылысуы) бар
болады.
(басты идеалдар қиылысуы) бар
болады.



Теорема 6 (ЕҮОБ
мен ЕКОЕ арасындағы байланыс): f
және  көпмүшелері F
өрісінен
тыс х-ке қатысты көпмүшелер
болсын, осылайша, мына қатынас бар болады:
көпмүшелері F
өрісінен
тыс х-ке қатысты көпмүшелер
болсын, осылайша, мына қатынас бар болады:  .
.
Дәлелдеуі:  белгілеулерін енгізейік.
белгілеулерін енгізейік.
 көпмүшесін қарастырайық.
көпмүшесін қарастырайық.
-
 , осылайша,
, осылайша,
 болатындай
болатындай
 және
және  көпмүшелері бар болады, мұндағы
көпмүшелері бар болады, мұндағы  .
. -
 көпмүшесін қарастырайық,
сонда
көпмүшесін қарастырайық,
сонда  , осылайша,
, осылайша,  .
. -
 шығады.
Д.К.О.
шығады.
Д.К.О.
Мысал.  .
.  табу керек.
табу керек.
Ш![]() ешуі.
ешуі.














0

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Осылайша,



Жауабы: 
1.17 Көпмүшенің формальды туындысы. Көпмүшенің келтірілмейтін еселіктері
 – F
өрісінен
тыс
– F
өрісінен
тыс  құрайтын көпмүшелер сақинасы
болсын.
құрайтын көпмүшелер сақинасы
болсын.  – у
арқылы
жасалған жай трансценденттік кеңейтілім
болсын.
– у
арқылы
жасалған жай трансценденттік кеңейтілім
болсын.
 .
.  элементі – коэффициенті F
өрісінен
тыс х-тен жасалған көпмүше
болатын у
айнымалысынан жасалған көпмүше. Егер
элементі – коэффициенті F
өрісінен
тыс х-тен жасалған көпмүше
болатын у
айнымалысынан жасалған көпмүше. Егер
 болса және
х-ке тәуелді болса,
онда
болса және
х-ке тәуелді болса,
онда  деп жазады.
деп жазады.
 ,
,

Мынадай белгілеу енгізейік:

Осылайша,

Анықтама
15:  болсын. f
көпмүшесінің формальды туындысы деп төмендегідей көпмүше
аталады:
болсын. f
көпмүшесінің формальды туындысы деп төмендегідей көпмүше
аталады:

Формальды туынды
 немесе
немесе  деп белгіленеді.
деп белгіленеді.
1.18 Туындылардың қасиеттері
Кез келген
f және  көпмүшелері үшін:
көпмүшелері үшін:




 дәлелдеу:
дәлелдеу:

Осылайша,
 Д.К.О.
Д.К.О.
 дәлелдеу:
дәлелдеу:
 ,
,

 Д.К.О.
Д.К.О.
 дәлелдеуі
дәлелдеуі
 болғандағы
болғандағы
 қасиеттен
шығады.
қасиеттен
шығады.
 дәлелдеуі
дәлелдеуі
 болғандағы
болғандағы
 қасиеттен
п дәреженің индукциясы бойынша
шығады.
қасиеттен
п дәреженің индукциясы бойынша
шығады.
2. «Көпмүшелер» тақырыбын оқып үйрену кезіндегі әдістемелік және психологиялық-педагогикалық аспектілері
2.1 Тақырыпты оқып үйрену кезіндегі логикалық ойлауды дамыту
Қоршаған ортамен танысу түйсіктен, қабылдаудан, сезімдерден басталып, ойлауға ауысады. Ойлаудың функциясы – белгілі түйсіктің шегінен шығып танымның шектерін кеңейту. Ойлау түйсік арқылы аша алмайтын нәрсені немесе құбылысты ақыл қорытындысы арқылы ашуға мүмкіндік береді.
Ойлаудың міндеті – заттар арасындағы қатынасты ашу, байланыстарды анықтау және оларды кездейсоқ сәйкестіктерден ажырату. Ойлау ұғымдарды пайдаланады және жалпылау мен жоспарлау функцияларын орындайды. Ойлау– түйсінетін объектілердің арасындағы байланысты орнататын психикалық бейнелеудің айрықша жалпыланған және жанамаланған түрі.
Қоғам дамыған сайын ойлау да бірте-бірте дамып келеді және ұғымдардағы жалпылама, теориялық ойлауға көшіп бара жатыр. Санның, кеңістіктің және уақыттың абстракциялары пайда болып, дамып келеді. Сонымен қатар ешқандай ұғым болып қалыптаспаған ұғымдарға сүйенуге әкеліп соғады.
Сондықтан баланың ойлау қабілетінің дамуы бірте-бірте жүреді. Алғашқыда ол заттарды мәнсіз қозғаудың дамуымен анықталады, сонан соң ойлау бағытталған объектімен анықталып, мәні бар құбылысқа айналады.
Баланың интеллектуалды дамуы оның іс-әрекетінің, қарым-қатынас жасаудың, қоғамдық тәжірибені меңгерудің барысында жүзеге асады.
Интеллектуалды дамудың тізбектелген сатылары – бұл көрнекі-әрекеттік және тілдік-логикалық ойлау. Сондай-ақ ойлаудың дамуына көптеген ұғымдардың пайда болуын қамтамасыз ететін дамытушы сөйлеу әрекеті үлкен ықпал етеді.
Сөздерді қабылдау (сенсорлы сөйлеу) әрекеті баланы объектіні және оның сипаттамаларын дұрыс түсінуге ықпал ететінін айта кету керек. Заттың немесе құбылыстың бір жақтарын ғана ерекшелеп, ал басқаларына назар аударуға баулитын қарапайым абстракция алғашқы қарапайым жалпылауға алып келеді.
Осылайша, бақылау – баланың ойлау әрекетінің негізгі болып табылады. Мысалы, көпмүшелер тақырыбын оқып үйрену барысында мүмкіндігінше көрнекі құралдарды пайдаланған жөн. Оның нәтижесінде ойлау әрекеті сәйкестендіру мен салыстыруда көрініс табады. Бұл ретте зат және заттың қасиеті ұғымдарының арасындағы айырмашылықтар меңгеріледі. Оның нәтижесінде бала заңдылық туралы қорытынды жасауды үйренеді. Бұл ретте практикалық әрекеттермен ойлау байланысы сақталса да, ол бұрынғыдай тығыз, түзу және тікелей болмайды. Бірқатар жағдайларда объектімен практикалық қимыл-әрекет жасау қажет болмайды, бірақ барлық жағдайда оны нақты қабылдау және көрнекі көрсету қажет. Себебі балалардың бейнелік ойлауы әлі тікелей жүзеге асады, сондықтан олар қарастырылып тұрған объектінің айқын көзге түсетін қасиеттерінен ұғымдар арқылы абстракциялана алмайды.
Ойлау қалыптасу барысында екі сатыдан өтеді: ұғымға дейінгі және ұғымдық.
Сонымен, ойлау нақты бір бейнеден сөзбен белгіленген әрекетке қарай дамиды. Түйсіну заттар мен құбылыстардағы ұқсас, өзгермейтін қасиеттерді бейнелейді.
Безу теоремасын және оның салдарын оқып үйрену барысында баланың интеллектуалды дамуындағы елеулі өзгерістер көпмүшелердің қасиеттерін оқуда, ол үшін қажетті ойлау амалдарының қалыптасуында, танымдық әрекеттің жаңа түрткілерінің пайда болуында байқалады.
Осының нәтижесінде бұдан да қиын танымдық міндеттер қолжетімді болады. Оларды шешу барысында ойлау амалдары жалпыланады, рәсімделеді және бұлар арқылы жаңа жағдайларда қолдану ауқымы кеңейеді. Өзара байланысқан, жалпыланған амалдардың жүйесі қалыптасады. Пайымдау, өзінің ойын дәлелдеу, пайымдау үрдісін түсіну және бақылау, оның жалпы әдістерін үйрену, пайымдаудың кеңейтілген түрлерінен қысқа түрлеріне ауысып тұру қабілеті дамиды. Нақты ұғымдық ойлаудан абстрактылы ұғымдық ойлауға ауысу орындалады.
Баланың интеллектуалды дамуы алдыңғысы келесісін дайындайтын сатылардың заңды түрде ауысуымен сипатталады. Ойлаудың жаңа түрлерінің пайда болуымен қатар ескі түрлері жойылмайды, керісінше, сақталады және дамиды.
Әрбір ойлау үрдісі ұғымдарды жалпылауда өтеді, алайда әдетте оның құрылымына ұғымдармен қатар бейнелер де кіреді. Мұндай үрдістің бастапқы кезеңі проблемалық жағдайды түсіну болып табылады. Проблеманы қоюдың өзі ойлаудың әрекеті болып табылады, көп жағдайда ол үлкен ойлау жұмысты талап етеді.
Ойланатын адамның бірінші белгісі – проблеманы дер кезінде көре білу. Сұрақтардың пайда болуы ой жұмысы дамуының белгісі болып табылады. Адамның білімі неғұрлым кең болса, соғұрлым ол көп проблема көре алады.
Проблеманы түсінуден кейін ой ол проблеманы шешуге ауысады. Есепті шешу әр түрлі тәсілдермен жүзеге асады. Ерекше есептер болады, оларды шешу үшін белгілі мәліметтерді жаңаша сәйкестендіріп, жағдайды қайта ойлау ғана қажет болады.
Көптеген жағдайда есепті шешу үшін теориялық жалпылама білімнің негізі керек болады. Есепті шешу үрдісі белгілі білімді есепті шешудің әдісі мен тәсілі ретінде қолдануды қажет етеді.
Есепті шешудің ережесін қолдану үрдісі екі ойлау амалын қамтиды:
-
есепті шешу үшін қандай «ережені» қолдану керектігін анықтау;
-
жалпы ережені есептің жеке шарттарына қолдану.
Мұндай есептерді шешуде ойлау дағдыларының рөлі білімнің жалпылама жүйесі бар бағыттарда аса жоғары болатынын ескерте кетейік.
Өте қиын проблеманы шешу кезінде әдетте болжам болып ұғынатын шешу жолы белгіленеді. Болжамды ұғыну тексеру жүргізуге деген қажеттілікті туындатады. Тексеру аяқталғаннан кейін ойлау үрдісі соңғы саты – берілген сұрақты талдау сатысына көшеді.
Осылайша, ойлау үрдісі – бастапқы жағдайды (есептің шартын) ұғынудан басталатын, саналы және мақсатты, ұғымдар мен бейнелерді пайдаланатын және белгілі бір нәтижемен аяқталатын үрдіс.
Проблеманы шешудің 4 сатысы бар:
-
дайындық;
-
шешімнің нақтылануы;
-
шабыт;
-
табылған шешімді тексеру.
Проблеманы шешудегі ойлау үрдісінің құрылымы:
-
Түрткі (проблеманы шешуге деген ықылас);
-
Проблеманы талдау («берілгенді», «табу керекті», жетпейтін немесе артық мәліметтерді және т.б. анықтау);
-
Шешу жолын іздеу:
-
Белгілі алгоритм негізінде есепті шешу жолын іздеу (ынталанған ойлау);
-
Көптеген белгілі алгоритмдердің ішінен тиімді нұсқасын таңдау арқылы есептің шешімін іздеу;
-
Әр түрлі алгоритмдердің жекелеген бөліктерін үйлестіру арқылы есепті шешу;
-
Есепті шешудің жаңаша түрін табу (шығармашылық ойлау):
-
Терең логикалық пайымдаулар (талдау, салыстыру, синтез, топтастыру, ақыл қорытындысы және т.б.) негізінде;
-
Ұқсастықтарды қолдану негізінде;
-
Эвристикалық амалдарды қолдану негізінде;
-
Сынау және қателесудің қарапайым әдістерін қолдану негізінде;
-
-
Қателескен жағдайда:
-
Ашулану, басқа әрекетке ауысып кету, «инкубациялық демалу» - «ойдың пісуі», нұрға бөлену, шабыттану, инсайд, белгілі бір проблеманы шешу жолын сол мезетте ұғыну (интуитивтік ойлау);
«Нұрға бөленуге» көмектесетін факторлар:
а) проблемаға деген үлкен қызығушылық;
ә) жетістікке, проблеманың шешілуіне деген сенімділік;
б) проблема туралы көп ақпаратты білу, жиналған тәжірибе;
в) мидың үлкен ассоциациялық әрекеті (ұйықтаған кезде, дене қызуы жоғарылағанда, безгек кезінде, жағымды эмоциялық түрткі кезінде);
-
Есепті шешудің табылған жолын логикалық түрде дәлелдеу, шешімнің дұрыстығының логикалық дәлелдеуі;
-
Шешімді іске асыру;
-
Табылған шешімді тексеру;
-
Түзету (қажет болған жағдайда 2-кезеңге қайта оралу).
Ойлау әрекеті саналы деңгейде де, санасыз деңгейде де жүзеге асады, күрделі ауысулар және бұл кезеңдердің өзара байланысымен сипатталады. Сәтті (мақсатты) әрекет нәтижесінде алдын ала мақсатқа сәйкес келетін нәтиже шығады.
Осылайша, ойлауды дамыту кезінде жеке-жеке іске аспайтын, бір-бірімен байланысатын амалдардың көптүрлілігі қажет.
2.2 Тақырыпты оқыту кезіндегі қолданылатын әдістер
Оқыту әдістері дегеніміз – оқу материалын анықтап алу арқылы белгілі бір мақсатқа жетуге бағытталған мұғалім мен оқушылар арасындағы өзара әрекетті тізбектеп алмастыру. «Әдіс» (грек тілінен – «бірдеңеге жету жолы») – мақсатқа жету тәсілі, білімді алу тәсілі. Педагогикалық әдебиеттерде «оқыту әдісі» ұғымына анықтама мен оның рөлі жөнінде бірыңғай пікір жоқ. Мысалы, Ю.К.Бабанский «оқыту әдісі» деген – білім берудің міндеттерін орындаудағы мұғалім мен оқушылардың арасындағы бірыңғай реттелген байланыс әрекеті деп есептейді. Т.А.Ильина оқыту әдістерін «оқушылардың танымдық іс-әрекетін ұйымдастырудың тәсілі» деп түсіндіреді.
Дидактика тарихында оқыту әдістерінің әр түрлі топтары бар. Әдістердің көп таралған тобы мазмұнды жеткізудің түрлеріне негізделеді. Бұл сөздік, практикалық және көрнекі әдістер:
-
Сөздік әдістер: әңгімелеу, баяндау;
-
Практикалық әдістер: жаттығу, машықтану;
-
Көрнекі әдістер: көрнекіліктерді, плакаттарды көрсету.
Әдістердің тағы бір тобы жеке тұлғаны қалыптастыру негізінде құрылған:
-
Сананы қалыптастыру әдістері: әңгімелеу, баяндау, нұсқама, көрсету, көрнекілеу;
-
Іс-әрекетті қалыптастыру әдістері: жаттығу, машықтану, өзін-өзі басқару;
-
Сезімдерді қалыптастыру әдістері (түрткі беру): мадақтау, бақылау.
Кесте 1
Оқушылардың әрекет түрлеріне қарай бөлінетін әдістер тобы
|
Әдіс |
Әрекет түрі |
Оқушының ой әрекетінің деңгейлері |
Білімнің деңгейлері |
Мазмұн |
Жақсарту |
|
1. Түсіндір-мелі көрнекі |
Мұғалім-нің көмегімен |
І – тану |
ІІ – тану білімі |
Дәстүрлі оқыту – белгілі дайын білімді беру үрдісі |
Бағдарламалы оқыту |
|
2. Репродук-тивті |
Оқушы-ның өзі |
ІІ – жаңғырту |
ІІ – тану білімі |
1-кестенің жалғасы
|
3. Пробле-малық оқыту |
Мұғалімнің көмегімен |
ІІІ – қолдану |
ІІІ – қолдану білімі |
Проблема-лық оқыту– белсенді ізденістің және оқушылар-дың жаңа білімді ашу үрдісі |
Іскерлік ойындар |
|
4. Жарты-лай ізден-гіш |
Мұғалімнің бақылауы-мен |
ІІІ – қолдану IV – шығарма-шылық |
ІІІ – қолдану білімі IV – өзгерту білімі |
||
|
5. Зерттеу-шілік |
Мұғалімнің көмегінсіз |
IV – шығарма-шылық |
IV – өзгерту білімі |
Сонымен қатар әдістердің монологтық (ақпараттық-хабарламалық) тобы да бар, мысалы: әңгіме, лекция, түсіндіру және оқу материалын диалогтік түрде айту (әңгімелесу, проблемалық оқыту, диспут).
Оқушылардың әрекет түрлеріне (өз бетімен жұмыстану және шығармашылық деңгейлері) қарай бөлінетін әдістер тобының тағы біреуіне тоқталайық. Бұл өнімді топты 1965 ж И.Я.Лернер мен М.Н.Скаткин ұсынған болатын. Олар оқыту әдістеріне деген бұрынғы көзқарастар әдістердің сыртқы құрылымының немесе дереккөздерінің әр түрлілігіне сүйеніп жасалғанын айтты. Оқытудың жетістігі оқушылардың белсенділігін мен бағытына, әрекет түрлеріне байланысты болғандықтан, осы аталған әрекет түрі, өз бетімен жұмыстану және шығармашылық деңгей әдісті таңдаудың маңызды критерийлері болуы керек. И.Я.Лернер мен М.Н.Скаткин оқыту әдістерінің бес түрін бөлуді ұсынды және бұл топтағы әрбір келесі әдісті қолдануда оқушылардың белсенділігі мен өз бетімен жұмыстану деңгейі арта береді.
-
Оқытудың түсіндірмелі-көрнекі әдісі (мұғалім түсіндіреді, оқу материалын көрнекі түрде көрсетеді) –лекция, әңгіме, тәжірибелерді көрсету, экскурсия және т.б. түрінде өткізіледі. Оқушының қызметі ақпаратты алуға, тануға бағытталады, нәтижесінде «тану білімі» қалыптасады.
-
Репродуктивті әдіс – мұғалім оқушылар алған білімін пайдалануға, қызмет тәсілдерін, есепті шешу, тәжірибелерді еске түсіруге бағытталған тапсырмалар әзірлейді, бұл арқылы оқушы өз бетімен белсенді түрде оқу материалын пайдаланады: сұрақтарға жауап береді, есептерді шешеді және т.б.; нәтижесінде «көшірме білім» қалыптасады.
-
Проблемалық оқыту әдісі. Әр түрлі дереккөздер мен тәсілдерді қолдана отырып мұғалім материалды берместен бұрын проблемалық сұрақ қояды, танымдық есепті береді, сонан соң дәлелдер жүйесін ашып, әр түрлі көзқарастарды салыстыра отырып, берілген есепті шешу тәсілін көрсетеді. Оқушылар өздерін ғылыми ізденістің куәсі болғандай сезінеді. Бұрынғы кезде де, қазіргі кезде бұл әдіс кеңінен қолданылады.
-
Жартылай ізденгіш немесе эвристикалық әдіс. Оқыту барысында берілген (немесе өз бетімен жасалған) танымдық есепті шешудің жолдарын мұғалімнің басшылығы немесе эвристикалық бағдарламалар мен нұсқаулар арқылы белсенді түрде іздеуді ұйымдастыруға негізделеді. Ойлау үрдісі өнімді түрде болады, бірақ бағдарламалармен (соның ішінде компьютерлік бағдарламалар) және оқу әдебиеттерімен жұмыстану арқылы мұғалім немесе оқушылардың өздері ойлау кезеңдерін бағыттайды және бақылайды. Түрлерінің бірі эвристикалық әңгімелесу болатын мұндай әдіс семинарлар мен коллоквиумдарда ойлауды жандандырудың танымдық әрекетке қызығушылықты арттырудың тиімді тәсілі болып табылады.
-
Зерттеушілік әдіс. Материалды талдау, проблеманы қою және ауызша немесе жазбаша қысқаша нұсқаулықпен танысқаннан кейін оқушылар өз бетімен әдебиеттермен, дереккөздермен танысады, бақылау жүргізеді және басқа да іздену жұмыстарын атқарады. Зерттеу әрекеті кезінде ықылас, ынта, өз бетімен жұмыс, шығармашылық ізденіс толық көрініс табады. Оқу жұмысының әдістері ғылыми зерттеу әдістеріне еріксіз айналып кетеді.
Оқыту үрдісінде әдіс белгілі бір оқу-тәрбиелік мақсаттарға жетудің мұғалім мен оқушылардың байланысқан қызметінің ыңғайластырылған тәсілі ретінде және оқушылардың оқу-танымдық іс-әрекеттерін ұйымдастырудың тәсілі ретінде қарастырылады.
Түсіндірмелі-көрнекі және репродуктивті әдістері – оқушылардың дайын белгілі білімді жеткізу үрдісі болып табылатын дәстүрлі оқытудың әдістері.
Дәстүрлі оқытудың кемшіліктері:
-
материалды оқудың жалпы орташа жылдамдығы;
-
оқушыларға берілетін білімнің бірыңғай орташа көлемі;
-
өзіндік жұмыстар қарастырылмаған мұғалім арқылы дайын түрде алынатын білімнің үлкен көлемі, оның нәтижесінде оқушы «ойлануды ұмытады»;
-
айтылған білімді оқушылардың түсінгенінен немесе түсінбегенінен мұғалімнің хабарсыз болуы;
-
материалды берудің сөздік әдістерінің көп болуы, ол зейіннің шашыраңқы болуына әкеледі;
-
оқу материалының бөлініп берілмеуінің салдарынан оқушылардың оқулықпен өз бетімен жұмыстана алмауы;
-
оқушылардың еске сақтауына үлкен ауырлық, себебі оқу материалын еске сақтап айту керек; кімнің еске сақтауы жақсы – сол жақсы айтып береді.
Бірақ болашақтағы кәсіптік қызметте ақпаратты жаттап алуды мен нақты айтып берудің мұндай әдістері қажет болмайды және қолданылмайды, сондықтан, басқа жағынан қарағанда, оқушы кәсіби қызметте кездесетін жұмыстың түрлеріне (өндірістік мәселені шешу үшін қажетті ақпаратты табу, күрделі жағдайларда шығармашылық шешімді таба білу біліктігі) дайын болмайды. Осылайша, дәстүрлі оқыту кезінде адамға оқу үрдісінде қойылатын талаптар мен кәсіптік қызметте қойылатын талаптар арасында қажетті сәйкестік байқалмайды.
Дәстүрлі оқытудың кейбір кемшіліктері 60-жылдары педагогика, психология және кибернетиканың тоғысында пайда болған бағдарламаланған оқыту арқылы түзетіледі. Бағдарламаланған оқыту негізінде оқыту туралы үш ой жатыр: 1) басқару үрдісі ретінде, 2) ақпараттық үрдіс ретінде және 3) жекелеген үрдіс ретінде.
Бағдарламаланған оқыту негізінде 1) оқу бағдарламасы; 2) оқу бағдарламасын меңгеру бойынша оқушының іс-әрекеті; 3) меңгеруді бақылау түрлері жүйеленген оқыту бағдарламасы бар.
Оқу материалы көлемі аз логикалық аяқталған шағын бөлімдерге бөлінеді, әрбір бөлімді меңгергеннен кейін мұғалім-программист алдын ала әзірлеген бірнеше жауаптың ішінен оқушы дұрыс жауабын таңдау арқылы бақылау сұрақтарына жауап береді немесе берілген символдар, әріптер, цифрлар арқылы жауапты өзі айтады. Егер дұрыс жауап берілсе, келесі оқу бөлімі беріледі. Қате жауап берілген болса, оқу бөлімін тағы бір қайталап, сұраққа тағы да жауап беру қажеттілігі туады.
Бейімделген бағдарламалар бағдарламаның оңай немесе қиын бөлімдеріне өтуге мүмкіндік береді және бұл ауысу оқушының алдыңғы жауаптары мен қателерін ескеру негізінде жүргізіледі. Бейімделген оқу бағдарламасына оқушылардың жауаптарын талдау схемасы, сондай-ақ оқушының жеке ерекшеліктеріне және жауаптарына қарай ақпаратты беру тәсілін, қиындық деңгейін, оқу материалының тереңдігі мен көлемін, сұрақтардың түрлерін және т.б. өзгерту мүмкіндігі қарастырылған параллельді ішкі бағдарламалар топтамасы енгізіледі.
Құрастырылған оқу бағдарламасы техникалық құрал – компьютер арқылы немесе «шатастырылған беттер» түрінде жасалған (берген жауабына сәйкес оқушы оқулықтың белгілі бір бетіне ауысады) бағдарламаланған оқулықтар арқылы жүзеге асырылуы мүмкін.
Бағдарламаланған оқытудың негізгі принциптері мен артықшылықтары:
-
оқу материалының мөлшерлі түрде болуы;
-
оқушының белсенді түрде өз бетімен жұмыстануы;
-
меңгеруді тұрақты бақылануы;
-
оқыту жылдамдығын, оқу материалының көлемін дараландыру;
-
оқытудың автоматтандырылған техникалық құралдарын қолдану мүмкіндігі.
Бағдарламаланған оқыту нақты материалға және біркелкі, нақты формулалары мен алгоритмдері бар қайталанатын іс-әрекеттерге негізделген пәндерді оқытуда пайдалы болмақ. Бағдарламаланған оқыту басты міндеті – автоматтандырылған дағды, берік біркелкі білім мен білікті қалыптастыру.
Бағдарламаланған оқыту оқытудың техникалық тәсілдерін қолдануға және дамытуға ықпал етті. Оқытудың техникалық тәсілдеріне (ОТТ) оқу үрдісінің тиімділігін арттыру мақсатында қолданылатын оқу-дидактикалық материалдармен қатар пайдаланылатын әр түрлі құрылғылар, машиналар және жүйелер жатады. Олар: 1) ақпараттық ОТТ – ақпаратты ұсынудың техникалық құралдары, 2) бақылаушы ОТТ, 3) оқытуды басқарудың тұйықталған циклын қамтамасыз ететін бағдарламаланған оқытуды орындайтын оқыту ОТТ деп бөлінеді.
2.3 Практикалық сабақтарды өткізуге арналған әдістемелік ұсыныстар
Сабақты бастау
Істі жаңадан бастау қиын, сабақты бастау да қиын болады. Себебі сабақтың бірінші минутынан-ақ мұғалім мен оқушылардың белгіленген мақсатқа жетудегі бірлескен қызметі жемісті болу үшін қажетті жағдай жасалуы керек. Бұл кезде туындаған қиындықтар төмендегі мәселелерді шешумен байланысты болады:
-
ұйымдастырушылық;
-
мазмұндық;
-
этикалық.
Ұйымдастырушылық мәселелерді шешу қажеттілігі мұғалім қоңырау соғылғаннан кейін сыныпқа кіргеннен-ақ басталады. Оның алғашқысы – мұғалім мен оқушының бір-бірімен амандасуы.
Егер бұл үрдіс оқушыларда қалыптаспаған болса, онда бұл жағдайды әдетте бір-екі сабақта өзгерту мүмкін болмайды. Бұл жағдайда шыдамдылық пен табандылық танытып, оқушылардан берілген әрекетті орындауларын, соның ішінде мұғаліммен амандасудан кейін жұмыс орындарына отыруларын талап ету керек.
Оқыту кезінде сабақтың басында әдетте ұйымдастырушылық мәселелерді шешу проблемасы болмайды: оқушылар сабақ басталысымен сабаққа кірісіп кетеді және мұғалімнің бастамасы мен ынтасын сақтай отырып, оқитын материалымен ғана шұғылданады. Шын мәнінде бұның артында оқушылардың бойында сабақ басындағы қажетті дағдыларды қалыптастырудағы мұғалімнің ұзақ және тыңғылықты жұмысы тұрады.
Кей кездері жоспарланған жұмысқа оқушылардың назарын аударту қажеттілігі туады. Бұл үшін оқушыларға «Назар аударыңдар, сабақты бастаймыз» деп айту жеткілікті болады. Егер оқушылар аса қозғалғыш күйде болса, онда мұндай үндеу нәтижесін болады. Мұндай жағдайлар бақылау жұмыстарынан кейін, сыныптағы жеке кикілжің жағдайлардан кейін болады. Бұл кезде сабақты оқылған материал негізінде құрылған қызықты тапсырмаларды қолдану арқылы бастаған жөн. Сонда оларды орындау үрдісінің өзі, әсіресе жазбаша жұмысты орындау үрдісі, қозғалғыш күйді төмендетуге және оқушыларды қалыпты жағдайға түсіріп, сабақты бастауға мүмкіндік береді. Көп жағдайда бұл уақытта үй тапсырмасын орындауды тексеру үрдісі жүргізіледі.
Сабақтың басында мазмұнды тапсырмаларды беру және шешу үрдісі бірнеше тәсілмен жүзеге асуы мүмкін. Олар кімнің және қалай таңдауына, жасауына және беруіне қарай топталады:
-
тек қана мұғаліммен (жаңа материалды оқып үйренуде қолданылады, басты рөл мұғалімге беріледі);
-
оқушылар және мұғаліммен (мұғалім өз ойын әдейі аяқтамайды да, оқушылардан аяқтауды сұрайды). Осылайша, оқушылар мысалдың соңын табу үшін логикалық ойланады, яғни шешу жолын ұсынады.
-
оқушылардың өздерімен.
Оқыту кезінде сабақтағы алдын ала жасалатын мазмұндық жұмыс көп жағдайда тек қана мұғаліммен ұйымдастырылады. Бұл жұмыс оқушылардың жаңа материалды оқып үйренуге, бұрыннан бар білімді пайдалануға, жаңа біліктерді меңгеруге дайындайды. Бұл мақсатта сабақтың басында математикалық диктанттар, ойын түріндегі тапсырмалар, заңдылықты анықтауға арналған тапсырмалар, берілген есепті шешудің тиімді жолын табуға арналған тапсырмалар беріледі. Алайда, тек бір ғана тапсырманы қайталап өткізе беруге болмайды. Қолданылатын тапсырмаларды әрдайым түрлендіру кенеттік және жаңашылдық элементтерін енгізеді, яғни оқушылардың сабаққа деген қызығушылығын бірінші минуттан оятуға көмектеседі.
Оқыту кезінде сабақтағы алдын ала жасалатын мазмұндық жұмысты түрлендіруге оқушыларды да тартуға болады. Бұл жерде тек оқушылардың қызығушылығын арттыру ғана емес, сонымен қатар олардың көмегінің қажет екенін көрсету арқылы сенімдерін арттыруға болады. Ол үшін оқушыларға математикалық сөзжұмбақ құрастыруды тапсыруға болады.
Әрине, алғашқы уақытта оқушылардың дайындаған жұмыстарында мұғалімнің жұмыстарынан көп айырмашылық болмайды. Бірақ, оқушыларды мадақтау және ынталандыру қажет, бұл олардың өз-өзін реттеу үрдісін жақсартады. Сол кезде оқушылар өз идеяларын терең ойлап, қосымша әдебиеттермен таныса бастайды. Бұл уақытта оқушылар мұғалімнің өзі де шеше алмайтын тапсырма алып келеді деп қорықпау керек. Мұндай жағдайларда оқушылардың өздері есептің шешімін көрсетіп, жақсы баға алуларына болады. Әрине, мұғалім осындай рөлде өте сирек болуы керек, ал ол үшін мұғалімнің өзі де ұдайы ізденісте болу керек.
Осылайша, сабақтағы алдын ала жасалатын мазмұндық жұмысты түрлендірудің тәсілдерін кешенді түрде жүзеге асыру арқылы әр сабақты бірдей әрекеттермен бастау мүмкін болмайды. Бұл жерде оқушылар «сабақтағы қызметтің біркелкі болуынан шаршайды, ал жаңа бастама қызықты болған жағдайда сабақтың басқа бөлігі дәстүрлі түрде ұйымдастырылған болса да, шаршаудан аулақ болуға көмектесетінін» ескерту орынды болады.
Сабақтың сәтті өтуіне оның бастамасынан оқушылар үшін жағымды эмоциялық климат орнатудың да маңызы зор.
Мұғалімнің жағымды құлшынысы, атқарып жатқан іспен әуестенуі, сабақты жақсы көңіл-күймен бастау және өткізу іскерлігі оқушылар тарапынан жоғары бағаланады. Сабақ кезінде өзіңнің жайсыздығыңызды, сабырсыздығыңызды, дөрекілігіңізді, ашық ызаңызды, жұмысқа деген немқұрайлығыңызды көрсетуге болмайды.
Мұғалім өзінің тілінің сауаттылығына назар аудару керек, қажет емесе дыбыстар мен сөздерден құтылып, негізгі ойды айту кезінде қысқа, нақты және логикалық түрде дұрыс айтып, тілді «ал», «қысқасы», «жаңағы» және т.б. тәрізді паразит сөздерден тазарту керек. Оқушыларды біркелкі тыныш немесе қатты дауыс ашуландыратындықтан, сыныптағы жағдайға байланысты дауыстың күші мен үнін өзгертіп отыру керек.
Сабақтың басында жоғарыда көрсетілген мәселелердің барлығын шешу іскерлігі сабақтың ары қарай өтуіне әсер етеді: ол сабақтың қажетті қарқынын, эмоциялық климатты, мұғалім мен оқушылардың өнімді жұмысын анықтайды.
Жаңа материалды оқып үйрену бойынша әдістемелік ұсыныстар
Сабақтың құрылымындағы басты мәселе – жаңа материалды оқып үйрену. Сабақтың барысындағы сұрақтар жаңа тақырыпқа негізделе отырып немесе байланыса отырып шешіледі. Математиканы оқыту кезінде ол көбіне математикалық ұғымдарды, сөйлемдерді, теоремаларды оқып үйренуге саяды. Бұл жағдайда үш негізгі кезеңді бөлуге болады: қабылдауға дайындық, кіріспе және жаңа материалды алғашқы ұғыну.
Жаңа материалды қабылдауға дайындық кезеңі тірек ұғымдардың қалыптасуымен байланысты. Оқушылардың жаңа білімді меңгеруге дайындығын қамтамасыз етуге бағытталады. Мұндай білім беру жаңаны меңгеруді немесе тірек білімді өзектендіруді ынталандыруға тиісті назар аудармауда байқалады.
-
Негізгі белгілерді анықтау мен тірек білімді өзектендіру арқылы оқып үйренуге дайындау алдын ала практикалық есептерді шешу, көрнекі материалдарды көрсету, тарихи мәліметтерді қысқаша баяндау үрдісі кезінде жүзеге асыруға болады. Расында да, қандай да бір математикалық ұғымды дәйектеуде оны одан да кең ұғымға, ал ол кең ұғымды одан да үлкен ұғымға әкелуге болады.
-
Оқушыларды көпмүшелердің қасиеттерін сипаттайтын теоремаларды, ұғынуға дайындау барысында теоремаларды, аксиомаларды, математикалық сөйлемдерді дәлелдеусіз алуға болады.
Оқушыларға теоремалардың тұжырымдамасын ұғынуды жеңілдету үшін болжамды ұсынуда бірлесіп жұмыстануды ұйымдастыруға болады. Ол үшін оқушыларда белгіленген өрнектерді жазу, оқу, орналастыру бойынша дағдылардың қалыптасуына бағытталған жоспарлы түрде бірнеше тізбектелген сабақтарда белгілі бір жаттығуларды орындау қажет.
Жаңа материалды оқып үйрену кезінде оқушылардың қызметін басқару психологиялық-дидактикалық заңдылықтарды ескеру арқылы жүргізілу керек. Бұл кезде оқушы сабаққа енжарлықпен қатысса, көптеген мәліметтерді ұқпай қалатынын есте сақтау қажет. Материалды толық ұғыну үшін төмендегідей шарттарды орындаған кезде мәліметтермен танысу барысында ұлғая беретін белсенді ой қызметі жүзеге асырылу қажет:
-
оқушылар материалмен танысу барысында берілген материалды терең түсінуге көмектесетін белгілі бір тапсырманы орындайды;
-
бұл тапсырма оқушының күшін ой қызметінің белгілі бір тәсілін қолдануға бағыттайды;
-
оқушының берілген тапсырманы орындауға қажет болатын білімі бар;
-
материал аса жеңіл емес.
Жұмыстың соңында жаңа материалдың ұғынуға тиісті негізгі мазмұнын және онымен жұмыстанудың тәсілдерін бекіту арқылы қол жеткізілетін «таңбаны» ерекшелеу керек.
Әрине, жаңа материалды оқып үйрену кезінде оны ұғыну, түсіну, еске сақтау, қолдану білігі тәрізді сұрақтар жаңадан шешіле бастайды. Аталған үрдістер оқып үйренген материалды бекіту кезінде дамиды, ал бекітуді келесі бөлімде жекелеп қарастырамыз.
Оқып үйренгенді бекіту бойынша әдістемелік ұсыныстар
Оқып үйренгенді бекіту кезінде оқушылардың оқу материалын меңгеруінің бағдарламаның шарттарына сай келетін деңгейде болуы қамтамасыз етіледі.
Белгілі болғандай, білім тек қана онымен өз бетімен тиісті деңгейде жұмыстануда меңгеріледі. Сондықтан мұғалім тарапынан барысы мен алынатын нәтижелерді бақылау мүмкіндігі болатындай оқушылардың өз бетімен жұмыстануды ұйымдастыруға назар аударылу керек. Мұндай іс-әрекет біртіндеп сыртқы бақылауды өткізумен аяқталып, бұл әрекеттерді ойша орындауға көшумен жалғасу керек.
Бекіту барысында оқу материалын есте сақтауды және есептер шығару кезінде қолдану білігін қалыптастыруды қамтамасыз етуге болады.
Әрине, оқып үйрену кезінде оқушыға көптеген мәліметті әдейі жаттауға тура келеді. Бұл кезде ол өзіне мақсат қою керек – өзі немесе мұғалім белгілеген материалды барынша толық, нақты және берік есте сақтау. Мұнда мұғалім оқушыларға осы тақырып бойынша бақылау жұмысын жазасыңдар деген уәж өткізу керек.
Әлбетте, оқушы материалды дұрыс түсінбеген жағдайда, оны есте сақтау қиындайды. Үлкен көлемді материалды оқып үйрену кезінде де мұндай қиындық кездеседі. Жалпы айтқанда, оқушылар белсенді ой қызметімен айналысқан жағдайда ғана берілген материалды терең түсініп, жақсы есте сақтайды.
Оқу материалын жаттау кезінде оны дауыстап немесе іштен оқумен ғана шектелмеу керек. Сондай-ақ оны еске түсіріп қайта жаңғырту арқылы жазбаша орындау керек. Сондықтан тақырыпты түсіндіруге қатысты мәселелер айтылғанды дәптерге түсіру арқылы беріледі. Бұл жағдайда материал берік есте сақталады, себебі көзден миға баратын жүйке талшықтары құлақтан миға баратын жүйке талшықтарынан жиырма бес есе қалың болады.
Есте сақтауға қарама-қарсы үрдіс ұмыту болып табылады. Ол адамның ағзасына биологиялық тұрғыдан алғанда абзал. Ұмытудың қарқындылығы жаттағаннан кейінгі алғашқы уақытта көп болады. Мәнсіз материалды ұмыту (оқығаннан кейінгі сегіз сағат ішінде келесі отыз күнге қарағанда көп ұмытылады) мәні терең материалды ұмытуға қарағанда тез жүргізілсе де, бұл заңдылық жалпы заңдылық болып табылады.
Ұмытудың алдын алудың бірден бір тәсілі оқығанды қайталау және оны жаңа есептерді шығаруға қосу болып табылады. Біртектес есептерді шығару арқылы біркелкі түрде қайталаудың нәтижелілігі өте аз. Бірақ бұл біртектес есептерден бас тарту керек дегенді білдірмейді. Бұл кезде мұндай қайталауды жиі өткізуге болмайтынын, біртектес есептердің санын үштен көп болмауын қадағалау керектігін ескеру керек.
Осылайша, сабақта өтілген материалды нәтижелі түрде қайталау және бекіту үшін тексеру жұмыстары және өзіндік жұмыстар қарастырылады. Сыныпта өткізілетін мұндай жұмыстардың мазмұны, түрі, ұзақтығы сабақтың қойылған мақсаттарына сай болу керек. Кей кездері олар те бірнеше минутта, ал кей кездері сабақтың өн бойында өтуі мүмкін.
Білім мен біліктің диагностикасы
Қазіргі заманғы мұғалім мен оқушылардың бағдарламалық материалды меңгеру қызметінің негізгі бөлімдері: бағыттаушылық, орындаушылық және тексерушілік. Тексерушілік бөлімде «Мұғалім – оқушы» жүйесінде кері байланыс орнатылады, кері байланыс оқушылардың оқу материалын меңгеру сапасын анықтауға, уақтылы диагностикалауға және олардың білімі мен біліктерді түзетуге арналған ақпаратты үнемі алып тұруға мүмкіндік береді. Басқаша айтқанда, тексеру кезінде оқушылардың білімі мен біліктері анықталып, бағаланады және оқушылардың оқуын, тәрбиесі мен дамуын ауызша басқару үшін қажетті ақпаратты алуға және жинақтауға мүмкіндік береді.
Осы орайда тексеруді үш түрге жіктейді:

Сырттай тексеру оқушыларды оқу жұмысын сапалы және жүйелі орындауға үйретеді, жұмысты одан да жақсы етіп істеуге деген құлшынысты арттырады, ал мақсатқа бағытталған жұмыс барысында мұғалімдер өзара тексеру мен өзін-өзі тексерудің дамуына ықпал етеді.
Өзін-өзі тексеру кезінде оқушының өзі жасаған әрекеттердің дұрыстығын сезінеді және болашақта қате жасамауға тырысатын болады.
Өзін-өзі тексеру сызбасын келтірейік:

Берілген сызбаны дәлелдейтін бірнеше мысал келтірейік.
-
Өзін-өзі тексеруге деген қажеттіліктің қалыптасуын тапсырмаларды өз бетімен орындау кезінде ұйымдастыруға болады. Мысалы, оқушылардың біреуіне «Горнер схемасы» тақырыбы бойынша тапсырмалар беріледі, оқушы оны орындағаннан кейін шығару жолын тақтада көрсетіп, шешу жолын түсіндіреді.
-
Оқушылардың мұғалімнің қызметін тексеруге ерекше назар аудару керек. Тақырыпты түсіндіру кезінде мұғалім әдейілеп қате жіберуі мүмкін. Егер оқушылар қатені бірден байқап қалмаса, онда мұғалім «жетекші» сұрақтар арқылы оқушыларды қажеттісіне алып келеді.
-
Оқушылардың бір-бірін өзара тексеруін келесідей ұйымдастыруға болады. 10 минутқа арналған тексеру жұмысын жүргізу керек. Сабақтың соңына қарай (2 минутқа таман) есептеуді тоқтату және «ал енді парақтарды көршілеріңмен ауыстырып, көршіңіздің жұмысын тексеріңдер. Тексеріп болғаннан кейін, көршіңіздің жұмысына сіздің ойыңызша лайық бағаны қойыңдар» деп айту керек.
Жалпы алғанда, тексеру мақсатты, объективті, жанжақты, жүйелі және жеке болу керек. Оның нәтижелілігі оқушының білімі мен білігінің бағдарламаның шарттарымен сәйкестік деңгейін сипаттайтын бағамен өрнектеледі. Бұл нормаларға сәйкестік белгі деп аталатын бағаны жазудың сандық немесе басқа да символдық түрде болуы мүмкін.
-
Көпмүшелердің бөлінгіштік қасиеттерін қолдану
Бұл тақырыпты оқып үйрену үшін оқушылардың бастапқы білімдерін және көпмүшелердің бөлінгіштік белгілері туралы теореманы қайталап алу керек. Оқушылардың қарастырылып отырған теореманың тұжырымы мен мәнін дұрыс түсінуін тексеріп алу керек. Оны төменде көрсетілген мысалдар арқылы тексеруге болады:
Оқушыларға «Оқып кеткен теореманы бекіту үшін мысалды қарастырайық» деген ұсыныс беру керек.
Оқушылардың біреуін тақтаға шақырып, қайталаған материалды қолдана отырып берілген мысалды шешуді сұрау керек. Бұл кезде басқа оқушылар осы мысалды орындарында өз беттерімен шығарып бастайды, тек тақтада шығарып жатқан оқушының есебімен әлсін-әлсін салыстырып отырады. Тақтадағы шығару жолы мұғалімнің бақылауымен жүргізілуі керек.
Мысал
1.  көпмүшесі
көпмүшесі  көпмүшесіне бөлінетіндігі белгілі. Бөліндіні
табыңдар.
көпмүшесіне бөлінетіндігі белгілі. Бөліндіні
табыңдар.
Шешу жолын анықтап алғаннан кейін, тақтада тұрған оқушыдан шығару жолын түсіндіріп тұруын сұрау ету керек. Бұл әрекет материалдың меңгерілуін тағы да бекітуге мүмкіндік береді.
Шешуі. Төртінші дәрежелі көпмүшені
екінші дәрежелі көпмүшеге бөлгендегі бөлінді екінші дәрежелі
көпмүше болады. Төртінші дәрежелі көпмүшені екінші дәрежелі
көпмүшеге бөлгендегі бөлінді болатын көпмүшені табу үшін жаңа
айнымалыны енгізу қажет. Ізделінді көпмүше  болсын. Онда мына теңдік дұрыс
болады:
болсын. Онда мына теңдік дұрыс
болады:

 көпмүшесіне тең
болатын
көпмүшесіне тең
болатын  көпмүшені қарастырамыз. Екі көпмүшеде де
х-тің дәрежелері бірдей, бірақ
коэффициенттері әр түрлі екені көрініп тұр.
х-тің бірдей дәрежелеріндегі
коэффициенттерді теңестіру арқылы, төмендегі жүйені
аламыз:
көпмүшені қарастырамыз. Екі көпмүшеде де
х-тің дәрежелері бірдей, бірақ
коэффициенттері әр түрлі екені көрініп тұр.
х-тің бірдей дәрежелеріндегі
коэффициенттерді теңестіру арқылы, төмендегі жүйені
аламыз:
 , бұдан
, бұдан
 .
.
Жаңа айнымалы болып
енгізілген  қайтып келеміз, құрылған және шешілген
жүйеден
қайтып келеміз, құрылған және шешілген
жүйеден  болады. Сонымен,
болады. Сонымен,  көпмүшесін
көпмүшесін  көпмүшесіне бөлгендегі бөлінді
көпмүшесіне бөлгендегі бөлінді  болады.
болады.
-
Безу теоремасы мен оның салдарларын оқып үйренудің әдістемесі
Осы тақырыпты оқып үйрену сабағын ұзақтығы 30 минуттан аспайтын лекция түрінде өткізуге болады.
Бұл әдісті педагогикалық әдебиеттерде түсіндірмелі-көрнекілік әдіс деп, әдістемелік әдебиеттерде – мектептік лекция деп аталады. Мұнда лекциялық әдістің негізгі ерекшеліктерін ерекшелеу үшін«жауаптың үлгісі» деген өзінше атау берілді.
Қарастырылып тұрған әдіске қойылатын негізгі талап – мұғалімнің түсіндіруін (қысқаша немесе ұзақ) жауаптың үлгілері ретінде қарастыру керек. Бұл жерде теориялық сұрақтарды баяндау үлгілері ғана емес, сондай-ақ, ең бастысы, есепті шығару үлгілері қарастырылу керек.
Есепті шығарудағы жауаптың үлгісі – байланысқан түрдегі әңгімелеудің маңызды тәсілдерінің бірі. Орындап жатқан тапсырманы жүйелі әңгіме ретінде мүлтіксіз баяндау және түсіндіру біліктерінің қалыптасуы мұғалімнің түсіндіруінен басталады. Мұғалім жаңа типті тапсырманы қалай орындалу керектігін, жазбаларды қалай орналастыру керектігін, орындап жатқан амалдарды қай уақытта және қалай түсіндіру керектігін көрсетеді.
Мұғалімнің баяндауымен беріліп тұрған жауап үлгісі – жүйелі әңгімелеуге үйретудегі қажетті кезең. Себебі мұғалімнің жаңа типтегі жаттығуды орындау үлгісінде (егер де бұл үлгі жоғарыда көрсетілген шарттарға сай болса) мазмұндық элементтер (қалай орындау қажет?) ғана емес, сонымен қатар дәл әдістемелік компоненттер (қалай түсіндіру керек, жазбаларды қалай орналастыру керек, сызбаларды қалай көрсету керек? және т.б.) болады. Жауап үлгісінің аталған дәл әдістемелік компоненттерін алғаш рет мұғалім беруі мүмкін.
Лекция сабағын өткізудегі ең бастысы – оқушылардың белсенді ойлау қабілеттеріне қол жеткізу. Мұғалімнің тәжірибесінде оқушылардың әңгімелеу барысында белсенді ойлауына қол жеткізуге көмектесетін тәсілдері көп болуы керек.
Түсіндіруге кіріспестен бұрын мұғалім сыныпқа жаңа материалды түсуге бағыттайтын нақты тапсырма береді. Мұғалімнің әңгімелеуі барысында бұл тапсырманың орындалуы оқушылардың ойлау қызметін жандандырады.
Оқыту тәсілдерін қарастырайық.
Мұғалім жаңа материалды түсіндірген кезде әдейі қате жіберетінін, ал оқушылар мұқият тыңдап, сол қатені табу керектігін оқушыларға хабарлайды. Бұл тәсілдің артықшылықтарын білу үшін мұғалім оны екі-үш рет қолданып, оқушылардың қатені табуға құлшынатындықтарын және сабаққа белсенді араласатынын көру керек.
Мысал
2. Теореманың тұжырымын мынадай
түрде беру керек: « көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі бөлінді
екімүшесіне бөлгендегі бөлінді  болғандағы
болғандағы  көпмүшесінің мәніне тең болады, яғни
көпмүшесінің мәніне тең болады, яғни
 ». Оқушылардан тұжырымды оқып,
ойланып, қатесін табуды сұрау
керек.
». Оқушылардан тұжырымды оқып,
ойланып, қатесін табуды сұрау
керек.
Теореманы түсіндіруді бастамастан бұрын мұғалім оны дәлелдеудің жоспарын береді. Жоспар дәлелдеу идеясын түсінуге көмектеседі. Нәтижесінде есте сақтауға деген нұсқау терең түсінуге мүмкіндік туғызады. Мұғалімнің түсіндіруін тыңдай отырып, оқушылар оның пайымдауларын берілген жоспармен сәйкестендіреді, материалдың бір логикалық бөлімінен екінші бөліміне өтуді жеңіл түйсінеді, олардың арасындағы байланысты орнатады. Оқытудың мұндай тәсілін қолданған уақытта оқушылар материалды жақсы меңгереді сондай-ақ, ең бастысы, тыңдауды, жоспарды қолдануды және болашақта мұғалімнің түсіндіруі кезінде жоспарды құруға үйренеді.
Берілген тарауды жақсы меңгеру үшін оқушылар баяндаушының айтқан сөзі мен ойын конспектілеу керек, себебі бұл кезде тек көру және есту арқылы есте сақтау ғана емес, сонымен қатар механикалық есте сақтау да жұмыс істейді.
Горнер схемасы
Горнер схемасын да лекцияға қосуға болады.
Келесідей мысалдарды қарастырып талдаған жөн:
Мысал
3.  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдықты
табыңдар.
екімүшесіне бөлгендегі қалдықты
табыңдар.
Шешуі.  теңдеуін қарастырайық, бұдан
теңдеуін қарастырайық, бұдан  болады. Безу теоремасына сәйкес
болады. Безу теоремасына сәйкес  мәнін
мәнін  көпмүшесіне қойып,
көпмүшесіне қойып,  аламыз. Осылайша,
аламыз. Осылайша,  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдық нөлінші дәрежелі 9 көпмүшесі
болады.
екімүшесіне бөлгендегі қалдық нөлінші дәрежелі 9 көпмүшесі
болады.
Мысал
4.  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдықты
табыңдар.
екімүшесіне бөлгендегі қалдықты
табыңдар.
Шешуі.  теңдеуін қарастырайық, бұдан
теңдеуін қарастырайық, бұдан  болады. Безу теоремасына сәйкес
болады. Безу теоремасына сәйкес  мәнін
мәнін  көпмүшесіне қойып,
көпмүшесіне қойып,
 аламыз.
аламыз.  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдық нөлінші
дәрежелі
екімүшесіне бөлгендегі қалдық нөлінші
дәрежелі  көпмүшесі болады.
көпмүшесі болады.
Мысал
5.  көпмүшесі а)
көпмүшесі а)  екімүшесіне;
екімүшесіне;
ә)  екімүшесіне бөлінеді
ме?
екімүшесіне бөлінеді
ме?
Шешуі. а)  болғандықтан
болғандықтан  екені шығады. Безу теоремасы бойынша:
екені шығады. Безу теоремасы бойынша:
 болады. Көпмүшелерді
бөлгендегі қалдық
болады. Көпмүшелерді
бөлгендегі қалдық  болғандықтан, берілген көпмүше
болғандықтан, берілген көпмүше  екімүшесіне қалдықсыз
бөлінбейді;
екімүшесіне қалдықсыз
бөлінбейді;
ә)
 болғандықтан
болғандықтан
 екені шығады. Безу теоремасы
бойынша:
екені шығады. Безу теоремасы
бойынша:  болады. Көпмүшелерді бөлгенде қалдық болмайтындықтан,
берілген көпмүше
болады. Көпмүшелерді бөлгенде қалдық болмайтындықтан,
берілген көпмүше  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
Мысал
6.  көпмүшесі
көпмүшесі  екімүшесіне бөлінетіндігін
дәлелдеңдер.
екімүшесіне бөлінетіндігін
дәлелдеңдер.
Шешуі.  теңдеуін қарастырайық, бұдан
теңдеуін қарастырайық, бұдан  болады. Безу теоремасына сәйкес:
болады. Безу теоремасына сәйкес:  шығады, яғни
шығады, яғни  көпмүшесі
көпмүшесі  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
Мысал
7.  көпмүшесін
көпмүшесін  екімүшесіне бөліңдер.
екімүшесіне бөліңдер.
Шешуі.  болғандықтан, Салдар 2 бойынша
болғандықтан, Салдар 2 бойынша
 көпмүшесі
көпмүшесі  екімүшесіне бөлінеді және
екімүшесіне бөлінеді және

Мысал
8. Горнер схемасын қолдана
отырып  көпмүшесін
көпмүшесін  екімүшесіне бөліңдер.
екімүшесіне бөліңдер.
Шешуі. Жеңіл және көрнекі болу үшін
бөлінгішті канондық түрде жазайық, яғни  түрінде жазамыз.
түрінде жазамыз.
Горнер схемасын қолданып,

аламыз.
 теңдеуін қарастырайық,
бұдан
теңдеуін қарастырайық,
бұдан  болады. Бұл санды Горнер схемасының сол жақ төменгі
бұрышына жазамыз. Горнер схемасы бойынша есептеудің алгоритмін
қолданамыз.
болады. Бұл санды Горнер схемасының сол жақ төменгі
бұрышына жазамыз. Горнер схемасы бойынша есептеудің алгоритмін
қолданамыз.
Алынған
 сандары
сандары
 көпмүшесін
көпмүшесін
 екімүшесіне бөлгендегі бөлінді
болып табылатын көпмүшенің коэффициенттері
болады.
екімүшесіне бөлгендегі бөлінді
болып табылатын көпмүшенің коэффициенттері
болады.
Сонымен,
бөлінді  және қалдық
және қалдық  болады.
болады.
Яғни
 .
.
Безу теоремасын оқып үйрену
Өткен білімді қайталау, берілген теореманың және салдардың тұжырымын беру, оқушылардың дұрыс түсінуін тексеру. Келесідей мысалды шешуді ұсыну. Мұғалім бұл есепті өз бетінше немесе тақтаға бір оқушыны шақыру арқылы шығаруға болады.
Мысал
9.  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдықты
табыңдар.
екімүшесіне бөлгендегі қалдықты
табыңдар.
Шешуі.  теңдеуін қарастырайық, бұдан
теңдеуін қарастырайық, бұдан  болады. Безу теоремасына сәйкес
болады. Безу теоремасына сәйкес  мәнін
мәнін  көпмүшесіне қойып,
көпмүшесіне қойып,  аламыз. Осылайша,
аламыз. Осылайша,  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдық нөлінші дәрежелі 9 көпмүшесі
болады.
екімүшесіне бөлгендегі қалдық нөлінші дәрежелі 9 көпмүшесі
болады.
Келесі мысалды өз беттерімен дәптерге шығаруды ұсынуға болады, содан соң оқушылар дәптерлерін көршілерімен алмастырып, бір-бірінің қателерін тексеріп, кейіннен дұрыс жауапты айту керек.
Мысал
10.  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдықты
табыңдар.
екімүшесіне бөлгендегі қалдықты
табыңдар.
Шешуі.  теңдеуін қарастырайық, бұдан
теңдеуін қарастырайық, бұдан  болады. Безу теоремасына сәйкес
болады. Безу теоремасына сәйкес  мәнін
мәнін  көпмүшесіне қойып,
көпмүшесіне қойып,  аламыз.
аламыз.  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі қалдық нөлінші
дәрежелі
екімүшесіне бөлгендегі қалдық нөлінші
дәрежелі  көпмүшесі болады.
көпмүшесі болады.
Мысал
11.  көпмүшесі а)
көпмүшесі а)  екімүшесіне;
екімүшесіне;
ә)  екімүшесіне бөлінеді
ме?
екімүшесіне бөлінеді
ме?
Шешуі. а)  болғаннан
болғаннан  екені шығады. Безу теоремасы бойынша:
екені шығады. Безу теоремасы бойынша:
 болады. Көпмүшелерді
бөлгендегі қалдық
болады. Көпмүшелерді
бөлгендегі қалдық  болғандықтан, берілген көпмүше
болғандықтан, берілген көпмүше  екімүшесіне қалдықсыз
бөлінбейді;
екімүшесіне қалдықсыз
бөлінбейді;
ә)
 болғаннан
болғаннан
 екені шығады. Безу теоремасы
бойынша:
екені шығады. Безу теоремасы
бойынша:  болады. Көпмүшелерді бөлгенде қалдық болмайтындықтан,
берілген көпмүше
болады. Көпмүшелерді бөлгенде қалдық болмайтындықтан,
берілген көпмүше  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
Безу теоремасының салдарын қолдану
Теореманы дұрыс түсінген оқушылар төмендегі мысалдарды өз бетінше шығара алады.
Мысал
12.  көпмүшесі
көпмүшесі  екімүшесіне бөлінетіндігін
дәлелдеңдер.
екімүшесіне бөлінетіндігін
дәлелдеңдер.
Шешуі.  теңдеуін қарастырайық, бұдан
теңдеуін қарастырайық, бұдан  болады. Безу теоремасына сәйкес:
болады. Безу теоремасына сәйкес:  шығады, яғни
шығады, яғни  көпмүшесі
көпмүшесі  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
Мысал
13.  көпмүшесін
көпмүшесін  екімүшесіне бөліңдер.
екімүшесіне бөліңдер.
Шешуі.  болғандықтан, Салдар 2 бойынша
болғандықтан, Салдар 2 бойынша
 көпмүшесі
көпмүшесі  екімүшесіне бөлінеді және
екімүшесіне бөлінеді және

Безу теоремасы мен Горнер схемасын қолдану
Өтілген материалды бекіту үшін оқушыларға 10-15 минутқа арналған шағын өзіндік жұмыс беруге болады. Одан кейін оқушылар бір-бірінің жұмысын тексере алады. Өзіндік жұмыс оқушылардың есеп шығару дағдысын нығайту үшін жүргізіледі.
Өзіндік жұмыс 2 нұсқада ұсынылады: 1-нұсқа а) және б) есептерін, 2-нұсқа ә) және в) есептерін орындайды.
Мысал 14. Көбейткіштерге жіктеңдер:
а)

ә)

б)

в)

Шешуі.
а) үлкен дәреженің
коэффициенті 1-ге тең, сондықтан  көпмүшесінің түбірлері бола алатын бүтін сандар бос мүше
12-нің бөлгіштері болады. бұл сандарды теріп жазайық:
көпмүшесінің түбірлері бола алатын бүтін сандар бос мүше
12-нің бөлгіштері болады. бұл сандарды теріп жазайық:
 . Әр санды берілген көпмүшеге
қою арқылы
. Әр санды берілген көпмүшеге
қою арқылы  аламыз.
аламыз.  болғандықтан,
болғандықтан,  саны
саны  көпмүшесінің түбірі болады, сондықтан
көпмүшесінің түбірі болады, сондықтан
 көпмүшесі
көпмүшесі
 екімүшесіне бөлінеді. Горнер
схемасы бойынша
екімүшесіне бөлінеді. Горнер
схемасы бойынша  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі бөліндінің коэффициенттерін табамыз.
(Мұнда және әрі қарай Горнер схемасы қысқартылған түрде беріледі):
осылайша,
екімүшесіне бөлгендегі бөліндінің коэффициенттерін табамыз.
(Мұнда және әрі қарай Горнер схемасы қысқартылған түрде беріледі):
осылайша,  .
.
 болғандықтан,
болғандықтан,
 болады.
болады.
ә) Егер
 көпмүшесінің
көпмүшесінің
 рационал түбірі бар болса,
онда р
саны (+1)
бос мүшенің бөлгіші болады, ал q
саны 2
коэффициентінің бөлгіші болады, сондықтан барлық рационал сандардың
ішінен тек қана
рационал түбірі бар болса,
онда р
саны (+1)
бос мүшенің бөлгіші болады, ал q
саны 2
коэффициентінің бөлгіші болады, сондықтан барлық рационал сандардың
ішінен тек қана  сандары түбірлер бола алады. Берілгенге табылған мәндерді
қою арқылы
сандары түбірлер бола алады. Берілгенге табылған мәндерді
қою арқылы  аламыз.
аламыз.
 болғандықтан,
болғандықтан,
 саны
саны  көпмүшесінің түбірі болады, сондықтан
көпмүшесінің түбірі болады, сондықтан
 көпмүшесі
көпмүшесі
 екімүшесіне
бөлінеді.
екімүшесіне
бөлінеді.
Осылайша,
 .
.  квадрат үшмүшенің дискриминантын табайық.
квадрат үшмүшенің дискриминантын табайық.
 болғандықтан,
онда
болғандықтан,
онда  және
және  сандары осы үшмүшенің түбірлері болады;
сондықтан
сандары осы үшмүшенің түбірлері болады;
сондықтан  .
.
Сонымен,
 .
.
б) Егер берілген
көпмүшенің түбірлерінің арасында бүтін сандар бар болса, онда бұл
сандар 1 немесе  болады.
болады.  табайық:
табайық:  .
.
 болғандықтан
болғандықтан
 саны
саны  көпмүшесінің түбірі болады, сондықтан
көпмүшесінің түбірі болады, сондықтан
 көпмүшесі
көпмүшесі
 екімүшесіне бөлінеді. Горнер
схемасы бойынша
екімүшесіне бөлінеді. Горнер
схемасы бойынша  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі бөліндінің коэффициенттерін
табамыз:
екімүшесіне бөлгендегі бөліндінің коэффициенттерін
табамыз:
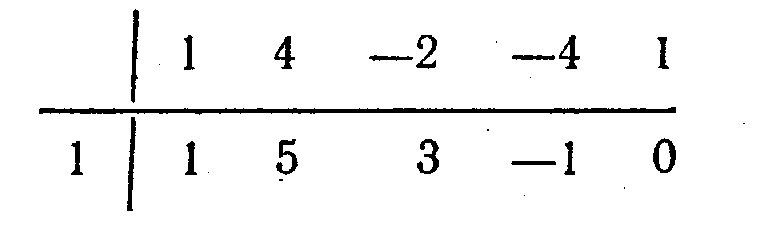
Осылайша,
 .
.
 көпмүшесі
көпмүшесі
 болғанда нөлге тең болады;
сондықтан ол
болғанда нөлге тең болады;
сондықтан ол  екімүшесіне бөлінеді.
екімүшесіне бөлінеді.
Горнер схемасы
бойынша  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі бөліндінің коэффициенттерін
табамыз.
екімүшесіне бөлгендегі бөліндінің коэффициенттерін
табамыз.

Осыдан
 шығады.
шығады.
 болғандықтан,
онда
болғандықтан,
онда  болады.
болады.
в)
 болғандықтан, онда Горнер
схемасына сәйкес мынаны аламыз:
болғандықтан, онда Горнер
схемасына сәйкес мынаны аламыз:
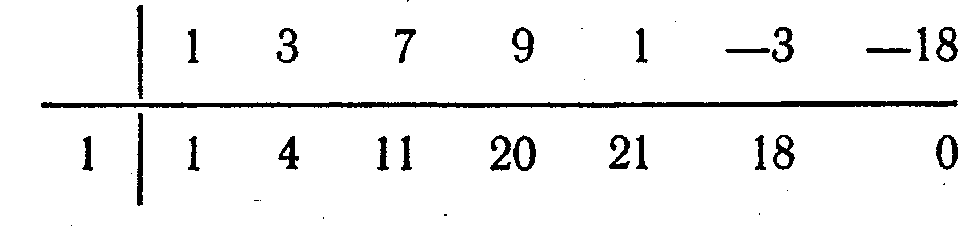
Бұдан

Горнер схемасын қолдана
отырып,  көпмүшесі
көпмүшесі  екімүшесіне бөлінетініне көз
жеткіземіз:
екімүшесіне бөлінетініне көз
жеткіземіз:
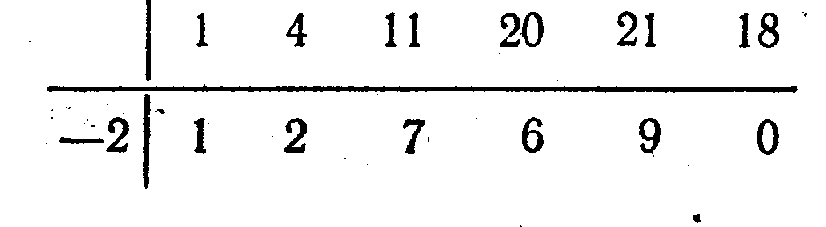
Осыдан,
 болады.
болады.
Топтастырып және толық квадратты шығарып, төмендегідей теңдікті аламыз:

 квадрат үшмүшенің
дискриминанты нөлден кем болғандықтан, бұл үшмүше сызықтық
көбейткіштерге жіктелмейді.
квадрат үшмүшенің
дискриминанты нөлден кем болғандықтан, бұл үшмүше сызықтық
көбейткіштерге жіктелмейді.
Сонымен,
 болады.
болады.
-
Көпмүшенің түбірлері туралы тұжырымды қолдану
Бұл тақырып оқушыларға бұрыннан таныс және олар осы бөлімнің мәнін өз бетімен аша алады. Бірнеше оқушыға бұл тақырыпты дайындап келіп, оны сабақта баяндама түрінде түсіндіруді тапсыруға болады. Бекіту үшін оқушыларға келесідей мысалдарды өз бетімен шығаруға ұсынуға болады. Оқушылардың барлық әрекеттері мұғалім тарапынан ұдайы тексеріліп тұруы керек, түсіндіру барысында мұғалімге баяндаушыны түзетуге және оқушылар тарапынан баяндамашыға қойылған қиын сұрақтарға жауап беруге болады.
Мысал
15.  көпмүшенің түбірлерін
табыңдар.
көпмүшенің түбірлерін
табыңдар.
Шешуі. Берілген көпмүшенің
түбірлерінің арасында рационал сан болатынын немесе болмайтынын
анықтайық. Айталық,  қысқартылмайтын бөлшегі берілген көпмүшенің түбірі болсын,
онда жоғарыда көрсетілген тұжырым бойынша р саны
қысқартылмайтын бөлшегі берілген көпмүшенің түбірі болсын,
онда жоғарыда көрсетілген тұжырым бойынша р саны  мәндеріне, ал q
саны
мәндеріне, ал q
саны  мәндеріне ие бола алады. Осылайша, берілген көпмүшенің
рационал түбірлері ретінде тек қана келесідей сандар болуы
мүмкін:
мәндеріне ие бола алады. Осылайша, берілген көпмүшенің
рационал түбірлері ретінде тек қана келесідей сандар болуы
мүмкін:  .
.
Осы сандардың әрқайсысын
берілген көпмүшеге қою арқылы  аламыз.
аламыз.
Осыдан,
 саны берілген
саны берілген
 көпмүшесінің түбірі болады
және
көпмүшесінің түбірі болады
және  .
.
Горнер схемасын қолдана
отырып, түбірлері  және
және  сандары болатын
сандары болатын  өрнегін табамыз. Сондықтан берілген көпмүшенің
түбірлері
өрнегін табамыз. Сондықтан берілген көпмүшенің
түбірлері  сандары болады.
сандары болады.
Мысал
16.  көпмүшесін көбейткіштерге
жіктеңдер.
көпмүшесін көбейткіштерге
жіктеңдер.
Шешуі. Берілген көпмүшенің
түбірлерінің арасында рационал сан болатынын немесе болмайтынын
анықтайық. Айталық,  қысқартылмайтын бөлшегі берілген көпмүшенің түбірі болсын,
онда жоғарыда көрсетілген тұжырым бойынша р саны
қысқартылмайтын бөлшегі берілген көпмүшенің түбірі болсын,
онда жоғарыда көрсетілген тұжырым бойынша р саны  мәндеріне, ал q
саны
мәндеріне, ал q
саны  мәндеріне ие бола алады. Осылайша, берілген көпмүшенің
рационал түбірлері ретінде тек қана келесідей сандар болуы
мүмкін:
мәндеріне ие бола алады. Осылайша, берілген көпмүшенің
рационал түбірлері ретінде тек қана келесідей сандар болуы
мүмкін:  .
.
Осы сандардың әрқайсысын
берілген көпмүшеге қою арқылы  аламыз.
аламыз.
 болғандықтан,
болғандықтан,
 және
және  сандары берілген
сандары берілген  көпмүшесінің түбірі болады, яғни
көпмүшесінің түбірі болады, яғни  .
.
 көпмүшесін
көпмүшесін
 көпмүшесін
көпмүшесін
 көпмүшесіне «бағандап» бөлу
арқылы немесе Горнер схемасы бойынша
көпмүшесіне «бағандап» бөлу
арқылы немесе Горнер схемасы бойынша  көпмүшесін
көпмүшесін  екімүшесіне, сонан соң шыққан бөліндіні
екімүшесіне, сонан соң шыққан бөліндіні
 екімүшесіне бөлу арқылы немесе
анықталмаған коэффициенттер әдісі арқылы табуға
болады.
екімүшесіне бөлу арқылы немесе
анықталмаған коэффициенттер әдісі арқылы табуға
болады.
 көпмүшесін анықталмаған
коэффициенттер әдісі арқылы
табайық.
көпмүшесін анықталмаған
коэффициенттер әдісі арқылы
табайық.
 тепе-теңдігі орындалатындықтан
және сол жақта тұрған көпмүшенің бос мүшесі
тепе-теңдігі орындалатындықтан
және сол жақта тұрған көпмүшенің бос мүшесі  -ге, ал оң жақта тұрған көпмүшенің бос мүшесі
-ге, ал оң жақта тұрған көпмүшенің бос мүшесі
 -ге тең
болғандықтан,
-ге тең
болғандықтан,  болады. Тепе-теңдіктегі с-ның орнына 4
санын, х-тің орнына 1-ді
қойып, b-ны
табамыз:
болады. Тепе-теңдіктегі с-ның орнына 4
санын, х-тің орнына 1-ді
қойып, b-ны
табамыз:

Бұдан  болады.
болады.
Сонымен,
 .
.
 көпмүшесінің нақты түбірлері
болмайды және ол көбейткіштерге жіктелмейді. Сондықтан есептің
шартында берілген көпмүше көбейткіштерге былай
жіктеледі:
көпмүшесінің нақты түбірлері
болмайды және ол көбейткіштерге жіктелмейді. Сондықтан есептің
шартында берілген көпмүше көбейткіштерге былай
жіктеледі:  .
.
-
Көпмүшені көбейткіштерге жіктеу әдістері
Бұл жұмысты оқушыларға қайталау сабағы ретінде ұсынуға болады. Оқушыларды тақтаға шақырып, мысалдарды шешуге болады. Мұндай есептерді шығару үшін оқушыларда қажетті білімнің барлығы бар. Басқа оқушылар орындарынан өз бетінше шығарады, басқаларынан «алға» шыққан оқушылар қосымша тапсырмалар алады және соларды орындайды.
Мысал 17. Көпмүшені көбейткіштерге жіктеңдер:
а)
ә)

Шешуі.
а)
 теңдеуін шешіп,
көбейтіндісі
теңдеуін шешіп,
көбейтіндісі  бос мүшеге, ал қосындысы
бос мүшеге, ал қосындысы  -ке тең болатын 2 және 3 сандарын аламыз, бұл
сандар
-ке тең болатын 2 және 3 сандарын аламыз, бұл
сандар
 көпмүшесінің түбірлері болады, яғни
көпмүшесінің түбірлері болады, яғни  көпмүшесі
көпмүшесі
 болып көбейткіштерге
жіктеледі;
болып көбейткіштерге
жіктеледі;
ә)
 теңдеуін шешіп,
теңдеуін шешіп,
 және
және
 болатындай
болатындай
 және
және  сандарын аламыз, бұл сандар
сандарын аламыз, бұл сандар
 көпмүшесінің түбірлері болады, яғни
көпмүшесінің түбірлері болады, яғни  көпмүшесін
көпмүшесін  болып көбейткіштерге жіктеуге
болады.
болып көбейткіштерге жіктеуге
болады.
Мысал 18. Көбейткіштерге жіктеңдер:
1)

2)
 .
.
Шешуі.
1)
 болғандықтан,
болғандықтан,
 көпмүшесі
көпмүшесі
 екімүшесіне бөлінеді.
Анықталмаған коэффициенттер әдісі арқылы
екімүшесіне бөлінеді.
Анықталмаған коэффициенттер әдісі арқылы  көпмүшесін
көпмүшесін  екімүшесіне бөлгендегі бөліндіні
табамыз.
екімүшесіне бөлгендегі бөліндіні
табамыз.
Бөлінді
 көпмүшесі
болсын.
көпмүшесі
болсын.  болғандықтан, төмендегі жүйені
аламыз:
болғандықтан, төмендегі жүйені
аламыз:

Бұдан
 болады. Яғни
болады. Яғни
 болады.
болады.
 болғандықтан,
болғандықтан,
 болады.
болады.
2)
 болғандықтан,
болғандықтан,
 көпмүшесі
көпмүшесі
 екімүшесіне бөлінеді.
Анықталмаған коэффициенттер әдісін қолдана отырып,
екімүшесіне бөлінеді.
Анықталмаған коэффициенттер әдісін қолдана отырып,
 бөліндіні
табамыз.
бөліндіні
табамыз.
 болғандықтан, төмендегі жүйені
аламыз:
болғандықтан, төмендегі жүйені
аламыз:

Бұдан
 болады. Яғни
болады. Яғни
 болады.
болады.
Оң жақтағы көпмүшені көбейткіштерге жіктейміз:

 квадрат үшмүшенің
дискриминантын табайық.
квадрат үшмүшенің
дискриминантын табайық.
 болғандықтан,
болғандықтан,
 және
және  сандары бұл үшмүшенің түбірлері болады.
Сондықтан
сандары бұл үшмүшенің түбірлері болады.
Сондықтан  болады.
болады.
Сонымен,
 .
.
Қорытынды
Дипломдық жұмыстың нәтижесі – «Көпмүшелер» тақырыбын оқып үйренуге арналған әдістеменің әзірленуі. Қазіргі уақытта білімнің жоғары бағалануына орай берілген тақырып бойынша білімді алу және тереңдету қажеттілігі туып отыр. Ал осы тақырыпты оқып үйрену кезінде оқушыларда ғылыми-зерттеу қызметіне деген қабілеті артады.
Анықтамаларды, теоремаларды және салдарларды дұрыс түсінуді жақсарту үшін оларды аналитикалық әдіс арқылы енгізу керек. Оның жүзеге асыру жолдары осы жұмыста көрсетілген. Сонымен қатар білімді толық меңгеруге көмектесетін әдістемелік ережелер жобаланып әзірленген.
Осы дипломдық жұмысын орындауда қол жеткізген жетістіктер:
-
«Көпмүшелер» тақырыбы бойынша материал жинақталып, жүйеленді;
-
әдістемелік нұсқаулар жобаланып, әзірленді;
-
тақырыпты оқып үйрену бойынша психологиялық-педагогикалық бөлім әзірленіп, жасалды.
Зерттеу жұмысында берілген материалды орта мектептің және математика бағытында мамандандырылған мектептердің мұғалімдеріне қолдануға болады. Сонымен қатар орта мектептердің, мектеп-лицейлерінің, мектеп-гимназияларының жоғары сынып оқушыларына, қорытынды емтихан мен жоғары оқу орнына түсуге арналған емтиханға дайындығын тереңдеткісі келетін оқушыларға, сонымен қатар педагогикалық институттар мен университеттердің физика-математика факультеттерінің студенттеріне ұсынылады.
Пайдаланылған әдебиеттер тізімі
-
«Математика» Большой справочник для школьников и поступающих в вузы – Дрофа 1998, 864 бет.
-
«Математика» Задачи М. И. Сканави с решениями – Минск 1996, 448 бет.
-
Бугров Я.С. Высшая математика.- Ростов-на-Дону 1997.
-
Винберг В.А. Алгебра.- Москва 1995.
-
Выгодский М.Я. Справочник по элементарной математике.- Москва 1997.
-
Зив Б.Г. Математика, 11. Уроки повторения. — СПб.: Мир и семья-95, 1998.
-
Кузнецова Г.Н. Миндюк Н.Г. «Программа» (Тематическое планирование к учебникам федерального комплекта «Математика») – М.:2002г 320 бет.
-
Курош А.Г. Курс высшей алгебры.- Наука 1973.
-
Мордкович А.Г. Алгебра және анализ бастамалары, 10-11. Оқулық, есептер жинағы.
-
Сборник задач по математике с решениями / под ред. М. И. Сканави –М.: Издательский дом Оникс 1999, 624 бет.
-
Фрижман Л.М., Турецкий Е.Н. «Как научиться решать задачи»: Просвещение 1984, 175 бет.
-
Шлярский Д.О., Ченцов Н.Н., Яглом И.М. "Избранные задачи и теоремы элементарной математики" Том 1 Арифметика и алгебра.-С-Петербург 1998, 328 бет.
Қосымшалар
Бұл бөлімде факультативтік сабақтарда қарастыруға арналған кейбір есептер келтіріледі. (*) таңбасымен берілген есептер – қиындығы жоғары тапсырмалар. Бұл есептерді үй немесе жеке жұмысқа беру ұсынылады.
1.
 өрнегінде жақшаларды ашып,
ұқсас мүшелерді біріктіргеннен кейін шығатын көпмүшенің
коэффициенттерінің қосындысын
табыңдар.
өрнегінде жақшаларды ашып,
ұқсас мүшелерді біріктіргеннен кейін шығатын көпмүшенің
коэффициенттерінің қосындысын
табыңдар.
Айталық, берілген
өрнекті х-тің дәрежелері арқылы
жіктеу  түрінде болады делік, мұндағы
түрінде болады делік, мұндағы  – қосындысын табуды қажет ететін анықталмаған
коэффициенттер, ал n
–
берілген өрнектің дәрежесі (ол оңай табылады және
– қосындысын табуды қажет ететін анықталмаған
коэффициенттер, ал n
–
берілген өрнектің дәрежесі (ол оңай табылады және
 болады). Егер бұл
теңдікте
болады). Егер бұл
теңдікте  болса, онда
болса, онда
 шығады.
шығады.
Осылайша, ізделінді қосынды 1-ге тең болады.
2. Қайсысында жақшаларды
ашып, ұқсас мүшелерді біріктіргеннен кейін  алдындағы коэффициент артық
болады?
алдындағы коэффициент артық
болады?
Екі өрнектің жақшаларын
ашып, ұқсас мүшелерді біріктіргеннен кейін
х-ке қатысты екі көпмүше
аламыз. Енді берілген өрнектердегі х-ті  -ке ауыстырайық. Сондай-ақ алынған көпмүшелерде
де х-ті
-ке ауыстырайық. Сондай-ақ алынған көпмүшелерде
де х-ті  -ке алмастырамыз, яғни олардың әрқайсысында
х-тің жұп дәрежелеріндегі
коэффициенттерді өзгертпей, х-тің тақ дәрежелеріндегі
коэффициенттердің таңбаларын ауыстырамыз. Әсіресе
-ке алмастырамыз, яғни олардың әрқайсысында
х-тің жұп дәрежелеріндегі
коэффициенттерді өзгертпей, х-тің тақ дәрежелеріндегі
коэффициенттердің таңбаларын ауыстырамыз. Әсіресе
 коэффициенттер өзгермейді.
Осылайша, алынған екі көпмүшедегі
коэффициенттер өзгермейді.
Осылайша, алынған екі көпмүшедегі  коэффициенттер
коэффициенттер  және
және  өрнектерінің жақшаларын ашып, ұқсас мүшелерді
біріктіргеннен кейін шығатын көпмүшелердегі
өрнектерінің жақшаларын ашып, ұқсас мүшелерді
біріктіргеннен кейін шығатын көпмүшелердегі  коэффициенттер тең екенін
көреміз.
коэффициенттер тең екенін
көреміз.
Бірақ, жаңа
көпмүшелердің біріншісінде коэффициенті ең үлкен болатыны анық. Расында да, бірінші
өрнекте жақшаларды ашқаннан кейін х-тің әр түрлі дәрежелерінде тек
қана оң таңбалы коэффициенттер шығады және ұқсас мүшелерді
біріктірген кезде осы коэффициенттер қосылады. Екінші өрнекте
жақшаларды ашқаннан кейін х-тің әр түрлі дәрежелерінде әр
түрлі таңбалы коэффициенттер шығады және ұқсас мүшелерді
біріктірген кезде осы коэффициенттер
азаяды.
коэффициенті ең үлкен болатыны анық. Расында да, бірінші
өрнекте жақшаларды ашқаннан кейін х-тің әр түрлі дәрежелерінде тек
қана оң таңбалы коэффициенттер шығады және ұқсас мүшелерді
біріктірген кезде осы коэффициенттер қосылады. Екінші өрнекте
жақшаларды ашқаннан кейін х-тің әр түрлі дәрежелерінде әр
түрлі таңбалы коэффициенттер шығады және ұқсас мүшелерді
біріктірген кезде осы коэффициенттер
азаяды.
Сонымен,
 және
және  өрнектерінің жақшаларын ашып, ұқсас мүшелерді
біріктіргеннен кейін бірінші өрнектегі
өрнектерінің жақшаларын ашып, ұқсас мүшелерді
біріктіргеннен кейін бірінші өрнектегі  коэффициенті екіншісіне қарағанда артық
болады.
коэффициенті екіншісіне қарағанда артық
болады.
3.
 көбейтіндісінде жақшаларды
ашып, ұқсас мүшелерді біріктіргеннен кейін
х-тің қандай да бір дәрежелерін
қамтитын мүшелер қалмайтынын дәлелдеу
керек.
көбейтіндісінде жақшаларды
ашып, ұқсас мүшелерді біріктіргеннен кейін
х-тің қандай да бір дәрежелерін
қамтитын мүшелер қалмайтынын дәлелдеу
керек.
Есептің тұжырымы төмендегідей түрлендіруден шығады:

 .
.
Төмендегі өрнектерде
жақшаларды ашып, ұқсас мүшелерді біріктіргеннен кейін
 коэффициентін табу:
а)
коэффициентін табу:
а)  ; ә)
; ә)  .
.
а) геометриялық прогрессияның қосындысының формуласына және Ньютон формуласына сәйкес:


Осылайша, ізделінді
коэффициент  болады.
болады.
ә) Берілген
өрнекті  деп белгілейік. Онда:
деп белгілейік. Онда:
 .
.
Бұдан
 .
.
Осылайша, ізделінді
коэффициент  болады.
болады.
4.
* (п
рет)
өрнегіндегі жақшаларды ашып, ұқсас мүшелерді біріктіргеннен кейін
шыққан
(п
рет)
өрнегіндегі жақшаларды ашып, ұқсас мүшелерді біріктіргеннен кейін
шыққан  алдындағы коэффициентті
анықтаңдар.
алдындағы коэффициентті
анықтаңдар.
Алдымен
 өрнегінде жақшаларды ашып,
ұқсас мүшелерді біріктіргеннен кейін шығатын бос мүшені табайық.
Ол
өрнегінде жақшаларды ашып,
ұқсас мүшелерді біріктіргеннен кейін шығатын бос мүшені табайық.
Ол  болғандағы осы өрнектің мәніне
тең, яғни
болғандағы осы өрнектің мәніне
тең, яғни

Келесі
кезекте х-тің
коэффициентін  деп,
деп,  -тың коэффициентін
-тың коэффициентін  деп,
деп,
х-тің жоғары дәрежелеріндегі
коэффициенттердің қосындысын  деп белгілейік. Онда
деп белгілейік. Онда  аламыз.
аламыз.
Басқаша алғанда,



Бұдан
 .
.
 болғандықтан,
болғандықтан,
 болады. Яғни
болады. Яғни
 болады. Енді
болады. Енді
 есептейік:
есептейік:

 .
.
Осы
өрнекке  қойып,
қойып,



5.
 көпмүшесін а)
көпмүшесін а)
 -ге; ә)
-ге; ә)
 -ге бөлгендегі қалдықты
табыңдар.
-ге бөлгендегі қалдықты
табыңдар.
а) Бірінші тәсілі. Кез
келген бүтін k
үшін  екімүшесі
екімүшесі  -ге бөлінетіндіктен,
-ге бөлінетіндіктен,  өрнегін
өрнегін  -ге бөлгенде 6 қалдық
қалады.
-ге бөлгенде 6 қалдық
қалады.
Екінші
тәсілі.  көпмүшесін
көпмүшесін  -ге бөлгендегі бөліндіні
-ге бөлгендегі бөліндіні  , ал қалдықты r
деп
белгілейік. Онда
, ал қалдықты r
деп
белгілейік. Онда  .
.
Осы
теңдікте  деп аламыз, сонда қалдықта 6
шығады.
деп аламыз, сонда қалдықта 6
шығады.
ә) Алдыңғы есептің
екінші тәсіліне сәйкес берілген көпмүшені  -ге бөлгендегі бөліндіні
-ге бөлгендегі бөліндіні  , ал қалдықты
, ал қалдықты  деп белгілейік (көпмүшені квадрат үшмүшеге бөлгендегі
қалдық бірінші дәрежелі екімүше
болады):
деп белгілейік (көпмүшені квадрат үшмүшеге бөлгендегі
қалдық бірінші дәрежелі екімүше
болады):
 , бұдан
, бұдан
 .
.
Осылайша, ізделінді
қалдық  -ке тең.
-ке тең.
6. Белгісіз
көпмүшені  -ге бөлгенде 2 қалдық, ал
-ге бөлгенде 2 қалдық, ал  -ге бөлгенде 1 қалдық қалады. Осы көпмүшені
-ге бөлгенде 1 қалдық қалады. Осы көпмүшені
 -ге бөлгенде қанша қалдық
қалады?
-ге бөлгенде қанша қалдық
қалады?
Айталық,
 – белгісіз
көпмүше,
– белгісіз
көпмүше,  – осы көпмүшені
– осы көпмүшені  -ге бөлгендегі бөлінді, ал
-ге бөлгендегі бөлінді, ал  – ізделінді қалдық болсын.
Онда
– ізделінді қалдық болсын.
Онда
 (*)
(*)
Есептің шарты
бойынша  , бұдан
, бұдан  ;
;
 , бұдан
, бұдан  болады.
болады.
 және
және  сандарын (*) теңдікке қойып,
сандарын (*) теңдікке қойып,  шығады, бұдан
шығады, бұдан  . Осылайша, ізделінді қалдық
. Осылайша, ізделінді қалдық  болады.
болады.
7.
 көпмүшесін
көпмүшесін
 -ге бөлгенде бөлінді мен
қалдық шығады. Бөліндідегі
-ге бөлгенде бөлінді мен
қалдық шығады. Бөліндідегі  коэффициентін табу.
коэффициентін табу.
 көпмүшесін көбейткіштерге
жіктеуге болады, ол
көпмүшесін көбейткіштерге
жіктеуге болады, ол  болады. Осы көпмүше
болады. Осы көпмүше  көпмүшесінің бөлгіші болатыны көрініп тұр.
Яғни
көпмүшесінің бөлгіші болатыны көрініп тұр.
Яғни

 көпмүшесін
көпмүшесін
 -ге бөлу
-ге бөлу
 көпмүшесін
көпмүшесін
 -ге бөліп,
нәтижесін
-ге бөліп,
нәтижесін  -ге көбейткенмен бірдей
болады.
-ге көбейткенмен бірдей
болады.
 екенін оңай көруге болады, ол
үшін берілген көпмүшелерді «бұрыштап» бөлуге немесе
екенін оңай көруге болады, ол
үшін берілген көпмүшелерді «бұрыштап» бөлуге немесе
 екенін байқап, жұп дәрежелі
екі бірмүшенің айырмасын дәреже негізінің айырмасына бөлу
формуласын қолдануға болады. Осыдан, ізделінді
коэффициент
екенін байқап, жұп дәрежелі
екі бірмүшенің айырмасын дәреже негізінің айырмасына бөлу
формуласын қолдануға болады. Осыдан, ізделінді
коэффициент  көбейтіндісіндегі
көбейтіндісіндегі  коэффициенті болатын
коэффициенті болатын  -ге тең болатыны шығады.
-ге тең болатыны шығады.
8.
 тепе-теңдігі орындалатын
барлық
тепе-теңдігі орындалатын
барлық  көпмүшелерін табу.
көпмүшелерін табу.
Есептің шартында
берілген тепе-теңдіктен ізделінді  (мұндағы п
–
көпмүшенің дәрежесі) көпмүшесі х-ке бөлінетіндігі шығады,
яғни
(мұндағы п
–
көпмүшенің дәрежесі) көпмүшесі х-ке бөлінетіндігі шығады,
яғни
 , мұндағы
, мұндағы  –
–  дәрежелі қандай да бір жаңа көпмүше.
Сондықтан
дәрежелі қандай да бір жаңа көпмүше.
Сондықтан  және
және  болады, осыдан
болады, осыдан  көпмүшесі
көпмүшесі  -ге бөлінеді, яғни
-ге бөлінеді, яғни  (
( -ге
-ге  бөлінеді). Онда
бөлінеді). Онда  болады және
болады және  шығады, бұдан
шығады, бұдан  көпмүшесі
көпмүшесі  -ге де бөлінетіндігі шығады (яғни
-ге де бөлінетіндігі шығады (яғни  көпмүшесі
көпмүшесі  -ге бөлінеді), яғни
-ге бөлінеді), яғни  . Осы
. Осы  мәнін берілген қатынасқа қою арқылы
мәнін берілген қатынасқа қою арқылы  көпмүшесінің
көпмүшесінің  -ке де бөлінетіндігін көреміз, яғни
-ке де бөлінетіндігін көреміз, яғни  болады және т.с.с.
болады және т.с.с.
Осы әдісті жалғастыра
берсек, соңында  көпмүшесінің келесідей түріне
келеміз:
көпмүшесінің келесідей түріне
келеміз:

Берілген
тепе-теңдікке  көпмүшесінің осы өрнегін қою
арқылы
көпмүшесінің осы өрнегін қою
арқылы

аламыз,
бұдан  дәрежелі
дәрежелі  көпмүшесі үшін
көпмүшесі үшін
 (*)
(*)
Егер  – дәрежесі нөлге тең көпмүше (сан!) болса, онда (*)
тепе-теңдігі орындалады; ол тек бір ғана жағдайда орындалатынын
көрсетейік. Расында да, егер
– дәрежесі нөлге тең көпмүше (сан!) болса, онда (*)
тепе-теңдігі орындалады; ол тек бір ғана жағдайда орындалатынын
көрсетейік. Расында да, егер  болса, онда (*) тепе-теңдігінің
болса, онда (*) тепе-теңдігінің  екі жағындағы
екі жағындағы  коэффициенттерін теңестіре отырып, Ньютон биномы
бойынша
коэффициенттерін теңестіре отырып, Ньютон биномы
бойынша  немесе
немесе  аламыз,
аламыз,  саны
саны  ұйғарымына қайшы келеді. Осылайша,
ұйғарымына қайшы келеді. Осылайша,  және
және
 – 26-шы дәрежелі көпмүше.
– 26-шы дәрежелі көпмүше.
9.  а) натурал
а) натурал  коэффициенттері бар; ә) бүтін
коэффициенттері бар; ә) бүтін  коэффициенттері бар көпмүшесі берілген;
коэффициенттері бар көпмүшесі берілген;
 санының цифрларының
қосындысын
санының цифрларының
қосындысын  деп белгілейік.
деп белгілейік.  тізбегінде шексіз көп сан болса, онда оның құрамында шексіз
көп бірдей сандар болатынын дәлелдеу
керек.
тізбегінде шексіз көп сан болса, онда оның құрамында шексіз
көп бірдей сандар болатынын дәлелдеу
керек.
а)  көпмүшесінің коэффициенттерінің барлығы теріс емес сандар
болса, онда
көпмүшесінің коэффициенттерінің барлығы теріс емес сандар
болса, онда  сандарының барлығы бар болады. Онның
сандарының барлығы бар болады. Онның
 түріндегі дәрежесін
қарастырайық, мұндағы N
–
түріндегі дәрежесін
қарастырайық, мұндағы N
–  көпмүшесінің
көпмүшесінің  коэффициенттерінен артық сан. Онда көпмүшенің
коэффициенттерінен артық сан. Онда көпмүшенің
 коэффициенті қандай цифрлармен
жазылса,
коэффициенті қандай цифрлармен
жазылса,  саны сол цифрлардан басталады; сонан соң (мүмкін бірнеше
нөлден кейін)
саны сол цифрлардан басталады; сонан соң (мүмкін бірнеше
нөлден кейін)  санының цифрлары жазылады; сонан соң (мүмкін тағы да
бірнеше нөлден кейін) –
санының цифрлары жазылады; сонан соң (мүмкін тағы да
бірнеше нөлден кейін) –  санының цифрлар және
санының цифрлар және  санына дейін т.с.с. жалғасады; сондықтан
санына дейін т.с.с. жалғасады; сондықтан
 саны
саны  сандарының барлық цифрларының қосындысына тең болады.
Осы S
санына
сандарының барлық цифрларының қосындысына тең болады.
Осы S
санына  шамалары да тең болады, осыдан
шамалары да тең болады, осыдан  тізбегінде S
саны
шексіз көп рет кездеседі деген қорытынды
шығады.
тізбегінде S
саны
шексіз көп рет кездеседі деген қорытынды
шығады.
ә)  көпмүшесінің ең үлкен коэффициенті теріс сан болса,
онда
көпмүшесінің ең үлкен коэффициенті теріс сан болса,
онда  сандарының арасында тек қана теріс сандар болатыны анық.
Олай болса, тек қана
сандарының арасында тек қана теріс сандар болатыны анық.
Олай болса, тек қана  жағдайын қарастыру қалды. Бірақ бұл жағдайда
жағдайын қарастыру қалды. Бірақ бұл жағдайда
 саны бар болады,
егер
саны бар болады,
егер  «жылжытылған» көпмүшенің коэффициенттерінің барлығы оң сан
болса. Осыдан
«жылжытылған» көпмүшенің коэффициенттерінің барлығы оң сан
болса. Осыдан  сандарының цифрларының қосындысынан тұратын
сандарының цифрларының қосындысынан тұратын
 тізбегінде шексіз көп бірдей
сандар болады және
тізбегінде шексіз көп бірдей
сандар болады және  болатындықтан,
болатындықтан,  тізбегінде де шексіз көп бірдей сандар болады деген
қорытынды шығады.
тізбегінде де шексіз көп бірдей сандар болады деген
қорытынды шығады.
Енді, жоғарыда жазылған
ұйғарымды дәлелдеу керек. Бірақ егер  боса, онда Ньютон биномы бойынша
боса, онда Ньютон биномы бойынша  болады. Осылайша,
болады. Осылайша,  ең үлкен коэффициенті
ең үлкен коэффициенті  болатын М-ге қатысты
болатын М-ге қатысты
 дәрежелі көпмүше түрінде
болады; сондықтан барлық
дәрежелі көпмүше түрінде
болады; сондықтан барлық  (мұндағы
(мұндағы  және
және  ) М-нің үлкен мәнінде оң мәнге ие
болады, дәлелдеу керегі осы.
) М-нің үлкен мәнінде оң мәнге ие
болады, дәлелдеу керегі осы.
10.  көпмүшесін
көпмүшесін  көбейтіндісі болатындай х
айнымалысы және у
айнымалысынан құралған екі көпмүше арқылы өрнектеуге
болмайтынын дәлелдеу керек.
көбейтіндісі болатындай х
айнымалысы және у
айнымалысынан құралған екі көпмүше арқылы өрнектеуге
болмайтынын дәлелдеу керек.
 және
және
 көпмүшелерінің
көпмүшелерінің
 (яғни
(яғни  ) және
) және  бос мүшелері болсын. Айталық,
бос мүшелері болсын. Айталық,  тепе-теңдігінде х
айнымалысы 0-ге тең болсын, онда
тепе-теңдігінде х
айнымалысы 0-ге тең болсын, онда  болады, яғни
болады, яғни  ; осылайша,
; осылайша,  барлық у
үшін
барлық у
үшін  -ге тең болады, яғни
-ге тең болады, яғни  тұрақты сан болады (нөлінші дәрежелі көпмүше). Дәл
осылайша
тұрақты сан болады (нөлінші дәрежелі көпмүше). Дәл
осылайша  екені оңай дәлелденеді, яғни
екені оңай дәлелденеді, яғни  . Алынған қарама-қайшылық есептің ұйғарымын
дәлелдейді.
. Алынған қарама-қайшылық есептің ұйғарымын
дәлелдейді.
11.  теңдеуінің (нақты) түбірлері болмайтындай
етіп
теңдеуінің (нақты) түбірлері болмайтындай
етіп  квадрат үшмүше берілген.
квадрат үшмүше берілген.  теңдеуінің де нақты түбірлері болмайтынын
дәлелдеңдер.
теңдеуінің де нақты түбірлері болмайтынын
дәлелдеңдер.
 (квадрат) теңдеуінің
нақты түбірлері болмайтындықтан,
(квадрат) теңдеуінің
нақты түбірлері болмайтындықтан,  квадрат үшмүше х-тің барлық мәнінде бірдей
таңбаның мәніне ие болады. Бірақ мұндай жағдайда кез
келген
квадрат үшмүше х-тің барлық мәнінде бірдей
таңбаның мәніне ие болады. Бірақ мұндай жағдайда кез
келген  үшін
үшін  , яғни
, яғни  болады және ұйғарым бойынша
болады және ұйғарым бойынша  , яғни
, яғни  болғандықтан,
болғандықтан,
 болады, осыдан
болады, осыдан  саны
саны  (4-ші дәрежелі) теңдеудің түбірі бола алмайды деген
қорытынды шығады.
(4-ші дәрежелі) теңдеудің түбірі бола алмайды деген
қорытынды шығады.
 деп есептейік, олай
болмаса,
деп есептейік, олай
болмаса,  көпмүшесін (берілген шарттарды
қанағаттандыратын)
көпмүшесін (берілген шарттарды
қанағаттандыратын)  көпмүшесіне алмастырамыз. Дәл солай
көпмүшесіне алмастырамыз. Дәл солай  деп есептейік, олай болмаса,
деп есептейік, олай болмаса,  көпмүшесін (берілген шарттарды
қанағаттандыратын)
көпмүшесін (берілген шарттарды
қанағаттандыратын)  көпмүшесіне алмастырамыз. Енді
көпмүшесіне алмастырамыз. Енді  мәндерін
мәндерін  теңсіздігіне қойып,
теңсіздігіне қойып,  аламыз, яғни
аламыз, яғни  болады. Сонан соң егер
болады. Сонан соң егер  болса, онда (
болса, онда ( болғанда)
болғанда)
 болады, осыдан
болады, осыдан  және
және  , бұдан
, бұдан
 шығады. Дәл осылай
шығады. Дәл осылай  үшін
үшін  болғанда
болғанда  және
және  , бұдан
, бұдан  шығады.
шығады.
12. Егер
 саны –
саны –  теңдеуінің түбірі, ал
теңдеуінің түбірі, ал  саны
саны  теңдеуінің түбірі болса, онда олардың арасында жататын,
яғни
теңдеуінің түбірі болса, онда олардың арасында жататын,
яғни
 немесе
немесе  және
және  теңдеуінің түбірі болатын
теңдеуінің түбірі болатын  саны табылатынын дәлелдеу
керек.
саны табылатынын дәлелдеу
керек.
Берілген үш теңдеу де бірінші
дәрежелі теңдеу болып шығатын, яғни бір-бірімен сәйкес келетін
бірдей түбірі (мұнда  ) бар болатын
) бар болатын  болатын жағдайды және
болатын жағдайды және  болып, үш теңдеудің түбірлері
болып, үш теңдеудің түбірлері  болатын жағдайды
қарастырмаймыз.
болатын жағдайды
қарастырмаймыз.
Егер  болса, онда
болса, онда  болады, осылайша егер
болады, осылайша егер  болса, онда
болса, онда  болады.
болады.
Осыдан,
 және
және  шамаларының таңбалары әр түрлі болады. Яғни
шамаларының таңбалары әр түрлі болады. Яғни
 параболасының
параболасының
 және
және  нүктелері х
өсінің
екі жағында орналасады, бұдан параболада осы екі нүктенің арасында
жататын және х
өсін осы
нүктеде қиып өтетін, сондай-ақ үшінші теңдеудің ізделінді түбірі
болатын
нүктелері х
өсінің
екі жағында орналасады, бұдан параболада осы екі нүктенің арасында
жататын және х
өсін осы
нүктеде қиып өтетін, сондай-ақ үшінші теңдеудің ізделінді түбірі
болатын  нүктесі табылады деген қорытынды
шығады.
нүктесі табылады деген қорытынды
шығады.
13.  және
және  сандары
сандары  теңдеуінің түбірлері, ал
теңдеуінің түбірлері, ал  және
және  сандары
сандары  теңдеуінің түбірлері болсын.
теңдеуінің түбірлері болсын.  көбейтіндісін берілген теңдеулердің коэффициенттері арқылы
өрнектеу керек.
көбейтіндісін берілген теңдеулердің коэффициенттері арқылы
өрнектеу керек.
Егер  және
және  сандары
сандары  теңдеуінің түбірлері болса, онда
теңдеуінің түбірлері болса, онда  . Яғни
. Яғни  .
.
Бірақ  , яғни
, яғни

14. а)  өрнегі b
және с
бүтін
сандары бар
өрнегі b
және с
бүтін
сандары бар
 көбейтіндісіне жіктелетіндей а
санын
табу керек; ә) коэффициенттері бүтін сандар болатын төртінші
дәрежелі
көбейтіндісіне жіктелетіндей а
санын
табу керек; ә) коэффициенттері бүтін сандар болатын төртінші
дәрежелі  көпмүшесін коэффициенттері бүтін сандар болатын екі
көпмүшенің көбейтіндісі түрінде жазуға болатындай бір-біріне тең
болмайтын нөлден өзге a, b, c
бүтін
сандарын табу керек.
көпмүшесін коэффициенттері бүтін сандар болатын екі
көпмүшенің көбейтіндісі түрінде жазуға болатындай бір-біріне тең
болмайтын нөлден өзге a, b, c
бүтін
сандарын табу керек.
а) Айталық,
 болсын. Теңдіктің екі
жағында
болсын. Теңдіктің екі
жағында  деп алып,
деп алып,  теңдігін аламыз. Бұдан
теңдігін аламыз. Бұдан  .
.
а
және b
– бүтін
сандар болғандықтан,  және
және  да – бүтін сандар болады. Бірақ
да – бүтін сандар болады. Бірақ  саны екі бүтін санның көбейтіндісі ретінде тек қана бір
әдіспен жазылады:
саны екі бүтін санның көбейтіндісі ретінде тек қана бір
әдіспен жазылады:  . Сондықтан тек қана екі жағдай болуы
мүмкін:
. Сондықтан тек қана екі жағдай болуы
мүмкін:
-
 ; онда
; онда  , яғни
, яғни  :
:
 .
. -
 ; онда
; онда  , яғни
, яғни  :
:
 .
.
ә) Төртінші дәрежелі көпмүшені бірінші дәрежелі көпмүше мен үшінші дәрежелі көпмүшенің көбейтіндісі түрінде немесе екінші дәрежелі екі көпмүшенің көбейтіндісі түрінде өрнектеуге болады, сондықтан бізге екі жағдайды қарастыру керек:
А)  (*) (теңдіктің оң жағындағы бірінші
көбейткіштегі х-ке қатысты коэффициенттер
және екінші көбейткіштегі
(*) (теңдіктің оң жағындағы бірінші
көбейткіштегі х-ке қатысты коэффициенттер
және екінші көбейткіштегі  -ке қатысты коэффициенттер екеуі де 1-ге
немесе
-ке қатысты коэффициенттер екеуі де 1-ге
немесе  -ге тең болады, себебі бұл көбейткіштердің көбейтіндісі
болатын өрнектегі
-ге тең болады, себебі бұл көбейткіштердің көбейтіндісі
болатын өрнектегі  коэффициенті
коэффициенті  өрнегіндегі
өрнегіндегі  коэффициентіне, яғни 1-ге тең болу керек; ал
коэффициентіне, яғни 1-ге тең болу керек; ал
 теңдігін оң
жағын
теңдігін оң
жағын  -ге көбейту арқылы (*) түріне келтіруге
болады).
-ге көбейту арқылы (*) түріне келтіруге
болады).
(*) теңдігіне
тізбектеп  қойып және 1 саны көбейткіштерге тек қана екі түрлі әдіспен
көбейткіштерге жіктелетінін, яғни
қойып және 1 саны көбейткіштерге тек қана екі түрлі әдіспен
көбейткіштерге жіктелетінін, яғни
 екенін ескере отырып, әр түрлі
екенін ескере отырып, әр түрлі  төрт сан (0, a, b, c
сандары
әр түрлі екенін еске саламыз) тек қана екі мәнге ие бола
алады:
төрт сан (0, a, b, c
сандары
әр түрлі екенін еске саламыз) тек қана екі мәнге ие бола
алады:  және
және  , ал бұл мүмкін емес.
, ал бұл мүмкін емес.
Ә)  . Бұдан, жоғарыдағы әдіспен
. Бұдан, жоғарыдағы әдіспен  қойғанда
қойғанда  және
және
 көпмүшелері 1 немесе
көпмүшелері 1 немесе  мәндеріне ие болады. Бірақ
мәндеріне ие болады. Бірақ  квадрат үшмүше х-тің әр түрлі үш мәнінде
бірдей
квадрат үшмүше х-тің әр түрлі үш мәнінде
бірдей  мәніне ие бола алмайды (әйтпесе,
мәніне ие бола алмайды (әйтпесе,  квадрат теңдеуінің әр түрлі үш түбірі болар еді),
бұдан
квадрат теңдеуінің әр түрлі үш түбірі болар еді),
бұдан  төрт мәннің ішінен екеуінде бұл үшмүше 1 санының мәнін, ал
басқа екеуінде
төрт мәннің ішінен екеуінде бұл үшмүше 1 санының мәнін, ал
басқа екеуінде  санының мәнін қабылдайды.
санының мәнін қабылдайды.  және
және  мәні
мәні мәндерінің ішінен бұл үшмүше 1 санының мәнін қабылдайтын
дәл сол болсын; бұл жағдайда
мәндерінің ішінен бұл үшмүше 1 санының мәнін қабылдайтын
дәл сол болсын; бұл жағдайда  және
және  мәндерінде бұл үшмүше
мәндерінде бұл үшмүше  санының мәнін қабылдайды.
Сонымен:
санының мәнін қабылдайды.
Сонымен:

 теңдігінен
теңдігінен
 екені шығады (себебі ұйығарым
бойынша
екені шығады (себебі ұйығарым
бойынша  ). Осылайша, соңғы екі теңдік
). Осылайша, соңғы екі теңдік  түріне келеді. Бірінші теңдіктен екінші теңдікті
азайтып,
түріне келеді. Бірінші теңдіктен екінші теңдікті
азайтып,  аламыз, бұдан
аламыз, бұдан  болғандықтан,
болғандықтан,  аламыз. Енді
аламыз. Енді  теңдігінен b,c
және а
үшін
мынадай мәндер табылады:
теңдігінен b,c
және а
үшін
мынадай мәндер табылады:




Осыған ұқсас,
егер  үшмүшесі
үшмүшесі  және
және  мәндерінде
мәндерінде  мәніне,
мәніне,  және
және  мәндерінде
мәндерінде  мәніне ие болса, онда:
мәніне ие болса, онда:
 ,
бұдан
,
бұдан


Осылайша, a, b, c үшін мүмкін болатын тағы екі жүйе аламыз:




15. Бір-бірінен әр түрлі
қандай  бүтін сандары үшін
бүтін сандары үшін
а)  ; ә)
; ә)  көпмүшелері басқа көпмүшелердің көбейтіндісіне жіктеледі
ме?
көпмүшелері басқа көпмүшелердің көбейтіндісіне жіктеледі
ме?
а)  деп алайық, мұндағы
деп алайық, мұндағы  пен
пен  – дәрежелерінің қосындысы п-ге тең бүтін коэффициенттері
бар көпмүшелер; осы екі көпмүшенің ең үлкен коэффициенті
– дәрежелерінің қосындысы п-ге тең бүтін коэффициенттері
бар көпмүшелер; осы екі көпмүшенің ең үлкен коэффициенті
1-ге тең деп есептейміз (алдыңғы есеппен салыстырыңдар). Осы
теңдікке
 мәндерін қойып және
мәндерін қойып және  саны екі бүтін көбейткіштерге бір ғана тәсілмен
жіктелетінін:
саны екі бүтін көбейткіштерге бір ғана тәсілмен
жіктелетінін:  ескере отырып,
ескере отырып,  аламыз. Осылайша,
аламыз. Осылайша,  қосындысы
қосындысы
 үшін нөлге тең екенін көреміз. Сонымен,
үшін нөлге тең екенін көреміз. Сонымен,
 теңдеуінің
түбірлері
теңдеуінің
түбірлері  болады, бұдан
болады, бұдан
 көпмүшесі
көпмүшесі  бөлінеді, яғни
бөлінеді, яғни
 көбейтіндісіне де бөлінетіндігі шығады. Бірақ
көбейтіндісіне де бөлінетіндігі шығады. Бірақ
 теңдеуінің
дәрежесі
теңдеуінің
дәрежесі  көпмүшелерінің ең үлкен дәрежесіне тең және
п-нен кем
(п саны –
көпмүшелерінің ең үлкен дәрежесіне тең және
п-нен кем
(п саны –  өрнегінің дәрежесі). Осыдан
өрнегінің дәрежесі). Осыдан  қосындысы
қосындысы  көбейтіндісіне жіктелмейтіні шығады, яғни біз ұйғарған
көбейткіштерге жіктеу мүмкін емес.
көбейтіндісіне жіктелмейтіні шығады, яғни біз ұйғарған
көбейткіштерге жіктеу мүмкін емес.
ә)  деп алайық, мұндағы
деп алайық, мұндағы  пен
пен  – ең үлкен дәрежелері 1-ге тең бүтін коэффициенттері бар
көпмүшелер. Осы теңдікке
– ең үлкен дәрежелері 1-ге тең бүтін коэффициенттері бар
көпмүшелер. Осы теңдікке  мәндерін қойып, әрбір қарастырған жағдайда
мәндерін қойып, әрбір қарастырған жағдайда
 немесе
немесе
 болатынын көреміз.
Осылайша,
болатынын көреміз.
Осылайша,  айырмасы
айырмасы
х-тің әр түрлі мәндерінде нөлге
айналатынын көреміз. Осыдан, біріншіден,  , екіншіден, п
саны –
жұп:
, екіншіден, п
саны –
жұп:  , мұндағы
, мұндағы
k
–  көпмүшелерінің әрқайсысының дәрежесі. Енді
теңдікті
көпмүшелерінің әрқайсысының дәрежесі. Енді
теңдікті
 немесе
немесе  түрінде жазайық.
түрінде жазайық.
Сонымен,
 және
және  көпмүшелерінің көбейтіндісі
көпмүшелерінің көбейтіндісі  кезінде нөлге айналады. Яғни х-тің әрбір мәнінде
көбейткіштердің ең болмағанда біреуі нөлге айналады,
бұдан
кезінде нөлге айналады. Яғни х-тің әрбір мәнінде
көбейткіштердің ең болмағанда біреуі нөлге айналады,
бұдан  немесе
немесе  көпмүшелерінің біреуі
көпмүшелерінің біреуі  екімүшесіне бөлінеді немесе
екімүшесіне бөлінеді немесе  немесе
немесе  көпмүшелерінің біреуі
көпмүшелерінің біреуі  екімүшесіне бөлінеді т.с.с. деген қорытынды
шығады. k
дәрежелі
көпмүше
екімүшесіне бөлінеді т.с.с. деген қорытынды
шығады. k
дәрежелі
көпмүше  түріндегі әр түрлі өрнектердің
түріндегі әр түрлі өрнектердің
k санынан артық көбейтіндісіне
бөлінбейтіндіктен және ең үлкен коэффициенті 1-ге тең
k дәрежелі көпмүше
 түріндегі
өрнектің k
санына
бөлінетіндіктен,
түріндегі
өрнектің k
санына
бөлінетіндіктен,  көпмүшесі соңғы теңдіктің сол жағындағы
2k көбейткіштердің
k көбейтіндісіне,
ал
көпмүшесі соңғы теңдіктің сол жағындағы
2k көбейткіштердің
k көбейтіндісіне,
ал  көпмүшесі қалған
k көбейтіндісіне тең
болады.
көпмүшесі қалған
k көбейтіндісіне тең
болады.
Айталық,
 деп алайық. Бірінші теңдіктен
екінші теңдікті азайтып,
деп алайық. Бірінші теңдіктен
екінші теңдікті азайтып,  . Осы теңдікке
. Осы теңдікке  қойып, 2 санының k
бүтін
көбейткішке жіктелуін аламыз:
қойып, 2 санының k
бүтін
көбейткішке жіктелуін аламыз:  .
.
2 санын әр түрлі үш
көбейткіштен артық көбейткіштерге жіктеу мүмкін емес,
сондықтан  екені белгілі болады. Бірақ
екені белгілі болады. Бірақ  болған жағдай да келесідей себеп үшін мүмкін емес. 2 саны
әр түрлі үш көбейткішке тек қана бір тәсілмен
жіктеледі:
болған жағдай да келесідей себеп үшін мүмкін емес. 2 саны
әр түрлі үш көбейткішке тек қана бір тәсілмен
жіктеледі:  .
.  деп алайық. Онда
деп алайық. Онда  , мұндағы
, мұндағы  және сәйкесінше
және сәйкесінше  .
.  мәнін
мәнін
 формуласына қойып, 2 санының басқа үш көбейткішке жіктелуін
аламыз:
формуласына қойып, 2 санының басқа үш көбейткішке жіктелуін
аламыз:  , мұндағы
, мұндағы  . Бұдан
. Бұдан  болады, яғни
болады, яғни  , ал ол есептің шартына қайшы
келеді.
, ал ол есептің шартына қайшы
келеді.
Сонымен, екі жағдай ғана болуы
мүмкін:  .
.
 . Егер
. Егер
 болса, онда:
болса, онда:
 , бұдан
, бұдан
 және
және  -ді а
арқылы
өрнектеп,
-ді а
арқылы
өрнектеп,  .
.
 . Егер
. Егер
 болса, онда:
болса, онда:
 болады, мұндағы
болады, мұндағы
 . Соңғы теңдікке
. Соңғы теңдікке
 және
және  қойып,
қойып,

 аламыз.
аламыз.
Бірақ 2 санын кему ретімен
орналасқан екі көбейткішке тек қана екі тәсілмен жіктеуге
болады:  және
және  . Сонымен қатар
. Сонымен қатар
 , сондықтан
, сондықтан  болады, бұдан
болады, бұдан  -ді а
арқылы
өрнектеп,
-ді а
арқылы
өрнектеп,  және
және  аламыз.
аламыз.
16. * Әр түрлі
 бүтін сандары
үшін
бүтін сандары
үшін  көпмүшесі бүтін коэффициенттері бар екі әр түрлі
көпмүшелердің көбейтіндісіне жіктелетінін
дәлелдеу.
көпмүшесі бүтін коэффициенттері бар екі әр түрлі
көпмүшелердің көбейтіндісіне жіктелетінін
дәлелдеу.
Алдыңғы есептің шешуіне
сәйкес  (*) ұйғарымынан
(*) ұйғарымынан  үшін
үшін
 немесе
немесе  болады, мұндағы
болады, мұндағы  – бүтін коэффициенттері бар қандай да бір
көпмүшелер.
– бүтін коэффициенттері бар қандай да бір
көпмүшелер.  көпмүшесі (әрине
көпмүшесі (әрине  көпмүшесі де)
көпмүшесі де)  барлық мәндерінде 1-ге тең болатынын немесе
барлық мәндерінде 1-ге тең болатынын немесе
 -ге тең болатынын
көрсетейік.
-ге тең болатынын
көрсетейік.
Расында да, егер
де  көпмүшесі
көпмүшесі
 мәнінде 1-ге тең,
ал
мәнінде 1-ге тең,
ал  мәнінде
мәнінде
 -ге тең болса,
онда
-ге тең болса,
онда  мен
мен  аралығындағы х-тің қандай да бір мәнінде
нөлге айналар еді (егер
аралығындағы х-тің қандай да бір мәнінде
нөлге айналар еді (егер  функциясының графигі
функциясының графигі  кезінде Ох
өсінен
жоғары, ал
кезінде Ох
өсінен
жоғары, ал  кезінде Ох
өсінен
төмен орналасатын болса, онда
кезінде Ох
өсінен
төмен орналасатын болса, онда  үзіліссіз қисығы Ох
өсін
үзіліссіз қисығы Ох
өсін  мен
мен  арасында қиып өтеді), ал бұл мүмкін емес, себебі (*)
теңдігінің сол жағы ылғи да 1-ге тең немесе 1-ден артық
болғандықтан нөлге айналмайды.
арасында қиып өтеді), ал бұл мүмкін емес, себебі (*)
теңдігінің сол жағы ылғи да 1-ге тең немесе 1-ден артық
болғандықтан нөлге айналмайды.
 те,
те,
 те
те  мәндерінде 1-ге тең болады делік. Бұл
жағдайда
мәндерінде 1-ге тең болады делік. Бұл
жағдайда  де,
де,  де
де  мәндерінде нөлге айналады, яғни
мәндерінде нөлге айналады, яғни  және
және  көпмүшелері
көпмүшелері  -ге бөлінеді.
-ге бөлінеді.  және
және  көпмүшелерінің дәрежелерінің қосындысы
көпмүшелерінің дәрежелерінің қосындысы
 дәрежесіне, яғни
дәрежесіне, яғни
 -ге тең
болғандықтан,
-ге тең
болғандықтан,  және
және  болады (алдыңғы есептің шешуімен
салыстырыңдар).
болады (алдыңғы есептің шешуімен
салыстырыңдар).
Осылайша,
 , бұдан
, бұдан
 болады, ал ол мүмкін
емес.
болады, ал ол мүмкін
емес.  және
және  көпмүшелері
көпмүшелері  нүктелерінде
нүктелерінде  мәнін қабылдай алмайды (бұл жағдайда
мәнін қабылдай алмайды (бұл жағдайда шығар еді).
шығар еді).
Сонымен,
 өрнегін коэффициенттері бүтін
сан болатын екі көпмүшенің көбейтіндісіне жіктеу мүмкін емес екенін
көреміз.
өрнегін коэффициенттері бүтін
сан болатын екі көпмүшенің көбейтіндісіне жіктеу мүмкін емес екенін
көреміз.
17. Коэффициенттері бүтін сан
болатын  көпмүшесі х-тің жұп мәндерінде 7-ге тең
болса, х-тің ешбір бүтін мәнінде 14-ке
тең бола алмайтынын дәлелдеу керек.
көпмүшесі х-тің жұп мәндерінде 7-ге тең
болса, х-тің ешбір бүтін мәнінде 14-ке
тең бола алмайтынын дәлелдеу керек.
 көпмүшесі
көпмүшесі
 мәндерінде 7-ге тең болсын.
Олай болса,
мәндерінде 7-ге тең болсын.
Олай болса,  теңдеуінің төрт бүтін түбірі бар:
теңдеуінің төрт бүтін түбірі бар:  . Бұдан
. Бұдан  көпмүшесі
көпмүшесі  -ға бөлінетіндігі шығады, яғни
-ға бөлінетіндігі шығады, яғни  болады, мұндағы
болады, мұндағы  мәні 1-ге тең бола алады.
мәні 1-ге тең бола алады.
Ендігі кезекте
 көпмүшесі
көпмүшесі
 бүтін мәнінде 14-ке тең болады
делік.
бүтін мәнінде 14-ке тең болады
делік.  мәнін соңғы теңдікке қойып,
мәнін соңғы теңдікке қойып,  аламыз, ал бұл мүмкін емес, себебі
аламыз, ал бұл мүмкін емес, себебі  бүтін сандарының барлығы әр түрлі, ал 7 санын ең болмағанда
төртеуі бір-біріне тең болмайтын әр түрлі бес санның көбейтіндісі
ретінде жіктеуге болмайды.
бүтін сандарының барлығы әр түрлі, ал 7 санын ең болмағанда
төртеуі бір-біріне тең болмайтын әр түрлі бес санның көбейтіндісі
ретінде жіктеуге болмайды.
18. Бүтін коэффициенттері
бар  көпмүшесі
х-тің 7 бүтін
мәнінде
көпмүшесі
х-тің 7 бүтін
мәнінде  және
және  мәндеріне тең болса, онда оны бүтін коэффициенттері бар екі
көпмүшенің көбейтіндісі ретінде жіктеуге болмайтынын дәлелдеу
керек.
мәндеріне тең болса, онда оны бүтін коэффициенттері бар екі
көпмүшенің көбейтіндісі ретінде жіктеуге болмайтынын дәлелдеу
керек.
Егер жетінші
дәрежелі  көпмүшесі бүтін коэффициентті
көпмүшесі бүтін коэффициентті  және
және  екі көпмүшенің көбейтіндісіне жіктелсе, онда
көбейткіштерінің біреуінің дәрежесі 3-тен артық болмайды; мұндай
көбейткіш
екі көпмүшенің көбейтіндісіне жіктелсе, онда
көбейткіштерінің біреуінің дәрежесі 3-тен артық болмайды; мұндай
көбейткіш  болсын. Егер
болсын. Егер  х-тің 7 бүтін
мәнінде
х-тің 7 бүтін
мәнінде  және
және  мәндеріне тең болса, онда
мәндеріне тең болса, онда  та х-тің 7 бүтін
мәнінде
та х-тің 7 бүтін
мәнінде  және
және  мәндеріне тең болады (себебі
мәндеріне тең болады (себебі  ).
). 
 мәніне тең
болатын х-тің бүтін жеті мәнінің
ішінен
мәніне тең
болатын х-тің бүтін жеті мәнінің
ішінен  1 санының мәніне тең болатындай төрт сан
немесе
1 санының мәніне тең болатындай төрт сан
немесе 
 санының мәніне тең болатындай
төрт сан табылады. Бірінші жағдайда үшінші дәрежелі
санының мәніне тең болатындай
төрт сан табылады. Бірінші жағдайда үшінші дәрежелі
 теңдеуінің төрт түбірі болады,
екінші жағдайда
теңдеуінің төрт түбірі болады,
екінші жағдайда  теңдеуінің төрт түбірі болады. Бірінші жағдай да, екінші
жағдай да орындалмайды, себебі бірінші жағдайда
теңдеуінің төрт түбірі болады. Бірінші жағдай да, екінші
жағдай да орындалмайды, себебі бірінші жағдайда
 төртінші дәрежелі көпмүшеге
бөліну керек еді.
төртінші дәрежелі көпмүшеге
бөліну керек еді.
19. Бүтін
коэффициентті  көпмүшесі
көпмүшесі  және
және  үшін тақ мәнге тең болса,
үшін тақ мәнге тең болса,  теңдеуінің a
рационал
түбірі болса, онда
теңдеуінің a
рационал
түбірі болса, онда  өрнегі 1 немесе 2-ге тең және
өрнегі 1 немесе 2-ге тең және  болатынын дәлелдеу керек.
болатынын дәлелдеу керек.
p
және q
– бір
мезгілде жұп немесе тақ екі бүтін сан болсын. Онда
 айырмасы жұп болады. Расында
да,
айырмасы жұп болады. Расында
да,  өрнегі
өрнегі  жұп өрнегіне бөлінеді.
жұп өрнегіне бөлінеді.
p
– жұп сан
болғанда,  жұп болады. Бірақ есептің шарты бойынша
жұп болады. Бірақ есептің шарты бойынша
 – тақ сан, яғни
– тақ сан, яғни
 да тақ сан болады, себебі
есептің шарты бойынша
да тақ сан болады, себебі
есептің шарты бойынша  тақ сан, осыдан
тақ сан, осыдан  екені шығады.
екені шығады.
Осылайша,
 көпмұшесі
х-тің ешбір бүтін мәнінде (жұп
болсын, тақ болсын) нөлге айнала алмайды, яғни
көпмұшесі
х-тің ешбір бүтін мәнінде (жұп
болсын, тақ болсын) нөлге айнала алмайды, яғни
 көпмүшесінің бүтін түбірлері
болмайды.
көпмүшесінің бүтін түбірлері
болмайды.
Айталық,
 теңдеуінің
теңдеуінің
 рационал түбірі болсын,
яғни
рационал түбірі болсын,
яғни
 .
.  көпмүшесін
көпмүшесін  дәрежелері бойынша жіктейік, яғни оны
дәрежелері бойынша жіктейік, яғни оны
 түрінде жазайық,
мұндағы
түрінде жазайық,
мұндағы  –
–  мәндері белгілі болған жағдайда оғай табылатын қандай да
бір сандар (
мәндері белгілі болған жағдайда оғай табылатын қандай да
бір сандар ( мәні
мәні  көпмүшесінің ең үлкен коэффициенті
көпмүшесінің ең үлкен коэффициенті  -ге тең,
-ге тең,  мәні
мәні  көпмүшесінің ең үлкен коэффициенті
көпмүшесінің ең үлкен коэффициенті  -ге тең,
-ге тең,  мәні
мәні  көпмүшесінің ең үлкен коэффициенті
көпмүшесінің ең үлкен коэффициенті  -ге тең, т.с.с.).
-ге тең, т.с.с.).  мәнін
мәнін  көпмүшесінің соңғы өрнегіне қойып,
көпмүшесінің соңғы өрнегіне қойып,  аламыз. Осы өрнекке
аламыз. Осы өрнекке  мәнін қойып, нәтижесін
мәнін қойып, нәтижесін  -не көбейтіп:
-не көбейтіп:

аламыз, бұдан
егер  болса, онда
болса, онда  бүтін сан болады. Бірақ
бүтін сан болады. Бірақ  көбейтіндісі l-ға бөлінетіндіктен,
ал k мен l – өзара жай сандар
болғандықтан (әйтпесе
көбейтіндісі l-ға бөлінетіндіктен,
ал k мен l – өзара жай сандар
болғандықтан (әйтпесе  бөлшегін қысқартуға болар еді), онда
бөлшегін қысқартуға болар еді), онда
 мен l – өзара жай сандар болады,
бұдан
мен l – өзара жай сандар болады,
бұдан  мен
мен  – өзара жай сандар болады деген қорытынды шығады.
Осыдан
– өзара жай сандар болады деген қорытынды шығады.
Осыдан  болған жағдайда ғана
болған жағдайда ғана  бүтін сан бола алатындығы
шығады.
бүтін сан бола алатындығы
шығады.
Дәл осылайша
 екенін
дәлелдейміз.
екенін
дәлелдейміз.
Енді  теңдігінен
теңдігінен  теңдігін азайтып,
теңдігін азайтып,  немесе
немесе  аламыз. Бірақ
аламыз. Бірақ  және
және  болғандықтан,
болғандықтан,
 болады, осыдан
болады, осыдан  .
.
Сонымен, егер
 болса, онда
болса, онда
 теңдеуінің рационал түбірлері
болмайды. Егер
теңдеуінің рационал түбірлері
болмайды. Егер  немесе
немесе  болса, онда
болса, онда  рационал түбірі бар болуы мүмкін. Осы жерде
рационал түбірі бар болуы мүмкін. Осы жерде
 теңдіктерін
қосып,
теңдіктерін
қосып,  аламыз. Дәлелдеу керегі
осы.
аламыз. Дәлелдеу керегі
осы.
3

шағым қалдыра аласыз


















