
Г. Шымкент Енбекшинский район
Общеобразовательная средняя школа №104 им Е.Юсупова
Доклад на научно-практическую конференцию «Число π»
для учащихся 8 – 10-х классов
Конкурсная работа
«Число π в современной математике»
Авторы: Сулайманкулов Шерзод, 10 класс
Пернибекова Дина, 10 класс
Наставник: Эргашова О.В.
учитель математики осш №104 им Е.Юсупова
2021 г.
Аннотация
Понятие числа служит исходным для многих основных математических теорий. Число позволяет выразить результаты счета или измерения. Учащиеся постепенно знакомятся со всеми числами, в том числе с натуральными, дробными, десятичными, отрицательными, рациональными и иррациональными. Среди этого большого количества есть особое число, точными вычислениями которого занимаются ученые уже много веков. Это число π.
Цель данной работы: выяснить, какие существуют современные методы вычисления числа π, в каких науках применяется это число и как используется в современной математике.
Учащимися было изучено много литературы. Они узнали, как появилось число π, проследили историю развития знаний о нём. В процессе изучения ребята встретились с интересными фактами, связанными с числом π, и особое внимание обратили на применении этого числа в современной математике.
Оглавление:
Введение
Основная часть:
Число π в эпоху цифровой техники
Применение числа π
Споры математиков
Заключение
Список литературы и источников информации
Введение
Обычно наши знания о числе π заканчиваются на этом: 3,14159. Не все даже помнят, что это число показывает отношение длины окружности к её диаметру.π — иррациональное число, то есть его можно представить в виде бесконечной непериодической десятичной дроби, что делает его одним из самых загадочных чисел, известных человеку.
В современной математике число π – это не только отношение длины окружности к диаметру, оно входит в большое число различных формул, в том числе и в формулы неевклидовой геометрии. Входит оно и в формулу Л.Эйлера, которая устанавливает связь числа “π” и числа “е”. Эта и другие взаимосвязи позволили математикам ещё глубже выяснить природу числа π.
Число π в эпоху цифровой техники
Эпоха цифровой техники в XX
веке привела к увеличению скорости появления вычислительных
рекордов. Джон фон Нейман и другие использовали в 1949
году ЭНИАК
для
вычисления 2037 цифр ![]() , которое заняло 70 часов. Ещё одна тысяча цифр
была получена в последующие десятилетия, а отметка в миллион была
пройдена в 1973 году. (Десяти знаков
числа
, которое заняло 70 часов. Ещё одна тысяча цифр
была получена в последующие десятилетия, а отметка в миллион была
пройдена в 1973 году. (Десяти знаков
числа ![]()
![]() вполне достаточно для всех практических
целей).
вполне достаточно для всех практических
целей).
В
начале XX века индийский
математик Сриниваса
Рамануджан обнаружил множество новых формул
для ![]() , некоторые из которых стали знаменитыми из-за
своей элегантности и математической глубины. Одна из этих
формул — это ряд:
, некоторые из которых стали знаменитыми из-за
своей элегантности и математической глубины. Одна из этих
формул — это ряд:
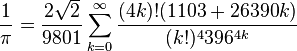 .
.
Братьями Чудновскими в 1987 году найдена похожая на неё:
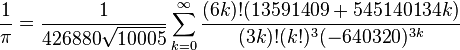 ,
,
Чудновские использовали эту формулу для того,
чтобы установить несколько рекордов в
вычислении ![]() в конце 1980-х, включая то, в результате
которого в 1989 году было получено 1 011 196 691
цифр десятичного разложения. Эта формула используется в программах,
вычисляющих
в конце 1980-х, включая то, в результате
которого в 1989 году было получено 1 011 196 691
цифр десятичного разложения. Эта формула используется в программах,
вычисляющих ![]() на персональных компьютерах, в отличие
от суперкомпьютеров, которые устанавливают современные
рекорды.
на персональных компьютерах, в отличие
от суперкомпьютеров, которые устанавливают современные
рекорды.
В 1975 году Ричард Брент и Юджин Саламин независимо друг от друга открыли алгоритм Брента — Саламина, который, используя лишь арифметику, на каждом шагу удваивает количество известных знаков. Алгоритм состоит из установки начальных значений
![]()
и итераций:
![]()
![]() ,
,
пока an и bn не станут достаточно близки. Тогда
оценка ![]() даётся формулой
даётся формулой
![]()
Похожий алгоритм, увеличивающий на каждом шаге
точность в четыре раза, был найден Джонатаном Боруэйном и
Питером Боруэйном. При помощи этих методов Ясумаса
Канада и его группа, начиная с 1980 года, установили
большинство рекордов вычисления ![]() вплоть до 206 158 430 000
знаков в 1999 году. В 2002 году Канада и его группа установили
новый рекорд — 1 241 100 000 000
десятичных знаков. Хотя большинство предыдущих рекордов Канады были
установлены при помощи алгоритма Брента — Саламина, вычисление
2002 года использовало две формулы типа мэчиновских, которые
работали медленнее, но радикально снижали использование памяти.
Вычисление было выполнено на
суперкомпьютере Hitachi из 64 узлов с
1 терабайтом оперативной памяти, способном выполнять 2
триллиона операций в секунду.
вплоть до 206 158 430 000
знаков в 1999 году. В 2002 году Канада и его группа установили
новый рекорд — 1 241 100 000 000
десятичных знаков. Хотя большинство предыдущих рекордов Канады были
установлены при помощи алгоритма Брента — Саламина, вычисление
2002 года использовало две формулы типа мэчиновских, которые
работали медленнее, но радикально снижали использование памяти.
Вычисление было выполнено на
суперкомпьютере Hitachi из 64 узлов с
1 терабайтом оперативной памяти, способном выполнять 2
триллиона операций в секунду.
Важным развитием недавнего времени стала формула Бэйли — Боруэйна — Плаффа, открытая в 1997 году Саймоном Плаффом и названная по авторам статьи, в которой она впервые была опубликована. Эта формула,
![]()
примечательна тем, что она позволяет извлечь
любую конкретную шестнадцатеричную или двоичную цифру
числа ![]() без вычисления предыдущих. С 1998 до 2000
года распределённый проект PiHex использовал
видоизменённую формулу ББП Фабриса
Беллара для
вычисления квадриллионного бита
числа
без вычисления предыдущих. С 1998 до 2000
года распределённый проект PiHex использовал
видоизменённую формулу ББП Фабриса
Беллара для
вычисления квадриллионного бита
числа ![]() , который оказался
нулём.
, который оказался
нулём.
В 2006 году Саймон Плафф, используя PSLQ, нашёл ряд красивых формул. Пусть q = eπ, тогда
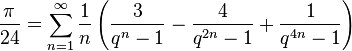
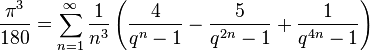
и другие вида
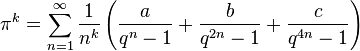 ,
,
где q = eπ, k — нечётное число, и a, b, c — рациональные числа. Если k — вида 4m + 3, то эта формула имеет особенно простой вид:
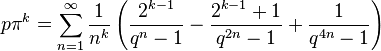
для рационального p, у которого знаменатель — число, хорошо разложимое на множители, хотя строгое доказательство ещё не предоставлено.
В августе 2009 года учёные из японского университета Цукубы рассчитали последовательность из 2 576 980 377 524 десятичных разрядов.
31 декабря 2009 года французский программист Фабрис Беллар на персональном компьютере рассчитал последовательность из 2 699 999 990 000 десятичных разрядов.
2 августа 2010 года американский студент Александр Йи и японский исследователь Сигэру Кондо рассчитали последовательность с точностью в 5 триллионов цифр после запятой.
19 октября 2011 года Александр Йи и Сигэру Кондо рассчитали последовательность с точностью в 10 триллионов цифр после запятой.
Голландский математик Брауэр в первой
половине XX века привёл в качестве примера бессмысленной задачи
поиск в десятичном разложении ![]() последовательности
последовательности ![]() — по его мнению, нужная для этого точность
никогда не будет достигнута. В конце XX века эта последовательность
была обнаружена, она начинается
с 17 387 594 880-го знака после
запятой.
— по его мнению, нужная для этого точность
никогда не будет достигнута. В конце XX века эта последовательность
была обнаружена, она начинается
с 17 387 594 880-го знака после
запятой.
Применение числа π
Величина π сейчас используется в самых различных областях современной науки. Это не только отношение длины окружности к ее диаметру, неевклидова геометрия не обходится без π. Эйлер вывел формулу, описывающую связь между π и e:
ei*π + 1 = 0.
С применением числа π можно вычислить любую другую константу, например, постоянную тонкой структуры, постоянную золотой пропорции.
Число π применяется в различных науках:
-
Алгебра: π - иррациональное и трансцендентное число.
-
Тригонометрия: радианная мера измерения углов.
-
Планиметрия: длина окружности и её дуги; площадь круга и его частей.
-
Стереометрия: объем шара и частей; объем цилиндра, конуса и усеченного конуса; площадь поверхности цилиндра, конуса и сферы.
-
Физика: теория относительности; квантовая механика; ядерная физика.
-
Теория вероятностей: формула Стирлинга для вычисления факториала.
Кроме этого, число π можно встретить в астрономии, космонавтике, архитектуре, навигации, электронике.
Число Пи одна из фундаментальных математических констант. Оно встречается во многих уравнениях различных направлений науки:
-
в уравнении гравитационного поля Эйнштейна
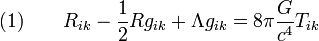
-
в уравнении нормального распределения Гаусса
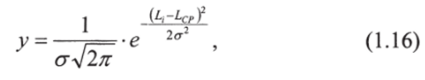
-
в уравнениях, связанных с образованием радуги;
-
в уравнениях описывающих распространение зыби при падении дождевой капли в воду;
-
в уравнении движения маятника;
-
во многих геометрических задачах;
-
в задачах связанных с волнами;
-
в задачах навигации и т.д.
В силу своей универсальности Пи используется в вычислениях для микро и макрокосмоса и входит, как и в формулы, описывающие движение комет, астероидов, космических кораблей и других небесных тел в астрономии, так и в формулы для вычислений электронных орбит в квантовой физике и квантовой химии.
Ученые выяснили, что в расшифрованном ДНК человека число π определяет структуру макромолекулы. Это произвело фурор. Руководитель исследования, доктор Чарльз Кантор, отметил: «Это феноменально, число π встречается повсюду, и при этом является неизменной величиной».
Люди, далекие от математики, скорее всего не знают, но так сложилось, что число Пи имеет брата, который больше его в два раза. Это число Тау(τ) , и, если Пи — это отношение длины окружности к диаметру, то Тау — это отношение этой длины к радиусу. "Тау", по мысли математиков-новаторов, должна прийти на смену "пи" и быть ровно вдвое больше привычной нам постоянной - 6,28.
И на сегодняшний день есть предложения некоторых математиков отказаться от числа Пи и заменить его на Тау, так как это во многом более удобно. По словам сторонников введения новой постоянной, при решении большинства математических задач "тау" имеет больше смысла, чем "пи", и может несколько упростить расчеты.
Однако с ними согласны далеко не все любители математики, а давняя традиция использования буквы "пи" дает основания полагать, что сбросить ее с математического пьедестала будет непросто.
И, как говорил Лев Давидович Ландау: «Новая теория начинает господствовать тогда, когда вымрут сторонники старой».
Заключение
С давних времен загадка этого числа не давала покоя многим ученым, особенно математикам - именно в этой области многие разделы науки не могут обойтись без законов этого таинственного числа.
Точное значение числа π в современном мире представляет собой не только собственную научную ценность, но и используется для очень точных вычислений (например, орбиты спутника, строительства гигантских мостов), а также оценки быстродействия и мощности современных компьютеров.
В настоящее время с числом π связано труднообозримое множество формул, математических и физических фактов. Их количество продолжает стремительно расти. Всё это говорит о возрастающем интересе к важнейшей математической константе, изучение которой насчитывает уже более двадцати двух веков.
Возможности, которые дает математикам число π, безграничны. В перспективе это бесконечное число может содержать всю информацию, находящуюся во Вселенной. Изучение числа π продолжается учеными до сих пор.
Список литературы:
1. Стройк Д.Я. Краткий очерк истории математики. Перевод с немецкого и дополнения И.Б. Погребысского - М.: «Наука» Главная редакция физико-математической литературы 2012г.
2. Глейзер. Г.И. История математики в средней школе / Г.И. Глейзер. – М.: Просвещение, 2011г.
3. Математика в школе, журнал, 2010 г.
4. Мантуров О.В. Толковый словарь математических терминов: Пособие для учителей / О.В. Мантуров, Ю.К. Солнцев, Ю.И. Соркин, Н.Г. Федин. – М.: Просвещение, 2013г.
Интернет ресурсы:
http:// crow.academy.ru/ materials_/pi/history.htm
http://hab/kp.ru// daily/24123/344634/
http://ru.wikipedia.org/
http://shkolazhizni.ru/archive/0/n-14621/
http://dic.academic.ru
http://www.bestreferat.ru/referat
http://statistic.su/blog/pi/2010-09-24-49
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Доклад на тему: «Число π в современной математике»
Доклад на тему: «Число π в современной математике»
Г. Шымкент Енбекшинский район
Общеобразовательная средняя школа №104 им Е.Юсупова
Доклад на научно-практическую конференцию «Число π»
для учащихся 8 – 10-х классов
Конкурсная работа
«Число π в современной математике»
Авторы: Сулайманкулов Шерзод, 10 класс
Пернибекова Дина, 10 класс
Наставник: Эргашова О.В.
учитель математики осш №104 им Е.Юсупова
2021 г.
Аннотация
Понятие числа служит исходным для многих основных математических теорий. Число позволяет выразить результаты счета или измерения. Учащиеся постепенно знакомятся со всеми числами, в том числе с натуральными, дробными, десятичными, отрицательными, рациональными и иррациональными. Среди этого большого количества есть особое число, точными вычислениями которого занимаются ученые уже много веков. Это число π.
Цель данной работы: выяснить, какие существуют современные методы вычисления числа π, в каких науках применяется это число и как используется в современной математике.
Учащимися было изучено много литературы. Они узнали, как появилось число π, проследили историю развития знаний о нём. В процессе изучения ребята встретились с интересными фактами, связанными с числом π, и особое внимание обратили на применении этого числа в современной математике.
Оглавление:
Введение
Основная часть:
Число π в эпоху цифровой техники
Применение числа π
Споры математиков
Заключение
Список литературы и источников информации
Введение
Обычно наши знания о числе π заканчиваются на этом: 3,14159. Не все даже помнят, что это число показывает отношение длины окружности к её диаметру.π — иррациональное число, то есть его можно представить в виде бесконечной непериодической десятичной дроби, что делает его одним из самых загадочных чисел, известных человеку.
В современной математике число π – это не только отношение длины окружности к диаметру, оно входит в большое число различных формул, в том числе и в формулы неевклидовой геометрии. Входит оно и в формулу Л.Эйлера, которая устанавливает связь числа “π” и числа “е”. Эта и другие взаимосвязи позволили математикам ещё глубже выяснить природу числа π.
Число π в эпоху цифровой техники
Эпоха цифровой техники в XX
веке привела к увеличению скорости появления вычислительных
рекордов. Джон фон Нейман и другие использовали в 1949
году ЭНИАК
для
вычисления 2037 цифр ![]() , которое заняло 70 часов. Ещё одна тысяча цифр
была получена в последующие десятилетия, а отметка в миллион была
пройдена в 1973 году. (Десяти знаков
числа
, которое заняло 70 часов. Ещё одна тысяча цифр
была получена в последующие десятилетия, а отметка в миллион была
пройдена в 1973 году. (Десяти знаков
числа ![]()
![]() вполне достаточно для всех практических
целей).
вполне достаточно для всех практических
целей).
В
начале XX века индийский
математик Сриниваса
Рамануджан обнаружил множество новых формул
для ![]() , некоторые из которых стали знаменитыми из-за
своей элегантности и математической глубины. Одна из этих
формул — это ряд:
, некоторые из которых стали знаменитыми из-за
своей элегантности и математической глубины. Одна из этих
формул — это ряд:
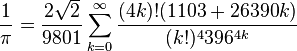 .
.
Братьями Чудновскими в 1987 году найдена похожая на неё:
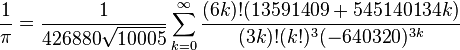 ,
,
Чудновские использовали эту формулу для того,
чтобы установить несколько рекордов в
вычислении ![]() в конце 1980-х, включая то, в результате
которого в 1989 году было получено 1 011 196 691
цифр десятичного разложения. Эта формула используется в программах,
вычисляющих
в конце 1980-х, включая то, в результате
которого в 1989 году было получено 1 011 196 691
цифр десятичного разложения. Эта формула используется в программах,
вычисляющих ![]() на персональных компьютерах, в отличие
от суперкомпьютеров, которые устанавливают современные
рекорды.
на персональных компьютерах, в отличие
от суперкомпьютеров, которые устанавливают современные
рекорды.
В 1975 году Ричард Брент и Юджин Саламин независимо друг от друга открыли алгоритм Брента — Саламина, который, используя лишь арифметику, на каждом шагу удваивает количество известных знаков. Алгоритм состоит из установки начальных значений
![]()
и итераций:
![]()
![]() ,
,
пока an и bn не станут достаточно близки. Тогда
оценка ![]() даётся формулой
даётся формулой
![]()
Похожий алгоритм, увеличивающий на каждом шаге
точность в четыре раза, был найден Джонатаном Боруэйном и
Питером Боруэйном. При помощи этих методов Ясумаса
Канада и его группа, начиная с 1980 года, установили
большинство рекордов вычисления ![]() вплоть до 206 158 430 000
знаков в 1999 году. В 2002 году Канада и его группа установили
новый рекорд — 1 241 100 000 000
десятичных знаков. Хотя большинство предыдущих рекордов Канады были
установлены при помощи алгоритма Брента — Саламина, вычисление
2002 года использовало две формулы типа мэчиновских, которые
работали медленнее, но радикально снижали использование памяти.
Вычисление было выполнено на
суперкомпьютере Hitachi из 64 узлов с
1 терабайтом оперативной памяти, способном выполнять 2
триллиона операций в секунду.
вплоть до 206 158 430 000
знаков в 1999 году. В 2002 году Канада и его группа установили
новый рекорд — 1 241 100 000 000
десятичных знаков. Хотя большинство предыдущих рекордов Канады были
установлены при помощи алгоритма Брента — Саламина, вычисление
2002 года использовало две формулы типа мэчиновских, которые
работали медленнее, но радикально снижали использование памяти.
Вычисление было выполнено на
суперкомпьютере Hitachi из 64 узлов с
1 терабайтом оперативной памяти, способном выполнять 2
триллиона операций в секунду.
Важным развитием недавнего времени стала формула Бэйли — Боруэйна — Плаффа, открытая в 1997 году Саймоном Плаффом и названная по авторам статьи, в которой она впервые была опубликована. Эта формула,
![]()
примечательна тем, что она позволяет извлечь
любую конкретную шестнадцатеричную или двоичную цифру
числа ![]() без вычисления предыдущих. С 1998 до 2000
года распределённый проект PiHex использовал
видоизменённую формулу ББП Фабриса
Беллара для
вычисления квадриллионного бита
числа
без вычисления предыдущих. С 1998 до 2000
года распределённый проект PiHex использовал
видоизменённую формулу ББП Фабриса
Беллара для
вычисления квадриллионного бита
числа ![]() , который оказался
нулём.
, который оказался
нулём.
В 2006 году Саймон Плафф, используя PSLQ, нашёл ряд красивых формул. Пусть q = eπ, тогда
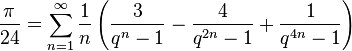
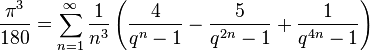
и другие вида
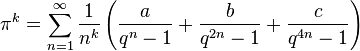 ,
,
где q = eπ, k — нечётное число, и a, b, c — рациональные числа. Если k — вида 4m + 3, то эта формула имеет особенно простой вид:
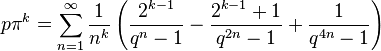
для рационального p, у которого знаменатель — число, хорошо разложимое на множители, хотя строгое доказательство ещё не предоставлено.
В августе 2009 года учёные из японского университета Цукубы рассчитали последовательность из 2 576 980 377 524 десятичных разрядов.
31 декабря 2009 года французский программист Фабрис Беллар на персональном компьютере рассчитал последовательность из 2 699 999 990 000 десятичных разрядов.
2 августа 2010 года американский студент Александр Йи и японский исследователь Сигэру Кондо рассчитали последовательность с точностью в 5 триллионов цифр после запятой.
19 октября 2011 года Александр Йи и Сигэру Кондо рассчитали последовательность с точностью в 10 триллионов цифр после запятой.
Голландский математик Брауэр в первой
половине XX века привёл в качестве примера бессмысленной задачи
поиск в десятичном разложении ![]() последовательности
последовательности ![]() — по его мнению, нужная для этого точность
никогда не будет достигнута. В конце XX века эта последовательность
была обнаружена, она начинается
с 17 387 594 880-го знака после
запятой.
— по его мнению, нужная для этого точность
никогда не будет достигнута. В конце XX века эта последовательность
была обнаружена, она начинается
с 17 387 594 880-го знака после
запятой.
Применение числа π
Величина π сейчас используется в самых различных областях современной науки. Это не только отношение длины окружности к ее диаметру, неевклидова геометрия не обходится без π. Эйлер вывел формулу, описывающую связь между π и e:
ei*π + 1 = 0.
С применением числа π можно вычислить любую другую константу, например, постоянную тонкой структуры, постоянную золотой пропорции.
Число π применяется в различных науках:
-
Алгебра: π - иррациональное и трансцендентное число.
-
Тригонометрия: радианная мера измерения углов.
-
Планиметрия: длина окружности и её дуги; площадь круга и его частей.
-
Стереометрия: объем шара и частей; объем цилиндра, конуса и усеченного конуса; площадь поверхности цилиндра, конуса и сферы.
-
Физика: теория относительности; квантовая механика; ядерная физика.
-
Теория вероятностей: формула Стирлинга для вычисления факториала.
Кроме этого, число π можно встретить в астрономии, космонавтике, архитектуре, навигации, электронике.
Число Пи одна из фундаментальных математических констант. Оно встречается во многих уравнениях различных направлений науки:
-
в уравнении гравитационного поля Эйнштейна
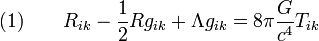
-
в уравнении нормального распределения Гаусса
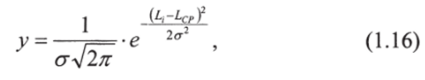
-
в уравнениях, связанных с образованием радуги;
-
в уравнениях описывающих распространение зыби при падении дождевой капли в воду;
-
в уравнении движения маятника;
-
во многих геометрических задачах;
-
в задачах связанных с волнами;
-
в задачах навигации и т.д.
В силу своей универсальности Пи используется в вычислениях для микро и макрокосмоса и входит, как и в формулы, описывающие движение комет, астероидов, космических кораблей и других небесных тел в астрономии, так и в формулы для вычислений электронных орбит в квантовой физике и квантовой химии.
Ученые выяснили, что в расшифрованном ДНК человека число π определяет структуру макромолекулы. Это произвело фурор. Руководитель исследования, доктор Чарльз Кантор, отметил: «Это феноменально, число π встречается повсюду, и при этом является неизменной величиной».
Люди, далекие от математики, скорее всего не знают, но так сложилось, что число Пи имеет брата, который больше его в два раза. Это число Тау(τ) , и, если Пи — это отношение длины окружности к диаметру, то Тау — это отношение этой длины к радиусу. "Тау", по мысли математиков-новаторов, должна прийти на смену "пи" и быть ровно вдвое больше привычной нам постоянной - 6,28.
И на сегодняшний день есть предложения некоторых математиков отказаться от числа Пи и заменить его на Тау, так как это во многом более удобно. По словам сторонников введения новой постоянной, при решении большинства математических задач "тау" имеет больше смысла, чем "пи", и может несколько упростить расчеты.
Однако с ними согласны далеко не все любители математики, а давняя традиция использования буквы "пи" дает основания полагать, что сбросить ее с математического пьедестала будет непросто.
И, как говорил Лев Давидович Ландау: «Новая теория начинает господствовать тогда, когда вымрут сторонники старой».
Заключение
С давних времен загадка этого числа не давала покоя многим ученым, особенно математикам - именно в этой области многие разделы науки не могут обойтись без законов этого таинственного числа.
Точное значение числа π в современном мире представляет собой не только собственную научную ценность, но и используется для очень точных вычислений (например, орбиты спутника, строительства гигантских мостов), а также оценки быстродействия и мощности современных компьютеров.
В настоящее время с числом π связано труднообозримое множество формул, математических и физических фактов. Их количество продолжает стремительно расти. Всё это говорит о возрастающем интересе к важнейшей математической константе, изучение которой насчитывает уже более двадцати двух веков.
Возможности, которые дает математикам число π, безграничны. В перспективе это бесконечное число может содержать всю информацию, находящуюся во Вселенной. Изучение числа π продолжается учеными до сих пор.
Список литературы:
1. Стройк Д.Я. Краткий очерк истории математики. Перевод с немецкого и дополнения И.Б. Погребысского - М.: «Наука» Главная редакция физико-математической литературы 2012г.
2. Глейзер. Г.И. История математики в средней школе / Г.И. Глейзер. – М.: Просвещение, 2011г.
3. Математика в школе, журнал, 2010 г.
4. Мантуров О.В. Толковый словарь математических терминов: Пособие для учителей / О.В. Мантуров, Ю.К. Солнцев, Ю.И. Соркин, Н.Г. Федин. – М.: Просвещение, 2013г.
Интернет ресурсы:
http:// crow.academy.ru/ materials_/pi/history.htm
http://hab/kp.ru// daily/24123/344634/
http://ru.wikipedia.org/
http://shkolazhizni.ru/archive/0/n-14621/
http://dic.academic.ru
http://www.bestreferat.ru/referat
http://statistic.su/blog/pi/2010-09-24-49

шағым қалдыра аласыз















