

№ 58
жалпы орта мектебі
58
жалпы орта мектебі
Қалалық ғылыми практикалық конференция
Оқыту процесінде заманауи инфрақұрлымдық, ақпараттық, коммуникациялық технологияларды және электрондық ресурстарды қолдану

Байболова Нұрбала Ізетбекқызы
Баяндама тақырыбы:
ЕКІ АЙНЫМАЛЫСЫ БАР СЫЗЫҚТЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДІҢ ТӘСІЛДЕРІ
Шымкент қаласы, Әл-Фараби ауданы
Қ айтпас -1 елді мекені Тел: 8702 611 04
75
айтпас -1 елді мекені Тел: 8702 611 04
75

№ 58 жалпы орта мектебі
Баяндама тақырыбы:
Жаңа технология әдістерін пайдаланып, математика
сабақтарында оқушылардың білім деңгейін
көтеру жолдары.

Байболова Нұрбала Ізетбекқызы
Қалалық ғылыми практикалық конференция
Тақырыбы: Оқыту процесінде заманауи инфрақұрлымдық, ақпараттық, коммуникациялық технологияларды және электрондық ресурстарды қолдану
Баяндама тақырыбы: ЕКІ АЙНЫМАЛЫСЫ БАР СЫЗЫҚТЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДІҢ ТӘСІЛДЕРІ
1.Кіріспе бөлім
Оқыту процесінде заманауи инфрақұрлымдық, ақпараттық, коммуникациялық технологияларды және электрондық ресурстарды қолдану
2. Негізгі бөлім
а) Екі айнымалысы бар сызықтық теңдеулер жүйесінің шығу тарихы.
б) Екі айнымалысы бар сызықтық теңдеулер жүйесінің шешу жолдары.
3.Қорытынды
4. Пайдаланылған әдебиеттер
Кіріспе
Еліміздің экономикалық, саяси-мәдени дамуына үлес қосатын әлеуметтік өркениетке көтерілетін, парасатты , денсаулығы мықты адамды тәрбиелеу- ұстаздар қауымының бүгінгі таңдағы мерейлі міндеті. Білім беру- оқыту мен тәрбиелеудің үздіксіз процесі.Қазіргі кездегі білім берудегі мақсат- жан-жақты,білімді,өмір сүруге бейім, өзіндік ой- талғамы бар,қабілетті жеке тұлғаны қалыптастыру, оқушылардың дүниетанымымын кеңейту,ой еркіндігіне жол ашу.
Жан –жақты үйлесімді өркениетті елдің елдің ұрпағын тәрбиелеп шығу бүгінгі мектептің алдына қойылған мақсаттардың бірі .Бұл мақсат әрбір орта мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын оқушы санасына жететіндей етіп оқытқанға ғана орындалады.
Мектепте математиканы оқытудың негізгі міндеті- оқушылардың нақты және жүйелі түрде білім алуын қамтамасыз ету. Математиканы тереңдетіп оқыту оқушының математикалық өрісін,шығармашылық дарынын, қызығушылығын арттырып,өздігіненізденісін қалыптастырады. Математиканы оқу- терең ойлап, кез-келген есепті шығару үшін, оның шығару жолын анықтау керек, қолданылатын формулаларды, ережелерді, теоремаларды т.б ұғымдарды білу қажет.
Математиканы оқыту – басты мақсат Оқыту үрдісінің негізгі мақсаты- арнайы педагогикалық әдістермен мақсатты түрде пайдаланып оқушылардың интеллектін ,шығармашылық ойлауын, ғылыми көзқарасы мен белсенділігін қалыптастыру,өз бетінше білім алу дағдыларын дамыту болып табылады
Бұл баяндама математика курсындада қарастырылатын екі айнымалысы бар сызықтық теңдеулер жүйесін және оларды шешу жолдарының әр түрлі әдістеріне негізделіп отыр.
Екі айнымалысы бар сызықтық теңдеулер жүйесі маңызды тақырыптардың бірі.Көптеген құбылыстар мен мазмұнды мәселе есептердің шығарылуы теңдеу және теңдеулер жүйесін құру арқылы шығарылады
Пьер Ферма- математик әрі заңгер
Пьер Ферма 1601 жылы 17 тамызда Францияның Монтобанда қаласында туған.Ферма Тулиза қаласында оқып, заң ғылымының маманы- заңгер болып шығады. Бүкіл өмірін осы сот қызметінде, сол Тулиза қаласындаөткізеді.
П.Ферма математиканы өз бетімен оқып үйренген .Грек және латын тілдеріндегі Аполлоний мен Диофанттың шығармаларын оқып, әуесқой математик болған.
Ферма сызықтарды теңдеулер арқылы өрнектейді. «Екі айнымалысы бар теңдеулер» -дейді. Екі айнымалысы бар теңдеулер мен теңдеулер жүйесіне келтіре отырып дәлелдеген. Ферма –әрдайым жазықтықта орналасқан сызықты анықтайды, түзу сызық бір ғана түрлі болады, ал қисық сызықтар сансыз көп Координаталарды Ферма кесінділер түріне алады. Түзудің ,шеңбердің ,параболаның теңдеулерін қорытып шығарды .Ескі математика тұрақты шамалардың ғана математикасыболатын.ал жаңа математика. Яғни айнымалы шамалардың математикасы болды.
Ферма 1665 жылы 12 қаңтарда Тулиза қаласында қайтыс болады
Екі айнымалысы бар теңдеулер жүйесін шешуде орындалатын түрлендіру-лердің тең шамалас болуына назар аудару, теңдеулер жүйесінде гі белгісіз айнымалылардың мәндеріне байланысты теңдеулер жүйесінің шешімдері болатынын немесе болмайтынын зерттейміз
Сызықтық теңдеулер жүйесін шешудің тәсілдері
Қосу тәсілі
1)кез-келген айнымалының коэффициенттерінің модульдерін теңестірукерек
2)жүйенің теңдеулерін мүшелеп қосу (азайту)керек
3)жаңа жүйе құру:біреуі-жаңа теңдеу,екіншісі-ескі теңдеулердің біреуі.
4)жаңа теңдеуді шешу және оның бір айнымалысының мәнін табу
5)табылған айнымалы мәнін ескі теңдеуге қою және екінші айнымалы мәнін табу
![]()


Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешуді қарастырып отырмыз.
1 жағдай.
у![]() 0,5х+2
0,5х+2
у-1,5х+6 жауабы (2; 3)

егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер қиылысса, онда теңдеулер жүйесінің бір ғана шешімі болады.
ІІ жағдай.
Теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер өзара параллель
х![]() +2у
= 4
+2у
= 4
3х+6у=-18
теңдеулер жүйесінің шешімдерін анықтайық, әрбір теңдеудегі у –ті х арқылы өрнектесек:
![]() у=-0,5х+2
у=-0,5х+2
у=-0,5х-3
у =-0,5х+2 теңдеуінің графигі
түзу . у=-0,5х-3 теңдеуінің графигі түзуі
Мұндағы
=-0,5х+2 теңдеуінің графигі
түзу . у=-0,5х-3 теңдеуінің графигі түзуі
Мұндағы
түзулердің бұрыштық коэффициенттері бірдей болғандықтан, олардың графиктері параллель түзулер .Параллель түзулердің бір-бірімен қиылыспайтыны белгілі, онда
х![]() +2у
= 4
+2у
= 4
3х+6у = -18 теңдеулер жүйесінің шешімдері болмайды, яғни теңдеулер жүйесінің шешімдері --бос жиын
жауабы: шешімдері болмайды, Ø
Егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер өзара параллель болса, онда теңдеулер жүйесінің шешімі болмайды.
ІІІ жағдай.
Жүйедегі теңдеулердің графигі болатын түзулер беттеседі.
7![]() х+2у12
х+2у12
35х+10у60

егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер беттесетін болса, онда теңдеулер жүйесінің шексіз көп шешімі болады.
Екі айнымалысы бар сызықтық теңдеулер жүйесін шешудің
алмастыру тәсілі
1-мысал Оқушы екі сан ойлады.Бірінші сан екінші саннан 7-ге аттық. Бірінші санды 3 еселеп, одан екінші санды 2 еселеп азайтқанда ,айырма 27-ге тең болады.Оқушы қандай сандар ойлады.
Шешуі:х- бірінші сан
у- екінші сан есептің шарты бойынша теңдеулер жүйесін құрамыз.
х-ті у арқылы өрнектеп, оны екінші теңдеудегі х-тің орнына қойғанда алғашқы теңдеулер жүйесіменмәндес теңдеулердің жүйесіалынады:
х = у+7
3(у+7)-2у =27 - бір айнымалысы бар теңдеу
мұндағы : 3(у+7)-2у = 27
3у+21-2у = 27
3у-2у = 27-21
у = 6 , 6-ны х=у+7 теңдеуіне қоямыз х=6+7 х=13
демек (13,6) сандар жұьы теңдеулер жүйесінің шешімі болады
Екі айнымалысы бар сызықтық теңдеулер жүйесінің
қосу тәсілі
* Айнымалылардың біреуінің коэффициенттері(бірінші және екінші теңдеудегі қарама-қарсы сандар болатындай көбейткіштерге жүйенің екі жағын да көбейту керек;{
*Жүйе теңдеулерінің оң жақтарын және сол жақтарын мүшелеп қосып немесе азайтып,оны бір айнымалысы бар теңдеуге айналдыру керек;
* шыққан бір айнымалысы бар теңдеуді шешіп,айнымалылының мәнін табу керек;
* айнымалылардың біреуінің табылған мәніне сәйкес екінші айнымалының мәнін табу керек;
1- жағдай. Теңдеулер жүйесіндегіайнымалылардың біреуінің коэффициенттері –қарама- қарсы сандар.
1-мысал
![]() теңдеулер жүйесін қосу
тәсілімен шешейік.
теңдеулер жүйесін қосу
тәсілімен шешейік.
Теңдеулердің сол және оң жақтарын мүшелеп қосайық:

9х![]() 36
36
Берілген жүйенің бір
теңдеуін 9х![]() 36 теңдеуімен алмастырайық
.
36 теңдеуімен алмастырайық
.
Сонда алғашқы берілген теңдеулер жүйесімен мәндес

теңдеулер жүйесі шығады,
ондағы бірінші теңдеуден х![]() . х –тің мәнін жүйенің екінші
6х+2у=30 теңдеуіне қойсақ :
. х –тің мәнін жүйенің екінші
6х+2у=30 теңдеуіне қойсақ :
6×4+2у=30, 24+2у =30 , у =3
Теңдеулер жүйесінің бір ғана : х = 4, у=3 шешімі бар.
Қысқаша:

9х![]() 36
36
х=4
6×4+2у=30, 24+2у =30 , у =3
Жауабы: х=4 , у =3
II Жағдай. Теңдеулер жүйесіндегі айнымалылардың біреуінің коэффициенттері тең.
2
мысал. 
теңдеулер жүйесін шешейік.
Теңдеулердің біреуінің екі жағын да -1 ге көбейтіп, теңдеулеоді мүшелеп қосу керек немесе теңдеулердің біреуінен екіншісін
азайту керек :

-2у =-4
у = 2
у тің табылған мәнін жүйедегі теңдеулердің кез келген біреуіне қоямыз.
Мысалы. 2х+5×2=16
2х=16-10
2х=6
х=3
Жауабы: х=3, у = 2
Екі ай нымалысы бар сызықтық теңдеулер жүйесін қосу тәсілімен
шешу үшін:
-
айнымалылардың біреуінің коэффициенттері (бірінші және екінші) қарама-қарсы сандар болатындай көбейткіштерге (көбейткішке) жүйенің теңдеулерінің екі жағын да( бір теңдеуін) көбейту керек;
2) жүйе теңдеулерінің оң жақтарын және сол жақтарын мүшелеп қосып немесе азайтып , оны бір айнымалысы бар теңдеуге айналдыру керек;
3) шыққан бір айнымалысы бар теңдеуді шешіп , айнымалының мәнән табу керек;
4) айнымалылаврдың біреуінің табылған мәніне сәйкес екінші айнымалының мәнін табу керек.
Егер айнымалылардың біреуінің коэффициенттері қарама-қарсы сандар болса , онда жүйені шешуді бірден теңдеулерді мүшелеп қосудан бастау керек.
Екі айнымалысы бар сызықтық теңдеулер жүйесін анықтауыштар арқылы шешу
![]() Екі айнымалысы бар сызықтық
теңдеулер жүйесін жалпы түрде шешуді
қарастырайық
Екі айнымалысы бар сызықтық
теңдеулер жүйесін жалпы түрде шешуді
қарастырайық ![]()
![]() →
→![]() →
х=
→
х=![]() =
=
(а2в1-а1в2) х = с2в1 –с1в2
=![]() =
х=
=
х= ![]()
![]()
![]() →
→![]() →
=
→
= ![]()
( а1в2-а2в1)у = а1с2-а2с1
Сонымен
![]() ⇛
х=
⇛
х=![]() ;
у=
;
у=![]()
Теңдеулердің коэффициенттерінен кесте құрып, оның мәнін мына ереже бойынша есептейміз : кестенің бас диогоналінің бойында тұрған цифрлардың көбейтіндісінен (а1в2) келесі диагональдардың бойындағы цифрлардың көбейтіндісін азайтамыз.
![]()
![]()
![]()
![]()
![]()
![]() а1 в1 с1 в1
а1 в1 с1 в1
∆ = а 2 в2 = а1в2-а2в1 ∆х= с2 в2 = с1 в2-с 2в1
( бірінші бағандағы элементтер сәйкес түрде жүйенің с 1және с 2 бос мүшелерімен алмастырылады)
Екінші бағандағы элементтер с1, с2 бос мүшелерімен сәйкес түрде алмастырылған.
![]()
![]() а1 с1
а1 с1
∆у = а2 с2 = а1 с2-а
2с1 ,
Сонда
х= ![]() және
у =
және
у =![]()
1)Егер ∆≠0 болса, жүйенің жалғыз ғана шешімі бар болады.
х
=![]() және
у=
және
у=![]()
2) егер ∆=0 ; және ∆х=0 ,∆у=0 болса жүйенің шексіз шешімі көп болады.
3) егер ∆=0, бірақ ∆х≠0 ( ∆у≠0) болса, жүйенің шешімі болмайды.
![]()
![]() 1-
мысалы:
1-
мысалы: ![]()
2 3
Шешуі:
![]() ⇛∆
= 3 -2 =
2*(-2)-3*3=-4-9=-13≠0
⇛∆
= 3 -2 =
2*(-2)-3*3=-4-9=-13≠0
Жүйенің жалғыз ғана шешімі бар.
![]()
![]() 4
3
4
3
∆х= 6
-2 =4*(-2)
-6*3 =
-8 -18 = -26 x
=![]() =
=![]() =2
→ x=2
=2
→ x=2
![]()
![]()
2 4
∆у= 3 6 = 2 *6 – 3 *4 = 0
у= ![]() =
=![]() = 0 → у
=0
= 0 → у
=0
Жауабы : ( 2; 0)
![]()
![]() 2 3
2 3
2-
Мысал ![]() →∆= 4 6 =2 *6 – 3* 4=
0
→∆= 4 6 =2 *6 – 3* 4=
0
![]()
![]()
∆х= 4 3
8 6 =4 * 6- 8 *3 = 0 Жүйенің шексіз көп шешімі болады
Қорытынды бөлім
Математика ғылымдардың әр саласында өте кең тараған сала болғандықтан, қойылатын талаптарға сай жас ұрпақты сапалы білім, саналы тәрбие бере отырып, математикалық мәдениетін көтеру керек.
Математикалық есептерді шешу,теоремаларды дәлелдеу оқушылардың ойлау ,есте сақтау қабілеттерін дамытады Ендеше оқушылардың математикалық сауаттылығын артыру-олардың алған білімінің тиянақты болуын қамтамасыз ету .
Негізінен жаңа технологиялар оқушылардың білім сапасын артыруға, ой санасының дамуына мүмкіндік жасайды.Үнемі өзгеріп тұрған әлем адамнан қабілет пенқажеттілікті талап етеді
Ереже білсек есеп шығару жеңіл болады.Әрбір есепті ереже тілмен айтсақ, математикалық тілде сөйлете алады екенбіз.Ьұғалім шеберлігінің негізгі көрсеткіштерінің бірі-әдәстеме саласындағы ғылыми жаңалықтар мен озық тәжірбиені жетік игеру және оларды күнделікті қызметте пайдалану .Демек оқушылардың бойында шығармашылық қабілетті дамыту жалпы пәндерді оқып үйрену кезінде және еңбек –оқу процесінде ойлаудың өмірлік тәжірбиесі негізінде алған білімдері мен дағдыларының негізінде жүзеге асады. Білім сапасын көтеруге ,қабілеті жоғары оқушыларды шығармашылыққа баулып ,ізденушілік қасиетерін жетілдіруге, уақытыт тиімді пайдалануға мүмкіндік туғызатын М.Жанпейісованың « Модульдік оқыту технологиясы» мен Ж.Қараевтың «Деңгейлеп оқыту технологиясын»
өз сабақтарымда қолданамын
Оқушылар «Екі айнымалысы бар теңдеулер жүйесін шешудің тәсілдері» тақырыбы бойынша алған білімдері
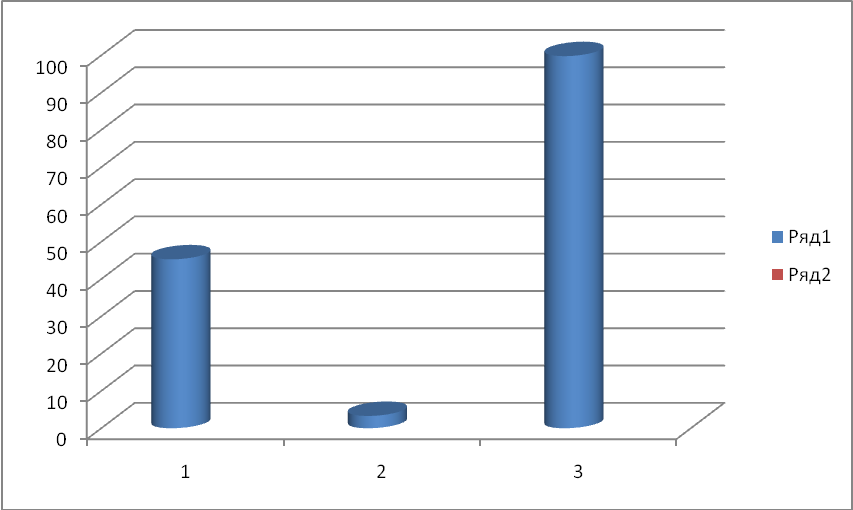
2009-2010 оқу жылындағы тест нәтижесі
2009-2010 оқу жылындағы тест нәтижесі
2010-2011 оқу жылындағы тест нәтижесі

Пайдаланылған әдебиеттер :
-
« Математиканың даму тарихы» . Алматы, Мектеп 1964 ж
Есмұханов М
-
«Матетематика мен математиктер жайында әңгімелер»
1 – ші кітап Алматы. Мектеп 1967 ж
2-ші кітап Алматы Мектеп 1970 ж Исқақов М .Ө
-
«Теңдеулер және теңдеулер жүйелері ».
Алматы ,Мектеп 1976 ж
Есмұханов М.Т
4. «Математика –физика» ғылыми әдістемелік журналы
№ 5, №7 2009ж, №4, №3 2010 ж-2011ж
-
Математика 6- сынып оқулығы
Алматы .Атамұра баспасы 2006ж
Т.А.Алдамұратова Т.С.Байшоланов.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
ЕКІ АЙНЫМАЛЫСЫ БАР СЫЗЫҚТЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДІҢ ТӘСІЛДЕРІ
ЕКІ АЙНЫМАЛЫСЫ БАР СЫЗЫҚТЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДІҢ ТӘСІЛДЕРІ

№ 58
жалпы орта мектебі
58
жалпы орта мектебі
Қалалық ғылыми практикалық конференция
Оқыту процесінде заманауи инфрақұрлымдық, ақпараттық, коммуникациялық технологияларды және электрондық ресурстарды қолдану

Байболова Нұрбала Ізетбекқызы
Баяндама тақырыбы:
ЕКІ АЙНЫМАЛЫСЫ БАР СЫЗЫҚТЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДІҢ ТӘСІЛДЕРІ
Шымкент қаласы, Әл-Фараби ауданы
Қ айтпас -1 елді мекені Тел: 8702 611 04
75
айтпас -1 елді мекені Тел: 8702 611 04
75

№ 58 жалпы орта мектебі
Баяндама тақырыбы:
Жаңа технология әдістерін пайдаланып, математика
сабақтарында оқушылардың білім деңгейін
көтеру жолдары.

Байболова Нұрбала Ізетбекқызы
Қалалық ғылыми практикалық конференция
Тақырыбы: Оқыту процесінде заманауи инфрақұрлымдық, ақпараттық, коммуникациялық технологияларды және электрондық ресурстарды қолдану
Баяндама тақырыбы: ЕКІ АЙНЫМАЛЫСЫ БАР СЫЗЫҚТЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДІҢ ТӘСІЛДЕРІ
1.Кіріспе бөлім
Оқыту процесінде заманауи инфрақұрлымдық, ақпараттық, коммуникациялық технологияларды және электрондық ресурстарды қолдану
2. Негізгі бөлім
а) Екі айнымалысы бар сызықтық теңдеулер жүйесінің шығу тарихы.
б) Екі айнымалысы бар сызықтық теңдеулер жүйесінің шешу жолдары.
3.Қорытынды
4. Пайдаланылған әдебиеттер
Кіріспе
Еліміздің экономикалық, саяси-мәдени дамуына үлес қосатын әлеуметтік өркениетке көтерілетін, парасатты , денсаулығы мықты адамды тәрбиелеу- ұстаздар қауымының бүгінгі таңдағы мерейлі міндеті. Білім беру- оқыту мен тәрбиелеудің үздіксіз процесі.Қазіргі кездегі білім берудегі мақсат- жан-жақты,білімді,өмір сүруге бейім, өзіндік ой- талғамы бар,қабілетті жеке тұлғаны қалыптастыру, оқушылардың дүниетанымымын кеңейту,ой еркіндігіне жол ашу.
Жан –жақты үйлесімді өркениетті елдің елдің ұрпағын тәрбиелеп шығу бүгінгі мектептің алдына қойылған мақсаттардың бірі .Бұл мақсат әрбір орта мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын оқушы санасына жететіндей етіп оқытқанға ғана орындалады.
Мектепте математиканы оқытудың негізгі міндеті- оқушылардың нақты және жүйелі түрде білім алуын қамтамасыз ету. Математиканы тереңдетіп оқыту оқушының математикалық өрісін,шығармашылық дарынын, қызығушылығын арттырып,өздігіненізденісін қалыптастырады. Математиканы оқу- терең ойлап, кез-келген есепті шығару үшін, оның шығару жолын анықтау керек, қолданылатын формулаларды, ережелерді, теоремаларды т.б ұғымдарды білу қажет.
Математиканы оқыту – басты мақсат Оқыту үрдісінің негізгі мақсаты- арнайы педагогикалық әдістермен мақсатты түрде пайдаланып оқушылардың интеллектін ,шығармашылық ойлауын, ғылыми көзқарасы мен белсенділігін қалыптастыру,өз бетінше білім алу дағдыларын дамыту болып табылады
Бұл баяндама математика курсындада қарастырылатын екі айнымалысы бар сызықтық теңдеулер жүйесін және оларды шешу жолдарының әр түрлі әдістеріне негізделіп отыр.
Екі айнымалысы бар сызықтық теңдеулер жүйесі маңызды тақырыптардың бірі.Көптеген құбылыстар мен мазмұнды мәселе есептердің шығарылуы теңдеу және теңдеулер жүйесін құру арқылы шығарылады
Пьер Ферма- математик әрі заңгер
Пьер Ферма 1601 жылы 17 тамызда Францияның Монтобанда қаласында туған.Ферма Тулиза қаласында оқып, заң ғылымының маманы- заңгер болып шығады. Бүкіл өмірін осы сот қызметінде, сол Тулиза қаласындаөткізеді.
П.Ферма математиканы өз бетімен оқып үйренген .Грек және латын тілдеріндегі Аполлоний мен Диофанттың шығармаларын оқып, әуесқой математик болған.
Ферма сызықтарды теңдеулер арқылы өрнектейді. «Екі айнымалысы бар теңдеулер» -дейді. Екі айнымалысы бар теңдеулер мен теңдеулер жүйесіне келтіре отырып дәлелдеген. Ферма –әрдайым жазықтықта орналасқан сызықты анықтайды, түзу сызық бір ғана түрлі болады, ал қисық сызықтар сансыз көп Координаталарды Ферма кесінділер түріне алады. Түзудің ,шеңбердің ,параболаның теңдеулерін қорытып шығарды .Ескі математика тұрақты шамалардың ғана математикасыболатын.ал жаңа математика. Яғни айнымалы шамалардың математикасы болды.
Ферма 1665 жылы 12 қаңтарда Тулиза қаласында қайтыс болады
Екі айнымалысы бар теңдеулер жүйесін шешуде орындалатын түрлендіру-лердің тең шамалас болуына назар аудару, теңдеулер жүйесінде гі белгісіз айнымалылардың мәндеріне байланысты теңдеулер жүйесінің шешімдері болатынын немесе болмайтынын зерттейміз
Сызықтық теңдеулер жүйесін шешудің тәсілдері
Қосу тәсілі
1)кез-келген айнымалының коэффициенттерінің модульдерін теңестірукерек
2)жүйенің теңдеулерін мүшелеп қосу (азайту)керек
3)жаңа жүйе құру:біреуі-жаңа теңдеу,екіншісі-ескі теңдеулердің біреуі.
4)жаңа теңдеуді шешу және оның бір айнымалысының мәнін табу
5)табылған айнымалы мәнін ескі теңдеуге қою және екінші айнымалы мәнін табу
![]()


Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешуді қарастырып отырмыз.
1 жағдай.
у![]() 0,5х+2
0,5х+2
у-1,5х+6 жауабы (2; 3)

егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер қиылысса, онда теңдеулер жүйесінің бір ғана шешімі болады.
ІІ жағдай.
Теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер өзара параллель
х![]() +2у
= 4
+2у
= 4
3х+6у=-18
теңдеулер жүйесінің шешімдерін анықтайық, әрбір теңдеудегі у –ті х арқылы өрнектесек:
![]() у=-0,5х+2
у=-0,5х+2
у=-0,5х-3
у =-0,5х+2 теңдеуінің графигі
түзу . у=-0,5х-3 теңдеуінің графигі түзуі
Мұндағы
=-0,5х+2 теңдеуінің графигі
түзу . у=-0,5х-3 теңдеуінің графигі түзуі
Мұндағы
түзулердің бұрыштық коэффициенттері бірдей болғандықтан, олардың графиктері параллель түзулер .Параллель түзулердің бір-бірімен қиылыспайтыны белгілі, онда
х![]() +2у
= 4
+2у
= 4
3х+6у = -18 теңдеулер жүйесінің шешімдері болмайды, яғни теңдеулер жүйесінің шешімдері --бос жиын
жауабы: шешімдері болмайды, Ø
Егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер өзара параллель болса, онда теңдеулер жүйесінің шешімі болмайды.
ІІІ жағдай.
Жүйедегі теңдеулердің графигі болатын түзулер беттеседі.
7![]() х+2у12
х+2у12
35х+10у60

егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер беттесетін болса, онда теңдеулер жүйесінің шексіз көп шешімі болады.
Екі айнымалысы бар сызықтық теңдеулер жүйесін шешудің
алмастыру тәсілі
1-мысал Оқушы екі сан ойлады.Бірінші сан екінші саннан 7-ге аттық. Бірінші санды 3 еселеп, одан екінші санды 2 еселеп азайтқанда ,айырма 27-ге тең болады.Оқушы қандай сандар ойлады.
Шешуі:х- бірінші сан
у- екінші сан есептің шарты бойынша теңдеулер жүйесін құрамыз.
х-ті у арқылы өрнектеп, оны екінші теңдеудегі х-тің орнына қойғанда алғашқы теңдеулер жүйесіменмәндес теңдеулердің жүйесіалынады:
х = у+7
3(у+7)-2у =27 - бір айнымалысы бар теңдеу
мұндағы : 3(у+7)-2у = 27
3у+21-2у = 27
3у-2у = 27-21
у = 6 , 6-ны х=у+7 теңдеуіне қоямыз х=6+7 х=13
демек (13,6) сандар жұьы теңдеулер жүйесінің шешімі болады
Екі айнымалысы бар сызықтық теңдеулер жүйесінің
қосу тәсілі
* Айнымалылардың біреуінің коэффициенттері(бірінші және екінші теңдеудегі қарама-қарсы сандар болатындай көбейткіштерге жүйенің екі жағын да көбейту керек;{
*Жүйе теңдеулерінің оң жақтарын және сол жақтарын мүшелеп қосып немесе азайтып,оны бір айнымалысы бар теңдеуге айналдыру керек;
* шыққан бір айнымалысы бар теңдеуді шешіп,айнымалылының мәнін табу керек;
* айнымалылардың біреуінің табылған мәніне сәйкес екінші айнымалының мәнін табу керек;
1- жағдай. Теңдеулер жүйесіндегіайнымалылардың біреуінің коэффициенттері –қарама- қарсы сандар.
1-мысал
![]() теңдеулер жүйесін қосу
тәсілімен шешейік.
теңдеулер жүйесін қосу
тәсілімен шешейік.
Теңдеулердің сол және оң жақтарын мүшелеп қосайық:

9х![]() 36
36
Берілген жүйенің бір
теңдеуін 9х![]() 36 теңдеуімен алмастырайық
.
36 теңдеуімен алмастырайық
.
Сонда алғашқы берілген теңдеулер жүйесімен мәндес

теңдеулер жүйесі шығады,
ондағы бірінші теңдеуден х![]() . х –тің мәнін жүйенің екінші
6х+2у=30 теңдеуіне қойсақ :
. х –тің мәнін жүйенің екінші
6х+2у=30 теңдеуіне қойсақ :
6×4+2у=30, 24+2у =30 , у =3
Теңдеулер жүйесінің бір ғана : х = 4, у=3 шешімі бар.
Қысқаша:

9х![]() 36
36
х=4
6×4+2у=30, 24+2у =30 , у =3
Жауабы: х=4 , у =3
II Жағдай. Теңдеулер жүйесіндегі айнымалылардың біреуінің коэффициенттері тең.
2
мысал. 
теңдеулер жүйесін шешейік.
Теңдеулердің біреуінің екі жағын да -1 ге көбейтіп, теңдеулеоді мүшелеп қосу керек немесе теңдеулердің біреуінен екіншісін
азайту керек :

-2у =-4
у = 2
у тің табылған мәнін жүйедегі теңдеулердің кез келген біреуіне қоямыз.
Мысалы. 2х+5×2=16
2х=16-10
2х=6
х=3
Жауабы: х=3, у = 2
Екі ай нымалысы бар сызықтық теңдеулер жүйесін қосу тәсілімен
шешу үшін:
-
айнымалылардың біреуінің коэффициенттері (бірінші және екінші) қарама-қарсы сандар болатындай көбейткіштерге (көбейткішке) жүйенің теңдеулерінің екі жағын да( бір теңдеуін) көбейту керек;
2) жүйе теңдеулерінің оң жақтарын және сол жақтарын мүшелеп қосып немесе азайтып , оны бір айнымалысы бар теңдеуге айналдыру керек;
3) шыққан бір айнымалысы бар теңдеуді шешіп , айнымалының мәнән табу керек;
4) айнымалылаврдың біреуінің табылған мәніне сәйкес екінші айнымалының мәнін табу керек.
Егер айнымалылардың біреуінің коэффициенттері қарама-қарсы сандар болса , онда жүйені шешуді бірден теңдеулерді мүшелеп қосудан бастау керек.
Екі айнымалысы бар сызықтық теңдеулер жүйесін анықтауыштар арқылы шешу
![]() Екі айнымалысы бар сызықтық
теңдеулер жүйесін жалпы түрде шешуді
қарастырайық
Екі айнымалысы бар сызықтық
теңдеулер жүйесін жалпы түрде шешуді
қарастырайық ![]()
![]() →
→![]() →
х=
→
х=![]() =
=
(а2в1-а1в2) х = с2в1 –с1в2
=![]() =
х=
=
х= ![]()
![]()
![]() →
→![]() →
=
→
= ![]()
( а1в2-а2в1)у = а1с2-а2с1
Сонымен
![]() ⇛
х=
⇛
х=![]() ;
у=
;
у=![]()
Теңдеулердің коэффициенттерінен кесте құрып, оның мәнін мына ереже бойынша есептейміз : кестенің бас диогоналінің бойында тұрған цифрлардың көбейтіндісінен (а1в2) келесі диагональдардың бойындағы цифрлардың көбейтіндісін азайтамыз.
![]()
![]()
![]()
![]()
![]()
![]() а1 в1 с1 в1
а1 в1 с1 в1
∆ = а 2 в2 = а1в2-а2в1 ∆х= с2 в2 = с1 в2-с 2в1
( бірінші бағандағы элементтер сәйкес түрде жүйенің с 1және с 2 бос мүшелерімен алмастырылады)
Екінші бағандағы элементтер с1, с2 бос мүшелерімен сәйкес түрде алмастырылған.
![]()
![]() а1 с1
а1 с1
∆у = а2 с2 = а1 с2-а
2с1 ,
Сонда
х= ![]() және
у =
және
у =![]()
1)Егер ∆≠0 болса, жүйенің жалғыз ғана шешімі бар болады.
х
=![]() және
у=
және
у=![]()
2) егер ∆=0 ; және ∆х=0 ,∆у=0 болса жүйенің шексіз шешімі көп болады.
3) егер ∆=0, бірақ ∆х≠0 ( ∆у≠0) болса, жүйенің шешімі болмайды.
![]()
![]() 1-
мысалы:
1-
мысалы: ![]()
2 3
Шешуі:
![]() ⇛∆
= 3 -2 =
2*(-2)-3*3=-4-9=-13≠0
⇛∆
= 3 -2 =
2*(-2)-3*3=-4-9=-13≠0
Жүйенің жалғыз ғана шешімі бар.
![]()
![]() 4
3
4
3
∆х= 6
-2 =4*(-2)
-6*3 =
-8 -18 = -26 x
=![]() =
=![]() =2
→ x=2
=2
→ x=2
![]()
![]()
2 4
∆у= 3 6 = 2 *6 – 3 *4 = 0
у= ![]() =
=![]() = 0 → у
=0
= 0 → у
=0
Жауабы : ( 2; 0)
![]()
![]() 2 3
2 3
2-
Мысал ![]() →∆= 4 6 =2 *6 – 3* 4=
0
→∆= 4 6 =2 *6 – 3* 4=
0
![]()
![]()
∆х= 4 3
8 6 =4 * 6- 8 *3 = 0 Жүйенің шексіз көп шешімі болады
Қорытынды бөлім
Математика ғылымдардың әр саласында өте кең тараған сала болғандықтан, қойылатын талаптарға сай жас ұрпақты сапалы білім, саналы тәрбие бере отырып, математикалық мәдениетін көтеру керек.
Математикалық есептерді шешу,теоремаларды дәлелдеу оқушылардың ойлау ,есте сақтау қабілеттерін дамытады Ендеше оқушылардың математикалық сауаттылығын артыру-олардың алған білімінің тиянақты болуын қамтамасыз ету .
Негізінен жаңа технологиялар оқушылардың білім сапасын артыруға, ой санасының дамуына мүмкіндік жасайды.Үнемі өзгеріп тұрған әлем адамнан қабілет пенқажеттілікті талап етеді
Ереже білсек есеп шығару жеңіл болады.Әрбір есепті ереже тілмен айтсақ, математикалық тілде сөйлете алады екенбіз.Ьұғалім шеберлігінің негізгі көрсеткіштерінің бірі-әдәстеме саласындағы ғылыми жаңалықтар мен озық тәжірбиені жетік игеру және оларды күнделікті қызметте пайдалану .Демек оқушылардың бойында шығармашылық қабілетті дамыту жалпы пәндерді оқып үйрену кезінде және еңбек –оқу процесінде ойлаудың өмірлік тәжірбиесі негізінде алған білімдері мен дағдыларының негізінде жүзеге асады. Білім сапасын көтеруге ,қабілеті жоғары оқушыларды шығармашылыққа баулып ,ізденушілік қасиетерін жетілдіруге, уақытыт тиімді пайдалануға мүмкіндік туғызатын М.Жанпейісованың « Модульдік оқыту технологиясы» мен Ж.Қараевтың «Деңгейлеп оқыту технологиясын»
өз сабақтарымда қолданамын
Оқушылар «Екі айнымалысы бар теңдеулер жүйесін шешудің тәсілдері» тақырыбы бойынша алған білімдері
2009-2010 оқу жылындағы тест нәтижесі
2009-2010 оқу жылындағы тест нәтижесі
2010-2011 оқу жылындағы тест нәтижесі


Пайдаланылған әдебиеттер :
-
« Математиканың даму тарихы» . Алматы, Мектеп 1964 ж
Есмұханов М
-
«Матетематика мен математиктер жайында әңгімелер»
1 – ші кітап Алматы. Мектеп 1967 ж
2-ші кітап Алматы Мектеп 1970 ж Исқақов М .Ө
-
«Теңдеулер және теңдеулер жүйелері ».
Алматы ,Мектеп 1976 ж
Есмұханов М.Т
4. «Математика –физика» ғылыми әдістемелік журналы
№ 5, №7 2009ж, №4, №3 2010 ж-2011ж
-
Математика 6- сынып оқулығы
Алматы .Атамұра баспасы 2006ж
Т.А.Алдамұратова Т.С.Байшоланов.

шағым қалдыра аласыз
















