|
Бөлім: |
9.3А Тригонометрия |
|||||
|
Педагогтің Тегі, Аты,Әкесінің аты |
Курманбаева Дарига |
|||||
|
Пән/Сынып: |
9 «Ә» сынып. Қатысқандар саны: Қатыспағандар саны: |
|||||
|
Күні: |
||||||
|
Сабақтың тақырыбы: |
Екі бұрыштың қосындысы мен айырмасының тригонометриялық формулалары. |
|||||
|
Оқу бағдарламасына сәйкес оқыту мақсаты: |
9.2.4.3 бұрыштардың қосындысы мен айырымының, жарты және қос бұрыштың тригонометриялық формулаларын қорытып шығару және қолдану; |
|||||
|
Сабақтың мақсаты: |
Қосу формулалары туралы түсінік беріп, екі бұрыштың қосындысы мен айырымының формулаларын қорытып шығару жолдарын үйрету; |
|||||
|
Сабақ барысы: |
||||||
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
|
5минут |
Ұйымдастыру |
Сәлеметсіздерме! Атмосфералық жағдайды қалыптастыру. Бүгін, Тригонометрия формулалары.Екі бұрыштың қосындысы мен айырмасының тригонометриялық формулалары. тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: - бұрыштардың қосындысы мен айырымының тригонометриялық формулалары. - бұрыштардың қосындысы мен айырымының тригонометриялық формулаларын қолдану. |
Сұрақтарға жауап береді.
|
|
Оқулық; оқу құралдары; тақта; бор; бағалау парағы. Интернет ресурстары |
|
|
10 мин |
Жаңа сабақ |
cos(α – β)=cosα cosβ + sinα sinβ (1) Екі бұрыштың айырымының косинусы осы бұрыштардың косинустарының көбейтіндісі мен синустарының көбейтіндісінің қосындысына тең. cos(α + β)=cosα cosβ – sinα sinβ (2)
Екі бұрыштың қосындысының косинусы осы бұрыштардың косинустарының көбейтіндісі мен синустарының көбейтіндісінің айырымына тең. Келтіру формулаларын қолдансақ: sin (α + β)= sinα cosβ + cosα sinβ (3) Екі бұрыштың қосындысының синусы бірінші бұрыштың синусы мен екінші бұрыштың косинусының көбейтіндісіне бірінші бұрыштың косинусы мен екінші бұрыштың синусы көбейтіндісін қосқанға тең. sin (α – β)= sinα cosβ – cosα sinβ (4) екі бұрыштың айырымының синусы бірінші бұрыштың синусының екінші бұрыштың косинусына көбейтіндісі мен бірінші бұрыштың косинусының екінші бұрыштың синусына көбейтіндісінің айырымына тең.
tg
(α+β)=
tg
(α
–
β)=
ctg(α
+
β)=
ctg(α
–
β)=
|
Қосымша ақпарат көздерін пайдалана отырып түсінеді Тақырып бойынша ресурстарды қарап, танысады |
«Екі жұлдыз бір ұсыныс» |
|
|
|
15мин |
Бекіту тапсырмалары |
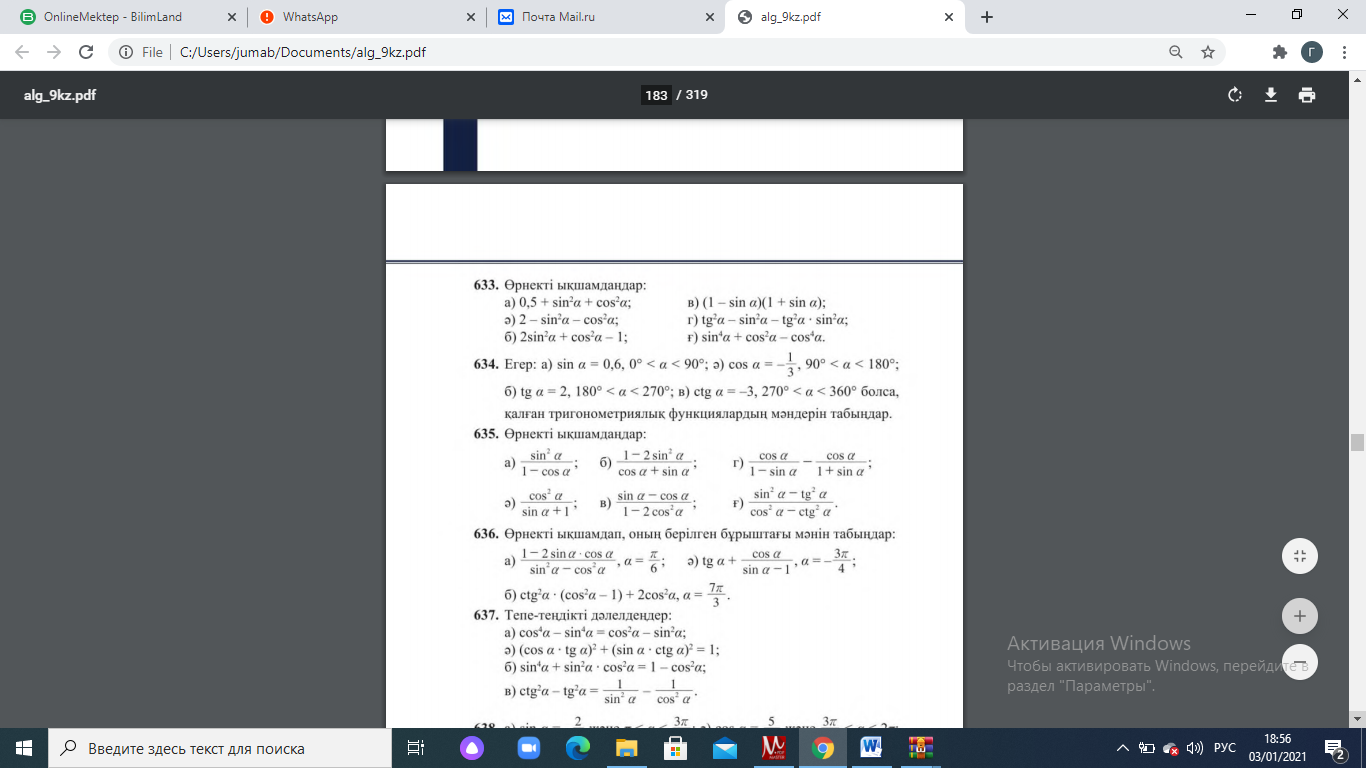
Есептер шығару.
|
Берілген тапсырма бойынша өз ойларын ортаға салып, пікірлерін білдіріп, жұптық талдау жасайды. Талқылау нәтижесінде өзара бір келісімге келіп есепті орындайды. Оқулықтан есептер шығарады. |
Дескриптор: -негізгі тригонометрія лық тепе-теңдік формуласын қолданады
Дескриптор: - Екі бұрыштың қосындысы мен айырмасының тригонометрия лық формулаларын қолданады. |
Интернет ресурстары Жалпы білім беретін мектептің 9–сыныбына арналған оқулық. Оқулық авторлары: А.Е.Әбілқасымова, Т.П.Кучер, В.Е.Корчевский, З.Ә.Жұмағұлова Алматы «Мектеп» баспасы 2019 жыл |
|
|
|
|
|
|
Дескриптор: - Екі бұрыштың қосындысы мен айырмасының тригонометрия лық формулаларын қолданады.
|
Оқулық; оқу құралдары; тақта; бор; бағалау парағы |
|
|
10мин |
Жеке жұмыс |
Оқулықтан есептер шығарады
|
Тапсырманы орындайды
|
Дескриптор: - Екі бұрыштың қосындысы мен айырмасының тригонометрия лық формулаларын қолданады. |
Оқулық; оқу құралдары; тақта; бор; бағалау парағы |
|
|
5минут |
|
Бүгінгі сабақта: - бұрыштардың қосындысы мен айырымының тригонометриялық формулалары. - бұрыштардың қосындысы мен айырымының тригонометриялық формулаларын қолдану. Рефлексия:БББ әдісі Үйге тапсырма. № 24.5 |
Тақырыпты меңгергенін анықтау . |
Кері байланыс |
Оқулық; оқу құралдары; тақта; бор; бағалау парағы |
|
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Екі бұрыштың қосындысы мен айырмасының тригонометриялық формулалары.
Екі бұрыштың қосындысы мен айырмасының тригонометриялық формулалары.
|
Бөлім: |
9.3А Тригонометрия |
|||||
|
Педагогтің Тегі, Аты,Әкесінің аты |
Курманбаева Дарига |
|||||
|
Пән/Сынып: |
9 «Ә» сынып. Қатысқандар саны: Қатыспағандар саны: |
|||||
|
Күні: |
||||||
|
Сабақтың тақырыбы: |
Екі бұрыштың қосындысы мен айырмасының тригонометриялық формулалары. |
|||||
|
Оқу бағдарламасына сәйкес оқыту мақсаты: |
9.2.4.3 бұрыштардың қосындысы мен айырымының, жарты және қос бұрыштың тригонометриялық формулаларын қорытып шығару және қолдану; |
|||||
|
Сабақтың мақсаты: |
Қосу формулалары туралы түсінік беріп, екі бұрыштың қосындысы мен айырымының формулаларын қорытып шығару жолдарын үйрету; |
|||||
|
Сабақ барысы: |
||||||
|
Уақыты |
Кезең дері |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
|
5минут |
Ұйымдастыру |
Сәлеметсіздерме! Атмосфералық жағдайды қалыптастыру. Бүгін, Тригонометрия формулалары.Екі бұрыштың қосындысы мен айырмасының тригонометриялық формулалары. тақырыбын қарастырамыз Бүгінгі сабақта меңгеретініңіз: - бұрыштардың қосындысы мен айырымының тригонометриялық формулалары. - бұрыштардың қосындысы мен айырымының тригонометриялық формулаларын қолдану. |
Сұрақтарға жауап береді.
|
|
Оқулық; оқу құралдары; тақта; бор; бағалау парағы. Интернет ресурстары |
|
|
10 мин |
Жаңа сабақ |
cos(α – β)=cosα cosβ + sinα sinβ (1) Екі бұрыштың айырымының косинусы осы бұрыштардың косинустарының көбейтіндісі мен синустарының көбейтіндісінің қосындысына тең. cos(α + β)=cosα cosβ – sinα sinβ (2)
Екі бұрыштың қосындысының косинусы осы бұрыштардың косинустарының көбейтіндісі мен синустарының көбейтіндісінің айырымына тең. Келтіру формулаларын қолдансақ: sin (α + β)= sinα cosβ + cosα sinβ (3) Екі бұрыштың қосындысының синусы бірінші бұрыштың синусы мен екінші бұрыштың косинусының көбейтіндісіне бірінші бұрыштың косинусы мен екінші бұрыштың синусы көбейтіндісін қосқанға тең. sin (α – β)= sinα cosβ – cosα sinβ (4) екі бұрыштың айырымының синусы бірінші бұрыштың синусының екінші бұрыштың косинусына көбейтіндісі мен бірінші бұрыштың косинусының екінші бұрыштың синусына көбейтіндісінің айырымына тең.
tg
(α+β)=
tg
(α
–
β)=
ctg(α
+
β)=
ctg(α
–
β)=
|
Қосымша ақпарат көздерін пайдалана отырып түсінеді Тақырып бойынша ресурстарды қарап, танысады |
«Екі жұлдыз бір ұсыныс» |
|
|
|
15мин |
Бекіту тапсырмалары |
Есептер шығару.
|
Берілген тапсырма бойынша өз ойларын ортаға салып, пікірлерін білдіріп, жұптық талдау жасайды. Талқылау нәтижесінде өзара бір келісімге келіп есепті орындайды. Оқулықтан есептер шығарады. |
Дескриптор: -негізгі тригонометрія лық тепе-теңдік формуласын қолданады
Дескриптор: - Екі бұрыштың қосындысы мен айырмасының тригонометрия лық формулаларын қолданады. |
Интернет ресурстары Жалпы білім беретін мектептің 9–сыныбына арналған оқулық. Оқулық авторлары: А.Е.Әбілқасымова, Т.П.Кучер, В.Е.Корчевский, З.Ә.Жұмағұлова Алматы «Мектеп» баспасы 2019 жыл |
|
|
|
|
|
|
Дескриптор: - Екі бұрыштың қосындысы мен айырмасының тригонометрия лық формулаларын қолданады.
|
Оқулық; оқу құралдары; тақта; бор; бағалау парағы |
|
|
10мин |
Жеке жұмыс |
Оқулықтан есептер шығарады
|
Тапсырманы орындайды
|
Дескриптор: - Екі бұрыштың қосындысы мен айырмасының тригонометрия лық формулаларын қолданады. |
Оқулық; оқу құралдары; тақта; бор; бағалау парағы |
|
|
5минут |
|
Бүгінгі сабақта: - бұрыштардың қосындысы мен айырымының тригонометриялық формулалары. - бұрыштардың қосындысы мен айырымының тригонометриялық формулаларын қолдану. Рефлексия:БББ әдісі Үйге тапсырма. № 24.5 |
Тақырыпты меңгергенін анықтау . |
Кері байланыс |
Оқулық; оқу құралдары; тақта; бор; бағалау парағы |
|

шағым қалдыра аласыз