
ЕКІ, ҮШ ТАҢБАЛЫ САНДАРДЫ АУЫЗША ЖЫЛДАМ ЕСЕПТЕУДІҢ ҒЫЛЫМИ ӘДІСТЕРІ
Шақарбекқызы Аман
«АйСаф» жеке қыздар мектебі
Жаратылыстану ғылымдарының магистрі,
Математика пәнінің мұғалімі
Алматы, Қарасай ауданы
Ғылым мен техниканың дамып, өркендеуі кез-келген салада, өндірісте, өнеркәсіпте әсіресе білім ордаларында ғылымның жаңа тұстарын қолданып, жаңа тәсілдермен оқытуды күнделікті өмірде қалыптастыруды талап етеді. Осы талапқа сай, төменде қарастырылып отырған екі таңбалы санды, екі таңбалы санға және үш таңбалы санды, үш таңбалы санға көбейтудің ауызша жылдам есептеудің бірнеше түрде келу формасының ғылыми жолмен есептеу әдістемесін қарастырамыз.
Бұл әдіс адам өмірінде де өте маңызды рөл атқарады деугу болады. Себебі ол адам тұлғасының ең маңызды құралы саналатын ми жүйесін іске қосып, сананы табысты әрекетке бағыттайтын, ойлау қабілетін жетілдіретін, үнемі тапқыр, ұтымды тәсілдерді ойлап табудың бірінші баспалдағы деп айтуға да болады.
Енді осы айтылған мәселенің негізгі шешімі болып табылатын тез есептеудің жаңа ғылыми әдістеріне толығымен тоқталып өтейік.
Бір таңбалы санды бір таңбалы санға көбейту кестесі мектеп қабырғасынан үйретілетіні айтпасақта көпшілікке мәлім. Сол сияқты бір таңбалы санды екітаңбалы, үш таңбалы т.с.с. көп таңбалы сандарға ойша көбейтудің де еш қиындығы жоқ. Ал екі таңбалы санды екі таңбалы санға, үш таңбалы санды үш таңбалы санға т.с.с көп таңбалы санды көп таңбалы санға ешқандай есептеу құралын (мысалы, колькуляторды) қолданбай, ауызша жылдам есептеудің жолдарын осы жұмыста баяндаймыз.
Осы жұмыста аталған екі, үш таңбалы сандарды өзара көбейту жолдары екі түрлі нұсқа арқылы көрсетілді. 1-нұсқада, 11-20 аралығындағы екі таңбалы сандарды өзара көбайтудің төрт түрлі әдісі көрсетілді. Ал 2-нұсқада, арнайы шарттармен топталған, мысалы, көбейткіштің құрамының қосындысы 10-ға тең болса (73), көбейгіш пен көбейткіштің ондықтары өзара бірдей цифр болса (47, 43), көбейгіш пен көбейткіштің ондықтарының қосындысы 10-ға тең болса (26, 86), көбейтілетін екі санның бірліктері бірдей цифр болса (41, 51), т.с.с., үш таңбалы сандарды өзара көбейтудің шарттары бойынша топтарға жіктеліп келтірілген. Аталған екі, үш таңбалы сандарды өзара көбейтудің ауызша дұрыс әрі жылдам есептеудің төмендегідей жаңа ғылыми әдісін саралап көрулеріңізге ұсынамыз.
-
Егер берілген екі таңбалы санның біреуінің бірліктер және ондықтар орнындағы цифрлары бірдей болып, екіншісанның бірліктер және ондықтар орнындағы цифрларының қосындысы 10 ға тең болатын болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады [1].
1-тәсіл: Ондықтар орнындағы «1» цифрларын өзара көбейтіп, теңдіктің оң жағына шығарып, жүздіктер орынына апарып тіркейміз, бірліктер орнындағы сандарды өзара қосып қосындыны ондықтар орнына апарып тіркейміз, кейін сол екі санды өзара көбейтіп, шыққан көбейтіндіні бірліктер орнына апарып тіркеп жазамыз. «Көбейту, қосу, көбейту» формуласы деп атауға болады.
Мысалы: 11 х 12 = 132
Шешуі: 1 х 1 = 1
(1+2) = 3
1 х 2 = 2
Қосындыны және көбейтінділерді тіркеп жазсақ 132
Мысалы: 11 х 18 = 198
Шешуі: 1 х 1 = 1
(1+8) = 9
1 х 8 =8
Қосындыны және көбейтінділерді тіркеп жазсақ 198
Мысалы: 12 х 14 = 168
Шешуі: 1 х 1 = 1
(2+4) = 6,
2 х 4 = 8
Қосындыны және көбейтінділерді тіркеп жазсақ 168
Мысалы: 16 х 11 = 176
Шешуі: 1 х 1 = 1
(6+1) = 7
6 х 1 =6
Қосындыны және көбейтінділерді тіркеп жазсақ 176
-
Егер берілген екі таңбалы санның екеуінің де ондықтар орнындағы цифрлары бірдей 1 ге тең болып, ал бірліктер орнындағы цифрларының қосындысы 10 нан кіші, ал көбейтіндісі 10 нан үлкен болсап, онда төмендегі тәсілді қолданып дұрыс әрі жылдам есептеуге болады [1].
2-тәсіл: Ондықтар орнындағы «1» цифрларын өзара көбейтіп, бірліктер орнындағы сандарды өзара қосып, олардың соңына «0» цифрын тіркеп жазамыз. Кейін сол екі санды өзара көбейтіп, шыққан көбейтіндіні алғашқы нәтижеге қосып жазамыз. «Көбейту, қосу, көбейту, қосу» формуласы деп атауға болады.
Мысалы: 13 х 15 = 195
Шешуі: 1 х 1 = 1
(3+5) = 8
3 х 5 = 15
180 + 15 = 195
Қосындыны және көбейтінділерді тіркеп жазсақ 195
Мысалы: 16 х 12 = 192
Шешуі: 1 х 1 = 1
(6+2 ) = 8
6 х 2 = 12
180 + 12 = 192
Қосындыны және көбейтінділерді тіркеп жазсақ 192
Мысалы: 15 х 14 = 168
Шешуі: 1 х 1 = 1
(5+4) = 9
5 х 4 = 20
190 + 20 = 210
Қосындыны және көбейтінділерді тіркеп жазсақ 210
Мысалы: 17 х 12 = 176
Шешуі: 1 х 1 = 1
(7+2) = 9
7 х 2 = 14
190 + 14 = 204
Қосындыны және көбейтінділерді тіркеп жазсақ 204
-
Егер берілген екі таңбалы санның екеуінің де ондықтар орнындағы цифрлары бірдей 1 ге тең болып, ал бірліктер орнындағы цифрларының қосындысы 10 ға тең болса, онда төмендегі тәсілді қолданып дұрыс әрі жылдам есептеуге болады [1].
3-тәсіл: Ондықтар орнындағы «1» цифрларының қосындысын, яғни «2» цифрын теңдіктің оң жағына шығарып, жүздіктер орынына апарып тұрақты етіп қоямыз, бірліктер орнындағы сандарды өзара қосып қосындыны ондықтар орнына апарып тіркейміз, кейін сол екі санды өзара көбейтіп, шыққан көбейтіндіні бірліктер орнына апарып тіркеп, шыққан мәннен 10 санын азайтамыз. «Қосу, қосу, көбейту, азайту 10» формуласы деп атауға болады.
Мысалы: 11 х 19 = 209
Шешуі: (1+1) = 2,
(1+9) = 10, тіркеу бойынша 210
1 х 9 = 9, тіркеу бойынша 210+009=219
219 - 10 = 209
Қосындыны және көбейтінділерді тіркеп жазсақ 209
Мысалы: 13 х 17 = 221
Шешуі: (1+1) = 2, тіркеу бойынша 200
(3+7) = 10, тіркеу бойынша 210
3 х 7 = 21, тіркеу бойынша 210 + 21 = 231
231 – 10 = 221
Қосындыны және көбейтінділерді тіркеп жазсақ 221
Мысалы: 15 х 15 = 225
Шешуі: (1+1) = 2,
(5+5) = 10, тіркеу бойынша 210
5 х 5 = 25, тіркеу бойынша 210+025=235
235 - 10 = 225
Қосындыны және көбейтінділерді тіркеп жазсақ 209
Мысалы: 18 х 12 = 216
Шешуі: (1+1) = 2, тіркеу бойынша 200
(8+2) = 10, тіркеу бойынша 210
8 х 2 = 16 тіркеу бойынша 210 + 16 = 226
226 – 10 = 216
Қосындыны және көбейтінділерді тіркеп жазсақ 216
-
Егер берілген екі таңбалы санның екеуінің де ондықтар орнындағы цифрлары бірдей 1 ге тең болып, ал бірліктер орнындағы цифрларының қосындысы және көбейтіндісі 10 нан үлкен болса, онда төмендегі тәсілді қолданып дұрыс әрі жылдам есептеуге болады [1].
4-тәсіл: Ондықтар орнындағы «1» цифрларының қосындысын, яғни «2» цифрын теңдіктің оң жағына шығарып, жүздіктер орынына апарып тұрақты етіп қоямыз, бірліктер орнындағы сандарды өзара қосып қосындыдан 10 санын аламыз да, ондықтар орнына апарып тіркейміз, кейін сол екі санды өзара көбейтіп, шыққан көбейтіндіні жоғарыда тіркелген ондықтарға апарып қосып, тіркеп жазамыз «Қосу, қосу, азайту 10, көбейту» формуласы деп атауға болады.
Мысалы: 14 х 17 = 238
Шешуі: (1+1) = 2,
(4+7) - 10 = 1, тіркеу бойынша 210
4 х 7 = 28, қосып, тіркеу бойынша 210+028=238
Қосындыны және көбейтінділерді тіркеп жазсақ 238
Мысалы: 13 х 18 = 234
Шешуі: (1+1) = 2,
(3+8) - 10 = 1, тіркеу бойынша 210
3 х 8 = 24, қосып, тіркеу бойынша 210+024=234
Қосындыны және көбейтінділерді тіркеп жазсақ 234
Мысалы: 16 х 19 = 238
Шешуі: (1+1) = 2,
(6+9) - 10 = 5, тіркеу бойынша 250
6 х 9 = 54, тіркеу бойынша 250+054=304
Қосындыны және көбейтінділерді тіркеп жазсақ 304
Мысалы: 15 х 18 = 270
Шешуі: (1+1) = 2,
(5+8) - 10 = 3, тіркеу бойынша 230
5 х 8 = 40, тіркеу бойынша 230+040=270
Қосындыны және көбейтінділерді тіркеп жазсақ 270
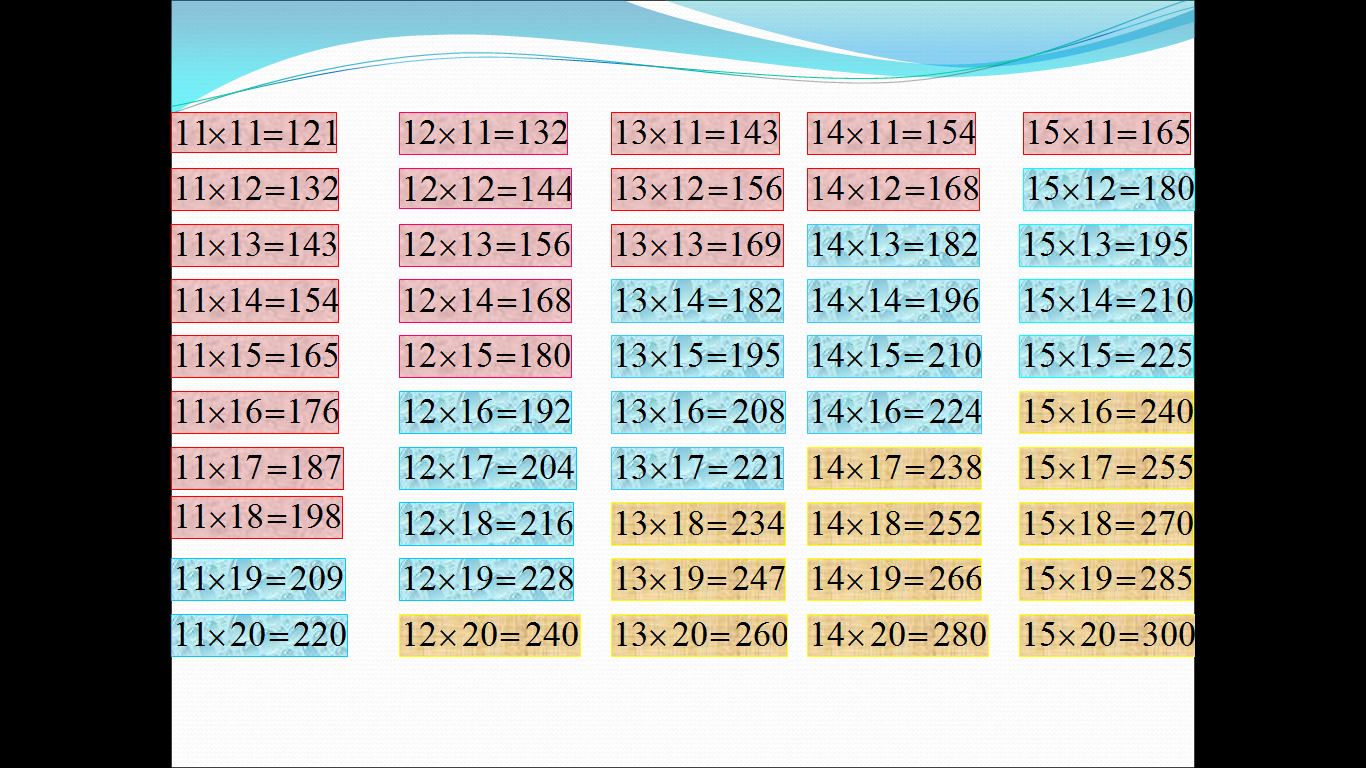
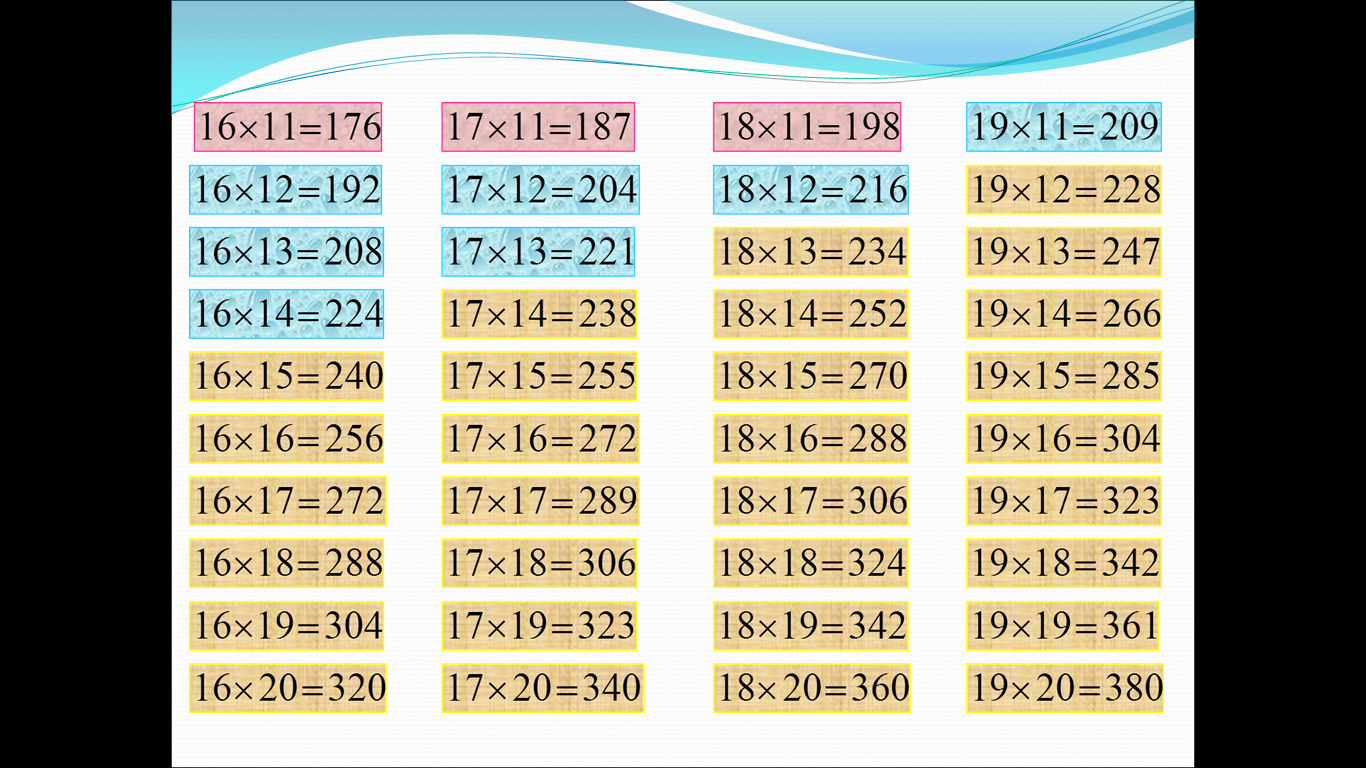
1-кесте. 11-ден 20-ға дейінгі екі таңбалы сандардың, қызғыл түспен боялғандары
1-әдіспен, көкшіл түспен боялғандары 2-әдіспен, ал сарғылт түспен боялғандары 3-,4-әдістермен көбейтіледі.
Ал енді 2-нұсқа бойынша топтастырылған екі, үш таңбалы сандарды көбейту әдістеріне тоқталамыз.
-
Егер берілген екі таңбалы санның біреуінің бірліктер және ондықтар орнындағы цифрлары бірдей болып, екіншісанның бірліктер және ондықтар орнындағы цифрларының қосындысы 10 ға тең болатын болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады [1].
1-тәсіл: қосындысы 10 болатын санның ондықтар орнындағы цифрына «1» санын қосып, «бірліктер * бірліктер», «ондықтар *ондықтар» бойынша көбейтіп, тіркеп жазамыз.
Мысалы: 66 х 28 = 1848
Шешуі: (2+1) х 6 = 18
6 х 8 = 48
Көбейтінділерді тіркеп жазсақ 1848
Мысалы: 22 х 73 = 1606
Шешуі: (7+1) х 2 = 16
2 х 3 =06
Көбейтінділерді тіркеп жазсақ 1606
-
Егер берілген екі таңбалы санның ондықтар орнындағы цифрлары бірдей болып, бірліктер орнындағы цифрларының қосындысы 10 ға тең болатын болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады.
2-тәсіл: ондықтар орнындағы сифрлардың біріне «1» санын қосып, «бірліктер * бірліктер», «ондықтар *ондықтар» бойынша көбейтіп, тіркеп жазамыз.
Мысалы: 47 х 43 = 2021
Шешуі: (4+1) х 4 = 20
7 х 3 = 21
Көбейтінділерд тіркеп жазсақ 2021
Мысалы: 83 х 87 = 7221
Шешуі: (8+1) х 8 = 72
3 х 7 = 21
Көбейтінділерді тіркеп жазсақ 7221 келіп шығады.
Осы түрдегі екі таңбалы сандарды көбейту әдісін « «1» санын қосу әдісі» деп атауға болады.
-
Егер берілген екі таңбалы санның бірліктер орнындағы цифрлары бірдей болып, ал ондықтар орнындағы цифрларының қосындысы 10 ға тең болатын болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады.
3-тәсіл: «ондықтар * ондықтар + бірліктер » «бірліктер * бірліктер», бойынша көбейтіп, тіркеп жазамыз.
Мысалы: 26 х 86 = 2236
Шешуі: 2 х 8 + 6 = 22
6 х 6 = 36
Көбейтінділерді тіркеп жазсақ 2236
Мысалы: 63 х 43 = 2709
6 х 4 + 3 = 27
3 х 3 = 09
Көбейтінділерді тіркеп жазсақ 2709
Осы түрдегі екі таңбалы сандарды көбейту әдісін «бірліктер цифрын қосу әдісі» деп атауға болады.
-
Егер берілген екі таңбалы санның бірліктер орнындағы цифрлары «1» болып, ал ондықтар орнындағы цифрлар кез келген сан болып, бірақ сол ондықтар орнындағы цифрлардың қосындысы 10 нан кіші болатын болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады [2].
4-тәсіл: «ондықтар * ондықтар», «ондықтар + ондықтар», бойынша көбейтіп, соңына «1» ді тіркеп жазамыз.
Мысалы: 41 х 51 = 2091
Шешуі: 4 х 5 = 20
4 + 5 = 9
Көбейтінділерді тіркеп, тағы «1» ді тіркеп жазсақ 2091
Мысалы: 61 х 21 = 1281
Шешуі: 6 х 2 = 12
6 + 2 = 8
Көбейтінділерді тіркеп, тағы «1» ді тіркеп жазсақ 1281
Осы түрдегі екі таңбалы сандарды көбейту әдісін « «1» санын тіркеу әдісі» деп атауға болады.
-
Егер берілген екі таңбалы санның бірліктер орнындағы цифрлары «1» болып, ал ондықтар орнындағы цифрлар кез келген сан болып, бірақ сол ондықтар орнындағы цифрлардың қосындысы 10 нан үлкен болатын болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады.
5-тәсіл: «ондықтар * ондықтар + 1» бойынша көбейтіп, «ондықтар + ондықтар = қосынды» қосындыдағы бірліктер мен ондықтар цифрларының орындарын алмастырып жазамыз.
Мысалы: 71 х 91 = 6461
Шешуі: 7 х 9 + 1 = 64
7 + 9 = 16 кері алмасу саны 61
Көбейтінді мен қосындының кері алмасу санын тіркеп жазсақ 6461
Мысалы: 81 х 61 = 4941
Шешуі: 8 х 6 + 1= 49
8 + 6 = 14 кері алмасу саны 41
Көбейтінді мен қосындының кері санын тіркеп жазсақ 4941 келіп шығады.
Осы түрдегі екі таңбалы сандарды көбейту әдісін « «қосындының кері алмасу санын» тіркеу әдісі» деп атауға болады.
-
Егер берілген екі таңбалы санның ондықтар орнындағы цифрлары «9» болып, ал бірліктер орнындағы цифрлар кез келген сан болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады [3].
6-тәсіл: бірінші саннан екінші санның 100 ге толықтаушы саны алынады, сонан кейін екі санның да 100 ге толықтауыштары өзара көбейтіліп, тіркеп жазылады.
Мысалы: 93 х 95 = 8835
Шешуі:
Жүктеу
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
ЕКІ, ҮШ ТАҢБАЛЫ САНДАРДЫ АУЫЗША ЖЫЛДАМ ЕСЕПТЕУДІҢ ҒЫЛЫМИ ӘДІСТЕРІ
ЕКІ, ҮШ ТАҢБАЛЫ САНДАРДЫ АУЫЗША ЖЫЛДАМ ЕСЕПТЕУДІҢ ҒЫЛЫМИ ӘДІСТЕРІ
ЕКІ, ҮШ ТАҢБАЛЫ САНДАРДЫ АУЫЗША ЖЫЛДАМ ЕСЕПТЕУДІҢ ҒЫЛЫМИ ӘДІСТЕРІ
Шақарбекқызы Аман
«АйСаф» жеке қыздар мектебі
Жаратылыстану ғылымдарының магистрі,
Математика пәнінің мұғалімі
Алматы, Қарасай ауданы
Ғылым мен техниканың дамып, өркендеуі кез-келген салада, өндірісте, өнеркәсіпте әсіресе білім ордаларында ғылымның жаңа тұстарын қолданып, жаңа тәсілдермен оқытуды күнделікті өмірде қалыптастыруды талап етеді. Осы талапқа сай, төменде қарастырылып отырған екі таңбалы санды, екі таңбалы санға және үш таңбалы санды, үш таңбалы санға көбейтудің ауызша жылдам есептеудің бірнеше түрде келу формасының ғылыми жолмен есептеу әдістемесін қарастырамыз.
Бұл әдіс адам өмірінде де өте маңызды рөл атқарады деугу болады. Себебі ол адам тұлғасының ең маңызды құралы саналатын ми жүйесін іске қосып, сананы табысты әрекетке бағыттайтын, ойлау қабілетін жетілдіретін, үнемі тапқыр, ұтымды тәсілдерді ойлап табудың бірінші баспалдағы деп айтуға да болады.
Енді осы айтылған мәселенің негізгі шешімі болып табылатын тез есептеудің жаңа ғылыми әдістеріне толығымен тоқталып өтейік.
Бір таңбалы санды бір таңбалы санға көбейту кестесі мектеп қабырғасынан үйретілетіні айтпасақта көпшілікке мәлім. Сол сияқты бір таңбалы санды екітаңбалы, үш таңбалы т.с.с. көп таңбалы сандарға ойша көбейтудің де еш қиындығы жоқ. Ал екі таңбалы санды екі таңбалы санға, үш таңбалы санды үш таңбалы санға т.с.с көп таңбалы санды көп таңбалы санға ешқандай есептеу құралын (мысалы, колькуляторды) қолданбай, ауызша жылдам есептеудің жолдарын осы жұмыста баяндаймыз.
Осы жұмыста аталған екі, үш таңбалы сандарды өзара көбейту жолдары екі түрлі нұсқа арқылы көрсетілді. 1-нұсқада, 11-20 аралығындағы екі таңбалы сандарды өзара көбайтудің төрт түрлі әдісі көрсетілді. Ал 2-нұсқада, арнайы шарттармен топталған, мысалы, көбейткіштің құрамының қосындысы 10-ға тең болса (73), көбейгіш пен көбейткіштің ондықтары өзара бірдей цифр болса (47, 43), көбейгіш пен көбейткіштің ондықтарының қосындысы 10-ға тең болса (26, 86), көбейтілетін екі санның бірліктері бірдей цифр болса (41, 51), т.с.с., үш таңбалы сандарды өзара көбейтудің шарттары бойынша топтарға жіктеліп келтірілген. Аталған екі, үш таңбалы сандарды өзара көбейтудің ауызша дұрыс әрі жылдам есептеудің төмендегідей жаңа ғылыми әдісін саралап көрулеріңізге ұсынамыз.
-
Егер берілген екі таңбалы санның біреуінің бірліктер және ондықтар орнындағы цифрлары бірдей болып, екіншісанның бірліктер және ондықтар орнындағы цифрларының қосындысы 10 ға тең болатын болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады [1].
1-тәсіл: Ондықтар орнындағы «1» цифрларын өзара көбейтіп, теңдіктің оң жағына шығарып, жүздіктер орынына апарып тіркейміз, бірліктер орнындағы сандарды өзара қосып қосындыны ондықтар орнына апарып тіркейміз, кейін сол екі санды өзара көбейтіп, шыққан көбейтіндіні бірліктер орнына апарып тіркеп жазамыз. «Көбейту, қосу, көбейту» формуласы деп атауға болады.
Мысалы: 11 х 12 = 132
Шешуі: 1 х 1 = 1
(1+2) = 3
1 х 2 = 2
Қосындыны және көбейтінділерді тіркеп жазсақ 132
Мысалы: 11 х 18 = 198
Шешуі: 1 х 1 = 1
(1+8) = 9
1 х 8 =8
Қосындыны және көбейтінділерді тіркеп жазсақ 198
Мысалы: 12 х 14 = 168
Шешуі: 1 х 1 = 1
(2+4) = 6,
2 х 4 = 8
Қосындыны және көбейтінділерді тіркеп жазсақ 168
Мысалы: 16 х 11 = 176
Шешуі: 1 х 1 = 1
(6+1) = 7
6 х 1 =6
Қосындыны және көбейтінділерді тіркеп жазсақ 176
-
Егер берілген екі таңбалы санның екеуінің де ондықтар орнындағы цифрлары бірдей 1 ге тең болып, ал бірліктер орнындағы цифрларының қосындысы 10 нан кіші, ал көбейтіндісі 10 нан үлкен болсап, онда төмендегі тәсілді қолданып дұрыс әрі жылдам есептеуге болады [1].
2-тәсіл: Ондықтар орнындағы «1» цифрларын өзара көбейтіп, бірліктер орнындағы сандарды өзара қосып, олардың соңына «0» цифрын тіркеп жазамыз. Кейін сол екі санды өзара көбейтіп, шыққан көбейтіндіні алғашқы нәтижеге қосып жазамыз. «Көбейту, қосу, көбейту, қосу» формуласы деп атауға болады.
Мысалы: 13 х 15 = 195
Шешуі: 1 х 1 = 1
(3+5) = 8
3 х 5 = 15
180 + 15 = 195
Қосындыны және көбейтінділерді тіркеп жазсақ 195
Мысалы: 16 х 12 = 192
Шешуі: 1 х 1 = 1
(6+2 ) = 8
6 х 2 = 12
180 + 12 = 192
Қосындыны және көбейтінділерді тіркеп жазсақ 192
Мысалы: 15 х 14 = 168
Шешуі: 1 х 1 = 1
(5+4) = 9
5 х 4 = 20
190 + 20 = 210
Қосындыны және көбейтінділерді тіркеп жазсақ 210
Мысалы: 17 х 12 = 176
Шешуі: 1 х 1 = 1
(7+2) = 9
7 х 2 = 14
190 + 14 = 204
Қосындыны және көбейтінділерді тіркеп жазсақ 204
-
Егер берілген екі таңбалы санның екеуінің де ондықтар орнындағы цифрлары бірдей 1 ге тең болып, ал бірліктер орнындағы цифрларының қосындысы 10 ға тең болса, онда төмендегі тәсілді қолданып дұрыс әрі жылдам есептеуге болады [1].
3-тәсіл: Ондықтар орнындағы «1» цифрларының қосындысын, яғни «2» цифрын теңдіктің оң жағына шығарып, жүздіктер орынына апарып тұрақты етіп қоямыз, бірліктер орнындағы сандарды өзара қосып қосындыны ондықтар орнына апарып тіркейміз, кейін сол екі санды өзара көбейтіп, шыққан көбейтіндіні бірліктер орнына апарып тіркеп, шыққан мәннен 10 санын азайтамыз. «Қосу, қосу, көбейту, азайту 10» формуласы деп атауға болады.
Мысалы: 11 х 19 = 209
Шешуі: (1+1) = 2,
(1+9) = 10, тіркеу бойынша 210
1 х 9 = 9, тіркеу бойынша 210+009=219
219 - 10 = 209
Қосындыны және көбейтінділерді тіркеп жазсақ 209
Мысалы: 13 х 17 = 221
Шешуі: (1+1) = 2, тіркеу бойынша 200
(3+7) = 10, тіркеу бойынша 210
3 х 7 = 21, тіркеу бойынша 210 + 21 = 231
231 – 10 = 221
Қосындыны және көбейтінділерді тіркеп жазсақ 221
Мысалы: 15 х 15 = 225
Шешуі: (1+1) = 2,
(5+5) = 10, тіркеу бойынша 210
5 х 5 = 25, тіркеу бойынша 210+025=235
235 - 10 = 225
Қосындыны және көбейтінділерді тіркеп жазсақ 209
Мысалы: 18 х 12 = 216
Шешуі: (1+1) = 2, тіркеу бойынша 200
(8+2) = 10, тіркеу бойынша 210
8 х 2 = 16 тіркеу бойынша 210 + 16 = 226
226 – 10 = 216
Қосындыны және көбейтінділерді тіркеп жазсақ 216
-
Егер берілген екі таңбалы санның екеуінің де ондықтар орнындағы цифрлары бірдей 1 ге тең болып, ал бірліктер орнындағы цифрларының қосындысы және көбейтіндісі 10 нан үлкен болса, онда төмендегі тәсілді қолданып дұрыс әрі жылдам есептеуге болады [1].
4-тәсіл: Ондықтар орнындағы «1» цифрларының қосындысын, яғни «2» цифрын теңдіктің оң жағына шығарып, жүздіктер орынына апарып тұрақты етіп қоямыз, бірліктер орнындағы сандарды өзара қосып қосындыдан 10 санын аламыз да, ондықтар орнына апарып тіркейміз, кейін сол екі санды өзара көбейтіп, шыққан көбейтіндіні жоғарыда тіркелген ондықтарға апарып қосып, тіркеп жазамыз «Қосу, қосу, азайту 10, көбейту» формуласы деп атауға болады.
Мысалы: 14 х 17 = 238
Шешуі: (1+1) = 2,
(4+7) - 10 = 1, тіркеу бойынша 210
4 х 7 = 28, қосып, тіркеу бойынша 210+028=238
Қосындыны және көбейтінділерді тіркеп жазсақ 238
Мысалы: 13 х 18 = 234
Шешуі: (1+1) = 2,
(3+8) - 10 = 1, тіркеу бойынша 210
3 х 8 = 24, қосып, тіркеу бойынша 210+024=234
Қосындыны және көбейтінділерді тіркеп жазсақ 234
Мысалы: 16 х 19 = 238
Шешуі: (1+1) = 2,
(6+9) - 10 = 5, тіркеу бойынша 250
6 х 9 = 54, тіркеу бойынша 250+054=304
Қосындыны және көбейтінділерді тіркеп жазсақ 304
Мысалы: 15 х 18 = 270
Шешуі: (1+1) = 2,
(5+8) - 10 = 3, тіркеу бойынша 230
5 х 8 = 40, тіркеу бойынша 230+040=270
Қосындыны және көбейтінділерді тіркеп жазсақ 270


1-кесте. 11-ден 20-ға дейінгі екі таңбалы сандардың, қызғыл түспен боялғандары
1-әдіспен, көкшіл түспен боялғандары 2-әдіспен, ал сарғылт түспен боялғандары 3-,4-әдістермен көбейтіледі.
Ал енді 2-нұсқа бойынша топтастырылған екі, үш таңбалы сандарды көбейту әдістеріне тоқталамыз.
-
Егер берілген екі таңбалы санның біреуінің бірліктер және ондықтар орнындағы цифрлары бірдей болып, екіншісанның бірліктер және ондықтар орнындағы цифрларының қосындысы 10 ға тең болатын болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады [1].
1-тәсіл: қосындысы 10 болатын санның ондықтар орнындағы цифрына «1» санын қосып, «бірліктер * бірліктер», «ондықтар *ондықтар» бойынша көбейтіп, тіркеп жазамыз.
Мысалы: 66 х 28 = 1848
Шешуі: (2+1) х 6 = 18
6 х 8 = 48
Көбейтінділерді тіркеп жазсақ 1848
Мысалы: 22 х 73 = 1606
Шешуі: (7+1) х 2 = 16
2 х 3 =06
Көбейтінділерді тіркеп жазсақ 1606
-
Егер берілген екі таңбалы санның ондықтар орнындағы цифрлары бірдей болып, бірліктер орнындағы цифрларының қосындысы 10 ға тең болатын болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады.
2-тәсіл: ондықтар орнындағы сифрлардың біріне «1» санын қосып, «бірліктер * бірліктер», «ондықтар *ондықтар» бойынша көбейтіп, тіркеп жазамыз.
Мысалы: 47 х 43 = 2021
Шешуі: (4+1) х 4 = 20
7 х 3 = 21
Көбейтінділерд тіркеп жазсақ 2021
Мысалы: 83 х 87 = 7221
Шешуі: (8+1) х 8 = 72
3 х 7 = 21
Көбейтінділерді тіркеп жазсақ 7221 келіп шығады.
Осы түрдегі екі таңбалы сандарды көбейту әдісін « «1» санын қосу әдісі» деп атауға болады.
-
Егер берілген екі таңбалы санның бірліктер орнындағы цифрлары бірдей болып, ал ондықтар орнындағы цифрларының қосындысы 10 ға тең болатын болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады.
3-тәсіл: «ондықтар * ондықтар + бірліктер » «бірліктер * бірліктер», бойынша көбейтіп, тіркеп жазамыз.
Мысалы: 26 х 86 = 2236
Шешуі: 2 х 8 + 6 = 22
6 х 6 = 36
Көбейтінділерді тіркеп жазсақ 2236
Мысалы: 63 х 43 = 2709
6 х 4 + 3 = 27
3 х 3 = 09
Көбейтінділерді тіркеп жазсақ 2709
Осы түрдегі екі таңбалы сандарды көбейту әдісін «бірліктер цифрын қосу әдісі» деп атауға болады.
-
Егер берілген екі таңбалы санның бірліктер орнындағы цифрлары «1» болып, ал ондықтар орнындағы цифрлар кез келген сан болып, бірақ сол ондықтар орнындағы цифрлардың қосындысы 10 нан кіші болатын болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады [2].
4-тәсіл: «ондықтар * ондықтар», «ондықтар + ондықтар», бойынша көбейтіп, соңына «1» ді тіркеп жазамыз.
Мысалы: 41 х 51 = 2091
Шешуі: 4 х 5 = 20
4 + 5 = 9
Көбейтінділерді тіркеп, тағы «1» ді тіркеп жазсақ 2091
Мысалы: 61 х 21 = 1281
Шешуі: 6 х 2 = 12
6 + 2 = 8
Көбейтінділерді тіркеп, тағы «1» ді тіркеп жазсақ 1281
Осы түрдегі екі таңбалы сандарды көбейту әдісін « «1» санын тіркеу әдісі» деп атауға болады.
-
Егер берілген екі таңбалы санның бірліктер орнындағы цифрлары «1» болып, ал ондықтар орнындағы цифрлар кез келген сан болып, бірақ сол ондықтар орнындағы цифрлардың қосындысы 10 нан үлкен болатын болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады.
5-тәсіл: «ондықтар * ондықтар + 1» бойынша көбейтіп, «ондықтар + ондықтар = қосынды» қосындыдағы бірліктер мен ондықтар цифрларының орындарын алмастырып жазамыз.
Мысалы: 71 х 91 = 6461
Шешуі: 7 х 9 + 1 = 64
7 + 9 = 16 кері алмасу саны 61
Көбейтінді мен қосындының кері алмасу санын тіркеп жазсақ 6461
Мысалы: 81 х 61 = 4941
Шешуі: 8 х 6 + 1= 49
8 + 6 = 14 кері алмасу саны 41
Көбейтінді мен қосындының кері санын тіркеп жазсақ 4941 келіп шығады.
Осы түрдегі екі таңбалы сандарды көбейту әдісін « «қосындының кері алмасу санын» тіркеу әдісі» деп атауға болады.
-
Егер берілген екі таңбалы санның ондықтар орнындағы цифрлары «9» болып, ал бірліктер орнындағы цифрлар кез келген сан болса, онда төмендегі тәсілмен дұрыс әрі жылдам есептеуге болады [3].
6-тәсіл: бірінші саннан екінші санның 100 ге толықтаушы саны алынады, сонан кейін екі санның да 100 ге толықтауыштары өзара көбейтіліп, тіркеп жазылады.
Мысалы: 93 х 95 = 8835
Шешуі:

шағым қалдыра аласыз















