Цилиндрлік беттер
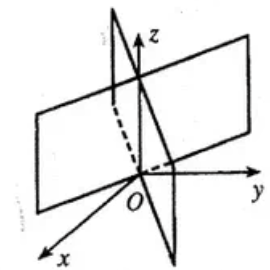
Берілген L сызықты қиятын және берілген l түзуге параллель түзулерден тұратын бетті цилиндрлік бет деп атайды. Мұндағы L цилиндрлік беттің бағыттаушысы, ал l түзуге параллель түзулер оны жолаушылары деп аталады. Егер цилиндрлік беттің бағыттаушы теңдеуі
 (1)
(1)
түрінде берілсе, ал осы беттің жасаушылары
 (2)
(2)
теңдеуімен берілсе,
онда M
 – бетке тиісті
нүкте,
– бетке тиісті
нүкте,  осьтік беттік ағымдық
координаталары,
осьтік беттік ағымдық
координаталары,  жасаушының негізгі
координаталары.
жасаушының негізгі
координаталары.
Егер
 +
+ =1 (1) теңдеуімен
берілсе,анықталатын бетті эллипстік цилиндр деп атайды. Оның
жасаушылары О
=1 (1) теңдеуімен
берілсе,анықталатын бетті эллипстік цилиндр деп атайды. Оның
жасаушылары О осіне параллель болатын,
ал бағыттау жолы ХОУ жазықтығында жаттатын жарты осьтер а және в
болады. Ал егер, а*в болса, онда теңдеуі
осіне параллель болатын,
ал бағыттау жолы ХОУ жазықтығында жаттатын жарты осьтер а және в
болады. Ал егер, а*в болса, онда теңдеуі
 -
- =
= болады.
болады.
Егер
 -
- =1 (2) теңдеуімен
анықталатын болса, бет гиперболасының цилиндрі деп аталады.Бұл
беттің де жасаушылары О
=1 (2) теңдеуімен
анықталатын болса, бет гиперболасының цилиндрі деп аталады.Бұл
беттің де жасаушылары О осіне бағыттаушысы ХОУ
жазықтығындағы нақты жарты ось а және жарымал осі в болатын
гипербола болады.
осіне бағыттаушысы ХОУ
жазықтығындағы нақты жарты ось а және жарымал осі в болатын
гипербола болады.
Егер
 -
- =0 теңдеуімен анықталса,
бет екі цилиндрлі жазықтықта бөлінетін
болады.
=0 теңдеуімен анықталса,
бет екі цилиндрлі жазықтықта бөлінетін
болады.
Егер
 =2рх(3) теңдеуімен
анықталатын бет параболалық цилиндр деп аталады. Бұл беттің
жасаушылары О
=2рх(3) теңдеуімен
анықталатын бет параболалық цилиндр деп аталады. Бұл беттің
жасаушылары О осіне параллель, ал
бағыттаушысы ОХУ жазықтығындағы жатқан парабола болады. (1)-(3)
теңдеулерде х пен у кездескен. Ал, оо белгісіздердің орнына у
пен
осіне параллель, ал
бағыттаушысы ОХУ жазықтығындағы жатқан парабола болады. (1)-(3)
теңдеулерде х пен у кездескен. Ал, оо белгісіздердің орнына у
пен  немеске х
пен
немеске х
пен  белгісіздерді беруі
мүмкін.
белгісіздерді беруі
мүмкін.
Сондай-ақ,  =
= және
және  =0 теңдеулері сияқты у=в
немесе
=0 теңдеулері сияқты у=в
немесе  2 =с2
теңдеулері де,
сондай-ақ,
2 =с2
теңдеулері де,
сондай-ақ,  =0,
=0,
 2
=0 теңдеулері кездесуі
мүмкін.
2
=0 теңдеулері кездесуі
мүмкін.
сурет 2 сурет 3 сурет 4


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]() х У
х У
сурет 5 сурет 6 сурет 7
№1.
 -
- =
= теңдеуі қандай бетті
анықтайды?
теңдеуі қандай бетті
анықтайды?
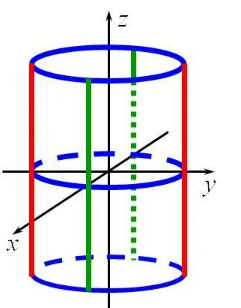
Шешуі: Берілген теңдеуде екі
айнымалы бар. Сондықтан берілген теңдеу цилиндрлік беті
О осіне параллель, ал
бағыттаушысы
осіне параллель, ал
бағыттаушысы  +
+ =
= шеңбер болып келген
бетті анықтайды.
шеңбер болып келген
бетті анықтайды.
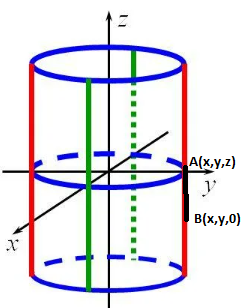
Жазықтықта ХУ-те жататын
шеңбердің центрі  болған және бағыттаушысы
О
болған және бағыттаушысы
О осіне параллель бетті
білдіреді. Сонымен
осіне параллель бетті
білдіреді. Сонымен  +
+ =
= теңдеуі кеңістікте тік
дөңгелек цилиндрді анықтайды.Бұл цилиндрдік жасаушылары
О
теңдеуі кеңістікте тік
дөңгелек цилиндрді анықтайды.Бұл цилиндрдік жасаушылары
О осіне параллель, ал
бағыттаушысы ОХУ жазықтығындағы шеңберге тең
болады.
осіне параллель, ал
бағыттаушысы ОХУ жазықтығындағы шеңберге тең
болады.
Демек,
 +
+ =
= теңдеуі тік дөңгелек
цилиндрлі дөңгелегі шеңбер, О
теңдеуі тік дөңгелек
цилиндрлі дөңгелегі шеңбер, О осіне параллель,
цилиндрді анықтайды.
осіне параллель,
цилиндрді анықтайды.
№2.
 +
+ =1 теңдеуі қандай бетті
анықтайды?
=1 теңдеуі қандай бетті
анықтайды?
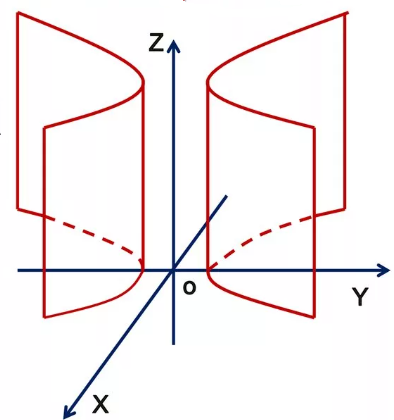
Шешуі: Берілген теңдеу
гиперболалық цилиндрді анықтайды. Бұл гиперболалық
цилиндрдің  -
- = бағыттаушысы ОХУ
жазықтығында, ал жасаушысы О
= бағыттаушысы ОХУ
жазықтығында, ал жасаушысы О осіне параллель болады.
Демек, берілген теңдеу гиперболалық цилиндрді
анықтайды.
осіне параллель болады.
Демек, берілген теңдеу гиперболалық цилиндрді
анықтайды.
 сурет
1
сурет
1
№3.
 =2рх теңдеуі қандай
бетті анықтайды?
=2рх теңдеуі қандай
бетті анықтайды?
Шешуі:
 =2рх теңдеуі
кеңістікте жасаушылары О
=2рх теңдеуі
кеңістікте жасаушылары О осіне параллель болатын
бетті анықтайды. Теңдеу
осіне параллель болатын
бетті анықтайды. Теңдеу  =2рх бағыттаушысы ХОУ
жазықтығындағы жататын параболаны анықтайды.
Сондықтан
=2рх бағыттаушысы ХОУ
жазықтығындағы жататын параболаны анықтайды.
Сондықтан  =2рх теңдеуі берілген
парабола ХОУ жазықтығында, ал жасаушысы
О
=2рх теңдеуі берілген
парабола ХОУ жазықтығында, ал жасаушысы
О осіне параллель болатын
бетті анықтайды. Демек,
осіне параллель болатын
бетті анықтайды. Демек,  =2рх теңдеуі параболалық
цилиндрді анықтайды.
=2рх теңдеуі параболалық
цилиндрді анықтайды.
14
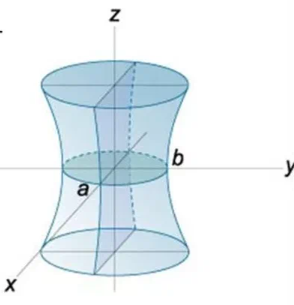
№5. Қандай
бетті  +у2
= 36
анықтайды?
+у2
= 36
анықтайды?
Шешуі:
ХОУ жазықтығындағы
жататын  +у2
= 36 теңдеуі цилиндрді
анықтайды. Бұл теңдеу кеңістікте жасаушысы
О
+у2
= 36 теңдеуі цилиндрді
анықтайды. Бұл теңдеу кеңістікте жасаушысы
О осіне параллель болатын
және бағыттаушысы 36-ға тең. Кеңістікте
осіне параллель болатын
және бағыттаушысы 36-ға тең. Кеңістікте
 +у2
= 36 теңдеуін анықтайтындығы,
яғни жасаушысы кеңістікте түзулер тік дөңгелек цилиндр
болады.
+у2
= 36 теңдеуін анықтайтындығы,
яғни жасаушысы кеңістікте түзулер тік дөңгелек цилиндр
болады.
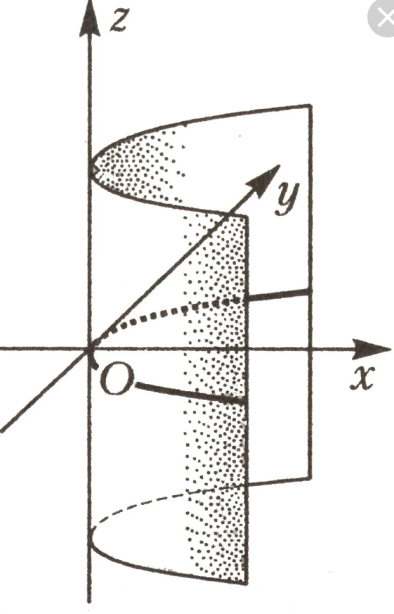
Демек,
 +у2
= 36 теңдеуі кеңістікте тік
дөңгелек цилиндрді анықтайды.
+у2
= 36 теңдеуі кеңістікте тік
дөңгелек цилиндрді анықтайды.
 15
15
№4
 = 4у теңдеуі
кеңістікте қандай бетті анықтайды?
= 4у теңдеуі
кеңістікте қандай бетті анықтайды?
Шешуі:
 = 4у теңдеуі
кеңістікте О
= 4у теңдеуі
кеңістікте О осіне параллель
параболалық цилиндрді анықтайды.
осіне параллель
параболалық цилиндрді анықтайды.
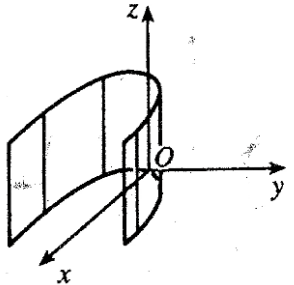
Цилиндрлік беттік
параболасы  = 4у
,
= 4у
,  =0 теңдеулермен
анықталады.
=0 теңдеулермен
анықталады.
Демек,
беттің  = 4у теңдеуі параболалық
цилиндрді анықтайды.
= 4у теңдеуі параболалық
цилиндрді анықтайды.
№6 Бағыттаушы
гипербола  -у2
= 25,
-у2
= 25,
 =0 теңдеуімен және
құраушылары уо
=0 теңдеуімен және
құраушылары уо теңдеуімен анықталатын
цилиндрдің таңдеуін табыңыздар.
теңдеуімен анықталатын
цилиндрдің таңдеуін табыңыздар.
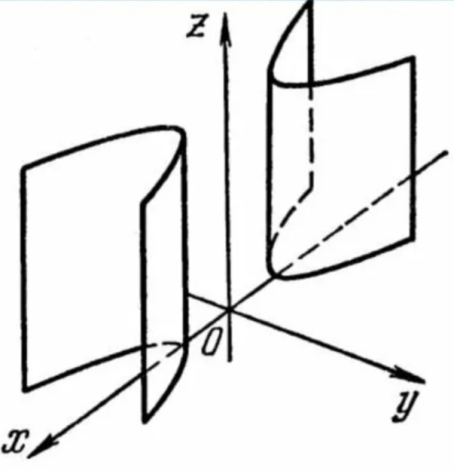
Шешуі:
уо бағыттаушы коэффициенті
бас нүктеден өтіп, координаталар системасының осімен
α=900,
бағыттаушы коэффициенті
бас нүктеден өтіп, координаталар системасының осімен
α=900,
 =450
бұрыш жасайды.
уо
=450
бұрыш жасайды.
уо бағыттаушы
бағыттаушы  коэффициенті
коэффициенті  ,
,
 болады. Түзудің
бағыттаушы коэффициенті бағыттаушы косинустарына пропорционал
болады.Оны мына түрде жазуға болады:
болады. Түзудің
бағыттаушы коэффициенті бағыттаушы косинустарына пропорционал
болады.Оны мына түрде жазуға болады:
n1:n:p=0: :
: =0:1:2. Сондықтан
m:n:p=0:1:1. Нәтижесінде цилиндрлік беттің
жасаушыларынан теңдеуді былайша жазуға
болады:
=0:1:2. Сондықтан
m:n:p=0:1:1. Нәтижесінде цилиндрлік беттің
жасаушыларынан теңдеуді былайша жазуға
болады:
 =
= =
=
Мұнда х,
у, - нүктелік беттің
координаталары
- нүктелік беттің
координаталары
 ,
,
 ,
,  1- бағыттаушыға тиісті
нүктелердің координаталары
1- бағыттаушыға тиісті
нүктелердің координаталары
Нәтижесінде мынадай теңдеулер алынады:
 және
және  =
= =
=
Бұл
теңдеулерден  ,
,
 тең екендігі
алынады.Осы теңдеудің мәнін сақинаның бірінші теңдеуіне қоссақ,
онда х1-
тең екендігі
алынады.Осы теңдеудің мәнін сақинаның бірінші теңдеуіне қоссақ,
онда х1- 2
2 немесе
х2-у2-
немесе
х2-у2- 2+27у-25
2+27у-25 теңдеуі
алынады.
теңдеуі
алынады.
Демек,
х2-у2- 2+27у-25
2+27у-25 теңдеуі есептің шартын
қанағаттандырады.
теңдеуі есептің шартын
қанағаттандырады.
№7 Дөңгелек цилиндрдің осі
х 9-t,
у
9-t,
у t,
t,
 t және
М0
(0;-2;3) оның бетінің нүктесі
берілген. Цилиндрлік теңдеуді табыңыздар.
t және
М0
(0;-2;3) оның бетінің нүктесі
берілген. Цилиндрлік теңдеуді табыңыздар.
Шешуі: Дөңгелек беттің
М(х,у, нүктесін алайық. Осы
нүктеден цилиндрдің осіне дейінгі қашықтық, цилиндрдің берілген
М0
(0;-2;3) нүктесіне дейінгі
қашықтыққа тең болады. Ал, М0(х0,у0,
нүктесін алайық. Осы
нүктеден цилиндрдің осіне дейінгі қашықтық, цилиндрдің берілген
М0
(0;-2;3) нүктесіне дейінгі
қашықтыққа тең болады. Ал, М0(х0,у0, нүктесін
х
нүктесін
х х1+l,t, y=y1+ m,t,
х1+l,t, y=y1+ m,t, 
 +n1t
+n1t
түрінде дейінгі қашықтық мына формуламен
d= 2+
2+ 2+
2+ 2
2

Есептелінеді. Сондықтан
d0= =
= =
= =10,
=10,
d1=
Дөңгелек цилиндрдің d0 мен d1 ұзындықтары тең болғандықтан, d0= d1 болады. Сондықтан
 =30
=30
Бұдан алатынымыз
8 -5
-5 +5
+5 -4ху+4х
-4ху+4х +8у
+8у +156х-60у-132
+156х-60у-132 -5х=0
-5х=0
Демек, дөңгелек цилиндрдің осі
х 9-t,
у
9-t,
у t,
t,
 t түзуінде берілген
және М0
(1;-1;3) нүктесінен өтетін
цилиндрлік беттің теңдеуі
t түзуінде берілген
және М0
(1;-1;3) нүктесінен өтетін
цилиндрлік беттің теңдеуі
8 -5
-5 +5
+5 -4ху+4х
-4ху+4х +8у
+8у +156х-60у-132
+156х-60у-132 -5х=0
болады.
-5х=0
болады.
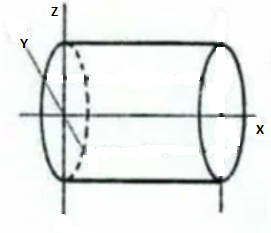
№8
у2+ =9 теңдеуімен берілген бетті
анықтаңыздар.
=9 теңдеуімен берілген бетті
анықтаңыздар.
![]()
Шешуі: Берілген теңдеуде х
айнымалысы жоқ.Сондықтан бұл беттің құрылысы ох осіне параллель.
у2+ =9 теңдеуі
уо
=9 теңдеуі
уо жазықтығында жататын
центр, координаталар системасының бас нүктесінен өтетін, радиусы
3-ке тең шеңбер алынады. Ал, кеңістікте
у2+
жазықтығында жататын
центр, координаталар системасының бас нүктесінен өтетін, радиусы
3-ке тең шеңбер алынады. Ал, кеңістікте
у2+ =9 теңдеуі кеңістікте
цилиндрді анықтайды. Бұл цилиндрдің табаны
у2+
=9 теңдеуі кеңістікте
цилиндрді анықтайды. Бұл цилиндрдің табаны
у2+ =9 теңдеуімен осы беттің ох
осіне параллель түзуді анықтайды.
=9 теңдеуімен осы беттің ох
осіне параллель түзуді анықтайды.
Демек, ізденілген цилиндрлік бет ох осіне параллель орналасады екен.
№9
 =9-х2
теңдеуімен берілген бетті
анықтаңыздар.
=9-х2
теңдеуімен берілген бетті
анықтаңыздар.
Шешуі:
 =9-х2
теңдеуі ох осіне параллель,
жасаушысы цилиндрлік бетке параллель болатын фигураны анықтайды.
Оның бағыттаушысы
=9-х2
теңдеуі ох осіне параллель,
жасаушысы цилиндрлік бетке параллель болатын фигураны анықтайды.
Оның бағыттаушысы  =9-х2
теңдеуімен анықталатын бет
болады. Бұл параболаның центрі (0; 0; 4) нүктесінде
болады.
=9-х2
теңдеуімен анықталатын бет
болады. Бұл параболаның центрі (0; 0; 4) нүктесінде
болады.
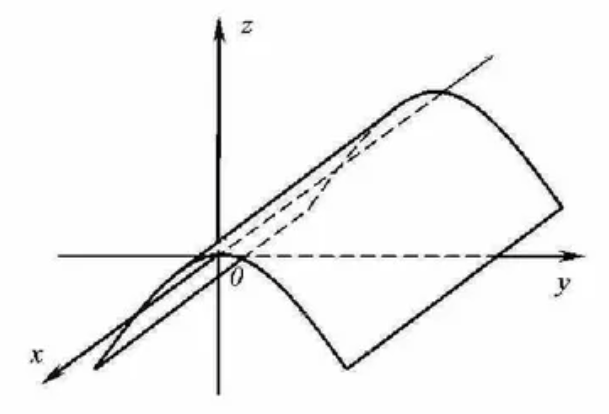
№10
 -
- =0 теңдеуі қандай бетті
анықтайды?
=0 теңдеуі қандай бетті
анықтайды?
Шешуі: Берілген теңдеуді келесі түрге келтіруге болады:
( -
- )
(
)
( +
+ )
=0
)
=0
Алынған теңдеуді
( -
- ) =0
(
) =0
( +
+ )
=0
)
=0
түріне келтіруге болады.Бұл теңдеулерді
 =
= х,
х,
 =-
=- х
х
түріне келтіреді.Мұндағы теңдеулер ох осі арқылы өтетін және ОУ осі арқылы қиылысатын екі жазықтықты көрсетеді.
№10 у2 -4х-6у+17=0 бетінің түрін анықтаңыздар.
Шешуі: Берілген бетінің түрін түрлендірейік:
у2 -4х-6у+17=0
(у2 -6у+9)-4х-9+17=0
(у-3 -4х+8=0
-4х+8=0
(у-3 =4(х-2)
=4(х-2)
Енді
у-3= ,
х-2
,
х-2 жаңа координаталар
енгізсек, онда
жаңа координаталар
енгізсек, онда  2
2 теңдеуі
алынады.
теңдеуі
алынады.
Демек, берілген
у2
-4х-6у+17=0
беті  2
2 бетіне сәйкес
параболалық цилиндр болады.
бетіне сәйкес
параболалық цилиндр болады.

алынады. Осы системаның екінші
теңдеуінен  ны тауып, біріншісіне
қайтсақ,
ны тауып, біріншісіне
қайтсақ,
(
теңдеуі алынады. Тұл теңдеуден:
 2-
2- +
+ 2-
2- +
+ 2-12 УƵ-4
Ƶ2-36
2-12 УƵ-4
Ƶ2-36 +12Ƶ
+12Ƶ
Демек,
 2-12 УƵ-4
Ƶ2-36
2-12 УƵ-4
Ƶ2-36 +12Ƶ
+12Ƶ теңдеуі цилиндрдің
теңдеуін жасады.
теңдеуі цилиндрдің
теңдеуін жасады.
№11
Жасаушысы  =
= векторына параллель, ал
бағыттаушысы х2+у2
векторына параллель, ал
бағыттаушысы х2+у2 ,
,
 теңдеуімен берілген
цилиндрдің теңдеуін табыңыздар.
теңдеуімен берілген
цилиндрдің теңдеуін табыңыздар.
Шешуі: Жасаушысы
х t,
у
t,
у t,
t,
 t теңдеулерімен,
басқаша
t теңдеулерімен,
басқаша

теңдеуімен берілген.Берілген теңдеуден
х 2
t+
2
t+ ,
у
,
у 3
t,
3
t,  +4 t. Соңғы
теңдеуден
+4 t. Соңғы
теңдеуден  +4
t
+4
t
Бұдан
t
Енді
 -2
t
-2
t  t
t +
+
Енді
 ,
,  -дерді теңдеуге қисақ,
онда
-дерді теңдеуге қисақ,
онда
(х- +(у+
+(у+ болады.
болады.
Енді амалдарды орындап, сәйкес мүшелерін қоссақ, онда
х2-х(1-2)- +у2+2у(
+у2+2у(
х2+
у2+х(1-2)+( +2у(
+2у(
16х2+16у2-16-16 +4-8
+4-8 +4
+4 2-24у-24у
2-24у-24у 9-19
9-19 +9
+9 2-144
2-144
16х2+16у2-13 2-16х+24у-26у
2-16х+24у-26у -144
-144
теңдеуі шықты.Демек, есептің мәнін қанағаттандыратын теңдеу алынды.
№ 16у2-9 2+32у+54
2+32у+54 -203
-203 теңдеуі қандай бетті
анықтайды?
теңдеуі қандай бетті
анықтайды?
Шешуі: Бұл теңдеу ох осіне параллель, гиперболалық цилиндрді анықтайды. Шындығында теңдеуде х айнымалысы жоқ, ал бағыттаушы гипербола болып тұр, яғни берілген теңдеудің толық квадратын бөліп шығарамыз. Сонда
16у2-9 2+32у+54
2+32у+54 -209
-209
16у2+3у-(9 2-54
2-54 -209
-209
16(у2+2у-1-1)-9 2-6
2-6 +9-9)
-209
+9-9)
-209
16(у2+1)2-10-9 -3)2+81
-209
-3)2+81
-209
16(у2+1)2-9 -3)2
-3)2
Енді соңғы теңдеуді 144-ке бөлсек, онда
 -
- теңдеуі
алынды.
теңдеуі
алынды.
Сонда

түзеді. (0,-1; 3) нүктесінде симметриялы және нақты ось, ОУ осіне тиісті болады. Демек, алынған теңдеу гиперболалық цилиндрді анықтайды.
№17 Цилиндрлік беттің жасаушысы
о осіне параллель, ал
бағыттаушысы х2+у2+
осіне параллель, ал
бағыттаушысы х2+у2+ 2
2 сферасына
х+у+
сферасына
х+у+ жазықтық қиылысуына
цилиндр бетінің теңдеуін табыңыздар.
жазықтық қиылысуына
цилиндр бетінің теңдеуін табыңыздар.
Шешуі: Цилиндрлік беттің жасаушысы сферамен жазықтық қиылысуы берілген, яғни

Осы схеманың екінші
теңдеуінен  тауып, бірінші бірінші
теңдеуді қоссақ, онда
тауып, бірінші бірінші
теңдеуді қоссақ, онда
х2+у2+( 2
2 немесе
х2+у2+
немесе
х2+у2+
Цилиндрлік беттің жасаушысы
х2+у2+ болады.
болады.
ІІбет 198/2
Жасаушысы
о осіне параллель, ал
бағыттаушысы х2+у2+
осіне параллель, ал
бағыттаушысы х2+у2+ 2
2 сферасының
х+у+
сферасының
х+у+ жазықтық қиылысу сызығы
болатын цилиндр бетінің теңдеуін
табыңыздар.
жазықтық қиылысу сызығы
болатын цилиндр бетінің теңдеуін
табыңыздар.
Шешуі:
 шешу үшін екінші
теңдеуден
шешу үшін екінші
теңдеуден  сызықтық схемасын оны
бірінші теңдеуге қоссақ, онда
сызықтық схемасын оны
бірінші теңдеуге қоссақ, онда
х2+у2+( 2
2 немесе
х2+у2+
немесе
х2+у2+ болып
алынады.
болып
алынады.
Сонда бағыттаушы


теңдеуі алынады. Мұндағы
бірінші теңдеу  цилиндр бетінің
теңдеуі.
цилиндр бетінің
теңдеуі.
Демек,
о осіне параллель, ал
бағыттаушысы х2+у2+
осіне параллель, ал
бағыттаушысы х2+у2+ 2
2 сферасының
х+у+
сферасының
х+у+ жазықтығымен қиылысу
сызығы
жазықтығымен қиылысу
сызығы  цилиндр беті
болады.
цилиндр беті
болады.
№19.
Бағыттаушысы 

теңдеуі арқылы анықталатын
шеңбер, ал жасаушысы  векторына параллель
цилиндр беттің теңдеуін табыңдар.
векторына параллель
цилиндр беттің теңдеуін табыңдар.
Шешуі:
М нүктесімен
нүктесімен  векторының бағытымен
жүргізілген түзу бағыттауыш сызығын әйтеуір бір
N(
векторының бағытымен
жүргізілген түзу бағыттауыш сызығын әйтеуір бір
N( нүктесінде қиғанда бұны
берілген цилиндрлік бетке тән болады.Ондай түзудің
теңдеулерін
нүктесінде қиғанда бұны
берілген цилиндрлік бетке тән болады.Ондай түзудің
теңдеулерін
х +
+
у +
+
 +
+
етіп орнатуға болады.Бұл
теңдеулерді  х-
х- ,
,
 у-
у- ,
,
 -
- түрінде жазамыз. Бұл
шамалар бағыттауышы сызықтың теңдеуін қанағаттандырады. Сондықтан:
х+
түрінде жазамыз. Бұл
шамалар бағыттауышы сызықтың теңдеуін қанағаттандырады. Сондықтан:
х+ +у-
+у- +
+
Бұдан
 +
+ .
.
Сонымен,
 х-
х- ,
,
 у-
у- ,
,
 -
- .
.
Векторларға бақыттаушы сызықты
анықтаутын теңдеулер системасының екінші тең бетке қиып, іздеген
цилиндр беттің х2+у2+ 2-ху-х
2-ху-х -у
-у -
- теңдеуін
табамыз.
теңдеуін
табамыз.
Демек,
х2+у2+ 2-ху-х
2-ху-х -у
-у -
- іздеуші цилиндр беттің
теңдеуі болады.
іздеуші цилиндр беттің
теңдеуі болады.
24
Айналу беті
Берілген L осі айналу сызығы
бойынша айналып алынған бетті Ф айналып беті деп атайды. Айналу
бетінің теңдеуін алу үшін, УО о
о осіне айналдырып алып,
F(х,у)
осіне айналдырып алып,
F(х,у) теңдеуінде
у-ті
теңдеуінде
у-ті  ауыстыру
керек.
ауыстыру
керек.
Егер
Уо жазықтығында
F(у,
жазықтығында
F(у, )
) ,
х
,
х теңдеудің қисығы СХ
алынатын жазықтығы болса, онда
теңдеудің қисығы СХ
алынатын жазықтығы болса, онда
F( )
) пайда болады. Осыған
ұқсас F(
пайда болады. Осыған
ұқсас F( теңдеуі
теңдеуі
ох осін айнала қозғаған кезде пайда болады.
Айналу эллипс
сызығы  о
о осін айналып қозғалу
кезінде (эллипстың а
осін айналып қозғалу
кезінде (эллипстың а с кезде) пайда
болады.
с кезде) пайда
болады.
Сонда ол сфераға айналады.Бір қуысты айналу гиперболасында
 айналдыру кезінде пайда
болар еді.
айналдыру кезінде пайда
болар еді.
Екі қуысты айналу
гиперболасында  о
о осін айналып қозғалу
кезінде пайда болады.
осін айналып қозғалу
кезінде пайда болады.
Айналу
параболоиды  2р
2р о
о осін айналу осі
болады.
осін айналу осі
болады.
Хо жазықтығында
эллипсті
жазықтығында
эллипсті
 (1)
(1)
о осіне айналдыратын болсақ,
алынған осынау бетті айналу эллипс сызығы деп атайды. Оның
теңдеуі
осіне айналдыратын болсақ,
алынған осынау бетті айналу эллипс сызығы деп атайды. Оның
теңдеуі
 (2) деп
аталады.
(2) деп
аталады.
Эллипс сызығы ХОУ жазықтығына
параллель бір  (/
(/ айналу
теңдігі
айналу
теңдігі 
Эллипс сызығы қиық,
оны  –с-дан +с-ға дейін
ордігенде эллипсоидты сызығы шығады. 36
–с-дан +с-ға дейін
ордігенде эллипсоидты сызығы шығады. 36
Эллипсоидты координаттық
с болса,
онда
болса,
онда  ,
,

эллипсоиді шығады. Жалпы
жағдайда (а болса), эллипсоид үш
осьті эллипсоид болады, егер а
болса), эллипсоид үш
осьті эллипсоид болады, егер а болса, эллипсоидтар
қысылықты эллипсоидтар деп аталады. 37
болса, эллипсоидтар
қысылықты эллипсоидтар деп аталады. 37
 2 шеңбері ох осінен айналады.
Айналу бетінің теңдігін сфераны
табыңыздар.
2 шеңбері ох осінен айналады.
Айналу бетінің теңдігін сфераны
табыңыздар.
Шешуі: ох осінен шеңберді
айналдыру керек.ох осін өзгеріссіз қалдыру керек. Ал екінші сызықта
у-х+ -пен ауыстырып, айналу
бетінің теңдігін жазу керек, яғни
у-х+
-пен ауыстырып, айналу
бетінің теңдігін жазу керек, яғни
у-х+ ауыстырып теңдеу жазылады.
Сонда
ауыстырып теңдеу жазылады.
Сонда
 +(
+( )2
)2 2
2
 +у2
+у2 2 айналу бетінің теңдігін
алынады немесе мұны сфералық беті дейміз. Айналу бетінің
теңдеуі
2 айналу бетінің теңдігін
алынады немесе мұны сфералық беті дейміз. Айналу бетінің
теңдеуі  +у2
+у2 2 түрінде жазылады.
38
2 түрінде жазылады.
38
Айналу эллипсоиды
 эллипсоид ОУ осінен
айналып шыққан, айналу эллипс сызығының теңдеуін
жазыңыздар.
эллипсоид ОУ осінен
айналып шыққан, айналу эллипс сызығының теңдеуін
жазыңыздар.
Шешуі: Айналу бетінің теңдеуін
табу ережесіне сәйкес эллипс сызығының
теңдеуіндегі  Нәтижесінде берілген
эллипстің теңдеуіндегі х-тың орнына
Нәтижесінде берілген
эллипстің теңдеуіндегі х-тың орнына  қойылады.Сонда
қойылады.Сонда
 +
+ немесе
немесе  теңдеуіне
айналады.
теңдеуіне
айналады.
Демек,
 айналу эллипс
сызығының теңдеуі алынады. 39
айналу эллипс
сызығының теңдеуі алынады. 39
Жарты осьтері 5 пен 3 болатын эллипс, өзінің үлкен осіның бойына айналады. Үлкен осі ОУ осінде, ал эллипс центрі координаталары системасының бас нүктесінде орналасқан.Осы эллипстің ОУ осіне айналу кезіндегі бетінің теңдеуін табыңыздар.
Шешуі: Берілуі бойынша
в және
уо
және
уо жазықтығында жатыр. Оның
теңдеуі
жазықтығында жатыр. Оның
теңдеуі

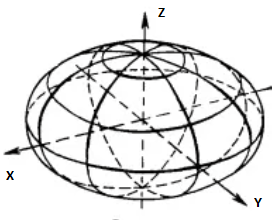
Берілгені бойынша қисықтың
теңдеуі уо жазықтығында жатыр.Ал
қисық ОУ осінен айналған кезде пайда болатын бетті алу
үшін
жазықтығында жатыр.Ал
қисық ОУ осінен айналған кезде пайда болатын бетті алу
үшін 
 Сонда қисықтың
теңдеуі
Сонда қисықтың
теңдеуі
 немесе
немесе  түрінде
жазылады.
түрінде
жазылады.
Демек,
алынған  ізделінді теңдеу
болады.
ізделінді теңдеу
болады.
х-2у ,
,
 айналғанда алынатын
айналу бетінің теңдеуін табыңыздар.
айналғанда алынатын
айналу бетінің теңдеуін табыңыздар.
Шешуі: М нүктесі сызығының
төбесі дейік. Оның координатасы (4; 0;0) болады. Осы конустың кез
келген А нүктесінің координатасы  десек, оның сәйкес
негізін В (х,у,о) нүктесі болады.А мен В ның координаталары А
(
десек, оның сәйкес
негізін В (х,у,о) нүктесі болады.А мен В ның координаталары А
( В(х,у,о) болады, сонда А
мен В координата нүктесінің әртүрлі нүктесі, ал В (х,у,о)
координатасында болады. Сонда
у2
В(х,у,о) болады, сонда А
мен В координата нүктесінің әртүрлі нүктесі, ал В (х,у,о)
координатасында болады. Сонда
у2 2. Ал бұдан
Х
2. Ал бұдан
Х у
у болады.
болады.
Сонда айналу бетінің ауданы
Х+ -4
-4
Х+ -4
-4
(
 )2
)2
4( 16+8
16+8 2
2
4( (
(
Демек,
4( (
( айналу беті болып
табылады.
айналу беті болып
табылады.
№5
.х2 теңдеуі қандай бетті
анықтайды?
теңдеуі қандай бетті
анықтайды?
Шешуі: Координаталық осьтерді
ОХ осінің айналасында  бұрышқа бұрайық. Мұнда
ОУ осінен ОХ осіне қажет нақты бағытта бұрылады. Сонда
х
бұрышқа бұрайық. Мұнда
ОУ осінен ОХ осіне қажет нақты бағытта бұрылады. Сонда
х 1,
у
1,
у 1
1  1
1 ,
,
 1
1 +
+ 1
1 .Сондықтан
.Сондықтан
 ,
онда
,
онда
х 1
,
у
1
,
у (
( 1-
1- 1),
1),
 (
( 1-
1- 1)
1)
Осы мәндерді беттің теңдеулеріне қоямыз, сонда
 -
- немесе
немесе  +
+ 0
0
Демек, конустың төбесі координаталар басында, ал координаталар осі болып табылады.
№6
 2) параболасы
о
2) параболасы
о осінің бойынан бұрылады
(вращается). Теңдеуді анықтаңыздар.
осінің бойынан бұрылады
(вращается). Теңдеуді анықтаңыздар.
Шешуі: Берілген мысал о*у
жазықтығында F(х,у )
) теңдеуімен берілген.
Парабола осінің бетінен айналады. Бұл жағдайда
х
теңдеуімен берілген.
Парабола осінің бетінен айналады. Бұл жағдайда
х 1,
у
1,
у теңдігінен және мына
теңдеулермен F(
теңдігінен және мына
теңдеулермен F( )
) болады. Осы теңдік
ізделінген теңдікті анықтайды.
болады. Осы теңдік
ізделінген теңдікті анықтайды.
№7
 -
- ОУ осі бойымен айналады.
Алынған екінші ретті беттің типін
анықтаңыздар.
ОУ осі бойымен айналады.
Алынған екінші ретті беттің типін
анықтаңыздар.
Шешуі: Берілген бет ОХУ
жазықтығында, ОУ осінің бойында айнала алады. Гипербола осінен
айналу кезінде у у
у теңдігі орындалады.
Айналған кезде
теңдігі орындалады.
Айналған кезде
F( )
) орындалады.
орындалады.
Берілген есептің шарты
бойынша 
яғни,
 -
- теңдеуі
алынады.
теңдеуі
алынады.
Сонда,
 -
- алынады. Демек, бұл
теңдеу бірқуысты гипербола. 42
алынады. Демек, бұл
теңдеу бірқуысты гипербола. 42
№9
х түзуі ОƵ осі бойымен
айналады. Айналу бетінің теңдеуін
табыңыздар.
түзуі ОƵ осі бойымен
айналады. Айналу бетінің теңдеуін
табыңыздар.
![]()
![]()


 900
900
![]()
![]()
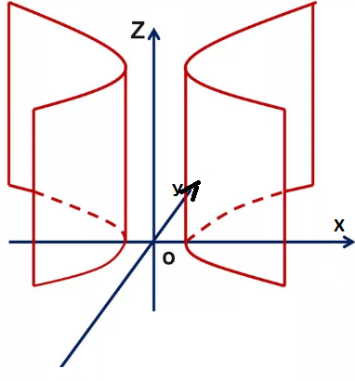
Шешуі:
х түзуінің ОƵ осі бойымен
айналуын табайық. х
түзуінің ОƵ осі бойымен
айналуын табайық. х түзуі ХоƵ жазықтығында
ОƵ осі бойымен айналғанда Ƶ өзгеріссіз қалады.Себебі, ол ОƵ осіне
байланысты.Ал екінші айнымалысы Х айналған кезде оның таңбасы оң
және теріс болып қалған Х пен У –тен квадрат түбір табу керек, яғни
сонда
түзуі ХоƵ жазықтығында
ОƵ осі бойымен айналғанда Ƶ өзгеріссіз қалады.Себебі, ол ОƵ осіне
байланысты.Ал екінші айнымалысы Х айналған кезде оның таңбасы оң
және теріс болып қалған Х пен У –тен квадрат түбір табу керек, яғни
сонда  (1) түрінде жазуға
болады. Бұл теңдікті квадраттасақ, онда теңдеу
(1) түрінде жазуға
болады. Бұл теңдікті квадраттасақ, онда теңдеу
 немесе
немесе  түрінде
жазылады.
түрінде
жазылады.
Демек,
 конустың теңдеуі
болады. 43
конустың теңдеуі
болады. 43
№8
х түзуі ОƵ осін айналады.
Айналу бетінің теңдеуін табыңыздар.
түзуі ОƵ осін айналады.
Айналу бетінің теңдеуін табыңыздар.
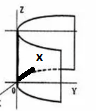
Шешуі:
х жазықтықта Х пен Ƶ
теңдеуге енген. Берілген теңдеуде Ƶ айнымалысы өзгеріссіз қалады.
Есепте берілуі бойынша ОƵ осі бойымен айналу осі болып тұр. Ал
теңдеудегі екінші айнымалы Х-тің өзі
жазықтықта Х пен Ƶ
теңдеуге енген. Берілген теңдеуде Ƶ айнымалысы өзгеріссіз қалады.
Есепте берілуі бойынша ОƵ осі бойымен айналу осі болып тұр. Ал
теңдеудегі екінші айнымалы Х-тің өзі  айнымалысымен алмасып
жазылуы керек. Сонда берілген теңдеу мынадай түрінде
жазылады:
айнымалысымен алмасып
жазылуы керек. Сонда берілген теңдеу мынадай түрінде
жазылады:
Бұл теңдеудің екі жағын
квадраттау арқылы  теңдеуі алынады.
Теңдеуді
теңдеуі алынады.
Теңдеуді  түрінде жазуға болады.
Бұл кезде теңдеудің төбесі координаталар сақинасының бас
нүктесінде, ал Х
түрінде жазуға болады.
Бұл кезде теңдеудің төбесі координаталар сақинасының бас
нүктесінде, ал Х Ƶ теңдеуі Ƶ бұрышының
биссектрисасы болады. Мұндағы у
Ƶ теңдеуі Ƶ бұрышының
биссектрисасы болады. Мұндағы у дегеніміз конус.... тең
конустық биссектрисасы болады.
дегеніміз конус.... тең
конустық биссектрисасы болады.
Бұл конустың осі
6 болады.
болады.
Демек,
 айналу бетінің
теңдеуі, нәтижесінде конус алынады.
айналу бетінің
теңдеуі, нәтижесінде конус алынады.
№10
 теңдеуімен берілген
параболаның ОƵ осі бойымен айналуынан пайда болған беттің теңдеуін
табыңыз.
теңдеуімен берілген
параболаның ОƵ осі бойымен айналуынан пайда болған беттің теңдеуін
табыңыз.
Шешуі: ху бетті табу үшін
теңдеудегі х-тың орнына  табу
керек.
табу
керек.  . Бұл
түзуден
. Бұл
түзуден  4х2+4у2.
4х2+4у2.
Демек, ізделінде теңдеу
-  4х2+4у2
болады.
44
4х2+4у2
болады.
44
№11 Гиперболаның ОƵ осі бойымен айналуынан алынған бірқуысты гиперболоидтың теңдеуін құрыңыздар.
Шешуі: Гиперболаның жорамал осін айналу арқылы алынған гиперболоидты табу керек. Сонымен ОƵ осін гиперболаның осі болса, онда гиперболаның теңдеуі

болады. Осы теңдеуде
х-ті  -қа ауыстырсақ, онда
бірқуысты гиперболоидтың теңдеуі
-қа ауыстырсақ, онда
бірқуысты гиперболоидтың теңдеуі
 немесе
немесе  +
+ болады.
болады.
Демек, Гиперболаны ОƵ осі бойымен айналдырғанда, шыққан бірқуысты гиперболоидтың теңдеуі
 +
+ алынады.
45
алынады.
45
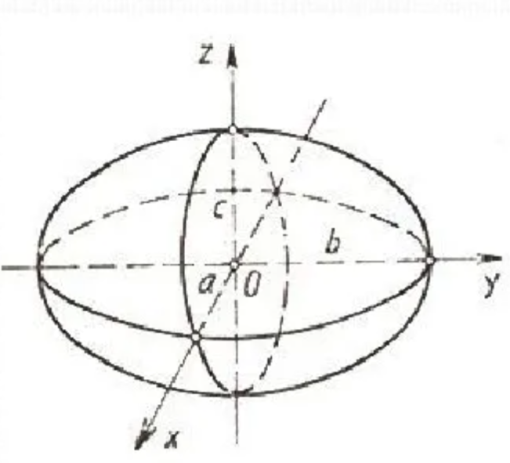
Эллипсоид
Үш осьті эллипсоид
 +
+ түрінде жазылған тұйық
бет. Мұнда а, е, с – эллипсоидтың жазық
беттері.
түрінде жазылған тұйық
бет. Мұнда а, е, с – эллипсоидтың жазық
беттері.
Мұндай эллипсоидтың центрі
координаталар басында жатады.Бас осьтері координаталар осінде
жатады. Төбелері А (-а; о;о),
А2(а; о;о), В (о; -в; о),
В2( о;в;о), С (о;о; с),
С2(о;о; с) нүктелерінде жатады.
А1А2 ,
В1В2
,
В1В2 ,
С1С2
,
С1С2 нүктелері эллипсоидтың
бас диаметрлері. Координаталар жазықтықтары (1) эллипсоиды үш
эллипстің бойымен қиылысады.
нүктелері эллипсоидтың
бас диаметрлері. Координаталар жазықтықтары (1) эллипсоиды үш
эллипстің бойымен қиылысады.
ХОУ жазықтығының
теңдеуі  сондықтан
сондықтан  эллипсі,
эллипсі,
ХоƵ жазықтығының
теңдеуі  сондықтан
сондықтан  эллипсі,
эллипсі,
УоƵ жазықтығының
теңдеуі  демек,
қимада
демек,
қимада  эллипсі
шығады.
эллипсі
шығады.
Эллипсоидтың жазық беттері
а болса, онда оның радиусы
а-ға тең центрі (0,0,0) нүктесінде орналасқан сфераға ауысады. Егер
радиусы а-ға тең, ал сфераның центрі
(
болса, онда оның радиусы
а-ға тең центрі (0,0,0) нүктесінде орналасқан сфераға ауысады. Егер
радиусы а-ға тең, ал сфераның центрі
( ) нүктесінде орналасса, онда
мұндай сфераның теңдеуі
) нүктесінде орналасса, онда
мұндай сфераның теңдеуі
(х- )2+
(у-
)2+
(у- )2+
(
)2+
( -
- )2
)2 2 болады.
2 болады.
Егер
 +
+ эллипсоидына
М0(х0;у0;
эллипсоидына
М0(х0;у0; нүктесінде жанама тұйықтық
жүргізсе, оның теңдеуі
нүктесінде жанама тұйықтық
жүргізсе, оның теңдеуі

болады.
Бір қуысты гиперболоид
Бір қуысты гиперболоидтың канондық теңдеуі
 +
+
түзуінде жатады. Нақты осьтері абциссалар мен ординаталар осьтерінің координаталар осі жорамал беттерінде жатады. а, в,с - бір қуысты гиперболоидтың жарты осьтері деп аталады.
Бір қуысты гиперболоидтың координаталар жазықтықтарымен қиса, онда төменгі сызықтар пайда болады.
Егер ХОУ жазықтықтарымен
қиса,  онда
онда
 +
+ эллипсі
шығады.
эллипсі
шығады.
Егер ХОƵ жазықтықтарымен
қиса,  онда
онда
 +
+ гиперболасы
шығады.
гиперболасы
шығады.
Егер уоƵ жазықтықтарымен
қиса,  онда
онда
 +
+ гиперболасы пайда
болады.
гиперболасы пайда
болады.
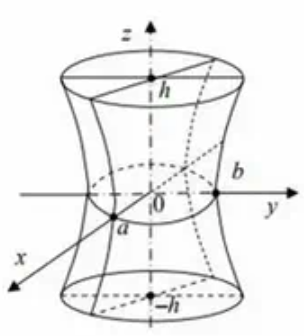
Бір қуысты
гиперболоидты 
 және
және
 координаталар
жазықтықтарымен қиғанда
координаталар
жазықтықтарымен қиғанда
 ,
,
 ,
, 
теңдеулері алынады. 58
Гиперболоноид

теңдеуіндегі ОƵ осі бойымен айналдыра отырып гиперболоидтың теңдеуін құрыңыздар.
Шешуі: Гиперболоид теңдеуін түрлендірейік. Бірінші теңдеуінен х2 тауып, оны екінші теңдеудің квадратынан мына теңдеулер алынады.

алынады. Енді бұл теңдеуді мынадай
 -
- немесе
немесе 

 +
+
түрінде жазылған гиперболоидтың теңдеуі алынады.
Демек,


 +
+
бір қуысты гиперболоидтың теңдеуі болып табылады.
№12
х2+2у2+3 +2х+8у+18
+2х+8у+18 54
54 қандай теңдеу екенін
табыңдар
қандай теңдеу екенін
табыңдар
Шешуі: Теңдеудегі
х,у,  тердің толық
квадраттарын бөлсек, онда
тердің толық
квадраттарын бөлсек, онда
х2+2у2+3 +2х+8у+18
+2х+8у+18 54
54
(х2+2у2+1)-1+2(у2+4у+4)-8-3(
(х2+1)2+2(у+2)2-36 -3)2
-1-8+27-54
-3)2
-1-8+27-54
(х2+1)2+2(у+2)2-36 -3)2
-3)2

......... 36 –ға бөлсек, онда
 +
+
Бұл түзудің центрі (-1;-2; 5)
нүктесінде орналасқан. Енді тік бұрыштар координаталар
сақинасын  х+1,
х+1,  у-2,
у-2, 
 -3 формулалары арқылы
ауыстырсақ, онда
-3 формулалары арқылы
ауыстырсақ, онда  +
+ -
-
 болып, гиперболоидтың
теңдеуіне ауысады.
болып, гиперболоидтың
теңдеуіне ауысады.
Демек, берілген бет бір қуысты гиперболоидты анықтайды. 60
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Эллипосид Цилиндрлік беттер Бір қуысты эллипсоид
Эллипосид Цилиндрлік беттер Бір қуысты эллипсоид
Цилиндрлік беттер
Берілген L сызықты қиятын және берілген l түзуге параллель түзулерден тұратын бетті цилиндрлік бет деп атайды. Мұндағы L цилиндрлік беттің бағыттаушысы, ал l түзуге параллель түзулер оны жолаушылары деп аталады. Егер цилиндрлік беттің бағыттаушы теңдеуі
 (1)
(1)
түрінде берілсе, ал осы беттің жасаушылары
 (2)
(2)
теңдеуімен берілсе,
онда M
 – бетке тиісті
нүкте,
– бетке тиісті
нүкте,  осьтік беттік ағымдық
координаталары,
осьтік беттік ағымдық
координаталары,  жасаушының негізгі
координаталары.
жасаушының негізгі
координаталары.
Егер
 +
+ =1 (1) теңдеуімен
берілсе,анықталатын бетті эллипстік цилиндр деп атайды. Оның
жасаушылары О
=1 (1) теңдеуімен
берілсе,анықталатын бетті эллипстік цилиндр деп атайды. Оның
жасаушылары О осіне параллель болатын,
ал бағыттау жолы ХОУ жазықтығында жаттатын жарты осьтер а және в
болады. Ал егер, а*в болса, онда теңдеуі
осіне параллель болатын,
ал бағыттау жолы ХОУ жазықтығында жаттатын жарты осьтер а және в
болады. Ал егер, а*в болса, онда теңдеуі
 -
- =
= болады.
болады.
Егер
 -
- =1 (2) теңдеуімен
анықталатын болса, бет гиперболасының цилиндрі деп аталады.Бұл
беттің де жасаушылары О
=1 (2) теңдеуімен
анықталатын болса, бет гиперболасының цилиндрі деп аталады.Бұл
беттің де жасаушылары О осіне бағыттаушысы ХОУ
жазықтығындағы нақты жарты ось а және жарымал осі в болатын
гипербола болады.
осіне бағыттаушысы ХОУ
жазықтығындағы нақты жарты ось а және жарымал осі в болатын
гипербола болады.
Егер
 -
- =0 теңдеуімен анықталса,
бет екі цилиндрлі жазықтықта бөлінетін
болады.
=0 теңдеуімен анықталса,
бет екі цилиндрлі жазықтықта бөлінетін
болады.
Егер
 =2рх(3) теңдеуімен
анықталатын бет параболалық цилиндр деп аталады. Бұл беттің
жасаушылары О
=2рх(3) теңдеуімен
анықталатын бет параболалық цилиндр деп аталады. Бұл беттің
жасаушылары О осіне параллель, ал
бағыттаушысы ОХУ жазықтығындағы жатқан парабола болады. (1)-(3)
теңдеулерде х пен у кездескен. Ал, оо белгісіздердің орнына у
пен
осіне параллель, ал
бағыттаушысы ОХУ жазықтығындағы жатқан парабола болады. (1)-(3)
теңдеулерде х пен у кездескен. Ал, оо белгісіздердің орнына у
пен  немеске х
пен
немеске х
пен  белгісіздерді беруі
мүмкін.
белгісіздерді беруі
мүмкін.
Сондай-ақ,  =
= және
және  =0 теңдеулері сияқты у=в
немесе
=0 теңдеулері сияқты у=в
немесе  2 =с2
теңдеулері де,
сондай-ақ,
2 =с2
теңдеулері де,
сондай-ақ,  =0,
=0,
 2
=0 теңдеулері кездесуі
мүмкін.
2
=0 теңдеулері кездесуі
мүмкін.



сурет 2 сурет 3 сурет 4



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]() х У
х У
сурет 5 сурет 6 сурет 7
№1.
 -
- =
= теңдеуі қандай бетті
анықтайды?
теңдеуі қандай бетті
анықтайды?
Шешуі: Берілген теңдеуде екі
айнымалы бар. Сондықтан берілген теңдеу цилиндрлік беті
О осіне параллель, ал
бағыттаушысы
осіне параллель, ал
бағыттаушысы  +
+ =
= шеңбер болып келген
бетті анықтайды.
шеңбер болып келген
бетті анықтайды.

Жазықтықта ХУ-те жататын
шеңбердің центрі  болған және бағыттаушысы
О
болған және бағыттаушысы
О осіне параллель бетті
білдіреді. Сонымен
осіне параллель бетті
білдіреді. Сонымен  +
+ =
= теңдеуі кеңістікте тік
дөңгелек цилиндрді анықтайды.Бұл цилиндрдік жасаушылары
О
теңдеуі кеңістікте тік
дөңгелек цилиндрді анықтайды.Бұл цилиндрдік жасаушылары
О осіне параллель, ал
бағыттаушысы ОХУ жазықтығындағы шеңберге тең
болады.
осіне параллель, ал
бағыттаушысы ОХУ жазықтығындағы шеңберге тең
болады.
Демек,
 +
+ =
= теңдеуі тік дөңгелек
цилиндрлі дөңгелегі шеңбер, О
теңдеуі тік дөңгелек
цилиндрлі дөңгелегі шеңбер, О осіне параллель,
цилиндрді анықтайды.
осіне параллель,
цилиндрді анықтайды.
№2.
 +
+ =1 теңдеуі қандай бетті
анықтайды?
=1 теңдеуі қандай бетті
анықтайды?
Шешуі: Берілген теңдеу
гиперболалық цилиндрді анықтайды. Бұл гиперболалық
цилиндрдің  -
- = бағыттаушысы ОХУ
жазықтығында, ал жасаушысы О
= бағыттаушысы ОХУ
жазықтығында, ал жасаушысы О осіне параллель болады.
Демек, берілген теңдеу гиперболалық цилиндрді
анықтайды.
осіне параллель болады.
Демек, берілген теңдеу гиперболалық цилиндрді
анықтайды.
 сурет
1
сурет
1
№3.
 =2рх теңдеуі қандай
бетті анықтайды?
=2рх теңдеуі қандай
бетті анықтайды?
Шешуі:
 =2рх теңдеуі
кеңістікте жасаушылары О
=2рх теңдеуі
кеңістікте жасаушылары О осіне параллель болатын
бетті анықтайды. Теңдеу
осіне параллель болатын
бетті анықтайды. Теңдеу  =2рх бағыттаушысы ХОУ
жазықтығындағы жататын параболаны анықтайды.
Сондықтан
=2рх бағыттаушысы ХОУ
жазықтығындағы жататын параболаны анықтайды.
Сондықтан  =2рх теңдеуі берілген
парабола ХОУ жазықтығында, ал жасаушысы
О
=2рх теңдеуі берілген
парабола ХОУ жазықтығында, ал жасаушысы
О осіне параллель болатын
бетті анықтайды. Демек,
осіне параллель болатын
бетті анықтайды. Демек,  =2рх теңдеуі параболалық
цилиндрді анықтайды.
=2рх теңдеуі параболалық
цилиндрді анықтайды.
14
№5. Қандай
бетті  +у2
= 36
анықтайды?
+у2
= 36
анықтайды?
Шешуі:
ХОУ жазықтығындағы
жататын  +у2
= 36 теңдеуі цилиндрді
анықтайды. Бұл теңдеу кеңістікте жасаушысы
О
+у2
= 36 теңдеуі цилиндрді
анықтайды. Бұл теңдеу кеңістікте жасаушысы
О осіне параллель болатын
және бағыттаушысы 36-ға тең. Кеңістікте
осіне параллель болатын
және бағыттаушысы 36-ға тең. Кеңістікте
 +у2
= 36 теңдеуін анықтайтындығы,
яғни жасаушысы кеңістікте түзулер тік дөңгелек цилиндр
болады.
+у2
= 36 теңдеуін анықтайтындығы,
яғни жасаушысы кеңістікте түзулер тік дөңгелек цилиндр
болады.

Демек,
 +у2
= 36 теңдеуі кеңістікте тік
дөңгелек цилиндрді анықтайды.
+у2
= 36 теңдеуі кеңістікте тік
дөңгелек цилиндрді анықтайды.
 15
15
№4
 = 4у теңдеуі
кеңістікте қандай бетті анықтайды?
= 4у теңдеуі
кеңістікте қандай бетті анықтайды?
Шешуі:
 = 4у теңдеуі
кеңістікте О
= 4у теңдеуі
кеңістікте О осіне параллель
параболалық цилиндрді анықтайды.
осіне параллель
параболалық цилиндрді анықтайды.

Цилиндрлік беттік
параболасы  = 4у
,
= 4у
,  =0 теңдеулермен
анықталады.
=0 теңдеулермен
анықталады.
Демек,
беттің  = 4у теңдеуі параболалық
цилиндрді анықтайды.
= 4у теңдеуі параболалық
цилиндрді анықтайды.
№6 Бағыттаушы
гипербола  -у2
= 25,
-у2
= 25,
 =0 теңдеуімен және
құраушылары уо
=0 теңдеуімен және
құраушылары уо теңдеуімен анықталатын
цилиндрдің таңдеуін табыңыздар.
теңдеуімен анықталатын
цилиндрдің таңдеуін табыңыздар.

Шешуі:
уо бағыттаушы коэффициенті
бас нүктеден өтіп, координаталар системасының осімен
α=900,
бағыттаушы коэффициенті
бас нүктеден өтіп, координаталар системасының осімен
α=900,
 =450
бұрыш жасайды.
уо
=450
бұрыш жасайды.
уо бағыттаушы
бағыттаушы  коэффициенті
коэффициенті  ,
,
 болады. Түзудің
бағыттаушы коэффициенті бағыттаушы косинустарына пропорционал
болады.Оны мына түрде жазуға болады:
болады. Түзудің
бағыттаушы коэффициенті бағыттаушы косинустарына пропорционал
болады.Оны мына түрде жазуға болады:
n1:n:p=0: :
: =0:1:2. Сондықтан
m:n:p=0:1:1. Нәтижесінде цилиндрлік беттің
жасаушыларынан теңдеуді былайша жазуға
болады:
=0:1:2. Сондықтан
m:n:p=0:1:1. Нәтижесінде цилиндрлік беттің
жасаушыларынан теңдеуді былайша жазуға
болады:
 =
= =
=
Мұнда х,
у, - нүктелік беттің
координаталары
- нүктелік беттің
координаталары
 ,
,
 ,
,  1- бағыттаушыға тиісті
нүктелердің координаталары
1- бағыттаушыға тиісті
нүктелердің координаталары
Нәтижесінде мынадай теңдеулер алынады:
 және
және  =
= =
=
Бұл
теңдеулерден  ,
,
 тең екендігі
алынады.Осы теңдеудің мәнін сақинаның бірінші теңдеуіне қоссақ,
онда х1-
тең екендігі
алынады.Осы теңдеудің мәнін сақинаның бірінші теңдеуіне қоссақ,
онда х1- 2
2 немесе
х2-у2-
немесе
х2-у2- 2+27у-25
2+27у-25 теңдеуі
алынады.
теңдеуі
алынады.
Демек,
х2-у2- 2+27у-25
2+27у-25 теңдеуі есептің шартын
қанағаттандырады.
теңдеуі есептің шартын
қанағаттандырады.
№7 Дөңгелек цилиндрдің осі
х 9-t,
у
9-t,
у t,
t,
 t және
М0
(0;-2;3) оның бетінің нүктесі
берілген. Цилиндрлік теңдеуді табыңыздар.
t және
М0
(0;-2;3) оның бетінің нүктесі
берілген. Цилиндрлік теңдеуді табыңыздар.
Шешуі: Дөңгелек беттің
М(х,у, нүктесін алайық. Осы
нүктеден цилиндрдің осіне дейінгі қашықтық, цилиндрдің берілген
М0
(0;-2;3) нүктесіне дейінгі
қашықтыққа тең болады. Ал, М0(х0,у0,
нүктесін алайық. Осы
нүктеден цилиндрдің осіне дейінгі қашықтық, цилиндрдің берілген
М0
(0;-2;3) нүктесіне дейінгі
қашықтыққа тең болады. Ал, М0(х0,у0, нүктесін
х
нүктесін
х х1+l,t, y=y1+ m,t,
х1+l,t, y=y1+ m,t, 
 +n1t
+n1t
түрінде дейінгі қашықтық мына формуламен
d= 2+
2+ 2+
2+ 2
2

Есептелінеді. Сондықтан
d0= =
= =
= =10,
=10,
d1=
Дөңгелек цилиндрдің d0 мен d1 ұзындықтары тең болғандықтан, d0= d1 болады. Сондықтан
 =30
=30
Бұдан алатынымыз
8 -5
-5 +5
+5 -4ху+4х
-4ху+4х +8у
+8у +156х-60у-132
+156х-60у-132 -5х=0
-5х=0
Демек, дөңгелек цилиндрдің осі
х 9-t,
у
9-t,
у t,
t,
 t түзуінде берілген
және М0
(1;-1;3) нүктесінен өтетін
цилиндрлік беттің теңдеуі
t түзуінде берілген
және М0
(1;-1;3) нүктесінен өтетін
цилиндрлік беттің теңдеуі
8 -5
-5 +5
+5 -4ху+4х
-4ху+4х +8у
+8у +156х-60у-132
+156х-60у-132 -5х=0
болады.
-5х=0
болады.
№8
у2+ =9 теңдеуімен берілген бетті
анықтаңыздар.
=9 теңдеуімен берілген бетті
анықтаңыздар.

![]()
Шешуі: Берілген теңдеуде х
айнымалысы жоқ.Сондықтан бұл беттің құрылысы ох осіне параллель.
у2+ =9 теңдеуі
уо
=9 теңдеуі
уо жазықтығында жататын
центр, координаталар системасының бас нүктесінен өтетін, радиусы
3-ке тең шеңбер алынады. Ал, кеңістікте
у2+
жазықтығында жататын
центр, координаталар системасының бас нүктесінен өтетін, радиусы
3-ке тең шеңбер алынады. Ал, кеңістікте
у2+ =9 теңдеуі кеңістікте
цилиндрді анықтайды. Бұл цилиндрдің табаны
у2+
=9 теңдеуі кеңістікте
цилиндрді анықтайды. Бұл цилиндрдің табаны
у2+ =9 теңдеуімен осы беттің ох
осіне параллель түзуді анықтайды.
=9 теңдеуімен осы беттің ох
осіне параллель түзуді анықтайды.
Демек, ізденілген цилиндрлік бет ох осіне параллель орналасады екен.
№9
 =9-х2
теңдеуімен берілген бетті
анықтаңыздар.
=9-х2
теңдеуімен берілген бетті
анықтаңыздар.
Шешуі:
 =9-х2
теңдеуі ох осіне параллель,
жасаушысы цилиндрлік бетке параллель болатын фигураны анықтайды.
Оның бағыттаушысы
=9-х2
теңдеуі ох осіне параллель,
жасаушысы цилиндрлік бетке параллель болатын фигураны анықтайды.
Оның бағыттаушысы  =9-х2
теңдеуімен анықталатын бет
болады. Бұл параболаның центрі (0; 0; 4) нүктесінде
болады.
=9-х2
теңдеуімен анықталатын бет
болады. Бұл параболаның центрі (0; 0; 4) нүктесінде
болады.

№10
 -
- =0 теңдеуі қандай бетті
анықтайды?
=0 теңдеуі қандай бетті
анықтайды?
Шешуі: Берілген теңдеуді келесі түрге келтіруге болады:
( -
- )
(
)
( +
+ )
=0
)
=0
Алынған теңдеуді
( -
- ) =0
(
) =0
( +
+ )
=0
)
=0
түріне келтіруге болады.Бұл теңдеулерді
 =
= х,
х,
 =-
=- х
х
түріне келтіреді.Мұндағы теңдеулер ох осі арқылы өтетін және ОУ осі арқылы қиылысатын екі жазықтықты көрсетеді.
№10 у2 -4х-6у+17=0 бетінің түрін анықтаңыздар.
Шешуі: Берілген бетінің түрін түрлендірейік:
у2 -4х-6у+17=0
(у2 -6у+9)-4х-9+17=0
(у-3 -4х+8=0
-4х+8=0
(у-3 =4(х-2)
=4(х-2)
Енді
у-3= ,
х-2
,
х-2 жаңа координаталар
енгізсек, онда
жаңа координаталар
енгізсек, онда  2
2 теңдеуі
алынады.
теңдеуі
алынады.
Демек, берілген
у2
-4х-6у+17=0
беті  2
2 бетіне сәйкес
параболалық цилиндр болады.
бетіне сәйкес
параболалық цилиндр болады.

алынады. Осы системаның екінші
теңдеуінен  ны тауып, біріншісіне
қайтсақ,
ны тауып, біріншісіне
қайтсақ,
(
теңдеуі алынады. Тұл теңдеуден:
 2-
2- +
+ 2-
2- +
+ 2-12 УƵ-4
Ƶ2-36
2-12 УƵ-4
Ƶ2-36 +12Ƶ
+12Ƶ
Демек,
 2-12 УƵ-4
Ƶ2-36
2-12 УƵ-4
Ƶ2-36 +12Ƶ
+12Ƶ теңдеуі цилиндрдің
теңдеуін жасады.
теңдеуі цилиндрдің
теңдеуін жасады.
№11
Жасаушысы  =
= векторына параллель, ал
бағыттаушысы х2+у2
векторына параллель, ал
бағыттаушысы х2+у2 ,
,
 теңдеуімен берілген
цилиндрдің теңдеуін табыңыздар.
теңдеуімен берілген
цилиндрдің теңдеуін табыңыздар.
Шешуі: Жасаушысы
х t,
у
t,
у t,
t,
 t теңдеулерімен,
басқаша
t теңдеулерімен,
басқаша

теңдеуімен берілген.Берілген теңдеуден
х 2
t+
2
t+ ,
у
,
у 3
t,
3
t,  +4 t. Соңғы
теңдеуден
+4 t. Соңғы
теңдеуден  +4
t
+4
t
Бұдан
t
Енді
 -2
t
-2
t  t
t +
+
Енді
 ,
,  -дерді теңдеуге қисақ,
онда
-дерді теңдеуге қисақ,
онда
(х- +(у+
+(у+ болады.
болады.
Енді амалдарды орындап, сәйкес мүшелерін қоссақ, онда
х2-х(1-2)- +у2+2у(
+у2+2у(
х2+
у2+х(1-2)+( +2у(
+2у(
16х2+16у2-16-16 +4-8
+4-8 +4
+4 2-24у-24у
2-24у-24у 9-19
9-19 +9
+9 2-144
2-144
16х2+16у2-13 2-16х+24у-26у
2-16х+24у-26у -144
-144
теңдеуі шықты.Демек, есептің мәнін қанағаттандыратын теңдеу алынды.
№ 16у2-9 2+32у+54
2+32у+54 -203
-203 теңдеуі қандай бетті
анықтайды?
теңдеуі қандай бетті
анықтайды?
Шешуі: Бұл теңдеу ох осіне параллель, гиперболалық цилиндрді анықтайды. Шындығында теңдеуде х айнымалысы жоқ, ал бағыттаушы гипербола болып тұр, яғни берілген теңдеудің толық квадратын бөліп шығарамыз. Сонда
16у2-9 2+32у+54
2+32у+54 -209
-209
16у2+3у-(9 2-54
2-54 -209
-209
16(у2+2у-1-1)-9 2-6
2-6 +9-9)
-209
+9-9)
-209
16(у2+1)2-10-9 -3)2+81
-209
-3)2+81
-209
16(у2+1)2-9 -3)2
-3)2
Енді соңғы теңдеуді 144-ке бөлсек, онда
 -
- теңдеуі
алынды.
теңдеуі
алынды.
Сонда

түзеді. (0,-1; 3) нүктесінде симметриялы және нақты ось, ОУ осіне тиісті болады. Демек, алынған теңдеу гиперболалық цилиндрді анықтайды.
№17 Цилиндрлік беттің жасаушысы
о осіне параллель, ал
бағыттаушысы х2+у2+
осіне параллель, ал
бағыттаушысы х2+у2+ 2
2 сферасына
х+у+
сферасына
х+у+ жазықтық қиылысуына
цилиндр бетінің теңдеуін табыңыздар.
жазықтық қиылысуына
цилиндр бетінің теңдеуін табыңыздар.
Шешуі: Цилиндрлік беттің жасаушысы сферамен жазықтық қиылысуы берілген, яғни

Осы схеманың екінші
теңдеуінен  тауып, бірінші бірінші
теңдеуді қоссақ, онда
тауып, бірінші бірінші
теңдеуді қоссақ, онда
х2+у2+( 2
2 немесе
х2+у2+
немесе
х2+у2+
Цилиндрлік беттің жасаушысы
х2+у2+ болады.
болады.
ІІбет 198/2
Жасаушысы
о осіне параллель, ал
бағыттаушысы х2+у2+
осіне параллель, ал
бағыттаушысы х2+у2+ 2
2 сферасының
х+у+
сферасының
х+у+ жазықтық қиылысу сызығы
болатын цилиндр бетінің теңдеуін
табыңыздар.
жазықтық қиылысу сызығы
болатын цилиндр бетінің теңдеуін
табыңыздар.
Шешуі:
 шешу үшін екінші
теңдеуден
шешу үшін екінші
теңдеуден  сызықтық схемасын оны
бірінші теңдеуге қоссақ, онда
сызықтық схемасын оны
бірінші теңдеуге қоссақ, онда
х2+у2+( 2
2 немесе
х2+у2+
немесе
х2+у2+ болып
алынады.
болып
алынады.
Сонда бағыттаушы


теңдеуі алынады. Мұндағы
бірінші теңдеу  цилиндр бетінің
теңдеуі.
цилиндр бетінің
теңдеуі.
Демек,
о осіне параллель, ал
бағыттаушысы х2+у2+
осіне параллель, ал
бағыттаушысы х2+у2+ 2
2 сферасының
х+у+
сферасының
х+у+ жазықтығымен қиылысу
сызығы
жазықтығымен қиылысу
сызығы  цилиндр беті
болады.
цилиндр беті
болады.
№19.
Бағыттаушысы 

теңдеуі арқылы анықталатын
шеңбер, ал жасаушысы  векторына параллель
цилиндр беттің теңдеуін табыңдар.
векторына параллель
цилиндр беттің теңдеуін табыңдар.
Шешуі:
М нүктесімен
нүктесімен  векторының бағытымен
жүргізілген түзу бағыттауыш сызығын әйтеуір бір
N(
векторының бағытымен
жүргізілген түзу бағыттауыш сызығын әйтеуір бір
N( нүктесінде қиғанда бұны
берілген цилиндрлік бетке тән болады.Ондай түзудің
теңдеулерін
нүктесінде қиғанда бұны
берілген цилиндрлік бетке тән болады.Ондай түзудің
теңдеулерін
х +
+
у +
+
 +
+
етіп орнатуға болады.Бұл
теңдеулерді  х-
х- ,
,
 у-
у- ,
,
 -
- түрінде жазамыз. Бұл
шамалар бағыттауышы сызықтың теңдеуін қанағаттандырады. Сондықтан:
х+
түрінде жазамыз. Бұл
шамалар бағыттауышы сызықтың теңдеуін қанағаттандырады. Сондықтан:
х+ +у-
+у- +
+
Бұдан
 +
+ .
.
Сонымен,
 х-
х- ,
,
 у-
у- ,
,
 -
- .
.
Векторларға бақыттаушы сызықты
анықтаутын теңдеулер системасының екінші тең бетке қиып, іздеген
цилиндр беттің х2+у2+ 2-ху-х
2-ху-х -у
-у -
- теңдеуін
табамыз.
теңдеуін
табамыз.
Демек,
х2+у2+ 2-ху-х
2-ху-х -у
-у -
- іздеуші цилиндр беттің
теңдеуі болады.
іздеуші цилиндр беттің
теңдеуі болады.
24
Айналу беті
Берілген L осі айналу сызығы
бойынша айналып алынған бетті Ф айналып беті деп атайды. Айналу
бетінің теңдеуін алу үшін, УО о
о осіне айналдырып алып,
F(х,у)
осіне айналдырып алып,
F(х,у) теңдеуінде
у-ті
теңдеуінде
у-ті  ауыстыру
керек.
ауыстыру
керек.
Егер
Уо жазықтығында
F(у,
жазықтығында
F(у, )
) ,
х
,
х теңдеудің қисығы СХ
алынатын жазықтығы болса, онда
теңдеудің қисығы СХ
алынатын жазықтығы болса, онда
F( )
) пайда болады. Осыған
ұқсас F(
пайда болады. Осыған
ұқсас F( теңдеуі
теңдеуі
ох осін айнала қозғаған кезде пайда болады.
Айналу эллипс
сызығы  о
о осін айналып қозғалу
кезінде (эллипстың а
осін айналып қозғалу
кезінде (эллипстың а с кезде) пайда
болады.
с кезде) пайда
болады.
Сонда ол сфераға айналады.Бір қуысты айналу гиперболасында
 айналдыру кезінде пайда
болар еді.
айналдыру кезінде пайда
болар еді.
Екі қуысты айналу
гиперболасында  о
о осін айналып қозғалу
кезінде пайда болады.
осін айналып қозғалу
кезінде пайда болады.
Айналу
параболоиды  2р
2р о
о осін айналу осі
болады.
осін айналу осі
болады.
Хо жазықтығында
эллипсті
жазықтығында
эллипсті
 (1)
(1)
о осіне айналдыратын болсақ,
алынған осынау бетті айналу эллипс сызығы деп атайды. Оның
теңдеуі
осіне айналдыратын болсақ,
алынған осынау бетті айналу эллипс сызығы деп атайды. Оның
теңдеуі
 (2) деп
аталады.
(2) деп
аталады.
Эллипс сызығы ХОУ жазықтығына
параллель бір  (/
(/ айналу
теңдігі
айналу
теңдігі 
Эллипс сызығы қиық,
оны  –с-дан +с-ға дейін
ордігенде эллипсоидты сызығы шығады. 36
–с-дан +с-ға дейін
ордігенде эллипсоидты сызығы шығады. 36
Эллипсоидты координаттық
с болса,
онда
болса,
онда  ,
,

эллипсоиді шығады. Жалпы
жағдайда (а болса), эллипсоид үш
осьті эллипсоид болады, егер а
болса), эллипсоид үш
осьті эллипсоид болады, егер а болса, эллипсоидтар
қысылықты эллипсоидтар деп аталады. 37
болса, эллипсоидтар
қысылықты эллипсоидтар деп аталады. 37
 2 шеңбері ох осінен айналады.
Айналу бетінің теңдігін сфераны
табыңыздар.
2 шеңбері ох осінен айналады.
Айналу бетінің теңдігін сфераны
табыңыздар.
Шешуі: ох осінен шеңберді
айналдыру керек.ох осін өзгеріссіз қалдыру керек. Ал екінші сызықта
у-х+ -пен ауыстырып, айналу
бетінің теңдігін жазу керек, яғни
у-х+
-пен ауыстырып, айналу
бетінің теңдігін жазу керек, яғни
у-х+ ауыстырып теңдеу жазылады.
Сонда
ауыстырып теңдеу жазылады.
Сонда
 +(
+( )2
)2 2
2
 +у2
+у2 2 айналу бетінің теңдігін
алынады немесе мұны сфералық беті дейміз. Айналу бетінің
теңдеуі
2 айналу бетінің теңдігін
алынады немесе мұны сфералық беті дейміз. Айналу бетінің
теңдеуі  +у2
+у2 2 түрінде жазылады.
38
2 түрінде жазылады.
38
Айналу эллипсоиды
 эллипсоид ОУ осінен
айналып шыққан, айналу эллипс сызығының теңдеуін
жазыңыздар.
эллипсоид ОУ осінен
айналып шыққан, айналу эллипс сызығының теңдеуін
жазыңыздар.
Шешуі: Айналу бетінің теңдеуін
табу ережесіне сәйкес эллипс сызығының
теңдеуіндегі  Нәтижесінде берілген
эллипстің теңдеуіндегі х-тың орнына
Нәтижесінде берілген
эллипстің теңдеуіндегі х-тың орнына  қойылады.Сонда
қойылады.Сонда
 +
+ немесе
немесе  теңдеуіне
айналады.
теңдеуіне
айналады.
Демек,
 айналу эллипс
сызығының теңдеуі алынады. 39
айналу эллипс
сызығының теңдеуі алынады. 39
Жарты осьтері 5 пен 3 болатын эллипс, өзінің үлкен осіның бойына айналады. Үлкен осі ОУ осінде, ал эллипс центрі координаталары системасының бас нүктесінде орналасқан.Осы эллипстің ОУ осіне айналу кезіндегі бетінің теңдеуін табыңыздар.
Шешуі: Берілуі бойынша
в және
уо
және
уо жазықтығында жатыр. Оның
теңдеуі
жазықтығында жатыр. Оның
теңдеуі


Берілгені бойынша қисықтың
теңдеуі уо жазықтығында жатыр.Ал
қисық ОУ осінен айналған кезде пайда болатын бетті алу
үшін
жазықтығында жатыр.Ал
қисық ОУ осінен айналған кезде пайда болатын бетті алу
үшін 
 Сонда қисықтың
теңдеуі
Сонда қисықтың
теңдеуі
 немесе
немесе  түрінде
жазылады.
түрінде
жазылады.
Демек,
алынған  ізделінді теңдеу
болады.
ізделінді теңдеу
болады.
х-2у ,
,
 айналғанда алынатын
айналу бетінің теңдеуін табыңыздар.
айналғанда алынатын
айналу бетінің теңдеуін табыңыздар.
Шешуі: М нүктесі сызығының
төбесі дейік. Оның координатасы (4; 0;0) болады. Осы конустың кез
келген А нүктесінің координатасы  десек, оның сәйкес
негізін В (х,у,о) нүктесі болады.А мен В ның координаталары А
(
десек, оның сәйкес
негізін В (х,у,о) нүктесі болады.А мен В ның координаталары А
( В(х,у,о) болады, сонда А
мен В координата нүктесінің әртүрлі нүктесі, ал В (х,у,о)
координатасында болады. Сонда
у2
В(х,у,о) болады, сонда А
мен В координата нүктесінің әртүрлі нүктесі, ал В (х,у,о)
координатасында болады. Сонда
у2 2. Ал бұдан
Х
2. Ал бұдан
Х у
у болады.
болады.
Сонда айналу бетінің ауданы
Х+ -4
-4
Х+ -4
-4
(
 )2
)2
4( 16+8
16+8 2
2
4( (
(
Демек,
4( (
( айналу беті болып
табылады.
айналу беті болып
табылады.
№5
.х2 теңдеуі қандай бетті
анықтайды?
теңдеуі қандай бетті
анықтайды?
Шешуі: Координаталық осьтерді
ОХ осінің айналасында  бұрышқа бұрайық. Мұнда
ОУ осінен ОХ осіне қажет нақты бағытта бұрылады. Сонда
х
бұрышқа бұрайық. Мұнда
ОУ осінен ОХ осіне қажет нақты бағытта бұрылады. Сонда
х 1,
у
1,
у 1
1  1
1 ,
,
 1
1 +
+ 1
1 .Сондықтан
.Сондықтан
 ,
онда
,
онда
х 1
,
у
1
,
у (
( 1-
1- 1),
1),
 (
( 1-
1- 1)
1)
Осы мәндерді беттің теңдеулеріне қоямыз, сонда
 -
- немесе
немесе  +
+ 0
0
Демек, конустың төбесі координаталар басында, ал координаталар осі болып табылады.
№6
 2) параболасы
о
2) параболасы
о осінің бойынан бұрылады
(вращается). Теңдеуді анықтаңыздар.
осінің бойынан бұрылады
(вращается). Теңдеуді анықтаңыздар.
Шешуі: Берілген мысал о*у
жазықтығында F(х,у )
) теңдеуімен берілген.
Парабола осінің бетінен айналады. Бұл жағдайда
х
теңдеуімен берілген.
Парабола осінің бетінен айналады. Бұл жағдайда
х 1,
у
1,
у теңдігінен және мына
теңдеулермен F(
теңдігінен және мына
теңдеулермен F( )
) болады. Осы теңдік
ізделінген теңдікті анықтайды.
болады. Осы теңдік
ізделінген теңдікті анықтайды.
№7
 -
- ОУ осі бойымен айналады.
Алынған екінші ретті беттің типін
анықтаңыздар.
ОУ осі бойымен айналады.
Алынған екінші ретті беттің типін
анықтаңыздар.
Шешуі: Берілген бет ОХУ
жазықтығында, ОУ осінің бойында айнала алады. Гипербола осінен
айналу кезінде у у
у теңдігі орындалады.
Айналған кезде
теңдігі орындалады.
Айналған кезде
F( )
) орындалады.
орындалады.
Берілген есептің шарты
бойынша 
яғни,
 -
- теңдеуі
алынады.
теңдеуі
алынады.
Сонда,
 -
- алынады. Демек, бұл
теңдеу бірқуысты гипербола. 42
алынады. Демек, бұл
теңдеу бірқуысты гипербола. 42
№9
х түзуі ОƵ осі бойымен
айналады. Айналу бетінің теңдеуін
табыңыздар.
түзуі ОƵ осі бойымен
айналады. Айналу бетінің теңдеуін
табыңыздар.
![]()
![]()


 900
900
![]()
![]()
Шешуі:
х түзуінің ОƵ осі бойымен
айналуын табайық. х
түзуінің ОƵ осі бойымен
айналуын табайық. х түзуі ХоƵ жазықтығында
ОƵ осі бойымен айналғанда Ƶ өзгеріссіз қалады.Себебі, ол ОƵ осіне
байланысты.Ал екінші айнымалысы Х айналған кезде оның таңбасы оң
және теріс болып қалған Х пен У –тен квадрат түбір табу керек, яғни
сонда
түзуі ХоƵ жазықтығында
ОƵ осі бойымен айналғанда Ƶ өзгеріссіз қалады.Себебі, ол ОƵ осіне
байланысты.Ал екінші айнымалысы Х айналған кезде оның таңбасы оң
және теріс болып қалған Х пен У –тен квадрат түбір табу керек, яғни
сонда  (1) түрінде жазуға
болады. Бұл теңдікті квадраттасақ, онда теңдеу
(1) түрінде жазуға
болады. Бұл теңдікті квадраттасақ, онда теңдеу
 немесе
немесе  түрінде
жазылады.
түрінде
жазылады.
Демек,
 конустың теңдеуі
болады. 43
конустың теңдеуі
болады. 43
№8
х түзуі ОƵ осін айналады.
Айналу бетінің теңдеуін табыңыздар.
түзуі ОƵ осін айналады.
Айналу бетінің теңдеуін табыңыздар.
Шешуі:
х жазықтықта Х пен Ƶ
теңдеуге енген. Берілген теңдеуде Ƶ айнымалысы өзгеріссіз қалады.
Есепте берілуі бойынша ОƵ осі бойымен айналу осі болып тұр. Ал
теңдеудегі екінші айнымалы Х-тің өзі
жазықтықта Х пен Ƶ
теңдеуге енген. Берілген теңдеуде Ƶ айнымалысы өзгеріссіз қалады.
Есепте берілуі бойынша ОƵ осі бойымен айналу осі болып тұр. Ал
теңдеудегі екінші айнымалы Х-тің өзі  айнымалысымен алмасып
жазылуы керек. Сонда берілген теңдеу мынадай түрінде
жазылады:
айнымалысымен алмасып
жазылуы керек. Сонда берілген теңдеу мынадай түрінде
жазылады:
Бұл теңдеудің екі жағын
квадраттау арқылы  теңдеуі алынады.
Теңдеуді
теңдеуі алынады.
Теңдеуді  түрінде жазуға болады.
Бұл кезде теңдеудің төбесі координаталар сақинасының бас
нүктесінде, ал Х
түрінде жазуға болады.
Бұл кезде теңдеудің төбесі координаталар сақинасының бас
нүктесінде, ал Х Ƶ теңдеуі Ƶ бұрышының
биссектрисасы болады. Мұндағы у
Ƶ теңдеуі Ƶ бұрышының
биссектрисасы болады. Мұндағы у дегеніміз конус.... тең
конустық биссектрисасы болады.
дегеніміз конус.... тең
конустық биссектрисасы болады.
Бұл конустың осі
6 болады.
болады.
Демек,
 айналу бетінің
теңдеуі, нәтижесінде конус алынады.
айналу бетінің
теңдеуі, нәтижесінде конус алынады.
№10
 теңдеуімен берілген
параболаның ОƵ осі бойымен айналуынан пайда болған беттің теңдеуін
табыңыз.
теңдеуімен берілген
параболаның ОƵ осі бойымен айналуынан пайда болған беттің теңдеуін
табыңыз.
Шешуі: ху бетті табу үшін
теңдеудегі х-тың орнына  табу
керек.
табу
керек.  . Бұл
түзуден
. Бұл
түзуден  4х2+4у2.
4х2+4у2.
Демек, ізделінде теңдеу
-  4х2+4у2
болады.
44
4х2+4у2
болады.
44
№11 Гиперболаның ОƵ осі бойымен айналуынан алынған бірқуысты гиперболоидтың теңдеуін құрыңыздар.
Шешуі: Гиперболаның жорамал осін айналу арқылы алынған гиперболоидты табу керек. Сонымен ОƵ осін гиперболаның осі болса, онда гиперболаның теңдеуі

болады. Осы теңдеуде
х-ті  -қа ауыстырсақ, онда
бірқуысты гиперболоидтың теңдеуі
-қа ауыстырсақ, онда
бірқуысты гиперболоидтың теңдеуі
 немесе
немесе  +
+ болады.
болады.
Демек, Гиперболаны ОƵ осі бойымен айналдырғанда, шыққан бірқуысты гиперболоидтың теңдеуі
 +
+ алынады.
45
алынады.
45
Эллипсоид
Үш осьті эллипсоид
 +
+ түрінде жазылған тұйық
бет. Мұнда а, е, с – эллипсоидтың жазық
беттері.
түрінде жазылған тұйық
бет. Мұнда а, е, с – эллипсоидтың жазық
беттері.
Мұндай эллипсоидтың центрі
координаталар басында жатады.Бас осьтері координаталар осінде
жатады. Төбелері А (-а; о;о),
А2(а; о;о), В (о; -в; о),
В2( о;в;о), С (о;о; с),
С2(о;о; с) нүктелерінде жатады.
А1А2 ,
В1В2
,
В1В2 ,
С1С2
,
С1С2 нүктелері эллипсоидтың
бас диаметрлері. Координаталар жазықтықтары (1) эллипсоиды үш
эллипстің бойымен қиылысады.
нүктелері эллипсоидтың
бас диаметрлері. Координаталар жазықтықтары (1) эллипсоиды үш
эллипстің бойымен қиылысады.
ХОУ жазықтығының
теңдеуі  сондықтан
сондықтан  эллипсі,
эллипсі,
ХоƵ жазықтығының
теңдеуі  сондықтан
сондықтан  эллипсі,
эллипсі,
УоƵ жазықтығының
теңдеуі  демек,
қимада
демек,
қимада  эллипсі
шығады.
эллипсі
шығады.
Эллипсоидтың жазық беттері
а болса, онда оның радиусы
а-ға тең центрі (0,0,0) нүктесінде орналасқан сфераға ауысады. Егер
радиусы а-ға тең, ал сфераның центрі
(
болса, онда оның радиусы
а-ға тең центрі (0,0,0) нүктесінде орналасқан сфераға ауысады. Егер
радиусы а-ға тең, ал сфераның центрі
( ) нүктесінде орналасса, онда
мұндай сфераның теңдеуі
) нүктесінде орналасса, онда
мұндай сфераның теңдеуі
(х- )2+
(у-
)2+
(у- )2+
(
)2+
( -
- )2
)2 2 болады.
2 болады.
Егер
 +
+ эллипсоидына
М0(х0;у0;
эллипсоидына
М0(х0;у0; нүктесінде жанама тұйықтық
жүргізсе, оның теңдеуі
нүктесінде жанама тұйықтық
жүргізсе, оның теңдеуі

болады.
Бір қуысты гиперболоид
Бір қуысты гиперболоидтың канондық теңдеуі
 +
+
түзуінде жатады. Нақты осьтері абциссалар мен ординаталар осьтерінің координаталар осі жорамал беттерінде жатады. а, в,с - бір қуысты гиперболоидтың жарты осьтері деп аталады.
Бір қуысты гиперболоидтың координаталар жазықтықтарымен қиса, онда төменгі сызықтар пайда болады.
Егер ХОУ жазықтықтарымен
қиса,  онда
онда
 +
+ эллипсі
шығады.
эллипсі
шығады.
Егер ХОƵ жазықтықтарымен
қиса,  онда
онда
 +
+ гиперболасы
шығады.
гиперболасы
шығады.
Егер уоƵ жазықтықтарымен
қиса,  онда
онда
 +
+ гиперболасы пайда
болады.
гиперболасы пайда
болады.

Бір қуысты
гиперболоидты 
 және
және
 координаталар
жазықтықтарымен қиғанда
координаталар
жазықтықтарымен қиғанда
 ,
,
 ,
, 
теңдеулері алынады. 58
Гиперболоноид

теңдеуіндегі ОƵ осі бойымен айналдыра отырып гиперболоидтың теңдеуін құрыңыздар.
Шешуі: Гиперболоид теңдеуін түрлендірейік. Бірінші теңдеуінен х2 тауып, оны екінші теңдеудің квадратынан мына теңдеулер алынады.

алынады. Енді бұл теңдеуді мынадай
 -
- немесе
немесе 

 +
+
түрінде жазылған гиперболоидтың теңдеуі алынады.
Демек,


 +
+
бір қуысты гиперболоидтың теңдеуі болып табылады.
№12
х2+2у2+3 +2х+8у+18
+2х+8у+18 54
54 қандай теңдеу екенін
табыңдар
қандай теңдеу екенін
табыңдар
Шешуі: Теңдеудегі
х,у,  тердің толық
квадраттарын бөлсек, онда
тердің толық
квадраттарын бөлсек, онда
х2+2у2+3 +2х+8у+18
+2х+8у+18 54
54
(х2+2у2+1)-1+2(у2+4у+4)-8-3(
(х2+1)2+2(у+2)2-36 -3)2
-1-8+27-54
-3)2
-1-8+27-54
(х2+1)2+2(у+2)2-36 -3)2
-3)2

......... 36 –ға бөлсек, онда
 +
+
Бұл түзудің центрі (-1;-2; 5)
нүктесінде орналасқан. Енді тік бұрыштар координаталар
сақинасын  х+1,
х+1,  у-2,
у-2, 
 -3 формулалары арқылы
ауыстырсақ, онда
-3 формулалары арқылы
ауыстырсақ, онда  +
+ -
-
 болып, гиперболоидтың
теңдеуіне ауысады.
болып, гиперболоидтың
теңдеуіне ауысады.
Демек, берілген бет бір қуысты гиперболоидты анықтайды. 60

шағым қалдыра аласыз