ЖИ көмекші
0 / 1
Барлық 400 000 материалдарды тегін жүктеу үшін
Ұнаған тарифті таңдаңыз
Айлық
Жылдық
1 - күндік
Танысу 690 ₸ / 1 күнге
Таңдау
UstazTilegi AI - ЖИ арқылы тегін ҚМЖ, БЖБ, ТЖБ, тест, презентация, авторлық бағдарлама т.б. 10 материал жасау
Материалдар бөлімі - Барлық 400 000 материалдарды тегін 30 материал жүктеу
Аттестация ПББ тестеріне доступ аласыз шексіз
Жеке ҚМЖ бөлімінде - дайын ҚМЖ-ларды, презентацияларды жүктеу5 файлды тегін жүктеу
Олимпиада, турнир, байқауларға 50% жеңілдік
1 - айлық
Стандарт
2990 ₸ / айына
UstazTilegi AI - ЖИ арқылы тегін ҚМЖ, БЖБ, ТЖБ, тест, презентация, авторлық бағдарлама т.б. жасау 30 материал жасау
Материалдар бөлімі - Барлық 400 000 материалдарды тегін 900 материал жүктеу
Аттестация ПББ тестеріне доступ аласыз шексіз
Жеке ҚМЖ бөлімінде - дайын ҚМЖ-ларды, презентацияларды жүктеу 150 файлды тегін жүктеу
Жинақталған ҚМЖ бөлімінде 10 файлды тегін жүктеу
Олимпиада, турнир, байқауларға 50% жеңілдік
Іс-шаралар (мини-курстар, семинарлар, конференциялар) тегін қатысу
1 - айлық
Шебер 7990 ₸ / айына
Таңдау
UstazTilegi AI - ЖИ арқылы тегін ҚМЖ, БЖБ, ТЖБ, тест, презентация, авторлық бағдарлама т.б. жасау 150 материал жасау
Материалдар бөлімі - Барлық 400 000 материалдарды тегін 900 материал жүктеу
Аттестация ПББ тестеріне доступ аласыз шексіз
Жеке ҚМЖ бөлімінде - дайын ҚМЖ-ларды, презентацияларды жүктеу 300 файлды тегін жүктеу
Жинақталған ҚМЖ бөлімінде 50 файлды тегін жүктеу
Олимпиада, турнир, байқауларға 50% жеңілдік
Іс-шаралар (мини-курстар, семинарлар, конференциялар) тегін қатысу
Назар аударыңыз!
Сіз барлық мүмкіндікті қолдандыңыз.
Қалған материалдарды ертең жүктей аласыз.
Ок
Материалдың қысқаша нұсқасы
Эллипсоид
Үш осьті эллипсоид
+
түрінде жазылған тұйық
бет. Мұнда а, е, с – эллипсоидтың жазық
беттері.
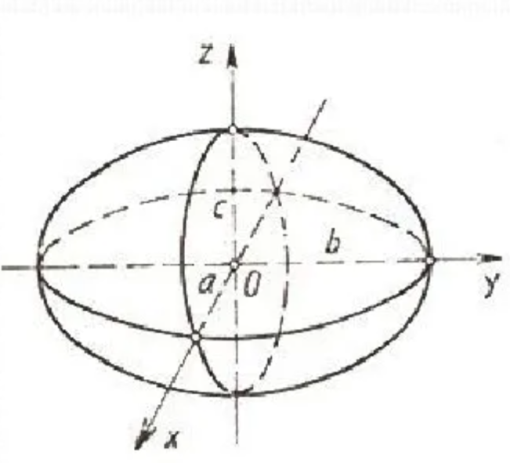
Мұндай эллипсоидтың центрі
координаталар басында жатады.Бас осьтері координаталар осінде
жатады. Төбелері А (-а; о;о),
А2(а; о;о), В (о; -в; о),
В2( о;в;о), С (о;о; с),
С2(о;о; с) нүктелерінде жатады.
А1А2
,
В1В2
,
С1С2
нүктелері эллипсоидтың
бас диаметрлері. Координаталар жазықтықтары (1) эллипсоиды үш
эллипстің бойымен қиылысады.
ХОУ жазықтығының
теңдеуі 
сондықтан 
эллипсі,
ХоƵ жазықтығының
теңдеуі 
сондықтан 
эллипсі,
УоƵ жазықтығының
теңдеуі демек,
қимада 
эллипсі
шығады.
Эллипсоидтың жазық беттері
а
болса, онда оның радиусы
а-ға тең центрі (0,0,0) нүктесінде орналасқан сфераға ауысады. Егер
радиусы а-ға тең, ал сфераның центрі
(
) нүктесінде орналасса, онда
мұндай сфераның теңдеуі
(х-
)2+
(у-
)2+
(
-
)2
2 болады.
Егер
+ эллипсоидына
М0(х0;у0;
нүктесінде жанама тұйықтық
жүргізсе, оның теңдеуі
болады.
Жүктеу
ЖИ арқылы жасау
ЖИ арқылы жасау
Бөлісу
1 - айлық
Материал тарифі-96% жеңілдік
00
05
00
ҚМЖ
Ашық сабақ
Тәрбие сағаты
Презентация
БЖБ, ТЖБ тесттер
Көрнекіліктер
Балабақшаға арнарлған құжаттар
Мақала, Эссе
Дидактикалық ойындар
және тағы басқа 400 000 материал
Барлық 400 000 материалдарды шексіз
жүктеу мүмкіндігіне ие боласыз
жүктеу мүмкіндігіне ие боласыз
1 990 ₸ 49 000₸
1 айға қосылу
Материалға шағымдану
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Жариялаған:
Мавленова Мапуза Ануаровна
16 Қырқүйек 2024
224Шағым жылдам қаралу үшін барынша толық ақпарат жіберіңіз
Эллипсоид
Тақырып бойынша 11 материал табылды
Эллипсоид
Материал туралы қысқаша түсінік
Эллипсоид
Материалдың қысқаша нұсқасы
Эллипсоид
Үш осьті эллипсоид
+ түрінде жазылған тұйық
бет. Мұнда а, е, с – эллипсоидтың жазық
беттері.
Мұндай эллипсоидтың центрі
координаталар басында жатады.Бас осьтері координаталар осінде
жатады. Төбелері А (-а; о;о),
А2(а; о;о), В (о; -в; о),
В2( о;в;о), С (о;о; с),
С2(о;о; с) нүктелерінде жатады.
А1А2 ,
В1В2 ,
С1С2 нүктелері эллипсоидтың
бас диаметрлері. Координаталар жазықтықтары (1) эллипсоиды үш
эллипстің бойымен қиылысады.
ХОУ жазықтығының
теңдеуі сондықтан эллипсі,
ХоƵ жазықтығының
теңдеуі сондықтан эллипсі,
УоƵ жазықтығының
теңдеуі демек,
қимада эллипсі
шығады.
Эллипсоидтың жазық беттері
а болса, онда оның радиусы
а-ға тең центрі (0,0,0) нүктесінде орналасқан сфераға ауысады. Егер
радиусы а-ға тең, ал сфераның центрі
( ) нүктесінде орналасса, онда
мұндай сфераның теңдеуі
(х- )2+
(у- )2+
( - )2 2 болады.
Егер
+ эллипсоидына
М0(х0;у0; нүктесінде жанама тұйықтық
жүргізсе, оның теңдеуі
болады.
Жүктеу Бөлісу
ЖИ арқылы жасау
Файл форматы:
docx
16.00.2024
224
Жүктеу
ЖИ арқылы жасау
Жариялаған:
Бұл материалды қолданушы жариялаған. Ustaz Tilegi ақпаратты жеткізуші ғана болып табылады. Жарияланған материалдың мазмұны мен авторлық құқық толықтай автордың жауапкершілігінде. Егер материал авторлық құқықты бұзады немесе сайттан алынуы тиіс деп есептесеңіз,
шағым қалдыра аласыз
шағым қалдыра аласыз
