«ФИЗИКА ЕСЕПТЕРІН ШЫҒАРУДЫҢ ТӘСІЛДЕРІ МЕН ӘДІСТЕМЕСІ»
Әдістемелік құрал
Әдістемелік құралды “Алматы облысы білім басқармасының Еңбекшіқазақ ауданы бойынша білім бөлімі” мемлекеттік мекемесінің “Жамбыл атындағы орта мектебі” мемлекеттік мекемесінің педагогикалық кеңесінің шешімімен баспаға ұсынылған
Абықан Ақбота Бақтығалыйқызы
«Физика есептерін шығарудың тәсілдері мен әдістемесі» әдістемелік құрал. Алматы облысы білім басқармасының Еңбекшіқазақ ауданы бойынша білім бөлімі” КММ -43 бет, -2025 ж
Ұсынылып отырған «Физика есептерін шығарудың тәсілдері мен әдістемесі» әдістемелік құрал физика есептерін шығару білім алушылардың оқу материалдарын саналы түрде терең игеруіне қолайлы жағдай туғызады, олардың алған білімдерін пайдалана білу қабілетін қалыптастырады және бекітеді. Сонымен қатар, есептерді шығару білім алушылардың өздігінен ойлануын, қиыншылықтарды жеңуге деген жігерін және табандылығын арттыру құралдарының бірі болып есептелініп, оқу процесін жақсарта түседі.Есеп шығару – оқу үрдісінің бөліп алуға болмайтын бір бөлігі болып табылады. Себебі, ол физикалық ұйымдарды қалыптастыруға білім алушылардың физикалық құбылыстарды ойлау қабілетін дамытуға, оны практикада қолданып білуге үйретеді.Физикалық теорияны үйренуде оның мағынасын терең түсініп қолдану жолдарын іздестіруде білім алушыларға жаттығу ретінде класта,үйлерінде өз бетінше түрлі есептер шығарудың мәні ерекше.Әдістемелік құрал орта мектепте өткізілетін таңдау курстарына пайдаланумен қатар, теориялық және практикалық деңгейі жағынан физика пәні мұғалімдеріне көмекші құрал бола алады.
Әдістемелік құрал физика пәнінен сабақ беретін мұғалімдерге, әдіскерлер мен физика сүйер көпшілік қауымға арналған.
Кіріспе
Есеп шығару физиканы оқыту процесінің ұдайы бөлінбес құрамды бөлігі болып саналады, өйткені ол физика сабақтарының түгелдей барлық түрлері мен кездерінде және кластан тыс жұмыстарында кездеседі. Есеп шығару, физиканы оқытудың әдістері, тәсілдері, амалдары ретінде әр жақты мағынада қолданылады. Физика есептерін шығару білім алушылардың оқу материалдарын саналы түрде терең игеруіне қолайлы жағдай туғызады, олардың алған білімдерін пайдалана білу қабілетін қалыптастырады және бекітеді. Сонымен қатар, есептерді шығару білім алушылардың өздігінен ойлануын, қиыншылықтарды жеңуге деген жігерін және табандылығын арттыру құралдарының бірі болып есептелініп, оқу процесін жақсарта түседі.
Есеп шығару – оқу үрдісінің бөліп алуға болмайтын бір бөлігі болып табылады. Себебі, ол физикалық ұйымдарды қалыптастыруға білім алушылардың физикалық құбылыстарды ойлау қабілетін дамытуға, оны практикада қолданып білуге үйретеді.Физикалық теорияны үйренуде оның мағынасын терең түсініп қолдану жолдарын іздестіруде білім алушыларға жаттығу ретінде класта,үйлерінде өз бетінше түрлі есептер шығарудың мәні ерекше.
Физика есептерінің түрлері де, оларды шығарудың тәсілдері де көп.Есепті шығару - күрделі процесс. Білім алушылар есептерді тақырып бойынша шығара алмайтын болса, ол физиканы терең түсіне алмайды. Сондықтан оқу программасын меңгеру үшін физикалық есеп жаттығулар керек- ақ.
Физика есептерін шығару үшін теорияны терең түсініп,іс жүзінде практикада пайдалана білуі керек, терең ойланып күрделі мәселелерді, құбылыстарды талдап, зерттеп шеше алатындай болуы керек. Есептерді шығару кезінде білім алушылар көптеген құбылыстардың заңдарын анықтайды, теорияның мағынасын терең түсініп, өмірдегі ролін көреді, техниканың жаңалықтарымен танысады, олардың физикалық негіздерін анықтайды, жалпы білімдерін көтереді, политехникалық тәрбие береді.
Есеп шығару кезінде білім алушылар физикамен бірге өздерінің математикалық дайындықтарын тереңдетеді. Физика есептері математиканы жандандырады, оның мағынасын артырады, оны шығаруда білім алушылар түрлі электрондық есептеу машиналарымен жұмыс істеп, есептеу техникасын үйренеді.
Әрбір сабақта жеке білім алушылардың қабілеттерін ескерген жөн. Физикаға ереже қызығатын білім алушылар үшін үйірмелер ашып, олардың қаблеттерін жетілдіре түсіп, қиын есептерді ұсынып шығарту және де оларды физикалық олимпиадаларға қатыстыру керек.
Физика есептерін шығару әдістерін қарастыру алдында, қазіргі кезде қолданылып жүрген есеп шығарудың жалпы метадикасына тоқталайық.
1.Есептің шартымен танысу.
Есепте қарастырылып отырған мәселелерді толық ұғынып,қойылған сұрақтарды анық түсінуі керек. Есептің шартына байланысты берілген шамаларды, сұрақтарды, қосымша тұрақтыларды таңбалап жазу керек.Экспирменттік есеп болса, қажетті құрал - жабдықтарды алдын - ала түгелдеп, жұмыстың күйін тексеріп алу керек.
2.Есептің мазмұнын талқылау.
Есептің шартында берілген процестердің құбылыстардың қандай заңдарға бағынатынын анықтап,ол заңдарды сипаттайтын формулаларды жазу керек. Құбылыстар арасындағы байланыстарды анықтау қажет.Координаталар систамасын ыңғайлы етіп алып,секторлы шамалардың бағыттарын, кеңістіктегі орнын анықтау керек. Есепті талдау үшін мүмкін болған жағдайда оқиғаның суретін салу, оның графигін сызу керек.
3.Есепті жалпы түрде шығару керек.
Есептің сұрауларына талдау беретін, проблеманы анықтайтын теңдеуді жалпы формула түрінде қорытып шығару керек. Барлық уақытта осылау шығару міндет емес, кейде есепті бөлшектеп, есептеулерді жүргізіп шығарған ыңғайлы болады.
4.Есептеу.
Есепте берілген шамалардың барлығын ХБЖ өлшемдеріне келтіріліп, қорытып алынған жалпы формулаға шамалардың сандық мәндерін қойып,математикалық есептеулер жүргізу керек. Мүмкіндігі болса, арифметикалық жұмысты микрокалькуляторларда, есетеу машиналарында жүргізген жақсы.
5.Есептің жауабын тексеру.
Есептің жауабы шындыққа жақын болуы тиіс.Көп жағайда сандық мәннің шамасы есептің дұрыс шықпағандығын анықтауға мүмкіндік береді.Мысалы кез келген дене жылдамдығы жарықтың вакумдағы таралу жылдамдығынан артық бола алмайды.
Білімді игерудің нәтижелілігі таным үдерісіне адамның әртүрлі сезім мүшелерінің іске қосылуы және нақты заттар мен құбылыстарға бетпе-бет келгенде оны сезіну, көре білу және қабылдау арқылы артады. Бұл жағдайда физикалық эксперименттің маңызы зор.
Физикалық құбылыстардың негізін ұғыну, түсініктерді, теорияны игеру процесі әр білім алушыларда бірдей жүрмейді. Оқыған материалды біреулер тез игереді, енді біреулеріне ой қорытуына және есіне сақтауына көп уақыт қажет. Үйде білім алушылар әрқайсысы өз қарқынымен жұмыс істейді. Үй тапсырмасы дұрыс ұйымдастырылса сабақ кезіндегі алған білімдерін бекітуге және тереңдетуге көмектеседі. Үйге берілген бақылаулар мен тәжірибелердің қорытындылары, есептердің шешімі, шығармашылық тапсырмалардың орындалуы білім алушылардың үй жұмыстарына арналған дәптерлеріне жазылады. Үй жұмысының қорытындылары туралы мәліметтер жазу білім алушылардың өз ойын сауатты және қысқаша жеткізуге үйретеді. Сонымен қатар жазу мәдениеті, яғни белгілі жүйе, нақтылық пен реттілік қалыптасады. Үйдегі тәжірибелерді және бақылауларды баяндау оқушыға көргенін терең ойлауға, негізгіні ажырата білуге үйретеді. Эксперименттік есептерді шешу тәсілдері оларды шешудегі эксперименттік жұмыстың қойылуына тәуелді.
Физика сабақтарында есептер шығару білім алушылармен жұмыс жасау барысында әрбір мұғалімнің негізгі әдістемесінің құраушысына айналуы керек. Себебі, қазіргі заман талабына сай, білім алушыларды техникалық бағыттағы пәндерге атап айтқанда физика саласына бағыттау ең басты қажеттілік болып табылады.
ФИЗИКА БОЙЫНША ЕСЕП ШЫҒАРУДЫҢ ТИІМДІ ӘДІСТЕМЕСІН ҚҰРАСТЫРУДЫҢ ЗАМАНАУИ ТӘСІЛДЕРІ
«Қазіргі заманғы жастарға
ақпараттық технологиямен байланысты әлемдік стандартқа сай мүдделі
жаңа білім беру өте қажет»
Н.Ә.Назарбаев.
Қазақстан Республикасының «Білім туралы» Заңының 8 – бабында «Білім
беру жүйесінің басты міндеті – оқытудың жаңа технологияларын
енгізу, білім беруді ақпараттандыру, халықаралық коммуникациялық
желілерге шығу, ұлттық және жалпы адамзаттық құндылықтар, ғылым мен
практика жетістіктері негізінде жеке тұлғаны қалыптастыруға,
дамытуға және кәсіби шыңдауға бағытталған білім алу үшін қажетті
жағдайлар жасау» – деп атап көрсеткендей, қазіргі кезеңде әрбір
мұғалімнің алдына қойып отырған басты міндеттерінің бірі – оқытудың
әдіс – тәсілдерін үнемі жетілдіріп отыру және жаңа педагогикалық
технологияны меңгеру. Ал білім беру жүйесінің алдындағы жаңа
міндеттердің бірі инновациялық педагогикалық оқыту технологияларын
пайдаланып білім сапасын арттыру.
Жаңаша оқытудың «Кембридждік» жүйесі бойынша балаларға білім дайын
күйінде берілмейді, керісінше оқушылардың өздерін еркін ұстауға,
ойлануға мүмкіндік жасалады. Олар өз беттерімен және өзара
әрекеттесе оқып-үйреніп, ортақ бір шешімге келуге бағытталады.
Сондықтан да қазіргі таңдағы әрбір ұстаздың да, оқушының да
іс-әрекеті ерекше шығармашылық сипатта болуы керек.
Бағдарламаның мақсаты – оқушылар өздерінің қалай оқу керектігіне
назар аудара отырып, олардың өз ойлары мен дәлелдемелерін нақты
жеткізе алатын, яғни ойға жүйрік, тілге шешен, әрі жазбаша түрде
еркін, көркем бейнелеп жазуға төселген, бірнеше тілді қатар
меңгерген бәсекеге қабілетті жан-жақты жетілген жеке тұлға
қалыптастыру болып табылады.
Ондай «тұлға» болашаққа сенімді, ынталы, сыни пікір көзқарастары
жүйелі дамыған, қазіргі сандық технологияларды, өмірде өз білімін
қалыптан тыс жағдайда да еркін әрі терең пайдалана білетін жан
болуы тиіс.
Әлеуметтік –сыдарлылық тұрғыдан оқытуды түсну /Выготский, 1978;
Вуд, 1998 / мұғалімдерге арналған нұсқаулығында айтылғандай «Оқыту
мен оқытудағы жаңа тәсілдер» негізінде жатыр. Балалар өзінің
түсінігін өзіндік зерттеулері мен әлеуметтік өзара байанысқа сәйкес
құратын белсенді білім алушылар болып табылады.
Осы орайда «Кембридждік» әдіс-тәсілдер мен заманауи педагогикалық
технологияларды тиімді қолдану жолында әріптестерім де атсалысуда.
Әр сабақтың тиімді әрі нәтижелі өту үшін әр ұстаз өз шығармашылығын
дамыту мен ізденіс үстінде.
Мотивация тудыру немесе қызығушылық ояту
Үйренушінің оқуға, үйренуге деген ықылас- ынтасы, ниеті мен зауқы
болмаса, оқу нәтижксінің мардымды болуы екіталай. Француз жазушысы
Анатоль Франц кезінде «тамақ тек зор тәбетпен ішкенде ғана сіңеді»
деген екен. Оқу мотивациясы дегеніміз деп осы осы сияқты білімге,
білуге, үйренуге деген «тәбет».
Топтық жұмыс, біріншіден,
оқушыларға бірігіп жұмыс істеу мүмкіндігін тудырады. Екіншіден,
ұйымшылдыққа тәрбиелейді. Үшіншіден, бірін-бірі оқытуға,
бірінен-бірі үйренуге жағдай жасайды. Бұл әдіс сонымен қатар топ
болып ынтымақтастықпен бірігіп жұмыс жасауға,ойын еркін ортаға
салуға, бірінен- бірі үйренуге септігін тигізді. Яғни, топтық жұмыс
оқушылар арасында әлеуметтік өзара қарым-қатынасты, тиімді араласу,
проблемаларды шешу және топ ішінде шығарманы жан-жақты талдауға
көмектеседі.
Топтық жұмыстың тиімділігі:
• Оқушылар өзара достық қатынаста болады;
• Бір-бірінен сұрай отырып білімдерін жетілдіреді
• Өзгелерге ойын жеткізу үшін өз шешімін дәлелдеп үйренеді;
• Менен сұрап қалады-ау деп қорықпайды,топ болып жауап береді;
• Оқушылардың мектепке деген көзқарасы өзгереді. Уақыттары қызықты
әрі тиімді өтеді.
• Топтық жұмыста бос отыратын оқушы
болмайды.
Ғылыми зерттеу нәтижелері
сабақта диалогтің маңызды рөл атқаратынын көрсетті. Мерсер мен
Литлтон (2007) өз еңбектерінде диалог сабақта оқушылардың
қызығушылығын арттырумен қатар олардың білім деңгейінің өсуіне үлес
қосатындығын атап көрсетеді. Мерсердің зерттеуіне сәйкес,
әңгімелесу оқушылардың білім алуының ажырамас бөлшегі болып
табылады және әңгімелесудің үш түрі бар,олар:
-Әңгіме-дебат барысында;
-Топтық әңгіме барысында;
-Зерттеушілік әңгіме жүргізілу үстінде байқалады екен.
«Диалогті оқыту арқылы оқушылардың қызығушылығын арттыру, олардың
білім деңгейін көтеру, сөйлеу мәдениетін қалыптастыру. Балаға
күштеп білім беруден гөрі, баланың білімге деген құштарлығын ояту
ең маңызды мақсат» деп К.Д.Ушинский айтқандай баланың білім алуға
деген құштарлығын ояту үшін мұғалім көп ізденіп, сабақтың тиімді
өтуіне жұмыс жасап, сабақ барысында оқудың белсенді әдістері,
диалогтік оқыту және оқу әдісін қолдануда білім сапасын арттыруға
көп көмегін тигізеді деп ойлаймын. Оқушылар диалог әдісін қолдана
отырып, білімді бірлесіп құру, талқылау, түсіну мен дағдыларды
қалыптастыру арқылы білім алады. Әр сабағымда оқушыларға сұрақтар
қою арқылы, тақырып бойынша өз ойларын ашық, еркін айтуға мүмкіндік
бердім. Өзара талқылау арқылы, түрлі ойлардың болатындығын, бір
бірінің түсінуіне көмектесетінін көрсетсе, сұхбаттасу арқылы өз
ойларын дәлелдеуге тырысты. Бұл оқушылардың қандай деңгейде екенін
түсінуге көмектеседі. Біз көбінесе диалогтік оқытуды сұрақ – жауап
ретінде қолданамыз. Яғни, бала теорияны меңгерумен қатар тәжірибе
жүзінде де қалай жасау қажеттігін ұғынуы керек. Тәжірибелік жұмыс
жасау барысында көптеген сұрақтар туындайды. Оқушылар өзара
пікірлер мен болжамдар айта отырып, бірлесе жұмыс жасайды. Жұмыс
жасау барысында оқушыларға көптеген сұрақтарды қоюға болады.
Мысалы, кез келген сабақтың басталуы сұрақ – жауаптан тұрады.
Сұрақтардың берілуіне байланысты оқушының пәнге деген қызығушылығын
арттыруға болады. Оқушы мен мұғалім арасында жақсы қарым-қатынас
орнайды. Диалогтік оқыту оқушы мен оқушы арасында да туындауы
мүмкін. Мұнда оқушылар бір-біріне сұрақтар қояды. Бір-бірінің
жауабына қанағаттанбаса, қосымша да сұрақтар беруі
мүмкін.
Оқу процесінде қолдануға
тиімді ойындардың маңызды түрлерінің бірі:
1. Рөлдік ойындар
2. Іскерлік ойындар
3. Имитациялық ойындар
Рөлдік ойындар –тиімді интербелсенді әдістердің бірі. Педагогика
саласында зерттеу жүргізетін ғалымдардың басым көпшілігі
оқу/оқутудың ойын әдістердің кәсіби дамыуды қамтамассыздандырудағы
ең тиімді әрі болашағы зор тәсілдер деп есептеледі. Өйткені
іс-әрекет арқылы үйрену/үйрету –танымның тиімді тәсілі екендігі
баршаға аян; адамның жадында бірінші мезетте өзінің жасағаны мен
бастан кешкен әсерлері қалады. Ал рөлдік ойындар оқушылардың
өздерін басқа адамдардың орнына қойып, мәселе немесе проблеманы
солардың тұрғысынан қарастырып, шешімді өз «қолдарымен» жасауды
меңзейді. «Ойын» сөзі сабақта инсценировканың орын алып,
әрекеттердің спектакль түрінде көрсетілетіндігін меңзейді.
Іскерлік оқу ойындарында қандайда бір сценарий ауқымында рөлдерді
өзара бөлісіп зерттеу жұмыстарын жүргізу және деректерді талдау
арқылы нақты практикалық мәселелерді бірлесе отырып шешеді. Оқу
ойындарының сценарийлері тақырып ауқымында болып, күрделі
мәселеерді ойын тұрғысынан «ойнап» шешуге ағытталады.
Имитациялық ойындар дегеніміз адамдардын қалыптан тыс /экстремалды/
жағдайлардағы әрекетерін анықтайтын өмір сүру ортасынан үлгісін
/модель/ құру. Мұндай жағдайлар қатарына «жан-жал», «әуе апаты»,
«жер сілкінісі» «жау тылында», «робинзон»секілді оқиғаларды
жатқызуға болады.
«Алдын ала берілген атаулар» –
сабақ басында жаңа тақырып бойынша тақтаға бірнеше атау /терминдер/
жазып қойып, оқушыларға олардың мағынасы, мақмұны және өзара
қатынасы мен байланысы туралы ойлануы керек. Бұл жұмысты оқушылар
жеке, жұппен нмесе шағын топ ішінде ауызша яки жазбаша /соңғысы
тиімдірек/ орвндауы иқтимал. Содан кейін бірнеше оқушының ойы мен
пікірі тыңдалады.
«Үш қадамды сұқбат»-тақырып бойынша оқушылардың бір-бірінен
кезектесіп интервью алу тәсілі. Бұл тәсіл «Сұрақ қою, қайтадан
сұрақ қою»
Тәсіліне ұқсас, алайда мұнда басты назарды жауапқа аудару
керек.
«Төрт сөйлем тәсілі» – сабақ
соңында қушылар өздерінің түсінік және жұмыс жасау деңгейлерін
бағалау үшін мынадай тапсырмаларды орындайды:
1 пікір.
Мәтін бойынша туындаған өзіндік пікірін /негізгі идеясын/ бір
сөйлеммен келтіру керек.
2. дәлел.
Келтірілген өзіндік пікірі бар сөйлеммен дәлелдеп шығу керек. Дәлел
дегеніміз ұстанған көзқарасты логикалық тұрғыдан дәйектеу,
негіздеу.
3.Мысал.
Енді келтірілген өзіндік пікірді тағыда бір негізден кету үшін бір
сөйлеммен мыса келтіру қажет. Мысал, өмірден, практикадан алынуы
керек; ақпарат көздеріне немесе көп тараған пікірлерге сілтеме
жасау, практикада орын алған үрдіс, басқа адамдардың пікірі;
4.Қорытынды.
Есеп шығару – оқыту үрдісінің маңызды элементы. Есептер қандай да бір нақты жағдайларда болып өтетін құбылыстарға физикалық заңдарды қолдануды талап ететін жаттығулар үшін материалдар береді. Сондықтан есептердің оқушылардың білімін нақтылауда, жалпы заңдардың түрлі көрінісін көруде үлкен маңызы бар. Мұндай нақтылаусыз білімнің практикалық маңызы болмайды. Есептер шығару физикалық заңдарды тереңірек және берік меңгеруге, логикалық ойлаудың дамуына ықпал етеді, оқушылардың қызығушылығыноятады, өзіндік жұмыс дағдыларын игеруге көмектеседі, әрі өзіндік ой қорытудың бірден-бір құралы болып табылады. Физикалық есептердің мазмұны оқушылардың табиғат пен техника жөніндегі білім шеңберін кеңейтеді. Сондай-ақ, есептер шығару – қайталаудың, пысықтаудың, оқушылардың білімін тексерудің маңызды құралы.
Физикалық есептерді шығару әдістемесі
Есеп шығару әдістемесі есептің мазмұнына, оқушылардың дайындығына, олардың алдына қойылған міндеттерге т.с.с. тәуелді. Дегенмен де көптеген есептерді шығару барысында жеткілікті көңіл бөлетін жағдайлар бар.
VII – XI сыныптар аралығында оқушылар шамамен 170 негізгі формуланы оқып-үйренеді. Әр формулада кем дегенде үш шама болатынын ескерсек, әрбір оқушы негізгі заңдылықтарға арналған бірнеше жүздеген есептердің типтерін меңгеруі тиіс.
Физикалық есептер шығарудағы анализдік – синтездік әдіс
Анализдік – синтездік әдіс – орта мектептің барлық сыныптарындағы физика есептерін шығарудаңы негізгі әдіс. Оқу процесінде оны ойдағыдай қолдану оқушыларға есептің шешуінің дұрыс жолын табуына жол ашып, олардың логикалық ойлауының дамуына септігін тигізеді.
Физикадан әдістеме құралдарында талдау (анализ) мен синтез екі тәуелсіз әдістер ретінде жиі қарастырылады. Алайда бұлай бөлуді дәл сол мағынасында түсінуге болмайды.Синтез бен анализ есептердің шығаруда, ойлау процесіндегі индукция және дедукция сияқты бөлінбейді. Физикалық есептерді шығарғанда анализ бен синтезді қолдану бірге алынады, яғни практикада анализдік әдіс қолданылады.
Бұл әдіспен есептің сұрағынан бастап, анализ жолымен шығарғанда, оны шығару үшін не істеу қажеттігін айқындайды және біртіндеп күрделі есепті жай есептер қатарына жіктей келе, шартында берілген белгілі шамаларға дейін жетеді.
Одан кейін синтез көмегімен пайымдауды кері тәртіпке жүргізеді: белгілі шамаларды пайдалана отырып, бірқатар амалдарды жүргізіп барып, нәтижесінде белгісізді табады.
Сапалық есептерді шығару әдістемесі
Оқушыларды сапалық есептерді саналы шығару дағдысын тәрбиелеу үшін, мұғалімнің белгілі бір жүйесі және ойластырылған оқыту әдістемесі болуы керек. Есепті дұрыс таңдаудың маңыздылығы да аз емес. Есептің алғашқы кездерінде оқушылардың өз тәжірибесінен белгілі құбылысқа немесе фактілерге түсінік беруі жүйелі енгізілсе, оқушылар өмірімен байланысты көреді. Ұсынылатын есептердің танымдық және тәрбиелік мағынасы артады.
Оқушылардың политехникалық ой өрісін кеңейту мақсатында 7-сыныптан бастап-ақ есептің шартына оқушылар үшін жаңа деректерді, техникалық мәліметтерді енгізген дұрыс. Есептерді таңдап алуда мектептің айналасындағы өндірістің сипатын және жергілікті жағдайларды ескерудің маңызы үлкен.
Сапалық есептердің шығару негізінен үш кезеңнен тұрады: шартын оқу, есепті талдау және шешу.
Есеп мазмұнын талдау кезінде ең алдымен оқушылар берілген тақырыптағы белгілі ортақ заңдылықтарды пайдаланады: осыдан кейін есептегі айтылған құбылыс қалай нақты түсіндіріулі керек екенің айқындайды. Сапалық есептерге шарттың талдауы негізделген керекті жауаппен тығыз байланысты.
Сандық есептерді шығару әдістемесі
Сабақта күрделі сандық есептерді шығару әдетте мына элементтерден құралады: есептің шартын қысқаша жазу және оны қайталау, суретін, схемасын жәнесызбасын салу, есептің физикалық мазмұның талдау және шығару жолдарын (тәсілдерін) айқындау, шешу жоспарын құру және жалпы түрдегі шешуін орындау, шамалау және есептеулер, нәтиженің талдауы және шешуін тексеру.
Күрделі есептерді шығарудың келтірілген схемасы оқушылардың оның мазмұны мен шешу барысын біртіндеп жан-жақты ойластырудын қамтамасыз етеді.
Келтірілген схема үлгі ретінде алынған. әрбір есепті шығарған сайын барлық жалпы түрде үнемі орындай бермейді; сұрақ – есептердің шығарған кезде есептеулердің қажеттігі болмайды.
Күрделі есепті шығару әдістемесінің кейбір кезеңдеріне қысқаша тоқталайық .
Есептің шартың оқу. Текст анық, мәнерлі, асықпай оқуылуы тиіс. Есептің шартын оқыған соң, мұғалім жаңа терминдердің, қиын ұғымдардың мағынасын (қажет болған жағдайда) түсіндіреді. Кейде мұғалім оқушылардың жаңа терминдерді олардың қалай түсінетінін өздеріне түсіндіруді ұсынады. Талқылау нәтижесінде дұрыс түсінікке келеді. Осыдан кейін есептің шартының қысқаша жазылуын орындайды.
Есеп шартының қысқаша жазылуы. Есептің толық мәтінің тақтаға да, оқушылардың дәптеріне де, әдетте толық жазбаған жөн.
Есептің шартын қайталау. Есептің шартының қысқаша жазылуы бойынша оқушылар оны қайталайды. Оқушылар есепті біле ме, оның шартын дұрыс түсіне ме, соны айқындау мақсатында есеп шартын қайталау ұсынылады. Ол үшін мұғалім кейбір оқушыларға оның мағынасын дәл жеткізе отырып, есеп шартының мазмұнын қайталауды ұсынады.
Осыдан кейін мұғалім, есептің шартын толық мағынасында түсінгендеріне көз жеткізу үшін, оқушыларға бірнеше сұрақтар қояды. Осыған байланысты оқушылар есепті шығару үшін суреттерді (схемаларды, сызбаларды) және кестелік мәліметтерді пайдалану қажет пе, соны анықтайды.
Сызбаны, схеманы, суретті орындау. Көп жағдайларда есептерді шығарғанда сызбалар, схемалар, суреттер пайдаланылады. Бұл есептің шартын түсінуді және оны шешудің тәсілін табуды жеңілдетеді.
Графиктік есептерді шығарғанда статика бойынша сызба есепті оқу барысында орындалуы мүмкін. Бірқатар басқа жағдайларда алдымен есептің шартына сәйкес жұмыстың сызбасын салып алады да, шығару барысында оны ұқыпты қарап, масштабы мен қажетті қатыстарды сақтай отырып орындайды. Оқушылар сызбаны дәптерлеріне салады.
Шарттың талдауы. Есепті талдау кезінде ең алдымен оның физикалық мәніне, берілген қарастырылатын физикалық шамалар арасындағы тәуелділікке көңіл аударады.
7 сыныптан бастап, шыдамдылықпен есептің дұрыс шешімін табу үшін есептің талдауын жүргізу керек, өйткені бұл оқушылардың логикалық ойлауын дамытып, есептерді шығаруға саналы тұрғыдан қарауға тәрбиелейді. Сабақта есепті талдауды көбінесе ұжым болып мұғалімнің оқушылармен әңгімесі түрінде өткізеді, оның барысында мұғалім өзара логикалық байланыста болатын мәселелерді талқылау нәтижесінде біртіндеп оқушыларды есептерді шығарудың неғұрлым тиімді әдісін алып келеді. Кейде бір ғана есептің бірнеше нұсқаларын қарастыру пайдалы, оларды салыстырып және неғұрлым ұтымдысын алу керек. Оқушылардан өз бетінше жасалғансаналы және негізделген пайымдауларды талап ете отырып, есепті талдауға үнемі үйрету керек.
Есеп шығару . есептін шартын талдаған соң оны шығаруға ауысады. Есеп шығаруды қысқаша түсіндірулермен қатар жүргізу керек. Есептеуде ұтымды әдістермен, ал жазудың атауларын мемлекеттік стандарт талаптарына сәйкес қабылданған белгілеулерін қолданып жүргізген дұрыс. Есептің жауабы айқын ерекшеленіп көрсетілуі керек.
Жауабын тексеру және бағалау. Есептің шыққан жауабын тексеру қажет. Ең алдымен оқушылардың жауабының шындыққа сәйкес болуына назар аудару керек. Кейбір жағдайларда оқушылар есеп шығарғанда есептің шартына тіпті сәйкес келмейтін, ал кейде қисыны келмейтін нәтижелер (жауаптар) алады. Оның себебі – есептеу процесінде есептің нақты шартымен байланысты болмауында. Осыдан қате шыққан шалағайлығы оқушылар назарынан тыс қалады.
Бұл кемшілікті болдырмау үшін оларды алдағы күтілетін нәтижені «болжауға» немесе алдын ала есептеуді пайдалануға, сондай-ақ шыққан жауаптың нақтылығы тұрғысынан сын-талдау жасауға үйрету пайдалы. Оқушыларды жауаптың тәртібін сақтай бағалауды, тек математикалық тұрғыдан емес, физикалық тұрғыдан да бағалай білуге үйрету қажет, мысалы, оқушылар мынадай жауаптардың мағынасыздығын бірден көру тиіс: қандай да бір механизмнің п.ә.к. 100%-дан артық, судың қалыпты жағдайдағы температурасы 0 С – тан аз немесе 100 С – дан көп, темірдің тығыздығы 78г/см .
Оқушылар есептің шешуінің дұрыстығын тексеру үшін оны басқа тәсілмен шығарып,нәтижелерді салыстырып,сондай-ақ физикалық шамалардың атау бірліктерімен амалдарды орындай отырып ж/е жауабын есептеп шығуға тиіс атауларымен салыстыра отырып тексереді.
Оқушылардың есепті шешудің атау бірліктеріне амалдар жасау жолымен тексеру әдісін қолдану дағдыларына машықтануына тиісті көңіл бөлу керек.Сабақта оны бірнеше қайтара пайдаланған соң тексерулдің осы әдісінің алгоритмін беруге болады.
Табылған шешудің жалпы түрде дұрыстығын тексеру үшін,шешуінің өрнектейтін формулаға әріпті белгілеулердің орнына физикалық шамалардың атау бірліктерін қойып, оларға шамалармен орындалатын амалдарды жасаймыз.
Есептің шартын және шешуін
жазу тәсілдері Есептің шартын жазудың түрлі формасын қолдануға
болады, бірақ олардың кез келгені негізгі талаптар – қысқалық және
айқындылықты қанағаттандыруы тиіс. Физика есептерінің шешуін жазуға
байланысты мұғалім оқушыларға түрілше талаптар қояды. Біреулер,
мысалы, шешуді жазуды жоспармен қоса орындауды талап етсе,
екіншілер – қысқаша түсінікпен, ал үшіншілері тек есептеулермен
шектеледі.
7-9-ШЫ СЫНЫП ЕСЕПТЕРІН ШЫҒАРУ ӘДІСІ
«Гидростатика» бөлімі бойынша есептерді шығарудың ерекше әдістері
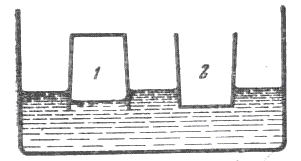
1. Суы бар ашық ыдысқа ашық стақан батырылады: бір рет түбімен жоғары қарай, ал келесісі түбімен астыға (сурет 21) бір тереңдікке батырылады. Осы екі жағдайда, стақанды батырған кезде, қайсысында көп жұмыс атқарылды. (Су ыдыстан ағып кетпейді, және түбімен төменге батырылған стақанға су құйылмайды.)
|
|
|
Сурет 21 |
Шешімі:
Стақан суға батырылған кезде, стақанның суға батуымен оны батыру үшін түсірілген күші жоғарылайды, өйткені кері итеруші күш арта бастайды. Алайда екі жағдайда қарастырылған күш бірдей емес: бірінші жағдайда стақан ішіндегі ауа сығылады және су ішінара стақанға кіреді. Осылайша, бірінші жағдайда стақандардың суға бірдей батырылған кездегі сығылған көлемі аз, демек көтергіш күші және оған тен кұш те аз, стақанды батыруға арналған күштің жұмысы бірдей түсірілген биіктікте аз болғаны.
2. Поршеннің салмағы P = 30 Н,радиусы r = 1 см жұқа қабырғалы түтікке тесігі бар R = 4 см радиусы дөңгелек дискке салынған.Поршень тығыз және үйкеліссіз стақанға кіруі мүмкін және алғашында стақанның төменгі жағында жатады. Поршень қандай Н биіктікке көтеріледі, егер трубкаға m=700 г суды құйса?
Шешімі:
|
|
|
Сурет 22 |
Барлық су поршеньді толтырмайды, оның жарты бөлігі түтікте қалады және қысым күшін тудырады, поршень салмағын теңестіріп.Осы негізінде, жазып алуға болады:


Нәтижесінде, поршень биіктікке көтеріледі

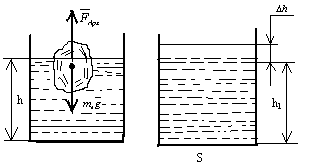
Түбінің ауданы 100 см2 болатын цилиндрлік ыдысқа сұйықтық құйылады, тығыздығы 1,2 г/см3. Оның ішінде массасы 300 г болатын мұз түйіршігі жүзіп жүр. Мұз салдарынан ыдыс түбі қаншалықты қысымды сезеді? Мұз ерігенде ыдыс түбіне түсірілген қысым қалай өзгереді?
S=100
см2=
10-2
м2;




|
|
|
Сурет 23 |


Шешімі: Мұздың жүзу шарты FАрх=mмg. Архимед заңы бойынша кері итеруші күш FАрх=ρgV', мұндағы V' – суға батқан бөлігінің көлемі. Егер мұз ыдыста болмаған жағдайда, онда сұйықтықтың деңгейі мынаған тең болар еді h1 және V'=S(h-h1). Түбіне түсірілген қысым мынаған тең болар еді P1=ратм+ρgh1. Мұз барда түбіне түсірілетін қысым P1=ратм+ρgh. Қысым айырмашылығы
∆р1=P2-P1=ρg(h-h1)=ρgV'/S= FАрх/S=mмg/S=
= .
.
Мұз еріген кезде, соның нәтижесіндегі су сұйықтық бетінде таралады (h1 тереңдікте болады) қалындығы ∆h тегіс қабаты. Енді түбіне түсірілген қысым
р'=ратм+ρgh1+ρсg∆h.
Анықтау бойынша, тығыздығы ρс=mм/Vс=mм/(S∆h). Бұдан ρс∆h=mм/S. Сондықтан, р'=ратм+ρgh1+mмg/S.
Қажетті қысым айырмасы
∆р2=р'-р2=ратм+ρgh1+ mмg/S-ратм-ρgh=р1+ mмg/S-р2= mмg/S-(р2-р1)=0.
Су көлемінің азаюына қарамастан, мұз еріген кезде, түбіне түсірілген жалпы қысымы өзгерген жоқ (мұз көлемімен салыстырғандағы).
-
Тығыздығы ρ1 және ρ2 екі араласпайтын сұйықтықтар ыдыста бар, бұл сұйықтықтар қабатының қалыңдығы тиісінше h1 және h2 тең. Ыдысқа сұйықтық бетінен кішкене аққыш зат түсіреді. Сұйықтық бетінен ыдысқа сумақайлық кішентай денені түсіреді, жылдамдағы нөлге тенелген кезде, дене түбіне түседі. Дененің жасалынған материал қалындығы қандай?
Шешімі.
Энергияның сақталу заңынан: Е2-Е1=А, мүнда А – сыртқы күш жұмысы. Берілген есепте Е2=0 (Жердің потенциалды энергия тартылысы түбінен саналады), сондықтан
mg(h1-h2)=FA1h1+FA2h2,
мұда FА1,2 – денеге әсерін тигізетін Архимед күші.
Нәтижесінде
|
|
|
Сурет 24 |
-
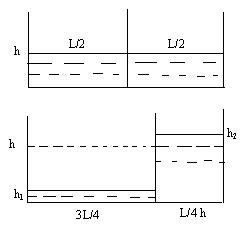
Ортасынан қалқанмен бөлінген h=1 м деңгейіне дейін сумен толтырылған бассейн ауданы S=100 м2. Бассейнді 1/3 бөлікке бөлетіндей етіп қалқанды жәймен жылжытып отырады. Су қалқаннан өтпейтін болса, қандай жұмыс жасау кере?
Шешімі.
Ауырлық күшінің жұмысы потенциалдық жүйесінің энергиясына шығынына тең А'=–∆Ер. ∆Ер=Ер2-Ер0, мұндағы Ер2 – соңғы күйдегі судың потенциалдық энергиясы; Ер0 – бастапқы күйдегі судың потенциалдық энергиясы. Потенциалдық энергиясын шыққаннан бастап бассейнінің төменгі деңгейіне түсуіне дейінгі уақыт, Ер2 үшіносыны аламыз:


(Потенциалдық энергиясының белгілеуін алғаннан кейін бассейнің екі жағында су массасы бірдей екенің ескереміз. Бұдан жұмысқа мынаны аламыз
А=
–А'=
Қорыта келе, мұғалімдерге заман өзгерісіне сай өзгеріп, биік шыңдардан көріне беру керек деген ойдамын. Осы әдіс-тәсілдерді қазақстандық мұғаімдер толық игеріп, тәжірибеге енгізілген жағдайда неге үздік жетістікке жетпеске деген ой түйдім. Болашақта теориялық және практикалық білімдерімізді ары қарай жалғастырып әлі де білімнің биік шыңдарына жетеміз деп ойлаймын
Физикалық есептері шығару тәсілдерінің мынадай түрлері кездеседі
1. Арифметикалық тәсілдер есептер математикалық теңдеулер құрылмай, арифметикалық амалдардың жәрдемімен, сұрақтар қою арқылы шығарылыды. Бұл тәсіл, мысалы, жылу мөлшерін анықтауда көп қолданылады.
2. Алгебралық тәсіл физикалық формулалардың негізінде математикалық теңдеулер құру арқылы есептер шығарғанда қолданылады. Мұндай есептер физиканың әр тарауында көп-ақ.
Күрделі, қиын есептердің көбісі осы тәсілмен шығарылады.
3. Геометриялық тәсіл физикалық есептерді шығаруда фигуралардың геометриялық және тригонометриялық қасиеттерін қолдану қажет болған жағдайда пайдаланылады. Мұндай тәсіл кинематика, статика, электростатика, фотометрия, геометриялық оптика тарауларында есептер шығаруда көп қолданылыды.
1. Графиктік тәсіл арқылы есептер шығарылғанда, олардың жауаптары, түрлі графиктерді талдау негізінде алынады.
2. Эксперименттік тәсіл бойынша есептер эксперимент жүргізудің негізінде шешіледі.
3. Аналитикалық тәсілде есептің мазмұны жеке қарапайым элементтерге жіктеліп, жан-жақты талданып, соның негізінде табуға қажетті шаманы бірден анықтаудың заңдылықтары қарастырылады (жалпыдан жекеге көшу). Бұл «өгізді тікелей мүйізден ұстаумен» бара-бар тіке төте жол, яғни есептің жауабына қатысты формуланы бірден тауып аламыз да, ол арқылы есепті басқа теріс жолдарға бұлтаңдатпай, оған берілген мәндерді қойып есептейміз.
4. Синтетикалық тәсілмен (жекеден жалпыға көшу) шығарғанда, есептің берілгендерді бойынша қандай шамаларды алдымен табуға болса, соны ретімен анықтап, ең ақырында ғана есептің шешуіне жетеміз. Сондықтан да, аналитикалық тәсілді жоғары, ал синтетикалық амалды төменгі кластарда пайдатанған әдістемелік жағынан тиімді деп есептелінеді.
Көп жағдайда физикалық есептер біріккен түрде аналитикалық- синтетикалық тәсілмен де шығарылады, ал кейде 4-5 тәсілдер араласып-қосылып, кешенді формада да шешіледі.
Физика есептерін шығаруда анықтамалық кестелер, логарифмдік сызғыш, микрокалкулятор, ЭЕМ, перфокарта, тексеру- оқыту машиналары, арнаулы дидактикалық тапсырмалар мен программаланған сын жұмыстары жайлы оқу құралдар кең қолданылуы керек.
Жалпы алғанда, физика есептерін шығарудың әдістемесі мынадай негізгі кезеңдерден (мұғалімнің не оқушының қызметінен) тұрады:
1) есептің текстін оқу және талдау, терминдер мен шамалардың мәндерін түсіндіру (мысалы, шығарылған №530 есепті шешудің әдістемесін қарастырайық);
Тексті кітаптан 1-2 рет оқу. Талдауды мынадай сұрақтарға жауап алу арқылы жүргізуге болады: Лифт қалай қозғалып барады? Ол қандай қозғалыста? 10 секундте қанша тереңдікке түскен? Нені табуды сұрайды? Канаттың керілу күші Fk қалай бағытталған?
2) есептің шартын жазу, тиісті сурет схемаларын салуды есептің шығарылуынан көріңіз;
3) физикалық мағыасын ашу мақсатында есептің мазмұнын ( құбылыстар-ды, процестерді) талдау, есепті шығаруға қажетті ұғымдар мен заңдарды қайталап, еске түсіру;
4) есепті шығарудың (эксперименттік жасаудың) жоспарын жасау, физикалық константа мен кесте мәліметтерін пайдалану, график- суретті талдау (мысалы, синтетикалық тәсіл үшін);
5) физикалық шамалардың мәндерін бірдей SI системасында келтіру
( g=9,8 м/с2);
6) берілген және табуға керекті шамалардың байланыстарын көрсететін заңдылықтарды анықтау, тиісті формулаларды табу:
Бір қалыпты үдемелі қозғалыс, Ньютонның екінші заңы: а =2h/t2
P=mg, R=ma, Fk =P- R
7) теңдеулер системасын шешу (эксперименттің приборларын дайындау) Fk =m(g-2h/t2 )
8) табуға керекті шаманы есептеп шығару және талқылау (эксперименттің нәтижелерін талдау, жазу);
9) есепті шығарудың басқа да тәсілдердің қарастыру (мысалы, аналитика-лық тәсіл), олардың ең тиімдісін таңдап алу (топ оқушыларының орташа дайындық жағдайында, синтетикалық тәсіл тиімді деп санаймыз).
Физика есептрін шығарудың тура төте жолы- есепті альгоритмдеу. Алгоритмді түзу процесін есептеп алгоритмдеу деп атайды. Ал алгоритм дегеніміз- есепті шығару тәсілдерінің реттелген дұрыс тізбегі. Алгоритмнің айны-қатесіз дұрыс (оптимал) жолы, жалпы алғанда, оның мынадай алгоритмдік құрылымына сүйеніп түзіледі: есепті шешу кезеңдері-
1) есептің шартымен танысу, 2) есепті шешудің жоспарын жасау,
3) жоспарды жүзеге асыру, 4) есептің шешімін тексеру; бұл кезеңдерді жүзеге асырудың амалдары- есеп шығарудың бағдар бағытын айқындау оны орындау, шығарылған есептің есептің нәтижесін байқап көру.
Осындай ұстамның (принциптің) негізінде есепті шығару процесі алгоритмделінеді.
Физикадан есептер шығарудың жалпы әдістері
Барлық физикалық есептер берілу әдісіне тәуелсіз, жалпы түрде шығарылады. Бұл жағдайда есепті шығару кезінде қолданылатын заңдар анық байқалады, есептің кез келген бөлігін тексеріп, мүмкін қателерді түзеуге мүмкіндік болады. Есептің шешімін алгебралық формула немесе теңдеу түрінде алған соң, оны талдап, іздеп отырған шаманың өзгерту сипаты мен шектерін тағайындауға болады. Бұлармен қоса, ең негізгісі, есепті жалпы түрде шығару физика курсының әр тарауының есептерін шығарудың әдістері мен тәсілдерін жалпылауға мүмкіндік береді.
Есептің шартымен танысқан соң назарды бірден ізделініп отырған шамаға аударып, оны бірден табуға тырыспаған жөн. Ең алдымен есептің шартында қандай физикалық құбылыс жатқанын,ол құбылыстардың негізі қандай заңдармен берілетінін және ол заңдардың математикалық жазылуын анықтауға көңіл аудару керек.
Есептің шартын дұрыс түсініп талдау үшін схемалық чертеждарын салып, берілген құбылысты сипаттайтын барлық шамаларды шартты түрде болса да көрсету керек. Чертеж салынған соң есептің шартын тағы бір рет оқып шығып, чертеждағы шамалардың қайсысы берілгенін және қайсысын анықтау керектігін белгілейді. Одан әрі физикалық заңдар мен формулалардың көмегімен жоғарыдағы айтылған шамалардың арасындағы математикалық байланыстар тағайындалады. Нәтижесінде берілген және белгісіз шамалар енетін бір немесе бірнеше теңдеулер жүйесі алынады. Алгебралық қатынастарды құрғанда, қандай да бір құбылыстарды сипаттайтын физикалық формулаларға енетін шамалардың кейбіреулерінің векторлық екендігіне ерекше назар аудару керек. Бұл шамаларды анықтау үшін олардың сандық мәндері ғана емес, бағыты да ескеріледі. Бұл үшін векторлық шамалардың координатостеріндегі проекциялары анықталып, теңдеулер осы проекциясы арқылы скаляр түрінде жазылады. Осымен физикалық есеп математикалық теңдеулер жүйесін шешпей тұрып берілген теңдеулер мен белгісіздер санының тең екендігіне көз жеткізу керек, әйтпесе теңдеулердің нақты шешуі болмайды.
Теңдеулер жүйесін тиімді әдіспен шешіп, есептің жалпы шешімі алынады да, талданады. Есептің жалпы шешімін талдауға оның өлшем бірліктерін тексеруден бастайды. СИ жүйесіне келтірілген өлшем бірліктер теңдеуге қойылып, қысқартылған соң ізделініп отырған физикалық шаманың өлшем бірлігі қалуы тиіс. Егер қалған өлшем бірлік ізделініп отырған шаманың өлшем бірлігімен сәйкес келмесе, есептің жалпы шешімінде қате бар, оны тексеру керек. Есептің жалпы шешімінің дұрыс екеніне көз жеткізген соң физикалық шамалардың сан мәндерін қойып, есептелініп, ізделініп отырған шаманың сандық мәні анықталады. Арифметикалық есептеулер кезінде дәлдігіне нұсқан келтірмейтін математикалық жуықтап есептеуді қолданған пайдалы. Бұнымен көп жағдайда уақытты ұтуға болады.
Есептің сандық жауабын тексеру және талдау есеп шығарудың соңғы кезеңі. Ең бірінші алынған жауаптың жуықталу реті бағаланады, одан соң оның шындыққа лайықтылығы ескеріледі.
Кинематикаға есептер шығару әдістері
Физиканың әр түрлі тарауларында есеп шығарудың жалпы ерекшеліктерінен басқа, сол тараулардың ерекшеліктеріне байланысты қосымша, өздік сипаттары болады.
Физика курсының кинематика тарауында негізінен есептер нүктенің түзу сызықты бірқалыпты және бірқалыпты үдемелі қозғалысына нүктенің шеңбер бойымен қозғалысына шығарылады.
а) Нүктенің түзу сызықты қозғалысына есеп шығарғанда есептің берілгенін оқыған соң схемалық чертежы салынып, онда санақ жүйесі мен нүктенің қозғалыс траекториясы көрсетіледі. Санақ жүйесін дұрыс таңдап алуға ерекше көңіл бөлу керек. Ол үшін координат жүйесінің бас нүктесін қозғалыстағы нұктенің қарастырылып отырған уақыттың бастапқы сәтіндегі орнына сәйкестендіреді және ості векторлар неғұрлым аз жіктелетіндей етіп бағыттайды. Сонда есептің шығарылуы неғұрлым қарапайым түрде болады және математикалық есептеулер оңайлайады. Санақ жүйесін таңдап алған соң чертежда қозғалыстың барлық кинематикалық сипаттамалары көрсетіледі: қарастырылып отырған уақытта орын ауыстыру, қозғалыстың басындағы және аяғындағы лездік жылдамдықтар, үдеу және уақыт. Егер есептің шарты бойынша қарастырылатын орын ауыстыруда қозғалыстың сипаты әр түрлі болса, немесе орын ауыстыру бірнеше бөліктерден тұрса, жүрілген қолды сонша бөліктерге бөліп әрқайсысындағы қозғалысты жеке қарастырады.
Чертеж салынған соң, қозғалысты сипаттайтын формулалар арқылы, чертеждағы физикалық шамалардың арасындағы байланыстарды тағайындаймыз. Нүктенің қозғалысының кинематикалық теңдеулерінің толық жүйесін құрған соң, есептің берілгеніндегі шарттарды қосымша теңдеулер түрінде жазып, теңдеулер саны белгісіздер санына сәйкестендіріледі. Осыдан соң теңдеулер жүйесін шешуге кірісіледі.
Мысал
1. самолет А пунктінен
шығысқа қарай 300 км қашықтыққа орналасқан В пунктіне ұшып келеді.
Егер: 1) жел жоқ болса, 2) жел оңтүстіктен солтүстікке қарй соғып
тұрса және 3) жел батыстан шығысқа қарай соғып тұрса, онда үшу
уақытының ұзақтығы қандай? Желдің
жылдамдығы ![]() =20 м\с, ауамен
салыстырғандағы самолеттің
жылдамдығы
=20 м\с, ауамен
салыстырғандағы самолеттің
жылдамдығы ![]() =600
км\сағ.
=600
км\сағ.
Берілгені: шығарылуы:
S=300
км= ![]() Есепті шығаруды санақ
жүйесін таңдап алудан
Есепті шығаруды санақ
жүйесін таңдап алудан
![]() =20 м\с, бастайық.
Қозғалмайтын санақ жүйесін жермен,
=20 м\с, бастайық.
Қозғалмайтын санақ жүйесін жермен,
![]() =600 км\сағ=166 м\с ал
қозғалыстағы санақ жүйесін ауамен байла-
=600 км\сағ=166 м\с ал
қозғалыстағы санақ жүйесін ауамен байла-
Тк ![]() ныстырамыз.
Онда
ныстырамыз.
Онда ![]() -ауыспалы (желдің жерге
-ауыспалы (желдің жерге
қарағандағы)
жылдамдық, ![]() - салыстырмалы (самолеттің ауаға
қарағандағы) жылдамдық болады. Абсолют жылдамдық
болса
- салыстырмалы (самолеттің ауаға
қарағандағы) жылдамдық болады. Абсолют жылдамдық
болса ![]() қатынасымен анықталады.
қатынасымен анықталады.
Есептің схемалық чертежін салайық:

Самолет А нүктесінен В нүктесіне түзу баруы үшін
абсолют жылдамдық міндетті түрде ОХ осімен бағытталуы керек. Үш
жағдайда да қозғалыс бірқалыпты түзу сызықты, ендеше қозғалыс
теңдеуі: ![]() немесе S=Vt түрінде
жазылады.
немесе S=Vt түрінде
жазылады.
Бұдан ![]() (V – абсолют жылдамдық)
(V – абсолют жылдамдық)
1) ![]() =0 онда, V=
=0 онда, V= ![]() және
және ![]()
![]()
2) ![]()
![]() , онда
, онда
![]()
Параллелограммға
толықтырылып, ![]() - бағыты анықталады. Самолет ОХ бойымен
қозғалу үшін,
- бағыты анықталады. Самолет ОХ бойымен
қозғалу үшін, ![]() суреттегідей бағытталуы керек.
Онда
суреттегідей бағытталуы керек.
Онда ![]() .
.
Суреттен ![]()
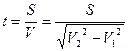
![]()
![]()
3) ![]() - ОХ бойымен бағытталған,
онда
- ОХ бойымен бағытталған,
онда ![]() де сол ось бойында жатады, сонда ғана –ОХ
бағытына сәйкес болады.
де сол ось бойында жатады, сонда ғана –ОХ
бағытына сәйкес болады.
![]()
Сондықтан ![]() , яғни
, яғни ![]() ;
;
![]()
Түзу сызықты бірқалыпты үдемелі қозғалысқа берілген есептер негізінен екі формуланы қолданумен шығарылады:
![]()
![]()
Немесе қозғалыс түзу сызықты болғандықтан
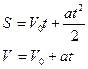
Мұндағы ![]() =сonst
=сonst ![]()
Осы теңдеулерге есептің шартынан қосымша теңдеулер жазылып, теңдеулер жүйесі құрылады. Теңднулер саны белгісіздер санынан кем болмаса, теңдеулер жүйесі ең тиімді тәсілмен шешіледі.
Мысал 2. Автомобиль 0,5 м\с үдеумен қозғала бастаған моментте оның жанынан бірқалыпты үдемелі қозғалып, 18 км\сағ жылдамдықпен трамвай өтеді. Трамвайдың үдеуі 0,3 м\с. Автомобиль трамвайды қуып жеткенде жылдамдығы қандай болады?
Берілгені:
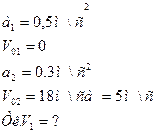
Шығарылуы:
Қозғалыстар бірқалыпты үдемелі. Санақ жүйесінің бас нүктесіне автомобиль мен трамвай кездескен нүктені сәйкестендіреміз. Уақытты есептеу де осы нүктеден басталады. Қозғалыстың схемалық чертежін саламыз.
Траекторияны бейнелеп, кинематикалық шамаларды белгілейміз. Екі дене үшін де қозғалыс теңдеулерін жазамыз: автомобиль үшін:
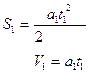
Трамвай үшін: 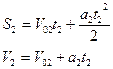
Есептің шартынан қосымша теңдеулер жазайық. Денелер бірдей уақытта бірдей жол жүреді (кездеседі).
![]()
Онда жоғарыдағы алғашқы үш теңдеу мына түрде жазылады:
![]()
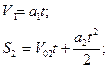 (1)
(1)
Немесе ![]() екенін
ескерсек
екенін
ескерсек 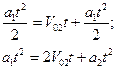
Бұдан ![]()
Уақыттың бұл мәнін (1) жүйедегі екінші теңдеуге қойсақ:
![]()
![]()
Есеп жалпы түрде шығарылды. өлшем бірлігінің дұрыс екендігі, яғни есептің дұрыс шыққаны оңай тексеріледі:
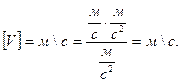
Жылдамдықтың сандық мәнін есептейміз.
![]()
Есептің жауабының мәні есептің шартына қарағанда нанымды.
Жанынан 5 м\с жылдамдықпен өткен трамвайды қуып жету үшін автомобиль осындай үлкен жылдамдық алу керек.
Вертикаль жоғары лақтырылған дененің қозғалысына есеп шығарғанда ерекше көңіл аудару қажет. Вертикаль жоғары лақтырылған дененің жылдамдығы (V) мен орын ауыстыруының (S=h) уақытқа (t) тәуелділік теңдеулері олардың арасындағы байланысты бүкіл қозғалыс барысында сипаттайды. Олар жоғары баяулай көтерілгенде ғана емес, траекторияның жоғарғы нүктесінде бір сәт тоқтап, бұрыңғы үдеумен төмен қозғалғанда да дұрыс, тек үдеудің таңбасының өзгеретіні ескеріледі, яғни қозғалыс теңдеулері жоғары көтерілгенде
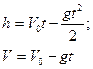
ал төмен қозғалғанда
![]()
түрінде жазылады.
Егер ауаның кедергісі ескерілмесе толық үдеу еркін түсу үдеуіне тең екендігі белгілі. Сонымен қоса дененің максималь биіктікке көтерілу уақыты оның құлау уақытына, ал құлау жылдамдығы жоғары лақтырылған бастапқы жылдамдыққа тең.
Мысал 3. доп һ=10 м биіктіктегі нүктеден вертикаль жоғары лақтырылған. Барлық қозғалыс уақытында ол 3һ жол ұшқан деп есептеп, доптың бастапқы жылдамдығын, қозғалу уақытын және құлау жылдамдығын табыңыздар.
Берілгені: шығарылуы:
Һ=10м қозғалыстың схемалық чертежын саламыз. Ол
l=3h үшін санақ жүйесінің бас нүктесіне доптың
Тк: ![]() =? t=? V=? лақтырылған
нүктесін немесе доптың жер бетіне құлаған нүктесін алуға болады.
Қай нүктені таңдағанымыздан есептің нәтижесі өзгермейді. Санақ
жүйесінің бас нүктесін (0) жермен байланыстырайық. Дененің қозғалыс
траекториясын белгілейік те
бастапқы
=? t=? V=? лақтырылған
нүктесін немесе доптың жер бетіне құлаған нүктесін алуға болады.
Қай нүктені таңдағанымыздан есептің нәтижесі өзгермейді. Санақ
жүйесінің бас нүктесін (0) жермен байланыстырайық. Дененің қозғалыс
траекториясын белгілейік те
бастапқы ![]() және соңғы V
жылдамдықтарды, биіктіктерді һ және
уақыттарын
және соңғы V
жылдамдықтарды, биіктіктерді һ және
уақыттарын ![]() көрсетейік. Есептің
шартынан егер дене 3һ жол жүрсе ол лақтырылған нүктеден биіктікке
көтеріліп, 2һ төмен құлайтынын табуға
болады
көрсетейік. Есептің
шартынан егер дене 3һ жол жүрсе ол лақтырылған нүктеден биіктікке
көтеріліп, 2һ төмен құлайтынын табуға
болады
Жоғары көтерілгендегі қозғалыс теңдеуін жазайық.
![]()
![]()
Ең жоғарғы нүктеде V=0,
онда ![]() Бұны бірінші теңдеуге
қойсақ
Бұны бірінші теңдеуге
қойсақ
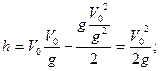
онда ![]() ал
ал 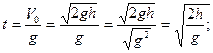
төмен қозғалғандағы қозғалыс
теңдеуі: ![]()
және ![]()
![]() , бұдан
, бұдан 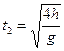 , ендеше
, ендеше
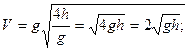
ал толық уақыт ![]() , жоғарғы мәндерін
қойсақ:
, жоғарғы мәндерін
қойсақ:
![]()
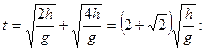
Сан мәндерін қойып есептейміз:
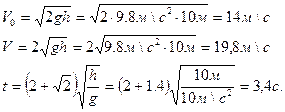
Формулалрға екі ғана шама енгендіктен өлшем бірліктерін жеке тексермей-ақ, бірден қоюға болады.
Қисық сызықты қозғалысқа берілетін есептерден негізінен нүктенің шеңбер бойымен қозғалысы және горизонтқа бұрыш жасай лақтырылған денелердің қозғалысы қарастырылады.
Нүктелердің шеңбер бойымен қозғалысына есептер шығарудың түзу сызықты қозғалысқа берілген есептерді шығарудан принципиалды айырмасы жоқ. Ерекшелігі айналмалы қозғалыс кинематикасы теңдеулерімен қоса айналмалы және сызықтың қозғалыс сипаттамаларының арасындағы байланысты ескеру керектігінде.
Егер дене тұрақты бұрыштық үдеумен айналса, онда оның қозғалыс теңдеулері түзу сызықты қозғалыстағы сияқты мынандай түрде жазылады:
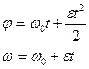
Егер қозғалыс бірқалыпты айналмалы болса ω=const,
ε=0, ε>0 ,болса ω> ![]()
Бұрыштық жылдамдық артады, ал ε<0 болса
кемиді: ω< ![]() . Екінші жағдайда теңдеулер теріс таңбамен
жазылады, яғни:
. Екінші жағдайда теңдеулер теріс таңбамен
жазылады, яғни:
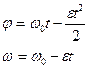
![]()
Сызықтық және бұрыштық жылдамдықтар арасындағы
байланыс V= ωR түрінде беріледі, бұдан ![]()
![]() - жанама үдеу. Осы теңдеулерге есептің
шартынан қосымша теңдеулер қосылып, кез келген есепті шығаруға
болады.
- жанама үдеу. Осы теңдеулерге есептің
шартынан қосымша теңдеулер қосылып, кез келген есепті шығаруға
болады.
Мысал 4.
Автомобиль қисықтық радиусы R=50 м-ге тең
шоссенің бойымен келе жатыр. Автомобильдің жүру
теңдеуі ![]() мұндағы А=10м, В=10 м\с, С=-0,5
м\с
мұндағы А=10м, В=10 м\с, С=-0,5
м\с ![]() . 1) t=5 с уақыт мезетіндегі автомобильдің
жылдамдығын v, тангенциал
. 1) t=5 с уақыт мезетіндегі автомобильдің
жылдамдығын v, тангенциал ![]() , нормаль
, нормаль ![]() және толық а үдеулерін; 2) автомобиль
қозғаннан бастап t=10с-қа дейінгі аралықта жол ұзындығын s және
ығысу модулін ∆r табу керек.
және толық а үдеулерін; 2) автомобиль
қозғаннан бастап t=10с-қа дейінгі аралықта жол ұзындығын s және
ығысу модулін ∆r табу керек.
![]()
|
|
|
|
|
|
|
|
|
|
Берілгені:
R=50м
ξ(t)=A+B+Ct ![]()
A=10м
В=10м\с
С=-0,5м\с ![]()
1) t=5c
2) t=0 c-тан t=10c-ге дейінгі аралықта
Табу керек: 1)
v, ![]() ,
, ![]() ,a;
,a;
2) s, ∆r
Шешуі:
1. бұл есепте жұру теңдеуін біле отырып жылдамдықты теңдеуден уақыт бойынша бірінші туындысын алу арқылы аламыз.
![]() Осы теңдеуге В,С және t-ның мәндерін қоя отырып жылдамдықтың сан мәнін табамыз
Осы теңдеуге В,С және t-ның мәндерін қоя отырып жылдамдықтың сан мәнін табамыз
![]() =10+2*(-0,5)*5=5м\с.
=10+2*(-0,5)*5=5м\с.
Жылдамдықтың уақыт бойынша бірінші туындысын алып тангенциал үдеуді ![]()
![]() табамыз.
С-ның мәнін қоя отырып::
табамыз.
С-ның мәнін қоя отырып::
![]() .
.
Нормаль үдеу келесі теңдеумен анықталады ![]() .
Осы теңдеуге табылған жылдамдықтың және берілген траекторияның қисықтық радиусының мәндерін қоя отырып нормаль үдеудің келесі мәнін аламыз:
.
Осы теңдеуге табылған жылдамдықтың және берілген траекторияның қисықтық радиусының мәндерін қоя отырып нормаль үдеудің келесі мәнін аламыз:
![]() =5
=5 ![]() .
.
Суретте көрсетілгендей,
толық үдеу ![]() және
және ![]() үдеулерінің геометриялық қосындыларына тең болатынын көреміз:
үдеулерінің геометриялық қосындыларына тең болатынын көреміз: ![]() .
Үдеудің модулі
.
Үдеудің модулі ![]() -ге тең.
Осы теңдеуге
-ге тең.
Осы теңдеуге ![]() және
және ![]() үдеулерінің сан мәндерін қоя отырып,
үдеулерінің сан мәндерін қоя отырып, ![]() =
= ![]() .
.
2. Автомобильдің жүрген s жолын анықтау үшін бір бағыттағы жүрген қозғалыс жағдайында жол ұзындығы s қисық сызықты координата ξ –дің өзгертетініне тең, яғни
S=
ξ(τ)-
ξ(0),
немесе s=A+Bt+C ![]() -A.
-A.
Алынған теңдеуге В,С және τ-лардың мәндерін қойып, есептесек:
s=A+Bt+C ![]() -A=10+10*10+(-0.5)*10
-A=10+10*10+(-0.5)*10 ![]() -A=50м.
-A=50м.
Суреттен көретініміздей орын ауыстыру модулі мынаған тең ∆r=2Rsin
(![]() \2).
\2).
Мұндағы ![]() -автомашинаның траекториясындағы бастапқы ξ(τ)
және ξ(0)
орындарын анықтайтын радиус-векторлар арасындағы бұрыш.
Бұл бұрышты (радиан өлшем бірлігінде) s
жолдың R
қисықтық радиусына қатынасы ретінде табамыз,
яғни
-автомашинаның траекториясындағы бастапқы ξ(τ)
және ξ(0)
орындарын анықтайтын радиус-векторлар арасындағы бұрыш.
Бұл бұрышты (радиан өлшем бірлігінде) s
жолдың R
қисықтық радиусына қатынасы ретінде табамыз,
яғни ![]() =s/R. Олай болса,
=s/R. Олай болса,
∆r=2Rsin (s/2R).
Бұл теңдеуге R, s мәндерін қойып есептеу нәтижесінде табатынымыз:
∆r=2Rsin (s/2R)=2*50*sin(50/2*50)=47.9 м.
Жауабы: v=5м/с, ![]() =-1 м/с
=-1 м/с ![]() ,
, ![]() =0,5 м/с
=0,5 м/с ![]() , а=1,12 м/с
, а=1,12 м/с ![]() ,s=50м, ∆r=47.9м.
,s=50м, ∆r=47.9м.
Горизонтқа бұрыш жасай лақтырылған дененің қозғалысы ОХ және ОY осьтерінің бойымен өтетін екі түзу сызықты қозғалыстарының қосындысы ретінде қарастырылады.
ОХ осі жер бетінің бағытымен,
ОY
осі оған перпендикуляр бағытталады. ОХ осі
бойымен өтетін қозғалыс бірқалыпты түзу сызықты, ал
ОY
осі бойындағы, қозғалыс вертикаль жоғары
лақтырылған дене қозғалысы сияқты, яғни бірқалыпты үдемелі қозғалыс
болып табылады. Бұл қозғалыстардың теңдеулерін, оларға жеке-жеке
есеп шығарудың әдістерін жоғарыда қарастырдық. Бұл қозғалысқа
арналған есептердің барлығын шығаруды, жоғарыда айтқанымызда
ескеріп, жылдамдық және үдеу векторларын ОХ және
ОY
остеріне жіктеуден бастайды. Кейін барып әр
бағытта қозғалыс теңдеулерін құрады. Дене горизонтқа бұрыш жасай
аса үлкен емес (бірінші космостық жылдамдықтан кіші) жылдамдықпен
лақтырылғанда, ауаның кедергісі ескерілмеген жағдайда, парабола
бойымен қозғалатыны және екі қозғалысқа дене бір мезгілде
қатысатындықтан ОХ бойымен қозғалу уақыты
ОY
бойымен қозғалу уақытына тең болатыны есте болу
керек. Тағы бір ескеретін жағдай траекторияның кез келген
нүктесінде толық үдеу еркін түсу үдеуіне тең де, жердің центріне
бағытталады, яғни a=g= ![]()
Бұл тақырыпқа есептер шығарар алдында, қозғалыстың схемалық чертежын жалпы жағдайға сызып алып (көрнекті етіп ), оны барлық дербес жағдайларға қолдануға болады. Чертежда санақ жүйесі, кинематикалық сипаттамалар (V,a), олардың остер бойынша t=0 және кез келген уақытта жіктелу, қозғалыс теңдеулері, траектория бейнесі, үдеудің жіктелуі көрсетіледі.
Мысал 5.
Допты горизонтқа ![]() бұрыш жасай
бұрыш жасай ![]() =10 м/с жылдамдықпен лақтырылған.
Мыналарды: 1) доптың қандай
=10 м/с жылдамдықпен лақтырылған.
Мыналарды: 1) доптың қандай ![]() биіктікке көтерілгенін .2) доптың лақтырған
жерінен жер бетіне түскен ℓ қашықтығын. 3) оның қанша уақыт
қозғалыста болатындығын табу керек. Ауаның кедергісі есепке
алынбайды.
биіктікке көтерілгенін .2) доптың лақтырған
жерінен жер бетіне түскен ℓ қашықтығын. 3) оның қанша уақыт
қозғалыста болатындығын табу керек. Ауаның кедергісі есепке
алынбайды.
![]() Берілгені: Шығарылуы:
Берілгені: Шығарылуы:
![]() 1-суреттен қозғалыс теңдеулерін
жазайық
1-суреттен қозғалыс теңдеулерін
жазайық
![]()
![]() =10 м/с
=10 м/с 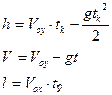
Т.к. ![]() =? ℓ=?
=? ℓ=? ![]() =?
=?
Мұндағы ![]() - көтерілу, ал
- көтерілу, ал ![]() - ұшу
уақыттары
- ұшу
уақыттары ![]() .
. ![]() болғандықтан
болғандықтан
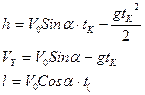
Максималь көтерілу
нүктесінде ![]() , ендеше
, ендеше ![]()
Бұдан ![]()
Онда 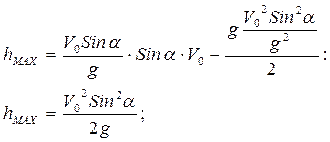
Көтерілу уақыты мен түсу уақыты бірдей және олардың қосындысы ұшу уақытына тең екенін ескерсек
![]()
Бұл өрнекті үшінші теңдеуге
қойсақ 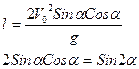
Немесе
![]()
![]()
Сан мәндерін қойып шығарамыз:
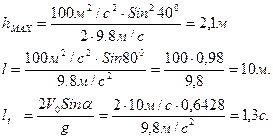
Өлшем бірліктерін сан мәнімен бірге қойып тексереміз. Физика есептерін шығару үшін теорияны терең түсініп,іс жүзінде практикада пайдалана білуі керек, терең ойланып күрделі мәселелерді, құбылыстарды талдап, зерттеп шеше алатындай болуы керек. Есептер қандай да бір нақты жағдайларда болып өтетін құбылыстарға физикалық заңдарды қолдануды талап ететін жаттығулар үшін материалдар береді. Сондықтан есептердің оқушылардың білімін нақтылауда, жалпы заңдардың түрлі көрінісін көруде үлкен маңызы бар.
Қорытынды
Қорытындылай келе, оқушылардың физика пәніне деген қызығушылығын, ынтасын арттыру үшін сапалық есептердің маңызы ерекше. Бұл есептерді физика пәнін жаңа бастаған 7 — сынып оқушылары үшін қолданыс аясын кеңейту олардың пәнді тереңірек түсінуіне елеулі әсерін тигізері анық. Біз білеміз, кез-келген есептерді шығару ол белгілі бір мақсатқа қарай бағытталады. Сондықтан да, біз оқушыларға есеп шығарудың айқын мақсатын қойған дұрыс деп санаймыз. Сапалық есептерді шешу арқылы оқушылардың шынайы әлемнің нақты объектілерін зерттеуде ғылыми түсініктері қалыптасады. Мектептегі физика курсын меңгеруде көптеген сапалық есептерді енгізу, білім сапасын арттыруға септігін тигізеді. Есеп түріндегі эксперименттік тапсырмаларды шешу және жазу келесі элементтерден тұрады: есептің қойылуы, шарттарды анализдеу, өлшеулер жүргізу, есептеулер, тәжірибеден тексеру. Эксперементтік есептердің бағалы жері - ол оқушылардың алған білімін практикада қолдана білуін тексеруге жол ашады.
Пәнаралық байланыстар: Алгебра, геометрия, информатика, химия, экономика, биология және өндірістік оқулықтар.
Кәсіби бағдарлау. Кәсіби бағдарлау, оны оқушыларды диагностикалық материалдарына сүйене отырып таңдауды негіздеу.
Оқушылар осы курсты оқу нәтижесінде мынадай мамандықтарды игеруге дайындалуға мүмкіндік алады: Педагогика, экономика, архитектор, әскери, құрылыс мамандары. Табиғатты саналы танудың міндетті ретінде алдынғы шартты ғылыми деректерді іздестіріп жинақтау. Байқау мен эксперимент жүргізу. Физикалық шамаларды анықтап, өлшем бірліктерін тағайындау және сан мәнін өлшей білу.
ӘДЕБИЕТТЕР ТІЗІМІ
Задачи по физике. Воробьев И.И., Зубков П.И., Кутузова Г.А. и др., М., 1999 г., 370 с.
-
Задачи по физике Пособие для учащихся 9-11-х классов. Гомонова А.И., Плетюшкин В.А., Погожев В.А., М., 1998 г., 192 с.
-
Задачи по физике для поступающих в вузы. Бендриков Г.А., Буховцев Б.Б., Керженцев В.В., Мякишев Г.Я., М., 2005 г., 344с.
-
Задачи по физике с анализом их решения. Савченко Н.Е., М., 2000 г., 320с.
5. Қазақстан Республикасының «Білім туралы» Заңы »
6. А.Б.Мәженова. Физика есептерінің жинағы. 9-11 сыныптар
7. Б.Дүйсембаев, Д.Қазақбаева. Физика анықтамалық құрал.
8. Баканина Л. П. и др. Сборник задач по физике: Учебное пособие для углубленного изучения физики в 10-11 класс, М.: Просвещение, 1995.
9. Балаш В. А. Задачи по физике и методы их решения. М.: Просвещение, 1983.
10. Д.Қазақбаева, Ш.Кәрібаева. Бағдарлы оқытуды ұйымдастыру жолдары. Физика және Астрономия, №1, 2006ж.
МАЗМҰНЫ:
-
Кіріспе..........................................................................................3
2.Физика бойынша есеп шығарудың тиімді әдістемесін
құрастырудың заманауи тәсілдері..................................................6
3.Сапалық есептерді шығару әдістемесі........................................12
4. 7-9-шы сынып есептерін шығару әдісі«Гидростатика»
бөлімі бойынша есептерді шығарудың ерекше әдістері..............16
5. Физикалық есептері шығару тәсілдерінің мынадай
түрлері кездеседі..............................................................................21
6. Физикадан есептер шығарудың жалпы әдістері.......................24
7 Кинематикаға есептер шығару әдістері......................................26
8 Қорытынды.....................................................................................41
-
Әдeбиeттep тізімі.........................................................................42
43
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Физика есептерін шығару тәсілдері
Физика есептерін шығару тәсілдері
«ФИЗИКА ЕСЕПТЕРІН ШЫҒАРУДЫҢ ТӘСІЛДЕРІ МЕН ӘДІСТЕМЕСІ»
Әдістемелік құрал
Әдістемелік құралды “Алматы облысы білім басқармасының Еңбекшіқазақ ауданы бойынша білім бөлімі” мемлекеттік мекемесінің “Жамбыл атындағы орта мектебі” мемлекеттік мекемесінің педагогикалық кеңесінің шешімімен баспаға ұсынылған
Абықан Ақбота Бақтығалыйқызы
«Физика есептерін шығарудың тәсілдері мен әдістемесі» әдістемелік құрал. Алматы облысы білім басқармасының Еңбекшіқазақ ауданы бойынша білім бөлімі” КММ -43 бет, -2025 ж
Ұсынылып отырған «Физика есептерін шығарудың тәсілдері мен әдістемесі» әдістемелік құрал физика есептерін шығару білім алушылардың оқу материалдарын саналы түрде терең игеруіне қолайлы жағдай туғызады, олардың алған білімдерін пайдалана білу қабілетін қалыптастырады және бекітеді. Сонымен қатар, есептерді шығару білім алушылардың өздігінен ойлануын, қиыншылықтарды жеңуге деген жігерін және табандылығын арттыру құралдарының бірі болып есептелініп, оқу процесін жақсарта түседі.Есеп шығару – оқу үрдісінің бөліп алуға болмайтын бір бөлігі болып табылады. Себебі, ол физикалық ұйымдарды қалыптастыруға білім алушылардың физикалық құбылыстарды ойлау қабілетін дамытуға, оны практикада қолданып білуге үйретеді.Физикалық теорияны үйренуде оның мағынасын терең түсініп қолдану жолдарын іздестіруде білім алушыларға жаттығу ретінде класта,үйлерінде өз бетінше түрлі есептер шығарудың мәні ерекше.Әдістемелік құрал орта мектепте өткізілетін таңдау курстарына пайдаланумен қатар, теориялық және практикалық деңгейі жағынан физика пәні мұғалімдеріне көмекші құрал бола алады.
Әдістемелік құрал физика пәнінен сабақ беретін мұғалімдерге, әдіскерлер мен физика сүйер көпшілік қауымға арналған.
Кіріспе
Есеп шығару физиканы оқыту процесінің ұдайы бөлінбес құрамды бөлігі болып саналады, өйткені ол физика сабақтарының түгелдей барлық түрлері мен кездерінде және кластан тыс жұмыстарында кездеседі. Есеп шығару, физиканы оқытудың әдістері, тәсілдері, амалдары ретінде әр жақты мағынада қолданылады. Физика есептерін шығару білім алушылардың оқу материалдарын саналы түрде терең игеруіне қолайлы жағдай туғызады, олардың алған білімдерін пайдалана білу қабілетін қалыптастырады және бекітеді. Сонымен қатар, есептерді шығару білім алушылардың өздігінен ойлануын, қиыншылықтарды жеңуге деген жігерін және табандылығын арттыру құралдарының бірі болып есептелініп, оқу процесін жақсарта түседі.
Есеп шығару – оқу үрдісінің бөліп алуға болмайтын бір бөлігі болып табылады. Себебі, ол физикалық ұйымдарды қалыптастыруға білім алушылардың физикалық құбылыстарды ойлау қабілетін дамытуға, оны практикада қолданып білуге үйретеді.Физикалық теорияны үйренуде оның мағынасын терең түсініп қолдану жолдарын іздестіруде білім алушыларға жаттығу ретінде класта,үйлерінде өз бетінше түрлі есептер шығарудың мәні ерекше.
Физика есептерінің түрлері де, оларды шығарудың тәсілдері де көп.Есепті шығару - күрделі процесс. Білім алушылар есептерді тақырып бойынша шығара алмайтын болса, ол физиканы терең түсіне алмайды. Сондықтан оқу программасын меңгеру үшін физикалық есеп жаттығулар керек- ақ.
Физика есептерін шығару үшін теорияны терең түсініп,іс жүзінде практикада пайдалана білуі керек, терең ойланып күрделі мәселелерді, құбылыстарды талдап, зерттеп шеше алатындай болуы керек. Есептерді шығару кезінде білім алушылар көптеген құбылыстардың заңдарын анықтайды, теорияның мағынасын терең түсініп, өмірдегі ролін көреді, техниканың жаңалықтарымен танысады, олардың физикалық негіздерін анықтайды, жалпы білімдерін көтереді, политехникалық тәрбие береді.
Есеп шығару кезінде білім алушылар физикамен бірге өздерінің математикалық дайындықтарын тереңдетеді. Физика есептері математиканы жандандырады, оның мағынасын артырады, оны шығаруда білім алушылар түрлі электрондық есептеу машиналарымен жұмыс істеп, есептеу техникасын үйренеді.
Әрбір сабақта жеке білім алушылардың қабілеттерін ескерген жөн. Физикаға ереже қызығатын білім алушылар үшін үйірмелер ашып, олардың қаблеттерін жетілдіре түсіп, қиын есептерді ұсынып шығарту және де оларды физикалық олимпиадаларға қатыстыру керек.
Физика есептерін шығару әдістерін қарастыру алдында, қазіргі кезде қолданылып жүрген есеп шығарудың жалпы метадикасына тоқталайық.
1.Есептің шартымен танысу.
Есепте қарастырылып отырған мәселелерді толық ұғынып,қойылған сұрақтарды анық түсінуі керек. Есептің шартына байланысты берілген шамаларды, сұрақтарды, қосымша тұрақтыларды таңбалап жазу керек.Экспирменттік есеп болса, қажетті құрал - жабдықтарды алдын - ала түгелдеп, жұмыстың күйін тексеріп алу керек.
2.Есептің мазмұнын талқылау.
Есептің шартында берілген процестердің құбылыстардың қандай заңдарға бағынатынын анықтап,ол заңдарды сипаттайтын формулаларды жазу керек. Құбылыстар арасындағы байланыстарды анықтау қажет.Координаталар систамасын ыңғайлы етіп алып,секторлы шамалардың бағыттарын, кеңістіктегі орнын анықтау керек. Есепті талдау үшін мүмкін болған жағдайда оқиғаның суретін салу, оның графигін сызу керек.
3.Есепті жалпы түрде шығару керек.
Есептің сұрауларына талдау беретін, проблеманы анықтайтын теңдеуді жалпы формула түрінде қорытып шығару керек. Барлық уақытта осылау шығару міндет емес, кейде есепті бөлшектеп, есептеулерді жүргізіп шығарған ыңғайлы болады.
4.Есептеу.
Есепте берілген шамалардың барлығын ХБЖ өлшемдеріне келтіріліп, қорытып алынған жалпы формулаға шамалардың сандық мәндерін қойып,математикалық есептеулер жүргізу керек. Мүмкіндігі болса, арифметикалық жұмысты микрокалькуляторларда, есетеу машиналарында жүргізген жақсы.
5.Есептің жауабын тексеру.
Есептің жауабы шындыққа жақын болуы тиіс.Көп жағайда сандық мәннің шамасы есептің дұрыс шықпағандығын анықтауға мүмкіндік береді.Мысалы кез келген дене жылдамдығы жарықтың вакумдағы таралу жылдамдығынан артық бола алмайды.
Білімді игерудің нәтижелілігі таным үдерісіне адамның әртүрлі сезім мүшелерінің іске қосылуы және нақты заттар мен құбылыстарға бетпе-бет келгенде оны сезіну, көре білу және қабылдау арқылы артады. Бұл жағдайда физикалық эксперименттің маңызы зор.
Физикалық құбылыстардың негізін ұғыну, түсініктерді, теорияны игеру процесі әр білім алушыларда бірдей жүрмейді. Оқыған материалды біреулер тез игереді, енді біреулеріне ой қорытуына және есіне сақтауына көп уақыт қажет. Үйде білім алушылар әрқайсысы өз қарқынымен жұмыс істейді. Үй тапсырмасы дұрыс ұйымдастырылса сабақ кезіндегі алған білімдерін бекітуге және тереңдетуге көмектеседі. Үйге берілген бақылаулар мен тәжірибелердің қорытындылары, есептердің шешімі, шығармашылық тапсырмалардың орындалуы білім алушылардың үй жұмыстарына арналған дәптерлеріне жазылады. Үй жұмысының қорытындылары туралы мәліметтер жазу білім алушылардың өз ойын сауатты және қысқаша жеткізуге үйретеді. Сонымен қатар жазу мәдениеті, яғни белгілі жүйе, нақтылық пен реттілік қалыптасады. Үйдегі тәжірибелерді және бақылауларды баяндау оқушыға көргенін терең ойлауға, негізгіні ажырата білуге үйретеді. Эксперименттік есептерді шешу тәсілдері оларды шешудегі эксперименттік жұмыстың қойылуына тәуелді.
Физика сабақтарында есептер шығару білім алушылармен жұмыс жасау барысында әрбір мұғалімнің негізгі әдістемесінің құраушысына айналуы керек. Себебі, қазіргі заман талабына сай, білім алушыларды техникалық бағыттағы пәндерге атап айтқанда физика саласына бағыттау ең басты қажеттілік болып табылады.
ФИЗИКА БОЙЫНША ЕСЕП ШЫҒАРУДЫҢ ТИІМДІ ӘДІСТЕМЕСІН ҚҰРАСТЫРУДЫҢ ЗАМАНАУИ ТӘСІЛДЕРІ
«Қазіргі заманғы жастарға
ақпараттық технологиямен байланысты әлемдік стандартқа сай мүдделі
жаңа білім беру өте қажет»
Н.Ә.Назарбаев.
Қазақстан Республикасының «Білім туралы» Заңының 8 – бабында «Білім
беру жүйесінің басты міндеті – оқытудың жаңа технологияларын
енгізу, білім беруді ақпараттандыру, халықаралық коммуникациялық
желілерге шығу, ұлттық және жалпы адамзаттық құндылықтар, ғылым мен
практика жетістіктері негізінде жеке тұлғаны қалыптастыруға,
дамытуға және кәсіби шыңдауға бағытталған білім алу үшін қажетті
жағдайлар жасау» – деп атап көрсеткендей, қазіргі кезеңде әрбір
мұғалімнің алдына қойып отырған басты міндеттерінің бірі – оқытудың
әдіс – тәсілдерін үнемі жетілдіріп отыру және жаңа педагогикалық
технологияны меңгеру. Ал білім беру жүйесінің алдындағы жаңа
міндеттердің бірі инновациялық педагогикалық оқыту технологияларын
пайдаланып білім сапасын арттыру.
Жаңаша оқытудың «Кембридждік» жүйесі бойынша балаларға білім дайын
күйінде берілмейді, керісінше оқушылардың өздерін еркін ұстауға,
ойлануға мүмкіндік жасалады. Олар өз беттерімен және өзара
әрекеттесе оқып-үйреніп, ортақ бір шешімге келуге бағытталады.
Сондықтан да қазіргі таңдағы әрбір ұстаздың да, оқушының да
іс-әрекеті ерекше шығармашылық сипатта болуы керек.
Бағдарламаның мақсаты – оқушылар өздерінің қалай оқу керектігіне
назар аудара отырып, олардың өз ойлары мен дәлелдемелерін нақты
жеткізе алатын, яғни ойға жүйрік, тілге шешен, әрі жазбаша түрде
еркін, көркем бейнелеп жазуға төселген, бірнеше тілді қатар
меңгерген бәсекеге қабілетті жан-жақты жетілген жеке тұлға
қалыптастыру болып табылады.
Ондай «тұлға» болашаққа сенімді, ынталы, сыни пікір көзқарастары
жүйелі дамыған, қазіргі сандық технологияларды, өмірде өз білімін
қалыптан тыс жағдайда да еркін әрі терең пайдалана білетін жан
болуы тиіс.
Әлеуметтік –сыдарлылық тұрғыдан оқытуды түсну /Выготский, 1978;
Вуд, 1998 / мұғалімдерге арналған нұсқаулығында айтылғандай «Оқыту
мен оқытудағы жаңа тәсілдер» негізінде жатыр. Балалар өзінің
түсінігін өзіндік зерттеулері мен әлеуметтік өзара байанысқа сәйкес
құратын белсенді білім алушылар болып табылады.
Осы орайда «Кембридждік» әдіс-тәсілдер мен заманауи педагогикалық
технологияларды тиімді қолдану жолында әріптестерім де атсалысуда.
Әр сабақтың тиімді әрі нәтижелі өту үшін әр ұстаз өз шығармашылығын
дамыту мен ізденіс үстінде.
Мотивация тудыру немесе қызығушылық ояту
Үйренушінің оқуға, үйренуге деген ықылас- ынтасы, ниеті мен зауқы
болмаса, оқу нәтижксінің мардымды болуы екіталай. Француз жазушысы
Анатоль Франц кезінде «тамақ тек зор тәбетпен ішкенде ғана сіңеді»
деген екен. Оқу мотивациясы дегеніміз деп осы осы сияқты білімге,
білуге, үйренуге деген «тәбет».
Топтық жұмыс, біріншіден,
оқушыларға бірігіп жұмыс істеу мүмкіндігін тудырады. Екіншіден,
ұйымшылдыққа тәрбиелейді. Үшіншіден, бірін-бірі оқытуға,
бірінен-бірі үйренуге жағдай жасайды. Бұл әдіс сонымен қатар топ
болып ынтымақтастықпен бірігіп жұмыс жасауға,ойын еркін ортаға
салуға, бірінен- бірі үйренуге септігін тигізді. Яғни, топтық жұмыс
оқушылар арасында әлеуметтік өзара қарым-қатынасты, тиімді араласу,
проблемаларды шешу және топ ішінде шығарманы жан-жақты талдауға
көмектеседі.
Топтық жұмыстың тиімділігі:
• Оқушылар өзара достық қатынаста болады;
• Бір-бірінен сұрай отырып білімдерін жетілдіреді
• Өзгелерге ойын жеткізу үшін өз шешімін дәлелдеп үйренеді;
• Менен сұрап қалады-ау деп қорықпайды,топ болып жауап береді;
• Оқушылардың мектепке деген көзқарасы өзгереді. Уақыттары қызықты
әрі тиімді өтеді.
• Топтық жұмыста бос отыратын оқушы
болмайды.
Ғылыми зерттеу нәтижелері
сабақта диалогтің маңызды рөл атқаратынын көрсетті. Мерсер мен
Литлтон (2007) өз еңбектерінде диалог сабақта оқушылардың
қызығушылығын арттырумен қатар олардың білім деңгейінің өсуіне үлес
қосатындығын атап көрсетеді. Мерсердің зерттеуіне сәйкес,
әңгімелесу оқушылардың білім алуының ажырамас бөлшегі болып
табылады және әңгімелесудің үш түрі бар,олар:
-Әңгіме-дебат барысында;
-Топтық әңгіме барысында;
-Зерттеушілік әңгіме жүргізілу үстінде байқалады екен.
«Диалогті оқыту арқылы оқушылардың қызығушылығын арттыру, олардың
білім деңгейін көтеру, сөйлеу мәдениетін қалыптастыру. Балаға
күштеп білім беруден гөрі, баланың білімге деген құштарлығын ояту
ең маңызды мақсат» деп К.Д.Ушинский айтқандай баланың білім алуға
деген құштарлығын ояту үшін мұғалім көп ізденіп, сабақтың тиімді
өтуіне жұмыс жасап, сабақ барысында оқудың белсенді әдістері,
диалогтік оқыту және оқу әдісін қолдануда білім сапасын арттыруға
көп көмегін тигізеді деп ойлаймын. Оқушылар диалог әдісін қолдана
отырып, білімді бірлесіп құру, талқылау, түсіну мен дағдыларды
қалыптастыру арқылы білім алады. Әр сабағымда оқушыларға сұрақтар
қою арқылы, тақырып бойынша өз ойларын ашық, еркін айтуға мүмкіндік
бердім. Өзара талқылау арқылы, түрлі ойлардың болатындығын, бір
бірінің түсінуіне көмектесетінін көрсетсе, сұхбаттасу арқылы өз
ойларын дәлелдеуге тырысты. Бұл оқушылардың қандай деңгейде екенін
түсінуге көмектеседі. Біз көбінесе диалогтік оқытуды сұрақ – жауап
ретінде қолданамыз. Яғни, бала теорияны меңгерумен қатар тәжірибе
жүзінде де қалай жасау қажеттігін ұғынуы керек. Тәжірибелік жұмыс
жасау барысында көптеген сұрақтар туындайды. Оқушылар өзара
пікірлер мен болжамдар айта отырып, бірлесе жұмыс жасайды. Жұмыс
жасау барысында оқушыларға көптеген сұрақтарды қоюға болады.
Мысалы, кез келген сабақтың басталуы сұрақ – жауаптан тұрады.
Сұрақтардың берілуіне байланысты оқушының пәнге деген қызығушылығын
арттыруға болады. Оқушы мен мұғалім арасында жақсы қарым-қатынас
орнайды. Диалогтік оқыту оқушы мен оқушы арасында да туындауы
мүмкін. Мұнда оқушылар бір-біріне сұрақтар қояды. Бір-бірінің
жауабына қанағаттанбаса, қосымша да сұрақтар беруі
мүмкін.
Оқу процесінде қолдануға
тиімді ойындардың маңызды түрлерінің бірі:
1. Рөлдік ойындар
2. Іскерлік ойындар
3. Имитациялық ойындар
Рөлдік ойындар –тиімді интербелсенді әдістердің бірі. Педагогика
саласында зерттеу жүргізетін ғалымдардың басым көпшілігі
оқу/оқутудың ойын әдістердің кәсіби дамыуды қамтамассыздандырудағы
ең тиімді әрі болашағы зор тәсілдер деп есептеледі. Өйткені
іс-әрекет арқылы үйрену/үйрету –танымның тиімді тәсілі екендігі
баршаға аян; адамның жадында бірінші мезетте өзінің жасағаны мен
бастан кешкен әсерлері қалады. Ал рөлдік ойындар оқушылардың
өздерін басқа адамдардың орнына қойып, мәселе немесе проблеманы
солардың тұрғысынан қарастырып, шешімді өз «қолдарымен» жасауды
меңзейді. «Ойын» сөзі сабақта инсценировканың орын алып,
әрекеттердің спектакль түрінде көрсетілетіндігін меңзейді.
Іскерлік оқу ойындарында қандайда бір сценарий ауқымында рөлдерді
өзара бөлісіп зерттеу жұмыстарын жүргізу және деректерді талдау
арқылы нақты практикалық мәселелерді бірлесе отырып шешеді. Оқу
ойындарының сценарийлері тақырып ауқымында болып, күрделі
мәселеерді ойын тұрғысынан «ойнап» шешуге ағытталады.
Имитациялық ойындар дегеніміз адамдардын қалыптан тыс /экстремалды/
жағдайлардағы әрекетерін анықтайтын өмір сүру ортасынан үлгісін
/модель/ құру. Мұндай жағдайлар қатарына «жан-жал», «әуе апаты»,
«жер сілкінісі» «жау тылында», «робинзон»секілді оқиғаларды
жатқызуға болады.
«Алдын ала берілген атаулар» –
сабақ басында жаңа тақырып бойынша тақтаға бірнеше атау /терминдер/
жазып қойып, оқушыларға олардың мағынасы, мақмұны және өзара
қатынасы мен байланысы туралы ойлануы керек. Бұл жұмысты оқушылар
жеке, жұппен нмесе шағын топ ішінде ауызша яки жазбаша /соңғысы
тиімдірек/ орвндауы иқтимал. Содан кейін бірнеше оқушының ойы мен
пікірі тыңдалады.
«Үш қадамды сұқбат»-тақырып бойынша оқушылардың бір-бірінен
кезектесіп интервью алу тәсілі. Бұл тәсіл «Сұрақ қою, қайтадан
сұрақ қою»
Тәсіліне ұқсас, алайда мұнда басты назарды жауапқа аудару
керек.
«Төрт сөйлем тәсілі» – сабақ
соңында қушылар өздерінің түсінік және жұмыс жасау деңгейлерін
бағалау үшін мынадай тапсырмаларды орындайды:
1 пікір.
Мәтін бойынша туындаған өзіндік пікірін /негізгі идеясын/ бір
сөйлеммен келтіру керек.
2. дәлел.
Келтірілген өзіндік пікірі бар сөйлеммен дәлелдеп шығу керек. Дәлел
дегеніміз ұстанған көзқарасты логикалық тұрғыдан дәйектеу,
негіздеу.
3.Мысал.
Енді келтірілген өзіндік пікірді тағыда бір негізден кету үшін бір
сөйлеммен мыса келтіру қажет. Мысал, өмірден, практикадан алынуы
керек; ақпарат көздеріне немесе көп тараған пікірлерге сілтеме
жасау, практикада орын алған үрдіс, басқа адамдардың пікірі;
4.Қорытынды.
Есеп шығару – оқыту үрдісінің маңызды элементы. Есептер қандай да бір нақты жағдайларда болып өтетін құбылыстарға физикалық заңдарды қолдануды талап ететін жаттығулар үшін материалдар береді. Сондықтан есептердің оқушылардың білімін нақтылауда, жалпы заңдардың түрлі көрінісін көруде үлкен маңызы бар. Мұндай нақтылаусыз білімнің практикалық маңызы болмайды. Есептер шығару физикалық заңдарды тереңірек және берік меңгеруге, логикалық ойлаудың дамуына ықпал етеді, оқушылардың қызығушылығыноятады, өзіндік жұмыс дағдыларын игеруге көмектеседі, әрі өзіндік ой қорытудың бірден-бір құралы болып табылады. Физикалық есептердің мазмұны оқушылардың табиғат пен техника жөніндегі білім шеңберін кеңейтеді. Сондай-ақ, есептер шығару – қайталаудың, пысықтаудың, оқушылардың білімін тексерудің маңызды құралы.
Физикалық есептерді шығару әдістемесі
Есеп шығару әдістемесі есептің мазмұнына, оқушылардың дайындығына, олардың алдына қойылған міндеттерге т.с.с. тәуелді. Дегенмен де көптеген есептерді шығару барысында жеткілікті көңіл бөлетін жағдайлар бар.
VII – XI сыныптар аралығында оқушылар шамамен 170 негізгі формуланы оқып-үйренеді. Әр формулада кем дегенде үш шама болатынын ескерсек, әрбір оқушы негізгі заңдылықтарға арналған бірнеше жүздеген есептердің типтерін меңгеруі тиіс.
Физикалық есептер шығарудағы анализдік – синтездік әдіс
Анализдік – синтездік әдіс – орта мектептің барлық сыныптарындағы физика есептерін шығарудаңы негізгі әдіс. Оқу процесінде оны ойдағыдай қолдану оқушыларға есептің шешуінің дұрыс жолын табуына жол ашып, олардың логикалық ойлауының дамуына септігін тигізеді.
Физикадан әдістеме құралдарында талдау (анализ) мен синтез екі тәуелсіз әдістер ретінде жиі қарастырылады. Алайда бұлай бөлуді дәл сол мағынасында түсінуге болмайды.Синтез бен анализ есептердің шығаруда, ойлау процесіндегі индукция және дедукция сияқты бөлінбейді. Физикалық есептерді шығарғанда анализ бен синтезді қолдану бірге алынады, яғни практикада анализдік әдіс қолданылады.
Бұл әдіспен есептің сұрағынан бастап, анализ жолымен шығарғанда, оны шығару үшін не істеу қажеттігін айқындайды және біртіндеп күрделі есепті жай есептер қатарына жіктей келе, шартында берілген белгілі шамаларға дейін жетеді.
Одан кейін синтез көмегімен пайымдауды кері тәртіпке жүргізеді: белгілі шамаларды пайдалана отырып, бірқатар амалдарды жүргізіп барып, нәтижесінде белгісізді табады.
Сапалық есептерді шығару әдістемесі
Оқушыларды сапалық есептерді саналы шығару дағдысын тәрбиелеу үшін, мұғалімнің белгілі бір жүйесі және ойластырылған оқыту әдістемесі болуы керек. Есепті дұрыс таңдаудың маңыздылығы да аз емес. Есептің алғашқы кездерінде оқушылардың өз тәжірибесінен белгілі құбылысқа немесе фактілерге түсінік беруі жүйелі енгізілсе, оқушылар өмірімен байланысты көреді. Ұсынылатын есептердің танымдық және тәрбиелік мағынасы артады.
Оқушылардың политехникалық ой өрісін кеңейту мақсатында 7-сыныптан бастап-ақ есептің шартына оқушылар үшін жаңа деректерді, техникалық мәліметтерді енгізген дұрыс. Есептерді таңдап алуда мектептің айналасындағы өндірістің сипатын және жергілікті жағдайларды ескерудің маңызы үлкен.
Сапалық есептердің шығару негізінен үш кезеңнен тұрады: шартын оқу, есепті талдау және шешу.
Есеп мазмұнын талдау кезінде ең алдымен оқушылар берілген тақырыптағы белгілі ортақ заңдылықтарды пайдаланады: осыдан кейін есептегі айтылған құбылыс қалай нақты түсіндіріулі керек екенің айқындайды. Сапалық есептерге шарттың талдауы негізделген керекті жауаппен тығыз байланысты.
Сандық есептерді шығару әдістемесі
Сабақта күрделі сандық есептерді шығару әдетте мына элементтерден құралады: есептің шартын қысқаша жазу және оны қайталау, суретін, схемасын жәнесызбасын салу, есептің физикалық мазмұның талдау және шығару жолдарын (тәсілдерін) айқындау, шешу жоспарын құру және жалпы түрдегі шешуін орындау, шамалау және есептеулер, нәтиженің талдауы және шешуін тексеру.
Күрделі есептерді шығарудың келтірілген схемасы оқушылардың оның мазмұны мен шешу барысын біртіндеп жан-жақты ойластырудын қамтамасыз етеді.
Келтірілген схема үлгі ретінде алынған. әрбір есепті шығарған сайын барлық жалпы түрде үнемі орындай бермейді; сұрақ – есептердің шығарған кезде есептеулердің қажеттігі болмайды.
Күрделі есепті шығару әдістемесінің кейбір кезеңдеріне қысқаша тоқталайық .
Есептің шартың оқу. Текст анық, мәнерлі, асықпай оқуылуы тиіс. Есептің шартын оқыған соң, мұғалім жаңа терминдердің, қиын ұғымдардың мағынасын (қажет болған жағдайда) түсіндіреді. Кейде мұғалім оқушылардың жаңа терминдерді олардың қалай түсінетінін өздеріне түсіндіруді ұсынады. Талқылау нәтижесінде дұрыс түсінікке келеді. Осыдан кейін есептің шартының қысқаша жазылуын орындайды.
Есеп шартының қысқаша жазылуы. Есептің толық мәтінің тақтаға да, оқушылардың дәптеріне де, әдетте толық жазбаған жөн.
Есептің шартын қайталау. Есептің шартының қысқаша жазылуы бойынша оқушылар оны қайталайды. Оқушылар есепті біле ме, оның шартын дұрыс түсіне ме, соны айқындау мақсатында есеп шартын қайталау ұсынылады. Ол үшін мұғалім кейбір оқушыларға оның мағынасын дәл жеткізе отырып, есеп шартының мазмұнын қайталауды ұсынады.
Осыдан кейін мұғалім, есептің шартын толық мағынасында түсінгендеріне көз жеткізу үшін, оқушыларға бірнеше сұрақтар қояды. Осыған байланысты оқушылар есепті шығару үшін суреттерді (схемаларды, сызбаларды) және кестелік мәліметтерді пайдалану қажет пе, соны анықтайды.
Сызбаны, схеманы, суретті орындау. Көп жағдайларда есептерді шығарғанда сызбалар, схемалар, суреттер пайдаланылады. Бұл есептің шартын түсінуді және оны шешудің тәсілін табуды жеңілдетеді.
Графиктік есептерді шығарғанда статика бойынша сызба есепті оқу барысында орындалуы мүмкін. Бірқатар басқа жағдайларда алдымен есептің шартына сәйкес жұмыстың сызбасын салып алады да, шығару барысында оны ұқыпты қарап, масштабы мен қажетті қатыстарды сақтай отырып орындайды. Оқушылар сызбаны дәптерлеріне салады.
Шарттың талдауы. Есепті талдау кезінде ең алдымен оның физикалық мәніне, берілген қарастырылатын физикалық шамалар арасындағы тәуелділікке көңіл аударады.
7 сыныптан бастап, шыдамдылықпен есептің дұрыс шешімін табу үшін есептің талдауын жүргізу керек, өйткені бұл оқушылардың логикалық ойлауын дамытып, есептерді шығаруға саналы тұрғыдан қарауға тәрбиелейді. Сабақта есепті талдауды көбінесе ұжым болып мұғалімнің оқушылармен әңгімесі түрінде өткізеді, оның барысында мұғалім өзара логикалық байланыста болатын мәселелерді талқылау нәтижесінде біртіндеп оқушыларды есептерді шығарудың неғұрлым тиімді әдісін алып келеді. Кейде бір ғана есептің бірнеше нұсқаларын қарастыру пайдалы, оларды салыстырып және неғұрлым ұтымдысын алу керек. Оқушылардан өз бетінше жасалғансаналы және негізделген пайымдауларды талап ете отырып, есепті талдауға үнемі үйрету керек.
Есеп шығару . есептін шартын талдаған соң оны шығаруға ауысады. Есеп шығаруды қысқаша түсіндірулермен қатар жүргізу керек. Есептеуде ұтымды әдістермен, ал жазудың атауларын мемлекеттік стандарт талаптарына сәйкес қабылданған белгілеулерін қолданып жүргізген дұрыс. Есептің жауабы айқын ерекшеленіп көрсетілуі керек.
Жауабын тексеру және бағалау. Есептің шыққан жауабын тексеру қажет. Ең алдымен оқушылардың жауабының шындыққа сәйкес болуына назар аудару керек. Кейбір жағдайларда оқушылар есеп шығарғанда есептің шартына тіпті сәйкес келмейтін, ал кейде қисыны келмейтін нәтижелер (жауаптар) алады. Оның себебі – есептеу процесінде есептің нақты шартымен байланысты болмауында. Осыдан қате шыққан шалағайлығы оқушылар назарынан тыс қалады.
Бұл кемшілікті болдырмау үшін оларды алдағы күтілетін нәтижені «болжауға» немесе алдын ала есептеуді пайдалануға, сондай-ақ шыққан жауаптың нақтылығы тұрғысынан сын-талдау жасауға үйрету пайдалы. Оқушыларды жауаптың тәртібін сақтай бағалауды, тек математикалық тұрғыдан емес, физикалық тұрғыдан да бағалай білуге үйрету қажет, мысалы, оқушылар мынадай жауаптардың мағынасыздығын бірден көру тиіс: қандай да бір механизмнің п.ә.к. 100%-дан артық, судың қалыпты жағдайдағы температурасы 0 С – тан аз немесе 100 С – дан көп, темірдің тығыздығы 78г/см .
Оқушылар есептің шешуінің дұрыстығын тексеру үшін оны басқа тәсілмен шығарып,нәтижелерді салыстырып,сондай-ақ физикалық шамалардың атау бірліктерімен амалдарды орындай отырып ж/е жауабын есептеп шығуға тиіс атауларымен салыстыра отырып тексереді.
Оқушылардың есепті шешудің атау бірліктеріне амалдар жасау жолымен тексеру әдісін қолдану дағдыларына машықтануына тиісті көңіл бөлу керек.Сабақта оны бірнеше қайтара пайдаланған соң тексерулдің осы әдісінің алгоритмін беруге болады.
Табылған шешудің жалпы түрде дұрыстығын тексеру үшін,шешуінің өрнектейтін формулаға әріпті белгілеулердің орнына физикалық шамалардың атау бірліктерін қойып, оларға шамалармен орындалатын амалдарды жасаймыз.
Есептің шартын және шешуін
жазу тәсілдері Есептің шартын жазудың түрлі формасын қолдануға
болады, бірақ олардың кез келгені негізгі талаптар – қысқалық және
айқындылықты қанағаттандыруы тиіс. Физика есептерінің шешуін жазуға
байланысты мұғалім оқушыларға түрілше талаптар қояды. Біреулер,
мысалы, шешуді жазуды жоспармен қоса орындауды талап етсе,
екіншілер – қысқаша түсінікпен, ал үшіншілері тек есептеулермен
шектеледі.
7-9-ШЫ СЫНЫП ЕСЕПТЕРІН ШЫҒАРУ ӘДІСІ
«Гидростатика» бөлімі бойынша есептерді шығарудың ерекше әдістері
1. Суы бар ашық ыдысқа ашық стақан батырылады: бір рет түбімен жоғары қарай, ал келесісі түбімен астыға (сурет 21) бір тереңдікке батырылады. Осы екі жағдайда, стақанды батырған кезде, қайсысында көп жұмыс атқарылды. (Су ыдыстан ағып кетпейді, және түбімен төменге батырылған стақанға су құйылмайды.)
|
|
|
Сурет 21 |
Шешімі:
Стақан суға батырылған кезде, стақанның суға батуымен оны батыру үшін түсірілген күші жоғарылайды, өйткені кері итеруші күш арта бастайды. Алайда екі жағдайда қарастырылған күш бірдей емес: бірінші жағдайда стақан ішіндегі ауа сығылады және су ішінара стақанға кіреді. Осылайша, бірінші жағдайда стақандардың суға бірдей батырылған кездегі сығылған көлемі аз, демек көтергіш күші және оған тен кұш те аз, стақанды батыруға арналған күштің жұмысы бірдей түсірілген биіктікте аз болғаны.
2. Поршеннің салмағы P = 30 Н,радиусы r = 1 см жұқа қабырғалы түтікке тесігі бар R = 4 см радиусы дөңгелек дискке салынған.Поршень тығыз және үйкеліссіз стақанға кіруі мүмкін және алғашында стақанның төменгі жағында жатады. Поршень қандай Н биіктікке көтеріледі, егер трубкаға m=700 г суды құйса?
Шешімі:
|
|
|
Сурет 22 |
Барлық су поршеньді толтырмайды, оның жарты бөлігі түтікте қалады және қысым күшін тудырады, поршень салмағын теңестіріп.Осы негізінде, жазып алуға болады:


Нәтижесінде, поршень биіктікке көтеріледі

Түбінің ауданы 100 см2 болатын цилиндрлік ыдысқа сұйықтық құйылады, тығыздығы 1,2 г/см3. Оның ішінде массасы 300 г болатын мұз түйіршігі жүзіп жүр. Мұз салдарынан ыдыс түбі қаншалықты қысымды сезеді? Мұз ерігенде ыдыс түбіне түсірілген қысым қалай өзгереді?
S=100
см2=
10-2
м2;




|
|
|
Сурет 23 |


Шешімі: Мұздың жүзу шарты FАрх=mмg. Архимед заңы бойынша кері итеруші күш FАрх=ρgV', мұндағы V' – суға батқан бөлігінің көлемі. Егер мұз ыдыста болмаған жағдайда, онда сұйықтықтың деңгейі мынаған тең болар еді h1 және V'=S(h-h1). Түбіне түсірілген қысым мынаған тең болар еді P1=ратм+ρgh1. Мұз барда түбіне түсірілетін қысым P1=ратм+ρgh. Қысым айырмашылығы
∆р1=P2-P1=ρg(h-h1)=ρgV'/S= FАрх/S=mмg/S=
= .
.
Мұз еріген кезде, соның нәтижесіндегі су сұйықтық бетінде таралады (h1 тереңдікте болады) қалындығы ∆h тегіс қабаты. Енді түбіне түсірілген қысым
р'=ратм+ρgh1+ρсg∆h.
Анықтау бойынша, тығыздығы ρс=mм/Vс=mм/(S∆h). Бұдан ρс∆h=mм/S. Сондықтан, р'=ратм+ρgh1+mмg/S.
Қажетті қысым айырмасы
∆р2=р'-р2=ратм+ρgh1+ mмg/S-ратм-ρgh=р1+ mмg/S-р2= mмg/S-(р2-р1)=0.
Су көлемінің азаюына қарамастан, мұз еріген кезде, түбіне түсірілген жалпы қысымы өзгерген жоқ (мұз көлемімен салыстырғандағы).
-
Тығыздығы ρ1 және ρ2 екі араласпайтын сұйықтықтар ыдыста бар, бұл сұйықтықтар қабатының қалыңдығы тиісінше h1 және h2 тең. Ыдысқа сұйықтық бетінен кішкене аққыш зат түсіреді. Сұйықтық бетінен ыдысқа сумақайлық кішентай денені түсіреді, жылдамдағы нөлге тенелген кезде, дене түбіне түседі. Дененің жасалынған материал қалындығы қандай?
Шешімі.
Энергияның сақталу заңынан: Е2-Е1=А, мүнда А – сыртқы күш жұмысы. Берілген есепте Е2=0 (Жердің потенциалды энергия тартылысы түбінен саналады), сондықтан
mg(h1-h2)=FA1h1+FA2h2,
мұда FА1,2 – денеге әсерін тигізетін Архимед күші.
Нәтижесінде
|
|
|
Сурет 24 |
-
Ортасынан қалқанмен бөлінген h=1 м деңгейіне дейін сумен толтырылған бассейн ауданы S=100 м2. Бассейнді 1/3 бөлікке бөлетіндей етіп қалқанды жәймен жылжытып отырады. Су қалқаннан өтпейтін болса, қандай жұмыс жасау кере?
Шешімі.
Ауырлық күшінің жұмысы потенциалдық жүйесінің энергиясына шығынына тең А'=–∆Ер. ∆Ер=Ер2-Ер0, мұндағы Ер2 – соңғы күйдегі судың потенциалдық энергиясы; Ер0 – бастапқы күйдегі судың потенциалдық энергиясы. Потенциалдық энергиясын шыққаннан бастап бассейнінің төменгі деңгейіне түсуіне дейінгі уақыт, Ер2 үшіносыны аламыз:


(Потенциалдық энергиясының белгілеуін алғаннан кейін бассейнің екі жағында су массасы бірдей екенің ескереміз. Бұдан жұмысқа мынаны аламыз
А=
–А'=
Қорыта келе, мұғалімдерге заман өзгерісіне сай өзгеріп, биік шыңдардан көріне беру керек деген ойдамын. Осы әдіс-тәсілдерді қазақстандық мұғаімдер толық игеріп, тәжірибеге енгізілген жағдайда неге үздік жетістікке жетпеске деген ой түйдім. Болашақта теориялық және практикалық білімдерімізді ары қарай жалғастырып әлі де білімнің биік шыңдарына жетеміз деп ойлаймын
Физикалық есептері шығару тәсілдерінің мынадай түрлері кездеседі
1. Арифметикалық тәсілдер есептер математикалық теңдеулер құрылмай, арифметикалық амалдардың жәрдемімен, сұрақтар қою арқылы шығарылыды. Бұл тәсіл, мысалы, жылу мөлшерін анықтауда көп қолданылады.
2. Алгебралық тәсіл физикалық формулалардың негізінде математикалық теңдеулер құру арқылы есептер шығарғанда қолданылады. Мұндай есептер физиканың әр тарауында көп-ақ.
Күрделі, қиын есептердің көбісі осы тәсілмен шығарылады.
3. Геометриялық тәсіл физикалық есептерді шығаруда фигуралардың геометриялық және тригонометриялық қасиеттерін қолдану қажет болған жағдайда пайдаланылады. Мұндай тәсіл кинематика, статика, электростатика, фотометрия, геометриялық оптика тарауларында есептер шығаруда көп қолданылыды.
1. Графиктік тәсіл арқылы есептер шығарылғанда, олардың жауаптары, түрлі графиктерді талдау негізінде алынады.
2. Эксперименттік тәсіл бойынша есептер эксперимент жүргізудің негізінде шешіледі.
3. Аналитикалық тәсілде есептің мазмұны жеке қарапайым элементтерге жіктеліп, жан-жақты талданып, соның негізінде табуға қажетті шаманы бірден анықтаудың заңдылықтары қарастырылады (жалпыдан жекеге көшу). Бұл «өгізді тікелей мүйізден ұстаумен» бара-бар тіке төте жол, яғни есептің жауабына қатысты формуланы бірден тауып аламыз да, ол арқылы есепті басқа теріс жолдарға бұлтаңдатпай, оған берілген мәндерді қойып есептейміз.
4. Синтетикалық тәсілмен (жекеден жалпыға көшу) шығарғанда, есептің берілгендерді бойынша қандай шамаларды алдымен табуға болса, соны ретімен анықтап, ең ақырында ғана есептің шешуіне жетеміз. Сондықтан да, аналитикалық тәсілді жоғары, ал синтетикалық амалды төменгі кластарда пайдатанған әдістемелік жағынан тиімді деп есептелінеді.
Көп жағдайда физикалық есептер біріккен түрде аналитикалық- синтетикалық тәсілмен де шығарылады, ал кейде 4-5 тәсілдер араласып-қосылып, кешенді формада да шешіледі.
Физика есептерін шығаруда анықтамалық кестелер, логарифмдік сызғыш, микрокалкулятор, ЭЕМ, перфокарта, тексеру- оқыту машиналары, арнаулы дидактикалық тапсырмалар мен программаланған сын жұмыстары жайлы оқу құралдар кең қолданылуы керек.
Жалпы алғанда, физика есептерін шығарудың әдістемесі мынадай негізгі кезеңдерден (мұғалімнің не оқушының қызметінен) тұрады:
1) есептің текстін оқу және талдау, терминдер мен шамалардың мәндерін түсіндіру (мысалы, шығарылған №530 есепті шешудің әдістемесін қарастырайық);
Тексті кітаптан 1-2 рет оқу. Талдауды мынадай сұрақтарға жауап алу арқылы жүргізуге болады: Лифт қалай қозғалып барады? Ол қандай қозғалыста? 10 секундте қанша тереңдікке түскен? Нені табуды сұрайды? Канаттың керілу күші Fk қалай бағытталған?
2) есептің шартын жазу, тиісті сурет схемаларын салуды есептің шығарылуынан көріңіз;
3) физикалық мағыасын ашу мақсатында есептің мазмұнын ( құбылыстар-ды, процестерді) талдау, есепті шығаруға қажетті ұғымдар мен заңдарды қайталап, еске түсіру;
4) есепті шығарудың (эксперименттік жасаудың) жоспарын жасау, физикалық константа мен кесте мәліметтерін пайдалану, график- суретті талдау (мысалы, синтетикалық тәсіл үшін);
5) физикалық шамалардың мәндерін бірдей SI системасында келтіру
( g=9,8 м/с2);
6) берілген және табуға керекті шамалардың байланыстарын көрсететін заңдылықтарды анықтау, тиісті формулаларды табу:
Бір қалыпты үдемелі қозғалыс, Ньютонның екінші заңы: а =2h/t2
P=mg, R=ma, Fk =P- R
7) теңдеулер системасын шешу (эксперименттің приборларын дайындау) Fk =m(g-2h/t2 )
8) табуға керекті шаманы есептеп шығару және талқылау (эксперименттің нәтижелерін талдау, жазу);
9) есепті шығарудың басқа да тәсілдердің қарастыру (мысалы, аналитика-лық тәсіл), олардың ең тиімдісін таңдап алу (топ оқушыларының орташа дайындық жағдайында, синтетикалық тәсіл тиімді деп санаймыз).
Физика есептрін шығарудың тура төте жолы- есепті альгоритмдеу. Алгоритмді түзу процесін есептеп алгоритмдеу деп атайды. Ал алгоритм дегеніміз- есепті шығару тәсілдерінің реттелген дұрыс тізбегі. Алгоритмнің айны-қатесіз дұрыс (оптимал) жолы, жалпы алғанда, оның мынадай алгоритмдік құрылымына сүйеніп түзіледі: есепті шешу кезеңдері-
1) есептің шартымен танысу, 2) есепті шешудің жоспарын жасау,
3) жоспарды жүзеге асыру, 4) есептің шешімін тексеру; бұл кезеңдерді жүзеге асырудың амалдары- есеп шығарудың бағдар бағытын айқындау оны орындау, шығарылған есептің есептің нәтижесін байқап көру.
Осындай ұстамның (принциптің) негізінде есепті шығару процесі алгоритмделінеді.
Физикадан есептер шығарудың жалпы әдістері
Барлық физикалық есептер берілу әдісіне тәуелсіз, жалпы түрде шығарылады. Бұл жағдайда есепті шығару кезінде қолданылатын заңдар анық байқалады, есептің кез келген бөлігін тексеріп, мүмкін қателерді түзеуге мүмкіндік болады. Есептің шешімін алгебралық формула немесе теңдеу түрінде алған соң, оны талдап, іздеп отырған шаманың өзгерту сипаты мен шектерін тағайындауға болады. Бұлармен қоса, ең негізгісі, есепті жалпы түрде шығару физика курсының әр тарауының есептерін шығарудың әдістері мен тәсілдерін жалпылауға мүмкіндік береді.
Есептің шартымен танысқан соң назарды бірден ізделініп отырған шамаға аударып, оны бірден табуға тырыспаған жөн. Ең алдымен есептің шартында қандай физикалық құбылыс жатқанын,ол құбылыстардың негізі қандай заңдармен берілетінін және ол заңдардың математикалық жазылуын анықтауға көңіл аудару керек.
Есептің шартын дұрыс түсініп талдау үшін схемалық чертеждарын салып, берілген құбылысты сипаттайтын барлық шамаларды шартты түрде болса да көрсету керек. Чертеж салынған соң есептің шартын тағы бір рет оқып шығып, чертеждағы шамалардың қайсысы берілгенін және қайсысын анықтау керектігін белгілейді. Одан әрі физикалық заңдар мен формулалардың көмегімен жоғарыдағы айтылған шамалардың арасындағы математикалық байланыстар тағайындалады. Нәтижесінде берілген және белгісіз шамалар енетін бір немесе бірнеше теңдеулер жүйесі алынады. Алгебралық қатынастарды құрғанда, қандай да бір құбылыстарды сипаттайтын физикалық формулаларға енетін шамалардың кейбіреулерінің векторлық екендігіне ерекше назар аудару керек. Бұл шамаларды анықтау үшін олардың сандық мәндері ғана емес, бағыты да ескеріледі. Бұл үшін векторлық шамалардың координатостеріндегі проекциялары анықталып, теңдеулер осы проекциясы арқылы скаляр түрінде жазылады. Осымен физикалық есеп математикалық теңдеулер жүйесін шешпей тұрып берілген теңдеулер мен белгісіздер санының тең екендігіне көз жеткізу керек, әйтпесе теңдеулердің нақты шешуі болмайды.
Теңдеулер жүйесін тиімді әдіспен шешіп, есептің жалпы шешімі алынады да, талданады. Есептің жалпы шешімін талдауға оның өлшем бірліктерін тексеруден бастайды. СИ жүйесіне келтірілген өлшем бірліктер теңдеуге қойылып, қысқартылған соң ізделініп отырған физикалық шаманың өлшем бірлігі қалуы тиіс. Егер қалған өлшем бірлік ізделініп отырған шаманың өлшем бірлігімен сәйкес келмесе, есептің жалпы шешімінде қате бар, оны тексеру керек. Есептің жалпы шешімінің дұрыс екеніне көз жеткізген соң физикалық шамалардың сан мәндерін қойып, есептелініп, ізделініп отырған шаманың сандық мәні анықталады. Арифметикалық есептеулер кезінде дәлдігіне нұсқан келтірмейтін математикалық жуықтап есептеуді қолданған пайдалы. Бұнымен көп жағдайда уақытты ұтуға болады.
Есептің сандық жауабын тексеру және талдау есеп шығарудың соңғы кезеңі. Ең бірінші алынған жауаптың жуықталу реті бағаланады, одан соң оның шындыққа лайықтылығы ескеріледі.
Кинематикаға есептер шығару әдістері
Физиканың әр түрлі тарауларында есеп шығарудың жалпы ерекшеліктерінен басқа, сол тараулардың ерекшеліктеріне байланысты қосымша, өздік сипаттары болады.
Физика курсының кинематика тарауында негізінен есептер нүктенің түзу сызықты бірқалыпты және бірқалыпты үдемелі қозғалысына нүктенің шеңбер бойымен қозғалысына шығарылады.
а) Нүктенің түзу сызықты қозғалысына есеп шығарғанда есептің берілгенін оқыған соң схемалық чертежы салынып, онда санақ жүйесі мен нүктенің қозғалыс траекториясы көрсетіледі. Санақ жүйесін дұрыс таңдап алуға ерекше көңіл бөлу керек. Ол үшін координат жүйесінің бас нүктесін қозғалыстағы нұктенің қарастырылып отырған уақыттың бастапқы сәтіндегі орнына сәйкестендіреді және ості векторлар неғұрлым аз жіктелетіндей етіп бағыттайды. Сонда есептің шығарылуы неғұрлым қарапайым түрде болады және математикалық есептеулер оңайлайады. Санақ жүйесін таңдап алған соң чертежда қозғалыстың барлық кинематикалық сипаттамалары көрсетіледі: қарастырылып отырған уақытта орын ауыстыру, қозғалыстың басындағы және аяғындағы лездік жылдамдықтар, үдеу және уақыт. Егер есептің шарты бойынша қарастырылатын орын ауыстыруда қозғалыстың сипаты әр түрлі болса, немесе орын ауыстыру бірнеше бөліктерден тұрса, жүрілген қолды сонша бөліктерге бөліп әрқайсысындағы қозғалысты жеке қарастырады.
Чертеж салынған соң, қозғалысты сипаттайтын формулалар арқылы, чертеждағы физикалық шамалардың арасындағы байланыстарды тағайындаймыз. Нүктенің қозғалысының кинематикалық теңдеулерінің толық жүйесін құрған соң, есептің берілгеніндегі шарттарды қосымша теңдеулер түрінде жазып, теңдеулер саны белгісіздер санына сәйкестендіріледі. Осыдан соң теңдеулер жүйесін шешуге кірісіледі.
Мысал
1. самолет А пунктінен
шығысқа қарай 300 км қашықтыққа орналасқан В пунктіне ұшып келеді.
Егер: 1) жел жоқ болса, 2) жел оңтүстіктен солтүстікке қарй соғып
тұрса және 3) жел батыстан шығысқа қарай соғып тұрса, онда үшу
уақытының ұзақтығы қандай? Желдің
жылдамдығы ![]() =20 м\с, ауамен
салыстырғандағы самолеттің
жылдамдығы
=20 м\с, ауамен
салыстырғандағы самолеттің
жылдамдығы ![]() =600
км\сағ.
=600
км\сағ.
Берілгені: шығарылуы:
S=300
км= ![]() Есепті шығаруды санақ
жүйесін таңдап алудан
Есепті шығаруды санақ
жүйесін таңдап алудан
![]() =20 м\с, бастайық.
Қозғалмайтын санақ жүйесін жермен,
=20 м\с, бастайық.
Қозғалмайтын санақ жүйесін жермен,
![]() =600 км\сағ=166 м\с ал
қозғалыстағы санақ жүйесін ауамен байла-
=600 км\сағ=166 м\с ал
қозғалыстағы санақ жүйесін ауамен байла-
Тк ![]() ныстырамыз.
Онда
ныстырамыз.
Онда ![]() -ауыспалы (желдің жерге
-ауыспалы (желдің жерге
қарағандағы)
жылдамдық, ![]() - салыстырмалы (самолеттің ауаға
қарағандағы) жылдамдық болады. Абсолют жылдамдық
болса
- салыстырмалы (самолеттің ауаға
қарағандағы) жылдамдық болады. Абсолют жылдамдық
болса ![]() қатынасымен анықталады.
қатынасымен анықталады.
Есептің схемалық чертежін салайық:

Самолет А нүктесінен В нүктесіне түзу баруы үшін
абсолют жылдамдық міндетті түрде ОХ осімен бағытталуы керек. Үш
жағдайда да қозғалыс бірқалыпты түзу сызықты, ендеше қозғалыс
теңдеуі: ![]() немесе S=Vt түрінде
жазылады.
немесе S=Vt түрінде
жазылады.
Бұдан ![]() (V – абсолют жылдамдық)
(V – абсолют жылдамдық)
1) ![]() =0 онда, V=
=0 онда, V= ![]() және
және ![]()
![]()
2) ![]()
![]() , онда
, онда
![]()
Параллелограммға
толықтырылып, ![]() - бағыты анықталады. Самолет ОХ бойымен
қозғалу үшін,
- бағыты анықталады. Самолет ОХ бойымен
қозғалу үшін, ![]() суреттегідей бағытталуы керек.
Онда
суреттегідей бағытталуы керек.
Онда ![]() .
.
Суреттен ![]()
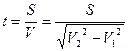
![]()
![]()
3) ![]() - ОХ бойымен бағытталған,
онда
- ОХ бойымен бағытталған,
онда ![]() де сол ось бойында жатады, сонда ғана –ОХ
бағытына сәйкес болады.
де сол ось бойында жатады, сонда ғана –ОХ
бағытына сәйкес болады.
![]()
Сондықтан ![]() , яғни
, яғни ![]() ;
;
![]()
Түзу сызықты бірқалыпты үдемелі қозғалысқа берілген есептер негізінен екі формуланы қолданумен шығарылады:
![]()
![]()
Немесе қозғалыс түзу сызықты болғандықтан
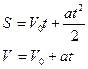
Мұндағы ![]() =сonst
=сonst ![]()
Осы теңдеулерге есептің шартынан қосымша теңдеулер жазылып, теңдеулер жүйесі құрылады. Теңднулер саны белгісіздер санынан кем болмаса, теңдеулер жүйесі ең тиімді тәсілмен шешіледі.
Мысал 2. Автомобиль 0,5 м\с үдеумен қозғала бастаған моментте оның жанынан бірқалыпты үдемелі қозғалып, 18 км\сағ жылдамдықпен трамвай өтеді. Трамвайдың үдеуі 0,3 м\с. Автомобиль трамвайды қуып жеткенде жылдамдығы қандай болады?
Берілгені:
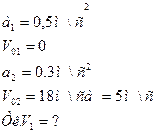
Шығарылуы:
Қозғалыстар бірқалыпты үдемелі. Санақ жүйесінің бас нүктесіне автомобиль мен трамвай кездескен нүктені сәйкестендіреміз. Уақытты есептеу де осы нүктеден басталады. Қозғалыстың схемалық чертежін саламыз.
Траекторияны бейнелеп, кинематикалық шамаларды белгілейміз. Екі дене үшін де қозғалыс теңдеулерін жазамыз: автомобиль үшін:
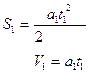
Трамвай үшін: 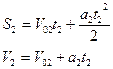
Есептің шартынан қосымша теңдеулер жазайық. Денелер бірдей уақытта бірдей жол жүреді (кездеседі).
![]()
Онда жоғарыдағы алғашқы үш теңдеу мына түрде жазылады:
![]()
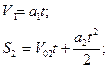 (1)
(1)
Немесе ![]() екенін
ескерсек
екенін
ескерсек 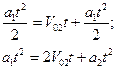
Бұдан ![]()
Уақыттың бұл мәнін (1) жүйедегі екінші теңдеуге қойсақ:
![]()
![]()
Есеп жалпы түрде шығарылды. өлшем бірлігінің дұрыс екендігі, яғни есептің дұрыс шыққаны оңай тексеріледі:
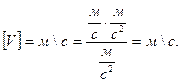
Жылдамдықтың сандық мәнін есептейміз.
![]()
Есептің жауабының мәні есептің шартына қарағанда нанымды.
Жанынан 5 м\с жылдамдықпен өткен трамвайды қуып жету үшін автомобиль осындай үлкен жылдамдық алу керек.
Вертикаль жоғары лақтырылған дененің қозғалысына есеп шығарғанда ерекше көңіл аудару қажет. Вертикаль жоғары лақтырылған дененің жылдамдығы (V) мен орын ауыстыруының (S=h) уақытқа (t) тәуелділік теңдеулері олардың арасындағы байланысты бүкіл қозғалыс барысында сипаттайды. Олар жоғары баяулай көтерілгенде ғана емес, траекторияның жоғарғы нүктесінде бір сәт тоқтап, бұрыңғы үдеумен төмен қозғалғанда да дұрыс, тек үдеудің таңбасының өзгеретіні ескеріледі, яғни қозғалыс теңдеулері жоғары көтерілгенде
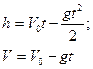
ал төмен қозғалғанда
![]()
түрінде жазылады.
Егер ауаның кедергісі ескерілмесе толық үдеу еркін түсу үдеуіне тең екендігі белгілі. Сонымен қоса дененің максималь биіктікке көтерілу уақыты оның құлау уақытына, ал құлау жылдамдығы жоғары лақтырылған бастапқы жылдамдыққа тең.
Мысал 3. доп һ=10 м биіктіктегі нүктеден вертикаль жоғары лақтырылған. Барлық қозғалыс уақытында ол 3һ жол ұшқан деп есептеп, доптың бастапқы жылдамдығын, қозғалу уақытын және құлау жылдамдығын табыңыздар.
Берілгені: шығарылуы:
Һ=10м қозғалыстың схемалық чертежын саламыз. Ол
l=3h үшін санақ жүйесінің бас нүктесіне доптың
Тк: ![]() =? t=? V=? лақтырылған
нүктесін немесе доптың жер бетіне құлаған нүктесін алуға болады.
Қай нүктені таңдағанымыздан есептің нәтижесі өзгермейді. Санақ
жүйесінің бас нүктесін (0) жермен байланыстырайық. Дененің қозғалыс
траекториясын белгілейік те
бастапқы
=? t=? V=? лақтырылған
нүктесін немесе доптың жер бетіне құлаған нүктесін алуға болады.
Қай нүктені таңдағанымыздан есептің нәтижесі өзгермейді. Санақ
жүйесінің бас нүктесін (0) жермен байланыстырайық. Дененің қозғалыс
траекториясын белгілейік те
бастапқы ![]() және соңғы V
жылдамдықтарды, биіктіктерді һ және
уақыттарын
және соңғы V
жылдамдықтарды, биіктіктерді һ және
уақыттарын ![]() көрсетейік. Есептің
шартынан егер дене 3һ жол жүрсе ол лақтырылған нүктеден биіктікке
көтеріліп, 2һ төмен құлайтынын табуға
болады
көрсетейік. Есептің
шартынан егер дене 3һ жол жүрсе ол лақтырылған нүктеден биіктікке
көтеріліп, 2һ төмен құлайтынын табуға
болады
Жоғары көтерілгендегі қозғалыс теңдеуін жазайық.
![]()
![]()
Ең жоғарғы нүктеде V=0,
онда ![]() Бұны бірінші теңдеуге
қойсақ
Бұны бірінші теңдеуге
қойсақ
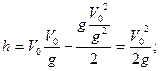
онда ![]() ал
ал 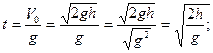
төмен қозғалғандағы қозғалыс
теңдеуі: ![]()
және ![]()
![]() , бұдан
, бұдан 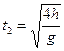 , ендеше
, ендеше
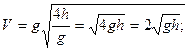
ал толық уақыт ![]() , жоғарғы мәндерін
қойсақ:
, жоғарғы мәндерін
қойсақ:
![]()
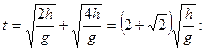
Сан мәндерін қойып есептейміз:
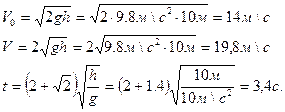
Формулалрға екі ғана шама енгендіктен өлшем бірліктерін жеке тексермей-ақ, бірден қоюға болады.
Қисық сызықты қозғалысқа берілетін есептерден негізінен нүктенің шеңбер бойымен қозғалысы және горизонтқа бұрыш жасай лақтырылған денелердің қозғалысы қарастырылады.
Нүктелердің шеңбер бойымен қозғалысына есептер шығарудың түзу сызықты қозғалысқа берілген есептерді шығарудан принципиалды айырмасы жоқ. Ерекшелігі айналмалы қозғалыс кинематикасы теңдеулерімен қоса айналмалы және сызықтың қозғалыс сипаттамаларының арасындағы байланысты ескеру керектігінде.
Егер дене тұрақты бұрыштық үдеумен айналса, онда оның қозғалыс теңдеулері түзу сызықты қозғалыстағы сияқты мынандай түрде жазылады:
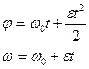
Егер қозғалыс бірқалыпты айналмалы болса ω=const,
ε=0, ε>0 ,болса ω> ![]()
Бұрыштық жылдамдық артады, ал ε<0 болса
кемиді: ω< ![]() . Екінші жағдайда теңдеулер теріс таңбамен
жазылады, яғни:
. Екінші жағдайда теңдеулер теріс таңбамен
жазылады, яғни:
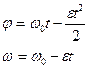
![]()
Сызықтық және бұрыштық жылдамдықтар арасындағы
байланыс V= ωR түрінде беріледі, бұдан ![]()
![]() - жанама үдеу. Осы теңдеулерге есептің
шартынан қосымша теңдеулер қосылып, кез келген есепті шығаруға
болады.
- жанама үдеу. Осы теңдеулерге есептің
шартынан қосымша теңдеулер қосылып, кез келген есепті шығаруға
болады.
Мысал 4.
Автомобиль қисықтық радиусы R=50 м-ге тең
шоссенің бойымен келе жатыр. Автомобильдің жүру
теңдеуі ![]() мұндағы А=10м, В=10 м\с, С=-0,5
м\с
мұндағы А=10м, В=10 м\с, С=-0,5
м\с ![]() . 1) t=5 с уақыт мезетіндегі автомобильдің
жылдамдығын v, тангенциал
. 1) t=5 с уақыт мезетіндегі автомобильдің
жылдамдығын v, тангенциал ![]() , нормаль
, нормаль ![]() және толық а үдеулерін; 2) автомобиль
қозғаннан бастап t=10с-қа дейінгі аралықта жол ұзындығын s және
ығысу модулін ∆r табу керек.
және толық а үдеулерін; 2) автомобиль
қозғаннан бастап t=10с-қа дейінгі аралықта жол ұзындығын s және
ығысу модулін ∆r табу керек.
![]()
|
|
|
|
|
|
|
|
|
|
Берілгені:
R=50м
ξ(t)=A+B+Ct ![]()
A=10м
В=10м\с
С=-0,5м\с ![]()
1) t=5c
2) t=0 c-тан t=10c-ге дейінгі аралықта
Табу керек: 1)
v, ![]() ,
, ![]() ,a;
,a;
2) s, ∆r
Шешуі:
1. бұл есепте жұру теңдеуін біле отырып жылдамдықты теңдеуден уақыт бойынша бірінші туындысын алу арқылы аламыз.
![]() Осы теңдеуге В,С және t-ның мәндерін қоя отырып жылдамдықтың сан мәнін табамыз
Осы теңдеуге В,С және t-ның мәндерін қоя отырып жылдамдықтың сан мәнін табамыз
![]() =10+2*(-0,5)*5=5м\с.
=10+2*(-0,5)*5=5м\с.
Жылдамдықтың уақыт бойынша бірінші туындысын алып тангенциал үдеуді ![]()
![]() табамыз.
С-ның мәнін қоя отырып::
табамыз.
С-ның мәнін қоя отырып::
![]() .
.
Нормаль үдеу келесі теңдеумен анықталады ![]() .
Осы теңдеуге табылған жылдамдықтың және берілген траекторияның қисықтық радиусының мәндерін қоя отырып нормаль үдеудің келесі мәнін аламыз:
.
Осы теңдеуге табылған жылдамдықтың және берілген траекторияның қисықтық радиусының мәндерін қоя отырып нормаль үдеудің келесі мәнін аламыз:
![]() =5
=5 ![]() .
.
Суретте көрсетілгендей,
толық үдеу ![]() және
және ![]() үдеулерінің геометриялық қосындыларына тең болатынын көреміз:
үдеулерінің геометриялық қосындыларына тең болатынын көреміз: ![]() .
Үдеудің модулі
.
Үдеудің модулі ![]() -ге тең.
Осы теңдеуге
-ге тең.
Осы теңдеуге ![]() және
және ![]() үдеулерінің сан мәндерін қоя отырып,
үдеулерінің сан мәндерін қоя отырып, ![]() =
= ![]() .
.
2. Автомобильдің жүрген s жолын анықтау үшін бір бағыттағы жүрген қозғалыс жағдайында жол ұзындығы s қисық сызықты координата ξ –дің өзгертетініне тең, яғни
S=
ξ(τ)-
ξ(0),
немесе s=A+Bt+C ![]() -A.
-A.
Алынған теңдеуге В,С және τ-лардың мәндерін қойып, есептесек:
s=A+Bt+C ![]() -A=10+10*10+(-0.5)*10
-A=10+10*10+(-0.5)*10 ![]() -A=50м.
-A=50м.
Суреттен көретініміздей орын ауыстыру модулі мынаған тең ∆r=2Rsin
(![]() \2).
\2).
Мұндағы ![]() -автомашинаның траекториясындағы бастапқы ξ(τ)
және ξ(0)
орындарын анықтайтын радиус-векторлар арасындағы бұрыш.
Бұл бұрышты (радиан өлшем бірлігінде) s
жолдың R
қисықтық радиусына қатынасы ретінде табамыз,
яғни
-автомашинаның траекториясындағы бастапқы ξ(τ)
және ξ(0)
орындарын анықтайтын радиус-векторлар арасындағы бұрыш.
Бұл бұрышты (радиан өлшем бірлігінде) s
жолдың R
қисықтық радиусына қатынасы ретінде табамыз,
яғни ![]() =s/R. Олай болса,
=s/R. Олай болса,
∆r=2Rsin (s/2R).
Бұл теңдеуге R, s мәндерін қойып есептеу нәтижесінде табатынымыз:
∆r=2Rsin (s/2R)=2*50*sin(50/2*50)=47.9 м.
Жауабы: v=5м/с, ![]() =-1 м/с
=-1 м/с ![]() ,
, ![]() =0,5 м/с
=0,5 м/с ![]() , а=1,12 м/с
, а=1,12 м/с ![]() ,s=50м, ∆r=47.9м.
,s=50м, ∆r=47.9м.
Горизонтқа бұрыш жасай лақтырылған дененің қозғалысы ОХ және ОY осьтерінің бойымен өтетін екі түзу сызықты қозғалыстарының қосындысы ретінде қарастырылады.
ОХ осі жер бетінің бағытымен,
ОY
осі оған перпендикуляр бағытталады. ОХ осі
бойымен өтетін қозғалыс бірқалыпты түзу сызықты, ал
ОY
осі бойындағы, қозғалыс вертикаль жоғары
лақтырылған дене қозғалысы сияқты, яғни бірқалыпты үдемелі қозғалыс
болып табылады. Бұл қозғалыстардың теңдеулерін, оларға жеке-жеке
есеп шығарудың әдістерін жоғарыда қарастырдық. Бұл қозғалысқа
арналған есептердің барлығын шығаруды, жоғарыда айтқанымызда
ескеріп, жылдамдық және үдеу векторларын ОХ және
ОY
остеріне жіктеуден бастайды. Кейін барып әр
бағытта қозғалыс теңдеулерін құрады. Дене горизонтқа бұрыш жасай
аса үлкен емес (бірінші космостық жылдамдықтан кіші) жылдамдықпен
лақтырылғанда, ауаның кедергісі ескерілмеген жағдайда, парабола
бойымен қозғалатыны және екі қозғалысқа дене бір мезгілде
қатысатындықтан ОХ бойымен қозғалу уақыты
ОY
бойымен қозғалу уақытына тең болатыны есте болу
керек. Тағы бір ескеретін жағдай траекторияның кез келген
нүктесінде толық үдеу еркін түсу үдеуіне тең де, жердің центріне
бағытталады, яғни a=g= ![]()
Бұл тақырыпқа есептер шығарар алдында, қозғалыстың схемалық чертежын жалпы жағдайға сызып алып (көрнекті етіп ), оны барлық дербес жағдайларға қолдануға болады. Чертежда санақ жүйесі, кинематикалық сипаттамалар (V,a), олардың остер бойынша t=0 және кез келген уақытта жіктелу, қозғалыс теңдеулері, траектория бейнесі, үдеудің жіктелуі көрсетіледі.
Мысал 5.
Допты горизонтқа ![]() бұрыш жасай
бұрыш жасай ![]() =10 м/с жылдамдықпен лақтырылған.
Мыналарды: 1) доптың қандай
=10 м/с жылдамдықпен лақтырылған.
Мыналарды: 1) доптың қандай ![]() биіктікке көтерілгенін .2) доптың лақтырған
жерінен жер бетіне түскен ℓ қашықтығын. 3) оның қанша уақыт
қозғалыста болатындығын табу керек. Ауаның кедергісі есепке
алынбайды.
биіктікке көтерілгенін .2) доптың лақтырған
жерінен жер бетіне түскен ℓ қашықтығын. 3) оның қанша уақыт
қозғалыста болатындығын табу керек. Ауаның кедергісі есепке
алынбайды.
![]() Берілгені: Шығарылуы:
Берілгені: Шығарылуы:
![]() 1-суреттен қозғалыс теңдеулерін
жазайық
1-суреттен қозғалыс теңдеулерін
жазайық
![]()
![]() =10 м/с
=10 м/с 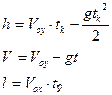
Т.к. ![]() =? ℓ=?
=? ℓ=? ![]() =?
=?
Мұндағы ![]() - көтерілу, ал
- көтерілу, ал ![]() - ұшу
уақыттары
- ұшу
уақыттары ![]() .
. ![]() болғандықтан
болғандықтан
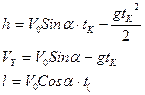
Максималь көтерілу
нүктесінде ![]() , ендеше
, ендеше ![]()
Бұдан ![]()
Онда 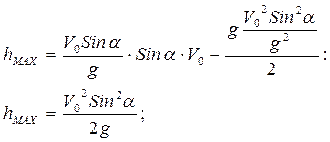
Көтерілу уақыты мен түсу уақыты бірдей және олардың қосындысы ұшу уақытына тең екенін ескерсек
![]()
Бұл өрнекті үшінші теңдеуге
қойсақ 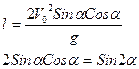
Немесе
![]()
![]()
Сан мәндерін қойып шығарамыз:
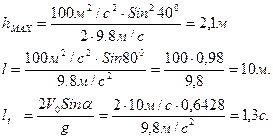
Өлшем бірліктерін сан мәнімен бірге қойып тексереміз. Физика есептерін шығару үшін теорияны терең түсініп,іс жүзінде практикада пайдалана білуі керек, терең ойланып күрделі мәселелерді, құбылыстарды талдап, зерттеп шеше алатындай болуы керек. Есептер қандай да бір нақты жағдайларда болып өтетін құбылыстарға физикалық заңдарды қолдануды талап ететін жаттығулар үшін материалдар береді. Сондықтан есептердің оқушылардың білімін нақтылауда, жалпы заңдардың түрлі көрінісін көруде үлкен маңызы бар.
Қорытынды
Қорытындылай келе, оқушылардың физика пәніне деген қызығушылығын, ынтасын арттыру үшін сапалық есептердің маңызы ерекше. Бұл есептерді физика пәнін жаңа бастаған 7 — сынып оқушылары үшін қолданыс аясын кеңейту олардың пәнді тереңірек түсінуіне елеулі әсерін тигізері анық. Біз білеміз, кез-келген есептерді шығару ол белгілі бір мақсатқа қарай бағытталады. Сондықтан да, біз оқушыларға есеп шығарудың айқын мақсатын қойған дұрыс деп санаймыз. Сапалық есептерді шешу арқылы оқушылардың шынайы әлемнің нақты объектілерін зерттеуде ғылыми түсініктері қалыптасады. Мектептегі физика курсын меңгеруде көптеген сапалық есептерді енгізу, білім сапасын арттыруға септігін тигізеді. Есеп түріндегі эксперименттік тапсырмаларды шешу және жазу келесі элементтерден тұрады: есептің қойылуы, шарттарды анализдеу, өлшеулер жүргізу, есептеулер, тәжірибеден тексеру. Эксперементтік есептердің бағалы жері - ол оқушылардың алған білімін практикада қолдана білуін тексеруге жол ашады.
Пәнаралық байланыстар: Алгебра, геометрия, информатика, химия, экономика, биология және өндірістік оқулықтар.
Кәсіби бағдарлау. Кәсіби бағдарлау, оны оқушыларды диагностикалық материалдарына сүйене отырып таңдауды негіздеу.
Оқушылар осы курсты оқу нәтижесінде мынадай мамандықтарды игеруге дайындалуға мүмкіндік алады: Педагогика, экономика, архитектор, әскери, құрылыс мамандары. Табиғатты саналы танудың міндетті ретінде алдынғы шартты ғылыми деректерді іздестіріп жинақтау. Байқау мен эксперимент жүргізу. Физикалық шамаларды анықтап, өлшем бірліктерін тағайындау және сан мәнін өлшей білу.
ӘДЕБИЕТТЕР ТІЗІМІ
Задачи по физике. Воробьев И.И., Зубков П.И., Кутузова Г.А. и др., М., 1999 г., 370 с.
-
Задачи по физике Пособие для учащихся 9-11-х классов. Гомонова А.И., Плетюшкин В.А., Погожев В.А., М., 1998 г., 192 с.
-
Задачи по физике для поступающих в вузы. Бендриков Г.А., Буховцев Б.Б., Керженцев В.В., Мякишев Г.Я., М., 2005 г., 344с.
-
Задачи по физике с анализом их решения. Савченко Н.Е., М., 2000 г., 320с.
5. Қазақстан Республикасының «Білім туралы» Заңы »
6. А.Б.Мәженова. Физика есептерінің жинағы. 9-11 сыныптар
7. Б.Дүйсембаев, Д.Қазақбаева. Физика анықтамалық құрал.
8. Баканина Л. П. и др. Сборник задач по физике: Учебное пособие для углубленного изучения физики в 10-11 класс, М.: Просвещение, 1995.
9. Балаш В. А. Задачи по физике и методы их решения. М.: Просвещение, 1983.
10. Д.Қазақбаева, Ш.Кәрібаева. Бағдарлы оқытуды ұйымдастыру жолдары. Физика және Астрономия, №1, 2006ж.
МАЗМҰНЫ:
-
Кіріспе..........................................................................................3
2.Физика бойынша есеп шығарудың тиімді әдістемесін
құрастырудың заманауи тәсілдері..................................................6
3.Сапалық есептерді шығару әдістемесі........................................12
4. 7-9-шы сынып есептерін шығару әдісі«Гидростатика»
бөлімі бойынша есептерді шығарудың ерекше әдістері..............16
5. Физикалық есептері шығару тәсілдерінің мынадай
түрлері кездеседі..............................................................................21
6. Физикадан есептер шығарудың жалпы әдістері.......................24
7 Кинематикаға есептер шығару әдістері......................................26
8 Қорытынды.....................................................................................41
-
Әдeбиeттep тізімі.........................................................................42
43

шағым қалдыра аласыз