
Мазмұны
1. Кіріспе
2. Физикадағы ғылыми есептеулерде математиканың рөлі
3. Математика мен физиканың өзара байланысы: пәнаралық байланыстар
4. Физика сабақтарында математикалық білімді қолдану
5. Физикадағы математикалық әдістер: негізгі тәсілдерге шолу
6. Физикалық заңдарды тұжырымдау негізі ретінде математика
7. Физикадағы математикалық модельдеу: практикалық қолдану
8. Физикадағы математикалық талдау: негізгі аспектілер
9. Физикадағы математикалық теңдеулер: мысалдар және қолдану
10. Физиканы зерттеуде математикалық білімнің маңызы
11. Физикадағы математикалық аппарат: заманауи тенденциялар
12.«Физикадағы математиканың рөлі» ғылыми-зерттеу жұмысы
13. Қорытынды
14. Әдебиеттер тізімі
Кіріспе
Жоба физика саласындағы математикалық есептеулердің рөліне арналған. Математика физикада негізгі рөл атқарып, физикалық заңдарды тұжырымдау, ғылыми есептеулер жүргізу және эксперименттік деректерді талдау үшін негіз болып табылады. Бұл жобада физикадағы математикалық әдістердің маңызы және олардың осы ғылымның әртүрлі аспектілерінде қолданылуы қарастырылады.Математика мен физика әдетте мектеп бағдарламасындағы ең қиын пәндер болып саналады. Мектептегі сабақтарға физика мен математиканы кіріктіру тек осы пәндерді тереңдетіп оқытылатын сыныптарда ғана мүмкін болады деп жалпы есептейді. Біз мұндай интеграцияның көптеген элементтері физика презентациясын оқудың барлық деңгейлерінде айқынырақ және қолжетімді ете алады деп есептейміз. оқушылар физика сабағында сұрағын түсіне алмауы немесе физика есептерін шеше алмауы көбінесе функционалдық тәуелділіктерді талдау, математикалық теңдеулерді құру және шешу дағдыларының жеткіліксіздігімен, алгебралық және геометриялық тапсырмаларды орындай алмауымен байланысты. байланысқан конструкциялар.Бірінші дүниежүзілік соғыс кезінде кейінірек Америка азаматтығын алған неміс физигі және математигі Альберт Эйнштейн дүние жүзіндегі астрономдарды, физиктер мен математиктерді таң қалдырған ерекше және күтпеген жаңалық жасады. Көптеген ғалымдарға қате болып көрінген ұстанымдарға сүйене отырып, Эйнштейн математикалық есептеулер арқылы жарық сәулесінің ауырлық күшіне ұшырайтынын және ол ауыр дененің жанынан өткенде, оның сол денеге қарай тартылып, итерілетінін дәл есептеді. Эйнштейн күн сәулесінің қаншалықты ауытқуы керектігін есептеді. Дүние жүзіндегі астрономдар бірден Эйнштейннің есебін тексеруге кірісті. Британдық астрономиялық қоғам үкіметтің мақұлдауымен екі жылдан кейін болатын күннің толық тұтылуы кезінде осы сынаққа дайындықты бастады. Күннің осындай толық тұтылуы кезінде ғана Күннің артында орналасқан жұлдыздың сәулелерін Күнге жақындаған кезде байқауға болады. Күн тұтылуын бақылаудың келесі ең жақсы жері Оңтүстік Африканың шөлінде болғандықтан, экспедицияға көптеген техника мен көптеген қызметкерлер дайындалуға тура келді. Мұның бәрі жасалды және сынақ нәтижелері Эйнштейннің есептеулерін растады.Эйнштейннің есебінің ақиқатқа жетуі жемісті гипотезаны басшылыққа ала отырып, адам санасының неге қабілетті екенін көрсетті. Эйнштейннің жаңалығы математиканы ойлаудың нақты және қатаң құралы ретінде пайдалануға болатынын тағы бір рет көрсетеді. Ежелгі дәуірдегі ең ұлы ғалымдардың барлығының бір мезгілде математиктер, физиктер және астрономдар болуы бұл ғылымдардың жеке өмір сүрмейтінін растайды. Әрбір физикалық мәлімдеме эксперименттік деректер мен математикалық есептеулерге негізделген дұрыс. Өкінішке орай, студенттер үшін физика - ақылға қонымсыз, ал математика - ақылға қонымсыз екені жиі шығады.
Бұл жұмыста біз зерттелетін материал мен математикадан алынған білімдерді физикалық есептерді шешу үшін және керісінше пайдалану мүмкіндігі арасындағы байланысты көрсетуді жөн көрдім.
Мақсаты: физикадағы математикалық есептеулердің рөлін қарастыру, математика мен физиканың өзара байланысының негізгі аспектілерін анықтау және физика сабақтарында математикалық білімдерді практикалық қолдануды талдау.
1) Пәнаралық байланыстардың мәнін, қызметін және олардың жіктелуін анықтау;
2) Математикада қандай ұғымдар және олардың физикада қалай қолданылатынын көрсетіңіз.
№1 тапсырма
Математика білімін не үшін қажет ететінін көрсетіңіз.
№2 тапсырма
Физикаға қажетті математикалық ұғымдарды анықтау.
Жобаның міндеттері:
-
Физикада қолданылатын негізгі математикалық әдістерді зерттеу.
-
Ғылыми және оқу контексттерінде математика мен физиканың өзара байланысын талдау.
-
Физика сабақтарында математикалық білімдерді практикалық қолдануды зерттеу.
Зерттеу нысаны: физикадағы математикалық әдістер
Зерттеу пәні: математика мен физиканың өзара байланысы
Зерттеу әдістері: ғылыми әдебиеттерді талдау, сұхбаттар, сауалнамалар
Ғылыми жаңалығы:Оқыту контекстінде математика мен физиканың өзара байланысын зерттеу
Жобаның идеясы:Жобаның идеясы – физиканы табысты оқып-үйрену және практикалық қолдану үшін математикалық әдістерді түсінудің маңыздылығын атап көрсету, сондай-ақ осы екі ғылымның өзара әрекеттесуінің негізгі аспектілерін анықтау.
Жаңалығы :Жоба физикадағы математикалық есептеулердің маңыздылығы туралы жеткіліксіз хабардарлықты және физиканы оқу кезінде математикалық білімдерді практикада қолданудағы қиындықтарды шешеді.
Ресурстар: Оқу әдебиеті, ғылыми мақалалар, оқу құралдары, әдістемелік әзірлемелер
Әдістері : жалпы ғылыми, нақты ғылыми, логикалық.Математиканың физикада қандай рөл атқаратынын сізге көрсетіп, дәлелдеуге тырысайық.
Пәнаралық байланыс принципі физиканы зерттеудің негізінде жатыр, өйткені бұл ғылым басқа салалардағы білімдерді қамтиды және олар өз кезегінде оларды түсіну үшін қажет. Физика сабақтарында көптеген құбылыстар мен процестерді қарастыру кезінде көптеген басқа пәндерді білу қажет, мысалы, математика, география, химия, биология және т.б. Сонымен бірге бұл оқу пәндерін оқу физиканы және физика ғылымдарының әдістерін терең және берік білуді талап етеді (мысалы, энергия ұғымдарын және биологиялық процестерде энергияның сақталу және түрлену заңын қолдану; физикалық құбылыстар). . , астрономиядағы заңдар мен әдістер және т.б.). Бұл пәнаралық байланыс принципі қазіргі уақытта жоғары дамыған ғылымдардың дифференциациясын және бірігуін қамтиды дегенді білдіреді.
Физикадағы ғылыми есептеулерде математиканың рөлі
Математиканың физикадағы рөлін асыра бағалау мүмкін емес. Галилео Галилей: «Математика - бұл табиғат кітабы жазылған тіл», - деп атайды. Математиктердің жұмысы – жаңа математикалық объектілерді табу және олардың қасиеттері мен байланыстарын зерттеу. Галилео заманынан бері математиканың көптеген жаңа салалары математикалық объектілерді сипаттауға арналған өз тілімен пайда болды.
Белгілі математикалық объект – функцияны алайық. Ол мектеп бағдарламасына нысан бойынша енгізілген y = f ( x ) және айнымалылардың қандай да бір тәуелділігінің көрсеткішін білдіреді j айнымалыдан X.
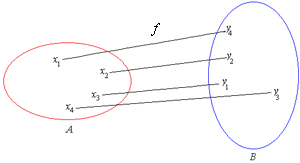
 Дегенмен, жиынтық теориясы тұрғысынан функция
болып табылады Жарнама бір сөйлемнен
екіншісіне:
Дегенмен, жиынтық теориясы тұрғысынан функция
болып табылады Жарнама бір сөйлемнен
екіншісіне:
A → fB
Ал абстрактілі алгебраның көмегімен функцияны оператор және мәндер
жиыны ретінде көрсетуге
болады X Және j векторлар болып саналады. Бұл сипаттамада
функцияны көрсету оператор матрицасын көрсетуге сәйкес
келеді F ^ F^
.
Y = F ^ X
Y=F^X
Ал пертурбация теориясында функцияларды шексіз қатар арқылы анықтау жиі кездеседі. Сонымен қатар, қатардың ерекше табиғаты функцияны анықтаудың әртүрлі облыстары үшін әртүрлі болуы мүмкін.
f ( x )=∑ n = 0 ∞anxn
Яғни, функция әртүрлі математикалық әдістерді қолдану арқылы «көрінетін» абстрактілі математикалық нысанның бір түрі ретінде өмір сүреді. Бұл аргументтерді кез келген дерлік математикалық объектіге қолдануға болады. Мысалы, векторды абстрактілі символ арқылы көрсетуге болады v немесе нақты координаттың көрінісі ( vx , vy , vz ) . Сонымен қатар, бұл координаттардың сандық мәндері таңдалған координаталар жүйесі мен негізіне байланысты.
Дегенмен, авторлар құбылыстардың физикалық
мазмұнын жасыратын және ішінара бұрмалайтын физиканың шамадан тыс
математикалану процесін сынайтын басылымдар барған сайын пайда
болуда.
Физика нақты табиғатты сипаттауы керек, ал математика адам ойының
жемісі. Математика формальды логикаға негізделген; олар үшін,
мысалы, Евклидтің де, Лобачевскийдің де геометриясы бірдей, ал
физика тек табиғатта бар нақты геометрияны көрсетуі керек. Бірақ
бұл тек математикаға тән формализм туралы емес. Қосымша екі
жағдайды ескеру қажет.
Біріншіден, белгілі бір математикалық теорияның
тұжырымдары эксперименттік фактілермен әлі расталған жоқ.Бұл
математикалық теорияның жалғыз дұрыс екенін айтады. Дәл сол
эксперименттік фактілерді кейіннен басқа математикалық теориямен
растауға болады және мұндай мысалдар физикада бар. Мысалы,
тербелмелі процестер тригонометриялық және көрсеткіштік
функциялармен, сондай-ақ векторлық диаграммалар әдісімен бірдей
сәтті сипатталады.
Екіншіден, физикада математикалық функцияларды қатардағы кеңейту,
олардың кішілігіне байланысты кеңейтудің үшінші және одан кейінгі
мүшелерін елеусіз қалдыру жиі қолданылады. Дегенмен, физика
дамуының осы кезеңінде елеусіз кішкентай және байқалмайтын нәрсе
болашақта физика дамуының басқа кезеңінде өте маңызды рөл атқаруы
мүмкін. Бұл супержолдар теориясына арналған Б.Гриннің (2004)
кітабында анық сипатталған.
Осы себептердің барлығына байланысты физиканы оқығанда ең алдымен
шамалардың физикалық мазмұнына назар аудару керек. Тіпті олардың
математикалық сипаттамасы физикалық мазмұнға сәйкес келмейтін
жағдайларда. Сонымен қатар, мұндай жағдайларда бұл тақырып ерекше
маңызға ие, өйткені бұл неліктен болғанын және ұсынылған оқу
материалын осы тұрғыдан қалай түсіну керек екенін түсіндіру
қажет.
Математика мен физиканыңөзарабайланысы: пәнаралықбайланыстар
Физика мен математика – ғылымныңеңтығызбайланысқанекісаласыболыптабылады. Математика физикадағызаңдардытұжырымдау, ғылымиесептеулержүргізужәнетәжірибелікмәліметтердіталдауүшінқажеттіқұралболыптабылады. Физикадағыкөптегенқұбылыстар мен процестерматематикалықформулаларжәнетеңдеулерарқылысипатталады. Сондықтан математика физикадағылымидәлдік пен нақтылықтықамтамасызететіннегізгітетікретіндеәрекететеді.
Пәнаралық байланыстар:
-
Теңдеулер мен формулалар:Физикадағызаңдар мен теорияларкөбінесематематикалықтеңдеулерарқылыөрнектеледі. Мысалы, Ньютонныңекіншізаңы F=maF = maF=ma (күш, масса жәнеүдеуарасындағыбайланыс) математикалықтүрдеанықталады.
-
Дифференциалдықесептеулер:Дифференциалдықтеңдеулерфизикадағыкөптегенқұбылыстардысипаттайды. Мысалы, тербеліспроцестері мен электрмагниттіктолқындарсияқтықұбылыстардысипаттауүшінқолданылады.
-
Функцияларжәнеграфиктер:Физикадафункциялар мен графиктерқозғалысты, электрлікжәнемагниттікөрістерді, жылупроцестерінжәнебасқақұбылыстардысипаттауүшінкеңіненқолданылады.
-
Векторлықталдау:Физикадавекторларкүштер, жылдамдықтаржәнеөрістерсияқтыфизикалықшамалардысипаттауүшінқолданылады. Векторлықталдауарқылы осы шамалардыңбағыттары мен шамаларыанықталады.
-
Математикалықмодельдеу:Физикалықжүйелер мен процестердіматематикалықмодельдерарқылыбейнелеуфизикадаөтемаңызды. Бұлмодельдерфизикалыққұбылыстардыболжауға, талдауғажәнетүсінугемүмкіндікбереді.
-
Статистика жәнеықтималдық:Физикадастатистикалықәдістер мен ықтималдықтеориясыкездейсоқпроцестер мен кванттық механика сияқтысалалардақолданылады.
Математика мен физиканыңөзарабайланысыпәнаралықбайланыстарарқылыоқушылардыңлогикалықойлауындамытуға, деректердіталдауқабілетінарттыруғажәнекүрделіфизикалыққұбылыстардытүсінугекөмектеседі. Бұлекіпәнніңбір-біріменүйлесімділігіфизиканытереңіректүсінугежәнеғылымибілімдітолықмеңгеругемүмкіндікбереді.
Физика сабақтарындаматематикалықбілімдіқолдану
Физика пәні – табиғаттыңзаңдарынтүсіндіретінжәнетәжірибелікесептеулерарқылығылымдымеңгеругебағытталғанмаңыздыпәндердіңбірі. Физикадағықұбылыстардытүсінуүшінматематикалықбілімдермаңыздырөлатқарады. Сабақбарысындаматематиканықолдануфизикалықпроцестердітереңіректүсінуге, есептердідұрысшығаруғажәнетеориялықбілімдітәжірибедеқолдануғамүмкіндікбереді.
-
Математикалықбілімдіқолданудыңнегізгіаспектілері:
-
Формулалардыпайдалану:Физикадакөптегензаңдар мен принциптерматематикалықформулаларарқылыберіледі. Оқушыларғаформулалардыдұрысқолданужәнеолардыесептердішығарудапайдалану физика сабақтарыныңнегізгіміндеттерініңбіріболыптабылады. Мысалы, жылдамдықтыесептеуүшін v=dtv = \frac{d}{t}v=td формуласы, немесекинетикалықэнергияныесептеуүшінEk=12mv2E_k = \frac{1}{2}mv^2Ek=21mv2 формуласықолданылады.
-
Теңдеулердішешу:Физикалықесептердішешубарысындатеңдеулердіқұружәнешешудағдыларыөтемаңызды. Бұлдағдыфизикалықшамалардыңөзарабайланысынанықтауғажәненақтышешімдергеқолжеткізугемүмкіндікбереді. Мысалы, кинематиканыңнегізгітеңдеулеріншешуарқылыдененіңқозғалысынсипаттайтынпараметрлердіанықтайаламыз.
-
Графикалықталдау:Физикадафункциялардыңграфиктерінқұружәнеолардыталдаумаңыздырөлатқарады. Мысалы, қозғалысграфиктеріарқылыжылдамдықты, үдеудінемесежүрілгенқашықтықтыанықтаумүмкіндігіпайдаболады. Графиктерфизикалықшамалардыңөзарабайланысынкөрнекітүрдекөрсетіп, оқушыларғатақырыптыжақсырақтүсінугекөмектеседі.
-
Дифференциалдықжәнеинтегралдықесептеулер:Кейбірфизикалыққұбылыстардысипаттауүшіндифференциалдықжәнеинтегралдықесептеулердіқолдануқажет. Мысалы, қозғалыстыңүдеуі мен жылдамдығыарасындағыбайланыстытүсінуүшіндифференциалдауәдістеріқолданылады, ал жиынтыққозғалыснемесекеңістікаумағынесептеуүшінинтегралдыпайдалануқажет.
-
Моделдеу:Математикалықмодельдеу – физикалықпроцестердіматематикалықформулаларарқылысипаттауәдісі. Бұләдіскүрделіжүйелердіқарапайыммодельдерарқылытүсінугежәнеолардызерттеугемүмкіндікбереді. Мысалы, электртізбектеріннемесемеханикалықжүйелердімодельдеуарқылыолардыңжұмысістеупринциптерінтүсіндіругеболады.
-
Статистика жәнеықтималдық:Физикадастатистикалықәдістер мен ықтималдықтеориясынқолданукездейсоққұбылыстардытүсіндірудемаңыздырөлатқарады. Бұләдістерәсіресе термодинамика, кванттық физика жәнеатомдықдеңгейдегіпроцестердісипаттаудақолданылады.
Физика сабақтарындаматематикалықбілімдіқолдануоқушыларғафизикалыққұбылыстардытереңіректүсінугежәнеолардыпрактикалықтұрғыдақолдануғамүмкіндікбереді. Математикалықесептеулерарқылыфизикалықзаңдылықтардыдәланықтап, ғылымиесептеулердіорындаумүмкіндігіартады. Осылайша, математикалықәдістерфизикадағыбілімдінығайтып, оқушылардыңғылымиойлауындамытуғасептігінтигізеді.
Физикалықзаңдардытұжырымдаунегізіретінде математика
Физика – бұлтабиғатқұбылыстарынзерттейтінғылым, ал математика – осы құбылыстардыдәлсипаттауғамүмкіндікберетінқұрал. Физикалықзаңдартабиғаттыңнегізгіпринциптерінтүсіндіреді, ал бұлзаңдардытұжырымдауүшін математика маңыздырөлатқарады. Физикалықзаңдардытұжырымдауүшінматематикалықтілдіңқолданылуыолардыңдәлдігі мен әмбебаптылығынқамтамасызетеді.
Математиканыңфизикалықзаңдардағырөлі:
-
Символдықөрнектержәнеформулалар: Математика физикалықзаңдардысимволдар мен формулаларарқылыөрнектеугемүмкіндікбереді. Бұлзаңдардыңнегізгісипаттарынқысқаәрінақтытүрдекөрсетугеболады. Мысалы, Ньютонныңекіншізаңы F=maF = maF=maтүріндежазылады, мұнда FFF – күш, mmm – масса, aaa – үдеу. Осы қарапайым формула арқылықозғалысзаңдылықтарынтүсіндіругеболады.
-
Математикалықмодельдеу:Физикалыққұбылыстардыматематикалықмодельдерарқылысипаттауоларғаталдаужасауғажәнеболжауғамүмкіндікбереді. Мысалы, электртізбектерін, термодинамикалықпроцестердінемесекванттықжүйелердімодельдеуүшіндифференциалдықтеңдеулерқолданылады. Модельдерфизикалықжүйелердіңмінез-құлқынматематикалықтұрғыдантүсінугежәнеолардынақтытәжірибелерменсалыстыруғамүмкіндікбереді.
-
Дифференциалдықтеңдеулер:Көптегенфизикалыққұбылыстаруақытнемесекеңістікбойыншаөзгеретіншамаларретіндесипатталады. Бұлөзгерістердісипаттауүшіндифференциалдықтеңдеулерқолданылады. Мысалы, гармоникалықтербелістердісипаттайтынтеңдеунемесежылуөткізупроцесіүшін Фурье теңдеуі. Осы теңдеулерарқылыжүйелердіңдинамикасынталдап, олардыңболашақтағыкүйінболжауғаболады.
-
Физикалықтұрақтыларжәне пропорция: Математика физикалықшамалардыңарасындағыпропорционалдыққатынастардыкөрсетудеқолданылады. Мысалы, Ом заңы V=IRV = IRV=IR түріндежазылады, мұнда VVV – кернеу, III – ток күші, RRR – кедергі. Мұндайқатынастарфизикалықшамалардыңөзарабайланысынтүсіндіредіжәнетәжірибелікдеректердіталдауғакөмектеседі.
-
Абстракция және идеализация:Математикалықәдістерфизикада абстракция мен идеализация жасауғамүмкіндікбереді, бұлкүрделіқұбылыстардықарапайыммодельдергедейінқысқартуғамүмкіндікбереді. Мысалы, идеалдыгаздармоделінемесеқаттыденелертеориясыарқылынақтыобъектілердіқарапайымтүрдесипаттауғаболады. Бұлабстракцияларфизикалықзаңдардыңнегізінтүсінугежәнеолардызерттеугемүмкіндікбереді.Математика физикалық заңдарды тұжырымдау негізі ретінде қызмет етіп, табиғаттың заңдылықтарын дәл және түсінікті түрде сипаттауға мүмкіндік береді. Математикалықәдістердіңкөмегіменфизикадағыкүрделіпроцестердіқарапайымтүрдесипаттап, олардыңмінез-құлқынболжауғаболады. Осылайша, математика физика ғылымыныңнегізіретіндемаңыздырөлатқарадыжәнеоныңдамуынаайтарлықтайықпалетеді.
Физикадағыматематикалықмодельдеу: практикалыққолдану
Математикалықмодельдеуфизикадатабиғиқұбылыстардысипаттаужәнетүсінуүшінқолданылатынмаңыздықұралдардыңбіріболыптабылады. Бұләдісфизикалықжүйелердіматематикалықтеңдеулер, формулаларнемесеалгоритмдерарқылыкөрсетіп, олардыңмінез-құлқынболжауғажәнеталдауғамүмкіндікбереді.
Математикалық модельдеудің рөлі:
-
Табиғи құбылыстарды сипаттау: Физикалық құбылыстардың көпшілігі математикалық модельдер арқылы сипатталады. Мысалы, Ньютона қозғалыс заңдары механикадағы денелердің қозғалысын модельдеуге мүмкіндік береді, ал Максвелл теңдеулері электромагниттік толқындарды сипаттайды. Бұл модельдер физикалық заңдылықтарды түсінуге және оларды математикалық тұрғыдан көрсетуге мүмкіндік береді.
-
Эксперименттік мәліметтерді талдау: Математикалық модельдеу физикадағы эксперименттік мәліметтерді талдауға және интерпретациялауға көмектеседі. Мысалы, радиоактивті ыдырау процесін модельдеу арқылы радиоактивті материалдардың жартылай ыдырау кезеңін есептеуге болады. Сондай-ақ, модельдеу тәжірибелік нәтижелерді болжауға және оларды нақты деректермен салыстыруға мүмкіндік береді.
-
Техникалық және инженерлік қолданбалар: Математикалық модельдеу физикада техникалық және инженерлік мәселелерді шешуде кеңінен қолданылады. Мысалы, құрылыс инженерлері ғимараттар мен көпірлердің беріктігін бағалау үшін құрылымдық механиканың математикалық модельдерін пайдаланады. Электротехникалық жүйелерді модельдеу арқылы электр тізбектерінің жұмысын талдау және оларды оңтайландыру мүмкіндігі бар.
-
Күрделі жүйелерді модельдеу: Физикадағы күрделі жүйелер, мысалы, атмосфералық құбылыстар, сұйықтық динамикасы немесе кванттық жүйелер, математикалық модельдер арқылы зерттеледі. Бұл модельдер табиғаттағы күрделі процестерді қарапайым түсіндіруге және олардың болашақтағы күйін болжауға мүмкіндік береді.
-
Компьютерлік модельдеу: Қазіргі заманғы математикалық модельдеу компьютерлік бағдарламалар арқылы жүзеге асырылады. Мысалы, климаттық өзгерістерді болжау үшін атмосфераның жаһандық циркуляциясын модельдейтін компьютерлік модельдер қолданылады. Сондай-ақ, ядролық реакторлардың жұмысын модельдеу немесе ғарыш аппараттарының траекториясын есептеу үшін де компьютерлік модельдеу қолданылады.
Математикалық модельдеудің практикалық мысалдары:
-
Қозғалыс теңдеулері: Механикада денелердің қозғалысын сипаттау үшін дифференциалдық теңдеулер қолданылады. Мысалы, еркін құлау қозғалысын модельдеу үшін s(t)=12gt2s(t) = \frac{1}{2}gt^2s(t)=21gt2 теңдеуі пайдаланылады, мұнда s(t)s(t)s(t) – уақытқа байланысты орын ауыстыру, ggg – еркін түсу үдеуі, ttt – уақыт.
-
Электр өрісін модельдеу: Электростатиканың негізгі заңдарын сипаттау үшін Кулон заңы және потенциалдық өрістердің теңдеулері қолданылады. Бұл модельдер арқылы электр зарядтарының өзара әрекеттесуін және олардың айналасындағы электр өрісін зерттеуге болады.
-
Толқындық процестер: Математикалық модельдеу толқындардың таралуын сипаттау үшін де қолданылады. Мысалы, су бетіндегі толқындарды немесе дыбыс толқындарын сипаттау үшін толқын теңдеуі ∂2u∂t2=c2∂2u∂x2\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2}∂t2∂2u=c2∂x2∂2u қолданылады, мұнда uuu – толқын амплитудасы, ccc – толқынның таралу жылдамдығы.Физикадағы математикалық модельдеу табиғи құбылыстарды түсіну және болжау үшін маңызды құрал болып табылады. Бұл әдіс физикалық заңдарды формулировка жасауға, тәжірибелік деректерді талдауға, инженерлік және техникалық мәселелерді шешуге мүмкіндік береді. Математикалық модельдеу физикадағы күрделі жүйелердің мінез-құлқын зерттеу үшін қажетті негізді қамтамасыз етеді және бұл ғылымның дамуына зор үлес қосады.
Физикадағы математикалық талдау: негізгі аспектілер
Математикалық талдау физикадағы маңызды құралдардың бірі болып табылады. Ол физикалық құбылыстарды сандық түрде сипаттау, түсіндіру және болжау үшін қолданылады. Математикалық талдау физикалық заңдарды зерттеу, физикалық жүйелердің мінез-құлқын түсіну және тәжірибелік мәліметтерді интерпретациялау үшін негіз болып табылады.
Математикалықталдаудыңрөлі:
-
Дифференциалдықтеңдеулердіқолдану:Физикадағыкөптегензаңдар мен процестердифференциалдықтеңдеулерарқылысипатталады. Мысалы, қозғалысзаңдары, жылуөткізу, сұйықтықдинамикасысияқтықұбылыстар осы теңдеулердішешуарқылытүсіндіріледі. Ньютонныңекіншізаңы F=maF = maF=maжиідифференциалдықтеңдеугеайналып, нақтыжүйелердегіқозғалыстысипаттайды.
-
Интегралдықесептеулер:Интегралдықесептеулерфизикадажүйелердіңжалпымінез-құлқынсипаттауүшінқолданылады. Мысалы, заттыңмассасыннемесеэлектрзарядынанықтауүшінинтегралдарқолданылады. Бұданбөлек, физикалықөрістердіесептеуде де интегралдармаңыздырөлатқарады.
-
Шектеуесептеулері:Физикадашектеупринциптерібелгілібіршарттардағыжүйелердіңмінез-құлқынзерттеуүшінқолданылады. Мысалы, шексізшамадағызарядтардыңөрісінемесеуақытөтешексіздіккеұмтылатынжүйелердізерттеушектеуәдістерініңкөмегіменжүзегеасады.
-
Сериялар мен қатарлар:Математикалыққатарларфизикадажүйелердіжуықтапесептеуүшінқолданылады. Тейлор немесе Фурье қатарларыкүрделіфункциялардықарапайымбөліктергежіктеугемүмкіндікбереді, бұлфизикалықжүйелердіталдаудыжеңілдетеді.
-
Вариациялықәдістер:Физикадағыкөптегенмәселелердішешуүшінвариациялықәдістерқолданылады. Бұләдістержүйеніңеңықтималкүйінанықтауүшінқолданылады, мысалы, Лагранж және Гамильтон әдістері механика мен электродинамикадакеңіненқолданылады.
Математикалықталдаудыңфизикадағынегізгіаспектілері:
-
Механикадағыталдау:Классикалықмеханикададенелердіңқозғалысынсипаттауүшіндифференциалдықтеңдеулер мен интегралдаркеңіненқолданылады. Мысалы, тербелмеліқозғалыстызерттеуүшінгармониялықосциллятордыңтеңдеуіқолданылады.
-
Электродинамикадағыталдау: Электр және магнит өрістерінзерттеуде Максвелл теңдеулеріматематикалықталдаудыңнегізгіқұралыболыптабылады. Бұлтеңдеулерэлектромагниттіктолқындардыңтаралуын, электрзарядтарыныңөзараәрекеттесуінжәнеэлектрөрістерініңқалыптасуынтүсіндіреді.
-
Термодинамика жәнестатистикалық физика:Термодинамикадажүйелердіңмакроскопиялыққасиеттерінзерттеуүшінинтегралдар мен ықтималдықтеориясықолданылады. Статистикалықфизикадакөпбөлшектердіңжүйелерінталдауүшінықтималдықтыесептеуәдістеріқолданылады.
-
Кванттықмеханикадағыталдау:Кванттықмеханикадатолқындықфункциялардысипаттауүшін Шредингер теңдеуіқолданылады. Бұлтеңдеукванттықжүйелердіңмінез-құлқынсипаттауүшінматематикалықталдаудыңнегізгіаспектіболыптабылады.
-
Тасымалдауқұбылыстарындағыталдау:Жылу, масса жәнеэлектрзарядтарыныңтасымалдануынсипаттауүшінматематикалықталдауқолданылады. Фурье теңдеуі, ОмынзаңыжәнеФикзаңдары осы құбылыстардытүсіндіруүшінқолданылады.Физикадағы математикалық талдау физикалық жүйелердің күрделі құбылыстарын түсіну және сипаттау үшін маңызды құрал болып табылады. Бұләдісфизикалықзаңдарды формулировка жасауға, жүйелердіңмінез-құлқынзерттеугежәнетәжірибелікнәтижелердіинтерпретациялауғамүмкіндікбереді. Математикалықталдауфизикадағызерттеулердіңмаңыздыаспектісіболыптабыладыжәнеолфизиканыңкөптегенсалаларындакеңіненқолданылады.
Физикадағыматематикалықтеңдеулер: мысалдаржәнеқолдану
Физикадағыматематикалықтеңдеулертабиғиқұбылыстардысипаттаудыңнегізгіқұралыболыптабылады. Оларфизикалықжүйелердіңдинамикасын, тепе-теңдігінжәнеэволюциясынсипаттап, физикалықзаңдардысандықтүрдетұжырымдауғамүмкіндікбереді. Математикалықтеңдеулерфизикадағызерттеулердіңнегізіболыптабыладыжәнеолардықолданукөптегенмаңыздыфизикалықнәтижелергеәкеледі.
1. Ньютонныңекіншізаңы:
Мысал:Ньютонныңекіншізаңықозғалыстысипаттауүшінқолданылады: F=maF = maF=maМұндағы FFF — күш, mmm — дененіңмассасы, aaa — үдеу. Бұлтеңдеуденегеәсерететінкүш пен оныңқозғалысындағыөзгерістерарасындағыбайланыстысипаттайды.
Қолдану:
-
Классикалықмеханикадағыденелердіңқозғалысынсипаттау.
-
Инженериядажәнетехникадақұрылғылардыңдинамикасынесептеу.
2. Шредингер теңдеуі:
Мысал:Кванттықмеханикадабөлшектердіңкүйінсипаттауүшін Шредингер теңдеуіқолданылады: H^Ψ=EΨ\hat{H}\Psi = E\PsiH^Ψ=EΨ Мұндағы H^\hat{H}H^ — Гамильтониан операторы, Ψ\PsiΨ — толқындық функция, EEE — энергия.
Қолдану:
-
Микробөлшектердің (электрондар, атомдар, молекулалар) қасиеттерінзерттеу.
-
Кванттықхимиядамолекулалардыңэлектрондыққұрылымынесептеу.
3. Максвелл теңдеулері:
Мысал:Электромагниттікөрістердісипаттауүшінқолданылатын Максвелл теңдеулері: ∇⋅E=ρϵ0\nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0}∇⋅E=ϵ0ρ ∇⋅B=0\nabla \cdot \mathbf{B} = 0∇⋅B=0 ∇×E=−∂B∂t\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}∇×E=−∂t∂B ∇×B=μ0J+μ0ϵ0∂E∂t\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}∇×B=μ0J+μ0ϵ0∂t∂E Мұндағы E\mathbf{E}E — электрөрісі, B\mathbf{B}B — магнит өрісі, ρ\rhoρ — электрзарядтарыныңтығыздығы, J\mathbf{J}J — ток тығыздығы.
Қолдану:
-
Электромагниттіктолқындардыңтаралуы.
-
Радиотолқындар, жарық, рентген сәулелерісияқтыэлектромагниттіксәулеленулердізерттеу.
4. Термодинамиканыңбіріншізаңы:
Мысал:Термодинамикадағыэнергияныңсақталузаңы: ΔU=Q−W\Delta U = Q - WΔU=Q−W Мұндағы ΔU\Delta UΔU — жүйеніңішкіэнергиясыныңөзгеруі, QQQ — жүйегеберілгенжылу, WWW — жүйежасағанжұмыс.
Қолдану:
-
Жылумашиналарының, тоңазытқыштардың, жәнебасқа да энергия түрлендіргіштердіңжұмысынсипаттау.
-
Химиялықреакциялардыңтермодинамикасынзерттеу.
5. Екіншіреттідифференциалдықтеңдеу:
Мысал:Гармониялықосциллятордысипаттайтынтеңдеу: md2xdt2+kx=0m\frac{d^2x}{dt^2} + kx = 0mdt2d2x+kx=0 Мұндағыmmm — масса, kkk — серіппеніңқатаңдығы, xxx — ауытқу.
Қолдану:
-
Серіппеліжүйелердіңтербелісінзерттеу.
-
Электрлікконтурлардағытербелістердісипаттау.
6. Фурье теңдеуі:
Мысал:Жылуөткізгіштікпроцесінсипаттауүшінқолданылатын Фурье теңдеуі: ∂u∂t=α∇2u\frac{\partial u}{\partial t} = \alpha \nabla^2 u∂t∂u=α∇2u Мұндағыuuu — температура, α\alphaα — жылуөткізгіштіккоэффициенті.
Қолдану:
-
Қаттыденелердежылутаралуынзерттеу.
-
Жылуоқшаулауматериалдарыныңтиімділігінбағалау.
Физикадағыматематикалықтеңдеулертабиғиқұбылыстардысандықтүрдесипаттаудыңжәнеталдаудыңнегізгіқұралыболыптабылады. Оларфизикалықзаңдарды формулировка жасауға, жүйелердіңмінез-құлқынмодельдеугежәнеболжауғамүмкіндікбереді. Мысалдардакелтірілгентеңдеулерәртүрліфизикалыққұбылыстардызерттеуүшінкеңіненқолданыладыжәнеолардыдұрысқолдануарқылыкүрделіжүйелердіңмінез-құлқынтүсінугеболады.
Физиканызерттеудематематикалықбілімніңмаңызы
Физика мен математика тығызбайланысқанғылымсалаларыболыптабылады. Физикадатабиғиқұбылыстардытүсіндіружәнеболжауүшінматематикалықәдістер мен құралдаркеңіненқолданылады. Математикалықбілімфизикалықзаңдардытұжырымдауда, эксперименттікнәтижелердіталдауда, жәнекүрделіжүйелердіңмінез-құлқынмодельдеуденегізгірөлатқарады.
1. Физикалықзаңдардытұжырымдау:
Математикалықбілімфизиканыңнегізгізаңдарынтұжырымдауғамүмкіндікбереді. Мысалы, Ньютонныңекіншізаңы( F=maF = maF=ma ) немесеЭйнштейнніңсалыстырмалықтеориясындағыэнергияныңтеңдеуі ( E=mc2E = mc^2E=mc2 ) сияқтыматематикалықформулаларфизикалыққұбылыстардыңдәлжәненақтысипаттамасынбереді.
2. Эксперименттікдеректердіталдау:
Физикалықзерттеулердіңкөпшілігіэксперименттікдеректердіжинаудықамтиды. Осы деректердідұрысталдауүшін статистика, ықтималдықтеориясыжәнебасқа да математикалықәдістерқажет. Математикалықбілімніңарқасындафизиктерэксперименттердіңнәтижелерінтүсіндіріп, қателіктердібағалайаладыжәнетеориялықмодельдердінақтыдеректерменсалыстыраалады.
3. Модельдеужәне симуляция:
Күрделіфизикалықжүйелердізерттеуүшінматематикалықмодельдерқолданылады. Модельдерфизикалыққұбылыстардықарапайымжәнетүсініктітүрдебейнелеугемүмкіндікбереді. Мысалы, климаттықөзгерістердіболжаунемесежаңаматериалдардыңқасиеттерінзерттеуүшінматематикалықмодельдерпайдаланылады. Бұлмодельдерсандықесептеулергенегізделеді, сондықтанматематикалықбілімфизикалықжүйелердісимуляциялауүшінөтемаңызды.
4. Теориялық физика:
Теориялықфизикадаматематикалыққұралдаререкшемаңыздырөлатқарады. Кванттық механика, салыстырмалықтеориясы, және термодинамика сияқтыфизиканыңбөлімдеріматематикалықнегіздеқұрылған. Мысалы, кванттықмеханикада Шредингер теңдеуібөлшектердіңтолқындықфункцияларынсипаттайды, ал салыстырмалықтеориясындаЭйнштейнніңтеңдеулерікеңістік пен уақыттыңқұрылымынсипаттайды.
5. Жаңафизикалықтеориялардыдамыту:
Физикадажаңатеориялардыдамытуүшінматематикалықжаңалықтарқажет. Мысалы, қарақұрдымдардың (қаратесіктердің) теориясындамытуүшінматематикалықталдау, дифференциалдықтеңдеулержәне топология сияқтыкүрделіматематикалықбөлімдерқолданылды.Физиканызерттеудематематикалықбілімніңмаңызызор. Математика физикалыққұбылыстардыдәлсипаттауға, эксперименттікдеректердіталдауға, күрделіжүйелердімодельдеугежәнежаңатеориялардыдамытуғамүмкіндікбереді. Математикалықбілімсізфизикалыққұбылыстардытолықтүсінумүмкінемес, сондықтан физика саласындатабысты болу үшінматематикаментереңтаныс болу қажет.
Физикадағыматематикалық аппарат: заманауитенденциялар
Физикадаматематикалықаппараттыңрөлікүнсанапартыпкеледі. Заманауифизикалықзерттеулердематематикалықәдістер мен құралдарфизикалықтеориялардыдамытудың, жаңаашылуларжасаудыңжәнеғылымипроблемалардышешудіңнегізіболыптабылады. Осығанбайланысты математика мен физика арасындағыөзарабайланыстереңдейтүсуде. Заманауитенденциялартөмендегідейбағыттардабайқалады:
1. Сандықәдістердіңдамуы:
Сандықәдістер мен компьютерлікмоделдеуфизикалықжүйелердізерттеудекеңіненқолданылуда. Қазіргізаманғысуперкомпьютерлер мен алгоритмдерфизикалыққұбылыстардысандықтұрғыдамодельдеугемүмкіндікбереді. Бұләдістеркүрделітеңдеулердішешуге, үлкенкөлемдегідеректердіөңдеугежәненақтыәлемдікжүйелердіңсимуляцияларынжүргізугемүмкіндікбереді.
2. Деректердіғылым мен аналитика:
Үлкендеректердің (Big Data) анализіфизикадамаңыздырөлатқарады. Ғылымиэксперименттер мен бақылауларданалынғанүлкенкөлемдегідеректердіөңдеуүшінкүрделістатистикалықжәнеесептеуәдістеріқолданылуда. Бұлфизикалықтеориялардытестілеуге, жаңамодельдержасауғажәнеболжамдардыдәлелдеугекөмектеседі.
3. Құрылымдықтеңдеулер мен симметриялар:
Физикадасимметриялар мен құрылымдықтеңдеулердіңмаңызызор. Қазіргізаманғызерттеулердесимметриялартеориясы мен жоғарыөлшемдікеңістіктердегітеңдеулеркеңіненқолданылуда. Мысалы, теориялықфизикада, стандарттымодельдежәнежалпысалыстырмалықтеориясындасимметриялар мен топологиялармаңыздырөлатқарады.
4. Қосымшаөлшемдер мен көпөлшемдімодельдер:
Көпөлшемдімодельдер мен қосымшаөлшемдерфизиканыңжаңатеорияларындакеңіненқолданылады. Мысалы, суперсимметрия, струндық теория және M-теория сияқтықосымшаөлшемдердіқамтитынтеорияларқазіргізамандабелсендізерттелуде. Бұлтеорияларфизикалыққұбылыстардытүсінугежаңаперспективаларұсынады.
5. Математикалық физика жәнеабстрактілітеориялар:
Математикалық физика, яғни математика мен физиканыңарасындағытереңбайланыстардызерттеу, маңыздызерттеубағытыболыптабылады. Абстрактіліматематикалыққұрылымдар мен теориялар, мысалы, топология, дифференциалдық геометрия жәнеалгебралық геометрия, физикалықмәселелердішешудеқолданылуда.
6. Жаңаалгоритмдер мен есептеутехникасы:
Заманауифизикадағыесептеулер мен моделдеуүшінжаңаалгоритмдер мен есептеуәдістеріәзірленуде. Мысалы, кванттықесептеу, нейрондықжелілержәнежасанды интеллект сияқтыжаңатехнологияларфизикалықпроблемалардышешудепайдаланылуда.
7. Тәжірибелікжәнетеориялық синтез:
Физикадатеориялықмодельдер мен эксперименттікнәтижелерарасындағыбайланыстыңнығаюымаңыздытенденциялардыңбіріболыптабылады. Теориялықболжамдардытәжірибелікдәлелдерментексеружәнекерісінше, эксперименттікдеректердітеориялықтүсініктерменсалыстырудықамтамасызететінәдістердамытылуда.Физикадағы математикалық аппараттың заманауи тенденциялары сандық әдістердің, деректерді анализдеудің, көп өлшемді модельдердің және жаңа математикалық теориялардың дамуымен байланысты. Бұлтенденцияларфизикалықтеориялардыкеңейтуге, жаңазерттеубағыттарынашуғажәнефизикадағыжаңаашылуларжасауғамүмкіндікбереді. Заманауиматематикалық аппарат физика ғылымыныңнегізіболыптабыладыжәнеғылымизерттеулердіңболашағынайқындайды.
«Физикадағы математиканың рөлі» ғылыми-зерттеу жұмысы
1. Математика физикаға қажет пе?

2. Физика
сабағында математиканы пайдаланасыз
ба?

3. Сіз не үйрететініңізді әрқашан түсінесіз бе?

4. Физиканы
математикасыз оқуға болады ма?

5. Математика
мен физика сізге оңай деп ойлайсыз
ба?

6.Физика мен
математиканы оқығанда қайталанатын тақырыптарды кездестірдіңіз
бе?

7.1.
Физика-математикадан тест тапсырмаларын тақырыптарды қайталаумен
біріктірсе, пәндерді меңгеру сапасы жоғары болады деп ойлайсыз
ба?

7.2. Оқушылардың эмоционалдық және физикалық жүктемелері төмендей ме?

7.3.Осы пәндер
бойынша жіберіп алған емтихандар саны азая
ма?

Осы зерттеу нәтижелеріне сүйене отырып, физикада математика қажет деп сеніммен айта аламыз.
Қорытынды
Математика қажет.
Физика үшін математиканың маңызы орасан зор. Математика табиғат заңдарының көпшілігін анықтайды. Бұл бізді қоршаған әлемді ғана емес, бүкіл ғаламды зерттеуге көмектесетін ерекше тіл. Математика іргелі ғылым ретінде жаратылыстану ғылымдарының әртүрлі бағыттағы дамуын қамтамасыз ететін әртүрлі әдістер жүйесі болып табылады. Математиканы физика мен жаратылыстану ғылымдарында қолдану өте үлкен, әрбір ғылымда жоғарыда келтірілген мысалдарда келтірілген математиканы қолданудың кем дегенде бір саласы бар. Математика басқа ғылыми пәндерге көмектесетін ғылым. Математика – жаратылыстану ғылымдары пәндерінің даму тілі. Математика – әртүрлі ғылымдардың зерттеу әдістерінің жиынтығы. Математиканы барлық жаратылыстану ғылымдары кеңінен қолданады. Математика жаратылыстану ғылымымен тығыз байланысты, бұл еңбекте көрсетілген.
Ұсыныс: Физикадағы математикалық әдістерге шолу, математика мен физиканың өзара байланысын талдау және физика сабақтарында математикалық білімдерді практикалық қолдану бойынша ұсыныстарды қамтитын зерттеу есебі.
Пайдаланылған әдебиеттер:
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Физикадағы математикалық есептеулер
Физикадағы математикалық есептеулер
Мазмұны
1. Кіріспе
2. Физикадағы ғылыми есептеулерде математиканың рөлі
3. Математика мен физиканың өзара байланысы: пәнаралық байланыстар
4. Физика сабақтарында математикалық білімді қолдану
5. Физикадағы математикалық әдістер: негізгі тәсілдерге шолу
6. Физикалық заңдарды тұжырымдау негізі ретінде математика
7. Физикадағы математикалық модельдеу: практикалық қолдану
8. Физикадағы математикалық талдау: негізгі аспектілер
9. Физикадағы математикалық теңдеулер: мысалдар және қолдану
10. Физиканы зерттеуде математикалық білімнің маңызы
11. Физикадағы математикалық аппарат: заманауи тенденциялар
12.«Физикадағы математиканың рөлі» ғылыми-зерттеу жұмысы
13. Қорытынды
14. Әдебиеттер тізімі
Кіріспе
Жоба физика саласындағы математикалық есептеулердің рөліне арналған. Математика физикада негізгі рөл атқарып, физикалық заңдарды тұжырымдау, ғылыми есептеулер жүргізу және эксперименттік деректерді талдау үшін негіз болып табылады. Бұл жобада физикадағы математикалық әдістердің маңызы және олардың осы ғылымның әртүрлі аспектілерінде қолданылуы қарастырылады.Математика мен физика әдетте мектеп бағдарламасындағы ең қиын пәндер болып саналады. Мектептегі сабақтарға физика мен математиканы кіріктіру тек осы пәндерді тереңдетіп оқытылатын сыныптарда ғана мүмкін болады деп жалпы есептейді. Біз мұндай интеграцияның көптеген элементтері физика презентациясын оқудың барлық деңгейлерінде айқынырақ және қолжетімді ете алады деп есептейміз. оқушылар физика сабағында сұрағын түсіне алмауы немесе физика есептерін шеше алмауы көбінесе функционалдық тәуелділіктерді талдау, математикалық теңдеулерді құру және шешу дағдыларының жеткіліксіздігімен, алгебралық және геометриялық тапсырмаларды орындай алмауымен байланысты. байланысқан конструкциялар.Бірінші дүниежүзілік соғыс кезінде кейінірек Америка азаматтығын алған неміс физигі және математигі Альберт Эйнштейн дүние жүзіндегі астрономдарды, физиктер мен математиктерді таң қалдырған ерекше және күтпеген жаңалық жасады. Көптеген ғалымдарға қате болып көрінген ұстанымдарға сүйене отырып, Эйнштейн математикалық есептеулер арқылы жарық сәулесінің ауырлық күшіне ұшырайтынын және ол ауыр дененің жанынан өткенде, оның сол денеге қарай тартылып, итерілетінін дәл есептеді. Эйнштейн күн сәулесінің қаншалықты ауытқуы керектігін есептеді. Дүние жүзіндегі астрономдар бірден Эйнштейннің есебін тексеруге кірісті. Британдық астрономиялық қоғам үкіметтің мақұлдауымен екі жылдан кейін болатын күннің толық тұтылуы кезінде осы сынаққа дайындықты бастады. Күннің осындай толық тұтылуы кезінде ғана Күннің артында орналасқан жұлдыздың сәулелерін Күнге жақындаған кезде байқауға болады. Күн тұтылуын бақылаудың келесі ең жақсы жері Оңтүстік Африканың шөлінде болғандықтан, экспедицияға көптеген техника мен көптеген қызметкерлер дайындалуға тура келді. Мұның бәрі жасалды және сынақ нәтижелері Эйнштейннің есептеулерін растады.Эйнштейннің есебінің ақиқатқа жетуі жемісті гипотезаны басшылыққа ала отырып, адам санасының неге қабілетті екенін көрсетті. Эйнштейннің жаңалығы математиканы ойлаудың нақты және қатаң құралы ретінде пайдалануға болатынын тағы бір рет көрсетеді. Ежелгі дәуірдегі ең ұлы ғалымдардың барлығының бір мезгілде математиктер, физиктер және астрономдар болуы бұл ғылымдардың жеке өмір сүрмейтінін растайды. Әрбір физикалық мәлімдеме эксперименттік деректер мен математикалық есептеулерге негізделген дұрыс. Өкінішке орай, студенттер үшін физика - ақылға қонымсыз, ал математика - ақылға қонымсыз екені жиі шығады.
Бұл жұмыста біз зерттелетін материал мен математикадан алынған білімдерді физикалық есептерді шешу үшін және керісінше пайдалану мүмкіндігі арасындағы байланысты көрсетуді жөн көрдім.
Мақсаты: физикадағы математикалық есептеулердің рөлін қарастыру, математика мен физиканың өзара байланысының негізгі аспектілерін анықтау және физика сабақтарында математикалық білімдерді практикалық қолдануды талдау.
1) Пәнаралық байланыстардың мәнін, қызметін және олардың жіктелуін анықтау;
2) Математикада қандай ұғымдар және олардың физикада қалай қолданылатынын көрсетіңіз.
№1 тапсырма
Математика білімін не үшін қажет ететінін көрсетіңіз.
№2 тапсырма
Физикаға қажетті математикалық ұғымдарды анықтау.
Жобаның міндеттері:
-
Физикада қолданылатын негізгі математикалық әдістерді зерттеу.
-
Ғылыми және оқу контексттерінде математика мен физиканың өзара байланысын талдау.
-
Физика сабақтарында математикалық білімдерді практикалық қолдануды зерттеу.
Зерттеу нысаны: физикадағы математикалық әдістер
Зерттеу пәні: математика мен физиканың өзара байланысы
Зерттеу әдістері: ғылыми әдебиеттерді талдау, сұхбаттар, сауалнамалар
Ғылыми жаңалығы:Оқыту контекстінде математика мен физиканың өзара байланысын зерттеу
Жобаның идеясы:Жобаның идеясы – физиканы табысты оқып-үйрену және практикалық қолдану үшін математикалық әдістерді түсінудің маңыздылығын атап көрсету, сондай-ақ осы екі ғылымның өзара әрекеттесуінің негізгі аспектілерін анықтау.
Жаңалығы :Жоба физикадағы математикалық есептеулердің маңыздылығы туралы жеткіліксіз хабардарлықты және физиканы оқу кезінде математикалық білімдерді практикада қолданудағы қиындықтарды шешеді.
Ресурстар: Оқу әдебиеті, ғылыми мақалалар, оқу құралдары, әдістемелік әзірлемелер
Әдістері : жалпы ғылыми, нақты ғылыми, логикалық.Математиканың физикада қандай рөл атқаратынын сізге көрсетіп, дәлелдеуге тырысайық.
Пәнаралық байланыс принципі физиканы зерттеудің негізінде жатыр, өйткені бұл ғылым басқа салалардағы білімдерді қамтиды және олар өз кезегінде оларды түсіну үшін қажет. Физика сабақтарында көптеген құбылыстар мен процестерді қарастыру кезінде көптеген басқа пәндерді білу қажет, мысалы, математика, география, химия, биология және т.б. Сонымен бірге бұл оқу пәндерін оқу физиканы және физика ғылымдарының әдістерін терең және берік білуді талап етеді (мысалы, энергия ұғымдарын және биологиялық процестерде энергияның сақталу және түрлену заңын қолдану; физикалық құбылыстар). . , астрономиядағы заңдар мен әдістер және т.б.). Бұл пәнаралық байланыс принципі қазіргі уақытта жоғары дамыған ғылымдардың дифференциациясын және бірігуін қамтиды дегенді білдіреді.
Физикадағы ғылыми есептеулерде математиканың рөлі
Математиканың физикадағы рөлін асыра бағалау мүмкін емес. Галилео Галилей: «Математика - бұл табиғат кітабы жазылған тіл», - деп атайды. Математиктердің жұмысы – жаңа математикалық объектілерді табу және олардың қасиеттері мен байланыстарын зерттеу. Галилео заманынан бері математиканың көптеген жаңа салалары математикалық объектілерді сипаттауға арналған өз тілімен пайда болды.
Белгілі математикалық объект – функцияны алайық. Ол мектеп бағдарламасына нысан бойынша енгізілген y = f ( x ) және айнымалылардың қандай да бір тәуелділігінің көрсеткішін білдіреді j айнымалыдан X.
 Дегенмен, жиынтық теориясы тұрғысынан функция
болып табылады Жарнама бір сөйлемнен
екіншісіне:
Дегенмен, жиынтық теориясы тұрғысынан функция
болып табылады Жарнама бір сөйлемнен
екіншісіне:
A → fB

Ал абстрактілі алгебраның көмегімен функцияны оператор және мәндер
жиыны ретінде көрсетуге
болады X Және j векторлар болып саналады. Бұл сипаттамада
функцияны көрсету оператор матрицасын көрсетуге сәйкес
келеді F ^ F^
.
Y = F ^ X
Y=F^X
Ал пертурбация теориясында функцияларды шексіз қатар арқылы анықтау жиі кездеседі. Сонымен қатар, қатардың ерекше табиғаты функцияны анықтаудың әртүрлі облыстары үшін әртүрлі болуы мүмкін.
f ( x )=∑ n = 0 ∞anxn
Яғни, функция әртүрлі математикалық әдістерді қолдану арқылы «көрінетін» абстрактілі математикалық нысанның бір түрі ретінде өмір сүреді. Бұл аргументтерді кез келген дерлік математикалық объектіге қолдануға болады. Мысалы, векторды абстрактілі символ арқылы көрсетуге болады v немесе нақты координаттың көрінісі ( vx , vy , vz ) . Сонымен қатар, бұл координаттардың сандық мәндері таңдалған координаталар жүйесі мен негізіне байланысты.
Дегенмен, авторлар құбылыстардың физикалық
мазмұнын жасыратын және ішінара бұрмалайтын физиканың шамадан тыс
математикалану процесін сынайтын басылымдар барған сайын пайда
болуда.
Физика нақты табиғатты сипаттауы керек, ал математика адам ойының
жемісі. Математика формальды логикаға негізделген; олар үшін,
мысалы, Евклидтің де, Лобачевскийдің де геометриясы бірдей, ал
физика тек табиғатта бар нақты геометрияны көрсетуі керек. Бірақ
бұл тек математикаға тән формализм туралы емес. Қосымша екі
жағдайды ескеру қажет.
Біріншіден, белгілі бір математикалық теорияның
тұжырымдары эксперименттік фактілермен әлі расталған жоқ.Бұл
математикалық теорияның жалғыз дұрыс екенін айтады. Дәл сол
эксперименттік фактілерді кейіннен басқа математикалық теориямен
растауға болады және мұндай мысалдар физикада бар. Мысалы,
тербелмелі процестер тригонометриялық және көрсеткіштік
функциялармен, сондай-ақ векторлық диаграммалар әдісімен бірдей
сәтті сипатталады.
Екіншіден, физикада математикалық функцияларды қатардағы кеңейту,
олардың кішілігіне байланысты кеңейтудің үшінші және одан кейінгі
мүшелерін елеусіз қалдыру жиі қолданылады. Дегенмен, физика
дамуының осы кезеңінде елеусіз кішкентай және байқалмайтын нәрсе
болашақта физика дамуының басқа кезеңінде өте маңызды рөл атқаруы
мүмкін. Бұл супержолдар теориясына арналған Б.Гриннің (2004)
кітабында анық сипатталған.
Осы себептердің барлығына байланысты физиканы оқығанда ең алдымен
шамалардың физикалық мазмұнына назар аудару керек. Тіпті олардың
математикалық сипаттамасы физикалық мазмұнға сәйкес келмейтін
жағдайларда. Сонымен қатар, мұндай жағдайларда бұл тақырып ерекше
маңызға ие, өйткені бұл неліктен болғанын және ұсынылған оқу
материалын осы тұрғыдан қалай түсіну керек екенін түсіндіру
қажет.
Математика мен физиканыңөзарабайланысы: пәнаралықбайланыстар
Физика мен математика – ғылымныңеңтығызбайланысқанекісаласыболыптабылады. Математика физикадағызаңдардытұжырымдау, ғылымиесептеулержүргізужәнетәжірибелікмәліметтердіталдауүшінқажеттіқұралболыптабылады. Физикадағыкөптегенқұбылыстар мен процестерматематикалықформулаларжәнетеңдеулерарқылысипатталады. Сондықтан математика физикадағылымидәлдік пен нақтылықтықамтамасызететіннегізгітетікретіндеәрекететеді.
Пәнаралық байланыстар:
-
Теңдеулер мен формулалар:Физикадағызаңдар мен теорияларкөбінесематематикалықтеңдеулерарқылыөрнектеледі. Мысалы, Ньютонныңекіншізаңы F=maF = maF=ma (күш, масса жәнеүдеуарасындағыбайланыс) математикалықтүрдеанықталады.
-
Дифференциалдықесептеулер:Дифференциалдықтеңдеулерфизикадағыкөптегенқұбылыстардысипаттайды. Мысалы, тербеліспроцестері мен электрмагниттіктолқындарсияқтықұбылыстардысипаттауүшінқолданылады.
-
Функцияларжәнеграфиктер:Физикадафункциялар мен графиктерқозғалысты, электрлікжәнемагниттікөрістерді, жылупроцестерінжәнебасқақұбылыстардысипаттауүшінкеңіненқолданылады.
-
Векторлықталдау:Физикадавекторларкүштер, жылдамдықтаржәнеөрістерсияқтыфизикалықшамалардысипаттауүшінқолданылады. Векторлықталдауарқылы осы шамалардыңбағыттары мен шамаларыанықталады.
-
Математикалықмодельдеу:Физикалықжүйелер мен процестердіматематикалықмодельдерарқылыбейнелеуфизикадаөтемаңызды. Бұлмодельдерфизикалыққұбылыстардыболжауға, талдауғажәнетүсінугемүмкіндікбереді.
-
Статистика жәнеықтималдық:Физикадастатистикалықәдістер мен ықтималдықтеориясыкездейсоқпроцестер мен кванттық механика сияқтысалалардақолданылады.
Математика мен физиканыңөзарабайланысыпәнаралықбайланыстарарқылыоқушылардыңлогикалықойлауындамытуға, деректердіталдауқабілетінарттыруғажәнекүрделіфизикалыққұбылыстардытүсінугекөмектеседі. Бұлекіпәнніңбір-біріменүйлесімділігіфизиканытереңіректүсінугежәнеғылымибілімдітолықмеңгеругемүмкіндікбереді.
Физика сабақтарындаматематикалықбілімдіқолдану
Физика пәні – табиғаттыңзаңдарынтүсіндіретінжәнетәжірибелікесептеулерарқылығылымдымеңгеругебағытталғанмаңыздыпәндердіңбірі. Физикадағықұбылыстардытүсінуүшінматематикалықбілімдермаңыздырөлатқарады. Сабақбарысындаматематиканықолдануфизикалықпроцестердітереңіректүсінуге, есептердідұрысшығаруғажәнетеориялықбілімдітәжірибедеқолдануғамүмкіндікбереді.
-
Математикалықбілімдіқолданудыңнегізгіаспектілері:
-
Формулалардыпайдалану:Физикадакөптегензаңдар мен принциптерматематикалықформулаларарқылыберіледі. Оқушыларғаформулалардыдұрысқолданужәнеолардыесептердішығарудапайдалану физика сабақтарыныңнегізгіміндеттерініңбіріболыптабылады. Мысалы, жылдамдықтыесептеуүшін v=dtv = \frac{d}{t}v=td формуласы, немесекинетикалықэнергияныесептеуүшінEk=12mv2E_k = \frac{1}{2}mv^2Ek=21mv2 формуласықолданылады.
-
Теңдеулердішешу:Физикалықесептердішешубарысындатеңдеулердіқұружәнешешудағдыларыөтемаңызды. Бұлдағдыфизикалықшамалардыңөзарабайланысынанықтауғажәненақтышешімдергеқолжеткізугемүмкіндікбереді. Мысалы, кинематиканыңнегізгітеңдеулеріншешуарқылыдененіңқозғалысынсипаттайтынпараметрлердіанықтайаламыз.
-
Графикалықталдау:Физикадафункциялардыңграфиктерінқұружәнеолардыталдаумаңыздырөлатқарады. Мысалы, қозғалысграфиктеріарқылыжылдамдықты, үдеудінемесежүрілгенқашықтықтыанықтаумүмкіндігіпайдаболады. Графиктерфизикалықшамалардыңөзарабайланысынкөрнекітүрдекөрсетіп, оқушыларғатақырыптыжақсырақтүсінугекөмектеседі.
-
Дифференциалдықжәнеинтегралдықесептеулер:Кейбірфизикалыққұбылыстардысипаттауүшіндифференциалдықжәнеинтегралдықесептеулердіқолдануқажет. Мысалы, қозғалыстыңүдеуі мен жылдамдығыарасындағыбайланыстытүсінуүшіндифференциалдауәдістеріқолданылады, ал жиынтыққозғалыснемесекеңістікаумағынесептеуүшінинтегралдыпайдалануқажет.
-
Моделдеу:Математикалықмодельдеу – физикалықпроцестердіматематикалықформулаларарқылысипаттауәдісі. Бұләдіскүрделіжүйелердіқарапайыммодельдерарқылытүсінугежәнеолардызерттеугемүмкіндікбереді. Мысалы, электртізбектеріннемесемеханикалықжүйелердімодельдеуарқылыолардыңжұмысістеупринциптерінтүсіндіругеболады.
-
Статистика жәнеықтималдық:Физикадастатистикалықәдістер мен ықтималдықтеориясынқолданукездейсоққұбылыстардытүсіндірудемаңыздырөлатқарады. Бұләдістерәсіресе термодинамика, кванттық физика жәнеатомдықдеңгейдегіпроцестердісипаттаудақолданылады.
Физика сабақтарындаматематикалықбілімдіқолдануоқушыларғафизикалыққұбылыстардытереңіректүсінугежәнеолардыпрактикалықтұрғыдақолдануғамүмкіндікбереді. Математикалықесептеулерарқылыфизикалықзаңдылықтардыдәланықтап, ғылымиесептеулердіорындаумүмкіндігіартады. Осылайша, математикалықәдістерфизикадағыбілімдінығайтып, оқушылардыңғылымиойлауындамытуғасептігінтигізеді.
Физикалықзаңдардытұжырымдаунегізіретінде математика
Физика – бұлтабиғатқұбылыстарынзерттейтінғылым, ал математика – осы құбылыстардыдәлсипаттауғамүмкіндікберетінқұрал. Физикалықзаңдартабиғаттыңнегізгіпринциптерінтүсіндіреді, ал бұлзаңдардытұжырымдауүшін математика маңыздырөлатқарады. Физикалықзаңдардытұжырымдауүшінматематикалықтілдіңқолданылуыолардыңдәлдігі мен әмбебаптылығынқамтамасызетеді.
Математиканыңфизикалықзаңдардағырөлі:
-
Символдықөрнектержәнеформулалар: Математика физикалықзаңдардысимволдар мен формулаларарқылыөрнектеугемүмкіндікбереді. Бұлзаңдардыңнегізгісипаттарынқысқаәрінақтытүрдекөрсетугеболады. Мысалы, Ньютонныңекіншізаңы F=maF = maF=maтүріндежазылады, мұнда FFF – күш, mmm – масса, aaa – үдеу. Осы қарапайым формула арқылықозғалысзаңдылықтарынтүсіндіругеболады.
-
Математикалықмодельдеу:Физикалыққұбылыстардыматематикалықмодельдерарқылысипаттауоларғаталдаужасауғажәнеболжауғамүмкіндікбереді. Мысалы, электртізбектерін, термодинамикалықпроцестердінемесекванттықжүйелердімодельдеуүшіндифференциалдықтеңдеулерқолданылады. Модельдерфизикалықжүйелердіңмінез-құлқынматематикалықтұрғыдантүсінугежәнеолардынақтытәжірибелерменсалыстыруғамүмкіндікбереді.
-
Дифференциалдықтеңдеулер:Көптегенфизикалыққұбылыстаруақытнемесекеңістікбойыншаөзгеретіншамаларретіндесипатталады. Бұлөзгерістердісипаттауүшіндифференциалдықтеңдеулерқолданылады. Мысалы, гармоникалықтербелістердісипаттайтынтеңдеунемесежылуөткізупроцесіүшін Фурье теңдеуі. Осы теңдеулерарқылыжүйелердіңдинамикасынталдап, олардыңболашақтағыкүйінболжауғаболады.
-
Физикалықтұрақтыларжәне пропорция: Математика физикалықшамалардыңарасындағыпропорционалдыққатынастардыкөрсетудеқолданылады. Мысалы, Ом заңы V=IRV = IRV=IR түріндежазылады, мұнда VVV – кернеу, III – ток күші, RRR – кедергі. Мұндайқатынастарфизикалықшамалардыңөзарабайланысынтүсіндіредіжәнетәжірибелікдеректердіталдауғакөмектеседі.
-
Абстракция және идеализация:Математикалықәдістерфизикада абстракция мен идеализация жасауғамүмкіндікбереді, бұлкүрделіқұбылыстардықарапайыммодельдергедейінқысқартуғамүмкіндікбереді. Мысалы, идеалдыгаздармоделінемесеқаттыденелертеориясыарқылынақтыобъектілердіқарапайымтүрдесипаттауғаболады. Бұлабстракцияларфизикалықзаңдардыңнегізінтүсінугежәнеолардызерттеугемүмкіндікбереді.Математика физикалық заңдарды тұжырымдау негізі ретінде қызмет етіп, табиғаттың заңдылықтарын дәл және түсінікті түрде сипаттауға мүмкіндік береді. Математикалықәдістердіңкөмегіменфизикадағыкүрделіпроцестердіқарапайымтүрдесипаттап, олардыңмінез-құлқынболжауғаболады. Осылайша, математика физика ғылымыныңнегізіретіндемаңыздырөлатқарадыжәнеоныңдамуынаайтарлықтайықпалетеді.
Физикадағыматематикалықмодельдеу: практикалыққолдану
Математикалықмодельдеуфизикадатабиғиқұбылыстардысипаттаужәнетүсінуүшінқолданылатынмаңыздықұралдардыңбіріболыптабылады. Бұләдісфизикалықжүйелердіматематикалықтеңдеулер, формулаларнемесеалгоритмдерарқылыкөрсетіп, олардыңмінез-құлқынболжауғажәнеталдауғамүмкіндікбереді.
Математикалық модельдеудің рөлі:
-
Табиғи құбылыстарды сипаттау: Физикалық құбылыстардың көпшілігі математикалық модельдер арқылы сипатталады. Мысалы, Ньютона қозғалыс заңдары механикадағы денелердің қозғалысын модельдеуге мүмкіндік береді, ал Максвелл теңдеулері электромагниттік толқындарды сипаттайды. Бұл модельдер физикалық заңдылықтарды түсінуге және оларды математикалық тұрғыдан көрсетуге мүмкіндік береді.
-
Эксперименттік мәліметтерді талдау: Математикалық модельдеу физикадағы эксперименттік мәліметтерді талдауға және интерпретациялауға көмектеседі. Мысалы, радиоактивті ыдырау процесін модельдеу арқылы радиоактивті материалдардың жартылай ыдырау кезеңін есептеуге болады. Сондай-ақ, модельдеу тәжірибелік нәтижелерді болжауға және оларды нақты деректермен салыстыруға мүмкіндік береді.
-
Техникалық және инженерлік қолданбалар: Математикалық модельдеу физикада техникалық және инженерлік мәселелерді шешуде кеңінен қолданылады. Мысалы, құрылыс инженерлері ғимараттар мен көпірлердің беріктігін бағалау үшін құрылымдық механиканың математикалық модельдерін пайдаланады. Электротехникалық жүйелерді модельдеу арқылы электр тізбектерінің жұмысын талдау және оларды оңтайландыру мүмкіндігі бар.
-
Күрделі жүйелерді модельдеу: Физикадағы күрделі жүйелер, мысалы, атмосфералық құбылыстар, сұйықтық динамикасы немесе кванттық жүйелер, математикалық модельдер арқылы зерттеледі. Бұл модельдер табиғаттағы күрделі процестерді қарапайым түсіндіруге және олардың болашақтағы күйін болжауға мүмкіндік береді.
-
Компьютерлік модельдеу: Қазіргі заманғы математикалық модельдеу компьютерлік бағдарламалар арқылы жүзеге асырылады. Мысалы, климаттық өзгерістерді болжау үшін атмосфераның жаһандық циркуляциясын модельдейтін компьютерлік модельдер қолданылады. Сондай-ақ, ядролық реакторлардың жұмысын модельдеу немесе ғарыш аппараттарының траекториясын есептеу үшін де компьютерлік модельдеу қолданылады.
Математикалық модельдеудің практикалық мысалдары:
-
Қозғалыс теңдеулері: Механикада денелердің қозғалысын сипаттау үшін дифференциалдық теңдеулер қолданылады. Мысалы, еркін құлау қозғалысын модельдеу үшін s(t)=12gt2s(t) = \frac{1}{2}gt^2s(t)=21gt2 теңдеуі пайдаланылады, мұнда s(t)s(t)s(t) – уақытқа байланысты орын ауыстыру, ggg – еркін түсу үдеуі, ttt – уақыт.
-
Электр өрісін модельдеу: Электростатиканың негізгі заңдарын сипаттау үшін Кулон заңы және потенциалдық өрістердің теңдеулері қолданылады. Бұл модельдер арқылы электр зарядтарының өзара әрекеттесуін және олардың айналасындағы электр өрісін зерттеуге болады.
-
Толқындық процестер: Математикалық модельдеу толқындардың таралуын сипаттау үшін де қолданылады. Мысалы, су бетіндегі толқындарды немесе дыбыс толқындарын сипаттау үшін толқын теңдеуі ∂2u∂t2=c2∂2u∂x2\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2}∂t2∂2u=c2∂x2∂2u қолданылады, мұнда uuu – толқын амплитудасы, ccc – толқынның таралу жылдамдығы.Физикадағы математикалық модельдеу табиғи құбылыстарды түсіну және болжау үшін маңызды құрал болып табылады. Бұл әдіс физикалық заңдарды формулировка жасауға, тәжірибелік деректерді талдауға, инженерлік және техникалық мәселелерді шешуге мүмкіндік береді. Математикалық модельдеу физикадағы күрделі жүйелердің мінез-құлқын зерттеу үшін қажетті негізді қамтамасыз етеді және бұл ғылымның дамуына зор үлес қосады.
Физикадағы математикалық талдау: негізгі аспектілер
Математикалық талдау физикадағы маңызды құралдардың бірі болып табылады. Ол физикалық құбылыстарды сандық түрде сипаттау, түсіндіру және болжау үшін қолданылады. Математикалық талдау физикалық заңдарды зерттеу, физикалық жүйелердің мінез-құлқын түсіну және тәжірибелік мәліметтерді интерпретациялау үшін негіз болып табылады.
Математикалықталдаудыңрөлі:
-
Дифференциалдықтеңдеулердіқолдану:Физикадағыкөптегензаңдар мен процестердифференциалдықтеңдеулерарқылысипатталады. Мысалы, қозғалысзаңдары, жылуөткізу, сұйықтықдинамикасысияқтықұбылыстар осы теңдеулердішешуарқылытүсіндіріледі. Ньютонныңекіншізаңы F=maF = maF=maжиідифференциалдықтеңдеугеайналып, нақтыжүйелердегіқозғалыстысипаттайды.
-
Интегралдықесептеулер:Интегралдықесептеулерфизикадажүйелердіңжалпымінез-құлқынсипаттауүшінқолданылады. Мысалы, заттыңмассасыннемесеэлектрзарядынанықтауүшінинтегралдарқолданылады. Бұданбөлек, физикалықөрістердіесептеуде де интегралдармаңыздырөлатқарады.
-
Шектеуесептеулері:Физикадашектеупринциптерібелгілібіршарттардағыжүйелердіңмінез-құлқынзерттеуүшінқолданылады. Мысалы, шексізшамадағызарядтардыңөрісінемесеуақытөтешексіздіккеұмтылатынжүйелердізерттеушектеуәдістерініңкөмегіменжүзегеасады.
-
Сериялар мен қатарлар:Математикалыққатарларфизикадажүйелердіжуықтапесептеуүшінқолданылады. Тейлор немесе Фурье қатарларыкүрделіфункциялардықарапайымбөліктергежіктеугемүмкіндікбереді, бұлфизикалықжүйелердіталдаудыжеңілдетеді.
-
Вариациялықәдістер:Физикадағыкөптегенмәселелердішешуүшінвариациялықәдістерқолданылады. Бұләдістержүйеніңеңықтималкүйінанықтауүшінқолданылады, мысалы, Лагранж және Гамильтон әдістері механика мен электродинамикадакеңіненқолданылады.
Математикалықталдаудыңфизикадағынегізгіаспектілері:
-
Механикадағыталдау:Классикалықмеханикададенелердіңқозғалысынсипаттауүшіндифференциалдықтеңдеулер мен интегралдаркеңіненқолданылады. Мысалы, тербелмеліқозғалыстызерттеуүшінгармониялықосциллятордыңтеңдеуіқолданылады.
-
Электродинамикадағыталдау: Электр және магнит өрістерінзерттеуде Максвелл теңдеулеріматематикалықталдаудыңнегізгіқұралыболыптабылады. Бұлтеңдеулерэлектромагниттіктолқындардыңтаралуын, электрзарядтарыныңөзараәрекеттесуінжәнеэлектрөрістерініңқалыптасуынтүсіндіреді.
-
Термодинамика жәнестатистикалық физика:Термодинамикадажүйелердіңмакроскопиялыққасиеттерінзерттеуүшінинтегралдар мен ықтималдықтеориясықолданылады. Статистикалықфизикадакөпбөлшектердіңжүйелерінталдауүшінықтималдықтыесептеуәдістеріқолданылады.
-
Кванттықмеханикадағыталдау:Кванттықмеханикадатолқындықфункциялардысипаттауүшін Шредингер теңдеуіқолданылады. Бұлтеңдеукванттықжүйелердіңмінез-құлқынсипаттауүшінматематикалықталдаудыңнегізгіаспектіболыптабылады.
-
Тасымалдауқұбылыстарындағыталдау:Жылу, масса жәнеэлектрзарядтарыныңтасымалдануынсипаттауүшінматематикалықталдауқолданылады. Фурье теңдеуі, ОмынзаңыжәнеФикзаңдары осы құбылыстардытүсіндіруүшінқолданылады.Физикадағы математикалық талдау физикалық жүйелердің күрделі құбылыстарын түсіну және сипаттау үшін маңызды құрал болып табылады. Бұләдісфизикалықзаңдарды формулировка жасауға, жүйелердіңмінез-құлқынзерттеугежәнетәжірибелікнәтижелердіинтерпретациялауғамүмкіндікбереді. Математикалықталдауфизикадағызерттеулердіңмаңыздыаспектісіболыптабыладыжәнеолфизиканыңкөптегенсалаларындакеңіненқолданылады.
Физикадағыматематикалықтеңдеулер: мысалдаржәнеқолдану
Физикадағыматематикалықтеңдеулертабиғиқұбылыстардысипаттаудыңнегізгіқұралыболыптабылады. Оларфизикалықжүйелердіңдинамикасын, тепе-теңдігінжәнеэволюциясынсипаттап, физикалықзаңдардысандықтүрдетұжырымдауғамүмкіндікбереді. Математикалықтеңдеулерфизикадағызерттеулердіңнегізіболыптабыладыжәнеолардықолданукөптегенмаңыздыфизикалықнәтижелергеәкеледі.
1. Ньютонныңекіншізаңы:
Мысал:Ньютонныңекіншізаңықозғалыстысипаттауүшінқолданылады: F=maF = maF=maМұндағы FFF — күш, mmm — дененіңмассасы, aaa — үдеу. Бұлтеңдеуденегеәсерететінкүш пен оныңқозғалысындағыөзгерістерарасындағыбайланыстысипаттайды.
Қолдану:
-
Классикалықмеханикадағыденелердіңқозғалысынсипаттау.
-
Инженериядажәнетехникадақұрылғылардыңдинамикасынесептеу.
2. Шредингер теңдеуі:
Мысал:Кванттықмеханикадабөлшектердіңкүйінсипаттауүшін Шредингер теңдеуіқолданылады: H^Ψ=EΨ\hat{H}\Psi = E\PsiH^Ψ=EΨ Мұндағы H^\hat{H}H^ — Гамильтониан операторы, Ψ\PsiΨ — толқындық функция, EEE — энергия.
Қолдану:
-
Микробөлшектердің (электрондар, атомдар, молекулалар) қасиеттерінзерттеу.
-
Кванттықхимиядамолекулалардыңэлектрондыққұрылымынесептеу.
3. Максвелл теңдеулері:
Мысал:Электромагниттікөрістердісипаттауүшінқолданылатын Максвелл теңдеулері: ∇⋅E=ρϵ0\nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0}∇⋅E=ϵ0ρ ∇⋅B=0\nabla \cdot \mathbf{B} = 0∇⋅B=0 ∇×E=−∂B∂t\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}∇×E=−∂t∂B ∇×B=μ0J+μ0ϵ0∂E∂t\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}∇×B=μ0J+μ0ϵ0∂t∂E Мұндағы E\mathbf{E}E — электрөрісі, B\mathbf{B}B — магнит өрісі, ρ\rhoρ — электрзарядтарыныңтығыздығы, J\mathbf{J}J — ток тығыздығы.
Қолдану:
-
Электромагниттіктолқындардыңтаралуы.
-
Радиотолқындар, жарық, рентген сәулелерісияқтыэлектромагниттіксәулеленулердізерттеу.
4. Термодинамиканыңбіріншізаңы:
Мысал:Термодинамикадағыэнергияныңсақталузаңы: ΔU=Q−W\Delta U = Q - WΔU=Q−W Мұндағы ΔU\Delta UΔU — жүйеніңішкіэнергиясыныңөзгеруі, QQQ — жүйегеберілгенжылу, WWW — жүйежасағанжұмыс.
Қолдану:
-
Жылумашиналарының, тоңазытқыштардың, жәнебасқа да энергия түрлендіргіштердіңжұмысынсипаттау.
-
Химиялықреакциялардыңтермодинамикасынзерттеу.
5. Екіншіреттідифференциалдықтеңдеу:
Мысал:Гармониялықосциллятордысипаттайтынтеңдеу: md2xdt2+kx=0m\frac{d^2x}{dt^2} + kx = 0mdt2d2x+kx=0 Мұндағыmmm — масса, kkk — серіппеніңқатаңдығы, xxx — ауытқу.
Қолдану:
-
Серіппеліжүйелердіңтербелісінзерттеу.
-
Электрлікконтурлардағытербелістердісипаттау.
6. Фурье теңдеуі:
Мысал:Жылуөткізгіштікпроцесінсипаттауүшінқолданылатын Фурье теңдеуі: ∂u∂t=α∇2u\frac{\partial u}{\partial t} = \alpha \nabla^2 u∂t∂u=α∇2u Мұндағыuuu — температура, α\alphaα — жылуөткізгіштіккоэффициенті.
Қолдану:
-
Қаттыденелердежылутаралуынзерттеу.
-
Жылуоқшаулауматериалдарыныңтиімділігінбағалау.
Физикадағыматематикалықтеңдеулертабиғиқұбылыстардысандықтүрдесипаттаудыңжәнеталдаудыңнегізгіқұралыболыптабылады. Оларфизикалықзаңдарды формулировка жасауға, жүйелердіңмінез-құлқынмодельдеугежәнеболжауғамүмкіндікбереді. Мысалдардакелтірілгентеңдеулерәртүрліфизикалыққұбылыстардызерттеуүшінкеңіненқолданыладыжәнеолардыдұрысқолдануарқылыкүрделіжүйелердіңмінез-құлқынтүсінугеболады.
Физиканызерттеудематематикалықбілімніңмаңызы
Физика мен математика тығызбайланысқанғылымсалаларыболыптабылады. Физикадатабиғиқұбылыстардытүсіндіружәнеболжауүшінматематикалықәдістер мен құралдаркеңіненқолданылады. Математикалықбілімфизикалықзаңдардытұжырымдауда, эксперименттікнәтижелердіталдауда, жәнекүрделіжүйелердіңмінез-құлқынмодельдеуденегізгірөлатқарады.
1. Физикалықзаңдардытұжырымдау:
Математикалықбілімфизиканыңнегізгізаңдарынтұжырымдауғамүмкіндікбереді. Мысалы, Ньютонныңекіншізаңы( F=maF = maF=ma ) немесеЭйнштейнніңсалыстырмалықтеориясындағыэнергияныңтеңдеуі ( E=mc2E = mc^2E=mc2 ) сияқтыматематикалықформулаларфизикалыққұбылыстардыңдәлжәненақтысипаттамасынбереді.
2. Эксперименттікдеректердіталдау:
Физикалықзерттеулердіңкөпшілігіэксперименттікдеректердіжинаудықамтиды. Осы деректердідұрысталдауүшін статистика, ықтималдықтеориясыжәнебасқа да математикалықәдістерқажет. Математикалықбілімніңарқасындафизиктерэксперименттердіңнәтижелерінтүсіндіріп, қателіктердібағалайаладыжәнетеориялықмодельдердінақтыдеректерменсалыстыраалады.
3. Модельдеужәне симуляция:
Күрделіфизикалықжүйелердізерттеуүшінматематикалықмодельдерқолданылады. Модельдерфизикалыққұбылыстардықарапайымжәнетүсініктітүрдебейнелеугемүмкіндікбереді. Мысалы, климаттықөзгерістердіболжаунемесежаңаматериалдардыңқасиеттерінзерттеуүшінматематикалықмодельдерпайдаланылады. Бұлмодельдерсандықесептеулергенегізделеді, сондықтанматематикалықбілімфизикалықжүйелердісимуляциялауүшінөтемаңызды.
4. Теориялық физика:
Теориялықфизикадаматематикалыққұралдаререкшемаңыздырөлатқарады. Кванттық механика, салыстырмалықтеориясы, және термодинамика сияқтыфизиканыңбөлімдеріматематикалықнегіздеқұрылған. Мысалы, кванттықмеханикада Шредингер теңдеуібөлшектердіңтолқындықфункцияларынсипаттайды, ал салыстырмалықтеориясындаЭйнштейнніңтеңдеулерікеңістік пен уақыттыңқұрылымынсипаттайды.
5. Жаңафизикалықтеориялардыдамыту:
Физикадажаңатеориялардыдамытуүшінматематикалықжаңалықтарқажет. Мысалы, қарақұрдымдардың (қаратесіктердің) теориясындамытуүшінматематикалықталдау, дифференциалдықтеңдеулержәне топология сияқтыкүрделіматематикалықбөлімдерқолданылды.Физиканызерттеудематематикалықбілімніңмаңызызор. Математика физикалыққұбылыстардыдәлсипаттауға, эксперименттікдеректердіталдауға, күрделіжүйелердімодельдеугежәнежаңатеориялардыдамытуғамүмкіндікбереді. Математикалықбілімсізфизикалыққұбылыстардытолықтүсінумүмкінемес, сондықтан физика саласындатабысты болу үшінматематикаментереңтаныс болу қажет.
Физикадағыматематикалық аппарат: заманауитенденциялар
Физикадаматематикалықаппараттыңрөлікүнсанапартыпкеледі. Заманауифизикалықзерттеулердематематикалықәдістер мен құралдарфизикалықтеориялардыдамытудың, жаңаашылуларжасаудыңжәнеғылымипроблемалардышешудіңнегізіболыптабылады. Осығанбайланысты математика мен физика арасындағыөзарабайланыстереңдейтүсуде. Заманауитенденциялартөмендегідейбағыттардабайқалады:
1. Сандықәдістердіңдамуы:
Сандықәдістер мен компьютерлікмоделдеуфизикалықжүйелердізерттеудекеңіненқолданылуда. Қазіргізаманғысуперкомпьютерлер мен алгоритмдерфизикалыққұбылыстардысандықтұрғыдамодельдеугемүмкіндікбереді. Бұләдістеркүрделітеңдеулердішешуге, үлкенкөлемдегідеректердіөңдеугежәненақтыәлемдікжүйелердіңсимуляцияларынжүргізугемүмкіндікбереді.
2. Деректердіғылым мен аналитика:
Үлкендеректердің (Big Data) анализіфизикадамаңыздырөлатқарады. Ғылымиэксперименттер мен бақылауларданалынғанүлкенкөлемдегідеректердіөңдеуүшінкүрделістатистикалықжәнеесептеуәдістеріқолданылуда. Бұлфизикалықтеориялардытестілеуге, жаңамодельдержасауғажәнеболжамдардыдәлелдеугекөмектеседі.
3. Құрылымдықтеңдеулер мен симметриялар:
Физикадасимметриялар мен құрылымдықтеңдеулердіңмаңызызор. Қазіргізаманғызерттеулердесимметриялартеориясы мен жоғарыөлшемдікеңістіктердегітеңдеулеркеңіненқолданылуда. Мысалы, теориялықфизикада, стандарттымодельдежәнежалпысалыстырмалықтеориясындасимметриялар мен топологиялармаңыздырөлатқарады.
4. Қосымшаөлшемдер мен көпөлшемдімодельдер:
Көпөлшемдімодельдер мен қосымшаөлшемдерфизиканыңжаңатеорияларындакеңіненқолданылады. Мысалы, суперсимметрия, струндық теория және M-теория сияқтықосымшаөлшемдердіқамтитынтеорияларқазіргізамандабелсендізерттелуде. Бұлтеорияларфизикалыққұбылыстардытүсінугежаңаперспективаларұсынады.
5. Математикалық физика жәнеабстрактілітеориялар:
Математикалық физика, яғни математика мен физиканыңарасындағытереңбайланыстардызерттеу, маңыздызерттеубағытыболыптабылады. Абстрактіліматематикалыққұрылымдар мен теориялар, мысалы, топология, дифференциалдық геометрия жәнеалгебралық геометрия, физикалықмәселелердішешудеқолданылуда.
6. Жаңаалгоритмдер мен есептеутехникасы:
Заманауифизикадағыесептеулер мен моделдеуүшінжаңаалгоритмдер мен есептеуәдістеріәзірленуде. Мысалы, кванттықесептеу, нейрондықжелілержәнежасанды интеллект сияқтыжаңатехнологияларфизикалықпроблемалардышешудепайдаланылуда.
7. Тәжірибелікжәнетеориялық синтез:
Физикадатеориялықмодельдер мен эксперименттікнәтижелерарасындағыбайланыстыңнығаюымаңыздытенденциялардыңбіріболыптабылады. Теориялықболжамдардытәжірибелікдәлелдерментексеружәнекерісінше, эксперименттікдеректердітеориялықтүсініктерменсалыстырудықамтамасызететінәдістердамытылуда.Физикадағы математикалық аппараттың заманауи тенденциялары сандық әдістердің, деректерді анализдеудің, көп өлшемді модельдердің және жаңа математикалық теориялардың дамуымен байланысты. Бұлтенденцияларфизикалықтеориялардыкеңейтуге, жаңазерттеубағыттарынашуғажәнефизикадағыжаңаашылуларжасауғамүмкіндікбереді. Заманауиматематикалық аппарат физика ғылымыныңнегізіболыптабыладыжәнеғылымизерттеулердіңболашағынайқындайды.
«Физикадағы математиканың рөлі» ғылыми-зерттеу жұмысы
1. Математика физикаға қажет пе?

2. Физика
сабағында математиканы пайдаланасыз
ба?

3. Сіз не үйрететініңізді әрқашан түсінесіз бе?

4. Физиканы
математикасыз оқуға болады ма?

5. Математика
мен физика сізге оңай деп ойлайсыз
ба?

6.Физика мен
математиканы оқығанда қайталанатын тақырыптарды кездестірдіңіз
бе?

7.1.
Физика-математикадан тест тапсырмаларын тақырыптарды қайталаумен
біріктірсе, пәндерді меңгеру сапасы жоғары болады деп ойлайсыз
ба?

7.2. Оқушылардың эмоционалдық және физикалық жүктемелері төмендей ме?

7.3.Осы пәндер
бойынша жіберіп алған емтихандар саны азая
ма?

Осы зерттеу нәтижелеріне сүйене отырып, физикада математика қажет деп сеніммен айта аламыз.
Қорытынды
Математика қажет.
Физика үшін математиканың маңызы орасан зор. Математика табиғат заңдарының көпшілігін анықтайды. Бұл бізді қоршаған әлемді ғана емес, бүкіл ғаламды зерттеуге көмектесетін ерекше тіл. Математика іргелі ғылым ретінде жаратылыстану ғылымдарының әртүрлі бағыттағы дамуын қамтамасыз ететін әртүрлі әдістер жүйесі болып табылады. Математиканы физика мен жаратылыстану ғылымдарында қолдану өте үлкен, әрбір ғылымда жоғарыда келтірілген мысалдарда келтірілген математиканы қолданудың кем дегенде бір саласы бар. Математика басқа ғылыми пәндерге көмектесетін ғылым. Математика – жаратылыстану ғылымдары пәндерінің даму тілі. Математика – әртүрлі ғылымдардың зерттеу әдістерінің жиынтығы. Математиканы барлық жаратылыстану ғылымдары кеңінен қолданады. Математика жаратылыстану ғылымымен тығыз байланысты, бұл еңбекте көрсетілген.
Ұсыныс: Физикадағы математикалық әдістерге шолу, математика мен физиканың өзара байланысын талдау және физика сабақтарында математикалық білімдерді практикалық қолдану бойынша ұсыныстарды қамтитын зерттеу есебі.
Пайдаланылған әдебиеттер:

шағым қалдыра аласыз















