Формирование функциональной грамотности первоклассников на уроках математики

Сысоева И.В.

КГУ «Основная средняя школа №14»

Формирование функциональной грамотности первоклассников

на уроках математики

Современному обществу требуются люди, умеющие быстро адаптироваться к изменениям, происходящим в мире. В новых обстоятельствах процесс обучения в школе должен быть ориентирован на формирование определенного уровня функциональной грамотности. Функциональная грамотность – это уровень образованности, который может быть достигнут учащимися за время обучения в школе, и предполагает способность человека решать стандартные жизненные задачи в различных сферах жизни. В международном исследовании PISA термин «функциональная математическая грамотность» означает «способность учащегося использовать математические знания, приобретенные им за время обучения в школе, для решения разнообразных задач межпредметного и практико-ориентированного содержания, для дальнейшего обучения и успешной социализации в обществе». Математическая грамотность - способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину.

На начальном этапе обучения главное – развивать умение каждого ребенка мыслить с помощью таких логических приемов, как анализ, синтез, сравнение, обобщение, классификация умозаключение, систематизация, отрицание, ограничение. Учебный предмет  математика предполагает формирование арифметических счетных навыков, ознакомление с основами геометрии; формирование навыка самостоятельного распознавания расположения предметов на плоскости и обозначение этого расположения языковым средствами: внизу, вверху, между, рядом, сзади, ближе, дальше; практическое умение ориентироваться во времени, умение решать задачи, сюжет которых связан с жизненными ситуациями. Учебные задания, предлагаемые учащимся должны способствовать достижению целей обучения, формировать умения и навыки первоклассников, функциональную грамотность. Согласно таксономии Б.Блума задания в соответствии с уровнями учебных целей формируют различные навыки. Первые три уровня - знание, понимание и применение формируют репродуктивные навыки- виды деятельности, заключающиеся в умении ученика повторить или воспроизвести усвоенную информацию. Учебные задания уровня анализа и синтеза направлены на развитие навыков требующих познавательного умения, направленного на трансформацию явной и скрытой информации. Задания уровня оценивания направлены на формирование поведенческих навыков - это внешние и внутренние формы поведения, посредством которых ученик проявляет себя, свое самовосприятие, воспритие окружающих, восприятие различных жизненных ситуаций.

Задание 1 уровня (знание). Объясни значение понятий «больше, меньше, столько же», используя предметы в классе.

Задание 2 уровня (понимание). Сравни количество предметов, используя природный материал, проиллюстрируй равенства и неравенства.

Задание 3 уровня (применение). Выполни из бумаги модели прямоугольников по заданным величинам 5см.*3см., 7см.*2см.

Задание 4 уровня (анализ). Сравни прямоугольники разных размеров. Обоснуй свою точку зрения.

Задание 5 уровня (синтез). Создай модель «Возрастной цепочки» своей семьи, используй слово «старше», «младше».

Задание 6 уровня (оценивание). Аргументируй свою причастность относительно «Возрастной цепочки» своей семьи.

Предлагая первоклассникам задания различного уровня, процесс обучения приобретает форму активного исследования, позиция учащихся характеризуется готовностью включиться в учебный процесс, так как задания являются стимулятором активной познавательной деятельности. Деятельность позволяет формировать функциональную математическую грамотность.

В помощь учителю можно предложить следующие задания:

Математическая разминка 1

1. Какой день наступает после понедельника? 

2. Какой день следует за вторником? 

3. Какой день недели наступает раньше других? 

4. Какой день недели наступает позже других? 

5. Какой день недели предшествует субботе? 

6. Какой день недели находится между средой и пятницей? 

7. Как перечислить пять дней недели, не называя их? Ответ: позавчера, вчера, сегодня, завтра, послезавтра.

Математическая разминка 2

а) Если стол выше стула, то стул_______________________________________

б) Если 2 больше одного, то один ______________________________________

в) Если Ерлан вышел из дома раньше Сережи, то Сережа __________________

г) Если река глубже ручейка, то ручеек__________________________________

д) Если сестра старше брата, то брат____________________________________

е) Если правая рука справа, то левая ___________________________________

Математическая разминка 3

А) Из-за куста торчат 8 ушек. Там спрятались зайчики. Сколько зайчиков?___

Б) За оградой спрятались медвежата. Видны 12 лапок. Сколько медвежат?___

В) Из будки торчат хвостики всех щенков. Сколько щенков в будке, если мы видим 6 хвостиков? _________________________________________________

Г) За калиткой спрятались цыплята. Видны 10 лапок. Сколько цыплят?______

Д) Из гнезда выглядывают 4 клювика. Сколько там птенцов?______________

Задачи на логику

1. Шоколадка состоит из 9 квадратиков. Сколько разломов надо сделать, чтобы отделить все квадратики? (Каждый раз ломается один кусок по прямой линии.)
Ломаем шоколадку 2 раза и получаем 3 шоколадные полоски. Ломаем полоску на отдельные квадраты: каждую полоску по 3 раза. Получаем всего 8 разломов. Для других вариантов разламывания тоже нужно будет 8 разломов.

2. а) Ахмет решает задачи лучше, чем Коля. Коля решает задачи лучше, чем Мирас. Напиши, кто решает задачи лучше всех. (Лучше всех решает задачи Ахмет)

б) Полкан лает чаще, чем Жучка, но реже, чем Барбос. Напиши, кто лает чаще всех. (Чаще всех лает Барбос)

в) Мурка мяукает тише Барсика, но громче Пушка. Напиши, кто мяукает громче всех. (Громче всех мяукает Барсик).

 Развитие логического мышления школьников основывается на решении нестандартных задач на уроках математики, которые требуют повышенного внимания к анализу условия и построения цепочки взаимосвязанных логических рассуждений. Они позволяют рассматривать объект с разных точек зрения, учат анализу, синтезу, оценочным суждениям, воспитывают внимание, способствуют развитию познавательного интереса и активности учащихся.

Первоклассникам в основном предлагаются не учебные, а практические ситуации, характерные для повседневной жизни. Материал помогает активизировать мыслительные процессы, развивает познавательную активность, наблюдательность, внимание, память, поддерживает интерес к предмету. Задания предполагают повысить у учащихся мотивацию к изучению предмета, развить аналитико-синтетические способности, сообразительность, математическую речь, гибкость ума.

Закономерности:

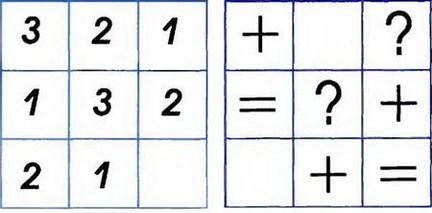
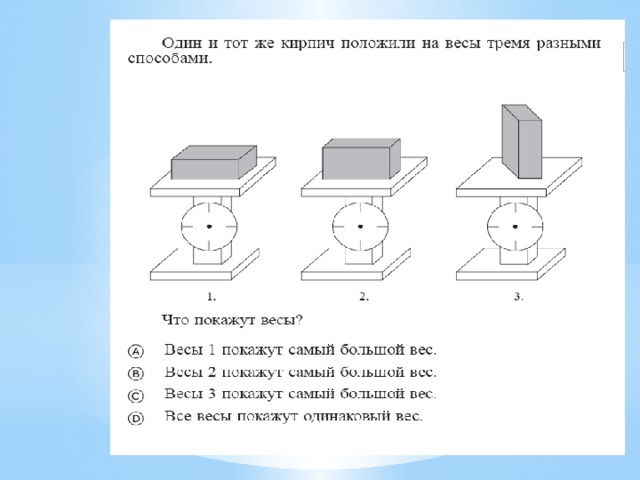
Основной целью математического образования должно быть развитие умения математически, логично и осознанно исследовать явления реального мира. Реализации этой цели может и должно способствовать решение на уроках математики разного рода нестандартных логических задач. Нестандартные задачи требуют повышенного внимания к анализу условия и построения цепочки взаимосвязанных логических рассуждений.   Примеры таких задач, ответ на которые необходимо логически обосновать.

1. В коробке лежат 5 карандашей: 2 синих и 3 красных. Сколько карандашей надо взять из коробки, не заглядывая в нее, чтобы среди них был хотя бы 1 красный карандаш?

2. Задумали число и к нему прибавили 4. Сколько нужно вычесть из полученного числа, чтобы снова получить задуманное число? Приведи несколько примеров, подтверждающих твой ответ.

При решении занимательных задач преследуются следующие цели: формирование и развитие мыслительных операций: анализа и синтеза; сравнения, аналогии, обобщения; развитие и тренинг мышления вообще и творческого в частности; поддержание интереса к предмету, к учебной деятельности (уникальность занимательной задачи служит мотивом к учебной деятельности); развитие качеств творческой личности, таких, как познавательная активность, усидчивость, упорство в достижении цели, самостоятельность; подготовка учащихся к творческой деятельности (творческое усвоение знаний, способов действий, умение переносить знания и способы действий в незнакомые ситуации и видеть новые функции объекта).

Нестандартные логические задачи - отличный инструмент для развития функциональной грамотности.

Задачи.

1. Расставить 6 книг на две полки так, чтобы на одной было на 2 книги больше, чем на  другой.

2. В шкафу было 16 чашек с синими цветочками, чашек в горошек – на 2 меньше, чайных ложек – на 12 больше, чем чашек в горошек. Сколько одновременно человек смогут пить чай, если у каждого должна быть своя чашка и своя чайная ложка?

Однако что зачастую наблюдается на практике? Учащимся предлагается задача, они знакомятся с нею и вместе с учителем анализируют условие и решают ее. Но извлекается ли из такой работы максимум пользы? Нет. Если дать эту задачу через день-два, то часть учащихся может вновь испытывать затруднения при решении. Наибольший эффект при этом может быть достигнут в результате применения различных форм работы над задачей:

1. Работа над решенной задачей. Многие учащиеся только после повторного анализа осознают план решения задачи. Это путь к выработке твердых знаний по математике.

2. Решение задач различными способами. Мало уделяется внимания решению задач разными способами в основном из-за нехватки времени. А ведь это умение свидетельствует о достаточно высоком математическом развитии. Кроме того, привычка нахождения другого способа решения сыграет большую роль в будущем.

3. Правильно организованный способ анализа задачи - от вопроса или от данных к вопросу.

4. Представление ситуации, описанной в задаче (нарисовать «картинку»). Учитель обращает внимание детей на детали, которые нужно обязательно представить, а которые можно опустить. Мысленное участие в этой ситуации. Разбиение текста задачи на смысловые части. Моделирование ситуации с помощью чертежа, рисунка.

5. Самостоятельное составление задач учащимися.

Составить задачу, используя слова: больше на, столько, сколько, меньше в, на столько больше, на столько меньше

6. Решение задач с недостающими данными.

7. Изменение вопроса задачи.

8. Составление различных выражений по данным задачи и объяснение, что означает то или иное выражение. Выбрать те выражения, которые являются ответом на вопрос задачи.

9. Объяснение готового решения задачи.

10. Использование приема сравнения задач и их решений.

11. Запись двух решений на доске - одного верного и другого неверного.

12. Изменение условия задачи так, чтобы задача решалась другим действием.

13. Закончить решение задачи.

14. Какой вопрос и какое действие лишнее в решении задачи (или, наоборот, восстановить пропущенный вопрос и действие в задаче).

15. Составление аналогичной задачи с измененными данными.

16. Решение обратных задач.

Систематическое использование на уроках математики задач и заданий, направленных на развитие логического мышления, расширяет математический кругозор младших школьников и позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.

Часто учителя начальных классов на своих уроках используют парную и групповую работу. При организации работы в парах и группах каждый ученик мыслит, предлагает своё мнение, пусть оно и неверное, в группах рождаются споры, обсуждаются разные варианты решения, идёт взаимообучение детей в процессе учебной дискуссии, учебного диалога. Используемые на уроках формы и методы работы способствуют развитию информационно-образовательной среды, направленной на повышение функциональной грамотности учащихся, обеспечивающей личное саморазвитие, самостоятельность в приобретении знаний, формирующей коммуникативные навыки, умения использовать информацию и технологии, решать проблемы, предприимчивость и креативность. Учитель должен увлечь и «заразить» детей, показать им значимость их деятельности и вселить уверенность в своих силах.

Учащиеся, овладевшие математической грамотностью, способны:
распознавать проблемы, которые возникают в окружающей действительности и могут быть решены средствами математики;
формулировать эти проблемы на языке математики;
решать проблемы, используя математические факты и методы;
анализировать использованные методы решения;
интерпретировать полученные результаты с учетом поставленной проблемы;
формулировать и записывать результаты решения.

Сущность функциональной грамотности состоит в способности личности самостоятельно осуществлять деятельность учения, а также применять все постоянно приобретаемые в жизни знания, умения и навыки для решения широкого диапазона жизненных задач в различных сферах жизни.

Задача учителя научить школьников добывать знания, умения, навыки и применять их в практических ситуациях, оценивая факты, явления, события и на основе полученных знаний принимать решения, действовать. Все приемы и методы, используемые педагогом, должны быть направлены на развитие познавательной, мыслительной активности, которая в свою очередь направлена на отработку, обогащение знаний каждого учащегося, развитие его функциональной грамотности. При условии успешности решения поставленных задач мы выполним главную цель формирования функционально-грамотной личности т.е. формирование в общеобразовательных школах интеллектуального, физически и духовно развитого гражданина РК.