
Мазмұны
1. Кіріспе …………………………………………………………………….3-4 бет
1.1. Формула әдемілігі
2. Негізгі бөлім …………………………….....................................................5 бет
2.1. Фракталдар дегеніміз не?…………………………................................5 бет
2.2. Қар қылауы және галактика - фракталдар………………....................6 бет
2.3. Тірі табиғаттағы фракталдар…………………………………...............7 бет
2.4. Математикадағы және адам ойлап тапқан заттардағы фракталдар…8-9 бет
3. Зерттеу бөлімі..........................................................................................10-11 бет
4. Тәжірибе жүзінде қолдану..................................................................12-13 бет
5. Қорытынды бөлім........................................................................................14 бет
6. Әдебиеттер тізімі .......................................................................................15 бет
7. Қосымша материалдар..........................................................................16-18 бет
Мақсаты:
Ою-өрнектердің үйлесімділігін сандық заңдылықтармен тексере отырып, түрлі облыстарда көрінетін дене арқылы көрінбейтін заттың ұқсастық негіздерін айқындап зерттеу жүргізу.
Міндеттері:
1) Фракталдарға анықтама беру;
-
Фракталдардың түрлерін сипаттау;
-
Фракталдардың ғылымдағы қолданысын тану;
-
Фракталды геометрия тұрғысынан адам ағзасының, өсімдіктер әлемінің, өлі табиғаттың байланысын көру.
Өзектілігі: Қоршаған айналамыздағы құбылыстарды зерттеу фракталды геометрия болып табылады.
Болжам: Қоршаған айналамыздағы құбылыстардың үйлесімді заңдылықтары математикалық нақтылықпен құрылған.
Зерттеу объектісі: Үй тұрмыс заттары, адам ойлап тапқан объектілер, адам қолынан жасалған заттар, айналаны қоршаған өсімдіктер әлемі.
Зерттеу нысаны: Қоршаған айналамыздағы фракталдардың ашылуы.
Зерттеу әдістері:
Эмпиризмдік (қадағалау, өлшеу, тәжірибе)
Теориялық (танымның логикалық сатысы)
Зерттеу кезеңдері:
Әдебиеттер тізімін қолдану
Зерттеу материалдарын жинақтау
Тәжірибе жүргізу
Жұмысты рәсімдеу
Күтілетін нәтиже: Өлі және тірі табиғатағы фракталдарға суреттер жинағын шығару.
Кіріспе
«Математика өзінің әдемілігімен
және үйлесімділігімен көрікті,
бірақ-та бұл әдемілікті көре білу керек ».
Бенуа Мандельброт
Өрнектерді мүмкіндігінше біз күнде көреміз. Оларды көру үшін әлдекім оған бар күшін салғаны бізге белгілі. Табиғаттағы біз кездестіретін өрнектер туралы не айтуға болады? Олар нені білдіреді? Қоршаған айналамыздағы үйлесімділікті математикалық нақтылықпен көре аламыз ба? деген сұрақтар туындай түседі.
Біз бұл туралы ақпаратты жан-жақты және ғаламтор желісінен іздестіруді жөн көрдік.
Қоршаған әлемдегі табиғат құбылыстарының жалпы теориясы, соның ішінде айқыш өрнектер фракталдар болып табылады. Фрактал құрылымының қиындығы бір мезгілде айқын болса, екінші жағынан айқын емес болып көрінеді. Себебі, бұл фрактал құрылымының кішкентай ғана бөлігі деп түсінеміз. Егер осы қағида дұрыс болса, онда барлық әлемді математикалық нақтылықпен есептеуге болар еді.
Фракталдар бұл оғаш, жұмбақ құбылыс. Ол қоршаған айналамызда шиыршықталып, дөңгеленіп, тармақталып бейнеленетін дүние. Фракталдар адам ағзасында, өсімдіктер әлемінде, галактика жұлдыздарында, тіпті біздің ұялы телефонымыздың сымында үздіксіз қайталанатын құбылыс болып көрінеді.
Фракталдар - таңғажайып математикалық өнердің саласы, күрделі формулалар және алгоритмдер көлемі мен адам айтқысыз әсем және күрделі суреттер жасауға болады. Бұл жаңа ұғым ғаламшар бойын өз әдемiлiгiмен және тылсымдылығымен арбай адымдайды, көптеген облыстарда: метеорологияда, философияда, биологияда, механикада, географияда және тiптi тарихта да айқындалады. Сондықтан оларды зерттеу бүгiнгi ғаламшар ойшылдарының мәселесіне айналуда.
Фракталдар біздің жан-жағымызда: тау жоталары сызығында, теңіз жағалауының ирелең сызықтарында кездеседі. Кейбір фракталдар жылжыған бұлттар мен жанып жатқан от іспеттес үздіксіз өзгереді, кейбіреулері тал ағаштар мен біздің қан тамырлары жүйелеріміз сияқты өзінің даму нәтижесінде қабылдаған құрылымын сақтайды. Мектепте зерделеген және күнделікті өмірде қолданатын геометрия Эвклидтен басталады (мөлшермен біздің дәуірімізге дейінгі 300 жыл бұрын). Үшбұрыштар, квадраттар, дөңгелектер, параллелограммдар, параллелепипедтер, пирамидалар, шарлар, призмалар – классикалық геометрия қарастыратын типтік объектілер. Адам қолынан туындаған заттар осы фигуралар мен олардың жеке бөліктерінен тұрады. Бірақ табиғатта олар жиі кездесе бермейді. Мысалы, орман шыршалары аталған заттар мен олардың комбинацияларына ұқсай ма? Расында да, Эвклид формаларына қарағанда, табиғи объектілер тегіс, жатық емес, шеттері сынық, беттері бұдыр, жарылып, тесіктер мен жолақтармен желінген. «Неге геометрияны суық, құрғақ деп атайды? Оның бір себебі – бұлттардың, таулар мен теңіз жағалауының түрлерін сипаттап бере алмауында. Бұлттар – сфера емес, таулар – конус емес, жағалау сызықтары – шеңберлер емес, қабықтар тегіс емес, найзағай түзу сызықпен шашырамайды. Табиғат тек қана жоғары деңгейдегі ғана емес, мүлде басқа деңгейдегі күрделілікті танытады» деген сөздерімен Бенуа Мандельброттың «Табиғаттың фракталды геометриясы» оқулығынан бастау алады. Фракталдар үшін осындай ұқсастық сипаттамалар анықталады.



1- сурет 2-сурет 3-сурет


4-сурет 5-сурет
2. Негізгі бөлім
2.1. Фракталдар дегеніміз не?
Фрактал ұғымын, фракталды геометрияның негізін салушы 1970 жылы Бенуа Мандельброт енгізген. Fractal - латын тілінің fractus деген сөзінен шыққан, бөліктерге бөлінген деген мағынаны береді. Фрактал - бұл әрбiр бөлiгi масштабын кiшiрейткенде өзін қайталайтын шексiз өзiне ұқсас геометриялық фигура. Масштабы үлкен құрылым, масштабы кіші құрылымды қайталайды. Өзінің бір мысалында Мандельброт ұшақтың үстінде тұрып жағалауды үлкейткіш әйнек арқылы қарауды ұсынады.
Барлық жағдайда ұқсас кескін
алады, бірақ масштабы әр түрлі болады.
1975 жылы математик Б. Мандельброт осы ұшы-қиырсыз, ретсіз
формаларға фрактал деген атау берді. Бұл фигураны ағаш бұтақтары,
тау шыңдары, жағалау сызықтары сияқты күрделі табиғи жүйелердің
моделі түрінде көруге болады. Ағаш тәрізді фракталдар тек
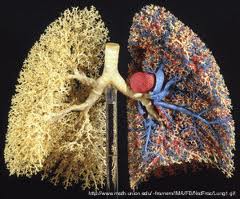
өсімдіктердің бейнесін ғана емес, сонымен бірге бронхы
тармақтарының, бүйректің, қан тамырларының т.б. жұмыс моделін жасау
үшін пайдаланылады. Көтеген тәжірибелік есептерді шығару барысында
пайда болатын құбылыстарды зерттеген американ
профессоры
Б. Мандельброт «Табиғаттың фрактал геометриясы» атты еңбегінде: фракталдар- бөлшектелген деген мағынаны береді – деп жазған. Ең қарапайым фрактал геометриялық фигуралардан тұрады. Олар бөлінгенде үлкенінің ұқсас көшірмесі пайда болады. Бір-бірімен шексіз бөліне отырып, бірігіп, керемет суреттер құрайды.
Фракталдар мынандай топтарға бөлінеді:
алгербралық, геометриялық,
итерацияланатын функциялар жүйесі, стохастикалық фракталдар және
т.б.
Фракталдар машиналық графикада үлкен рөл атқарады. Мысалы, олар
бірнеше коэффициент арқылы, формасы өте күрделі сызықтар мен
жазықтықтарды жасау кезінде көмекке келеді. Машиналық графиканың
пікірі бойынша, жасанды бұлттарды, тауларды, мұхит бетін
генерациялауда фракталдық графика таптырмайтын құрал. Нақтырақ
айтсақ, кескіндері табиғатқа ұқсас, әрі өте күрделi, Евклидтiк емес
объектiлерді ұсыну мүмкіндік береді.
Фракталды алгоритмдер ақпараттық технологияларда, мысалы табиғи
ландшафтылардың үшөлшемді компьютерлік бейнелеуін енгізуге,
деректерді қысып жинақтауға қолданылады. Фрактал түсінігі тағы да
бір таңғажайып көрініспен – динамикалық жүйелердегі хаоспен тығыз
байланысты.
Жалпы фракталдардың тарихы геометриялық фракталдардан бастау алады.
Бұл фракталдардың типі қарапайым геометриялық құрастырулардан пайда
болады. Негізінен ол былай жасалады, ең алдымен – “бастама” -
аксиома алынады, яғни солар арқылы салынатын, кескіндер жиынтығы
беріледі. Содан соң “бастамаға”, оны белгілі бір геометриялық
фигураға айналдыратын ережелер жиынтығы қолданылады. Сосын сол
фигураның әрбір бөлігіне қайтадан сол ережелерді қолданады. Әрбір
қадам сайын фигура күрделене түседі. Егер де осы операцияларды
шексіз көп қайталайтын болсақ (қажетінше) онда біз геометриялық
фракталды аламыз.
Геометриялық фракталдар – өзінің пішінін кішірейтілген түрде
қайталайтын геометриялық фигуралар. Машиналық графикада
геометриялық фракталдарды ағаштың, өсімдіктің суретін және жағалау
сызығын алу үшін қолданылады.
Бізді қоршаған айналамыздағы
құбылыстардың құрылымы фракталдарға ұқсас болатынын анықтауға
болады. Олар: дауыл соққан кездегі бұлттардың көшуі, теңіз
жағалауларының шекаралары, беттері жарылған жерлер, терезеге
салынған қылау өрнектері болып
табылады.
2.2. Қар қылауы және галактика – фракталдар.
Қар қылауы немесе ұлпалар ауадағы су буынан, салқын тұман тамшыларынан түрлі заттар бетіне крисалл түрінде бейнеленеді. Кристалдардың көбеюінен нәзік өрнектер пайда болады. Оның сәулелері тармақталған сайын оның пішіндері кіші өлшемдермен бейнелене түседі. Сондықтан да осындай ұқсастық қасиеттер математикада фракталдар болып табылады.
Тағы бір фракталдардың түрі - бұл камераларға бөлінген наутилус қабыршағы. Бұл нутилус қабыршағы дамып, көбейген сайын көптеген камераларға бөлініп, өзіне қажетсіз қабыршақтарды тастайды. Нәтижесінде өзінің пішінін сақтай отырып, фракталды шиыршық түрінде бейнеленеді. Осындай ұқсас шиыршық тәрізді бейнелер дауыл болғанда бұлттардың құбылысы және галактикадағы жұлдыздарда байқалады.



6-сурет 7-сурет 8-сурет
2.3. Тірі табиғаттағы фракталдар.
Фракталдар бізді қоршаған әлемнің үйреншікті көріністерінің көбін өзгертеді. Фракталдар табиғи және жасанды объектілердің геометриялық қасиеттеріне деген біздің көзқарасымызды қайта бағалауға мәжбүр етеді, ал динамикалық хаос осы объектілердің уақыт барысында өздерін ұстау түсінігіне күрт өзгерістер енгізеді. Осы түсініктер негізінде құрылған теориялар білімнің әртүрлі салаларында, оның ішінде ақпараттық және коммуникациялық технологияларда жаңа мүмкіндіктер ашады.
Қоршаған айналамыздағы фракталдар өте көп кездеседі. Табиғи құрылымдардың барлығының фракталды құрылысы болады. Егер фракталды объектіге толығымен қараса, содан кейін оның үлкейтілген жеке бөлігіне қараса, содан кейін осы бөліктің бөлігіне қараса т.с.с., онда олардың бірдей екендігін көруге болады. Фракталдар өз-өзіне баламалы – олардың пішіндері әртүрлі өлшемдерде қайталанады. Фракталды алгоритмдер ақпараттық технологияларда, мысалы табиғи ландшафтылардың үшөлшемді компьютерлік бейнелеуін енгізуге, деректерді қысып (компрессиялау) жинақтауға қолданылады. Фрактал түсінігі тағы да бір таңғажайып көрініспен – динамикалық жүйелердегі хаоспен тығыз байланысты.
Мысал келтіретін болсақ, фракталдардың ұқсастық қасиеттері ағаштарда да байқалады. Ағаштардан көптеген бөліктерге тал шыбықтары бөлініп шығады, ал осы тал шыбықтардан ұсақ шыбықтар, одан тағы да өте ұсақ шыбықтар т.с.с бөлініп шығатыны байқалады. Сол сияқты гүл өсімдіктері, адам ағзасының құрылыстары да фракталдар түрінде бейнеленеді.
Өсімдіктер, ағаштар, шөптер, телефон антенналары т.б. объектілер белгілі бір фракталды пішін түрінде көрінеді.
Гүлді қырыққабат та, оның "әсерлі" түрі - фракталдар түсінігін түсіндіруге мүмкіндік беретін табиғи нысандар болып табылады. Оны математикаға
70-ші жылдары Иель университетінің француз ғалымы Бенуа Мандельброт енгізді. Фракталдың өзіне ғана тән қасиеті оның өзіне өзі ұқсастығы, яғни оның бөлігі - бұл бүтіннің кішірейтілген көшірмесі. Сонымен әр гүл шоғыры бүтін гүлді қырыққабаттың бейнесі болып табылады. Фракталдар медицина, гидрология және қаржы сияқты әртүрлі салаларда қолданылады.


 -
-
9- сурет 10-сурет 11-сурет

12-сурет 13-сурет
2.4. Математикадағы және адам ойлап тапқан заттардағы фракталдар
Адамзат тарихының өткен барлық кезеңдерінде әрқашан да табиғат құпияларын танып-білудің негізгі құралы математика болған. Математика бізді айнала қоршаған сандар мен фигуралардан тұратын ерекше әлемнің құпия-сырын ашып береді. Табиғатта көптеп кездесетін барлық тірі нәрселердің арасындағы байланыс математикалық дәлдікпен жасалған.
Шамамен бұдан 100 жылдай бұрын математиктер тек үшбұрыштар мен шеңберлер сияқты қалыптасқан формаларды зерттеумен ғана айналысқан. Бірақ мұндай формалар табиғатта сирек кездеседі. Табиғат жаратылыстары ретсіз формаға, мысалы, жағалаудың ирек толқынды жиек сызығы немесе құз жартасты таулар. Жақыннан қарағанда тегіс және жалпақ болып көрінетін шеңберден айырмашылығы таулар құз шыңды күйде қалады. Оларға жақыннан қарайтын болсақ, одан да тек бұралаңдар мен қыртыс-қатпарларды көреміз.
Фракталдар өздеріне ұқсас кішкентай көшірмелерінен тұрады. Б. Мандельброт өзінің компьютерінде ғажайып фрактал үлгілерін жасады. Ол математикадағы жорамал сандардың көмегімен графтар сызды. Ең танымал үлгіні Мандельброт жиыны деп атайды. Ол математикадағы ең күрделі фигура болып саналады. Егер оны көбейтетін болса, ол одан сайын ою-өрнекті болады және құлпыра түседі. Ал егер оның майда фрагменттерін көбейтетін болса, онда ою-өрнектің ұшы-қиырсыз шексіз екеніне көзің жетеді. Тіпті математикаға ешқандай қатысы жоқ адамның өзі де фигуралардың негізгі формаларының түрленгенінде қайталана беретінін байқайды.
Қазіргі таңда ғылымдардың математикалануы күрделілігі әртүрлі математиалық модельдердің қолдануымен сипатталады. Табиғаттағы құбылыстар мен процестерді зерттеуде, табиғат ананың рухани және материалдық байлықтарын ұқыптап теруде алдын-ала өлшеп, есептеп және саралап алмай, мәселені түбегейлң шешуге болмайтындығы белгілі. Міне, осы кезде математиканың табиғаттағы, адам өміріндегі рөлі айқындала түседі.
-
«Серпіндік үшбұрыш»
Бұл «Серпіндік үшбұрыш» 1915 жылы поль математигі Вацлов Серпинский ойлап тапқан ұқсастық фракталдары болып табылады.
Бұл теңбүйірлі үшбұрышты құру үшін үшбұрыштың ортасын қиып алып тастағанда, дұрыс төрт үшбұрыштарға бөлінеді. Осындай ретпен ішкі үшбұрыштың ортасын алып тастағанда тағы да ұсақ үшбұрыштарға бөлінеді. Алынған үшбұрыштарды осындай реттілікпен қайталап орындағанда, бірте-бірте кішірейтілген объектілердің ұқастық қасиеттері байқалады. Демек бұл объектілер фракталдар болып табылады.


14-сурет 15-сурет
-
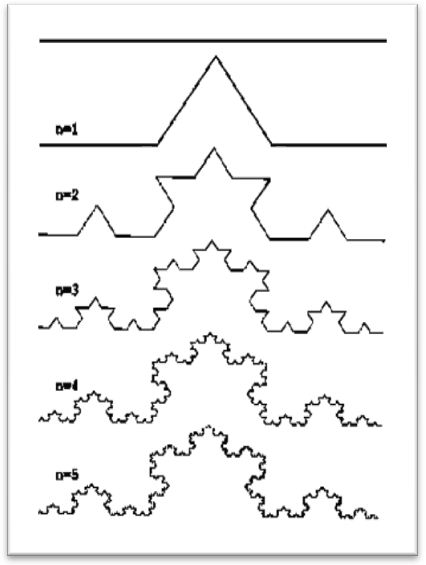
«Кох» ұлпасы
Бұл «Кох» ұлпасы 1904 жылы Гильгом фон Кох ойлап шығарған. Оның құрылымы мына суретте көрсетілген.
Кесіндіні теңдей үш бөлікке бөліп, ортаңғы 1/3 бөлігін алып тастайды. Содан соң осындай ұзындықта тағы екі кесінді қосылады. Әрбір жасалған қадамда теңдей үш бөлікке бөлінген кесіндіні екі жаңа кесіндімен қосып алады және бірнеше рет қайталанып отырады. Нәтижесінде кесінділерден ұлпа тәрізді фигура пайда болып табылады болады. Демек, бірте-бірте кішірейтілетін объектіле фракталдар болып табылады.

16-сурет 17-сурет
-
Зерттеу бөлімі.
Расында да дауыл кезіндегі бұлттардың құбылысы, ұсақ камераларға бөлінген наутилус қабыршақтары, галактикадағы жұлдыздар – барлығы да фракталдар болып табылады.
Осы объектілердің негізі шиыршық тәрізді болатынына тәжірибе жүргізіп көрейік.
-
Күнбағыс
-
Ананас
-
Түймедақ
-
Жабайы сәбіздің шатыр гүлі
-
Күнбағысты микроскоп арқылы бақылаймыз. Бұл күнбағыстың дәндері
шиыршық тәрізді орналасқанын байқадық. Оның дәндері қандайда бір бұрыш түрінде көрінеді. Бұл бұрыш шамамен доғал бұрышқа ұқсас, яғни 137,50 градусты көрсетеді. Бұл ерекше бұрыш болғандықтан оны «алтын бұрыш» деп атайды екен. Осы бұрышқа байланысты нақты шиыршық тәрізді сурет құралады. Ал егер бұл бұрышыты 1400 деп өзгертсек, онда күнбағыстың құрылымы радиалды, ал дәндерінің орналасуы тиімді болмас еді. Осы тәжірибені жасау кезінде мен мынадай ойға келдім. Күнбағыстың себет гүлінің өсуі ретсіз болмайды, ол қандай да бір заңдылыққа тәуелді болады екен. Егжей-тегжейлі қарастырылғандықтан, «алтын бұрыш» пен сандар қатары арасындағы тамаша тәуелділікті байқауға болады.
Бұл тәуелділік тізбектелінген Фибоначчии сандары болып табылады.
1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 4181;...
Бұл сандар қатарындағы әрбір келесі сан алдыңғы екі санның қосындысына тең болады. Шынында да, тізбектелінген Фибоначчи сандарын барлық өсімдіктерден анықтауға болады.
Күнбағыстың бір жағында 34 иірмек шиыршық бейнеленген болса, екінші жағына 55 иірмек шиыршық болады екен. Бұл екі сан тізбектелінген Фибоначчи сандарына жатады.


18-сурет 19-сурет
-
Ананас
Кез келген екі ананасты аламыз. Бірінші ананастың 8 иірмек шиыршығы бар, ал екінші ананаста 13 иірмек шиыршығы болады. Бұл екі сандар тізбектелінген Фибоначчи сандарына жатады. Бұл экзотикалық жемістің құрылымы фракталдар болып табылады.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
"ФРАКТАЛДАР" ғылыми-зерттеу жобасы
"ФРАКТАЛДАР" ғылыми-зерттеу жобасы
Мазмұны
1. Кіріспе …………………………………………………………………….3-4 бет
1.1. Формула әдемілігі
2. Негізгі бөлім …………………………….....................................................5 бет
2.1. Фракталдар дегеніміз не?…………………………................................5 бет
2.2. Қар қылауы және галактика - фракталдар………………....................6 бет
2.3. Тірі табиғаттағы фракталдар…………………………………...............7 бет
2.4. Математикадағы және адам ойлап тапқан заттардағы фракталдар…8-9 бет
3. Зерттеу бөлімі..........................................................................................10-11 бет
4. Тәжірибе жүзінде қолдану..................................................................12-13 бет
5. Қорытынды бөлім........................................................................................14 бет
6. Әдебиеттер тізімі .......................................................................................15 бет
7. Қосымша материалдар..........................................................................16-18 бет
Мақсаты:
Ою-өрнектердің үйлесімділігін сандық заңдылықтармен тексере отырып, түрлі облыстарда көрінетін дене арқылы көрінбейтін заттың ұқсастық негіздерін айқындап зерттеу жүргізу.
Міндеттері:
1) Фракталдарға анықтама беру;
-
Фракталдардың түрлерін сипаттау;
-
Фракталдардың ғылымдағы қолданысын тану;
-
Фракталды геометрия тұрғысынан адам ағзасының, өсімдіктер әлемінің, өлі табиғаттың байланысын көру.
Өзектілігі: Қоршаған айналамыздағы құбылыстарды зерттеу фракталды геометрия болып табылады.
Болжам: Қоршаған айналамыздағы құбылыстардың үйлесімді заңдылықтары математикалық нақтылықпен құрылған.
Зерттеу объектісі: Үй тұрмыс заттары, адам ойлап тапқан объектілер, адам қолынан жасалған заттар, айналаны қоршаған өсімдіктер әлемі.
Зерттеу нысаны: Қоршаған айналамыздағы фракталдардың ашылуы.
Зерттеу әдістері:
Эмпиризмдік (қадағалау, өлшеу, тәжірибе)
Теориялық (танымның логикалық сатысы)
Зерттеу кезеңдері:
Әдебиеттер тізімін қолдану
Зерттеу материалдарын жинақтау
Тәжірибе жүргізу
Жұмысты рәсімдеу
Күтілетін нәтиже: Өлі және тірі табиғатағы фракталдарға суреттер жинағын шығару.
Кіріспе
«Математика өзінің әдемілігімен
және үйлесімділігімен көрікті,
бірақ-та бұл әдемілікті көре білу керек ».
Бенуа Мандельброт
Өрнектерді мүмкіндігінше біз күнде көреміз. Оларды көру үшін әлдекім оған бар күшін салғаны бізге белгілі. Табиғаттағы біз кездестіретін өрнектер туралы не айтуға болады? Олар нені білдіреді? Қоршаған айналамыздағы үйлесімділікті математикалық нақтылықпен көре аламыз ба? деген сұрақтар туындай түседі.
Біз бұл туралы ақпаратты жан-жақты және ғаламтор желісінен іздестіруді жөн көрдік.
Қоршаған әлемдегі табиғат құбылыстарының жалпы теориясы, соның ішінде айқыш өрнектер фракталдар болып табылады. Фрактал құрылымының қиындығы бір мезгілде айқын болса, екінші жағынан айқын емес болып көрінеді. Себебі, бұл фрактал құрылымының кішкентай ғана бөлігі деп түсінеміз. Егер осы қағида дұрыс болса, онда барлық әлемді математикалық нақтылықпен есептеуге болар еді.
Фракталдар бұл оғаш, жұмбақ құбылыс. Ол қоршаған айналамызда шиыршықталып, дөңгеленіп, тармақталып бейнеленетін дүние. Фракталдар адам ағзасында, өсімдіктер әлемінде, галактика жұлдыздарында, тіпті біздің ұялы телефонымыздың сымында үздіксіз қайталанатын құбылыс болып көрінеді.
Фракталдар - таңғажайып математикалық өнердің саласы, күрделі формулалар және алгоритмдер көлемі мен адам айтқысыз әсем және күрделі суреттер жасауға болады. Бұл жаңа ұғым ғаламшар бойын өз әдемiлiгiмен және тылсымдылығымен арбай адымдайды, көптеген облыстарда: метеорологияда, философияда, биологияда, механикада, географияда және тiптi тарихта да айқындалады. Сондықтан оларды зерттеу бүгiнгi ғаламшар ойшылдарының мәселесіне айналуда.
Фракталдар біздің жан-жағымызда: тау жоталары сызығында, теңіз жағалауының ирелең сызықтарында кездеседі. Кейбір фракталдар жылжыған бұлттар мен жанып жатқан от іспеттес үздіксіз өзгереді, кейбіреулері тал ағаштар мен біздің қан тамырлары жүйелеріміз сияқты өзінің даму нәтижесінде қабылдаған құрылымын сақтайды. Мектепте зерделеген және күнделікті өмірде қолданатын геометрия Эвклидтен басталады (мөлшермен біздің дәуірімізге дейінгі 300 жыл бұрын). Үшбұрыштар, квадраттар, дөңгелектер, параллелограммдар, параллелепипедтер, пирамидалар, шарлар, призмалар – классикалық геометрия қарастыратын типтік объектілер. Адам қолынан туындаған заттар осы фигуралар мен олардың жеке бөліктерінен тұрады. Бірақ табиғатта олар жиі кездесе бермейді. Мысалы, орман шыршалары аталған заттар мен олардың комбинацияларына ұқсай ма? Расында да, Эвклид формаларына қарағанда, табиғи объектілер тегіс, жатық емес, шеттері сынық, беттері бұдыр, жарылып, тесіктер мен жолақтармен желінген. «Неге геометрияны суық, құрғақ деп атайды? Оның бір себебі – бұлттардың, таулар мен теңіз жағалауының түрлерін сипаттап бере алмауында. Бұлттар – сфера емес, таулар – конус емес, жағалау сызықтары – шеңберлер емес, қабықтар тегіс емес, найзағай түзу сызықпен шашырамайды. Табиғат тек қана жоғары деңгейдегі ғана емес, мүлде басқа деңгейдегі күрделілікті танытады» деген сөздерімен Бенуа Мандельброттың «Табиғаттың фракталды геометриясы» оқулығынан бастау алады. Фракталдар үшін осындай ұқсастық сипаттамалар анықталады.



1- сурет 2-сурет 3-сурет


4-сурет 5-сурет
2. Негізгі бөлім
2.1. Фракталдар дегеніміз не?
Фрактал ұғымын, фракталды геометрияның негізін салушы 1970 жылы Бенуа Мандельброт енгізген. Fractal - латын тілінің fractus деген сөзінен шыққан, бөліктерге бөлінген деген мағынаны береді. Фрактал - бұл әрбiр бөлiгi масштабын кiшiрейткенде өзін қайталайтын шексiз өзiне ұқсас геометриялық фигура. Масштабы үлкен құрылым, масштабы кіші құрылымды қайталайды. Өзінің бір мысалында Мандельброт ұшақтың үстінде тұрып жағалауды үлкейткіш әйнек арқылы қарауды ұсынады.
Барлық жағдайда ұқсас кескін
алады, бірақ масштабы әр түрлі болады.
1975 жылы математик Б. Мандельброт осы ұшы-қиырсыз, ретсіз
формаларға фрактал деген атау берді. Бұл фигураны ағаш бұтақтары,
тау шыңдары, жағалау сызықтары сияқты күрделі табиғи жүйелердің
моделі түрінде көруге болады. Ағаш тәрізді фракталдар тек
өсімдіктердің бейнесін ғана емес, сонымен бірге бронхы
тармақтарының, бүйректің, қан тамырларының т.б. жұмыс моделін жасау
үшін пайдаланылады. Көтеген тәжірибелік есептерді шығару барысында
пайда болатын құбылыстарды зерттеген американ
профессоры
Б. Мандельброт «Табиғаттың фрактал геометриясы» атты еңбегінде: фракталдар- бөлшектелген деген мағынаны береді – деп жазған. Ең қарапайым фрактал геометриялық фигуралардан тұрады. Олар бөлінгенде үлкенінің ұқсас көшірмесі пайда болады. Бір-бірімен шексіз бөліне отырып, бірігіп, керемет суреттер құрайды.
Фракталдар мынандай топтарға бөлінеді:
алгербралық, геометриялық,
итерацияланатын функциялар жүйесі, стохастикалық фракталдар және
т.б.
Фракталдар машиналық графикада үлкен рөл атқарады. Мысалы, олар
бірнеше коэффициент арқылы, формасы өте күрделі сызықтар мен
жазықтықтарды жасау кезінде көмекке келеді. Машиналық графиканың
пікірі бойынша, жасанды бұлттарды, тауларды, мұхит бетін
генерациялауда фракталдық графика таптырмайтын құрал. Нақтырақ
айтсақ, кескіндері табиғатқа ұқсас, әрі өте күрделi, Евклидтiк емес
объектiлерді ұсыну мүмкіндік береді.
Фракталды алгоритмдер ақпараттық технологияларда, мысалы табиғи
ландшафтылардың үшөлшемді компьютерлік бейнелеуін енгізуге,
деректерді қысып жинақтауға қолданылады. Фрактал түсінігі тағы да
бір таңғажайып көрініспен – динамикалық жүйелердегі хаоспен тығыз
байланысты.
Жалпы фракталдардың тарихы геометриялық фракталдардан бастау алады.
Бұл фракталдардың типі қарапайым геометриялық құрастырулардан пайда
болады. Негізінен ол былай жасалады, ең алдымен – “бастама” -
аксиома алынады, яғни солар арқылы салынатын, кескіндер жиынтығы
беріледі. Содан соң “бастамаға”, оны белгілі бір геометриялық
фигураға айналдыратын ережелер жиынтығы қолданылады. Сосын сол
фигураның әрбір бөлігіне қайтадан сол ережелерді қолданады. Әрбір
қадам сайын фигура күрделене түседі. Егер де осы операцияларды
шексіз көп қайталайтын болсақ (қажетінше) онда біз геометриялық
фракталды аламыз.
Геометриялық фракталдар – өзінің пішінін кішірейтілген түрде
қайталайтын геометриялық фигуралар. Машиналық графикада
геометриялық фракталдарды ағаштың, өсімдіктің суретін және жағалау
сызығын алу үшін қолданылады.
Бізді қоршаған айналамыздағы
құбылыстардың құрылымы фракталдарға ұқсас болатынын анықтауға
болады. Олар: дауыл соққан кездегі бұлттардың көшуі, теңіз
жағалауларының шекаралары, беттері жарылған жерлер, терезеге
салынған қылау өрнектері болып
табылады.
2.2. Қар қылауы және галактика – фракталдар.
Қар қылауы немесе ұлпалар ауадағы су буынан, салқын тұман тамшыларынан түрлі заттар бетіне крисалл түрінде бейнеленеді. Кристалдардың көбеюінен нәзік өрнектер пайда болады. Оның сәулелері тармақталған сайын оның пішіндері кіші өлшемдермен бейнелене түседі. Сондықтан да осындай ұқсастық қасиеттер математикада фракталдар болып табылады.
Тағы бір фракталдардың түрі - бұл камераларға бөлінген наутилус қабыршағы. Бұл нутилус қабыршағы дамып, көбейген сайын көптеген камераларға бөлініп, өзіне қажетсіз қабыршақтарды тастайды. Нәтижесінде өзінің пішінін сақтай отырып, фракталды шиыршық түрінде бейнеленеді. Осындай ұқсас шиыршық тәрізді бейнелер дауыл болғанда бұлттардың құбылысы және галактикадағы жұлдыздарда байқалады.



6-сурет 7-сурет 8-сурет
2.3. Тірі табиғаттағы фракталдар.
Фракталдар бізді қоршаған әлемнің үйреншікті көріністерінің көбін өзгертеді. Фракталдар табиғи және жасанды объектілердің геометриялық қасиеттеріне деген біздің көзқарасымызды қайта бағалауға мәжбүр етеді, ал динамикалық хаос осы объектілердің уақыт барысында өздерін ұстау түсінігіне күрт өзгерістер енгізеді. Осы түсініктер негізінде құрылған теориялар білімнің әртүрлі салаларында, оның ішінде ақпараттық және коммуникациялық технологияларда жаңа мүмкіндіктер ашады.
Қоршаған айналамыздағы фракталдар өте көп кездеседі. Табиғи құрылымдардың барлығының фракталды құрылысы болады. Егер фракталды объектіге толығымен қараса, содан кейін оның үлкейтілген жеке бөлігіне қараса, содан кейін осы бөліктің бөлігіне қараса т.с.с., онда олардың бірдей екендігін көруге болады. Фракталдар өз-өзіне баламалы – олардың пішіндері әртүрлі өлшемдерде қайталанады. Фракталды алгоритмдер ақпараттық технологияларда, мысалы табиғи ландшафтылардың үшөлшемді компьютерлік бейнелеуін енгізуге, деректерді қысып (компрессиялау) жинақтауға қолданылады. Фрактал түсінігі тағы да бір таңғажайып көрініспен – динамикалық жүйелердегі хаоспен тығыз байланысты.
Мысал келтіретін болсақ, фракталдардың ұқсастық қасиеттері ағаштарда да байқалады. Ағаштардан көптеген бөліктерге тал шыбықтары бөлініп шығады, ал осы тал шыбықтардан ұсақ шыбықтар, одан тағы да өте ұсақ шыбықтар т.с.с бөлініп шығатыны байқалады. Сол сияқты гүл өсімдіктері, адам ағзасының құрылыстары да фракталдар түрінде бейнеленеді.
Өсімдіктер, ағаштар, шөптер, телефон антенналары т.б. объектілер белгілі бір фракталды пішін түрінде көрінеді.
Гүлді қырыққабат та, оның "әсерлі" түрі - фракталдар түсінігін түсіндіруге мүмкіндік беретін табиғи нысандар болып табылады. Оны математикаға
70-ші жылдары Иель университетінің француз ғалымы Бенуа Мандельброт енгізді. Фракталдың өзіне ғана тән қасиеті оның өзіне өзі ұқсастығы, яғни оның бөлігі - бұл бүтіннің кішірейтілген көшірмесі. Сонымен әр гүл шоғыры бүтін гүлді қырыққабаттың бейнесі болып табылады. Фракталдар медицина, гидрология және қаржы сияқты әртүрлі салаларда қолданылады.


 -
-
9- сурет 10-сурет 11-сурет


12-сурет 13-сурет
2.4. Математикадағы және адам ойлап тапқан заттардағы фракталдар
Адамзат тарихының өткен барлық кезеңдерінде әрқашан да табиғат құпияларын танып-білудің негізгі құралы математика болған. Математика бізді айнала қоршаған сандар мен фигуралардан тұратын ерекше әлемнің құпия-сырын ашып береді. Табиғатта көптеп кездесетін барлық тірі нәрселердің арасындағы байланыс математикалық дәлдікпен жасалған.
Шамамен бұдан 100 жылдай бұрын математиктер тек үшбұрыштар мен шеңберлер сияқты қалыптасқан формаларды зерттеумен ғана айналысқан. Бірақ мұндай формалар табиғатта сирек кездеседі. Табиғат жаратылыстары ретсіз формаға, мысалы, жағалаудың ирек толқынды жиек сызығы немесе құз жартасты таулар. Жақыннан қарағанда тегіс және жалпақ болып көрінетін шеңберден айырмашылығы таулар құз шыңды күйде қалады. Оларға жақыннан қарайтын болсақ, одан да тек бұралаңдар мен қыртыс-қатпарларды көреміз.
Фракталдар өздеріне ұқсас кішкентай көшірмелерінен тұрады. Б. Мандельброт өзінің компьютерінде ғажайып фрактал үлгілерін жасады. Ол математикадағы жорамал сандардың көмегімен графтар сызды. Ең танымал үлгіні Мандельброт жиыны деп атайды. Ол математикадағы ең күрделі фигура болып саналады. Егер оны көбейтетін болса, ол одан сайын ою-өрнекті болады және құлпыра түседі. Ал егер оның майда фрагменттерін көбейтетін болса, онда ою-өрнектің ұшы-қиырсыз шексіз екеніне көзің жетеді. Тіпті математикаға ешқандай қатысы жоқ адамның өзі де фигуралардың негізгі формаларының түрленгенінде қайталана беретінін байқайды.
Қазіргі таңда ғылымдардың математикалануы күрделілігі әртүрлі математиалық модельдердің қолдануымен сипатталады. Табиғаттағы құбылыстар мен процестерді зерттеуде, табиғат ананың рухани және материалдық байлықтарын ұқыптап теруде алдын-ала өлшеп, есептеп және саралап алмай, мәселені түбегейлң шешуге болмайтындығы белгілі. Міне, осы кезде математиканың табиғаттағы, адам өміріндегі рөлі айқындала түседі.
-
«Серпіндік үшбұрыш»
Бұл «Серпіндік үшбұрыш» 1915 жылы поль математигі Вацлов Серпинский ойлап тапқан ұқсастық фракталдары болып табылады.
Бұл теңбүйірлі үшбұрышты құру үшін үшбұрыштың ортасын қиып алып тастағанда, дұрыс төрт үшбұрыштарға бөлінеді. Осындай ретпен ішкі үшбұрыштың ортасын алып тастағанда тағы да ұсақ үшбұрыштарға бөлінеді. Алынған үшбұрыштарды осындай реттілікпен қайталап орындағанда, бірте-бірте кішірейтілген объектілердің ұқастық қасиеттері байқалады. Демек бұл объектілер фракталдар болып табылады.


14-сурет 15-сурет
-
«Кох» ұлпасы
Бұл «Кох» ұлпасы 1904 жылы Гильгом фон Кох ойлап шығарған. Оның құрылымы мына суретте көрсетілген.
Кесіндіні теңдей үш бөлікке бөліп, ортаңғы 1/3 бөлігін алып тастайды. Содан соң осындай ұзындықта тағы екі кесінді қосылады. Әрбір жасалған қадамда теңдей үш бөлікке бөлінген кесіндіні екі жаңа кесіндімен қосып алады және бірнеше рет қайталанып отырады. Нәтижесінде кесінділерден ұлпа тәрізді фигура пайда болып табылады болады. Демек, бірте-бірте кішірейтілетін объектіле фракталдар болып табылады.


16-сурет 17-сурет
-
Зерттеу бөлімі.
Расында да дауыл кезіндегі бұлттардың құбылысы, ұсақ камераларға бөлінген наутилус қабыршақтары, галактикадағы жұлдыздар – барлығы да фракталдар болып табылады.
Осы объектілердің негізі шиыршық тәрізді болатынына тәжірибе жүргізіп көрейік.
-
Күнбағыс
-
Ананас
-
Түймедақ
-
Жабайы сәбіздің шатыр гүлі
-
Күнбағысты микроскоп арқылы бақылаймыз. Бұл күнбағыстың дәндері
шиыршық тәрізді орналасқанын байқадық. Оның дәндері қандайда бір бұрыш түрінде көрінеді. Бұл бұрыш шамамен доғал бұрышқа ұқсас, яғни 137,50 градусты көрсетеді. Бұл ерекше бұрыш болғандықтан оны «алтын бұрыш» деп атайды екен. Осы бұрышқа байланысты нақты шиыршық тәрізді сурет құралады. Ал егер бұл бұрышыты 1400 деп өзгертсек, онда күнбағыстың құрылымы радиалды, ал дәндерінің орналасуы тиімді болмас еді. Осы тәжірибені жасау кезінде мен мынадай ойға келдім. Күнбағыстың себет гүлінің өсуі ретсіз болмайды, ол қандай да бір заңдылыққа тәуелді болады екен. Егжей-тегжейлі қарастырылғандықтан, «алтын бұрыш» пен сандар қатары арасындағы тамаша тәуелділікті байқауға болады.
Бұл тәуелділік тізбектелінген Фибоначчии сандары болып табылады.
1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 4181;...
Бұл сандар қатарындағы әрбір келесі сан алдыңғы екі санның қосындысына тең болады. Шынында да, тізбектелінген Фибоначчи сандарын барлық өсімдіктерден анықтауға болады.
Күнбағыстың бір жағында 34 иірмек шиыршық бейнеленген болса, екінші жағына 55 иірмек шиыршық болады екен. Бұл екі сан тізбектелінген Фибоначчи сандарына жатады.


18-сурет 19-сурет
-
Ананас
Кез келген екі ананасты аламыз. Бірінші ананастың 8 иірмек шиыршығы бар, ал екінші ананаста 13 иірмек шиыршығы болады. Бұл екі сандар тізбектелінген Фибоначчи сандарына жатады. Бұл экзотикалық жемістің құрылымы фракталдар болып табылады.

шағым қалдыра аласыз















