Сандық функция. Функцияның берілу тәсілдері мен графигі. Функция графигін түрлендіру арқылы салу.
Анықтама: Егер х-тің әрбір мәніне у-тің
жалғыз ғана мәні сәйкес болса, онда у айнымалысының х-айнымалысынан
тәуелділігі функция деп аталады.х- айнымалысын тәуелсіз айнымалы
немесе аргумент деп, ал у- айнымалысын тәуелді айнымалы деп атайды.
Берілген х-тің мәніне сәйкес у-тің мәнін функцияның мәні деп
аталады. Тәуелсіз айнымалы қабылдайтын мәндердің бәрі функцияның
анықталу облысын құрайды. ![]() функциясы қабылдайтын мәндердің
бәрі функцияның мәндерін қабылдайды.
функциясы қабылдайтын мәндердің
бәрі функцияның мәндерін қабылдайды.
Функцияның берілу тәсілдері:
-
Функцияның аналитикалық берілуі
Функцияны беру үшін аргументтің әрбір мәніне сәйкес келетін функцияның мәнін табуға мүмкіндік беретін тәсілді көрсету керек. Ең көп қолданылатын тәсіл функцияның формула арқылы берілу тәсілі болады.
-
Функцияның кестелік берілуі
Практикада функцияның кестелік берілуі жиі қолданылады. Бұл тәсілде аргументтің белгілі мәндеріне сәйкес функцияның мәндері көрсетілген кесте келтіріледі.
3. Функцияның графиктік берілуі Функцияның графигі деп координаталық жазықтықтағы абсциссалары функция аргументіне тең, ал ординаталары функцияның сәйкес мәндеріне тең нүктелердің жиынынан тұратын сызбаны айтады.
Функция графигін түрлендіру арқылы салу
![]()
![]()
![]() функциясының графигін біле
отырып, қарапайым геометриялық түрдендірулер арқылы көптеген басқа
функциялардың графиктерін салуға болады. Ең негізгілеріне тоқталып
өтейік.
функциясының графигін біле
отырып, қарапайым геометриялық түрдендірулер арқылы көптеген басқа
функциялардың графиктерін салуға болады. Ең негізгілеріне тоқталып
өтейік.
1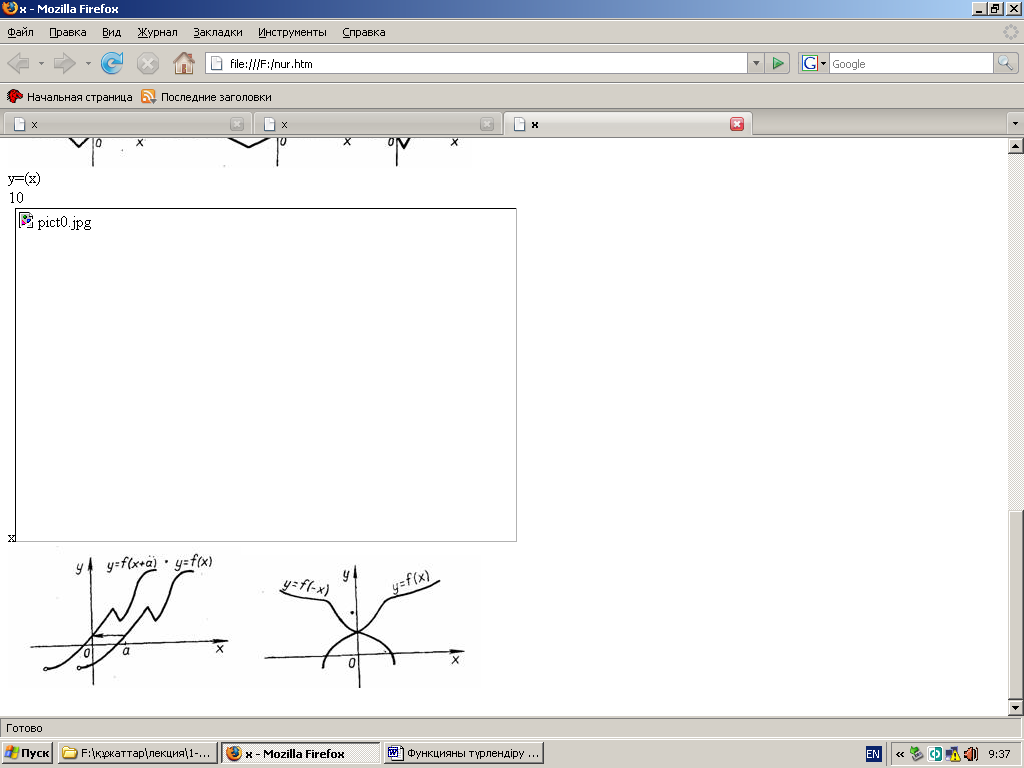 .
. ![]() функциясының
графигі
функциясының
графигі ![]() функциясының
графигінен
функциясының
графигінен ![]() осіне қарағанда
симметриялы болады (бұл симметрияда әрбір
осіне қарағанда
симметриялы болады (бұл симметрияда әрбір ![]() нүкте ординатасы қарама-қарсы
нүкте ординатасы қарама-қарсы
![]() нүктеге
көшеді).
нүктеге
көшеді).
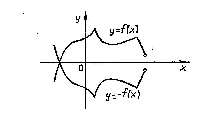
2.
![]() функциясының
графигі
функциясының
графигі![]() функциясының
графигін
функциясының
графигін ![]() осіне
қарағанда симметриялы болады (бұл симметрияда әрбір
осіне
қарағанда симметриялы болады (бұл симметрияда әрбір ![]() нүкте қарама-қарсы
нүкте қарама-қарсы ![]() нүктеге
көшеді).
нүктеге
көшеді).
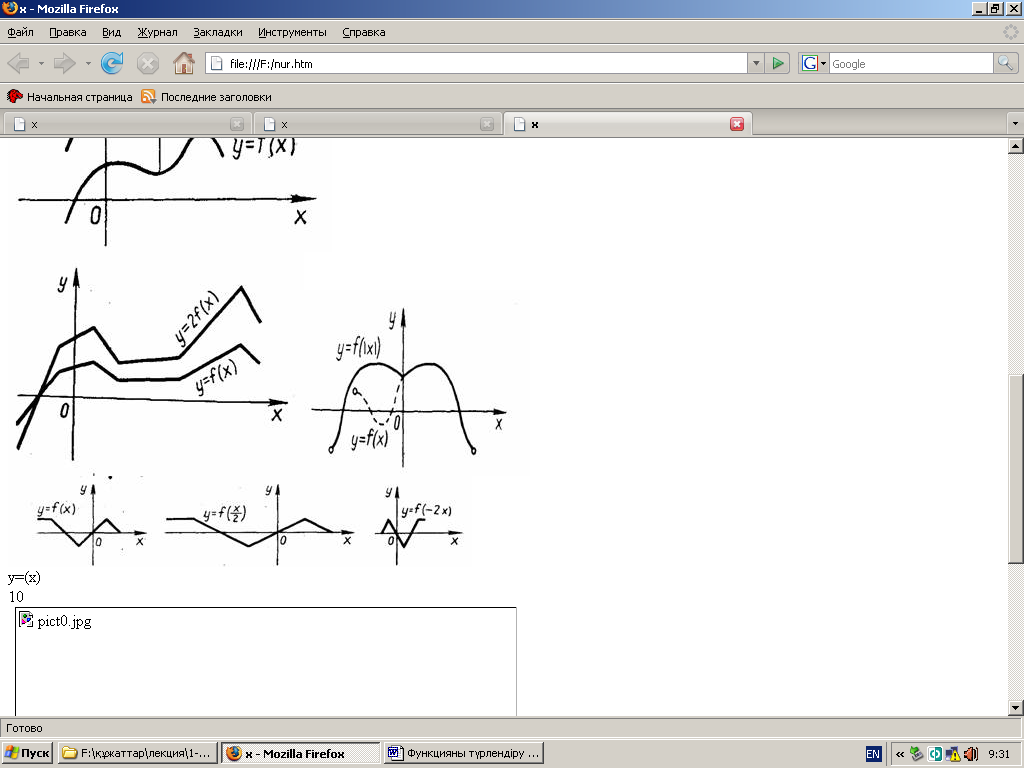
3.
![]() функциясының графигі,
функциясының графигі,
![]() болғанда
болғанда ![]() функциясының графигінің әрбір
нүктесінің ординатасын
функциясының графигінің әрбір
нүктесінің ординатасын ![]() санына көбейту, яғни
санына көбейту, яғни ![]() осіне қарай
осіне қарай ![]() қатынаста сығу арқылы
(
қатынаста сығу арқылы
(![]() болғанда, ондай сығу
болғанда, ондай сығу
![]() есе созылады). Егер
есе созылады). Егер
![]() болса, ондай да сәйкес
түрлендіру
болса, ондай да сәйкес
түрлендіру
![]() осіне қарағанда симметриялы
және сол оське қарай
осіне қарағанда симметриялы
және сол оське қарай ![]() қатынасында сығу композициясы
кез-келген ретпен болып табылады.
қатынасында сығу композициясы
кез-келген ретпен болып табылады.
4.
![]() функциясының графигі
функциясының графигі
![]() ,
,![]() ,
, ![]() болғанда графиктері келесідей
болады.
болғанда графиктері келесідей
болады.
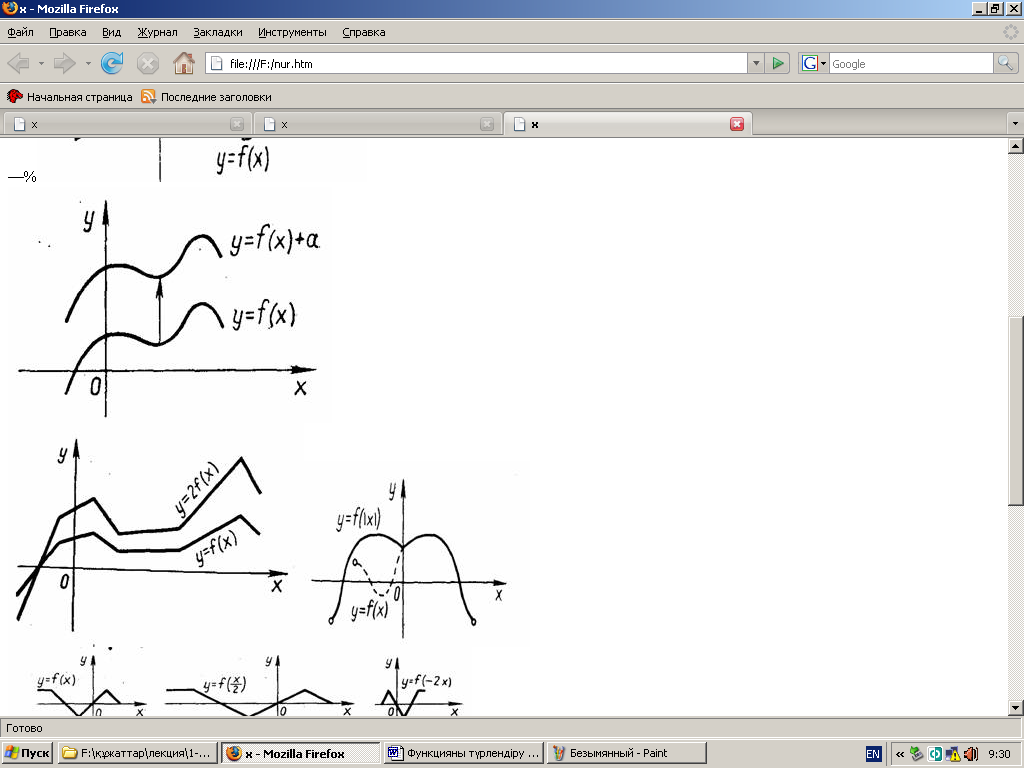
5
 .
.
![]() функциясы графигінің
әрбір нүктесінің ординатасын бір ғана
функциясы графигінің
әрбір нүктесінің ординатасын бір ғана ![]() шамаға арттырсақ,
шамаға арттырсақ, ![]() функциясы графигі шығады.
Сонымен,
функциясы графигі шығады.
Сонымен, ![]() функциясының
графигі
функциясының
графигі ![]() функциясы
графигінін
функциясы
графигінін ![]() осі бойымен
осі бойымен
![]() шамаға параллель көшіру
арқылы, яғни координаталары
шамаға параллель көшіру
арқылы, яғни координаталары ![]() қашықтыққа көшіру арқылы
табылады, ал
қашықтыққа көшіру арқылы
табылады, ал ![]() функциясы
графигі
функциясы
графигі![]() қашықтыққа
көшіру арқылы табылады.
қашықтыққа
көшіру арқылы табылады.
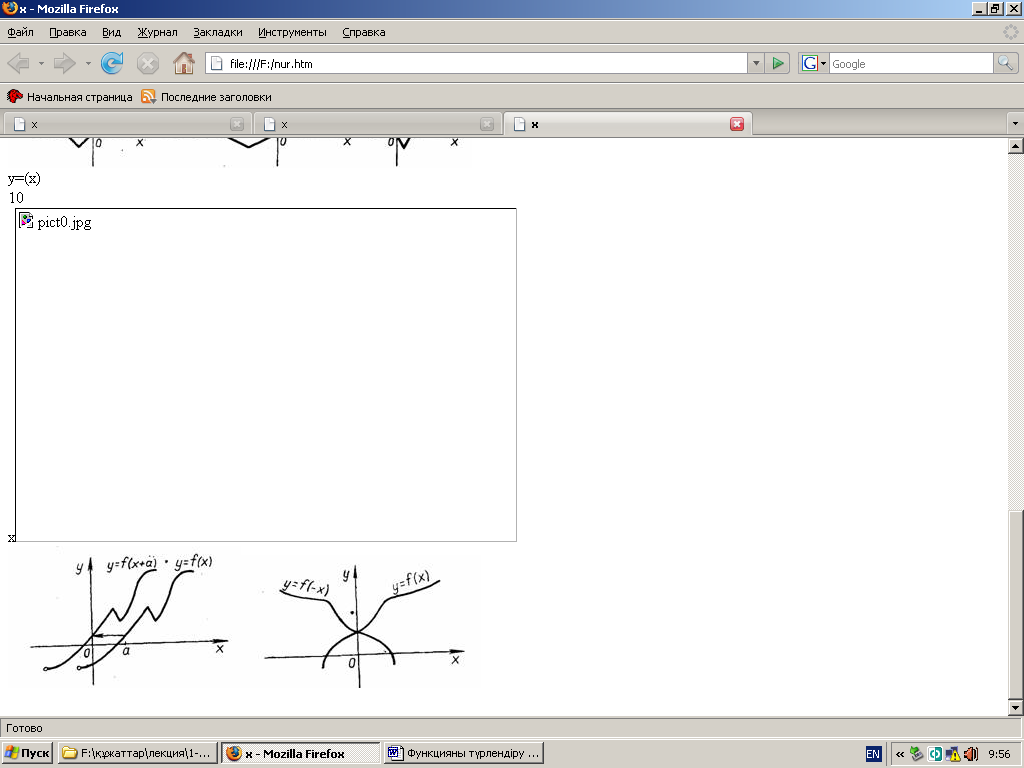
6.
![]() функциясы графигі бойынша
функциясы графигі бойынша
![]() функциясы графигін
функциясы графигін
![]() координаталарын
координаталарын ![]() осі бойымен параллель көшіру
арқылы, ал
осі бойымен параллель көшіру
арқылы, ал ![]() функциясының
графигін
функциясының
графигін![]() координаталарын
координаталарын ![]() осі
бойымен параллель көшіру арқылы табылады.
осі
бойымен параллель көшіру арқылы табылады.

7.
Функцияның ![]() болғанда
графигі
болғанда
графигі ![]() функциясы
графигінің
функциясы
графигінің ![]() осінен жоғары
орналасқан (ол үшін
осінен жоғары
орналасқан (ол үшін ![]() бөлігі
мен
бөлігі
мен ![]() қалған бөлігінің
қалған бөлігінің
![]() осіне қарағандағы
симметрияда шығатын бейнесінің бірігуінен
тұрады).
осіне қарағандағы
симметрияда шығатын бейнесінің бірігуінен
тұрады).
8 . Мына функцуияның
. Мына функцуияның ![]() графигін салу үшін
графигін салу үшін ![]() функциясы графигінің
функциясы графигінің ![]() осінің оң жағында жатқан бөлігі
мен осы бөліктің
осінің оң жағында жатқан бөлігі
мен осы бөліктің ![]() осіне
қарағандағы симметрияда шығатын бейнесін біріктіру
керек.
осіне
қарағандағы симметрияда шығатын бейнесін біріктіру
керек.
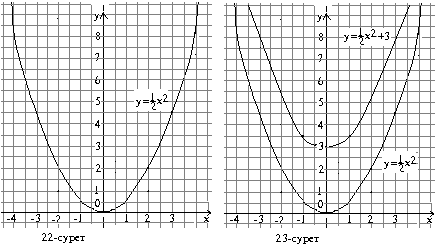
![]() функциясының графигі 22-суретте
кескінделген.
функциясының графигі 22-суретте
кескінделген.
Аргументтің осы
мәндеріне арналған ![]() функция
мәндерінің кестесін құру үшін
функция
мәндерінің кестесін құру үшін ![]() функциясының табылған мәндеріне
3-ті қосу жеткілікті .
функциясының табылған мәндеріне
3-ті қосу жеткілікті .
Координаталары
кестеде берілген нүктелерді қоссақ, ![]() +3 функциясының графигін
аламыз (23
–сурет)
+3 функциясының графигін
аламыз (23
–сурет) ![]() функциясының графигі
функциясының графигі ![]() функциясының графигін жогары
қарай жылжыту нәтижесінде алынган
парабола.
функциясының графигін жогары
қарай жылжыту нәтижесінде алынган
парабола.
Жалпы алғанда,
![]() функциясының грфигі
функциясының грфигі
![]() функциясының графигінен у
осінің бойымен ( егер n>0 болса ) n бірлік жоғары қарай немесе (
егер n<0 болса) n бірлік төмен қарай параллель көшіру арқылы
алуға болады.
функциясының графигінен у
осінің бойымен ( егер n>0 болса ) n бірлік жоғары қарай немесе (
егер n<0 болса) n бірлік төмен қарай параллель көшіру арқылы
алуға болады. ![]() функциясының
графигі
функциясының
графигі ![]() функциясының
графигінен х осінің бойымен оңға қарай mбірлік (мұндағы m>0)
немесе солға қарай m бірлік (мұндағы m<0 ) параллель көшіру
арқылы алынады. Мысалы,
функциясының
графигінен х осінің бойымен оңға қарай mбірлік (мұндағы m>0)
немесе солға қарай m бірлік (мұндағы m<0 ) параллель көшіру
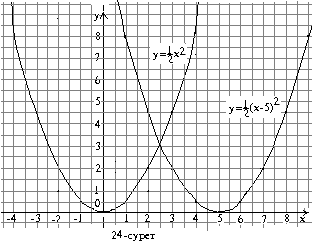
арқылы алынады. Мысалы, ![]() функциясын қарастырайық. Ол
үшін
функциясын қарастырайық. Ол
үшін ![]()
![]() функциясының графигін саламыз
(24- сурет).
Осыдан кейін
функциясының графигін саламыз
(24- сурет).
Осыдан кейін
![]() функциясының мәндерінің
кестесін құрып, графигін саламыз.
функциясының мәндерінің
кестесін құрып, графигін саламыз. ![]() және
және ![]() функцияларының графигін бір
координаталық жазықтыққа саламыз (24-сурет).
функцияларының графигін бір
координаталық жазықтыққа саламыз (24-сурет). ![]() функциясының графигі
функциясының графигі ![]() функциясының графигін оңға
қарай жылжыту нәтижесінде алынған
парабола.
функциясының графигін оңға
қарай жылжыту нәтижесінде алынған
парабола.
![]() функциясының графигі екі
параллель көшіру арқылы х осі бойымен оңға қарай m бірлік (m>0
болса) немесе солға қарай –m бірлік (m<0 болса) және у
осібойымен жогары қарай n бірлік (n>0болса) немесе төмен қарай –
n бірлік (n>0 болса ) жылжыту арқылы
функциясының графигі екі
параллель көшіру арқылы х осі бойымен оңға қарай m бірлік (m>0
болса) немесе солға қарай –m бірлік (m<0 болса) және у
осібойымен жогары қарай n бірлік (n>0болса) немесе төмен қарай –
n бірлік (n>0 болса ) жылжыту арқылы ![]() функциясының графигінен
алынатын парабола. Мысалы,
функциясының графигінен
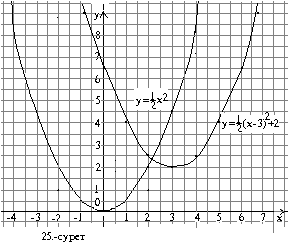
алынатын парабола. Мысалы, ![]() функциясының графигін екі
паралльл көшіру арқылы:
функциясының графигін екі
паралльл көшіру арқылы:![]() параболасын 3бірлік оңға қарай
және 2 бірлік жоғары қарай жылжыту арқылы алуға
болады.(25-сурет).
параболасын 3бірлік оңға қарай
және 2 бірлік жоғары қарай жылжыту арқылы алуға
болады.(25-сурет).
Оқулықта берілген мысалдарға ұқсас функцияның графигін салуға арналған есептер жеткілікті берілген. №87-90 жаттығулары оқушылардың тақырыпты қаншалықты меңгергенін көрсетсе, ал №91-97 жаттығулары тақырыпты тиянақты және толық меңгеруге арналған күрделірек есептер.
Оқушылардың өткен тақырып бойынша білім деңгейін тесеру үшін тест тапсырмаларын ұсынуға болады. [ *]
Тест тапсырмасы
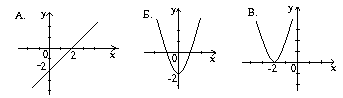
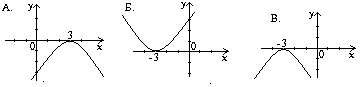
1. ![]() формуласымен берілген функцияға
сәйкес графикті табыңыз?
формуласымен берілген функцияға
сәйкес графикті табыңыз?
2. Қай суретте ![]() функциясының графигі
бейнеленген?
функциясының графигі
бейнеленген?
3. Функция ![]() формуласымен берілген. Қай
суретте оның графигі бейнеленген?
формуласымен берілген. Қай
суретте оның графигі бейнеленген?
Деңгейлік тапсырмалар.
I вариант
1. ![]() функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
а)
![]() ;
;
б)
![]() ?
?
2. ![]() ,
, ![]() функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
а)
![]() ;
;
б)
![]() .
.
3. ![]() функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
а)
![]() ;
;
б)
![]() .
.
4. Функцияның графигін салыңыз:
а)
![]() ;
;
б)
![]() .
.
ll вариант
1. ![]() функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
а)
![]() ;
;
б)
![]() ?
?
2. ![]() ,
, ![]() функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
а)
![]() ;
;
б)
![]() .
.
3. ![]() функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
а)
![]() ;
;
б)
![]() .
.
4. Функцияның графигін салыңыз:
а)
![]() ;
;
б)
![]() .
.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Функция және оның берілу тәсілдері.
Функция және оның берілу тәсілдері.
Сандық функция. Функцияның берілу тәсілдері мен графигі. Функция графигін түрлендіру арқылы салу.
Анықтама: Егер х-тің әрбір мәніне у-тің
жалғыз ғана мәні сәйкес болса, онда у айнымалысының х-айнымалысынан
тәуелділігі функция деп аталады.х- айнымалысын тәуелсіз айнымалы
немесе аргумент деп, ал у- айнымалысын тәуелді айнымалы деп атайды.
Берілген х-тің мәніне сәйкес у-тің мәнін функцияның мәні деп
аталады. Тәуелсіз айнымалы қабылдайтын мәндердің бәрі функцияның
анықталу облысын құрайды. ![]() функциясы қабылдайтын мәндердің
бәрі функцияның мәндерін қабылдайды.
функциясы қабылдайтын мәндердің
бәрі функцияның мәндерін қабылдайды.
Функцияның берілу тәсілдері:
-
Функцияның аналитикалық берілуі
Функцияны беру үшін аргументтің әрбір мәніне сәйкес келетін функцияның мәнін табуға мүмкіндік беретін тәсілді көрсету керек. Ең көп қолданылатын тәсіл функцияның формула арқылы берілу тәсілі болады.
-
Функцияның кестелік берілуі
Практикада функцияның кестелік берілуі жиі қолданылады. Бұл тәсілде аргументтің белгілі мәндеріне сәйкес функцияның мәндері көрсетілген кесте келтіріледі.
3. Функцияның графиктік берілуі Функцияның графигі деп координаталық жазықтықтағы абсциссалары функция аргументіне тең, ал ординаталары функцияның сәйкес мәндеріне тең нүктелердің жиынынан тұратын сызбаны айтады.
Функция графигін түрлендіру арқылы салу
![]()

![]()
![]() функциясының графигін біле
отырып, қарапайым геометриялық түрдендірулер арқылы көптеген басқа
функциялардың графиктерін салуға болады. Ең негізгілеріне тоқталып
өтейік.
функциясының графигін біле
отырып, қарапайым геометриялық түрдендірулер арқылы көптеген басқа
функциялардың графиктерін салуға болады. Ең негізгілеріне тоқталып
өтейік.
1 .
. ![]() функциясының
графигі
функциясының
графигі ![]() функциясының
графигінен
функциясының
графигінен ![]() осіне қарағанда
симметриялы болады (бұл симметрияда әрбір
осіне қарағанда
симметриялы болады (бұл симметрияда әрбір ![]() нүкте ординатасы қарама-қарсы
нүкте ординатасы қарама-қарсы
![]() нүктеге
көшеді).
нүктеге
көшеді).
2.
![]() функциясының
графигі
функциясының
графигі![]() функциясының
графигін
функциясының
графигін ![]() осіне
қарағанда симметриялы болады (бұл симметрияда әрбір
осіне
қарағанда симметриялы болады (бұл симметрияда әрбір ![]() нүкте қарама-қарсы
нүкте қарама-қарсы ![]() нүктеге
көшеді).
нүктеге
көшеді).

3.
![]() функциясының графигі,
функциясының графигі,
![]() болғанда
болғанда ![]() функциясының графигінің әрбір
нүктесінің ординатасын
функциясының графигінің әрбір
нүктесінің ординатасын ![]() санына көбейту, яғни
санына көбейту, яғни ![]() осіне қарай
осіне қарай ![]() қатынаста сығу арқылы
(
қатынаста сығу арқылы
(![]() болғанда, ондай сығу
болғанда, ондай сығу
![]() есе созылады). Егер
есе созылады). Егер
![]() болса, ондай да сәйкес
түрлендіру
болса, ондай да сәйкес
түрлендіру
![]() осіне қарағанда симметриялы
және сол оське қарай
осіне қарағанда симметриялы
және сол оське қарай ![]() қатынасында сығу композициясы
кез-келген ретпен болып табылады.
қатынасында сығу композициясы
кез-келген ретпен болып табылады.
4.
![]() функциясының графигі
функциясының графигі
![]() ,
,![]() ,
, ![]() болғанда графиктері келесідей
болады.
болғанда графиктері келесідей
болады.

5
 .
.
![]() функциясы графигінің
әрбір нүктесінің ординатасын бір ғана
функциясы графигінің
әрбір нүктесінің ординатасын бір ғана ![]() шамаға арттырсақ,
шамаға арттырсақ, ![]() функциясы графигі шығады.
Сонымен,
функциясы графигі шығады.
Сонымен, ![]() функциясының
графигі
функциясының
графигі ![]() функциясы
графигінін
функциясы
графигінін ![]() осі бойымен
осі бойымен
![]() шамаға параллель көшіру
арқылы, яғни координаталары
шамаға параллель көшіру
арқылы, яғни координаталары ![]() қашықтыққа көшіру арқылы
табылады, ал
қашықтыққа көшіру арқылы
табылады, ал ![]() функциясы
графигі
функциясы
графигі![]() қашықтыққа
көшіру арқылы табылады.
қашықтыққа
көшіру арқылы табылады.
6.
![]() функциясы графигі бойынша
функциясы графигі бойынша
![]() функциясы графигін
функциясы графигін
![]() координаталарын
координаталарын ![]() осі бойымен параллель көшіру
арқылы, ал
осі бойымен параллель көшіру
арқылы, ал ![]() функциясының
графигін
функциясының
графигін![]() координаталарын
координаталарын ![]() осі
бойымен параллель көшіру арқылы табылады.
осі
бойымен параллель көшіру арқылы табылады.

7.
Функцияның ![]() болғанда
графигі
болғанда
графигі ![]() функциясы
графигінің
функциясы
графигінің ![]() осінен жоғары
орналасқан (ол үшін
осінен жоғары
орналасқан (ол үшін ![]() бөлігі
мен
бөлігі
мен ![]() қалған бөлігінің
қалған бөлігінің
![]() осіне қарағандағы
симметрияда шығатын бейнесінің бірігуінен
тұрады).
осіне қарағандағы
симметрияда шығатын бейнесінің бірігуінен
тұрады).
8 . Мына функцуияның
. Мына функцуияның ![]() графигін салу үшін
графигін салу үшін ![]() функциясы графигінің
функциясы графигінің ![]() осінің оң жағында жатқан бөлігі
мен осы бөліктің
осінің оң жағында жатқан бөлігі
мен осы бөліктің ![]() осіне
қарағандағы симметрияда шығатын бейнесін біріктіру
керек.
осіне
қарағандағы симметрияда шығатын бейнесін біріктіру
керек.
![]() функциясының графигі 22-суретте
кескінделген.
функциясының графигі 22-суретте
кескінделген.
Аргументтің осы
мәндеріне арналған ![]() функция
мәндерінің кестесін құру үшін
функция
мәндерінің кестесін құру үшін ![]() функциясының табылған мәндеріне
3-ті қосу жеткілікті .
функциясының табылған мәндеріне
3-ті қосу жеткілікті .
Координаталары
кестеде берілген нүктелерді қоссақ, ![]() +3 функциясының графигін
аламыз (23
–сурет)
+3 функциясының графигін
аламыз (23
–сурет) ![]() функциясының графигі
функциясының графигі ![]() функциясының графигін жогары
қарай жылжыту нәтижесінде алынган
парабола.
функциясының графигін жогары
қарай жылжыту нәтижесінде алынган
парабола.
Жалпы алғанда,
![]() функциясының грфигі
функциясының грфигі
![]() функциясының графигінен у
осінің бойымен ( егер n>0 болса ) n бірлік жоғары қарай немесе (
егер n<0 болса) n бірлік төмен қарай параллель көшіру арқылы
алуға болады.
функциясының графигінен у
осінің бойымен ( егер n>0 болса ) n бірлік жоғары қарай немесе (
егер n<0 болса) n бірлік төмен қарай параллель көшіру арқылы
алуға болады. ![]() функциясының
графигі
функциясының
графигі ![]() функциясының
графигінен х осінің бойымен оңға қарай mбірлік (мұндағы m>0)
немесе солға қарай m бірлік (мұндағы m<0 ) параллель көшіру
арқылы алынады. Мысалы,
функциясының
графигінен х осінің бойымен оңға қарай mбірлік (мұндағы m>0)
немесе солға қарай m бірлік (мұндағы m<0 ) параллель көшіру
арқылы алынады. Мысалы, ![]() функциясын қарастырайық. Ол
үшін
функциясын қарастырайық. Ол
үшін ![]()
![]() функциясының графигін саламыз
(24- сурет).
Осыдан кейін
функциясының графигін саламыз
(24- сурет).
Осыдан кейін
![]() функциясының мәндерінің
кестесін құрып, графигін саламыз.
функциясының мәндерінің
кестесін құрып, графигін саламыз. ![]() және
және ![]() функцияларының графигін бір
координаталық жазықтыққа саламыз (24-сурет).
функцияларының графигін бір
координаталық жазықтыққа саламыз (24-сурет). ![]() функциясының графигі
функциясының графигі ![]() функциясының графигін оңға
қарай жылжыту нәтижесінде алынған
парабола.
функциясының графигін оңға
қарай жылжыту нәтижесінде алынған
парабола.
![]() функциясының графигі екі
параллель көшіру арқылы х осі бойымен оңға қарай m бірлік (m>0
болса) немесе солға қарай –m бірлік (m<0 болса) және у
осібойымен жогары қарай n бірлік (n>0болса) немесе төмен қарай –
n бірлік (n>0 болса ) жылжыту арқылы
функциясының графигі екі
параллель көшіру арқылы х осі бойымен оңға қарай m бірлік (m>0
болса) немесе солға қарай –m бірлік (m<0 болса) және у
осібойымен жогары қарай n бірлік (n>0болса) немесе төмен қарай –
n бірлік (n>0 болса ) жылжыту арқылы ![]() функциясының графигінен
алынатын парабола. Мысалы,
функциясының графигінен
алынатын парабола. Мысалы, ![]() функциясының графигін екі
паралльл көшіру арқылы:
функциясының графигін екі
паралльл көшіру арқылы:![]() параболасын 3бірлік оңға қарай
және 2 бірлік жоғары қарай жылжыту арқылы алуға
болады.(25-сурет).
параболасын 3бірлік оңға қарай
және 2 бірлік жоғары қарай жылжыту арқылы алуға
болады.(25-сурет).
Оқулықта берілген мысалдарға ұқсас функцияның графигін салуға арналған есептер жеткілікті берілген. №87-90 жаттығулары оқушылардың тақырыпты қаншалықты меңгергенін көрсетсе, ал №91-97 жаттығулары тақырыпты тиянақты және толық меңгеруге арналған күрделірек есептер.
Оқушылардың өткен тақырып бойынша білім деңгейін тесеру үшін тест тапсырмаларын ұсынуға болады. [ *]
Тест тапсырмасы
1. ![]() формуласымен берілген функцияға
сәйкес графикті табыңыз?
формуласымен берілген функцияға
сәйкес графикті табыңыз?
2. Қай суретте ![]() функциясының графигі
бейнеленген?
функциясының графигі
бейнеленген?
3. Функция ![]() формуласымен берілген. Қай
суретте оның графигі бейнеленген?
формуласымен берілген. Қай
суретте оның графигі бейнеленген?
Деңгейлік тапсырмалар.
I вариант
1. ![]() функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
а)
![]() ;
;
б)
![]() ?
?
2. ![]() ,
, ![]() функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
а)
![]() ;
;
б)
![]() .
.
3. ![]() функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
а)
![]() ;
;
б)
![]() .
.
4. Функцияның графигін салыңыз:
а)
![]() ;
;
б)
![]() .
.
ll вариант
1. ![]() функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
а)
![]() ;
;
б)
![]() ?
?
2. ![]() ,
, ![]() функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
а)
![]() ;
;
б)
![]() .
.
3. ![]() функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
функциясының графигін
пайдаланып, мына функциялардың графигін
салыңыз:
а)
![]() ;
;
б)
![]() .
.
4. Функцияның графигін салыңыз:
а)
![]() ;
;
б)
![]() .
.

шағым қалдыра аласыз