|
Тақырыбы Сабақ 3 |
10.4АТуындының қолданылуы Функцияның кризистік нүктелері мен экстремум нүктелері |
|
|
Күні,айы:30.03 |
Мұғалімнің аты-жөні: Әбдірахман М.Е. |
|
|
10 ә, б |
Сабаққа қатысқан оқушылар саны: |
Сабаққа қатыспаған оқушылар саны: |
|
Оқу бағдарламасына сәйкес оқу мақсаты |
10.4.1.28 - функцияның кризистік нүктелерінің және экстремум нүктелерінің анықтамаларын, функция экстремумының бар болу шартын білу; 10.4.1.29 - функцияның кризистік нүктелері мен экстремум нүктелерін табу |
|
|
Сабақ мақсаты |
- функцияның кризистік нүктелерінің және экстремум нүктелерінің анықтамаларын, функция экстремумының бар болу шартын білу; функцияның кризистік нүктелері мен экстремум нүктелерін табу |
|
Сабақтың барысы
|
Сабақтың кезеңі |
Педагогтың әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
||||||
|
Сабақтың басы |
Математикалықлогикалықесептер беру арқылы «Миғашабу 1.
Функцияның туындысын
тап 1) у ´= 4 х3– 12 х2 + 7 2) у´ = 10 х3 – 12 х2 – 5 3) у´= 5 х3 – 3 х2 + 7 4) у´ = 10 х3 – 12 х2 + 7 Жауабы: 4 |
2.
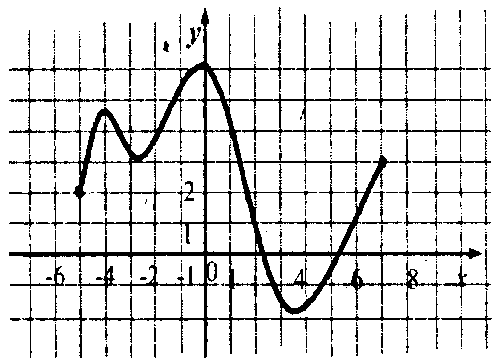
суретте у = f(х) графигі берілген. 1) [- 5; 7] 2) [- 2; 6] 3) [- 2; 4] 4) [0; 7] Жауабы:1 |
Оқушылардың белсенділіген байланысты бағаланады. |
https://youtu.be/HS0LtA-NbEM |
||||||
|
Сабақтың ортасы |
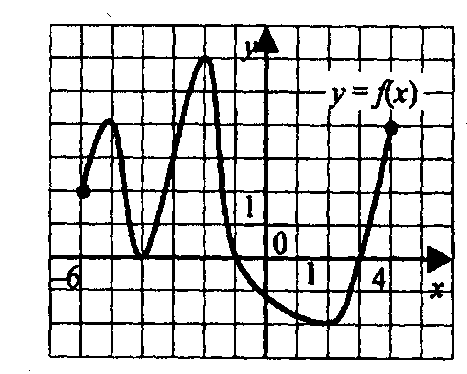
у = f(х) функцияның графигі [– 6; 4]
аралықта.
1) [- 6; - 5] [- 4; - 2] [2; 4] 2) [- 6; - 5] [- 4; 2] [3; 4] 3) [- 6; - 4) (- 4; - 1) (3; 4 ] 4)[- 6;- 1) (3;4] Жауабы: 4 Оқушыларды түгендеу және оқушылардың сабаққа дайындығын тексеру. Сыныпта жақсы атмосфера қалыптастыру. Үй тапсырмасын тексеру:
Жаңа тақырыпты ашу: Қайталаутапсырмалары 1. Функцияның туындысын тап: у = 2,5 х4 – 4 х3 + 7 х – 5. Жауабы: у´ = 10 х3 – 12 х2 + 7 2.
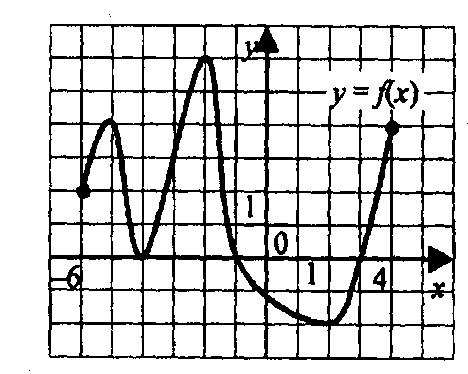
суретте у = f(х)
графигіберілген.
Жауабы: [- 5; 7] 3.
у = f(х)
функцияныңграфигі [– 6; 4] аралықта.
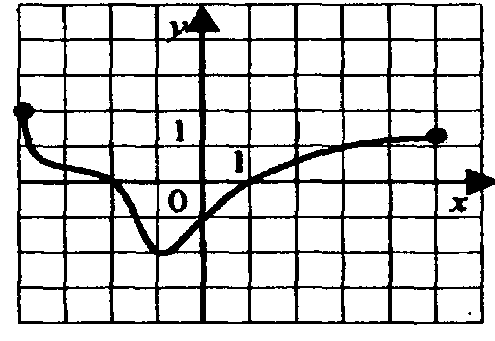
Жауабы: [- 6;- 1) (3;4] 4.Функцияның қайаралықтакемімелі
Жауабы: [– 4;– 1] Оқушыларға тапсырмалары беріледі. М: Оқушылар бұл функцияны біз төменгі сыныпта қарастырдық, ал енді қалай ойлайсыздар қазіргі біздің оқып жатқан бөлімімізге бұның не қатысы бар. О: Туындының көмегімен функцияны зерттеуді қарастырамыз. М:Олай болса онда біздің бүгінгі оқу мақсатымыз: 10.5.1.31 функцияның кризистік нүктелерінің анықтамасын біледі және оларды табады;
Функцияның туындысы нольге тең немесе туындысы болмайтын анықталу облысының ішкі нүктелері кризистік нүктелер деп атайды.
|
Анықтама :
Қажетті шарты
тең , яғни f’(x )=0 Жеткілікті шарты Егер х нүктесінде f(x) функциясы үзіліссіз, ал (а;х0 ) аралығында f’(x)>0 (f’(x)<0)және (х0 ;b) аралығында f’(x)<0 (f’(x)>0 ) болса , онда х0 нүктесінде f(x) функцияның максимум (минимум) нүктесі болады. х0 нүктесінің аймағында туынды таңбасы плюстен минуске ауыстырлыса , онда х0 нүктесі максимум нүтесі болады.
х Функцияның экстремум нүктелерін табу алгоритмі
|
Оқушылардың белсенділіген байланысты бағаланады. |
Оқулық Аудидиск: 1.4.1; 1.4.4; Жұмыс дәптері |
||||||
|
Сабақтың соңы |
Жаңа тақырып бойынша мұғалімнің сұрақтары: 1)Функцияның өсу, кему белгісін табу алгоритмән жаз? 2)Функция максимумының белгісі қандай? 3)Функция минимумының белгісі қандай? |
|
Оқушылардың белсенділіген байланысты бағаланады. |
|
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Функцияның кризистік нүктелері мен экстремум нүктелері
Функцияның кризистік нүктелері мен экстремум нүктелері
|
Тақырыбы Сабақ 3 |
10.4АТуындының қолданылуы Функцияның кризистік нүктелері мен экстремум нүктелері |
|
|
Күні,айы:30.03 |
Мұғалімнің аты-жөні: Әбдірахман М.Е. |
|
|
10 ә, б |
Сабаққа қатысқан оқушылар саны: |
Сабаққа қатыспаған оқушылар саны: |
|
Оқу бағдарламасына сәйкес оқу мақсаты |
10.4.1.28 - функцияның кризистік нүктелерінің және экстремум нүктелерінің анықтамаларын, функция экстремумының бар болу шартын білу; 10.4.1.29 - функцияның кризистік нүктелері мен экстремум нүктелерін табу |
|
|
Сабақ мақсаты |
- функцияның кризистік нүктелерінің және экстремум нүктелерінің анықтамаларын, функция экстремумының бар болу шартын білу; функцияның кризистік нүктелері мен экстремум нүктелерін табу |
|
Сабақтың барысы
|
Сабақтың кезеңі |
Педагогтың әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
||||||
|
Сабақтың басы |
Математикалықлогикалықесептер беру арқылы «Миғашабу 1.
Функцияның туындысын
тап 1) у ´= 4 х3– 12 х2 + 7 2) у´ = 10 х3 – 12 х2 – 5 3) у´= 5 х3 – 3 х2 + 7 4) у´ = 10 х3 – 12 х2 + 7 Жауабы: 4 |
2.
суретте у = f(х) графигі берілген. 1) [- 5; 7] 2) [- 2; 6] 3) [- 2; 4] 4) [0; 7] Жауабы:1 |
Оқушылардың белсенділіген байланысты бағаланады. |
https://youtu.be/HS0LtA-NbEM |
||||||
|
Сабақтың ортасы |
у = f(х) функцияның графигі [– 6; 4]
аралықта.
1) [- 6; - 5] [- 4; - 2] [2; 4] 2) [- 6; - 5] [- 4; 2] [3; 4] 3) [- 6; - 4) (- 4; - 1) (3; 4 ] 4)[- 6;- 1) (3;4] Жауабы: 4 Оқушыларды түгендеу және оқушылардың сабаққа дайындығын тексеру. Сыныпта жақсы атмосфера қалыптастыру. Үй тапсырмасын тексеру:
Жаңа тақырыпты ашу: Қайталаутапсырмалары 1. Функцияның туындысын тап: у = 2,5 х4 – 4 х3 + 7 х – 5. Жауабы: у´ = 10 х3 – 12 х2 + 7 2.
суретте у = f(х)
графигіберілген.
Жауабы: [- 5; 7] 3.
у = f(х)
функцияныңграфигі [– 6; 4] аралықта.
Жауабы: [- 6;- 1) (3;4] 4.Функцияның қайаралықтакемімелі
Жауабы: [– 4;– 1] Оқушыларға тапсырмалары беріледі. М: Оқушылар бұл функцияны біз төменгі сыныпта қарастырдық, ал енді қалай ойлайсыздар қазіргі біздің оқып жатқан бөлімімізге бұның не қатысы бар. О: Туындының көмегімен функцияны зерттеуді қарастырамыз. М:Олай болса онда біздің бүгінгі оқу мақсатымыз: 10.5.1.31 функцияның кризистік нүктелерінің анықтамасын біледі және оларды табады;
Функцияның туындысы нольге тең немесе туындысы болмайтын анықталу облысының ішкі нүктелері кризистік нүктелер деп атайды.
|
Анықтама :
Қажетті шарты
тең , яғни f’(x )=0 Жеткілікті шарты Егер х нүктесінде f(x) функциясы үзіліссіз, ал (а;х0 ) аралығында f’(x)>0 (f’(x)<0)және (х0 ;b) аралығында f’(x)<0 (f’(x)>0 ) болса , онда х0 нүктесінде f(x) функцияның максимум (минимум) нүктесі болады. х0 нүктесінің аймағында туынды таңбасы плюстен минуске ауыстырлыса , онда х0 нүктесі максимум нүтесі болады.
х Функцияның экстремум нүктелерін табу алгоритмі
|
Оқушылардың белсенділіген байланысты бағаланады. |
Оқулық Аудидиск: 1.4.1; 1.4.4; Жұмыс дәптері |
||||||
|
Сабақтың соңы |
Жаңа тақырып бойынша мұғалімнің сұрақтары: 1)Функцияның өсу, кему белгісін табу алгоритмән жаз? 2)Функция максимумының белгісі қандай? 3)Функция минимумының белгісі қандай? |
|
Оқушылардың белсенділіген байланысты бағаланады. |
|

шағым қалдыра аласыз