ӘОЖ 37.013.2
ГЕОМЕТРИЯ ПӘНІНЕН СТАНДАРТ ЕМЕС ЕСЕПТЕРДІҢ ШЫҒАРЫЛУ ТӘСІЛДЕРІ
Халил Айгүл Оралбайқызы
М.Х. Дулати атындағы Тараз университетінің студенті,
Ғылыми жетекші – Дунбаева Айгуль,
Тараз, Қазақстан
Аннотация: бұл мақалада стандарт емес есептерді шешу арқылы логикалық ойлау, шығармашылық қабілеттер мен аналитикалық дағдыларды дамыту мәселелері қарастырылады. Стандарт емес есептер дәстүрлі геометриялық принциптерді тереңірек түсінуге мүмкіндік беріп, оқушылардың проблемаларды шешу тәсілдерін әртараптандыруға ықпал етеді. Мақала стандарт емес есептердің білім беру жүйесіндегі маңызын, оларды шешудің шығармашылық жолдарын және оқушылардың математикалық сауаттылығын арттырудағы рөлін талқылайды.
Кілт сөздер: геометрия, стандарт емес есептер, логика, шеңбер, үшбұрыш.
Стандарт емес есептер — классикалық есептерден ерекшеленетін, күрделі немесе ерекше шешу тәсілдерін талап ететін математикалық мәселелер. Олар логикалық ойлауды, шығармашылықты және жаңаша көзқарасты қажет етеді, жиі олимпиадалық немесе конкурстық деңгейде кездеседі. Мұндай есептер оқушыларды тереңірек түсінік қалыптастыруға және проблема шешу дағдыларын дамытуға ынталандырады[1].
Стандарт емес есептердің логикалық, геометриялық, комбинаторика, алгебралық, құрылымдық түрлері бар. Соның ішінде геомериялық есептерге тоқталайық. Геометриялық стандарт емес есептер геометриялық фигуралар мен олардың қасиеттерін пайдалана отырып, ерекше жағдайларды зерттейді.
Мысалдар келтірейік:
Мысал 1.
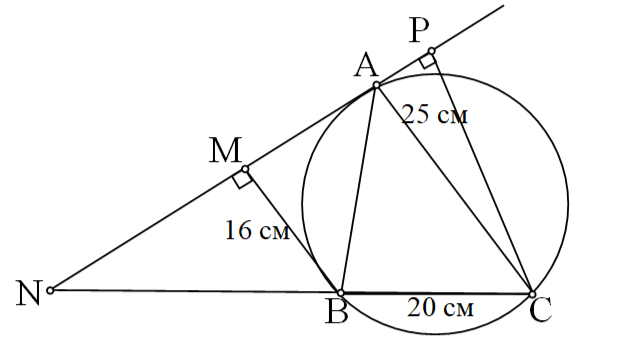
Берілгені: АВС шеңберге іштей сызылған үшбұрыштың табаны 20 см. АВС үшбұрышының табанының ұштарына қарама-қарсы төбе арқылы жүргізілген жанамаға түскен биіктіктері 25 см және 16 см. АВС үшбұрышының ауданын табыңыз.
Шешеуі:
 және
және  болса, онда
болса, онда 
 ~
~  ұқсас
үшбұрыштар
ұқсас
үшбұрыштар
















Формула: 










 см2
см2
Жауабы: 200 см2.
Мысал 2.
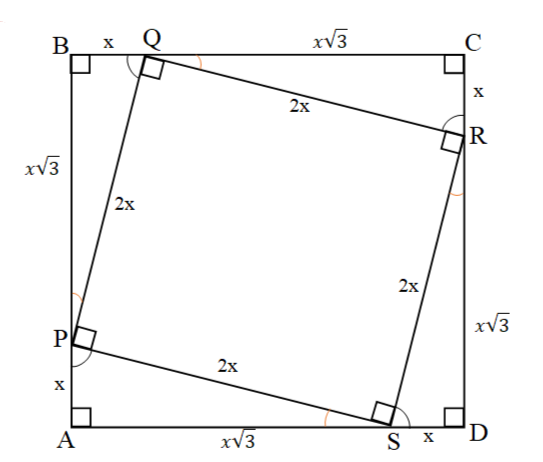
Берілгені: ABCD квадратының ішіне PQRS квадраты салынған PQRS квадратының қырлары ABCD квадратының қабырғасында жанады. Екі квадрат қабырғалары арасындағы бұрыш 30°-ты құрайды. PQRS квадратының ауданының ABCD квадратының ауданына қатынасын табыңыз.
Шешеуі:


сонда  ұқсас үшбұрыштар, яғни тең
үшбұрыштар
ұқсас үшбұрыштар, яғни тең
үшбұрыштар
PQRS - квадрат болғандықтан: PQ = QR = PS = SP
Сонда BQ = CR = DS = AP және BP = CQ = DR = AS
Пифагор теоремасы бойынша:
AP = BQ = CR = DS = x
BP = CQ = RD = AS =

BC = CD = AD = AB =

PQ = QR = RS = SP = 2x




Жауабы:  .
.
Мысал 3.
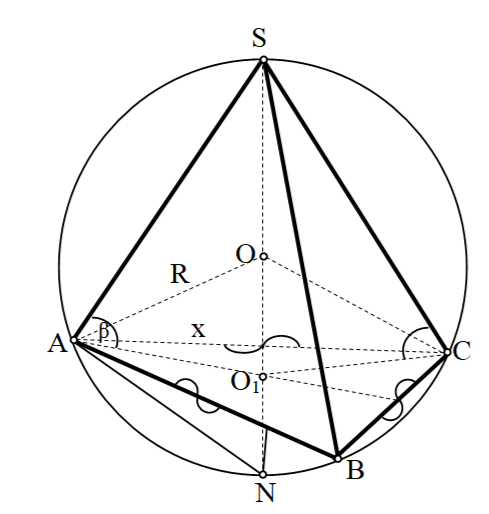
Берілгені: Радиусы R шарды іштей дұрыс пирамида сызылған.Пирамиданың бүйір қыры табан жазықтығымен , бұрышын жасайды деп,пирамиданың көлемін есептеп табыңыздар.
Шешеуі: Уақытша табатынындағы дұрыс үшбұрыштығы қабырғасының ұзындығын x деп белгілейік. Сонда

Енді ізделінді көлемді табу
үшін пирамиданың  биіктігін х арқылы екі рет
өрнектеп, оларды теңістірейік.
Ол үшін пирамиданың төбесі арқылы шардың
диаметірі жүргізіп, сонда табылған N
нүктесін А нүктесімен қоссақ, тік бұрышты SAN үшбұрышының тік
бұрышына гипотенузага түсірілген
биіктігін х арқылы екі рет
өрнектеп, оларды теңістірейік.
Ол үшін пирамиданың төбесі арқылы шардың
диаметірі жүргізіп, сонда табылған N
нүктесін А нүктесімен қоссақ, тік бұрышты SAN үшбұрышының тік
бұрышына гипотенузага түсірілген  биіктігі
биіктігі  мен
мен  геометриялық ортасы
болады:
геометриялық ортасы
болады:
 (1)
(1)
 - АBC үшбұрышының
- АBC үшбұрышының
 медиасының
медиасының  бөлігі екендігін
ескерсек,
бөлігі екендігін
ескерсек,
 (2)
(2)
-
мен (2) қатыстан мынау шығады:
 (3)
(3)
Тік бұрышты  үшбұрыштан:
үшбұрыштан:

Мұны (3)-ге қойып,
 ескеріп, х-ке мүшелеп
бөлсек:
ескеріп, х-ке мүшелеп
бөлсек:
 ,
,

Олай болса,


 .
.
Ақырында,  (куб бірлік)
(куб бірлік)
Жауабы:  .
.
Мысал 4.
Берілгені:
n бұрышты дұрыс пирамиданың биіктігінің табан қабырғасына қатынасы k болса:
-
Пирамиданың төбесіндегі жазық бұрышты,
-
Бүйір қыры мен табан жазықтығының арасындағы бұрышы,
-
Бүйір жақтарының арасындығы екі жақты бұрышы неге тең болады?
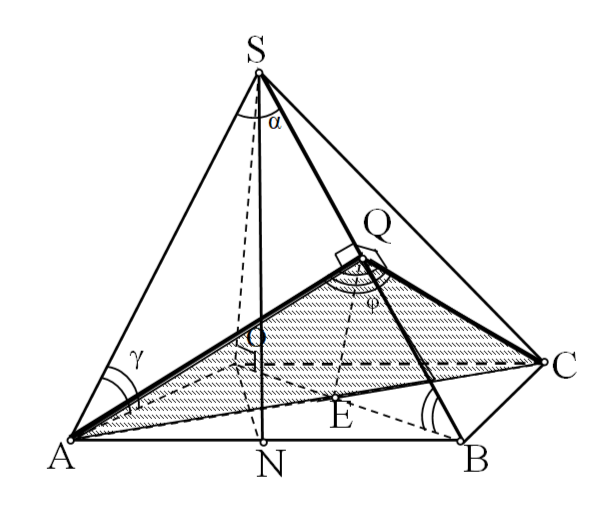
Шешеуі: Табан қабырғасы
 деп, пирамида биіктігін h деп
белгілейік. АSB жағының
деп, пирамида биіктігін h деп
белгілейік. АSB жағының  апофемасын жүргізейік, яғни
апофемасын жүргізейік, яғни
 .
.
Сонда тік бұрышынан:

 (1)
(1)

Тік бұрышты АNO үшбұрышынан:
 .
.
-
қатысты былай түсіндірейік:
 ,
, (2)
(2)
Бұдан  . (2’)
. (2’)

 ;
;  .
.
SNB және ONB, SOB тік бұрышты үшбұрыштарынан:
 ,
,  .
.

 (3)
(3)



Егер  жүргізсек, онда
жүргізсек, онда  ізделетін
бұрыш.
ізделетін
бұрыш.
 .
.
AEB және AQB тік бұрышты үшбұрышынан:

 ,
,  .
.
Олай болса,
 .
(4)
.
(4)
(2), (3) және (4) формулалар есептерді шешуде жиі қолданылады.
Пайдаланылған әдебиеттер тізімі:
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
ГЕОМЕТРИЯ ПӘНІНЕН СТАНДАРТ ЕМЕС ЕСЕПТЕРДІҢ ШЫҒАРЫЛУ ТӘСІЛДЕРІ
ГЕОМЕТРИЯ ПӘНІНЕН СТАНДАРТ ЕМЕС ЕСЕПТЕРДІҢ ШЫҒАРЫЛУ ТӘСІЛДЕРІ
ӘОЖ 37.013.2
ГЕОМЕТРИЯ ПӘНІНЕН СТАНДАРТ ЕМЕС ЕСЕПТЕРДІҢ ШЫҒАРЫЛУ ТӘСІЛДЕРІ
Халил Айгүл Оралбайқызы
М.Х. Дулати атындағы Тараз университетінің студенті,
Ғылыми жетекші – Дунбаева Айгуль,
Тараз, Қазақстан
Аннотация: бұл мақалада стандарт емес есептерді шешу арқылы логикалық ойлау, шығармашылық қабілеттер мен аналитикалық дағдыларды дамыту мәселелері қарастырылады. Стандарт емес есептер дәстүрлі геометриялық принциптерді тереңірек түсінуге мүмкіндік беріп, оқушылардың проблемаларды шешу тәсілдерін әртараптандыруға ықпал етеді. Мақала стандарт емес есептердің білім беру жүйесіндегі маңызын, оларды шешудің шығармашылық жолдарын және оқушылардың математикалық сауаттылығын арттырудағы рөлін талқылайды.
Кілт сөздер: геометрия, стандарт емес есептер, логика, шеңбер, үшбұрыш.
Стандарт емес есептер — классикалық есептерден ерекшеленетін, күрделі немесе ерекше шешу тәсілдерін талап ететін математикалық мәселелер. Олар логикалық ойлауды, шығармашылықты және жаңаша көзқарасты қажет етеді, жиі олимпиадалық немесе конкурстық деңгейде кездеседі. Мұндай есептер оқушыларды тереңірек түсінік қалыптастыруға және проблема шешу дағдыларын дамытуға ынталандырады[1].
Стандарт емес есептердің логикалық, геометриялық, комбинаторика, алгебралық, құрылымдық түрлері бар. Соның ішінде геомериялық есептерге тоқталайық. Геометриялық стандарт емес есептер геометриялық фигуралар мен олардың қасиеттерін пайдалана отырып, ерекше жағдайларды зерттейді.
Мысалдар келтірейік:
Мысал 1.
Берілгені: АВС шеңберге іштей сызылған үшбұрыштың табаны 20 см. АВС үшбұрышының табанының ұштарына қарама-қарсы төбе арқылы жүргізілген жанамаға түскен биіктіктері 25 см және 16 см. АВС үшбұрышының ауданын табыңыз.
Шешеуі:
 және
және  болса, онда
болса, онда 
 ~
~  ұқсас
үшбұрыштар
ұқсас
үшбұрыштар
















Формула: 










 см2
см2
Жауабы: 200 см2.
Мысал 2.
Берілгені: ABCD квадратының ішіне PQRS квадраты салынған PQRS квадратының қырлары ABCD квадратының қабырғасында жанады. Екі квадрат қабырғалары арасындағы бұрыш 30°-ты құрайды. PQRS квадратының ауданының ABCD квадратының ауданына қатынасын табыңыз.

Шешеуі:


сонда  ұқсас үшбұрыштар, яғни тең
үшбұрыштар
ұқсас үшбұрыштар, яғни тең
үшбұрыштар
PQRS - квадрат болғандықтан: PQ = QR = PS = SP
Сонда BQ = CR = DS = AP және BP = CQ = DR = AS
Пифагор теоремасы бойынша:
AP = BQ = CR = DS = x
BP = CQ = RD = AS =

BC = CD = AD = AB =

PQ = QR = RS = SP = 2x




Жауабы:  .
.
Мысал 3.
Берілгені: Радиусы R шарды іштей дұрыс пирамида сызылған.Пирамиданың бүйір қыры табан жазықтығымен , бұрышын жасайды деп,пирамиданың көлемін есептеп табыңыздар.

Шешеуі: Уақытша табатынындағы дұрыс үшбұрыштығы қабырғасының ұзындығын x деп белгілейік. Сонда

Енді ізделінді көлемді табу
үшін пирамиданың  биіктігін х арқылы екі рет
өрнектеп, оларды теңістірейік.
Ол үшін пирамиданың төбесі арқылы шардың
диаметірі жүргізіп, сонда табылған N
нүктесін А нүктесімен қоссақ, тік бұрышты SAN үшбұрышының тік
бұрышына гипотенузага түсірілген
биіктігін х арқылы екі рет
өрнектеп, оларды теңістірейік.
Ол үшін пирамиданың төбесі арқылы шардың
диаметірі жүргізіп, сонда табылған N
нүктесін А нүктесімен қоссақ, тік бұрышты SAN үшбұрышының тік
бұрышына гипотенузага түсірілген  биіктігі
биіктігі  мен
мен  геометриялық ортасы
болады:
геометриялық ортасы
болады:
 (1)
(1)
 - АBC үшбұрышының
- АBC үшбұрышының
 медиасының
медиасының  бөлігі екендігін
ескерсек,
бөлігі екендігін
ескерсек,
 (2)
(2)
-
мен (2) қатыстан мынау шығады:
 (3)
(3)
Тік бұрышты  үшбұрыштан:
үшбұрыштан:

Мұны (3)-ге қойып,
 ескеріп, х-ке мүшелеп
бөлсек:
ескеріп, х-ке мүшелеп
бөлсек:
 ,
,

Олай болса,


 .
.
Ақырында,  (куб бірлік)
(куб бірлік)
Жауабы:  .
.
Мысал 4.
Берілгені:
n бұрышты дұрыс пирамиданың биіктігінің табан қабырғасына қатынасы k болса:
-
Пирамиданың төбесіндегі жазық бұрышты,
-
Бүйір қыры мен табан жазықтығының арасындағы бұрышы,
-
Бүйір жақтарының арасындығы екі жақты бұрышы неге тең болады?

Шешеуі: Табан қабырғасы
 деп, пирамида биіктігін h деп
белгілейік. АSB жағының
деп, пирамида биіктігін h деп
белгілейік. АSB жағының  апофемасын жүргізейік, яғни
апофемасын жүргізейік, яғни
 .
.
Сонда тік бұрышынан:

 (1)
(1)

Тік бұрышты АNO үшбұрышынан:
 .
.
-
қатысты былай түсіндірейік:
 ,
, (2)
(2)
Бұдан  . (2’)
. (2’)

 ;
;  .
.
SNB және ONB, SOB тік бұрышты үшбұрыштарынан:
 ,
,  .
.

 (3)
(3)



Егер  жүргізсек, онда
жүргізсек, онда  ізделетін
бұрыш.
ізделетін
бұрыш.
 .
.
AEB және AQB тік бұрышты үшбұрышынан:

 ,
,  .
.
Олай болса,
 .
(4)
.
(4)
(2), (3) және (4) формулалар есептерді шешуде жиі қолданылады.
Пайдаланылған әдебиеттер тізімі:

шағым қалдыра аласыз