
Мәншүк Мәметова атындағы шағын орталықты
орта мектебінің математика пәнінің мұғалімі
Дүйсембиева Бағдат Әлішқызы
ҰБТ есептерін шығару жолдары
1.Дұрыс үшбұрышқа қабырғасы 6-ға тең квадрат іштей сызылған. Үшбұрыштың қабырғасын табыңыз.
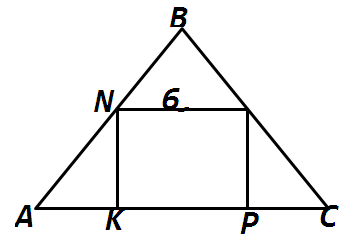 Берілгені: NK=6
т/к:АС
Берілгені: NK=6
т/к:АС
шешуі:
tg60= ,
AK=
,
AK=
Жауабы:
6+4
2.Тік төртбұрыштың қабырғалары 30см және 20см. Егер кіші қабырғасын 25% азайтып,үлкен қабырғасын 20% үлкейткенде тік төртбұрыштың ауданы неше процентк өзгереді?
Берілгені: а=30 , b=20 т/к: ауданы канша процентке өзгереді
шешуі:
100%-25%=75%;
100%+20%=120%;
75 :100=0,75;120:100=1,2;1,2 0,75=0,9
0,75=0,9
100-0,9*100=100-90=10 Жауабы:
10 азаяды
азаяды
3. Трапецияның диагоналдары оны төрт үшбұрышқа бөлген. Бір қабырғасы табаны болатын үшбұрыштар ауданы 6 және 24. Трапеция ауданын табыңыз.
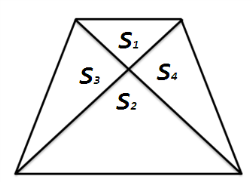
Берілгені:
S1=6,
S2=24; т/к:
Sтр шешуі:
S3=
S4 ,S1S2=S3S4
теңдігінен  =6*24=144
=6*24=144
S3=S4=12; Sтр=6+24+12+12=54
2-ші
әдіс: Sтр= 2=(
2=( +
+ )2=6+2
)2=6+2 +24=54;
Жауабы:
54.
+24=54;
Жауабы:
54.
4. Үлкен табаны 2, қалған қабырғалары 1-ге тең трапецияға сырттай сызылған шеңбердің радиусын табыңыз.
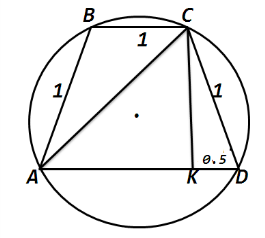
Берілгені: АД=2,
АВ=ВС=СД=1; т/к: R; шешуі: КД= AK=1,5; CK2=1-0,25=0,75=
AK=1,5; CK2=1-0,25=0,75= ;
;
CK= ; AC2=2,25+0,75=3;
AC=
; AC2=2,25+0,75=3;
AC= .
S=
.
S= ;
S=
;
S= =
= ; R=
; R=
Жауабы: 1
5. АВСД ромб АВД үшбұрышына сырттай сызылған шеңбер ромбының үлкен АС диагоналын Е нүктесінде қияды. Егер АВ=8√5 , ВД=16 болса, онда СЕ-ні табыңыз.
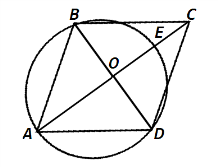
Берілгені:
АB=8 ,BD=16;
т/к: CE;
шешуі: АО2=AB2-BO2=(8
,BD=16;
т/к: CE;
шешуі: АО2=AB2-BO2=(8 2-82==320-64=256; AO=16,
AC=2AO=32; SABD=
2-82==320-64=256; AO=16,
AC=2AO=32; SABD= AO
AO BD=
BD= . R=
. R= =
= =10, AB=2R=20;
=10, AB=2R=20;
CE=AC-AE=32-20=12 Жауабы: 12
6. Радиустары 3 см және 8 см болатын екі шеңбер сырттай жанасады. Жанасу нүктесінен осы шеңберлерге жүргізілген ортақ жанамаға дейінгі қашықтықты табыңыз.
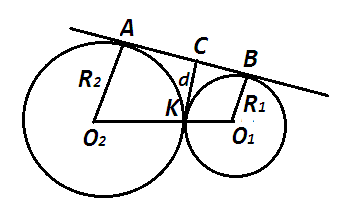
Берілгені:
R1=3,
R2=8; т/к: d;
шешуі: d= ;
d=
;
d= см.
Жауабы:
см.
Жауабы:  см
см
7. A(-3;2;-1), B(2;-1;-3), C(1;-4;3), D(-1;2;-2) нүктелерінің координаталары берілген.
 табыңыз.
табыңыз.
Берілгені: A(-3;2;-1),
B(2;-1;-3), C(1;-4;3), D(-1;2;-2) т/к: 
шешуі: АВ=(2+3;-1-2;-3+1)=(5;-3;-2);CD=(-1-1;2+4;-2-3)=(-2;6;-5); 2АВ+3СД=
(10;-6;-4)+(-6;18;-15)=(4;12;-19); =
= =
= =
=
Жауабы:

8. А(-2;4) , В(5;2) және С(3;0) үшбұрыш төбелері. Оның ауданын табыңыз.
Берілгені: A(-2;4), B(5;2), C(3;0) т/к : S
шешуі:
АВ=(5+2;2-4)=(7;-2),
AC=(3+2;0-4)=(5;-4);S= 9
9
Жауабы:9
9. Дұрыс үшбұрышты пирамиданың бүйір қыры 6, ол табанымен 300 бұрыш жасайды. Пирамиданың көлемін табыңыз.
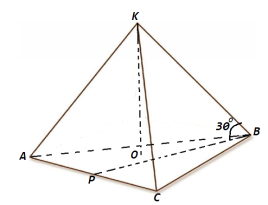
Берілгені: <KBO=300, KB=6; т/к : V;
шешуі:
BO=KB Cos300=6
Cos300=6 ;КО=3,
BP=
;КО=3,
BP= ;S=
;S= 2=
2=
V= Жауабы:
Жауабы: 
10. Конустың остік қимасы қабырғалары 1-ге тең үшбұрыш. Конустың осімен, оның табанымен және бүйір жағымен жанасатын сфераның радиусын табыңыз.
![]()
Берілгені: SA=SB=AB=1; т/к : r;
шешуі: OB= ,
SO=
,
SO= ;
r=
;
r=
Жауабы:
11.Дұрыс төртбұрышты призма шарға іштей сызылған. Шар радиусы 5 см, призма
табанының қыры 6 см. Призма биіктігін табыңыз.
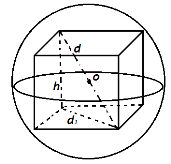
Берілгені: d1=6 см, d=10см; т/к : h
;шешуі: h=
см, d=10см; т/к : h
;шешуі: h=
Жауабы:
12.Екі шардың беттерінің аудандарының қатынасы 4:1. Көлемдерінің қатынасын табыңыз.
Берілгені:  ;т/к :
;т/к :  ; шешуі:
; шешуі:
 =(
=( Жауабы: 8:1
Жауабы: 8:1
13.Табанының қабырғасы 9 см және биіктігі 10 см болатын үшбұрышты дұрыс
пирамидаға сырттай шар сызылған. Шардың радиусын табыңыз.
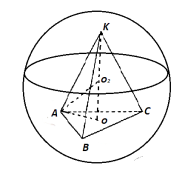
Берілгені: a=9
,h=10 т/к
: R
;шешуі: AO= ;AO=3
;AO=3
L= R=
R= см. Жауабы :
см. Жауабы : см
см
Жамбыл облысы, Шу ауданы, Бәйдібек ауылы
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Геометрия пәнінен ҰБТ есептерін шығару жолдары
Геометрия пәнінен ҰБТ есептерін шығару жолдары
Мәншүк Мәметова атындағы шағын орталықты
орта мектебінің математика пәнінің мұғалімі
Дүйсембиева Бағдат Әлішқызы
ҰБТ есептерін шығару жолдары
1.Дұрыс үшбұрышқа қабырғасы 6-ға тең квадрат іштей сызылған. Үшбұрыштың қабырғасын табыңыз.
 Берілгені: NK=6
т/к:АС
Берілгені: NK=6
т/к:АС
шешуі:
tg60= ,
AK=
,
AK=
Жауабы:
6+4
2.Тік төртбұрыштың қабырғалары 30см және 20см. Егер кіші қабырғасын 25% азайтып,үлкен қабырғасын 20% үлкейткенде тік төртбұрыштың ауданы неше процентк өзгереді?
Берілгені: а=30 , b=20 т/к: ауданы канша процентке өзгереді
шешуі:
100%-25%=75%;
100%+20%=120%;
75 :100=0,75;120:100=1,2;1,2 0,75=0,9
0,75=0,9
100-0,9*100=100-90=10 Жауабы:
10 азаяды
азаяды
3. Трапецияның диагоналдары оны төрт үшбұрышқа бөлген. Бір қабырғасы табаны болатын үшбұрыштар ауданы 6 және 24. Трапеция ауданын табыңыз.

Берілгені:
S1=6,
S2=24; т/к:
Sтр шешуі:
S3=
S4 ,S1S2=S3S4
теңдігінен  =6*24=144
=6*24=144
S3=S4=12; Sтр=6+24+12+12=54
2-ші
әдіс: Sтр= 2=(
2=( +
+ )2=6+2
)2=6+2 +24=54;
Жауабы:
54.
+24=54;
Жауабы:
54.
4. Үлкен табаны 2, қалған қабырғалары 1-ге тең трапецияға сырттай сызылған шеңбердің радиусын табыңыз.

Берілгені: АД=2,
АВ=ВС=СД=1; т/к: R; шешуі: КД= AK=1,5; CK2=1-0,25=0,75=
AK=1,5; CK2=1-0,25=0,75= ;
;
CK= ; AC2=2,25+0,75=3;
AC=
; AC2=2,25+0,75=3;
AC= .
S=
.
S= ;
S=
;
S= =
= ; R=
; R=
Жауабы: 1
5. АВСД ромб АВД үшбұрышына сырттай сызылған шеңбер ромбының үлкен АС диагоналын Е нүктесінде қияды. Егер АВ=8√5 , ВД=16 болса, онда СЕ-ні табыңыз.

Берілгені:
АB=8 ,BD=16;
т/к: CE;
шешуі: АО2=AB2-BO2=(8
,BD=16;
т/к: CE;
шешуі: АО2=AB2-BO2=(8 2-82==320-64=256; AO=16,
AC=2AO=32; SABD=
2-82==320-64=256; AO=16,
AC=2AO=32; SABD= AO
AO BD=
BD= . R=
. R= =
= =10, AB=2R=20;
=10, AB=2R=20;
CE=AC-AE=32-20=12 Жауабы: 12
6. Радиустары 3 см және 8 см болатын екі шеңбер сырттай жанасады. Жанасу нүктесінен осы шеңберлерге жүргізілген ортақ жанамаға дейінгі қашықтықты табыңыз.

Берілгені:
R1=3,
R2=8; т/к: d;
шешуі: d= ;
d=
;
d= см.
Жауабы:
см.
Жауабы:  см
см
7. A(-3;2;-1), B(2;-1;-3), C(1;-4;3), D(-1;2;-2) нүктелерінің координаталары берілген.
 табыңыз.
табыңыз.
Берілгені: A(-3;2;-1),
B(2;-1;-3), C(1;-4;3), D(-1;2;-2) т/к: 
шешуі: АВ=(2+3;-1-2;-3+1)=(5;-3;-2);CD=(-1-1;2+4;-2-3)=(-2;6;-5); 2АВ+3СД=
(10;-6;-4)+(-6;18;-15)=(4;12;-19); =
= =
= =
=
Жауабы:

8. А(-2;4) , В(5;2) және С(3;0) үшбұрыш төбелері. Оның ауданын табыңыз.
Берілгені: A(-2;4), B(5;2), C(3;0) т/к : S
шешуі:
АВ=(5+2;2-4)=(7;-2),
AC=(3+2;0-4)=(5;-4);S= 9
9
Жауабы:9
9. Дұрыс үшбұрышты пирамиданың бүйір қыры 6, ол табанымен 300 бұрыш жасайды. Пирамиданың көлемін табыңыз.

Берілгені: <KBO=300, KB=6; т/к : V;
шешуі:
BO=KB Cos300=6
Cos300=6 ;КО=3,
BP=
;КО=3,
BP= ;S=
;S= 2=
2=
V= Жауабы:
Жауабы: 
10. Конустың остік қимасы қабырғалары 1-ге тең үшбұрыш. Конустың осімен, оның табанымен және бүйір жағымен жанасатын сфераның радиусын табыңыз.
![]()
Берілгені: SA=SB=AB=1; т/к : r;
шешуі: OB= ,
SO=
,
SO= ;
r=
;
r=
Жауабы:
11.Дұрыс төртбұрышты призма шарға іштей сызылған. Шар радиусы 5 см, призма
табанының қыры 6 см. Призма биіктігін табыңыз.

Берілгені: d1=6 см, d=10см; т/к : h
;шешуі: h=
см, d=10см; т/к : h
;шешуі: h=
Жауабы:
12.Екі шардың беттерінің аудандарының қатынасы 4:1. Көлемдерінің қатынасын табыңыз.
Берілгені:  ;т/к :
;т/к :  ; шешуі:
; шешуі:
 =(
=( Жауабы: 8:1
Жауабы: 8:1
13.Табанының қабырғасы 9 см және биіктігі 10 см болатын үшбұрышты дұрыс
пирамидаға сырттай шар сызылған. Шардың радиусын табыңыз.

Берілгені: a=9
,h=10 т/к
: R
;шешуі: AO= ;AO=3
;AO=3
L= R=
R= см. Жауабы :
см. Жауабы : см
см
Жамбыл облысы, Шу ауданы, Бәйдібек ауылы

шағым қалдыра аласыз















