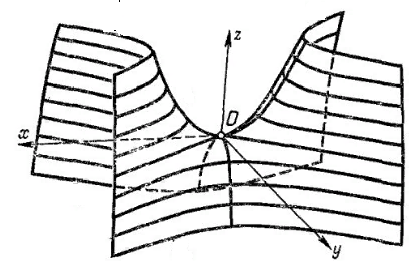
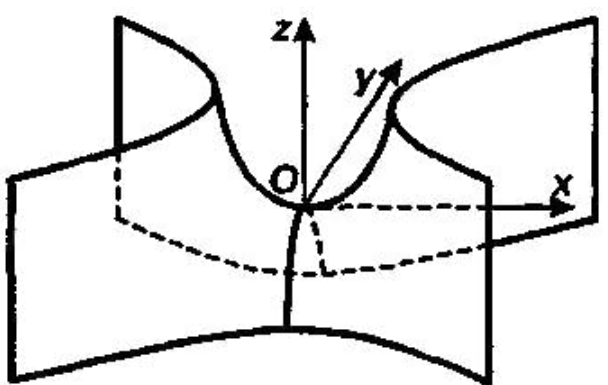
Гиперболалық параболоидтар
Гиперболалық параболидтың канондық теңдеуі
 -
- =2ƶ. (p>0, q>0)
(31) туынды түрінде жазылады.
=2ƶ. (p>0, q>0)
(31) туынды түрінде жазылады.
Гиперболалық параболоидты Х0 ƶ жазықтығында қиса, қиынды х2=2pƶ теңдеуімен анықталады.Параллель бойынша қияды, уоƶ жазықтығынан қиса, у=2qƶ парабола шығады.
№1. х2+2у2-6х-20у-8ƶ+43=0 теңдеуін канондық түрге келтіріңіздер.
Шешуі: Берілген теңдеуді төмендегіше түрлендірейік:
х2+2у2-6х-20у-8ƶ+43=0,
(х2+6х+9)-9+2(у2-10у+25)-50+8ƶ+43=0,
(х+3)2+2(у-5)2-9-50-8ƶ-43=0,
(х+3)2+2(у-5)2-8ƶ=16,
Соңғы теңдеуді 8-ге бөлсек,
онда  +
+ =
ƶ+2
=
ƶ+2
Енді
х-3= ; у-5= ¯У¯;
ƶ+2=Ƶ1
деп белгілесек,
онда
; у-5= ¯У¯;
ƶ+2=Ƶ1
деп белгілесек,
онда  +
+ =
Ƶ1
=
Ƶ1
Демек, бұл теңдеу гиперболалық параболидты анықтайды.
2. 82-у2= 8 ƶ теңдеуімен берілген гиперболалық параболидты шешіңіздер.
Шешуі: Берілген бетті
уо ƶ жазықтығымен қияйық.
Онда 
Онда
у теңдеуін х2-у2= 8 ƶ теңдеуіне қисақ,
онда х2-8 ƶ теңдеуі
қалады.
теңдеуін х2-у2= 8 ƶ теңдеуіне қисақ,
онда х2-8 ƶ теңдеуі
қалады.
Бұл бет хоƶ жазықтығында, о ƶ осіне қарағанда симметриялы болады. Сонда хо ƶ жазықтығында параболаны салайық. (Сурет 1)
![]()
![]()
![]()
![]()
![]()
 ƶ
ƶ
у
ƶ
ƶ
у
![]()
![]()
![]()

о х о у х
у
Сурет 1 Сурет 2 Сурет 3
Осыған ұқсас уоƶ жазықтығында қиса, у2= 8 ƶ болады. Бұл сызықта уоƶ жазықтығында салайық (сурет 2)
Енді Хоу
жазықтығында 
Теңдеуінің схемасын шешсек,
онда  0 немесе
у
0 немесе
у у
у
Мұнда екі түзу алынады.Бұл жағдайларда қарастырылып отырған беттік тік бұрышты жазықтары бар.
Енді ондықтар беттері координаталық жазықтықтарға параллель беттермен қияйық.Сонда мынадай жағдайлар болуы мүмкін. Беттің теңдеуі х = ±h (уоƶ жазықтығына параллель) екі жазықтықтарға бөлінеді.
х= h және х=- h. Бұл жағдайда
![]()
![]()
![]()
 h2-у2= 8 ƶ,
у2= -8 ƶ+
h, у2= -2*4 ƶ+
h
h2-у2= 8 ƶ,
у2= -8 ƶ+
h, у2= -2*4 ƶ+
h
Алынған қисық парабола
(р=-4)
уоƶ
жазықтығында жатады және
теңдеуі у2= -8 ƶ түрінде болады. Мұның
төбелері аппликоты осінде жатады және
 –ге тең және
парабола х2= 8 ƶ - те жатады. Сондықтан
ƶ=
–ге тең және
парабола х2= 8 ƶ - те жатады. Сондықтан
ƶ= параболаның х2= 8 ƶ мәнін қанағаттандырады.
Параболаның сызығы төмен қарайды.
параболаның х2= 8 ƶ мәнін қанағаттандырады.
Параболаның сызығы төмен қарайды.
Бұл бетті
 ху жазықтығына
параллель) қарастырайық. Алдымен
ху жазықтығына
параллель) қарастырайық. Алдымен 
А![]() лсақ, онда
лсақ, онда 

ƶ= h тың жазықтығындағы қабырға гиперболаны аласыз, оның жақтығы h және нақты ох осіне параллель.
Егер ƶ = ±h десек, онда гиперболаның теңдеуі осы оске жатады және
 болады, бұл сызық
гиперболаның нақты ОУ осіне параллель болады. Сонда у х түзулері
гиперболаның үйірі бір үйрінен
болады, бұл сызық
гиперболаның нақты ОУ осіне параллель болады. Сонда у х түзулері
гиперболаның үйірі бір үйрінен  екінші бір үйіріне
(
екінші бір үйіріне
( көшеді.
көшеді.
93 Досжан
Қимасының у = ±h
(хоƶ
параллель жазықтығында)
параболасы: 
у= ±h кеңістігінің жазықтық
қимасынан парабола 

қиясыз. Бұл жазықтық симметрия осі, уоƶ жазықтығында орналасқан, оның тармақтары жағдайында бағытталған.
Симметрия үшін алынған чертеж сызықтарын қарастырайық.
1) Хоƶ жазықтығында х2= 8ƶ параболаны алдық;
2) Хоƶ жазықтығында у2=- 8х параболаны алдық;
3) ХОУ жазықтығында у=-х түрлерін алдық;
4) х= ±h жазықтығында у2= -8ƶ+ h2 параболаны алдық;
5) у=- h жазықтығында х2= -8ƶ+ h2 параболаны алдық;
6) ƶ= h жазықтығында х2 -у2= 8 h гиперболаны алдық;
7) ƶ=- h жазықтығында у2 -х2= 8 h гиперболаны алдық.
ƶ=ху теңдеуі гиперболалық параболоидты анықтайтынын дәлелдеңіздер.
Шешуі: Егер
Ох=
ƶ
координаты сияқты оны да
О ƶ осін
У= бұрышын беру арқылы жаңа
координаталар салынады. ОХУƵ-ке көшейік. Мынадай:
α1=
бұрышын беру арқылы жаңа
координаталар салынады. ОХУƵ-ке көшейік. Мынадай:
α1= ,
α2=
,
α2= ?,
α3=
?,
α3= ,
,
 1=
1= ,
,
 2=
2= ,
,
 3=
3= ,
ɤ1=
,
ɤ1= ,
ɤ2=
,
ɤ2= ,
ɤ1=0 формулалар арқылы
көшсек,
,
ɤ1=0 формулалар арқылы
көшсек,
онда х=
 -
¯У¯
-
¯У¯ у=
у= +
¯У¯
+
¯У¯ ƶ=
ƶ1
ƶ=
ƶ1
Осы мәндерді ƶ=ху формуласына қоссақ, онда
Ƶ=( -
¯У¯
-
¯У¯ (
( +
¯У¯
+
¯У¯
 (
( -
-

Және 2 Ƶ
 -
-  формуласы
алынады.
формуласы
алынады.
Нәтижесінде алынған теңдеу гиперболалық параболоидтың теңдеуі болып табылады.
Мысалы,
 -
- =
2ƶ гиперболалық параболоидтың
М(4;1;
=
2ƶ гиперболалық параболоидтың
М(4;1;  нүктесі арқылы өтетін
тік сызықты жасаушылардың арасындағы бұрышты
табыңыздар.
нүктесі арқылы өтетін
тік сызықты жасаушылардың арасындағы бұрышты
табыңыздар.
Шешуі: М нүктесінің координаталары берңлген гиперболаның теңдеуін қанағаттандырады, яғни
 ;
;
 – 2
*
– 2
*  ;
;
 -
- =
= ;
1-
;
1- =
= ;
;
 =
= .
.
Берілген теңдеуден мынаны аламыз:
( -
-
 )
(
)
( +
+
 ) =
2ƶ
) =
2ƶ
Осы теңдеудегі пик сызықты жасаушылардың екі үйірі келесі сызықтарды құрайды;


М нүктесінің координаталарын осы теңдеулерге қоссақ, онда


Мысалы,
 Р,
Р,  .
.
Нәтижесінде алынған теңдеу гиперболалық параболоидтың теңдеуі болып табылады.

Гиперболалық параболоидтың
бастаушы верторы 
 , ал екінші
бастаушысы
, ал екінші
бастаушысы 
 болады,
сондықтан
болады,
сондықтан

 ;
;
Сондағы М (4;
1;  нүктесінен
өтетін гиперболалық параболоидты
жасаушылардың арасындағы бұрыш
нүктесінен
өтетін гиперболалық параболоидты
жасаушылардың арасындағы бұрыш 
 болады.
болады.
х2-
у2
 2ƶ гиперболалық параболоидты
2х-12у- ƶ+19
2ƶ гиперболалық параболоидты
2х-12у- ƶ+19 жазықтық тік сызықты
құраушылар бойынша қиып өтеді. Тік сызықты құраушылар бойынша
қиылысатындығын анықтаңдар.
жазықтық тік сызықты
құраушылар бойынша қиып өтеді. Тік сызықты құраушылар бойынша
қиылысатындығын анықтаңдар.
Шешуі: Гиперболалық параболоид теңдеуімен жазықтық теңдеуі бойынша сызықтардың осі оның ж жазықтық теңдеуіне ƶ-ті бірінші теңдеуден алатын болсақ, онда:

Гиперболалық параболоидтың
соңғы теңдеуінде (х-2)-4(у-3) х-2у-(х+2у)-8
х-2у-(х+2у)-8 түрінде
жазылады.Сондықтан соңғы нәтиже мынадай
болады:
түрінде
жазылады.Сондықтан соңғы нәтиже мынадай
болады:
 немесе
немесе 
Осы координатадағы екінші теңдеу түзудің теңдеуі болып табылады. Бұл түзудің бойындағы гиперболалық параболоидқа жатады. Бұл түзулердің теңдеуін қанағаттандырады. Түзулердің әрқайсысы берілген түзуге 2х-2у- ке тиісті. Демек, бұл түзулер берілген тік сызықты қанағаттандырады.
Гиперболалық параболоидтың кесінді координаталары шаршысымен осі, нүктесімен, ал 6 ƶ осімен анықталатын осімен сәйкестенеді. Ал А (1; -2; -1) В (-3; 3, 2) нүктесімен өтеді.Тапсырма: Гиперболалық параболоидтың теңдеуін табыңдар.
Шешуі: Есептің шарты бойынша
о ƶ осі беттің
осіменсәйкестенеді. Берілген нүктелердің
гиперболалық параболоид
екендігі айқын. Сондықтан, ізденіп отырған
теңдеу  -
- берілген. А нүктесі және
В нүктесі үшін де бұл нүктелер ізденіп отырған жазықтыққа тиесілі,
сондықтан
берілген. А нүктесі және
В нүктесі үшін де бұл нүктелер ізденіп отырған жазықтыққа тиесілі,
сондықтан
 -
- =-4
(1)
=-4
(1)
 -
- =-6
(2)
=-6
(2)
Берілген екі теңдеуден мына шығады:
 -
- =-4
=-4
 -
- =-6
=-6
құрып, соны шешейік. Бірінші теңдеуді 9-ға көбейтіп, екінші теңдеуді (-1)-ге көбейтіп, оларды қоссақ, онда
- =-30
=-30
 =
=
тең шығады. Осы мәнді (1) теңдеуге қоссақ, онда
 -6 =-4
,
-6 =-4
,  = 2,
а2=
= 2,
а2=
Табылған мәндерді алғашқы
мәндерге қоссақ, онда 2 -6
-6 =2у
немесе
=2у
немесе  -
3
-
3 =у теңдеуі алынады.Демек
кесінді теңдеу
=у теңдеуі алынады.Демек
кесінді теңдеу  -
3
-
3 =у
болады.
=у
болады.
97.Омар
 -
- =-у
гиперболалық параболоидты
3х-3у+4
=-у
гиперболалық параболоидты
3х-3у+4 2=0 жазықтықпен
қиғандағы оның центрін табыңдар.
2=0 жазықтықпен
қиғандағы оның центрін табыңдар.
Шешуі: Жазықтық теңдеуін
у= түрінде жазайық.
Табылған у-тің мәнін гиперболалық параболоидтың
теңдеуіне қоссақ, онда
түрінде жазайық.
Табылған у-тің мәнін гиперболалық параболоидтың
теңдеуіне қоссақ, онда
 -
- =
=
шығады. Осы теңдеуді
түрлендірейік. Сонда  =2(3х+4х+2)
=2(3х+4х+2)
немесе
3(х-1 -2
(
-2
( +1=0
алынады.
+1=0
алынады.
Енді есепті мына түрде
жазайық: 2( -3(х-1
-3(х-1 =1. Бұл теңдеу
алынған гиперболалық параболоидты
анықтайды.
=1. Бұл теңдеу
алынған гиперболалық параболоидты
анықтайды.
у= =
= =
= =-1.
Сондықтан, гиперболалық параболоид пен
3х-3у+4
=-1.
Сондықтан, гиперболалық параболоид пен
3х-3у+4 +2=0 теңдеуінің қиылысу
сызығының үстіне (1, -1, -2) нүктесінде
орналасады.
+2=0 теңдеуінің қиылысу
сызығының үстіне (1, -1, -2) нүктесінде
орналасады.
 -
- =
= =6
=6 гиперболалық
параболоидтың у-6=0 жазықтық параллель бойынша
қиылысатындығын және параболоид төбесін
табыңдар.
гиперболалық
параболоидтың у-6=0 жазықтық параллель бойынша
қиылысатындығын және параболоид төбесін
табыңдар.
Шешуі: у-6=0 теңдеуін у=-6 түрінде алайық. Енді гиперболалық параболоидтың теңдеуін табыңдар.
Осы теңдеулер сәйкестігін у=-6 –ны бірінші теңдеуге қойсақ, онда
 -
- =6
=6 ,
,
 =6
=6 ,
,
 =30
=30 +45
+45
Бұл теңдеулердегі параметр
Р=12. Соңғы теңдеуден  =30(
=30( +
+ ),
у=-6,
),
у=-6,  =
= -
- =
= *
* )=-
)=- . Демек, координатасы
(0; -6;
. Демек, координатасы
(0; -6;  )
болады.
)
болады.
№9
 +
+  = 0 теңдеуін канондық
түрге келтіріңдер.
= 0 теңдеуін канондық
түрге келтіріңдер.
Шешуі: Берілген теңдеуді келесі түрде
 -4х)+(
-4х)+(  жазайық. Енді әрбір
жақшаны толық квадраттарға толтырсақ, онда
жазайық. Енді әрбір
жақшаны толық квадраттарға толтырсақ, онда
 -4х+4)+(
-4х+4)+(  +4-16
+4-16
 х-
х- +(
+(
 -12
-12
 х-
х- +(
+(
 -6).
-6).
Енді координаталари симасының бос нүктелерін 0(2;4;6) нүктесімен жазамыз.Енді

 ьелгілерін енгізсек,
онда
ьелгілерін енгізсек,
онда  -
- 2
2 түрінде жазуға болады.
Демек, бұл теңдеу гиперболалық параболоидты
анықтайды.
түрінде жазуға болады.
Демек, бұл теңдеу гиперболалық параболоидты
анықтайды.
99 Асқарұлы Н.
 -
- =-2
=-2
 теңдеуімен
берілген
теңдеуімен
берілген  бетті зерттеуді жазайық.
Берілген жазықтықпен бетті
қияйық.Нәтижесінде
бетті зерттеуді жазайық.
Берілген жазықтықпен бетті
қияйық.Нәтижесінде

Бұдан
 Бұл теңдеу
уо
Бұл теңдеу
уо жазықтығымен
параллельдеседі.
жазықтығымен
параллельдеседі.
Егер
 жазықтықта қисақ,
онда
жазықтықта қисақ,
онда

 жазықтықта қисақ,
онда
жазықтықта қисақ,
онда

Параллель жазықтықтар қимасымен қисақ, онда жазықтық

Олай болса, гиперболаның нақты осі ОХ осіне параллель, ал 4<0 болса, онда параллель болады. Демек, бұл теңдеу гиперболалық параболоидты белгілейді.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Гипрерболалық параболоидтар
Гипрерболалық параболоидтар
Гиперболалық параболоидтар
Гиперболалық параболидтың канондық теңдеуі
 -
- =2ƶ. (p>0, q>0)
(31) туынды түрінде жазылады.
=2ƶ. (p>0, q>0)
(31) туынды түрінде жазылады.
Гиперболалық параболоидты Х0 ƶ жазықтығында қиса, қиынды х2=2pƶ теңдеуімен анықталады.Параллель бойынша қияды, уоƶ жазықтығынан қиса, у=2qƶ парабола шығады.
№1. х2+2у2-6х-20у-8ƶ+43=0 теңдеуін канондық түрге келтіріңіздер.
Шешуі: Берілген теңдеуді төмендегіше түрлендірейік:
х2+2у2-6х-20у-8ƶ+43=0,
(х2+6х+9)-9+2(у2-10у+25)-50+8ƶ+43=0,
(х+3)2+2(у-5)2-9-50-8ƶ-43=0,
(х+3)2+2(у-5)2-8ƶ=16,
Соңғы теңдеуді 8-ге бөлсек,
онда  +
+ =
ƶ+2
=
ƶ+2
Енді
х-3= ; у-5= ¯У¯;
ƶ+2=Ƶ1
деп белгілесек,
онда
; у-5= ¯У¯;
ƶ+2=Ƶ1
деп белгілесек,
онда  +
+ =
Ƶ1
=
Ƶ1
Демек, бұл теңдеу гиперболалық параболидты анықтайды.
2. 82-у2= 8 ƶ теңдеуімен берілген гиперболалық параболидты шешіңіздер.
Шешуі: Берілген бетті
уо ƶ жазықтығымен қияйық.
Онда 
Онда
у теңдеуін х2-у2= 8 ƶ теңдеуіне қисақ,
онда х2-8 ƶ теңдеуі
қалады.
теңдеуін х2-у2= 8 ƶ теңдеуіне қисақ,
онда х2-8 ƶ теңдеуі
қалады.
Бұл бет хоƶ жазықтығында, о ƶ осіне қарағанда симметриялы болады. Сонда хо ƶ жазықтығында параболаны салайық. (Сурет 1)
![]()
![]()
![]()
![]()
![]()
 ƶ
ƶ
у
ƶ
ƶ
у
![]()
![]()
![]()

о х о у х
у
Сурет 1 Сурет 2 Сурет 3
Осыған ұқсас уоƶ жазықтығында қиса, у2= 8 ƶ болады. Бұл сызықта уоƶ жазықтығында салайық (сурет 2)
Енді Хоу
жазықтығында 
Теңдеуінің схемасын шешсек,
онда  0 немесе
у
0 немесе
у у
у
Мұнда екі түзу алынады.Бұл жағдайларда қарастырылып отырған беттік тік бұрышты жазықтары бар.
Енді ондықтар беттері координаталық жазықтықтарға параллель беттермен қияйық.Сонда мынадай жағдайлар болуы мүмкін. Беттің теңдеуі х = ±h (уоƶ жазықтығына параллель) екі жазықтықтарға бөлінеді.
х= h және х=- h. Бұл жағдайда
![]()
![]()
![]()
 h2-у2= 8 ƶ,
у2= -8 ƶ+
h, у2= -2*4 ƶ+
h
h2-у2= 8 ƶ,
у2= -8 ƶ+
h, у2= -2*4 ƶ+
h
Алынған қисық парабола
(р=-4)
уоƶ
жазықтығында жатады және
теңдеуі у2= -8 ƶ түрінде болады. Мұның
төбелері аппликоты осінде жатады және
 –ге тең және
парабола х2= 8 ƶ - те жатады. Сондықтан
ƶ=
–ге тең және
парабола х2= 8 ƶ - те жатады. Сондықтан
ƶ= параболаның х2= 8 ƶ мәнін қанағаттандырады.
Параболаның сызығы төмен қарайды.
параболаның х2= 8 ƶ мәнін қанағаттандырады.
Параболаның сызығы төмен қарайды.
Бұл бетті
 ху жазықтығына
параллель) қарастырайық. Алдымен
ху жазықтығына
параллель) қарастырайық. Алдымен 
А![]() лсақ, онда
лсақ, онда 

ƶ= h тың жазықтығындағы қабырға гиперболаны аласыз, оның жақтығы h және нақты ох осіне параллель.
Егер ƶ = ±h десек, онда гиперболаның теңдеуі осы оске жатады және
 болады, бұл сызық
гиперболаның нақты ОУ осіне параллель болады. Сонда у х түзулері
гиперболаның үйірі бір үйрінен
болады, бұл сызық
гиперболаның нақты ОУ осіне параллель болады. Сонда у х түзулері
гиперболаның үйірі бір үйрінен  екінші бір үйіріне
(
екінші бір үйіріне
( көшеді.
көшеді.
93 Досжан
Қимасының у = ±h
(хоƶ
параллель жазықтығында)
параболасы: 
у= ±h кеңістігінің жазықтық
қимасынан парабола 

қиясыз. Бұл жазықтық симметрия осі, уоƶ жазықтығында орналасқан, оның тармақтары жағдайында бағытталған.
Симметрия үшін алынған чертеж сызықтарын қарастырайық.
1) Хоƶ жазықтығында х2= 8ƶ параболаны алдық;
2) Хоƶ жазықтығында у2=- 8х параболаны алдық;
3) ХОУ жазықтығында у=-х түрлерін алдық;
4) х= ±h жазықтығында у2= -8ƶ+ h2 параболаны алдық;
5) у=- h жазықтығында х2= -8ƶ+ h2 параболаны алдық;
6) ƶ= h жазықтығында х2 -у2= 8 h гиперболаны алдық;
7) ƶ=- h жазықтығында у2 -х2= 8 h гиперболаны алдық.

ƶ=ху теңдеуі гиперболалық параболоидты анықтайтынын дәлелдеңіздер.
Шешуі: Егер
Ох=
ƶ
координаты сияқты оны да
О ƶ осін
У= бұрышын беру арқылы жаңа
координаталар салынады. ОХУƵ-ке көшейік. Мынадай:
α1=
бұрышын беру арқылы жаңа
координаталар салынады. ОХУƵ-ке көшейік. Мынадай:
α1= ,
α2=
,
α2= ?,
α3=
?,
α3= ,
,
 1=
1= ,
,
 2=
2= ,
,
 3=
3= ,
ɤ1=
,
ɤ1= ,
ɤ2=
,
ɤ2= ,
ɤ1=0 формулалар арқылы
көшсек,
,
ɤ1=0 формулалар арқылы
көшсек,
онда х=
 -
¯У¯
-
¯У¯ у=
у= +
¯У¯
+
¯У¯ ƶ=
ƶ1
ƶ=
ƶ1
Осы мәндерді ƶ=ху формуласына қоссақ, онда
Ƶ=( -
¯У¯
-
¯У¯ (
( +
¯У¯
+
¯У¯
 (
( -
-

Және 2 Ƶ
 -
-  формуласы
алынады.
формуласы
алынады.
Нәтижесінде алынған теңдеу гиперболалық параболоидтың теңдеуі болып табылады.
Мысалы,
 -
- =
2ƶ гиперболалық параболоидтың
М(4;1;
=
2ƶ гиперболалық параболоидтың
М(4;1;  нүктесі арқылы өтетін
тік сызықты жасаушылардың арасындағы бұрышты
табыңыздар.
нүктесі арқылы өтетін
тік сызықты жасаушылардың арасындағы бұрышты
табыңыздар.
Шешуі: М нүктесінің координаталары берңлген гиперболаның теңдеуін қанағаттандырады, яғни
 ;
;
 – 2
*
– 2
*  ;
;
 -
- =
= ;
1-
;
1- =
= ;
;
 =
= .
.
Берілген теңдеуден мынаны аламыз:
( -
-
 )
(
)
( +
+
 ) =
2ƶ
) =
2ƶ
Осы теңдеудегі пик сызықты жасаушылардың екі үйірі келесі сызықтарды құрайды;


М нүктесінің координаталарын осы теңдеулерге қоссақ, онда


Мысалы,
 Р,
Р,  .
.
Нәтижесінде алынған теңдеу гиперболалық параболоидтың теңдеуі болып табылады.

Гиперболалық параболоидтың
бастаушы верторы 
 , ал екінші
бастаушысы
, ал екінші
бастаушысы 
 болады,
сондықтан
болады,
сондықтан

 ;
;
Сондағы М (4;
1;  нүктесінен
өтетін гиперболалық параболоидты
жасаушылардың арасындағы бұрыш
нүктесінен
өтетін гиперболалық параболоидты
жасаушылардың арасындағы бұрыш 
 болады.
болады.
х2-
у2
 2ƶ гиперболалық параболоидты
2х-12у- ƶ+19
2ƶ гиперболалық параболоидты
2х-12у- ƶ+19 жазықтық тік сызықты
құраушылар бойынша қиып өтеді. Тік сызықты құраушылар бойынша
қиылысатындығын анықтаңдар.
жазықтық тік сызықты
құраушылар бойынша қиып өтеді. Тік сызықты құраушылар бойынша
қиылысатындығын анықтаңдар.
Шешуі: Гиперболалық параболоид теңдеуімен жазықтық теңдеуі бойынша сызықтардың осі оның ж жазықтық теңдеуіне ƶ-ті бірінші теңдеуден алатын болсақ, онда:

Гиперболалық параболоидтың
соңғы теңдеуінде (х-2)-4(у-3) х-2у-(х+2у)-8
х-2у-(х+2у)-8 түрінде
жазылады.Сондықтан соңғы нәтиже мынадай
болады:
түрінде
жазылады.Сондықтан соңғы нәтиже мынадай
болады:
 немесе
немесе 
Осы координатадағы екінші теңдеу түзудің теңдеуі болып табылады. Бұл түзудің бойындағы гиперболалық параболоидқа жатады. Бұл түзулердің теңдеуін қанағаттандырады. Түзулердің әрқайсысы берілген түзуге 2х-2у- ке тиісті. Демек, бұл түзулер берілген тік сызықты қанағаттандырады.
Гиперболалық параболоидтың кесінді координаталары шаршысымен осі, нүктесімен, ал 6 ƶ осімен анықталатын осімен сәйкестенеді. Ал А (1; -2; -1) В (-3; 3, 2) нүктесімен өтеді.Тапсырма: Гиперболалық параболоидтың теңдеуін табыңдар.
Шешуі: Есептің шарты бойынша
о ƶ осі беттің
осіменсәйкестенеді. Берілген нүктелердің
гиперболалық параболоид
екендігі айқын. Сондықтан, ізденіп отырған
теңдеу  -
- берілген. А нүктесі және
В нүктесі үшін де бұл нүктелер ізденіп отырған жазықтыққа тиесілі,
сондықтан
берілген. А нүктесі және
В нүктесі үшін де бұл нүктелер ізденіп отырған жазықтыққа тиесілі,
сондықтан
 -
- =-4
(1)
=-4
(1)
 -
- =-6
(2)
=-6
(2)
Берілген екі теңдеуден мына шығады:
 -
- =-4
=-4
 -
- =-6
=-6
құрып, соны шешейік. Бірінші теңдеуді 9-ға көбейтіп, екінші теңдеуді (-1)-ге көбейтіп, оларды қоссақ, онда
- =-30
=-30
 =
=
тең шығады. Осы мәнді (1) теңдеуге қоссақ, онда
 -6 =-4
,
-6 =-4
,  = 2,
а2=
= 2,
а2=
Табылған мәндерді алғашқы
мәндерге қоссақ, онда 2 -6
-6 =2у
немесе
=2у
немесе  -
3
-
3 =у теңдеуі алынады.Демек
кесінді теңдеу
=у теңдеуі алынады.Демек
кесінді теңдеу  -
3
-
3 =у
болады.
=у
болады.
97.Омар
 -
- =-у
гиперболалық параболоидты
3х-3у+4
=-у
гиперболалық параболоидты
3х-3у+4 2=0 жазықтықпен
қиғандағы оның центрін табыңдар.
2=0 жазықтықпен
қиғандағы оның центрін табыңдар.
Шешуі: Жазықтық теңдеуін
у= түрінде жазайық.
Табылған у-тің мәнін гиперболалық параболоидтың
теңдеуіне қоссақ, онда
түрінде жазайық.
Табылған у-тің мәнін гиперболалық параболоидтың
теңдеуіне қоссақ, онда
 -
- =
=
шығады. Осы теңдеуді
түрлендірейік. Сонда  =2(3х+4х+2)
=2(3х+4х+2)
немесе
3(х-1 -2
(
-2
( +1=0
алынады.
+1=0
алынады.
Енді есепті мына түрде
жазайық: 2( -3(х-1
-3(х-1 =1. Бұл теңдеу
алынған гиперболалық параболоидты
анықтайды.
=1. Бұл теңдеу
алынған гиперболалық параболоидты
анықтайды.
у= =
= =
= =-1.
Сондықтан, гиперболалық параболоид пен
3х-3у+4
=-1.
Сондықтан, гиперболалық параболоид пен
3х-3у+4 +2=0 теңдеуінің қиылысу
сызығының үстіне (1, -1, -2) нүктесінде
орналасады.
+2=0 теңдеуінің қиылысу
сызығының үстіне (1, -1, -2) нүктесінде
орналасады.
 -
- =
= =6
=6 гиперболалық
параболоидтың у-6=0 жазықтық параллель бойынша
қиылысатындығын және параболоид төбесін
табыңдар.
гиперболалық
параболоидтың у-6=0 жазықтық параллель бойынша
қиылысатындығын және параболоид төбесін
табыңдар.
Шешуі: у-6=0 теңдеуін у=-6 түрінде алайық. Енді гиперболалық параболоидтың теңдеуін табыңдар.
Осы теңдеулер сәйкестігін у=-6 –ны бірінші теңдеуге қойсақ, онда
 -
- =6
=6 ,
,
 =6
=6 ,
,
 =30
=30 +45
+45
Бұл теңдеулердегі параметр
Р=12. Соңғы теңдеуден  =30(
=30( +
+ ),
у=-6,
),
у=-6,  =
= -
- =
= *
* )=-
)=- . Демек, координатасы
(0; -6;
. Демек, координатасы
(0; -6;  )
болады.
)
болады.
№9
 +
+  = 0 теңдеуін канондық
түрге келтіріңдер.
= 0 теңдеуін канондық
түрге келтіріңдер.
Шешуі: Берілген теңдеуді келесі түрде
 -4х)+(
-4х)+(  жазайық. Енді әрбір
жақшаны толық квадраттарға толтырсақ, онда
жазайық. Енді әрбір
жақшаны толық квадраттарға толтырсақ, онда
 -4х+4)+(
-4х+4)+(  +4-16
+4-16
 х-
х- +(
+(
 -12
-12
 х-
х- +(
+(
 -6).
-6).
Енді координаталари симасының бос нүктелерін 0(2;4;6) нүктесімен жазамыз.Енді

 ьелгілерін енгізсек,
онда
ьелгілерін енгізсек,
онда  -
- 2
2 түрінде жазуға болады.
Демек, бұл теңдеу гиперболалық параболоидты
анықтайды.
түрінде жазуға болады.
Демек, бұл теңдеу гиперболалық параболоидты
анықтайды.
99 Асқарұлы Н.
 -
- =-2
=-2
 теңдеуімен
берілген
теңдеуімен
берілген  бетті зерттеуді жазайық.
Берілген жазықтықпен бетті
қияйық.Нәтижесінде
бетті зерттеуді жазайық.
Берілген жазықтықпен бетті
қияйық.Нәтижесінде

Бұдан
 Бұл теңдеу
уо
Бұл теңдеу
уо жазықтығымен
параллельдеседі.
жазықтығымен
параллельдеседі.
Егер
 жазықтықта қисақ,
онда
жазықтықта қисақ,
онда

 жазықтықта қисақ,
онда
жазықтықта қисақ,
онда

Параллель жазықтықтар қимасымен қисақ, онда жазықтық

Олай болса, гиперболаның нақты осі ОХ осіне параллель, ал 4<0 болса, онда параллель болады. Демек, бұл теңдеу гиперболалық параболоидты белгілейді.

шағым қалдыра аласыз