1. Математикалық зерттеу жобасы

2. «Геометриялық иллюзиялар»

Авторы: Жумадилова Жадыра Шарипхановна

Абай Облысы, Семей қаласы, «Көлік колледжі» КМҚК

1. Мазмұны

2. Кіріспе
   1. Иллюзияның геометриялық негіздемесі.

3. 2. Геометриялық иллюзияның түрлері.

4. 3. Геометриялық иллюзияларды қолдану салалары

5. 3.1 Өнер.

6. 3.2 Сән дизайны.

7. 3.3 Сәулет өнеріндегі иллюзиялар.

8. 3.4 Менің геометриялық иллюзияларым.

9. Қорытынды

10. Ақпарат көздері
    Кіріспе

7-11 сыныптардағы геометрия сабақтарында әртүрлі жазық фигуралардың белгілері мен қасиеттерін зерттейміз. Бірақ 5-сыныпта біз үш өлшемді фигуралар: тік бұрышты параллелепипед және текшемен де таныстық, ал Л.С.Атанасянның 7-9 геометрия оқулығында XIV тарауда әртүрлі көп қырлылар туралы алғашқы мәліметтер бар. Геометриялық есептерді шығару үшін фигуралардың сызбаларын саламыз. Бірақ кейде сызбаны аяқтағаннан кейін, егер біз тек көрнекі қабылдауға сүйенсек, қате шешімді көреміз.

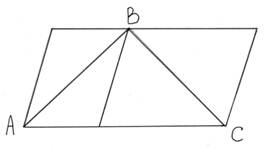
Мысалы, егер біз тік бұрышты параллелепипед тұрғызатын болсақ, онда сызбада табандары параллелограммдар, бірақ табандары тіктөртбұрыштар екенін көреміз. Біз әрқашан сызбадан сызықтардың параллельдігін анықтай алмаймыз;

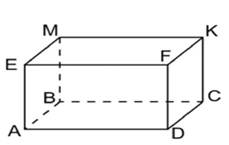
Берілген суреттен АВ ІІ DE дәлелдейміз.

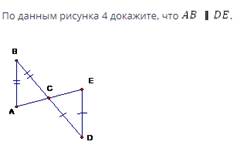
Сондай-ақ суретті көргенде иллюзияларды жиі кездестіреміз. Әрдайым сұрақ туындайды: «Суретшілер үш өлшемді бейнені қалай жасай алады? Олар қандай әдістерді қолданады?

Кейбір суреттерде қандай сызықтар (параллель немесе жоқ), қандай сегменттер (тең немесе жоқ) көрсетілгенін түсіну мүмкін емес.

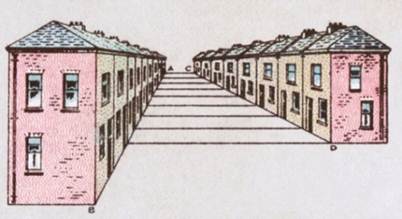
Сыныпта мен сыныптастарыма бірнеше сызбаларды көрсетіп, келесі сұрақтарға жауап берулерін сұрадым

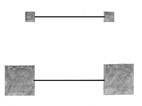
1) Кесінділердің қайсысының ұзындығы ең үлкен, қайсысының ұзындығы ең қысқа?

2) Қызыл сызықтардың қайсысы ұзын?

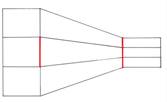
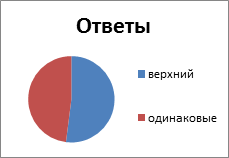
3) Сегменттердің қайсысы ұзын?

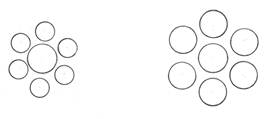
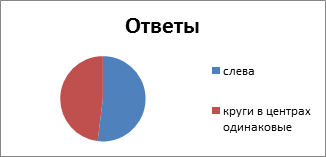
4) Орталықтағы қай шеңбер үлкенірек: оң жақта ма, сол жақта ма?

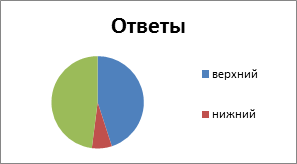
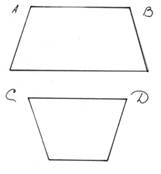
5) Қай тіктөртбұрыштың ауданы ең үлкен?

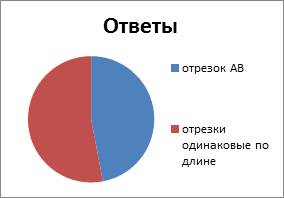
6) Қандай сегмент AB немесе CD-ден ұзын?

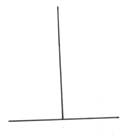
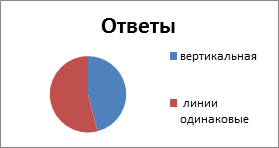
7) Қай сызық ұзынырақ: тік пе, көлденең бе?

Б ірдей

Төменгі

ұзын

8) Қандай кесінді АВ немесе ВС-тан ұзын?

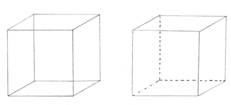
9) Геометрияны оқығанда кубтың қандай бейнесі қолданылады және неліктен?

Жігіттер нүктелі сызықтар текшенің біз көре алмайтын шеттерін білдіреді деп дұрыс жауап берді.

Сыныптастарымның мысалын қолдана отырып, мен адамның визуалды адасушылықтары шынымен бар екеніне және олардың «елес» ұғымымен байланысты екеніне көз жеткіздім. Мен геометриялық иллюзиялармен толығырақ танысып, адам өмірінің қандай салаларында кездесетінін білгім келді.

«Иллюзия» латын тілінен аударғанда адасу, қателік.

Тақырыптың өзектілігі:біздің әлемде біз жиі иллюзиялармен, соның ішінде геометриялықпен кездесеміз.

Мәселе:Геометриялық иллюзиялар мектеп курстарында оқытылмайды, бірақ біз геометриялық есептерді шешу үшін сызбаларды құрастыру кезінде кездесеміз.

Жұмыс мақсаты: геометриялық иллюзиялармен танысу.

Ол үшін мен өзіме мынадай міндеттер қойдым:

1. осы тақырып бойынша теориялық материалды оқу;

2. геометриялық иллюзиялардың шынымен бар екеніне тәжірибе арқылы көз жеткізу;

3. геометриялық иллюзия түрлерін қарастыру;

4. геометриялық иллюзиялар қолданылатын аймақтарды анықтау;

5. геометриялық иллюзияларды өзіңіз жасауға тырысыңыз.

Кез келген геометриялық иллюзияны математикалық білім арқылы түсіндіруге болады деп ойладым.

Зерттеу пәні:геометриялық иллюзиялар;

Зерттеу объектілері:сызбалар, суреттер, фигуралар, сәулет құрылымдары.

Зерттеу әдістері:іздеу, зерттеу, талдау, синтез, сұрақ қою, эксперимент, жалпылау.

2. Иллюзияның геометриялық негіздемесі

Иллюзияобъектінің қасиеттерінің бұрмалануы болып табылады. Иллюзия ұзақ уақыт бойы көру жүйесіндегі ақаулар ретінде қабылданады.

Бұл геометриялық иллюзияның табиғатын түсіну үшін адамның көру арқылы заттарды қалай қабылдайтынын түсінуіміз керек дегенді білдіреді.

Объектіні әр түрлі нүктеден қарасақ, біз оны әр түрлі бұрыштан көреміз, яғни объектінің бұрыштық өлшемі екі жақты анықталмайды. Оның мәні объектінің көзден қашықтығына байланысты. Нысан көзден неғұрлым алыс болса, соғұрлым ол кішірек болып көрінеді.

Неліктен бұл орын алғанын геометриялық заңдар арқылы түсіндіруге болады.

Қарастырылып отырған заттың алдымен бір қашықтықтан, содан кейін одан әрі қашықтықтан қаралған биіктігі h болсын.

AB,AC – сәйкесінше екі жағдайда да көз торындағы объектінің кескіндері.

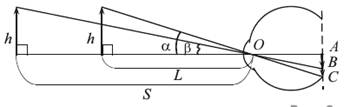
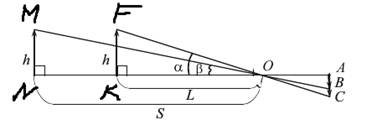
NMO тікбұрышты үшбұрышты қарастырайық: tg b= MN/NO= h/S ;

FKO тікбұрышты үшбұрышын қарастырайық: tg a=FK/KO=h/L;

)=h/S:h/L=L/S;)/( тг (тг)

D ABO : Ð AOB = Ðb (тік ретінде).

tg b= AB/AO

D ACO: ÐAOC=Ða (тік ретінде).

tg a=AC/AO

)= AB/AO:AC/AO=AB/AC;)/( тг (тг)

L/S=AB/AC

Егер S=2L болса, онда AC= 2AB, сондықтан S қашықтықтағы нысан L қашықтықтағыдан жарты есе үлкен болып көрінеді.

Бұл көру бұрышы объектіге дейінгі қашықтыққа кері пропорционалды екенін білдіреді. Егер затты көзден 1 метр қашықтықта қойып, содан кейін тағы 1 метр жылжытса, ол жарты есе үлкен болып көрінеді.

Бұл фактіні тәжірибе жүзінде растауға болады:

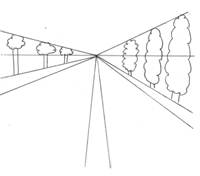
Егер зат өте алыс орналасса, онда ол нүкте ретінде қабылданады. Көз екі нүктені бөлек көре алатын көру бұрышының шекті мәні бар. Сондықтан теміржол рельстері, аллея ағаштары, шам бағаналары көкжиектегі бір нүктеде түйісетін сияқты, ал нүктенің өзі шексіз алыс болып көрінеді.

Бір бұрыштан әртүрлі өлшемдегі объектілерді бақыланатын болса, олардың өлшемдері бірдей көрінеді.

Мұны, мысалы, күн тұтылуымен растауға болады. Күн тұтылу кезінде Ай Күнді толығымен жауып тұрады және олардың өлшемдері бірдей болып көрінеді, өйткені екі дене де Жерден бір бұрышта көрінеді.

Бұл құбылысты геометрия заңдарымен түсіндіруге болады.

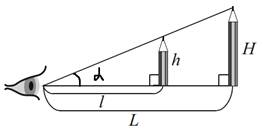
D AOB : tg a=AB/OB=h/l ; D COD: tg a = CD/OD=H/L

h/l=H/L, бұл h/H=l/L дегенді білдіреді. Егер екі нысан бір көру бұрышынан көрінетін болса, онда олардың сызықтық өлшемдері объектілерге дейінгі арақашықтықтар қанша болса, сонша рет ерекшеленеді.

Мен өз тәжірибемді жүргіздім және өз пікірімнің дұрыстығына көз жеткіздім.

Сызықтардың қисықтығы мен ұзындығын қабылдауға олардың орналасуы, олар кіретін фигуралардың өлшемі, қиылысатын немесе іргелес сызықтардың болуы әсер етеді. Көлденең сегменттің ұзындығы әрқашан тікке қарағанда дәлірек бағаланады. Кез келген кескінді әртүрлі тәсілдермен түсіндіруге болады, бірақ адамның көру жүйесі ең таныс интерпретацияға артықшылық береді.

Егер сіз текшені осылай сызсаңыз, текшенің беттері үнемі өз орнын өзгертетін сияқты болады. Бұл жағдайда көрнекі иллюзиядан құтылу үшін көрінбейтін жиектер нүктелі сызықпен ерекшеленіп, кескіннің тереңдігін береді.

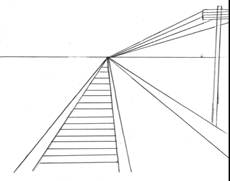
Кеңістіктік фигураларды бейнелеу тек геометрлерді ғана емес, сонымен қатар кенепте үш өлшемді заттарды салуды үйренуге ұмтылған суретшілерді де бұрыннан мазалайды. Сурет салу кезінде адам көзінің механизмін ескеруге мүмкіндік беретін әдіс сызықтық перспектива деп аталды (латын тілінен аударғанда «мен анық көремін» деп аударылады)

Сонымен, сызықтық перспектива - бұл түзу сызықтарды пайдаланып жазықтықта кеңістік объектілерін салудың геометриялық тәсілі. Бұл әдісті пайдаланған кезде орталық маңызды - объектілер арқылы өтетін, алдыңғы планнан алшақтайтын сызықтар біріктірілетін тұрақты нүкте.

Параллельді дизайнның қасиеттеріне негізделген жазықтықта көлемдік фигураларды бейнелеу ережелері де бар:

• түзудің жазықтықтағы проекциясы түзу;

• сегменттің проекциясы кесінді болып табылады;

• параллель кесінділердің проекциясы – параллель кесінділер немесе бір түзуге жататын кесінділер.

Жазықтықта көлемді фигуралардың кескіндерін салу ережелері:

1. түзу сызық түзу сызыққа айналады;

2. нүктеден нүктеге;

3. сегменттен сегментке;

4. бұрыш бұрышқа айналады, ал бұрыштың градустық өлшемі өзгермейді;

5. бір түзудің немесе параллель түзудің кесінділерінің ұзындықтарының қатынасы сақталады;

6. сегменттің ортасы сегменттің ортасына түседі;

7. параллель түзулерді параллель түзулерге немесе сәйкес келетін сызықтарға;

8. кез келген үшбұрышты кез келген үшбұрышқа;

9. параллелограмм, тіктөртбұрыш, ромб, шаршыдан параллелограммға;

10. трапеция трапецияға айналады, оның негіздері түпнұсқаның негіздеріне пропорционал;

11. шеңбер эллипске айналады.

Мен зерттеп жүрген Л.С.Атанасянның «Геометрия 7-9» оқулығында стереометриядан негізгі мәліметтер XIV тарау бар. Бұл тарауда қарапайым фигуралардың: текше, шар, цилиндр, параллелепипед, пирамида, конус және т.б., сондай-ақ олардың қималары сызбаларының мысалдары көрсетілген.

Мен жоғарыда жазылған кейбір құрылыс ережелерін сақтамай, бұл фигураларды салуға тырыстым және бұл менің алдым.

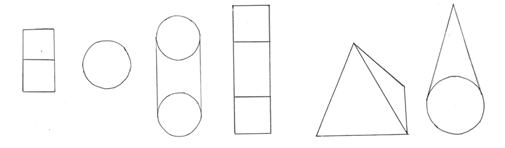
Мұндай сызбалардан қандай фигура сызылғанын түсіну қиын, мәселенің шешімін көру мүмкін емес.

Сонымен, геометриялық иллюзияларды геометрия заңдарын қолдана отырып түсіндіруге болады және сызбада үш өлшемді кескінді алу үшін белгілі бір ережелерді сақтау керек деген қорытынды жасауға болады.

3. Геометриялық иллюзияның түрлері

1) Менің сыныптастарыма көрсетілген алғашқы иллюзия Мюллер-Льер иллюзиясы деп аталады (алғаш рет 1889 жылы сипатталған)

Материалды жүктеу

Материал ұнаса әріптестеріңізбен бөлісіңіз

Ватсапта бөлісу Телеграммда бөлісу Фейсбукта бөлісу Сілтемені көшіру

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Тізімді көру