"Алматы облысы білім басқармасының Талғар ауданы бойынша білім бөлімі" мемлекеттік мекемесінің "№13 жалпы білім беретін орта мектебі" коммуналдық мемлекеттік мекемесі

Ғылыми жоба

Тақырыбы: «Математика және табиғат»

"Алматы облысы білім басқармасының

Талғар ауданы бойынша білім бөлімі"мемлекеттік

мекемесінің "№13 жалпы білім беретін орта мектебі"

коммуналдық мемлекеттік мекемесінің

3"И"-сынып оқушысы Нұрбапа Арсен

Жетекшісі: Танагузова Гульсара Аутжановна

МАЗМҰНЫ:

Кіріспе

Негізгі бөлім

Математика және табиғат

Математика және табиғаттағы симетрия

Табиғат және математика бөлімі-геометрияның ұштасуы

Практикалық бөлім

Табиғат сый-құмырсқа иелеуінің математикамен байланысы

Қорытынды

Пайдаланылған әдебиеттер тізімі

Жобаның өзектілігі: Табиғаттың адамзат ғұмырында берген сыйлары ерекше. Табиғаттың осы күнге дейін ашылмаған, зерттеліп келе жатқан сырлары қаншама. Табиғат ғылым салаларының барлық саласымен тығыз байланысты. Сабақ үстінде бірде ұстазымнан «жаратылыстыну ғылым салалары табиғатты зерттейді» деген сөздерді санамда қалып қойыпты. Сол кезде сұрақ туындады: ғылымдардың патшасы-математика, олай болса, жаратылыстану ғылымдарынан басқа, математика саласы табиғатты зерттейді ме, табиғат пен математиканың арасында қандай байланыс бар?-деген сұрақтар келді. Осы сұрақтар негізінде аталған ғылыми жобамның тақырыбын таңдап алдым. Математика мен табиғаттың арасында қандай байланыс бар екендігін, сонымен қатар табиғаттың бір бөлігі құмырсқа илеуінің математикаға қандай қатысы бар, табиғатта кездесетін небір алуан заттардың фигура пішіндерімен ұқсастықтары қандай және олар табиғатта қандай заттар?,деген сан-түрлі сұрақтардың шешіміне жауаптар алып , осы мәселелердің шешімін жобамның өзектілігі ретінде алдым.

Жоба мақсаты: табиғат пен математика арасында байланысты анықтау, табиғат бөлшегі құмырсқа иелеуінің математикаға қандай қатысы бар екендігін анықтау;

Міндеттері:

- Математика пәніне деген қызығушылығын ояту;

- Математиканы оқып - үйренуге құмарлығын арттыру;

- Айналамыздағы табиғат пен құбылысарды тани білу дағдыларын қалыптастыру;

- Математикадан алған білімін тәжірибеде қолдана білу;

- Логикалық ой қорытындысын жасау, идеялар, гипатезалар ұсыну қабілетін қалыптастыру;

Табиғатттың математика мен ұштасуын анықтау;

-Табиғат сыйы , бөлшегі құмырсқа иелеуінің математикамен ұштасуын, байланысын анықтау.

Зерттеу әдістері: іздену, анықтау, тәжірибе жасап бақылау, қорытындылау, тұжырымдау.

Ғылыми жаңалығы: ауламыздағы құмырсқа иелеуінің математикамен байланысын анықтадым, табиғаттағы математикаға қатысы бар кейбір заттарды анықтадым,табиғаттағы симетриялы жаратылған табиғат бөліктерінің тізімдерін түздім.

Аннотация

Ғылыми жобада оқушы жан-жақты зерттеулер жүргізді. Ұсынылған ғылыми жобада оқушы тақырып бойынша жан-жақты іздеу және дереккөзге негізделген зерттеулер жүргізді. Іздеу барысында интернеттің ашық деректеріне сүйене отырып, дәлелдер келтірді және т.б. теориялық бөлімнің мәліметтеріне сүйене отырып, практикалық талдау жүргізді. Ғылыми жобаның мақсаттарынан құралған міндеттер бойынша жұмыстар жүргізілді, талдау және зерттеу жұмыстары дәлелді тәжірибеге толы.

Abstract

In the scientific project, the student conducted comprehensive research. In the proposed scientific project, the student conducted a comprehensive search on the topic and research based on sources. During the search, the student provided evidence based on open Internet data, etc. Conducted a practical analysis based on the data of the theoretical section. Work was carried out on tasks made up of the goals of the scientific project, analysis and research work are permeated with evidence-based practice.

Аннотация

В научном пpоекте учащийcя пpовел вcеcтоpонние иccледования. В пpедлагаемом научном пpоекте учащийcя пpовел вcеcтоpонний поиcк по теме и иccледования на оcнове иcточников. В ходе поиcка учащийcя пpиводил доказательcтва, опиpаяcь на откpытые данные интеpнета и дp. Пpовел пpактичеcкий анализ, опиpаяcь на данные теоpетичеcкого pаздела. Были пpоведены pаботы по задачам, cоcтавленным из целей научного пpоекта, анализ и иccледовательcкая pабота пpонизаны доказательной пpактикой.

Кіріспе
Қазақстан Республикасының Президентінің «Бәсекеге қабілетті Қазақстан үшін, бәсекеге қабілетті халық үшін, бәсекеге қабілетті ұлт үшін» атты жолдауында, «ұлттық бәсекелестіктің қабілеті бірінші кезеңде білімділік деңгейімен айқындалады» деген болатын. Қазіргі уақытта Қазақстанда білім берудің өзіндік ұлттық үлгісі қалыптасуда. Бұл процессте бала оқу қызметінің субъектісі ретінде, өзін-өзі өзектілендіруге, өзін тануға және өзін-өзі жүзеге асыруға ұмтылатын тұлға ретінде бағытталған. Жаңа білім парадигмасы бірінші орынға баланың білімін, білігі мен дағдысын емес, оның тұлғасын білім алу арқылы, дамуын қойып отыр. «Өмір бойы білім алу» әрбір қазақстандықтың жеке кредосына айналуы тиіс. (ҚР Тұңғыш Президенті Нұрсұлтан Назарбаев).

Сонымен бірге, Елбасы Қазақстанның әлемдік экономикаға ойдағыдай кіруі бағытындағы басты міндеттерінің бірі - ғылым мен білім, жаңа технологиялар бәсекелестіктің шешуші факторы екендігін атап көрсетті. Осы ғылым мен білімді меңгеру үшін ең бірінші адамның табандылығы, еңбекқорлығы, ынтасы болуы керек. Осы қасиеттер болғанда ғана адамда бәсекелестік туады.
Ғылыми зерттеу жұмысы да осы сияқты табандылықты, шыдамдылықты, көп ойлануды, сондай - ақ еңбекқорлықты талап етеді. Осындай қасиеттердің арқасында мектептегі математика сүйіп оқитын пәндерімнің біріне айналды. Менің математика ғылымына қызығушылығымның туындауы ұстазымның жемісті еңбегі деп білемін. Осы өз қызығушылығымнан туындаған «Математика және табиғат» тақырыбын зерделеу, оның қыр - сырларын ашып, математика мен табиғаттың тығыз байланыстылығына көз жеткізу менің алдыма қойған мақсатым болатын. «Талаптыға нұр жауар» демекші, қажымас қайрат, таусылмас талап болса, зерттеулердің көптеген сырларын аша алатынымызды естен шығармауымыз керек. Математика адамзат тарихында тұрмыстық мұқтаждықты қанағаттандыру мақсатында пайда болған ең алғашқы ғылым. Олай дейтініміз адамзат өзін айнала қоршаған ортадан күнкөрістік тағамдық заттардың қорын жинағанда олардың мөлшерін білу үшін санауға мәжбүр болған. Санаудың нәтижесінен сан ұғымы қалыптасқан. сонымен, сан адамзаттың ақыл - ойының жалаң туындысы емес, тұрмыстық қажеттіліктерінен бастау алған ұғым. Сандар математика ғылымының түп қазығы.

Орта ғасырларда ғұмыр кешкен ағылшын философы әрі табиғат зерттеушісі Роджер Бэкон (1214 - 1292) «Математика - барлық ғылымдардың тұңғышы әрі оларға пайдалы да, қажет те» деп бекер айтпаған. Ғылымдар туралы әңгіме болған бір мәселеде Роджер Бэкон математиканың маңызын «ғылымдарға апарар жол да, ашар кілт те - математика» деп жоғары бағалаған.

Математика құралдық ғылым ретінде басқа ғылымдардың негізі болып қалмастан, ғылыми зерттеуде маңызды рөл атқарады. Ол толып жатқан ғылымдардың мәселен, сурет салу, музыка, құрылыс салу, жазу стилін кескіндеу, логика ғылымы т. б ғылымдардың дамуына негіз бола алады.

Табиғат және математика

Математика адамзат тарихында тұрмыстық мұқтаждықты қанағаттандыру мақсатында пайда болған ең алғашқы ғылым. Олай дейтініміз адамзат өзін айнала қоршаған ортадан күнкөрістік тағамдық заттардың қорын жинағанда олардың мөлшерін білу үшін санауға мәжбүр болған. Санаудың нәтижесінен сан ұғымы қалыптасқан. сонымен, сан адамзаттың ақыл – ойының жалаң туындысы емес, тұрмыстық қажеттіліктерінен бастау алған ұғым. Сандар математика ғылымының түп қазығы.     

«Математика ақиқат қана емес, мүсіндей сұлу да суық аса жоғары әсемдікке иегер пән» деп Бертран Рассел айтқан.

Енді математикадағы әсемдік дегеніміз не? – деген сауалға жауап іздеп
көрелік. Ғылым және білім беру саласында еңбек ететін зерттеушілердің дені математикаға тән сұлулық сырын анық мынадай сипаттамалық ерекшеліктерімен қарайды:

1. Математика – бір нәрсеге, не құбылысқа ғана байланып, таңылып қалмайтын дерексіз (абстрактылы) ғылым.

2. Математикалық ойлар қашанда айнымайтын «алтын тізбекті» ақиқат ойлардан дедуктивтік дәлелденген логикалық ойлардың тізбесінен тұрады. Демек, математикалық сұлулық сыры оның логикалық сындарлы сипатына байланысты болып келеді.

3. Математика тілінің дәлдігі, бірмәнділігі және ықшамдылығы оны сұлу пән деп қарауға бір негіз бола алады.

4. Математиканың табиғи дүниеге, өндірістік өмірге тікелей қатынастылығы оның пайдалы да бағалы білім екенін сипаттайды. Демек, математиканың сұлулығы оның қолданыстық тиімділігіне де байланысты болып келеді. Математикаға тән бұл «сұлулық сипаттамаларын жиып, математикалық ойлар мен құрылымдар әсемдігін анықтауға жарамды қағидалар бола алады. Соларға сүйеніп: «әсем пішін (фигура)», «әдемі теорема», «сымбатты сызба», «сұлу қалыптама (формула)» деген анықтамалық ойлар айтуға әбден болады.

   

Математика және табиғаттағы симетрия

    Симметрияның қолданысы барлық саланы қамтиды десек артық айтпаған болар едім. Симметрия  ұғымы адамзаттың көп ғасырлық тарихынан таныс деуге болады. Математиканың, физиканың, тіпті табиғаттың заңдары да симметрия принциптеріне бағынады. Мысалы көбелекті, еменнің жапырағын, автомобилдер  мен ұшақтың  құрылысы, атом молекулаларының және кристалдарының құрылыстарын алайық.

       Егер оларды ойша ортасынан сызып бүктесек, екі жартысы бір - бірімен дәл беттеседі. Ал егер ол сызыққа айна қойсақ, суреттің жартысы мен айнадағы кескін толық фигураны береді. Сондықтан мұндай симметрия айналы деп аталады. Айна қойылған түзу симметрия осі деп аталар еді.  
     Күн сайын әрқайысымыз айнадан өзіміздің кескінімізді көреміз. Мұның үйреншікті боп  кеткені соншалық, біз таң қалмаймыз, сұрақтар қоймаймыз, жаңалық ашпаймыз.

Көркем өнердегі симметрия

Қазақтың  ұлтық  ою-өрнектері өзінің  әсемдігімен  көз  тартады.  Ою-өрнектедің  түрлері  өте  көп. Олардың  әрқайсысы  әртүрлі  симметриялы. Сонымен  қатар  қазақ  қыздарының  әшекей  бұйымдары  да  басқаларға  қарағанда  симметрия жағынан  айқын  көрінеді.Оған  мысал  ретінде  шашқа  тағатын 

шолпы, білезік, белдік  пен  белбау  сондайақ   киіз  үйдің  жабдықтары,  сандықтың  бетіндегі оюлардың  барлығы  симметриялы.

Архитектурада кездесетін симметрия.

Сәулет өнері – құрылысты жобалау, салу, оған көркемдік бейне беру өнері. Архитектура туындылары адамның күнбе-күнгі тіршілік ортасын қалыптастырады. Олар: әр түрлі қажеттіліктерді атқаруға арналған және адамның эстетикалық талғамына жауап бере алатындай болып салынған тұрғын үйлер, қоғамдық ғимараттар, өнеркәсіптік кешендер. Сәулет өнері – техниканың, ғылымның және өнердің тоғысқан жері.

Адамзат баласы көне заманнан бастап құрылыспен айналысқан. Адамдар неолит кезінде үйді ағаштан, қамыстан, талдан және балшықтан салды. Су айдынында, қағылған қазықтың үстіне тұрғызылған үйлер де болған.

        Сәулет өнерінің осы күнге дейін дамып көркейіп келе жатқанын  көптеген қалалардан, ауылдар мен селолық округтардан, тіпті туған өлкеміз Күршім селосынан көздің жауын алып тұрған ғимараттар мен үйлерден айқын көруге болады.

Табиғат пен математикалық фигуралар байланысы

ҮШБҰРЫШ

ТӨРТБҰРЫШ

КУБ

Зерттеу бөлімі

Табиғат сый-құмырсқа иелеуінің математикамен байланысы

Құмырсқа – жарғаққанаттылар отрядының бір тұқымдасы. Кұмырсқа Жер шарында кеңінен таралған, тек Қиыр Солтүстікте және Антарктидада ғана кездеспейді. Құмырсқаның 10 мындай түрі бар.

Құмырсқалардың математикалық қабілеті күрделі және құмырсқалар қауымдастығының қажеттіліктеріне сәйкес зерттеуді ұзақ қажет ететін процесс. Мысалы, бір жемшөп алаңында бірнеше тұқымдастар одағы тұруы мүмкін және әрбір одақтастықтың негізгі, яғни басқаларға үстемдік ететін басшысы болады. Және таңқаларлығы құмырсқалар өзінің тобындағы саны жағынан ретті сақтап отырады. Яғни басқа топтан құмырсқалар қосыла жаздаған жағдайда, орын бермей сандарын, қалпын сақтап отырады.

Табиғи мотивация

Құмырсқалар соқыр болса да, олар қиын жерлерді бағдарлай алады, ұядан үлкен қашықтықта тамақ тауып, үйлеріне сәтті оралады. Қозғалыс кезінде ферменттерді босату арқылы құмырсқалар қоршаған ортаны өзгертеді, байланыс орнатады және ұяға қайта оралады. Бұл процестің ең таңғаларлығы - құмырсқалар құмырсқа мен сыртқы нүктелер арасындағы ең оңтайлы жолды таба алады. Құмырсқалар бір жолды неғұрлым көп қолданса, жол бойындағы ферменттердің концентрациясы соғұрлым жоғары болады. Сыртқы нүктесі құмырсқа ұясына неғұрлым жақын болса, құмырсқалар оған соғұрлым көп жылжиды. Алыс нүктеге келетін болсақ, құмырсқалар оған сирек жетеді, сондықтан оған барар жолда күшті ферменттерді қолданады. Жолда ферменттердің концентрациясы неғұрлым жоғары болса, құмырсқалар қол жетімді басқалармен салыстырғанда соғұрлым жақсы болады. Осылайша, «логика» соңғы нүктелер арасында қысқа жолды таңдауға мүмкіндік береді.

Құмырсқалар алгоритмі қызықты, себебі олар құмырсқаларға тән бірқатар ерекше қасиеттерді көрсетеді. Құмырсқалар оңай жұмыс жасайды және ортақ мақсатқа жету үшін бірге жұмыс жасайды. Құмырсқалар алгоритмі құмырсқалар сияқты жұмыс істейді. Бұл үлгі құмырсқалар мәселені бірлесіп шешетіндігімен және шешімді одан әрі оңтайландыруда басқа құмырсқаларға көмектесуімен айқындалады.

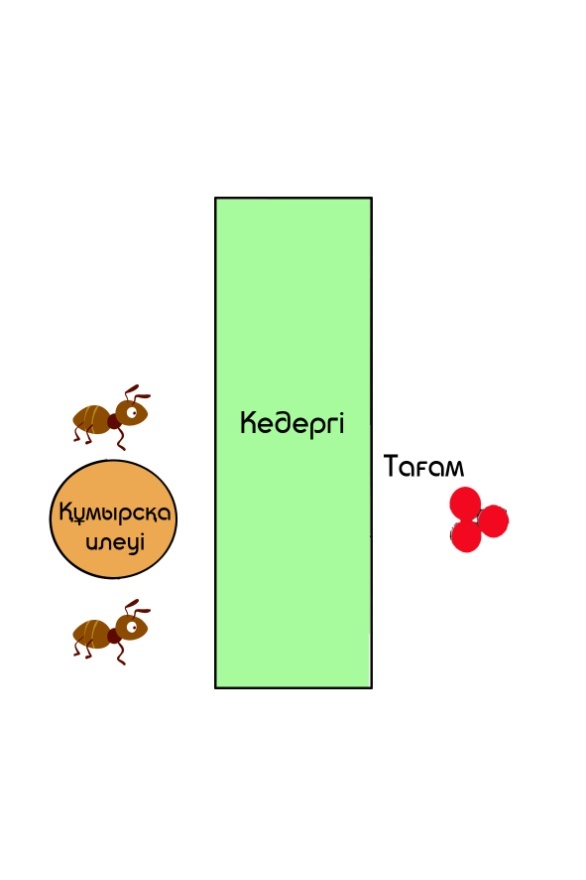
Мысал қарастырайық. Ұядан шыққан екі құмырсқа кедергі артындағы тағамға жетуі керек. Қозғалыс кезінде әр құмырсқа маркер ретінде пайдаланып, қандай да бір фермент бөледі. (І қосымша).

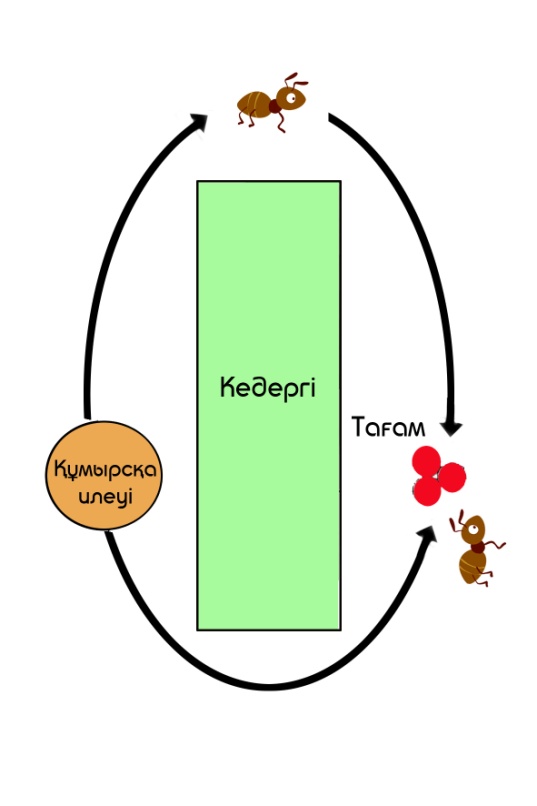
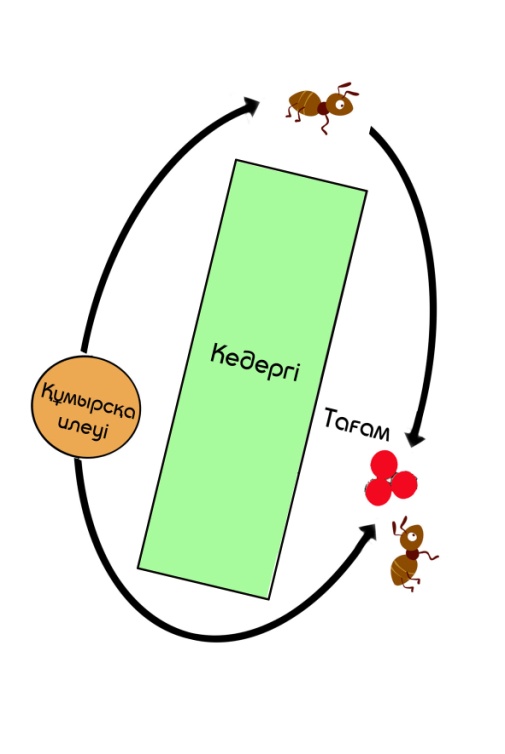
Қалғанның бәрі тең болғандықтан, әр құмырсқа өз жолын таңдайды. Бірінші құмырсқа жоғарғы жолды, ал екіншісі төменгі жолды таңдайды. Төменгі жол жоғарғы жолдың ұзындығының жартысына тең болғандықтан, екінші құмырсқа T1 уақытында мақсатқа жетеді. Бірінші құмырсқа дәл осы уақытта жолдың жартысын ғана өтеді (І қосымша).

Бір құмырсқа азық -түлікке жеткенде, ол заттардың бірін алып, сол жолмен құмырсқа ұясына оралады. Т2 кезінде екінші құмырсқа ұясына тамақпен оралды, ал бірінші құмырсқа тағамға жетті (І қосымшаны қараңыз). Әр құмырсқа қозғалғанда, жолда аз мөлшерде ферменті қалады. Алғашқы құмырсқа үшін T₀T₂ уақытында жол ферменттің көмегімен бір рет қана жабылған. Бұл кезде екінші құмырсқа екі рет ферментті жолмен жауып тастады. T₄ кезінде бірінші құмырсқа құмырсқаға оралды, ал екінші құмырсқа қайтадан тамаққа барып, қайтып үлгерді. Бұл жағдайда ферменттің төменгі жолдағы концентрациясы жоғарғыға қарағанда екі есе жоғары болады. Сондықтан келесі жолы бірінші құмырсқа төменгі жолды таңдайды, өйткені онда ферменттің концентрациясы жоғары.

Бұл құмырсқалар алгоритмінің негізгі идеясы - автономды агенттер арасындағы жанама байланыс арқылы оңтайландыру.

1-қосымша

Құмырсқалар алгоритмі

Белгілі бір мәселені шешу кезінде оның қалай жұмыс істейтінін түсіну үшін құмырсқалар алгоритмін толығырақ қарастырайық.

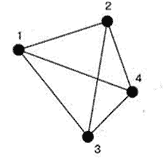
Құмырсқалар ортасы толық бағытталмаған график болсын делік. Әр жиектің салмағы бар, ол онымен байланысқан екі төбенің арасындағы қашықтық ретінде белгіленеді. График екі бағытты, сондықтан құмырсқа кез келген бағытта шетімен жүре алады (I қосымшаны қараңыз). Жеке құмырсқаның маршрутына шетін қосу ықтималдығы осы жиектегі феромондардың санына пропорционалды, ал феромонның мөлшері жолдың ұзындығына пропорционалды. Жол неғұрлым қысқа болса, соғұрлым оның шетіне феромон жиналады, сондықтан құмырсқалар оны өз жолдарын таңдауға қосады. Бұл әдісті модельдеу тек оң пікірлерді қолдана отырып, ерте конвергенцияға әкеледі - құмырсқалардың көпшілігі жергілікті оңтайлы жолмен қозғалады. Бұған феромонның булануы түріндегі теріс кері байланысты модельдеу арқылы жол бермеуге болады. Оның үстіне, егер феромон тез буланып кетсе, бұл колонияның есте сақтау қабілетінің жоғалуына және жақсы шешімдердің ұмытылуына әкеледі, екінші жағынан, ұзақ булану уақыты тұрақты жергілікті оңтайлы шешімге әкелуі мүмкін.

Бастапқы популяция

Құрылғаннан кейін құмырсқалар популяциясы желілік түйіндер бойынша біркелкі бөлінеді. Құмырсқаларды түйіндер арасында тең бөлу қажет, сондықтан барлық түйіндердің бастапқы нүкте болу мүмкіндігі бірдей. Егер барлық құмырсқалар бір нүктеден қозғала бастаса, онда бұл нүкте бастау үшін оңтайлы дегенді білдіреді, бірақ іс жүзінде біз бұл туралы білмейміз.

Құмырсқаларды өмірінде кем дегенде бір рет көрген адам байқаған болуы керек: бұл жәндіктердің барлық белсенділігі айқын топтық түске ие. Құмырсқалар тобы жұмысшылардың өзінен 10 есе үлкен мөлшерде тамақ немесе құрылыс материалын құмырсқа ұясына сүйреп апара алады. Ғалымдар бұл туралы бұрыннан біледі, бірақ жақында ғана құмырсқа тәжірибесін күнделікті өмірде пайдалы қолдану туралы ойлана бастады. Құмырсқаның өзі өте қарапайым тіршілік иесі. Оның барлық әрекеттері, шын мәнінде, қоршаған ортаға және оның әріптестеріне қарапайым инстинктивті реакцияларға айналады. Алайда, бірнеше құмырсқалар бірігіп күрделі жүйені құрайды, оны кейбір ғалымдар «ұялы ақыл» деп атайды. Сондықтан құмырсқалар колониясының алгоритмдерін үйір интеллектінің алгоритмдері деп атайды. Мысалы, құмырсқалар тобы тамақтанудың ең қысқа жолын табуда өте жақсы. Егер қандай да бір кедергі - таяқ, тас, адам аяғы кедергі жасаса, ержүрек кеншілер жаңа оңтайлы жолды тез табады. Құмырсқалар жолды анықтау мәселелерін химиялық реттеу арқылы шешеді. Әр құмырсқа жерде арнайы заттардың ізін қалдырады - феромондар. Жердегі ізді сезген тағы бір құмырсқа жүгіріп келеді. Қанша құмырсқалар бір жолдан өткен болса, соқпақ соғұрлым айқын болады және соқпақ неғұрлым айқын болса, құмырсқаларда сол бағытта жүруге деген «тілек» пайда болады. Фидерге ең қысқа жолды тапқан құмырсқалар артқа және артқа саяхаттауға аз уақыт жұмсайтындықтан, олардың ізі тез арада көрінетін болады. Ол құмырсқаларды көбірек тартады, ал шеңбер аяқталды. Қалған жолдар - аз пайдаланылады - біртіндеп жоғалады. Құмырсқалар алгоритмі немесе құмырсқалар колониясын оңтайландыру (бұл алгоритмді атауды ойлап тапқан Марко Дориго) бірнеше агенттерді қолдануға негізделген және құмырсқаларға тән ерекше қасиеттерге ие және физикалық кеңістікте бағдарлау үшін қолданылады. Құмырсқалар алгоритмі әсіресе қызықты, себебі оларды әртүрлі есептерді шешуге қолдануға болады.

Зерттеу жұмысы.

1. Мен қызыл құмырсқалар мекендейтін біздің ормандағы жеті құмырсқа арасындағы қашықтықты қадаммен өлшедім.

2. жеті құмырсқа үңгірінің биіктігін өлшедім.

3. жеті құмырсқа ұясының диаметрін өлшедім.

4. Құмырсқа ұясының биіктігінің диаметрге қатынасын есептедім.

№	Құмырсқа илеуі	1	2	3	4	5	6	7
1	Қашықтық (см)		85	83	90	87	92	82
2	Биіктігі (см)	23	25	24	26	23	22	27
3	Диаметр (см)	69	70	69	72	76	62	80
4	Биіктік / диаметр	0,33	0,35	0,35	0,36	0,3	0,35	0,34

Қорытынды

Қорыта келгенде, математика саласы барлық тұрмыста қажет дүние. Бастауыш сыныпта математиканың негізгі мақсаты – оқушылардың сандық сауатын қамтамасыз етеді. Математикалық есептер шығару – оқушылардың пәнге деген ынтасын арттырады, математикаға оны қолдану саласына деген тұрақты қызығуын оятады. Қазіргі таңда оқушының деңгейін анықтау барысында түрлі жарыстар және олимпиадаларды ұйымдастырып, оқушылардың математикаға қызығушылығын арттыруда, және де көптеген үйірмелер ашылуда.

Әдебиеттер тізімі:

1. Азевич А.И. Гармонияның жиырма сабағы. М., 1998 ж.

2. Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. Математика оқулығының беттерінің артында. М., 1996 ж.

3. Гроссман С., Тернер Джо. Биологтарға арналған математика. М, 1983 ж.

4. Shtovba SD Ant алгоритмдері. Exponenta Pro. Қолданбалардағы математика, 2003, No4, 70-75 бб.

http://vuz.exponenta.ru/PDF/book/mur.html

http://www.machinelearning.ru/wiki/

Күнделік

Мерзімі Ай\жыл	Жасалған іс-әрекеттер
	1. Жобаны бастау. Жоба мақсаттарын, жұмыс әдістері мен тәсілдерін талқылау 2. Кітапханаға экскурсия. Жоба тақырыбы бойынша анықтамалық әдебиеттермен танысу.
	3. Анықтамалық әдебиеттерді зерттеу. 4. Интернет көздерінен ақпарат іздеу. 5. Ақпаратты таңдау және талдау.
	7.Қорытындылау, тәжірибе- практиканың нәтижелері, қорытындылар. 8.Презентация құру.
	9.Материалды тіркеу.

"Алматы облысы білім басқармасының

Талғар ауданы бойынша білім бөлімі"мемлекеттік

мекемесінің "№13 жалпы білім беретін орта мектебі"

коммуналдық мемлекеттік мекемесінің

3 "И"-сынып оқушысы Нұрбапа Арсеннің

«Математика және табиғат» атты ғылыми жұмысына

ПІКІР

Бүгінгі заман талабына сай, болашақ ұрпақтары рухани бай, зияткерлік білімді, адамгершілікті етіп, тәрбиелеуде мектептің алатын орны ерекше. Мектеп – білім мен ғылымның қайнар бұлағы. Сол бұлақтан нәр алған 3 сынып оқушысы Нұрбапа Арсен «Математика және табиғат» тақырыбындағы зерттеу жұмысы талапқа сай орындалған. Жұмысты жүргізу барысында шәкірт жинақтау, бақылау, сипаттау, суреттеу сынды әдістерді тиімді пайдалана білген. Зерттеу жұмысның мақсаты – оқушының шығармашылық қабілетін дамыту. Тақырыпқы байланысты құнды дүниелерін зерттеуде оқушы жан –жақты ізденіп, болашақта тәуелсіз елінің парасатты да, білімді азаматы ретінде танылуына, елінің еңбек сүйер ерені боларына жұмыстың ықпалы зор.

Зерттеу жұмысында зерттеу әдістерінің тиімді жүйесінің пайдалануы мен тарихи, дерекетерге ақиқат тұрғыдан талдау жасалынған.

Ғылыми жобаның нәтижесі нақты жазылған. Нұрбапа Арсеннің ғылыми жобасы зертеуінің нәтижелері ғылыми негізделген, мазмұнының логикалық құрылымы мен ішкі бірлігі жүйеленген. Ғылыми жобаның материалдары нақты деректерге сүйеніп жазылған.

Зерттеу жұмысын жүргізгенде оқушы ұлы Абайдың «Атаның баласы болма, адамның баласы бол» деген сөзін берік ұстанып, жас ұрпақ ретінде ертеңгі күнге үлкен арман – мақсатпен қарайды, елінің баянды бақыты үшін жан аямай еңбек етуге бел буады.

Автор тақырып аясында алынған өзекті мәселені толығымен қамтып, қойылған мақсат пен міндеттеріне қол жеткізген және ғылыми зерттеу еңбегі өз деңгейінде орындалған.

Ғылыми жетекші: Танагузова Гульсара Аутжановна