
Кіріспе
«Үлкен алаңда бұрыш жоқ»
Лао-цзы
Oригами - бұл таңғажайып көңілді тәжірибе. Бала кезімде мені осы ерекше фигуралар қызықтырды, оларды ойында да қолдануға болады. Ол кезде біз геометрия ғылымын білмейтін едік. Тиісінше, біз осындай әртүрлі қағаздан жасалған ойыншықтарды жинау ережелері туралы ойлаған жоқпыз.
Оригамиді геометрия туралы білімді және математикалық есептеулерді қолдану арқылы жасауға болады екен.
Жұмыстың мақсаты: оригами мен математиканың сәндік-қолданбалы өнері арасындағы байланысты анықтау.
Тапсырмалар:
1. оригами тарихын зерттеу;
2. оригами мен бүктеу техникасының негізгі формаларын сипаттау;
3. оригами мен математиканың өзара байланысын анықтау және дәлелдеу, оригаметрияны сипаттау;
4. қағаз фигураларын жасауға көмектесетін практикалық мәселелерді шешу.
Нысан – оригамеметрия.
Зерттеу пәні: оригами техникасы.
Гипотеза: оригами сабағы жазықтық пен кеңістіктік геометрияның практикалық дамуына ықпал етеді.
Зерттеу әдістері:талдау, синтез, салыстыру, модельдеу.
I тарау. Оригами техникасы сәндік-қолданбалы өнердің бір түрі ретінде
1.1. Оригами тарихы
Көптеген адамдар «оригами» сөзін естігенде таң қалады. «Ал бұл не?» Олар сұрайды. Сонымен қатар, әрбір адам өмірінде кем дегенде бір рет төртбұрышты қағаздан ең қарапайым өнімді - қайықты немесе ұшақты жасады. Дүкендерде сабан шляпалар мен панамаларды мұндай таңдау болмаған кезде, адамдар жазда өздерін газеттен «қақпақ» жасайтын. Қағаз қайықтары да, қалпақшасы да оригами қағидасына сәйкес жасалған.
Оригами - Жапонияда кеңінен таралған қағаздан жасалған көлемді және жалпақ фигуралардың әр түрін бүктеудің ежелгі қытайлық өнері.
Қағаз үлгілерін жасау өнері Қытайда біздің дәуіріміздің 1 - 2 ғасырлар тоғысында пайда болып, 6 ғасырға қарай Жапонияға жетіп, жаңа өмір тапты.
Бұл оригами өнері бүкіл жапон мәдениетінің ажырамас бөлігіне айналды.
Жапондық дәстүрлер бойынша қағаз модельдері құстардың, жануарлардың немесе гүлдердің формаларын берудегі шынайылық үшін емес, ішкі сезім, табиғаттың белгілі бір жаратылысына тән «рух» сезімі үшін бағаланды. Бұл сезім қағаз парағындағы бірнеше бүктемелермен жеткізілді.
Хейя дәуірінде (794-1185) оригами оның маңызды бөлігіне айналды ең жоғары жапон қоғамы арасында қабылданған рәсімдер. Самурай «ауыртпалықтар» деп аталып, олардан жасалған оригами тұмарларын жасады
акула терісінің
жолақтары немесе кептірілген ет талшықтары қосылған
қағаз.
Мұндай тұмарлар
самурайды қорғау және оған жеңіс әкелу үшін жасалған. Шыныаяқтарды
оригами қағаздан жасалған мүсіншелермен безендірген шай
басқарушылар өз қолөнерінің құпияларын мұқият сақтады. Олардың
оригамиі фигураны жайып салғаннан кейін оны бұрынғы қалпына
келтіру, басқаша айтқанда, оның жасалу құпиясына ену мүмкін
болмайтындай етіп қалыптасты. Сонымен қатар, жаңадан бүктелген
фигура жаңаға ие болуы керек еді. Бүктемелер, және олардың ойынша
шеберлер өздерінің оригами құпиясында біреу екенін анықтай алады,
содан кейін тырысты.
Оригами өз атын жапонның «ори» - бүктеу және «гами» - қағаз сөздерінен алды. Сөздіктерден кейде оригамидің қағаздан құстар мен жануарлардың бейнелерін жасау өнері ретінде анықтамасын кездестіруге болады. Бұл қысқа фазаның сипаттамасы біздің балалық шақ туралы естеліктер оятады: қағаз ұшақтар, жәрмеңке алаңында жанып тұрған шамдар. Алайда, оригамиге деген шынайы қызығушылық Еуропада және Америкада осы ежелгі өнер бірінші көзқараста көрінгеннен әлдеқайда терең екендігі белгілі болған кезде ғана пайда болды. Ақыр соңында, қарапайым қағаз парағынан алынған оригамидің көмегімен сіз ең керемет нәрселерді жасай аласыз!
Нағыз оригами өнері тек қағазбен ғана шектелмейді. Қазіргі уақытта көптеген оригами әуесқойлары батылдықпен жаңа материалдармен тәжірибе жасау, модель құрудың жаңа тәсілдерін іздеу және табу . Мысалы, американдық Лэйн Аллен оригамидің «оригами» деп аталатын жаңа тармағын құрды. Ол өз модельдерін металлдалған дәкенің бүктелген парақтарынан жасайды. Бұл материалда дәстүрлі оригами материалынан - қағаздан екі түбегейлі айырмашылық бар. Біріншіден, ол пішінді қатаң ұстайды, екіншіден, оның иілуін тегіс етіп жасауға болады.
Бұл оригамиді сүйетіндер үшін жаңа мүмкіндіктер ашады. Тағы бір американдық Джереми Шефер одан да алға жылжып, өз модельдерін металл фольгадан жасайды, сондықтан оның қайықтарын ылғалданудан қорықпай жіберуге болады. Англиядан келген Дэвид Брилл барлық оригами білгірлерін өз модельдерін бос бөтелкелерге салып таң қалдырды.
Қазіргі кезде бүкіл әлемде көптеген адамдар оригами өнеріне тәуелді. Қағаз фигураларын балалар мен ересектер, суретшілер мен дизайнерлер жасайды. Бұл тіпті мектептерде оқытылады, бұл туралы кітаптар жазылады және журналдар қызықты мақалалармен және әртүрлі модельдердің сипаттамаларымен шығарылады.
Біздің уақытымызда оригами тек ойыншық емес. Бұл өнерге ғалымдар мен дизайнерлер қызығушылық таныта бастады. Оригами бойынша ғылыми симпозиумдар өткізілуде. Қазірдің өзінде ең күрделі техникалық құрылымдар - қағаз үлгілері жасалуда.
Бірақ балалар, әрине, оригамиді жаңа ойыншық жасау мүмкіндігі ретінде қызықтырады. Сіз өзіңіздің көлемді қағаздан жаңа, жеке фигуралар жасай аласыз.
1.2 Оригами формалары
Ежелгі дәуірден бастап жапондық оригамиде негізгі болып саналатын кейбір формалары болған. Бұл кейіннен жүздеген вариациялар жасауға болатын стандартты, оңай танылатын бланкілер. Барлық осы негізгі модельдер сізге таныс болуы керек, және сіз олардың әрқайсысының бүктемелері мен кезектілігін біле отырып, әрбір негізгі бланкті автоматты түрде жасауыңыз керек. Негізгі формаларды игере отырып, сіз классикалық модельдерді ғана емес, сонымен қатар өзіңіздің модельдеріңізді де сәтті қоса аласыз.
Жұмыстың алғашқы кезеңдерінде квадрат парақты бірнеше тәсілмен бүктеуге болады. Олардың көпшілігі жоқ - он бір, және әрқайсысының өз атауы бар. Міне олар:
Қарапайым:
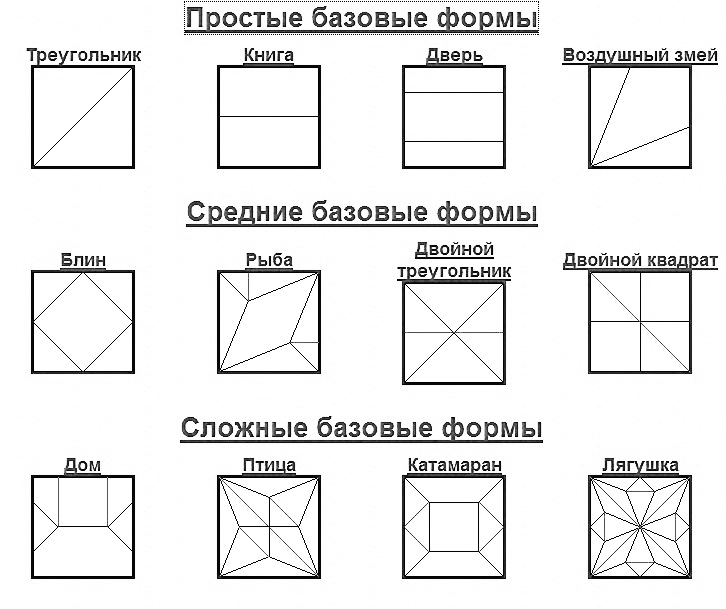
Үшбұрыш кітап есік батпырауық
Орташа:

Ромб балық үшбұрыштар квадра
Күрделі:

Үйшік құс қайық бақа
Кез-келген оригами фигурасы белгілі бір өлшемдегі квадрат парақтардан тұрады (егер сіз схемада өзгеше көрсетілмесе, өлшемді өз қалауыңыз бойынша таңдайсыз). Бастапқы кезеңдегі барлық негізгі формалар дәл осылай бүктелген. Үшбұрыштан негізгі «үшбұрыш», «құймақ», «балық», «батпырауық» сияқты негізгі пішіндер алынады. Қос квадрат төртбұрыштан, «құстан» және «бақадан» жасалады. Тік бұрышты «кітап» пішінінен «үй», «есік» және «катамаран» алынады.
Осы пішіндерді көріп, біз оригами көмегімен келесі түсініктерді қайталауға болатындығын түсінеміз:
– көлденең, тік, қиғаш сызықтар;
– квадратты әртүрлі тәсілдермен бүктеу, көршілес жақтарын, диагональдарын көрсету;
– квадраттар;
– барлық үшбұрыштар.
Классикалық техниканы игере отырып, сіз модульдік оригамиден бастауға болады. Бұл техникалардың арасындағы түбегейлі айырмашылықтар - классикалық фигуралар тегіс және бір парақтан бүктелген, ал модульдік оригами жасау үшін үш өлшемді фигураға айнала отырып, бір-біріне енгізілген бірдей қағаз бөліктерінің (модульдердің) белгілі бір саны қажет. Тегіс оригамиді бір жақты оригами деп те атайды: объект тек бір жағында ғана анықталады. Әдетте мұндай өнімдер аппликация жұмысында қолданылады.
Модульдік (көлемдік) оригами неғұрлым күрделі және көп уақытты қажет етеді, бірақ бұл техникада сіз тұтас қағаздан жасалған мүсіндер, сонымен қатар күнделікті өмірде қолдануға және сыйлық ретінде ұсынуға болатын әр түрлі пайдалы заттарды жасай аласыз: қораптар, ұсақ-түйек заттарға арналған стендтер, қораптар, вазалар.
Модульдік оригами түрлерінің бірі - кусудама техникасы - конус тәрізді қағаздың белгілі бір санынан сфералық пішіндерді бүктеу. Көптеген оригамистер кусудаманы түбегейлі өзгеше әдіс деп санайды, өйткені бөлшектерді тігу көбінесе фигураларды жасау және құрастыру үшін қолданылады. Кусудаманы игере отырып, сіз өзіңіздің үйіңізді фантастикалық әдемі гүл композицияларымен безендіре аласыз, оған қарап олардың қағаздан жиналғанына сену қиын. Оригами принципінің жалпы негізі екі өлшемді затты үш өлшемді затқа айналдыру болып табылады.
II тарау. Оригами мен математиканың байланысы
2.1. Математикті оригами жасау үшін қолдану
Осы өнермен алғашқы танысу кезінде біз тіктөртбұрыш және үшбұрыш сияқты қарапайым пішіндер туралы білеміз. Қарапайым пішінді қосқанда, біз квадратпен танысамыз, оның бұрыштары ортасына қарай иіліп, квадрат төрт бірдей үшбұрыштан тұруы мүмкін екенін көруге болады. «Батпырауық» пішінін бүктеп, біз ромбпен танысамыз. Оригами алфавиті нүкте мен сызық сияқты геометриялық түсініктерді қамтиды.
Осылайша, оригами мен математика (атап айтқанда геометрия) бір-бірімен тығыз байланысты. Математикадан көптеген ұғымдарды (мысалы, нүкте, түзу, квадрат, тіктөртбұрыш, үшбұрыш) оригами жасау кезінде қолданамыз.
Инженер, математик және суретші болмай-ақ, сіз әдістің барлық тапқыр қарапайымдылығын түсіне алмайсыз, соның арқасында оригами шеберінің қолындағы тегіс бет күрделі кеңістіктік құрылымға айналуы мүмкін. Қағаздың оңай бүктелуіне, кесілуіне және желімделуіне арналған жоғары қасиеттерін ескере отырып, бұл материал архитектуралық орналасу және декоративті модельдеу үшін бұрыннан қолданылып келеді. Шынында да, өнімнің немесе құрылымның прототипін жасамас бұрын, алдымен қағаздан модель жасау әлдеқайда оңай. Сол себепті қағаз шаблондарды, өрнектер мен трафареттерді жасауда қолданылады. Тұлпарларды кесіп тастауды, коллаждар мен аппликацияларды осы материалсыз елестету қиынға соғады.
Оригами өнері, керісінше, кесу, желімдеу және одан да беткей созуды мүлдем жоққа шығарады. Классикалық оригамидегі барлық ықтимал әдістердің тек иілуіне және бүктелуіне жол беріледі. Бұл шектеу форманы модельдеу міндетін шексіз қиындатады, бірақ, екінші жағынан, шеберді өзі үшін күтпеген жерден онымен жұмыс істеудің барлық басқа тәсілдерінде талап етілмеген материалдың осындай мүмкіндіктерін ашуға мәжбүр етеді.
Бірақ, өкінішке орай, тіпті оригамиді білетіндер бұл туралы үнемі ойлана бермейді. Әдетте, бүктеу, ең алдымен, нәзік қолөнер, фигуралардың белгілі конструкцияларының схемалары бойынша қайталау немесе жаңаларын ойлап табу ретінде қарастырылады.
Оригами туралы математикалық түсінік бетті материалдан абстракциялауға мүмкіндік беретіні және парақтың топологиялық бүктелген түрлендірулерін беттің құрылымдық негізделген бөліктерін енгізу және оның түсінігін кеңістіктен, қисыққа, жабық көлемнің қабығына, үш өлшемді құрылымға және т.б. кеңейту арқылы толықтыруға болатындығы айқын болды.
Ресейде Михаил Максимович Литвинов «оригами» тұжырымдамасын тұжырымдап қана қоймай, сонымен бірге Ресейдегі пікірлес адамдардың жаңа қозғалысын көрсетіп, үйретіп, құрды, оларды кейіннен Мәскеудегі Оригами клубына айналдырған Оригами өнер және оқу орталығының айналасына біріктірді.
Осылайша, жазықсыз ойын мен қолөнерден шыққан оригами интеллектуалды кәсіпке айналды, оның жаппай ынта-жігері ғылыми және көркем шығармашылыққа бағытталды. Оригами үшінші мыңжылдықтың заманауи мәдениетімен және технологияларымен біртіндеп араласа бастады.
Классикалық оригами бойынша, бүктелудің нысаны - кесектерсіз, белгіленбеген квадрат парақ.
Математикалық тұрғыдан алғанда, оригамистің мақсаты - соңғы нысанды қалыптастыру үшін қажетті бүктемелерді анықтайтын парақтағы бір немесе бірнеше нүктелердің орнын дәл анықтау. Бүктеу процесі келесі ережелерге сәйкес нақты анықталған әрекеттер тізбегін орындауды қамтиды:
-
Жол парақтың шетімен немесе қағаздың бүктелген сызығымен анықталады.
-
Нүктелер сызықтардың қиылысуымен анықталады.
-
Барлық қатпарлар туралау арқылы бірегей анықталады
-
парақтың әртүрлі элементтері - сызықтар немесе нүктелер.
-
Қатпар бір бүктеме арқылы пайда болады, ал бүктеу нәтижесінде фигура тегіс болып қалады.
Соңғы нүкте бүктеуді қатаң түрде шектейді, бір уақытта бір бүктеуге мүмкіндік береді. Іс жүзінде, ең қарапайым оригами модельдері де бір операцияда бірнеше қатпар жасауды көздейді.
Оригами фигураларын бүктеу барысында біз әртүрлі геометриялық фигуралармен танысамыз: үшбұрыш, квадрат, трапеция және т.с.с., біз кеңістікте және қағаз парағында оңай шарлауды, тұтас бөліктерге бөлуді, тік, көлденең, диагональды табуды үйренеміз, одан да көп нәрсені білеміз геометрия мен математикаға қатысты. ХІХ ғасырдың ортасында американдық ағартушы Ф.Фребел оригамидің геометриялық ерекшелігін байқап, оны мектеп пәні ретінде енгізді.
Мысалы, ол геометрия негіздерін циркуль, сызғыш және кейбір ұғымдардың көмегімен емес, қағаз фигураларын бүктеу мысалында оқып үйренуді ұсынды. Ол оригамиді педагогикалық процеске белсенді түрде енгізді. Өкінішке орай, ол кезде Фребель фигураларды бүгу техникасын дәл қазіргідей меңгерген емес.
Оригами теориясында математиканың көмегімен дәлелденетін ережелер, заңдылықтар бар, ал үш өлшемді денелердің жалпы қасиеттерін арнайы математика ғылымы - топология зерттейді.
2.2. Оригамидің практикалық тапсырмалары
Табиғатта барлығы симметриялы болады. Ал оригамидің өзінде: парақтың екі жағы бар; квадрат - бұрыштар мен қабырғалардың екі жұбы, екі симметрия осі.
Барлық негізгі оригами пішіндерін бүктеуге, содан кейін топтастыруға және квадраттың екі симметрия осі бойымен орналастыруға болады. Мұны қарапайым мысалдармен қалай жасауға болатынын көрейік:
-
Қағаз квадратын симметрия осі бойымен өзіңізге қарай бүктеңіз. Негізгі «Үшбұрыш» пішіні алынды.
-
Қағаз квадратын симметрия осі бойымен өзіңізге қарай бүктеңіз. Негізгі «Тіктөртбұрыш» формасы шықты
-
Қағаздың төртбұрышын өзіңізге қарай бүктеңіз, оның оң және сол жақ төменгі жақтары симметрия осімен сәйкес келеді. Негізгі формасы «Батпырауық» алынды.
-
Қағаз квадратын өзіңізге қарай бүктеңіз, оның оң және сол жағы симметрия осімен сәйкес келеді. «Есік» негізгі формасы алынды.
Математика сабағында оригамиді келесі тапсырмаларда қолдануға болады: а) көлденең, тік, қиғаш сызықтарды табу; б) барлық квадраттарды табу; в) барлық үшбұрыштарды табу; г) кескіндерді атаңыз; в) төртбұрышты, көршілес жақтарын, диагональды бүктеу.
Мысалы, бірнеше мәселені шешейік:
1-мақсат.
Тік бұрышты бөлу
Бұрышты 30 немесе 60 градусқа
кешіктіру қиындық тудырмайды. Квадраттың бүйіріне тең бүйірлі
үшбұрыш салу жеткілікті. Ол үшін алдымен тік бүктелген квадратты
екі тең төртбұрышқа бөлу керек. Содан кейін біз квадраттың бұрышын
белгіленген сызыққа жеткізетін бүктемені
саламыз. 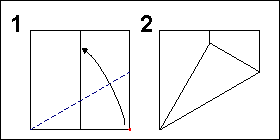
Мақсат 2.
Оригами әдісін қолдана отырып, квадраттың бір бұрышын тең үш бұрышқа бөліңіз.
Бұл мәселені оригами әдісі арқылы шешкен кезде, оригамиде қолданылатын кейбір шарттылықтарды білу қажет. Олар келесі кестеде көрсетілген:
![]()
«Аңғар», «өзіне қарай» қатпар
сызығы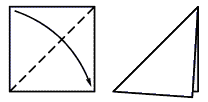
![]()
«Алқап», «өзіне қарай» бүктелген
көрсеткі![]()
Белгіленген нүктелерді
туралаңыз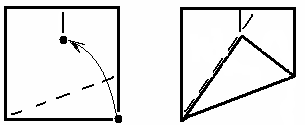
![]()
Созу және иілу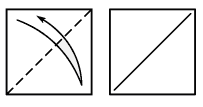
Оригами ерітіндісі
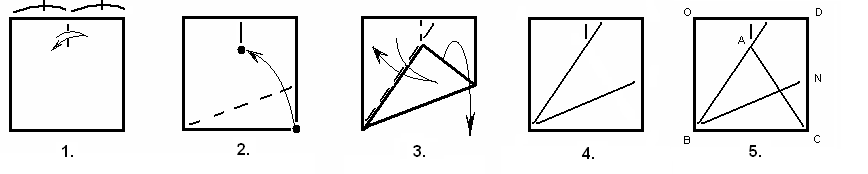
1. Квадраттың жоғарғы жағын екіге бөлетін бүктеме салыңыз.
2. Квадраттың оң жақ төменгі бұрышының жоғарғы жағын белгіленген бү
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Ғылыми жоба "Қағаз қимасының математикасы"
Ғылыми жоба "Қағаз қимасының математикасы"
Кіріспе
«Үлкен алаңда бұрыш жоқ»
Лао-цзы
Oригами - бұл таңғажайып көңілді тәжірибе. Бала кезімде мені осы ерекше фигуралар қызықтырды, оларды ойында да қолдануға болады. Ол кезде біз геометрия ғылымын білмейтін едік. Тиісінше, біз осындай әртүрлі қағаздан жасалған ойыншықтарды жинау ережелері туралы ойлаған жоқпыз.
Оригамиді геометрия туралы білімді және математикалық есептеулерді қолдану арқылы жасауға болады екен.
Жұмыстың мақсаты: оригами мен математиканың сәндік-қолданбалы өнері арасындағы байланысты анықтау.
Тапсырмалар:
1. оригами тарихын зерттеу;
2. оригами мен бүктеу техникасының негізгі формаларын сипаттау;
3. оригами мен математиканың өзара байланысын анықтау және дәлелдеу, оригаметрияны сипаттау;
4. қағаз фигураларын жасауға көмектесетін практикалық мәселелерді шешу.
Нысан – оригамеметрия.
Зерттеу пәні: оригами техникасы.
Гипотеза: оригами сабағы жазықтық пен кеңістіктік геометрияның практикалық дамуына ықпал етеді.
Зерттеу әдістері:талдау, синтез, салыстыру, модельдеу.
I тарау. Оригами техникасы сәндік-қолданбалы өнердің бір түрі ретінде
1.1. Оригами тарихы
Көптеген адамдар «оригами» сөзін естігенде таң қалады. «Ал бұл не?» Олар сұрайды. Сонымен қатар, әрбір адам өмірінде кем дегенде бір рет төртбұрышты қағаздан ең қарапайым өнімді - қайықты немесе ұшақты жасады. Дүкендерде сабан шляпалар мен панамаларды мұндай таңдау болмаған кезде, адамдар жазда өздерін газеттен «қақпақ» жасайтын. Қағаз қайықтары да, қалпақшасы да оригами қағидасына сәйкес жасалған.
Оригами - Жапонияда кеңінен таралған қағаздан жасалған көлемді және жалпақ фигуралардың әр түрін бүктеудің ежелгі қытайлық өнері.
Қағаз үлгілерін жасау өнері Қытайда біздің дәуіріміздің 1 - 2 ғасырлар тоғысында пайда болып, 6 ғасырға қарай Жапонияға жетіп, жаңа өмір тапты.
Бұл оригами өнері бүкіл жапон мәдениетінің ажырамас бөлігіне айналды.
Жапондық дәстүрлер бойынша қағаз модельдері құстардың, жануарлардың немесе гүлдердің формаларын берудегі шынайылық үшін емес, ішкі сезім, табиғаттың белгілі бір жаратылысына тән «рух» сезімі үшін бағаланды. Бұл сезім қағаз парағындағы бірнеше бүктемелермен жеткізілді.
Хейя дәуірінде (794-1185) оригами оның маңызды бөлігіне айналды ең жоғары жапон қоғамы арасында қабылданған рәсімдер. Самурай «ауыртпалықтар» деп аталып, олардан жасалған оригами тұмарларын жасады
акула терісінің
жолақтары немесе кептірілген ет талшықтары қосылған
қағаз.
Мұндай тұмарлар
самурайды қорғау және оған жеңіс әкелу үшін жасалған. Шыныаяқтарды
оригами қағаздан жасалған мүсіншелермен безендірген шай
басқарушылар өз қолөнерінің құпияларын мұқият сақтады. Олардың
оригамиі фигураны жайып салғаннан кейін оны бұрынғы қалпына
келтіру, басқаша айтқанда, оның жасалу құпиясына ену мүмкін
болмайтындай етіп қалыптасты. Сонымен қатар, жаңадан бүктелген
фигура жаңаға ие болуы керек еді. Бүктемелер, және олардың ойынша
шеберлер өздерінің оригами құпиясында біреу екенін анықтай алады,
содан кейін тырысты.
Оригами өз атын жапонның «ори» - бүктеу және «гами» - қағаз сөздерінен алды. Сөздіктерден кейде оригамидің қағаздан құстар мен жануарлардың бейнелерін жасау өнері ретінде анықтамасын кездестіруге болады. Бұл қысқа фазаның сипаттамасы біздің балалық шақ туралы естеліктер оятады: қағаз ұшақтар, жәрмеңке алаңында жанып тұрған шамдар. Алайда, оригамиге деген шынайы қызығушылық Еуропада және Америкада осы ежелгі өнер бірінші көзқараста көрінгеннен әлдеқайда терең екендігі белгілі болған кезде ғана пайда болды. Ақыр соңында, қарапайым қағаз парағынан алынған оригамидің көмегімен сіз ең керемет нәрселерді жасай аласыз!
Нағыз оригами өнері тек қағазбен ғана шектелмейді. Қазіргі уақытта көптеген оригами әуесқойлары батылдықпен жаңа материалдармен тәжірибе жасау, модель құрудың жаңа тәсілдерін іздеу және табу . Мысалы, американдық Лэйн Аллен оригамидің «оригами» деп аталатын жаңа тармағын құрды. Ол өз модельдерін металлдалған дәкенің бүктелген парақтарынан жасайды. Бұл материалда дәстүрлі оригами материалынан - қағаздан екі түбегейлі айырмашылық бар. Біріншіден, ол пішінді қатаң ұстайды, екіншіден, оның иілуін тегіс етіп жасауға болады.
Бұл оригамиді сүйетіндер үшін жаңа мүмкіндіктер ашады. Тағы бір американдық Джереми Шефер одан да алға жылжып, өз модельдерін металл фольгадан жасайды, сондықтан оның қайықтарын ылғалданудан қорықпай жіберуге болады. Англиядан келген Дэвид Брилл барлық оригами білгірлерін өз модельдерін бос бөтелкелерге салып таң қалдырды.
Қазіргі кезде бүкіл әлемде көптеген адамдар оригами өнеріне тәуелді. Қағаз фигураларын балалар мен ересектер, суретшілер мен дизайнерлер жасайды. Бұл тіпті мектептерде оқытылады, бұл туралы кітаптар жазылады және журналдар қызықты мақалалармен және әртүрлі модельдердің сипаттамаларымен шығарылады.
Біздің уақытымызда оригами тек ойыншық емес. Бұл өнерге ғалымдар мен дизайнерлер қызығушылық таныта бастады. Оригами бойынша ғылыми симпозиумдар өткізілуде. Қазірдің өзінде ең күрделі техникалық құрылымдар - қағаз үлгілері жасалуда.
Бірақ балалар, әрине, оригамиді жаңа ойыншық жасау мүмкіндігі ретінде қызықтырады. Сіз өзіңіздің көлемді қағаздан жаңа, жеке фигуралар жасай аласыз.
1.2 Оригами формалары
Ежелгі дәуірден бастап жапондық оригамиде негізгі болып саналатын кейбір формалары болған. Бұл кейіннен жүздеген вариациялар жасауға болатын стандартты, оңай танылатын бланкілер. Барлық осы негізгі модельдер сізге таныс болуы керек, және сіз олардың әрқайсысының бүктемелері мен кезектілігін біле отырып, әрбір негізгі бланкті автоматты түрде жасауыңыз керек. Негізгі формаларды игере отырып, сіз классикалық модельдерді ғана емес, сонымен қатар өзіңіздің модельдеріңізді де сәтті қоса аласыз.
Жұмыстың алғашқы кезеңдерінде квадрат парақты бірнеше тәсілмен бүктеуге болады. Олардың көпшілігі жоқ - он бір, және әрқайсысының өз атауы бар. Міне олар:
Қарапайым:

Үшбұрыш кітап есік батпырауық
Орташа:

Ромб балық үшбұрыштар квадра
Күрделі:

Үйшік құс қайық бақа
Кез-келген оригами фигурасы белгілі бір өлшемдегі квадрат парақтардан тұрады (егер сіз схемада өзгеше көрсетілмесе, өлшемді өз қалауыңыз бойынша таңдайсыз). Бастапқы кезеңдегі барлық негізгі формалар дәл осылай бүктелген. Үшбұрыштан негізгі «үшбұрыш», «құймақ», «балық», «батпырауық» сияқты негізгі пішіндер алынады. Қос квадрат төртбұрыштан, «құстан» және «бақадан» жасалады. Тік бұрышты «кітап» пішінінен «үй», «есік» және «катамаран» алынады.
Осы пішіндерді көріп, біз оригами көмегімен келесі түсініктерді қайталауға болатындығын түсінеміз:
– көлденең, тік, қиғаш сызықтар;
– квадратты әртүрлі тәсілдермен бүктеу, көршілес жақтарын, диагональдарын көрсету;
– квадраттар;
– барлық үшбұрыштар.
Классикалық техниканы игере отырып, сіз модульдік оригамиден бастауға болады. Бұл техникалардың арасындағы түбегейлі айырмашылықтар - классикалық фигуралар тегіс және бір парақтан бүктелген, ал модульдік оригами жасау үшін үш өлшемді фигураға айнала отырып, бір-біріне енгізілген бірдей қағаз бөліктерінің (модульдердің) белгілі бір саны қажет. Тегіс оригамиді бір жақты оригами деп те атайды: объект тек бір жағында ғана анықталады. Әдетте мұндай өнімдер аппликация жұмысында қолданылады.
Модульдік (көлемдік) оригами неғұрлым күрделі және көп уақытты қажет етеді, бірақ бұл техникада сіз тұтас қағаздан жасалған мүсіндер, сонымен қатар күнделікті өмірде қолдануға және сыйлық ретінде ұсынуға болатын әр түрлі пайдалы заттарды жасай аласыз: қораптар, ұсақ-түйек заттарға арналған стендтер, қораптар, вазалар.
Модульдік оригами түрлерінің бірі - кусудама техникасы - конус тәрізді қағаздың белгілі бір санынан сфералық пішіндерді бүктеу. Көптеген оригамистер кусудаманы түбегейлі өзгеше әдіс деп санайды, өйткені бөлшектерді тігу көбінесе фигураларды жасау және құрастыру үшін қолданылады. Кусудаманы игере отырып, сіз өзіңіздің үйіңізді фантастикалық әдемі гүл композицияларымен безендіре аласыз, оған қарап олардың қағаздан жиналғанына сену қиын. Оригами принципінің жалпы негізі екі өлшемді затты үш өлшемді затқа айналдыру болып табылады.
II тарау. Оригами мен математиканың байланысы
2.1. Математикті оригами жасау үшін қолдану
Осы өнермен алғашқы танысу кезінде біз тіктөртбұрыш және үшбұрыш сияқты қарапайым пішіндер туралы білеміз. Қарапайым пішінді қосқанда, біз квадратпен танысамыз, оның бұрыштары ортасына қарай иіліп, квадрат төрт бірдей үшбұрыштан тұруы мүмкін екенін көруге болады. «Батпырауық» пішінін бүктеп, біз ромбпен танысамыз. Оригами алфавиті нүкте мен сызық сияқты геометриялық түсініктерді қамтиды.
Осылайша, оригами мен математика (атап айтқанда геометрия) бір-бірімен тығыз байланысты. Математикадан көптеген ұғымдарды (мысалы, нүкте, түзу, квадрат, тіктөртбұрыш, үшбұрыш) оригами жасау кезінде қолданамыз.
Инженер, математик және суретші болмай-ақ, сіз әдістің барлық тапқыр қарапайымдылығын түсіне алмайсыз, соның арқасында оригами шеберінің қолындағы тегіс бет күрделі кеңістіктік құрылымға айналуы мүмкін. Қағаздың оңай бүктелуіне, кесілуіне және желімделуіне арналған жоғары қасиеттерін ескере отырып, бұл материал архитектуралық орналасу және декоративті модельдеу үшін бұрыннан қолданылып келеді. Шынында да, өнімнің немесе құрылымның прототипін жасамас бұрын, алдымен қағаздан модель жасау әлдеқайда оңай. Сол себепті қағаз шаблондарды, өрнектер мен трафареттерді жасауда қолданылады. Тұлпарларды кесіп тастауды, коллаждар мен аппликацияларды осы материалсыз елестету қиынға соғады.
Оригами өнері, керісінше, кесу, желімдеу және одан да беткей созуды мүлдем жоққа шығарады. Классикалық оригамидегі барлық ықтимал әдістердің тек иілуіне және бүктелуіне жол беріледі. Бұл шектеу форманы модельдеу міндетін шексіз қиындатады, бірақ, екінші жағынан, шеберді өзі үшін күтпеген жерден онымен жұмыс істеудің барлық басқа тәсілдерінде талап етілмеген материалдың осындай мүмкіндіктерін ашуға мәжбүр етеді.
Бірақ, өкінішке орай, тіпті оригамиді білетіндер бұл туралы үнемі ойлана бермейді. Әдетте, бүктеу, ең алдымен, нәзік қолөнер, фигуралардың белгілі конструкцияларының схемалары бойынша қайталау немесе жаңаларын ойлап табу ретінде қарастырылады.
Оригами туралы математикалық түсінік бетті материалдан абстракциялауға мүмкіндік беретіні және парақтың топологиялық бүктелген түрлендірулерін беттің құрылымдық негізделген бөліктерін енгізу және оның түсінігін кеңістіктен, қисыққа, жабық көлемнің қабығына, үш өлшемді құрылымға және т.б. кеңейту арқылы толықтыруға болатындығы айқын болды.
Ресейде Михаил Максимович Литвинов «оригами» тұжырымдамасын тұжырымдап қана қоймай, сонымен бірге Ресейдегі пікірлес адамдардың жаңа қозғалысын көрсетіп, үйретіп, құрды, оларды кейіннен Мәскеудегі Оригами клубына айналдырған Оригами өнер және оқу орталығының айналасына біріктірді.
Осылайша, жазықсыз ойын мен қолөнерден шыққан оригами интеллектуалды кәсіпке айналды, оның жаппай ынта-жігері ғылыми және көркем шығармашылыққа бағытталды. Оригами үшінші мыңжылдықтың заманауи мәдениетімен және технологияларымен біртіндеп араласа бастады.
Классикалық оригами бойынша, бүктелудің нысаны - кесектерсіз, белгіленбеген квадрат парақ.
Математикалық тұрғыдан алғанда, оригамистің мақсаты - соңғы нысанды қалыптастыру үшін қажетті бүктемелерді анықтайтын парақтағы бір немесе бірнеше нүктелердің орнын дәл анықтау. Бүктеу процесі келесі ережелерге сәйкес нақты анықталған әрекеттер тізбегін орындауды қамтиды:
-
Жол парақтың шетімен немесе қағаздың бүктелген сызығымен анықталады.
-
Нүктелер сызықтардың қиылысуымен анықталады.
-
Барлық қатпарлар туралау арқылы бірегей анықталады
-
парақтың әртүрлі элементтері - сызықтар немесе нүктелер.
-
Қатпар бір бүктеме арқылы пайда болады, ал бүктеу нәтижесінде фигура тегіс болып қалады.
Соңғы нүкте бүктеуді қатаң түрде шектейді, бір уақытта бір бүктеуге мүмкіндік береді. Іс жүзінде, ең қарапайым оригами модельдері де бір операцияда бірнеше қатпар жасауды көздейді.
Оригами фигураларын бүктеу барысында біз әртүрлі геометриялық фигуралармен танысамыз: үшбұрыш, квадрат, трапеция және т.с.с., біз кеңістікте және қағаз парағында оңай шарлауды, тұтас бөліктерге бөлуді, тік, көлденең, диагональды табуды үйренеміз, одан да көп нәрсені білеміз геометрия мен математикаға қатысты. ХІХ ғасырдың ортасында американдық ағартушы Ф.Фребел оригамидің геометриялық ерекшелігін байқап, оны мектеп пәні ретінде енгізді.
Мысалы, ол геометрия негіздерін циркуль, сызғыш және кейбір ұғымдардың көмегімен емес, қағаз фигураларын бүктеу мысалында оқып үйренуді ұсынды. Ол оригамиді педагогикалық процеске белсенді түрде енгізді. Өкінішке орай, ол кезде Фребель фигураларды бүгу техникасын дәл қазіргідей меңгерген емес.
Оригами теориясында математиканың көмегімен дәлелденетін ережелер, заңдылықтар бар, ал үш өлшемді денелердің жалпы қасиеттерін арнайы математика ғылымы - топология зерттейді.
2.2. Оригамидің практикалық тапсырмалары
Табиғатта барлығы симметриялы болады. Ал оригамидің өзінде: парақтың екі жағы бар; квадрат - бұрыштар мен қабырғалардың екі жұбы, екі симметрия осі.
Барлық негізгі оригами пішіндерін бүктеуге, содан кейін топтастыруға және квадраттың екі симметрия осі бойымен орналастыруға болады. Мұны қарапайым мысалдармен қалай жасауға болатынын көрейік:
-
Қағаз квадратын симметрия осі бойымен өзіңізге қарай бүктеңіз. Негізгі «Үшбұрыш» пішіні алынды.
-
Қағаз квадратын симметрия осі бойымен өзіңізге қарай бүктеңіз. Негізгі «Тіктөртбұрыш» формасы шықты
-
Қағаздың төртбұрышын өзіңізге қарай бүктеңіз, оның оң және сол жақ төменгі жақтары симметрия осімен сәйкес келеді. Негізгі формасы «Батпырауық» алынды.
-
Қағаз квадратын өзіңізге қарай бүктеңіз, оның оң және сол жағы симметрия осімен сәйкес келеді. «Есік» негізгі формасы алынды.
Математика сабағында оригамиді келесі тапсырмаларда қолдануға болады: а) көлденең, тік, қиғаш сызықтарды табу; б) барлық квадраттарды табу; в) барлық үшбұрыштарды табу; г) кескіндерді атаңыз; в) төртбұрышты, көршілес жақтарын, диагональды бүктеу.
Мысалы, бірнеше мәселені шешейік:
1-мақсат.
Тік бұрышты бөлу
Бұрышты 30 немесе 60 градусқа
кешіктіру қиындық тудырмайды. Квадраттың бүйіріне тең бүйірлі
үшбұрыш салу жеткілікті. Ол үшін алдымен тік бүктелген квадратты
екі тең төртбұрышқа бөлу керек. Содан кейін біз квадраттың бұрышын
белгіленген сызыққа жеткізетін бүктемені
саламыз. 
Мақсат 2.
Оригами әдісін қолдана отырып, квадраттың бір бұрышын тең үш бұрышқа бөліңіз.
Бұл мәселені оригами әдісі арқылы шешкен кезде, оригамиде қолданылатын кейбір шарттылықтарды білу қажет. Олар келесі кестеде көрсетілген:
![]()
«Аңғар», «өзіне қарай» қатпар
сызығы
![]()
«Алқап», «өзіне қарай» бүктелген
көрсеткі![]()
Белгіленген нүктелерді
туралаңыз
![]()
Созу және иілу
Оригами ерітіндісі

1. Квадраттың жоғарғы жағын екіге бөлетін бүктеме салыңыз.
2. Квадраттың оң жақ төменгі бұрышының жоғарғы жағын белгіленген бү

шағым қалдыра аласыз















