
Геометриялық және физикалық есептерде интегралды қолдану
Геометрия мен физика
курстарында анықталған интегралдың кейбір қолдануларын
қарастырайық.  анықталған интегралы
жоғарыдан
анықталған интегралы
жоғарыдан  функциясының графигімен,
төменгі жағынан Ох
осіне
тиісті
функциясының графигімен,
төменгі жағынан Ох
осіне
тиісті  кесіндісімен, ал екі
жағынан
кесіндісімен, ал екі
жағынан  =а,
=а,  =
= түзулерімен
шектелгенқисықсызықты трапецияның ауданын беретінін
білеміз.
түзулерімен
шектелгенқисықсызықты трапецияның ауданын беретінін
білеміз.
Кейбір жағдайларда жоғарыдан да, төменнен де әртүрлі функциялардың графиктерімен (әртүрлі қисықтар) шектелген жазық фигураның ауданын табуға тура келеді.
Жазық фигураның ауданын
кескіндеу үшін жоғарыдан  функциясының графигімен
шектелген қисықсызықты трапецияның ауданынан
жоғарыдан
функциясының графигімен
шектелген қисықсызықты трапецияның ауданынан
жоғарыдан  функциясының графигімен
шектелген қисықсызықты трапецияның ауданын азайту
керек.
функциясының графигімен
шектелген қисықсызықты трапецияның ауданын азайту
керек.
Сонда ізделінді ауданды былай табамыз:


Кейбір дербес жағдайларда
Ох
осіне
параллель  түзулерімен,
түзулерімен,  =0 түзуі және бір бүйір жағынан
қисықпен
=0 түзуі және бір бүйір жағынан
қисықпен =
= (у) функциясының графигімен)
шектелген фигураның ауданын есептеу қажет
болады.
(у) функциясының графигімен)
шектелген фигураның ауданын есептеу қажет
болады.
Мұндай фигураның ауданы

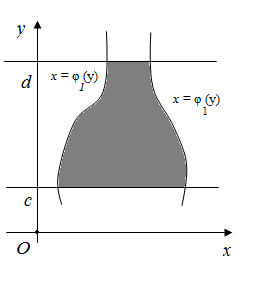
Сурет – 13.
Мысал – 1.11y=x3+1 қисығымен,y=2 түзуіменOyосімен шектелген фигураның ауданын табайық( 1 – сурет)
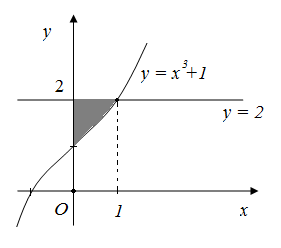
Сурет - 14
Шешуі. Берілген жазық фигураның ауданын (1.6) формула бойынша есептейміз:

Мысал –
1.12 түзулерімен және Ох
осімен шектелген фигураның ауданын
есептейік(15–сурет).
түзулерімен және Ох
осімен шектелген фигураның ауданын
есептейік(15–сурет).
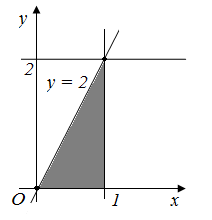
Сурет – 15
Шешуі: Берілген үшбұрыштың ауданын (1.6) формуланың көмегімен табамыз:

Тура осындай қорытындыны
үшбұрыштың ауданын есептеу формуласы
 арқылы да алуға
болады. Бұл жағдайда
арқылы да алуға
болады. Бұл жағдайда  Демек,
Демек,

Мысал –
1.13 интегралы түрінде
берілген функцияның графигімен және
интегралы түрінде
берілген функцияның графигімен және  түзуімен шектелген
фигураның ауданын табайық.
түзуімен шектелген
фигураның ауданын табайық.
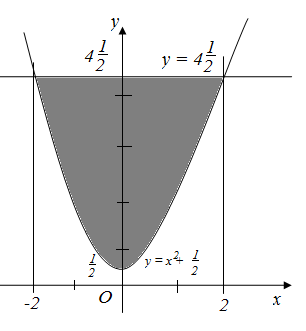
Сурет - 16
Шешуі. Алдымен интегралды табайық:

Сонымен, есепті
шығару  параболасы
және
параболасы
және  түзуімен шектелген
фигураның ауданын табуға
әкеледі.
түзуімен шектелген
фигураның ауданын табуға
әкеледі.
Алдымен интегралдау шектерін
табайық. Ол үшін  теңдеуін шешеміз.
Теңдеудің түбірлері
теңдеуін шешеміз.
Теңдеудің түбірлері 
Берілген жазық фигура Оу осіне
қарағанда симметриялы. Сондықтан қисықсызықты трапецияның
ауданын  кесіндісінде еспетеп,
екіге көбейтсе жеткілікті.
кесіндісінде еспетеп,
екіге көбейтсе жеткілікті.

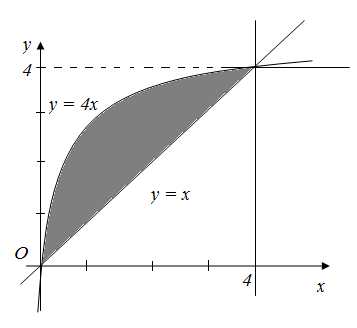
Мысал –
1.14 параболасы
және у=х түзуімен шектелгенфигураның
ауданын есептейік(
17–сурет)
параболасы
және у=х түзуімен шектелгенфигураның
ауданын есептейік(
17–сурет)
Сурет - 17
Шешуі. Берілген қисықтармен шектелген жазық фигураның ауданын есептеу. Осы жазық фигураның ауданын есептеу үшін алдымен берілген парабола мен түзудің қиылысқан нүктелерінің координаталарын табайық. Ол үшін екі теңдеуден тұратын теңдеулер жүйесін шешеміз:
 немесе
немесе  осыдан
осыдан 
Демек, ізделінді фигураның ауданын (1.6) формула бойынша анықтаймыз:

Мысал –
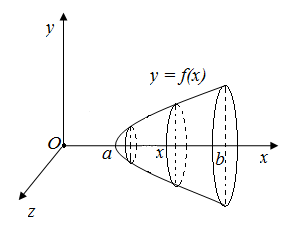
1.15Айналу денесінің көлемін табу
үшін интегралдың қолданылуын қарастырайық. Ол
үшін  кесіндісінде
үзіліссіз
кесіндісінде
үзіліссіз  функциясының графигімен
шектелген қисықсызықты трапеция берілсін(18 –
сурет)
функциясының графигімен
шектелген қисықсызықты трапеция берілсін(18 –
сурет)
Сурет – 18
Осы қисықсызықты трапецияны Ох осінен айналдырғанда пайда болған геометриялық көлемін табу керек болсын.
 кесіндісінің бойынан кез
келген х
нүктесін алайық. Егер осы
нүкте арқылы Ох осіне перпендикуляр жазықтық жүргізсек, онда
жазықтық айналу денесін дөңгелек бойымен қиып өтеді (яғни қимада
дөңгелек пайда болады). Ал шыққан дөңгелектің
радиусы у-ке тең. Демек, қиманың
ауданы Q(x)=πy2.
кесіндісінің бойынан кез
келген х
нүктесін алайық. Егер осы
нүкте арқылы Ох осіне перпендикуляр жазықтық жүргізсек, онда
жазықтық айналу денесін дөңгелек бойымен қиып өтеді (яғни қимада
дөңгелек пайда болады). Ал шыққан дөңгелектің
радиусы у-ке тең. Демек, қиманың
ауданы Q(x)=πy2.
Енді айналу денесінің көлемін табу үшін а– дан b– ға дейінгі аралықта Q(x)=πy2
Функциясының интегралын есептесек жеткілікті, яғни
 (1.9)
(1.9)
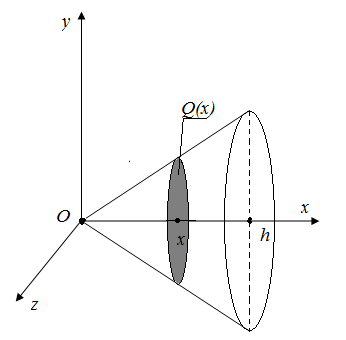
Мысал – 1.16 Табан ауданы Р – ға, биіктігі һ – қа тең конустың көлемін есептейік.
Шешуі. Конустың төбесін координаталар басына сәйкес етіп, биіктігін Ох осі бойымен бағыттайық(19 – сурет)
Сурет - 19
Кез келген х нүктесі арқылы Ох осіне перпендикуляр жазықтық жүргіземіз. Ол жазықтық конустан ауданы Q(x) болатын дөңгелекті қиып өтеді.
Конустың параллель қималарының
аудандары осы қималардан конустың төбесіне дейінгі қашықтықтардың
квадраттарының қатынасына тең екені геометрия курсынан белгілі,
яғни  ,
мұндағы Q(x)- конустың х нүктесі арқылы Ох
осіне перпендикуляр жазықтықпен қимасының ауданы, Р – конус
табанының ауданы, һ – конустың биіктігі, х шамасы х нүктесі арқылы
өтетін қимадан конустың төбесіне дейінгі
қашықтық.
,
мұндағы Q(x)- конустың х нүктесі арқылы Ох
осіне перпендикуляр жазықтықпен қимасының ауданы, Р – конус
табанының ауданы, һ – конустың биіктігі, х шамасы х нүктесі арқылы
өтетін қимадан конустың төбесіне дейінгі
қашықтық.
Соңғы
теңдіктен  шығады.
шығады.
Енді интеграл көмегімен конустың көлемін еспетейік:

Сонымен,
 конустың көлемін
есептеу формуласын алдық. Анықталған интегралдың физикалық
есептерді шығаруға қолданылуын
қарастырайық.
конустың көлемін
есептеу формуласын алдық. Анықталған интегралдың физикалық
есептерді шығаруға қолданылуын
қарастырайық.
Материялық нүктенің жылдамдығы оның жүрген s жолынан t уақыт бойынша алынған туынды, яғни v=s'(t), ал үдеу жылдамдықтан t уақыт бойынша алынған туынды, яғни а=s'(t) екені 10 – сыныптың физика мен алгебра және анализ бастамалары курсынан белгілі.
Берілген туынды (жылдамдықтың туындысы) бойынша дененің жүрген жолын анықтау керек болса, онда Ньютон-Лейбниц формуласын қолданып, мына теңдікті аламыз:

немесе
 (1.10)
(1.10)
мұндағы

Тура осылай туындысы бойынша (үдеуден) жылдамдықтың шамасын да анықтауға болады:

немесе

Мұнда
 бастапқы жылдамдықты
анықтайды және
бастапқы жылдамдықты
анықтайды және  арқылы белгіленеді.
Сондықтан соңғы теңдік былай
жазылады:
арқылы белгіленеді.
Сондықтан соңғы теңдік былай
жазылады:

(1.11) формула арқылы материялық нүктенің үдеуі бойынша жылдамдықты білсек, (1.10) формула арқылы материялық нүктенің жүрген жолын анықтауға болады.
Мысал –
1.17 Жылдамдығы  заңдылығымен өзгерген,
материялық нүктенің
заңдылығымен өзгерген,
материялық нүктенің  -ке дейінгі уақыт
аралығында жүрген жолын
анықтайық.
-ке дейінгі уақыт
аралығында жүрген жолын
анықтайық.
Шешуі. Есепті шығару үшін (1.10) формуланы қолданамыз. Сонда

Есептің берілгені
бойынша  (яғни
(яғни  ),
сондықтан
),
сондықтан 
Мысал – 1.18Табаны а-ға, биіктігі һ-қа тең, бір төбесі төмен бағытталған үшбұрыш пішінді пластина берілген. Осы пластинаға (пластинаның табаны судың бетінде орналасқан) жіберілген судың қысымын табайық.
Шешуі. тереңдікте орналасқан
биіктігі шексіз аз
тереңдікте орналасқан
биіктігі шексіз аз 

Демек, жолақтың
ауданы  Ал оған жіберілген судың
қысымы
Ал оған жіберілген судың
қысымы 
Барлық пластинаға жіберілген
судың қысымын табу үшін  –ны
–ны

Сонда,

Демек, пластинаға жіберілген
судың қысымы 
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
"интегралдың геометрияда қолданылуы"
"интегралдың геометрияда қолданылуы"
Геометриялық және физикалық есептерде интегралды қолдану
Геометрия мен физика
курстарында анықталған интегралдың кейбір қолдануларын
қарастырайық.  анықталған интегралы
жоғарыдан
анықталған интегралы
жоғарыдан  функциясының графигімен,
төменгі жағынан Ох
осіне
тиісті
функциясының графигімен,
төменгі жағынан Ох
осіне
тиісті  кесіндісімен, ал екі
жағынан
кесіндісімен, ал екі
жағынан  =а,
=а,  =
= түзулерімен
шектелгенқисықсызықты трапецияның ауданын беретінін
білеміз.
түзулерімен
шектелгенқисықсызықты трапецияның ауданын беретінін
білеміз.
Кейбір жағдайларда жоғарыдан да, төменнен де әртүрлі функциялардың графиктерімен (әртүрлі қисықтар) шектелген жазық фигураның ауданын табуға тура келеді.
Жазық фигураның ауданын
кескіндеу үшін жоғарыдан  функциясының графигімен
шектелген қисықсызықты трапецияның ауданынан
жоғарыдан
функциясының графигімен
шектелген қисықсызықты трапецияның ауданынан
жоғарыдан  функциясының графигімен
шектелген қисықсызықты трапецияның ауданын азайту
керек.
функциясының графигімен
шектелген қисықсызықты трапецияның ауданын азайту
керек.
Сонда ізделінді ауданды былай табамыз:


Кейбір дербес жағдайларда
Ох
осіне
параллель  түзулерімен,
түзулерімен,  =0 түзуі және бір бүйір жағынан
қисықпен
=0 түзуі және бір бүйір жағынан
қисықпен =
= (у) функциясының графигімен)
шектелген фигураның ауданын есептеу қажет
болады.
(у) функциясының графигімен)
шектелген фигураның ауданын есептеу қажет
болады.
Мұндай фигураның ауданы


Сурет – 13.
Мысал – 1.11y=x3+1 қисығымен,y=2 түзуіменOyосімен шектелген фигураның ауданын табайық( 1 – сурет)
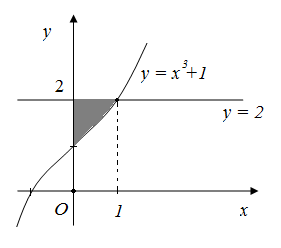
Сурет - 14
Шешуі. Берілген жазық фигураның ауданын (1.6) формула бойынша есептейміз:

Мысал –
1.12 түзулерімен және Ох
осімен шектелген фигураның ауданын
есептейік(15–сурет).
түзулерімен және Ох
осімен шектелген фигураның ауданын
есептейік(15–сурет).
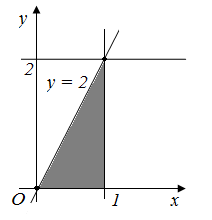
Сурет – 15
Шешуі: Берілген үшбұрыштың ауданын (1.6) формуланың көмегімен табамыз:

Тура осындай қорытындыны
үшбұрыштың ауданын есептеу формуласы
 арқылы да алуға
болады. Бұл жағдайда
арқылы да алуға
болады. Бұл жағдайда  Демек,
Демек,

Мысал –
1.13 интегралы түрінде
берілген функцияның графигімен және
интегралы түрінде
берілген функцияның графигімен және  түзуімен шектелген
фигураның ауданын табайық.
түзуімен шектелген
фигураның ауданын табайық.

Сурет - 16
Шешуі. Алдымен интегралды табайық:

Сонымен, есепті
шығару  параболасы
және
параболасы
және  түзуімен шектелген
фигураның ауданын табуға
әкеледі.
түзуімен шектелген
фигураның ауданын табуға
әкеледі.
Алдымен интегралдау шектерін
табайық. Ол үшін  теңдеуін шешеміз.
Теңдеудің түбірлері
теңдеуін шешеміз.
Теңдеудің түбірлері 
Берілген жазық фигура Оу осіне
қарағанда симметриялы. Сондықтан қисықсызықты трапецияның
ауданын  кесіндісінде еспетеп,
екіге көбейтсе жеткілікті.
кесіндісінде еспетеп,
екіге көбейтсе жеткілікті.

Мысал –
1.14 параболасы
және у=х түзуімен шектелгенфигураның
ауданын есептейік(
17–сурет)
параболасы
және у=х түзуімен шектелгенфигураның
ауданын есептейік(
17–сурет)

Сурет - 17
Шешуі. Берілген қисықтармен шектелген жазық фигураның ауданын есептеу. Осы жазық фигураның ауданын есептеу үшін алдымен берілген парабола мен түзудің қиылысқан нүктелерінің координаталарын табайық. Ол үшін екі теңдеуден тұратын теңдеулер жүйесін шешеміз:
 немесе
немесе  осыдан
осыдан 
Демек, ізделінді фигураның ауданын (1.6) формула бойынша анықтаймыз:

Мысал –
1.15Айналу денесінің көлемін табу
үшін интегралдың қолданылуын қарастырайық. Ол
үшін  кесіндісінде
үзіліссіз
кесіндісінде
үзіліссіз  функциясының графигімен
шектелген қисықсызықты трапеция берілсін(18 –
сурет)
функциясының графигімен
шектелген қисықсызықты трапеция берілсін(18 –
сурет)

Сурет – 18
Осы қисықсызықты трапецияны Ох осінен айналдырғанда пайда болған геометриялық көлемін табу керек болсын.
 кесіндісінің бойынан кез
келген х
нүктесін алайық. Егер осы
нүкте арқылы Ох осіне перпендикуляр жазықтық жүргізсек, онда
жазықтық айналу денесін дөңгелек бойымен қиып өтеді (яғни қимада
дөңгелек пайда болады). Ал шыққан дөңгелектің
радиусы у-ке тең. Демек, қиманың
ауданы Q(x)=πy2.
кесіндісінің бойынан кез
келген х
нүктесін алайық. Егер осы
нүкте арқылы Ох осіне перпендикуляр жазықтық жүргізсек, онда
жазықтық айналу денесін дөңгелек бойымен қиып өтеді (яғни қимада
дөңгелек пайда болады). Ал шыққан дөңгелектің
радиусы у-ке тең. Демек, қиманың
ауданы Q(x)=πy2.
Енді айналу денесінің көлемін табу үшін а– дан b– ға дейінгі аралықта Q(x)=πy2
Функциясының интегралын есептесек жеткілікті, яғни
 (1.9)
(1.9)
Мысал – 1.16 Табан ауданы Р – ға, биіктігі һ – қа тең конустың көлемін есептейік.
Шешуі. Конустың төбесін координаталар басына сәйкес етіп, биіктігін Ох осі бойымен бағыттайық(19 – сурет)

Сурет - 19
Кез келген х нүктесі арқылы Ох осіне перпендикуляр жазықтық жүргіземіз. Ол жазықтық конустан ауданы Q(x) болатын дөңгелекті қиып өтеді.
Конустың параллель қималарының
аудандары осы қималардан конустың төбесіне дейінгі қашықтықтардың
квадраттарының қатынасына тең екені геометрия курсынан белгілі,
яғни  ,
мұндағы Q(x)- конустың х нүктесі арқылы Ох
осіне перпендикуляр жазықтықпен қимасының ауданы, Р – конус
табанының ауданы, һ – конустың биіктігі, х шамасы х нүктесі арқылы
өтетін қимадан конустың төбесіне дейінгі
қашықтық.
,
мұндағы Q(x)- конустың х нүктесі арқылы Ох
осіне перпендикуляр жазықтықпен қимасының ауданы, Р – конус
табанының ауданы, һ – конустың биіктігі, х шамасы х нүктесі арқылы
өтетін қимадан конустың төбесіне дейінгі
қашықтық.
Соңғы
теңдіктен  шығады.
шығады.
Енді интеграл көмегімен конустың көлемін еспетейік:

Сонымен,
 конустың көлемін
есептеу формуласын алдық. Анықталған интегралдың физикалық
есептерді шығаруға қолданылуын
қарастырайық.
конустың көлемін
есептеу формуласын алдық. Анықталған интегралдың физикалық
есептерді шығаруға қолданылуын
қарастырайық.
Материялық нүктенің жылдамдығы оның жүрген s жолынан t уақыт бойынша алынған туынды, яғни v=s'(t), ал үдеу жылдамдықтан t уақыт бойынша алынған туынды, яғни а=s'(t) екені 10 – сыныптың физика мен алгебра және анализ бастамалары курсынан белгілі.
Берілген туынды (жылдамдықтың туындысы) бойынша дененің жүрген жолын анықтау керек болса, онда Ньютон-Лейбниц формуласын қолданып, мына теңдікті аламыз:

немесе
 (1.10)
(1.10)
мұндағы

Тура осылай туындысы бойынша (үдеуден) жылдамдықтың шамасын да анықтауға болады:

немесе

Мұнда
 бастапқы жылдамдықты
анықтайды және
бастапқы жылдамдықты
анықтайды және  арқылы белгіленеді.
Сондықтан соңғы теңдік былай
жазылады:
арқылы белгіленеді.
Сондықтан соңғы теңдік былай
жазылады:

(1.11) формула арқылы материялық нүктенің үдеуі бойынша жылдамдықты білсек, (1.10) формула арқылы материялық нүктенің жүрген жолын анықтауға болады.
Мысал –
1.17 Жылдамдығы  заңдылығымен өзгерген,
материялық нүктенің
заңдылығымен өзгерген,
материялық нүктенің  -ке дейінгі уақыт
аралығында жүрген жолын
анықтайық.
-ке дейінгі уақыт
аралығында жүрген жолын
анықтайық.
Шешуі. Есепті шығару үшін (1.10) формуланы қолданамыз. Сонда

Есептің берілгені
бойынша  (яғни
(яғни  ),
сондықтан
),
сондықтан 
Мысал – 1.18Табаны а-ға, биіктігі һ-қа тең, бір төбесі төмен бағытталған үшбұрыш пішінді пластина берілген. Осы пластинаға (пластинаның табаны судың бетінде орналасқан) жіберілген судың қысымын табайық.
Шешуі. тереңдікте орналасқан
биіктігі шексіз аз
тереңдікте орналасқан
биіктігі шексіз аз 

Демек, жолақтың
ауданы  Ал оған жіберілген судың
қысымы
Ал оған жіберілген судың
қысымы 
Барлық пластинаға жіберілген
судың қысымын табу үшін  –ны
–ны

Сонда,

Демек, пластинаға жіберілген
судың қысымы 

шағым қалдыра аласыз















