
ТҮРКІСТАН ОБЛЫСЫНЫҢ БІЛІМ БАСҚАРМАСЫ
Ғ.МҰРАТБАЕВ АТЫНДАҒЫ ЖЕТІСАЙ ГУМАНИТАРЛЫҚ-ТЕХНИКАЛЫҚ КОЛЛЕДЖІ
АШЫҚ САБАҚ
Тақырыбы: Жазық фигуралар аудандарын анықталған интегралдың көмегімен есептеу.
Оқытушы: Жакупова У.Т.
Хаттама № «___» «____» 2024ж
Кафедра меңгерушісі: _________
(қолы)
2024 ж
Ғ.Мұратбаев атындағы Жетісай гуманитарлық-техникалық колледжі
Оқу сабағының жоспары
Сабақтың тақырыбы: Жазық фигуралар аудандарын анықталған интегралдың көмегімен есептеу.
Модуль /пән атауы:Математика
Педагог: Жакупова Улжалгас Турапбаевна дайындады
2024 жылғы «14» ақпан.
Жалпы
мәліметтер
Курс, топ: 1-курс, РБ 23-9/1.2
Сабақ түрі: Тәжірибелік сабақ
2.Мақсаты, міндеттері:
Тақырыпты игере отырып, Жазық фигуралар аудандарын анықталған интегралдың көмегімен есептеу. Анықталған интегралдың қолданумен танысу. Есептер шығару
3.Күтілетін нәтижелер:
- Жазық фигуралар аудандарын анықтайды;
- Анықталған интегралдың қолдануды біледі;
- Оларға берілген есептерді шығара алады.
4.Қажетті ресурстар:
«Алгебра және анализ бастамалары» әдістемелік кешен 2012ж, шаршы, канверт,стикер,үлестірме қағаздар, панель т.б
5.Сабақтың барысы:
а) Ұйымдастыру.
ә) Үй тапсырмасын пысықтау
б) Жаңа материалды түсіндіру
в) Пысықтау жұмыстары
г) Сабақты бекіту
д) Қорытынды
Жағымды атмосфера қалыптастыру: «Кубизм» әдісі арқылы амандасу.

Топқа бөлу: « Пазыл» әдісі арқылы. Студенттер суреттерді құрастыру арқылы топқа бөлінеді.

Үй тапсырмасын пысықтау «Банкомат» әдісі. Студенттер картичканы банкоматқа салады, алатын соманы таңдайды сұраққа жауап береді , сол соманы шешіп алады.

-
500тг- Кез келген Х жиынында өзгеретін х үшін F´(x) = f(x), теңдігі орындалса, онда F(x) функциясы осы жиында f(x) функциясының ............... деп аталады.
алғашқы функциясы;
-
1000тг- Ньютон - Лейбниц формуласымен ...................есептейді
анықталған интеграл;
-
2000 тг- Берілген функция үшін алғашқы функцияның жалпы түрін жаз f(x) = 2
2х + С;
-
5000тг- F(в) -Ғ(а) айырманын у= f(x) үзіліссіз функциясының [а;в] кеіндісіндегі ................... деп аталады
анықталған интеграл
-
10000тг- Алғашқы функцияның жалпы түрін жазыңдар f(x) = 2Sin3x
-
-
20000тг- Есептеңіз:
 ;
;

-
30000тг- Есептеңіз:

 ;
;
-
40000тг- Есептеңіз:


Жаңа сабақ. « Баяндау» әдісі.


Жазық фигуралар аудандарын анықталған интегралдың көмегімен есептеу.
1. Анықталған интеграл арқылы қисық сызықты трапеция ауданы.
2. Анықталған интеграл арқылы жазық фигура ауданы.
Қисық сызықты трапецияның ауданы төмендегідей алгоритм бойынша есептелінеді:
-
Бір координаталық жазықтықта берілген сызықтардың графиктерін салу;
-
Фигураны OX осі бйымен шектелген кесіндісінің шеткі нүктелерін, яғни a және b-ның мәндерін анықтау;
-
f(x) функциясының алғашқы функциясын табу;
-
S=F(b)-F(a) формуласы бойынша қисықсызықты трапецияның ауданын есептеу.
[a;b] кесіндісінде үзілліссіз у=f(х) функциясы берілсін
-
[a;b] кесіндісінде у=f(х) функциясының графигімен және у=0 түзуімен
Шектелген фигураның ауданы
а) ![]() болғанда
болғанда
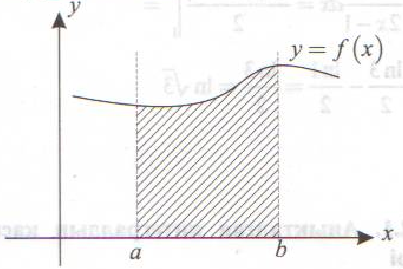
![]()
b) ![]() болғанда
болғанда

![]()
b)![]()
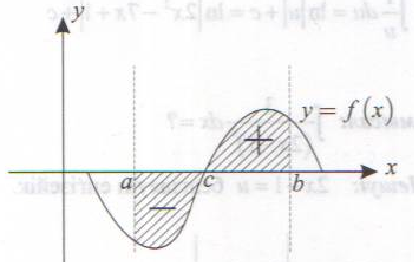
-
мысал.
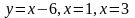 түзулерімен Ох
осімен шектелген фигураның
ауданын есептеңіз.
түзулерімен Ох
осімен шектелген фигураның
ауданын есептеңіз.
Шешуі:
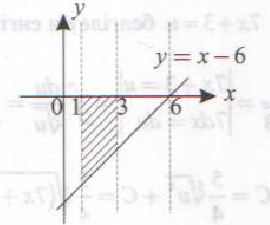
![]()
Жауабы: ![]() (ш.б)
(ш.б)
Егер ![]() үшін
үшін![]() функция үзілліссіз болса,
онда
функция үзілліссіз болса,
онда ![]() кесіндісінде
кесіндісінде ![]() (үстіңгі)
және
(үстіңгі)
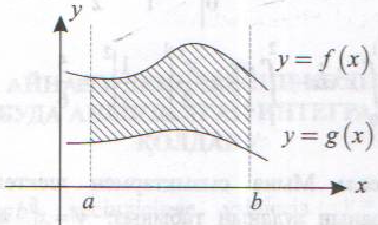
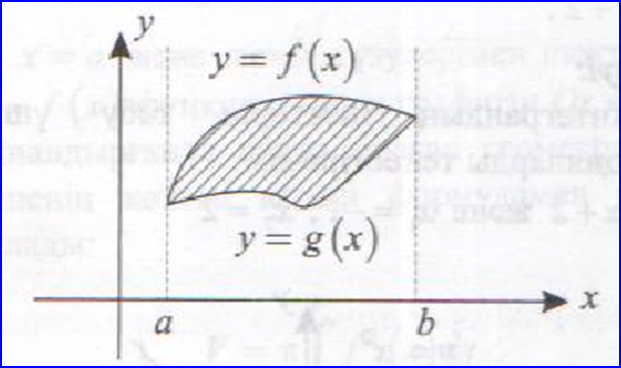
және ![]() (төменгі) функцияларының
графиктерімен шектелген фигураның ауданы:
(төменгі) функцияларының
графиктерімен шектелген фигураның ауданы:
![]()
Ескерту: Егер а және bшектері берілмесе, онда интегралдың шектері
f(x)=g(x) теңдеуінің түбірлері болады.
-
мысал.y = 4 –x2, y = x + 2 сызықтарымен және Ox осімен шектелген фигураның ауданын табыңыз.


Топтық жұмыс. «Айналмалы бекет» әдісі. Студенттер топта тапсырманы орындайды, сағат тілінің бағытымен тапсырманы шығару жолымен бөліседі. Басқа топтар кері байланыс береді.


Топ -1. Алғыр тобы
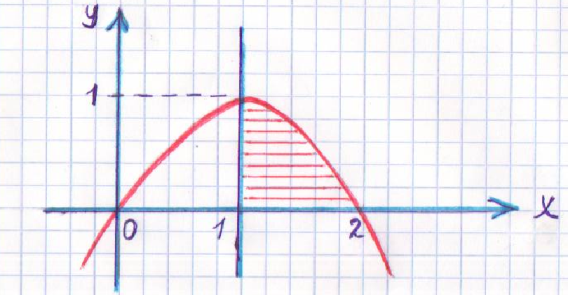
№1
![]() ,
, ![]() сызықтарыменшектелген (боялған)
фигура ауданын табыңыздар.
сызықтарыменшектелген (боялған)
фигура ауданын табыңыздар.
![]()
Жауабы: ![]() (ш.б)
(ш.б)
№ 2. y = -х2 + 4х - 4, y = 0, х = -1 және x = 4 сызықтарымен шектелген фигураның ауданын табыңыз.

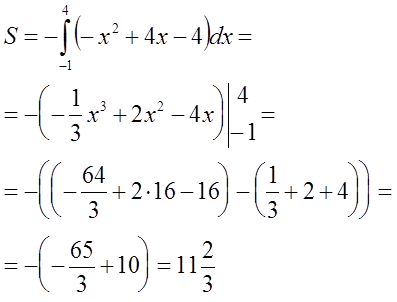
Топ -2. Тапқыр тобы.
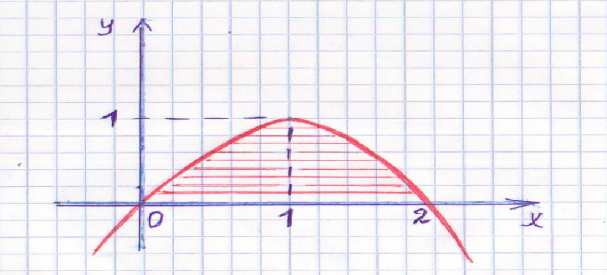
№1.
![]() ,
, ![]() сызықтарымен шектелген фигура
ауданын табыңыздар.
сызықтарымен шектелген фигура
ауданын табыңыздар.
![]()
Жауабы: ![]() (ш.б)
(ш.б)
№2. y = 9 – 0.5x2 параболасымен және x = -1, x = 2 түзулері мен Ox осі арқылы шектелген фигураның ауданын табыңыз.


Жауабы: 25.5 ед2
Сергіту сәті: Шапалақпен әннің ырғағына ілесу.

Сабақтың соңы: Суреттегі штрихталған фигуралардың қайсысы қисық трапеция болып табылады және қайсысы жоқ? « Ия, Жоқ»
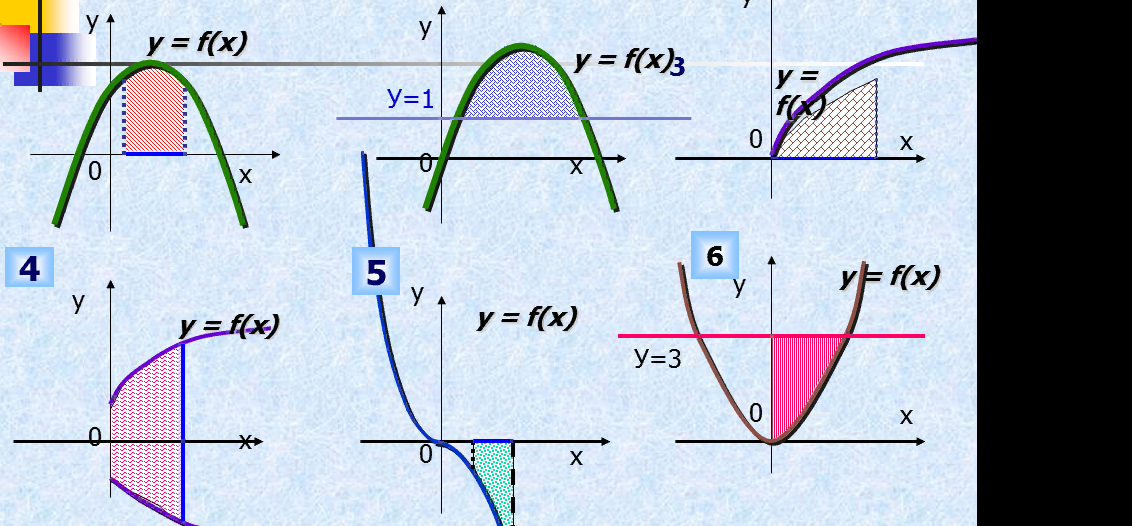
«Сиқырлы сандық» ойыны. Логикалық сұрақтарға жауап береді.

-
Ол сізге тиесілі, бірақ адамдар оны сізден жиі қолданады? (сіздің есіміңіз)
-
Жабық көзбен нені көруге болады? (түсті)
-
Алғашында төрт аяқты, кейін екіаяқты, сосын үш аяқты. Ол не? (бала)
-
Теңізде қандай тас болмайды? (құрғақ тас)
-
Адам аттан неге құлайды? (жерге)
-
Қаз, адам, қарақат. Үшеуін не байланыстырады?( а - әріпі)
-
Кім отырып жүреді? (шахматшы)
-
Қызыл теңізге ақ орамал салсақ не болады? (сулы орамал болады)
Қорытынды: Жетісітіктер критерийлеріне байланысты білім алушылар өз жұмыстарын бағалайды, Оқытушы жұмысты жақсарту үшін ұсыныс жасайды.
Бағалау. Бағалау парақтары студенттердің алдына беріледі.
5. Рефлексия
«Тик ток »
әдісі.
- Ұнады
- Айтарым бар
- Достарыммен бөлісемін
- Есіме сақтадым.


Үй тапсырмасы. № 17.1, 17.3

жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Жазық фигуралар аудандарын анықталған интегралдың көмегімен есептеу
Жазық фигуралар аудандарын анықталған интегралдың көмегімен есептеу
ТҮРКІСТАН ОБЛЫСЫНЫҢ БІЛІМ БАСҚАРМАСЫ
Ғ.МҰРАТБАЕВ АТЫНДАҒЫ ЖЕТІСАЙ ГУМАНИТАРЛЫҚ-ТЕХНИКАЛЫҚ КОЛЛЕДЖІ
АШЫҚ САБАҚ
Тақырыбы: Жазық фигуралар аудандарын анықталған интегралдың көмегімен есептеу.
Оқытушы: Жакупова У.Т.
Хаттама № «___» «____» 2024ж
Кафедра меңгерушісі: _________
(қолы)
2024 ж
Ғ.Мұратбаев атындағы Жетісай гуманитарлық-техникалық колледжі
Оқу сабағының жоспары
Сабақтың тақырыбы: Жазық фигуралар аудандарын анықталған интегралдың көмегімен есептеу.
Модуль /пән атауы:Математика
Педагог: Жакупова Улжалгас Турапбаевна дайындады
2024 жылғы «14» ақпан.
Жалпы
мәліметтер
Курс, топ: 1-курс, РБ 23-9/1.2
Сабақ түрі: Тәжірибелік сабақ
2.Мақсаты, міндеттері:
Тақырыпты игере отырып, Жазық фигуралар аудандарын анықталған интегралдың көмегімен есептеу. Анықталған интегралдың қолданумен танысу. Есептер шығару
3.Күтілетін нәтижелер:
- Жазық фигуралар аудандарын анықтайды;
- Анықталған интегралдың қолдануды біледі;
- Оларға берілген есептерді шығара алады.
4.Қажетті ресурстар:
«Алгебра және анализ бастамалары» әдістемелік кешен 2012ж, шаршы, канверт,стикер,үлестірме қағаздар, панель т.б
5.Сабақтың барысы:
а) Ұйымдастыру.
ә) Үй тапсырмасын пысықтау
б) Жаңа материалды түсіндіру
в) Пысықтау жұмыстары
г) Сабақты бекіту
д) Қорытынды
Жағымды атмосфера қалыптастыру: «Кубизм» әдісі арқылы амандасу.

Топқа бөлу: « Пазыл» әдісі арқылы. Студенттер суреттерді құрастыру арқылы топқа бөлінеді.

Үй тапсырмасын пысықтау «Банкомат» әдісі. Студенттер картичканы банкоматқа салады, алатын соманы таңдайды сұраққа жауап береді , сол соманы шешіп алады.

-
500тг- Кез келген Х жиынында өзгеретін х үшін F´(x) = f(x), теңдігі орындалса, онда F(x) функциясы осы жиында f(x) функциясының ............... деп аталады.
алғашқы функциясы;
-
1000тг- Ньютон - Лейбниц формуласымен ...................есептейді
анықталған интеграл;
-
2000 тг- Берілген функция үшін алғашқы функцияның жалпы түрін жаз f(x) = 2
2х + С;
-
5000тг- F(в) -Ғ(а) айырманын у= f(x) үзіліссіз функциясының [а;в] кеіндісіндегі ................... деп аталады
анықталған интеграл
-
10000тг- Алғашқы функцияның жалпы түрін жазыңдар f(x) = 2Sin3x
-
-
20000тг- Есептеңіз:
 ;
;

-
30000тг- Есептеңіз:

 ;
;
-
40000тг- Есептеңіз:


Жаңа сабақ. « Баяндау» әдісі.


Жазық фигуралар аудандарын анықталған интегралдың көмегімен есептеу.
1. Анықталған интеграл арқылы қисық сызықты трапеция ауданы.
2. Анықталған интеграл арқылы жазық фигура ауданы.
Қисық сызықты трапецияның ауданы төмендегідей алгоритм бойынша есептелінеді:
-
Бір координаталық жазықтықта берілген сызықтардың графиктерін салу;
-
Фигураны OX осі бйымен шектелген кесіндісінің шеткі нүктелерін, яғни a және b-ның мәндерін анықтау;
-
f(x) функциясының алғашқы функциясын табу;
-
S=F(b)-F(a) формуласы бойынша қисықсызықты трапецияның ауданын есептеу.
[a;b] кесіндісінде үзілліссіз у=f(х) функциясы берілсін
-
[a;b] кесіндісінде у=f(х) функциясының графигімен және у=0 түзуімен
Шектелген фигураның ауданы
а) ![]() болғанда
болғанда

![]()
b) ![]() болғанда
болғанда

![]()
b)![]()

-
мысал.
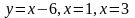 түзулерімен Ох
осімен шектелген фигураның
ауданын есептеңіз.
түзулерімен Ох
осімен шектелген фигураның
ауданын есептеңіз.
Шешуі:

![]()
Жауабы: ![]() (ш.б)
(ш.б)
Егер ![]() үшін
үшін![]() функция үзілліссіз болса,
онда
функция үзілліссіз болса,
онда ![]() кесіндісінде
кесіндісінде ![]() (үстіңгі)
және
(үстіңгі)
және ![]() (төменгі) функцияларының
графиктерімен шектелген фигураның ауданы:
(төменгі) функцияларының
графиктерімен шектелген фигураның ауданы:


![]()
Ескерту: Егер а және bшектері берілмесе, онда интегралдың шектері
f(x)=g(x) теңдеуінің түбірлері болады.
-
мысал.y = 4 –x2, y = x + 2 сызықтарымен және Ox осімен шектелген фигураның ауданын табыңыз.


Топтық жұмыс. «Айналмалы бекет» әдісі. Студенттер топта тапсырманы орындайды, сағат тілінің бағытымен тапсырманы шығару жолымен бөліседі. Басқа топтар кері байланыс береді.


Топ -1. Алғыр тобы
№1
![]() ,
, ![]() сызықтарыменшектелген (боялған)
фигура ауданын табыңыздар.
сызықтарыменшектелген (боялған)
фигура ауданын табыңыздар.

![]()
Жауабы: ![]() (ш.б)
(ш.б)
№ 2. y = -х2 + 4х - 4, y = 0, х = -1 және x = 4 сызықтарымен шектелген фигураның ауданын табыңыз.

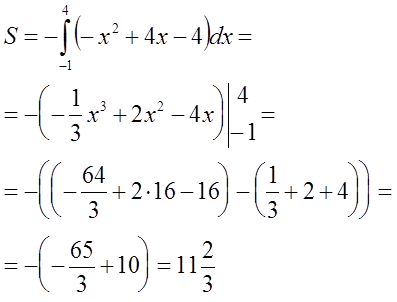
Топ -2. Тапқыр тобы.
№1.
![]() ,
, ![]() сызықтарымен шектелген фигура
ауданын табыңыздар.
сызықтарымен шектелген фигура
ауданын табыңыздар.

![]()
Жауабы: ![]() (ш.б)
(ш.б)
№2. y = 9 – 0.5x2 параболасымен және x = -1, x = 2 түзулері мен Ox осі арқылы шектелген фигураның ауданын табыңыз.


Жауабы: 25.5 ед2
Сергіту сәті: Шапалақпен әннің ырғағына ілесу.

Сабақтың соңы: Суреттегі штрихталған фигуралардың қайсысы қисық трапеция болып табылады және қайсысы жоқ? « Ия, Жоқ»

«Сиқырлы сандық» ойыны. Логикалық сұрақтарға жауап береді.

-
Ол сізге тиесілі, бірақ адамдар оны сізден жиі қолданады? (сіздің есіміңіз)
-
Жабық көзбен нені көруге болады? (түсті)
-
Алғашында төрт аяқты, кейін екіаяқты, сосын үш аяқты. Ол не? (бала)
-
Теңізде қандай тас болмайды? (құрғақ тас)
-
Адам аттан неге құлайды? (жерге)
-
Қаз, адам, қарақат. Үшеуін не байланыстырады?( а - әріпі)
-
Кім отырып жүреді? (шахматшы)
-
Қызыл теңізге ақ орамал салсақ не болады? (сулы орамал болады)
Қорытынды: Жетісітіктер критерийлеріне байланысты білім алушылар өз жұмыстарын бағалайды, Оқытушы жұмысты жақсарту үшін ұсыныс жасайды.
Бағалау. Бағалау парақтары студенттердің алдына беріледі.
5. Рефлексия
«Тик ток »
әдісі.
- Ұнады
- Айтарым бар
- Достарыммен бөлісемін
- Есіме сақтадым.


Үй тапсырмасы. № 17.1, 17.3


шағым қалдыра аласыз















