Аңдатпа (қазақша)

Бұл мақалада тригонометриялық теңсіздіктерді бірлік шеңбер көмегімен шешу әдістері қарастырылады. Бірлік шеңбердің тригонометриялық функциялармен байланысы және олардың теңсіздіктерді шешудегі рөлі талданады.

Аннотация (орысша)

В этой статье рассматриваются методы решения тригонометрических неравенств с помощью единичной окружности. Анализируется связь единичной окружности с тригонометрическими функциями и их роль в решении неравенств.

Annotation (ағылшынша)

This article discusses methods for solving trigonometric inequalities using the unit circle. The relationship between the unit circle and trigonometric functions and their role in solving inequalities are analyzed.

Кіріспе

Тригонометриялық теңсіздіктерді шешу математикада маңызды орын алады. Тригонометриялық теңсіздіктерді шешу кезінде бірлік шеңбердің маңызды рөлін анықтау қажет. Бірлік шеңбер - радиусы 1-ге тең шеңбер, ол тригонометриялық функциялардың мәндерін визуализациялауға мүмкіндік береді. Бұл кітапшада тригонометриялық теңсіздіктерді бірлік шеңбер арқылы қалай шешуге болатыны туралы талқыланатын болады.
Оқушылар үшін тригонометриялық функциялардың қасиеттерін түсіну және оларды есептерде қолдану дағдыларын дамыту қажет. Синус, косинус және тангенс - негізгі тригонометриялық функциялар болып табылады. Бұл функциялар бірлік шеңбердің әртүрлі бұрыштарындағы нүктелердің координаталары арқылы анықталады. Мысалы, синус функциясы y-координатаны, ал косинус функциясы x-координатаны білдіреді.
Бұл кітапшада тригонометриялық теңсіздіктерді бірлік шеңбер көмегімен шешу әдістері қарастырылады.

Негізгі бөлім

Бірлік шеңбер тригонометриялық функцияларды көрнекі түрде түсіндіруге мүмкіндік береді. Мысалы, синус және косинус функцияларының мәндері шеңбердің сәйкес координаталары ретінде беріледі. Бірлік шеңберді қолдану арқылы тригонометриялық теңсіздіктерді шешу бірнеше артықшылықтарға ие. Біріншіден, ол теңсіздіктердің шешімдерін графикалық түрде көруге мүмкіндік береді, бұл оқушыларға түсінікті әрі жеңіл болады. Екіншіден, бұл әдіс арқылы тригонометриялық функциялардың периодтылығын ескеру жеңілдейді. 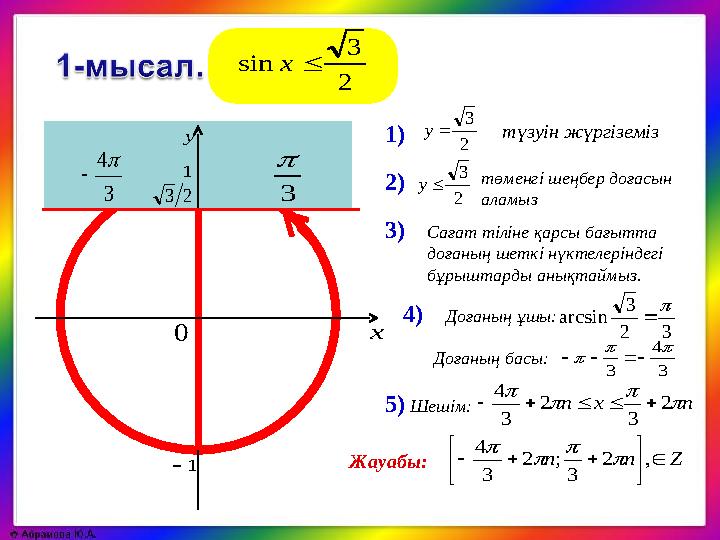Мысалы, теңсіздік sin(x) > 1/2 теңдеуін қарастырсақ, бірлік шеңберде бұл мәнге сәйкес келетін барлық бұрыштарды оңай табуға болады. Үшіншіден, бірлік шеңбер тригонометриялық теңсіздіктердің шешімдерін тексеру үшін статистикалық мәліметтерді қолдануға мүмкіндік береді. Бұл әдістің тиімділігі бірнеше зерттеулермен дәлелденген. Бірлік шеңберде әрбір бұрышқа сәйкес тригонометриялық мәндер бар. Мысалы, 0°, 90°, 180°, 270° бұрыштарында синус және косинус мәндері белгілі бір тұрақты сандарға тең. Бұл мәндер теңсіздіктерді шешуде пайдаланылады, себебі олар функциялардың өзгеру аймақтарын анықтайды. Тригонометриялық теңсіздіктерді шешу үшін алдымен теңдеуді түрлендіріп, бірлік шеңберде шешімін табу қажет. Бірлік шеңберді пайдалану арқылы теңсіздіктердің шешімдерін визуализациялау оңай болып келеді. 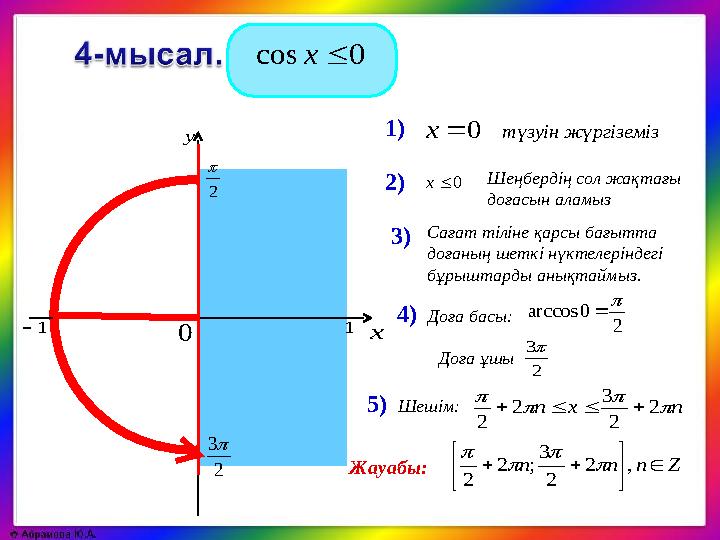Бұл әдіс арқылы теңсіздіктің шешімін нақты және түсінікті түрде көрсетуге боладыКейбір тригонометриялық теңсіздіктер күрделі болуы мүмкін, мысалы, cos(x) ≤ sin(x) сияқты. Мұндай теңсіздіктерді шешу үшін бірлік шеңберде әрбір функцияның графигін салыстырып, олардың қиылысу нүктелерін анықтау қажет. Бұл тәсіл арқылы күрделі теңсіздіктердің шешімін табуға болады.
Тригонометриялық теңсіздіктер физика, инженерия және басқа да ғылым салаларында кеңінен қолданылады. Мысалы, механикалық тербелістерді зерттеу кезінде теңсіздіктерді пайдалану арқылы жүйенің тұрақтылығын анықтауға болады. Бұл тригонометриялық теңсіздіктердің нақты өмірде қолданылуын көрсетеді.

Қорытынды

Бірлік шеңбер тригонометриялық теңсіздіктерді шешуде тиімді құрал болып табылады. Ол тригонометриялық функциялардың қасиеттерін көрнекі түрде түсінуге және оларды есептерде қолдануға мүмкіндік береді. Тригонометриялық теңсіздіктерді бірлік шеңбер көмегімен шешу - математикада маңызды әдістердің бірі. Бірлік шеңбердің көмегімен тригонометриялық функциялардың мәндерін визуализациялау және теңсіздіктерді шешу жеңілдейді. Бұл әдіс математикалық есептерді тиімді әрі түсінікті түрде шешуге мүмкіндік бередіМұғалімдер үшін бұл әдісті оқыту процесінде қолдану оқушылардың материалды игеру деңгейін арттыруға көмектеседі.

Пайдаланылған әдебиеттер

1. Кенжеғали А. Тригонометрия негіздері. Алматы: Мектеп, 2018.

2. Сүлейменов Б. Математикалық талдау. Астана: Фолиант, 2019.

3. Иванов И. Введение в тригонометрию. Москва: Наука, 2017.