Сабақтың тақырыбы: Шеңбердің хордалары мен қиюшы кесінділерінің пропорционалдығы туралы теорема. Геометрия-9 класс.
Садуахасова Гуляйм Алексеевна
І санатты математика пәні мұғалімі.
Батыс Қазақстан облысы
Зеленов ауданы
Достық ауылы
Достық жалпы орта білім беретін мектебі
Мақсаты:
Білімділік: шеңбер ішінде қиылысқан хордалардың кесінділерінің қасиетін, сондай-ақ шеңбер сыртында жатқан нүкте арқылы жүргізілген қиюшылардың кесінділерінің қасиетін көрсету, бұл кесінділердің қасиеттерін геометриялық есептер шығарғанда қолдану дағдысын меңгерту.
Дамытушылық: Алған білімдерін есептер шығаруда, жаңа білімді бекітуде қолдана білу, оқушылардың пәнге қызығушылығын арттыру, дамыту;
Тәрбиелік: Оқуға, саналы жауапкершілікке, өз бетінше еңбектенуге тәрбиелеу. Жан жақты дамыған салауатты тұлға тәрбиелеу.
Сабақтың түрі: аралас
Типі: жаңа сабақты меңгерту
Әдісі: сұрақ-жауап, топтастыру, рефлексия, сто элементтері
Көрнекілігі: интерактивті тақта, слайдтар, топшамалар.
Сабақтың барысы: І. Ұйымдастыру бөлімі.
а) Оқушылармен амандасу, класты түгендеу;
ә) 2 топқа бөлу, топ басшыларын сайлау.
ІІ. Үй тапсырмасын тексеру. «Ой қозғау»
Қайталау сұрақтары:
Слайд №1 «Ғажайып үштік» (терезе сұрақтарына жауап беру)
-
Шеңбер деп қандай фигураны айтамыз?
-
Шеңбердің хордасы, қиюшысы деген не?
-
Вертикаль бұрыштар деп қандай бұрыштарды айтамыз?
-
Ұқсас үшбұрыштар
-
Үшбұрыштардың ұқсастық белгілері
-
Центрлік бұрыш
-
Шеңберге іштей сызылған бұрыш
-
Іштей сызылған бұрыштың қандай қасиеттері бар?
-
Ауызша есептерді шығару.
ІІІ. Жаңа сабақ түсіндіру.
«Қызығушылықты ояту»
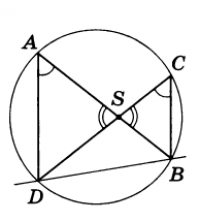
Теорема 1. Егер шеңбердің АВ және СD хордалары S нүктесінде қиылысса, онда AS*BS = CS*DS.
АВ СD
=S
СD
=S
д/к: AS*BS = CS*DS.
д/уі: АD, ВС хордаларын жүргіземіз.
 ASD
ASD ~
~ CSD,
себебі
CSD,
себебі  ASD=
ASD= CSD
(вертикаль),
CSD
(вертикаль),  DАS=
DАS= BCD (DВ доғасына тірелетін
іштей сызылған
бұрыш)
BCD (DВ доғасына тірелетін
іштей сызылған
бұрыш)
Үшбұрыштардың ұқсастығынан :
AS:CS =DS: BS
AS*BS= CS*DS
Дәлелденді.
Теорема
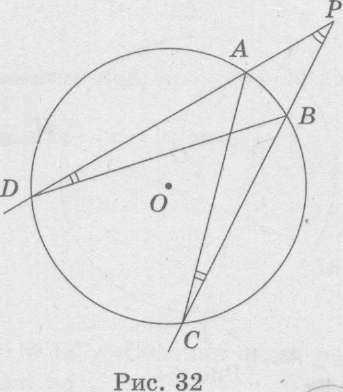
2. Егер шеңбер сыртында жатқан P
нүктесінен шеңберді А,В және С, D нүктелерінде қиятын екі қиюшы
жүргізілсе,
онда
PA * РD = PB * PC.
Мұндағы А,B нүктелері P-ге жақын орналасқан нүктелер.
(өз беттерімен дәлелдеу)
 Бер:
шеңбер
Бер:
шеңбер
DP және PC- қиюшылар.
д/к: PA * РD = PB * PC
д/уі: АС, ВD – хордаларын жүргіземіз.
 AСP
AСP ~
~ BDP,
себебі
BDP,
себебі  D=
D= C (АВ доғасына тірелген іштей
сызылған бұрыштар) ,
C (АВ доғасына тірелген іштей
сызылған бұрыштар) ,  P-ортақ.
P-ортақ.
Үшбұрыштардың ұқсастығынан :
PA: PB=PC: PD
PA*PD= PB*PC.
Дәлелденді.
ІҮ. Бекіту.
(екі топқа бірдей есептер беріледі, орындарынан ақылдасып, шығарып, тақтада түсіндіріп, орындап береді)
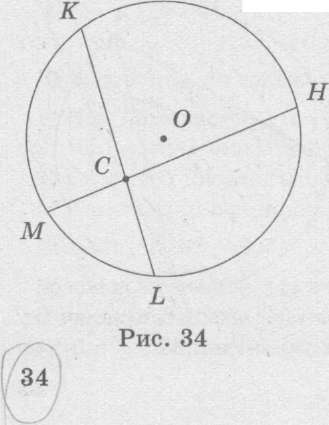
№1.

 Бер:
шеңбер
Бер:
шеңбер
КС=6см, МС=3 см, СН=9 см.
т/к: СL
Шешуі:
1-теорема б/ша:
МС*СН=КС* СL
СL= =
= =
=
Жауабы: 4,5 см.
№2. (осы суретті пайдаланып, белгісіз кесіндіні табыңдар)
Бер: шеңбер
KL = 14 дм, СМ = 4 дм, СН = 12 дм.
т/к: КС.
Шешуі: 1-теорема б/ша: МС*СН=КС* СL
КС және СL кесінділері белгісіз. КС=х дм болсын, ал СL=(14-х) дм.
4*12=х*(х-14) теңдеуін шешеміз.
х2-14х-48=0. Виет теоремасы бойынша х1=6, х2=8.
Сонымен, КС=6 дм болса, СL=14-6=8 дм немесе керісінше.
Жауабы: 6дм, 8дм.
№3.
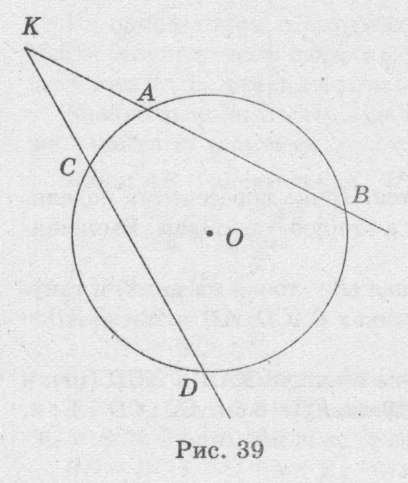 А)Бер: КВ,
КD-қиюшылар
А)Бер: КВ,
КD-қиюшылар
КВ=10 дм, КD=15 дм
СD=KA
т/к: СD
Шешуі:
КА*КВ=КС*КD
10* СD=15(15- СD)
25* СD=225
СD =9
Жауабы: 9 дм.
Ә) Бер: КВ, КD-қиюшылар
КА=18 см, АВ=12 см
КС:СD=5:7
т/к: КD
Шешуі:
КС= КD- СD,
КС= СD
СD
КА*КВ=КС*КD
18*30= СD*(
СD*( СD+
СD)=
СD+
СD)=
 *
* СD2
СD2
18*30= СD2, СD=21,
КС=15см,
СD2, СD=21,
КС=15см,
КD=21+15=36 см.
Жауабы: 36 см.
Топтар бір-бірін бағалайды. Бағалау критериалды.
-
Оқушы тапсырманы мүлдем орындамаса - 0 ұпай.
-
Оқушы тапсырманы орындау алгоритмін біледі, бірақ есептеулерде қателіктер кеткендіктен есептің шешуі дұрыс емес – 1 ұпай.
-
Оқушы тапсырманы дұрыс орындаған, бірақ есептің жауабы толық жазылмаған – 2 ұпай.
-
Оқушы тапсырманы толық, дұрыс орындаған, есептің жауабы жазылған -4 ұпай.
Ү. Үйге тапсырма беру
ҮІ. Қорытындылау, оқушыларды бағалау.
-
Бүгінгі сабақ туралы пікір айту.
-
Рефлексия
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Келтіріу формулалары
Келтіріу формулалары
Сабақтың тақырыбы: Шеңбердің хордалары мен қиюшы кесінділерінің пропорционалдығы туралы теорема. Геометрия-9 класс.
Садуахасова Гуляйм Алексеевна
І санатты математика пәні мұғалімі.
Батыс Қазақстан облысы
Зеленов ауданы
Достық ауылы
Достық жалпы орта білім беретін мектебі
Мақсаты:
Білімділік: шеңбер ішінде қиылысқан хордалардың кесінділерінің қасиетін, сондай-ақ шеңбер сыртында жатқан нүкте арқылы жүргізілген қиюшылардың кесінділерінің қасиетін көрсету, бұл кесінділердің қасиеттерін геометриялық есептер шығарғанда қолдану дағдысын меңгерту.
Дамытушылық: Алған білімдерін есептер шығаруда, жаңа білімді бекітуде қолдана білу, оқушылардың пәнге қызығушылығын арттыру, дамыту;
Тәрбиелік: Оқуға, саналы жауапкершілікке, өз бетінше еңбектенуге тәрбиелеу. Жан жақты дамыған салауатты тұлға тәрбиелеу.
Сабақтың түрі: аралас
Типі: жаңа сабақты меңгерту
Әдісі: сұрақ-жауап, топтастыру, рефлексия, сто элементтері
Көрнекілігі: интерактивті тақта, слайдтар, топшамалар.
Сабақтың барысы: І. Ұйымдастыру бөлімі.
а) Оқушылармен амандасу, класты түгендеу;
ә) 2 топқа бөлу, топ басшыларын сайлау.
ІІ. Үй тапсырмасын тексеру. «Ой қозғау»
Қайталау сұрақтары:
Слайд №1 «Ғажайып үштік» (терезе сұрақтарына жауап беру)
-
Шеңбер деп қандай фигураны айтамыз?
-
Шеңбердің хордасы, қиюшысы деген не?
-
Вертикаль бұрыштар деп қандай бұрыштарды айтамыз?
-
Ұқсас үшбұрыштар
-
Үшбұрыштардың ұқсастық белгілері
-
Центрлік бұрыш
-
Шеңберге іштей сызылған бұрыш
-
Іштей сызылған бұрыштың қандай қасиеттері бар?
-
Ауызша есептерді шығару.

ІІІ. Жаңа сабақ түсіндіру.
«Қызығушылықты ояту»
Теорема 1. Егер шеңбердің АВ және СD хордалары S нүктесінде қиылысса, онда AS*BS = CS*DS.
АВ СD
=S
СD
=S
д/к: AS*BS = CS*DS.
д/уі: АD, ВС хордаларын жүргіземіз.
 ASD
ASD ~
~ CSD,
себебі
CSD,
себебі  ASD=
ASD= CSD
(вертикаль),
CSD
(вертикаль),  DАS=
DАS= BCD (DВ доғасына тірелетін
іштей сызылған
бұрыш)
BCD (DВ доғасына тірелетін
іштей сызылған
бұрыш)
Үшбұрыштардың ұқсастығынан :
AS:CS =DS: BS
AS*BS= CS*DS
Дәлелденді.
Теорема
2. Егер шеңбер сыртында жатқан P
нүктесінен шеңберді А,В және С, D нүктелерінде қиятын екі қиюшы
жүргізілсе,
онда
PA * РD = PB * PC.
Мұндағы А,B нүктелері P-ге жақын орналасқан нүктелер.
(өз беттерімен дәлелдеу)

 Бер:
шеңбер
Бер:
шеңбер
DP және PC- қиюшылар.
д/к: PA * РD = PB * PC
д/уі: АС, ВD – хордаларын жүргіземіз.
 AСP
AСP ~
~ BDP,
себебі
BDP,
себебі  D=
D= C (АВ доғасына тірелген іштей
сызылған бұрыштар) ,
C (АВ доғасына тірелген іштей
сызылған бұрыштар) ,  P-ортақ.
P-ортақ.
Үшбұрыштардың ұқсастығынан :
PA: PB=PC: PD
PA*PD= PB*PC.
Дәлелденді.
ІҮ. Бекіту.
(екі топқа бірдей есептер беріледі, орындарынан ақылдасып, шығарып, тақтада түсіндіріп, орындап береді)
№1.

 Бер:
шеңбер
Бер:
шеңбер
КС=6см, МС=3 см, СН=9 см.
т/к: СL
Шешуі:
1-теорема б/ша:
МС*СН=КС* СL
СL= =
= =
=
Жауабы: 4,5 см.
№2. (осы суретті пайдаланып, белгісіз кесіндіні табыңдар)
Бер: шеңбер
KL = 14 дм, СМ = 4 дм, СН = 12 дм.
т/к: КС.
Шешуі: 1-теорема б/ша: МС*СН=КС* СL
КС және СL кесінділері белгісіз. КС=х дм болсын, ал СL=(14-х) дм.
4*12=х*(х-14) теңдеуін шешеміз.
х2-14х-48=0. Виет теоремасы бойынша х1=6, х2=8.
Сонымен, КС=6 дм болса, СL=14-6=8 дм немесе керісінше.
Жауабы: 6дм, 8дм.
№3.
 А)Бер: КВ,
КD-қиюшылар
А)Бер: КВ,
КD-қиюшылар
КВ=10 дм, КD=15 дм
СD=KA
т/к: СD
Шешуі:
КА*КВ=КС*КD
10* СD=15(15- СD)
25* СD=225
СD =9
Жауабы: 9 дм.
Ә) Бер: КВ, КD-қиюшылар
КА=18 см, АВ=12 см
КС:СD=5:7
т/к: КD
Шешуі:
КС= КD- СD,
КС= СD
СD
КА*КВ=КС*КD
18*30= СD*(
СD*( СD+
СD)=
СD+
СD)=
 *
* СD2
СD2
18*30= СD2, СD=21,
КС=15см,
СD2, СD=21,
КС=15см,
КD=21+15=36 см.
Жауабы: 36 см.
Топтар бір-бірін бағалайды. Бағалау критериалды.
-
Оқушы тапсырманы мүлдем орындамаса - 0 ұпай.
-
Оқушы тапсырманы орындау алгоритмін біледі, бірақ есептеулерде қателіктер кеткендіктен есептің шешуі дұрыс емес – 1 ұпай.
-
Оқушы тапсырманы дұрыс орындаған, бірақ есептің жауабы толық жазылмаған – 2 ұпай.
-
Оқушы тапсырманы толық, дұрыс орындаған, есептің жауабы жазылған -4 ұпай.
Ү. Үйге тапсырма беру
ҮІ. Қорытындылау, оқушыларды бағалау.
-
Бүгінгі сабақ туралы пікір айту.
-
Рефлексия

шағым қалдыра аласыз