келтіру формулалары

Күні: 24.02.2016

Сыныбы: 9Ә

Пәні: алгебра

Сабақтың тақырыбы: Келтіру формулалары

Сабақтың мақсаты: Оқушыларға сүйір бұрыштың тригонометриялық функциясының  әрбір бұрышындағы синустың, косинустың, тангенстің, котангенстің келтіру формулаларымен таныстыру, осы формулаларды тригонометриялық  өрнектерді түрлендіруде және есептерді шығару кезінде қолдануды үйрету; Оқушылардың ойлау қабілетін жетілдіру, шапшандыққа тәрбиелеу.

Күтілетін нәтиже: Оқушылар келтіру формулаларын пайдаланып, тригонометриялық функциялардың кез-келген бұрыштагы мәндерін таба біледі.

Сабақтың әдіс-тәсілдері: «Мига шабуыл», «Үнсіз оқу», түсіндіру, сұрақ – жауап, есептер шыгару 
Сабақтың типі: жаңа тақырыпты меңгерту
Сабақтың барысы: 

І. Ұйымдастыру кезеңі

ІІ. Қайталау – оқу анасы

• Тригонометриялық функциялар

• Негізгі тригонометриялық теңбе-теңдік

• Орнектерді ықшамдауда қолданылатын формулалар

ІІІ. «Үнсіз оқу»

ІҮ. Тақырыпты талдау

Берілген тақырыпты игере отырып, сүйір бұрыштың тригонометриялық функциясының әрбір бұрышындағы синустың, косинустың, тангенстің, котангенстің келтіру формулаларымен танысып, осы формулаларды тригонометриялық өрнектерді түрлендіруде және есептерді шығару кезінде қолдануды үйренесіңдер.

Тригонометриялық функциялармен байланысты көптеген есептерді шығаруда тригонометриялық функцияның кез келген бұрышын тригонометриялық функциялардың сүйір бұрышына келтірудің маңызы зор. Басқаша айтқанда, егер (мұндағы k- кез келген бүтін сан, α - сүйір бұрыш) бұрышының функциялары берілсе, онда оларды α-бұрышына байланысты тригонометриялық функцияларға келтіру ыңғайлы. Ол үшін арнайы берілген келтіру формулалары қолданылады.

Біз тек кейбір жағдайларда ғана қолданылатын келтіру формулаларын

k = 1; 2; 3; 4 болған жағдайдағы өрнегін, яғни ; ; ; бұрыштарын қарастырамыз.

Басқа бұрыштар (k-ның бүтін мәніне сәйкес қалған бұрыштар) жоғарыда көрсетілген бүтін бұрыштардың шамаларына 2π; 4 π; 6π және т.б. қосу жолымен алынады.

Алдымен синус пен косинус үшін келтіру формулаларын қарастырайық. Ал олар арқылы тангенс және котангенс үшін келтіру формулаларын оңай қорытып шығаруға болады.

ІІ ширектегі синус және косинус үшін келтіру формулаларын қорытып шығарайық. ІІ ширектегі әрбір бұрышты түріне келтіру болады

( мұндағы α -сүйір бұрыш).

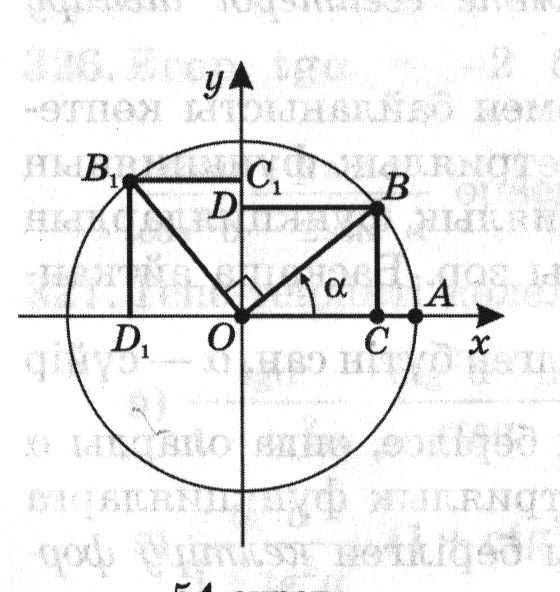
О нүктесін айналдыра шеңбердің R = OA радуысын – бұрышына бұрайық, сосын бұрышына тағы да бұрамыз. Осы бұрулар кезінде ОА радиусы сәйкес ОВ және ОВ₁ радиусына ауысады. В және В₁ нүктелерінен координаталық осьтерге перпендикуляр түсіреміз. Нәтижесінде ОСВД және ОС₁ В₁ Д₁ екі төртбұрышты аламыз. ОС₁ В₁ Д₁ тік төртбұрышын оң бағытта бұрышына бұру арқылы шықты. Расында ВОВ₁ = болғандықтан, бұру кезінде В нүктесі В₁ нүктесіне көшеді. Дәл осылай С нүктесі С₁ нүктесіне, ал Д нүктесі Д₁ нүктесіне көшеді. Содықтан В₁ нүктесінің ординатасы ретінде В нүктесінің абсциссасын, ал В₁ нүктесінің абсциссасы ретінде В нүктесінің ординатасын қарама-қарсы таңбамен алуға болады:

y₁ = x және x₁ = -y

немесе және

Аңықтама бойынша бұрыштың синусы ординатаның радиусқа қатынасына тең екенін білеміз, яғни

, sin α =

Дәл осылай

cos , ал cos α =

Осы берілгендерді ескере отырып, кейінгі теңдіктерден мынаны аламыз:

(1)

[2]

[3]

[4]

[5]

[6]

1-тапсырма.   (0⁰; 90⁰) аралығындағы бұрыштың тригонометриялық функциясына келтіріңдер:

а) tg137⁰ =  tg (90⁰ + 47⁰) = — ctg 47⁰ = — tg 43⁰.

б) sin (-178⁰) = — sin (180⁰ – 2⁰) = — sin2⁰ = — cos 78⁰.

в) sin 680⁰ = sin (720⁰ – 40⁰) = — sin 40⁰.

г) cos (-1000⁰) = cos (1080⁰ – 80⁰) = cos 80⁰.

2-тапсырма. Өрнектің мәнін табыңдар.

а) sin 240^o = sin (180^o+60^o)= — sin 60⁰ = — .

в) tg 300^o = tg (360^o — 60^o) = — tg 60⁰ = — .

с) ctg (- 225^o) = — ctg (180^o +45^o) = — ctg 45^o = -1.

д)  соs(-210) = cos(180⁰+30⁰) = — cos 30⁰ = — 0.5

ІҮ. Бекіту бөлімі.

1.Оқушыларға сәйкестендіру тесті беріледі

1.Қандай жағдайда функция өзгермейді? 

2.Қай уақытта тригонометриялықфункциялардың аттары өзгереді?

3.Келтіру формуласының оң жағындағы функцияның таңбасын қалай анықтауға болады?

Ү. Бағалау. 

ҮІ. Үйге  тапсырма: 1. §21- оқу. 2. №335